Refined Discontinuous Trigger Scheme for Event-Based Synchronization of Chaotic Neural Networks
Abstract
1. Introduction
2. Related Works
3. Preliminaries and Problem Formulation
4. Main Results
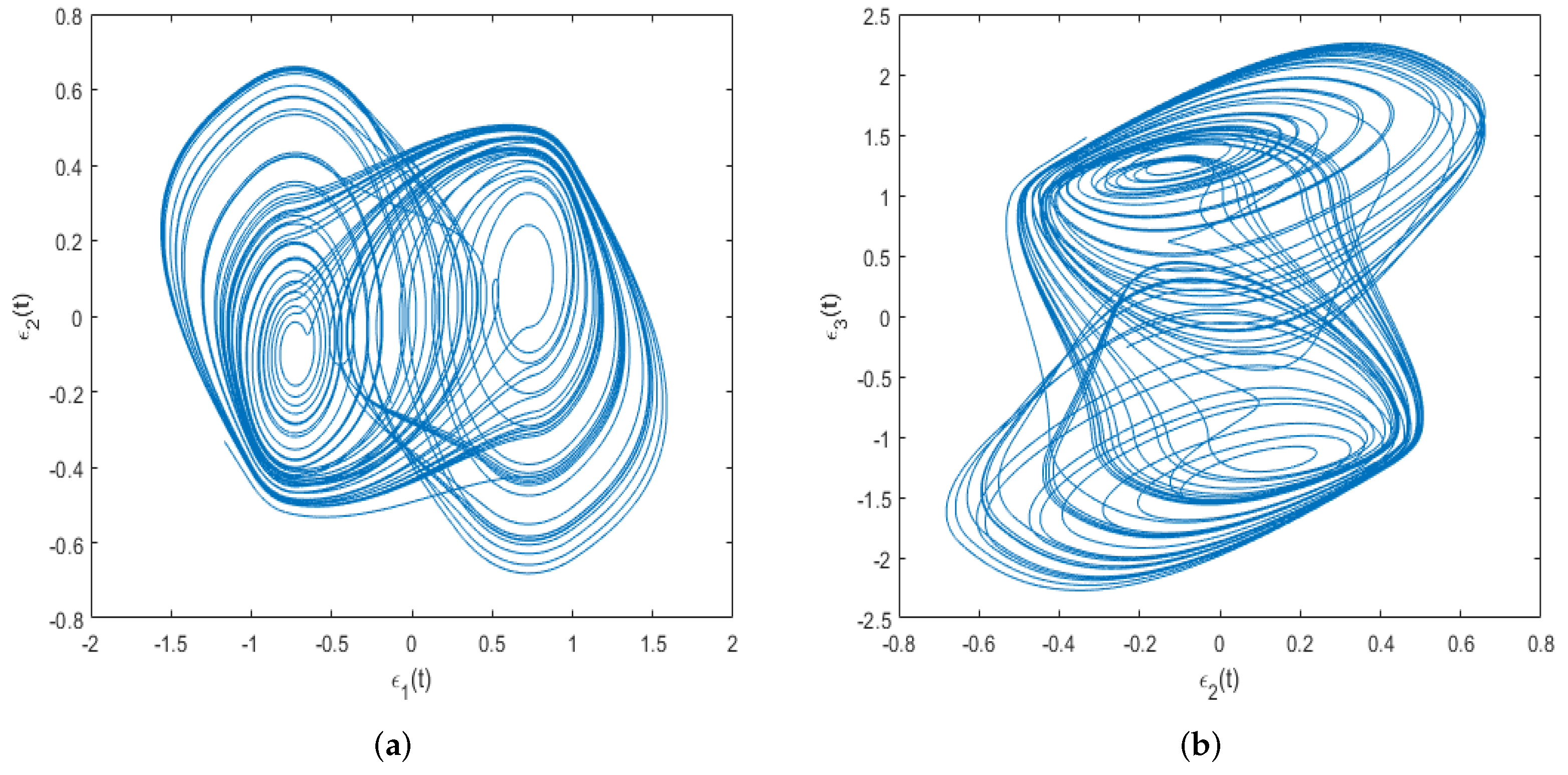
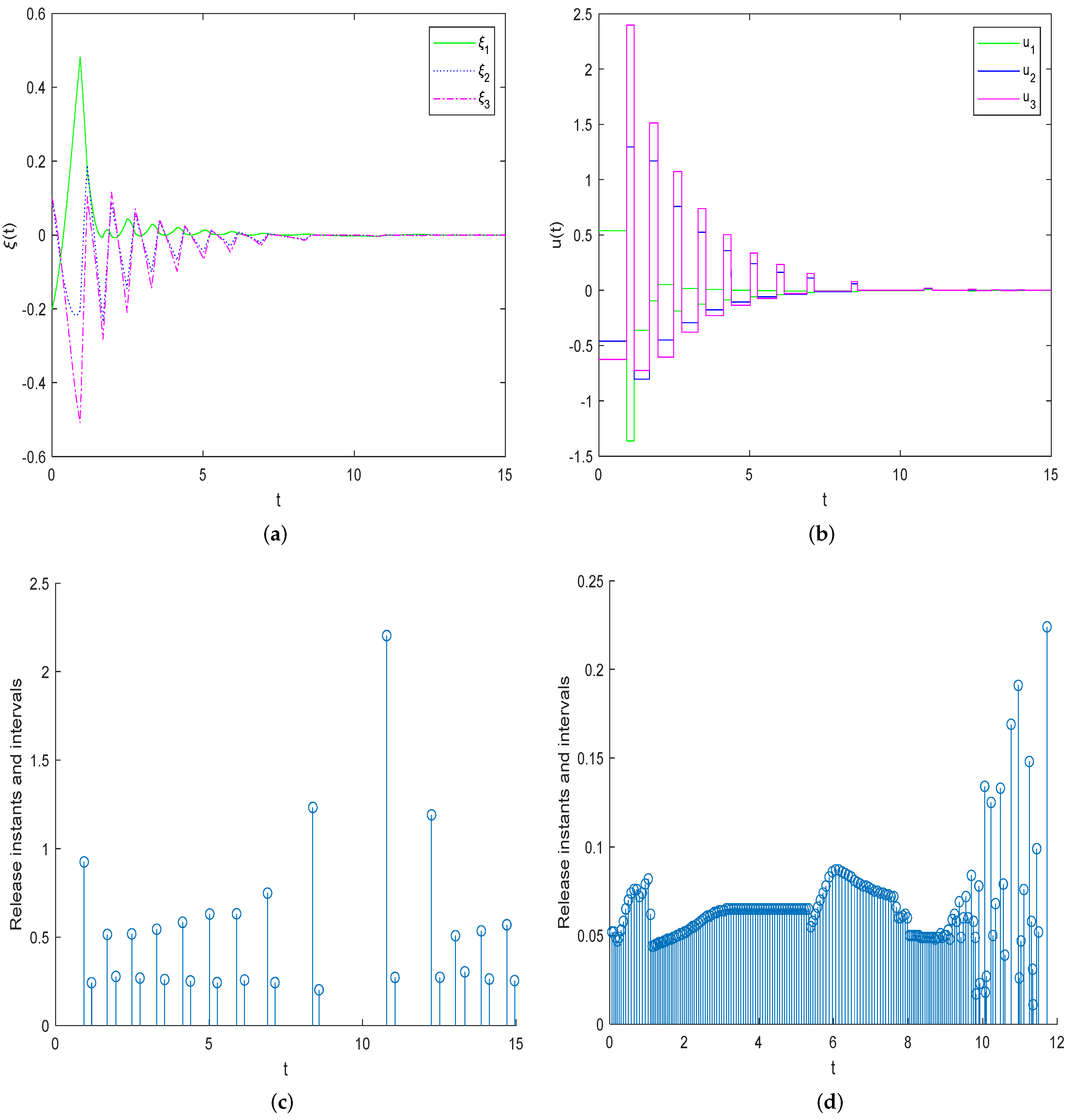
5. Numerical Examples
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RDET | refined discontinuous event-trigger |
| TLF | time-dependent Lyapunov function |
| NNs | neural networks |
| LMI | linear matrix inequality |
References
- Huang, Q.; Ma, N.; Tu, Z.W. Lagrange stability of quaternion-valued memristive neural networks. Math. Methods Appl. Sci. 2024, 47, 14796–14806. [Google Scholar] [CrossRef]
- Hu, X.; Wang, L.M.; Sheng, Y.; Hu, J. Finite-time stabilization of fuzzy spatiotemporal competitive neural networks with hybrid time-varying delays. IEEE Trans. Fuzzy Syst. 2023, 31, 3015–3024. [Google Scholar] [CrossRef]
- Liu, H.W.; Chen, X.Y.; Qiu, J.L.; Zhao, F. Finite-time synchronization of complex networks with hybrid-coupled time-varying delay via event-triggered aperiodically intermittent pinning control. Math. Methods Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Hu, B.; Guan, Z.H.; Xiong, N.; Chao, H.C. Intelligent impulsive synchronization of nonlinear interconnected neural networks for image protection. IEEE Trans. Ind. Inform. 2018, 14, 3775–3787. [Google Scholar] [CrossRef]
- Xu, X.Y.; Tan, M.X.; Corcoran, B.; Wu, J.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Hicks, D.G.; Morandotti, R.; et al. 11 TOPS photonic convolutional accelerator for optical neural networks. Nature 2021, 589, 44–51. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Wang, Z.; Liang, H.; Ahn, C.K. Neural-network-based predefined-time adaptive consensus in nonlinear multi-agent systems with switching topologies. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 9995–10005. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Xu, N.; Basin, M.V.; Zhou, D.; Chen, X. Stability and tracking recovery of continuous-time Markov jump piecewise affine systems using virtual-sensor-based reconfiguration. IEEE Trans. Autom. Control 2024, 69, 2705–2712. [Google Scholar] [CrossRef]
- Du, Z.B.; Kao, Y.G.; Zhao, X.D. An input delay approach to interval type-2 fuzzy exponential stabilization for nonlinear unreliable networked sampled-data control systems. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3488–3497. [Google Scholar] [CrossRef]
- Sun, Y.F.; Li, L.L.; Ho, D.W.C. Quantized synchronization control of networked nonlinear systems: Dynamic quantizer design with event-triggered mechanism. IEEE Trans. Cybern. 2023, 53, 184–196. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Liu, Y.J.; Tong, S.C.; Gao, Z.W. Relative threshold-based event-triggered control for nonlinear constrained systems with application to aircraft wing rock motion. IEEE Trans. Ind. Inform. 2022, 18, 911–921. [Google Scholar] [CrossRef]
- Shi, S.; Fei, Z.Y.; Karimi, H.R.; Lam, H. Event-triggered control for switched T-S fuzzy systems with general asynchronism. IEEE Trans. Fuzzy Syst. 2022, 30, 27–38. [Google Scholar] [CrossRef]
- Yan, S.; Shen, M.; Nguang, S.K.; Zhang, G.; Zhang, L. A distributed delay method for event-triggered control of T-S fuzzy networked systems with transmission delay. IEEE Trans. Fuzzy Syst. 2019, 27, 1963–1973. [Google Scholar] [CrossRef]
- Cao, Y.T.; Wang, S.B.; Guo, Z.Y.; Huang, T.W.; Wen, S.P. Synchronization of memristive neural networks with leakage delay and parameters mismatch via event-triggered control. Neural Netw. 2019, 119, 178–189. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.K.; Yang, J.; Li, S.H.; Zheng, W.X. Sampled-data-based event-triggered active disturbance rejection control for disturbed systems in networked environment. IEEE Trans. Cybern. 2019, 49, 556–566. [Google Scholar] [CrossRef] [PubMed]
- Song, X.; Zhang, Q.; Song, S.; Ahn, C.K. Sampled-data-based event-triggered fuzzy control for PDE systems under cyberattacks. IEEE Trans. Fuzzy Syst. 2022, 30, 2693–2705. [Google Scholar] [CrossRef]
- Fei, Z.Y.; Guan, C.X.; Gao, H.J. Exponential synchronization of networked chaotic delayed neural network by a hybrid event trigger scheme. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 2558–2567. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.H.; Park, J.H. Stability analysis of sampled-data systems via free-matrix-based time-dependent discontinuous Lyapunov approach. IEEE Trans. Autom. Control 2017, 62, 3653–3657. [Google Scholar] [CrossRef]
- Xu, X.Z.; Li, Y.; Zhang, H.B.; Chen, W.; Zheng, Q.X. Practical stability for switched affine systems via time-dependent switching function. Int. J. Robust Nonlinear Control 2021, 31, 9731–9744. [Google Scholar] [CrossRef]
| Notation | Description |
|---|---|
| the maximum eigenvalue of matrix Q | |
| transpose (or inverse) of matrix Q | |
| * | the symmetric element |
| Q is a positive | |
| (or | definite (or semi-definite) matrix |
| diag | a block diagonal matrix |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Fan, Y.; Li, M. Refined Discontinuous Trigger Scheme for Event-Based Synchronization of Chaotic Neural Networks. Axioms 2025, 14, 403. https://doi.org/10.3390/axioms14060403
Wang Y, Fan Y, Li M. Refined Discontinuous Trigger Scheme for Event-Based Synchronization of Chaotic Neural Networks. Axioms. 2025; 14(6):403. https://doi.org/10.3390/axioms14060403
Chicago/Turabian StyleWang, Yingjie, Yingjie Fan, and Meixuan Li. 2025. "Refined Discontinuous Trigger Scheme for Event-Based Synchronization of Chaotic Neural Networks" Axioms 14, no. 6: 403. https://doi.org/10.3390/axioms14060403
APA StyleWang, Y., Fan, Y., & Li, M. (2025). Refined Discontinuous Trigger Scheme for Event-Based Synchronization of Chaotic Neural Networks. Axioms, 14(6), 403. https://doi.org/10.3390/axioms14060403






