Assessing Expected Shortfall in Risk Analysis Through Generalized Autoregressive Conditional Heteroskedasticity Modeling and the Application of the Gumbel Distribution
Abstract
1. Preliminaries and Background
2. Some Background on ES
- Parametric Methods: These approaches assume that returns follow a specific distribution, like the normal or Student’s t distributions. The ES is computed using analytical formulas derived from the CDF.
- Non-Parametric Methods: These methods do not rely on distributional assumptions and use empirical data. For example, the historical simulation approach sorts past returns and averages the worst of losses to estimate ES.
- Monte Carlo Simulations: These involve generating a large number of hypothetical portfolio returns via a stochastic model and computing ES from the simulated distribution. This method is particularly effective for capturing complex dependencies in asset returns.
3. GARCH Models
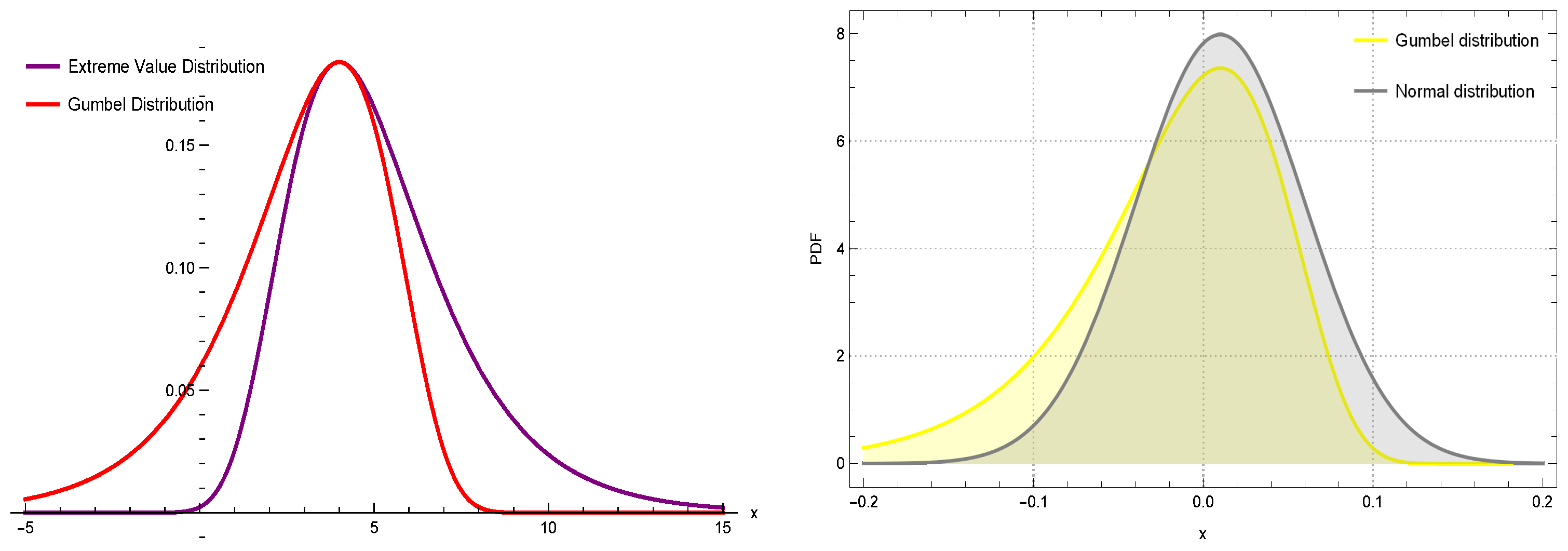
4. VaR Based on the Gumbel Distribution
- ;
- a is the parameter of location, which shifts the distribution along the x-axis;
- is the parameter of scale, which specifies the spread of the distribution.
5. ES via the Gumbel Distribution
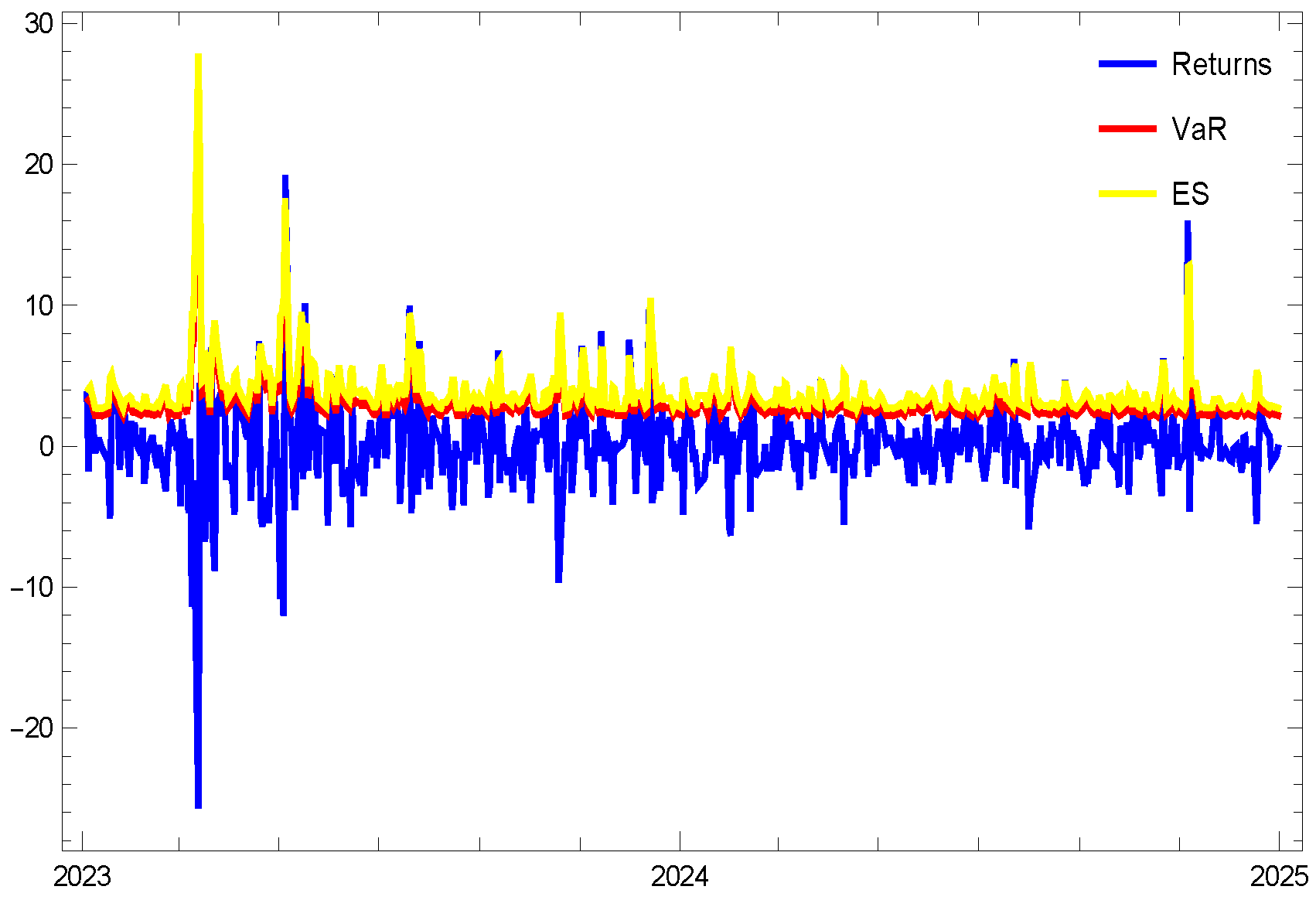
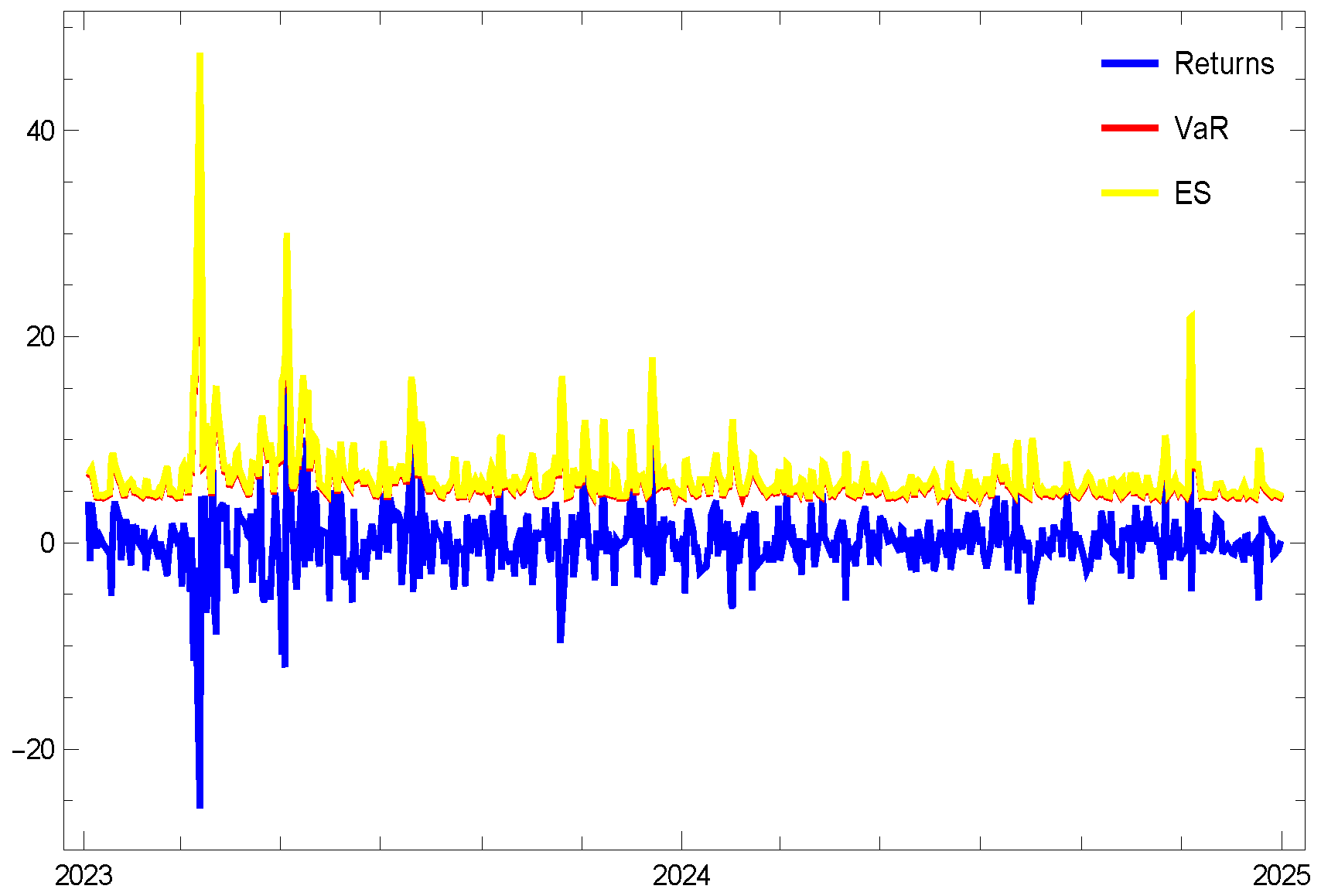
6. Numerical Validations
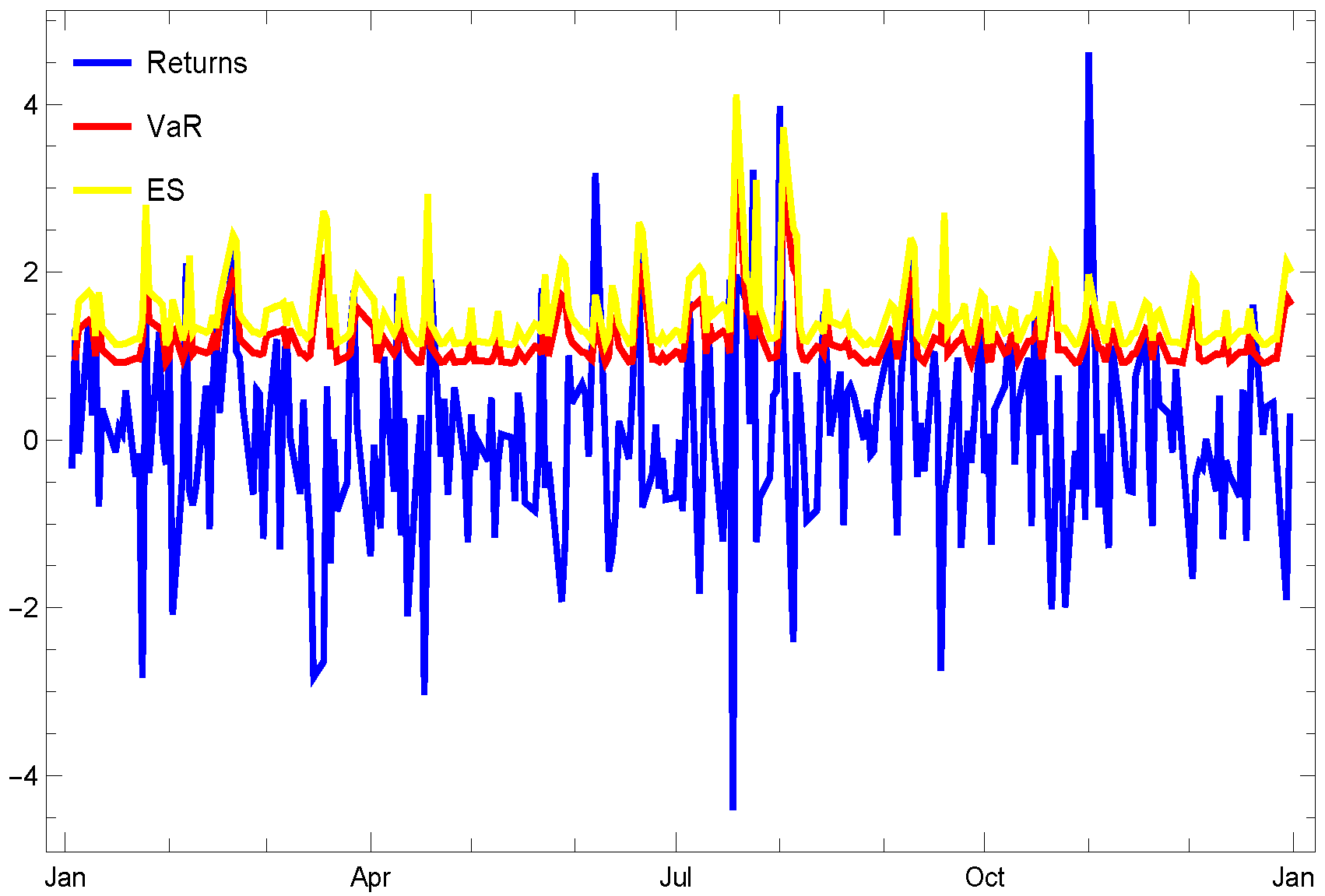
- The 1st experiment involves the stock ticker “NYSE:ABT”.
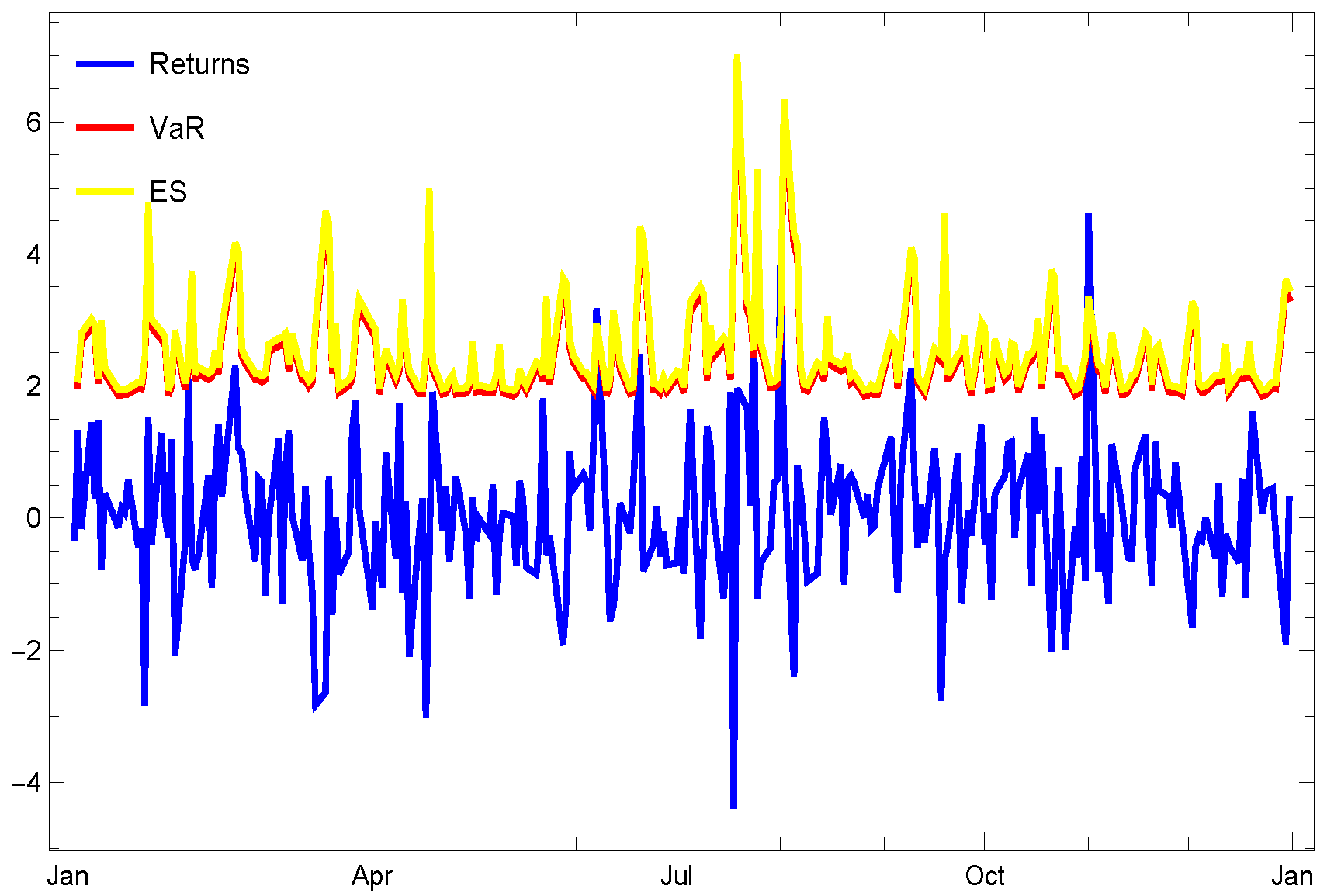
- The 2nd test focuses on “NASDAQ:ZION”.
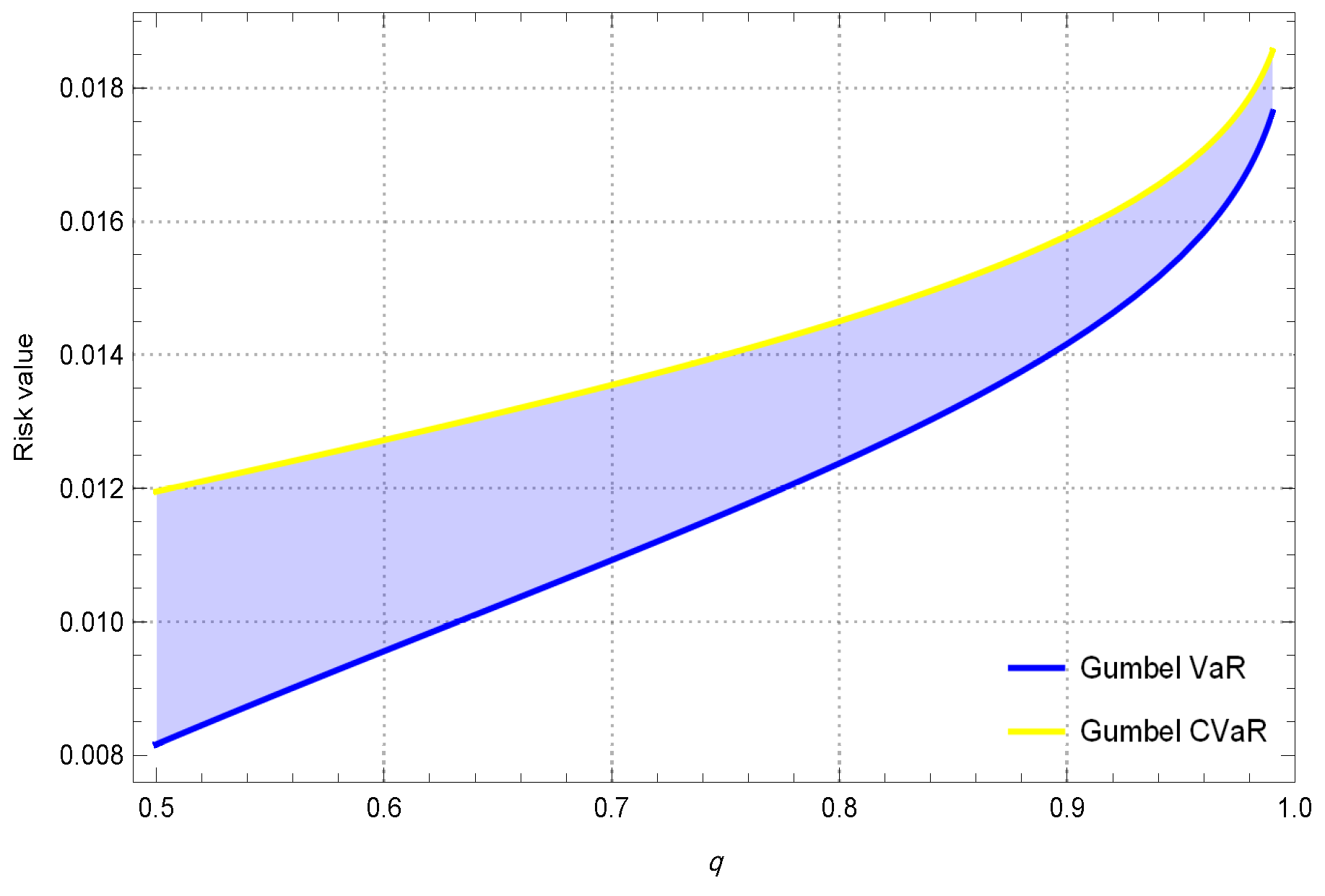
- Firstly, as the pre-specified tail level increases, both risk measures progressively converge toward one another.
- Selecting a pre-specified confidence level of appears to be a prudent selection for analyzing highly volatile stocks, particularly when employing these risk measures under the Gumbel distribution.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Albrecher, H.; Binder, A.; Lautscham, V.; Mayer, P. Introduction to Quantitative Methods for Financial Markets; Springer: Basel, Switzerland, 2013. [Google Scholar]
- Bormetti, G.; Cisana, E.; Montagna, G.; Nicrosini, O. A non-Gaussian approach to risk measures. Physica A 2007, 376, 532–542. [Google Scholar] [CrossRef]
- Galindo, J.; Tamayo, P. Credit risk assessment using statistical and machine learning basic methodology and risk modeling applications. Comput. Econ. 2000, 15, 107–143. [Google Scholar] [CrossRef]
- Wang, G.-J.; Zhu, C.-L. BP-CVaR: A novel model of estimating CVaR with back propagation algorithm. Econ. Lett. 2021, 209, 110125. [Google Scholar] [CrossRef]
- Martín, J.; Isabel Parra, M.; Pizarro, M.M.; Sanjuán, E.L. A new Bayesian method for estimation of value at risk and conditional value at risk. Empir. Econ. 2024, 68, 1171–1189. [Google Scholar] [CrossRef]
- Ahmed, D.; Soleymani, F.; Ullah, M.Z.; Hasan, H. Managing the risk based on entropic value-at-risk under a normal-Rayleigh distribution. Appl. Math. Comput. 2021, 402, 126129. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Roy, A. Safety first and the holding of assets. Econometrica 1952, 20, 431–449. [Google Scholar] [CrossRef]
- Lechner, L.A.; Ovaert, T.C. Value-at-risk: Techniques to account for leptokurtosis and asymmetric behavior in returns distributions. J. Risk Financ. 2010, 11, 464–480. [Google Scholar] [CrossRef]
- Benninga, S.; Wiener, Z. Value-at-Risk (VaR). Math. Edu. Res. 1998, 7, 1–8. [Google Scholar]
- Braione, M.; Scholtes, N.K. Forecasting value-at-risk under different distributional assumptions. Econometrics 2016, 4, 3. [Google Scholar] [CrossRef]
- Wang, Z.-R.; Chen, Y.-H.; Jin, Y.-B.; Zhou, Y.-J. Estimating risk of foreign exchange portfolio: Using VaR and CVaR based on GARCH-EVT-Copula model. Phys. A 2010, 389, 4918–4928. [Google Scholar] [CrossRef]
- Soleymani, F.; Itkin, A. Pricing foreign exchange options under stochastic volatility and interest rates using an RBF-FD method. J. Comput. Sci. 2019, 37, 101028. [Google Scholar] [CrossRef]
- Sarykalin, S.; Serraino, G.; Uryasev, S. Value-at-risk vs. conditional value-at-risk in risk management and optimization. In State-of-the-Art Decision-Making Tools in the Information-Intensive Age; Tutorials in Operations Research; Informs: Catonsville, MD, USA, 2008; pp. 270–294. [Google Scholar]
- Rockafellar, R.T.; Uryasev, S. Conditional value-at-risk for general loss distributions. J. Bank. Financ. 2002, 26, 1443–1471. [Google Scholar] [CrossRef]
- Herwartz, H. Stock return prediction under GARCH—An empirical assessment. Int. J. Forecast. 2017, 33, 569–580. [Google Scholar] [CrossRef]
- Norton, M.; Khokhlov, V.; Uryasev, S. Calculating CVaR and bPOE for common probability distributions with application to portfolio optimization and density estimation. Ann. Oper. Res. 2021, 299, 1281–1315. [Google Scholar] [CrossRef]
- Goode, J.; Kim, Y.S.; Fabozzi, F.J. Full versus quasi MLE for ARMA-GARCH models with infinitely divisible innovations. Appl. Econ. 2015, 47, 5147–5158. [Google Scholar] [CrossRef]
- McNeil, Q.J.; Frey, R.; Embrechts, P. Quantitative Risk Management, Revised ed.; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Viet Long, H.; Bin Jebreen, H.; Dassios, I.; Baleanu, D. On the statistical GARCH model for managing the risk by employing a fat-tailed distribution in finance. Symmetry 2020, 12, 1698. [Google Scholar] [CrossRef]
- Ullah, M.Z.; Mallawi, F.O.; Asma, M.; Shateyi, S. On the conditional value at risk based on the laplace distribution with application in GARCH model. Mathematics 2022, 10, 3018. [Google Scholar] [CrossRef]
- Williams, B. GARCH(1, 1) Models; Ruprecht-Karls-Universität Heidelberg: Heidelberg, Germany, 2011. [Google Scholar]
- De-Graft, E.; Owusu-Ansah, J.; Barnes, B.; Donkoh, E.K.; Appau, J.; Effah, B.; Mccall, M. Quantifying economic risk: An application of extreme value theory for measuring fire outbreaks financial loss. Financ. Math. Appl. 2019, 4, 1–12. [Google Scholar]
- Halkos, G.E.; Tsirivis, A.S. Value-at-risk methodologies for effective energy portfolio risk management. Econ. Anal. Policy 2019, 62, 197–212. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econometr. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Hlivka, I. VaR, CVaR and Their Time Series Applications; Research Note; Quant Solutions Group: London, UK, 2015; pp. 1–2. [Google Scholar]
- Chu, J.; Chan, S.; Nadarajah, S.; Osterrieder, J. GARCH Modelling of Cryptocurrencies. J. Risk Financ. Manag. 2017, 10, 17. [Google Scholar] [CrossRef]
- Echaust, K.; Just, M. Value at risk estimation using the GARCH-EVT approach with optimal tail selection. Mathematics 2020, 8, 114. [Google Scholar] [CrossRef]
- Davis, R.A.; Mikosch, T. Extreme value theory for GARCH processes. In Handbook of Financial Time Series; Springer: Berlin/Heidelberg, Germany, 2009; pp. 187–200. [Google Scholar]
- Gumbel, E.J. Les valeurs extrêmes des distributions statistiques (PDF). Ann. L’Institut Henri Poincaré 1935, 5, 115–158. [Google Scholar]
- Available online: https://reference.wolfram.com/language/ref/GumbelDistribution.html.en (accessed on 4 October 2016).
- Gumbel, E.J. The return period of flood flows. Ann. Math. Stat. 1941, 12, 163–190. [Google Scholar] [CrossRef]
- Georgakopoulos, N.L. Illustrating Finance Policy with Mathematica; Springer International Publishing: London, UK, 2018. [Google Scholar]
- Soleymani, F.; Ma, Q.; Liu, T. Managing the risk via the Chi-squared distribution in VaR and CVaR with the use in generalized autoregressive conditional heteroskedasticity model. Mathematics 2025, 13, 1410. [Google Scholar] [CrossRef]
- Engle, R.F. Autoregressive conditional heteroskedasticity with estimates of the variance of U.K. inflation. Econometrica 1982, 50, 987–1008. [Google Scholar] [CrossRef]

| a | b | q | VaR (Normal) | VaR (Gumbel Distribution) | ES (Normal) | ES (Gumbel Distribution) |
|---|---|---|---|---|---|---|
| 0.020 | 0.0020 | 0.85 | 0.022 | 0.021 | 0.023 | 0.022 |
| 0.020 | 0.0020 | 0.90 | 0.023 | 0.022 | 0.024 | 0.022 |
| 0.020 | 0.0020 | 0.95 | 0.023 | 0.022 | 0.024 | 0.023 |
| 0.020 | 0.0040 | 0.85 | 0.024 | 0.023 | 0.026 | 0.024 |
| 0.020 | 0.0040 | 0.90 | 0.025 | 0.023 | 0.027 | 0.025 |
| 0.020 | 0.0040 | 0.95 | 0.027 | 0.024 | 0.028 | 0.025 |
| 0.020 | 0.0060 | 0.85 | 0.026 | 0.024 | 0.029 | 0.026 |
| 0.020 | 0.0060 | 0.90 | 0.028 | 0.025 | 0.031 | 0.027 |
| 0.020 | 0.0060 | 0.95 | 0.030 | 0.027 | 0.032 | 0.028 |
| 0.020 | 0.0080 | 0.85 | 0.028 | 0.025 | 0.032 | 0.028 |
| 0.020 | 0.0080 | 0.90 | 0.030 | 0.027 | 0.034 | 0.029 |
| 0.020 | 0.0080 | 0.95 | 0.033 | 0.029 | 0.037 | 0.031 |
| 0.040 | 0.0020 | 0.85 | 0.042 | 0.041 | 0.043 | 0.042 |
| 0.040 | 0.0020 | 0.90 | 0.043 | 0.042 | 0.044 | 0.042 |
| 0.040 | 0.0020 | 0.95 | 0.043 | 0.042 | 0.044 | 0.043 |
| 0.040 | 0.0040 | 0.85 | 0.044 | 0.043 | 0.046 | 0.044 |
| 0.040 | 0.0040 | 0.90 | 0.045 | 0.043 | 0.047 | 0.045 |
| 0.040 | 0.0040 | 0.95 | 0.047 | 0.044 | 0.048 | 0.045 |
| 0.040 | 0.0060 | 0.85 | 0.046 | 0.044 | 0.049 | 0.046 |
| 0.040 | 0.0060 | 0.90 | 0.048 | 0.045 | 0.051 | 0.047 |
| 0.040 | 0.0060 | 0.95 | 0.050 | 0.047 | 0.052 | 0.048 |
| 0.040 | 0.0080 | 0.85 | 0.048 | 0.045 | 0.052 | 0.048 |
| 0.040 | 0.0080 | 0.90 | 0.050 | 0.047 | 0.054 | 0.049 |
| 0.040 | 0.0080 | 0.95 | 0.053 | 0.049 | 0.057 | 0.051 |
| 0.060 | 0.0020 | 0.85 | 0.062 | 0.061 | 0.063 | 0.062 |
| 0.060 | 0.0020 | 0.90 | 0.063 | 0.062 | 0.064 | 0.062 |
| 0.060 | 0.0020 | 0.95 | 0.063 | 0.062 | 0.064 | 0.063 |
| 0.060 | 0.0040 | 0.85 | 0.064 | 0.063 | 0.066 | 0.064 |
| 0.060 | 0.0040 | 0.90 | 0.065 | 0.063 | 0.067 | 0.065 |
| 0.060 | 0.0040 | 0.95 | 0.067 | 0.064 | 0.068 | 0.065 |
| 0.060 | 0.0060 | 0.85 | 0.066 | 0.064 | 0.069 | 0.066 |
| 0.060 | 0.0060 | 0.90 | 0.068 | 0.065 | 0.071 | 0.067 |
| 0.060 | 0.0060 | 0.95 | 0.070 | 0.067 | 0.072 | 0.068 |
| 0.060 | 0.0080 | 0.85 | 0.068 | 0.065 | 0.072 | 0.068 |
| 0.060 | 0.0080 | 0.90 | 0.070 | 0.067 | 0.074 | 0.069 |
| 0.060 | 0.0080 | 0.95 | 0.073 | 0.069 | 0.077 | 0.071 |
| 0.080 | 0.0020 | 0.85 | 0.082 | 0.081 | 0.083 | 0.082 |
| 0.080 | 0.0020 | 0.90 | 0.083 | 0.082 | 0.084 | 0.082 |
| 0.080 | 0.0020 | 0.95 | 0.083 | 0.082 | 0.084 | 0.083 |
| 0.080 | 0.0040 | 0.85 | 0.084 | 0.083 | 0.086 | 0.084 |
| 0.080 | 0.0040 | 0.90 | 0.085 | 0.083 | 0.087 | 0.085 |
| 0.080 | 0.0040 | 0.95 | 0.087 | 0.084 | 0.088 | 0.085 |
| 0.080 | 0.0060 | 0.85 | 0.086 | 0.084 | 0.089 | 0.086 |
| 0.080 | 0.0060 | 0.90 | 0.088 | 0.085 | 0.091 | 0.087 |
| 0.080 | 0.0060 | 0.95 | 0.090 | 0.087 | 0.092 | 0.088 |
| 0.080 | 0.0080 | 0.85 | 0.088 | 0.085 | 0.092 | 0.088 |
| 0.080 | 0.0080 | 0.90 | 0.090 | 0.087 | 0.094 | 0.089 |
| 0.080 | 0.0080 | 0.95 | 0.093 | 0.089 | 0.097 | 0.091 |
| Stock | Tickers | Market | Section | Float Shares | Starting | Ending | Data Size |
|---|---|---|---|---|---|---|---|
| Abbott Laboratories | NYSE:ABT | NYSE | Medical Devices | 1734455940 | 1 January 2024 | 1 January 2025 | 251 |
| Zions Bancorp NA | NASDAQ:ZION | NASDAQ | Banks Regional | 147699000 | 1 January 2023 | 1 January 2025 | 501 |
| w | The Variance for Error | ||
|---|---|---|---|
| 0.696408 | 0.426945 | 0.0481203 | 6.49298 |
| w | The Variance for Error | ||
|---|---|---|---|
| 3.83852 | 0.304459 | 0.323751 | 1241.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Zhang, Y.; Li, J.; Liu, T. Assessing Expected Shortfall in Risk Analysis Through Generalized Autoregressive Conditional Heteroskedasticity Modeling and the Application of the Gumbel Distribution. Axioms 2025, 14, 391. https://doi.org/10.3390/axioms14050391
Wang B, Zhang Y, Li J, Liu T. Assessing Expected Shortfall in Risk Analysis Through Generalized Autoregressive Conditional Heteroskedasticity Modeling and the Application of the Gumbel Distribution. Axioms. 2025; 14(5):391. https://doi.org/10.3390/axioms14050391
Chicago/Turabian StyleWang, Bingjie, Yihui Zhang, Jia Li, and Tao Liu. 2025. "Assessing Expected Shortfall in Risk Analysis Through Generalized Autoregressive Conditional Heteroskedasticity Modeling and the Application of the Gumbel Distribution" Axioms 14, no. 5: 391. https://doi.org/10.3390/axioms14050391
APA StyleWang, B., Zhang, Y., Li, J., & Liu, T. (2025). Assessing Expected Shortfall in Risk Analysis Through Generalized Autoregressive Conditional Heteroskedasticity Modeling and the Application of the Gumbel Distribution. Axioms, 14(5), 391. https://doi.org/10.3390/axioms14050391







