Stabilization and Synchronization of a New 3D Complex Chaotic System via Adaptive and Active Control Methods
Abstract
1. Introduction
2. The 3D Chaotic System and Its Equilibrium Points
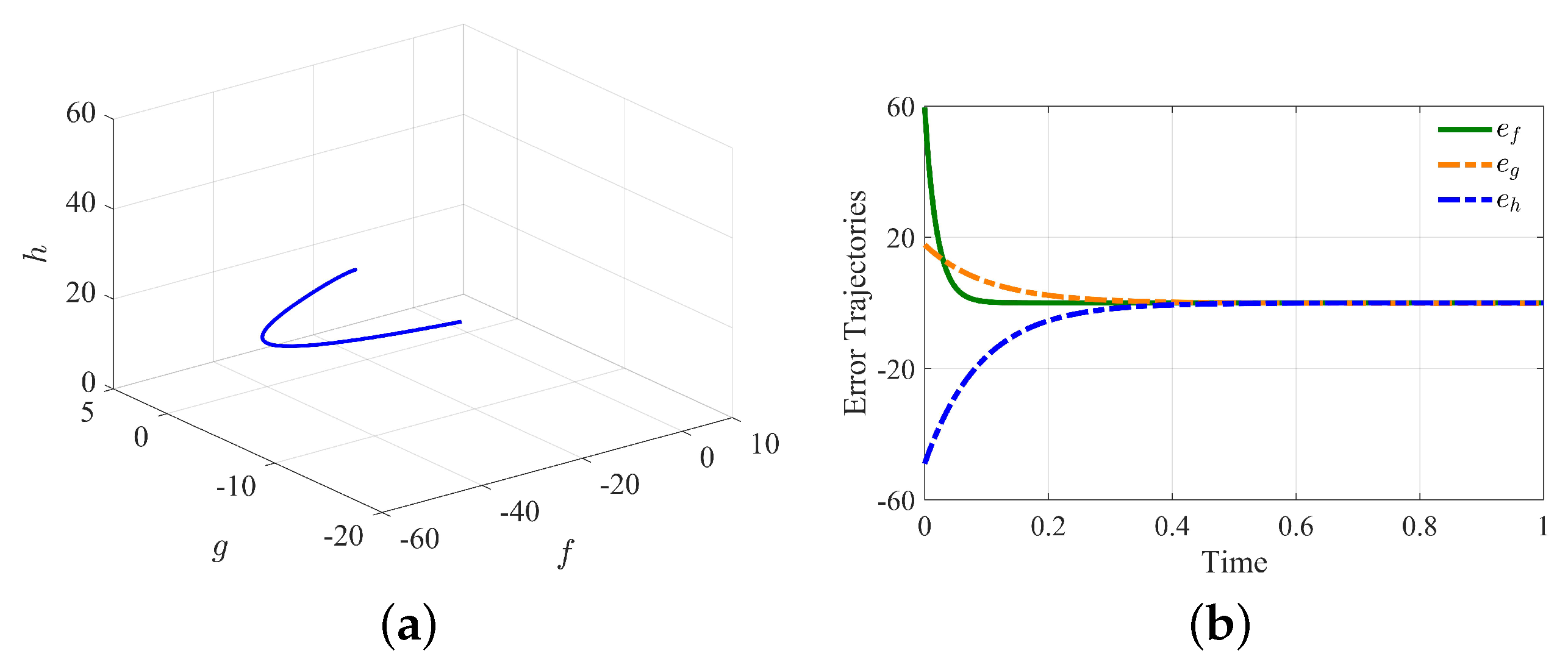
3. Stability Analysis of the 3D Chaotic System
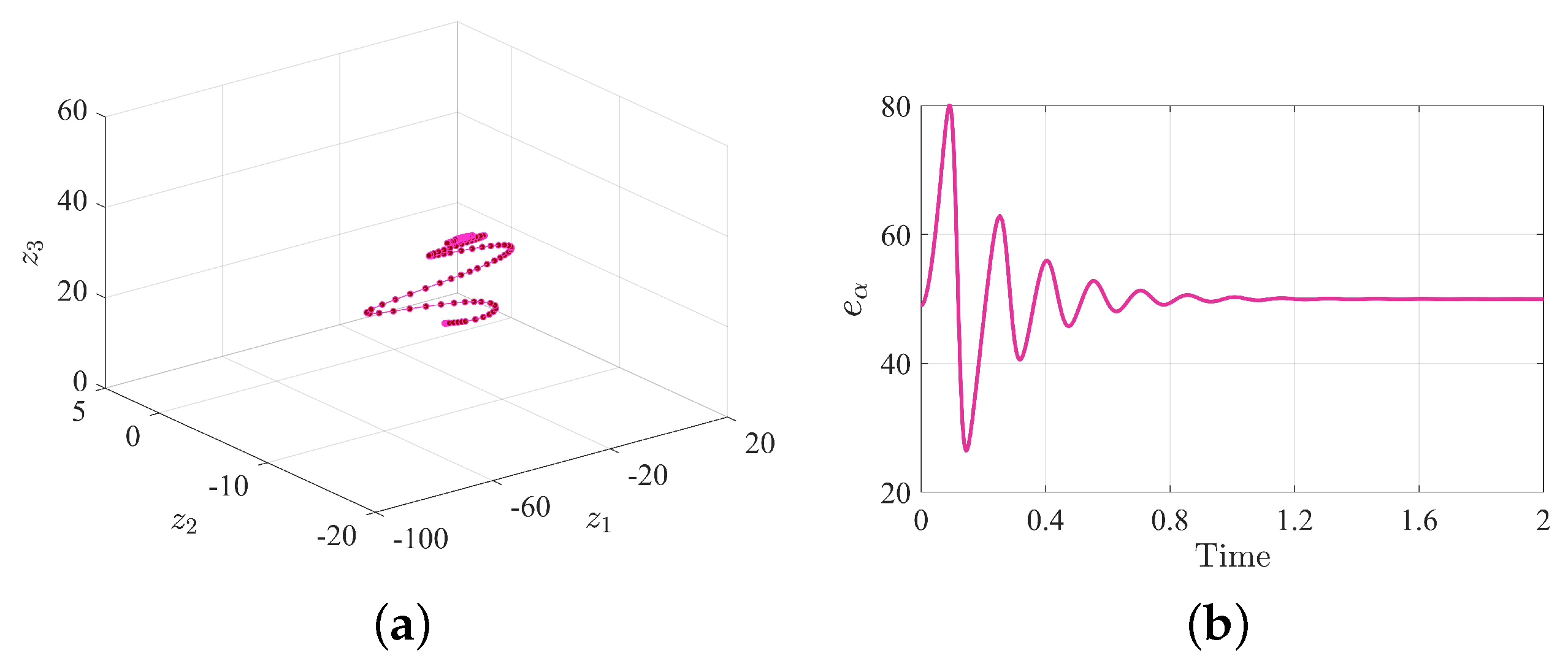
3.1. Active Control
3.2. Adaptive Control
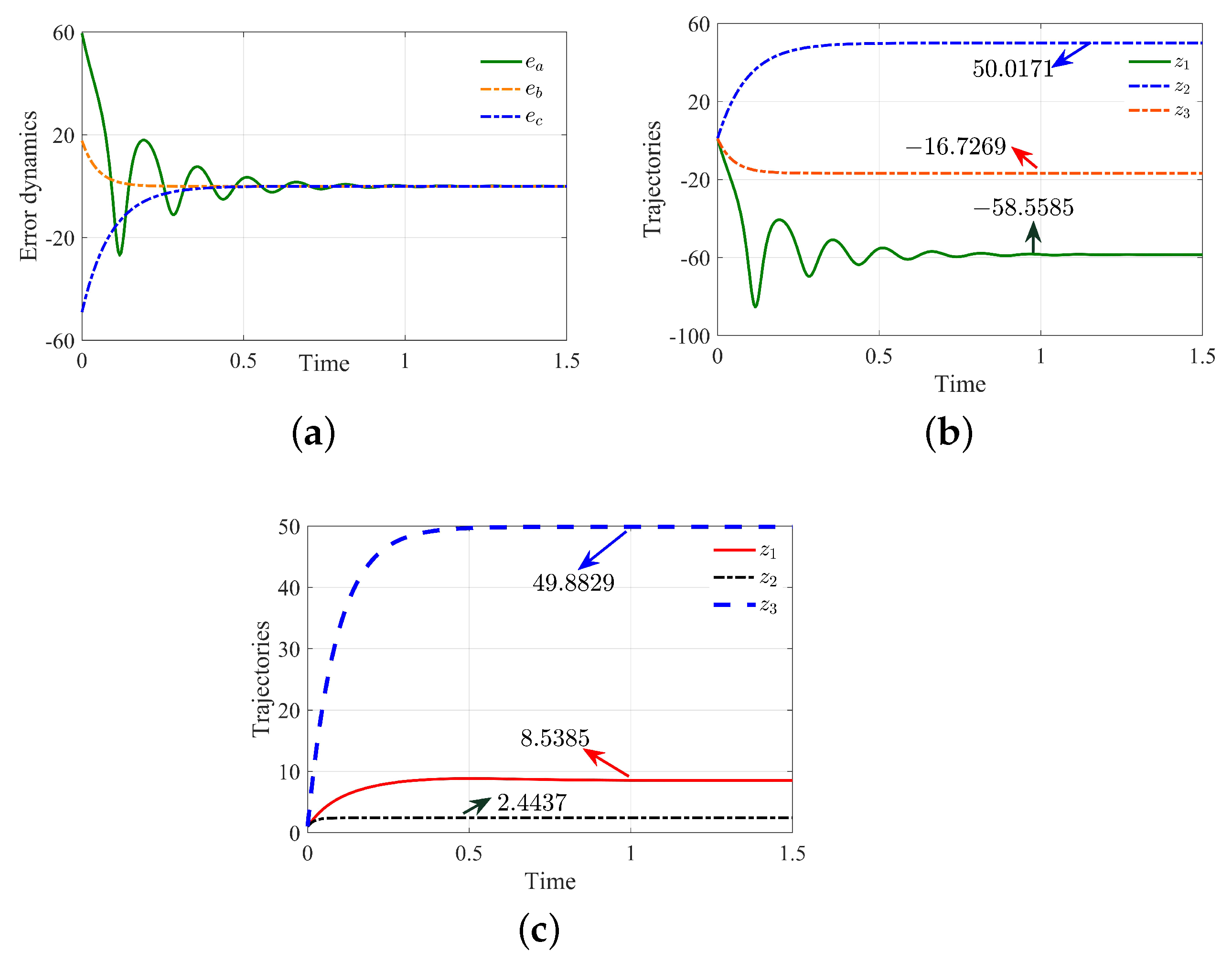
3.3. Stability: Results and Discussion
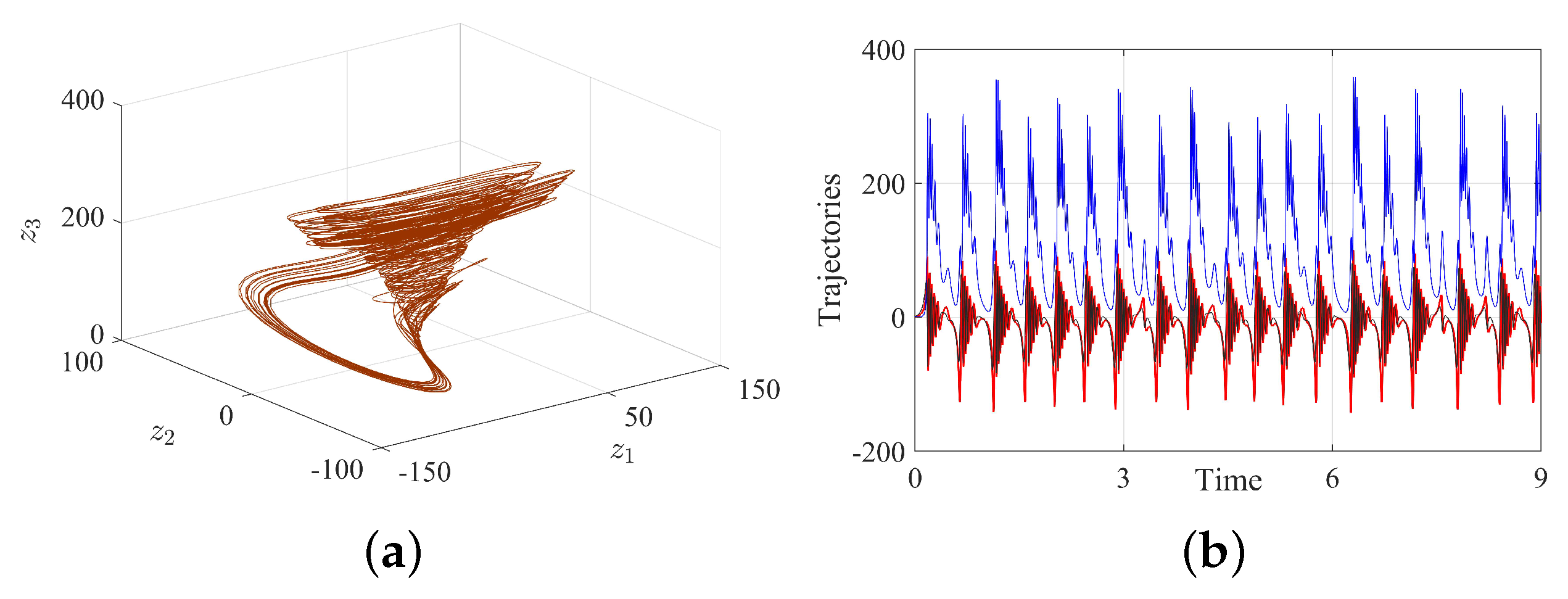
4. Synchronization of the 3D Chaotic System
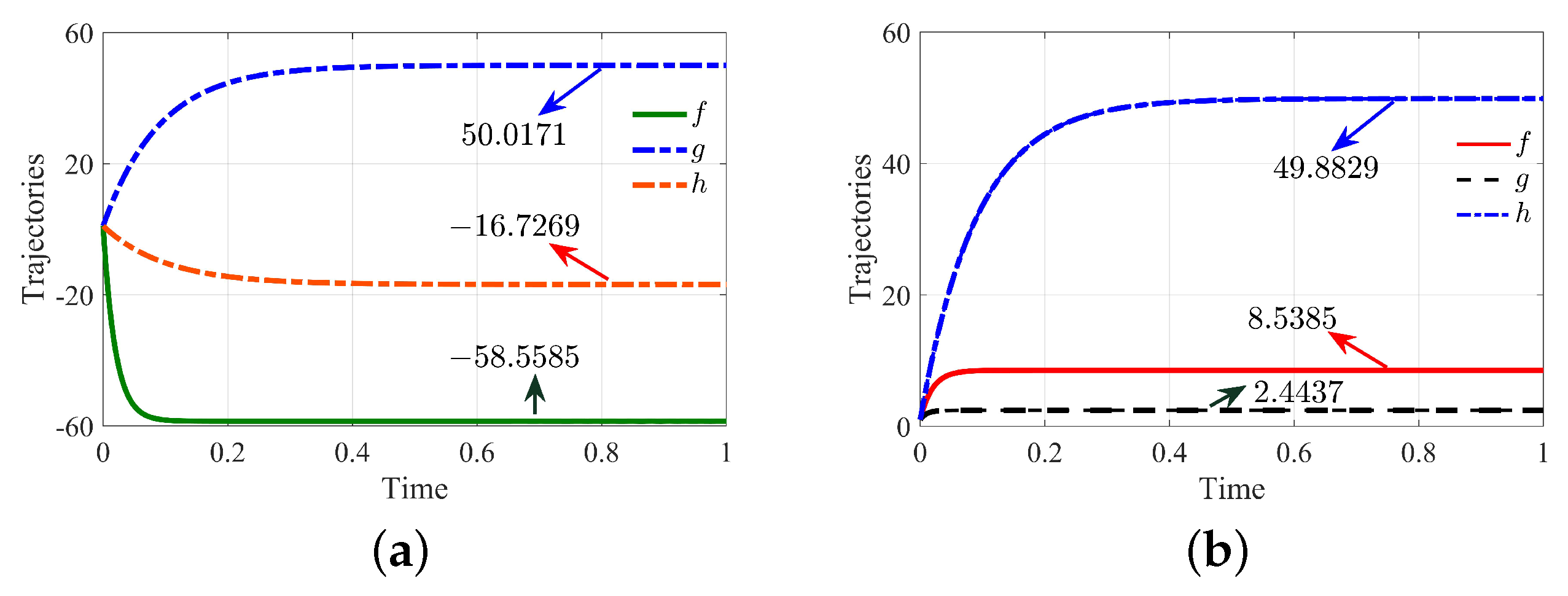
4.1. Active Control Synchronization
4.2. Adaptive Synchronization
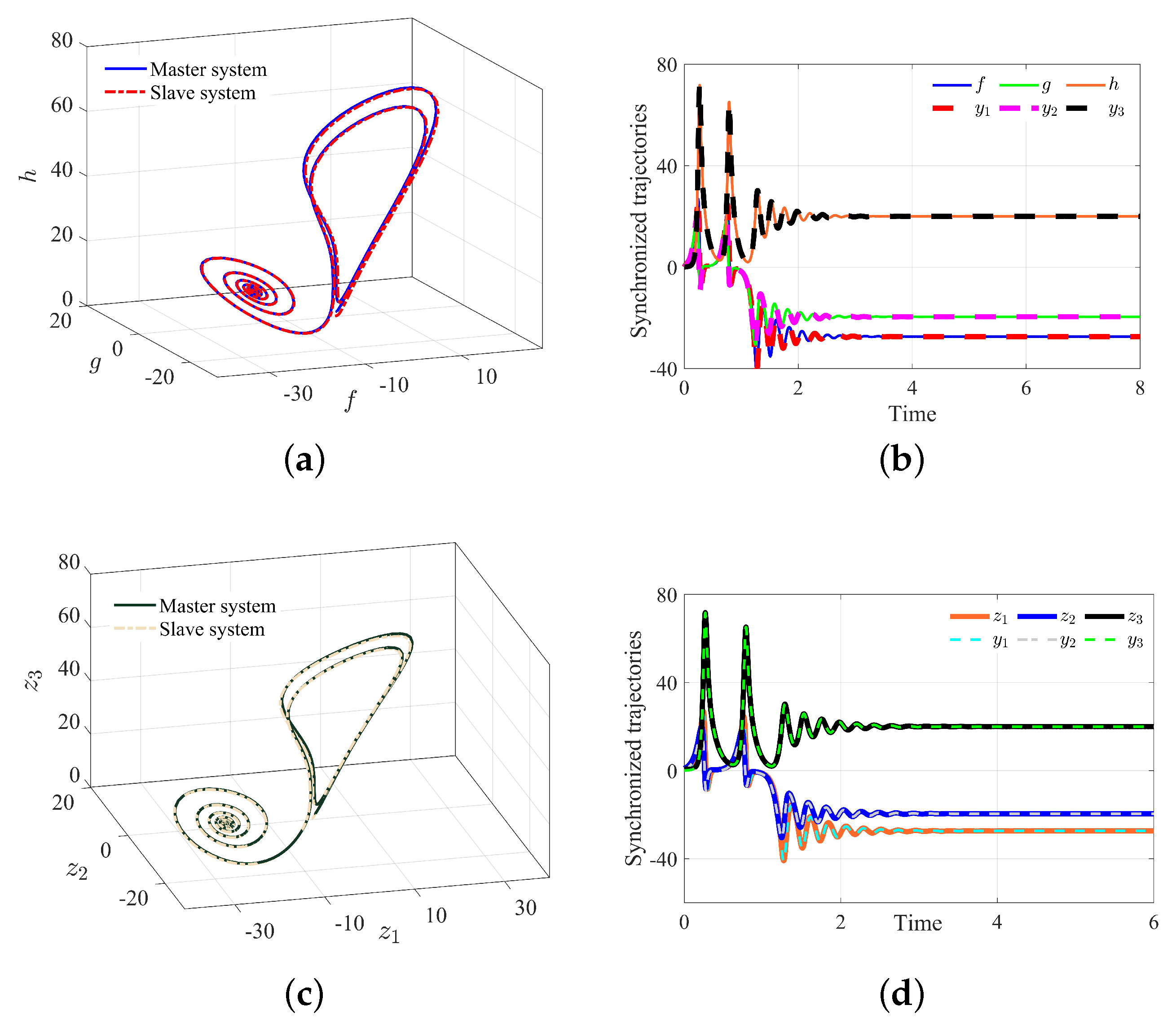
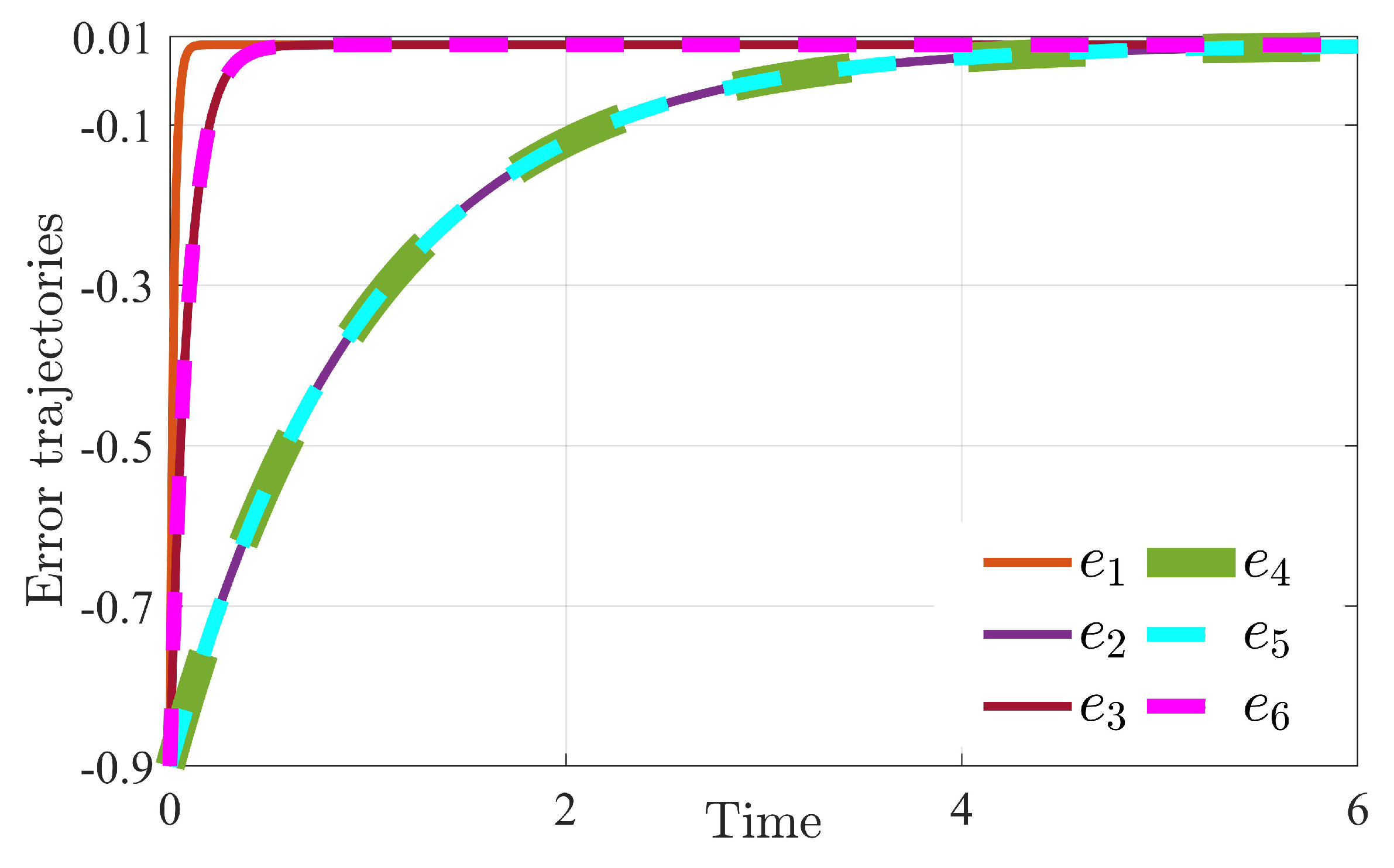
4.3. Synchronization: Discussion and Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, T.; Xing, H.; Xu, X.; Wang, Z.; Zhao, Y. Chaos-based coverage path planning framework for mobile robots and its digital signal processing implementation. Phys. Scr. 2024, 99, 125293. [Google Scholar] [CrossRef]
- Wang, N.; Marwan, M.; Yang, Y.; Chen, X.; Herbert, H.C.I.; Xu, Q. Designing nest-fold system via dual-route fractal process and application in chaotic mobile robot. IEEE Internet Things J. 2024, 12, 9206–9217. [Google Scholar] [CrossRef]
- Manhil, M.M.; Jamal, R.K. A novel secure communication system using Duffing’s chaotic model. Multimed. Tools Appl. 2024, 83, 89681–89694. [Google Scholar] [CrossRef]
- Gokyildirim, A.; Akgul, A.; Calgan, H.; Demirtas, M. Parametric fractional-order analysis of Arneodo chaotic system and microcontroller-based secure communication implementation. AEU-Int. J. Electron. Commun. 2024, 175, 155080. [Google Scholar] [CrossRef]
- Yan, S.; Zhang, H.; Jiang, D. Multi-wing chaotic system based on smooth function and its predefined time synchronization. Commun. Nonlinear Sci. Numer. Simul. 2024, 138, 108178. [Google Scholar] [CrossRef]
- Marwan, M.; Han, M.; Dai, Y.; Cai, M. The impact of global dynamics on the fractals of a Quadrotor Unmanned Aerial Vehicle (QUAV) chaotic system. Fractals 2024, 32, 2450043. [Google Scholar] [CrossRef]
- Matouk, A.E. Applications of the generalized gamma function to a fractional-order biological system. Heliyon 2023, 9, e18645. [Google Scholar] [CrossRef]
- Polyanovsky, V.O.; Kamenev, I.G. On stable and quasi-chaotic regimes in a one-dimensional unimodal mapping obtained by modeling the dynamics of a biological population. J. Phys. Conf. Ser. 2024, 2701, 012058. [Google Scholar] [CrossRef]
- Bi, H.; Qi, G.; Hu, J. Modeling and analysis of chaos and bifurcations for the attitude system of a quadrotor unmanned aerial vehicle. Complexity 2019, 2019, 6313925. [Google Scholar] [CrossRef]
- Ali, A.; Ahmad, J.; Javed, S.; Rehman, S. Analysis of chaotic structures, bifurcation and soliton solutions to fractional Boussinesq model. Phys. Scr. 2023, 98, 075217. [Google Scholar] [CrossRef]
- Kocamaz, U.E.; Cevher, B.; Uyaroglu, Y. Control and synchronization of chaos with sliding mode control based on cubic reaching rule. Chaos Solitons Fractals 2017, 105, 92–98. [Google Scholar] [CrossRef]
- Johansyah, M.D.; Sambas, A.; Mobayen, S.; Vaseghi, B.; Al-Azzawi, S.F.; Sukono; Sulaiman, I.M. Dynamical analysis and adaptive finite-time sliding mode control approach of the financial fractional-order chaotic system. Mathematics 2022, 11, 100. [Google Scholar] [CrossRef]
- Saeed, N.A.; Saleh, H.A.; El-Ganaini, W.A.; Kamel, M.; Mohamed, M.S. On a New Three-Dimensional Chaotic System with Adaptive Control and Chaos Synchronization. Shock Vib. 2023, 2023, 1969500. [Google Scholar] [CrossRef]
- Rahman, Z.A.; Al-Kashoash, H.A.; Ramadhan, S.M.; Al-Yasir, Y.I. Adaptive control synchronization of a novel memristive chaotic system for secure communication applications. Inventions 2019, 4, 30. [Google Scholar] [CrossRef]
- Marwan, M.; Ahmad, S.; Aqeel, M.; Sabir, M. Control analysis of Rucklidge chaotic system. J. Dyn. Syst. Meas. Control 2019, 141, 041010. [Google Scholar] [CrossRef]
- Yu, Z.; Zhao, F.; Ding, S.; Chen, X. Adaptive pre-assigned finite-time control of uncertain nonlinear systems with unknown control gains. Appl. Math. Comput. 2022, 417, 126784. [Google Scholar] [CrossRef]
- Dou, W.; Ding, S.; Chen, X. Practical adaptive finite-time stabilization for a class of second-order systems. Appl. Math. Comput. 2022, 431, 127340. [Google Scholar] [CrossRef]
- Cheng, L.; Lin, Y.; Hou, Z.; Tan, M.; Huang, J.; Zhang, W. Adaptive tracking control of hybrid machines: A closed-chain five-bar mechanism case. IEEE/ASME Trans. Mech. 2010, 16, 1155–1163. [Google Scholar] [CrossRef]
- Barzegar, A.; Lee, D.-J. Deep reinforcement learning-based adaptive controller for trajectory tracking and altitude control of an aerial robot. Appl. Sci. 2022, 12, 4764. [Google Scholar] [CrossRef]
- Jai, A.A.; Ouassaid, M. Three novel machine learning-based adaptive controllers for a photovoltaic shunt active power filter performance enhancement. Sci. Afr. 2024, 24, e02171. [Google Scholar]
- He, G.; Choudhary, Y.; Shi, G. Self-Supervised Meta-Learning for All-Layer DNN-Based Adaptive Control with Stability Guarantees. arXiv 2024, arXiv:2410.07575. [Google Scholar]
- Berkenkamp, F.; Turchetta, M.; Schoellig, A.P.; Krause, A. Safe model-based reinforcement learning with stability guarantees. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar]
- Aguilar-Lopez, R.; Martínez-Guerra, R. Chaos suppression via observer-based active control scheme: Application to Duffing’s oscillator. Chaos Solitons Fractals 2007, 32, 1887–1897. [Google Scholar] [CrossRef]
- Roldán-Caballero, A.; Pérez-Cruz, J.H.; Hernandez-Marquez, E.; Garcia-Sanchez, J.R.; Ponce-Silva, M.; Rubio, J.D.J.; Mendoza-Chegue, A. Synchronization of a new chaotic system using adaptive control: Design and experimental implementation. Complexity 2023, 2023, 2881192. [Google Scholar] [CrossRef]
- Kumar, A.; Handa, H. PI Sliding Mode Control and Active Control Based Stabilization Scheme for a Chaotic System Having Single Stable Equilibrium and its Circuit Implementation. In Proceedings of the 2024 5th International Conference for Emerging Technology (INCET), Belgaum, India, 24–26 May 2024; pp. 1–7. [Google Scholar]
- Akter, M.T.; Tarammim, A.; Hussen, S. Chaos control and synchronization of modified Lorenz system using active control and backstepping scheme. Waves Random Complex Media 2023, 16, 1–20. [Google Scholar] [CrossRef]
- Tarammim, A.; Akter, M.T. A comparative study of synchronization methods of rucklidge chaotic systems with design of active control and backstepping methods. Int. J. Mod. Nonlinear Theory Appl. 2022, 11, 31–51. [Google Scholar] [CrossRef]
- Iqbal, S.; Wang, J. A novel fractional-order 3-D chaotic system and its application to secure communication based on chaos synchronization. Phys. Scr. 2025, 100, 025243. [Google Scholar] [CrossRef]
- Tarammim, A.; Akter, M.T. Shimizu–Morioka’s chaos synchronization: An efficacy analysis of active control and backstepping methods. Front. Appl. Math. Stat. 2023, 9, 1100147. [Google Scholar] [CrossRef]
- Pakiriswamy, S.; Vaidyanathan, S. Generalized projective synchronization of three-scroll chaotic systems via active control. In Proceedings of the 2012 International Conference on Computer Science and Information Technology, Bangalore, India, 2–4 January 2012; pp. 146–155. [Google Scholar]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Driving systems with chaotic signals. Phys. Rev. A 1991, 44, 2374. [Google Scholar] [CrossRef]
- Wang, J.; Ye, X.; Si, W. Robust ISS-satisfying fuzzy control of chaotic systems. In Proceedings of the Sixth International Conference on Intelligent Systems Design and Applications, Jinan, China, 16–18 October 2006; Volume 1, pp. 293–298. [Google Scholar]
- Wang, X.; Liu, X.; She, K.; Zhong, S. Pinning impulsive synchronization of complex dynamical networks with various time-varying delay sizes. Nonlinear Anal. Hybrid Syst. 2017, 26, 307–318. [Google Scholar] [CrossRef]
- Azar, A.T.; Serrano, F.; Kamal, N.A.; Koubaa, A. Robust Kinematic Control of Unmanned Aerial Vehicles with Non-holonomic Constraints. Proc. Int. Conf. Adv. Intell. Syst. Inform. 2020, 1261, 839–850. [Google Scholar]
- Wang, L.; Dong, W.; Ding, Q. A new fixed-time sliding mode control scheme for synchronization of chaotic systems. Phys. Scr. 2024, 99, 095240. [Google Scholar] [CrossRef]
- Marwan, M.; Mehboob, M.; Ahmad, S.; Aqeel, M. Hopf bifurcation of forced Chen system and its stability via adaptive control with arbitrary parameters. Soft Comput. 2020, 24, 4333–4341. [Google Scholar] [CrossRef]
- Jia, T.; Chen, X.; He, L.; Zhao, F.; Qiu, J. Finite-time synchronization of uncertain fractional-order delayed memristive neural networks via adaptive sliding mode control and its application. Fractal Fract. 2022, 6, 502. [Google Scholar] [CrossRef]
- Ogorzalek, M.J. Taming chaos. I. Synchronization. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1993, 40, 693–699. [Google Scholar] [CrossRef]
- Zeng, Y.; Singh, S.N. Adaptive control in Lorenz system. Int. J. Dyn. Control 1998, 8, 255–267. [Google Scholar]
- Sambas, A.; Benkouider, K.; Kaçar, S.; Ceylan, N.; Vaidyanathan, S.; Sulaiman, I.M.; Mohamed, M.A.; Ayob, A.F.M.; Muni, S.S. Dynamic Analysis and Circuit Design of a New 3D Highly Chaotic System and its Application to Pseudo Random Number Generator (PRNG) and Image Encryption. SN Comput. Sci. 2024, 5, 420. [Google Scholar] [CrossRef]
- Dong, Y.; Li, Y.; Li, X.; Yang, J. Active Control of Dynamic Behaviors of Graded Graphene Reinforced Cylindrical Shells with Piezoelectric Actuator/Sensor Layers. Appl. Math. Model. 2020, 82, 252–270. [Google Scholar] [CrossRef]
- Wang, L.; Liu, J.; Yang, C.; Wu, D. A Novel Interval Dynamic Reliability Computation Approach for the Risk Evaluation of Vibration Active Control Systems Based on PID Controllers. Appl. Math. Model. 2021, 92, 422–446. [Google Scholar] [CrossRef]
- Qin, G.; Wu, H.; Cheng, Y.; Pan, H.; Zhao, W.; Shi, S.; Song, Y.; Ji, A. Adaptive Trajectory Control of an Under-Actuated Snake Robot. Appl. Math. Model. 2022, 106, 756–769. [Google Scholar] [CrossRef]
- Guo, X.; Wang, H.; Liu, H. Adaptive Sliding Mode Control with Disturbance Estimation for Hydraulic Actuator Systems and Application to Rock Drilling Jumbo. Appl. Math. Model. 2024, 136, 115637. [Google Scholar] [CrossRef]
- He, Y.; Yang, M.; Zhao, X.; He, C.; Chen, Y.-H.; Li, D.; Huang, J. Adaptive Control Scheme for Cooperative Transport Systems Navigation Under Uncertainty. Appl. Math. Model. 2025, 138, 115778. [Google Scholar] [CrossRef]
- Fiori, S. A control-theoretic approach to the synchronization of second-order continuous-time dynamical systems on real connected Riemannian manifolds. SIAM J. Control Optim. 2020, 58, 787–813. [Google Scholar] [CrossRef]
- Rieger, C.G.; David, I.G.; McQueen, M.A. Resilient control systems: Next generation design research. In Proceedings of the 2009 2nd Conference on Human System Interactions, Catania, Italy, 21–23 May 2009. [Google Scholar]
- Wei, D.; Ji, K. Resilient industrial control system (RICS): Concepts, formulation, metrics, and insights. In Proceedings of the 2010 3rd International Symposium on Resilient Control Systems, Idaho Falls, ID, USA, 10–12 August 2010. [Google Scholar]
- Zhang, W.J.; Van Luttervelt, C.A. Toward a resilient manufacturing system. CIRP Ann. 2011, 60, 469–472. [Google Scholar] [CrossRef]
- Zhang, W.; Lin, Y. On the principle of design of resilient systems–application to enterprise information systems. Enterp. Inf. Syst. 2010, 4, 99–110. [Google Scholar] [CrossRef]
- Soliman, H.M.; Elshafei, A.L.; Shaltout, A.A.; Morsi, M.F. Robust power system stabiliser. IEE Proc.-Gener. Transm. Distrib. 2000, 147, 285–291. [Google Scholar] [CrossRef]
- Liu, C.C.; Jung, J.; Heydt, G.T.; Vittal, V.; Phadke, A.G. The strategic power infrastructure defense (SPID) system. A conceptual design. IEEE Control Syst. Mag. 2000, 20, 40–52. [Google Scholar]
- Leonessa, A.; Haddad, W.M.; Chellaboina, V. Hierarchical Nonlinear Switching Control Design with Applications to Propulsion Systems; Springer Science & Business Media: London, UK, 2000. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loudahi, L.; Yuan, J.; Dehbi, L.; Osman, M. Stabilization and Synchronization of a New 3D Complex Chaotic System via Adaptive and Active Control Methods. Axioms 2025, 14, 383. https://doi.org/10.3390/axioms14050383
Loudahi L, Yuan J, Dehbi L, Osman M. Stabilization and Synchronization of a New 3D Complex Chaotic System via Adaptive and Active Control Methods. Axioms. 2025; 14(5):383. https://doi.org/10.3390/axioms14050383
Chicago/Turabian StyleLoudahi, Lamia, Jing Yuan, Lydia Dehbi, and Mawia Osman. 2025. "Stabilization and Synchronization of a New 3D Complex Chaotic System via Adaptive and Active Control Methods" Axioms 14, no. 5: 383. https://doi.org/10.3390/axioms14050383
APA StyleLoudahi, L., Yuan, J., Dehbi, L., & Osman, M. (2025). Stabilization and Synchronization of a New 3D Complex Chaotic System via Adaptive and Active Control Methods. Axioms, 14(5), 383. https://doi.org/10.3390/axioms14050383






