Slant Helices and Darboux Helices in Myller Configuration

Abstract

In this paper, we study slant helices (or ${\stackrel{\_}{\xi }}_2$-helices) and Darboux helices in the Myller configuration M. We demonstrate that a curve in M is a slant helix if and only if it is a Darboux helix. We present the alternative frame for a curve in M. Furthermore, we derive the differential equations that characterize the curves in M using both the Frenet-type frame and the alternative frame.

1. Introduction

Orthonormal frames are essential tools for studying the differential geometry of curves and surfaces [1,2,3]. The Frenet–Serret frame of a space curve and the Darboux frame of a surface curve are among the most well-known of these frames [4,5,6]. More general frames along space curves or surface curves have been introduced by Myller. He defined a configuration in $E^3$, known as the Myller configuration $M(C,\stackrel{\_}{\xi },\pi )$, by considering a unit vector field $\stackrel{\_}{\xi }$ and a plane $\pi$ along a curve C, referring to them as a versor field $(C,\stackrel{\_}{\xi })$ and a plane field $(C,\pi )$, respectively, with the condition that $\stackrel{\_}{\xi }\in \pi$. When the planes $\pi$ are tangent to C, this configuration becomes a special case called the tangent Myller configuration, denoted by $M_t(C,\stackrel{\_}{\xi },\pi )$. Specifically, if the curve C is a surface curve lying on a surface $S\subset E^3$ with arclength parameter s, $\stackrel{\_}{\xi }\left(s\right)$ serves as the tangent versor field to S along C, and $\pi \left(s\right)$ is the tangent plane field to S along $C.$ In this context, $M_t(C,\stackrel{\_}{\xi },\pi )$ is referred to as the tangent Myller configuration intrinsically associated with the geometric objects $S,C,$ and $\stackrel{\_}{\xi }$. Thus, the geometry of the versor field $(C,\stackrel{\_}{\xi })$ on a surface S corresponds to the geometry of the associated Myller configurations $M_t(C,\stackrel{\_}{\xi },\pi )$, which in turn represents a particular case of $M(C,\stackrel{\_}{\xi },\pi )$. In the special instance where the tangent Myller configuration $M_t(C,\stackrel{\_}{\xi },\pi )$ is the associated Myller configuration to a curve C on a surface $S,$ we obtain the classical theory of surface curves (curves lying on a surface).

Myller studied the parallelism of versor field $(C,\stackrel{\_}{\xi })$ in the plane field $(C,\pi )$ [7]. He obtained a generalization of the parallelism of Levi-Civita on the curved surfaces. Later, Mayer introduced some new invariants for $M(C,\stackrel{\_}{\xi },\pi )$ and $M_t(C,\stackrel{\_}{\xi },\pi )$ [8]. Miron extended the notion of Myller configuration in Riemannian geometry [9]. Vaisman considered the Myller configuration in the symplectic geometry [10]. Furthermore, Myller configuration has been studied in different spaces [11,12,13]. Macsim, Mihai, and Olteanu have investigated rectifying-type curves in a Myller configuration [14]. Recently, the authors defined some special helices in M and provided the characterizations for those curves [15]. In recent years, several works have further expanded the study of geometric structures in Euclidean spaces, such as the study of sweeping surfaces and directional developable surfaces [16,17,18]. Li and other researchers also explored osculating curves [19,20,21] and generalized Bertrand curve pairs [22,23,24]. These works contribute to a deeper understanding of geometric curves in higher-dimensional spaces and offer a broader context for our exploration of slant helices and Darboux helices in the Myller configuration M [25,26,27].

In the present paper, we study slant helices and Darboux helices in the Myller configuration M. We provide characterizations and axes for these curves. Moreover, we introduce the alternative frame of a curve C in M and present the geometric interpretations of alternative invariants of C. Finally, we obtain the differential equations related to curves, helices, and slant helices in M.

2. Preliminaries

In this section, a brief summary of curves in Myller configuration $M(C,\stackrel{\_}{\xi },\pi )$ are introduced. For more detailed information, we refer to [9].

Let $(C,\stackrel{\_}{\xi })$ be a versor field and $(C,\pi )$ be a plane field such that $\stackrel{\_}{\xi }\in \pi$ in $E^3$. The pair $((C,\stackrel{\_}{\xi }),(C,\pi ))$ is called Myller configuration in $E^3$ and is denoted by $M(C,\stackrel{\_}{\xi },\pi )$ or, briefly, M. Let $R=(O;{\stackrel{\_}{i}}_1,{\stackrel{\_}{i}}_2,{\stackrel{\_}{i}}_3)$ denotes an orthonormal frame. Then, $(C,\stackrel{\_}{\xi })$ can be expressed in the form

$$\begin{array}{ccc}\hfill \stackrel{\_}{r}& =& \stackrel{\_}{r}\left(s\right),\stackrel{\_}{\xi }=\stackrel{\_}{\xi }\left(s\right),s\in I=(s_1,s_2),\hfill \\ \hfill \stackrel{\_}{r}\left(s\right)& =& x\left(s\right){\stackrel{\_}{i}}_1+y\left(s\right){\stackrel{\_}{i}}_2+z\left(s\right){\stackrel{\_}{i}}_3=\overrightarrow{OP}\left(s\right),\hfill \\ \hfill \stackrel{\_}{\xi }\left(s\right)& =& {\xi }_1\left(s\right){\stackrel{\_}{i}}_1+{\xi }_2\left(s\right){\stackrel{\_}{i}}_2+{\xi }_3\left(s\right){\stackrel{\_}{i}}_3=\overrightarrow{PQ},\hfill \end{array}$$

where $\stackrel{\_}{r}=\stackrel{\_}{r}\left(s\right)$ is the position vector of C, s is the arclength parameter of $C,$ and ${∥\stackrel{\_}{\xi }\left(s\right)∥}^2=〈\stackrel{\_}{\xi }\left(s\right),\stackrel{\_}{\xi }\left(s\right)〉=1.$ Writing ${\stackrel{\_}{\xi }}_1\left(s\right)=\stackrel{\_}{\xi }\left(s\right)$ and considering ${\displaystyle \frac{d{\stackrel{\_}{\xi }}_1\left(s\right)}{ds}},$ one can define versor field ${\stackrel{\_}{\xi }}_2\left(s\right)$ as follows:

$${\displaystyle \frac{d{\stackrel{\_}{\xi }}_1\left(s\right)}{ds}}=K_1\left(s\right){\stackrel{\_}{\xi }}_2\left(s\right),$$

where $K_1\left(s\right)=∥{\displaystyle \frac{d\stackrel{\_}{\xi }}{ds}}∥>0$ is called the curvature (or $K_1$-curvature) of $(C,\stackrel{\_}{\xi })$. The versor field ${\stackrel{\_}{\xi }}_2\left(s\right)$ is orthogonal to ${\stackrel{\_}{\xi }}_1\left(s\right)$ and exists when $K_1\left(s\right)\ne 0$. By defining the versor field ${\stackrel{\_}{\xi }}_3\left(s\right)={\stackrel{\_}{\xi }}_1\left(s\right)\times {\stackrel{\_}{\xi }}_2\left(s\right),$ an orthonormal and positively oriented frame is obtained. This frame is called the invariant frame of Frenet type for the versor field $(C,\stackrel{\_}{\xi })$ and denoted by $R_F\left(P\left(s\right);{\stackrel{\_}{\xi }}_1\left(s\right),{\stackrel{\_}{\xi }}_2\left(s\right),{\stackrel{\_}{\xi }}_3\left(s\right)\right)$ or, briefly, $R_F$ [9].

The derivative formulas for $R_F$ are

$${\displaystyle \frac{d\stackrel{\_}{r}\left(s\right)}{ds}}=\stackrel{\_}{\alpha }\left(s\right)=a_1\left(s\right){\stackrel{\_}{\xi }}_1\left(s\right)+a_2\left(s\right){\stackrel{\_}{\xi }}_2\left(s\right)+a_3\left(s\right){\stackrel{\_}{\xi }}_3\left(s\right),$$

(1)

with $a_1^2\left(s\right)+a_2^2\left(s\right)+a_3^2\left(s\right)=1$ and

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d{\stackrel{\_}{\xi }}_1\left(s\right)}{ds}}& =& K_1\left(s\right){\stackrel{\_}{\xi }}_2\left(s\right),\hfill \\ \hfill {\displaystyle \frac{d{\stackrel{\_}{\xi }}_2\left(s\right)}{ds}}& =& -K_1\left(s\right){\stackrel{\_}{\xi }}_1\left(s\right)+K_2\left(s\right){\stackrel{\_}{\xi }}_3\left(s\right),\hfill \\ \hfill {\displaystyle \frac{d{\stackrel{\_}{\xi }}_3\left(s\right)}{ds}}& =& -K_2\left(s\right){\stackrel{\_}{\xi }}_2\left(s\right),\hfill \end{array}$$

where $K_2\left(s\right)=〈{\displaystyle \frac{d{\stackrel{\_}{\xi }}_3\left(s\right)}{ds}},{\stackrel{\_}{\xi }}_3\left(s\right)〉$ is called the torsion (or $K_2$-torsion) of $(C,\stackrel{\_}{\xi }).$ The curvatures $K_1\left(s\right)$ and $K_2\left(s\right)$ have the same geometrical interpretation as the curvature and torsion of a curve in $E^3$, and the functions $a_1\left(s\right),a_2\left(s\right)$, $a_3\left(s\right),K_1\left(s\right),K_2\left(s\right),(s\in I)$ are invariants of the versor field $(C,\stackrel{\_}{\xi })$ [9]. If $a_1\left(s\right)=1,a_2\left(s\right)=0,a_3\left(s\right)=0$, one obtains the Frenet equations of a curve in $E^3.$

The following theorem serves as the fundamental theorem for the versor field $(C,\xi )$:

Theorem 1 

([9]). If the functions $K_1\left(s\right),K_2\left(s\right),a_1\left(s\right),a_2\left(s\right)$, and $a_3\left(s\right)$, $(a_1^2\left(s\right)+a_2^2\left(s\right)+a_3^2\left(s\right)=1)$ of class $C^{\infty }$ and are given a priori, for $s\in [a,b]$, then there exists a curve $C:[a,b]\to E^3$ with arclength s and a versor field $\stackrel{\_}{\xi }\left(s\right)$, $s\in [a,b]$ such that the functions $a_i\left(s\right)$, $(i=1,2,3),$ $K_1\left(s\right),$ and $K_2\left(s\right)$ are the invariants of $(C,\stackrel{\_}{\xi })$. Any two such versor fields $(C,\stackrel{\_}{\xi })$ differ by a proper Euclidean motion.

We give the definition of ${\stackrel{\_}{\xi }}_i$-helix ($i=1,2,3)$ as follows.

Definition 1 

([15]). Let the curve C with the invariant type Frenet frame $R_F\left(P\left(s\right);{\stackrel{\_}{\xi }}_1\left(s\right),{\stackrel{\_}{\xi }}_2\left(s\right),\right.$ $\left.{\stackrel{\_}{\xi }}_3\left(s\right)\right)$ in M be a helix in $E^3$ with the unit axis $\stackrel{\_}{d}$, that is, $〈\stackrel{\_}{\alpha },\stackrel{\_}{d}〉$ is constant. Then, the curve C is called ${\stackrel{\_}{\xi }}_i$-helix if the versor field ${\stackrel{\_}{\xi }}_i$ makes a constant angle with the same fixed direction $\stackrel{\_}{d}$, where $i=1,2,3$.

3. Slant Helices in Myller Configuration $M(C,\stackrel{\_}{\xi },\pi )$

In this section, we focus on slant helices (or ${\stackrel{\_}{\xi }}_2$-helices) in the Myller configuration $M(C,\stackrel{\_}{\xi },\pi ).$ We provide characterizations for slant helices in this context. Specifically, we explore the geometric properties and conditions that define a curve as a slant helix in the Myller configuration, analyzing its behavior and relationships with other curve types, and we give the characterizations for slant helix in M.

Definition 2. 

Let the curve C with the invariant-type Frenet frame $R_F\left(P\left(s\right);{\stackrel{\_}{\xi }}_1\left(s\right),{\stackrel{\_}{\xi }}_2\left(s\right),{\stackrel{\_}{\xi }}_3\left(s\right)\right)$ in M be a helix in $E^3$ with the unit axis $\stackrel{\_}{d}$, that is, $〈\stackrel{\_}{\alpha },\stackrel{\_}{d}〉$ is constant. The curve C is called a slant helix(or ${\stackrel{\_}{\xi }}_2$-helix) in M if the versor field ${\stackrel{\_}{\xi }}_2$ makes a constant angle with the same fixed unit direction $\stackrel{\_}{d.}$

Theorem 2. 

The curve C in M with Frenet frame $R_F$ and $\left(K_1,K_2\right)\ne (0,0)$ is a slant helix iff the following functions are constant:

$$\begin{array}{ccc}\hfill \sigma & =& cot\theta =\mp {\displaystyle \frac{K_1^2}{{\left(K_1^2+K_2^2\right)}^{\frac{3}{2}}}}{\left({\displaystyle \frac{K_2}{K_1}}\right)}^{\prime },\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill \rho & =& \mp a_1\sin \theta {\displaystyle \frac{K_2}{\sqrt{K_1^2+K_2^2}}}+a_2\cos \theta \mp a_3\sin \theta {\displaystyle \frac{K_1}{\sqrt{K_1^2+K_2^2}}}.\hfill \end{array}$$

(3)

Proof. 

From Definition 2, there exists a constant angle $\theta$ such that $〈{\stackrel{\_}{\xi }}_2,\stackrel{\_}{d}〉=\cos \theta .$ Then, for the axis $\stackrel{\_}{d}$, we can write

$$\stackrel{\_}{d}=x_1{\stackrel{\_}{\xi }}_1+\left(\cos \theta \right){\stackrel{\_}{\xi }}_2+x_3{\stackrel{\_}{\xi }}_3,$$

(4)

where $x_1=x_1\left(s\right)$ and $x_3=x_3\left(s\right)$ are smooth functions of s. Since $\stackrel{\_}{d}$ is constant, differentiating (4) with respect to s yields

$$0=\left(x_1^{\prime }-K_1\cos \theta \right){\stackrel{\_}{\xi }}_1+\left(x_1{K}_1-x_3{K}_2\right){\stackrel{\_}{\xi }}_2+\left(K_2\cos \theta +x_3^{\prime }\right){\stackrel{\_}{\xi }}_3,$$

and we have the system

$$\left\{\begin{array}{c}{x}_1^{\prime }-K_1\cos \theta =0,\\ x_1{K}_1-x_3{K}_2=0,\\ K_2\cos \theta +x_3^{\prime }=0.\end{array}\right.$$

(5)

From the second equation in (5), it follows that $x_1=x_3{\displaystyle \frac{K_2}{K_1}}$. Substituting this into the first and third equations in (5) gives the differential equation

$$x_3^{\prime }\left(1+{\left({\displaystyle \frac{K_2}{K_1}}\right)}^2\right)+x_3{\displaystyle \frac{K_2}{K_1}}{\left({\displaystyle \frac{K_2}{K_1}}\right)}^{\prime }=0.$$

(6)

Considering the transformation $t={\displaystyle \frac{K_2}{K_1}},$ the differential equation given in (6) becomes ${\displaystyle \frac{d{x}_3}{dt}}\left(1+t^2\right)+x_{3}t{t}^{\prime }=0$, which has the solution $x_3=\lambda {\displaystyle \frac{K_1}{\sqrt{K_1^2+K_2^2}}}$, where $\lambda$ is the integration constant. Hence, $x_1=\lambda {\displaystyle \frac{K_2}{\sqrt{K_1^2+K_2^2}}}$. Since $∥\stackrel{\_}{d}∥=1$, from (4), we have $\lambda =\mp \sin \theta .$ Then, (4) becomes

$$\stackrel{\_}{d}=\mp \sin \theta {\displaystyle \frac{K_2}{\sqrt{K_1^2+K_2^2}}}{\stackrel{\_}{\xi }}_1+\left(\cos \theta \right){\stackrel{\_}{\xi }}_2\mp \sin \theta {\displaystyle \frac{K_1}{\sqrt{K_1^2+K_2^2}}}{\stackrel{\_}{\xi }}_3.$$

(7)

From the third equation in (5), it follows that ${\left(\mp \sin \theta {\displaystyle \frac{K_1}{\sqrt{K_1^2+K_2^2}}}\right)}^{\prime }=-\cos \theta K_2.$ Hence, we have that $\sigma =cot\theta =\mp {\displaystyle \frac{K_1^2}{{\left(K_1^2+K_2^2\right)}^{\frac{3}{2}}}}{\left({\displaystyle \frac{K_2}{K_1}}\right)}^{\prime }$ is a constant function. Also, from Definition 2, it follows that $〈\stackrel{\_}{\alpha },\stackrel{\_}{d}〉=\rho$ is constant.

Conversely, let the functions $\sigma$ and $\rho$ given in (2) be constants and $\stackrel{\_}{d}$ be a unit vector defined by

$$\stackrel{\_}{d}=\mp \sin \theta {\displaystyle \frac{K_2}{\sqrt{K_1^2+K_2^2}}}{\stackrel{\_}{\xi }}_1+\left(\cos \theta \right){\stackrel{\_}{\xi }}_2\mp \sin \theta {\displaystyle \frac{K_1}{\sqrt{K_1^2+K_2^2}}}{\stackrel{\_}{\xi }}_3,$$

where $\theta$ is constant. Differentiating the last equality gives

$${\stackrel{\_}{d}}^{\prime }=K_1(\mp \left(\sin \theta \right)\sigma -\cos \theta ){\stackrel{\_}{\xi }}_1+K_2(\pm \left(\sin \theta \right)\sigma +\cos \theta ){\stackrel{\_}{\xi }}_3.$$

Now, substituting (2) in this result, we have ${\stackrel{\_}{d}}^{\prime }=0$, i.e., $\stackrel{\_}{d}$ is a constant vector field and, since $〈\stackrel{\_}{{\xi }_2},\stackrel{\_}{d}〉$ and $〈\stackrel{\_}{\alpha },\stackrel{\_}{d}〉$ are constants, we obtain that C is a slant helix in Myller configuration $M.$ □

From Theorem 2, the following corollary is obtained.

Corollary 1. 

The axis of slant helix C in the Myller configuration M is given by

$$\stackrel{\_}{d}=\mp \sin \theta {\displaystyle \frac{K_2}{\sqrt{K_1^2+K_2^2}}}{\stackrel{\_}{\xi }}_1+\left(\cos \theta \right){\stackrel{\_}{\xi }}_2\mp \sin \theta {\displaystyle \frac{K_1}{\sqrt{K_1^2+K_2^2}}}{\stackrel{\_}{\xi }}_3,$$

where θ is the constant angle defined by $〈\stackrel{\_}{{\xi }_2},\stackrel{\_}{d}〉=\cos \theta .$

4. Darboux Helices in Myller Configuration $\mathbf{M}$($\mathbf{C}$,$\stackrel{\_}{\xi }$,$\pi$)

The alternative frame of a curve is a useful tool to study the properties of the curve in the Euclidean 3-space. This frame is obtained from the Frenet frame of the curve and provides advantages in characterizing certain special curves and surfaces [28,29,30,31]. In this section, we first define the alternative frame of a curve C and provide the geometric interpretations of the alternative curvatures. Next, we define Darboux helices in M and characterize these helices by means of an alternative frame.

Let $(C,\stackrel{\_}{\xi })$ be a versor field with invariant-type Frenet frame $R_F\left(P\left(s\right);{\stackrel{\_}{\xi }}_1\left(s\right),{\stackrel{\_}{\xi }}_2\left(s\right),{\stackrel{\_}{\xi }}_3\left(s\right)\right)$ in the Myller configuration M. The vector $D=K_2{\stackrel{\_}{\xi }}_1+K_1{\stackrel{\_}{\xi }}_3$ is called the Darboux vector field of the Frenet frame $R_F$.

Let us define $\stackrel{\_}{Y}={\displaystyle \frac{{\stackrel{\_}{\xi }}_2^{\prime }}{∥{\stackrel{\_}{\xi }}_2^{\prime }∥}}$ and $\stackrel{\_}{D}={\displaystyle \frac{K_2}{\sqrt{K_1^2+K_2^2}}}{\stackrel{\_}{\xi }}_1+{\displaystyle \frac{K_1}{\sqrt{K_1^2+K_2^2}}}{\stackrel{\_}{\xi }}_3$. Then, $R_A\{P\left(s\right);{\stackrel{\_}{\xi }}_2\left(s\right),\stackrel{\_}{Y}\left(s\right),\stackrel{\_}{D}\left(s\right)$ = ${\stackrel{\_}{\xi }}_2\times \stackrel{\_}{Y}\}$ is an othonormal frame of the versor field $(C,\stackrel{\_}{\xi })$ in M called the alternative Frenet frame (or AF-frame) of $(C,\stackrel{\_}{\xi })$. The moving equations of the AF-frame are as follows:

$${\displaystyle \frac{d\stackrel{\_}{r}\left(s\right)}{ds}}=\stackrel{\_}{\alpha }\left(s\right)=d_1\left(s\right){\stackrel{\_}{\xi }}_2\left(s\right)+d_2\left(s\right)\stackrel{\_}{Y}\left(s\right)+d_3\left(s\right)\stackrel{\_}{D}\left(s\right),$$

(8)

with $d_1^2\left(s\right)+d_2^2\left(s\right)+d_3^2\left(s\right)=1$ and

$$\begin{array}{c}{\stackrel{\_}{\xi }}_2^{\prime }=p\stackrel{\_}{Y},\\ {\stackrel{\_}{Y}}^{\prime }=-p{\stackrel{\_}{\xi }}_2+q\stackrel{\_}{D},\\ {\stackrel{\_}{D}}^{\prime }=-q\stackrel{\_}{Y},\end{array}$$

(9)

where $d_i\left(s\right),(i=1,2,3),p=\sqrt{K_1^2+K_2^2},$ and $q={\displaystyle \frac{K_1^2}{K_1^2+K_2^2}}{\left({\displaystyle \frac{K_2}{K_1}}\right)}^{\prime }$ are invariants and called the alternative curvatures of versor field $(C,\stackrel{\_}{\xi })$.

The geometric interpretations of the functions $d_i\left(s\right),(i=1,2,3)$ can be expressed as follows:

$$d_1\left(s\right)=\cos \sphericalangle (\stackrel{\_}{\alpha },{\stackrel{\_}{\xi }}_2),d_2\left(s\right)=\cos \sphericalangle (\stackrel{\_}{\alpha },\stackrel{\_}{Y}),d_3\left(s\right)=\cos \sphericalangle (\stackrel{\_}{\alpha },\stackrel{\_}{D}).$$

For the geometric interpretations of the invariants $p,q,$ we present the following theorem.

Theorem 3. 

Let us consider a variation of an alternative frame

$R_A\{P\left(s\right);{\stackrel{\_}{\xi }}_2\left(s\right),\stackrel{\_}{Y}\left(s\right),\stackrel{\_}{D}\left(s\right)\}\to R_A^{*}\{P^{*}(s+\Delta s);{\stackrel{\_}{\xi }}_2(s+\Delta s),\stackrel{\_}{Y}(s+\Delta s),\stackrel{\_}{D}(s+\Delta s)\}$

And let ${\phi }_1$ be the oriented angle between the successive versor fields ${\stackrel{\_}{\xi }}_2\left(s\right)$ and ${\phi }_2$ be the oriented angle between the successive versor fields $\stackrel{\_}{D}\left(s\right)$. Alternative curvatures p and q of the versor field $(C,\stackrel{\_}{\xi })$ are given by

$$p=\left|{\displaystyle \frac{d{\phi }_1}{ds}}\right|,q=\left|{\displaystyle \frac{d{\phi }_2}{ds}}\right|,$$

(10)

respectively.

Proof. 

Let ${\phi }_1\left(s\right)$ be the oriented angle between the successive versor fields ${\stackrel{\_}{\xi }}_2\left(s\right)$. Then, the angle function between versor fields ${\stackrel{\_}{\xi }}_2\left(s\right)$ and ${\stackrel{\_}{\xi }}_2(s+\Delta s)$ is defined by $\left|{\phi }_1(s+\Delta s)-{\phi }_1\left(s\right)\right|=h\left(s\right)$. From (9), we have $p\left(s\right)=∥{\stackrel{\_}{\xi }}_2^{\prime }\left(s\right)∥$. Then, we can write

$$\begin{array}{ccc}\hfill p\left(s\right)& =& ∥{\stackrel{\_}{\xi }}_2^{\prime }\left(s\right)∥\hfill \\ & =& \underset{\Delta s\to 0}{\lim }∥{\displaystyle \frac{{\stackrel{\_}{\xi }}_2(s+\Delta s)-{\stackrel{\_}{\xi }}_2\left(s\right)}{\Delta s}}∥\hfill \\ & =& \underset{\Delta s\to 0}{\lim }∥{\displaystyle \frac{{\phi }_1(s+\Delta s)-{\phi }_1\left(s\right)}{\Delta s}}{\displaystyle \frac{{\stackrel{\_}{\xi }}_2(s+\Delta s)-{\stackrel{\_}{\xi }}_2\left(s\right)}{{\phi }_1(s+\Delta s)-{\phi }_1\left(s\right)}}∥\hfill \\ & =& \underset{\Delta s\to 0}{\lim }\left|{\displaystyle \frac{{\phi }_1(s+\Delta s)-{\phi }_1\left(s\right)}{\Delta s}}\right|\underset{\Delta s\to 0}{\lim }∥{\displaystyle \frac{{\stackrel{\_}{\xi }}_2(s+\Delta s)-{\stackrel{\_}{\xi }}_2\left(s\right)}{{\phi }_1(s+\Delta s)-{\phi }_1\left(s\right)}}∥\hfill \\ & =& \left|{\displaystyle \frac{d{\phi }_1}{ds}}\right|\underset{\Delta s\to 0}{\lim }∥{\displaystyle \frac{{\stackrel{\_}{\xi }}_2(s+\Delta s)-{\stackrel{\_}{\xi }}_2\left(s\right)}{{\phi }_1(s+\Delta s)-{\phi }_1\left(s\right)}}∥.\hfill \end{array}$$

(11)

Considering the cosine theorem, we have

$${∥{\stackrel{\_}{\xi }}_2(s+\Delta s)-{\stackrel{\_}{\xi }}_2\left(s\right)∥}^2={∥{\stackrel{\_}{\xi }}_2(s+\Delta s)∥}^2+{∥{\stackrel{\_}{\xi }}_2\left(s\right)∥}^2-2∥{\stackrel{\_}{\xi }}_2(s+\Delta s)∥∥{\stackrel{\_}{\xi }}_2\left(s\right)∥\cos h.$$

(12)

Since ${\stackrel{\_}{\xi }}_2\left(s\right)$ and ${\stackrel{\_}{\xi }}_2(s+\Delta s)$ are unit, (12) becomes

$${∥{\stackrel{\_}{\xi }}_2(s+\Delta s)-{\stackrel{\_}{\xi }}_2\left(s\right)∥}^2=2-2\cos h.$$

By using trigonometric relation $\cos h=1-2{\sin }^2{\displaystyle \frac{h}{2}},$ the last equality gives $∥{\stackrel{\_}{\xi }}_2(s+\Delta s)$ $-{\stackrel{\_}{\xi }}_2\left(s\right)∥=2\sin {\displaystyle \frac{h}{2}}$. Hence,

$$\begin{array}{ccc}\hfill \underset{\Delta s\to 0}{\lim }∥{\displaystyle \frac{{\stackrel{\_}{\xi }}_2(s+\Delta s)-{\stackrel{\_}{\xi }}_2\left(s\right)}{{\phi }_1(s+\Delta s)-{\phi }_1\left(s\right)}}∥& =& \underset{\Delta s\to 0}{\lim }\left|{\displaystyle \frac{1}{{\phi }_1(s+\Delta s)-{\phi }_1\left(s\right)}}\right|∥{\stackrel{\_}{\xi }}_2(s+\Delta s)-{\stackrel{\_}{\xi }}_2\left(s\right)∥\hfill \\ & =& \underset{h\to 0}{\lim }{\displaystyle \frac{1}{h}}\left(2\sin {\displaystyle \frac{h}{2}}\right)\hfill \\ & =& \underset{h\to 0}{\lim }{\displaystyle \frac{\sin (h/2)}{h/2}}\hfill \\ & =& 1.\hfill \end{array}$$

Then, from (11), we have $p=\left|{\displaystyle \frac{d{\phi }_1}{ds}}\right|$. The proof of second equality in (10) can be provided in a similar manner. □

Theorem 4. 

Let $(C,\stackrel{\_}{\xi })$ be a versor field with curvatures $K_1,K_2,$ and alternative curvatures p and q. The relationship between these curvatures are given as follows:

$$K_1\left(s\right)=p\left(s\right)\cos \left(q\left(s\right)ds\right),K_2\left(s\right)=p\left(s\right)\sin \left(q\left(s\right)ds\right),$$

(13)

$$\begin{array}{c}{a}_1\left(s\right)=-d_2\left(s\right)\cos \left(q\left(s\right)ds\right)+d_3\left(s\right)\sin \left(q\left(s\right)ds\right),\\ a_2\left(s\right)=d_1\left(s\right),\\ a_3\left(s\right)=d_2\left(s\right)\sin \left(q\left(s\right)ds\right)+d_3\left(s\right)\cos \left(q\left(s\right)ds\right).\end{array}$$

(14)

Proof. 

Let define the function $\omega \left(s\right)={\displaystyle \frac{K_2}{K_1}}\left(s\right).$ Thus, the alternative curvature q takes the form $q={\displaystyle \frac{{\omega }^{\prime }}{1+{\omega }^2}}$. Integrating the last equality gives $qds=arctan\left(\omega \right)$. Hence, we obtain $\omega =tan\left(qds\right)$. Considering the relation $p=\sqrt{K_1^2+K_2^2}$ and trigonometric relations, we obtained Equalities (13). Now, comparing (1) and (8) and using (13), we have Equalities (14) □

Definition 3. 

Let the curve C with the invariant-type Frenet frame $R_F\left(P\left(s\right);{\stackrel{\_}{\xi }}_1\left(s\right),{\stackrel{\_}{\xi }}_2\left(s\right),{\stackrel{\_}{\xi }}_3\left(s\right)\right)$ in M be a helix in $E^3$ with the unit axis $\stackrel{\_}{l}$, that is, $〈\stackrel{\_}{\alpha },\stackrel{\_}{l}〉$ is constant. Let $R_A\{P\left(s\right);{\stackrel{\_}{\xi }}_2\left(s\right),\stackrel{\_}{Y}\left(s\right),\stackrel{\_}{D}\left(s\right)\}$ denote the AF-frame of C in the Myller configuration M. The curve C is called a Darboux helix in M if the versor field $\stackrel{\_}{D}$ makes a constant angle with the constant versor field $\stackrel{\_}{l.}$

Theorem 5. 

The curve C with AF-frame $R_A$ and $\left(K_1,K_2\right)\ne (0,0)$ in M is a Darboux helix if and only if the following functions are constant:

$$f=\mp {\displaystyle \frac{p}{q}},g=\mp d_1\sin \varphi +d_3{p}^2\cos \varphi .$$

(15)

Proof. 

Let C be a Darboux helix in M. Then, there exists a constant angle $\varphi$ such that $〈\stackrel{\_}{D},\stackrel{\_}{l}〉=\cos \varphi .$ Differentiating the last equality with respect to s and considering (9), we obtain $〈\stackrel{\_}{Y},\stackrel{\_}{l}〉=0$. Hence, we have $\stackrel{\_}{l}\in sp\{{\stackrel{\_}{\xi }}_2,\stackrel{\_}{D}\}$. Now, we can write $\stackrel{\_}{l}=\mp \sin \varphi {\stackrel{\_}{\xi }}_2+\cos \varphi \stackrel{\_}{D}$. Since $\stackrel{\_}{l}$ is a constant versor field, the differentiation of the last equality yields

$$(\mp p\sin \varphi -q\cos \varphi )\stackrel{\_}{Y}=0.$$

Hence, we have that $cot\theta =\mp {\displaystyle \frac{p}{q}}=\mp {\displaystyle \frac{1}{\sigma }}$ is constant. Furthermore, since $\theta +\varphi =\pi /2,$ by considering (13) and (14), we have

$$\begin{array}{ccc}\hfill g& =& 〈\stackrel{\_}{\alpha },\stackrel{\_}{l}〉=a_1\cos \varphi {\displaystyle \frac{K_2}{\sqrt{K_1^2+K_2^2}}}\mp a_2\sin \varphi +a_3\cos \varphi {\displaystyle \frac{K_1}{\sqrt{K_1^2+K_2^2}}}\hfill \\ & =& K_2(d_3{K}_2-d_2{K}_1)\cos \varphi \mp d_1\sin \varphi +K_1(d_2{K}_2+d_3{K}_1)\cos \varphi \hfill \\ & =& \mp d_1\sin \varphi +d_3{p}^2\cos \varphi \hfill \\ & =& \mp \rho ,\hfill \end{array}$$

which finishes the proof. □

From Theorem 5, the following corollaries are obtained.

Corollary 2. 

The curve C in M is a Darboux helix if and only if C is a slant helix.

Corollary 3. 

The axis $\stackrel{\_}{l}$ of a Darboux helix C in terms of Frenet frame $R_F$ is given by

$$\stackrel{\_}{l}=\cos \varphi {\displaystyle \frac{K_2}{\sqrt{K_1^2+K_2^2}}}{\stackrel{\_}{\xi }}_1\mp \sin \varphi {\stackrel{\_}{\xi }}_2+\cos \varphi {\displaystyle \frac{K_1}{\sqrt{K_1^2+K_2^2}}}{\stackrel{\_}{\xi }}_3=\mp \stackrel{\_}{d}.$$

5. Differential Equations Characterizing Slant Helices and Darboux Helices in $\mathit{M}$

In this section, we present general differential equations for a versor field $(C,\stackrel{\_}{\xi })$ in M with respect to both AF-frame $R_A$ and the Frenet-type frame $R_F$. Furthermore, we derive differential equations that characterize helices, slant helices, and Darboux helices in M.

Theorem 6. 

Let $(C,\stackrel{\_}{\xi })$ be a versor field with AF-frame $R_A$ and non-zero alternative curvatures p and q. The versor field ${\stackrel{\_}{\xi }}_2$ satisfies the following differential equation:

$${\stackrel{\_}{\xi }}_2^{\prime \prime \prime }-\left[{\displaystyle \frac{p^{\prime }}{p}}+{\displaystyle \frac{{\left(pq\right)}^{\prime }}{pq}}\right]{\stackrel{\_}{\xi }}_2^{\prime \prime }+\left\{pq{\left[{\left({\displaystyle \frac{1}{p}}\right)}^{\prime }{\displaystyle \frac{1}{q}}\right]}^{\prime }+p^2+q^2\right\}{\stackrel{\_}{\xi }}_2^{\prime }+pq{\left({\displaystyle \frac{p}{q}}\right)}^{\prime }{\stackrel{\_}{\xi }}_2=0.$$

(16)

Proof. 

From the second equation in (9), it follows that

$$\stackrel{\_}{D}={\displaystyle \frac{1}{q}}{\stackrel{\_}{Y}}^{\prime }+{\displaystyle \frac{p}{q}}{\stackrel{\_}{\xi }}_2,$$

(17)

and, from the first equation in (9), we obtain $\stackrel{\_}{Y}={\displaystyle \frac{1}{p}}{\stackrel{\_}{\xi }}_2^{\prime }$. Considering the last equality and third equation in (9), we obtain

$${\stackrel{\_}{D}}^{\prime }=-{\displaystyle \frac{q}{p}}{\stackrel{\_}{\xi }}_2^{\prime }.$$

(18)

Differentiating $\stackrel{\_}{Y}={\displaystyle \frac{1}{p}}{\stackrel{\_}{\xi }}_2^{\prime }$, we have

$${\stackrel{\_}{Y}}^{\prime }={\left({\displaystyle \frac{1}{p}}\right)}^{\prime }{\stackrel{\_}{\xi }}_2^{\prime }+{\displaystyle \frac{1}{p}}{\stackrel{\_}{\xi }}_2^{\prime \prime }.$$

(19)

Writing (19) in (17) gives

$$\stackrel{\_}{D}={\displaystyle \frac{1}{q}}{\left({\displaystyle \frac{1}{p}}\right)}^{\prime }{\stackrel{\_}{\xi }}_2^{\prime }+{\displaystyle \frac{1}{q}}{\displaystyle \frac{1}{p}}{\stackrel{\_}{\xi }}_2^{\prime \prime }+{\displaystyle \frac{p}{q}}{\stackrel{\_}{\xi }}_2.$$

By differentiating the last equality and taking into account (18), we have (16). □

Corollary 4. 

The curve C with AF-frame $R_A$ and non-zero curvatures $p,q$ is a slant helix (or Darboux helix) iff $g=\mp d_1\sin \varphi +d_3{p}^2\cos \varphi$ is constant and the versor field ${\stackrel{\_}{\xi }}_2$ satisfies the following differential equation:

$${\stackrel{\_}{\xi }}_2^{\prime \prime \prime }-\left[{\displaystyle \frac{p^{\prime }}{p}}+{\displaystyle \frac{{\left(pq\right)}^{\prime }}{pq}}\right]{\stackrel{\_}{\xi }}_2^{\prime \prime }+\left\{pq{\left[{\left({\displaystyle \frac{1}{p}}\right)}^{\prime }{\displaystyle \frac{1}{q}}\right]}^{\prime }+p^2+q^2\right\}{\stackrel{\_}{\xi }}_2^{\prime }=0.$$

(20)

Proof. 

From Theorem 5, we have that the curve C is a slant helix (or Darboux helix) if and only if ${\displaystyle \frac{p}{q}}$ and g are constants. By applying this to (16), (20) is obtained. □

Theorem 7. 

Let $(C,\stackrel{\_}{\xi })$ be a versor field with AF-frame $R_A$ and non-zero alternative curvatures $p,q$. The versor field $\stackrel{\_}{Y}$ satisfies the following differential equation:

$${\stackrel{\_}{Y}}^{\prime \prime \prime }+{\displaystyle \frac{1}{{\lambda }_1}}\left({\lambda }_1^{\prime }-{\lambda }_2\right){\stackrel{\_}{Y}}^{\prime \prime }+{\displaystyle \frac{1}{{\lambda }_1}}\left({\lambda }_3-{\lambda }_2^{\prime }\right){\stackrel{\_}{Y}}^{\prime }+{\displaystyle \frac{1}{{\lambda }_1}}\left({\lambda }_3^{\prime }-p\right)\stackrel{\_}{Y}=0,$$

where ${\lambda }_1={\displaystyle \frac{q}{q^{\prime }p-q{p}^{\prime }}},$ ${\lambda }_2={\displaystyle \frac{1}{p}}\left(1+p^{\prime }{\lambda }_1\right)$, and ${\lambda }_3=\left(p^2+q^2\right){\lambda }_1.$

Proof. 

From the second equality in (9), we have

$${\stackrel{\_}{\xi }}_2=-{\displaystyle \frac{1}{p}}{\stackrel{\_}{Y}}^{\prime }+{\displaystyle \frac{q}{p}}\stackrel{\_}{D}.$$

(21)

Differentiating (21) and considering the first and third equalities in (9), it follows that

$$\stackrel{\_}{D}={\displaystyle \frac{p^2}{q^{\prime }p-p^{\prime }q}}\left[{\displaystyle \frac{1}{p}}{\stackrel{\_}{Y}}^{\prime \prime }+{\left({\displaystyle \frac{1}{p}}\right)}^{\prime }{\stackrel{\_}{Y}}^{\prime }+{\displaystyle \frac{p^2+q^2}{p}}\stackrel{\_}{Y}\right].$$

(22)

Writing (22) in (21), we have

$${\stackrel{\_}{\xi }}_2={\displaystyle \frac{q}{q^{\prime }p-p^{\prime }q}}{\stackrel{\_}{Y}}^{\prime \prime }+\left[{\displaystyle \frac{pq}{q^{\prime }p-p^{\prime }q}}{\left({\displaystyle \frac{1}{p}}\right)}^{\prime }-{\displaystyle \frac{1}{p}}\right]{\stackrel{\_}{Y}}^{\prime }+{\displaystyle \frac{q(p^2+q^2)}{q^{\prime }p-p^{\prime }q}}\stackrel{\_}{Y}.$$

(23)

Now, differentiating (23), we obtain the desired equation. □

Corollary 5. 

The curve C with AF-frame $R_A$ and non-zero curvatures $p,q$ is a slant helix (or Darboux helix) iff $g=\mp d_1\sin \varphi +d_3{p}^2\cos \varphi$ is constant and the versor field $\stackrel{\_}{Y}$ satisfies the following differential equation

$${\stackrel{\_}{Y}}^{\prime \prime }+q{\left({\displaystyle \frac{1}{q}}\right)}^{\prime }{\stackrel{\_}{Y}}^{\prime }+(p^2+q^2)\stackrel{\_}{Y}=0.$$

(24)

Proof. 

From the second equality in (9), it follows $\stackrel{\_}{D}={\displaystyle \frac{1}{q}}{\stackrel{\_}{Y}}^{\prime }+{\displaystyle \frac{p}{q}}{\stackrel{\_}{\xi }}_2$ and differentiating that gives

$$\stackrel{\_}{D^{\prime }}={\left({\displaystyle \frac{1}{q}}\right)}^{\prime }{\stackrel{\_}{Y}}^{\prime }+{\displaystyle \frac{1}{q}}{\stackrel{\_}{Y}}^{\prime \prime }+{\left({\displaystyle \frac{p}{q}}\right)}^{\prime }{\stackrel{\_}{\xi }}_2+{\displaystyle \frac{p}{q}}{\stackrel{\_}{\xi }}_2^{\prime }.$$

By taking into account the first and third equations in (9), the last equality becomes

$${\displaystyle \frac{1}{q}}{\stackrel{\_}{Y}}^{\prime \prime }+{\left({\displaystyle \frac{1}{q}}\right)}^{\prime }{\stackrel{\_}{Y}}^{\prime }+\left({\displaystyle \frac{p^2+q^2}{q}}\right)\stackrel{\_}{Y}+{\left({\displaystyle \frac{p}{q}}\right)}^{\prime }{\stackrel{\_}{\xi }}_2=0.$$

(25)

From (25), C is a slant helix (or Darboux helix) if and only if ${\stackrel{\_}{Y}}^{\prime \prime }+q{\left({\displaystyle \frac{1}{q}}\right)}^{\prime }{\stackrel{\_}{Y}}^{\prime }+(p^2+q^2)\stackrel{\_}{Y}=0$ holds. □

Theorem 8. 

Let $(C,\stackrel{\_}{\xi })$ be a versor field with AF-frame $R_A$ and non-zero alternative curvatures $p,q$. The versor field $\stackrel{\_}{D}$ satisfies the following differential equation:

$${\stackrel{\_}{D}}^{\prime \prime \prime }-\left[{\displaystyle \frac{{\left(pq\right)}^{\prime }}{pq}}+{\displaystyle \frac{q^{\prime }}{q}}\right]{\stackrel{\_}{D}}^{\prime \prime }+\left\{pq{\left[{\displaystyle \frac{1}{p}}{\left({\displaystyle \frac{1}{q}}\right)}^{\prime }\right]}^{\prime }+p^2+q^2\right\}{\stackrel{\_}{D}}^{\prime }+pq{\left({\displaystyle \frac{q}{p}}\right)}^{\prime }\stackrel{\_}{D}=0.$$

(26)

Proof. 

From the third equation in (9), we obtain $\stackrel{\_}{Y}=-{\displaystyle \frac{1}{q}}\stackrel{\_}{D^{\prime }}$, and differentiating this gives

$$\stackrel{\_}{Y^{\prime }}={\left(-{\displaystyle \frac{1}{q}}\right)}^{\prime }\stackrel{\_}{D^{\prime }}+\left(-{\displaystyle \frac{1}{q}}\right)\stackrel{\_}{D^{\prime \prime }.}$$

Writing that in the second equation in (9), it follows that

$${\stackrel{\_}{\xi }}_2={\displaystyle \frac{1}{pq}}{\stackrel{\_}{D}}^{\prime \prime }+{\displaystyle \frac{1}{p}}{\left({\displaystyle \frac{1}{q}}\right)}^{\prime }{\stackrel{\_}{D}}^{\prime }+{\displaystyle \frac{q}{p}}\stackrel{\_}{D}.$$

Differentiating the last equality gives

$${\stackrel{\_}{\xi }}_2^{\prime }={\displaystyle \frac{1}{pq}}{\stackrel{\_}{D}}^{\prime \prime \prime }+\left[{\left({\displaystyle \frac{1}{pq}}\right)}^{\prime }+{\displaystyle \frac{1}{p}}{\left({\displaystyle \frac{1}{q}}\right)}^{\prime }\right]{\stackrel{\_}{D}}^{\prime \prime }\left\{{\left[{\displaystyle \frac{1}{p}}{\left({\displaystyle \frac{1}{q}}\right)}^{\prime }\right]}^{\prime }+{\displaystyle \frac{q}{p}}\right\}{\stackrel{\_}{D}}^{\prime }+{\left({\displaystyle \frac{q}{p}}\right)}^{\prime }\stackrel{\_}{D}.$$

(27)

Writing $\stackrel{\_}{Y}=-{\displaystyle \frac{1}{q}}\stackrel{\_}{D^{\prime }}$ in the first equation in (9), we have ${\stackrel{\_}{\xi }}_2^{\prime }=-{\displaystyle \frac{p}{q}}{\stackrel{\_}{D}}^{\prime }$. Considering this in (27), we have (26). □

Corollary 6. 

The curve C with AF-frame $R_A$ and non-zero curvatures $p,q$ is a slant helix (or Darboux helix) iff $g=\mp d_1\sin \varphi +d_3{p}^2\cos \varphi$ is constant and the versor field $\stackrel{\_}{D}$ satisfies the following differential equation:

$${\stackrel{\_}{D}}^{\prime \prime \prime }-\left[{\displaystyle \frac{{\left(pq\right)}^{\prime }}{pq}}+{\displaystyle \frac{q^{\prime }}{q}}\right]{\stackrel{\_}{D}}^{\prime \prime }+\left\{pq{\left[{\displaystyle \frac{1}{p}}{\left({\displaystyle \frac{1}{q}}\right)}^{\prime }\right]}^{\prime }+p^2+q^2\right\}{\stackrel{\_}{D}}^{\prime }=0.$$

(28)

Proof. 

The proof can be clearly established based on the assertions made in Theorem 9. □

In Theorem 6, we present the differential equation of a curve C in M with respect to versor field ${\stackrel{\_}{\xi }}_2.$ In the following theorems, we provide the differential equations of a curve C in M with respect to versor fields ${\stackrel{\_}{\xi }}_1$ and ${\stackrel{\_}{\xi }}_3.$ The proofs of these theorems can be derived in a manner similar to that described above.

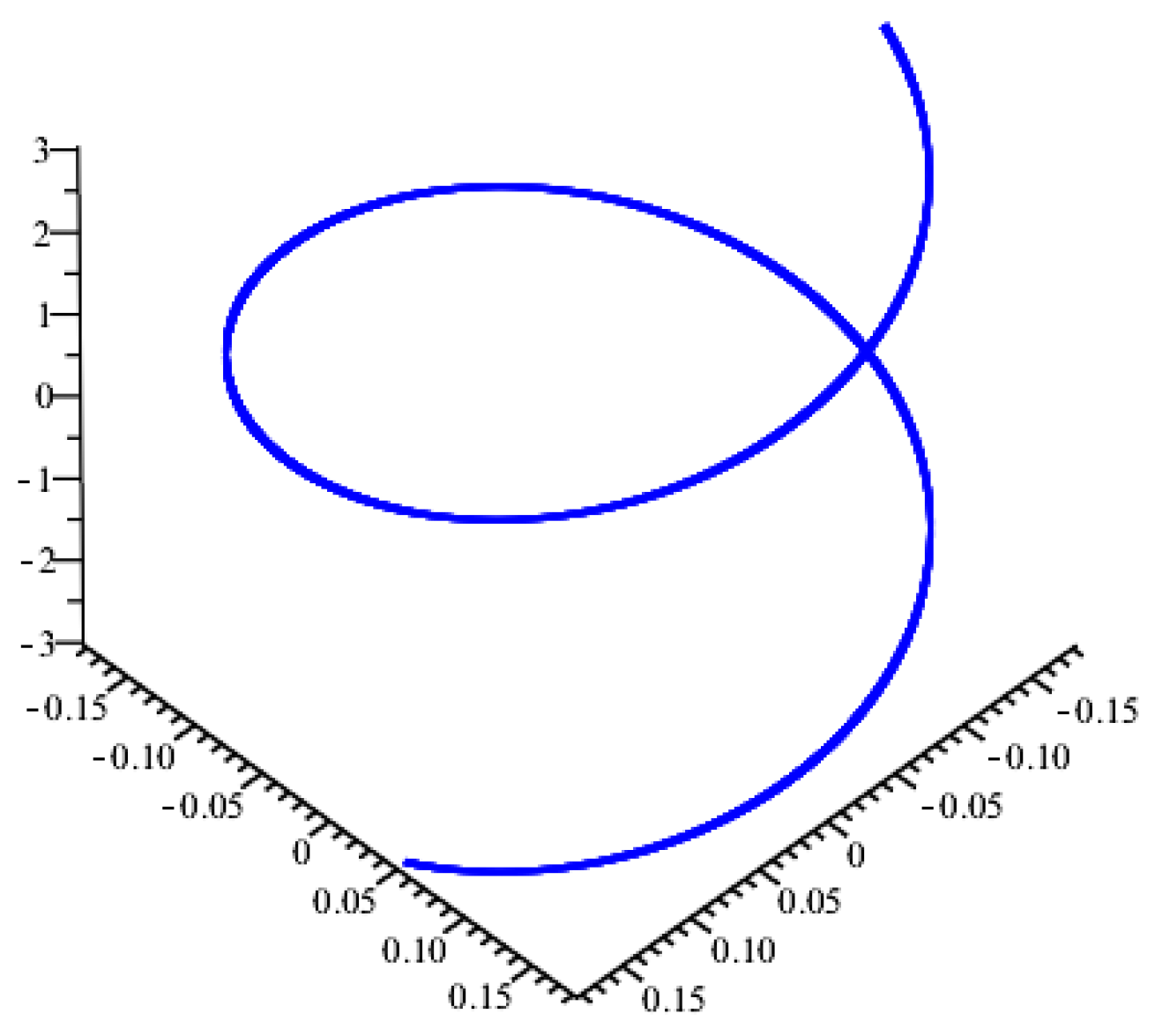
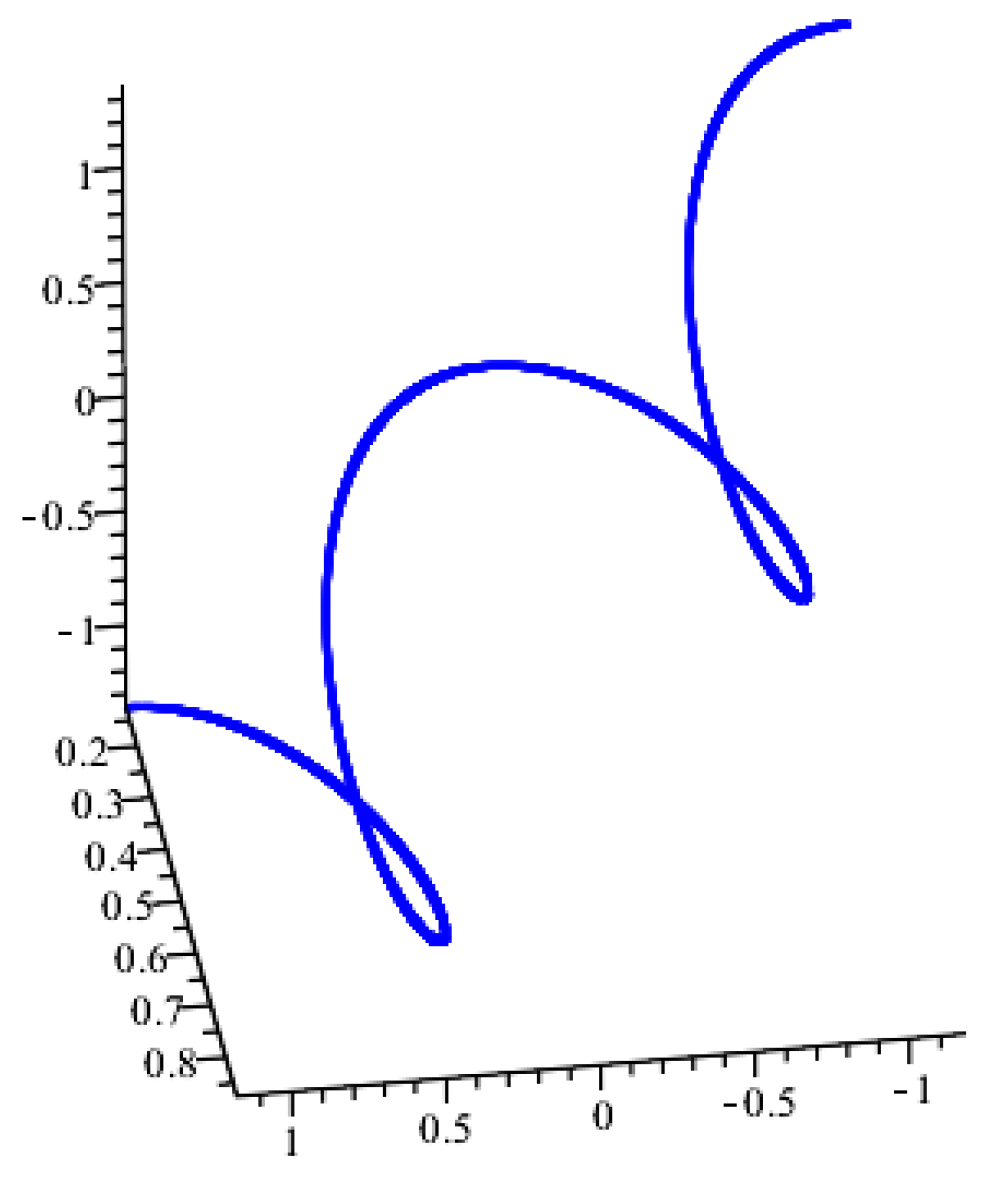
Theorem 9. 

The versor field ${\stackrel{\_}{\xi }}_1$ of the versor field $(C,\stackrel{\_}{\xi })$ with Frenet frame $R_F$ and non-zero curvatures $K_1,K_2$ satisfies the following differential equation:

$$\begin{array}{c}{\stackrel{\_}{\xi }}_1^{\prime \prime \prime }-\left[{\displaystyle \frac{{\left(K_1{K}_2\right)}^{\prime }}{K_1{K}_2}}+{\displaystyle \frac{K_1^{\prime }}{K_1}}\right]{\stackrel{\_}{\xi }}_1^{\prime \prime }\\ +\left\{K_1{K}_2{\left[{\displaystyle \frac{1}{K_2}}{\left({\displaystyle \frac{1}{K_1}}\right)}^{\prime }\right]}^{\prime }+K_1^2+K_2^2\right\}{\stackrel{\_}{\xi }}_1^{\prime }+K_1{K}_2{\left({\displaystyle \frac{K_1}{K_2}}\right)}^{\prime }{\stackrel{\_}{\xi }}_1=0.\end{array}$$

(29)

Theorem 10. 

The versor field ${\stackrel{\_}{\xi }}_2$ of the versor field $(C,\stackrel{\_}{\xi })$ with Frenet frame $R_F$ and non-zero curvatures $K_1,K_2$ satisfies the following differential equation:

$${\stackrel{\_}{\xi }}_2^{\prime \prime \prime }+{\displaystyle \frac{1}{{\rho }_1}}\left({\rho }_1^{\prime }-{\rho }_2\right){\stackrel{\_}{\xi }}_2^{\prime \prime }+{\displaystyle \frac{1}{{\rho }_1}}\left({\rho }_3-{\rho }_2^{\prime }\right){\stackrel{\_}{\xi }}_2^{\prime }+{\displaystyle \frac{1}{{\rho }_1}}\left({\rho }_3^{\prime }-K_1\right){\stackrel{\_}{\xi }}_2=0,$$

(30)

where ${\rho }_1={\displaystyle \frac{K_2}{K_2^{\prime }{K}_1-K_2{K}_1^{\prime }}},$ ${\rho }_2={\displaystyle \frac{1}{K_1}}\left(1+K_1^{\prime }{\rho }_1\right)$ and ${\rho }_3=\left(K_1^2+K_2^2\right){\rho }_1.$

Theorem 11. 

The versor field ${\stackrel{\_}{\xi }}_3$ of the versor field $(C,\stackrel{\_}{\xi })$ with Frenet frame $R_F$ and non-zero curvatures $K_1,K_2$ satisfies the following differential equation:

$$\begin{array}{c}{\stackrel{\_}{\xi }}_3^{\prime \prime \prime }-\left[{\displaystyle \frac{{\left(K_1{K}_2\right)}^{\prime }}{K_1{K}_2}}+{\displaystyle \frac{K_2^{\prime }}{K_2}}\right]{\stackrel{\_}{\xi }}_3^{\prime \prime }\\ +\left\{K_1{K}_2{\left[{\displaystyle \frac{1}{K_1}}{\left({\displaystyle \frac{1}{K_2}}\right)}^{\prime }\right]}^{\prime }+K_1^2+K_2^2\right\}{\stackrel{\_}{\xi }}_3^{\prime }+K_1{K}_2{\left({\displaystyle \frac{K_2}{K_1}}\right)}^{\prime }{\stackrel{\_}{\xi }}_3=0.\end{array}$$

(31)

Example 1. 

Let us consider the versor fields

$$\begin{array}{ccc}\hfill {\stackrel{\_}{\xi }}_1& =& \left(\sin \left(\sqrt{2}s\right)\cos \left(s\right)-{\displaystyle \frac{\sqrt{2}}{2}}\sin \left(s\right)\cos \left(\sqrt{2}s\right),-\cos \left(\sqrt{2}s\right)\cos \left(s\right)-{\displaystyle \frac{\sqrt{2}}{2}}\sin \left(\sqrt{2}s\right)\sin \left(s\right),{\displaystyle \frac{\sqrt{2}}{2}}\sin \left(s\right)\right),\hfill \\ \hfill {\stackrel{\_}{\xi }}_2& =& \left({\displaystyle \frac{\sqrt{2}}{2}}\cos \left(\sqrt{2}s\right),{\displaystyle \frac{\sqrt{2}}{2}}\sin \left(\sqrt{2}s\right),{\displaystyle \frac{\sqrt{2}}{2}}\right),\hfill \\ \hfill {\stackrel{\_}{\xi }}_3& =& \left(-{\displaystyle \frac{\sqrt{2}}{2}}\cos \left(\sqrt{2}s\right)\cos \left(s\right)-\sin \left(\sqrt{2}s\right)\sin \left(s\right),-{\displaystyle \frac{\sqrt{2}}{2}}\sin \left(\sqrt{2}s\right)\cos \left(s\right)+\sin \left(s\right)\cos \left(\sqrt{2}s\right),{\displaystyle \frac{\sqrt{2}}{2}}\cos \left(s\right)\right).\hfill \end{array}$$

The curvatures $K_1$ and $K_2$ are computed as $K_1\left(s\right)=\cos \left(s\right),$ $K_2\left(s\right)=\sin \left(s\right),$ which gives $p=q=1.$ Then, we have $\sigma =cot\theta =\mp 1$. This results in $\theta ={\displaystyle \frac{3\pi }{4}}$ or $\theta ={\displaystyle \frac{\pi }{4}}.$ By choosing $\theta ={\displaystyle \frac{\pi }{4}},$ $a_1=-\cos \left(s\right)$, $a_2=0,$ and $a_3=\sin \left(s\right),$ we obtain $\rho =0,$ i.e., σ and ρ are constants. Then, the curve $C_1$ given by the parametric form $r_1\left(s\right)=\left({\displaystyle \frac{\sqrt{2}}{2}}\cos \left(\sqrt{2}s\right),s,{\displaystyle \frac{\sqrt{2}}{2}}\sin \left(\sqrt{2}s\right),0\right)$ is a slant helix in M (Figure 1). If we choose $\theta ={\displaystyle \frac{\pi }{4}},$ $a_1={\displaystyle \frac{1}{2}}\sin \left(s\right)$, $a_2={\displaystyle \frac{\sqrt{3}}{2}},$ and $a_3={\displaystyle \frac{1}{2}}\cos \left(s\right),$ it follows that $\rho ={\displaystyle \frac{1+\sqrt{3}}{2}}$, meaning that both σ and ρ are constants. Consequently, the curve $C_2$ given by the parametrization $r_2\left(s\right)=\left({\displaystyle \frac{\sqrt{3}-1}{4}}\sin \left(\sqrt{2}s\right),-{\displaystyle \frac{\sqrt{3}-1}{4}}\cos \left(\sqrt{2}s\right),{\displaystyle \frac{\sqrt{2}(\sqrt{3}+1)}{4}}s\right)$ is a slant helix in M (Figure 2). Both curves $C_1$ and $C_2$ are also Darboux helices in M and they satisfy the differential Equations (20), (24) and (28).

Example 2. 

Let us consider the versor fields

$$\begin{array}{ccc}\hfill {\stackrel{\_}{\xi }}_1& =& \left({\displaystyle \frac{1}{4}}\sin \left(3s\right)+{\displaystyle \frac{3}{4}}\sin \left(s\right),-{\cos }^3\left(s\right),-{\displaystyle \frac{\sqrt{3}}{2}}\sin \left(s\right)\right),\hfill \\ \hfill {\stackrel{\_}{\xi }}_2& =& \left({\displaystyle \frac{\sqrt{3}}{4}}\left(1+{\displaystyle \frac{\cos \left(3s\right)}{\cos \left(s\right)}}\right),\sqrt{3}\sin \left(s\right)\cos \left(s\right),-{\displaystyle \frac{1}{2}}\right),\hfill \\ \hfill {\stackrel{\_}{\xi }}_3& =& \left(-{\displaystyle \frac{1}{2}}\cos \left(s\right)\left(2{\cos }^2\left(s\right)-3\right),{\sin }^3\left(s\right),{\displaystyle \frac{\sqrt{3}}{2}}\cos \left(s\right)\right).\hfill \end{array}$$

The curvatures $K_1$ and $K_2$ are computed as $K_1\left(s\right)=\sqrt{3}\cos \left(s\right),$ $K_2\left(s\right)=-\sqrt{3}\sin \left(s\right),$ which gives $p=\sqrt{3},q=-1.$ Then, we have $\sigma =cot\theta =\pm {\displaystyle \frac{\sqrt{3}}{3}}$. This results in $\theta ={\displaystyle \frac{\pi }{3}}$ or $\theta ={\displaystyle \frac{2\pi }{3}}.$ By choosing $\theta ={\displaystyle \frac{\pi }{3}},$ $a_1=\sin \left(s\right)$, $a_2=0,$ and $a_3=\cos \left(s\right),$ we obtain $\rho =-{\displaystyle \frac{\sqrt{3}}{2}},$ i.e., σ and ρ are constants. Then, the curve $C_3$ given by the parametric form

$$r_1\left(s\right)=\left(-{\displaystyle \frac{1}{2}}\sin \left(s\right){\cos }^3\left(s\right)+{\displaystyle \frac{1}{4}}\sin \left(s\right)\cos \left(s\right)+{\displaystyle \frac{3s}{4}},{\displaystyle \frac{1}{2}}{\cos }^4\left(s\right)-{\displaystyle \frac{1}{2}}{\cos }^2\left(s\right)+{\displaystyle \frac{1}{4}},{\displaystyle \frac{\sqrt{3}}{2}}\sin \left(s\right)\cos \left(s\right)\right)$$

is a slant helix in M (Figure 3). If we choose $\theta ={\displaystyle \frac{\pi }{3}},$ $a_1={\displaystyle \frac{1}{2}}\sin \left(s\right)$, $a_2={\displaystyle \frac{\sqrt{3}}{2}},$ and $a_3={\displaystyle \frac{1}{2}}\cos \left(s\right),$ it follows that $\rho =0$, meaning that both σ and ρ are constants. Consequently, the curve $C_4$ given by the parametrization

$$r_2\left(s\right)=\left(-{\displaystyle \frac{1}{4}}\sin \left(s\right){\cos }^3\left(s\right)+{\displaystyle \frac{7}{8}}\sin \left(s\right)\cos \left(s\right)+{\displaystyle \frac{3}{8}}s,{\displaystyle \frac{1}{4}}{\cos }^4\left(s\right)-{\cos }^2\left(s\right)+{\displaystyle \frac{7}{8}},{\displaystyle \frac{\sqrt{3}}{4}}(\sin \left(s\right)\cos \left(s\right)-s)\right)$$

is a slant helix in M (Figure 4). Both curves $C_3$ and $C_4$ are also Darboux helices in M and they satisfy the differential Equations (20), (24) and (28).

6. Conclusions

Slant helices and Darboux helices in the Myller configuration M are introduced and studied. It is shown that a curve C in M is a slant helix if and only if it is also a Darboux helix in M. Moreover, the alternative frame of a curve C in M is introduced, and geometric interpretations of alternative curvatures are provided. Subsequently, general differential equations for a curve C in M are derived with respect to both the alternative frame $R_A$ and the Frenet-type frame $R_F$. Finally, differential equations characterizing helices, slant helices, and Darboux helices in M are presented.