Multiple Solutions of Fractional Kazdan–Warner Equation for Negative Case on Finite Graphs
Abstract
1. Introduction
2. Preparation
- (i)
- is bijective;
- (ii)
- if , then .
3. Proof of Theorem 1
4. Proof of Theorem 2
4.1. Multiplicity When
4.2. Solvability When
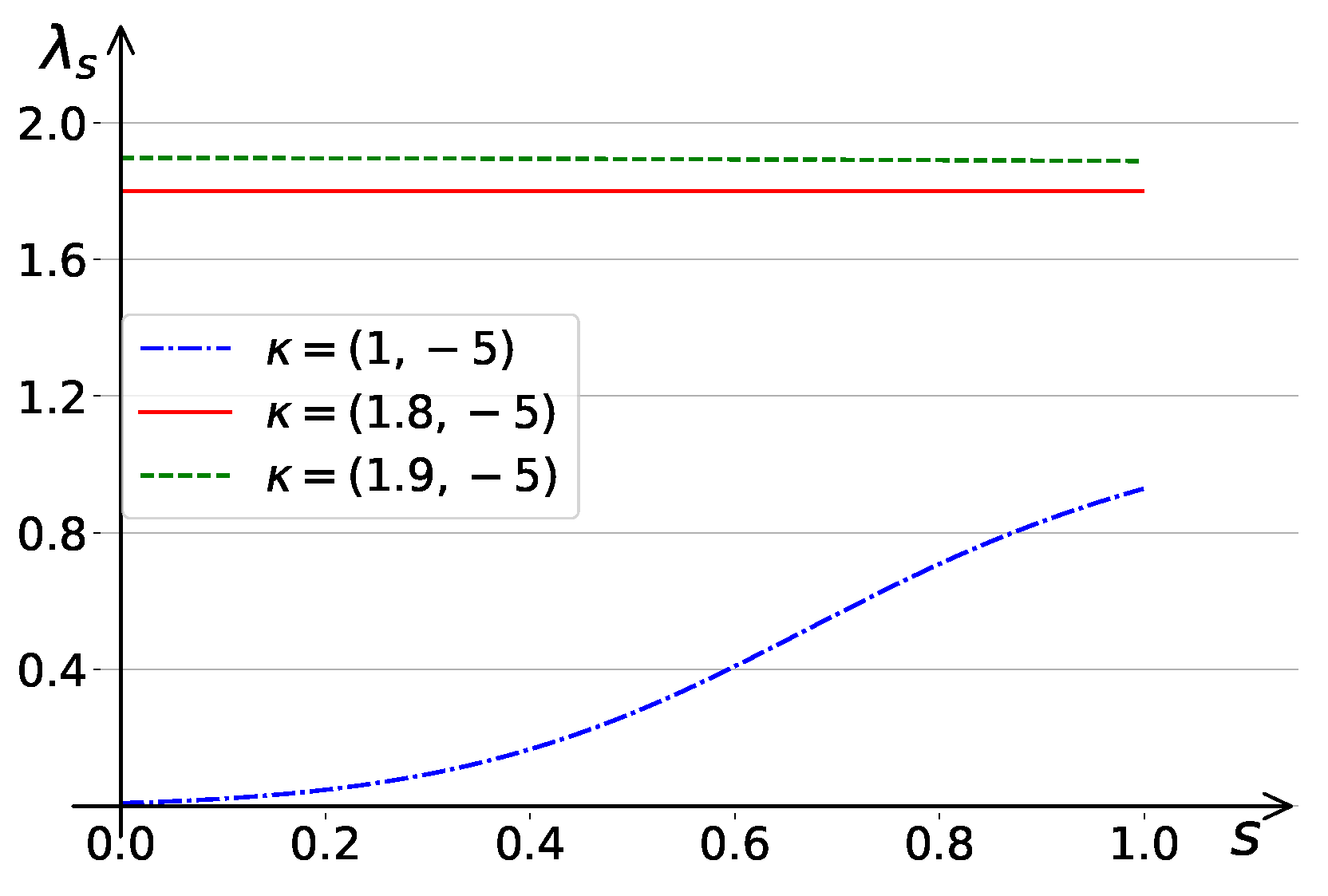
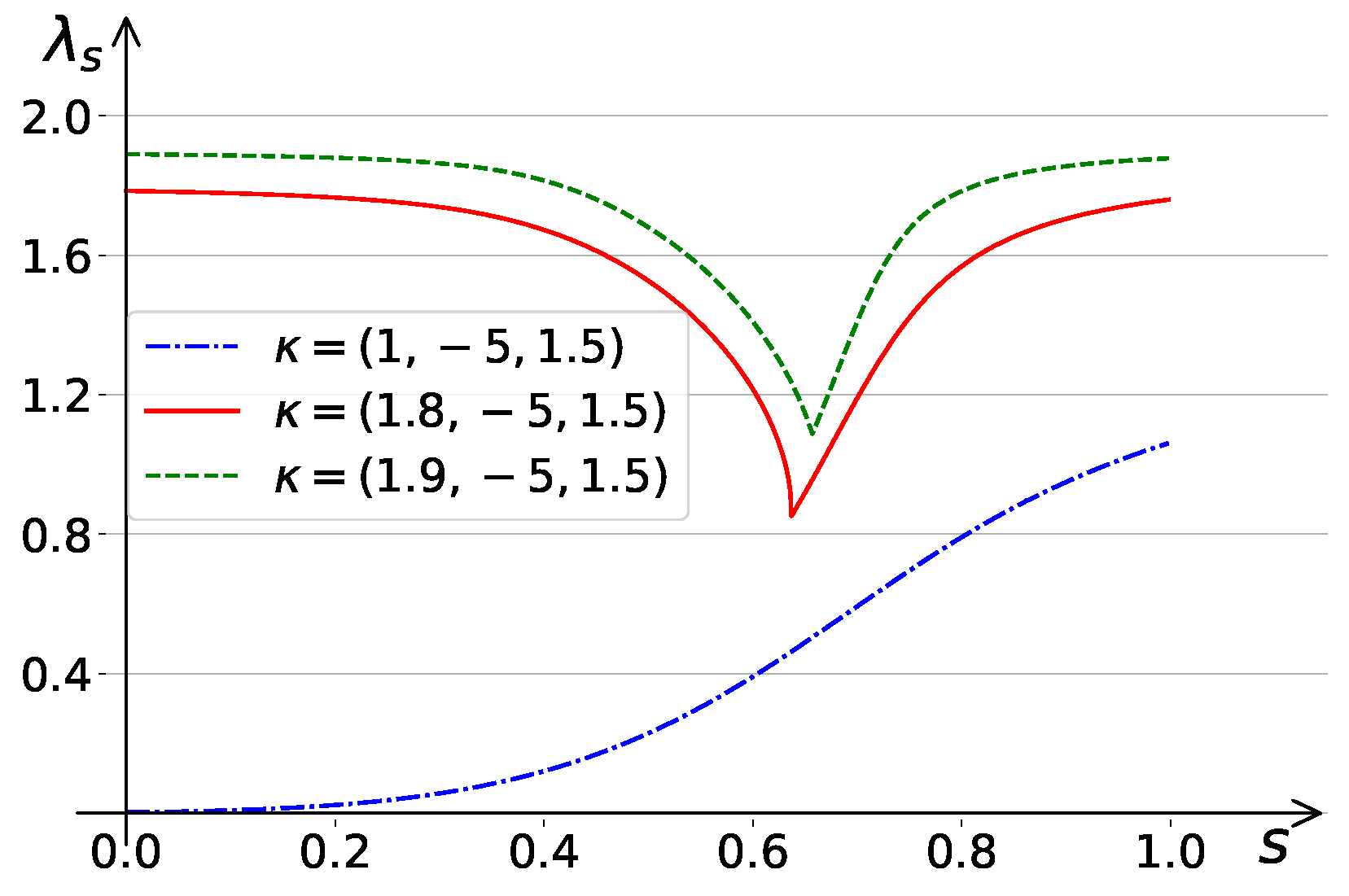
5. Experimental Results
5.1. Experimental Setting
5.2. Results
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kazdan, J.; Warner, F. Curvature functions for compact 2-manifolds. Ann. Math. 1974, 99, 14–47. [Google Scholar] [CrossRef]
- Kazdan, J.; Warner, F. Curvature functions for open 2-manifolds. Ann. Math. 1974, 99, 203–219. [Google Scholar] [CrossRef]
- Chen, W.; Li, C. Gaussian curvature on singular surfaces. J. Geom. Anal. 1993, 3, 315–334. [Google Scholar] [CrossRef]
- Ding, W.; Jost, J.; Li, J.; Wang, G. The differential equation Δu = 8π − 8πheu on a compact Riemann Surface. Asian J. Math. 1997, 1, 230–248. [Google Scholar] [CrossRef]
- Ding, W.; Liu, J. A note on the problem of prescribing Gaussian curvature on surfaces. Trans. Amer. Math. Soc. 1995, 347, 1059–1066. [Google Scholar] [CrossRef]
- Borer, F.; Galimberti, L.; Struwe, M. “Large” conformal metrics of prescribed Gauss curvature on surfaces of higher genus. Comment. Math. Helv. 2015, 90, 407–428. [Google Scholar] [CrossRef]
- Struwe, M. The existence of surfaces of constant mean curvature with free boundaries. Acta Math. 1988, 160, 19–64. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, X. Prescribing Gaussian curvature on closed Riemann surface with conical singularity in the negative case. Ann. Acad. Sci. Fenn. Math. 2019, 44, 167–181. [Google Scholar] [CrossRef]
- Grigor, A.; Lin, Y.; Yang, Y. Kazdan-Warner equation on graph. Calc. Var. Partial Differ. Equ. 2016, 55, 92. [Google Scholar] [CrossRef]
- Ge, H. Kazdan-Warner equation on graph in the negative case. J. Math. Anal. Appl. 2017, 453, 1022–1027. [Google Scholar] [CrossRef]
- Ge, H. The p-th Kazdan-Warner equation on graphs. Commun. Contemp. Math. 2020, 22, 1950052. [Google Scholar] [CrossRef]
- Zhang, X.; Chang, Y. p-th Kazdan-Warner equation on graph in the negative case. J. Math. Anal. Appl. 2018, 466, 400–407. [Google Scholar] [CrossRef]
- Ge, H.; Jiang, W. Kazdan-Warner equation on infinite graphs. J. Korean Math. Soc. 2018, 55, 1091–1101. [Google Scholar]
- Keller, M.; Schwarz, M. The Kazdan-Warner equation on canonically compactifiable graphs. Calc. Var. Partial Differ. Equ. 2018, 57, 70. [Google Scholar] [CrossRef]
- Sun, L.; Wang, L. Brouwer degree for Kazdan-Warner equations on a connected finite graph. Adv. Math. 2022, 404, 108422. [Google Scholar] [CrossRef]
- Liu, S.; Yang, Y. Multiple solutions of Kazdan-Warner equation on graphs in the negative case. Calc. Var. Partial Differ. Equ. 2020, 59, 164. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Y. Topological degree for Kazdan-Warner equation in the negative case on finite graph. Ann. Glob. Anal. Geom. 2024, 65, 29. [Google Scholar] [CrossRef]
- Grigor, A.; Lin, Y.; Yang, Y. Yamabe type equations on graphs. J. Differ. Equ. 2016, 261, 4924–4943. [Google Scholar] [CrossRef]
- Grigor, A.; Lin, Y.; Yang, Y. Existence of positive solutions to some nonlinear equations on locally finite graphs. Sci. China Math. 2017, 60, 1311–1324. [Google Scholar] [CrossRef]
- Han, X.; Shao, M. p-Laplacian equations on locally finite graphs. Acta Math. Sin. (Engl. Ser.) 2021, 37, 1645–1678. [Google Scholar] [CrossRef]
- Hou, S.; Sun, J. Existence of solutions to Chern-Simons-Higgs equations on graphs. Calc. Var. Partial Differ. Equ. 2022, 61, 139. [Google Scholar] [CrossRef]
- Hua, B.; Wang, L. Dirichlet p-Laplacian eigenvalues and Cheeger constants on symmetric graphs. Adv. Math. 2020, 364, 106997. [Google Scholar] [CrossRef]
- Huang, H.; Wang, J.; Yang, W. Mean field equation and relativistic Abelian Chern-Simons model on finite graphs. J. Funct. Anal. 2021, 281, 109218. [Google Scholar] [CrossRef]
- Li, J.; Sun, L.; Yang, Y. Topological degree for Chern-Simons Higgs models on finite graphs. arXiv 2023, arXiv:2309.12024v1. [Google Scholar] [CrossRef]
- Riesz, M. L’intégrale de Riemann-Liouville et le problème de Cauchy pour l’équation des ondes. Bull. Soc. Math. Fr. 1939, 67, 153–170. [Google Scholar] [CrossRef]
- Biler, P.; Karch, G.; Woyczyński, W. Critical nonlinearity exponent and self-similar asymptotics for Lévy conservation laws. Ann. Inst. Henri Poincarè C Anal. Non Linéaire 2001, 18, 613–637. [Google Scholar]
- Caffarelli, L.; Valdinoci, E. Uniform estimates and limiting arguments for nonlocal minimal surfaces. Calc. Var. Partial Differ. Equ. 2011, 41, 203–240. [Google Scholar] [CrossRef]
- Iomin, A. Fractional Schrödinger equation in gravitational optics. Mod. Phys. Lett. A 2021, 36, 2140003. [Google Scholar] [CrossRef]
- Savin, O.; Valdinoci, E. Elliptic PDEs with fibered nonlinearities. J. Geom. Anal. 2009, 19, 420–432. [Google Scholar] [CrossRef]
- Maz’ya, V.; Verbitsky, I. The form boundedness criterion for the relativistic Schrödinger operator. Ann. Inst. Fourier 2004, 54, 317–339. [Google Scholar] [CrossRef]
- Meerschaert, M. Fractional Calculus, Anomalous Diffusion, and Probability; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 2012; pp. 265–284. [Google Scholar]
- Adams, R. Sobolev Spaces, Pure and Applied Mathematics; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Brezis, H.; Mironescu, P. Gagliardo-Nirenberg, composition and products in fractional Sobolev spaces. J. Evol. Equ. 2001, 1, 387–404. [Google Scholar] [CrossRef]
- Di Nezza, E.; Palatucci, G.; Valdinoci, E. Hitchhiker’s guide to the fractional Sobolev spaces. Bull. Sci. Math. 2012, 136, 521–573. [Google Scholar] [CrossRef]
- Kwaśnicki, M. Ten equivalent definitions of the fractional laplace operator. Fract. Calc. Appl. Anal. 2017, 20, 7–51. [Google Scholar] [CrossRef]
- Runst, T.; Sickel, W. Sobolev Spaces of Fractional Order, Nemytskij Operators, and Nonlinear Partial Differential Equations; De Gruyter Series in Nonlinear Analysis and Applications; Walter de Gruyter & Co.: Berlin, Germany, 1996; Volume 3. [Google Scholar]
- Ciaurri, Ó.; Roncal, L.; Stinga, P.; Torrea, J.; Varona, J. Nonlocal discrete diffusion equations and the fractional discrete Laplacian, regularity and applications. Adv. Math. 2018, 330, 688–738. [Google Scholar] [CrossRef]
- Keller, M.; Nietschmann, M. Optimal Hardy inequality for fractional Laplacians on the integers. Ann. Henri Poincaré 2023, 24, 2729–2741. [Google Scholar] [CrossRef]
- Lizama, C.; Roncal, L. Hölder-Lebesgue regularity and almost periodicity for semidiscrete equations with a fractional Laplacian. Discret. Contin. Dyn. Syst. 2018, 38, 1365–1403. [Google Scholar] [CrossRef]
- Wang, J. Eigenvalue estimates for the fractional Laplacian on lattice subgraphs. arXiv 2024, arXiv:2303.15766. [Google Scholar]
- Zhang, M.; Lin, Y.; Yang, Y. Fractional Laplace operator on finite graphs. arXiv 2024, arXiv:2403.19987. [Google Scholar]
- Zhang, M.; Lin, Y.; Yang, Y. Fractional Laplace operator and related Schrödinger equations on locally finite graphs. arXiv 2024, arXiv:2408.02902. [Google Scholar]
- Ciaurri, Ó.; Gillespie, T.; Roncal, L.; Torrea, J.; Varona, J. Harmonic analysis associated with a discrete Laplacian. J. Anal. Math. 2017, 132, 109–131. [Google Scholar] [CrossRef]
- Ciaurri, Ó.; Lizama, C.; Roncal, L.; Varona, J. On a connection between the discrete fractional Laplacian and superdiffusion. Appl. Math. Lett. 2015, 49, 119–125. [Google Scholar] [CrossRef]
- Ju, C.; Zhang, B. On fractional discrete p-Laplacian equations via Clark’s theorem. Appl. Math. Comput. 2022, 434, 127443. [Google Scholar] [CrossRef]
- Lizama, C.; Murillo-Arcila, M. On a connection between the N-dimensional fractional Laplacian and 1-D operators on lattices. J. Math. Anal. Appl. 2022, 511, 126051. [Google Scholar] [CrossRef]
- Tarasov, V. Exact discretization of fractional Laplacian. Comput. Math. Appl. 2017, 73, 855–863. [Google Scholar] [CrossRef]
- Ambrosetti, A.; Rabinowitz, P. Dual variational methods in critical point theory and applications. J. Funct. Anal. 1973, 14, 349–381. [Google Scholar] [CrossRef]
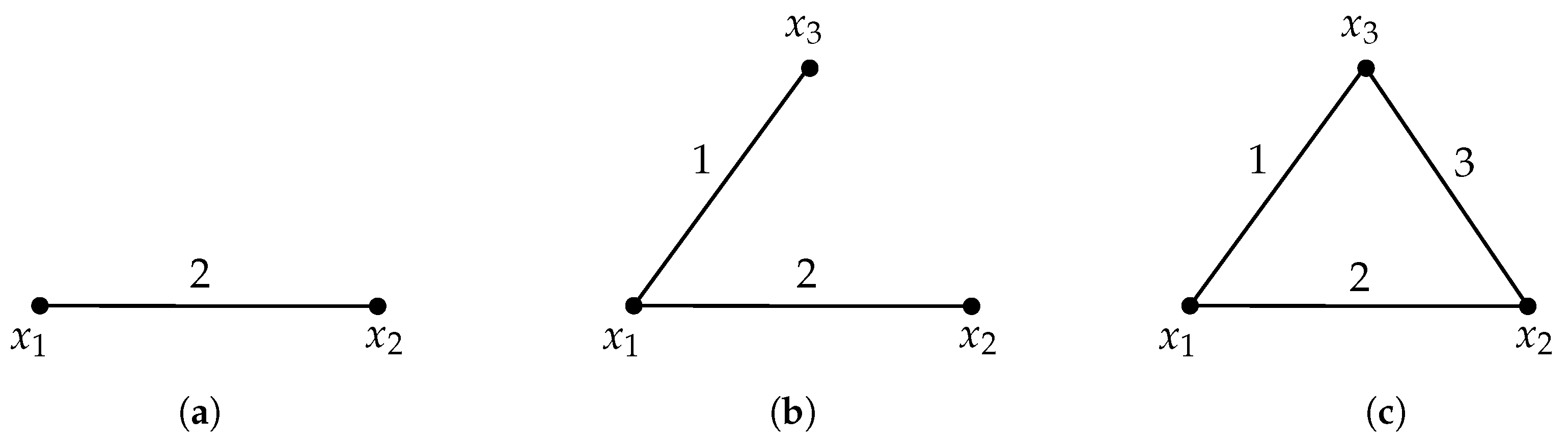

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, L.; Liu, Y. Multiple Solutions of Fractional Kazdan–Warner Equation for Negative Case on Finite Graphs. Axioms 2025, 14, 345. https://doi.org/10.3390/axioms14050345
Shan L, Liu Y. Multiple Solutions of Fractional Kazdan–Warner Equation for Negative Case on Finite Graphs. Axioms. 2025; 14(5):345. https://doi.org/10.3390/axioms14050345
Chicago/Turabian StyleShan, Liang, and Yang Liu. 2025. "Multiple Solutions of Fractional Kazdan–Warner Equation for Negative Case on Finite Graphs" Axioms 14, no. 5: 345. https://doi.org/10.3390/axioms14050345
APA StyleShan, L., & Liu, Y. (2025). Multiple Solutions of Fractional Kazdan–Warner Equation for Negative Case on Finite Graphs. Axioms, 14(5), 345. https://doi.org/10.3390/axioms14050345





