Involute Partner-Ruled Surfaces Formed by Involutes of Spacelike Curves in Minkowski Three-Space

Abstract

We introduced the concept of involute partner-ruled surfaces, which are formed by the involutes of spacelike curves and additional conditions ensuring the presence of definite surface normals in Minkowski three-space. First, we provided the criteria for each couple of involute partner-ruled surfaces to be simultaneously developable and minimal. Then, we established the requirements for the coordinate curves lying on these surfaces to be geodesic, asymptotic, and lines of curvature. We also expanded this paper with an example by providing graphical illustrations of the involute partner-ruled surfaces.

1. Introduction and Preliminaries

The notion of surfaces has been crucial in the field of differential geometry for thousands of years, with a wide range of applications in various disciplines. Among the different types of surfaces, ruled surfaces, first defined by Garspard Monge, are of special importance to researchers. The ruled surfaces are formed by the motion of a straight line termed a generator line along a given curve called the base curve. The concept of ruled surfaces plays a critical role in various engineering fields. In particular, these surfaces are widely used in mechanical systems, computer graphics, animation, and industrial design problems [1,2]. Cylindrical and conical surfaces are the most common examples of ruled surfaces. Ruled surfaces can also be found in remarkable architectural designs, such as the Millennium Bridge, the Shukhov Tower, The Guggenheim Museum, the Munich Olympic Stadium, and the Golden Gate Bridge. In addition to these applications, researchers have defined new ruled surfaces by incorporating moving frames on and along a given curve [3,4,5,6,7,8]. Moreover, the examinations of some geometric properties for ruled surfaces, such as developability and minimality conditions, and for parametric curves to be asymptotic, geodesic, or lines of curvature in Euclidean and Minkowski three-spaces were studied in [9,10,11,12,13,14,15]. In addition, some recent works on a new concept for ruled surfaces were introduced, namely, partner-ruled surfaces, and their characteristics were studied in [16,17].

The involute–evolute curve pair, on the other hand, is another critical topic in the context of associated curves where the theory of these curves can be found in [18,19] for Euclidean space and in [20,21] for Minkowski space. By combining the concepts of associated curves and ruled surfaces, the involute-ruled surfaces with a Frenet frame in Euclidean and Minkowski three-spaces were defined and characterized in [22,23,24,25].

In this study, involute partner-ruled surfaces that are formed by involutes of spacelike curves with spacelike Darboux vectors in the Minkowski three-space are investigated. Firstly, the Gaussian curvatures and the mean curvature for these surfaces are calculated. Then, the constraints are given for each pair of involute partner-ruled surfaces that are to be classified as both developable and minimal at the same time. Moreover, necessary and sufficient conditions are established for the coordinate curves, which are geodesic, asymptotic, and lines of curvature on these surfaces. Finally, examples of these partner-ruled surfaces and their graphics are presented.

We first review the basic notions for Minkowski three-space, and please note that the vector notations are given with bold characters throughout the paper.

Let $\mathbf{a}=(a_1,a_2,a_3)$ and $\mathbf{b}=(b_1,b_2,b_3)\in {\mathbb{R}}^3$ be two vectors in the 3-dimensional Cartesian space ${\mathbb{R}}^3$, where $a_i,b_i\in \mathbb{R}(i=1,2,3)$. Then, the pseudoscalar product of $\mathbf{a}$, $\mathbf{b}$ is defined by

$${〈\mathbf{a},\mathbf{b}〉}_L=a_1{b}_1+a_2{b}_2-a_3{b}_3$$

(1)

Thus, a Minkowski 3-space denoted by $E_1^3=\left({\mathbb{R}}^3,{〈,〉}_L\right)$ is defined as the real vector space ${\mathbb{R}}^3$ with the pseudoscalar metric. The non-zero vector $\mathbf{a}\in E_1^3$ is spacelike, lightlike, or timelike if ${〈\mathbf{a},\mathbf{a}〉}_L>0$, ${〈\mathbf{a},\mathbf{a}〉}_L=0$ or ${〈\mathbf{a},\mathbf{a}〉}_L<0$, respectively. The norm of the vector $\mathbf{a}\in E_1^3$ is defined by ${∥\mathbf{a}∥}_L=\sqrt{\left|{〈\mathbf{a},\mathbf{a}〉}_L\right|}$. For any two vectors $\mathbf{a},\mathbf{b}\in E_1^3$, the vector product is defined by

$$\begin{array}{c}\hfill \begin{array}{c}\mathbf{a}\times \mathbf{b}=\left|\begin{array}{ccc}-{\mathbf{e}}_{\mathbf{1}}& -{\mathbf{e}}_{\mathbf{2}}& {\mathbf{e}}_{\mathbf{3}}\\ a_1& a_2& a_3\\ b_1& b_2& b_3\end{array}\right|=\left(a_3{b}_2-a_2{b}_3,a_1{b}_3-a_3{b}_1,a_1{b}_2-a_2{b}_1\right)\end{array}\end{array}$$

where ${\mathbf{e}}_{\mathbf{1}},{\mathbf{e}}_{\mathbf{2}},{\mathbf{e}}_{\mathbf{3}}$ is the canonical basis of $E_1^3$ [19,26,27].

For $\forall s\in I\subset \mathbb{R},$ let $\phi \left(s\right):I\to E_1^3$ be a unit-speed spacelike curve in $E_1^3$ with curvature $\kappa \left(s\right)$ and torsion $\tau \left(s\right)$ and $\{{\mathbf{V}}_1\left(s\right),{\mathbf{V}}_2\left(s\right),{\mathbf{V}}_3\left(s\right)\}$ be its Serret–Frenet (S-F) frame. If $\phi$ is a curve with a timelike binormal, then the (S-F) formulae for the curve are given by

$$\left[\begin{array}{c}{\mathbf{V}}_1^{\prime }\\ {\mathbf{V}}_2^{\prime }\\ {\mathbf{V}}_3^{\prime }\end{array}\right]=\left[\begin{array}{ccc}0& \kappa & 0\\ -\kappa & 0& \tau \\ 0& \tau & 0\end{array}\right]\left[\begin{array}{c}{\mathbf{V}}_1\\ {\mathbf{V}}_2\\ {\mathbf{V}}_3\end{array}\right]=\mathbf{w}\times \left[\begin{array}{c}{\mathbf{V}}_1\\ {\mathbf{V}}_2\\ {\mathbf{V}}_3\end{array}\right]$$

(2)

where $\mathbf{w}=\tau {\mathbf{V}}_1-\kappa {\mathbf{V}}_3$ defines the Darboux vector of the (S-F) frame.

The vectors ${\mathbf{V}}_1={\phi }^{\prime },{\mathbf{V}}_2={\phi }^{″}/∥{\phi }^{″}∥$, and ${\mathbf{V}}_3={\mathbf{V}}_1\times {\mathbf{V}}_2$ are called the unit tangent vector, the principal normal vector, and the binormal vector, respectively. The (S-F) vector fields satisfy the following relations [27]:

$$〈{\mathbf{V}}_1,{\mathbf{V}}_1〉=〈{\mathbf{V}}_2,{\mathbf{V}}_2〉=-〈{\mathbf{V}}_3,{\mathbf{V}}_3〉=1,{\mathbf{V}}_1\times {\mathbf{V}}_2={\mathbf{V}}_3,{\mathbf{V}}_2\times {\mathbf{V}}_3=-{\mathbf{V}}_1,{\mathbf{V}}_3\times {\mathbf{V}}_1=-{\mathbf{V}}_2.$$

Also, if $\left|\tau \right|>\left|\kappa \right|$, then $\mathbf{w}$ is a spacelike vector and we derive the following relations:

$$\kappa =∥\mathbf{w}∥sinh\wp ,\tau =∥\mathbf{w}∥cosh\wp ,{∥\mathbf{w}∥}^2={\tau }^2-{\kappa }^2$$

(3)

where $\wp =\angle (\mathbf{w},{\mathbf{V}}_3)$ [20].

If $\phi \left(s\right)$ is a spacelike curve with a spacelike binormal in $E_1^3$, then the (S-F) formulae for the curve $\phi \left(s\right)$ are given by

$$\left[\begin{array}{c}{\mathbf{V}}_1^{\prime }\\ {\mathbf{V}}_2^{\prime }\\ {\mathbf{V}}_3^{\prime }\end{array}\right]=\left[\begin{array}{ccc}0& \kappa & 0\\ \kappa & 0& \tau \\ 0& \tau & 0\end{array}\right]\left[\begin{array}{c}{\mathbf{V}}_1\\ {\mathbf{V}}_2\\ {\mathbf{V}}_3\end{array}\right]=\mathbf{w}\times \left[\begin{array}{c}{\mathbf{V}}_1\\ {\mathbf{V}}_2\\ {\mathbf{V}}_3\end{array}\right]$$

(4)

where $\mathbf{w}=-\tau {\mathbf{V}}_1+\kappa {\mathbf{V}}_3$ defines the Darboux vector of the (S-F) frame. The (S-F) vector fields satisfy the following relations [27]:

$$〈{\mathbf{V}}_1,{\mathbf{V}}_1〉=-〈{\mathbf{V}}_2,{\mathbf{V}}_2〉=〈{\mathbf{V}}_3,{\mathbf{V}}_3〉=1,{\mathbf{V}}_1\times {\mathbf{V}}_2=-{\mathbf{V}}_3,{\mathbf{V}}_2\times {\mathbf{V}}_3=-{\mathbf{V}}_1,{\mathbf{V}}_3\times {\mathbf{V}}_1={\mathbf{V}}_2.$$

Also, if ${\mathbf{V}}_3$ and $\mathbf{w}$ are both spacelike vectors that span a spacelike vector subspace, then we have

$$\kappa =∥\mathbf{w}∥cos\wp ,\tau =∥\mathbf{w}∥sin\wp ,{∥\mathbf{w}∥}^2={\tau }^2+{\kappa }^2$$

(5)

where $\wp =\angle (\mathbf{w},{\mathbf{V}}_3)$ [20].

Definition 1

([18,19]). Let $\phi \left(s\right)$ and $\overline{\phi }\left(s\right),$ $s\in I$ be two curves such that $\overline{\phi }$ intersects the tangents of φ orthogonally. Then, the curve $\overline{\phi }$ is called an involute of φ, and the curve $\overline{\phi }$ is called an evolute of the curve φ. The parametric equation of an involute of a curve $\phi \left(s\right)$ with arc length s is given by

$$\overline{\phi }\left(s\right)=\phi \left(s\right)+\lambda {\mathbf{V}}_1\left(s\right)$$

(6)

where $\lambda =c-s\ne 0$ and c is a real constant.

Lemma 1

([20,21]). Let $\phi \left(s\right)$ be a unit-speed spacelike curve in $E_1^3$ and $\overline{\phi }\left(s\right)$ be its involute curve with (S-F) frames $\{{\mathbf{V}}_1\left(s\right),{\mathbf{V}}_2\left(s\right),{\mathbf{V}}_3\left(s\right)\}$ and $\{{{\mathbf{V}}_1}^{\ast }\left(s\right),{\mathbf{V}}_2^{\ast }\left(s\right),{\mathbf{V}}_3^{\ast }\left(s\right)\}$, respectively. Then, the relations between the (S-F) frames of involute curve $\overline{\phi }$ and evolute curve φ can be given as follows:

(i) 

If $\phi \left(s\right)$ is a unit-speed spacelike curve with a timelike binormal and spacelike $\mathbf{w}$ vector, then

$$\left[\begin{array}{c}{\mathbf{V}}_1^{\ast }\\ {\mathbf{V}}_2^{\ast }\\ {\mathbf{V}}_3^{\ast }\end{array}\right]=\left[\begin{array}{ccc}0& 1& 0\\ sinh\wp & 0& -cosh\wp \\ -cosh\wp & 0& sinh\wp \end{array}\right]\left[\begin{array}{c}{\mathbf{V}}_1\\ {\mathbf{V}}_2\\ {\mathbf{V}}_3\end{array}\right];$$

(7)

(ii) 

If $\phi \left(s\right)$ is a unit-speed spacelike curve with a spacelike binormal, then

$$\left[\begin{array}{c}{\mathbf{V}}_1^{\ast }\\ {\mathbf{V}}_2^{\ast }\\ {\mathbf{V}}_3^{\ast }\end{array}\right]=\left[\begin{array}{ccc}0& 1& 0\\ cos\wp & 0& sin\wp \\ -sin\wp & 0& cos\wp \end{array}\right]\left[\begin{array}{c}{\mathbf{V}}_1\\ {\mathbf{V}}_2\\ {\mathbf{V}}_3\end{array}\right].$$

(8)

Definition 2

([13,14]). A ruled surface is formed by moving a straight line along a curve. The parametric equation of the ruled surface can be expressed as follows:

$$\psi (s,v)=\phi \left(s\right)+vr\left(s\right)$$

(9)

where $\phi \left(s\right)$ is the base (or directrix) curve and $r\left(s\right)$ is the ruling (or generator line) of a ruled surface.

Lemma 2

([26,28]). Let $\psi (s,v)$ be a ruled surface in $E_1^3$. Then, the Gaussian curvature and the mean curvature for $\psi (s,v)$ are defined by, respectively,

$$K=\epsilon {\displaystyle \frac{eg-f^2}{EG-F^2}},H=\epsilon {\displaystyle \frac{Eg-2Ff+Ge}{2(EG-F^2)}}$$

(10)

where

$$\begin{array}{c}E={〈{\psi }_s,{\phi }_s〉}_L,F={〈{\psi }_s,{\psi }_v〉}_L,G={〈{\psi }_v,{\psi }_v〉}_L,\hfill \\ e={〈{\psi }_{ss},\mathbf{U}〉}_L,f={〈{\psi }_{sv},\mathbf{U}〉}_L,g={〈{\psi }_{vv},\mathbf{U}〉}_L,\\ {\displaystyle \mathbf{U}(s,v)=\frac{{\psi }_s\times {\psi }_v}{∥{\psi }_s\times {\psi }_v∥}}\hfill \end{array}$$

(11)

and ${〈\mathbf{U}(s,v),\mathbf{U}(s,v)〉}_L=\epsilon =\pm 1$. The surface in Minkowski 3-space $E_1^3$ is spacelike if $EG-F^2>0$ and it is timelike if $EG-F^2<0$.

2. Involute Partner-Ruled Surfaces Formed by Involutes of Spacelike Curve

Partner-ruled surfaces are formed when two ruling lines move along their respective curves. Based on this definition, we consider the following:

Let $\overline{\phi }\left(s\right)$ be the involute of a regular spacelike curve $\phi \left(s\right)$ and $\left\{{\mathbf{V}}_1^{\ast },{\mathbf{V}}_2^{\ast },{\mathbf{V}}_3^{\ast }\right\}$ be its (S-F) frame in $E_1^3$ with spacelike Darboux vector $\mathbf{w}$. Then, by considering the tangent, principal normal, and binormal vectors of the Frenet frame of the involute of a unit-speed spacelike curve as ruling lines of partner-ruled surfaces, we study the following surfaces couples.

2.1. ${\mathbf{V}}_1^{\ast }{\mathbf{V}}_2^{\ast }$-Involute Partner-Ruled Surfaces Formed by Involutes of Spacelike Curves

Definition 3.

Let ${\psi }_1$ and ${\psi }_2$ be the surfaces obtained using the tangent and principal normal vectors of the involute curve $\overline{\phi }\left(s\right)$. Then, the pair of involute partner-ruled surfaces $({\psi }_1,{\psi }_2)$ defined by

$$\begin{array}{cc}\hfill {\psi }_1(s,v)=& {\mathbf{V}}_1^{\ast }\left(s\right)+v{\mathbf{V}}_2^{\ast }\left(s\right),\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill {\psi }_2(s,v)=& {\mathbf{V}}_2^{\ast }\left(s\right)+v{\mathbf{V}}_1^{\ast }\left(s\right)\hfill \end{array}$$

(13)

is called the $({\psi }_1,{\psi }_2)$-involute partner-ruled surfaces (IPRSs) with the (S-F) frame of the involute of a spacelike curve $\phi \left(s\right)$ in $E_1^3$.

The results given in Theorems 1–4 are obtained considering the characteristics of involute partner-ruled surfaces for a given unit-speed spacelike curve with a timelike binormal in $E_1^3$.

Theorem 1.

Let the $({\psi }_1,{\psi }_2)$-IPRS be formed by involute curve $\overline{\phi }\left(s\right)$ in $E_1^3$. Then, the $({\psi }_1,{\psi }_2)$-IPRSs are simultaneously developable and minimal if and only if $\wp =constant$.

Proof. 

By taking the derivatives of relation (12) in terms of s and v, and using relations (2), (3), and (7), we obtain

$$\begin{array}{c}{\left({\psi }_1\right)}_s=\begin{array}{c}(v{\wp }^{\prime }cosh\wp -∥\mathbf{w}∥sinh\wp ){\mathbf{V}}_1-v∥\mathbf{w}∥{\mathbf{V}}_2+(∥\mathbf{w}∥cosh\wp -v{\wp }^{\prime }sinh\wp ){\mathbf{V}}_3\hfill \end{array},\hfill \\ {\left({\psi }_1\right)}_v=sinh\wp {\mathbf{V}}_1-cosh\wp {\mathbf{V}}_3.\hfill \end{array}$$

(14)

Then, using the relation (14), the unit normal vector of the surface ${\psi }_1$ is found as

$$\begin{array}{c}{\mathbf{U}}_{{\psi }_1}={\displaystyle \frac{v(-∥\mathbf{w}∥cosh\wp ,-{\wp }^{\prime },∥\mathbf{w}∥sinh\wp )}{\sqrt{v^2{∥\mathbf{w}∥}^2+v^2{{\wp }^{\prime }}^2}}}=\pm {\displaystyle \frac{(-∥\mathbf{w}∥cosh\wp ,-{\wp }^{\prime },∥\mathbf{w}∥sinh\wp )}{\sqrt{{∥\mathbf{w}∥}^2+{{\wp }^{\prime }}^2}}}.\end{array}$$

(15)

By using the relation (14), the coefficients of the 1st fundamental form for ${\psi }_1$ can be obtained as follows:

$$E_{{\psi }_1}=v^2{∥\mathbf{w}∥}^2+v^2{\wp }^{\prime 2}-{∥\mathbf{w}∥}^2,F_{{\psi }_1}=∥\mathbf{w}∥,G{\psi }_1=-1.$$

(16)

Then, by the aid of (16), we obtain $EG-F^2=-\left(v^2{∥\mathbf{w}∥}^2+v^2{{\wp }^{\prime }}^2\right)<0$. Hence, the ${\psi }_1$-IPRS is timelike.

Taking the derivatives of relation (14) in terms of s and v, we obtain

$$\begin{array}{c}{\left({\psi }_1\right)}_{ss}=\left(\left(v{{\wp }^{\prime }}^2+v{∥\mathbf{w}∥}^2-{∥\mathbf{w}∥}^{\prime }\right)sinh\wp +\left(v{\wp }^{″}-{\wp }^{\prime }∥\mathbf{w}∥\right)cosh\wp \right){\mathbf{V}}_1\hfill \\ +\left({∥\mathbf{w}∥}^2-v{∥\mathbf{w}∥}^{\prime }\right){\mathbf{V}}_2\hfill \\ +\left(\left({∥\mathbf{w}∥}^{\prime }-v{{\wp }^{\prime }}^2-v{∥\mathbf{w}∥}^2\right)cosh\wp +\left({\wp }^{\prime }∥\mathbf{w}∥-v{\wp }^{″}\right)sinh\wp \right){\mathbf{V}}_3,\hfill \\ {\left({\psi }_1\right)}_{sv}={\wp }^{\prime }cosh\wp {\mathbf{V}}_1-∥\mathbf{w}∥{\mathbf{V}}_2-{\wp }^{\prime }sinh\wp {\mathbf{V}}_3,\hfill \\ {\left({\psi }_1\right)}_{vv}=0.\hfill \end{array}$$

(17)

By using the relations (15) and (17), the coefficients of the 2nd fundamental form for ${\psi }_1$ are determined as follows:

$$e_{{\psi }_1}={\displaystyle \frac{v^2\left({\wp }^{\prime }{∥\mathbf{w}∥}^{\prime }-{\wp }^{″}∥\mathbf{w}∥\right)}{\sqrt{v^2{∥\mathbf{w}∥}^2+v^2{{\wp }^{\prime }}^2}}},f_{{\psi }_1}=0,g_{{\psi }_1}=0.$$

(18)

Thus, by substituting relations (16) and (18) into relation (10), the Gaussian curvature and the mean curvature for ${\psi }_1$ can be found as follows:

$$K_{{\psi }_1}=0,H_{{\psi }_1}={\displaystyle \frac{{\wp }^{″}∥\mathbf{w}∥-{\wp }^{\prime }{∥\mathbf{w}∥}^{\prime }}{2\sqrt{v^2{∥\mathbf{w}∥}^2+v^2{{\wp }^{\prime }}^2}\left({∥\mathbf{w}∥}^2+{{\wp }^{\prime }}^2\right)}}.$$

(19)

Moreover, by taking the derivatives of relation (13) in terms of s and v and using Equations (2), (3), and (7), we obtain

$$\begin{array}{c}{\left({\psi }_2\right)}_s=({\wp }^{\prime }cosh\wp -v∥\mathbf{w}∥sinh\wp ){\mathbf{V}}_1-∥\mathbf{w}∥{\mathbf{V}}_2\hfill \\ +(v∥\mathbf{w}∥cosh\wp -{\wp }^{\prime }sinh\wp ){\mathbf{V}}_3,\hfill \\ {\left({\psi }_2\right)}_v={\mathbf{V}}_2.\hfill \end{array}$$

(20)

Then, using (20), the unit normal vector of the surface ${\psi }_2$ is determined as

$${\mathbf{U}}_{{\psi }_2}={\displaystyle \frac{\left(\begin{array}{c}v∥\mathbf{w}∥cosh\wp -{\wp }^{\prime }sinh\wp ,0,{\wp }^{\prime }cosh\wp -v∥\mathbf{w}∥sinh\wp \hfill \end{array}\right)}{\sqrt{\left|v^2{∥\mathbf{w}∥}^2-{{\wp }^{\prime }}^2\right|}}}$$

(21)

where ${\wp }^{\prime }\left(s\right)\ne \pm v∥\mathbf{w}\left(s\right)∥$.

By using relation (20), the coefficients of the 1st fundamental form for ${\psi }_2$ are as follows:

$$E_{{\psi }_2}={\wp }^{\prime 2}-v^2{∥\mathbf{w}∥}^2+{∥\mathbf{w}∥}^2,F_{{\psi }_2}=-∥\mathbf{w}∥,G_{{\psi }_2}=1.$$

(22)

Then, by the aid of (22), we obtain $EG-F^2={\wp }^{\prime 2}-v^2{∥\mathbf{w}∥}^2$. Hence, the ${\psi }_2$-IPRS is spacelike if ${\wp }^{\prime 2}-v^2{∥\mathbf{w}∥}^2>0$ and the ${\psi }_2$-IPRS is timelike if ${\wp }^{\prime 2}-v^2{∥\mathbf{w}∥}^2<0$.

Taking the derivatives of relation (20) in terms of s and v, we obtain

$$\begin{array}{c}{\left({\psi }_2\right)}_{ss}=\left(\left({{\wp }^{\prime }}^2+{∥\mathbf{w}∥}^2-v{∥\mathbf{w}∥}^{\prime }\right)sinh\wp +\left({\wp }^{″}-v{\wp }^{\prime }∥\mathbf{w}∥\right)cosh\wp \right){\mathbf{V}}_1\hfill \\ +\left(v{∥\mathbf{w}∥}^2-{∥\mathbf{w}∥}^{\prime }\right){\mathbf{V}}_2\hfill \\ +\left(\left(v{∥\mathbf{w}∥}^{\prime }-{{\wp }^{\prime }}^2-{∥\mathbf{w}∥}^2\right)cosh\wp +\left(v{\wp }^{\prime }∥\mathbf{w}∥-{\wp }^{″}\right)sinh\wp \right){\mathbf{V}}_3,\hfill \\ {\left({\psi }_2\right)}_{sv}=-∥\mathbf{w}∥sinh\wp {\mathbf{V}}_1+∥\mathbf{w}∥cosh\wp {\mathbf{V}}_3,\hfill \\ {\left({\psi }_2\right)}_{vv}=0.\hfill \end{array}$$

(23)

By using the relations (21) and (23), the coefficients of the 2nd fundamental form for ${\psi }_2$ are determined as follows:

$$\begin{array}{c}{e}_{{\psi }_2}={\displaystyle \frac{\begin{array}{c}{{\wp }^{\prime }}^3-v{\wp }^{\prime }{∥\mathbf{w}∥}^{\prime }+{∥\mathbf{w}∥}^2{\wp }^{\prime }-v^2{∥\mathbf{w}∥}^2{\wp }^{\prime }+v{\wp }^{″}∥\mathbf{w}∥\end{array}}{\sqrt{\left|v^2{∥\mathbf{w}∥}^2-{{\wp }^{\prime }}^2\right|}}},\hfill \\ f_{{\psi }_2}={\displaystyle \frac{-∥\mathbf{w}∥{\wp }^{\prime }}{\sqrt{\left|v^2{∥\mathbf{w}∥}^2-{{\wp }^{\prime }}^2\right|}}},g_{{\psi }_2}=0.\end{array}$$

(24)

By substituting relations (22) and (24) into relation (10), the Gaussian curvature and the mean curvature for ${\psi }_2$ can be found as follows:

$$\begin{array}{c}{K}_{{\psi }_2}=\epsilon {\displaystyle \frac{{∥\mathbf{w}∥}^2{{\wp }^{\prime }}^2}{\left|v^2{∥\mathbf{w}∥}^2-{{\wp }^{\prime }}^2\right|\left({{\wp }^{\prime }}^2-v^2{∥\mathbf{w}∥}^2\right)}},\hfill \\ H_{{\psi }_2}=\epsilon {\displaystyle \frac{{{\wp }^{\prime }}^3-{∥\mathbf{w}∥}^2{\wp }^{\prime }-v{∥\mathbf{w}∥}^{\prime }{\wp }^{\prime }-v^2{∥\mathbf{w}∥}^2{\wp }^{\prime }+v∥\mathbf{w}∥{\wp }^{″}}{2\sqrt{\left|v^2{∥\mathbf{w}∥}^2-{{\wp }^{\prime }}^2\right|}\left({{\wp }^{\prime }}^2-v^2{∥\mathbf{w}∥}^2\right)}}.\hfill \end{array}$$

(25)

Consequently, from Equations (19) and (25), the proof is complete. □

Theorem 2.

The s-coordinate curves of $({\psi }_1,{\psi }_2)$-IPRS are simultaneously as follows:

(i) 

Not geodesics;

(ii) 

Asymptotic curves if $\wp =constant$.

Proof. 

(i) By using Equations (15), (17), (21), and (23), we obtain

$${\left({\psi }_1\right)}_{ss}\times \left({\mathbf{U}}_{{\psi }_1}\right)=\pm {\displaystyle \frac{\left(\begin{array}{c}\left({\wp }^{\prime }v{∥\mathbf{w}∥}^2+{{\wp }^{\prime }}^{3}v-{∥\mathbf{w}∥}^{\prime }{\wp }^{\prime }\right)cosh\wp \hfill \\ +\left({\wp }^{\prime }{\wp }^{″}v-{∥\mathbf{w}∥}^3-∥\mathbf{w}∥{{\wp }^{\prime }}^2+∥\mathbf{w}∥{∥\mathbf{w}∥}^{\prime }v\right)sinh\wp ,\hfill \\ ∥\mathbf{w}∥\left({∥\mathbf{w}∥}^{\prime }+{∥\mathbf{w}∥}^{2}v+{{\varphi }^{\prime }}^2\right),\hfill \\ \left({∥\mathbf{w}∥}^{\prime }{\wp }^{\prime }-{∥\mathbf{w}∥}^2{\wp }^{\prime }v-{{\wp }^{\prime }}^{3}v\right)sinh\wp \hfill \\ +\left({∥\mathbf{w}∥}^3+∥\mathbf{w}∥{{\wp }^{\prime }}^2-{\wp }^{\prime }{\wp }^{″}v-∥\mathbf{w}∥{∥\mathbf{w}∥}^{\prime }v\right)cosh\wp \hfill \end{array}\right)}{\sqrt{{∥\mathbf{w}∥}^2+{{\wp }^{\prime }}^2}}}$$

and

$${\left({\psi }_2\right)}_{ss}\times \left({\mathbf{U}}_{{\psi }_2}\right)={\displaystyle \frac{\left(\begin{array}{c}\left({∥\mathbf{w}∥}^{\prime }{\wp }^{\prime }-{∥\mathbf{w}∥}^2{\wp }^{\prime }v\right)cosh\wp +\left({∥\mathbf{w}∥}^3{v}^2-∥\mathbf{w}∥{∥\mathbf{w}∥}^{\prime }v\right)sinh\wp ,\hfill \\ {∥\mathbf{w}∥}^{3}v-∥\mathbf{w}∥{∥\mathbf{w}∥}^{\prime }{v}^2+{\wp }^{\prime }{\wp }^{″},\hfill \\ \left({∥\mathbf{w}∥}^2{\wp }^{\prime }v-{∥\mathbf{w}∥}^{\prime }{\wp }^{\prime }\right)sinh\wp +\left(∥\mathbf{w}∥{∥\mathbf{w}∥}^{\prime }v-{∥\mathbf{w}∥}^3{v}^2\right)cosh\wp \hfill \end{array}\right)}{\sqrt{\left|v^2{∥\mathbf{w}∥}^2-{{\wp }^{\prime }}^2\right|}}}$$

Since ${\left({\psi }_1\right)}_{ss}\times \left({\mathbf{U}}_{{\psi }_1}\right)\ne 0$ and ${\left({\psi }_2\right)}_{ss}\times \left({\mathbf{U}}_{{\psi }_2}\right)\ne 0$, the s-coordinate curves of the $({\psi }_1,{\psi }_2)$-IPRS are not simultaneously geodesic.

(ii) By using Equations (15), (17), (21), and (23), we obtain

$$\begin{array}{cc}\hfill 〈{\left({\psi }_1\right)}_{ss},{\mathbf{U}}_{{\psi }_1}〉=& {\displaystyle \frac{\left|v\right|\left({\wp }^{\prime }{∥\mathbf{w}∥}^{\prime }-{\wp }^{″}∥\mathbf{w}∥\right)}{\sqrt{{∥\mathbf{w}∥}^2+{{\wp }^{\prime }}^2}}}\hfill \\ \hfill 〈{\left({\psi }_2\right)}_{ss},{\mathbf{U}}_{{\psi }_2}〉=& {\displaystyle \frac{{{\wp }^{\prime }}^3-v{\wp }^{\prime }{∥\mathbf{w}∥}^{\prime }+{∥\mathbf{w}∥}^2{\wp }^{\prime }-v^2{∥\mathbf{w}∥}^2{\wp }^{\prime }+v{\wp }^{″}∥\mathbf{w}∥}{\sqrt{\left|v^2{∥\mathbf{w}∥}^2-{{\wp }^{\prime }}^2\right|}}}\hfill \end{array}$$

(26)

From (26), if $\wp =constant$, then $〈{\left({\psi }_1\right)}_{ss},{\mathbf{U}}_{{\psi }_1}〉=0$ and $〈{\left({\psi }_2\right)}_{ss},{\mathbf{U}}_{{\psi }_2}〉=0$. Finally, the s-coordinate curves of the $({\psi }_1,{\psi }_2)$-IPRS are simultaneously asymptotic if $\wp =constant$. □

Theorem 3.

The v-coordinate curves of the $({\psi }_1,{\psi }_2)$-IPRS are simultaneously geodesics and asymptotic curves.

Proof. 

Since ${\left({\psi }_1\right)}_{vv}\times \left({\mathbf{U}}_{{\psi }_1}\right)=0$ and ${\left({\psi }_2\right)}_{vv}\times \left({\mathbf{U}}_{{\psi }_2}\right)=0$, the v-coordinate curves of the $({\psi }_1,{\psi }_2)$-IPRS are simultaneously geodesic.

Further, since $〈{\left({\psi }_1\right)}_{vv},{\mathbf{U}}_{{\psi }_1}〉=0$ and $〈{\left({\psi }_2\right)}_{vv},{\mathbf{U}}_{{\psi }_2}〉=0$, the v-coordinate curves of the $({\psi }_1,{\psi }_2)$-IPRS are simultaneously asymptotic. □

Theorem 4.

The s-coordinate and the v-coordinate curves of the $({\psi }_1,{\psi }_2)$-IPRS are simultaneously not lines of curvature.

Proof. 

Since $F_{{\psi }_1}\ne 0$ and $F_{{\psi }_2}\ne 0$, the proof is complete. □

Further, let us consider the characteristics of involute partner-ruled surfaces for a given unit-speed spacelike curve with a spacelike binormal in Theorems 5–8. By utilizing the same relations given in Equations (12) and (13), we denote this pair of ruled surfaces with $({\overline{\psi }}_1,{\overline{\psi }}_2)$.

Theorem 5.

Let the $({\overline{\psi }}_1,{\overline{\psi }}_2)$-IPRS be formed by involute curve $\overline{\phi }\left(s\right)$ in $E_1^3$. Then, the $({\overline{\psi }}_1,{\overline{\psi }}_2)$-IPRSs are simultaneously developable and minimal if and only if $\wp =constant$.

Proof. 

Taking the derivatives of relation (12) in terms of s and v and utilizing relations (4), (5), and (8), we obtain

$$\begin{array}{c}{\left({\overline{\psi }}_1\right)}_s=(∥\mathbf{w}∥cos\wp -v{\wp }^{\prime }sin\wp ){\mathbf{V}}_1+v∥\mathbf{w}∥{\mathbf{V}}_2+(∥\mathbf{w}∥sin\wp +v{\wp }^{\prime }cos\wp ){\mathbf{V}}_3,\hfill \\ {\left({\overline{\psi }}_1\right)}_v=cos\wp {\mathbf{V}}_1+sin\wp {\mathbf{V}}_3.\hfill \end{array}$$

(27)

Then, using relation (27), the unit normal vector of the surface ${\overline{\psi }}_1$ is obtained by

$$\begin{array}{c}{\mathbf{U}}_{{\overline{\psi }}_1}={\displaystyle \frac{(-v∥\mathbf{w}∥sin\wp ,v{\wp }^{\prime },v∥\mathbf{w}∥cos\wp )}{\sqrt{\left|v^2{∥\mathbf{w}∥}^2-v^2{{\wp }^{\prime }}^2\right|}}}=\pm {\displaystyle \frac{(-∥\mathbf{w}∥sin\wp ,{\wp }^{\prime },∥\mathbf{w}∥cos\wp )}{\sqrt{\left|{∥\mathbf{w}∥}^2-{{\wp }^{\prime }}^2\right|}}}\hfill \end{array}$$

(28)

where ${\wp }^{\prime }\left(s\right)\ne \pm ∥\mathbf{w}\left(s\right)∥$.

By using relation (27), the coefficients of the 1st fundamental form for ${\overline{\psi }}_1$ can be obtained as follows:

$$E_{{\overline{\psi }}_1}={∥\mathbf{w}∥}^2+v^2{\wp }^{\prime 2}-v^2{∥\mathbf{w}∥}^2,F_{{\overline{\psi }}_1}=-∥\mathbf{w}∥,G_{{\overline{\psi }}_1}=1.$$

(29)

Then, by the aid of (29), we obtain $EG-F^2=v^2{\wp }^{\prime 2}-v^2{∥\mathbf{w}∥}^2$. Hence, the ${\overline{\psi }}_1$-IPRS is spacelike if $v^2{\wp }^{\prime 2}-v^2{∥\mathbf{w}∥}^2>0$ and the ${\overline{\psi }}_1$-IPRS is timelike if $v^2{\wp }^{\prime 2}-v^2{∥\mathbf{w}∥}^2<0$.

Taking the derivatives of relation (27) in terms of s and v, we obtain

$$\begin{array}{c}{\left({\overline{\psi }}_1\right)}_{ss}=\left(\left({∥\mathbf{w}∥}^{\prime }-v{{\wp }^{\prime }}^2+v{∥\mathbf{w}∥}^2\right)cos\wp -\left(v{\wp }^{″}+{\wp }^{\prime }∥\mathbf{w}∥\right)sin\wp \right){\mathbf{V}}_1\hfill \\ +\left({∥\mathbf{w}∥}^2+v{∥\mathbf{w}∥}^{\prime }\right){\mathbf{V}}_2\hfill \\ +\left(\left({∥\mathbf{w}∥}^{\prime }-v{{\wp }^{\prime }}^2+v{∥\mathbf{w}∥}^2\right)sin\wp +\left({\wp }^{\prime }∥\mathbf{w}∥+v{\wp }^{″}\right)cos\wp \right){\mathbf{V}}_3,\hfill \\ {\left({\overline{\psi }}_1\right)}_{sv}=-{\wp }^{\prime }sin\wp {\mathbf{V}}_1+∥\mathbf{w}∥{\mathbf{V}}_2+{\wp }^{\prime }cos\wp {\mathbf{V}}_3,\hfill \\ {\left({\overline{\psi }}_1\right)}_{vv}=0.\hfill \end{array}$$

(30)

By using relations (28) and (30), the coefficients of the 2nd fundamental form for ${\overline{\psi }}_1$ are determined as follows:

$$e_{{\overline{\psi }}_1}={\displaystyle \frac{v^2\left({\wp }^{″}∥\mathbf{w}∥-{\wp }^{\prime }{∥\mathbf{w}∥}^{\prime }\right)}{\sqrt{\left|v^2{∥\mathbf{w}∥}^2-v^2{{\wp }^{\prime }}^2\right|}}},f_{{\overline{\psi }}_1}=0,g_{{\overline{\psi }}_1}=0.$$

(31)

By substituting relations (29) and (31) into relation (10), the Gaussian curvature and the mean curvature for ${\overline{\psi }}_1$ can be found as follows:

$$K_{{\overline{\psi }}_1}=0,H_{{\overline{\psi }}_1}=\epsilon {\displaystyle \frac{{\wp }^{″}∥\mathbf{w}∥-{\wp }^{\prime }{∥\mathbf{w}∥}^{\prime }}{2\sqrt{\left|v^2{∥\mathbf{w}∥}^2-v^2{{\wp }^{\prime }}^2\right|}\left({{\wp }^{\prime }}^2-{∥\mathbf{w}∥}^2\right)}}.$$

(32)

Moreover, by taking the derivatives of (13) in terms of s and v, and using Equations (4), (5), and (8), we obtain the following:

$$\begin{array}{c}{\left({\overline{\psi }}_2\right)}_s=\left(v∥\mathbf{w}∥cos\wp -{\wp }^{\prime }sin\wp \right){\mathbf{V}}_1+∥\mathbf{w}∥{\mathbf{V}}_2+(v∥\mathbf{w}∥sin\wp +{\wp }^{\prime }cos\wp ){\mathbf{V}}_3,\hfill \\ {\left({\overline{\psi }}_2\right)}_v={\mathbf{V}}_2.\hfill \end{array}$$

(33)

Then, using (33), we obtain the normal vector of the surface ${\overline{\psi }}_2$ as follows:

$${\mathbf{U}}_{{\overline{\psi }}_2}={\displaystyle \frac{(v∥\mathbf{w}∥sin\wp +{\wp }^{\prime }cos\wp ,0,{\wp }^{\prime }sin\wp -v∥\mathbf{w}∥cos\wp )}{\sqrt{v^2{∥\mathbf{w}∥}^2+{{\wp }^{\prime }}^2}}}.$$

(34)

By using relation (33), the coefficients of the 1st fundamental form for ${\overline{\psi }}_2$ are given by

$$E_{{\overline{\psi }}_2}={\wp }^{\prime 2}+v^2{∥\mathbf{w}∥}^2-{∥\mathbf{w}∥}^2,F_{{\overline{\psi }}_2}=-∥\mathbf{w}∥,G_{{\overline{\psi }}_2}=-1.$$

(35)

Hence, by the aid of (35), we obtain $EG-F^2=-\left({{\wp }^{\prime }}^2+v^2{∥\mathbf{w}∥}^2\right)<0$. Hence, the ${\overline{\psi }}_2$-IPRS is timelike.

Taking the derivatives of relation (33) in terms of s and v, we obtain

$$\begin{array}{c}{\left({\overline{\psi }}_2\right)}_{ss}=\left(\left({∥\mathbf{w}∥}^2+v{∥\mathbf{w}∥}^{\prime }-{{\wp }^{\prime }}^2\right)cos\wp -\left({\wp }^{″}+v{\wp }^{\prime }∥\mathbf{w}∥\right)sin\wp \right){\mathbf{V}}_1+\left(v{∥\mathbf{w}∥}^2+{∥\mathbf{w}∥}^{\prime }\right){\mathbf{V}}_2\hfill \\ +\left(\left(v{∥\mathbf{w}∥}^{\prime }-{{\wp }^{\prime }}^2+{∥\mathbf{w}∥}^2\right)sin\wp +\left(v{\wp }^{\prime }∥\mathbf{w}∥+{\wp }^{″}\right)cos\wp \right){\mathbf{V}}_3,\hfill \\ {\left({\overline{\psi }}_2\right)}_{sv}=∥\mathbf{w}∥cos\wp {\mathbf{V}}_1+∥\mathbf{w}∥sin\wp {\mathbf{V}}_3,\hfill \\ {\left({\overline{\psi }}_2\right)}_{vv}=0.\hfill \end{array}$$

(36)

By using relations (34) and (36), the coefficients of the 2nd fundamental form for ${\overline{\psi }}_2$ are determined as follows:

$$e_{{\overline{\psi }}_2}={\displaystyle \frac{\left(\begin{array}{c}v{\wp }^{\prime }{∥\mathbf{w}∥}^{\prime }-{{\wp }^{\prime }}^3+{∥\mathbf{w}∥}^2{\wp }^{\prime }\hfill \\ -v^2{∥\mathbf{w}∥}^2{\wp }^{\prime }-v{\wp }^{″}∥\mathbf{w}∥\hfill \end{array}\right)}{\sqrt{v^2{∥\mathbf{w}∥}^2+{{\wp }^{\prime }}^2}}},f_{{\overline{\psi }}_2}={\displaystyle \frac{∥\mathbf{w}∥{\wp }^{\prime }}{\sqrt{v^2{∥\mathbf{w}∥}^2+{{\wp }^{\prime }}^2}}},g_{{\overline{\psi }}_2}=0.$$

(37)

By substituting relations (34) and (37) into relation (10), the Gaussian curvature and the mean curvature for ${\overline{\psi }}_2$ can be found as follows:

$$\begin{array}{c}{K}_{{\overline{\psi }}_2}=-{\displaystyle \frac{{∥\mathbf{w}∥}^2{{\wp }^{\prime }}^2}{{\left(v^2{∥\mathbf{w}∥}^2+{{\wp }^{\prime }}^2\right)}^2}},\hfill \\ H_{{\overline{\psi }}_2}={\displaystyle \frac{v{\wp }^{\prime }{∥\mathbf{w}∥}^{\prime }-{{\wp }^{\prime }}^3-{∥\mathbf{w}∥}^2{\wp }^{\prime }-v^2{∥\mathbf{w}∥}^2{\wp }^{\prime }-v{\wp }^{″}∥\mathbf{w}∥}{2\sqrt{\left|v^2{∥\mathbf{w}∥}^2+{{\wp }^{\prime }}^2\right|}\left(v^2{∥\mathbf{w}∥}^2+{{\wp }^{\prime }}^2\right)}}.\hfill \end{array}$$

(38)

Consequently, from Equations (32) and (38), the proof is complete. □

Theorem 6.

The s-coordinate curves of the $({\overline{\psi }}_1,{\overline{\psi }}_2)$-IPRS are simultaneously as follows:

(i) 

Not geodesics;

(ii) 

Asymptotic curves if $\wp =constant$.

Proof. 

(i) By using relations (28), (30), (34) and (36), we obtain

$${\left({\overline{\psi }}_1\right)}_{ss}\times \left({\mathbf{U}}_{{\overline{\psi }}_1}\right)=\pm {\displaystyle \frac{\left(\begin{array}{c}\left({∥\mathbf{w}∥}^2{\wp }^{\prime }v-{{\wp }^{\prime }}^{3}v+{∥\mathbf{w}∥}^{\prime }{\wp }^{\prime }\right)sin\wp \hfill \\ +\left({\wp }^{\prime }{\wp }^{″}v-{∥\mathbf{w}∥}^3+∥\mathbf{w}∥{{\wp }^{\prime }}^2-∥\mathbf{w}∥{∥\mathbf{w}∥}^{\prime }v\right)cos\wp ,\hfill \\ ∥\mathbf{w}∥\left({{\wp }^{\prime }}^2-{∥\mathbf{w}∥}^{\prime }-{∥\mathbf{w}∥}^{2}v\right),\hfill \\ \left({{\wp }^{\prime }}^{3}v-{∥\mathbf{w}∥}^{\prime }{\wp }^{\prime }-{∥\mathbf{w}∥}^2{\wp }^{\prime }v\right)cos\wp \hfill \\ +\left({\wp }^{\prime }{\wp }^{″}v-{∥\mathbf{w}∥}^3+∥\mathbf{w}∥{{\wp }^{\prime }}^2-∥\mathbf{w}∥{∥\mathbf{w}∥}^{\prime }v\right)sin\wp \hfill \end{array}\right)}{\sqrt{\left|{∥\mathbf{w}∥}^2-{{\wp }^{\prime }}^2\right|}}}$$

and

$${\left({\overline{\psi }}_2\right)}_{ss}\times \left({\mathbf{U}}_{{\overline{\psi }}_2}\right)={\displaystyle \frac{\left(\begin{array}{c}\left({∥\mathbf{w}∥}^3{v}^2+∥\mathbf{w}∥{∥\mathbf{w}∥}^{\prime }v\right)cos\wp -\left({∥\mathbf{w}∥}^{\prime }{\wp }^{\prime }+{∥\mathbf{w}∥}^2{\wp }^{\prime }v\right)sin\wp ,\hfill \\ -∥\mathbf{w}∥{∥\mathbf{w}∥}^{\prime }{v}^2-{∥\mathbf{w}∥}^{3}v-{\wp }^{″}{\wp }^{\prime },\hfill \\ \left(∥\mathbf{w}∥{∥\mathbf{w}∥}^{\prime }v+{∥\mathbf{w}∥}^3{v}^2\right)sin\wp +\left({∥\mathbf{w}∥}^2{\wp }^{\prime }v+{∥\mathbf{w}∥}^{\prime }{\wp }^{\prime }\right)cos\wp \hfill \end{array}\right)}{\sqrt{v^2{∥\mathbf{w}∥}^2+{{\wp }^{\prime }}^2}}}$$

Since ${\left({\overline{\psi }}_1\right)}_{ss}\times \left({\mathbf{U}}_{{\overline{\psi }}_1}\right)\ne 0$ and ${\left({\overline{\psi }}_2\right)}_{ss}\times \left({\mathbf{U}}_{{\overline{\psi }}_2}\right)\ne 0$, the s-coordinate curves of the $({\overline{\psi }}_1,{\overline{\psi }}_2)$-IPRS are not simultaneously geodesic.

(ii) By using relations (28), (30), (34) and (36), we obtain

$$\begin{array}{c}〈{\left({\overline{\psi }}_1\right)}_{ss},{\mathbf{U}}_{{\overline{\psi }}_1}〉={\displaystyle \frac{\left|v\right|\left({\wp }^{″}∥\mathbf{w}∥-{\wp }^{\prime }{∥\mathbf{w}∥}^{\prime }\right)}{\sqrt{\left|{∥\mathbf{w}∥}^2-{{\wp }^{\prime }}^2\right|}}},\hfill \\ 〈{\left({\overline{\psi }}_2\right)}_{ss},{\mathbf{U}}_{{\overline{\psi }}_2}〉={\displaystyle \frac{v{\wp }^{\prime }{∥\mathbf{w}∥}^{\prime }-{{\wp }^{\prime }}^3+{∥\mathbf{w}∥}^2{\wp }^{\prime }-v^2{∥\mathbf{w}∥}^2{\wp }^{\prime }-v{\wp }^{″}∥\mathbf{w}∥}{\sqrt{v^2{∥\mathbf{w}∥}^2+{{\wp }^{\prime }}^2}}}.\hfill \end{array}$$

(39)

Hence, if $\wp =constant$, then $〈{\left({\overline{\psi }}_1\right)}_{ss},{\mathbf{U}}_{{\overline{\psi }}_1}〉=0$ and $〈{\left({\overline{\psi }}_2\right)}_{ss},{\mathbf{U}}_{{\overline{\psi }}_2}〉=0$, which means that the s-coordinate curves of the $({\overline{\psi }}_1,{\overline{\psi }}_2)$-IPRS are simultaneously asymptotic if $\wp =constant$. □

Theorem 7.

The v-coordinate curves of the $({\overline{\psi }}_1,{\overline{\psi }}_2)$-IPRS are simultaneously geodesics and asymptotic curves.

Proof. 

Since ${\left({\overline{\psi }}_1\right)}_{vv}\times \left({\mathbf{U}}_{{\overline{\psi }}_1}\right)=0$ and ${\left({\overline{\psi }}_2\right)}_{vv}\times \left({\mathbf{U}}_{{\overline{\psi }}_2}\right)=0$, the v-coordinate curves of the $({\overline{\psi }}_1,{\overline{\psi }}_2)$-IPRS are simultaneously geodesic.

Further, since $〈{\left({\overline{\psi }}_1\right)}_{vv},{\mathbf{U}}_{{\overline{\psi }}_1}〉=0$ and $〈{\left({\overline{\psi }}_2\right)}_{ss},{\mathbf{U}}_{{\overline{\psi }}_2}〉=0$, the v-coordinate curves of the $({\overline{\psi }}_1,{\overline{\psi }}_2)$-IPRS are simultaneously asymptotic. □

Theorem 8.

The s-coordinate and v-coordinate curves of the $({\overline{\psi }}_1,{\overline{\psi }}_2)$-IPRS are simultaneously not lines of curvature.

Proof. 

Since $F_{{\overline{\psi }}_1}\ne 0$ and $F_{{\overline{\psi }}_2}\ne 0$, the proof is complete. □

2.2. ${\mathbf{V}}_1^{\ast }{\mathbf{V}}_3^{\ast }$-Involute Partner-Ruled Surfaces Formed by Involutes of Spacelike Curve

Definition 4.

Let ${\xi }_1$ and ${\xi }_2$ be the surfaces obtained using the tangent and binormal vectors of the involute curve $\overline{\phi }\left(s\right)$. Then, the pair of involute partner-ruled surfaces $({\xi }_1,{\xi }_2)$ defined by

$$\begin{array}{cc}\hfill {\xi }_1(s,v)=& {\mathbf{V}}_1^{\ast }\left(s\right)+v{\mathbf{V}}_3^{\ast }\left(s\right),\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill {\xi }_2(s,v)=& {\mathbf{V}}_3^{\ast }\left(s\right)+v{\mathbf{V}}_1^{\ast }\left(s\right)\hfill \end{array}$$

(41)

is called the $({\xi }_1,{\xi }_2)$-involute partner-ruled surfaces (IPRSs) with the (S-F) frame of the involute of a spacelike curve $\phi \left(s\right)$ in $E_1^3$.

The results given in Theorems 9 and 10 are obtained considering the characteristics of involute partner-ruled surfaces for a given unit-speed spacelike curve with a timelike binormal in $E_1^3$.

Theorem 9.

Let the $({\xi }_1,{\xi }_2)$-IPRS be formed by involute curve $\overline{\phi }\left(s\right)$ in $E_1^3$. Then, the $({\xi }_1,{\xi }_2)$-IPRSs are simultaneously developable but not minimal surfaces.

Proof. 

Taking the derivatives of relation (40) in terms of s and v and utilizing relations (2), (3), and (7), we obtain

$$\begin{array}{c}{\left({\xi }_1\right)}_s=-(v{\wp }^{\prime }+∥\mathbf{w}∥)sinh\wp {\mathbf{V}}_1+(∥\mathbf{w}∥+v{\wp }^{\prime })cosh\wp {\mathbf{V}}_3,\hfill \\ {\left({\xi }_1\right)}_v=-cosh\wp {\mathbf{V}}_1+sinh\wp {\mathbf{V}}_3.\hfill \end{array}$$

(42)

Then, using relation (42), the unit normal vector of the surface ${\xi }_1$ is obtained by

$${\mathbf{U}}_{{\xi }_1}={\displaystyle \frac{(0,∥\mathbf{w}∥+v{\wp }^{\prime },0)}{\left|∥\mathbf{w}∥+v{\wp }^{\prime }\right|}}=\pm N$$

(43)

where $∥\mathbf{w}∥\ne -v{\wp }^{\prime }$.

By using relation (42), the coefficients of the 1^nd fundamental form for ${\xi }_1$ can be obtained as follows:

$$E_{{\xi }_1}=-{(∥\mathbf{w}∥+v{\wp }^{\prime })}^2,F_{{\xi }_1}=0,G_{{\xi }_1}=1.$$

(44)

Then, by the aid of (44), we obtain $EG-F^2=-{\left(∥\mathbf{w}∥+v{\wp }^{\prime }\right)}^2<0$. Hence, the ${\xi }_1$-IPRS is timelike.

Taking a derivative of relation (42) in terms of s and v, we obtain

$$\begin{array}{c}{\left({\xi }_1\right)}_{ss}=\left(\left(-v{\wp }^{″}-{∥\mathbf{w}∥}^{\prime }\right)sinh\wp -\left(v{{\wp }^{\prime }}^2+{\wp }^{\prime }∥\mathbf{w}∥\right)cosh\wp \right){\mathbf{V}}_1+\left({∥\mathbf{w}∥}^2+v{∥\mathbf{w}∥}^{\prime }{\wp }^{\prime }\right){\mathbf{V}}_2\hfill \\ +\left(\left(v{\wp }^{″}+{∥\mathbf{w}∥}^{\prime }\right)cosh\wp +\left(v{{\wp }^{\prime }}^2+{\wp }^{\prime }∥\mathbf{w}∥\right)sinh\wp \right){\mathbf{V}}_3,\hfill \\ {\left({\xi }_1\right)}_{sv}=-{\wp }^{\prime }sinh\wp {\mathbf{V}}_1+{\wp }^{\prime }cosh\wp {\mathbf{V}}_3,\hfill \\ {\left({\xi }_1\right)}_{vv}=0.\hfill \end{array}$$

(45)

By using relations (43) and (45), the coefficients of the 2nd fundamental form for ${\xi }_1$ are determined as follows:

$$e_{{\xi }_1}={\displaystyle \frac{∥\mathbf{w}∥{\left(∥\mathbf{w}∥+v{\wp }^{\prime }\right)}^2}{\left|∥\mathbf{w}∥+v{\wp }^{\prime }\right|}},f_{{\xi }_1}=0,g_{{\xi }_1}=0.$$

(46)

By substituting relations (44) and (46) into relation (10), the Gaussian curvature and the mean curvature for ${\xi }_1$ can be found as follows:

$$K_{{\xi }_1}=0,H_{{\xi }_1}=-{\displaystyle \frac{∥\mathbf{w}∥}{2\left|∥\mathbf{w}∥+v{\wp }^{\prime }\right|}}.$$

(47)

Moreover, by taking the derivatives of (41) in terms of s and v and using Equations (2), (3), and (7), we obtain

$$\begin{array}{c}{\left({\xi }_2\right)}_s=-\left(v∥\mathbf{w}∥+{\wp }^{\prime }\right)sinh\wp {\mathbf{V}}_1+(v∥\mathbf{w}∥+{\wp }^{\prime })cosh\wp {\mathbf{V}}_3,\hfill \\ {\left({\xi }_2\right)}_v={\mathbf{V}}_2.\hfill \end{array}$$

(48)

Then, using relation (48), the unit normal vector of the ruled surface ${\xi }_2$ is obtained by

$${\mathbf{U}}_{{\xi }_2}={\displaystyle \frac{({\wp }^{\prime }+v∥\mathbf{w}∥)(cosh\wp ,0,-sinh\wp )}{\left|{\wp }^{\prime }+v∥\mathbf{w}∥\right|}}=\pm (cosh\wp ,0,-sinh\wp ).$$

(49)

where ${\wp }^{\prime }\ne -v∥\mathbf{w}∥$.

By using relation (48), the coefficients of the 1st fundamental form for ${\xi }_2$ can be obtained as follows:

$$E_{{\xi }_2}=-{\left({\wp }^{\prime }+v∥\mathbf{w}∥\right)}^2,F_{{\xi }_2}=0,G_{{\xi }_2}=1.$$

(50)

By the aid of (50), we obtain $EG-F^2=-{\left({\wp }^{\prime }+v∥\mathbf{w}∥\right)}^2<0$. Hence, the ${\xi }_2$-IPRS is timelike.

Taking the derivatives of relation (48) in terms of s and v, we obtain

$$\begin{array}{c}{\left({\xi }_2\right)}_{ss}=\left(\left(-{\wp }^{″}-v{∥\mathbf{w}∥}^{\prime }\right)sinh\wp -\left({{\wp }^{\prime }}^2+v{\wp }^{\prime }∥\mathbf{w}∥\right)cosh\wp \right){\mathbf{V}}_1-\left({\wp }^{\prime }∥\mathbf{w}∥+v{∥\mathbf{w}∥}^2\right){\mathbf{V}}_2\hfill \\ +\left(\left({\wp }^{″}+v{∥\mathbf{w}∥}^{\prime }\right)cosh\wp +\left({{\wp }^{\prime }}^2+v{\wp }^{\prime }∥\mathbf{w}∥\right)sinh\wp \right){\mathbf{V}}_3,\hfill \\ {\left({\xi }_2\right)}_{sv}=-∥\mathbf{w}∥sinh\wp {\mathbf{V}}_1+∥\mathbf{w}∥cosh\wp {\mathbf{V}}_3,\hfill \\ {\left({\xi }_2\right)}_{vv}=0.\hfill \end{array}$$

(51)

By using relations (49) and (51), the coefficients of the 2nd fundamental form for ${\xi }_2$ are determined as follows:

$$e_{{\xi }_2}=-{\displaystyle \frac{{\wp }^{\prime }{\left({\wp }^{\prime }+v∥\mathbf{w}∥\right)}^2}{\left|{\wp }^{\prime }+v∥\mathbf{w}∥\right|}},f_{{\xi }_2}=0,g_{{\xi }_2}=0.$$

(52)

By substituting relations (50) and (52) into relation (10), the Gaussian curvature and the mean curvature for ${\xi }_2$ can be found as follows:

$$K_{{\xi }_2}=0,H_{{\xi }_2}={\displaystyle \frac{{\wp }^{\prime }}{2\left|{\wp }^{\prime }+v∥\mathbf{w}∥\right|}}.$$

(53)

Consequently, from Equations (47) and (53), the $({\xi }_1,{\xi }_2)$-IPRSs are simultaneously developable but not minimal surfaces. □

Theorem 10.

Let the $({\xi }_1,{\xi }_2)$-IPRS be formed by involute curve $\overline{\phi }\left(s\right)$ in $E_1^3$. Then, we obtain the following:

(i) 

The s-coordinate curves of the $({\xi }_1,{\xi }_2)$-IPRS are simultaneously neither geodesics nor asymptotic curves.

(ii) 

The v-coordinate curves of the $({\xi }_1,{\xi }_2)$-IPRS are simultaneously geodesics and asymptotic curves.

(iii) 

The s-coordinate and v-coordinate curves of the $({\xi }_1,{\xi }_2)$-IPRS are simultaneously lines of curvature.

Proof. 

The proofs are similar to that of Theorems 2–4 given for the $({\psi }_1,{\psi }_2)$-IPRS. □

Now, let us consider a unit-speed spacelike curve with a spacelike binormal with the same relations given in Equations (40) and (41). We denote this pair of ruled surfaces with $({\overline{\xi }}_1,{\overline{\xi }}_2)$ and obtain the following Theorems 11–12.

Theorem 11.

Let the $({\overline{\xi }}_1,{\overline{\xi }}_2)$-IPRS be formed by involute curve $\overline{\phi }\left(s\right)$ in $E_1^3$. Then, the $({\overline{\xi }}_1,{\overline{\xi }}_2)$-IPRSs are simultaneously developable but not minimal surfaces.

Proof. 

By taking the derivatives of relation (40) in terms of s and v, and utilizing relations (4), (5), and (8), we obtain

$$\begin{array}{c}{\left({\overline{\xi }}_1\right)}_s=(∥\mathbf{w}∥-v{\wp }^{\prime })cos\wp {\mathbf{V}}_1+(∥\mathbf{w}∥-v{\wp }^{\prime })sin\wp {\mathbf{V}}_3,\hfill \\ {\left({\overline{\xi }}_1\right)}_v=-sin\wp {\mathbf{V}}_1+cos\wp {\mathbf{V}}_3.\hfill \end{array}$$

(54)

Then, using (54), the unit normal vector of the surface ${\overline{\xi }}_1$ is obtained by

$${\mathbf{U}}_{{\overline{\xi }}_1}={\displaystyle \frac{(0,v{\wp }^{\prime }-∥\mathbf{w}∥,0)}{\left|∥\mathbf{w}∥-v{\wp }^{\prime }\right|}}=\pm N$$

(55)

where $∥\mathbf{w}∥\ne v{\wp }^{\prime }$.

By using relation (54), the coefficients of the 1st fundamental form can be obtained as follows:

$$E_{{\overline{\xi }}_1}={(∥\mathbf{w}∥-v{\wp }^{\prime })}^2,F_{{\overline{\xi }}_1}=0,G_{{\overline{\xi }}_1}=1.$$

(56)

Then, by the aid of (56), we obtain $EG-F^2={\left(∥\mathbf{w}∥-v{\wp }^{\prime }\right)}^2>0$. Hence, the ${\overline{\xi }}_1$-IPRS is spacelike.

Taking the derivatives of (54) in terms of s and v, we obtain

$$\begin{array}{c}{\left({\overline{\xi }}_1\right)}_{ss}=\left(\left({∥\mathbf{w}∥}^{\prime }-v{\wp }^{″}\right)cos\wp +\left(v{{\wp }^{\prime }}^2-{\wp }^{\prime }∥\mathbf{w}∥\right)sin\wp \right){\mathbf{V}}_1+\left({∥\mathbf{w}∥}^2-v∥\mathbf{w}∥{\wp }^{\prime }\right){\mathbf{V}}_2\hfill \\ +\left(\left({∥\mathbf{w}∥}^{\prime }-v{\wp }^{″}\right)sin\wp +\left({\wp }^{\prime }∥\mathbf{w}∥-v{{\wp }^{\prime }}^2\right)cos\wp \right){\mathbf{V}}_3,\hfill \\ {\left({\overline{\xi }}_1\right)}_{sv}=-{\wp }^{\prime }cos\wp {\mathbf{V}}_1-{\wp }^{\prime }sin\wp {\mathbf{V}}_3,\hfill \\ {\left({\overline{\xi }}_1\right)}_{vv}=0.\hfill \end{array}$$

(57)

By using relations (55) and (57), the coefficients of the 2nd fundamental form for ${\overline{\xi }}_1$ are determined as follows:

$$e_{{\overline{\xi }}_1}={\displaystyle \frac{∥\mathbf{w}∥{\left(∥\mathbf{w}∥-v{\wp }^{\prime }\right)}^2}{\left|∥\mathbf{w}∥-v{\wp }^{\prime }\right|}},f_{{\overline{\xi }}_1}=0,g_{{\overline{\xi }}_1}=0.$$

(58)

By substituting relations (56) and (58) into relation (10), the Gaussian curvature and the mean curvature for ${\overline{\xi }}_1$ can be found as follows:

$$K_{{\overline{\xi }}_1}=0,H_{{\overline{\xi }}_1}={\displaystyle \frac{∥\mathbf{w}∥}{2\left|∥\mathbf{w}∥-v{\wp }^{\prime }\right|}}.$$

(59)

On the other hand, taking the derivatives of relation (41) in terms of s and v, and using relations (4), (5), and (8), we obtain

$$\begin{array}{c}{\left({\overline{\xi }}_2\right)}_s=\left(v∥\mathbf{w}∥-{\wp }^{\prime }\right)cos\wp {\mathbf{V}}_1+(v∥\mathbf{w}∥-{\wp }^{\prime })sin\wp {\mathbf{V}}_3,\hfill \\ {\left({\overline{\xi }}_2\right)}_v={\mathbf{V}}_2.\hfill \end{array}$$

(60)

Then, using relation (60), we obtain the unit normal vector of the surface ${\overline{\xi }}_2$ as follows:

$${\mathbf{U}}_{{\overline{\xi }}_2}={\displaystyle \frac{({\wp }^{\prime }-v∥\mathbf{w}∥)(-sin\wp ,0,cos\wp )}{\left|{\wp }^{\prime }-v∥\mathbf{w}∥\right|}}=\pm (-sin\wp ,0,cos\wp )$$

(61)

where ${\wp }^{\prime }\ne v∥\mathbf{w}∥$.

By using relation (60), the coefficients of the 1st fundamental form for ${\overline{\xi }}_2$ can be obtained as follows:

$$E_{{\overline{\xi }}_2}={\left({\wp }^{\prime }-v∥\mathbf{w}∥\right)}^2,F_{{\overline{\xi }}_2}=0,G_{{\overline{\xi }}_2}=-1.$$

(62)

By the aid of (62), we obtain $EG-F^2=-{\left({\wp }^{\prime }-v∥\mathbf{w}∥\right)}^2<0$. Hence, the ${\overline{\xi }}_2$-IPRS is timelike.

Taking the derivatives of relation (60) in terms of s and v, we obtain

$$\begin{array}{c}{\left({\overline{\xi }}_2\right)}_{ss}=\left(\left(v{∥\mathbf{w}∥}^{\prime }-{\wp }^{″}\right)cos\wp +\left({{\wp }^{\prime }}^2-v{\wp }^{\prime }∥\mathbf{w}∥\right)sin\wp \right){\mathbf{V}}_1-\left(v{∥\mathbf{w}∥}^2-{\wp }^{\prime }∥\mathbf{w}∥\right){\mathbf{V}}_2\hfill \\ +\left(\left(v{∥\mathbf{w}∥}^{\prime }-{\wp }^{″}\right)sin\wp +\left(v{\wp }^{\prime }∥\mathbf{w}∥-{{\wp }^{\prime }}^2\right)cos\wp \right){\mathbf{V}}_3,\hfill \\ {\left({\overline{\xi }}_2\right)}_{sv}=∥\mathbf{w}∥cos\wp {\mathbf{V}}_1+∥\mathbf{w}∥sin\wp {\mathbf{V}}_3,\hfill \\ {\left({\overline{\xi }}_2\right)}_{vv}=0.\hfill \end{array}$$

(63)

By using relations (63) and (61), the coefficients of the 2nd fundamental form for ${\overline{\xi }}_2$ are determined as follows:

$$e_{{\overline{\xi }}_2}=-{\displaystyle \frac{{\wp }^{\prime }{\left(v∥\mathbf{w}∥-{\wp }^{\prime }\right)}^2}{\left|{\wp }^{\prime }-v∥\mathbf{w}∥\right|}},f_{{\overline{\xi }}_2}=0,g_{{\overline{\xi }}_2}=0.$$

(64)

By substituting relations (62) and (64) into relation (10), the Gaussian curvature and the mean curvature for ${\overline{\xi }}_2$ can be found as follows:

$$K_{{\overline{\xi }}_2}=0,H_{{\overline{\xi }}_2}={\displaystyle \frac{{\wp }^{\prime }}{2\left|{\wp }^{\prime }-v∥\mathbf{w}∥\right|}}.$$

(65)

Consequently, from Equations (59) and (65), the $({\overline{\xi }}_1,{\overline{\xi }}_2)$-IPRSs are simultaneously developable but not minimal surfaces. □

Theorem 12.

Let the $({\overline{\xi }}_1,{\overline{\xi }}_2)$-IPRS be formed by involute curve $\overline{\phi }\left(s\right)$ in $E_1^3$. Then, we obtain the following:

(i) 

The s-coordinate curves of the $({\overline{\xi }}_1,{\overline{\xi }}_2)$-IPRS are simultaneously neither geodesics nor asymptotic curves.

(ii) 

The v-coordinate curves of the $({\overline{\xi }}_1,{\overline{\xi }}_2)$-IPRS are simultaneously geodesics and asymptotic curves.

(iii) 

The s coordinate and v-coordinate curves of the $({\overline{\xi }}_1,{\overline{\xi }}_2)$-IPRS are simultaneously lines of curvature.

Proof. 

The proofs are similar to that of Theorems 6, 7, and 8 given for the $({\overline{\psi }}_1,{\overline{\psi }}_2)$-IPRS. □

2.3. ${\mathbf{V}}_2^{\ast }{\mathbf{V}}_3^{\ast }$-Involute Partner-Ruled Surfaces Formed by Involutes of Spacelike Curve

Definition 5.

Let ${\zeta }_1$ and ${\zeta }_2$ be the surfaces obtained using the principal normal and binormal vectors of the involute curve $\overline{\phi }\left(s\right)$. Then, the pair of involute partner-ruled surfaces $({\zeta }_1,{\zeta }_2)$ defined by

$$\begin{array}{cc}\hfill {\zeta }_1(s,v)=& {\mathbf{V}}_2^{\ast }\left(s\right)+v{\mathbf{V}}_3^{\ast }\left(s\right),\hfill \end{array}$$

(66)

$$\begin{array}{cc}\hfill {\zeta }_2(s,v)=& {\mathbf{V}}_3^{\ast }\left(s\right)+v{\mathbf{V}}_2^{\ast }\left(s\right)\hfill \end{array}$$

(67)

is called the $({\zeta }_1,{\zeta }_2)$-involute partner-ruled surfaces (IPRSs) with the (S-F) frame of the involute of a spacelike curve $\phi \left(s\right)$ in $E_1^3$.

The results given in Theorems 13 and 14 are obtained considering the characteristics of involute partner-ruled surfaces for a given unit-speed spacelike curve with a timelike binormal in $E_1^3$.

Theorem 13.

Let the $({\zeta }_1,{\zeta }_2)$-IPRS be formed by involute curve $\overline{\phi }\left(s\right)$ in $E_1^3$. Then, the $({\zeta }_1,{\zeta }_2)$-IPRSs are simultaneously developable surfaces if and only if $\wp =constant$ but not minimal surfaces.

Proof. 

By taking the derivative of relation (66) in terms of s and v and using relations (2), (3), and (7), we obtain

$$\begin{array}{c}{\left({\zeta }_1\right)}_s=({\wp }^{\prime }cosh\wp -v{\wp }^{\prime }sinh\wp ){\mathbf{V}}_1-∥\mathbf{w}∥{\mathbf{V}}_2+(v{\wp }^{\prime }cosh\wp -{\wp }^{\prime }sinh\wp ){\mathbf{V}}_3,\hfill \\ {\left({\zeta }_1\right)}_v=-cosh\wp {\mathbf{V}}_1+sinh\wp {\mathbf{V}}_3.\hfill \end{array}$$

(68)

Then, using relation (68), the unit normal vector of the surface ${\zeta }_1$ is obtained by

$${\mathbf{U}}_{{\zeta }_1}={\displaystyle \frac{\left(∥\mathbf{w}∥sinh\wp ,v{\wp }^{\prime },-∥\mathbf{w}∥cosh\wp \right)}{\sqrt{\left|v^2{{\wp }^{\prime }}^2-{∥\mathbf{w}∥}^2\right|}}}$$

(69)

where $∥\mathbf{w}∥\ne \pm v{\varphi }^{\prime }$.

By using relation (68), the coefficients of the 1st fundamental form for ${\zeta }_1$ can be obtained as follows:

$$E_{{\zeta }_1}={\wp }^{\prime 2}-v^2{\wp }^{\prime 2}+{∥\mathbf{w}∥}^2,F_{{\zeta }_1}=-{\wp }^{\prime },G_{{\zeta }_1}=1.$$

(70)

Then, by the aid of (70), we obtain $EG-F^2={∥\mathbf{w}∥}^2-v^2{\wp }^{\prime 2}$. Hence, the ${\zeta }_1$-IPRS is spacelike if ${∥\mathbf{w}∥}^2-v^2{\wp }^{\prime 2}\rangle 0$, and the ${\zeta }_1$-IPRS is timelike if ${∥\mathbf{w}∥}^2-v^2{\wp }^{\prime 2}<0$.

Taking the derivatives of relation (68) in terms of s and v, we obtain

$$\begin{array}{c}{\left({\zeta }_1\right)}_{ss}=\left(\left({\wp }^{″}-v{{\wp }^{\prime }}^2\right)cosh\wp +\left({{\wp }^{\prime }}^2-v{\wp }^{″}+{∥\mathbf{w}∥}^2\right)sinh\wp \right){\mathbf{V}}_1+\left(v∥\mathbf{w}∥{\wp }^{\prime }-{∥\mathbf{w}∥}^{\prime }\right){\mathbf{V}}_2\hfill \\ +\left(\left(v{{\wp }^{\prime }}^2-{\wp }^{″}\right)sinh\wp +\left(v{\wp }^{″}-{{\wp }^{\prime }}^2-{∥\mathbf{w}∥}^2\right)cosh\wp \right){\mathbf{V}}_3,\hfill \\ {\left({\zeta }_1\right)}_{sv}=-{\wp }^{\prime }sinh\wp {\mathbf{V}}_1+{\wp }^{\prime }cosh\wp {\mathbf{V}}_3,\hfill \\ {\left({\zeta }_1\right)}_{vv}=0.\hfill \end{array}$$

(71)

By using relations (69) and (71), the coefficients of the 2nd fundamental form for ${\zeta }_1$ are determined as follows:

$$\begin{array}{c}{e}_{{\zeta }_1}={\displaystyle \frac{v\left({\wp }^{″}∥\mathbf{w}∥-{∥\mathbf{w}∥}^{\prime }{\wp }^{\prime }\right)+∥\mathbf{w}∥{{\wp }^{\prime }}^2\left(v^2+1\right)-{∥\mathbf{w}∥}^3}{\sqrt{\left|v^2{{\wp }^{\prime }}^2-{∥\mathbf{w}∥}^2\right|}}},\hfill \\ f_{{\zeta }_1}={\displaystyle \frac{{\wp }^{\prime }∥\mathbf{w}∥}{\sqrt{\left|v^2{{\wp }^{\prime }}^2-{∥\mathbf{w}∥}^2\right|}}},g_{{\zeta }_1}=0.\hfill \end{array}$$

(72)

By substituting relations (70) and (72) into relation (10), the Gaussian curvature and the mean curvature for ${\zeta }_1$ can be found as follows:

$$\begin{array}{c}{K}_{{\zeta }_1}=\epsilon {\displaystyle \frac{{{\wp }^{\prime }}^2{∥\mathbf{w}∥}^2}{\left|v^2{{\wp }^{\prime }}^2-{∥\mathbf{w}∥}^2\right|\left({∥\mathbf{w}∥}^2-v^2{{\wp }^{\prime }}^2\right)}},\hfill \\ H_{{\zeta }_1}=\epsilon {\displaystyle \frac{∥\mathbf{w}∥\left(3{{\wp }^{\prime }}^2+v{\wp }^{″}-{∥\mathbf{w}∥}^2+v^2{{\wp }^{\prime }}^2\right)-v{∥\mathbf{w}∥}^{\prime }{\wp }^{\prime }}{2\sqrt{\left|v^2{{\wp }^{\prime }}^2-{∥\mathbf{w}∥}^2\right|}\left({∥\mathbf{w}∥}^2-v^2{{\wp }^{\prime }}^2\right)}}.\hfill \end{array}$$

(73)

Moreover, by taking the derivatives of (67) in terms of s and v, and using Equations (2), (3), and (7), we obtain

$$\begin{array}{c}{\left({\zeta }_2\right)}_s=(v{\wp }^{\prime }cosh\wp -{\wp }^{\prime }sinh\wp ){\mathbf{V}}_1-∥\mathbf{w}∥v{\mathbf{V}}_2+({\wp }^{\prime }cosh\wp -v{\wp }^{\prime }sinh\wp ){\mathbf{V}}_3,\hfill \\ {\left({\zeta }_2\right)}_v=sinh\wp {\mathbf{V}}_1-cosh\wp {\mathbf{V}}_3.\hfill \end{array}$$

(74)

Then, using (74), the unit normal vector of the ruled surface ${\zeta }_2$ is obtained by

$${\mathbf{U}}_{{\zeta }_2}={\displaystyle \frac{\left(-v∥\mathbf{w}∥cosh\wp ,-v{\wp }^{\prime },v∥\mathbf{w}∥sinh\wp \right)}{\sqrt{v^2{{\wp }^{\prime }}^2+v^2{∥\mathbf{w}∥}^2}}}$$

(75)

By using relation (74), the coefficients of the 1st fundamental form for ${\zeta }_2$ can be obtained as follows:

$$E_{{\zeta }_2}={\wp }^{\prime 2}\left(v^2-1\right)+v^2{∥\mathbf{w}∥}^2,F_{{\zeta }_2}={\wp }^{\prime },G_{{\zeta }_2}=-1.$$

(76)

By the aid of (76), we obtain $EG-F^2=-v^2({∥\mathbf{w}∥}^2+{\wp }^{\prime 2})$. Hence, the ${\zeta }_2$-IPRS is timelike.

Taking the derivative of relation (74) in terms of s and v, we obtain

$$\begin{array}{c}{\left({\zeta }_2\right)}_{ss}=\left(\left(v{{\wp }^{\prime }}^2-{\wp }^{″}+v{∥\mathbf{w}∥}^2\right)sinh\wp +\left(v{\wp }^{″}-{{\wp }^{\prime }}^2\right)cosh\wp \right){\mathbf{V}}_1+\left({\wp }^{\prime }∥\mathbf{w}∥-v{∥\mathbf{w}∥}^{\prime }\right){\mathbf{V}}_2\hfill \\ +\left(\left({\wp }^{″}-v{{\wp }^{\prime }}^2-v{∥\mathbf{w}∥}^2\right)cosh\wp +\left({{\wp }^{\prime }}^2-v{\wp }^{″}\right)sinh\wp \right){\mathbf{V}}_3,\hfill \\ {\left({\zeta }_2\right)}_{sv}={\wp }^{\prime }cosh\wp {\mathbf{V}}_1-∥\mathbf{w}∥{\mathbf{V}}_2-{\wp }^{\prime }sinh\wp {\mathbf{V}}_3,\hfill \\ {\left({\zeta }_2\right)}_{vv}=0.\hfill \end{array}$$

(77)

By using relations (75) and (77), the coefficients of the 2nd fundamental form for ${\zeta }_2$ are determined as follows:

$$e_{{\zeta }_2}={\displaystyle \frac{v^2\left({∥\mathbf{w}∥}^{\prime }{\wp }^{\prime }-{\wp }^{″}∥\mathbf{w}∥\right)}{\sqrt{v^2{{\wp }^{\prime }}^2+v^2{∥\mathbf{w}∥}^2}}},f_{{\zeta }_2}=0,g_{{\zeta }_2}=0.$$

(78)

By substituting relations (76) and (78) into relation (10), the Gaussian curvature and the mean curvature for ${\zeta }_2$ can be found as follows:

$$K_{{\zeta }_2}=0,H_{{\zeta }_2}={\displaystyle \frac{{∥\mathbf{w}∥}^{\prime }{\wp }^{\prime }-∥\mathbf{w}∥{\wp }^{″}}{2\sqrt{v^2{{\wp }^{\prime }}^2+v^2{∥\mathbf{w}∥}^2}\left({{\wp }^{\prime }}^2+{∥\mathbf{w}∥}^2\right)}}.$$

(79)

Therefore, the $({\zeta }_1,{\zeta }_2)$-IPRSs can be simultaneously developable if and only if $\wp =constant$ but can not be minimal surfaces. □

Theorem 14.

Let the $({\zeta }_1,{\zeta }_2)$-IPRS be formed by involute curve $\overline{\phi }\left(s\right)$ in $E_1^3$. Then, we obtain the following:

(i) 

The s-coordinate curves of the $({\zeta }_1,{\zeta }_2)$-IPRS are simultaneously neither geodesics nor asymptotic curves.

(ii) 

The v-coordinate curves of the $({\zeta }_1,{\zeta }_2)$-IPRS are simultaneously geodesics and asymptotic curves.

(iii) 

The s-coordinate and v-coordinate curves of the $({\zeta }_1,{\zeta }_2)$-IPRS are simultaneously lines of curvature if and only if $\wp =constant$.

Proof. 

The proofs are similar to that of Theorems 2–4 given for the $({\psi }_1,{\psi }_2)$-IPRS. □

Similarly, if we consider a unit-speed spacelike curve with a spacelike binormal in $E_1^3$ with the same relations (66) and (67), then we denote this pair of ruled surfaces with $({\overline{\zeta }}_1,{\overline{\zeta }}_2)$, and we have the Theorems 15 and 16.

Theorem 15.

Let the $({\overline{\zeta }}_1,{\overline{\zeta }}_2)$-IPRS be formed by involute curve $\overline{\phi }\left(s\right)$ in $E_1^3$. Then, the $({\overline{\zeta }}_1,{\overline{\zeta }}_2)$-IPRSs are simultaneously developable surfaces if and only if $\wp =constant$ but not minimal surfaces.

Proof. 

By taking the derivatives of relation (66) in terms of s and v and using relations (4), (5), and (8), we obtain

$$\begin{array}{c}{\left({\overline{\zeta }}_1\right)}_s=-({\wp }^{\prime }sin\wp +v{\wp }^{\prime }cos\wp ){\mathbf{V}}_1+∥\mathbf{w}∥{\mathbf{V}}_2+({\wp }^{\prime }cos\wp -v{\wp }^{\prime }sin\wp ){\mathbf{V}}_3,\hfill \\ {\left({\overline{\zeta }}_1\right)}_v=-sin\wp {\mathbf{V}}_1+cos\wp {\mathbf{V}}_3.\hfill \end{array}$$

(80)

Then, using (80), the unit normal vector of the ruled surface ${\overline{\zeta }}_1$ is obtained by

$${\mathbf{U}}_{{\overline{\zeta }}_1}={\displaystyle \frac{\left(-∥\mathbf{w}∥cos\wp ,v{\wp }^{\prime },-∥\mathbf{w}∥sin\wp \right)}{\sqrt{\left|{∥\mathbf{w}∥}^2-v^2{{\wp }^{\prime }}^2\right|}}}$$

(81)

where $∥\mathbf{w}∥\ne \pm v{\varphi }^{\prime }$.

By using (80), the coefficients of the 1st fundamental form for ${\overline{\zeta }}_1$ can be obtained as follows:

$$E_{{\overline{\zeta }}_1}={\wp }^{\prime 2}(v^2+1)-{∥\mathbf{w}∥}^2,F_{{\overline{\zeta }}_1}={\wp }^{\prime },G_{{\overline{\zeta }}_1}=1.$$

(82)

Then, by the aid of (82), we obtain $EG-F^2=v^2{\wp }^{\prime 2}-{∥\mathbf{w}∥}^2$. Hence, the ${\overline{\zeta }}_1$-IPRS is spacelike if $v^2{\wp }^{\prime 2}-{∥\mathbf{w}∥}^2\rangle 0$, and the ${\overline{\zeta }}_1$-IPRS is timelike if $v^2{\wp }^{\prime 2}-{∥\mathbf{w}∥}^2<0$.

Taking the derivatives of relation (80) in terms of s and v, we obtain

$$\begin{array}{c}{\left({\overline{\zeta }}_1\right)}_{ss}=\left(\left(v{{\wp }^{\prime }}^2-{\wp }^{″}\right)sin\wp +\left({∥\mathbf{w}∥}^2-{{\wp }^{\prime }}^2-v{\wp }^{″}\right)cos\wp \right){\mathbf{V}}_1+\left({∥\mathbf{w}∥}^{\prime }-v∥\mathbf{w}∥{\wp }^{\prime }\right){\mathbf{V}}_2\hfill \\ +\left(\left({\wp }^{″}-v{{\wp }^{\prime }}^2\right)cos\wp +\left({∥\mathbf{w}∥}^2-v{\wp }^{″}-{{\wp }^{\prime }}^2\right)sin\wp \right){\mathbf{V}}_3,\hfill \\ {\left({\overline{\zeta }}_1\right)}_{sv}=-{\wp }^{\prime }cos\wp {\mathbf{V}}_1-{\wp }^{\prime }sin\wp {\mathbf{V}}_3,\hfill \\ {\left({\overline{\zeta }}_1\right)}_{vv}=0.\hfill \end{array}$$

(83)

By using relations (81) and (83), the coefficients of the 2nd fundamental form for ${\overline{\zeta }}_1$ are determined as follows:

$$\begin{array}{c}{e}_{{\overline{\zeta }}_1}={\displaystyle \frac{v\left({\wp }^{″}∥\mathbf{w}∥-{∥\mathbf{w}∥}^{\prime }{\wp }^{\prime }\right)+∥\mathbf{w}∥{{\wp }^{\prime }}^2\left(1+v^2\right)-{∥\mathbf{w}∥}^3}{\sqrt{\left|{∥\mathbf{w}∥}^2-v^2{{\wp }^{\prime }}^2\right|}}},\hfill \\ f_{{\overline{\zeta }}_1}=-{\displaystyle \frac{{\wp }^{\prime }∥\mathbf{w}∥}{\sqrt{\left|{∥\mathbf{w}∥}^2-v^2{{\wp }^{\prime }}^2\right|}}},g_{{\overline{\zeta }}_1}=0.\hfill \end{array}$$

(84)

By substituting relations (82) and (84) into relation (10), the Gaussian curvature and the mean curvature for ${\overline{\zeta }}_1$ can be found as follows:

$$\begin{array}{c}{K}_{{\overline{\zeta }}_1}=\epsilon {\displaystyle \frac{{{\wp }^{\prime }}^2{∥\mathbf{w}∥}^2}{\left|{∥\mathbf{w}∥}^2-v^2{{\wp }^{\prime }}^2\right|\left({∥\mathbf{w}∥}^2-v^2{{\wp }^{\prime }}^2\right)}},\hfill \\ H_{{\overline{\zeta }}_1}=\epsilon {\displaystyle \frac{∥\mathbf{w}∥\left(3{{\wp }^{\prime }}^2+v{\wp }^{″}-{∥\mathbf{w}∥}^2+v^2{{\wp }^{\prime }}^2\right)-v{∥\mathbf{w}∥}^{\prime }{\wp }^{\prime }}{2\sqrt{\left|{∥\mathbf{w}∥}^2-v^2{{\wp }^{\prime }}^2\right|}\left(v^2{{\wp }^{\prime }}^2-{∥\mathbf{w}∥}^2\right)}}.\hfill \end{array}$$

(85)

Moreover, by taking the derivatives of relation (67) in terms of s and v and using relations (4), (5), and (8), we obtain

$$\begin{array}{c}{\left({\overline{\zeta }}_2\right)}_s=-(v{\wp }^{\prime }sin\wp +{\wp }^{\prime }cos\wp ){\mathbf{V}}_1+∥\mathbf{w}∥v{\mathbf{V}}_2+(v{\wp }^{\prime }cos\wp -{\wp }^{\prime }sin\wp ){\mathbf{V}}_3,\hfill \\ {\left({\overline{\zeta }}_2\right)}_v=cos\wp {\mathbf{V}}_1+sin\wp {\mathbf{V}}_3.\hfill \end{array}$$

(86)

Then, using (86), the unit normal vector of the ruled surface ${\overline{\zeta }}_2$ is obtained by

$$\begin{array}{c}{\mathbf{U}}_{{\overline{\zeta }}_2}={\displaystyle \frac{\left(-v∥\mathbf{w}∥sin\wp ,v{\wp }^{\prime },v∥\mathbf{w}∥cos\wp \right)}{\sqrt{\left|v^2{∥\mathbf{w}∥}^2-v^2{{\wp }^{\prime }}^2\right|}}}=\pm {\displaystyle \frac{\left(-∥\mathbf{w}∥sin\wp ,{\wp }^{\prime },∥\mathbf{w}∥cos\wp \right)}{\sqrt{\left|{∥\mathbf{w}∥}^2-{{\wp }^{\prime }}^2\right|}}}\hfill \end{array}$$

(87)

where $∥\mathbf{w}∥\ne \pm {\varphi }^{\prime }$.

By using relation (86), the coefficients the of 1st fundamental form for ${\overline{\zeta }}_2$ can be obtained as follows:

$$E_{{\overline{\zeta }}_2}={\wp }^{\prime 2}\left(v^2+1\right)-v^2{∥\mathbf{w}∥}^2,F_{{\overline{\zeta }}_2}=-{\wp }^{\prime },G_{{\overline{\zeta }}_2}=1.$$

(88)

By the aid of (88), we obtain $EG-F^2=v^2{\wp }^{\prime 2}-v^2{∥\mathbf{w}∥}^2$. Hence, the ${\overline{\zeta }}_2$-IPRS is spacelike if $v^2{\wp }^{\prime 2}-v^2{∥\mathbf{w}∥}^2>0$ and the ${\overline{\zeta }}_2$-IPRS is timelike if $v^2{\wp }^{\prime 2}-v^2{∥\mathbf{w}∥}^2<0$.

Taking the derivative of relation (86) in terms of s and v, we obtain

$$\begin{array}{c}{\left({\overline{\zeta }}_2\right)}_{ss}=\left(\left(v{∥\mathbf{w}∥}^2-v{{\wp }^{\prime }}^2-{\wp }^{″}\right)cos\wp +\left({{\wp }^{\prime }}^2-v{\wp }^{″}\right)sin\wp \right){\mathbf{V}}_1\hfill \\ -\left(v{∥\mathbf{w}∥}^{\prime }-{\wp }^{\prime }∥\mathbf{w}∥\right){\mathbf{V}}_2\hfill \\ +\left(\left(v{∥\mathbf{w}∥}^2-{\wp }^{″}-v{{\wp }^{\prime }}^2\right)sin\wp +\left(v{\wp }^{″}-{{\wp }^{\prime }}^2\right)cos\wp \right){\mathbf{V}}_3,\hfill \\ {\left({\overline{\zeta }}_2\right)}_{sv}=-{\wp }^{\prime }sin\wp {\mathbf{V}}_1+∥\mathbf{w}∥{\mathbf{V}}_2+{\wp }^{\prime }cos\wp {\mathbf{V}}_3,\hfill \\ {\left({\overline{\zeta }}_2\right)}_{vv}=0.\hfill \end{array}$$

(89)

By using relations (87) and (89), the coefficients of the 2nd fundamental form for ${\overline{\zeta }}_2$ are determined as follows:

$$e_{{\overline{\zeta }}_2}={\displaystyle \frac{v^2\left({\wp }^{″}∥\mathbf{w}∥-{∥\mathbf{w}∥}^{\prime }{\wp }^{\prime }\right)}{\sqrt{\left|v^2{∥\mathbf{w}∥}^2-v^2{{\wp }^{\prime }}^2\right|}}},f_{{\overline{\zeta }}_2}=0,g_{{\overline{\zeta }}_2}=0.$$

(90)

By substituting relations (88) and (90) into relation (10), the Gaussian curvature and the mean curvature for ${\overline{\zeta }}_2$ can be found as follows:

$$K_{{\overline{\zeta }}_2}=0,H_{{\overline{\zeta }}_2}={\displaystyle \frac{{\wp }^{″}∥\mathbf{w}∥-{∥\mathbf{w}∥}^{\prime }{\wp }^{\prime }}{2\sqrt{v^2{∥\mathbf{w}∥}^2-v^2{{\wp }^{\prime }}^2}\left({{\wp }^{\prime }}^2-{∥\mathbf{w}∥}^2\right)}}.$$

(91)

Therefore, $({\overline{\zeta }}_1,{\overline{\zeta }}_2)$-IPRSs can be simultaneously developable if and only if $\wp =constant$ but can not be minimal surfaces. □

Theorem 16.

Let the $({\overline{\zeta }}_1,{\overline{\zeta }}_2)$-IPRS be formed by involute curve $\overline{\phi }\left(s\right)$ in $E_1^3$. Then, we obtain the following:

(i) 

The s-coordinate curves of the $({\overline{\zeta }}_1,{\overline{\zeta }}_2)$-IPRS are simultaneously neither geodesics nor asymptotic curves.

(ii) 

The v-coordinate curves of the $({\overline{\zeta }}_1,{\overline{\zeta }}_2)$-IPRS are simultaneously both geodesics and asymptotic curves.

(iii) 

The s-coordinate and v-coordinate curves of the $({\overline{\zeta }}_1,{\overline{\zeta }}_2)$-IPRS are simultaneously lines of curvature if and only if $\wp =constant$.

Proof. 

The proofs are similar to that of Theorems 6–8 given for the $({\overline{\psi }}_1,{\overline{\psi }}_2)$-IPRS. □

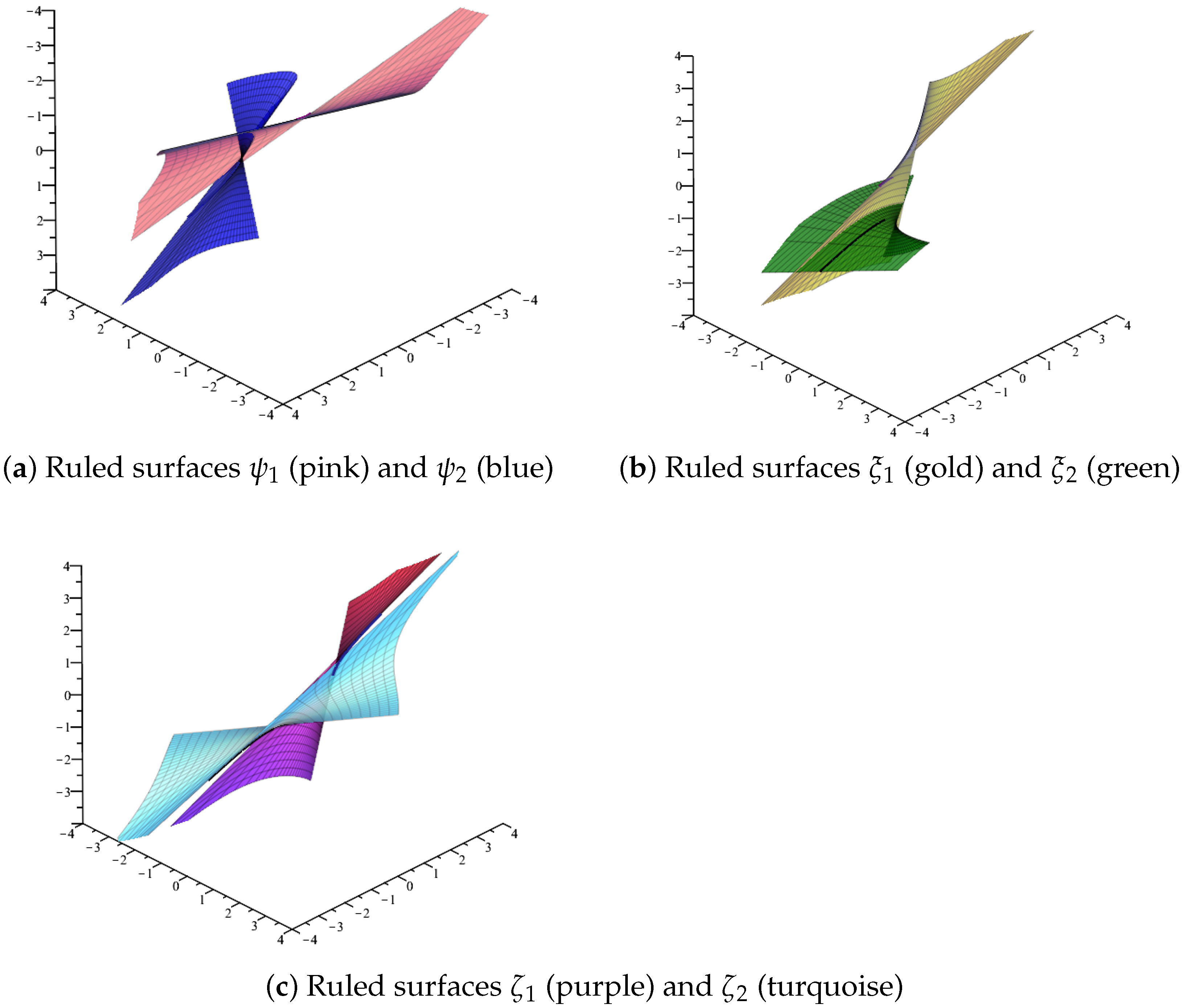
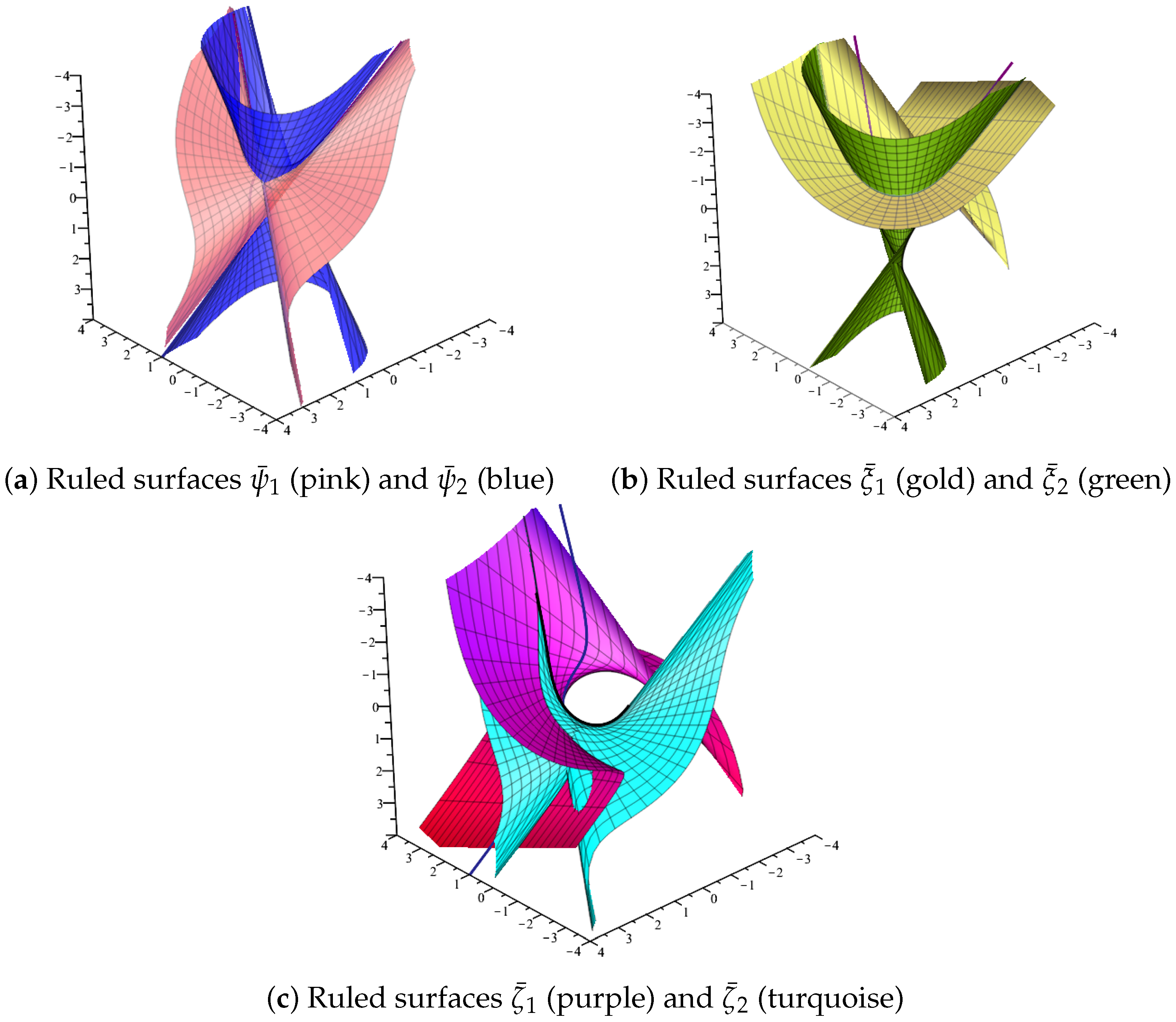
Example 1.

Let $\phi :s\in \left(0,\infty \right)\to {\mathbb{R}}^3$ be a unit-speed spacelike curve with the following parametrization:

$$\phi \left(s\right)=\left(sin\left(ln\left(s\right)\right)-scos\left(ln\left(s\right)\right),cos\left(ln\left(s\right)\right)+ssin\left(ln\left(s\right)\right),s-ln\left(s\right)\right).$$

As ${∥{\phi }^{\prime }\left(s\right)∥}_L=1$, the Frenet vectors and curvatures for $\phi =\phi \left(s\right)$ are computed as

$$\begin{array}{cc}\hfill T_{\phi }\left(s\right)=& {\displaystyle \frac{\left(\left(1-s\right)cos\left(ln\left(s\right)\right)+ssin\left(ln\left(s\right)\right),\left(s-1\right)sin\left(ln\left(s\right)\right)+scos\left(ln\left(s\right)\right),s-1\right)}{s}},\hfill \\ \hfill N_{\phi }\left(s\right)=& {\displaystyle \frac{\left(\left(s-1\right)\left(sin\left(ln\left(s\right)\right)+cos\left(ln\left(s\right)\right)\right),\left(s-1\right)\left(cos\left(ln\left(s\right)\right)-sin\left(ln\left(s\right)\right)\right),1\right)}{\sqrt{|2s^2-4s+1|}}},\hfill \\ \hfill B_{\phi }\left(s\right)=& {\displaystyle \frac{\left(\begin{array}{c}\left(s^2-3s+1\right)cos\left(ln\left(s\right)\right)-ssin\left(ln\left(s\right)\right)\left(s-1\right),\hfill \\ \left(-s^2+s\right)cos\left(ln\left(s\right)\right)-\left(s^2-3s+1\right)sin\left(ln\left(s\right)\right),-2s^2+3s-1\hfill \end{array}\right)}{s\sqrt{|2s^2-4s+1|}}},\hfill \\ \hfill {\kappa }_{\phi }\left(s\right)=& {\displaystyle \frac{\sqrt{|2s^2-4s+1|}}{s^2}},{\tau }_{\phi }\left(s\right)={\displaystyle \frac{-2s^3+8s^2-6s+1}{|2s^2-4s+1|s^2}}.\hfill \end{array}$$

Note that for the given curve, the causal character of ${T_{\phi }}^{\prime }\left(s\right)$ is determined by the sign of $2s^2-4s+1$ since ${\displaystyle {〈{\phi }^{″}\left(s\right),{\phi }^{″}\left(s\right)〉}_L=\frac{2s^2-4s+1}{s^4}.}$ Thus, we note that ${T_{\phi }}^{\prime }\left(s\right)$ is timelike if $s\in \left(1-{\displaystyle \frac{\sqrt{2}}{2}},1+{\displaystyle \frac{\sqrt{2}}{2}}\right)$, and spacelike if otherwise, except for the roots.

Further, the involute of the curve $\phi =\phi \left(s\right)$, which is defined by $\overline{\phi }\left(s\right)=\phi \left(s\right)+\left(c-s\right)T_{\phi }\left(s\right)$, can be given as follows:

$$\overline{\phi }\left(s\right)=\left(\left(1-s\right)sin\left(ln\left(s\right)\right)-cos\left(ln\left(s\right)\right),\left(1-s\right)cos\left(ln\left(s\right)\right)+sin\left(ln\left(s\right)\right),1-ln\left(s\right)\right),$$

where $c=0$. The Frenet vectors and the curvatures of the involute curve $\overline{\phi }=\overline{\phi }\left(s\right)$ are computed as in the following:

$$\begin{array}{cc}\hfill T_{\overline{\phi }}\left(s\right)=& {\displaystyle \frac{\left(\left(s-1\right)\left(sin\left(ln\left(s\right)\right)+cos\left(ln\left(s\right)\right)\right),\left(s-1\right)\left(cos\left(ln\left(s\right)\right)-sin\left(ln\left(s\right)\right)\right),1\right)}{\sqrt{|2s^2-4s+1|}}}=-N_{\phi }\left(s\right),\hfill \\ \hfill N_{\overline{\phi }}\left(s\right)=& {\displaystyle \frac{\sqrt{2}\left(\begin{array}{c}-\left(\left(s^3-3s^2+2s-0.5\right)\left(sin\left(ln\left(s\right)\right)-cos\left(ln\left(s\right)\right)\right)+ssin\left(ln\left(s\right)\right)\right),\hfill \\ \left(\left(s^3-3s^2+2s-0.5\right)\left(sin\left(ln\left(s\right)\right)+cos\left(ln\left(s\right)\right)\right)+scos\left(ln\left(s\right)\right)\right),s\left(s-1\right)\hfill \end{array}\right)}{\sqrt{|2s^4-8s^3+10s^2-6s+1|}\sqrt{|2s^2-4s+1|}}},\hfill \\ \hfill B_{\overline{\phi }}\left(s\right)=& {\displaystyle \frac{\left(\left(1-2s\right)sin\left(ln\left(s\right)\right)+cos\left(ln\left(s\right)\right),\left(1-2s\right)cos\left(ln\left(s\right)\right)-sin\left(ln\left(s\right)\right),-2{\left(s-1\right)}^2\right)}{\sqrt{2}\sqrt{|2s^4-8s^3+10s^2-6s+1|}}}\hfill \\ \hfill {\kappa }_{\overline{\phi }}\left(s\right)=& {\displaystyle \frac{\sqrt{2}\sqrt{|2s^4-8s^3+10s^2-6s+1|}}{|2s^2-4s+1{|}^{\frac{3}{2}}}},{\tau }_{\overline{\phi }}\left(s\right)={\displaystyle \frac{2s^2-s+1}{2s^4-8s^3+10s^2-6s+1}}\hfill \end{array}$$

As the casual characteristics of the curve change in its domain $I=\left(0,\infty \right)$, we illustrate the corresponding involutive partner-ruled surfaces in two folds.

Case 1.

For $1+{\displaystyle \frac{1}{\sqrt{2}}}<s$, the curve $\phi =\phi \left(s\right)$ is a unit-speed spacelike curve with a timelike binormal. For this case, the illustrations of the involutive partner-ruled surfaces are given in Figure 1.

Case 2.

For $s\in \left(1-{\displaystyle \frac{\sqrt{2}}{2}},1+{\displaystyle \frac{\sqrt{2}}{2}}\right)$, the curve $\phi =\phi \left(s\right)$ is considered to be a unit-speed spacelike curve with a spacelike binormal. For such a situation, the illustrations of the involutive partner-ruled surfaces are given in Figure 2.

3. Conclusions

This study focuses on constructing involute partner-ruled surfaces, which are formed by involutes of spacelike curves in Minkowski 3-space $E_1^3.$ First, the involute partner-ruled surfaces formed by the involutes of spacelike curves are defined in Minkowski three-space. Then, the curvatures of Gaussian surfaces and the mean for these surfaces are calculated, and the conditions for these surfaces to be developable and minimal are examined. Also, the criteria for the coordinate curves on the surface to be asymptotic, geodesic, and lines of curvature on the surface are obtained. Examples of these surfaces are provided, and their graphical representations are drawn. Partner-ruled surfaces are critical in differential geometry because they provide insight into the geometric relationships between curves and their associated ruled surfaces.