Exploring Geometrical Properties of Annihilator Intersection Graph of Commutative Rings

Abstract

Let $\Lambda$ denote a commutative ring with unity and $\mathfrak{D}\left(\Lambda \right)$ denote a collection of all annihilating ideals from $\Lambda$. An annihilator intersection graph of $\Lambda$ is represented by the notation $\mathcal{AIG}\left(\Lambda \right)$. This graph is not directed in nature, where the vertex set is represented by $\mathfrak{D}{\left(\Lambda \right)}^{*}$. There is a connection in the form of an edge between two distinct vertices $\varsigma$ and $\varrho$ in $\mathcal{AIG}\left(\Lambda \right)$ iff $Ann\left(\varsigma \varrho \right)\ne Ann\left(\varsigma \right)\cap Ann\left(\varrho \right)$. In this work, we begin by categorizing commutative rings $\Lambda$, which are finite in structure, so that $\mathcal{AIG}\left(\Lambda \right)$ forms a star graph/2-outerplanar graph, and we identify the inner vertex number of $\mathcal{AIG}\left(\Lambda \right)$. In addition, a classification of the finite rings where the genus of $\mathcal{AIG}\left(\Lambda \right)$ is 2, meaning $\mathcal{AIG}\left(\Lambda \right)$ is a double-toroidal graph, is also investigated. Further, we determine $\Lambda$, having a crosscap 1 of $\mathcal{AIG}\left(\Lambda \right),$ indicating that $\mathcal{AIG}\left(\Lambda \right)$ is a projective plane. Finally, we examine the domination number for the annihilator intersection graph and demonstrate that it is at maximum, two.

1. Introduction

Algebra, combinatorics and discrete mathematics are three crucial branches of mathematical sciences. These branches frequently intersect, using techniques from one to the other. The first occurrence of forming a group from a graph resulted from studying the automorphic groups of graphs. This led to the essential question of identifying classes of groups that can be represented as automorphic groups of graphs. Conversely, this research involves creating graphs from groups. The earliest example of this was given in 1878 for the formation of graphs with finite groups due to Arthur Cayley, known as pictorial representation for a class of groups. Today, Cayley graphs are important discrete structures in parallel computing and they are applied in routing problems to resolve and correct any type of error that appears.

In classical algebra, the notable construction involves graphs that are derived from rings with finite or infinite characteristics. Investigating graphs originating from rings enhances the relationship between structural properties of rings with their corresponding graph structures. The present research starts with the extensively studied zero-divisor graphs of commutative rings. The concept of a graph, which is represented by ${\Gamma }_0\left(\Lambda \right)$ and is associated with a set of zero-divisor elements of a commutative ring $\Lambda$, was initially defined by Beck [1] in 1988. The author explored the colors of these graphs. Beck hypothesized that the clique number and the chromatic number are not different for the graph ${\Gamma }_0\left(\Lambda \right).$ However, Anderson and Naseer [2], in 1993, refuted Beck’s hypothesis by presenting a counterexample. In 1999, Anderson and Livingston [3] not only coined the term zero-divisor graph but also revised Beck’s definition. They interlinked the relationship between the structural properties of commutative rings and the corresponding theoretic properties of the graphs due to a set of zero-divisor elements. Beck’s initial definition of a zero-divisor graph includes all elements of $\Lambda$ as vertices of ${\Gamma }_0\left(\Lambda \right)$, while in $\Gamma \left(\Lambda \right)$, a set of vertices consists of all zero-divisor elements of $\Lambda$.

In the theory of rings, the structural properties are often more closed to the behavior of associated ideals rather individual elements of rings. Ideals gives structural details that might be missed when focusing solely on elements, making it logical to introduce a graph with its corresponding ideals as all of its vertex. Then, Behboodi and Rakeei [4,5] introduced a different graph that would come prior to it and named it the annihilating-ideal graph $\mathcal{AG}\left(\Lambda \right)$ on $\Lambda$, whose vertices belong to the set of nonzero annihilating ideals of $\Lambda$ instead of those in the previously known zero-divisor graphs. This makes annihilating-ideal graphs of rings a valuable tool to study certain features of properties of rings with commutativity, particularly structures based on associated ideals of the ring.

In a related development, Vafaei et al. [6] introduced a class of ideal-based graphs that are undirected over a ring and named these graphs based on the annihilator intersection of $\Lambda$, which is denoted by the symbol $\mathcal{AIG}\left(\Lambda \right)$. This graph has $\mathfrak{D}{\left(\Lambda \right)}^{*}$ as its vertex set, and there is connection in form of an edge between two distinct vertices $\varsigma$ and $\varrho$ in $\mathcal{AIG}\left(\Lambda \right)$ iff $Ann\left(\varsigma \varrho \right)\ne Ann\left(\varsigma \right)\cap Ann\left(\varrho \right)$.

In [7], Rehman et al. characterized finite commutative rings that have the annihilator intersection graph as either a unicycle, a tree, an outerplanar graph, or a split graph. They also classified isomorphic properties of $\Lambda$, whose graph based on the annihilator intersection is either a toroidal or a planar graph. Minimal non-outerplanar graphs are discussed in [8]. Algebraic graphs are not only studied in classical structures but in logical algebras and lattice theory as well, e.g., Moin et al. [9] investigated a graph associated with UP-algebras that is a class of logical algebras.

This article begins with the classification of the finite commutative rings $\Lambda$ to determine whether $\mathcal{AIG}\left(\Lambda \right)$ is a star graph or a 2-outerplanar graph, and we determine the inner vertex number of $\mathcal{AIG}\left(\Lambda \right)$. We also identify the class of finite rings to determine that the genus of $\mathcal{AIG}\left(\Lambda \right)$ is 2, meaning that $\mathcal{AIG}\left(\Lambda \right)$ is a double-toroidal graph. In addition, we determine the class of finite rings $\Lambda$ to determine that the crosscap of $\mathcal{AIG}\left(\Lambda \right)$ is 1, indicating that $\mathcal{AIG}\left(\Lambda \right)$ is a projective plane. Finally, we examine the domination number of the annihilator intersection graph and prove that it is at maximum, two.

The set $\mathfrak{G}=(V,E)$ is a collection of vertices V and edges E in such a way that its edges are undirected. The structure formed by the collection of edges and vertices is simple; it is called a graph. A graph has a number of classes. Among the classes of graphs, we denote a complete graph by the notation $K_n$, in which every pair of distinct vertices is connected by an edge. In an r-partite graph, the set of vertices are partitioned into r subsets, ensuring that there is no connection between vertices within the same partition. Specifically, a complete r-partite graph has vertices connected to all vertices not in the same subset. $K_{m,n}$ is another special class of r-partite graph that is from the family of 2-partite graph, whose part sizes are m and n, where each vertex from one part is connected to every vertex in the opposite part. A dominating set S of $\mathfrak{G}$ is a subset of $V\left(\mathfrak{G}\right)$ such that every vertex in $V\left(\mathfrak{G}\right)\setminus S$ has at least one neighbor in S. $\delta \left(\mathfrak{G}\right)$ is the domination number of $\mathfrak{G}$ by the size of the smallest dominating set in $\mathfrak{G}$. In [10], the smallest k in a complete graph, such that G is k-outerplanar, is determined.

Mohar and Thomassen [11] introduced the concept of graphs on surfaces. Let $S_k$ represent a sphere with k handles for $k\ge 0,$ indicating the surface of genus oriented to k. $\gamma \left(\mathfrak{G}\right)$ represents the genus of graph $\mathfrak{G}$, which is the least positive integer n so that $\mathfrak{G}$ can be embedded in $S_n$. Visually, a graph $\mathfrak{G}$ is considered embedded in a surface if it can be depicted on that surface such that its edges only intersect at their common vertices. A planar graph is a class of graphs whose genus is $0,$ while a toroidal graph is another class of graphs with genus $1.$ A graph with genus 2 is called a double-toroidal graph. In addition, it is important to note that $\gamma \left(\mathfrak{G}\right)\ge \gamma \left(H\right)$ indicates that H is a subgraph of $\mathfrak{G}$. The genus of a graph is given in more detail in [7,12]. For other terminologies based on graph theoretic concepts, the reader may refer to [13].

Throughout this research, commutative rings are considered those that have a unit element 1 other than $0.$ For $\Lambda$, $\Theta \left(\Lambda \right)$ denotes the collection of ideals of $\Lambda$ and $\Theta {\left(\Lambda \right)}^{*}=\Theta \left(\Lambda \right)\setminus \left\{0\right\}$. An ideal $\varsigma$ of $\Lambda$ is called an annihilator ideal if ∃ is an ideal $(\ne 0)\varrho$ of $\Lambda \ni \varsigma \varrho =0$. For $\varsigma \in \Theta \left(\Lambda \right)$, the annihilator of $\varsigma$ is defined as $Ann\left(\varsigma \right)=\{\varrho \in \Theta (\Lambda ):\varsigma \varrho =0\}$. Let $\mathfrak{D}\left(\Lambda \right)$ represent the collection of annihilator ideals where $\mathfrak{D}{\left(\Lambda \right)}^{*}=\mathfrak{D}\left(\Lambda \right)\setminus \left\{0\right\}$. The sets of minimal prime ideals, nilpotent elements, zero-divisors, and unity of $\Lambda$ are denoted correspondingly by $M\left(\Lambda \right),$$N\left(\Lambda \right)$, $Z\left(\Lambda \right)$, and $U\left(\Lambda \right)$. More details with different notations and other terminologies for the ring theoretic concept can be found in [14].

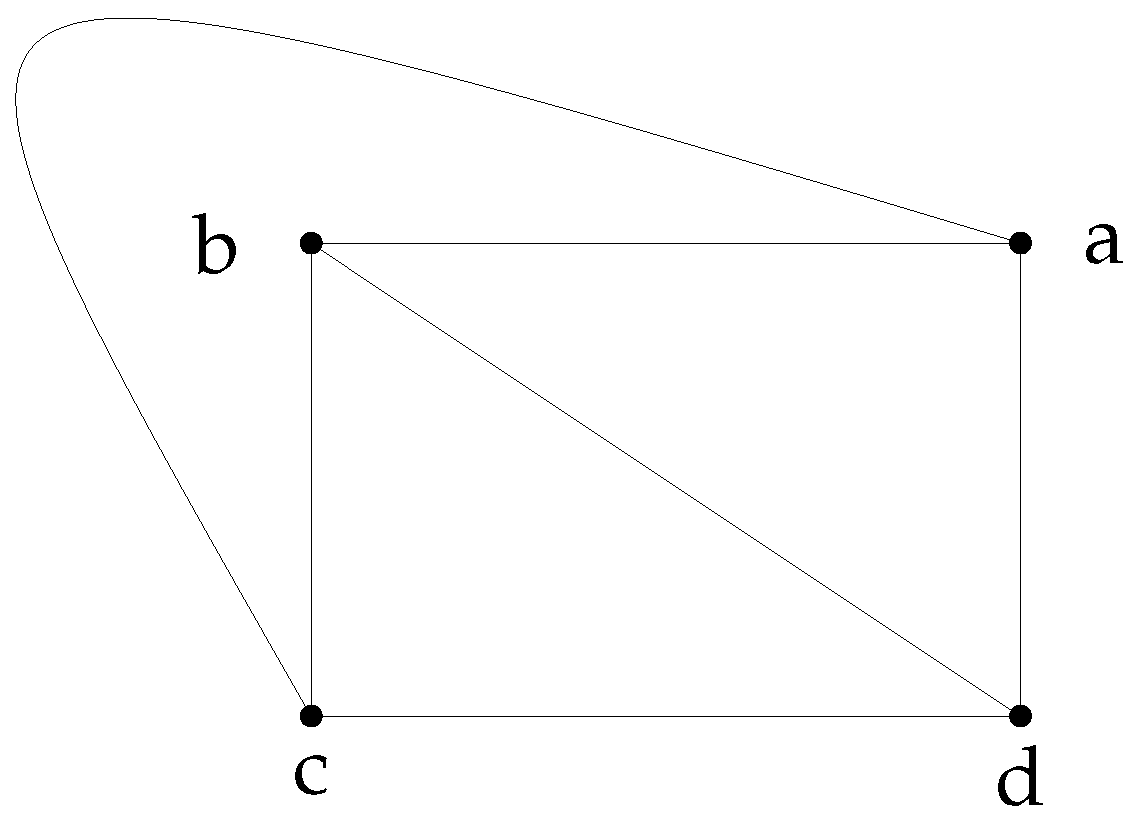
2. Basic Properties of $\mathcal{AIG}\left(\Lambda \right)$

This section comprises the characterization of $\Lambda$ to determine that $\mathcal{AIG}\left(\Lambda \right)$ is a ring graph, star graph, or a 2-outerplanar graph. In addition, we determine the inner vertex number of $\mathcal{AIG}\left(\Lambda \right)$ for a finite commutative ring.

The subsequent observations of [6] are frequently utilized throughout this paper.

Lemma 1

([6]). Let Λ be a commutative ring, where $\varsigma ,\varrho \in \mathfrak{D}{\left(\Lambda \right)}^{*}$. Consequently, the subsequent statements are valid:

1.

If $\varsigma \sim \varrho$∉$E\left(\mathcal{AIG}\right(\Lambda \left)\right)$, then $Ann\left(\varsigma \right)=Ann\left(\varrho \right)$.

2.

If $\varsigma \sim \varrho$∈$E\left(\mathcal{AG}\right(\Lambda \left)\right)$, then $\varsigma \sim \varrho$∈$E\left(\mathcal{AIG}\right(\Lambda \left)\right)$.

3.

If $\varsigma \sim \varrho$∉$E\left(\mathcal{AIG}\right(\Lambda \left)\right)$, then there exists a vertex ${\varrho }_1\in \mathfrak{D}{\left(\Lambda \right)}^{*}$ such that $\varsigma \sim {\varrho }_1\sim \varrho$ forms a path in $\mathcal{AIG}\left(\Lambda \right)$.

Lemma 2

([6]). Let Λ be a non-reduced ring. Then, every nilpotent ideal of Λ other than zero is connected with every other vertex in $\mathcal{AIG}\left(\Lambda \right)$. Specifically, the subgraph or subpart formed with nilpotent ideals is a complete subgraph or subpart of $\mathcal{AIG}\left(\Lambda \right)$.

Theorem 1

([7]). Let Λ be a local commutative ring. Then, $\mathcal{AIG}\left(\Lambda \right)$ generates a complete graph.

In the subsequent ring, we investigate the class of finite commutative rings $\Lambda$ to determine that $\mathcal{AIG}\left(\Lambda \right)$ forms a star graph.

Theorem 2.

The structure $\mathcal{AIG}\left(\Lambda \right)$ turns to a star graph in a finite commutative ring Λ iff either Λ is a local ring having a maximum of two different ideals other than zero or $\Lambda \cong {{\rm Y}}_1\times {{\rm Y}}_2$, where ${{\rm Y}}_1$ and ${{\rm Y}}_2$ are fields.

Proof. 

First, consider whether $\mathcal{AIG}\left(\Lambda \right)$ is a star graph. Now, it is known that $\Lambda$ is non-infinite, $\Lambda \cong {\Lambda }_1\times {\Lambda }_2\times \cdots \times {\Lambda }_m$, where $({\Lambda }_i,{\varkappa }_i)$ is a local ring for each i and $m\ge 1$. Assume $m\ge 3$. Consider $a_1={\Lambda }_1\times \left(0\right)\times \left(0\right)\times \cdots \times \left(0\right)$, $a_2=\left(0\right)\times {\Lambda }_2\times \left(0\right)\times \cdots \times \left(0\right)$, and $a_3=\left(0\right)\times \left(0\right)\times {\Lambda }_3\times \left(0\right)\times \cdots \times \left(0\right)\in \Theta {\left(\Lambda \right)}^{*}$. Since $Ann\left(a_i{a}_j\right)\ne Ann\left(a_i\right)\cap Ann\left(a_j\right)$ for each $i,j$, $a_1\sim a_2\sim a_3\sim a_1$ forms a cycle in $\mathcal{AIG}\left(\Lambda \right)$, this contradicts the fact. Hence, $2\ge m$.

Case (1) Suppose $m=2$ and ${\varkappa }_1\ne 0$. Consider $w_1={\Lambda }_1\times \left(0\right)$, $w_2=\left(0\right)\times {\Lambda }_2$, and $w_3={\varkappa }_1\times \left(0\right)\in \Theta {\left(\Lambda \right)}^{*}$. Since $Ann\left(w_i{w}_j\right)\ne Ann\left(w_i\right)\cap Ann\left(w_j\right)$ for each $i,j$, $w_1\sim w_2\sim w_3\sim w_1$ forms a cycle in $\mathcal{AIG}\left(\Lambda \right)$, it is contradictory. Therefore, ${\Lambda }_1$ is a field. In similar fashion, ${\Lambda }_2$ is a field.

Case (2) Suppose $m=1$, i.e., $\Lambda$ is a local ring. Using Theorem 1, graph $\mathcal{AIG}\left(\Lambda \right)$ is complete. Since $\mathcal{AIG}\left(\Lambda \right)$ is a star graph, ${1\le |\Theta \left(\Lambda \right)}^{*}|\le 2$.

Conversely, if $\Lambda$ is a local ring with ${1\le |\Theta \left(\Lambda \right)}^{*}|\le 2$, then $\mathcal{AIG}\left(\Lambda \right)\cong K_1$ or $K_2.$ Using Theorem 1, if $\Lambda \cong {{\rm Y}}_1\times {{\rm Y}}_2$, where ${{\rm Y}}_1$ and ${{\rm Y}}_2$ are fields, then $\mathcal{AIG}\left(\Lambda \right)\cong K_2$. This confirms that it is a star graph. □

The results for a planar graph established by Rehman et al. [7] are presented as follows:

Theorem 3

([7]). The structure $\mathcal{AIG}\left(\Lambda \right)$ is a planar graph in the finite commutative ring Λ iff any one subsequent below is satisfied:

1.

Λ is a local ring with maximum 4 non-trivial ideals.

2.

$\Lambda \cong {{\rm Y}}_1\times {{\rm Y}}_2$, where ${{\rm Y}}_1$ and ${{\rm Y}}_2$ are fields.

3.

$\Lambda \cong {\rm Y}\times \mathfrak{S}$, where Υ is a field, $(\mathfrak{S},\varkappa )$ is a local ring, and ϰ is a unique non-trivial ideal of $\mathfrak{S}$.

Theorem 4

([7]). The structure $\mathcal{AIG}\left(\Lambda \right)$ in a finite commutative ring Λ is an outerplanar graph iff either Λ is local with ${|\Theta \left(\Lambda \right)}^{*}|\le 3$ or $\Lambda \cong {{\rm Y}}_1\times {{\rm Y}}_2$, where ${{\rm Y}}_1$ and ${{\rm Y}}_2$ are fields.

Consider the graph $\mathfrak{G}(p,q)$. A chord in $\mathfrak{G}$ is an edge that connects two non-adjacent vertices within a cycle of $\mathfrak{G}$. A cycle C in $\mathfrak{G}$ is called primitive if there are no chords in it. A graph $\mathfrak{G}$ is said to have the primitive cycle property (PCP) if any two primitive cycles share a maximum of one edge. The notation $frank\left(\mathfrak{G}\right)$ stands for a free rank of $\mathfrak{G}$, and it is the number of primitive cycles in $\mathfrak{G}$. The cycle rank of $\mathfrak{G}$, denoted by $rank\left(\mathfrak{G}\right)$, is given by $q-p+k$, where k indicates the number of connected components of $\mathfrak{G}$. The cycle rank is also known as the dimension of the cycle space of $\mathfrak{G}$. Due to [15], $rank\left(\mathfrak{G}\right)\le frank\left(\mathfrak{G}\right)$. A graph $\mathfrak{G}$ is referred as a ring graph, meeting any one subsequent equivalent assertions [15]:

• $rank\left(\mathfrak{G}\right)=frank\left(\mathfrak{G}\right)$;
• $\mathfrak{G}$ satisfies the PCP without having a subdivision of $K_4$ as a subpart.

We are now ready to identify the class of rings $\Lambda$ to determine that $\mathcal{AIG}\left(\Lambda \right)$ is a ring graph.

Theorem 5.

The structure $\mathcal{AIG}\left(\Lambda \right)$ is a ring graph in the finite commutative ring Λ iff any one of the following assertions is met:

1.

Λ is a local ring with a maximum of 3 non-trivial ideals.

2.

$\Lambda \cong {{\rm Y}}_1\times {{\rm Y}}_2$, where ${{\rm Y}}_1$ and ${{\rm Y}}_2$ are fields.

Proof. 

Since all ring graphs are planar, we only need to verify the rings listed in Theorem 3 to determine if they form ring graphs. If $\Lambda$ is a local ring with ${|\Theta \left(\Lambda \right)}^{*}|=1$ or 2, or if $\Lambda \cong {{\rm Y}}_1\times {{\rm Y}}_2$, where ${{\rm Y}}_1$ and ${{\rm Y}}_2$ are fields, then using Theorem 1, $\mathcal{AIG}\left(\Lambda \right)\cong K_1$ or $K_2$. In such cases, $rank\left(\mathcal{AIG}\right(\Lambda \left)\right)=frank\left(\mathcal{AIG}\right(\Lambda \left)\right)=0$, making $\mathcal{AIG}\left(\Lambda \right)$ a ring graph.

If $\Lambda$ is a local ring with ${|\Theta \left(\Lambda \right)}^{*}|=3$, then using Theorem 1, $\mathcal{AIG}\left(\Lambda \right)\cong K_3$. Here, $rank\left(\mathcal{AIG}\right(\Lambda \left)\right)=frank\left(\mathcal{AIG}\right(\Lambda \left)\right)=1$, so $\mathcal{AIG}\left(\Lambda \right)$ is also a ring graph.

However, if $\Lambda$ is a local ring with ${|\Theta \left(\Lambda \right)}^{*}|=4$ or if $\Lambda \cong {\rm Y}\times \mathfrak{S}$, where ${\rm Y}$ is a field and $(\mathfrak{S},\varkappa )$ is a local ring with $\varkappa$ as a unique non-trivial ideal of $\mathfrak{S}$, then using Theorem 1, $\mathcal{AIG}\left(\Lambda \right)\cong K_4$. In this situation, $rank\left(\mathcal{AIG}\right(\Lambda \left)\right)=3$ and $frank\left(\mathcal{AIG}\right(\Lambda \left)\right)=4$, meaning $\mathcal{AIG}\left(\Lambda \right)$ is not a ring graph. □

A planar graph embedding of $\Lambda$ is called 1-outerplanar if the planar graph itself is outerplanar, which means the collection of vertices are connected to the outer face in the embedding. This idea extends to k-outerplanar embeddings, where, once the vertex set is removed from the outer face corresponding to incident edges, the remaining graph is $(k-1)$-outerplanar. We call a graph to be k-outerplanar if it allows for such a k-outerplanar embedding. The outerplanarity index of a graph $\mathfrak{G}$ is the smallest k such that $\mathfrak{G}$ is k-outerplanar. For a planar graph $\mathfrak{G}$, the inner vertex number $i\left(\mathfrak{G}\right)$ is defined as the minimum number of vertices not on the boundary of the exterior face in any plane embedding of $\mathfrak{G}$. A graph $\mathfrak{G}$ is termed minimally non-outerplanar if $i\left(\mathfrak{G}\right)$ equals 1. For additional details on k-outerplanarity, refer to [8,10].

The subsequent observations are crucial for deriving the results in this section.

Theorem 6

([16]). A graph $\mathfrak{G}$ is outerplanar iff it is not contained in a subdivision of $K_4$ or $K_{2,3}$.

In the next result, the classification of the finite rings $\Lambda$ as a 2-outerplanar graph $\mathcal{AIG}\left(\Lambda \right)$ is given.

Theorem 7.

The structure $\mathcal{AIG}\left(\Lambda \right)$ in the finite commutative ring Λ has an outerplanarity index of 2 iff any of the subsequent conditions is satisfied:

1.

Λ is a local ring with exactly 4 non-trivial ideals.

2.

$\Lambda \cong {\rm Y}\times \mathfrak{S}$, where Υ is a field and $(\mathfrak{S},\varkappa )$ is a local ring with ϰ as a unique non-trivial ideal of $\mathfrak{S}$.

Proof. 

Suppose that $\mathcal{AIG}\left(\Lambda \right)$ has an outerplanarity index of 2. This means that $\mathcal{AIG}\left(\Lambda \right)$ is a planar graph. Hence, according to Theorem 3, $\Lambda$ must be any one of the rings identified in Theorem 3.

If $\Lambda$ is a local ring with ${|\Theta \left(\Lambda \right)}^{|}\le 3$ or if $\Lambda \cong {{\rm Y}}_1\times {{\rm Y}}_2$, where ${{\rm Y}}_1$ and ${{\rm Y}}_2$ are fields, then, using Theorem 4, the outerplanarity index of $\mathcal{AIG}\left(\Lambda \right)$ is 1, which is contradictory. Therefore, $\Lambda$ must be a local ring with ${|\Theta \left(\Lambda \right)}^{*}|=4$ or $\Lambda \cong {\rm Y}\times \mathfrak{S}$, where ${\rm Y}$ is a field and $(\mathfrak{S},\varkappa )$ is a local ring with $\varkappa$ as a unique non-trivial ideal of $\mathfrak{S}$.

Conversely, if $\Lambda$ is a local ring with ${|\Theta \left(\Lambda \right)}^{*}|=4$ or if $\Lambda \cong {\rm Y}\times \mathfrak{S}$, where ${\rm Y}$ is a field and $(\mathfrak{S},\varkappa )$ is a local ring with $\varkappa$ as a unique non-trivial ideal of $\mathfrak{S}$, then $\mathcal{AIG}\left(\Lambda \right)\cong K_4$. So, using Theorem 6, $\mathcal{AIG}\left(\Lambda \right)$ is not a 1-outerplanar graph. Removing the vertices from the outer face results in a graph that is $K_1$, which is 1-outerplanar (refer to Figure 1). Therefore, by definition, $\mathcal{AIG}\left(\Lambda \right)$ is 2-outerplanar, establishing 2 as the minimum. Thus, the outerplanarity index of $\mathcal{AIG}\left(\Lambda \right)$ is 2. □

Corollary 1.

The structure $\mathcal{AIG}\left(\Lambda \right)$ in a finite commutative ring Λ has an outerplanarity index of maximum two.

Lastly, we determine the inner vertex number of $\mathcal{AIG}\left(\Lambda \right)$ for the class of finite rings $\Lambda$ in the subsequent result.

Theorem 8.

The inner vertex number of $\mathcal{AIG}\left(\Lambda \right)$ in a finite commutative ring Λ is given by

$$\begin{gathered} i\left(\mathcal{AIG}\left(\Lambda \right)\right)= \\ \left\{\begin{array}{cc}1\hfill & {\mathit{if}\Lambda \mathit{is}a\mathit{local}\mathit{ring}\mathit{with}|\Theta \left(\Lambda \right)}^{*}|=4;\hfill \\ 1\hfill & \mathit{if}\Lambda \cong {\rm Y}\times \mathfrak{S}\mathit{where}{\rm Y}\mathit{is}a\mathit{field}\mathit{and}(\mathfrak{S},\varkappa )\mathit{is}a\mathit{local}\mathit{ring}\mathit{with}\mathit{the}\mathit{unique}\mathit{ideal}\varkappa ;\hfill \\ 0\hfill & \mathit{otherwise}.\hfill \end{array}\right. \end{gathered}$$

Proof. 

By using Theorem 4 and Figure 1, the following proof is directly obtained. □

Corollary 2.

The structure $\mathcal{AIG}\left(\Lambda \right)$ is minimally non-outerplanar in a finite commutative ring Λ iff either Λ is a local ring with exactly 4 non-trivial ideals or $\Lambda \cong {\rm Y}\times \mathfrak{S}$, where Υ is a field and $(\mathfrak{S},\varkappa )$ is a local ring with ϰ as a unique non-trivial ideal of $\mathfrak{S}$.

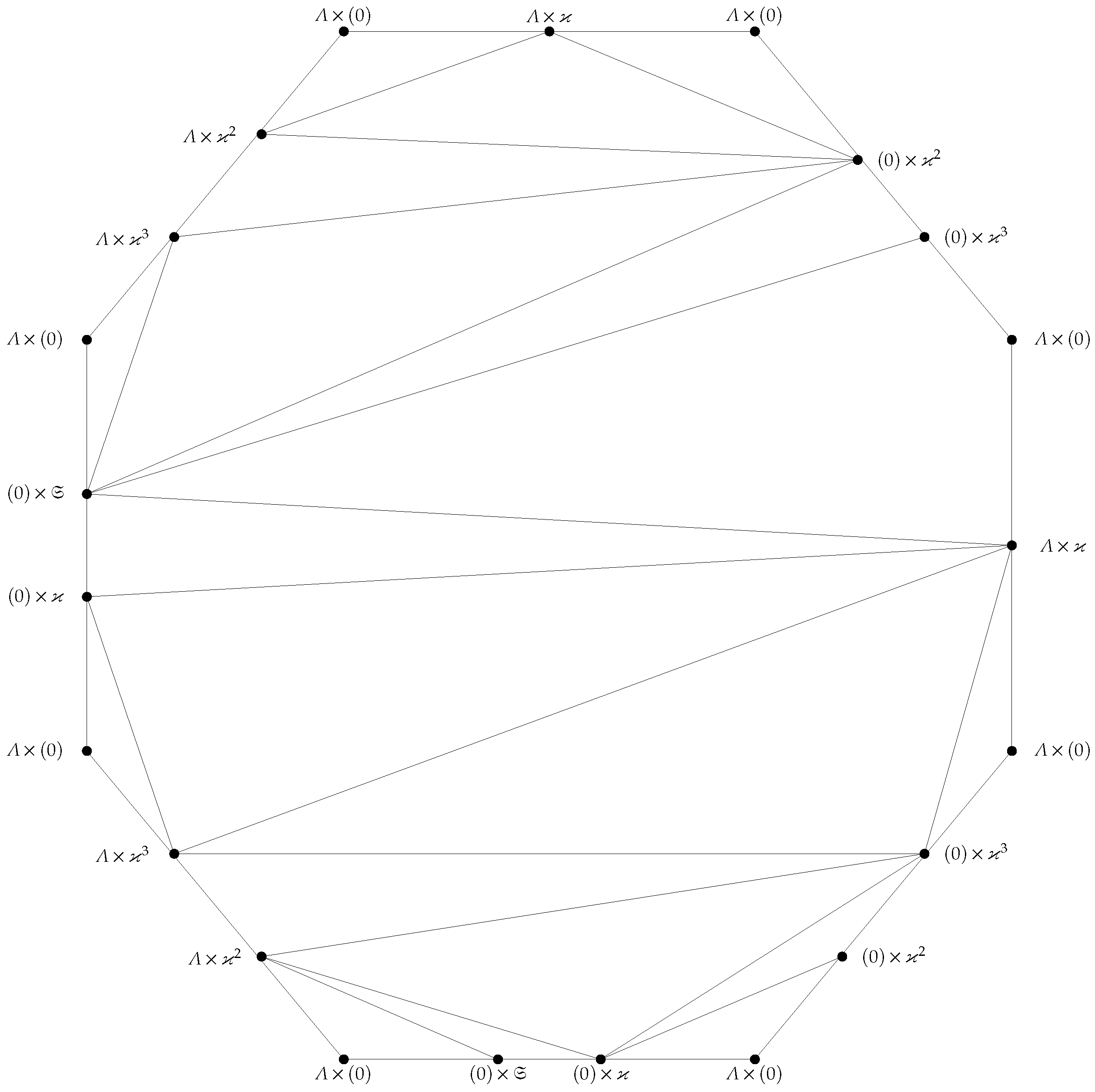
3. Genus of $\mathcal{AIG}\left(\Lambda \right)$

This section comprises the classification of finite rings $\Lambda$ to determine that $\mathcal{AIG}\left(\Lambda \right)$ is a double-toroidal graph, i.e., $\gamma \left(\mathcal{AIG}\right(\Lambda \left)\right)=2$.

For a given real number w, let $\lceil w\rceil =minimum\{a\in \mathbb{Z};a\ge x\}.$

Lemma 3

([16]). Let $p,q\ge 2$. Then,

$$\gamma \left(K_{p,q}\right)=⌈{\displaystyle \frac{1}{4}}(p-2)(q-2)⌉.$$

Specifically, $\gamma \left(K_{4,4}\right)=\gamma \left(K_{3,q}\right)=1$ for $q=3,4,5,6$. In addition, $\gamma \left(K_{5,4}\right)=\gamma \left(K_{6,4}\right)=\gamma \left(K_{3,p}\right)=2$ for $p=7,8,9,10$.

Lemma 4

([16]). Let $p\ge 3$. Then,

$$\gamma \left(K_p\right)=⌈{\displaystyle \frac{1}{12}}(p-3)(p-4)⌉.$$

In particular, $\gamma \left(K_p\right)=1$ for $p=5,6,7$ and $\gamma \left(K_8\right)=2$.

In [7], Rehman et al. identify the class of finite rings to determine that $\mathcal{AIG}\left(\Lambda \right)$ is a toroidal graph, as follows:

Theorem 9

([7] (Theorems 4.3, 4.4, 4.5, 4.6)). Let Λ be a finite commutative ring. Then, $\gamma \left(\mathcal{AIG}\right(\Lambda \left)\right)=1$ iff any one ot these subsequent conditions is satisfied:

1.

Λ is a local ring between 5 and 7 non-trivial ideals.

2.

$\Lambda \cong {{\rm Y}}_1\times {{\rm Y}}_2\times {{\rm Y}}_3$, where ${{\rm Y}}_1$, ${{\rm Y}}_2$, and ${{\rm Y}}_3$ are fields.

3.

$\Lambda \cong {\mathfrak{S}}_1\times {\mathfrak{S}}_2$, where each $({\mathfrak{S}}_i,{\varkappa }_i)$ is a local ring having unique non-trivial ideal ${\varkappa }_i$ for $i=1$ and $i=2$.

4.

$\Lambda \cong {\rm Y}\times \mathfrak{S}$, where Υ is a field and $(\mathfrak{S},\varkappa )$ is a local ring with ϰ and ${\varkappa }^2$ as its only non-trivial ideals.

We now determine the finite commutative rings to determine that the annihilator intersection graph is a double-toroidal graph.

Theorem 10.

$\gamma \left(\mathcal{AIG}\right(\Lambda \left)\right)=2$ in a finite commutative ring Λ iff any one of the conditions below is met:

1.

Λ is a local ring with exactly 8 non-trivial ideals.

2.

$\Lambda \cong {\rm Y}\times \mathfrak{S}$, where Υ is a field and $(\mathfrak{S},\varkappa )$ is a local ring with ϰ, ${\varkappa }^2$, and ${\varkappa }^3$ as its only non-trivial ideals.

Proof. 

Assume that $\gamma \left(\mathcal{AIG}\right(\Lambda \left)\right)=2$. Since $\Lambda$ is a finite non-local ring, it can be expressed as $\Lambda \cong {\Lambda }_1\times {\Lambda }_2\times \cdots \times {\Lambda }_m$, where each $({\Lambda }_i,{\mathrm{m}}_i)$ is a local ring and $m\ge 1$. Suppose $m\ge 4$. Define the subsequent vertices: $a_1={\Lambda }_1\times \left(0\right)\times \cdots \times \left(0\right),a_2=\left(0\right)\times {\Lambda }_2\times \left(0\right)\times \cdots \times \left(0\right),a_3=\left(0\right)\times \left(0\right)\times {\Lambda }_3\times \left(0\right)\times \cdots \times \left(0\right),a_4=\left(0\right)\times \left(0\right)\times \left(0\right)\times {\Lambda }_4\times \left(0\right)\times \cdots \times \left(0\right),b_1={\Lambda }_1\times {\Lambda }_2\times \left(0\right)\times \cdots \times \left(0\right),b_2={\Lambda }_1\times \left(0\right)\times {\Lambda }_3\times \left(0\right)\cdots \times \left(0\right),b_3={\Lambda }_1\times \left(0\right)\times \left(0\right)\times {\Lambda }_4\times \left(0\right)\cdots \times \left(0\right),b_4={\Lambda }_1\times {\Lambda }_2\times {\Lambda }_3\times \left(0\right)\times \cdots \times \left(0\right),b_5=\left(0\right)\times {\Lambda }_2\times {\Lambda }_3\times \left(0\right)\cdots \times \left(0\right),b_6=\left(0\right)\times {\Lambda }_2\times \left(0\right)\times {\Lambda }_4\times \left(0\right)\cdots \times \left(0\right),b_7=\left(0\right)\times \left(0\right)\times {\Lambda }_3\times {\Lambda }_4\times \left(0\right)\cdots \times \left(0\right)\in \Theta {\left(\Lambda \right)}^{*}$. Since $Ann\left(a_i{b}_j\right)\ne Ann\left(a_i\right)\cap Ann\left(b_j\right)$ for every i and j, the graph $\mathcal{AIG}\left(\Lambda \right)$ contains a subgraph isomorphic to $K_{4,7}$, induced by the set $\{a_1,a_2,a_3,a_4\}\cup \{b_1,b_2,\dots ,b_7\}$. Therefore, by Lemma 3, it follows that $\gamma \left(\mathcal{AIG}\right(\Lambda \left)\right)\ge 3$, which is contradictory. Consequently, we must have $m\le 3$.

Case (1) Assume $m=3$ and ${\varkappa }_1\ne 0$. Let us consider the subsequent vertices: $w_1={\Lambda }_1\times \left(0\right)\times \left(0\right)$, $w_2=\left(0\right)\times {\Lambda }_2\times \left(0\right)$, $w_3=\left(0\right)\times \left(0\right)\times {\Lambda }_3$, $w_4={\varkappa }_1\times \left(0\right)\times \left(0\right)$, $w_5={\varkappa }_1\times {\Lambda }_2\times \left(0\right)$, $w_6={\varkappa }_1\times \left(0\right)\times {\Lambda }_3$, $w_7={\varkappa }_1\times {\Lambda }_2\times {\Lambda }_3$, $w_8={\Lambda }_1\times {\Lambda }_2\times \left(0\right)$, and $w_9={\Lambda }_1\times \left(0\right)\times {\Lambda }_3$, all of which are vertices of $\Theta {\left(\Lambda \right)}^{*}$.

Since $Ann\left(w_i{w}_j\right)\ne Ann\left(w_i\right)\cap Ann\left(w_j\right)$ for i and j, $\mathcal{AIG}\left(\Lambda \right)$ has a $K_9$ subgraph induced by the set $\{w_1,w_2,\dots ,w_9\}$. Therefore, by Lemma 4, we have $\gamma \left(\mathcal{AIG}\right(\Lambda \left)\right)\ge 3$, which contradicts. Hence, ${\varkappa }_1=0$, meaning that ${\Lambda }_1$ must be a field. By a similar reasoning, it follows that ${\Lambda }_2$ and ${\Lambda }_3$ are also fields. Consequently, according to Theorem 9, $\gamma \left(\mathcal{AIG}\right(\Lambda \left)\right)=1$, which again contradicts.

Case (2) Suppose $m=2$, with ${\varkappa }_1\ne 0$ and ${\varkappa }_2\ne 0$. Let $\varsigma \in \Theta {\left(\Lambda \right)}^{*}$ such that $\varsigma \ne {\varkappa }_1$. Define the subsequent vertices: $y_1={\Lambda }_1\times \left(0\right)$, $y_2=\left(0\right)\times {\Lambda }_2$, $y_3={\varkappa }_1\times \left(0\right)$, $y_4=\left(0\right)\times {\varkappa }_2$, $z_1={\varkappa }_1\times {\varkappa }_2$, $z_2={\varkappa }_1\times {\Lambda }_2$, $z_3={\Lambda }_1\times {\varkappa }_2$, $z_4=\varsigma \times \left(0\right)$, $z_5=\varsigma \times {\varkappa }_2$, and $z_6=\varsigma \times {\Lambda }_2\in \Theta {\left(\Lambda \right)}^{*}$.

Since $Ann\left(y_i{z}_j\right)\ne Ann\left(y_i\right)\cap Ann\left(z_j\right)$ for i and j, $\mathcal{AIG}\left(\Lambda \right)$ has a $K_{4,7}$ subgraph induced by the set $\{y_1,y_2,y_3,y_4\}\cup \{z_1,z_2,\dots ,z_6\}$. Therefore, by Lemma 4, we have $\gamma \left(\mathcal{AIG}\right(\Lambda \left)\right)\ge 3$, which contradicts. Thus, ${\varkappa }_1$ must be the sole non-trivial ideal of ${\Lambda }_1$. Similarly, ${\varkappa }_2$ must be a unique non-trivial ideal of ${\Lambda }_2$. Consequently, using Theorem 9, $\gamma \left(\mathcal{AIG}\right(\Lambda \left)\right)=1$, which again contradicts. Therefore, any one ${\varkappa }_i$ must be zero; let us assume ${\varkappa }_1=0$, implying that ${\Lambda }_1$ is a field.

If ${\Lambda }_2$ were also a field, then using Theorem 3, $\gamma \left(\mathcal{AIG}\right(\Lambda \left)\right)=0$, which contradicts. Hence, ${\Lambda }_2$ is not a field and has a non-trivial maximal ideal ${\varkappa }_2$. Let $\eta$ denote the nilpotency index of ${\varkappa }_2$. Suppose $\eta \ge 5$. Consider the subsequent vertices: $u_1={\Lambda }_1\times \left(0\right)$, $u_2=\left(0\right)\times {\Lambda }_2$, $u_3=\left(0\right)\times {\varkappa }_2$, $u_4={\Lambda }_1\times {\varkappa }_2$, $v_1=\left(0\right)\times {\varkappa }_2^{\eta -1}$, $v_2=\left(0\right)\times {\varkappa }_2^{\eta -2}$, $v_3=\left(0\right)\times {\varkappa }_2^{\eta -3}$, $v_4={\Lambda }_1\times {\varkappa }_2^{\eta -1}$, $v_5={\Lambda }_1\times {\varkappa }_2^{\eta -2}$, $v_6={\Lambda }_1\times {\varkappa }_2^{\eta -3}$, and $v_7={\Lambda }_1\times {\varkappa }_2^{\eta -4}\in \Theta {\left(\Lambda \right)}^{*}$.

Since $Ann\left(u_i{v}_j\right)\ne Ann\left(u_i\right)\cap Ann\left(v_j\right)$ for i and j, $\mathcal{AIG}\left(\Lambda \right)$ has $K_{4,7}$ subgraph induced by the set $\{u_1,u_2,u_3,u_4\}\cup \{v_1,v_2,\dots ,v_7\}$, which contradicts Lemma 3. Thus, $\eta \le 4$. Based on Theorems 3 and 9, it is evident that $\eta \ne 2$ and $\eta \ne 3$, so $\eta =4$.

Let $\varrho \in \Theta {\left(\Lambda \right)}^{*}$ such that $\varrho \ne {\varkappa }_2$, ${\varkappa }_2^2$, or ${\varkappa }_2^3$. Define the vertices $r_1={\Lambda }_1\times \left(0\right)$, $r_2=\left(0\right)\times {\Lambda }_2$, $r_3=\left(0\right)\times {\varkappa }_2$, $r_4={\Lambda }_1\times {\varkappa }_2$, $r_5=\left(0\right)\times {\varkappa }_2^2$, $r_6=\left(0\right)\times {\varkappa }_2^3$, $r_7={\Lambda }_1\times {\varkappa }_2^2$, $r_8=\left(0\right)\times \varrho$, and $r_9={\Lambda }_1\times \varrho \in \Theta {\left(\Lambda \right)}^{*}$.

Since $Ann\left(r_i{r}_j\right)\ne Ann\left(r_i\right)\cap Ann\left(r_j\right)$ for each i and j, $\mathcal{AIG}\left(\Lambda \right)$ contains a $K_9$ subgraph induced by the set $\{r_1,r_2,\dots ,r_9\}$, which contradicts Lemma 4. Hence, ${\varkappa }_2$, ${\varkappa }_2^2$, and ${\varkappa }_2^3$ must be unique non-trivial ideals of ${\Lambda }_2$.

Case (3) Assume $m=1$, which means $\Lambda$ is a local ring. According to Theorem 1, $\mathcal{AIG}\left(\Lambda \right)$ is a complete graph. Hence, $\Lambda$ must have exactly 8 non-trivial ideals by using Lemma 4.

Conversely, if $\Lambda \cong {\rm Y}\times \mathfrak{S}$, where ${\rm Y}$ is a field and $(\mathfrak{S},\varkappa )$ is a local ring with $\varkappa$, ${\varkappa }^2$, and ${\varkappa }^3$ as unique non-trivial ideals of $\mathfrak{S}$, then the double-toroidal embedding of $\mathcal{AIG}\left(\Lambda \right)$ is illustrated in Figure 2. In addition, if $\Lambda$ is a local ring having precisely 8 non-trivial ideals, this implies that $\mathcal{AIG}\left(\Lambda \right)\cong K_8$, using Theorem 1. Thus, applying Lemma 4, we find that $\gamma \left(\mathcal{AIG}\right(\Lambda \left)\right)=2$. □

Example 1.

Let $\Lambda ={\mathbb{Z}}_5\times {\mathbb{Z}}_{16}$; then, using Theorem 10, $\gamma \left(\mathcal{AIG}\right(\Lambda \left)\right)=2$.

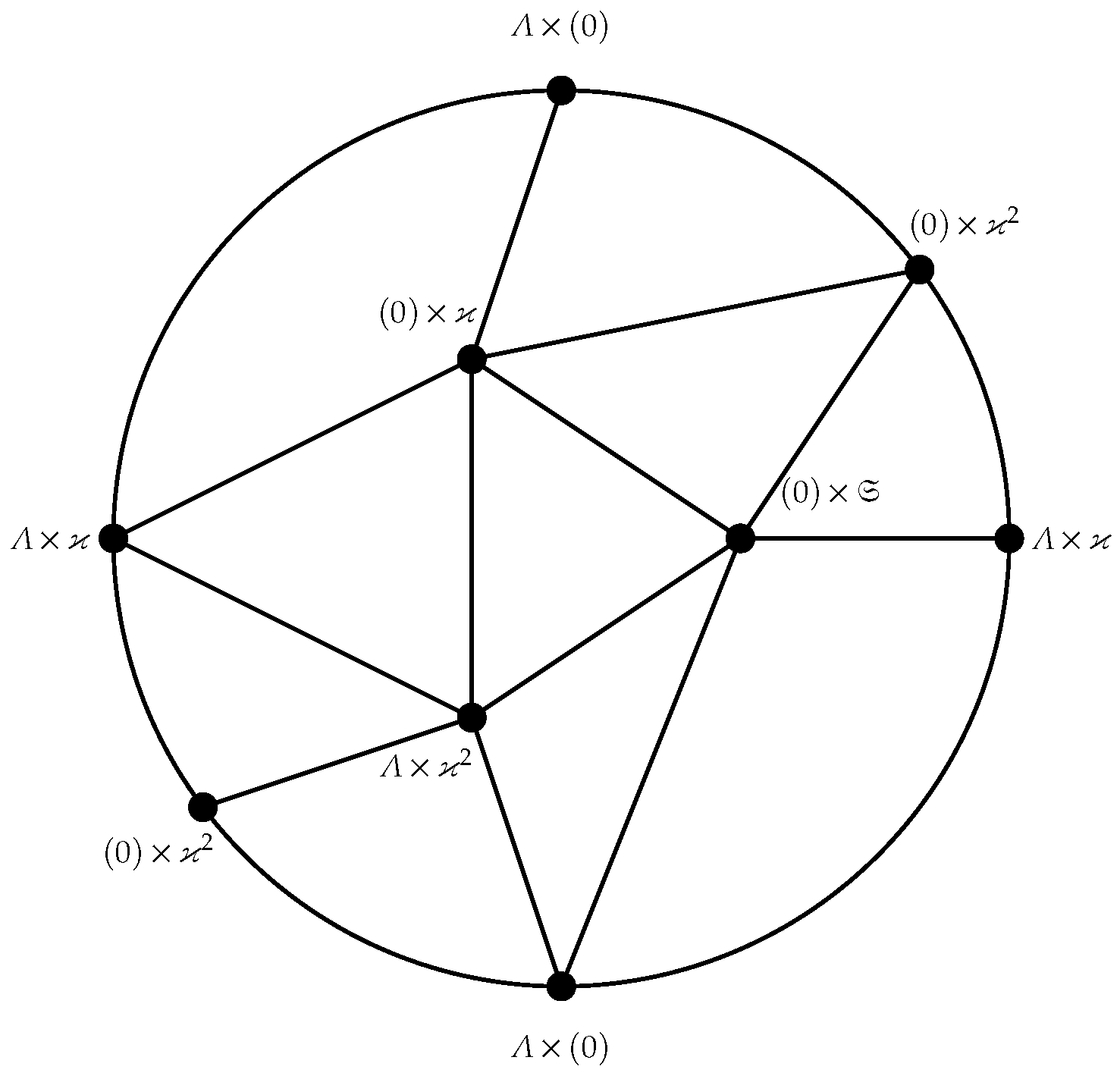
4. Crosscap of $\mathcal{AIG}\left(\Lambda \right)$

This section comprises the identification of the class of rings $\Lambda$ to determine that the crosscap number of the annihilator intersection graph equals one, i.e., $\overline{\gamma }\left(\mathcal{AIG}\left(\Lambda \right)\right)=1$.

For non-negative integers k, $N_k$ denotes a sphere with k crosscaps attached. Any connected compact surface can be topologically represented as $N_k$ for some non-negative integer k. The crosscap number, also referred to as $\overline{\gamma }\left(H\right)$ or a nonorientable genus, is the least positive integer k in such a way that H can be embedded in $N_k$. The projective and Klein bottle graphs correspond to crosscap numbers 1 and 2, respectively. Moreover, if L is a subgraph of H, then $\overline{\gamma }\left(L\right)\le \overline{\gamma }\left(H\right)$.

The subsequent results specify the crosscap numbers for complete graphs and complete bipartite graphs. In this context, the notation $\lceil w\rceil =minimum\{a\in \mathbb{Z};a\ge x\}$.

Lemma 5

([16]). For $p\ge 3$, we have

$$\overline{\gamma }\left(K_p\right)=\left\{\begin{array}{cc}⌈{\displaystyle \frac{(p-3)(p-4)}{6}}⌉\hfill & \mathit{if}p\ge 3\mathit{and}p\ne 7;\hfill \\ 3\hfill & \mathit{if}p=7.\hfill \end{array}\right.$$

Lemma 

([16]). For $p,q\ge 2$, it holds that

$$\overline{\gamma }\left(K_{p,q}\right)=⌈{\displaystyle \frac{(p-2)(q-2)}{2}}⌉.$$

We now proceed to classify finite commutative rings $\Lambda$ to determine that $\mathcal{AIG}\left(\Lambda \right)$ is a projective plane.

Theorem 11.

$\overline{\gamma }\left(\mathcal{AIG}\left(\Lambda \right)\right)=1$ in a finite commutative ring Λ iff any one of the subsequent conditions is satisfied:

1.

Λ is a local ring with 5 or 6 non-trivial ideals.

2.

$\Lambda \cong {{\rm Y}}_1\times {{\rm Y}}_2\times {{\rm Y}}_3$, where each ${{\rm Y}}_i$ is a field for $i=1,2,3$.

3.

$\Lambda \cong {\rm Y}\times \mathfrak{S}$, where Υ is a field and $(\mathfrak{S},\varkappa )$ is a local ring with ϰ and ${\varkappa }^2$ as its only non-trivial ideals.

Proof. 

Assume $\overline{\gamma }\left(\mathcal{AIG}\left(\Lambda \right)\right)=1$. Since $\Lambda$ is finite, hence $\Lambda \cong {\Lambda }_1\times {\Lambda }_2\times \cdots \times {\Lambda }_m$, with each $({\Lambda }_i,{\varkappa }_i)$ is a local ring and $m\ge 1$. If $m\ge 4$, consider the vertices $e_1={\Lambda }_1\times \left(0\right)\times \cdots \times \left(0\right)$, $e_2=\left(0\right)\times {\Lambda }_2\times \left(0\right)\times \cdots \times \left(0\right)$, $e_3=\left(0\right)\times \left(0\right)\times {\Lambda }_3\times \left(0\right)\times \cdots \times \left(0\right)$, $e_4=\left(0\right)\times \left(0\right)\times \left(0\right)\times {\Lambda }_4\times \left(0\right)\times \cdots \times \left(0\right)$, $e_5={\Lambda }_1\times {\Lambda }_2\times \left(0\right)\times \cdots \times \left(0\right)$, and $e_7={\Lambda }_1\times \left(0\right)\times {\Lambda }_3\times \left(0\right)\cdots \times \left(0\right)\in \Theta {\left(\Lambda \right)}^{*}$. Since $Ann\left(e_i{e}_j\right)\ne Ann\left(e_i\right)\cap Ann\left(e_j\right)$ for every $i,j$, the graph $\mathcal{AIG}\left(\Lambda \right)$ has a subgraph isomorphic to $K_{4,7}$ induced by the set $\{e_1,e_2,\dots ,e_7\}$, which contradicts Lemma 3. Therefore, $m\le 3$.

Case (1) Assume $m=3$ and ${\varkappa }_1\ne 0$. Let us consider the subsequent vertices: $f_1={\Lambda }_1\times \left(0\right)\times \left(0\right)$, $f_2=\left(0\right)\times {\Lambda }_2\times \left(0\right)$, $f_3=\left(0\right)\times \left(0\right)\times {\Lambda }_3$, $f_4={\varkappa }_1\times \left(0\right)\times \left(0\right)$, $f_5={\varkappa }_1\times {\Lambda }_2\times \left(0\right)$, $f_6={\varkappa }_1\times \left(0\right)\times {\Lambda }_3$, and $f_7={\varkappa }_1\times {\Lambda }_2\times {\Lambda }_3$, all of which are in $\Theta {\left(\Lambda \right)}^{*}$. Since $Ann\left(f_i{f}_j\right)\ne Ann\left(f_i\right)\cap Ann\left(f_j\right)$ for each pair $(i,j)$, the subgraph induced by $\{f_1,f_2,\dots ,f_7\}$ in $\mathcal{AIG}\left(\Lambda \right)$ is isomorphic to $K_7$. By Lemma 5, this implies $\overline{\gamma }\left(\mathcal{AIG}\left(\Lambda \right)\right)=3$, which contradicts. Therefore, ${\varkappa }_1$ must be zero, meaning ${\Lambda }_1$ is a field. Similarly, it follows that ${\Lambda }_2$ and ${\Lambda }_3$ must also be fields.

Case (2) Assume $m=2$, and both ${\varkappa }_1\ne 0$ and ${\varkappa }_2\ne 0$. Let us define the subsequent vertices: $g_1={\Lambda }_1\times \left(0\right)$, $g_2=\left(0\right)\times {\Lambda }_2$, $g_3={\varkappa }_1\times \left(0\right)$, $g_4=\left(0\right)\times {\varkappa }_2$, $g_5={\varkappa }_1\times {\varkappa }_2$, $g_6={\varkappa }_1\times {\Lambda }_2$, and $g_7={\Lambda }_1\times {\varkappa }_2$, all of which are in $\Theta {\left(\Lambda \right)}^{*}$. Since $Ann\left(g_i{g}_j\right)\ne Ann\left(g_i\right)\cap Ann\left(g_j\right)$ for every pair $(i,j)$, the subgraph induced by $\{g_1,g_2,\dots ,g_7\}$ in $\mathcal{AIG}\left(\Lambda \right)$ is isomorphic to $K_7$. This leads to a contradiction of Lemma 3, implying that at least one of ${\varkappa }_i$ must be zero. Assume ${\varkappa }_1=0$, which means ${\Lambda }_1$ is a field.

If ${\Lambda }_2$ were also a field, then by Lemma 3, $\overline{\gamma }\left(\mathcal{AIG}\left(\Lambda \right)\right)$ would be 0, which is contradictory. Therefore, ${\Lambda }_2$ must not be a field and must have a nonzero maximal ideal ${\varkappa }_2$. Let $\eta$ denote the nilpotency index of ${\varkappa }_2$. Suppose $\eta \ge 4$. Define the following vertices: $h_1={\Lambda }_1\times \left(0\right)$, $h_2=\left(0\right)\times {\Lambda }_2$, $h_3=\left(0\right)\times {\varkappa }_2$, $h_4={\Lambda }_1\times {\varkappa }_2$, $h_5=\left(0\right)\times {\varkappa }_2^{\eta -1}$, $h_6=\left(0\right)\times {\varkappa }_2^{\eta -2}$, and $h_7={\Lambda }_1\times {\varkappa }_2^{\eta -1}$, which are in $\Theta {\left(\Lambda \right)}^{*}$. Since $Ann\left(h_i{h}_j\right)\ne Ann\left(h_i\right)\cap Ann\left(h_j\right)$ for each pair $(i,j)$, the subgraph induced by $\{h_1,h_2,\dots ,h_7\}$ in $\mathcal{AIG}\left(\Lambda \right)$ is isomorphic to $K_7$, which contradicts with Lemma 5. Thus, $\eta \le 3$.

If $\eta =2$, then $\mathcal{AIG}\left(\Lambda \right)\cong K_4$. According to Lemma 5, this would imply $\overline{\gamma }\left(\mathcal{AIG}\left(\Lambda \right)\right)=0$, which contradicts it. Consequently, $\eta$ must be 3.

Consider $\varsigma \in \Theta {\left(\Lambda \right)}^{*}$ such that $\varsigma \ne {\varkappa }_2$ and $\varsigma \ne {\varkappa }_2^2$. Define the following vertices: $r_1={\Lambda }_1\times \left(0\right)$, $r_2=\left(0\right)\times {\Lambda }_2$, $r_3=\left(0\right)\times {\varkappa }_2$, $r_4={\Lambda }_1\times {\varkappa }_2$, $r_5=\left(0\right)\times \varsigma$, $r_6=\left(0\right)\times {\varkappa }_2^2$, and $r_7={\Lambda }_1\times {\varkappa }_2^2$, all of which are in $\Theta {\left(\Lambda \right)}^{*}$. Since $Ann\left(r_i{r}_j\right)\ne Ann\left(r_i\right)\cap Ann\left(r_j\right)$ for every pair $(i,j)$, the subgraph induced by the set $\{r_1,r_2,\dots ,r_7\}$ contains a subgraph isomorphic to $K_7$ in $\mathcal{AIG}\left(\Lambda \right)$, which contradicts Lemma 5. Therefore, ${\varkappa }_2$ and ${\varkappa }_2^2$ must be unique non-trivial ideals of ${\Lambda }_2$.

Case (3) Assume $m=1$. Using Theorem 1, the graph $\mathcal{AIG}\left(\Lambda \right)$ must be a complete graph. Given that $\overline{\gamma }\left(\mathcal{AIG}\left(\Lambda \right)\right)=1$, Lemma 5 implies that $\Lambda$ must have 5 or 6 non-trivial ideals.

On the other hand, if the number of non-trivial ideals in $\Lambda$ satisfies ${5\le |\Theta \left(\Lambda \right)}^{*}|\le 6$, then $\mathcal{AIG}\left(\Lambda \right)$ is either $K_5$ or $K_6$. By Lemma 5, this confirms that $\overline{\gamma }\left(\mathcal{AIG}\left(\Lambda \right)\right)=1$.

Specifically, if $\Lambda \cong {{\rm Y}}_1\times {{\rm Y}}_2\times {{\rm Y}}_3$, where each ${{\rm Y}}_i$ is in the form of a field for a selection of $i=1,2,3$, then $\mathcal{AIG}\left(\Lambda \right)$ is isomorphic to $K_6$. Thus, applying Lemma 5 again, $\overline{\gamma }\left(\mathcal{AIG}\left(\Lambda \right)\right)=1$.

In addition, if $\Lambda \cong {\rm Y}\times \mathfrak{S}$, where ${\rm Y}$ is a field and $(\mathfrak{S},\varkappa )$ is a local ring with $\varkappa$ and ${\varkappa }^2$ being unique non-trivial ideals of $\mathfrak{S}$, then the projective embedding of $\mathcal{AIG}\left(\Lambda \right)$ is illustrated in Figure 3. □

Example 2.

Let $\Lambda ={\mathbb{Z}}_7\times {\mathbb{Z}}_3\times {\mathbb{Z}}_2$; then, using Theorem 11, $\overline{\gamma }\left(\mathcal{AIG}\left(\Lambda \right)\right)=2$.

Example 3.

Let $\Lambda ={\mathbb{Z}}_5\times {\mathbb{Z}}_8$; then, using Theorem 11, $\overline{\gamma }\left(\mathcal{AIG}\left(\Lambda \right)\right)=2$.

5. Domination Number of $\mathcal{AIG}\left(\Lambda \right)$

This section comprises an exploration of the domination number of the annihilator intersection graph.

Lemma 7.

Let $\Lambda \cong {{\rm Y}}_1\times {{\rm Y}}_2\times \cdots \times {{\rm Y}}_m$ be a commutative ring, where each ${{\rm Y}}_i$ is an integral domain for $1\le i\le m$ and $m\ge 2$. The subsequent statements are true:

1.

For $m=2$, the graph $\mathcal{AIG}\left(\Lambda \right)$ is a complete bipartite graph.

2.

For $m\ge 3$, $\mathcal{AIG}\left(\Lambda \right)\cong K_m\vee H$, where H denotes a multipartite graph and m is a positive integer with $m\ge 1$.

Proof. 

(1) When $m=2$, the graph $\mathcal{AIG}\left(\Lambda \right)$ is a complete bipartite graph with the partitions $\{\varsigma \times \left(0\right):\varsigma \in \Theta {\left({{\rm Y}}_1\right)}^{*}\}$ and $\{\left(0\right)\times \varrho :\varrho \in \Theta {\left({{\rm Y}}_2\right)}^{*}\}$.

(2) For $m\ge 3$, let us define the subsequent sets:

$${\Pi }_1=\{{\varsigma }_1\times {\varsigma }_2\times \cdots \times {\varsigma }_m\in \Theta {\left(\Lambda \right)}^{*}:\mathrm{exactly}\mathrm{any}\mathrm{one}{\varsigma }_i\mathrm{is}\mathrm{zero}\}$$

and

$${\Pi }_2=\{{\varsigma }_1\times {\varsigma }_2\times \cdots \times {\varsigma }_m\in \Theta {\left(\Lambda \right)}^{*}:\mathrm{at}\mathrm{least}\mathrm{two}\mathrm{of}\mathrm{the}{\varsigma }_i\mathrm{are}\mathrm{zero}\}$$

.

It follows that $V\left(\mathcal{AIG}\left(\Lambda \right)\right)={\Pi }_1\cup {\Pi }_2$ and ${\Pi }_1\cap {\Pi }_2=\varnothing$. We establish the subsequent claims:

Claim(1): The subgraph $\mathcal{AIG}\left(\Lambda \right)\left[{\Pi }_1\right]$ is a multipartite graph. Let $\varsigma ={\varsigma }_1\times {\varsigma }_2\times \cdots \times {\varsigma }_m$ and $\varrho ={\varrho }_1\times {\varrho }_2\times \cdots \times {\varrho }_m$ be two vertices of ${\Pi }_1$. Define a relation ∼ on ${\Pi }_1$ by $\varsigma \sim \varrho$ iff ${\varsigma }_i=0$ iff ${\varrho }_i=0$ for each $1\le i\le m$. It is straightforward to verify that ∼ is an equivalence relation on ${\Pi }_1$. The equivalence classes under ∼ are $\left[{\Pi }_i\right]$, where ${\Pi }_i={{\rm Y}}_1\times {{\rm Y}}_2\times \cdots \times {{\rm Y}}_{i-1}\times \left(0\right)\times {{\rm Y}}_{i+1}\times \cdots \times {{\rm Y}}_m$ with only the $i^{\mathrm{th}}$ ideal being zero for each $1\le i\le m$. Therefore, ${\Pi }_1={\bigcup }_{i=1}^m\left[{\Pi }_i\right]$. Consider two distinct vertices $\varsigma ={\varsigma }_1\times {\varsigma }_2\times \cdots \times {\varsigma }_m$ and $\varrho ={\varrho }_1\times {\varrho }_2\times \cdots \times {\varrho }_m$ in $\mathcal{AIG}\left(\Lambda \right)\left[{\Pi }_1\right]$. Analyze the subsequent cases:

Case (i): Let $\varsigma ,\varrho \in \left[{\Pi }_i\right]$ for some $1\le i\le m$. In this case, ${\varsigma }_i={\varrho }_i=0$. Given that $Ann\left(\varsigma \varrho \right)=Ann\left(\varsigma \right)=Ann\left(\varrho \right)=\{\left(0\right)\times \left(0\right)\times \cdots \times L\times \cdots \times \left(0\right):L\in \Theta \left({{\rm Y}}_i\right)\}$, it follows that no edge exists between $\varsigma$ and $\varrho$ in $\mathcal{AIG}\left(\Lambda \right)$. Consequently, no two vertices within $\left[{\Pi }_i\right]$ are connected in $\mathcal{AIG}\left(\Lambda \right)$ for each $1\le i\le m$.

Case (ii): Suppose $\varsigma \in \left[{\Pi }_i\right]$ and $\varrho \in \left[{\Pi }_j\right]$ for some $1\le i,j\le m$. Here, $i\ne j$ and ${\varsigma }_i={\varrho }_j=0$. Since $L=\left(0\right)\times \left(0\right)\times \cdots \times {{\rm Y}}_i\times \cdots \times \left(0\right)\times {{\rm Y}}_j\times \left(0\right)\times \cdots \times \left(0\right)\in Ann\left(\varsigma \varrho \right)$ but $L\notin Ann\left(\varsigma \right)\cap Ann\left(\varrho \right)$, we have $Ann\left(\varsigma \varrho \right)\ne Ann\left(\varsigma \right)\cap Ann\left(\varrho \right)$. Therefore, $\varsigma \sim \varrho$ forms an edge in $\mathcal{AIG}\left(\Lambda \right)$. Thus, each vertex in $\left[{\Pi }_i\right]$ is adjacent to every vertex in $\left[{\Pi }_j\right]$ for all $1\le i,j\le m$.

Combining the results from Case (i) and Case (ii), we conclude that $\mathcal{AIG}\left(\Lambda \right)\left[{\Pi }_1\right]$ is indeed a multipartite subgraph of $\mathcal{AIG}\left(\Lambda \right)$.

Claim (2): The subgraph $\mathcal{AIG}\left(\Lambda \right)\left[{\Pi }_2\right]$ is a complete subgraph of $\mathcal{AIG}\left(\Lambda \right)$. Consider two distinct vertices $\varsigma ={\varsigma }_1\times {\varsigma }_2\times \cdots \times {\varsigma }_m$ and $\varrho ={\varrho }_1\times {\varrho }_2\times \cdots \times {\varrho }_m$ in $\mathcal{AIG}\left(\Lambda \right)\left[{\Pi }_2\right]$. There exist indices $1\le i,j,k,l\le m$ such that the $i^{th}$ and $j^{th}$ ideals of $\varsigma$ are zero, and the $k^{th}$ and $l^{th}$ ideals of $\varrho$ are zero. Without loss of generality, $i\ne k$. Then, $P=\left(0\right)\times \left(0\right)\times \cdots \times {{\rm Y}}_i\times \cdots \times \left(0\right)\times {{\rm Y}}_k\times \left(0\right)\times \cdots \times \left(0\right)\in Ann\left(\varsigma \varrho \right)$, but $P\notin Ann\left(\varsigma \right)\cap Ann\left(\varrho \right)$. Therefore, $Ann\left(\varsigma \varrho \right)\ne Ann\left(\varsigma \right)\cap Ann\left(\varrho \right)$. This implies that $\mathcal{AIG}\left(\Lambda \right)\left[{\Pi }_2\right]$ is a complete subgraph of $\mathcal{AIG}\left(\Lambda \right)$.

Combining Claims (1) and (2), we conclude that $\mathcal{AIG}\left(\Lambda \right)\cong \mathcal{AIG}\left(\Lambda \right)\left[{\Pi }_1\right]\vee \mathcal{AIG}\left(\Lambda \right)\left[{\Pi }_2\right]$, where $\mathcal{AIG}\left(\Lambda \right)\left[{\Pi }_1\right]$ is a multipartite graph and $\mathcal{AIG}\left(\Lambda \right)\left[{\Pi }_2\right]$ is a complete graph. □

Theorem 12.

Let $\Lambda \cong {{\rm Y}}_1\times {{\rm Y}}_2\times \cdots \times {{\rm Y}}_m$ be a commutative ring, where each ${{\rm Y}}_i$ is an integral domain for $1\le i\le m$ and $m\ge 2$. Then, the subsequent statements are true:

1.

If $m=2$, then $\delta \left(\mathcal{AIG}\right(\Lambda \left)\right)\le 2$.

2.

If $m\ge 3$, then $\delta \left(\mathcal{AIG}\right(\Lambda \left)\right)=1$.

Proof. 

(1) For the case $m=2$, according to Lemma 7(1), we have $\mathcal{AIG}\left(\Lambda \right)\cong K_{|\Theta {\left({{\rm Y}}_1\right)}^{*}|,|\Theta {\left({{\rm Y}}_2\right)}^{*}|}$. If $min\left\{\right|\Theta {\left({{\rm Y}}_1\right)}^{*}|,|\Theta {\left({{\rm Y}}_2\right)}^{*}\left|\right\}=2$, it follows that $\delta \left(\mathcal{AIG}\right(\Lambda \left)\right)=1$. On the other hand, if $min\left\{\right|\Theta {\left({{\rm Y}}_1\right)}^{*}|,|\Theta {\left({{\rm Y}}_2\right)}^{*}\left|\right\}\ge 3$, then $\delta \left(\mathcal{AIG}\right(\Lambda \left)\right)=2$.

(2) For the case $m\ge 3$, by Lemma 7(2), $\mathcal{AIG}\left(\Lambda \right)\cong K_m\vee H$, where H denotes a multipartite graph with $m\ge 1$. Hence, $\delta \left(\mathcal{AIG}\right(\Lambda \left)\right)=1$. □

Lemma 8

([17] (2.7)). Let Λ be a reduced commutative ring containing a nonzero minimal ideal, then Λ is decomposable.

Lemma 9.

Let $\Lambda \cong {\Lambda }_1\times {\Lambda }_2\times \cdots \times {\Lambda }_m$ be a commutative ring, where each ${\Lambda }_i$ is a commutative ring and $m\ge 3$. Then, $\delta \left(\mathcal{AIG}\right(\Lambda \left)\right)=1$.

Proof. 

For $\mathcal{AIG}\left(\Lambda \right)$, the set of vertices is shown by $V\left(\mathcal{AIG}\left(\Lambda \right)\right)=\{{\varsigma }_1\times {\varsigma }_2\times \cdots \times {\varsigma }_n\in \Theta {\left(\Lambda \right)}^{*}\mid {\varsigma }_i\in \mathfrak{D}\left({\Lambda }_i\right)\mathrm{for}\mathrm{some}1\le i\le n\}$. We claim that the set $\{\varsigma ={\Lambda }_1\times \left(0\right)\times \cdots \times \left(0\right)\}$ is a dominating set in $\mathcal{AIG}\left(\Lambda \right)$.

Consider any vertex $\varrho ={\varsigma }_1\times {\varsigma }_2\times \cdots \times {\varsigma }_n\in V\left(\mathcal{AIG}\left(\Lambda \right)\right)\setminus \left\{\varsigma \right\}$. There exists at least one index $1\le i\le n$ such that ${\varsigma }_i\in \mathfrak{D}\left({\Lambda }_i\right)$, implying that there is ${\varrho }_i\in \Theta {\left({\Lambda }_i\right)}^{*}$ to that ${\varsigma }_i{\varrho }_i=0$.

If $i=1$, then $P_1={\varrho }_1\times \left(0\right)\times \left(0\right)\times \cdots \times \left(0\right)\in Ann\left(\varsigma \varrho \right)$, but $P_1\notin Ann\left(\varsigma \right)\cap Ann\left(\varrho \right)$, hence $Ann\left(\varsigma \varrho \right)\ne Ann\left(\varsigma \right)\cap Ann\left(\varrho \right)$. Therefore, $\varsigma \sim \varrho$ is an edge in $\mathcal{AIG}\left(\Lambda \right)$.

If $i\ge 2$ and ${\varrho }_i\ne 0$, then $P_2=\left(0\right)\times \left(0\right)\times \cdots \times \left(0\right)\times {\Lambda }_i\times \left(0\right)\times \cdots \times \left(0\right)\in Ann\left(\varsigma \varrho \right)$, but $P_2\notin Ann\left(\varsigma \right)\cap Ann\left(\varrho \right)$, thus $Ann\left(\varsigma \varrho \right)\ne Ann\left(\varsigma \right)\cap Ann\left(\varrho \right)$. This indicates that $\varsigma \sim \varrho$ forms an edge in $\mathcal{AIG}\left(\Lambda \right)$.

If $i\ge 2$ and ${\varrho }_i=0$, then there must exist ${\varrho }_k\in \Theta \left({\Lambda }_k\right)$. Here, $P_3=\left(0\right)\times \left(0\right)\times \cdots \times \left(0\right)\times {\Lambda }_k\times \left(0\right)\times \cdots \times \left(0\right)\in Ann\left(\varsigma \varrho \right)$, but $P_3\notin Ann\left(\varsigma \right)\cap Ann\left(\varrho \right)$, leading to $Ann\left(\varsigma \varrho \right)\ne Ann\left(\varsigma \right)\cap Ann\left(\varrho \right)$. Thus, $\varsigma \sim \varrho$ is an edge in $\mathcal{AIG}\left(\Lambda \right)$.

Combining these observations, we conclude that there is an edge between $\varsigma$ and $\varrho$ in $\mathcal{AIG}\left(\Lambda \right)$. Therefore, $\left\{\varsigma \right\}$ is indeed a dominating set in $\mathcal{AIG}\left(\Lambda \right)$. Consequently, $\delta \left(\mathcal{AIG}\right(\Lambda \left)\right)=1$. □

Theorem 13.

Let Λ be a reduced commutative ring; the domination number of $\mathcal{AIG}\left(\Lambda \right)$ is at most two.

Proof. 

If $\left|M\right(\Lambda \left)\right|=2$, then using Theorem [6] (thm 2.2), the annihilator intersection graph $\mathcal{AIG}\left(\Lambda \right)$ is isomorphic to $\mathcal{AG}\left(\Lambda \right)=K_{m,n}$, where $m,n\ge 1$. Therefore, $\delta \left(\mathcal{AIG}\right(\Lambda \left)\right)\le 2$.

If $\left|M\right(\Lambda \left)\right|\ge 3$, then according to Lemma 8, we can decompose $\Lambda$ as $\Lambda \cong {\Lambda }_1\times {\Lambda }_2$, where ${\Lambda }_1$ and ${\Lambda }_2$ are commutative rings. Without loss of generality, $\left|M\right({\Lambda }_2\left)\right|=n-1$. Applying similar reasoning as before, we find that $\Lambda$ can be further decomposed into ${\Lambda }_1\times {\Lambda }_2\times \cdots \times {\Lambda }_n$, where each ${\Lambda }_i$ is a commutative ring. By Lemma 9, the set $\{{\Lambda }_1\times \left(0\right)\times \cdots \times \left(0\right)\}$ is a dominating set in $\mathcal{AIG}\left(\Lambda \right)$. Consequently, $\delta \left(\mathcal{AIG}\right(\Lambda \left)\right)=1$. □

Corollary 3.

Let Λ be a reduced commutative ring with $\left|M\right(\Lambda \left)\right|=2$. Then, the subsequent statements are true:

1.

If $\delta \left(\mathcal{AIG}\right(\Lambda \left)\right)=1$, then $\Lambda \cong {\Lambda }_1\times {\Lambda }_2$, where at least one of ${\Lambda }_1$ or ${\Lambda }_2$ is a field.

2.

If $\delta \left(\mathcal{AIG}\right(\Lambda \left)\right)=2$, then $\Lambda \cong {\Lambda }_1\times {\Lambda }_2$, where neither ${\Lambda }_1$ nor ${\Lambda }_2$ is a field.

Theorem 14.

Let Λ be a non-reduced commutative ring. Then, $\delta \left(\mathcal{AIG}\right(\Lambda \left)\right)=1$.

Proof. 

Assume $N\left(\Lambda \right)\ne 0$ and consider any $a\in N{\left(\Lambda \right)}^{*}$. By Lemma 2, $\alpha \Lambda$ is connected to every other vertex in $\mathcal{AIG}\left(\Lambda \right)$. Therefore, $\delta \left(\mathcal{AIG}\right(\Lambda \left)\right)=1$. □

6. Conclusions

In this paper, we have extensively studied the annihilator intersection graph $\mathcal{AIG}\left(\Lambda \right)$ for a commutative ring $\Lambda$ with unity. We classify finite commutative rings to $\mathcal{AIG}\left(\Lambda \right)$ that exhibits the structure of a star graph and a 2-outerplanar graph. Furthermore, we have determined the inner vertex number of $\mathcal{AIG}\left(\Lambda \right)$, enriching our understanding of its structural properties.

Our investigation has led to the identification of finite rings to determine that the genus of $\mathcal{AIG}\left(\Lambda \right)$ is 2, categorizing $\mathcal{AIG}\left(\Lambda \right)$ as a double-toroidal graph. In addition, we have identified the finite rings to determine that the crosscap of $\mathcal{AIG}\left(\Lambda \right)$ is 1, thereby classifying $\mathcal{AIG}\left(\Lambda \right)$ as a projective plane.

Finally, we have explored the domination number of the annihilator intersection graph, establishing that it is at maximum, two. These findings contribute to the broader comprehension of the graphical properties of $\mathcal{AIG}\left(\Lambda \right)$ and its behavior across different classes of commutative rings.