Simulation-Based Evaluation of Robust Transformation Techniques for Median Estimation Under Simple Random Sampling

Abstract

An efficient estimator can reduce both bias and mean squared error to provide more accurate results by using the transformation strategy. In this paper, an enhanced class of ratio–product types of estimators is introduced, which employs the transformation technique by linearly combining two robust measures, the trimean and decile mean, and five non-conventional measures, the range, inter-quartile range, mid-range, quartile average, and quartile deviation, on auxiliary variables with a simple random sampling method to estimate the finite population median. This transformation approach improves efficiency and enables estimators to manage data variability better. Using these estimators, we investigate their bias and mean squared error up to the first order of approximation. A comparison of the proposed estimators and existing methods is conducted through five simulated populations generated through different suitable distributions and three real datasets. By improving the precision and efficiency of median estimation, the proposed estimators ensure accurate and reliable results. Comparing the new estimators to traditional estimators, the findings show superior performance for new estimators in terms of mean squared errors (MSEs).

1. Introduction

At the planning and estimate stages, the utilization of auxiliary information is important to improving the performance of estimators in survey sampling. The median often gives a more accurate picture of the central tendency than the mean when working with highly skewed data distributions, such as those in income, expenditure, taxation, consumption, and production. For datasets with significant skewness, this is especially true because the median provides a more reliable representation of the information in the middle. The development of effective techniques for accurately estimating medians in finite populations has received less attention, despite the massive quantity of research on estimating population parameters, such as means, variances, proportions, and totals. This contrast highlights the importance of more research on improving methods that use auxiliary variables to improve median estimation. More details about auxiliary information can be found in [1,2,3,4,5].

In many cases, the median is important for analyzing skewed data or outliers. For reflecting survey responses in the social sciences, income in economics, pollution levels in environmental research, patient outcomes in health, and variations in the real estate market, it increases statistical accuracy. The estimation of the median using auxiliary information in simple random sampling has been significantly enhanced by the fundamental contributions [6,7,8,9]. Their efforts laid the foundation for subsequent research and enhancement in this area. A number of estimators have been developed for estimating the finite population median using various sampling techniques in subsequent years of the work [9]. Some novel techniques for improving regression estimators and ratios for the median were proposed by [10]. To address median estimation, ref. [11] presented a few techniques utilizing double sampling techniques. The population median was estimated by [12] using a generalized class of estimators that employs two auxiliary variables in double sampling. By employing the known median of the auxiliary variable, ref. [13] presented the minimum unbiased estimator. Subsequently, later on, the accuracy of the median estimation was improved by using two auxiliary variables under the two-phase sampling technique as discussed by [14]. To approximate the population median using simple random and stratified random sampling methods, refs. [15,16] developed several improved estimators. Using auxiliary data for various population parameters under different sampling designs, some new estimators were developed by [17,18,19]. In recent years, many researchers have been focusing on introducing new efficient estimators to estimate population median with different sampling methods. For more details about median estimation, we refer the reader to [20,21,22,23,24,25,26,27], and references therein.

The precision of estimators typically decreases and may lead to misleading results when extreme values are present. All ratio, product, regression, and exponential estimators used to determine the finite population median significantly rely on traditional auxiliary variable measures, which is a drawback. This dependence can reduce their efficacy, especially in outlier-influenced datasets. An efficient estimator can reduce both bias and mean squared error to provide more accurate results by using the transformation strategy. In this paper, an enhanced class of ratio–product types of estimators is introduced that employs the transformation technique by linearly combining two robust measures, the trimean and decile mean, and five non-conventional measures, the inter-quartile range, mid-range, quartile average, and quartile deviation, on auxiliary variables with a simple random sampling method to estimate the finite population median. This transformation approach improves efficiency and helps estimators manage data variability. The suggested estimators are flexible to skewed distributions and datasets with outliers, in contrast to many other estimators previously in use. Because of their flexibility, they are especially useful in domains such as environmental research, healthcare, and income analysis.

Real-Life Applications

In real-life applications, the improved median-estimation method proposed in this study can provide valuable insights across various fields:

• Economic income-distribution analysis: In economics, accurate estimations of median income are crucial for understanding income inequality. The proposed method can offer more reliable median estimates even in the presence of extreme incomes or outliers, providing a clearer understanding of wealth distribution, which is critical for policy making and economic planning.
• Climate research: In climate studies, data often contain extreme values due to rare events like heatwaves or storms. By applying the improved median estimation, researchers can obtain a more stable and robust estimate of climate variables (e.g., average temperature or rainfall) without the distortion caused by these extreme outliers. This can improve the reliability of climate models and help in formulating better strategies for climate change adaptation.
• Medical studies: In healthcare, particularly when dealing with patient data or clinical trials, outliers can significantly affect the analysis of treatment efficacy or patient outcomes. The proposed method can be instrumental in estimating more accurate median values of health metrics (e.g., blood pressure, cholesterol levels) in populations with heterogeneous health conditions, thus ensuring more robust conclusions and better healthcare decision-making.
• Environmental monitoring: For environmental monitoring, where pollutants or rare events (e.g., oil spills, radioactive leaks) can distort data, the improved median estimator can offer a more reliable measure of the central tendency, improving the accuracy of risk assessments and mitigation strategies.
• Education and social sciences: The method could be applied in educational assessments or social research, where extreme test scores or outlier responses could otherwise skew the interpretation of central tendencies. By providing more robust median estimates, researchers can better understand the typical performance or behavior in a population, leading to more informed decisions in policy or education strategy development.

The structure of this paper can be outlined as follows: Section 2 provides a comprehensive explanation of the methods and notations employed in the study, followed by a review of existing estimators in Section 2 to establish a foundation for comparison. Section 3 introduces and elaborates on the proposed class of estimators. Section 4 presents a detailed mathematical comparison of the estimators under consideration. To verify the theoretical findings discussed in this section, a simulation study is conducted in Section 5. This study involves the construction of five distinct artificial populations utilizing various probability distributions. Furthermore, this section includes numerical examples to illustrate the practical application of the theoretical results. Finally, Section 6 provides a summary of the key findings and proposes potential paths for future research.

2. Concepts and Existing Estimators

Suppose the auxiliary variable is denoted by X and the study variable by Y for a finite population consisting of N units, denoted as $\Omega =({\Omega }_1,{\Omega }_2,\dots ,{\Omega }_N)$. For each unit i where $i=1,2,\dots ,N$, the corresponding values of the auxiliary and study variables are $x_i$ and $y_i$, respectively. Let a random sample of size n be selected from the population of size N with the condition that $n<N$ under simple random sampling without replacement (SRSWOR). The population medians for the study and auxiliary variables are represented as ${\delta }_{M_y}$ and ${\delta }_{M_x}$, and the sample medians as ${\widehat{\delta }}_{M_y}$ and ${\widehat{\delta }}_{M_x}$. The associated probability density functions for the population medians are $f_y\left({\delta }_{M_y}\right)$ and $f_x\left({\delta }_{M_x}\right)$. The correlation coefficient between ${\delta }_{M_y}$ and ${\delta }_{M_x}$ is denoted by ${\rho }_{yx}$ and is defined as $\rho ({\delta }_{M_y},{\delta }_{M_x})=4P_{11}(y,x)-1,$ where $P_{11}=P(y\le {\delta }_{M_y}\cap x\le {\delta }_{M_x}).$

To determine the mathematical properties of different estimators, the following relative error terms are utilized:

$${\delta }_{e_0}=\left({\displaystyle \frac{{\widehat{\delta }}_{M_y}-{\delta }_{M_y}}{{\delta }_{M_y}}}\right)$$

and

$${\delta }_{e_1}=\left({\displaystyle \frac{{\widehat{\delta }}_{M_x}-{\delta }_{M_x}}{{\delta }_{M_x}}}\right),$$

such that $E\left({\delta }_{e_i}\right)=0$ for $i=0,1$.

$$E\left({\delta }_{e_0}^2\right)=\theta {\Delta }_{M_y}^2,$$

$$E\left({\delta }_{e_1}^2\right)=\theta {\Delta }_{M_x}^2,$$

$$E\left({\delta }_{e_0}{\delta }_{e_1}\right)=\theta {\Delta }_{M_{yx}}={\rho }_{yx}{\Delta }_{M_y}{\Delta }_{M_x},$$

where

$${\Delta }_{M_y}={\displaystyle \frac{1}{{\delta }_{M_y}{f}_y\left({\delta }_{M_y}\right)}},$$

$${\Delta }_{M_x}={\displaystyle \frac{1}{{\delta }_{M_x}{f}_x\left({\delta }_{M_x}\right)}},$$

denote the population coefficient of variations of the study variable Y and the auxiliary variable X, and let

$$\theta ={\displaystyle \frac{1}{4}}\left({\displaystyle \frac{1}{n}}-{\displaystyle \frac{1}{N}}\right)$$

be the finite population-correction factor.

Now, the biases and mean squared errors of the existing estimators used to estimate the finite population mean are investigated. We then compare these results with those of our suggested class of estimators to identify potential improvements.

The population median is generally estimated by the unbiased estimator, defined as:

$${\widehat{\delta }}_{M_{GR}}={\widehat{\delta }}_{M_y}.$$

(1)

The variance of ${\widehat{\delta }}_{M_{GR}}$ is given by:

$$V\left({\widehat{\delta }}_{M_y}\right)=\theta {\delta }_{M_y}^2{\Delta }_{M_y}^2.$$

(2)

Assuming the median of the X variable is known, ref. [9] proposed a ratio-type estimator for ${\widehat{\delta }}_{M_R}$, which is defined as:

$${\widehat{\delta }}_{M_R}=\left({\displaystyle \frac{{\widehat{\delta }}_{M_y}}{{\widehat{\delta }}_{M_x}}}\right){\delta }_{M_x}.$$

(3)

The following formulas are used to express the bias and MSE of ${\widehat{\delta }}_{M_R}$:

$$Bias\left({\widehat{\delta }}_{M_R}\right)\cong \theta {\Delta }_{M_y}\left({\Delta }_{M_x}^2-{\Delta }_{M_{yx}}\right)$$

(4)

and

$$MSE\left({\widehat{\delta }}_{M_R}\right)\cong \theta {\delta }_{M_y}^2\left({\Delta }_{M_y}^2+{\Delta }_{M_x}^2-2{\Delta }_{M_{yx}}\right).$$

(5)

The difference estimator for ${\widehat{\delta }}_{M_D}$ introduced by [13] is defined as:

$${\widehat{\delta }}_{M_D}={\widehat{\Delta }}_{M_y}+d\left({\delta }_{M_x}-{\widehat{\delta }}_{M_x}\right),$$

(6)

where d is an unknown constant, and the optimum value of d is as given below:

$$d_{min}={\displaystyle \frac{{\rho }_{yx}{\delta }_{M_y}{\Delta }_{M_y}}{{\delta }_{M_x}{\Delta }_{M_x}}}.$$

The minimum MSE of ${\widehat{\delta }}_{M_D}$ is given below:

$$MSE{\left({\widehat{\delta }}_{M_D}\right)}_{min}\cong \theta {\delta }_{M_y}^2{\Delta }_{M_y}^2\left(1-{\rho }_{yx}^2\right).$$

(7)

We present an exponential ratio and product-type estimators in terms of median using the idea provided by [28]:

$${\widehat{\delta }}_{M_{Re}}={\widehat{\delta }}_{M_y}exp\left({\displaystyle \frac{{\delta }_{M_x}-{\widehat{\delta }}_{M_x}}{{\delta }_{M_x}+{\widehat{\delta }}_{M_x}}}\right)$$

(8)

and

$${\widehat{\delta }}_{M_{Pe}}={\widehat{\delta }}_{M_y}exp\left({\displaystyle \frac{{\widehat{\delta }}_{M_x}-{\delta }_{M_x}}{{\delta }_{M_x}+{\widehat{\delta }}_{M_x}}}\right).$$

(9)

The biases and MSEs for (${\widehat{\delta }}_{M_{Re}},{\widehat{\delta }}_{M_{Pe}}$) are as follows:

$$Bias\left({\widehat{\delta }}_{M_{Re}}\right)\cong \theta {\delta }_{M_y}\left({\displaystyle \frac{3}{8}}{\Delta }_{M_x}^2-{\displaystyle \frac{1}{2}}{\Delta }_{M_{yx}}\right),$$

(10)

$$Bias\left({\widehat{\delta }}_{M_{Pe}}\right)\cong \theta {\delta }_{M_y}\left({\displaystyle \frac{1}{2}}{\Delta }_{M_{yx}}-{\displaystyle \frac{3}{8}}{\Delta }_{M_x}^2\right),$$

(11)

$$MSE\left({\widehat{\delta }}_{M_{Re}}\right)\cong \theta {\delta }_{M_y}^2\left({\Delta }_{M_y}^2+{\displaystyle \frac{1}{4}}{\Delta }_{M_x}^2-{\Delta }_{M_{yx}}\right)$$

(12)

and

$$MSE\left({\widehat{\delta }}_{M_{Pe}}\right)\cong \theta {\delta }_{M_y}^2\left({\Delta }_{M_y}^2+{\displaystyle \frac{1}{4}}{\Delta }_{M_x}^2+{\Delta }_{M_{yx}}\right).$$

(13)

The difference type estimators for estimating median introduced by [10,14] are:

$${\widehat{\delta }}_{M_{D_1}}=d_1{\widehat{\delta }}_{M_y}+d_2\left({\delta }_{M_x}-{\widehat{\delta }}_{M_x}\right),$$

(14)

$${\widehat{\delta }}_{M_{D_2}}=\left[d_3{\widehat{\delta }}_{M_y}+d_4\left({\delta }_{M_x}-{\widehat{\delta }}_{M_x}\right)\right]\left({\displaystyle \frac{{\delta }_{M_x}}{{\widehat{\delta }}_{M_x}}}\right),$$

(15)

$${\widehat{\delta }}_{M_{D_3}}=\left[d_5{\widehat{\delta }}_{M_y}+d_6\left({\delta }_{M_x}-{\widehat{\delta }}_{M_x}\right)\right]\left({\displaystyle \frac{{\delta }_{M_x}-{\widehat{\delta }}_{M_x}}{{\delta }_{M_x}+{\widehat{\delta }}_{M_x}}}\right).$$

(16)

The optimum values of the unknown constants $d_i(i=1,2,\dots ,6)$ are given below:

$$d_{1\left(opt\right)}={\displaystyle \frac{1}{1+\theta {\Delta }_{M_y}^2\left(1-{\rho }_{yx}^2\right)}},$$

$$d_{2\left(opt\right)}={\displaystyle \frac{{\delta }_{M_y}}{{\delta }_{M_x}}}\left[{\displaystyle \frac{{\rho }_{yx}{\Delta }_{M_y}}{1+\theta {\Delta }_{M_y}^2\left(1-{\rho }_{yx}^2\right)}}\right],$$

$$d_{3\left(opt\right)}={\displaystyle \frac{1-\theta {\Delta }_{M_y}^2}{1-\theta {\Delta }_{M_y}^2+\theta {\Delta }_{M_y}^2\left(1-{\rho }_{yx}^2\right)}},$$

$$d_{4\left(opt\right)}={\displaystyle \frac{{\delta }_{M_y}}{{\delta }_{M_x}}}\left[1+d_{3\left(opt\right)}\left({\displaystyle \frac{{\rho }_{yx}{\Delta }_{M_y}}{{\Delta }_{M_x}}}\right)-2\right],$$

$$d_{5\left(opt\right)}={\displaystyle \frac{1}{8}}\left[{\displaystyle \frac{8-\theta {\Delta }_{M_x}^2}{1+\theta {\Delta }_{M_x}^2\left(1-{\rho }_{yx}^2\right)}}\right]$$

and

$$d_{6\left(opt\right)}={\displaystyle \frac{{\delta }_{M_y}}{{\delta }_{M_x}}}\left[{\displaystyle \frac{1}{2}}+d_{5\left(opt\right)}\left({\displaystyle \frac{{\rho }_{yx}{\Delta }_{M_y}}{{\Delta }_{M_x}}}\right)-1\right].$$

The minimum biases and mean squared errors of ${\widehat{\delta }}_{M_{D_i}}(i=1,2,3)$ are given by the following expressions, using the optimal values of $d_i(i=1,2,\dots ,6)$:

$$Bias\left({\widehat{\delta }}_{M_{D_1}}\right)\cong {\delta }_{M_y}\left(d_1-1\right),$$

(17)

$$Bias\left({\widehat{\delta }}_{M_{D_2}}\right)\cong {\delta }_{M_y}\left(d_3-1\right)+\theta d_3{\delta }_{M_y}\left({\Delta }_{M_x}^2-{\Delta }_{M_{yx}}\right)+\theta d_4{\delta }_{M_x}{\Delta }_{M_x}^2,$$

(18)

$$Bias\left({\widehat{\delta }}_{M_{D_3}}\right)\cong {\delta }_{M_y}\left(d_5-1\right)+\theta d_5{\delta }_{M_y}\left\{{\displaystyle \frac{3}{8}}{\Delta }_{M_x}^2-{\displaystyle \frac{1}{2}}{\Delta }_{M_{yx}}\right\}+{\displaystyle \frac{\theta }{2}}{d}_6{\delta }_{M_x}{\Delta }_{M_x}^2,$$

(19)

$$MSE{\left({\widehat{\delta }}_{M_{D_1}}\right)}_{min}\cong {\displaystyle \frac{\theta {\delta }_{M_y}^2{\Delta }_{M_y}^2\left(1-{\rho }_{yx}^2\right)}{1+\theta {\Delta }_{M_y}^2\left(1-{\rho }_{yx}^2\right)}},$$

(20)

$$MSE{\left({\widehat{\delta }}_{M_{D_2}}\right)}_{min}\cong {\displaystyle \frac{\theta {\delta }_{M_y}^2\left(1-\theta {\Delta }_{M_x}^2\right){\Delta }_{M_y}^2\left(1-{\rho }_{yx}^2\right)}{\left(1-\theta {\Delta }_{M_x}^2\right)+\theta {\Delta }_{M_y}^2\left(1-{\rho }_{yx}^2\right)}}$$

(21)

and

$$MSE{\left({\widehat{\delta }}_{M_{D_3}}\right)}_{min}\cong {\displaystyle \frac{\theta {\delta }_{M_y}^2\left[{\Delta }_{M_x}^2\left(1-{\rho }_{yx}^2\right)-\frac{\theta }{4}{\Delta }_{M_x}^2\left\{\frac{1}{16}{\Delta }_{M_x}^2+{\Delta }_{M_y}^2\left(1-{\rho }_{yx}^2\right)\right\}\right]}{1+\theta {\Delta }_{M_y}^2\left(1-{\rho }_{yx}^2\right)}}.$$

(22)

3. Proposed Family of Estimators

In this section, we discuss a family of ratio–product-type estimators, which employs the transformation technique by linearly combining robust measures such as the trimean and decile mean and five non-conventional measures, the range, inter-quartile range, mid-range, quartile average, and quartile deviation, on auxiliary variables with the simple random sampling method to estimate the finite population median. This transformation approach improves efficiency and helps estimators manage data variability. The proposed estimator is defined below:

$${\widehat{\delta }}_{M_e}={\widehat{\delta }}_{M_y}exp\left[L_1\left\{{\displaystyle \frac{a_1\left({\widehat{\delta }}_{M_x}-{\delta }_{M_x}\right)}{a_1\left({\delta }_{M_x}+{\widehat{\delta }}_{M_x}\right)+2a_2}}\right\}\right]exp\left[L_2\left\{{\displaystyle \frac{b_1\left({\delta }_{M_x}-{\widehat{\delta }}_{M_x}\right)}{b_1\left({\delta }_{M_x}+{\widehat{\delta }}_{M_x}\right)+2b_2}}\right\}\right],$$

(23)

where the terms $\left(L_i,i=1,2\right)$ represent fixed constant values either 1 or 2, while the known population parameters ($a_1,a_2,b_1,b_2$) are associated with the auxiliary variable X. From Equation (23), a set of new estimators can be derived by varying the population parameters $(a_1,a_2)$, including the interquartile range ($Q_R$), mid-range ($M_R$), quartile average ($Q_A$), quartile deviation ($Q_D$), tri-mean ($T_M$), and decile mean ($D_M$), as shown in

Table 1. Some classes of the proposed estimator.

Subsets of the Proposed Estimator ${\widehat{\mathit{\delta }}}_{{\mathit{M}}_{\mathit{e}}}$	${\mathit{a}}_1$	${\mathit{a}}_2$
${\widehat{\delta }}_{M_{e_1}}={\widehat{\delta }}_{M_y}exp\left[L_1\left\{{\displaystyle \frac{Q_R\left({\widehat{\delta }}_{M_x}-{\delta }_{M_x}\right)}{Q_R\left({\delta }_{M_x}+{\widehat{\delta }}_{M_x}\right)+2D_M}}\right\}\right]exp\left[K\right]$	$Q_R$	$D_M$
${\widehat{\delta }}_{M_{e_2}}={\widehat{\delta }}_{M_y}exp\left[L_1\left\{{\displaystyle \frac{M_R\left({\widehat{\delta }}_{M_x}-{\delta }_{M_x}\right)}{M_R\left({\delta }_{M_x}+{\widehat{\delta }}_{M_x}\right)+2T_M}}\right\}\right]exp\left[K\right]$	$M_R$	$T_M$
${\widehat{\delta }}_{M_{e_3}}={\widehat{\delta }}_{M_y}exp\left[L_1\left\{{\displaystyle \frac{Q_A\left({\widehat{\delta }}_{M_x}-{\delta }_{M_x}\right)}{Q_A\left({\delta }_{M_x}+{\widehat{\delta }}_{M_x}\right)+2Q_D}}\right\}\right]exp\left[K\right]$	$Q_A$	$Q_D$
${\widehat{\delta }}_{M_{e_4}}={\widehat{\delta }}_{M_y}exp\left[L_1\left\{{\displaystyle \frac{Q_D\left({\widehat{\delta }}_{M_x}-{\delta }_{M_x}\right)}{Q_D\left({\delta }_{M_x}+{\widehat{\delta }}_{M_x}\right)+2Q_A}}\right\}\right]exp\left[K\right]$	$Q_D$	$Q_A$
${\widehat{\delta }}_{M_{e_5}}={\widehat{\delta }}_{M_y}exp\left[L_1\left\{{\displaystyle \frac{T_M\left({\widehat{\delta }}_{M_x}-{\delta }_{M_x}\right)}{T_M\left({\delta }_{M_x}+{\widehat{\delta }}_{M_x}\right)+2M_R}}\right\}\right]exp\left[K\right]$	$T_M$	$M_R$
${\widehat{\delta }}_{M_{e_6}}={\widehat{\delta }}_{M_y}exp\left[L_1\left\{{\displaystyle \frac{D_M\left({\widehat{\delta }}_{M_x}-{\delta }_{M_x}\right)}{D_M\left({\delta }_{M_x}+{\widehat{\delta }}_{M_x}\right)+2Q_R}}\right\}\right]exp\left[K\right]$	$D_M$	$Q_R$
${\widehat{\delta }}_{M_{e_7}}={\widehat{\delta }}_{M_y}exp\left[L_1\left\{{\displaystyle \frac{M_R\left({\widehat{\delta }}_{M_x}-{\delta }_{M_x}\right)}{M_R\left({\delta }_{M_x}+{\widehat{\delta }}_{M_x}\right)+2Q_A}}\right\}\right]exp\left[K\right]$	$M_R$	$Q_A$
${\widehat{\delta }}_{M_{e_8}}={\widehat{\delta }}_{M_y}exp\left[L_1\left\{{\displaystyle \frac{Q_D\left({\widehat{\delta }}_{M_x}-{\delta }_{M_x}\right)}{Q_D\left({\delta }_{M_x}+{\widehat{\delta }}_{M_x}\right)+2T_M}}\right\}\right]exp\left[K\right]$	$Q_D$	$T_M$

.

Here

$$K=L_2\left[{\displaystyle \frac{{\delta }_{M_x}-{\widehat{\delta }}_{M_x}}{{\delta }_{M_x}+{\widehat{\delta }}_{M_x}+2\left(X_{max}-X_{min}\right)}}\right],$$

$$b_1=1,$$

$$b_2=X_{max}-X_{min},$$

$$Q_R=Q_3-Q_1,$$

$$M_R={\displaystyle \frac{X_{max}+X_{min}}{2}},$$

$$Q_A={\displaystyle \frac{Q_3+Q_1}{2}},$$

$$Q_D={\displaystyle \frac{Q_3-Q_1}{2}},$$

$$T_M={\displaystyle \frac{Q_1+2Q_2+Q_3}{4}},$$

$$D_M={\displaystyle \frac{{\sum }_{i=1}^9{D}_i}{9}}.$$

The following theorem provides the bias and mean squared error of the family of ratio–product-type estimators ${\widehat{\delta }}_{M_e}.$

Theorem 1. 

Consider ${\widehat{\delta }}_{M_e}$ as a set of ratio–product estimators used to estimate the finite population median ${\delta }_{M_y}$ in a simple random sampling scheme. The expressions for the bias and mean squared error (MSE) of ${\widehat{\delta }}_{M_e}$ are provided below:

$$\begin{array}{c}Bias\left({\widehat{\delta }}_{M_e}\right)\cong -{\displaystyle \frac{\theta }{8}}{\delta }_{M_y}\left[\left(g_1^2-g_2^2\right){\Delta }_{M_x}^2-2\left(2g_1-2g_2-g_1{g}_2\right){\Delta }_{M_{yx}}\right].\hfill \end{array}$$

and

$$\begin{array}{c}MSE\left({\widehat{\delta }}_{M_e}\right)\cong \theta {\delta }_{M_y}^2\left[{\Delta }_{M_y}^2+\left({\displaystyle \frac{g_1^2+g_2^2-2g_1{g}_2}{4}}\right){\Delta }_{M_x}^2-\left(g_1-g_2\right){\Delta }_{M_{yx}}\right].\hfill \end{array}$$

Proof. 

To prove this theorem, we recall some concepts:

$${\delta }_{e_0}=\left({\displaystyle \frac{{\widehat{\delta }}_{M_y}-{\delta }_{M_y}}{{\delta }_{M_y}}}\right),{\delta }_{e_1}=\left({\displaystyle \frac{{\widehat{\delta }}_{M_x}-{\delta }_{M_x}}{{\delta }_{M_x}}}\right),$$

such that $E\left({\delta }_{e_i}\right)=0$ for $i=0,1$,

$$E\left({\delta }_{e_0}^2\right)=\theta {\Delta }_{M_y}^2,$$

$$E\left({\delta }_{e_1}^2\right)=\theta {\Delta }_{M_x}^2$$

and

$$E\left({\delta }_{e_0}{\delta }_{e_1}\right)=\theta {\Delta }_{M_{yx}},$$

where

$${\Delta }_{M_y}={\displaystyle \frac{1}{{\delta }_{M_y}{f}_y\left({\delta }_{M_y}\right)}},$$

$${\Delta }_{M_x}={\displaystyle \frac{1}{{\delta }_{M_x}{f}_x\left({\delta }_{M_x}\right)}}.$$

In order to examine the properties of the suggested estimator, we simplify Equation (23) by expressing it in terms of relative errors, which allows us to calculate the bias and mean squared error (MSE) of ${\widehat{\delta }}_{M_e}^2$, as follows:

$$\begin{array}{c}{\widehat{\delta }}_{M_e}={\delta }_{M_y}\left(1+{\delta }_{e_0}\right)exp\left[{\displaystyle \frac{L_1{g}_1{\delta }_{e_1}}{2}}{\left(1+{\displaystyle \frac{g_1{\delta }_{e_1}}{2}}\right)}^1\right]exp\left[{\displaystyle \frac{-L_2{g}_2{\delta }_{e_1}}{2}}{\left(1+{\displaystyle \frac{g_2{\delta }_{e_1}}{2}}\right)}^{-1}\right]\hfill \end{array}$$

(24)

where $g_1$ and $g_2$ are defined as:

$$g_1={\displaystyle \frac{a_1{\delta }_{M_x}}{a_1{\delta }_{M_x}+a_2}}$$

and

$$g_2={\displaystyle \frac{{\delta }_{M_x}}{{\delta }_{M_X}+b_2}}.$$

We examine the right-hand side of Equation (24) using the first-order Taylor series expansion. To simplify, we neglect terms where $e_i>2$, as their contributions are considered negligible in this context. This approach allows us to derive the following key expression:

$$\begin{array}{c}{\widehat{\delta }}_{M_e}={\delta }_{M_y}\left(1+{\delta }_{e_0}\right)exp\left[{\displaystyle \frac{L_1{g}_1{\delta }_{e_1}}{2}}\left(1-{\displaystyle \frac{g_1{\delta }_{e_1}}{2}}+{\displaystyle \frac{g_1^2{\delta }_{e_1}^2}{4}}\right)\right]exp\left[{\displaystyle \frac{-L_2{g}_2{\delta }_{e_1}}{2}}\left(1-{\displaystyle \frac{g_2{\delta }_{e_1}}{2}}+{\displaystyle \frac{g_2^2{\delta }_{e_1}^2}{4}}\right)\right],\end{array}$$

$$\begin{array}{c}{\widehat{\delta }}_{M_e}={\delta }_{M_y}\left(1+{\delta }_{e_0}\right)exp\left[{\displaystyle \frac{L_1{g}_1{\delta }_{e_1}}{2}}-{\displaystyle \frac{L_1{g}_1^2{\delta }_{e_1}^2}{4}}\right]exp\left[{\displaystyle \frac{-L_2{g}_2{\delta }_{e_1}}{2}}+{\displaystyle \frac{L_2{g}_1^2{\delta }_{e_1}^2}{4}}\right].\hfill \end{array}$$

After simplifying, we obtain:

$$\begin{array}{c}{\widehat{\delta }}_{M_e}-{\delta }_{M_y}\cong {\delta }_{M_y}\left[{\delta }_{e_0}-\left({\displaystyle \frac{L_1{g}_1-L_2{g}_2}{2}}\right){\delta }_{e_1}-{\displaystyle \frac{\left(2L_1{g}_1^2-2L_2{g}_2^2-L_1^2{g}_1^2-L_2^2{g}_2^2\right)}{8}}{\delta }_{e_1}^2+\left({\displaystyle \frac{2L1g_1-2L_2{g}_2-L_1{L}_2{g}_1{g}_2}{4}}\right){\delta }_{e_0}{\delta }_{e_1}\right].\hfill \end{array}$$

(25)

The bias of ${\widehat{\delta }}_{M_e}$ is derived by applying the expectation to both sides of Equation (25) and replacing the terms (${\delta }_{e_0},{\delta }_{e_1},{\delta }_{e_1}^2,{\delta }_{e_0}{\delta }_{e_1}$) with their expected values, which is expressed as:

$$\begin{array}{c}Bias\left({\widehat{\delta }}_{M_e}\right)\cong -{\displaystyle \frac{\theta }{8}}{\delta }_{M_y}\left[\left(2L_1{g}_1^2-2L_2{g}_2^2-L_1^2{g}_1^2-L_2^2{g}_2^2\right){\Delta }_{M_x}^2-2\left(2L_1{g}_1-2L_2{g}_2-L_1{L}_2{g}_1{g}_2\right){\Delta }_{M_{yx}}\right].\hfill \end{array}$$

(26)

The MSE of ${\widehat{\delta }}_{M_e}$ can be derived by squaring both sides of Equation (25) and taking the expectation, resulting in the equation shown below:

$$\begin{array}{c}MSE\left({\widehat{\delta }}_{M_e}\right)\cong \theta {\delta }_{M_y}^2\left[{\Delta }_{M_y}^2+\left({\displaystyle \frac{L_1^2{g}_1^2+L_2^2{g}_2^2-2L_1{L}_2{g}_1{g}_2}{4}}\right){\Delta }_{M_x}^2-\left(L_1{g}_1-L_2{g}_2\right){\Delta }_{M_{yx}}\right].\hfill \end{array}$$

(27)

We can obtain the final results if we substitute the known constant values of $(L_1=L_2=1)$ into Equations (26) and (27), and after some straightforward simplification, we obtain:

$$\begin{array}{c}Bias\left({\widehat{\delta }}_{M_e}\right)\cong -{\displaystyle \frac{\theta }{8}}{\delta }_{M_y}\left[\left(g_1^2-g_2^2\right){\Delta }_{M_x}^2-2\left(2g_1-2g_2-g_1{g}_2\right){\Delta }_{M_{yx}}\right].\hfill \end{array}$$

(28)

and

$$\begin{array}{c}MSE\left({\widehat{\delta }}_{M_e}\right)\cong \theta {\delta }_{M_y}^2\left[{\Delta }_{M_y}^2+\left({\displaystyle \frac{g_1^2+g_2^2-2g_1{g}_2}{4}}\right){\Delta }_{M_x}^2-\left(g_1-g_2\right){\Delta }_{M_{yx}}\right].\hfill \end{array}$$

(29)

□

4. Mathematical Comparison

In this section, we obtain the efficiency conditions by using the mean squared error equations of the proposed family of estimators ${\delta }_{M_e}$ with the mean squared error equations of existing estimators, such as ${\widehat{\delta }}_{M_y}$, ${\widehat{\delta }}_{M_R}$, ${\widehat{\delta }}_{M_D}$, ${\widehat{\delta }}_{M_{Re}}$, ${\widehat{\delta }}_{M_{Pe}}$, ${\widehat{\delta }}_{M_{D_1}},$${\widehat{\delta }}_{M_{D_2}},$ and ${\widehat{\delta }}_{M_{D_3}}$.

(i)

The following condition results from comparing the MSE of the new family of estimators proved in (29) with the variance of the sample median mentioned in (2):

$$V\left({\widehat{\delta }}_{M_y}\right)>MSE\left({\widehat{\delta }}_{M_e}\right) \mathrm{if}$$

$$\left(g_1^2+g_2^2-2g_1{g}_2\right){\Delta }_{M_x}^2<4\left(g_1-g_2\right){\Delta }_{M_{yx}}$$

(ii)

The following condition results from comparing the MSE of the new family of estimators proved in (29) with the MSE of the ratio estimator mentioned in (5):

$$MSE\left({\widehat{\delta }}_{M_R}\right)>MSE\left({\widehat{\delta }}_{M_e}\right) \mathrm{if}$$

$$\left(g_1^2+g_2^2-2g_1{g}_2-4\right){\Delta }_{M_x}^2<4\left(g_1-g_2-2\right){\Delta }_{M_{yx}}.$$

(iii)

The following condition results from comparing the MSE of the new family of estimators proved in (29) with the the MSE of the difference-type estimator mentioned in (7):

$$MSE{\left({\widehat{\delta }}_{M_D}\right)}_{min}>MSE\left({\widehat{\delta }}_{M_e}\right) \mathrm{if}$$

$$\left(g_1^2+g_2^2-2g_1{g}_2\right){\Delta }_{M_x}^2<4\left[\left(g_1-g_2\right){\Delta }_{M_{yx}}-{\Delta }_{M_y}^2{\rho }_{yx}^2\right].$$

(iv)

The following condition results from comparing the MSE of the new family of estimators proved in (29) with the MSE of the exponential ratio-type estimator mentioned in (12):

$$MSE\left({\widehat{\delta }}_{M_{Re}}\right)>MSE\left({\widehat{\delta }}_{M_e}\right) \mathrm{if}$$

$$\left(g_1^2+g_2^2-2g_1{g}_2-1\right){\Delta }_{M_x}^2<4\left(g_1-g_2+1\right){\Delta }_{M_{yx}}.$$

(v)

The following condition results from comparing the MSE of the new family of estimators proved in (29) with the MSE of the exponential product-type estimator mentioned in (13):

$$MSE\left({\widehat{\delta }}_{M_{Pe}}\right)>MSE\left({\widehat{\delta }}_{M_e}\right) \mathrm{if}$$

$$\left(g_1^2+g_2^2-2g_1{g}_2-1\right){\Delta }_{M_x}^2<4\left(g_1-g_2-1\right){\Delta }_{M_{yx}}.$$

(vi)

The following condition results from comparing the MSE of the new family of estimators proved in (29) with the MSE of difference estimator ${\widehat{M}}_{D_1}$ mentioned in (20):

$$MSE{\left({\widehat{\delta }}_{M_{D1}}\right)}_{min}>MSE\left({\widehat{\delta }}_{M_e}\right) \mathrm{if}$$

$$\left(g_1^2+g_2^2-2g_1{g}_2-1\right){\Delta }_{M_x}^2+4\left(g_1-g_2\right){\Delta }_{M_{yx}}<4{\Delta }_{M_y}^2\left[{\displaystyle \frac{\left(\theta {\Delta }_{M_y}^2-1\right){\rho }_{yx}^2-\theta {\Delta }_{M_y}^2}{1+\theta {\Delta }_{M_y}^2\left(1-{\rho }_{yx}^2\right)}}\right].$$

(vii)

The following condition results from comparing the MSE of the new family of estimators proved in (29) with the MSE of difference estimator ${\widehat{M}}_{D_2}$ mentioned in (21):

$$MSE{\left({\widehat{\delta }}_{M_{D2}}\right)}_{min}>MSE\left({\widehat{\delta }}_{M_e}\right)\mathrm{if}$$

$$\left(g_1^2+g_2^2-2g_1{g}_2\right){\Delta }_{M_x}^2-4\left(g_1-g_2\right){\Delta }_{M_{yx}}<4{\Delta }_{M_y}^2\left[{\displaystyle \frac{\theta {\rho }_{yx}^2\left({\Delta }_{M_y}^2+{\Delta }_{M_x}^2\right)-\left(\theta {\Delta }_{M_y}^2+{\rho }_{yx}^2\right)}{\left(1-\theta {\Delta }_{M_x}^2\right)+\theta {\Delta }_{M_y}^2\left(1-{\rho }_{yx}^2\right)}}\right].$$

(viii)

The following condition results from comparing the MSE of the new family of estimators proved in (29) with the MSE of difference estimator ${\widehat{M}}_{D_3}$ mentioned in (22):

$$MSE{\left({\widehat{\delta }}_{M_{D_3}}\right)}_{min}>MSE{\left({\widehat{\delta }}_{M_e}\right)}_{min}\mathrm{if}$$

$$4{\Delta }_{M_y}^2+\left(g_1^2+g_2^2-2g_1{g}_2\right){\Delta }_{M_x}^2-4\left(g_1-g_2\right){\Delta }_{M_{yx}}<{\Delta }_{M_x}^2\left[{\displaystyle \frac{\left\{\left(1-{\rho }_{yx}^2\right)\left(4-\theta {\Delta }_{M_x}^2\right)-\frac{\theta }{16}{\Delta }_{M_x}^2\right\}}{1+\theta {\Delta }_{M_y}^2\left(1-{\rho }_{yx}^2\right)}}\right].$$

5. Results and Discussion

To compare the effectiveness of the new family of estimators with all other existing estimators, we generate the five different simulated populations in this part using suitable positively skewed distributions. Additionally, four datasets are used to confirm the performance of the newly suggested estimators.

5.1. Simulation Study

The distribution that is best suited for a median estimate depends on the statistical properties of the data and the distribution itself; the median is particularly helpful and compatible with skewed, outlier-containing, and non-normal data. To obtain the variable X, we chose one of the five distributions provided below:

• Population 1: X∼Moderate skew and spread Gamma distribution $(\alpha =5,\beta =2)$ with ${\rho }_{yx}=0.5;$
• Population 2: X∼Slight skew Log-Normal distribution $(\mu =3,\sigma =2)$ with ${\rho }_{yx}=0.35;$
• Population 3: X∼Heavy tails Cauchy distribution $({\gamma }_0=6,\gamma =3)$ with ${\rho }_{yx}=-0.45;$
• Population 4: X∼Baseline Uniform distribution $(a=6,b=19)$ with ${\rho }_{yx}=0;$
• Population 5: X∼High skew Exponential $(\mu ={\displaystyle \frac{1}{2}})$ with ${\rho }_{yx}=0.75.$

For analyzing and showing the robustness of the proposed estimators under different scenarios and their characteristics, these five distributions are most suited. We can use the following equation to find the variable Y:

$$Y={\rho }_{yx}\times X+e,$$

where ${\rho }_{yx}$ is the correlation, and e∼$N(0,1)$ represents the error term.

We analyzed the MSEs of the proposed estimators and other existing estimators for each distribution and correlation setting using the following techniques proposed by [29,30,31] in the R software (latest v. 4.4.0) to evaluate their robustness and efficiency.

Step 1:

Using the techniques described above, simulate $N=800$ observations for X and $Y.$

Step 2:

Samples of size n were chosen using simple random sampling without replacement (SRSWOR). The sample sizes are $n=25,100,150,$ and 200.

Step 3:

To measure the performance of the estimators, compute the required statistics (such as sample mean, median, variance, or covariance) from the sampled data using the procedures outlined above. The optimal values for existing estimators, which consider unknown constants, are also determined.

Step 4:

For every sample size, MSE values for each estimator discussed in this article are computed.

Step 5:

After 50,000 iterations of steps 3 and 4, compute the mean squared error values using the formula provided below:

$$MSE{\left({\widehat{\delta }}_{M_t}\right)}_{min}={\displaystyle \frac{{\sum }_{k=1}^{50,000}{\left({\widehat{\delta }}_{M_{tk}}-{\delta }_{M_y}\right)}^2}{50,000}},$$

where t ($t=R,D,Re,Pe,D_1,D_2{D}_3,e_1,e_2,\dots ,e_8$) denotes the subscripts of the existing and new family of estimators.

5.2. Real-Life Application

The performance of the suggested family of estimators in comparison with the other estimators is now assessed by analyzing the MSE values of three different datasets. An extensive description of the datasets is given in the following part, along with statistical summaries that emphasize the most significant parameters and characteristics.

Population 1 

(Source: [32]). Y: Denotes the total number of households; X: Denotes the total area in square miles.

$$\begin{array}{c}N=128,n=45,X_{min}=5.961,X_{max}=10.579,{\delta }_{M_x}=4.715,{\delta }_{M_y}=686,f_x\left({\delta }_{M_x}\right)=0.1154,\hfill \\ f_y\left({\delta }_{M_y}\right)=0.00092,{\rho }_{yx}=0.468,T_M=5.385,D_M=5.378,Q_R=4.618,Q_A=5.316,\hfill \\ Q_D=2.309,M_R=8.270.\hfill \end{array}$$

Population 2 

(Source: [33]). Y: Denotes the overall count of educators employed within educational institutions; X: Denotes the overall count of students enrolled in educational institutions in 2012.

$$\begin{array}{c}N=923,n=180,X_{min}=85,388.5,X_{max}=93,671.5,{\delta }_{M_x}=4123,{\delta }_{M_y}=171,{\rho }_{yx}=0.155,\hfill \\ f_x\left({\delta }_{M_x}\right)=0.00009409,f_y\left({\delta }_{M_y}\right)=0.002676,T_M=7726,D_M=7348.3,Q_R=8283,\hfill \\ Q_A=5870.5,Q_D=4141.5,M_R=89,530.\hfill \end{array}$$

Population 3 

(Source: [13]). Y: The overall amount of fish harvested in 1995; X: Denotes the total number of fish harvested by recreational marine fisherman in 1994.

$$\begin{array}{c}N=69,n=17,X_{min}=15,055,X_{max}=19,005,{\delta }_{M_x}=2007,{\delta }_{M_y}=2068,{\rho }_{yx}=0.314,\hfill \\ f_x\left({\delta }_{M_x}\right)=0.00014,f_y\left({\delta }_{M_y}\right)=0.00014,T_M=3777,D_M=3615.2,Q_R=3936,Q_A=3002,\hfill \\ Q_D=1975,M_R=17,030.\hfill \end{array}$$

Now, proceed with the calculation of mean squared error values for all available estimators. The results of this analysis, which highlight the performance of our proposed family of estimators, can be found in

Table 2. Mean squared error of various estimators using real populations.

Estimator	Population-1	Population-2	Population-3
[1] ${\widehat{\delta }}_{M_y}$	4256.180	156.129	565,443.600
[2] ${\widehat{\delta }}_{M_R}$	5361.578	316.274	799,889.900
[3] ${\widehat{\delta }}_{M_D}$	3323.974	152.378	509,693.100
[4] ${\widehat{\delta }}_{M_{Re}}$	3377.321	181.892	532,582.300
[5] ${\widehat{\delta }}_{M_{Pe}}$	7998.154	238.983	898,473.600
[6] ${\widehat{\delta }}_{M_{D_1}}$	3300.661	151.588	455,416.100
[7] ${\widehat{\delta }}_{M_{D_2}}$	3300.375	151.582	447,631.900
[8] ${\widehat{\delta }}_{M_{D_3}}$	4429.561	210.612	466,361.300
[9] ${\widehat{\delta }}_{M_{e_1}}$	3011.078	142.217	388,892.200
[10] ${\widehat{\delta }}_{M_{e_2}}$	2730.148	142.220	388,834.300
[11] ${\widehat{\delta }}_{M_{e_3}}$	2640.630	142.219	388,857.600
[12] ${\widehat{\delta }}_{M_{e_4}}$	2629.768	142.215	388,942.200
[13] ${\widehat{\delta }}_{M_{e_5}}$	2619.683	142.178	389,190.600
[14] ${\widehat{\delta }}_{M_{e_6}}$	2599.298	141.967	388,830.500
[15] ${\widehat{\delta }}_{M_{e_7}}$	2725.291	142.220	388,618.400
[16] ${\widehat{\delta }}_{M_{e_8}}$	2702.546	142.214	388,974.800

.

5.3. Discussion

We performed simulations using suitable distributions with different ${\rho }_{yx}$ values and sample sizes to support the median estimations. The performance of the proposed family of estimators was also evaluated by analyzing three datasets. The mean squared error (MSE) criterion is used to measure the different estimators. From five simulated distributions, the MSE values for the new family and other existing estimators are shown in

Table 3. Mean squared error (MSE) values for $n=25$.

Estimator	$\mathit{Gam}(5,2)$	$\mathit{LN}(3,2)$	$\mathit{C}(6,3)$	$\mathit{Uni}(6,19)$	$\mathit{Exp}\left(0.5\right)$
[1] ${\widehat{\delta }}_{M_y}$	$5.3\times {10}^{-3}$	$6.1\times {10}^{-2}$	$7.0\times {10}^{-3}$	$3.0\times {10}^{-2}$	$4.0\times {10}^{-2}$
[2] ${\widehat{\delta }}_{M_R}$	$6.0\times {10}^{-3}$	$6.8\times {10}^{-2}$	$7.5\times {10}^{-3}$	$3.7\times {10}^{-2}$	$4.9\times {10}^{-2}$
[3] ${\widehat{\delta }}_{M_D}$	$4.1\times {10}^{-3}$	$4.9\times {10}^{-2}$	$6.1\times {10}^{-3}$	$2.7\times {10}^{-2}$	$3.5\times {10}^{-2}$
[4] ${\widehat{\delta }}_{M_{Re}}$	$3.6\times {10}^{-3}$	$4.7\times {10}^{-2}$	$5.4\times {10}^{-3}$	$2.5\times {10}^{-2}$	$3.2\times {10}^{-2}$
[5] ${\widehat{\delta }}_{M_{Pe}}$	$4.5\times {10}^{-3}$	$5.4\times {10}^{-2}$	$6.3\times {10}^{-3}$	$2.9\times {10}^{-2}$	$3.6\times {10}^{-2}$
[6] ${\widehat{\delta }}_{M_{D_1}}$	$2.8\times {10}^{-3}$	$3.7\times {10}^{-2}$	$4.7\times {10}^{-3}$	$2.0\times {10}^{-2}$	$2.6\times {10}^{-2}$
[7] ${\widehat{\delta }}_{M_{D_2}}$	$2.3\times {10}^{-3}$	$3.5\times {10}^{-2}$	$4.4\times {10}^{-3}$	$1.9\times {10}^{-2}$	$2.4\times {10}^{-2}$
[8] ${\widehat{\delta }}_{M_{D_3}}$	$3.5\times {10}^{-3}$	$4.4\times {10}^{-2}$	$4.9\times {10}^{-3}$	$2.4\times {10}^{-2}$	$3.0\times {10}^{-2}$
[9] ${\widehat{\delta }}_{M_{e_1}}$	$1.7\times {10}^{-3}$	$2.8\times {10}^{-2}$	$3.4\times {10}^{-3}$	$1.5\times {10}^{-2}$	$1.8\times {10}^{-2}$
[10] ${\widehat{\delta }}_{M_{e_2}}$	$1.8\times {10}^{-3}$	$2.9\times {10}^{-2}$	$3.6\times {10}^{-3}$	$1.6\times {10}^{-2}$	$1.9\times {10}^{-2}$
[11] ${\widehat{\delta }}_{M_{e_3}}$	$1.9\times {10}^{-3}$	$3.0\times {10}^{-2}$	$3.9\times {10}^{-3}$	$1.7\times {10}^{-2}$	$1.9\times {10}^{-2}$
[12] ${\widehat{\delta }}_{M_{e_4}}$	$1.7\times {10}^{-3}$	$2.5\times {10}^{-2}$	$3.3\times {10}^{-3}$	$1.2\times {10}^{-2}$	$1.7\times {10}^{-2}$
[13] ${\widehat{\delta }}_{M_{e_5}}$	$1.5\times {10}^{-3}$	$2.4\times {10}^{-2}$	$3.2\times {10}^{-3}$	$1.1\times {10}^{-2}$	$1.5\times {10}^{-2}$
[14] ${\widehat{\delta }}_{M_{e_6}}$	$1.7\times {10}^{-3}$	$2.6\times {10}^{-2}$	$3.1\times {10}^{-3}$	$1.3\times {10}^{-2}$	$1.6\times {10}^{-2}$
[15] ${\widehat{\delta }}_{M_{e_7}}$	$1.4\times {10}^{-3}$	$2.3\times {10}^{-2}$	$2.9\times {10}^{-3}$	$1.0\times {10}^{-2}$	$1.4\times {10}^{-2}$
[16] ${\widehat{\delta }}_{M_{e_8}}$	$1.5\times {10}^{-3}$	$2.4\times {10}^{-2}$	$3.0\times {10}^{-3}$	$1.2\times {10}^{-2}$	$1.5\times {10}^{-2}$

,

Table 4. Mean squared error (MSE) values for $n=100$.

Estimator	$\mathit{Gam}(5,2)$	$\mathit{LN}(3,2)$	$\mathit{C}(6,3)$	$\mathit{Uni}(6,19)$	$\mathit{Exp}\left(0.5\right)$
[1] ${\widehat{\delta }}_{M_y}$	$4.7\times {10}^{-3}$	$5.6\times {10}^{-2}$	$6.5\times {10}^{-3}$	$2.7\times {10}^{-2}$	$3.6\times {10}^{-2}$
[2] ${\widehat{\delta }}_{M_R}$	$5.5\times {10}^{-3}$	$6.4\times {10}^{-2}$	$7.3\times {10}^{-3}$	$3.5\times {10}^{-2}$	$4.5\times {10}^{-2}$
[3] ${\widehat{\delta }}_{M_D}$	$3.6\times {10}^{-3}$	$4.5\times {10}^{-2}$	$5.3\times {10}^{-3}$	$2.3\times {10}^{-2}$	$3.0\times {10}^{-2}$
[4] ${\widehat{\delta }}_{M_{Re}}$	$3.5\times {10}^{-3}$	$4.3\times {10}^{-2}$	$5.1\times {10}^{-3}$	$2.2\times {10}^{-2}$	$2.9\times {10}^{-2}$
[5] ${\widehat{\delta }}_{M_{Pe}}$	$4.2\times {10}^{-3}$	$5.1\times {10}^{-2}$	$6.0\times {10}^{-3}$	$2.5\times {10}^{-2}$	$3.4\times {10}^{-2}$
[6] ${\widehat{\delta }}_{M_{D_1}}$	$2.5\times {10}^{-3}$	$3.4\times {10}^{-2}$	$4.2\times {10}^{-3}$	$1.7\times {10}^{-2}$	$2.3\times {10}^{-2}$
[7] ${\widehat{\delta }}_{M_{D_2}}$	$2.0\times {10}^{-3}$	$3.0\times {10}^{-2}$	$4.0\times {10}^{-3}$	$1.5\times {10}^{-2}$	$2.1\times {10}^{-2}$
[8] ${\widehat{\delta }}_{M_{D_3}}$	$3.2\times {10}^{-3}$	$4.1\times {10}^{-2}$	$4.5\times {10}^{-3}$	$2.1\times {10}^{-2}$	$2.7\times {10}^{-2}$
[9] ${\widehat{\delta }}_{M_{e_1}}$	$1.5\times {10}^{-3}$	$2.5\times {10}^{-2}$	$3.2\times {10}^{-3}$	$1.2\times {10}^{-2}$	$1.6\times {10}^{-2}$
[10] ${\widehat{\delta }}_{M_{e_2}}$	$1.6\times {10}^{-3}$	$2.6\times {10}^{-2}$	$3.3\times {10}^{-3}$	$1.3\times {10}^{-2}$	$1.7\times {10}^{-2}$
[11] ${\widehat{\delta }}_{M_{e_3}}$	$1.7\times {10}^{-3}$	$2.7\times {10}^{-2}$	$3.4\times {10}^{-3}$	$1.4\times {10}^{-2}$	$1.7\times {10}^{-2}$
[12] ${\widehat{\delta }}_{M_{e_4}}$	$1.4\times {10}^{-3}$	$2.3\times {10}^{-2}$	$3.1\times {10}^{-3}$	$1.1\times {10}^{-2}$	$1.5\times {10}^{-2}$
[13] ${\widehat{\delta }}_{M_{e_5}}$	$1.3\times {10}^{-3}$	$2.2\times {10}^{-2}$	$2.9\times {10}^{-3}$	$1.0\times {10}^{-2}$	$1.4\times {10}^{-2}$
[14] ${\widehat{\delta }}_{M_{e_6}}$	$1.4\times {10}^{-3}$	$2.4\times {10}^{-2}$	$3.0\times {10}^{-3}$	$1.2\times {10}^{-2}$	$1.5\times {10}^{-2}$
[15] ${\widehat{\delta }}_{M_{e_7}}$	$1.2\times {10}^{-3}$	$2.1\times {10}^{-2}$	$2.7\times {10}^{-3}$	$0.9\times {10}^{-2}$	$1.3\times {10}^{-2}$
[16] ${\widehat{\delta }}_{M_{e_8}}$	$1.3\times {10}^{-3}$	$2.2\times {10}^{-2}$	$2.8\times {10}^{-3}$	$1.0\times {10}^{-2}$	$1.4\times {10}^{-2}$

,

Table 5. Mean squared error (MSE) values for $n=150$.

Estimator	$\mathit{Gam}(5,2)$	$\mathit{LN}(3,2)$	$\mathit{C}(6,3)$	$\mathit{Uni}(6,19)$	$\mathit{Exp}\left(0.5\right)$
[1] ${\widehat{\delta }}_{M_y}$	$4.5\times {10}^{-3}$	$5.4\times {10}^{-2}$	$6.3\times {10}^{-3}$	$2.6\times {10}^{-2}$	$3.5\times {10}^{-2}$
[2] ${\widehat{\delta }}_{M_R}$	$5.3\times {10}^{-3}$	$6.2\times {10}^{-2}$	$7.1\times {10}^{-3}$	$3.4\times {10}^{-2}$	$4.4\times {10}^{-2}$
[3] ${\widehat{\delta }}_{M_D}$	$3.5\times {10}^{-3}$	$4.4\times {10}^{-2}$	$5.2\times {10}^{-3}$	$2.2\times {10}^{-2}$	$2.9\times {10}^{-2}$
[4] ${\widehat{\delta }}_{M_{Re}}$	$3.4\times {10}^{-3}$	$4.2\times {10}^{-2}$	$5.0\times {10}^{-3}$	$2.1\times {10}^{-2}$	$2.8\times {10}^{-2}$
[5] ${\widehat{\delta }}_{M_{Pe}}$	$4.1\times {10}^{-3}$	$5.0\times {10}^{-2}$	$5.9\times {10}^{-3}$	$2.4\times {10}^{-2}$	$3.3\times {10}^{-2}$
[6] ${\widehat{\delta }}_{M_{D_1}}$	$2.4\times {10}^{-3}$	$3.3\times {10}^{-2}$	$4.1\times {10}^{-3}$	$1.6\times {10}^{-2}$	$2.2\times {10}^{-2}$
[7] ${\widehat{\delta }}_{M_{D_2}}$	$1.9\times {10}^{-3}$	$2.9\times {10}^{-2}$	$3.9\times {10}^{-3}$	$1.4\times {10}^{-2}$	$2.0\times {10}^{-2}$
[8] ${\widehat{\delta }}_{M_{D_3}}$	$3.1\times {10}^{-3}$	$4.0\times {10}^{-2}$	$4.4\times {10}^{-3}$	$2.0\times {10}^{-2}$	$2.6\times {10}^{-2}$
[9] ${\widehat{\delta }}_{M_{e_1}}$	$1.4\times {10}^{-3}$	$2.4\times {10}^{-2}$	$3.1\times {10}^{-3}$	$1.1\times {10}^{-2}$	$1.5\times {10}^{-2}$
[10] ${\widehat{\delta }}_{M_{e_2}}$	$1.5\times {10}^{-3}$	$2.5\times {10}^{-2}$	$3.2\times {10}^{-3}$	$1.2\times {10}^{-2}$	$1.6\times {10}^{-2}$
[11] ${\widehat{\delta }}_{M_{e_3}}$	$1.6\times {10}^{-3}$	$2.6\times {10}^{-2}$	$3.3\times {10}^{-3}$	$1.3\times {10}^{-2}$	$1.6\times {10}^{-2}$
[12] ${\widehat{\delta }}_{M_{e_4}}$	$1.3\times {10}^{-3}$	$2.2\times {10}^{-2}$	$3.0\times {10}^{-3}$	$1.0\times {10}^{-2}$	$1.4\times {10}^{-2}$
[13] ${\widehat{\delta }}_{M_{e_5}}$	$1.2\times {10}^{-3}$	$2.1\times {10}^{-2}$	$2.8\times {10}^{-3}$	$0.9\times {10}^{-2}$	$1.3\times {10}^{-2}$
[14] ${\widehat{\delta }}_{M_{e_6}}$	$1.3\times {10}^{-3}$	$2.3\times {10}^{-2}$	$2.9\times {10}^{-3}$	$1.1\times {10}^{-2}$	$1.4\times {10}^{-2}$
[15] ${\widehat{\delta }}_{M_{e_7}}$	$1.1\times {10}^{-3}$	$2.0\times {10}^{-2}$	$2.6\times {10}^{-3}$	$0.8\times {10}^{-2}$	$1.2\times {10}^{-2}$
[16] ${\widehat{\delta }}_{M_{e_8}}$	$1.2\times {10}^{-3}$	$2.1\times {10}^{-2}$	$2.7\times {10}^{-3}$	$0.9\times {10}^{-2}$	$1.3\times {10}^{-2}$

and

Table 6. Mean squared error (MSE) values for $n=200$.

Estimator	$\mathit{Gam}(5,2)$	$\mathit{LN}(3,2)$	$\mathit{C}(6,3)$	$\mathit{Uni}(6,19)$	$\mathit{Exp}\left(0.5\right)$
[1] ${\widehat{\delta }}_{M_y}$	$4.3\times {10}^{-3}$	$5.2\times {10}^{-2}$	$6.1\times {10}^{-3}$	$2.5\times {10}^{-2}$	$3.4\times {10}^{-2}$
[2] ${\widehat{\delta }}_{M_R}$	$5.1\times {10}^{-3}$	$6.0\times {10}^{-2}$	$7.0\times {10}^{-3}$	$3.2\times {10}^{-2}$	$4.2\times {10}^{-2}$
[3] ${\widehat{\delta }}_{M_D}$	$3.3\times {10}^{-3}$	$4.2\times {10}^{-2}$	$5.0\times {10}^{-3}$	$2.1\times {10}^{-2}$	$2.8\times {10}^{-2}$
[4] ${\widehat{\delta }}_{M_{Re}}$	$3.2\times {10}^{-3}$	$4.0\times {10}^{-2}$	$4.8\times {10}^{-3}$	$2.0\times {10}^{-2}$	$2.6\times {10}^{-2}$
[5] ${\widehat{\delta }}_{M_{Pe}}$	$3.9\times {10}^{-3}$	$4.8\times {10}^{-2}$	$5.7\times {10}^{-3}$	$2.3\times {10}^{-2}$	$3.2\times {10}^{-2}$
[6] ${\widehat{\delta }}_{M_{D_1}}$	$2.3\times {10}^{-3}$	$3.2\times {10}^{-2}$	$4.0\times {10}^{-3}$	$1.5\times {10}^{-2}$	$2.1\times {10}^{-2}$
[7] ${\widehat{\delta }}_{M_{D_2}}$	$1.8\times {10}^{-3}$	$2.8\times {10}^{-2}$	$3.7\times {10}^{-3}$	$1.3\times {10}^{-2}$	$1.9\times {10}^{-2}$
[8] ${\widehat{\delta }}_{M_{D_3}}$	$3.0\times {10}^{-3}$	$3.9\times {10}^{-2}$	$4.3\times {10}^{-3}$	$1.9\times {10}^{-2}$	$2.5\times {10}^{-2}$
[9] ${\widehat{\delta }}_{M_{e_1}}$	$1.3\times {10}^{-3}$	$2.3\times {10}^{-2}$	$3.0\times {10}^{-3}$	$1.0\times {10}^{-2}$	$1.4\times {10}^{-2}$
[10] ${\widehat{\delta }}_{M_{e_2}}$	$1.4\times {10}^{-3}$	$2.4\times {10}^{-2}$	$3.1\times {10}^{-3}$	$1.1\times {10}^{-2}$	$1.5\times {10}^{-2}$
[11] ${\widehat{\delta }}_{M_{e_3}}$	$1.5\times {10}^{-3}$	$2.5\times {10}^{-2}$	$3.2\times {10}^{-3}$	$1.2\times {10}^{-2}$	$1.6\times {10}^{-2}$
[12] ${\widehat{\delta }}_{M_{e_4}}$	$1.2\times {10}^{-3}$	$2.1\times {10}^{-2}$	$2.9\times {10}^{-3}$	$0.9\times {10}^{-2}$	$1.3\times {10}^{-2}$
[13] ${\widehat{\delta }}_{M_{e_5}}$	$1.1\times {10}^{-3}$	$2.0\times {10}^{-2}$	$2.7\times {10}^{-3}$	$0.8\times {10}^{-2}$	$1.2\times {10}^{-2}$
[14] ${\widehat{\delta }}_{M_{e_6}}$	$1.2\times {10}^{-3}$	$2.2\times {10}^{-2}$	$2.8\times {10}^{-3}$	$1.0\times {10}^{-2}$	$1.3\times {10}^{-2}$
[15] ${\widehat{\delta }}_{M_{e_7}}$	$1.0\times {10}^{-3}$	$1.9\times {10}^{-2}$	$2.5\times {10}^{-3}$	$0.7\times {10}^{-2}$	$1.1\times {10}^{-2}$
[16] ${\widehat{\delta }}_{M_{e_8}}$	$1.1\times {10}^{-3}$	$2.0\times {10}^{-2}$	$2.6\times {10}^{-3}$	$0.8\times {10}^{-2}$	$1.2\times {10}^{-2}$

. The outcomes from the real datasets are shown in Table 2. We derive the following significant conclusions from these analyses:

• The MSE values for all new estimators are less than those of the other existing estimators covered in Section 2, according to the findings of both simulated and real datasets, which are shown in Table 2, Table 3, Table 4, Table 5 and Table 6. This illustrates the better performance of the newly proposed estimators over existing ones.
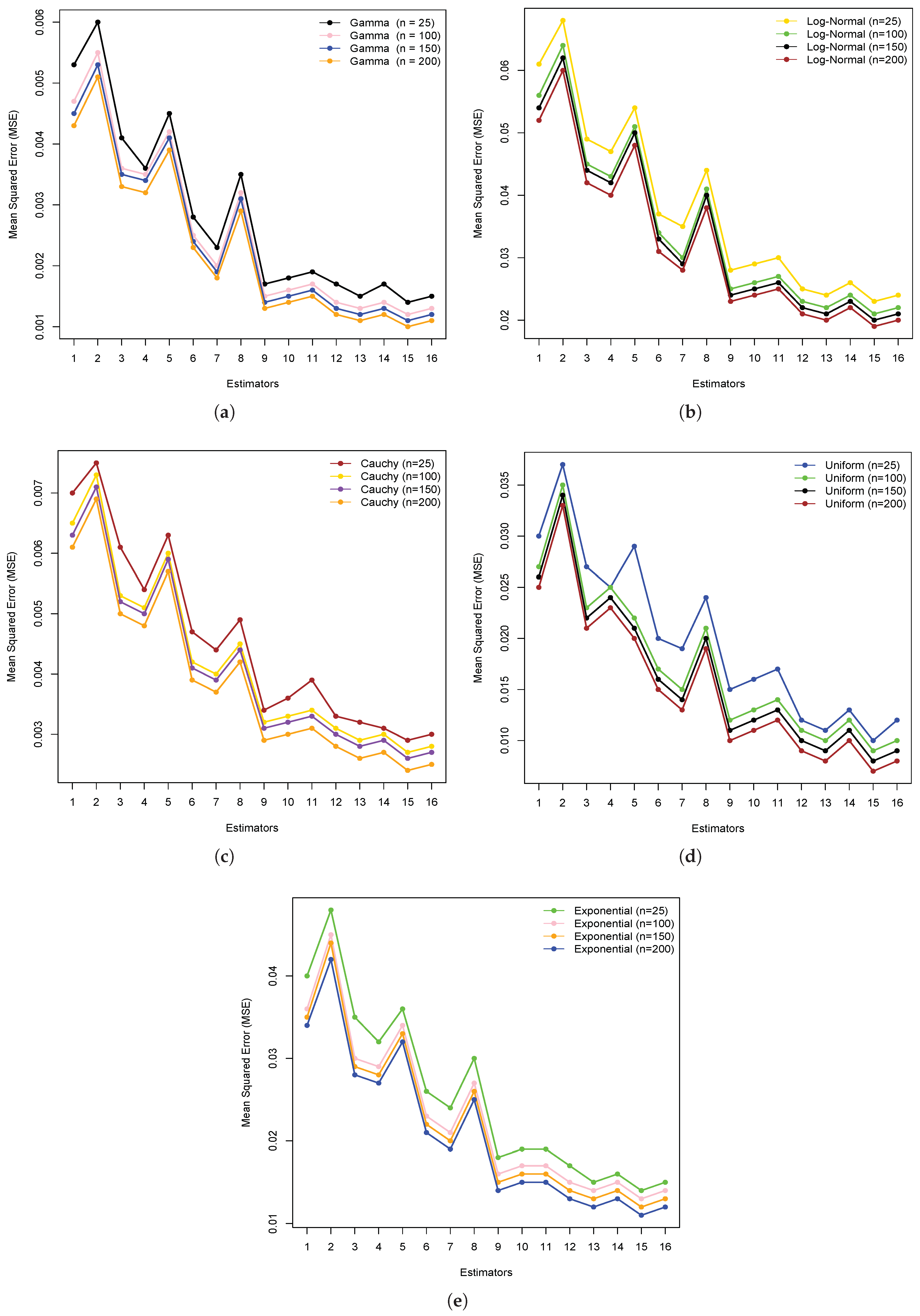
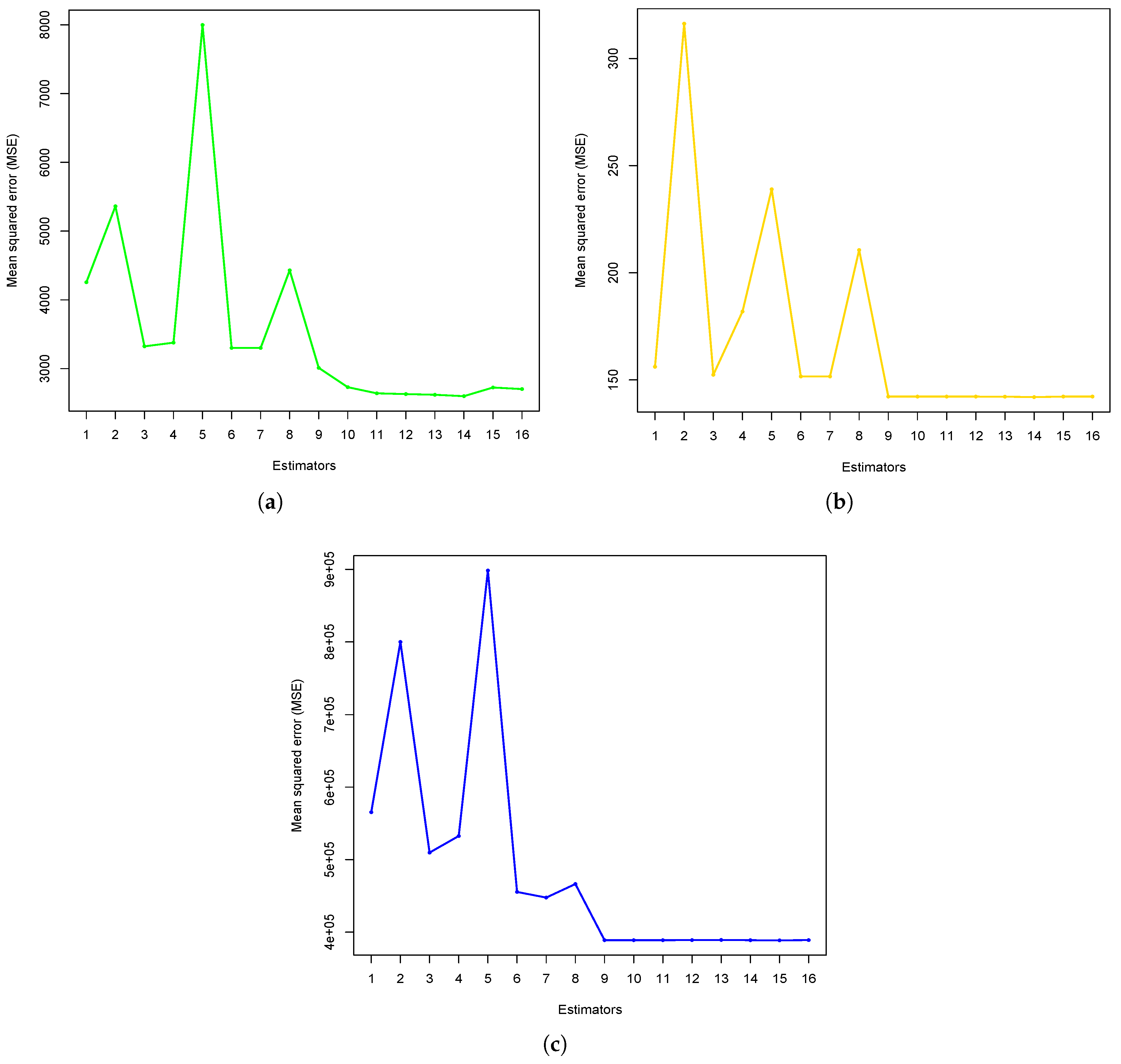
• Furthermore, the downward-trending graph lines in Figure 1 and Figure 2 for both five simulated distributions and three real datasets prove that all new estimators have MSE values that are consistently lower than those of existing estimators. The inverse relationship between the MSE values for the new estimators and the existing estimators led to the conclusion that the new family of estimators outperforms existing methods.
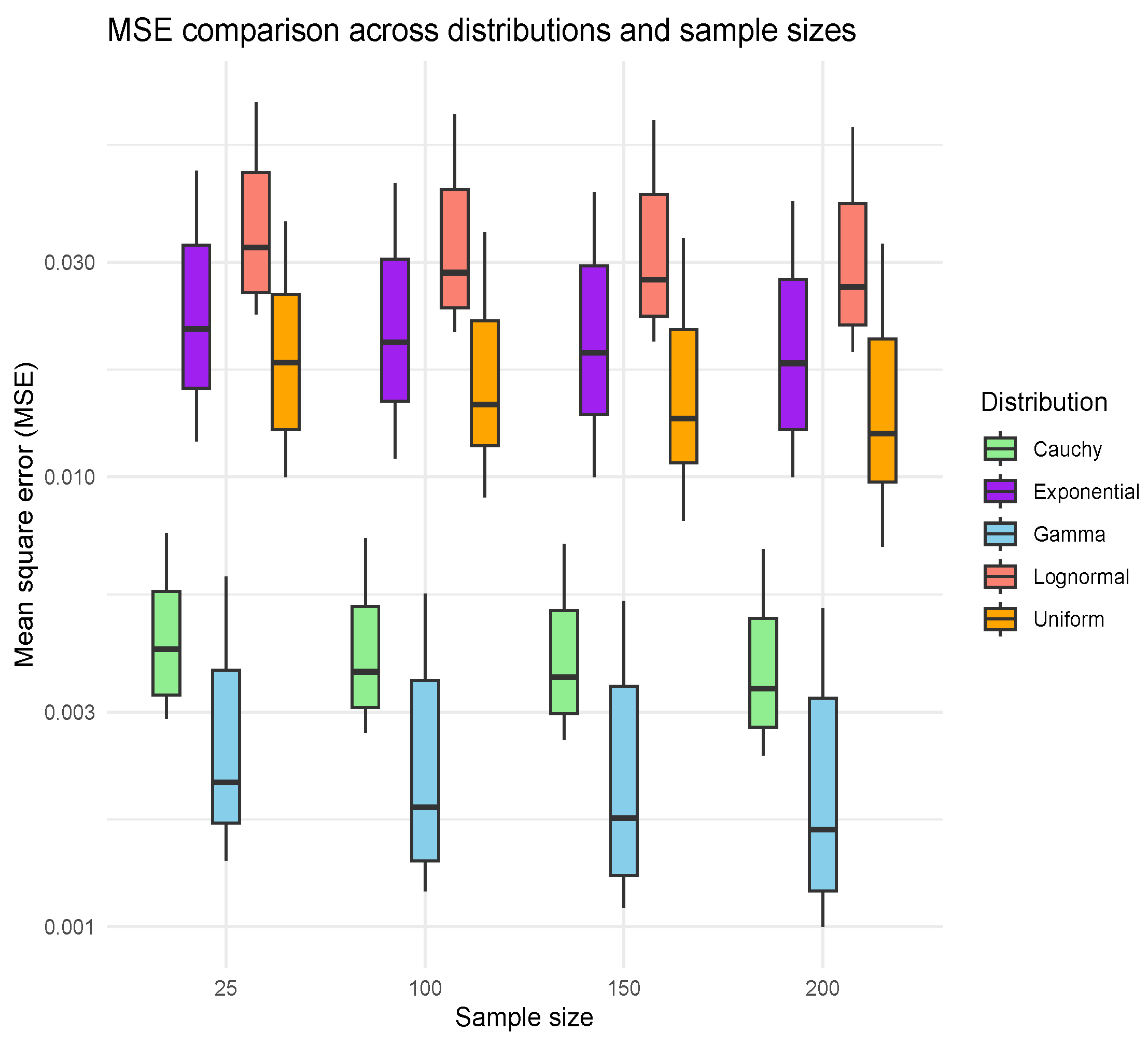
• The box plot given in Figure 3 illustrates the distribution of mean squared error (MSE) values for different sample sizes (25, 100, 150, and 200) across five distributions: Gamma, Lognormal, Cauchy, Uniform, and Exponential. As sample size increases, the MSE values tend to decrease, indicating improved estimation accuracy with larger samples. The plot also highlights variability in MSE across the different distributions, with some showing wider spreads and others demonstrating more consistent performance.
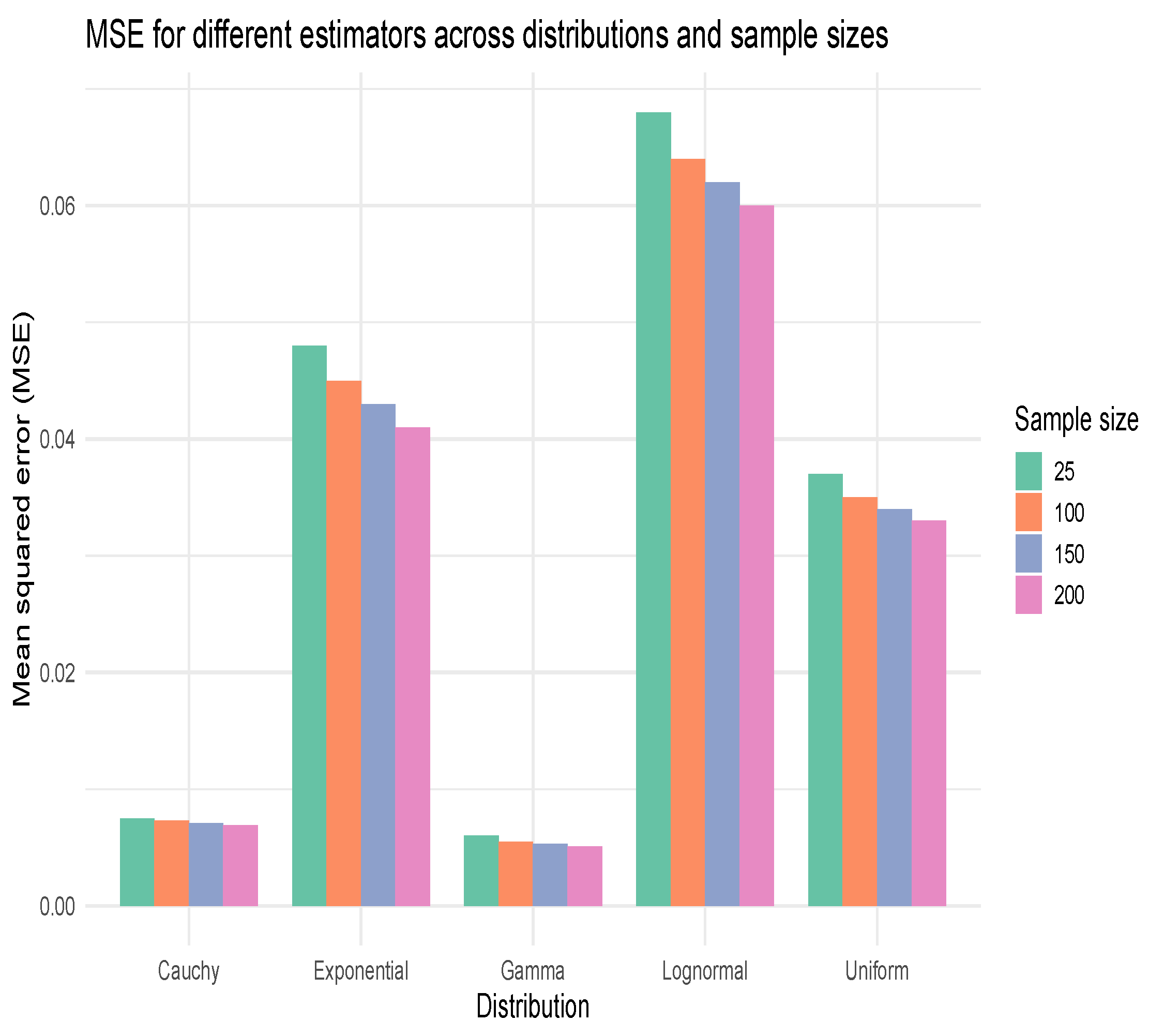
• The bar chart displayed in Figure 4 shows MSE values for different estimators across five distributions and four sample sizes. MSE generally decreases with larger sample sizes, indicating better estimator performance. Distributions like Lognormal and Exponential show higher MSEs, suggesting more estimation difficulty compared to Gamma and Uniform.

6. Conclusions

In this work, we used robust measurements of an auxiliary variable to obtain a new family of estimators to determine the finite population median under simple random sampling. The first degree of approximation provided a valuable framework for obtaining the biases and mean squared errors associated with both existing estimators and several newly developed ones. This approach enhances our understanding of their performance and potential areas for improvement. We conducted simulation analysis through five distributions with all possible different conditions and three real-life datasets to check the potential performance of new estimators with existing estimators by applying the mean squared error criterion. The simulation and numerical real-life dataset results are given in Table 2, Table 3, Table 4, Table 5 and Table 6, which show that the new family of estimators performs well and can obtain the optimum estimators as compared to other existing estimators. We noticed that all the new estimators have higher efficiency than other estimators.

The improved median estimation method has broad practical relevance. In economics, it enhances the accuracy of income-distribution analysis by reducing the impact of outliers. In climate research and environmental monitoring, it provides stable estimates despite extreme events, aiding in model reliability and risk assessment. Medical studies benefit from more robust estimates of patient health indicators, leading to sounder conclusions. In education and social sciences, it helps interpret central tendencies accurately, even in the presence of skewed data, thereby supporting better policy and decision-making.

Furthermore, our analysis focused on the properties of the new improved estimators within the context of a simple random sampling technique. It is worth exploring the potential of developing new estimators based on these findings, with the goal of achieving even lower MSE values under systemmatic sampling and stratified random sampling. This topic offers an interesting direction for further investigation.