A Comprehensive Study of Nonlinear Mixed Integro-Differential Equations of the Third Kind for Initial Value Problems: Existence, Uniqueness and Numerical Solutions
Abstract
1. Introduction
- Converting the IVPs to a form of NM-IDEs of the third kind.
- Investigating the solvability of the second- and the third-kind NM-IDEs via Picard’s method.
- Applying the homotoy analysis method to express the solution of the equation under consideration in addition to the convergence of the approach.
2. Solvability of NM-IDEs of the Third Kind
- 1.
- The kernels and are continuous in and fulfill the following: and , .
- 2.
- The functions and are continuous in the space , satisfying and .
- 3.
- The nonlinear function satisfies
- i.
- The Lipschitz condition.
- ii.
- The inequality ,
3. Homotopy Analysis Method for NM-IDEs
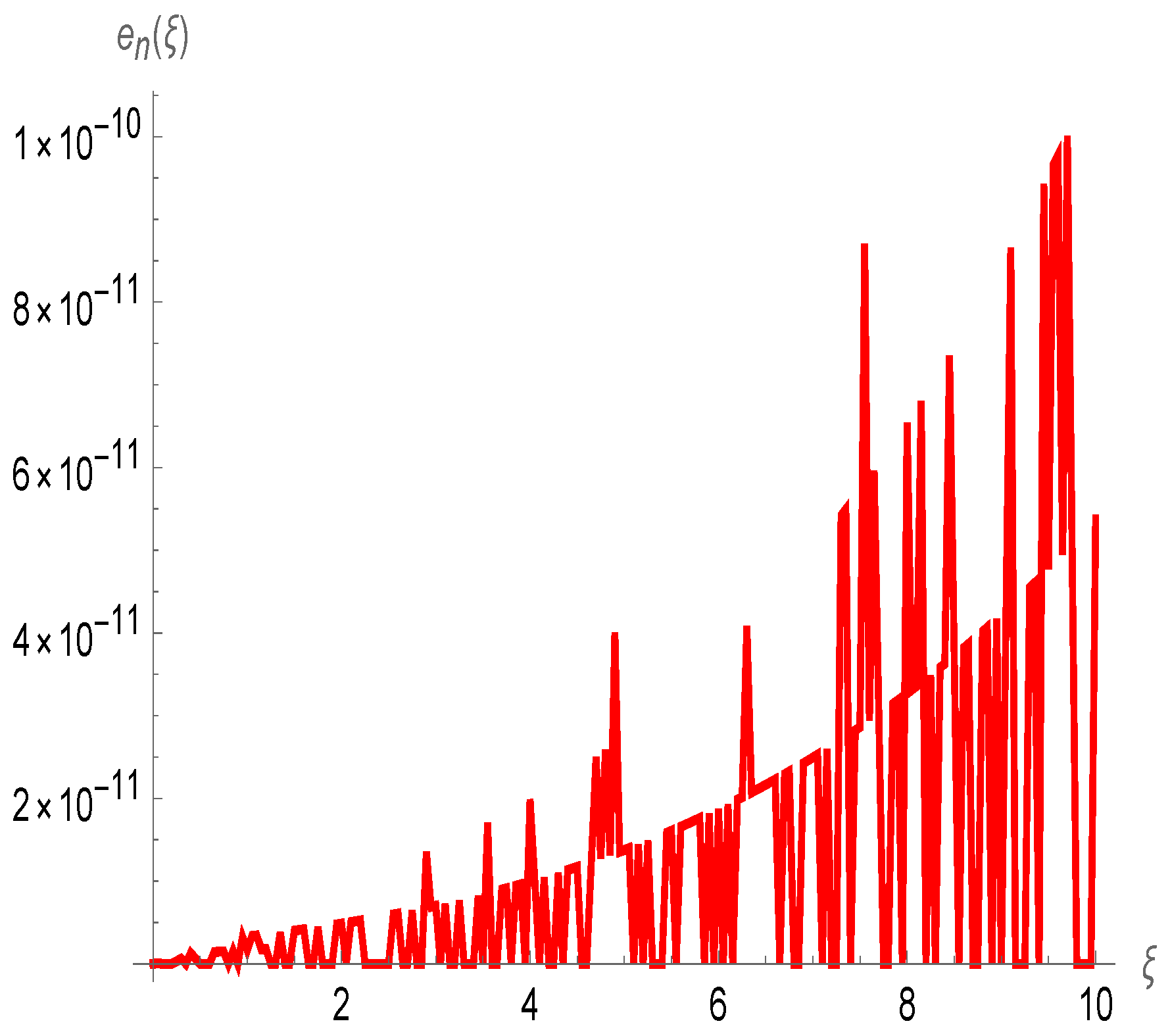
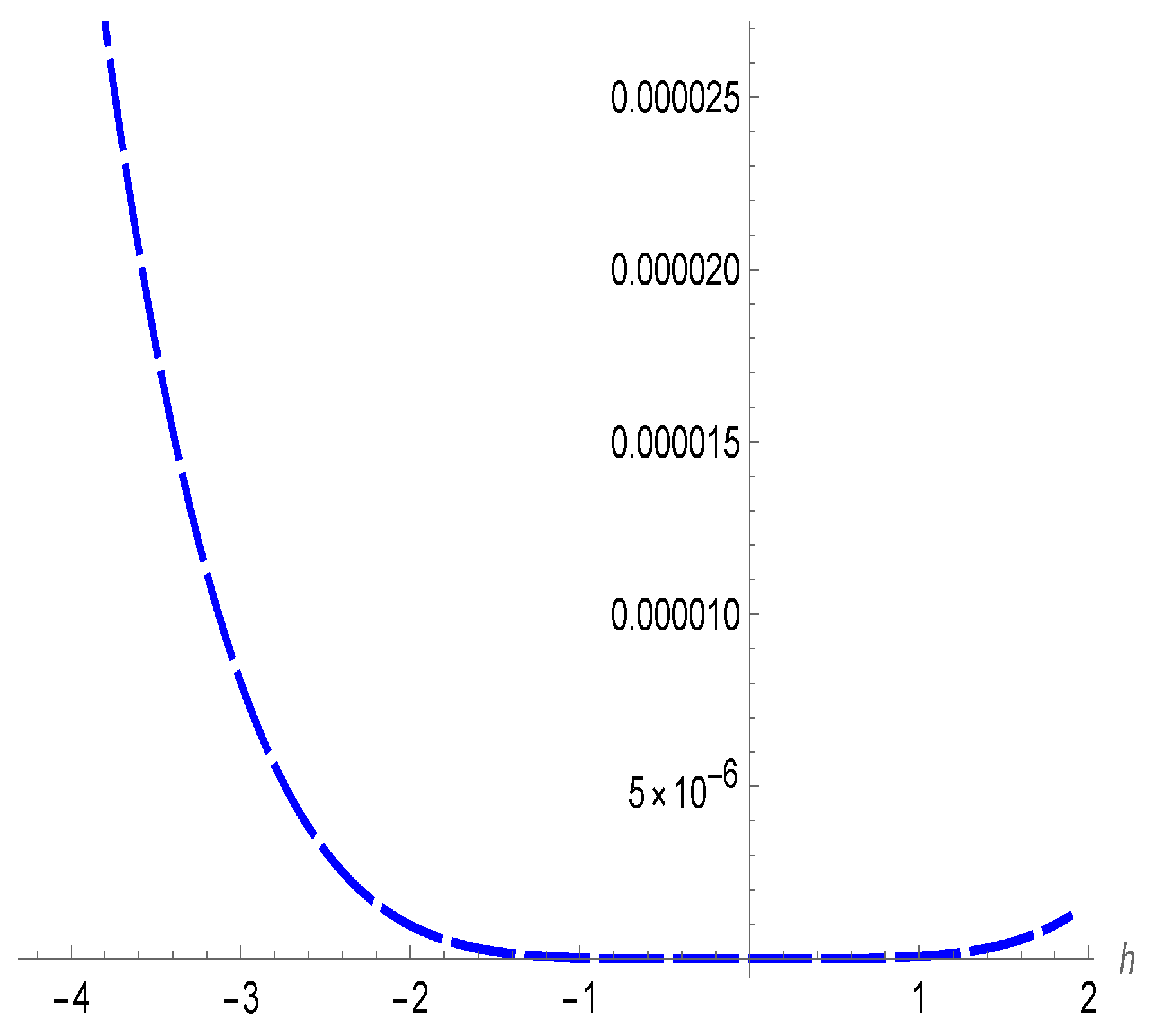
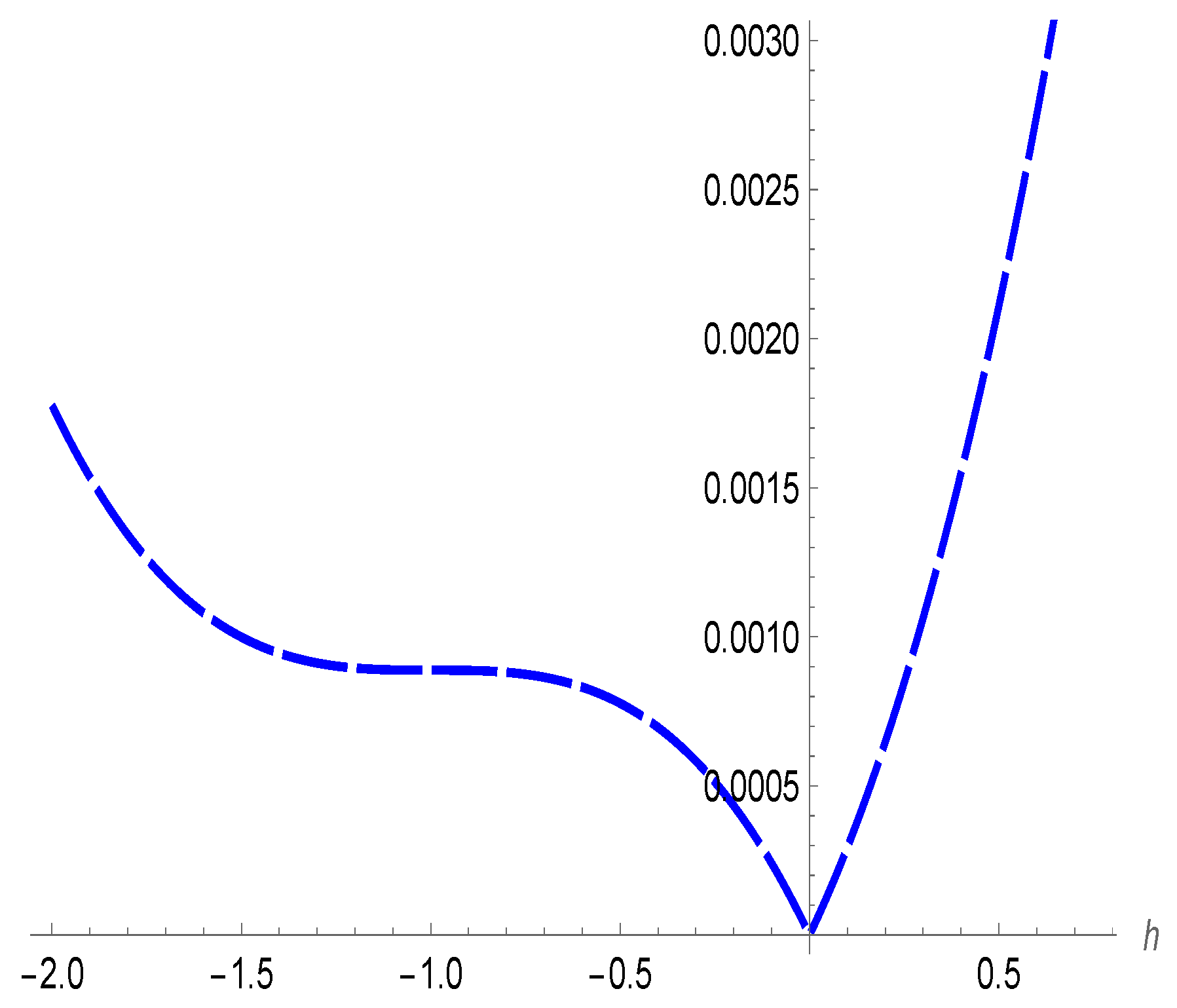
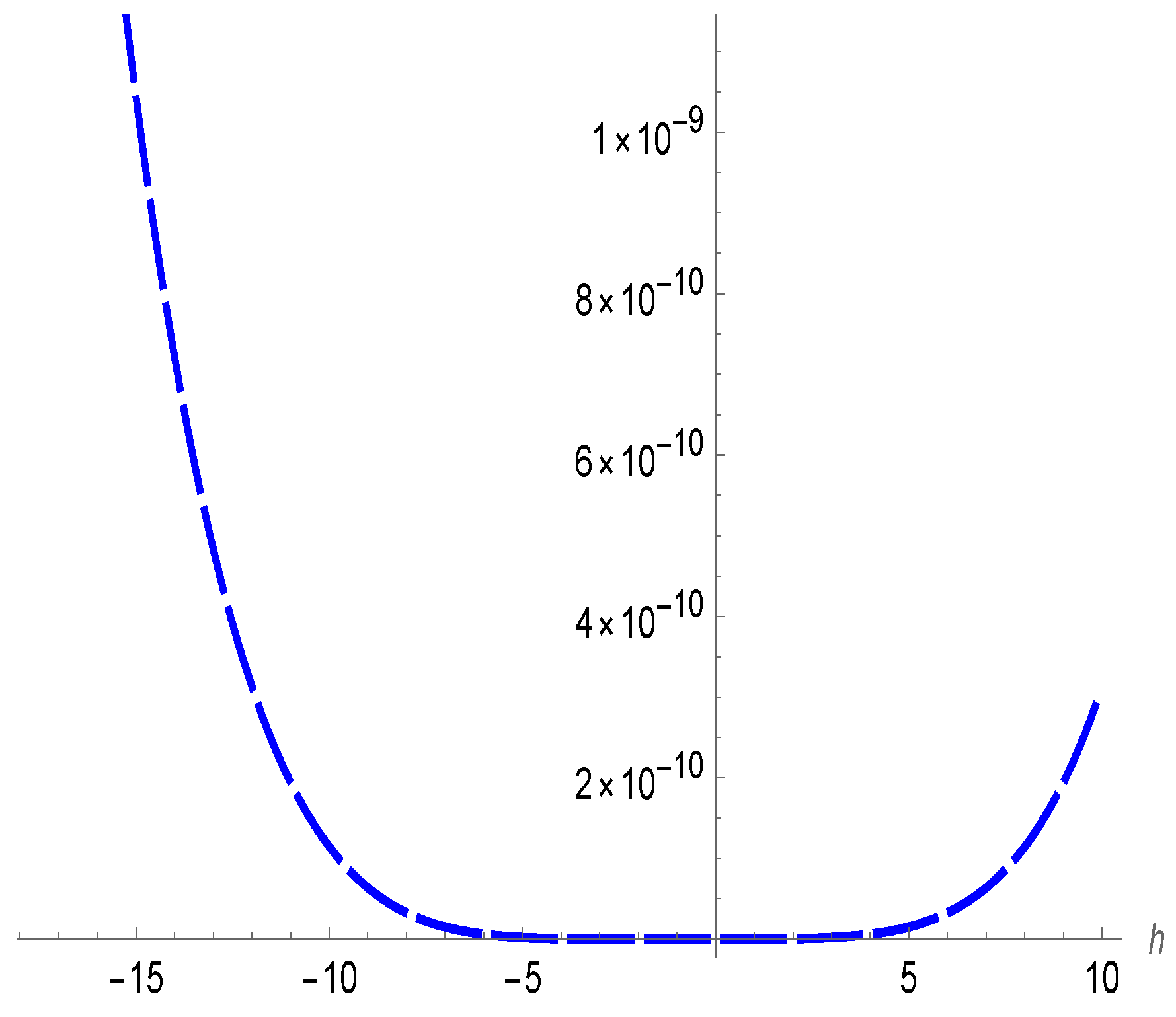
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brenan, K.E.; Campbell, S.L.; Petzold, L.R. Numerical Solution of Initial-Value Problems in Differential-Algebraic Equations; SIAM: Philadelphia, PA, USA, 1995. [Google Scholar]
- Wanner, G.; Hairer, E. Solving Ordinary Differential Equations II; Springer: Berlin/Heidelberg, Germany, 1996; Volume 375. [Google Scholar]
- Mickens, R.E. Truly Nonlinear Oscillations: Harmonic Balance, Parameter Expansions, Iteration, and Averaging Methods; World Scientific: Singapore, 2010. [Google Scholar]
- Biazar, J.; Ghanbari, B. HAM solution of some initial value problems arising in heat radiation equations. J. King Saud Univ. Sci. 2012, 24, 161–165. [Google Scholar]
- Mosa, G.A.; Abdou, M.A.; Rahby, A.S. Numerical solutions for nonlinear Volterra-Fredholm integral equations of the second kind with a phase lag. AIMS Math. 2021, 6, 8525–8543. [Google Scholar]
- Rahby, A.S.; Abdou, M.A.; Mosa, G.A. On the solutions of the second kind nonlinear Volterra-Fredholm integral equations via homotopy analysis method. Int. J. Anal. Appl. 2022, 20, 35. [Google Scholar]
- Shiralashetti, S.C.; Deshi, A.B.; Desai, P.B.M. Haar wavelet collocation method for the numerical solution of singular initial value problems. Ain Shams Eng. J. 2016, 7, 663–670. [Google Scholar]
- Gámez, D.; Guillem, A.I.G.; Galán, M.R. Nonlinear initial-value problems and Schauder bases. Nonlinear Anal. Theory Methods Appl. 2005, 63, 97–105. [Google Scholar]
- Chen, Z.; Jiang, W.; Du, H. A new reproducing kernel method for Duffing equations. Int. J. Comput. Math. 2021, 98, 2341–2354. [Google Scholar]
- Geng, F.; Cui, M.; Zhang, B. Method for solving nonlinear initial value problems by combining homotopy perturbation and reproducing kernel Hilbert space methods. Nonlinear Anal. Real World Appl. 2010, 11, 637–644. [Google Scholar]
- Abdulqader, A.J.; Abdulmaged, R.B.; Abdali, B.M. Numerical solution for solving nonlinear Volterra-Fredholm system by using iterative techniques. J. Interdiscip. Math. 2024, 27, 991–1000. [Google Scholar]
- Mahdy, A.M.S.; Abdou, M.A.; Mohamed, D.S. Numerical solution, convergence and stability of error to solve quadratic mixed integral equation. J. Appl. Math. Comput. 2024, 70, 5887–5916. [Google Scholar] [CrossRef]
- Alalyani, A.; Abdou, M.A.; Basseem, M. The orthogonal polynomials method using Gegenbauer polynomials to solve mixed integral equations with a Carleman kernel. AIMS Math. 2024, 9, 19240–19260. [Google Scholar]
- Achar, S.D. Symmetric multistep Obrechkoff methods with zero phase-lag for periodic initial value problems of second order differential equations. Appl. Math. Comput. 2011, 218, 2237–2248. [Google Scholar]
- Wang, B.; Liu, K.; Wu, X. A Filon-type asymptotic approach to solving highly oscillatory second-order initial value problems. J. Comput. Phys. 2013, 243, 210–223. [Google Scholar] [CrossRef]
- Rahmanzadeh, M.; Cai, L.; White, R.E. A new method for solving initial value problems. Comput. Chem. Eng. 2013, 58, 33–39. [Google Scholar] [CrossRef]
- Baccouch, M. A posteriori error estimates and adaptivity for the discontinuous Galerkin solutions of nonlinear second-order initial-value problems. Appl. Numer. Math. 2017, 121, 18–37. [Google Scholar] [CrossRef]
- Baccouch, M. Superconvergence of the discontinuous Galerkin method for nonlinear second-order initial-value problems for ordinary differential equations. Appl. Numer. Math. 2017, 115, 160–179. [Google Scholar] [CrossRef]
- Ramos, H.; Mehta, S.; Vigo-Aguiar, J. A unified approach for the development of k-step block Falkner-type methods for solving general second-order initial-value problems in ODEs. J. Comput. Appl. Math. 2017, 318, 550–564. [Google Scholar] [CrossRef]
- Khalsaraei, M.M.; Shokri, A. An explicit six-step singularly P-stable Obrechkoff method for the numerical solution of second-order oscillatory initial value problems. Numer. Algorithms 2020, 84, 871–886. [Google Scholar] [CrossRef]
- Yüzbaşı, S. A collocation method based on Bernstein polynomials to solve nonlinear Fredholm–Volterra integro-differential equations. Appl. Math. Comput. 2016, 273, 142–154. [Google Scholar] [CrossRef]
- Alalyani, A.; Abdou, M.A.; Basseem, M. On a Solution of a Third Kind Mixed Integro-Differential Equation with Singular Kernel Using Orthogonal Polynomial Method. J. Appl. Math. 2023, 2023, 5163398. [Google Scholar] [CrossRef]
- Hemeda, A.A. A friendly iterative technique for solving nonlinear integro-differential and systems of nonlinear integro-differential equations. Int. J. Comput. Methods 2018, 15, 1850016. [Google Scholar] [CrossRef]
- Hamed, Y.S.; Amer, Y.A. Nonlinear saturation controller for vibration supersession of a nonlinear composite beam. J. Mech. Sci. Technol. 2014, 28, 2987–3002. [Google Scholar] [CrossRef]
- Warminski, J.; Bochenski, M.; Jarzyna, W.; Filipek, P.; Augustyniak, M. Active suppression of nonlinear composite beam vibrations by selected control algorithms. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 2237–2248. [Google Scholar]
- Warminski, J.; Cartmell, M.P.; Bochenski, M.; Ivanov, I. Analytical and experimental investigations of an autoparametric beam structure. J. Sound Vib. 2008, 315, 486–508. [Google Scholar] [CrossRef]
- Liao, S. Homotopy analysis method: A new analytic method for nonlinear problems. Appl. Math. Mech. 1998, 19, 957–962. [Google Scholar]
- Cherruault, Y. Convergence of Adomian’s method. Kybernetes 1989, 18, 31–38. [Google Scholar]




| HAM | HWCM |
|---|---|
| HAM | RKHSA with HPM |
|---|---|
| HAM | SB |
|---|---|
| HAM | RKM |
|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahby, A.S.; Askar, S.S.; Alshamrani, A.M.; Mosa, G.A. A Comprehensive Study of Nonlinear Mixed Integro-Differential Equations of the Third Kind for Initial Value Problems: Existence, Uniqueness and Numerical Solutions. Axioms 2025, 14, 282. https://doi.org/10.3390/axioms14040282
Rahby AS, Askar SS, Alshamrani AM, Mosa GA. A Comprehensive Study of Nonlinear Mixed Integro-Differential Equations of the Third Kind for Initial Value Problems: Existence, Uniqueness and Numerical Solutions. Axioms. 2025; 14(4):282. https://doi.org/10.3390/axioms14040282
Chicago/Turabian StyleRahby, Ahmed S., Sameh S. Askar, Ahmad M. Alshamrani, and Gamal A. Mosa. 2025. "A Comprehensive Study of Nonlinear Mixed Integro-Differential Equations of the Third Kind for Initial Value Problems: Existence, Uniqueness and Numerical Solutions" Axioms 14, no. 4: 282. https://doi.org/10.3390/axioms14040282
APA StyleRahby, A. S., Askar, S. S., Alshamrani, A. M., & Mosa, G. A. (2025). A Comprehensive Study of Nonlinear Mixed Integro-Differential Equations of the Third Kind for Initial Value Problems: Existence, Uniqueness and Numerical Solutions. Axioms, 14(4), 282. https://doi.org/10.3390/axioms14040282







