A Robust Framework for Probability Distribution Generation: Analyzing Structural Properties and Applications in Engineering and Medicine

Abstract

This study introduces a novel trigonometric-based family of distributions for modeling continuous data through a newly proposed framework known as the ASP family, where ‘ASP’ represents the initials of the authors Aadil, Shamshad, and Parvaiz. A specific subclass of this family, termed the “ASP Rayleigh distribution” (ASPRD), is introduced that features two parameters. We conducted a comprehensive statistical analysis of the ASPRD, exploring its key properties and demonstrating its superior adaptability. The model parameters are estimated using four classical estimation methods: maximum likelihood estimation (MLE), least squares estimation (LSE), weighted least squares estimation (WLSE), and maximum product of spaces estimation (MPSE). Extensive simulation studies confirm these estimation techniques’ robustness, showing that biases, mean squared errors, and root mean squared errors consistently decrease as sample sizes increase. To further validate its applicability, we employ ASPRD on three real-world engineering datasets, showcasing its effectiveness in modeling complex data structures. This work not only strengthens the theoretical framework of probability distributions but also provides valuable tools for practical applications, paving the way for future advancements in statistical modeling.

1. Introduction

In the past few decades, the increasing complexity of real-world data has motivated researchers to develop more advanced probability distributions. While traditional models form the foundation of statistical analysis, they often lack the necessary flexibility and accuracy for modern applications. To overcome these limitations, several generalized families of distributions have been introduced, extending classical models to enhance both theoretical insights and practical applications.

One of the earliest and most fundamental techniques for generating new probability distributions was introduced by [1], who proposed the exponentiated family of distributions. The cumulative distribution function (CDF) of this family is given by:

$$F(x;\alpha ,\zeta )={\left[G(x;\zeta )\right]}^{\alpha };\alpha ,\zeta >0,x\in \mathcal{R}.$$

(1)

where $\alpha >0$ acts as an additional shape parameter and $G(x;\zeta )$ denotes the CDF of the baseline distribution, parameterized by $\zeta$.

Marshall and Olkin [2] introduced an alternative approach, known as the “Marshall and Olkin Family” of distributions, designed to modify existing models. The CDF of this family is defined as:

$$F(x;\alpha ,\zeta )={\displaystyle \frac{G(x;\zeta )}{1-(1-\alpha )\left[1-G(x;\zeta )\right]}};\alpha ,\zeta >0,x\in \mathcal{R}.$$

(2)

Odhah et al. [3] proposed a new family of distributions based on trigonometric transformations, with the CDF given by:

$$F(x;\zeta )={\displaystyle \frac{e^{1-cos\left[\frac{\pi G(x;\zeta )}{1+G(x;\zeta )}\right]}-1}{e-1}};\zeta >0,x\in \mathcal{R}.$$

(3)

Additionally, Shah et al. [4] introduced a more flexible probability model using the T-X family methodology [5]. This led to the development of the New Exponent Power-X (NGEP-X) family, whose CDF is given by:

$$F(x;\alpha ,\zeta )=1-\left(e^{\alpha G(x;\zeta )}-e^{\alpha }G(x;\zeta )\right);\alpha \in {\mathcal{R}}^{+},x\in \mathcal{R}.$$

(4)

To further enhance flexibility, Mahdavi and Kundu [6] proposed the Alpha Power Transformation (APT) method, which introduces an additional shape parameter $\alpha$ to the baseline distribution $G(x;\zeta )$. The CDF of the APT family is given by:

$$F(x;\alpha ,\zeta )=\left\{\begin{array}{cc}{\displaystyle \frac{{\alpha }^{G(x;\zeta )}-1}{\alpha -1}},\hfill & \mathrm{if}\alpha >0,\alpha \ne 1\hfill \\ G(x;\zeta ),\hfill & \mathrm{if}\alpha =1\hfill \end{array}\right.$$

(5)

Trigonometric-based transformations have gained significant attention due to their ability to alter the shape of distributions without introducing additional parameters. A notable example is the sine-G family, introduced by [7], which applies a sine transformation to the CDF of a baseline distribution. This approach enhances shape flexibility while preserving the simplicity of the original model. The CDF and PDF of the sine-G family are defined as follows:

$$F(x;\zeta )=sin\left[{\displaystyle \frac{\pi }{2}}G(x;\zeta )\right]$$

(6)

$$f(x;\zeta )={\displaystyle \frac{\pi }{2}}g(x;\zeta )cos\left[{\displaystyle \frac{\pi }{2}}G(x;\zeta )\right]$$

(7)

where $G(x;\zeta )$ and $g(x;\zeta )$ represent the CDF and PDF of the baseline distribution, respectively. An extension of this method, the Exponentiated Sine-Generated Distributions, was introduced by [8] with the following CDF:

$$F(x;\alpha ,\xi )={\left[sin\left({\displaystyle \frac{\pi }{2}}G(x;\xi )\right)\right]}^{\alpha },\alpha >0.$$

(8)

More recently, Oramulu et al. [9] introduced the sine-generalized family of distributions, whose CDF is given by:

$$F\left(x\right)=sin\left[{\displaystyle \frac{\pi }{2}}\left(1-{\left(\overline{G}\left(x\right)\right)}^{\alpha }\right)\right],x>0,\alpha >0.$$

(9)

Several researchers have explored sine-based transformations to extend classical probability distributions. For instance, Ref. [10] introduced the sine-exponential distribution, while Ref. [11] proposed the sine-Weibull distribution, enhancing the flexibility of the Weibull model. Similarly, Ref. [12] developed the sine power Rayleigh distribution, Ref. [13] studied sine-G family of distributions, Ref. [14] studied Sine Topp Leone G family of distributions, Ref. [15] derived sine modified Lindley distribution, Ref. [10] studied Sine burr xii distribution, Ref. [16] discussed the new hyperbolic sine generator with an example of Rayleigh distribution, Ref. [17] derived sine Kumaraswamy-G family of distributions, Ref. [18] considered sine generalized odd log-logistic family of distributions, and Ref. [19] investigated the sine inverse Rayleigh distribution.

A seminal example in this evolution is the Rayleigh distribution, originally introduced by [20], which has been extensively used to model skewed data, particularly in lifetime analysis. Recognizing the limitations of the classical Rayleigh model, researchers have sought to extend its framework to better capture diverse data behaviors. For instance, the two-parameter Burr type X distribution, first described by [21], marked an important step in this direction. Building on that foundation, Ref. [22] rigorously investigated and estimated the parameters of this extended model using various innovative techniques.

In parallel, Bayesian methodologies have been applied to refine parameter estimation within the Rayleigh framework. Ref. [23] examined the properties of the Half Logistic Exponentiated Inverse Rayleigh distribution and its application to lifetime data. Furthermore, Ref. [24] studied the half logistic generalized Rayleigh distribution for modeling hydrological data, while Ref. [25] focused on parameter estimation for a weighted version of the Rayleigh distribution.

Building on this framework, Ref. [26] introduced a new extension of the Rayleigh distribution, discussing its methodology, classical and Bayesian estimation, and its application to industrial data; moreover, Ref. [27] demonstrated its practical relevance by applying a flexible variation to predict COVID-19 mortality rates. More recent contributions by [28,29,30,31] have continued to explore generalized distributions and their wide-ranging applications. Moreover, Ref. [32] examined an odd Lindley power extension of the Rayleigh distribution, while Refs. [33,34] further extended the model and investigated its reliability function. Collectively, these advancements underscore the ongoing evolution of probability distribution theory, paving the way for models that are both robust and adaptable to contemporary statistical challenges.

The development of new generalized families of distributions is driven by the need for models that can effectively capture the structural complexities and variability inherent in modern datasets. Traditional distributions often fall short in accommodating the intricate patterns observed in real-world data, necessitating more flexible and adaptive frameworks. As the complexity and dimensionality of data continue to expand, there is a growing demand for probability distributions capable of modeling high-dimensional structures while maintaining interpretability and stability. Such advancements enhance the precision and reliability of statistical analyses by providing a more accurate representation of underlying stochastic processes. In this study, we introduce the ASP family of distributions, a highly adaptable and versatile class designed to address these challenges across various domains. This family extends the Sine-G distribution by integrating the classical generalized function into its probability density structure, resulting in a novel and refined mathematical formulation. The motivation behind constructing the trigonometric ASP family stems from the need for greater flexibility in extending probability distributions. Existing sine-based transformations, while effective, modify the baseline distribution without incorporating additional parameters, thereby limiting their adaptability. To overcome this limitation, we propose the ASP family, which introduces a shape parameter $\alpha$, providing enhanced control over skewness and kurtosis. This structural improvement allows the ASP family to capture a broader range of distributional shapes, making it a more powerful tool for statistical modeling and data analysis.

In this manuscript, we introduce a novel method the ASP transformation designed to extend the classical Rayleigh distribution (RD) and enhance its engineering applications. Our primary goal is to construct new families of distributions with increased flexibility, thereby enabling a more comprehensive analysis of real-world data. The proposed approach not only generalizes the traditional RD but also provides improved adaptability for modeling skewed data, which is particularly valuable in lifetime and reliability studies.

The selection of maximum likelihood estimation (MLE), least squares estimation (LSE), weighted least squares estimation (WLSE), and maximum product of spacings estimation (MPSE) for estimating the parameters of the ASP Rayleigh Distribution (ASPRD) is driven by their theoretical strengths, computational feasibility and practical applicability. MLE is preferred for its asymptotic efficiency, while LSE provides a simpler alternative when direct likelihood optimization is challenging. WLSE improves estimation in heteroscedastic cases, and MPSE offers stability, particularly for small samples. These methods outperform alternatives like the method of moments or Bayesian estimation, which may impose restrictive assumptions or be computationally intensive. The inclusion of these four approaches ensures a well-rounded analysis of ASPRD, reinforcing the reliability and adaptability of the proposed model in practical applications.

The paper is organized as follows. In Section 2, we present a detailed outline of the ASP transformation technique, explaining its underlying principles and the rationale behind its development. Section 3 is dedicated to introducing the ASP Rayleigh Distribution (ASPRD), where we describe its formulation and key features. The expansion of this distribution is explored in Section 4, demonstrating how the ASP transformation broadens the scope of classical models. In Section 5, we derive and discuss the statistical properties of ASPRD, highlighting its theoretical foundations and practical implications. Estimation of unknown parameters is addressed in Section 6 using the MLE, LSE, WLSE, and MPSE methods, which provides robust techniques for parameter inference. To validate our approach, Section 7 presents extensive simulation studies and Section 8 illustrates the application of ASPRD to real-life datasets. Finally, Section 9 concludes the paper by summarizing our findings and suggesting potential avenues for future research.

2. ASP Method

The CDFs of the ASP method are given as:

$$F_{\mathrm{ASP}}(x;\alpha )=2sin\left[{\displaystyle \frac{\pi }{2}}{\left[C(x;\zeta )\right]}^{\alpha }\right]-{\left[C(x;\zeta )\right]}^{\alpha };\alpha >0.$$

(10)

It is evident that $F_{\mathrm{ASP}}(x;\alpha )$ is a valid CDF, provided that $C(x;\zeta )$ is a valid CDF. This holds because it satisfies the fundamental properties of CDF as:

• ${\mathrm{F}}_{\mathrm{ASP}}(-\infty )=0$; $F_{\mathrm{ASP}}(\infty )=1$
• ${\mathrm{F}}_{\mathrm{ASP}}\left(x\right)$ is a monotonic increasing function of x
• ${\mathrm{F}}_{\mathrm{ASP}}\left(x\right)$ is right continuous
• $0\le {\mathrm{F}}_{\mathrm{ASP}}\left(x\right)\le 1$

and the corresponding PDF is expressed as:

$$f_{\mathrm{ASP}}(x;\alpha )=\alpha \left[\pi cos\left[{\displaystyle \frac{\pi }{2}}{\left[C(x;\zeta )\right]}^{\alpha }\right]-1\right]{\left[C(x;\zeta )\right]}^{\alpha -1}c(x;\zeta );\alpha >0.$$

(11)

In Equations (10) and (11), $C(x;\zeta )$ and $c(x;\zeta )$, respectively, represent the CDF and PDF of the base line distribution with parameter vector $\zeta$.

The reliability function of the ASP method is defined as:

$$R_{\mathrm{ASP}}(x;\alpha )=1-2sin\left({\displaystyle \frac{\pi }{2}}{\left[C(x;\zeta )\right]}^{\alpha }\right)+{\left[C(x;\zeta )\right]}^{\alpha };\alpha >0.$$

(12)

By using the ASP approach, the hazard rate function is provided by

$$h_{\mathrm{ASP}}(x;\alpha )={\displaystyle \frac{\alpha \left[\pi cos\left(\frac{\pi }{2}{\left[C(x;\zeta )\right]}^{\alpha }\right)-1\right]{\left[C(x;\zeta )\right]}^{\alpha -1}c(x;\zeta )}{1-2sin\left(\frac{\pi }{2}{\left[C(x;\zeta )\right]}^{\alpha }\right)+{\left[C(x;\zeta )\right]}^{\alpha }}};\alpha >0.$$

(13)

3. ASP Rayleigh Distribution (ASPRD)

The PDF and CDF of the Rayleigh distribution (RD) are defined as follows:

$$\begin{array}{c}\hfill c(x;\theta )={\displaystyle \frac{x}{{\theta }^2}}exp\left(-{\displaystyle \frac{x^2}{2{\theta }^2}}\right);x>0,\theta >0\end{array}$$

(14)

$$\begin{array}{c}\hfill C(x;\theta )=1-exp\left(-{\displaystyle \frac{x^2}{2{\theta }^2}}\right);x>0,\theta >0\end{array}$$

(15)

By inserting Equation (15) in Equation (10), the CDF of ASPRD is obtained as

$$\begin{array}{c}\hfill F_{\mathrm{ASPRD}}(x;\alpha ,\theta )=2sin\left[{\displaystyle \frac{\pi }{2}}{\left[1-exp\left(-{\displaystyle \frac{x^2}{2{\theta }^2}}\right)\right]}^{\alpha }\right]-{\left[1-exp\left(-{\displaystyle \frac{x^2}{2{\theta }^2}}\right)\right]}^{\alpha };\alpha ,\theta >0.\end{array}$$

(16)

where $\alpha$ and $\theta$ are the shape and scale parameter of the model.

The corresponding PDF of ASPRD is obtained as

$$\begin{array}{c}\hfill f_{\mathrm{ASPRD}}(x;\alpha ,\theta )={\displaystyle \frac{\alpha x}{{\theta }^2}}exp\left(-{\displaystyle \frac{x^2}{2{\theta }^2}}\right)\left[\pi cos\left({\displaystyle \frac{\pi }{2}}{\left[1-exp\left(-{\displaystyle \frac{x^2}{2{\theta }^2}}\right)\right]}^{\alpha }\right)-1\right]{\left[1-exp\left(-{\displaystyle \frac{x^2}{2{\theta }^2}}\right)\right]}^{\alpha -1}.\end{array}$$

(17)

To analyze the asymptotic behavior of (17), we consider two cases:

• Case 1: As $x\to 0$

For small values of x, we observe that:

$${\displaystyle \frac{x^2}{2{\theta }^2}}\to 0\Rightarrow e^{-\frac{x^2}{2{\theta }^2}}\to 1.$$

Thus,

$$1-e^{-\frac{x^2}{2{\theta }^2}}\to 0.$$

For the cosine term, we have the following

$$\pi cos\left[{\displaystyle \frac{\pi }{2}}{\left(1-e^{-\frac{x^2}{2{\theta }^2}}\right)}^{\alpha }\right]=\pi cos\left(0\right)=\pi ;\mathrm{as}{\left[1-e^{-\frac{x^2}{2{\theta }^2}}\right]}^{\alpha }\to 0.$$

Therefore, combining all these results, we conclude the following:

$$\underset{x\to 0}{lim}{f}_{\mathrm{ASPRD}}(x;\alpha ,\theta )=0.$$

(18)

• Case 2: As $x\to \infty$

For large values of x, we observe that:

$${\displaystyle \frac{x^2}{2{\theta }^2}}\to \infty \Rightarrow e^{-\frac{x^2}{2{\theta }^2}}\to 0.$$

Thus,

$$1-e^{-\frac{x^2}{2{\theta }^2}}\to 1.$$

This simplifies to:

$$\pi cos\left[{\displaystyle \frac{\pi }{2}}{\left(1-e^{-\frac{x^2}{2{\theta }^2}}\right)}^{\alpha }\right]\to 0.$$

Therefore, combining all these results, we conclude the following:

$$\underset{x\to \infty }{lim}{f}_{\mathrm{ASPRD}}(x;\alpha ,\theta )=0.$$

(19)

Thus, the PDF of the ASPRD tends to 0 as $x\to 0$ and as $x\to \infty$. Therefore, its asymptotic behavior is such that it decays to 0 at both the left and right tails of its domain.

The reliability function of ASPRD is given by

$$R_{\mathrm{ASPRD}}(x;\alpha ,\theta )=1-2sin\left[{\displaystyle \frac{\pi }{2}}{\left[1-exp\left(-{\displaystyle \frac{x^2}{2{\theta }^2}}\right)\right]}^{\alpha }\right]+{\left[1-exp\left(-{\displaystyle \frac{x^2}{2{\theta }^2}}\right)\right]}^{\alpha }.$$

(20)

The ASPRD hazard rate function is obtained as

$$h_{\mathrm{ASPRD}}(x;\alpha ,\theta )={\displaystyle \frac{\alpha \left[\pi cos\left(\frac{\pi }{2}{\left[1-exp\left(-\frac{x^2}{2{\theta }^2}\right)\right]}^{\alpha }\right)-1\right]{\left[1-exp\left(-\frac{x^2}{2{\theta }^2}\right)\right]}^{\alpha -1}\frac{x}{{\theta }^2}exp\left(-\frac{x^2}{2{\theta }^2}\right)}{1-2sin\left[\frac{\pi }{2}{\left[1-exp\left(-\frac{x^2}{2{\theta }^2}\right)\right]}^{\alpha }\right]+{\left[1-exp\left(-\frac{x^2}{2{\theta }^2}\right)\right]}^{\alpha }}}.$$

(21)

To analyze the asymptotic behavior of (21), we consider two cases here as well:

• Case 1: As $x\to 0$

For small values of x, we observe that:

$${\displaystyle \frac{x^2}{2{\theta }^2}}\to 0\Rightarrow e^{-\frac{x^2}{2{\theta }^2}}\to 1.$$

Thus,

$$1-e^{-\frac{x^2}{2{\theta }^2}}\to 0.$$

For the cosine term, we have the following

$$\pi cos\left[{\displaystyle \frac{\pi }{2}}{\left(1-e^{-\frac{x^2}{2{\theta }^2}}\right)}^{\alpha }\right]=\pi cos\left[{\displaystyle \frac{\pi }{2}}\left(0\right)\right]=\pi$$

Substituting this in the numerator of (21), we have the following

$${\displaystyle \frac{\alpha (\pi -1)0^{\alpha -1}x}{{\theta }^2}}=0.$$

For the denominator, we have the following

$$1-2sin\left[{\displaystyle \frac{\pi }{2}}\left(0\right)\right]+0=1.$$

Therefore, combining all these results, we conclude the following:

$$\underset{x\to 0}{lim}{h}_{\mathrm{ASPRD}}(x;\alpha ,\theta )=0.$$

(22)

• Case 2: As $x\to \infty$

For large values of x, we observe that:

$${\displaystyle \frac{x^2}{2{\theta }^2}}\to \infty \Rightarrow e^{-\frac{x^2}{2{\theta }^2}}\to 0.$$

Thus,

$$1-e^{-\frac{x^2}{2{\theta }^2}}\to 1.$$

For the cosine term, we have the following

$$cos\left[{\displaystyle \frac{\pi }{2}}{\left(1-e^{-\frac{x^2}{2{\theta }^2}}\right)}^{\alpha }\right]\to 0.$$

Therefore, the numerator simplifies to:

$${\displaystyle \frac{\alpha \left[\pi \left(0\right)-1\right]1^{\alpha -1}x}{{\theta }^2}}\left(0\right)\to 0.$$

Thus, we conclude the following:

$$\underset{x\to \infty }{lim}{h}_{\mathrm{ASPRD}}(x;\alpha ,\theta )=0.$$

(23)

The density plots of the ASPRD is plotted using different combinations of shape parameter $\alpha$ and scale parameter $\theta$. The density plots have distinct shapes for varying parameter values, as seen in Figure 1.

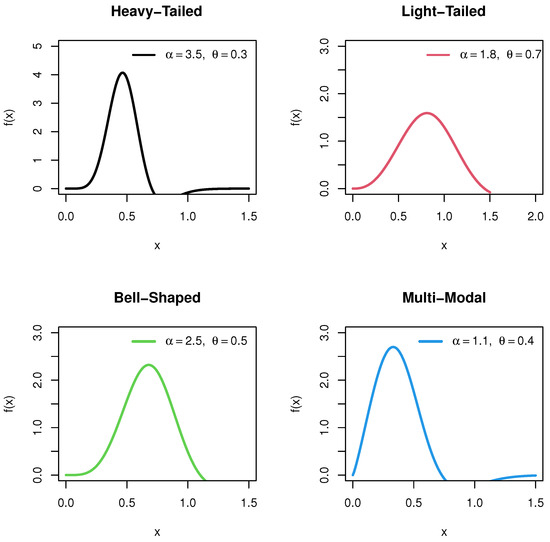
Figure 1. Density plots of ASPRD for different combinations of shape parameter $\alpha$ and scale parameter $\theta$.

According to Figure 2, the proposed model is capable of representing datasets characterized by failure rates that are positively skewed, increasing, decreasing, constant, inverted J-shaped, and unimodal.

Figure 2. Hazard rate plots of ASPRD for different combinations of shape parameter $\alpha$ and scale parameter $\theta$.

4. Expanded Forms of the Model

Various statistical properties can be conveniently derived using the mixture representation of the PDF and CDF of the proposed model. The expression

$$cos\left[{\displaystyle \frac{\pi }{2}}{\left(1-e^{-\frac{x^2}{2{\theta }^2}}\right)}^{\alpha }\right]$$

can be expanded as

$$cos\left[{\displaystyle \frac{\pi }{2}}{\left(1-e^{-\frac{x^2}{2{\theta }^2}}\right)}^{\alpha }\right]=\sum _{s=0}^{\infty }{\displaystyle \frac{{(-1)}^s}{2s!}}{\displaystyle \frac{{\pi }^{2s}}{2^{2s}}}{\left(1-e^{-\frac{x^2}{2{\theta }^2}}\right)}^{2\alpha s}.$$

Furthermore, the term ${\left(1-e^{-\frac{x^2}{2{\theta }^2}}\right)}^{2\alpha s}$ can be written as

$${\left(1-e^{-\frac{x^2}{2{\theta }^2}}\right)}^{2\alpha s}=\sum _{t=0}^{\infty }{(-1)}^t\left({\displaystyle \genfrac{}{}{0pt}{}{2\alpha s}{t}}\right)e^{-\frac{t{x}^2}{2{\theta }^2}}.$$

Similarly, the expansion for ${\left(1-e^{-\frac{x^2}{2{\theta }^2}}\right)}^{\alpha -1}$ is given by

$${\left(1-e^{-\frac{x^2}{2{\theta }^2}}\right)}^{\alpha -1}=\sum _{u=0}^{\infty }{(-1)}^u\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right)e^{-\frac{u{x}^2}{2{\theta }^2}}.$$

The sine term, $sin\left[{\displaystyle \frac{\pi }{2}}{\left(1-e^{-\frac{x^{2\beta }}{2{\theta }^2}}\right)}^{\alpha }\right]$, can be expanded as

$$sin\left[{\displaystyle \frac{\pi }{2}}{\left(1-e^{-\frac{x^{2\beta }}{2{\theta }^2}}\right)}^{\alpha }\right]=\sum _{v=0}^{\infty }{\displaystyle \frac{{(-1)}^v}{(2v+1)!}}{\displaystyle \frac{{\pi }^{2v+1}}{2^{2v+1}}}{\left(1-e^{-\frac{x^2}{2{\theta }^2}}\right)}^{(2v+1)\alpha }.$$

Also, ${\left(1-e^{-\frac{x^2}{2{\theta }^2}}\right)}^{(2v+1)\alpha }$ can be expanded as

$${\left(1-e^{-\frac{x^2}{2{\theta }^2}}\right)}^{(2v+1)\alpha }=\sum _{w=0}^{\infty }{(-1)}^w\left({\displaystyle \genfrac{}{}{0pt}{}{(2v+1)\alpha }{w}}\right)e^{-\frac{w{x}^2}{2{\theta }^2}}.$$

$${\left(1-e^{-\frac{x^2}{2{\theta }^2}}\right)}^{\alpha }=\sum _{j=0}^{\infty }{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha }{j}}\right)e^{-\frac{j{x}^2}{2{\theta }^2}}.$$

As a result, the probability density function (PDF) of the proposed model can be represented in its mixture form as:

$$f(x;\alpha ,\theta )={\displaystyle \frac{\alpha x}{{\theta }^2}}\left\{\sum _{s=0}^{\infty }\sum _{t=0}^{\infty }\sum _{u=0}^{\infty }{\displaystyle \frac{{(-1)}^{s+t+u}}{2s!}}\left({\displaystyle \genfrac{}{}{0pt}{}{2\alpha s}{t}}\right){\displaystyle \frac{{\pi }^{2s+1}}{2^{2s}}}\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right)e^{-\frac{(t+u+1)x^2}{2{\theta }^2}}-\sum _{u=0}^{\infty }{(-1)}^u\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right)e^{-\frac{(u+1)x^2}{2{\theta }^2}}\right\}.$$

(24)

Similarly, the cumulative distribution function (CDF) can be expressed as:

$$F(x;\alpha ,\theta )=\sum _{v=0}^{\infty }\sum _{w=0}^{\infty }{\displaystyle \frac{{(-1)}^{v+w}}{(2v+1)!}}{\displaystyle \frac{{\pi }^{2v+1}}{2^{2v}}}\left({\displaystyle \genfrac{}{}{0pt}{}{(2v+1)\alpha }{w}}\right)e^{-\frac{w{x}^2}{2{\theta }^2}}-\sum _{j=0}^{\infty }{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha }{j}}\right)e^{-\frac{j{x}^2}{2{\theta }^2}}.$$

(25)

5. Statistical Properties of ASPRD

Some of the mathematical properties, such as the $r^{th}$ moment, moment-generating function, conditional moments and associated measures, the entropy, and order statistics of ASPRD, are derived.

5.1. Moments

Theorem 1.

If X∼$\mathrm{ASPRD}(\alpha ,\theta )$, then the $r^{\mathit{th}}$ moment of the ASPRD about the origin is given by:

$$\begin{array}{cc}\hfill E\left(X^r\right)={\displaystyle \frac{\alpha }{2{\theta }^2}}& \left\{\sum _{s=0}^{\infty }\sum _{t=0}^{\infty }\sum _{u=0}^{\infty }{\displaystyle \frac{{(-1)}^{t+u+1}}{2s!}}\left({\displaystyle \genfrac{}{}{0pt}{}{2\alpha s}{t}}\right){\displaystyle \frac{{\pi }^{2s+1}}{2^{2s}}}\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{s+t+1}}\right)}^{{\displaystyle \frac{r+2}{2}}}\right.\hfill \\ \hfill & \left.-\sum _{u=0}^{\infty }{(-1)}^u\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{u+1}}\right)}^{{\displaystyle \frac{r+2}{2}}}\right\}\Gamma \left({\displaystyle \frac{r+2}{2}}\right)\hfill \end{array}$$

(26)

Proof. 

The $r^{\mathrm{th}}$ moment of the ASPRD can be directly computed by expanding the PDF as given in Equation (24):

$$\begin{array}{cc}\hfill E\left(X^r\right)& =\underset{0}{\overset{\infty }{\int }}{x}^{r}f(x;\alpha ,\theta )dx,\mathrm{for}r=1,2,\dots \hfill \end{array}$$

where $f\left(x\right)$ is the PDF of the ASPRD as provided in Equation (24). Therefore,

$$\begin{array}{cc}\hfill E\left(X^r\right)& ={\displaystyle \frac{\alpha }{{\theta }^2}}\left\{\sum _{s=0}^{\infty }\sum _{t=0}^{\infty }\sum _{u=0}^{\infty }{\displaystyle \frac{{(-1)}^{s+t+1}}{2s!}}\left({\displaystyle \genfrac{}{}{0pt}{}{2\alpha s}{t}}\right){\displaystyle \frac{{\pi }^{2s+1}}{2^{2s}}}\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right)\underset{0}{\overset{\infty }{\int }}{x}^{r+1}{e}^{-{\displaystyle \frac{(t+u+1)x^2}{2{\theta }^2}}}dx\right.\hfill \\ \hfill & \left.-\sum _{u=0}^{\infty }{(-1)}^u\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right)\underset{0}{\overset{\infty }{\int }}{x}^{r+1}{e}^{-{\displaystyle \frac{(u+1)x^2}{2{\theta }^2}}}dx\right\}.\hfill \end{array}$$

(27)

□

We now use the method of substitution for the integrals in Equation (27).

Let

$${\displaystyle \frac{(t+u+1)x^2}{2{\theta }^2}}=z\Rightarrow x={\left({\displaystyle \frac{2{\theta }^{2}z}{t+u+1}}\right)}^{\frac{1}{2}},$$

which implies

$$dx={\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{2{\theta }^2}{t+u+1}}\right)}^{\frac{1}{2}}{z}^{-\frac{1}{2}}dz.$$

Similarly, for the second term, let,

$${\displaystyle \frac{(u+1)x^2}{2{\theta }^2}}=t\Rightarrow x={\left({\displaystyle \frac{2{\theta }^{2}t}{u+1}}\right)}^{\frac{1}{2}},$$

which implies

$$dx={\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{2{\theta }^2}{u+1}}\right)}^{\frac{1}{2}}{t}^{-\frac{1}{2}}dt.$$

Simplifying Equation (27) yields the following:

$$\begin{array}{cc}\hfill E\left(X^r\right)={\displaystyle \frac{\alpha }{2{\theta }^2}}& \left\{\sum _{s=0}^{\infty }\sum _{t=0}^{\infty }\sum _{u=0}^{\infty }{\displaystyle \frac{{(-1)}^{t+u+1}}{2s!}}\left({\displaystyle \genfrac{}{}{0pt}{}{2\alpha s}{t}}\right){\displaystyle \frac{{\pi }^{2s+1}}{2^{2s}}}\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{s+t+1}}\right)}^{{\displaystyle \frac{r+2}{2}}}\right.\hfill \\ \hfill & \left.-\sum _{u=0}^{\infty }{(-1)}^u\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{u+1}}\right)}^{{\displaystyle \frac{r+2}{2}}}\right\}\Gamma \left({\displaystyle \frac{r+2}{2}}\right).\hfill \end{array}$$

(28)

Here, the Gamma function $\Gamma \left({\displaystyle \frac{r}{2}}+1\right)$ is defined as:

$$\Gamma \left({\displaystyle \frac{r}{2}}+1\right)=\underset{0}{\overset{\infty }{\int }}{z}^{\left({\displaystyle \frac{r}{2}}+1\right)-1}{e}^{-z}dz.$$

Setting $r=1$ in Equation (28), the mean of the model is computed as:

$$\begin{array}{cc}\hfill E\left(X\right)={\displaystyle \frac{\alpha }{2{\theta }^2}}& \left\{\sum _{s=0}^{\infty }\sum _{t=0}^{\infty }\sum _{u=0}^{\infty }{\displaystyle \frac{{(-1)}^{t+u+1}}{2s!}}\left({\displaystyle \genfrac{}{}{0pt}{}{2\alpha s}{t}}\right){\displaystyle \frac{{\pi }^{2s+1}}{2^{2s}}}\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{s+t+1}}\right)}^{{\displaystyle \frac{3}{2}}}\right.\hfill \\ \hfill & \left.-\sum _{u=0}^{\infty }{(-1)}^u\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{u+1}}\right)}^{{\displaystyle \frac{3}{2}}}\right\}\Gamma \left({\displaystyle \frac{3}{2}}\right).\hfill \end{array}$$

(29)

Similarly for r = 2, 3, and 4 in Equation (28), the second, third, and fourth moments about the origin can be calculated.

5.2. Moment Generating Function (MGF) of ASPRD

The moments of a distribution are represented by the moment generating function (MGF). The following theorem provides the MGF for the ASPRD.

Theorem 2.

If $X\sim \mathrm{ASPRD}(\alpha ,\theta )$, then the moment generating function, $M_X\left(m\right)$, is expressed as

$$\begin{array}{cc}\hfill M_X\left(m\right)={\displaystyle \frac{\alpha }{2{\theta }^2}}& \left\{\sum _{s=0}^{\infty }\sum _{t=0}^{\infty }\sum _{u=0}^{\infty }\sum _{r=0}^{\infty }{\displaystyle \frac{{(-1)}^{s+t+u}}{2s!}}{\displaystyle \frac{m^r}{r!}}\left({\displaystyle \genfrac{}{}{0pt}{}{2\alpha s}{t}}\right){\displaystyle \frac{{\pi }^{2s+1}}{2^{2s}}}\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{t+u+1}}\right)}^{{\displaystyle \frac{r+2}{2}}}\right.\hfill \\ \hfill & \left.-\sum _{u=0}^{\infty }\sum _{r=0}^{\infty }{(-1)}^u{\displaystyle \frac{m^r}{r!}}\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{u+1}}\right)}^{{\displaystyle \frac{r+2}{2}}}\right\}\Gamma \left({\displaystyle \frac{r+2}{2}}\right)\hfill \end{array}$$

(30)

Proof. 

The moment generating function (MGF) for the ASPRD can be defined as

$$M_X\left(m\right)={\int }_0^{\infty }{e}^{mx}f(x;\alpha ,\theta )dx.$$

(31)

Using the power series expansion of $e^{mx}$, we obtain the following

$$M_X\left(m\right)=\sum _{r=0}^{\infty }{\displaystyle \frac{m^r}{r!}}E\left(X^r\right)$$

(32)

Inserting the expression for $E\left(X^r\right)$ from Equation (28) into (32), we derive the following:

$$\begin{array}{cc}\hfill M_X\left(m\right)={\displaystyle \frac{\alpha }{2{\theta }^2}}& \left\{\sum _{s=0}^{\infty }\sum _{t=0}^{\infty }\sum _{u=0}^{\infty }\sum _{r=0}^{\infty }{\displaystyle \frac{{(-1)}^{s+t+u}}{2s!}}{\displaystyle \frac{m^r}{r!}}\left({\displaystyle \genfrac{}{}{0pt}{}{2\alpha s}{t}}\right){\displaystyle \frac{{\pi }^{2s+1}}{2^{2s}}}\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{t+u+1}}\right)}^{{\displaystyle \frac{r+2}{2}}}\right.\hfill \\ \hfill & \left.-\sum _{u=0}^{\infty }\sum _{r=0}^{\infty }{(-1)}^u{\displaystyle \frac{m^r}{r!}}\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{u+1}}\right)}^{{\displaystyle \frac{r+2}{2}}}\right\}\Gamma \left({\displaystyle \frac{r+2}{2}}\right)\hfill \end{array}$$

(33)

□

5.3. Conditional Moments and Associated Measures

Theorem 3.

Consider a random variable X that follows the ASPRD distribution parameterized by $(\alpha ,\theta )$, with its probability density function (PDF) expressed in Equation (24). Let’s ${\phi }_r\left(z\right)={\int }_0^z{x}^{r}f(x;\alpha ,\theta )dx$ represent the rth incomplete moment. Then, the following holds:

$$\begin{array}{cc}\hfill {\phi }_r\left(z\right)={\displaystyle \frac{\alpha }{2{\theta }^2}}& \left\{\sum _{s=0}^{\infty }\sum _{t=0}^{\infty }\sum _{u=0}^{\infty }{\displaystyle \frac{{(-1)}^{s+t+u}}{2s!}}\left({\displaystyle \genfrac{}{}{0pt}{}{2\alpha s}{t}}\right){\displaystyle \frac{{\pi }^{2s+1}}{2^{2s}}}\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{t+u+1}}\right)}^{{\displaystyle \frac{r+2}{2}}}\gamma \left(\left({\displaystyle \frac{r+2}{2}}\right),{\displaystyle \frac{(t+u+1)z^2}{2{\theta }^2}}\right)\right.\hfill \\ \hfill & \left.-\sum _{u=0}^{\infty }{(-1)}^u\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{u+1}}\right)}^{{\displaystyle \frac{r+2}{2}}}\gamma \left(\left({\displaystyle \frac{r+2}{2}}\right),{\displaystyle \frac{(u+1)z^2}{2{\theta }^2}}\right)\right\}\hfill \end{array}$$

(34)

where $\gamma (a,b)={\int }_0^b{z}^{a-1}{e}^{-z}dz$ denotes the lower incomplete gamma function.

Proof. 

Starting from the PDF of the ASPRD distribution given in Equation (24), we have the following:

$$\begin{array}{cc}\hfill {\phi }_r\left(z\right)& ={\int }_0^z{x}^{r}f(x;\alpha ,\theta )dx\hfill \\ \hfill & ={\displaystyle \frac{\alpha }{{\theta }^2}}\left\{\sum _{s=0}^{\infty }\sum _{t=0}^{\infty }\sum _{u=0}^{\infty }{\displaystyle \frac{{(-1)}^{s+t+u}}{2s!}}\left({\displaystyle \genfrac{}{}{0pt}{}{2\alpha s}{t}}\right){\displaystyle \frac{{\pi }^{2s+1}}{2^{2s}}}\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\int }_0^{\infty }{x}^{r+1}{e}^{-{\displaystyle \frac{(t+u+1)x^2}{2{\theta }^2}}}dx\right.\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill & \left.-\sum _{u=0}^{\infty }{(-1)}^u\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\int }_0^{\infty }{x}^{r+1}{e}^{-{\displaystyle \frac{(u+1)x^2}{2{\theta }^2}}}dx\right\}\hfill \end{array}$$

(36)

Upon simplification, we arrive at:

$$\begin{array}{cc}\hfill {\phi }_r\left(z\right)={\displaystyle \frac{\alpha }{2{\theta }^2}}& \left\{\sum _{s=0}^{\infty }\sum _{t=0}^{\infty }\sum _{u=0}^{\infty }{\displaystyle \frac{{(-1)}^{s+t+u}}{2s!}}\left({\displaystyle \genfrac{}{}{0pt}{}{2\alpha s}{t}}\right){\displaystyle \frac{{\pi }^{2s+1}}{2^{2s}}}\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{t+u+1}}\right)}^{{\displaystyle \frac{r+2}{2}}}\gamma \left(\left({\displaystyle \frac{r+2}{2}}\right),{\displaystyle \frac{(t+u+1)z^2}{2{\theta }^2}}\right)\right.\hfill \\ \hfill & \left.-\sum _{u=0}^{\infty }{(-1)}^u\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{u+1}}\right)}^{{\displaystyle \frac{r+2}{2}}}\gamma \left(\left({\displaystyle \frac{r+2}{2}}\right),{\displaystyle \frac{(u+1)z^2}{2{\theta }^2}}\right)\right\}\hfill \end{array}$$

(37)

By setting $r=1$ in Equation (37), we obtain the first incomplete moment as follows:

$$\begin{array}{cc}\hfill {\phi }_1\left(z\right)={\displaystyle \frac{\alpha }{2{\theta }^2}}& \left\{\sum _{s=0}^{\infty }\sum _{t=0}^{\infty }\sum _{u=0}^{\infty }{\displaystyle \frac{{(-1)}^{s+t+u}}{2s!}}\left({\displaystyle \genfrac{}{}{0pt}{}{2\alpha s}{t}}\right){\displaystyle \frac{{\pi }^{2s+1}}{2^{2s}}}\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{t+u+1}}\right)}^{{\displaystyle \frac{3}{2}}}\gamma \left({\displaystyle \frac{3}{2}},{\displaystyle \frac{(t+u+1)z^2}{2{\theta }^2}}\right)\right.\hfill \\ \hfill & \left.-\sum _{u=0}^{\infty }{(-1)}^u\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{u+1}}\right)}^{{\displaystyle \frac{3}{2}}}\gamma \left({\displaystyle \frac{3}{2}},{\displaystyle \frac{(u+1)z^2}{2{\theta }^2}}\right)\right\}\hfill \end{array}$$

(38)

□

5.3.1. Lorenz and Bonferroni Inequality Curves

The Lorenz and Bonferroni inequality curves represent significant applications of the first incomplete moment. For a given probability distribution, these curves are defined as follows:

$$L_p={\displaystyle \frac{1}{E\left(X\right)}}{\int }_0^{m}xf(x;\alpha ,\theta )dx={\displaystyle \frac{{\phi }_1\left(m\right)}{E\left(X\right)}}$$

Utilizing Equations (29) and (38), we can express $L_p$ as:

$$L_p={\displaystyle \frac{(A_1-B_1)}{(A_2-B_2)\Gamma \left(\frac{3}{2}\right)}}$$

In a similar manner, the Bonferroni inequality can be expressed as:

$$\begin{array}{c}\hfill B_P={\displaystyle \frac{1}{pE\left(X\right)}}{\int }_0^{m}xf(x;\alpha ,\theta )dx={\displaystyle \frac{{\phi }_1\left(m\right)}{pE\left(X\right)}}\end{array}$$

This leads to the following formulation for $B_p$:

$$\begin{array}{cc}\hfill B_p=& {\displaystyle \frac{(A_1-B_1)}{p(A_2-B_2)\Gamma \left(\frac{3}{2}\right)}}\hfill \end{array}$$

where the components are defined as follows:

$$A_1=\sum _{s=0}^{\infty }\sum _{t=0}^{\infty }\sum _{u=0}^{\infty }{\displaystyle \frac{{(-1)}^{s+t+u}}{2s!}}\left({\displaystyle \genfrac{}{}{0pt}{}{2\alpha s}{t}}\right){\displaystyle \frac{{\pi }^{2s+1}}{2^{2s}}}\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{t+u+1}}\right)}^{{\displaystyle \frac{3}{2}}}\gamma \left({\displaystyle \frac{3}{2}},{\displaystyle \frac{(t+u+1)m^2}{2{\theta }^2}}\right)$$

$$B_1=\sum _{u=0}^{\infty }{(-1)}^u\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{u+1}}\right)}^{{\displaystyle \frac{3}{2}}}\gamma \left({\displaystyle \frac{3}{2}},{\displaystyle \frac{(u+1)m^2}{2{\theta }^2}}\right)$$

$$A_2=\sum _{s=0}^{\infty }\sum _{t=0}^{\infty }\sum _{u=0}^{\infty }{\displaystyle \frac{{(-1)}^{s+t+u}}{2s!}}\left({\displaystyle \genfrac{}{}{0pt}{}{2\alpha s}{t}}\right){\displaystyle \frac{{\pi }^{2s+1}}{2^{2s}}}\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{t+u+1}}\right)}^{{\displaystyle \frac{3}{2}}}$$

$$B_2=\sum _{u=0}^{\infty }{(-1)}^u\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{u+1}}\right)}^{{\displaystyle \frac{3}{2}}}$$

5.3.2. $r^{th}$ Conditional Moment and $r^{th}$ Reversed Conditional Moment of ASPRD

The $r^{th}$ conditional moment of the ASPRD can be computed using the following expression:

$$E\left[X^r|x>m\right]={\displaystyle \frac{1}{R\left(m\right)}}{\int }_m^{\infty }{x}^{r}f(x;\alpha ,\theta )dx={\displaystyle \frac{1}{R\left(m\right)}}\left[E\left(X^r\right)-{\phi }_r\left(m\right)\right]$$

where $R\left(m\right)$ denotes the reliability of ASPRD at time m.

By substituting the values from Equations (20), (28), and (37), we derive the following:

$$E\left[X^r|x>m\right]={\displaystyle \frac{\frac{\alpha }{2{\theta }^2}(A_3+B_3)}{1-2sin\left[\frac{\pi }{2}{\left[1-exp\left(-\frac{m^2}{2{\theta }^2}\right)\right]}^{\alpha }\right]+{\left[1-exp\left(-\frac{m^2}{2{\theta }^2}\right)\right]}^{\alpha }}}$$

In a similar fashion, the $r^{th}$ reversed conditional moment of the ASPRD is defined as:

$$E\left[X^r|x\le m\right]={\displaystyle \frac{1}{F\left(m\right)}}{\int }_0^m{x}^{r}f(x;\alpha ,\theta )dx={\displaystyle \frac{{\phi }_r\left(m\right)}{F\left(m\right)}}$$

Thus, we can express the reversed conditional moment as:

$$E\left[X^r\mid x\le m\right]={\displaystyle \frac{\frac{\alpha }{2{\theta }^2}(A_4-B_4)}{{\sum }_{v=0}^{\infty }{\sum }_{w=0}^{\infty }\frac{{(-1)}^{v+w}}{(2v+1)!}\frac{{\pi }^{2v+1}}{2^{2v}}\left(\genfrac{}{}{0pt}{}{(2v+1)\alpha }{w}\right)e^{-\frac{w{m}^2}{2{\theta }^2}}-{\sum }_{j=0}^{\infty }{(-1)}^j\left(\genfrac{}{}{0pt}{}{\alpha }{j}\right)e^{-\frac{j{m}^2}{2{\theta }^2}}}}$$

where the components are defined as follows:

$$\begin{array}{c}\hfill A_3=\sum _{s=0}^{\infty }\sum _{t=0}^{\infty }\sum _{u=0}^{\infty }{\displaystyle \frac{{(-1)}^{s+t+u}}{2s!}}\left({\displaystyle \genfrac{}{}{0pt}{}{2\alpha s}{t}}\right){\displaystyle \frac{{\pi }^{2s+1}}{2^{2s}}}\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right)\\ \hfill \times {\left({\displaystyle \frac{2{\theta }^2}{t+u+1}}\right)}^{{\displaystyle \frac{r+2}{2}}}\left(\Gamma \left({\displaystyle \frac{r+2}{2}}\right)-\gamma \left({\displaystyle \frac{r+2}{2}},{\displaystyle \frac{(t+u+1)m^2}{2{\theta }^2}}\right)\right)\end{array}$$

$$B_3=\sum _{u=0}^{\infty }{(-1)}^u\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{u+1}}\right)}^{{\displaystyle \frac{r+2}{2}}}\left(\gamma \left({\displaystyle \frac{r+2}{2}},{\displaystyle \frac{(u+1)m^2}{2{\theta }^2}}\right)-\Gamma \left({\displaystyle \frac{r+2}{2}}\right)\right)$$

$$A_4=\sum _{s=0}^{\infty }\sum _{t=0}^{\infty }\sum _{u=0}^{\infty }{\displaystyle \frac{{(-1)}^{s+t+u}}{2s!}}\left({\displaystyle \genfrac{}{}{0pt}{}{2\alpha s}{t}}\right){\displaystyle \frac{{\pi }^{2s+1}}{2^{2s}}}\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{t+u+1}}\right)}^{{\displaystyle \frac{r+2}{2}}}\gamma \left({\displaystyle \frac{r+2}{2}},{\displaystyle \frac{(t+u+1)m^2}{2{\theta }^2}}\right)$$

$$B_4=\sum _{u=0}^{\infty }{(-1)}^u\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{u+1}}\right)}^{{\displaystyle \frac{r+2}{2}}}\gamma \left({\displaystyle \frac{r+2}{2}},{\displaystyle \frac{(u+1)m^2}{2{\theta }^2}}\right)$$

5.3.3. Mean Residual Life (MRL) and Mean Waiting Time (MWT)

The Mean Residual Life (MRL) is defined as follows:

$$\mu \left(m\right)={\displaystyle \frac{1}{R\left(m\right)}}\left[E\left(m\right)-{\int }_0^{m}xf(x;\alpha ,\theta )dx\right]-m={\displaystyle \frac{1}{R\left(m\right)}}\left[E\left(m\right)-{\phi }_1\left(m\right)\right]-m$$

After substituting the values from Equations (20), (29), and (38), we arrive at the expression for the mean residual life:

$$\mu \left(m\right)={\displaystyle \frac{\frac{\alpha }{2{\theta }^2}(A_5+B_5)}{1-2sin\left[\frac{\pi }{2}{\left[1-exp\left(-\frac{m^2}{2{\theta }^2}\right)\right]}^{\alpha }\right]+{\left[1-exp\left(-\frac{m^2}{2{\theta }^2}\right)\right]}^{\alpha }}}-m$$

The Mean Waiting Time (MWT) is defined as:

$$\overline{\mu }\left(m\right)=m-{\displaystyle \frac{1}{F\left(m\right)}}{\int }_0^{m}xf(x;\alpha ,\theta )dx=m-{\displaystyle \frac{{\phi }_1\left(m\right)}{F\left(m\right)}}$$

Thus, we can express the Mean Waiting Time as:

$$\overline{\mu }\left(m\right)=m-{\displaystyle \frac{\frac{\alpha }{2{\theta }^2}(A_6-B_6)}{{\sum }_{p=0}^{\infty }{\sum }_{q=0}^{\infty }\frac{{(-1)}^{p+q}}{(2p+1)!}\frac{{\pi }^{2p+1}}{2^{2p}}\left(\genfrac{}{}{0pt}{}{(2p+1)\alpha }{q}\right)e^{-\frac{q{m}^2}{2{\theta }^2}}-{\sum }_{j=0}^{\infty }{(-1)}^j\left(\genfrac{}{}{0pt}{}{\alpha }{j}\right)e^{-\frac{j{m}^2}{2{\theta }^2}}}}$$

where the components are defined as:

$$A_5=\sum _{s=0}^{\infty }\sum _{t=0}^{\infty }\sum _{u=0}^{\infty }{\displaystyle \frac{{(-1)}^{s+t+u}}{2s!}}\left({\displaystyle \genfrac{}{}{0pt}{}{2\alpha s}{t}}\right){\displaystyle \frac{{\pi }^{2s+1}}{2^{2s}}}\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{t+u+1}}\right)}^{{\displaystyle \frac{3}{2}}}\left(\Gamma \left({\displaystyle \frac{3}{2}}\right)-\gamma \left({\displaystyle \frac{3}{2}},{\displaystyle \frac{(t+u+1)m^2}{2{\theta }^2}}\right)\right)$$

$$B_5=\sum _{u=0}^{\infty }{(-1)}^u\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{u+1}}\right)}^{{\displaystyle \frac{3}{2}}}\left(\gamma \left({\displaystyle \frac{3}{2}},{\displaystyle \frac{(u+1)m^2}{2{\theta }^2}}\right)-\Gamma \left({\displaystyle \frac{3}{2}}\right)\right)$$

$$A_6=\sum _{s=0}^{\infty }\sum _{t=0}^{\infty }\sum _{u=0}^{\infty }{\displaystyle \frac{{(-1)}^{s+t+u}}{2s!}}\left({\displaystyle \genfrac{}{}{0pt}{}{2\alpha s}{t}}\right){\displaystyle \frac{{\pi }^{2s+1}}{2^{2s}}}\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{s+t+1}}\right)}^{{\displaystyle \frac{3}{2}}}\gamma \left({\displaystyle \frac{3}{2}},{\displaystyle \frac{(t+u+1)m^2}{2{\theta }^2}}\right)$$

$$B_6=\sum _{u=0}^{\infty }{(-1)}^u\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right){\left({\displaystyle \frac{2{\theta }^2}{u+1}}\right)}^{{\displaystyle \frac{3}{2}}}\gamma \left({\displaystyle \frac{3}{2}},{\displaystyle \frac{(u+1)m^2}{2{\theta }^2}}\right)$$

5.4. Renyi Entropy

Theorem 4.

If X∼$\mathrm{ASPRD}(\alpha ,\theta )$, then the Renyi entropy of the ASPRD is given as

$$\begin{array}{cc}\hfill R{E}_X\left(p\right)& ={\displaystyle \frac{1}{1-p}}log\left\{{\left({\displaystyle \frac{\alpha }{{\theta }^2}}\right)}^p\left[{\left(\sum _{s=0}^{\infty }\sum _{t=0}^{\infty }\sum _{u=0}^{\infty }{\displaystyle \frac{{(-1)}^{s+t+u}}{2s!}}\left({\displaystyle \genfrac{}{}{0pt}{}{2\alpha s}{t}}\right){\displaystyle \frac{{\pi }^{2s+1}}{2^{2s}}}\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right)\right)}^p\underset{0}{\overset{\infty }{\int }}{x}^p{e}^{-{\displaystyle \frac{p(t+u+1)x^2}{2{\theta }^2}}}dx\right.\right.\hfill \\ \hfill & \left.\left.-{\left(\sum _{u=0}^{\infty }{(-1)}^u\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right)\right)}^p\underset{0}{\overset{\infty }{\int }}{x}^p{e}^{-{\displaystyle \frac{p(u+1)x^2}{2{\theta }^2}}}dx\right]\right\}.\hfill \end{array}$$

(39)

Proof. 

The Renyi entropy, denoted as $R{E}_X\left(p\right)$, of ASPRD can be defined as

$$\begin{array}{cc}\hfill R{E}_X\left(p\right)=& {\displaystyle \frac{1}{1-p}}log\left(\underset{-\infty }{\overset{\infty }{\int }}{f}^p(x,\alpha ,\theta )dx\right);p>0,p\ne 1.\hfill \end{array}$$

(40)

Substituting Equation (24) into Equation (40), we obtain

$$\begin{array}{cc}\hfill R{E}_X\left(p\right)& ={\displaystyle \frac{1}{1-p}}log\left\{{\left({\displaystyle \frac{\alpha }{{\theta }^2}}\right)}^p\left[{\left(\sum _{s=0}^{\infty }\sum _{t=0}^{\infty }\sum _{u=0}^{\infty }{\displaystyle \frac{{(-1)}^{s+t+u}}{2s!}}\left({\displaystyle \genfrac{}{}{0pt}{}{2\alpha s}{t}}\right){\displaystyle \frac{{\pi }^{2s+1}}{2^{2s}}}\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right)\right)}^p\underset{0}{\overset{\infty }{\int }}{x}^p{e}^{-{\displaystyle \frac{p(t+u+1)x^2}{2{\theta }^2}}}dx\right.\right.\hfill \\ \hfill & \left.\left.-{\left(\sum _{u=0}^{\infty }{(-1)}^u\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right)\right)}^p\underset{0}{\overset{\infty }{\int }}{x}^p{e}^{-{\displaystyle \frac{p(u+1)x^2}{2{\theta }^2}}}dx\right]\right\}.\hfill \end{array}$$

(41)

□

Using the same procedure as in Equation (28), we obtain the final expression for Renyi entropy as

$$\begin{array}{cc}\hfill R{E}_X\left(p\right)& ={\displaystyle \frac{1}{1-p}}log\left\{{\displaystyle \frac{\Gamma \left(\frac{p+1}{2}\right)}{2}}{\left({\displaystyle \frac{\alpha }{{\theta }^2}}\right)}^p\left[{\left(\sum _{s=0}^{\infty }\sum _{t=0}^{\infty }\sum _{u=0}^{\infty }{\displaystyle \frac{{(-1)}^{s+t+u}}{2s!}}\left({\displaystyle \genfrac{}{}{0pt}{}{2\alpha s}{t}}\right){\displaystyle \frac{{\pi }^{2s+1}}{2^{2s}}}\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right)\right)}^p{\left({\displaystyle \frac{2{\theta }^2}{p(t+u+1)}}\right)}^{{\displaystyle \frac{p+1}{2}}}\right.\right.\hfill \\ \hfill & \left.\left.-{\left(\sum _{u=0}^{\infty }{(-1)}^u\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha -1}{u}}\right)\right)}^p{\left({\displaystyle \frac{2{\theta }^2}{p(u+1)}}\right)}^{{\displaystyle \frac{p+1}{2}}}\right]\right\}.\hfill \end{array}$$

(42)

5.5. Order Statistics of ASPRD

In real-world applications incorporating data from life testing studies, order statistics are very important. Let $x_{(r;n)}$ be the $r^{th}$ order statistics with the random sample $x_{\left(1\right)},x_{\left(2\right)},x_{\left(3\right)},\dots x_{\left(n\right)}$ derived from the ASPRD having the PDF $f(x;\alpha ,\theta )$ and CDF $F(x;\alpha ,\theta )$. Therefore, the PDF and CDF of $x_{(r;n)}$ say $f_{(r;n)}\left(x\right)$ and $F_{(r;n)}\left(x\right)$ for the ASPRD are derived and are expressed as:

$$\begin{array}{cc}\hfill f_{(r;n)}\left(x\right)& ={\displaystyle \frac{\frac{\alpha x}{{\theta }^2}exp\left(-\frac{x^2}{2{\theta }^2}\right)\left[\pi cos\left(\frac{\pi }{2}{\left(1-exp\left(-\frac{x^2}{2{\theta }^2}\right)\right)}^{\alpha }\right)-1\right]{\left[1-exp\left(-\frac{x^2}{2{\theta }^2}\right)\right]}^{\alpha -1}}{B(n,n-r+1)}}\hfill \\ \hfill & \times {\left\{\left[2sin\left({\displaystyle \frac{\pi }{2}}{\left(1-exp\left(-{\displaystyle \frac{x^2}{2{\theta }^2}}\right)\right)}^{\alpha }\right)-{\left(1-exp\left(-{\displaystyle \frac{x^2}{2{\theta }^2}}\right)\right)}^{\alpha }\right]\right\}}^{r-1}\hfill \\ \hfill & \times {\left\{\left[2sin\left({\displaystyle \frac{\pi }{2}}{\left(1-exp\left(-{\displaystyle \frac{x^2}{2{\theta }^2}}\right)\right)}^{\alpha }\right)-{\left(1-exp\left(-{\displaystyle \frac{x^2}{2{\theta }^2}}\right)\right)}^{\alpha }\right]\right\}}^{n-r}\hfill \end{array}$$

$$\begin{array}{cc}\hfill F_{(r;n)}\left(x\right)=\sum _{j=r}^n\left({\displaystyle \genfrac{}{}{0pt}{}{n}{j}}\right)\{& {\left[2sin\left({\displaystyle \frac{\pi }{2}}{\left(1-exp\left(-{\displaystyle \frac{x^2}{2{\theta }^2}}\right)\right)}^{\alpha }\right)-{\left(1-exp\left(-{\displaystyle \frac{x^2}{2{\theta }^2}}\right)\right)}^{\alpha }\right]}^j\hfill \\ \hfill & \times {\left[1-2sin\left({\displaystyle \frac{\pi }{2}}{\left(1-exp\left(-{\displaystyle \frac{x^2}{2{\theta }^2}}\right)\right)}^{\alpha }\right)-{\left(1-exp\left(-{\displaystyle \frac{x^2}{2{\theta }^2}}\right)\right)}^{\alpha }\right]}^{n-j}\}\hfill \end{array}$$

where $B(a,b)={\displaystyle \frac{\Gamma \left(a\right)\Gamma \left(b\right)}{\Gamma (a+b)}}$ is the beta function.

6. Estimation

This section discusses the different estimation approaches used to estimate the unknown parameters, $\alpha$ and $\theta$, of the ASPRD.

6.1. Maximum Likelihood Estimation (MLE)

Let $x_1,x_2,\dots ,x_n$ represent a random sample drawn from the ASPRD distribution. The parameters of the distribution are $\alpha$ and $\theta >0$. The logarithm of the likelihood function for the ASPRD can be expressed as:

$$\begin{array}{cc}\hfill l=& nlog\alpha -2nlog\theta -{\displaystyle \frac{1}{2{\theta }^2}}\sum _{i=1}^n{x}_i^2+\sum _{i=1}^{n}log{x}_i+\sum _{i=1}^{n}log\left[\pi cos\left({\displaystyle \frac{\pi }{2}}{\left(1-exp\left(-{\displaystyle \frac{x_i^2}{2{\theta }^2}}\right)\right)}^{\alpha }\right)-1\right]\hfill \\ \hfill & +(\alpha -1)log\left[1-exp\left(-{\displaystyle \frac{x_i^2}{2{\theta }^2}}\right)\right]\hfill \end{array}$$

(43)

The maximum likelihood estimates (MLEs) of $\alpha$ and $\theta$ are obtained by taking the partial derivatives of Equation (43) concerning each parameter and setting them to zero. This gives us the following equations:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial \ell }{\partial \alpha }}& ={\displaystyle \frac{n}{\alpha }}+\sum _{i=1}^{n}log\left[1-exp\left(-{\displaystyle \frac{x_i^2}{2{\theta }^2}}\right)\right]\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill & -{\displaystyle \frac{{\pi }^2}{2}}\sum _{i=1}^n{\displaystyle \frac{sin\left(\frac{\pi }{2}{\left(1-exp\left(-\frac{x_i^2}{2{\theta }^2}\right)\right)}^{\alpha }\right)\left(1-exp{\left(-\frac{x_i^2}{2{\theta }^2}\right)}^{\alpha }log\left(1-exp\left(-\frac{x_i^2}{2{\theta }^2}\right)\right)\right)}{\left[\pi cos\left(\frac{\pi }{2}{\left(1-exp\left(-\frac{x_i^2}{2{\theta }^2}\right)\right)}^{\alpha }\right)-1\right]}}=0\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial \ell }{\partial \theta }}& ={\displaystyle \frac{1}{{\theta }^3}}\sum _{i=1}^n{x}_i^2-{\displaystyle \frac{2n}{\theta }}+{\displaystyle \frac{(\alpha -1)}{{\theta }^3}}\sum _{i=1}^n{\displaystyle \frac{x_i^{2}exp\left(-\frac{x_i^2}{2{\theta }^2}\right)}{\left(1-exp\left(-\frac{x_i^2}{2{\theta }^2}\right)\right)}}\hfill \\ \hfill & -{\displaystyle \frac{\alpha {\pi }^2}{2{\theta }^3}}\sum _{i=1}^n{\displaystyle \frac{x_i^{2}sin\left(\frac{\pi }{2}{\left(1-exp\left(-\frac{x_i^2}{2{\theta }^2}\right)\right)}^{\alpha }\right){\left(1-exp\left(-\frac{x_i^2}{2{\theta }^2}\right)\right)}^{\alpha -1}exp\left(-\frac{x_i^2}{2{\theta }^2}\right)}{\pi cos\left(\frac{\pi }{2}{\left(1-exp\left(-\frac{x_i^2}{2{\theta }^2}\right)\right)}^{\alpha }\right)-1}}=0\hfill \end{array}$$

(46)

Equations (45) and (46) are nonlinear and lack closed-form solutions. Therefore, we will employ R software (version 4.4.2.) to find estimates for these parameters.

6.2. Least Square Estimation (LSE) and Weighted Least Square Estimation (WLSE)

Ref. [35] introduced the LSE and WLSE methods to estimate the parameters of the Beta distribution. By minimizing the least squares function $LS$ concerning the unknown parameters, the parameters of the proposed model can be estimated using the least squares estimation approach, where

$$\begin{array}{cc}\hfill S& =\sum _{k=1}^n{\left[F\left(x_{\left(k\right)}\right)-{\displaystyle \frac{k}{n+1}}\right]}^2\hfill \\ & =2\sum _{k=1}^{n+1}{\left[sin\left[{\displaystyle \frac{\pi }{2}}{\left[1-exp\left(-{\displaystyle \frac{x_{\left(k\right)}^2}{2{\theta }^2}}\right)\right]}^{\alpha }\right]-{\left[1-exp\left(-{\displaystyle \frac{x_{\left(k\right)}^2}{2{\theta }^2}}\right)\right]}^{\alpha }-{\displaystyle \frac{k}{n+1}}\right]}^2.\hfill \end{array}$$

Similarly, to get the WLS estimate for the unknown parameters, the weighted least squares function $WLS$ is minimized:

$$\begin{array}{cc}\hfill W& =\sum _{k=1}^n{\displaystyle \frac{{(n+1)}^2(n+2)}{k(n-k+1)}}{\left[F\left(x_{\left(k\right)}\right)-{\displaystyle \frac{k}{n+1}}\right]}^2\hfill \\ & =2\sum _{k=1}^n{\displaystyle \frac{{(n+1)}^2(n+2)}{k(n-k+1)}}{\left[sin\left[{\displaystyle \frac{\pi }{2}}{\left[1-exp\left(-{\displaystyle \frac{x_{\left(k\right)}^2}{2{\theta }^2}}\right)\right]}^{\alpha }\right]-{\left[1-exp\left(-{\displaystyle \frac{x_{\left(k\right)}^2}{2{\theta }^2}}\right)\right]}^{\alpha }-{\displaystyle \frac{k}{n+1}}\right]}^2.\hfill \end{array}$$

6.3. Maximum Product of Spacings Estimation (MPSE)

For estimating parameters of continuous univariate distributions, the maximum product of the spacing method—first presented by [36] and then examined by [37]—offers an alternative to maximum likelihood estimation. Its consistency and connection to the Kullback–Leibler measure of information were explained by [37]. This approach is a solid choice for estimating parameters in our study since it has been demonstrated to be effective and reliable in a wider range of circumstances. For a random sample of size n from the proposed model, with the order statistics $X_{\left(1\right)},X_{\left(2\right)},\dots ,X_{\left(n\right)}$, the uniform spacings are the differences between each pair of consecutive order statistics, expressed as follows:

$$D_k=F\left(x_{\left(k\right)}\right)-F\left(x_{(k-1)}\right);k=1,2,\dots ,n+1$$

where $F\left(x_{\left(0\right)}\right)=0$ and $F\left(x_{\left(n\right)}\right)=1$. The maximum product of spacing estimators is obtained by maximizing the following function:

$$\begin{array}{cc}\hfill M& ={\displaystyle \frac{1}{n+1}}\sum _{k=1}^{n+1}ln\left[D_k\right]\hfill \\ & ={\displaystyle \frac{1}{n+1}}\sum _{k=1}^{n+1}ln{\left[F\left(x_{\left(k\right)}\right)-{\displaystyle \frac{k}{n+1}}\right]}^2.\hfill \end{array}$$

where

$$F(x_{\left(k\right)})=\left[2sin\left\{{\displaystyle \frac{\pi }{2}}{\left[1-exp\left(-{\displaystyle \frac{x_{\left(k\right)}^2}{2{\theta }^2}}\right)\right]}^{\alpha }\right\}-{\left[1-exp\left(-{\displaystyle \frac{x_{\left(k\right)}^2}{2{\theta }^2}}\right)\right]}^{\alpha }\right]$$

and

$$F\left(x_{(k-1)}\right)=\left[2sin\left\{{\displaystyle \frac{\pi }{2}}{\left[1-exp\left(-{\displaystyle \frac{x_{(k-1)}^2}{2{\theta }^2}}\right)\right]}^{\alpha }\right\}-{\left[1-exp\left(-{\displaystyle \frac{x_{(k-1)}^2}{2{\theta }^2}}\right)\right]}^{\alpha }\right].$$

By solving the nonlinear equations ${\displaystyle \frac{\partial M}{\partial \alpha }}=0$ and ${\displaystyle \frac{\partial M}{\partial \theta }}=0$, we procure the maximum product of spacing estimates for the parameters of the ASPRD model.

7. Simulated Analysis

A simulation experiment is conducted using R software (version 4.4.2.) to evaluate the efficiency of different estimation techniques using varying sample sizes like $n=25,50,75,100,150,250$, and 350. The procedure is replicated 1000 times, and the parameters were set at $(0.25,0.75)$ and $(2.1,1.2)$ concerning the standard order $(\alpha ,\theta )$. The biases, mean square errors (MSE), and mean relative errors (MRE) are determined for each scenario.

The findings from the simulation analysis are displayed in Table 1 and Table 2. We can comprehend the relative benefits and efficacy of the various estimation techniques taken into consideration in our simulation study by integrating these tables. A graphical depiction of these tabular findings is shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, which further facilitates the interpretation of efficacy and performance of each method. These insights play a crucial role in determining which estimating method is best for upcoming applications and research projects.

Table 1. Results of simulations for various estimation techniques with parameter combination $\alpha =0.25$ and $\theta =0.75$.

Sample Size	Estimate	Parameter	MLE	LSE	WLSE	MPSE
25	Bias	$\alpha$	0.02805	0.03051	0.03364	0.02831
		$\theta$	0.09298	0.09642	0.07372	0.07422
	MSE	$\alpha$	0.00212	0.00149	0.00171	0.00122
		$\theta$	0.01943	0.01527	0.00901	0.00909
	MRE	$\alpha$	0.11219	0.12204	0.13454	0.11323
		$\theta$	0.12397	0.12856	0.09831	0.09896
50	Bias	$\alpha$	0.01125	0.02154	0.02291	0.01879
		$\theta$	0.03827	0.05474	0.04988	0.04262
	MSE	$\alpha$	0.00064	0.00072	0.00075	0.00053
		$\theta$	0.00599	0.00489	0.00438	0.00322
	MRE	$\alpha$	0.04501	0.08617	0.09168	0.07517
		$\theta$	0.05103	0.07298	0.06651	0.05682
75	Bias	$\alpha$	0.00711	0.02062	0.01945	0.01611
		$\theta$	0.02671	0.05194	0.04021	0.03195
	MSE	$\alpha$	0.00026	0.00067	0.00056	0.00041
		$\theta$	0.00381	0.00472	0.00246	0.00182
	MRE	$\alpha$	0.02846	0.08246	0.07779	0.06444
		$\theta$	0.03562	0.06925	0.05360	0.04260
100	Bias	$\alpha$	0.00438	0.01727	0.01374	0.01224
		$\theta$	0.01752	0.03987	0.02963	0.02242
	MSE	$\alpha$	0.00011	0.00048	0.00028	0.00026
		$\theta$	0.00209	0.00259	0.00145	0.00089
	MRE	$\alpha$	0.01751	0.06906	0.05497	0.04897
		$\theta$	0.02336	0.05315	0.03951	0.02989
150	Bias	$\alpha$	0.00068	0.01197	0.01163	0.01004
		$\theta$	0.00213	0.03204	0.02448	0.01754
	MSE	$\alpha$	0.00009	0.00023	0.00021	0.00017
		$\theta$	0.00013	0.00164	0.00096	0.00051
	MRE	$\alpha$	0.00274	0.04788	0.04651	0.04017
		$\theta$	0.00285	0.04272	0.03264	0.02339
250	Bias	$\alpha$	0.00031	0.01059	0.00998	0.00728
		$\theta$	0.00119	0.02972	0.01799	0.01249
	MSE	$\alpha$	0.00007	0.00018	0.00017	0.00010
		$\theta$	0.00011	0.00145	0.00052	0.00024
	MRE	$\alpha$	0.00123	0.04235	0.03991	0.02915
		$\theta$	0.00159	0.03963	0.02399	0.01665
350	Bias	$\alpha$	0.00019	0.00925	0.00701	0.00568
		$\theta$	0.00089	0.02396	0.01608	0.01189
	MSE	$\alpha$	0.00000	0.00013	0.00008	0.00006
		$\theta$	0.00000	0.00088	0.00044	0.00021
	MRE	$\alpha$	0.00000	0.03699	0.02805	0.02275
		$\theta$	0.00000	0.03196	0.02144	0.01584

Table 2. Results of simulations for various estimation techniques with parameter combination $\alpha =1.2$ and $\theta =2.1$.

Sample Size	Estimate	Parameter	MLE	LSE	WLSE	MPSE
25	Bias	$\alpha$	1.32625	0.35759	0.34229	0.31972
		$\theta$	0.31609	0.03433	0.02697	0.02045
	MSE	$\alpha$	3.35358	0.22367	0.25568	0.18201
		$\theta$	0.10652	0.00206	0.00165	0.00099
	MRE	$\alpha$	0.63155	0.17029	0.16300	0.15225
		$\theta$	0.26341	0.02861	0.02248	0.01705
50	Bias	$\alpha$	1.00687	0.25018	0.23172	0.21356
		$\theta$	0.30595	0.02348	0.01664	0.01118
	MSE	$\alpha$	1.58685	0.09976	0.09059	0.07347
		$\theta$	0.09641	0.00090	0.00051	0.00025
	MRE	$\alpha$	0.47946	0.11914	0.11034	0.10169
		$\theta$	0.25645	0.01957	0.01387	0.00932
75	Bias	$\alpha$	0.98021	0.20135	0.17713	0.16951
		$\theta$	0.30586	0.01908	0.01133	0.00808
	MSE	$\alpha$	1.32003	0.06645	0.05114	0.04664
		$\theta$	0.09570	0.00061	0.00023	0.00013
	MRE	$\alpha$	0.46677	0.09588	0.08435	0.08072
		$\theta$	0.25488	0.01590	0.00944	0.00674
100	Bias	$\alpha$	0.94272	0.17480	0.15237	0.14242
		$\theta$	0.30578	0.01569	0.00934	0.00642
	MSE	$\alpha$	1.13016	0.04849	0.03667	0.03301
		$\theta$	0.09507	0.00040	0.00015	0.00008
	MRE	$\alpha$	0.44891	0.08324	0.07256	0.06782
		$\theta$	0.25481	0.01308	0.00778	0.00535
150	Bias	$\alpha$	0.87893	0.14396	0.12519	0.10934
		$\theta$	0.30219	0.01320	0.00709	0.00443
	MSE	$\alpha$	0.92882	0.03257	0.02564	0.01914
		$\theta$	0.09239	0.00027	0.00008	0.00003
	MRE	$\alpha$	0.41853	0.06856	0.05962	0.05206
		$\theta$	0.25183	0.01100	0.00591	0.00369
250	Bias	$\alpha$	0.86596	0.11063	0.09879	0.08878
		$\theta$	0.30203	0.01001	0.00528	0.00350
	MSE	$\alpha$	0.83929	0.01927	0.01532	0.01227
		$\theta$	09186	0.00016	0.00004	0.00002
	MRE	$\alpha$	0.41236	0.05268	0.04705	0.04228
		$\theta$	0.25169	0.00834	0.00440	0.00292
350	Bias	$\alpha$	0.83590	0.09183	0.08192	0.07930
		$\theta$	0.30063	0.00866	0.00438	0.00289
	MSE	$\alpha$	0.78402	0.01355	0.01052	0.01004
		$\theta$	0.09140	0.00012	0.00003	0.00001
	MRE	$\alpha$	0.40469	0.04372	0.03901	0.03776
		$\theta$	0.25131	0.00722	0.00365	0.00249

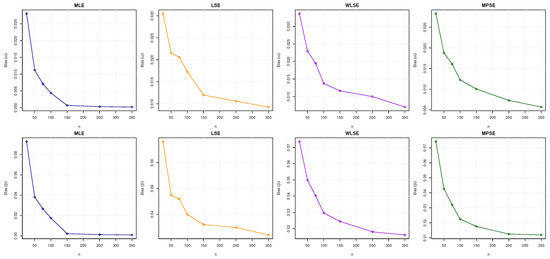
Figure 3. Visual summary of bias values for $\alpha$ and $\theta$ as reported in Table 3.

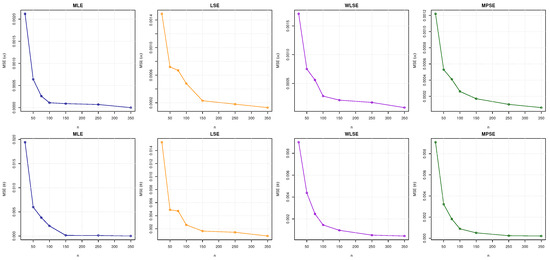
Figure 4. Visual summary of MSE values for $\alpha$ and $\theta$ as reported in Table 3.

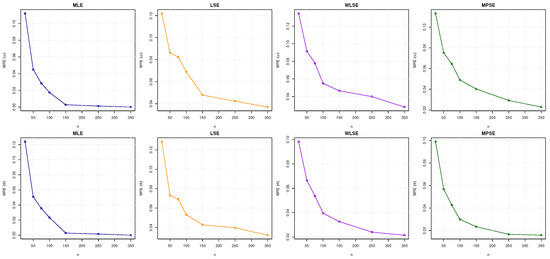
Figure 5. Visual summary of MRE values for $\alpha$ and $\theta$ as reported in Table 3.

Figure 6. Visual summary of bias values for $\alpha$ and $\theta$ as reported in Table 4.

Figure 7. Visual summary of MSE values for $\alpha$ and $\theta$ as reported in Table 4.

Figure 8. Visual summary of MSE values for $\alpha$ and $\theta$ as reported in Table 4.

Many inferences can be made from the thorough examination of the ranking tables and simulation results, including the following:

• All estimators analyzed in this research demonstrate the property of consistency. This suggests that as the sample size (n) rises, the estimators converge to the true parameter values.
• Regardless of the estimation approach employed, the bias of all estimators diminishes as sample size (n) grows. This suggests that larger sample sizes yield more precise estimates with reduced systematic errors.
• For all estimation strategies, the MSE of the estimates decreases as n increases. This implies that larger sample sizes improve the precision of the estimates by minimizing random and systematic errors.
• Regardless of the estimation approach utilized, the RMSE of all estimators decreases as n increases. This indicates that higher sample numbers lead to more precise approximations as the relative error gradually decreases.

8. Application

To illustrate the importance of the ASPRD model, we present three practical applications to evaluate the adaptability of the subject model. For comparison, multiple goodness-of-fit (GoF) metrics have been evaluated, including Akaike Information Criteria (AIC), Bayesian Information Criteria (BIC), Akaike Information Criteria Corrected (AICC) and Hannan–Quinn Information Criteria (HQIC). The optimal distribution has lower values for all GoF metrics.

Dataset 1: The first data on the breaking stress of carbon fibers of 50 mm length (GPa) are obtained from [38]. These data were used by [12] to illustrate the applications of the sine power Rayleigh distribution. The dataset is unimodal and is approximately symmetric (skewness = −0.13 and kurtosis = 3.22). The data are as follows: 3.70, 2.74, 2.73, 2.50, 3.60, 3.11, 3.27, 2.87, 1.47, 3.11, 3.56, 4.42, 2.41, 3.19, 3.22, 1.69, 3.28, 3.09, 1.87, 3.15, 4.90, 1.57, 2.67, 2.93, 3.22, 3.39, 2.81, 4.20, 3.33, 2.55, 3.31, 3.31, 2.85, 1.25, 4.38, 1.84, 0.39, 3.68, 2.48, 0.85, 1.61, 2.79, 4.70, 2.03, 1.89, 2.88, 2.82, 2.05, 3.65, 3.75, 2.43, 2.95, 2.97, 3.39, 2.96, 2.35, 2.55, 2.59, 2.03, 1.61, 2.12, 3.15, 1.08, 2.56, 1.80, 2.53.

Dataset 2: The data consist of 63 observations of the strengths of 1.5 cm glass fibers, which are obtained from [39]. This dataset was also analyzed by [32] to demonstrate the properties and applications of power exponentiated Rayleigh distribution. The dataset is unimodal and is left skewed (skewness = −0.89 and kurtosis = 3.92). The data are as follows: 0.55, 0.74, 0.77, 0.81, 0.84, 0.93, 1.04, 1.11, 1.13, 1.24, 1.25, 1.27, 1.28, 1.29, 1.30, 1.36, 1.39, 1.42, 1.48, 1.48, 1.49, 1.49, 1.50, 1.50, 1.51, 1.52, 1.53, 1.54, 1.55, 1.55, 1.58, 1.59, 1.60, 1.61, 1.61,1.61, 1.61, 1.62, 1.62, 1.63, 1.64, 1.66, 1.66, 1.66, 1.67,1.68, 1.68, 1.69, 1.70, 1.70, 1.73, 1.76, 1.76, 1.77, 1.78, 1.81, 1.82, 1.84, 1.84, 1.89, 2.00, 2.01, 2.24.

Dataset 3: Data were collected from a group of 46 patients, per year, on recurrence of leukemia who received autologous marrow. The dataset is unimodal and is positively skewed (skewness = 1.03 and kurtosis = 2.65), reported by Ahmad et al. [40], as follows: 0.0301, 0.0384, 0.0630, 0.0849, 0.0877, 0.0959, 0.1397, 0.1616, 0.1699, 0.2137, 0.2137, 0.2164, 0.2384, 0.2712, 0.2740, 0.3863, 0.4384, 0.4548, 0.5918, 0.6000, 0.6438, 0.6849, 0.7397, 0.8575, 0.9096, 0.9644, 1.0082, 1.2822, 1.3452, 1.4000, 1.5260, 1.7205, 1.9890, 2.2438, 2.5068, 2.6466, 3.0384, 3.1726, 3.4411, 4.4219, 4.4356, 4.5863, 4.6904, 4.7808, 4.9863, 5.

The potentiality of the proposed model is determined by comparing its performance with several other competitive models, namely Weighted Rayleigh Distribution (WRD) [25], Transmuted Rayleigh Distribution (TRD) [41], Exponentiated Rayleigh Distribution (ERD) [21], Rayleigh Distribution (RD) [20], Power Exponentiated Rayleigh Distribution (PERD) [32], Weibull Distribution (WD) [42], Power Rayleigh Distribution (PRD) [43], and Sine Power Rayleigh Distribution (SPRD) [12].

The findings presented in Table 3, Table 4 and Table 5 indicate that the ASPRD exhibits the lowest values for AIC, BIC, AICC, and HQIC when compared with the existing models discussed. This demonstrates that it surpasses the baseline Rayleigh distribution model and existing competing models. Figure 9, Figure 10, Figure 11 and Figure 12 compare the estimated density, P-P, survival, and TTT plots of the ASPRD model for the three datasets. In summary, the ASPRD model shows its practical applicability in real-world circumstances and is the most appropriate model for the three datasets.

Table 3. ML estimates and model selection criteria for different models for dataset 1.

Model	ML Estimates (Standard Errors)	Model Selection Criteria
		$-\mathbf{2}\mathit{l}$	AIC	BIC	AICC	HQIC
ASPRD	$\widehat{\alpha }$ = 1.661 (0.231)	160.172	164.173	168.553	164.364	165.904
	$\widehat{\theta }$ = 2.526 (0.135)
WRD	$\widehat{\beta }$ = 2.572 (0.745)	175.710	179.710	184.090	179.901	181.441
	$\widehat{\theta }$ = 1.355 (0.123)
TRD	$\widehat{\eta }$ = −0.958 (0.092)	177.748	181.748	186.128	181.939	183.479
	$\widehat{\theta }$ = 1.696 (0.082)
ERD	$\widehat{\alpha }$ = 2.348 (0.431)	177.273	181.273	185.652	181.463	183.003
	$\widehat{\theta }$ = 0.191 (0.024)
RD	$\widehat{\theta }$ = 2.049 (0.126)	196.416	198.416	200.606	198.479	199.282
PERD	$\widehat{\alpha }$ = 1.868 (0.343)	171.917	177.917	184.486	178.304	180.513
	$\widehat{\beta }$ = 0.859 (0.270)
	$\widehat{\theta }$ = 0.013 (0.014)
WD	$\widehat{\delta }$ = 3.441 (0.330)	172.135	176.135	180.514	176.325	177.865
	$\widehat{\lambda }$ = 3.062 (0.114)
ED	$\widehat{\theta }$ = 0.362 (0.044)	265.989	267.989	270.179	268.052	268.854
PRD	$\widehat{\beta }$ = 1.720 (0.165)	172.135	176.135	180.514	176.325	177.865
	$\widehat{\theta }$ = 4.850 (1.036)
SPRD	$\widehat{\beta }$ = 1.636 (0.159)	171.682	175.682	180.061	175.873	177.412
	$\widehat{\theta }$ = 5.851 (1.205)
GD	$\widehat{\alpha }$ = 7.488 (1.276)	182.335	186.335	190.714	186.526	188.066
	$\widehat{\theta }$ = 2.713 (0.478)

Table 4. ML estimates and model selection criteria for different models for dataset 2.

Model	ML Estimates (Standard Errors)	Model Selection Criteria
		$-\mathbf{2}\mathit{l}$	AIC	BIC	AICC	HQIC
ASPRD	$\widehat{\alpha }$ = 3.723 (0.609)	22.943	26.943	31.229	27.143	28.629
	$\widehat{\theta }$ = 0.970 (0.042)
WRD	$\widehat{\beta }$ = 8.084 (1.740)	41.687	45.686	49.973	45.886	47.372
	$\widehat{\theta }$ = 0.485 (0.044)
TRD	$\widehat{\eta }$ = −1.212 (0.381)	67.313	71.313	75.599	71.513	72.999
	$\widehat{\theta }$ = 0.901 (0.056)
ERD	$\widehat{\alpha }$ = 5.486 (1.184)	47.857	51.857	56.143	52.057	53.543
	$\widehat{\theta }$ = 0.974 (0.106)
RD	$\widehat{\theta }$ = 1.289 (0.068)	99.581	101.581	103.724	101.647	102.424
PERD	$\widehat{\alpha }$ = 3.611 (0.716)	29.352	35.352	41.781	35.759	37.881
	$\widehat{\beta }$ = 0.679 (0.218)
	$\widehat{\theta }$ = 0.020 (0.021)
WD	$\widehat{\delta }$ = 5.780 (0.576)	30.413	34.413	38.699	34.613	36.099
	$\widehat{\lambda }$ = 1.628 (0.037)
ED	$\widehat{\theta }$ = 0.663 (0.083)	177.660	179.660	181.803	179.726	180.503
PRD	$\widehat{\beta }$ = 2.890 (0.288)	30.413	34.413	38.699	34.613	36.099
	$\widehat{\theta }$ = 2.892 (0.496)
SPRD	$\widehat{\beta }$ = 2.764 (0.278)	29.404	33.404	37.690	33.604	35.090
	$\widehat{\theta }$ = 3.608 (0.596)
GD	$\widehat{\alpha }$ = 17.139 (3.077)	47.902	51.902	56.189	52.103	53.589
	$\widehat{\theta }$ = 11.574 (2.072)

Table 5. ML estimates and model selection criteria for different models for dataset 3.

Model	ML Estimates (Standard Errors)	Model Selection Criteria
		$-\mathbf{2}\mathit{l}$	AIC	BIC	AICC	HQIC
ASPRD	$\widehat{\alpha }$ = 0.307 (0.042)	117.667	121.667	125.324	121.946	123.037
	$\widehat{\theta }$ = 6.221 (1.114)
WRD	$\widehat{\beta }$ = 0.002 (0.367)	207.502	211.501	215.158	211.780	212.871
	$\widehat{\theta }$ = 1.566 (0.184)
TRD	$\widehat{\eta }$ = 0.539 (0.168)	198.828	202.828	206.485	203.107	204.198
	$\widehat{\theta }$ = 1.690 (0.149)
ERD	$\widehat{\alpha }$ = 0.295 (0.048)	128.448	132.448	136.106	132.727	133.818
	$\widehat{\theta }$ = 0.083 (0.024)
RD	$\widehat{\theta }$ = 1.566 (0.115)	207.422	209.422	211.250	209.512	210.107
PERD	$\widehat{\alpha }$ = 0.398 (0.326)	127.969	133.969	139.455	134.541	136.024
	$\widehat{\beta }$ = 1.094 (1.505)
	$\widehat{\theta }$ = 0.834 (1.156)
WD	$\widehat{\delta }$ = 1.385 (0.257)	127.974	131.974	135.631	132.252	133.344
	$\widehat{\lambda }$ = 0.840 (0.099)
ED	$\widehat{\theta }$ = 0.659 (0.097)	130.352	132.352	134.181	132.443	133.037
PRD	$\widehat{\beta }$ = 0.420 (0.049)	126.947	130.947	134.631	131.235	132.343
	$\widehat{\theta }$ = 0.811 (0.068)
SPRD	$\widehat{\beta }$ = 0.397 (0.047)	128.368	132.368	136.026	132.648	133.739
	$\widehat{\theta }$ = 1.069 (0.087)
GD	$\widehat{\alpha }$ = 0.771 (0.138)	128.082	132.082	135.740	132.362	133.453
	$\widehat{\theta }$ = 0.508 (0.125)

Figure 9. Histogram with fitted density plots for datasets I, II, and III.

Figure 10. P-P plots for datasets I, II, and III.

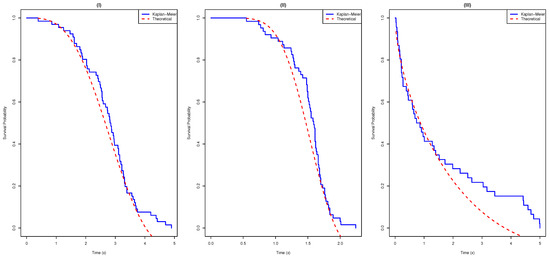
Figure 11. Survival plots for datasets I, II, and III.

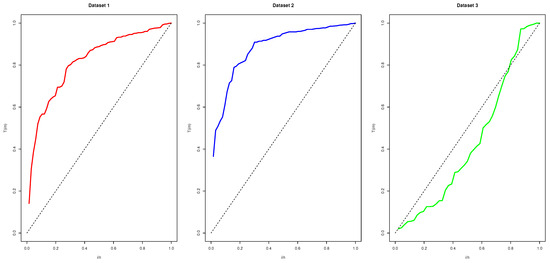
Figure 12. TTT plots for datasets I, II, and III.

9. Conclusions

This study introduces the ASP-X family of distributions, with an emphasis on the ASP Rayleigh Distribution (ASPRD), a versatile two-parameter model intended to improve data adaptability. A comprehensive statistical examination reveals its practical benefits and structural characteristics. We evaluated the precision of the parameter estimate using four traditional estimation techniques, including MLE, LSE, WLSE, and MPSE, and showed the resilience of the model through in-depth simulations. The application of ASPRD to real-world datasets further validates its effectiveness in capturing complex data patterns. In addition to an engineering dataset, we have incorporated a medical dataset, demonstrating the model’s adaptability and versatility across diverse fields.

The study has some limitations despite its encouraging results. Like many parametric distributions, the ASPRD model may be less flexible when dealing with multimodal or strongly skewed datasets. To increase adaptability, future studies should investigate expanded models that include more form factors or hybrid estimating methods. Additionally, ASPRD’s generalizability might be further evaluated by extending it to other fields, including economics or the biological sciences. These paths will contribute to the improvement of the framework and increase the scope of its statistical modeling applications.