Approximation Results: Szász–Kantorovich Operators Enhanced by Frobenius–Euler–Type Polynomials
Abstract
1. Introduction and Preliminaries
2. Approximation Properties—Uniform Convergence and the Approximation Order
3. Graphical and Numerical Approaches to a Convergence Analysis
4. Local Approximation Results
5. The Bivariate of a Frobenius–Euler–Simsek Polynomial Analog of Szász Operators
6. Order of Approximation
7. Numerical and Graphical Analyses of Bivariate Operators
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bernstein, S.N. Démonstration du théorème de Weierstrass fondée sur le calcul de probabilités. Commun. Soc. Math. Kharkow. 1913, 13, 1–2. [Google Scholar]
- Weierstrass, K. Über die analytische Darstellbarkeit sogenannter willkürlicher Functionen einer reellen Veränderlichen. Sitzungsberichte KöNiglichen PreußIschen Akad. Wiss. Berl. 1885, 2, 633–639. [Google Scholar]
- Kantorovich, L.V. Sur certain developpments suivant les polynomes de la forme de S. Bernstein, I, II. C. R. Acad. URSS 1930, 563–568, 595–600. [Google Scholar]
- Khan, K.; Lobiyal, D.K. Bézier curves based on Lupăs (p,q)-analogue of Bernstein functions in CAGD. Comput. Appl. Math. 2017, 317, 458–477. [Google Scholar] [CrossRef]
- Raiz, M.; Rao, N.; Mishra, V.N. Szász-type operators involving q-Appell polynomials. In Approximation Theory, Sequence Spaces and Applications; Mohiuddine, S.A., Hazarika, B., Nashine, H.K., Eds.; Industrial and Applied Mathematics; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- Khan, K.; Lobiyal, D.K.; Kilicman, A. Bézier curves and surfaces based on modified Bernstein polynomials. Azerb. J. Math. 2019, 9, 102–115. [Google Scholar]
- Izadbakhsh, A.; Kalat, A.A.; Khorashadizadeh, S. Observer-based adaptive control for HIV infection therapy using the Baskakov operator. Biomed. Signal Process. Control 2021, 65, 102343. [Google Scholar] [CrossRef]
- Uyan, H.; Aslan, A.O.; Karateke, S.; Büyükyazıcı, İ. Interpolation for neural network operators activated with a generalized logistic-type function. Neural Comput. Appl. 2024, in press. [CrossRef]
- Zhang, Q.; Mu, M.; Wang, X. A modified robotic manipulator controller based on Bernstein-Kantorovich-Stancu operator. Micromachines 2022, 14, 44. [Google Scholar] [CrossRef]
- Özger, F. Weighted statistical approximation properties of univariate and bivariate λ-Kantorovich operators. Filomat 2019, 33, 3473–3486. [Google Scholar] [CrossRef]
- Özger, F.; Ansari, K.J. Statistical convergence of bivariate generalized Bernstein operators via four-dimensional infinite matrices. Filomat 2022, 36, 543–555. [Google Scholar] [CrossRef]
- Cai, Q.B.; Lian, B.Y.; Zhou, G. Approximation properties of λ-Bernstein operators. J. Inequal. Appl. 2018, 2018, 61. [Google Scholar] [CrossRef] [PubMed]
- Cai, Q.B.; Zhou, G.; Li, J. Statistical approximation properties of λ-Bernstein operators based on q-integers. Open Math. 2019, 17, 487–498. [Google Scholar]
- Aslan, R. Rate of approximation of blending type modified univariate and bivariate λ-Schurer-Kantorovich operators. Kuwait J. Sci. 2024, 51, 100168. [Google Scholar]
- Aslan, R. Approximation properties of univariate and bivariate new class-Bernstein–Kantorovich operators and its associated GBS operators. Comput. Appl. Math. 2023, 42, 34. [Google Scholar] [CrossRef]
- Acu, A.M.; Gonska, H.; Rașa, I. Grüss-type and Ostrowski-type inequalities in approximation theory. Ukr. Math. J. 2011, 63, 843–864. [Google Scholar]
- Acu, A.M.; Acar, T.; Radu, V.A. Approximation by modified operators. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Math. 2019, 113, 2715–2729. [Google Scholar]
- Acu, A.M.; Tachev, G. Yet another new variant of Szász–Mirakyan operator. Symmetry 2021, 13, 2018. [Google Scholar] [CrossRef]
- Mohiuddine, S.A.; Acar, T.; Alotaibi, A. Construction of a new family of Bernstein-Kantorovich operators. Math. Methods Appl. Sci. 2017, 40, 7749–7759. [Google Scholar]
- Mohiuddine, S.A.; Ahmad, N.; Özger, F.; Alotaibi, A.; Hazarika, B. Approximation by the parametric generalization of Baskakov–Kantorovich operators linking with Stancu operators. Iran. J. Sci. Technol. Trans. A Math. 2021, 45, 593–605. [Google Scholar] [CrossRef]
- Mursaleen, M.; Ansari, K.J.; Khan, A. Approximation properties and error estimation of q-Bernstein shifted operators. Numer. Algorithms 2020, 84, 207–227. [Google Scholar] [CrossRef]
- Mursaleen, M.; Naaz, A.; Khan, A. Improved approximation and error estimations by King type (p, q)-Szász–Mirakjan Kantorovich operators. Appl. Math. Comput. 2019, 348, 2175–2185. [Google Scholar]
- Bustamante, J. Direct estimates and a Voronovskaja-type formula for Mihesan operators. Comput. Math. Appl. 2022, 5, 202–213. [Google Scholar]
- Ozsarac, F.; Gupta, V.; Aral, A. Approximation by some Baskakov–Kantorovich exponential-type operators. Bull. Iran. Math. Soc. 2022, 48, 227–241. [Google Scholar]
- Khan, A.; Mansoori, M.; Khan, K.; Mursaleen, M. Phillips-type q-Bernstein operators on triangles. J. Funct. Spaces 2021, 1–13. [Google Scholar] [CrossRef]
- Nasiruzzaman, M. Approximation properties by Szász–Mirakjan operators to bivariate functions via Dunkl analogue. Iran. J. Sci. Technol. Trans. A Math. 2011, 45, 259–269. [Google Scholar]
- Braha, N.L.; Loku, V.; Mansour, T.; Mursaleen, M. A new weighted statistical convergence and some associated approximation theorems. Math. Methods Appl. Sci. 2022, 45, 5682–5698. [Google Scholar]
- Rao, N.; Farid, M.; Ali, R.A. Study of Szász–Durremeyer-Type Operators Involving Adjoint Bernoulli Polynomials. Mathematics 2024, 12, 3645. [Google Scholar] [CrossRef]
- Rao, N.; Farid, M.; Raiz, M. Symmetric Properties of λ-Szász Operators Coupled with Generalized Beta Functions and Approximation Theory. Symmetry 2024, 16, 1703. [Google Scholar] [CrossRef]
- Çetin, N. Approximation and geometric properties of complex α-Bernstein operator. Results Math. 2019, 74, 40. [Google Scholar]
- Çetin, N.; Radu, V.A. Approximation by generalized Bernstein–Stancu operators. Turk. J. Math. 2019, 43, 2032–2048. [Google Scholar]
- Simsek, Y. Applications of constructed new families of generating-type functions interpolating new and known classes of polynomials and numbers. Math. Methods Appl. Sci. 2021, 44, 11245–11268. [Google Scholar] [CrossRef]
- Kucukoglu, I. Generating functions for multiparametric Hermite-based Peters-type Simsek numbers and polynomials in several variables. Montes Taurus J. Pure Appl. Math. 2024, 6, 217–238. [Google Scholar]
- Kucukoglu, I.; Simsek, Y. Identities and relations on the q-Apostol type Frobenius–Euler numbers and polynomials. J. Korean Math. Soc. 2019, 56, 265–284. [Google Scholar]
- Agyuz, E. On the convergence properties of generalized Szász–Kantorovich type operators involving Frobenius–Euler–Simsek-type polynomials. AIMS Math. 2024, 9, 28195–28210. [Google Scholar]
- DeVore, R.A.; Lorentz, G.G. Constructive Approximation; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Altomare, F.; Campiti, M. Korovkin-Type Approximation Theory and Its Applications; De Gruyter Studies in Mathematics; De Gruyter: Berlin, Germany, 1994; Volume 17, pp. 266–274. [Google Scholar]
- Özarslan, M.A.; Aktuğlu, H. Local approximation for certain King type operators. Filomat 2013, 27, 173–181. [Google Scholar]
- Volkov, V.I. On the convergence of sequences of linear positive operators in the space of continuous functions of two variables. Dokl. Akad. Nauk SSSR (NS) 1957, 115, 17–19. (In Russian) [Google Scholar]
- Stancu, F. Aproximarea Funcţiilor de Două şi Mai Multe Variabile Prin şIruri de Operatori Liniari şi Pozitivi. Ph.D. Thesis, University ”Babe¸s-Bolyai”, Cluj-Napoca, Romania, 1984. (In Russian). [Google Scholar]
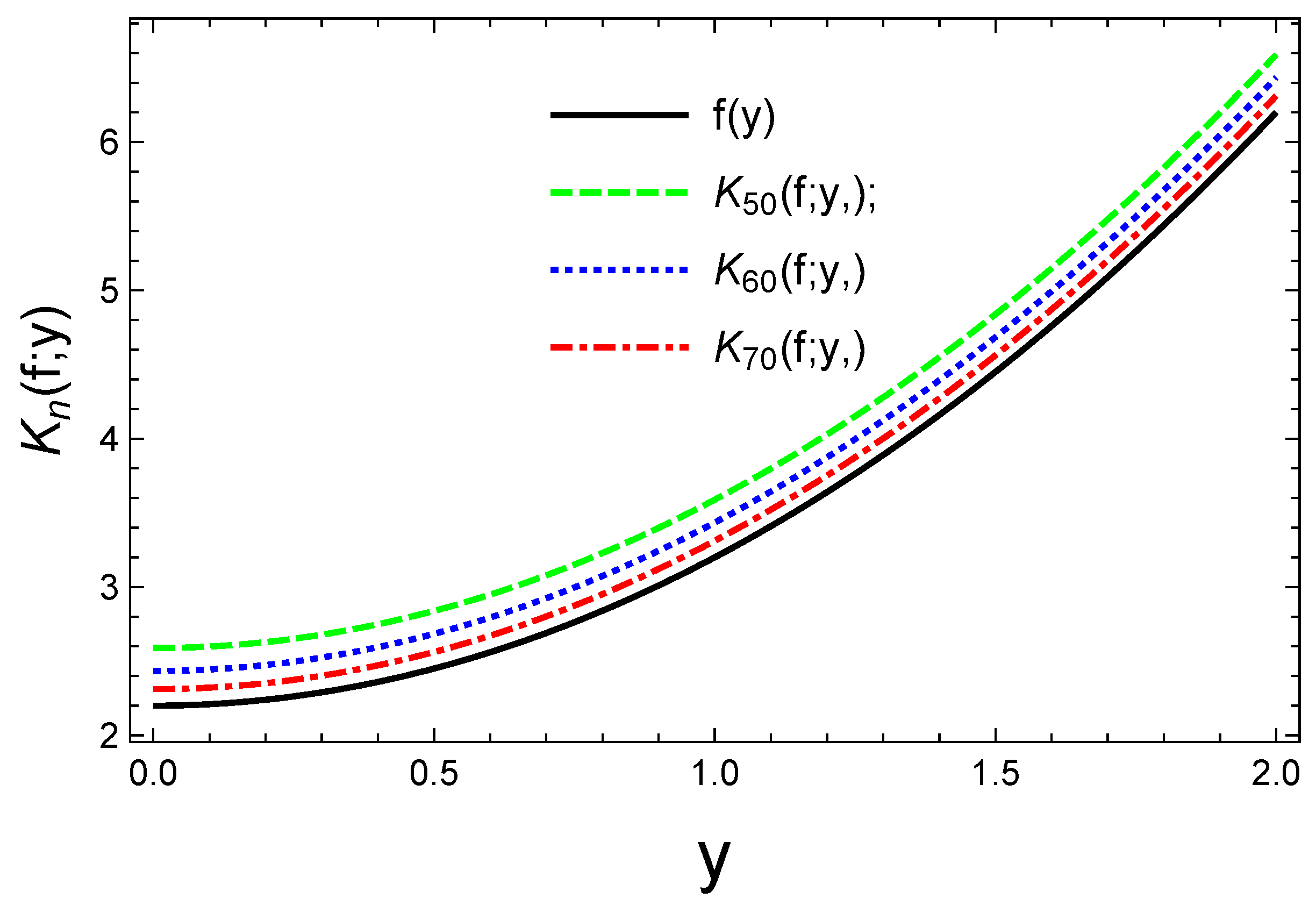
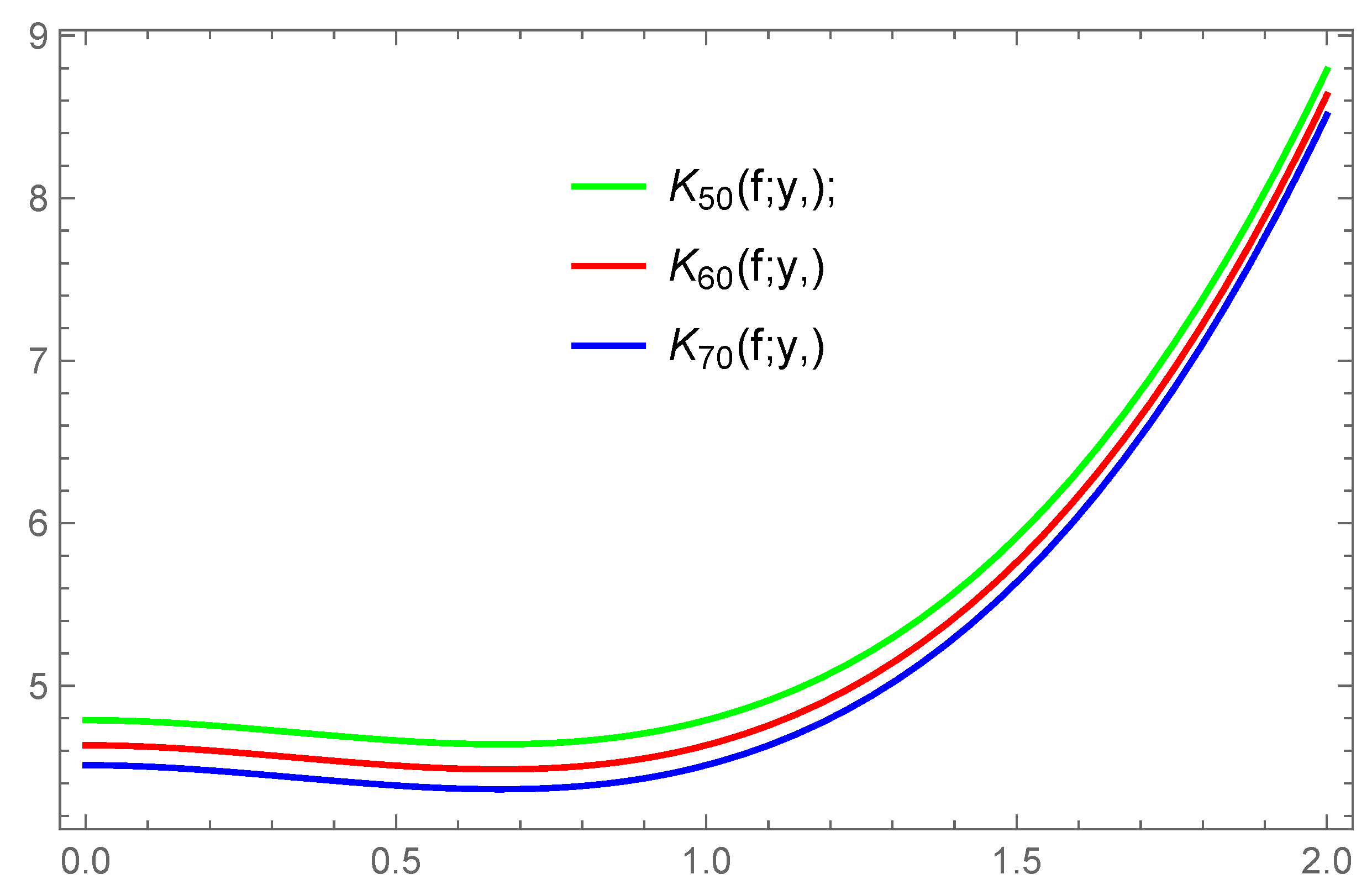
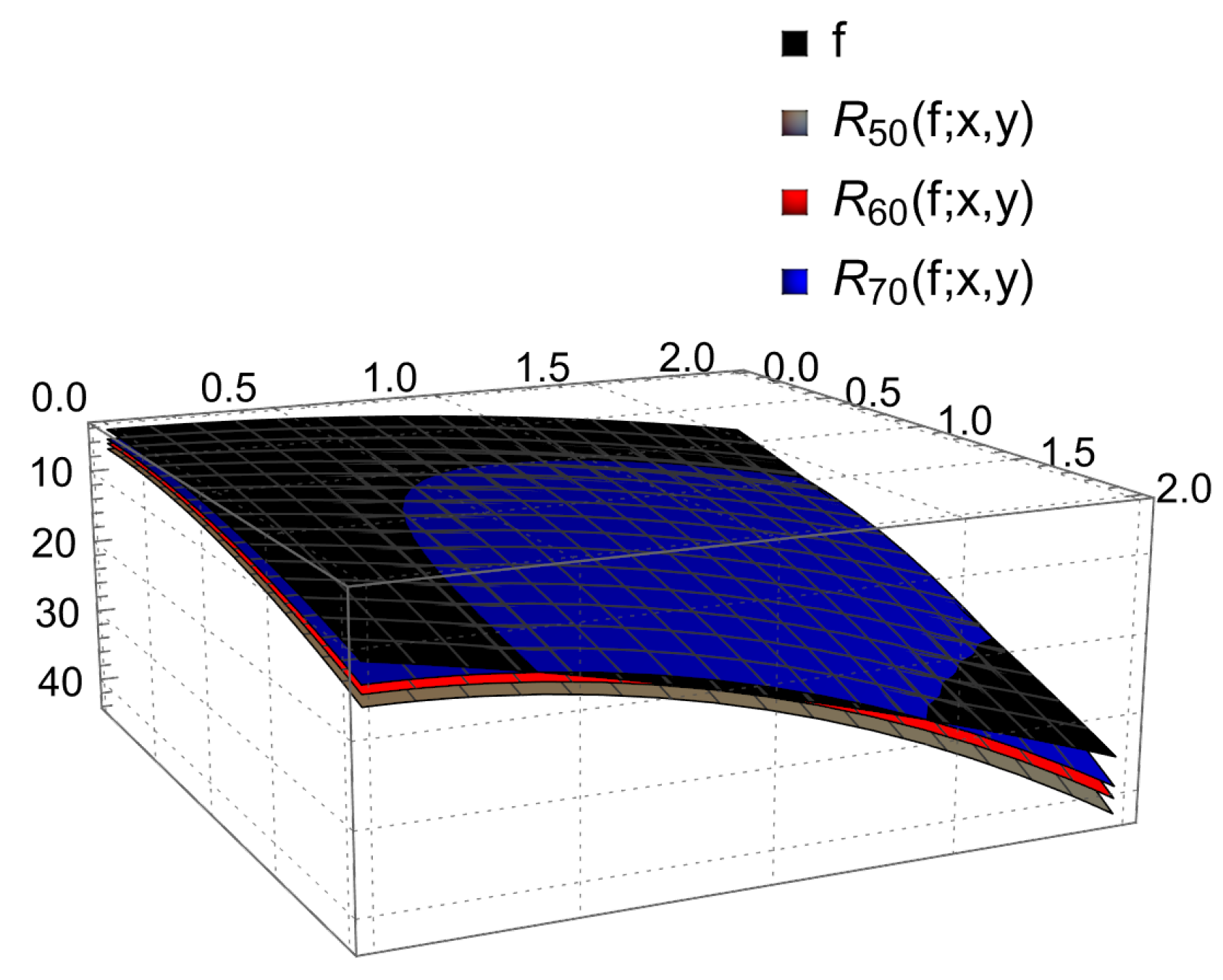
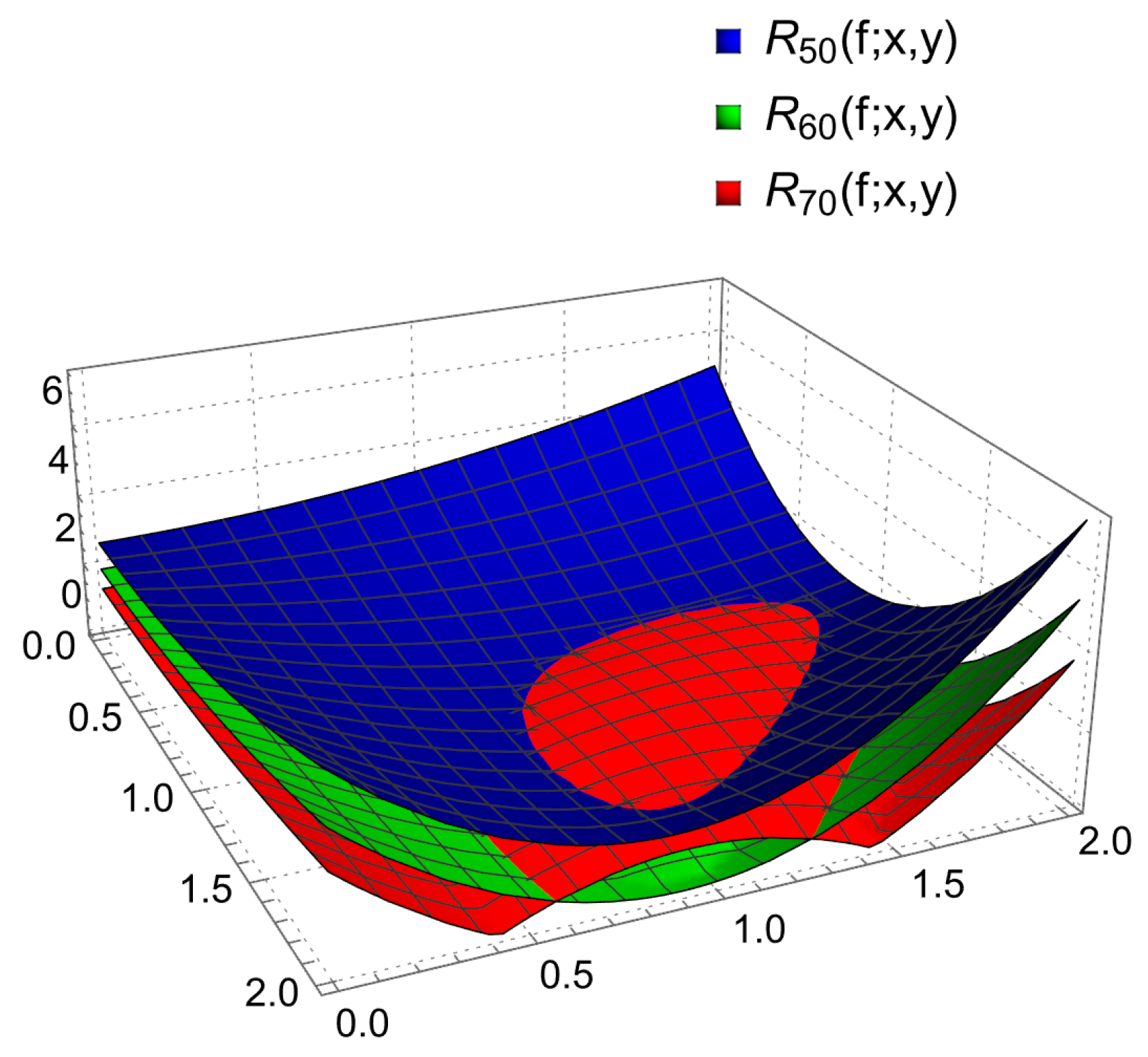
| y | |||
|---|---|---|---|
| 0.2 | 4.82078 | 4.66625 | 4.54366 |
| 0.4 | 4.88478 | 4.73025 | 4.60766 |
| 0.6 | 4.93278 | 4.77825 | 4.65566 |
| 0.8 | 4.91678 | 4.77825 | 4.63966 |
| 1.0 | 4.86978 | 4.76228 | 4.59266 |
| 1.2 | 4.78878 | 4.71525 | 4.51166 |
| 1.4 | 4.50078 | 4.63425 | 4.22366 |
| 1.6 | 4.00478 | 4.34625 | 3.72766 |
| 1.8 | 3.25278 | 3.85025 | 2.97566 |
| 2.0 | 2.19678 | 3.09825 | 1.91966 |
| 0.2, 0.2 | 2.59048 | 1.80191 | 1.210319 |
| 0.4, 0.4 | 2.27578 | 1.45012 | 0.829109 |
| 0.6, 0.6 | 1.81534 | 0.927824 | 0.257771 |
| 0.8, 0.8 | 1.30501 | 0.331003 | 0.407696 |
| 1.0, 1.0 | 0.87933 | 0.205938 | 1.032911 |
| 1.2, 1.2 | 0.71105 | 0.510199 | 1.44504 |
| 1.4, 1.4 | 1.01139 | 0.370581 | 1.432913 |
| 1.6, 1.6 | 2.02992 | 0.462517 | 0.746917 |
| 1.8, 1.8 | 4.05466 | 2.277118 | 0.900942 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rao, N.; Farid, M.; Raiz, M. Approximation Results: Szász–Kantorovich Operators Enhanced by Frobenius–Euler–Type Polynomials. Axioms 2025, 14, 252. https://doi.org/10.3390/axioms14040252
Rao N, Farid M, Raiz M. Approximation Results: Szász–Kantorovich Operators Enhanced by Frobenius–Euler–Type Polynomials. Axioms. 2025; 14(4):252. https://doi.org/10.3390/axioms14040252
Chicago/Turabian StyleRao, Nadeem, Mohammad Farid, and Mohd Raiz. 2025. "Approximation Results: Szász–Kantorovich Operators Enhanced by Frobenius–Euler–Type Polynomials" Axioms 14, no. 4: 252. https://doi.org/10.3390/axioms14040252
APA StyleRao, N., Farid, M., & Raiz, M. (2025). Approximation Results: Szász–Kantorovich Operators Enhanced by Frobenius–Euler–Type Polynomials. Axioms, 14(4), 252. https://doi.org/10.3390/axioms14040252







