A New Hybrid Class of Distributions: Model Characteristics and Stress–Strength Reliability Studies

Abstract

This study proposes a generalized family of distributions to enhance flexibility in modeling complex engineering and biomedical data. The framework unifies existing models and improves reliability analysis in both engineering and biomedical applications by capturing diverse system behaviors. We introduce a novel hybrid family of distributions that incorporates a flexible set of hybrid functions, enabling the extension of various existing distributions. Specifically, we present a three-parameter special member called the hybrid-Weibull–exponential (HWE) distribution. We derive several fundamental mathematical properties of this new family, including moments, random data generation processes, mean residual life (MRL) and its relationship with the failure rate function, and its related asymptotic behavior. Furthermore, we compute advanced information measures, such as extropy and cumulative residual entropy, and derive order statistics along with their asymptotic behaviors. Model identifiability is demonstrated numerically using the Kullback–Leibler divergence. Additionally, we perform a stress–strength (SS) reliability analysis of the HWE under two common scale parameters, supported by illustrative numerical evaluations. For parameter estimation, we adopt the maximum likelihood estimation (MLE) method in both density estimation and SS-parameter studies. The simulation results indicated that the MLE demonstrates consistency in both density and SS-parameter estimations, with the mean squared error of the MLEs decreasing as the sample size increases. Moreover, the average length of the confidence interval for the percentile and Student’s t-bootstrap for the SS-parameter becomes smaller with larger sample sizes, and the coverage probability progressively aligns with the nominal confidence level of 95%. To demonstrate the practical effectiveness of the hybrid family, we provide three real-world data applications in which the HWE distribution outperforms many existing Weibull-based models, as measured by AIC, BIC, CAIC, KS, Anderson–Darling, and Cramer–von Mises criteria. Furthermore, the HLW exhibits strong performance in SS-parameter analysis. Consequently, this hybrid family holds immense potential for modeling lifetime data and advancing reliability and survival analysis.

1. Introduction

With the advent of new technologies and innovative methods, the data they generate often exhibit characteristics that deviate from those described by traditional statistical models. These can include unusual patterns such as skewness, heavy tails, multimodal distributions, or atypical failure rates. Such discrepancies can make conventional models insufficient for accurate analysis and prediction, highlighting the need for more adaptable approaches. The creation of dynamic models that accurately encapsulate a variety of data types is a crucial challenge and opportunity within the realm of probability and applied statistics. This vital endeavor not only facilitates the integration of diverse aspects of real-world phenomena but also aids in the development of predictive insights. In this pursuit, statisticians have crafted numerous families of distributions using various methods, such as employing differential equations and manipulating parameters including location, scale, and shape, as well as incorporating confounding schemes and trigonometric and weighting techniques. These methodological advancements are similar to developing new data generation processes, which is comparable to creating fresh case studies. Such progress not only enhances our understanding of existing models but also improves our ability to tackle future challenges across various fields, including finance, engineering, biomedical sciences, and natural sciences. By extending these distributions, we develop more flexible and precise tools that contribute to both theoretical research and practical applications, particularly in analyzing complex and dynamic datasets. For instance, these advancements include various classes and extensions of distributions, see Table 1:

Table 1. G-classes of distributions.

Model Name	Cumulative Distribution Function
Beta-G [1]	$F\left(x\right)=I_{G(x;\xi )}(a,b),$
	where, $I_y(a,b)={\displaystyle \frac{B_y(a,b)}{B(a,b)}}$ is the incomplete beta function   $a,b>0,\xi \in \mathbb{R}.$
Generalized beta-G [2]	$F\left(x\right)=I_{G^c(x;\xi )}(a,b),a,b,c>0,\xi \in \mathbb{R}.$
New Kumaraswamy-G [3]	$F\left(x\right)=1-{\left(1-{\left(1-\overline{G}{(x;\eta )}^{G(x;\eta )}\right)}^a\right)}^b,a,b>0,\eta \in \mathbb{R}.$
Kumaraswamy–Poisson-G [4]	$F\left(x\right)=1-{\left(1-{\left({\displaystyle \frac{1-e^{-\lambda G(x;\eta )}}{1-e^{-\lambda }}}\right)}^a\right)}^b,\lambda a,b>0,\eta \in \mathbb{R}.$
Poisson-odd generalized exponential-G [5]	$F\left(x\right)={\displaystyle \frac{1-e^{-\lambda {\left(1-e^{-\alpha \frac{G(x;\xi )}{\overline{G}(x;\xi )}}\right)}^{\beta }}}{(1-e^{-\lambda })}},\alpha ,\beta ,\lambda >0,\xi \in \mathbb{R}.$
Extended Topp–Leone-G [6]	$F\left(x\right)=G^{\alpha }(x;\xi ){(2-G(x;\xi ))}^{\alpha \beta },\alpha >0,\beta ,\xi \in \mathbb{R}$
Power Topp–Leone-G [7]	$F\left(x\right)=e^{\alpha \beta \left(1-{\displaystyle \frac{1}{G(x;\xi )}}\right)}{\left(2-e^{\beta \left(1-{\displaystyle \frac{1}{G(x;\xi )}}\right)}\right)}^{\alpha },\alpha ,\beta >0,\xi \in \mathbb{R}.$
Weighted cosine-G [8]	$F\left(x\right)={\displaystyle \frac{e^{1-cos(\frac{\pi G(x;\eta )}{1+G(x;\eta )})}-1}{e-1}},\eta \in \mathbb{R}.$
Tan-G-loss family [9]	$F\left(x\right)=tan\left({\displaystyle \frac{\pi }{4}}\left(1-{\displaystyle \frac{\sigma \overline{G}(x;\xi )}{\sigma -log\overline{G}(x;\xi )}}\right)\right)\sigma >0,\xi \in \mathbb{R}.$
Exponent-G-exponential [10]	$F\left(x\right)=1-e^{-\lambda \left({\displaystyle \frac{1-e^{-G(x;\zeta )}}{e^{\overline{G}(x;\zeta )}-1}}\right)},\lambda >0,\zeta \in \mathbb{R}.$

Furthermore, the field has seen the introduction of several Weibull-related distributions such as the exponentiated additive Weibull [11], improved Weibull–Weibull [12], modified exponential Weibull [13], discrete bivariate Frechet–Weibull [14], Dhillon-exponential power [15], and Mustapha–Badamasi modified Weibull [16], among others. The family of distributions given by (1) was introduced in [17].

$$F\left(x\right)=1-e^{-\alpha H(x;\zeta )},\alpha >0.$$

(1)

where $H(x;\zeta )$ is a non-negative monotonically increasing function, $x\in \mathbb{R}$, and $\zeta$ is a parameter vector. Different $H(x;\zeta )$ include some statistical models such as the following: $H\left(x\right)=x$ gives the exponential; $H\left(x\right)=x^2,$ Rayleigh; $H\left(x\right)=log(x/a),$ Pareto; $H\left(x\right)=a^{-1}(e^{ax}-1),$ Gompertz; $H\left(x\right)=x^{\beta },$ Weibull; $H\left(x\right)=x^{\beta }{e}^{\lambda x},$ modified Weibull [18]; $H\left(x\right)=e^{\lambda x-\beta /x},$ flexible Weibull [19]; and $H\left(x\right)=(e^{{(x/\alpha )}^{\beta }}-1),$ modified Weibull extension [20]. This innovation extends the classical Weibull model. However, this method has limitations due to the restricted set of suitable functions $H(x;\zeta )$ that are non-negative and monotonically increasing. Therefore, it is necessary to extend the method and provide alternative approaches.

Objectives and Paper Organization

Our target is to investigate the pivotal role of the function in (1), represented as $\alpha H(x;\zeta )$, to decompose it into two separate components: one exhibiting monotonic growth on ${\mathbb{R}}^{+}$ and the other confined within a unit interval to allow us to develop a novel hybrid-G class of models. This approach will pave the way for more adaptable models and offer fresh insights into data modeling and applied statistical research. Such innovation introduces novel statistical methods for data analysis, among other benefits. This development will exemplify the dynamic evolution of statistical distributions in adapting to complex data analysis needs and demonstrate the ongoing evolution and adaptation in statistical modeling to meet practical demands.

(i)

We explored the key characteristics and practical illustrations of the proposed family, as well as various computational approaches and procedures for its implementation. This model not only facilitates the development of new probability models but also integrates with data simulation processes.

(ii)

A special member called hybrid-Weibull–exponential is discussed extensively. Mathematical and statistical properties such as shape properties, moments, mean residual life, information measures, order statistics, model identifiability, and stress–strength (SS) reliability are explored.

(iii)

The maximum likelihood estimation (MLE) method for parameter estimation is considered, and comprehensive simulation studies are conducted to rigorously assess the performance of the MLEs. We also employ nonparametric bootstrap techniques to construct confidence intervals and evaluate coverage probabilities associated with the SS-parameter.

(iv)

To illustrate the practical effectiveness of the hybrid family, three real-world applications are explored for illustration.

The advantage of extended models is allowing for flexible modeling of data with a variety of shapes. The parameters controlled the skewness or heavy-tailed characteristics of the model, providing additional flexibility to accommodate highly skewed data and various failure rates. Different probability models serve different purposes and represent different data generation processes; as such, the proposed model can be a better alternative to various distributions.

The subsequent contents of the article are structured as follows: In Section 2, we propose the hybrid-W-G family of distributions and some useful properties. In Section 3, a special member called hybrid-Weibull–exponential is proposed and discussed. Properties such as moments, mean residual life, order statistics, information measure, and model identifiability are explored. In Section 4, the maximum likelihood estimation and simulation studies are presented. In Section 5, the stress–strength reliability parameter and its maximum likelihood estimation together with bootstrap confidence interval are studied, and a simulation analysis is performed. In Section 6, we present the applications of the hybrid-Weibull–exponential. Conclusions of the study are placed in Section 7.

2. The Proposed Hybrid Model

Let $G(x;\zeta )\in (0,1)$ preferably be any valid cumulative distribution function (CDF), where $\zeta$ is a parameter vector in ${\mathbb{R}}^n$. We proposed the use of an increasing function defined as $w(x;\xi )\in (c,\infty )$, where $c\ge 0$ and $\xi$ is a parameter vector in ${\mathbb{R}}^n$. The proposed hybrid family of distribution is defined as

$$F(x;\xi ,\zeta )=1-e^{-w(x;\xi )G(x;\zeta )}.$$

(2)

The model should be called the hybrid-w-G family of distributions. For example, if $w(x;\xi )={\displaystyle \frac{1}{1-G\left(x\right)}}$, we have an odd-G family, and $w(x;\xi )$ ranges from $c=1$ to $\infty .$ Hence, it is necessary to provide some possible $w(x;\xi )$ to facilitate the model generating process and naming, and also to provide the opportunity of introducing various $w(x;\xi )$. Table 2 gives some possible $w(x;\xi )$ with their names and ranges for $a,b,\alpha ,\beta >0$.

Table 2. Some possible $w(x_i;\xi )$ functions and ranges.

Name	$\mathit{w}(\mathit{x};\mathit{\xi });\mathit{x}\in {\mathbb{R}}^{+}$	Range
Exponential	$\alpha x$	$(0,\infty )$
Exponent	$e^{\alpha x}$	$(1,\infty )$
Weibull	$\alpha x^{\beta }$	$(0,\infty )$
Extended Power	$a{x}^{\beta }+bx,a,b>0$	$(0,\infty )$
Hybrid-odd	${\displaystyle \frac{1}{1-G_2(x;\xi )}}$	$(1,\infty )$
Sine	${\displaystyle \frac{1}{sin\left(\frac{\pi }{2}(1-G(x;\xi ))\right)}}$	$(1,\infty )$
Cosine	${\displaystyle \frac{1}{cos\left(\frac{\pi }{2}G(x;\xi )\right)}}$	$(1,\infty )$
Tangent	${\displaystyle \frac{1}{tan\left(\frac{\pi }{4}(1-G(x;\xi ))\right)}}$	$(1,\infty )$

Note: The hybrid-odd-w-G implies using different baseline CDF as $w(x;\xi )G(x;\zeta )={\displaystyle \frac{G_1(x;\zeta )}{1-G_2(x;\xi )}}$—that is, $w(x;\xi )={\displaystyle \frac{1}{1-G_2(x;\xi )}}.$

The corresponding probability density function (PDF), reliability function (RF), and failure rate function (FRF) of the hybrid-w-G are given, respectively, as

$$\begin{array}{cc}\hfill f\left(x\right)& =[w^{\prime }(x;\xi )G(x;\zeta )+w(x;\xi )g(x;\zeta )]e^{-w(x;\xi )G(x;\zeta )},\hfill \\ \hfill R\left(x\right)& =e^{-w(x;\xi )G(x;\zeta )},\hfill \\ \hfill h\left(x\right)& =w^{\prime }(x;\xi )G(x;\zeta )+w(x;\xi )g(x;\zeta ).\hfill \end{array}$$

Moments and Mean Residual Life

Obtaining the mathematical characteristics of probability distributions holds significant importance for a numerous of reasons. Foremost among these is the capability to devise multiple statistical measures and to complexly regard the behaviors exhibited by the hybrid-w-G family. The moments of a probability distribution are essential tools in statistics for summarizing the shape and characteristics of distributions. The moments, including mean, variance, skewness, and kurtosis, provide insights into the central tendency, dispersion, asymmetry, and peakedness of the distribution. We can obtain the $r^{th}$ moments of X having hybrid-w-G:

$$\begin{array}{cc}\hfill E\left[X^r\right]& ={\int }_{-\infty }^{\infty }{x}^r[w^{\prime }(x;\xi )G(x;\zeta )+w(x;\xi )g(x;\zeta )]e^{-w(x;\xi )G(x;\zeta )}dx\hfill \\ \hfill & =\sum _{i=1}^{\infty }{\displaystyle \frac{{(-1)}^i}{i!}}{\int }_{-\infty }^{\infty }{x}^r{w}^{\prime }(x;\xi )w^i(x;\xi )G^{i+1}(x;\zeta )dx\hfill \\ \hfill & +\sum _{i=1}^{\infty }{\displaystyle \frac{{(-1)}^i}{i!}}{\int }_{-\infty }^{\infty }{x}^r{w}^{i+1}(x;\xi )G^i(x;\zeta )g(x;\zeta )dx.\hfill \end{array}$$

The mean residual life (MRL) at a given time t is a statistical measure representing the expected remaining lifetime or duration until an event of interest, given survival up to time t. It is a crucial concept in survival analysis and reliability engineering, offering insights into the longevity or reliability of a component or system beyond a specified point in time. The MRL of hybrid-w-G is given by

$${\mu }_X\left(t\right)={\displaystyle \frac{1}{R\left(t\right)}}{\int }_t^{\infty }{e}^{-w(x;\xi )G(x;\zeta )}dx={\displaystyle \frac{1}{R\left(t\right)}}\sum _{i=1}^{\infty }{\displaystyle \frac{{(-1)}^i}{i!}}{\int }_t^{\infty }{w}^i(x;\xi )G^i(x;\zeta )dx.$$

In the next section, we will discuss a special member of the hybrid-w-G and some of its important properties, namely, the hybrid-Weibull–exponential distributions.

3. The Hybrid-Weibull–Exponential (HWE)

The hybrid-Weibull–exponential is derived by taking $w(x_i;\alpha ,\beta )=\alpha x^{\beta }$ and $G(x;\lambda )=1-e^{-\lambda x}$ as the exponential distribution CDF; hence, HWE has PDF, $R\left(x\right)$, and FRF as

$$f\left(x\right)=\alpha \left[\beta x^{\beta -1}(1-e^{-\lambda x})+\lambda x^{\beta }{e}^{-\lambda x}\right]e^{-\alpha x^{\beta }(1-e^{-\lambda x})},$$

(3)

$$R\left(x\right)=e^{-\alpha x^{\beta }(1-e^{-\lambda x})},$$

(4)

and

$$h\left(x\right)=\alpha \beta x^{\beta -1}-\alpha \beta x^{\beta -1}{e}^{-\lambda x}+\alpha \lambda x^{\beta }{e}^{-\lambda x},$$

(5)

respectively.

Theorem 1. 

The FRF of the HWE in (5) can be unimodal with mode at $x_0={\displaystyle \frac{2\beta [2+(\beta -1\left)\right]}{\lambda [2-\beta (\beta -1\left)\right]}},$ for $\beta \le 1.$

Proof. 

This was proved by obtaining $h^{\prime }\left(x\right).$ The derivative of $h\left(x\right)$ is obtained as

$$h^{\prime }\left(x\right)=\alpha x^{\beta -2}{e}^{-\lambda x}\left[\beta (\beta -1)e^{\lambda x}-\beta (\beta -1)+2\beta \lambda x-{\lambda }^2{x}^2\right].$$

Some roots can be obtain by solving the following:

$${\displaystyle \frac{{\lambda }^2}{\beta (\beta -1)}}{x}^2-{\displaystyle \frac{2\lambda }{(\beta -1)}}x-e^{\lambda x}+1=0.$$

Since it has many roots—and thus, to obtain at least one root—it can be expressed as

$${\displaystyle \frac{{\lambda }^2}{\beta (\beta -1)}}{x}^2-{\displaystyle \frac{2\lambda }{(\beta -1)}}x-\left[1+\lambda x+{\displaystyle \frac{{\lambda }^2{x}^2}{2}}+\sum _{i=3}^{\infty }{\displaystyle \frac{{\lambda }^i{x}^i}{i!}}\right]+1=0.$$

For $i=2,$ we obtain

$${\displaystyle \frac{{\lambda }^2[2-\beta (\beta -1)]}{2\beta (\beta -1)}}{x}^2-{\displaystyle \frac{\lambda [2+(\beta -1\left)\right]}{(\beta -1)}}x=0.$$

Hence,

$$x={\displaystyle \frac{2\beta [2+(\beta -1\left)\right]}{\lambda [2-\beta (\beta -1\left)\right]}},$$

and $\beta \le 1.$    □

Figure 1 displays some possible shapes of the PDF and FRF of the HWE distribution for some parameter values.

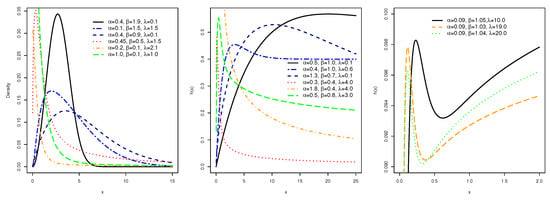
Figure 1. Graphical illustrations of PDF and FRF of HWE model for some selected parameters.

3.1. HWE Data Generating Process

To generate a dataset that follows HWE, we need the following alternative process since HWE does not have a closed form quantile function. The quantile function $q\left(u\right)$ of the HWE is essential for random sampling and other statistical studies regarding HWE, and it is possible to use the Markov chain Monte Carlo (MCMC) method or employ an alternative specified technique to achieve this goal, as shown below. The CDF of the HWE is given as

$$F\left(x\right)=1-e^{-\alpha x^{\beta }(1-e^{-\lambda x})}.$$

(6)

The quantiles, $q\left(u\right)=X$ of HWE, are the exact solution of the following equation. The solution can be obtained using numerical root-finding methods like Newton–Raphson; an alternative function called inverseCDF in the package named HDInterval [21] in R-software (version 4.3.2) can be used to obtain the solution. The inverseCDF used a uniroot function, which provides an implementation of Newton–Raphson for finding the root of an equation in a given interval.

$$log[1-u]=\alpha x^{\beta }(e^{-\lambda x}-1).$$

(7)

To produce a random sample from the proposed HWE, we present some useful steps in Algorithm 1 as follows:

Algorithm 1 HWE random sample procedure

1.    Select $\alpha ,\beta ,\lambda ,$

2.    Generate $u_i\sim U(0,1),i=1,2,\cdots ,n$,

3.    Apply $u_i$ from 2 to evaluate $x_i$ by solving         $log[1-u_i]=\alpha x_i^{\beta }(e^{-\lambda x_i}-1)$.

Under the quantile function, we subsequently discussed the skewness and kurtosis of the proposed HWE, which require the use of Algorithm 1. Bowley’s skewness (Bo) and Moor’s kurtosis (Mo) are quantile-based measures, respectively, defined as

$$Bo={\displaystyle \frac{q\left(\frac{3}{4}\right)-2q\left(\frac{2}{4}\right)+q\left(\frac{1}{4}\right)}{q\left(\frac{3}{4}\right)-q\left(\frac{1}{4}\right)}},\mathit{and}Mo={\displaystyle \frac{q\left(\frac{7}{8}\right)-q\left(\frac{5}{8}\right)+q\left(\frac{3}{8}\right)-q\left(\frac{1}{8}\right)}{q\left(\frac{6}{8}\right)-q\left(\frac{2}{8}\right)}}.$$

Figure 2 shows that for fixed $\alpha =1,$ the skewness is decreasing then increasing as both $\beta$ and $\lambda$ increase in the interval $[0.2,5]$; meanwhile, the kurtosis is also decreasing then increasing as both $\beta$ and $\lambda$ increase in $[1,6].$

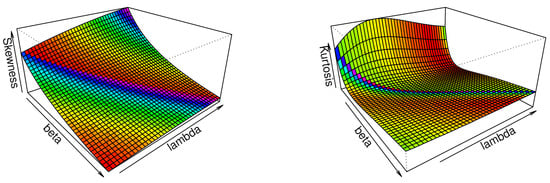
Figure 2. Plots of the Bo and Mo for the HWE model for fixed $\alpha =1$.

3.2. Moments

From the rth moments of HWE, we can obtain some characteristics including mean and variance, among others. The rth moment of HWE is derived as

$$\begin{array}{cc}\hfill E\left[X^r\right]& ={\int }_0^{\infty }{x}^r\alpha \left[\beta x^{\beta -1}(1-e^{-\lambda x})+\lambda x^{\beta }{e}^{-\lambda x}\right]e^{-\alpha x^{\beta }(1-e^{-\lambda x})}dx\hfill \\ \hfill & ={\displaystyle \sum _{i=0}^{\infty }}{\displaystyle \sum _{j=0}^{i+1}}{\displaystyle \frac{{(-1)}^{i+j}}{i!}}\left(\genfrac{}{}{0pt}{}{i}{j}\right){\alpha }^{i+1}\beta {\int }_0^{\infty }{x}^{\beta (i+1)+r-1}{e}^{-\lambda jx}dx\hfill \\ \hfill & +{\displaystyle \sum _{i=0}^{\infty }}{\displaystyle \sum _{j=0}^i}{\displaystyle \frac{{(-1)}^{i+k}}{i!}}\left(\genfrac{}{}{0pt}{}{i}{k}\right){\alpha }^{i+1}\lambda {\int }_0^{\infty }{x}^{\beta (i+1)+r-1}{e}^{-\lambda (k+1)x}dx\hfill \\ \hfill & ={\displaystyle \sum _{i=0}^{\infty }}{\displaystyle \sum _{j=0}^{i+1}}{\rho }_{i,j}^{\left(1\right)}\Gamma (\beta (i+1)+r)+{\displaystyle \sum _{i=0}^{\infty }}{\displaystyle \sum _{j=0}^i}{\rho }_{i,k}^{\left(2\right)}\Gamma (\beta (i+1)+r).\hfill \end{array}$$

(8)

where ${\rho }_{i,j}^{\left(1\right)}={\displaystyle \frac{{(-1)}^{i+j}{\alpha }^{i+1}\beta \left(\genfrac{}{}{0pt}{}{i}{j}\right)}{i!{\left[\lambda j\right]}^{\beta (i+1)+r}}}$ and ${\rho }_{i,k}^{\left(2\right)}={\displaystyle \frac{{(-1)}^{i+k}{\alpha }^{i+1}\lambda \left(\genfrac{}{}{0pt}{}{i}{k}\right)}{i!{\left[\lambda (k+1)\right]}^{\beta (i+1)+r}}}.$ Also, $\Gamma (·)$ is a gamma function. The mean $\left(E\right[X\left]\right)$ and variance $Var=E\left[X^2\right]-{\left(E\left[X\right]\right)}^2$ of the HWE can be obtained from (8) by setting $r=1$ and $r=2.$ Figure 3 shows that for fixed $\alpha =1,$ the mean of the HWE is decreasing when both $\beta$ and $\lambda$ are increasing in the interval $[0.8,20];$ also, the variance is decreasing when both $\beta$ and $\lambda$ are increasing in $[0.9,5].$

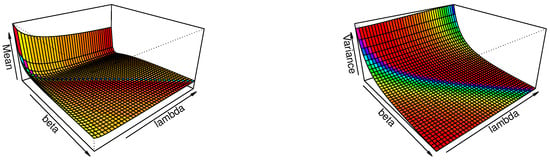
Figure 3. Plots of mean (left) and variance (right) for the HWE model for fixed $\alpha =1$.

3.3. Mean Residual Life and Asymptotic Behavior

In reliability engineering, statistical mechanics, and survival analysis, the mean residual life (MRL) is a key measure with broad applications. It represents the expected remaining lifetime of a system or entity at a given time, serving as an essential tool for evaluating the durability and performance of components, ranging from mechanical systems to software. The MRL for the HWE can be determined by solving the following integral:

$$\begin{array}{cc}\hfill {\mu }_X\left(t\right)& ={\displaystyle \frac{1}{R\left(t\right)}}{\int }_t^{\infty }{e}^{-\alpha x^{\beta }(1-e^{-\lambda x})}dx={\displaystyle \frac{1}{R\left(t\right)}}\sum _{i=0}^{\infty }\sum _{j=0}^i{\displaystyle \frac{{(-1)}^{i+j}{\alpha }^i\left(\genfrac{}{}{0pt}{}{i}{j}\right)}{i!}}{\int }_t^{\infty }{x}^{\beta i}{e}^{-\lambda jx}dx\hfill \\ \hfill & ={\displaystyle \frac{1}{R\left(t\right)}}\sum _{i=0}^{\infty }\sum _{j=0}^i{\displaystyle \frac{{(-1)}^{i+j}{\alpha }^i\left(\genfrac{}{}{0pt}{}{i}{j}\right)}{i!{\left[\lambda j\right]}^{\beta i+1}}}\Gamma (\beta i+1,t\lambda j).\hfill \end{array}$$

The MRL and FRF exhibit an inverse relationship, as they characterize different aspects of the same survival behavior. Mathematically, the MRL can be expressed using the FRF through the equation $s\left(t\right)=e^{\left[-{\int }_0^{t}h\left(x\right)dx\right]}.$ Furthermore, there exists another mathematical relationship between the MRL and FRF $h\left(t\right)$, defined as $h\left(t\right)=[{\mu }_X^{\prime }\left(t\right)+1]/{\mu }_X\left(t\right).$ It is evident that ${\mu }_X^{\prime }\left(t\right)\ge -1.$ The MRL and FRF uniquely determine a probability distribution, as discussed in [22,23]. Additionally, ref. [24] established the following relationships: an increasing MRL implies a decreasing FRF, while a decreasing MRL implies an increasing FRF. Moreover, [25] demonstrated that an upside-down bathtub-shaped MRL corresponds to a bathtub-shaped FRF. In addition, [26] highlighted that the MRL and FRF have a reciprocal relationship expressed as ${lim}_{t\to \infty }{\mu }_X\left(t\right)={lim}_{t\to \infty }{\displaystyle \frac{1}{h\left(t\right)}}.$ Consequently, a bathtub-shaped MRL implies an upside-down bathtub-shaped FRF. Figure 4 provides a graphical illustration of several relationships between the MRL and FRF for the proposed model at possible t.

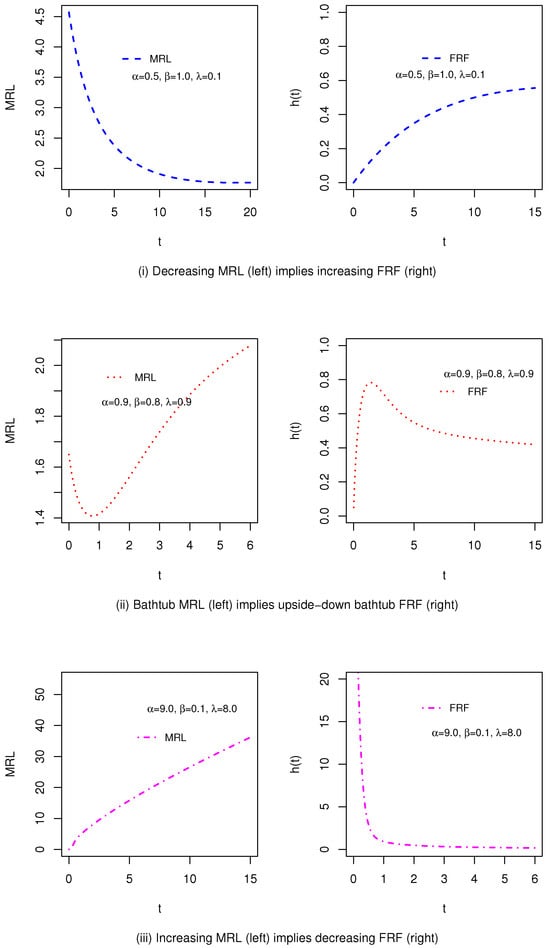
Figure 4. Graphical presentation demonstrating the reciprocal relationship between the MRL and FRF of the proposed model for some selected parameters shown in (i–iii).

The asymptotic behavior of the MRL is a key tool for evaluating the long-term reliability of systems. It is particularly useful in complex engineering applications, providing insights into the evolution of system reliability over time, especially for aging or deteriorating components.

Theorem 2. 

The asymptote of the MRL of HWE as $t\to \infty$ is

$${\mu }_X\left(t\right)\sim {\displaystyle \frac{e^{\alpha t^{\beta }}}{{\alpha }^{\frac{1}{\beta }}\beta }}\Gamma ({\displaystyle \frac{1}{\beta }},\alpha t^{\beta }).$$

(9)

Proof. 

Let us find the asymptote of $R\left(x\right)$ in (4),

$$\underset{x\to \infty }{lim}R\left(x\right)\sim e^{-\alpha x^{\beta }}.$$

Therefore, as $t\to \infty$,

$${\mu }_X\left(t\right)=E(X-t|X>t)={\int }_0^{\infty }{\displaystyle \frac{R(x+t)}{R\left(t\right)}}dx\sim e^{\alpha t^{\beta }}{\int }_0^{\infty }{e}^{-\alpha {(x+t)}^{\beta }}dx.$$

Setting $u=\alpha {(x+t)}^{\beta },$ we obtain

$${\mu }_X\left(t\right)\sim {\displaystyle \frac{e^{\alpha t^{\beta }}}{{\alpha }^{\frac{1}{\beta }}\beta }}{\int }_{\alpha t^{\beta }}^{\infty }{u}^{{\displaystyle \frac{1}{\beta }}-1}{e}^{-u}du={\displaystyle \frac{e^{\alpha t^{\beta }}}{{\alpha }^{\frac{1}{\beta }}\beta }}\Gamma ({\displaystyle \frac{1}{\beta }},\alpha t^{\beta }).$$

   □

Figure 5 displays how good the asymptote of the MRL of HWE can be used to approximate the actual MRL of the HWE in some possible scenarios using some selected parameter values.

Figure 5. Plots of the MRL and asymptote of the MRL of the HWE model.

3.4. Order Statistics and Asymptotic Behavior

Let $X_1,X_2,\cdots ,X_n$, $n\ge 1$ describe an ordered HWE sample; the j-th order statistics PDF is designated by $f_{j:n}\left(x\right)$:

$$\begin{array}{c}\hfill f_{X_{j:n}}\left(x\right)=\sum _{m=0}^{n-j}{\displaystyle \frac{n!{(-1)}^{m}f\left(x\right)F^{j+m-1}\left(x\right)}{(j-1)!(n-j-m)!m!}}.\end{array}$$

(10)

Therefore, for $F\left(x\right)$ in (6) and $f\left(x\right)$ in (3), we have

$$\begin{array}{cc}\hfill f_{X_{j:n}}\left(x\right)& =\sum _{m=0}^{n-j}{\displaystyle \frac{\alpha n!{(-1)}^m\left[\beta x^{\beta -1}(1-e^{-\lambda x})+\lambda x^{\beta }{e}^{-\lambda x}\right]}{(j-1)!(n-j-m)!m!}}\hfill \\ \hfill & \times e^{-\alpha x^{\beta }(1-e^{-\lambda x})}{\left(1-e^{-\alpha x^{\beta }(1-e^{-\lambda x})}\right)}^{j+m-1}.\hfill \end{array}$$

Thus, $f_{X_{j:n}}\left(x\right)$ can be written as a series of exponentiated-HWE with parameters $j+m-1,\alpha ,\beta$, and $\lambda$ as

$$f_{X_{j:n}}\left(x\right)=\sum _{m=0}^{n-j}{\displaystyle \frac{n!{(-1)}^{m}f(x;j+m-1,\alpha ,\beta ,\lambda )}{(j+m-1)(j-1)!(n-j-m)!m!}}.$$

The asymptotic distributions for the extreme order statistics, i.e., the minimum $X_{1:n}$ and maximum $X_{n:n}$ from $X_1,\dots ,X_n$ following HWE are built as follows. For more details and examples, one can see [27].

Theorem 3. 

Let $X_1,\cdots ,X_n$ be a random sample from HWE and let $B_n=(X_{n:n}-a_n)/b_n$; then, $B_n\stackrel{d}{\to }B$ implies that

$$\underset{n\to \infty }{lim}P(B_n\le x)=G\left(x\right)=e^{-e^{-x}},$$

$\vee x\in \Re$ of $G\left(x\right)$ is continuous; $a_n=q(1-n^{-1})$ and $b_n=E[X-a_n|X>a_n]$ can be derived according to Theorem 8.3.4 of [27], where $q(·)$ is the quantile function.

Proof. 

To follow Theorem 8.3.2 of [27], we start by considering the limit of the MRL in (9) with some algebra, we have

$$\underset{t\to \infty }{lim}E(X-t|X>t)\sim \underset{t\to \infty }{lim}{\displaystyle \frac{{\left(\alpha t^{\beta }\right)}^{\frac{1}{\beta }-1}}{{\alpha }^{\frac{1}{\beta }}\beta }}\underset{t\to \infty }{lim}{\displaystyle \frac{\Gamma (\frac{1}{\beta },\alpha t^{\beta })}{e^{-\alpha t^{\beta }}{\left(\alpha t^{\beta }\right)}^{\frac{1}{\beta }-1}}}=\underset{t\to \infty }{lim}{\displaystyle \frac{t^{1-\beta }}{\alpha \beta }}.$$

Thus, we can use the above result in Theorem 8.3.2 of [27] as

$$\underset{t\to \infty }{lim}{\displaystyle \frac{R(t+xE(X-t|X>t))}{R\left(t\right)}}\sim \underset{t\to \infty }{lim}{\displaystyle \frac{e^{-\alpha {\left(t+{\left(\alpha \beta \right)}^{-1}x{t}^{1-\beta }\right)}^{\beta }}}{e^{-\alpha t^{\beta }}}}\sim e^{-x}.$$

Clearly, if $\beta =1,$ the result holds; also, by binomial expansion with the power of $\beta \ge 2$ and a natural number, the result holds too.    □

Theorem 4. 

Let $X_1,\cdots ,X_n$ be a random sample from HWE and let $B_n^{*}=(X_{1:n}-a_n^{*})/b_n^{*}$; then, $B_n^{*}\stackrel{d}{\to }{B}^{*}$ is equivalent to saying

$$\underset{n\to \infty }{lim}P(B_n^{*}\le x)=G^{*}\left(x\right)=1-e^{-x^{\beta +1}},$$

for every point $x\in {\Re }^{+}$ of $G^{*}\left(x\right)$ for which $G^{*}\left(x\right)$ is continuous. From Theorem 8.3.6 of [27], $a_n^{*}=0$ and $b_n^{*}=q\left({\displaystyle \frac{1}{n}}\right)$, where $q(·)$ is the quantile function.

Proof. 

We start by

$$\underset{x\to 0}{lim}F\left(x\right)\sim \alpha x^{\beta }(1-e^{-\lambda x})\sim \alpha \lambda x^{\beta +1}.$$

By Theorem 8.3.6 of [27], we can consider

$$\underset{t\to 0}{lim}{\displaystyle \frac{F\left(tx\right)}{F\left(t\right)}}\sim \underset{t\to 0}{lim}{\displaystyle \frac{\alpha \lambda {\left(tx\right)}^{\beta +1}}{\alpha \lambda t^{\beta +1}}}=x^{\beta +1}.$$

   □

3.5. Extropy and Cumulative Residual Entropy

The concept of entropy, widely utilized in information theory and other scientific domains, serves as a measure of uncertainty associated with the occurrence of a specific event, given partial information about the event or system. Entropy plays a crucial role in a variety of studies. In this context, we introduce the notions of extropy and cumulative residual entropy. Recently, ref. [28] proposed a novel measure of randomness for a random variable, termed extropy (Ex), which is also regarded as the complement dual of Shannon entropy. For a recent application of Ex, see [29]. The Ex is defined as $Ex=-{\displaystyle \frac{1}{2}}{\int }_{-\infty }^{\infty }{f}^2\left(x\right)dx$, while the cumulative residual entropy (CRE) is given by $CRE=-{\int }_{-\infty }^{\infty }R\left(x\right)logR\left(x\right)dx$, where $R\left(x\right)$ denotes the reliability function.

• The Ex for the HWE is calculated as

  $$Ex=\sum _{k=0}^2\sum _{i=0}^{\infty }\sum _{j=0}^{k+i}{\psi }_{i,j,k}(\alpha ,\beta ,\lambda )\Gamma (\beta (i+2)-k+1).$$

  where ${\psi }_{i,j,k}(\alpha ,\beta ,\lambda )=\left(\genfrac{}{}{0pt}{}{2}{k}\right)\left(\genfrac{}{}{0pt}{}{k+i}{j}\right){\displaystyle \frac{{(-1)}^{i+j+1}{\alpha }^{2+i}{2}^i{\beta }^k{\lambda }^{2-k}}{2i!{\left[\lambda (j+2-k)\right]}^{\beta (i+2)-k+1}}}.$
• The CRE of the HWE model is derived as

  $$CRE=\sum _{i=0}^{\infty }\sum _{j=0}^{i+1}{\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{i+1}{j}\right){(-1)}^{i+j}{\alpha }^{i+1}}{{\left[\lambda j\right]}^{\beta (i+1)+1}i!}}\Gamma (\beta (i+1)+1).$$

Next, we discuss the nature of the above measures when the parameters values are growing. Figure 6 illustrated that for a fixed $\alpha =1,$ the Ex is decreasing when both $\beta$ and $\lambda$ are increasing in the interval $[0.001,5];$ further, the CRE decreases as both $\beta$ and $\lambda$ increase within the interval $[0.8,5].$

Figure 6. Plots of the Ex and CRE of the HWE for a fixed value of $\alpha =1$.

3.6. Identifiability of the HWE

Assessing the identifiability of a distribution with respect to its parameters involves determining whether sufficient information exists to differentiate between distinct parameter values within the distribution. The Kullback–Leibler divergence (KLD) is a widely used method for examining parameter identifiability, as highlighted by [30]. In this study, we outline the standard criterion for evaluating identifiability in statistical distributions as follows:

Let $\Lambda (\mathit{t},\mathit{\gamma })$ be a statistical model. The parameter $\mathit{\gamma }\in {\mathbf{R}}^d$ is locally (globally) identifiable if and only if $\mathit{\gamma }$ is the unique solution of the equation $KLD(\mathit{\gamma },\mathit{\delta })=0in{\mathbf{R}}^d$ (an open neighborhood of $\mathit{\gamma }$), where

$$KLD(\mathit{\gamma },\mathit{\delta })={\mathbb{E}}_{\mathit{\gamma }}\left(log{\displaystyle \frac{\Lambda (\mathit{t},\mathit{\gamma })}{\Lambda (\mathit{t},\mathit{\delta })}}\right)=\int \Lambda (\mathit{t},\mathit{\gamma })log{\displaystyle \frac{\Lambda (\mathit{t},\mathit{\gamma })}{\Lambda (\mathit{t},\mathit{\delta })}}\mathrm{dt}$$

(11)

Note that $KLD(\mathit{\gamma },\mathit{\delta })\ge 0$ for all $\mathit{\delta }$. Furthermore, $KLD(\mathit{\gamma },\mathit{\delta })=0⟺\Lambda (\mathit{t},\mathit{\gamma })=\Lambda (\mathit{t},\mathit{\delta })$ almost everywhere for $\mathit{t}\in {\mathbf{R}}^d$. However, it is important to highlight that obtaining an analytical solution for (11) is often challenging due to the complexity of many density functions; see [30,31] for more details.

In this study, we define and compute the equation $KLD(\mathit{\gamma },\mathit{\delta })$ for our model numerically. Suppose we have two random variables, $X_1\sim \mathrm{HWE}\left(\mathit{\gamma }\right)$ and $X_2\sim \mathrm{HWE}\left(\mathit{\delta }\right)$, where $\mathit{\gamma }={({\alpha }^{\circ },{\beta }^{\circ },{\lambda }^{\circ })}^{\prime }$ and $\mathit{\delta }={({\alpha }^{*},{\beta }^{*},{\lambda }^{*})}^{\prime }$. Then, based on (11), we can express

$$\begin{array}{cc}\hfill KLD(\mathit{\gamma },\mathit{\delta })& ={\mathbb{E}}_{\mathit{\gamma }}\left(log{\displaystyle \frac{f_1\left(\mathit{x}\right|\mathit{\gamma })}{f_2\left(\mathit{x}\right|\mathit{\delta })}}\right)\hfill \\ \hfill & ={\int }_0^{\infty }{f}_1\left(x\right|\mathit{\gamma })log\left[f_1\left(x\right|\mathit{\gamma })\right]dx-{\int }_0^{\infty }{f}_1\left(x\right|\mathit{\gamma })log\left[f_2\left(x\right|\mathit{\delta })\right]dx.\hfill \end{array}$$

(12)

By substituting the PDFs of $f_1$ and $f_2$ into (12), we obtain

$$\begin{array}{cc}\hfill KLD(\mathit{\gamma },\mathit{\delta })& ={\int }_0^{\infty }{\alpha }^{\circ }\left[{\beta }^{\circ }{x}^{{\beta }^{\circ }-1}(1-e^{-{\lambda }^{\circ }x})+{\lambda }^{\circ }{x}^{{\beta }^{\circ }}{e}^{-{\lambda }^{\circ }x}\right]e^{-{\alpha }^{\circ }{x}^{{\beta }^{\circ }}(1-e^{-{\lambda }^{\circ }x})}\hfill \\ \hfill & \times log\left[{\alpha }^{\circ }\left[{\beta }^{\circ }{x}^{{\beta }^{\circ }-1}(1-e^{-{\lambda }^{\circ }x})+{\lambda }^{\circ }{x}^{{\beta }^{\circ }}{e}^{-{\lambda }^{\circ }x}\right]e^{-{\alpha }^{\circ }{x}^{{\beta }^{\circ }}(1-e^{-{\lambda }^{\circ }x})}\right]dx\hfill \\ \hfill & -{\int }_0^{\infty }{\alpha }^{\circ }\left[{\beta }^{\circ }{x}^{{\beta }^{\circ }-1}(1-e^{-{\lambda }^{\circ }x})+{\lambda }^{\circ }{x}^{{\beta }^{\circ }}{e}^{-{\lambda }^{\circ }x}\right]e^{-{\alpha }^{\circ }{x}^{{\beta }^{\circ }}(1-e^{-{\lambda }^{\circ }x})}\hfill \\ \hfill & \times log\left[{\alpha }^{*}\left[{\beta }^{*}{x}^{{\beta }^{*}-1}(1-e^{-{\lambda }^{*}x})+{\lambda }^{*}{x}^{{\beta }^{*}}{e}^{-{\lambda }^{*}x}\right]e^{-{\alpha }^{*}{x}^{{\beta }^{*}}(1-e^{-{\lambda }^{*}x})}\right]dx.\hfill \end{array}$$

(13)

Here, $\mathit{\gamma }$ and $\mathit{\delta }$ represent vectors of real values derived from ${(\alpha ,\beta ,\lambda )}^{\prime }$. Solving (13) analytically may be infeasible; therefore, we adopt a numerical approach using the one-dimensional integral function in R-software by selecting specific cases to examine identifiability. We consider three cases of $\mathit{\gamma }$:

• Case I: $\mathit{\gamma }={({\alpha }^{\circ }=1.5,{\beta }^{\circ }=1.2,{\lambda }^{\circ }=3.0)}^{\prime }$.
• Case II: $\mathit{\gamma }={({\alpha }^{\circ }=0.5,{\beta }^{\circ }=0.9,{\lambda }^{\circ }=0.8)}^{\prime }$.
• Case III: $\mathit{\gamma }={({\alpha }^{\circ }=5.0,{\beta }^{\circ }=8.0,{\lambda }^{\circ }=12.0)}^{\prime }$.

Also, we form eight different $\mathit{\delta }$ based on the cases I, II, and III, where $\mathit{\gamma }\ne \mathit{\delta }$ in the seventh cases and $\mathit{\gamma }=\mathit{\delta }$ in the eighth case. The computed results for all cases are presented in Table 3. The results indicate that $KLD(\mathit{\gamma },\mathit{\delta })>0$ in the first seven cases, while it equals zero when $\mathit{\gamma }=\mathit{\delta }$. These findings substantiate the identifiability of the HWE. However, we acknowledge that these specific cases are not enough to generalize conclusions about the local or global identifiability of the HWE based on its parameters.

Table 3. Numerical evaluation of identifiability of the HWE model based on some parameters values (13).

Case I	Hypothesis $\mathit{\gamma }\mathbf{\ne }\mathit{\delta }$ and $\mathit{\gamma }=\mathit{\delta }$	$\mathit{KLD}$(γ, δ)	Absolute Error
1	${\alpha }^{\circ }\ne {\alpha }^{*},{\beta }^{\circ }={\beta }^{*}$, ${\lambda }^{\circ }={\lambda }^{*}$	$0.07213>0$	$1.9\times {10}^{-05}$
2	${\alpha }^{\circ }={\alpha }^{*},{\beta }^{\circ }\ne {\beta }^{*}$, ${\lambda }^{\circ }={\lambda }^{*}$	$0.63184>0$	$7.8\times {10}^{-05}$
3	${\alpha }^{\circ }={\alpha }^{*},{\beta }^{\circ }={\beta }^{*}$, ${\lambda }^{\circ }\ne {\lambda }^{*}$	$0.001113>0$	$6.9\times {10}^{-05}$
4	${\alpha }^{\circ }\ne {\alpha }^{*},{\beta }^{\circ }\ne {\beta }^{*}$, ${\lambda }^{\circ }={\lambda }^{*}$	$0.21883>0$	$7.3\times {10}^{-05}$
5	${\alpha }^{\circ }\ne {\alpha }^{*},{\beta }^{\circ }={\beta }^{*}$, ${\lambda }^{\circ }\ne {\lambda }^{*}$	$0.02205>0$	$8.2\times {10}^{-05}$
6	${\alpha }^{\circ }={\alpha }^{*},{\beta }^{\circ }\ne {\beta }^{*}$, ${\lambda }^{\circ }\ne {\lambda }^{*}$	$0.02658>0$	$6.0\times {10}^{-05}$
7	${\alpha }^{\circ }\ne {\alpha }^{*},{\beta }^{\circ }\ne {\beta }^{*}$, ${\lambda }^{\circ }\ne {\lambda }^{*}$	$0.35663>0$	$4.0\times {10}^{-05}$
8	${\alpha }^{\circ }={\alpha }^{*},{\beta }^{\circ }={\beta }^{*}$, ${\lambda }^{\circ }={\lambda }^{*}$	0	0
Case II
1	${\alpha }^{\circ }\ne {\alpha }^{*},{\beta }^{\circ }={\beta }^{*}$, ${\lambda }^{\circ }={\lambda }^{*}$	$2.39056>0$	$0.00011$
2	${\alpha }^{\circ }={\alpha }^{*},{\beta }^{\circ }\ne {\beta }^{*}$, ${\lambda }^{\circ }={\lambda }^{*}$	$2.84839>0$	$7.3\times {10}^{-05}$
3	${\alpha }^{\circ }={\alpha }^{*},{\beta }^{\circ }={\beta }^{*}$, ${\lambda }^{\circ }\ne {\lambda }^{*}$	$0.03128>0$	$6.6\times {10}^{-05}$
4	${\alpha }^{\circ }\ne {\alpha }^{*},{\beta }^{\circ }\ne {\beta }^{*}$, ${\lambda }^{\circ }={\lambda }^{*}$	$11.69699>0$	$0.0014$
5	${\alpha }^{\circ }\ne {\alpha }^{*},{\beta }^{\circ }={\beta }^{*}$, ${\lambda }^{\circ }\ne {\lambda }^{*}$	$1.14845>0$	$0.000011$
6	${\alpha }^{\circ }={\alpha }^{*},{\beta }^{\circ }\ne {\beta }^{*}$, ${\lambda }^{\circ }\ne {\lambda }^{*}$	$2.89721>0$	$7.3\times {10}^{-05}$
7	${\alpha }^{\circ }\ne {\alpha }^{*},{\beta }^{\circ }\ne {\beta }^{*}$, ${\lambda }^{\circ }\ne {\lambda }^{*}$	$12.15810>0$	$0.00120$
8	${\alpha }^{\circ }={\alpha }^{*},{\beta }^{\circ }={\beta }^{*}$, ${\lambda }^{\circ }={\lambda }^{*}$	0	0
Case III
1	${\alpha }^{\circ }\ne {\alpha }^{*},{\beta }^{\circ }={\beta }^{*}$, ${\lambda }^{\circ }={\lambda }^{*}$	$1.40259>0$	$7.1\times {10}^{-06}$
2	${\alpha }^{\circ }={\alpha }^{*},{\beta }^{\circ }\ne {\beta }^{*}$, ${\lambda }^{\circ }={\lambda }^{*}$	$3.381249>0$	$1.3\times {10}^{-05}$
3	${\alpha }^{\circ }={\alpha }^{*},{\beta }^{\circ }={\beta }^{*}$, ${\lambda }^{\circ }\ne {\lambda }^{*}$	$1.42533>0$	$6.5\times {10}^{-06}$
4	${\alpha }^{\circ }\ne {\alpha }^{*},{\beta }^{\circ }\ne {\beta }^{*}$, ${\lambda }^{\circ }={\lambda }^{*}$	$2.03998>0$	$1.9\times {10}^{-05}$
5	${\alpha }^{\circ }\ne {\alpha }^{*},{\beta }^{\circ }={\beta }^{*}$, ${\lambda }^{\circ }\ne {\lambda }^{*}$	$1.35215>0$	$1.2\times {10}^{-05}$
6	${\alpha }^{\circ }={\alpha }^{*},{\beta }^{\circ }\ne {\beta }^{*}$, ${\lambda }^{\circ }\ne {\lambda }^{*}$	$3.63908>0$	$1.4\times {10}^{-05}$
7	${\alpha }^{\circ }\ne {\alpha }^{*},{\beta }^{\circ }\ne {\beta }^{*}$, ${\lambda }^{\circ }\ne {\lambda }^{*}$	$3.32781>0$	$2.2\times {10}^{-05}$
8	${\alpha }^{\circ }={\alpha }^{*},{\beta }^{\circ }={\beta }^{*}$, ${\lambda }^{\circ }={\lambda }^{*}$	0	0

4. Estimation

In this section, MLE is used for parameter estimation and to aid in model comparison. Let $x_1,\cdots ,x_n$ be observed values from a sample of size n that follow the proposed hybrid-w-G. Let $\mathbf{\Theta }={(\xi ,\zeta )}^T$; then, the MLEs of $\mathbf{\Theta }$—that is, $\widehat{\mathbf{\Theta }}={(\widehat{\xi },\widehat{\zeta })}^T$—can be obtained by the maximization of $L\left(\mathrm{\Theta }\right):$

$$logL=\sum _{i=1}^{n}log[w^{\prime }(x_i;\xi )G(x_i;\zeta )+w(x_i;\xi )g(x_i;\zeta )]-\sum _{i=1}^{n}w(x_i;\xi )G(x_i;\zeta ).$$

(14)

Alternatively, maximizing the following equations can be accomplished using an iterative method such as Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm through the maxLik package in R software [32].

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial logL}{\partial \xi }}& =\sum _{i=1}^n{\displaystyle \frac{w^{\prime }{(x_i;\xi )}^{{\xi }^{\prime }}G(x_i;\zeta )+w{(x_i;\xi )}^{{\xi }^{\prime }}g(x_i;\zeta )}{w^{\prime }(x_i;\xi )G(x_i;\zeta )+w(x_i;\xi )g(x_i;\zeta )}}-\sum _{i=1}^{n}w{(x_i;\xi )}^{{\xi }^{\prime }}G(x_i;\zeta )\hfill \\ \hfill {\displaystyle \frac{\partial logL}{\partial \zeta }}& =\sum _{i=1}^n{\displaystyle \frac{w^{\prime }(x_i;\xi )G{(x_i;\xi )}^{{\xi }^{\prime }}+w(x_i;\xi )g{(x_i;\xi )}^{{\xi }^{\prime }}}{w^{\prime }(x_i;\xi )G(x_i;\zeta )+w(x_i;\xi )g(x_i;\zeta )}}-\sum _{i=1}^{n}w(x_i;\xi )G{(x_i;\zeta )}^{{\zeta }^{\prime }}.\hfill \end{array}$$

where ${\displaystyle \frac{\partial }{\partial \xi }}\left({\displaystyle \frac{\partial w}{\partial x}}\right)=w^{\prime }{(x_i;\xi )}^{{\xi }^{\prime }}$. The asymptotic distribution of the estimator $\widehat{\mathbf{\Theta }}$ can be approximated by $N_{p+q}(0,{\widehat{J}}^{-1})$, a multivariate normal, provided the standard boundary conditions for the parameters are satisfied. Here, p and q represent the number of parameters associated with the components $\xi$ and $\zeta$, respectively. The matrix J in this context is defined as the Hessian matrix of the $L\left(\mathbf{\Theta }\right)$, with its elements given by the second-order partial derivatives:

$$J_{ij}={\displaystyle \frac{{\partial }^{2}logL\left(\mathbf{\Theta }\right)}{\partial {\mathbf{\Theta }}_i\partial {\mathbf{\Theta }}_j}},\mathrm{for}i,j=1,\dots ,p+q.$$

where ${\mathbf{\Theta }}_r$ and r denote the $r^{\mathrm{th}}$ parameter in the vector $\mathbf{\Theta }$, an asymptotic confidence interval (ACI) can be constructed. The confidence interval provides an estimate of the range within which the true value of ${\mathbf{\Theta }}_r$ is expected to lie with a specified level of confidence, denoted by $100(1-ϵ)\%$. This interval is derived as

$$AC{I}_r=\left({\mathbf{\Theta }}_r\pm {\omega }_{ϵ/2}\sqrt{{\widehat{J}}_{rr}}\right).$$

where ${\widehat{J}}_{rr}$ is the $(r,r)$th diagonal element of the inverse Hessian matrix ${\widehat{J}}^{-1}$, which represents the estimated variance of ${\mathbf{\Theta }}_r$. ${\omega }_{ϵ/2}$ is the $(1-ϵ/2)$ quantile of the standard normal distribution, providing the critical value for the specified confidence level.

This approach ensures that the confidence intervals are asymptotically valid, meaning that they are reliable when the sample size is sufficiently large. The use of the Hessian matrix, a critical component in the computation, reflects the curvature of the log-likelihood function, thereby encapsulating information about parameter variability. Such intervals are particularly useful in assessing the precision of parameter estimates in complex models where analytical solutions may not be feasible.

Simulation Results I

In this section, we assess the MLEs for the parameters of the HWE. Following the procedures outlined in Section 3.1, we generate some moderate random samples of sizes $n=50,100,150,200$ from the HWE using specific parameters and replicate this process $N=1000$ times. The selected parameters allow us to explore a variety of distributional behaviors (shape), which we assumed to capture a broad range of possible scenarios relevant to various applications. For each sample, we compute the MLEs, and evaluate their biases and mean squared errors (MSEs). As evident from Table 4 and Table 5, the bias tends to decrease as the sample size grows, often approaching zero. This trend suggests that the accuracy of the estimates increases with larger sample sizes. Additionally, the MSE consistently diminishes as the sample size expands, indicating an overall enhancement in the precision and reliability of the estimates with increasing sample sizes. Particularly, we observe that when $\alpha =1.4,\beta =0.6$, and $\lambda =1.8$, the estimates converge well as n increases, with a noticeable decrease in bias and MSE. For lower values of $\alpha$ and $\lambda$, such as $\alpha =0.3,\beta =0.5$, and $\lambda =0.3$, estimates remain close to the true values even for smaller n and exhibit low MSEs. For small sample sizes ($n=50$), the estimates tend to have noticeable bias and higher MSE. Parameters such as $\lambda =1.0$ and $\lambda =0.6$ show instability at smaller n, but this improves significantly by $n=100$ or more. The estimation of $\beta$ appears more stable across different values of n.

Table 4. Simulation results for HWE: the average estimate (AE), MSE, and Bias in parenthesis-I.

n		$\alpha =1.1$	$\beta =0.5$	$\lambda =1.1$	$\alpha =1.4$	$\beta =0.6$	$\lambda =1.8$
50	AE	1.1647	0.5215	1.0525	1.9986	0.6703	1.5355
	MSE	0.7286	0.0421	0.6053	0.1876	0.0895	0.7451
	Bias	(1.0647)	(0.0215)	(0.9525)	(3.5986)	(0.0703)	(0.7355)
100		1.2153	0.5234	1.4455	1.5015	0.6379	1.9396
		0.6799	0.0217	0.5096	0.1236	0.0569	0.2240
		(0.1153)	(0.0234)	(0.3455)	(1.1015)	(0.0379)	(0.3996)
150		1.1779	0.5088	1.2756	1.8160	0.6488	1.6290
		0.2454	0.0137	0.5017	0.1173	0.0452	0.1857
		(0.0779)	(0.0088)	(0.1756)	(0.4160)	(0.0488)	(0.3690)
200		1.1249	0.5155	1.2585	1.4845	0.6326	1.6060
		0.0865	0.0097	0.3963	0.0861	0.0357	0.0780
		(0.0249)	(0.0155)	(0.1585)	(0.2845)	(0.0326)	(0.2660)
n		$\alpha =0.4$	$\beta =0.6$	$\lambda =1.0$	$\alpha =0.5$	$\beta =0.5$	$\lambda =0.5$
50		0.4686	0.6129	1.1136	0.5993	0.5249	0.7617
		0.2696	0.0208	0.7570	0.7640	0.0217	1.4837
		(0.0686)	(0.0129)	(2.4136)	(0.0993)	(0.0249)	(0.2617)
100		0.4207	0.6112	1.0092	0.5410	0.5175	0.7202
		0.0324	0.0106	0.3579	0.6182	0.0102	1.3801
		(0.0207)	(0.0112)	(0.3092)	(0.0410)	(0.0175)	(0.2202)
150		0.4117	0.6082	0.9483	0.5087	0.5086	0.5573
		0.0310	0.0064	0.2896	0.0194	0.0055	0.0523
		(0.0117)	(0.0082)	(0.2483)	(0.0087)	(0.0086)	(0.0573)
200		0.4091	0.6059	0.7651	0.5045	0.5086	0.5580
		0.0093	0.0048	0.0877	0.0134	0.0046	0.0142
		(0.0091)	(0.0059)	(0.0651)	(0.0045)	(0.0086)	(0.0580)
n		$\alpha =0.6$	$\beta =0.5$	$\lambda =0.6$	$\alpha =0.3$	$\beta =0.5$	$\lambda =0.3$
50		0.6297	0.5232	0.9092	0.3227	0.5219	0.4598
		0.2717	0.0170	1.8623	0.0422	0.0128	0.7901
		(0.1297)	(0.0232)	(0.3092)	(0.0227)	(0.0219)	(0.1598)
100		0.5216	0.5139	0.7284	0.3114	0.5077	0.4754
		0.0917	0.0087	0.3203	0.0131	0.0057	0.6813
		(0.0216)	(0.0139)	(0.1284)	(0.0114)	(0.0077)	(0.1754)
150		0.5123	0.5078	0.6834	0.3032	0.5084	0.3400
		0.0222	0.0053	0.2814	0.0062	0.0040	0.0688
		(0.0123)	(0.0078)	(0.0834)	(0.0032)	(0.0084)	(0.0400)
200		0.5090	0.5040	0.6375	0.3036	0.5057	0.3211
		0.0111	0.0035	0.0435	0.0047	0.0029	0.0140
		(0.0090)	(0.0040)	(0.0375)	(0.0036)	(0.0057)	(0.0211)
n		$\alpha =0.8$	$\beta =0.8$	$\lambda =0.8$	$\alpha =0.4$	$\beta =0.6$	$\lambda =0.4$
50		0.7147	0.7650	1.0193	0.5665	0.6335	0.5399
		0.8917	0.0858	1.0267	1.7151	0.0321	0.4472
		(2.9147)	(−0.0350)	(0.2193)	(0.1665)	(0.0335)	(0.5399)
100		0.8418	0.7839	0.9830	0.4531	0.6103	0.5258
		0.5853	0.0592	0.6344	0.0893	0.0168	0.3194
		(1.0418)	(−0.0161)	(0.1830)	(0.0531)	(0.0103)	(0.1258)
150		1.3960	0.7783	0.9133	0.4310	0.6107	0.4760
		0.5329	0.0478	0.4175	0.0626	0.0115	0.0842
		(0.5960)	(−0.0217)	(0.1133)	(0.0310)	(0.0107)	(0.0760)
200		1.0949	0.7952	0.9480	0.4201	0.6079	0.4593
		0.4051	0.0371	0.4013	0.0464	0.0087	0.0655
		(0.2949)	(−0.0048)	(0.1480)	(0.0201)	(0.0079)	(0.0593)

Table 5. Simulation results for HWE: the average estimate (AE), MSE, and Bias in parenthesis-II.

n		$\alpha =0.1$	$\beta =0.5$	$\lambda =0.1$	$\alpha =0.4$	$\beta =0.6$	$\lambda =0.7$
50	AE	0.1044	0.5232	0.2293	0.5777	0.6131	1.1722
	MSE	0.0068	0.0087	1.2860	0.7409	0.0218	1.5306
	Bias	(0.0044)	(0.0232)	(0.3293)	(0.1777)	(0.0131)	(0.4722)
100		0.1023	0.5105	0.2808	0.4282	0.6058	0.9120
		0.0016	0.0039	1.2025	0.0599	0.0103	1.0262
		(0.0023)	(0.0105)	(0.1808)	(0.0282)	(0.0058)	(0.2120)
150		0.1006	0.5077	0.1517	0.4102	0.6081	0.8076
		0.0009	0.0026	0.0587	0.0174	0.0067	0.4280
		(0.0006)	(0.0077)	(0.0517)	(0.0102)	(0.0081)	(0.1076)
200		0.1019	0.5035	0.1203	0.4036	0.6091	0.7943
		0.0007	0.0019	0.0146	0.0088	0.0048	0.1282
		(0.0019)	(0.0035)	(0.0203)	(0.0036)	(0.0091)	(0.0943)
n		$\alpha =0.4$	$\beta =0.3$	$\lambda =0.5$	$\alpha =2.0$	$\beta =0.9$	$\lambda =0.9$
50		0.4072	0.3109	0.5049	2.3740	0.8766	1.1057
		0.0153	0.0031	0.9124	1.3627	0.0972	1.1911
		(0.0072)	(0.0109)	(0.1049)	(3.4740)	(−0.0234)	(0.2057)
100		0.4076	0.3031	0.4218	1.6541	0.8622	1.0649
		0.0077	0.0014	0.0190	0.7120	0.0777	0.8293
		(0.0076)	(0.0031)	(0.0218)	(1.7541)	(−0.0378)	(0.1649)
150		0.4017	0.3029	0.4200	1.7929	0.8673	1.0268
		0.0043	0.0008	0.0114	0.0845	0.0596	0.6346
		(0.0017)	(0.0029)	(0.0200)	(0.8929)	(−0.0327)	(0.1268)
200		0.4027	0.3025	0.4137	1.3375	0.8809	1.0378
		0.0036	0.0006	0.0096	0.0197	0.0471	0.5277
		(0.0027)	(0.0025)	(0.0137)	(0.4375)	(−0.0191)	(0.1378)
n		$\alpha =1.0$	$\beta =0.9$	$\lambda =0.3$	$\alpha =1.5$	$\beta =1.1$	$\lambda =1.1$
50		1.4472	0.8512	0.3481	1.5807	1.0737	1.2864
		0.6709	0.0949	0.1440	0.8743	0.1247	0.5345
		(1.1472)	(−0.0488)	(0.0481)	(4.4807)	(−0.0263)	(0.1864)
100		1.0783	0.8539	0.3353	1.4598	1.0450	1.2122
		0.4591	0.0722	0.0738	0.8636	0.0907	0.1647
		(0.7783)	(−0.0461)	(0.0353)	(2.3598)	(−0.0550)	(0.1122)
150		0.7613	0.8472	0.3092	1.5477	1.0681	1.2462
		0.5897	0.0540	0.0460	0.8000	0.0757	0.0507
		(0.4613)	(−0.0528)	(0.0092)	(1.4477)	(−0.0319)	(0.1462)
200		0.9864	0.8538	0.3067	1.7882	1.0840	1.2905
		0.3148	0.0465	0.0386	0.5194	0.0574	0.0201
		(0.2864)	(−0.0462)	(0.0067)	(0.6882)	(−0.0160)	(0.1905)
n		$\alpha =1.1$	$\beta =1.1$	$\lambda =1.1$	$\alpha =0.5$	$\beta =0.1$	$\lambda =0.5$
50		1.2415	1.1620	1.4288	0.5724	0.0504	0.6447
		0.0672	0.1382	0.9878	0.2326	0.0927	0.3110
		(0.9415)	(−0.0380)	(0.1288)	(0.4724)	(−0.0496)	(0.5447)
100		1.2692	1.1377	1.4034	0.5909	0.0472	0.6221
		0.0460	0.0992	0.5514	0.2018	0.0028	0.2776
		(0.9692)	(−0.0623)	(0.1034)	(0.4909)	(−0.0528)	(0.5221)
150		1.0112	1.1631	1.4532	0.5936	0.064	0.6122
		0.0379	0.0786	0.3995	0.1036	0.0020	0.2048
		(0.7112)	(−0.0369)	(0.1532)	(0.4936)	(−0.0536)	(0.5122)
200		1.0366	1.1696	1.4625	0.5032	0.0463	0.6060
		0.0148	0.0308	0.2053	0.0115	0.0002	0.1006
		(0.2366)	(−0.0304)	(0.1625)	(0.4932)	(−0.0537)	(0.5060)

5. Stress–Strength Reliability Parameter $R_s$

In mechanical reliability analysis, the stress–strength (SS) parameter, denoted as $R_s=P(X<Y)$, plays a vital role in evaluating system performance. This parameter represents the probability that the strength Y of a component exceeds the applied stress X, with system failure occurring when the stress surpasses the strength. Beyond its primary application in reliability studies, $R_s$ is also a critical measure for comparing two distinct populations, making it applicable across various fields [33]. These fields include engineering, biomedical sciences, and economics, where the parameter’s usage is well-documented. Research on the SS-parameter $R_s$, under the assumption that X and Y are independent random variables, spans multiple distribution models. Examples under various perspectives include the studies on the generalized-exponential distribution [34], inverse Pareto [35], Poisson half logistic [36], Weibull distribution [37,38], weighted exponential-Lindley [39], Weibull [40], two-parameter exponential [41], alpha power exponential [42], and bivariate iterated Farlie–Gumbel–Morgenstern [43], among others.

Next, we outline the formulation of a reliability parameter within the context of the HWE. Let X be a random variable with a density function $f_1(x;\alpha ,{\beta }_1,\lambda )$, and let Y be another random variable with a cumulative distribution function $F_2(y;\alpha ,{\beta }_2,\lambda )$, where X and Y are independent. The SS-reliability parameter is then obtained using the computations described in (8).

$$\begin{array}{cc}\hfill R_s& ={\int }_0^{\infty }{f}_1\left(x\right)F_2\left(x\right)dx\hfill \\ \hfill & =\alpha {\int }_0^{\infty }\left[{\beta }_1{x}^{{\beta }_1-1}(1-e^{-\lambda x})+\lambda x^{{\beta }_1}{e}^{-\lambda x}\right]\left(1-e^{-\alpha x^{{\beta }_2}(1-e^{-\lambda x})}\right)e^{-\alpha x^{{\beta }_1}(1-e^{-\lambda x})}dx,\hfill \end{array}$$

thus,

$$R_s=1-\left[\sum _{i,j,k=0}^{\infty }{\rho }_{i,j,k}^{\left(1\right)*}\Gamma ({\beta }_1(j+1)+{\beta }_{2}i)+\sum _{i,j,l=0}^{\infty }{\rho }_{i,j,l}^{\left(2\right)*}\Gamma ({\beta }_1(j+1)+{\beta }_{2}i+1)\right].$$

Here, ${\rho }_{i,j,k}^{\left(1\right)*}={\displaystyle \frac{{\beta }_1{\alpha }^{i+j+1}{(-1)}^{i+j+k}\left(\genfrac{}{}{0pt}{}{i+j+1}{k}\right)}{i!j!{\left[\lambda k\right]}^{{\beta }_1(j+1)+{\beta }_{2}i}}}$ and ${\rho }_{i,j,l}^{\left(2\right)*}={\displaystyle \frac{\lambda {\alpha }^{i+j}{(-1)}^{i+j+l}\left(\genfrac{}{}{0pt}{}{i+j}{l}\right)}{i!j!{\left[\lambda l\right]}^{{\beta }_1(j+1)+{\beta }_{2}i+1}}}.$

Consider the random variables $X_1,X_2,\dots ,X_n$, where $n\ge 1$, as a sample of independent observations drawn from the $HWE(\alpha ,{\beta }_1,\lambda )$ distribution, and $Y_1,Y_2,\dots ,Y_m$, where $m\ge 1$, as a sample of independent observations drawn from the $HWE(\alpha ,{\beta }_2,\lambda )$ distribution. The observed values of these samples are denoted by $x_1,x_2,\dots ,x_n$ and $y_1,y_2,\dots ,y_m$, respectively. Let $\theta ={(\alpha ,{\beta }_1,{\beta }_2,\lambda )}^T$ represent the vector of parameters, and let $\widehat{\theta }={(\widehat{\alpha },{\widehat{\beta }}_1,{\widehat{\beta }}_2,\widehat{\lambda })}^T$ denote the MLE of $\theta$. Further, let $\widehat{R_s}$ denote the estimator of $R_s$. The log-likelihood function is then expressed as

$$\begin{array}{cc}\hfill log{L}_{R_s}& =(n+m)log\alpha +\sum _{i=1}^{n}log\left[{\beta }_1{x}_i^{{\beta }_1-1}(1-e^{-\lambda x_i})+\lambda x_i^{{\beta }_1}{e}^{-\lambda x_i}\right]-\alpha \sum _{i=1}^n{x}_i^{{\beta }_1}(1-e^{-\lambda x_i})\hfill \\ \hfill & +\sum _{j=1}^{m}log\left[{\beta }_2{y}_j^{{\beta }_2-1}(1-e^{-\lambda y_j})+\lambda y_j^{{\beta }_2}{e}^{-\lambda y_j}\right]-\alpha \sum _{j=1}^m{y}_j^{{\beta }_2}(1-e^{-\lambda y_j})\hfill \end{array}$$

Similarly, this can be accomplished using an iterative approach, such as the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm, to solve the nonlinear equation provided below. This method is implemented through the maxLik package [32] in the R programming environment.

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial log{L}_{R_s}}{\partial \alpha }}={\displaystyle \frac{n+m}{\alpha }}-\sum _{i=1}^n{x}_i^{{\beta }_1}(1-e^{-\lambda x_i})-\sum _{j=1}^m{y}_j^{{\beta }_2}(1-e^{-\lambda y_j})\end{array}$$

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial log{L}_{R_s}}{\partial {\beta }_1}}& =\sum _{i=1}^n{\displaystyle \frac{x_i^{{\beta }_1-1}(1-e^{-\lambda x_i})+{\beta }_1{x}_i^{{\beta }_1-1}(1-e^{-\lambda x_i})log{x}_i+\lambda x_i^{{\beta }_1}(1-e^{-\lambda x_i})log{x}_i}{\left[{\beta }_1{x}_i^{{\beta }_1-1}(1-e^{-\lambda x_i})+\lambda x_i^{{\beta }_1}{e}^{-\lambda x_i}\right]}}\hfill \\ \hfill & -\alpha \sum _{i=1}^n{x}_i^{{\beta }_1}(1-e^{-\lambda x_i})log{x}_i\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial log{L}_{R_s}}{\partial {\beta }_2}}& =\sum _{j=1}^m{\displaystyle \frac{y_j^{{\beta }_2-1}(1-e^{-\lambda y_j})+{\beta }_2{y}_j^{{\beta }_2-1}(1-e^{-\lambda y_j})log{y}_j+\lambda y_j^{{\beta }_2}(1-e^{-\lambda y_j})log{y}_j}{\left[{\beta }_2{y}_j^{{\beta }_2-1}(1-e^{-\lambda y_j})+\lambda y_j^{{\beta }_2}{e}^{-\lambda y_j}\right]}}\hfill \\ \hfill & -\alpha \sum _{j=1}^m{y}_j^{{\beta }_2}(1-e^{-\lambda y_j})log{y}_j\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial log{L}_{R_s}}{\partial \lambda }}& =\sum _{i=1}^n{\displaystyle \frac{{\beta }_1{x}_i^{{\beta }_1-1}{x}_i{e}^{-\lambda x_i}+x_i^{{\beta }_1}{e}^{-\lambda x_i}+\lambda x_i^{{\beta }_1+1}{e}^{-\lambda x_i}}{\left[{\beta }_1{x}_i^{{\beta }_1-1}(1-e^{-\lambda x_i})+\lambda x_i^{{\beta }_1}{e}^{-\lambda x_i}\right]}}\hfill \\ \hfill & +\sum _{j=1}^m{\displaystyle \frac{{\beta }_2{y}_j^{{\beta }_2-1}{y}_j{e}^{-\lambda y_j}+y_j^{{\beta }_2}{e}^{-\lambda y_j}+\lambda y_j^{{\beta }_2+1}{e}^{-\lambda y_j}}{\left[{\beta }_2{y}_j^{{\beta }_2-1}(1-e^{-\lambda y_j})+\lambda y_j^{{\beta }_2}{e}^{-\lambda y_j}\right]}}\hfill \\ \hfill & -\alpha \sum _{i=1}^n{x}_i^{{\beta }_1+1}{e}^{-\lambda x_i}-\alpha \sum _{j=1}^m{y}_j^{{\beta }_2+1}{e}^{-\lambda y_j}\hfill \end{array}$$

5.1. Bootstrap Confidence Interval for $R_s$

In this section, we propose the use of two non-parametric bootstrap confidence intervals: the percentile bootstrap confidence interval and the student’s t bootstrap confidence interval, as described in [44]. Algorithm 2 outlines the steps required to compute the bootstrap confidence intervals. Additionally, a flowchart in Figure 7 is provided to facilitate a clearer understanding of the algorithm. Then, bootstrap CIs of $R_s$ can be obtained in the following:

Algorithm 2 Bootstrap confidence interval for $R_s$

1.     Simulate independent data $x_1,\dots ,x_n$ from the $HW{E}_1(\alpha ,{\beta }_1,\lambda )$.

2.     Simulate independent data $y_1,\dots ,y_m$ from the $HW{E}_2(\alpha ,{\beta }_2,\lambda )$.

3.     For $j=1$.

4.     Draw independent bootstrap samples: $x_1^{*},x_2^{*},\dots ,x_n^{*}$           and $y_1^{*},y_2^{*},\dots ,y_m^{*}$ by sampling with replacement from steps 1           and 2 in above.

5.     Determine the MLEs of $\theta$ from the bootstrap sample in 4,           say ${\widehat{\theta }}^{*\left(j\right)}={({\widehat{\alpha }}^{*\left(j\right)},{\widehat{\beta }}_1^{*\left(j\right)},{\widehat{\beta }}_2^{*\left(j\right)},{\widehat{\lambda }}^{*\left(j\right)})}^T$.

6.     Calculate the MLE of ${\widehat{R_s}}^{*\left(j\right)}\left({\widehat{\theta }}^{*\left(j\right)}\right)$ using MLEs in 5.

7.     Repeat step 4 to 6 B-times to get a set of bootstrap samples of ${\widehat{R_s}}^{*\left(j\right)}$.

8.     Set the samples in 7 in increasing order: ${\widehat{R_s}}^{*\left(1\right)}\le {\widehat{R_s}}^{*\left(2\right)},\dots ,\le {\widehat{R_s}}^{*\left(B\right)}.j=1,\dots ,B.$

9.     Obtain the bootstrap CI of $\widehat{R_s}$.

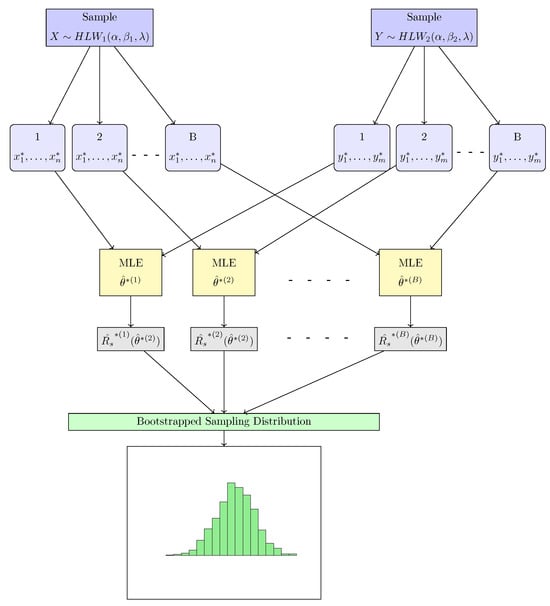
Figure 7. Flowchart demonstrating the bootstrap samples for the $\widehat{R_s}$.

5.1.1. Percentile Bootstrap Confidence Interval (BpCI):

Let ${\widehat{R_s}}_{\left(\delta \right)}^{*}$ be the $\delta$ percentile of ${\widehat{R_s}}_j^{*}$, $j=1,2,3,\dots ,B$—that is,

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{B}}\sum _{j=1}^B{I}_{\left\{{\widehat{R_s}}_j^{*}\le {\widehat{R_s}}_{\delta }^{*}\right\}}=\delta ,0<\delta <1\end{array}$$

where $I_{\{.\}}$ is an indicator function. A $100(1-ϵ)\%$ BpCI of $R_s$ is

$$\left({\widehat{R_s}}_{(ϵ/2)}^{*},{\widehat{R_s}}_{(1-ϵ/2)}^{*}\right).$$

5.1.2. Student’s t Bootstrap Confidence Interval (BtCI)

Let us set

$${\overline{\widehat{R_s}}}^{*}={\displaystyle \frac{1}{B}}\sum _{j=1}^B{\widehat{R_s}}_j^{*},se\left({\widehat{R_s}}^{*}\right)=\sqrt{{\displaystyle \frac{1}{B}}{\sum }_{j=1}^B{\left({\widehat{R_s}}_j^{*}-{\overline{\widehat{R_s}}}^{*}\right)}^2},$$

and ${\widehat{t}}_{\delta }^{*}$ be the $\delta$ percentile of $\left({\widehat{R_s}}_j^{*}-\widehat{R_s}\right)/se\left({\widehat{R_s}}^{*}\right)$, $j=1,2,\dots ,3$, such that

$${\displaystyle \frac{1}{B}}\sum _{j=1}^B{I}_{\left({\widehat{R_s}}_j^{*}-\widehat{R_s}\right)/se\left({\widehat{R_s}}^{*}\right)\le {\widehat{t}}_{\delta }^{*}}=\delta ,0<\tau <1,$$

with these, a $100(1-ϵ)\%$$BtCI$ of $R_s$ is given as

$$\left({\overline{\widehat{R_s}}}^{*}-{\widehat{t}}_{(ϵ/2)}^{*}se\left({\widehat{R_s}}^{*}\right),{\overline{\widehat{R_s}}}^{*}+{\widehat{t}}_{(ϵ/2)}^{*}se\left({\widehat{R_s}}^{*}\right)\right).$$

5.2. Simulation Results II

In this section, simulations are performed to evaluate the performance of the MLE for $R_s$ and the bootstrap confidence intervals (CIs) of $R_s$. Simulated samples of size 1000 were generated using Algorithm 1 for varied sample sizes and parameters from the distributions $HWE(\alpha ,{\beta }_1,\lambda )$ and $HWE(\alpha ,{\beta }_2,\lambda )$. Let n and m represent the sample sizes, respectively. The cases considered for $(n,m)$ are $(20,20)$, $(20,30)$, $(40,50)$, and $(60,60)$. The MLEs of $R_s$ were computed, and the standard deviation (SD), bias, and MSE of $R_s$ were analyzed. Additionally, a $95\%$ CI for $R_s$ was constructed using the non-parametric BpCI and the BtCI. The bootstrap procedure was carried out with $B=1000$ replications. The findings from the simulation study, summarized in Table 6, demonstrate notable trends as the sample sizes increase. Specifically, both the SD and the MSE of the estimates decrease, indicating improved precision and accuracy. Additionally, the estimated value of $R_s$ exhibits convergence towards its true value as the sample size grows, highlighting the consistency of the estimator. Moreover, the average length of the confidence interval (ALCI) for both bootstrap methods diminishes with larger sample sizes, reflecting tighter bounds around the estimates. This reduction in interval length is indicative of increased reliability in the parameter estimation. Importantly, the coverage probability (CP) progressively aligns with the nominal confidence level of $95\%$, demonstrating that the bootstrap methods maintain their validity under larger samples. These results collectively validate the robustness of the proposed methods in terms of both accuracy and reliability, especially as sample sizes grow. This behavior underscores the importance of larger datasets for achieving more precise and trustworthy statistical inferences.

Table 6. Parameter values, $R_s$, $\widehat{R_s}$ with (SD) below, MSE of $\widehat{R_s}$ with (bias) below, and ALCI with (CP) below in parenthesis.

($\mathit{\alpha },{\mathit{\beta }}_1,{\mathit{\beta }}_2,\mathit{\lambda }$)	${\mathit{R}}_{\mathit{s}}$	($\mathit{n},\mathit{m}$)	$\widehat{\mathit{R}}$(SD)	$\mathit{MSE}$(bias)	$\mathit{ALBpCI}$(CP)	$\mathit{ALBtCI}$(CP)
$(1.1,2.1,1.5,1.1)$	0.4965	(20,20)	0.4966	0.00026	0.0807	0.0836
			(0.0162)	(0.0012)	(0.98)	(0.99)
		(20,30)	0.4967	0.00021	0.0695	0.0719
			(0.01436)	(0.00020)	(0.98)	(0.98)
		(40,50)	0.4966	$8.015\times {10}^{-5}$	0.0422	0.0446
			(0.0089)	(0.00011)	(0.98)	(0.96)
		(60,60)	0.4965	$5.735\times {10}^{-5}$	0.0335	0.0355
			(0.0075)	($-3.165\times {10}^{-5}$)	(0.97)	(0.98)
$(2.0,3.0,1.0,1.5)$	0.6356	(20,20)	0.6374	0.0021	0.1821	0.1689
			(0.0459)	(0.0019)	(0.93)	(0.92)
		(20,30)	0.6342	0.0017	0.1606	0.1465
			(0.0407)	(−0.0036)	(0.94)	(0.91)
		(40,50)	0.6358	0.0008	0.1178	0.1098
			(0.0295)	(0.0003)	(0.95)	(0.93)
		(60,60)	0.6348	0.00067	0.1011	0.0956
			(0.0259)	(−0.00073)	(0.95)	(0.93)
$(1.9,0.9,0.8,0.8)$	0.5046	(20,20)	0.5050	0.00045	0.1008	0.0981
			(0.0213)	(0.0003)	(0.98)	(0.96)
		(20,30)	0.5059	0.00037	0.0875	0.0813
			(0.0192)	(0.0013)	(0.97)	(0.98)
		(40,50)	0.5056	0.00018	0.0562	0.0526
			(0.01333)	(0.0009)	(0.96)	(0.97)
		(60,60)	0.5047	0.00012	0.0456	0.0434
			(0.0108)	($4.665\times {10}^{-5}$)	(0.96)	(0.98)
$(1.5,1.5,1.9,1.5)$	0.4815	(20,20)	0.4817	0.00076	0.1232	0.1323
			(0.0276)	(0.00018)	(0.95)	(0.96)
		(20,30)	0.4832	0.00065	0.1075	0.1117
			(0.0254)	(0.0017)	(0.94)	(0.95)
		(40,50)	0.4818	0.00036	0.0734	0.0772
			(0.0189)	(0.00034)	(0.93)	(0.94)
		(60,60)	0.4801	0.00023	0.06121	0.0656
			(0.0152)	(−0.00095)	(0.95)	(0.96)
$(5.9,3.9,6.0,2.8)$	0.3074	(20,20)	0.3067	0.0059	0.3015	0.2887
			(0.0772)	(−0.00066)	(0.94)	(0.93)
		(20,30)	0.3069	0.0049	0.2732	0.2598
			(0.0702)	(−0.00051)	(0.94)	(0.93)
		(40,50)	0.3052	0.0028	0.2006	0.1943
			(0.0531)	(−0.0021)	(0.94)	(0.92)
		(60,60)	0.3087	0.0019	0.1735	0.1698
			(0.0444)	(0.0014)	(0.94)	(0.94)
$(1.0,1.0,1.0,1.0)$	0.500	(20,20)	0.4995	0.0028	0.0798	0.0806
			(0.0168)	(−0.0044)	(0.98)	(0.98)
		(20,30)	0.4998	0.0017	0.0668	0.0702
			(0.0134)	(−0.00018)	(0.98)	(0.96)
		(40,50)	0.4997	$9.014\times {10}^{-5}$	0.0418	0.0429
			(0.0095)	(−0.00029)	(0.97)	(0.98)
		(60,60)	0.4997	$5.599\times {10}^{-5}$	0.0324	0.0326
			(0.0075)	(−0.00025)	(0.96)	(0.97)
$(0.5,0.5,0.5,0.5)$	0.4999	(20,20)	0.4997	0.0022	0.1881	0.1906
			(0.4704)	(−0.0003)	(0.89)	(0.90)
		(20,30)	0.4948	0.0017	0.1615	0.1740
			(0.0409)	(−0.0052)	(0.91)	(0.93)
		(40,50)	0.5001	0.0008	0.1075	0.1109
			(0.0285)	(0.0001)	(0.92)	(0.94)
		(60,60)	0.5001	0.0006	0.0906	0.0903
			(0.0239)	(0.0006)	(0.92)	(0.93)
$(5.0,5.5,3.5,6.5)$	0.6993	(20,20)	0.7016	0.0058	0.2904	0.3032
			(0.0759)	(0.0023)	(0.93)	(0.94)
		(20,30)	0.7027	0.0049	0.2614	0.2683
			(0.0704)	(0.0034)	(0.93)	(0.93)
		(40,50)	0.6979	0.0028	0.1961	0.2009
			(0.0529)	(−0.0014)	(0.93)	(0.94)
		(60,60)	0.6999	0.0019	0.1683	0.1720
			(0.0130)	(0.0007)	(0.94)	(0.95)

6. Application

In this section, we demonstrate the performance of the HWE distribution through three applications to real datasets by comparing the HWE with several other existing distributions and in SS-analysis. We estimated the parameters of all competing models using MLE and evaluated the fitted models using various information criteria such as the Akaike information criterion (AIC), Bayesian information criterion (BIC), and consistent Akaike information criterion (CAIC). Additionally, we considered goodness-of-fit statistics including the Kolmogorov–Smirnov (KS), Anderson–Darling (A), and Cramer–von Mises (W) tests. The goodness of fit comparison involves distributions with the reliability function given in Table 7.

Table 7. Reliability function of the competing distributions $x,\alpha ,\beta ,\lambda ,\gamma >0$.

Distribution	R(x)
Modified Weibull (MW) [18]	$exp(-\alpha x^{\beta }{e}^{\lambda x})$
Exponentiated Weibull (EW) [45]	$1-{(1-e^{-\alpha x^{\beta }})}^{\lambda }$
Exponentiated sine Weibull (ESW) [46]	${sin}^{\alpha }\left({\displaystyle \frac{\pi }{2}}[1-e^{-\alpha x^{\beta }}]\right)$
Additive Weibull (AddW) [47]	$e^{-\alpha x^{\beta }-\lambda x^{\gamma }}$
Sarhan–Zaindin modified Weibull (SZW) [48]	$e^{-\alpha x-\lambda x^{\gamma }}$
Modified Weibull extension (MWE) [20]	$exp\left(\alpha \lambda (1-e^{{(x/\alpha )}^{\beta }})\right)$
Extended cosine Weibull (ESW) [49]	$1-{\left(1-cos\left({\displaystyle \frac{\pi }{2}}{e}^{-\alpha x^{\beta }}\right)\right)}^{\lambda }$

6.1. Fitting HWE and Other Weibull Based Models

This subsection evaluates the performance of the HWE distribution by fitting it to two real-world datasets: remission times of bladder cancer patients and failure times of specific components. The assessment is carried out by comparing HWE against several Weibull-related distributions using the aforementioned model selection criteria and goodness-of-fit measures.

6.1.1. First Dataset

The dataset consists of remission times from 128 bladder cancer patients, originally documented by [50]. We calculated the maximum likelihood estimates and detailed the numerical results for each model in Table 8 and Table 9. The findings demonstrate that the HWE distribution provides a better fit than the competing models.

Table 8. MLEs for first datasets.

Distribution	$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\lambda }$	$\mathit{\gamma }$
HWE	0.592 (0.6431)	0.5103 (0.2616)	0.0973 (0.08700)	-
W	0.0939 (0.0190)	1.0478 (0.0675)	-	-
MW	0.0939 (0.0172)	1.2 $\times {10}^{-7}$ (1.0035)	1.0478 (0.0955)	-
EW	0.4539 (0.2386)	0.6542 (0.1338)	2.7973 (1.2577)	-
AddW	0.0120 (5.2031)	1.0480 (0.1545)	0.0818(7.8070)	1.0477 (0.0415)
MWE	1.5 $\times {10}^5$ (0.5461)	1.0490 (0.8420)	1.6740 (0.1306)	-
ESW	2.7589 (1.0894)	0.6208 (0.1138)	0.2666 (0.1174)	-
ECSW	0.3199 (0.0282)	0.1749 (0.0001)	1.0030 (1.1 $\times {10}^6$)	-

Table 9. L, AIC, BIC, CAIC, A, W, KS, and p-value for first data sets.

Distribution	L	$\mathit{AIC}$	$\mathit{BIC}$	CAIC	A	W	$\mathit{KS}$(PV)
HWE	−409.80	825.61	834.17	825.80	0.1234	0.0174	0.0310 (0.9997)
W	−414.09	832.17	837.88	832.27	0.7817	0.1309	0.0701 (0.5552)
MW	−414.09	834.17	842.73	834.37	0.7815	0.1308	0.0704 (0.5507)
EW	−410.68	827.36	835.92	827.55	0.2885	0.0437	0.0450 (0.9578)
AddW	−414.09	836.17	847.58	836.49	0.1314	0.7863	0.0700 (0.5573)
MWE	−414.08	834.18	842.73	834.37	0.7831	0.1311	0.0710 (0.5388)
ESW	−410.48	826.95	835.51	827.15	0.2595	0.0394	0.0436 (0.9682)
ECSW	−413.44	832.88	841.44	833.07	0.6917	0.1154	0.0660 (0.6335)

In Table 9, the HWE distribution is notable for its log-likelihood value of $-409.80$, the most favorable among the models compared, indicating its superior fit to the data. The HWE distribution also excels in other statistical criteria and goodness-of-fit measures, achieving a balanced and effective representation of the data. Notably, it records the lowest values for AIC, CAIC, BIC, A, W, and KS among all considered distributions, strongly advocating for its appropriateness for this dataset. Furthermore, Figure 8 illustrates an exemplary match with the empirical data through the fitted PDF and survival functions, while Figure 9 includes a box plot and quantile–quantile (QQ) plot, affirming the HWE’s consistency with the observed data.

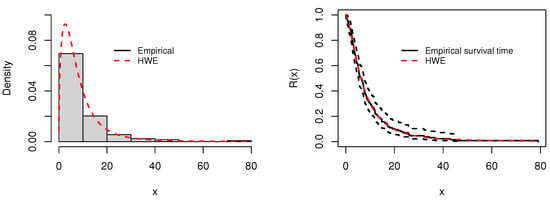
Figure 8. Plots of the histogram and fitted PDF (left), and empirical and fitted survival functions (right), for the first data.

Figure 9. Box plot (left) and quantile–quantile plot (right) for the first data.

6.1.2. Second Dataset

This dataset, initially reported in [51], consists of failure times for fifty components over 1000 h. Table 10 presents the MLEs for each model, while Table 11 shows that the HWE distribution provides a superior fit compared to other models. The HWE distribution consistently achieves more of the smallest values in the evaluative criteria and goodness-of-fit measures, positioning it as the first ranked model. This indicates its excellent capability to accurately represent the data, suggesting that it is the most appropriate model for these data according to these metrics. Additionally, to support our findings, Figure 10 illustrates the HWE’s excellent fit with the displayed fitted PDF and survival function. Furthermore, Figure 11 includes a box plot and a quantile–quantile (QQ) plot, demonstrating the HWE’s alignment with the data.

Table 10. MLEs for second dataset.

Distribution	$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\lambda }$	$\mathit{\gamma }$
HWE	(0.6015) (0.1123)	0.5989 (0.0785)	13.5171 (6.2122)	-
W	0.5412 (0.0995)	0.6611 (0.0747)	-	-
MW	0.4964 (0.0.0990)	0.5615 (0.0975)	0.0335 (0.0248)	-
EW	0.3859 (1.1141)	0.7698 (0.9441)	0.7856 (1.4754)	-
AddW	0.5289 (8.8612)	0.6611 (0.0830)	0.0124 (8.8614)	0.6603 (1.5778)
SZMW	0.4926 (0.1807)	0.6197 (0.1544)	0.0438 (0.1314)	-
MWE	21.4159 (7.0007)	0.5845 (0.0766)	0.1319 (0.0264)	-
ESW	0.4288 (0.7410)	1.1379 (1.5183)	0.0695 (0.3030)	-
ECSW	6.3682 (7.0763)	0.0528 (0.0582)	0.6489 (0.0744)	-

Table 11. L, AIC, BIC, CAIC, A, W, KS, and p-value for second datasets.

Distribution	L	$\mathit{AIC}$	$\mathit{BIC}$	CAIC	W	A	$\mathit{KS}$(PV)
HWE	−99.07	204.15	209.88	204.67	0.6765	0.1109	0.1122 (0.5186)
W	−102.36	208.73	212.55	208.98	0.9393	0.1507	0.1269 (0.3652)
MW	−101.36	208.73	214.46	209.25	0.8504	0.1300	0.1326 (0.3144)
EW	−102.37	210.71	216.45	211.23	0.9459	0.1499	0.1333 (0.3083)
AddW	−102.36	212.73	220.38	213.62	0.9393	0.1507	0.1270 (0.3642)
SZMW	−102.32	210.64	216.38	211.16	0.9304	0.1487	0.1278 (0.3563)
MWE	−101.94	209.88	215.62	210.40	0.8908	0.1402	0.1375 (0.2747)
ESW	−102.51	211.02	216.76	211.54	0.9417	0.1453	0.1504 (0.1877)
ECSW	−102.30	210.59	216.33	211.11	0.1489	0.9305	0.1289 (0.3471)

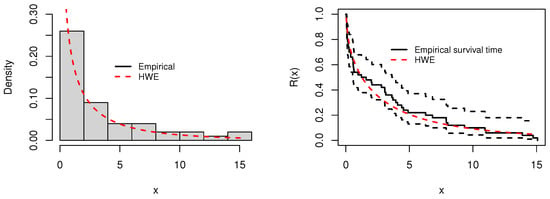
Figure 10. Plots of the histogram and fitted PDF (left), and empirical and fitted survival functions (right), for the second data.

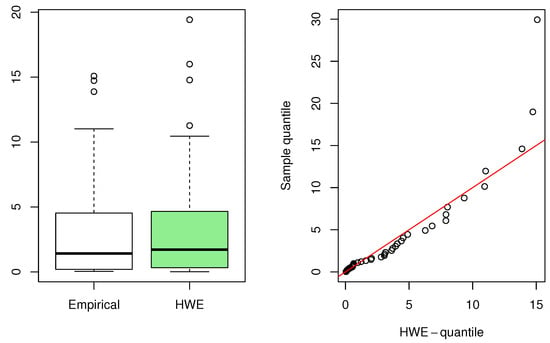
Figure 11. Box plot (left) and quantile–quantile plot (right) for the second data.

6.1.3. On the Performance of HWE on the Fitted Datasets

HWE performed well in comparison with the other models based on the presented datasets. HWE exhibits enhanced flexibility due to its three parameters: $\alpha$(scale), $\beta$ (shape), and $\lambda$ from the hybridization. This structure allows HWE to adapt to a wider range of shape behaviors, which are common in reliability and biomedical applications. Compared to classical models (e.g., Weibull, Exponential), the HWE model offers some key advantages: the term $(1-e^{-\lambda x})$ introduces an additional degree of flexibility in shaping the distribution’s tail. This helps to capture heavy-tailed or light-tailed behaviors, improving the fit for datasets exhibiting deviations from standard Weibull or Exponential assumptions. The hybrid structure can allows for a better trade-off between short-term and long-term failure risks, making it particularly suitable for lifetime and reliability data. In addition, the MLE adoption shows that HWE’s parameter estimates align well with the underlying dataset’s distributions by reducing model bias. Thus, based on the two datasets, we can say that the HWE can capture complex data structures better by balancing the flexibility of Weibull and exponential components while retaining interpretability in reliability and survival studies.

6.2. Third Dataset (Stress–Strength Reliability $\left(R_s\right)$)

In this section, we illustrate the applicability of the HWE model in reliability analysis by applying it to two real-world datasets. This demonstration highlights the practical utility of the proposed estimation techniques. The reliability parameter $R_s$ is estimated using the MLE method. Additionally, $95\%$ confidence intervals for $R_s$ are constructed using non-parametric bootstrap BpCI and BtCI, based on $B=1000$ bootstrap replications. To evaluate the fit of the HWE model to the datasets, the KS test is employed, providing a rigorous assessment of the model’s goodness-of-fit. The datasets, as described in [52], consist of two distinct types of measurements. The first dataset, denoted as X, corresponds to single fibers tested under tension at a gauge length of 10 mm, with a sample size of $n=63$. The second dataset, denoted as Y, pertains to impregnated tows of 1000 fibers tested at a gauge length of 20 mm, with a sample size of $m=69$.

This analysis not only validates the practical feasibility of the HWE model in handling real-world data but also demonstrates its capability in providing reliable estimates of $R_s$ and its associated confidence intervals. The application of the KS test further reinforces the suitability of the HWE model for these datasets, ensuring its robustness in SS-reliability studies.

The estimated values from the analysis are presented in Table 12. The results clearly demonstrate that the HWE model provides a good fit to both datasets, as indicated by the KS test for the $HW{E}_1(\alpha ,{\beta }_1,\lambda )$ distribution for dataset (X) and the $HW{E}_2(\alpha ,{\beta }_2,\lambda )$ distribution for dataset (Y). These findings suggest that the HWE model is a suitable candidate for reliability analysis. Figure 12 illustrates the empirical and fitted CDFs of the HWE model, along with the density of the estimated bootstrap values of $R_s$ for the datasets. Figure 13 displays the bootstrap estimates of $R_s$ and their density, which clearly approximate normality, demonstrating that the bootstrap CIs are reliable. Additionally, Figure 14 presents the profile log-likelihood of the estimated parameters, confirming the uniqueness of the maximum.

Table 12. MLEs, $L_{R_s}$, $R_s$, KS with p-value in parenthesis, and ALCI with $95\%$ CI within parentheses for the stress–strength dataset.

$\widehat{\mathit{\theta }}$	${\mathit{L}}_{{\mathit{R}}_{\mathit{s}}}$	${\mathit{HWE}}_1-\mathit{KS}$	${\mathit{HWE}}_2-\mathit{KS}$	$\widehat{{\mathit{R}}_{\mathit{s}}}$	$\mathit{BpCI}$	$\mathit{BtCI}$
$\widehat{\alpha }=0.00599$	111.4004	0.1057	0.0654	0.7299	0.1323	0.1284
$\widehat{{\beta }_1}=4.43233$		(0.45103)	(0.9107)		(0.6657, 0.7979)	(0.6657, 0.7941)
$\widehat{{\beta }_2}=5.43053$
$\widehat{\lambda }=0.62129$

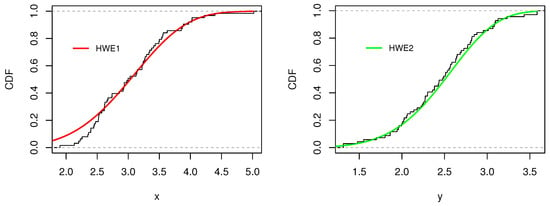
Figure 12. Plots of the empirical and fitted $HW{E}_1$ and $HW{E}_2$ models for the SS-datasets.

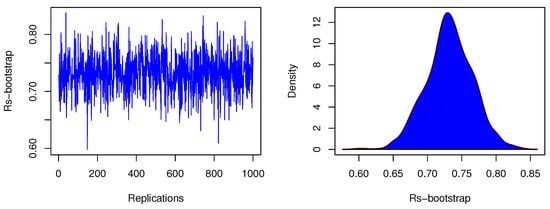
Figure 13. Plots illustrating the estimated bootstrap values of $R_s$ and their density for the SS-datasets.

Figure 14. Plots of the profile log-likelihood of the parameters for the SS-data.

7. Conclusions

In this paper, we introduced a novel hybrid family of distributions that includes a flexible set of hybrid functions to extend a variety of existing distributions. Another key contribution of this family is the three-parameter hybrid-Weibull–exponential distribution, for which we thoroughly investigated several core mathematical properties, including moments, random data generation procedures, MRL analyses that involve the study of its reciprocal relationship with FRF, and relevant asymptotic of the MRL. Additionally, we computed advanced information metrics such as the extropy and cumulative residual entropy, and derived order statistics along with their asymptotic behaviors. The model’s identifiability was further verified numerically using the Kullback–Leibler divergence; based on some selected parameters, the findings substantiate the identifiability of the HWE. Parameter estimation was performed via MLE, with extensive simulations assessing the performance of the MLEs in density estimation and SS-parameter studies. We also utilized nonparametric bootstrap techniques to construct confidence intervals and evaluate coverage probabilities for the SS-parameter. Notably, the MSE of the density estimates and the SS-parameter estimates decreased as sample size increased. Similarly, as sample size increases, the average width of nonparametric percentile and Student’s t bootstrap confidence intervals narrowed, and the coverage probabilities converged to the nominal $95\%$ level for the SS-parameter. We validated the practical effectiveness of this hybrid family using three real-world datasets. The HWE outperforms several prominent Weibull-based models in fitting the remission times of bladder cancer patients, and failure times for some components, as discussed based on AIC, BIC, CAIC, KS, A, and W metrics. Furthermore, HWE exhibited robust performance in the SS-parameter analysis of two sets of fiber data tested under tension at various gauge lengths, thus underscoring the potential of this hybrid family for advancing reliability and survival studies.

This research not only spotlights the versatility of the hybrid-w-G family in a broad range of statistical applications but also sets the stage for further theoretical and applied developments. Future work may focus on constructing additional hybrid-w-G distributions with different $w(x;\xi )$ and $G(x;\zeta )$ configurations, extending the inferential approaches (e.g., Bayesian methods), addressing censored data, and providing more analytical framework. In addition, several applied studies based on Weibull and other distributions (for instance, refs. [53,54,55]) can be advanced by considering members of the hybrid-w-G family as an alternative. The limitations of the hybrid-w-G family is that many members might have non-closed form quantile functions for random data generation, but this limitations was overcome using the package stated in Section 3.1.