Some Bounds for the Fragmentation Coefficient of Random Graphs

Abstract

Graph fragmentation aims to find the smallest vertex subset whose removal breaks a graph into components of bounded size. While this problem has applications in network dismantling and combinatorics, theoretical bounds on optimal solutions remain limited. We derive rigorous bounds for several graph classes, characterize hard instances, and illuminate the relationship between graph structure and optimal fragmentation strategies. Specifically, we show that for random d-regular graphs with n vertices, the minimal size of the fragmenting subset of nodes is asymptotically almost surely $\left|S\right|\ge {\displaystyle \frac{d-2}{2d-2}}n-o(n)$, and that asymptotically almost surely, $n-2\alpha (G)-o(n)\le \left|S\right|\le n-\alpha (G)+o(n)$, where $\alpha (G)$ is the independence number of G. For $d\gg 1$, we prove that asymptotically almost surely, $\left|S\right|/n\approx 1-logd/d$. However, we show that the line graphs of random regular graphs are considerably harder to fragment, with $\left|S\right|/n\ge 1-c/d$ for some constant c.

1. Introduction

Graph fragmentation is the removal of the smallest possible subset of a graph’s vertices such that all the connected components in the remaining graph are of small size. Equivalently, we may consider the largest induced subgraph in which none of its connected components is larger than that size. This problem has been studied in the context of network resilience in the field of complex networks and is known as network dismantling. Additionally, it has been studied in the combinatorics community, where it is known as graph fragmentation.

In recent years, a few heuristic algorithms have been developed to handle the dismantling problem in various types of networks [1]. Providing bounds for the size of the set to be removed may help evaluate the performance of these algorithms.

In this paper, we prove bounds on the graph fragmentation problem for several classes of graphs and discuss hard classes of instances to be fragmented.

A fundamental result by Janson and Thomason [2] considers the dependence of the number of vertices to be removed on the size of the remaining connected components in the context of random graphs. They show that the asymptotic fraction of the vertices to be removed in order to fragment the graph G into components of size at most k is essentially the same for all values of k that satisfy both $k\to \infty$ and $k=o(n)$, if G is a sparse random graph from the Erdős–Rényi model, henceforth denoted $G(n,p)$, or a random regular graph, denoted as $G_{n,d}$.

Edwards and Farr [3,4] addressed this question for some classes of graphs. They parameterized it by $ϵ$ for the fraction of the vertices to be removed and an upper bound C on the number of vertices in any connected component after removal. That is, a graph $G=(V,E)$ is $(ϵ,C)$-fragmentable if there exists $S\subseteq V$ with $\left|S\right|\le ϵ\left|V\right|$ such that every connected component of $G\backslash$S has at most C vertices. The set S is called the fragmenting set. A class of graphs $\mathrm{\Gamma }$ is $ϵ$-fragmentable if there is an integer C such that any member of $\mathrm{\Gamma }$ is $(ϵ,C)$-fragmentable. The coefficient of fragmentability$c_f(\mathrm{\Gamma })$ is defined as

$$c_f(\mathrm{\Gamma })=inf\{ϵ\mid \mathrm{\Gamma }\mathrm{is}ϵ\text{-}\mathrm{fragmentable}\}.$$

The general strategy taken in [3,4] was to remove vertices until a planar graph remains and then fragment it using separators. They were able to achieve the following bounds for ${\mathrm{\Gamma }}_d$, the class of graphs with maximum degree d, with $d\ge 2$:

$${\displaystyle \frac{d-2}{2d-2}}\le c_f({\mathrm{\Gamma }}_d)\le {\displaystyle \frac{d-2}{d+1}}.$$

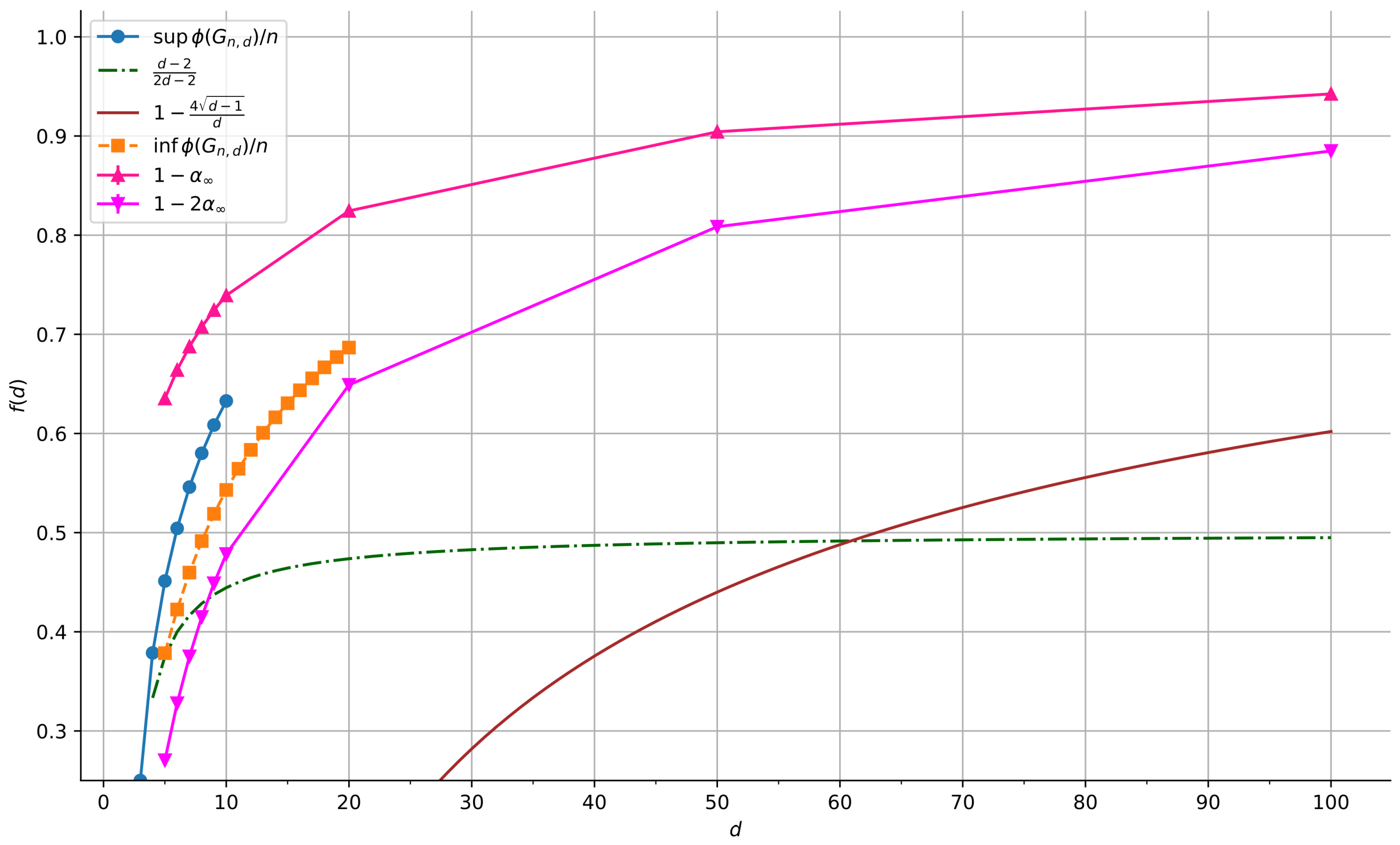
Similar bounds hold for the class of connected graphs of average degree d for a real $d\ge 2$, as well as for the class of graphs of average degree d for a real $d\ge 4$.

In [5], the same authors improved the upper bounds by replacing the fraction ${\displaystyle \frac{d-2}{d+1}}$ with a function $g(d)$, defined as follows: Set $g(2)=0$, $g(3)={\displaystyle \frac{1}{4}}$, and, for any integer $d\ge 4$,

$$g(d)=(d-2)g(d-1)+g(d-2)+1.$$

Then, they extended the definition to real numbers by linear interpolation—that is, for any integer $d\ge 2$ and real number r satisfying $0<r<1$, set $g(d+r)=(1-r)g(d)+rg(d+1)$. The following can then be shown:

• $g(d)<{\displaystyle \frac{d-2}{d+1}}$ for all $d>3$;
• $g(d)={\displaystyle \frac{d-\frac{9}{4}}{d+1}}+O(d^{-3})$;
• $g(d)={\displaystyle \frac{13}{4}}{\displaystyle \frac{A(d)}{d!}}+{\displaystyle \frac{5}{4}}{(-1)}^d{\displaystyle \frac{1}{d!}}-{\displaystyle \frac{9}{4}}$ when d is an integer, where $A(d)$ is the alternating factorial function given by $A(d)=d!-(d-1)!+\dots -{(-1)}^{d}1!$.

In this paper, we are interested in the case where the size of the remaining connected components may depend on n, and generally, our setting is that of random graphs. Hence we define the $(ϵ,f)$-fragmentability of a graph G. A vertex set $S\subseteq V$ is said to f-fragment a graph $G=(V,E)$ if the induced graph $G[V\backslash S]$ does not contain any component of size at least f. A graph G is $(ϵ,f)$-fragmentable if there exists a subset S of the vertices of V with $\left|S\right|\le ϵn$, whose removal leaves a graph with no component having more than f vertices.

Definition 1. 

Let $\mathrm{\Gamma }={\left\{{\mathrm{\Gamma }}_n\right\}}_{n=1}^{\infty }$ be a sequence of probability distributions over graphs, and let $G_n$ be a randomly chosen graph from ${\mathrm{\Gamma }}_n$. The fragmentation coefficient of Γ, ${\sigma }_f({\mathrm{\Gamma }}_n)$ is

$${\sigma }_f({\mathrm{\Gamma }}_n)=inf\left\{ϵ\mid P_{G\sim {\mathrm{\Gamma }}_n}(G_n\mathrm{is}(ϵ,f)\text{-}\mathit{fragmentable})\ge {\displaystyle \frac{1}{2}}\right\}.$$

For the random graph models, we consider $G(n,p)$ and $G_{n,d}$. Any probability strictly between zero and one can be taken instead of ${\displaystyle \frac{1}{2}}$ in the definition above. This was shown in [6] for the decycling number of $G_{n,d}$ and in Lemma 1 for $G(n,p)$.

Lemma 1. 

For $p>1$, the constant $1/2$ in Definition 1 has an asymptotically negligible effect on ${\sigma }_f(G(n,p))$ and can be replaced with any constant in the interval $(0,1)$.

Proof. 

Let $G\sim G(n,p)$, and let $s(G)$ be the size of the fragmentation set of G. We show that for every $ϵ>0$, there is a constant C and a segment of integers I such that $\left|I\right|\le C\sqrt{n}$ and

$$Pr[s\in I]\ge 1-ϵ.$$

We consider the vertex-exposure martingale (see [7]). Note that if $G^{\prime }$ differs from G in only one vertex, then $|s(G^{\prime })-s(G)|\le 1$. Hence, the vertex Lipschitz condition holds, and by Azuma’s inequality:

$$Pr[|s-Es|>C\sqrt{n}/2]<2e^{-C^2/8}.$$

□

Note that while, for large enough n, the size of the fragmentation set is close to its mean with probability tending to one, this lemma does not provide anything regarding the mean $Es$. In particular, for small values of c, we do not know the expected size of the fragmentation set $Es$. Additionally, we do not gain any insight regarding the dependency of s in n, and we only know it in some cases. In fact, we generally cannot answer the question of whether the limit ${lim}_{n\to \infty }{\sigma }_f({\mathrm{\Gamma }}_n)$ exists. Hence, we define

Definition 2. 

$$\begin{array}{cc}\hfill m(\mathrm{\Gamma })& =\underset{n\to \infty }{lim\; inf}{\sigma }_f({\mathrm{\Gamma }}_n)\hfill \\ \hfill M(\mathrm{\Gamma })& =\underset{n\to \infty }{lim\; sup}{\sigma }_f({\mathrm{\Gamma }}_n)\hfill \end{array}$$

Note that $m(\mathrm{\Gamma })$ and $M(\mathrm{\Gamma })$ are related to the typical behavior of graphs, whereas $c_f({\mathrm{\Gamma }}_d)$ is related to the external behavior of graphs in the family. In these studies, Edwards and Farr [3,4] used d-regular graphs with high girth to establish their lower bound for $c_f({\mathrm{\Gamma }}_d)$. We show below that ${\displaystyle \frac{d-2}{2d-2}}$ is also a lower bound for the fragmentation coefficient of a random d-regular graph. We approach the problem by considering the vertex expansion properties of random regular graphs.

Haxell et al. [6] studied a closely related parameter called the decycling number of a graph. They answered a question by Edwards and Farr and showed that ${lim}_{d\to \infty }{c}_f({\mathrm{\Gamma }}_d)=1$ by proving the following lower bound for every $d\ge 4$:

$$c_f({\mathrm{\Gamma }}_d)\ge \{\begin{array}{l}1-{\displaystyle \frac{4}{d+2}}\mathrm{if}d\mathrm{is}\mathrm{even};\\ 1-{\displaystyle \frac{4(d+2)}{(d+1)(d+3)}}\mathrm{if}d\mathrm{is}\mathrm{odd}.\end{array}$$

We show below that if d is large enough, then a line graph of a random d-regular graph actually slightly improves that bound, meaning that it is asymptotically the hardest graph to be fragmented up to a constant factor (in the number of remaining vertices), in the sense that to fragment it, we have to remove almost all the vertices since its fragmentation coefficient satisfies

$${\sigma }_f\left(L\left(G_{{\displaystyle \frac{2n}{d}},{\displaystyle \frac{d+2}{2}}}\right)\right)=1-\mathrm{\Theta }\left({\displaystyle \frac{1}{d}}\right)$$

where n is the order of the line graph and d is the degree of its vertices. It should be noted that in [6,8], it was proven that decycling and fragmentation of sparse random graphs are almost the same, in the sense that asymptotically, to decycle a random graph costs almost no more than to fragment. This property is used in our study as well. In the same paper, Haxell et al. [6] showed that the lower bound for the decycling number of random d-regular graphs for large d is $1-{\displaystyle \frac{2ln(d)}{d}}-O\left({\displaystyle \frac{1}{d}}\right)$.

Bau et al. [8] gave bounds for the decycling number $\varphi$ of random d-regular graphs. The upper bounds are based on an algorithmic approach to decycling, and the lower bounds are based on the combinatorial counting of forests. A related question is the computational complexity of finding a minimum fragmenting set. It is known that finding the minimum fragmenting set for an $(ϵ,1)$-fragmentable graph is equivalent to the maximum independent set problem, which is known to be NP-hard. In fact, it has been shown that even approximating the size of the maximum independent set (which is at least $n(1-ϵ)$ for any $(ϵ,1)$-fragmentable graph) up to a constant factor is Poly-APX-complete [9]. Deciding whether a graph is $(ϵ,{\displaystyle \frac{n}{2}})$-fragmentable corresponds to the vertex separator problem, which is also known to be NP-hard. It is, therefore, reasonable to assume that many instances of the fragmentation problem are computationally hard. The complexity of finding a shattering set in the case of random graphs remains unknown. In some cases (e.g., random 3-regular graphs), asymptotically optimal solutions are known to be computable in polynomial time.

Organization

In the second section, we give all the necessary background for our work. This background consists of basic notations of asymptotics and graph theory, definitions of the two models of random graphs studied here, and basic definitions from spectral graph theory. In Section 3.1, we prove some bounds on the fragmenting set of general graphs, and in Section 3.2, we find general lower and upper bounds for two models of random graphs: $\mathcal{G}(n,p)$ where $p={\displaystyle \frac{c}{n}}$ and $c>0$ is a constant and $\mathcal{G}(n,d)$. In Section 4, we improve the lower bound for the size of the fragmenting set of $\mathcal{G}(n,p)$ random graphs, where $p={\displaystyle \frac{c}{n}}$, and c is a large constant. Section 5 deals with the fragmenting set of random d-regular graphs. In Section 5.1, we show that asymptotically, the hardest regular graph to be fragmented is a line graph of a random regular graph. In Section 5.2, we show two lower bounds based on spectral graph theory.

2. Theoretical Background and Notations

We denote by $[n]=\{1,2,\dots n\}$ the set of n vertices.

We denote the set of neighbors of some set $S\subset V$ as

$$N(S)=N_G(S)=\left\{w\right|\exists v\in S,\{v,w\}\in E\},$$

where $S\subset V$. The boundary of some set $S\subset V$ is denoted by $\partial S=N(S)\backslash S$. A set $S\subset V$ is an independent set if no two of its vertices are adjacent. A maximum independent set is an independent set of the largest possible cardinality in G, and its size is denoted by $\alpha (G)$. The chromatic number is the minimum number of colors needed to properly color a graph, where no pair of neighbors is colored by the same color, denoted by $\chi \left(G\right)$.

A set $S\subset V$ is a dominating set if every vertex of G outside of S has a neighbor in S. A minimum dominating set is a dominating set of the smallest possible cardinality in G, and is denoted by $\gamma \left(G\right)$.

An induced subgraph of a graph G is a subset of vertices $U\subset V$ together with every edge whose endpoints are both in U and is denoted by $G\left[U\right]$, we say that such a U spans $G[U]$. For a graph $G=(V,E)$ and a set of vertices $S\subset V$, we denote by $G\backslash S$ the induced graph $G\left[V\backslash S\right]$. A subgraph of a graph $G=(V,E)$ spanned by a set of edges $E_0\subset E$ is a graph with a set of edges $E_0$, and its set of vertices includes the endpoints of every edge in $E_0$ and possibly some isolated vertices.

Given a graph $G=(V,E)$, we denote by P a partition of $V(G)$ into disjoint sets of vertices. The graph induced by a partition consists of connected components that are induced subgraphs of the sets in the partition.

The line graph of a graph G is a graph, denoted by $L(G)$, whose set of vertices is the set of edges of G, and every two vertices of $L(G)$ are connected by an edge if and only if their respective edges share a vertex in common as edges in G.

The density of a graph $G=(V,E)$ is defined as ${\displaystyle \frac{\left|E\right|}{\left|V\right|}}$.

Since every graph G satisfies $\chi (G)\le \mathrm{\Delta }(G)+1$, where $\mathrm{\Delta }(G)$ is the maximum vertex degree in G [10],

Conclusion 1. 

it follows that every d-regular graph has an independent set of order at least ${\displaystyle \frac{n}{d+1}}$.

Together with the known inequality $\alpha (G)\chi (G)\ge n$, it follows that

$$\alpha (G)\ge {\displaystyle \frac{n}{\chi (G)}}\ge {\displaystyle \frac{n}{d+1}}.$$

We use the following notation for random graphs. Given a real number $0\le p\le 1$, the binomial model of random graphs is a probability space, denoted by $\mathcal{G}(n,p)$, consisting of all graphs on the vertex set $[n]$, where each graph G with $e_G$ edges occurs with probability $P(G)=p^{e_G}{(1-p)}^{\left({\displaystyle \genfrac{}{}{0pt}{}{n}{2}}\right)-e_G}$. We define a random graph in this model as a graph randomly chosen from $\mathcal{G}(n,p)$ with a $Bin(\left({\displaystyle \genfrac{}{}{0pt}{}{n}{2}}\right),p)$ distribution. We denote this distribution by $G(n,p)$. We say that $G\in \mathcal{G}(n,p)$ is distributed according to $G(n,p)$ and denote it by $G\sim G(n,p)$.

The model of random d-regular graphs is the probability space, denoted by $\mathcal{G}(n,d)$, consisting of all simple d-regular graphs with the vertex set $[n]$. A random d-regular graph is a graph chosen from $\mathcal{G}(n,d)$ with a uniform distribution. We denote this distribution by $G(n,d)$, and we say that $G\in \mathcal{G}(n,d)$ is distributed according to $G(n,d)$ and denote it by $G\sim G(n,d)$.

A random graph is sparse if with high probability, $\left|E\left(G\right)\right|=O\left(n\right)$.

Note that for positive constants d and c, $G\sim G\left(n,d\right)$ and $G\sim G\left(n,{\displaystyle \frac{c}{n}}\right)$ are sparse graphs.

The following theorems were derived by A. Frieze et al. [11,12], for the size of the maximum independent set.

Theorem 1. 

Let $d=np$ and ϵ be fixed. Suppose that $d_{ϵ}\le d=o(n)$ for some sufficiently large fixed constant $d_{ϵ}$. Then,

$$\left|\alpha (G(n,p))-{\displaystyle \frac{2n}{d}}(log(d)-log(log(d))-log(2)+1)\right|\le {\displaystyle \frac{ϵn}{d}}$$

with high probability [11].

Theorem 2. 

Let $0<ϵ<1$ be fixed. There exists a constant $d_{ϵ}$ such that if $d\ge d_{ϵ},d=o(n^{\theta }),$ $\theta <{\displaystyle \frac{1}{3}}$ is a constant, then

$$\left|\alpha (G(n,d))-{\displaystyle \frac{2n}{d}}(log(d)-log(log(d))+1-log(2))\right|\le {\displaystyle \frac{ϵn}{d}}$$

with high probability [12].

Denote by A the adjacency matrix,

$$A_{ij}=\left\{\begin{array}{cc}1\hfill & \{v_i,v_j\}\in E\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

and by D the diagonal matrix, whose entries are $D_{ii}=\mathrm{deg}(v_i){\delta }_{i,j}$, with ${\delta }_{i,j}$ being the Kronecker delta. Note that for any k-regular graph G, $D=k·I$, where I is the identity matrix.

The Laplacian matrix of a graph G is defined as $L=D-A$, and the normalized Laplacian is $\mathcal{L}=D^{-{\displaystyle \frac{1}{2}}}L{D}^{{\displaystyle \frac{1}{2}}}$, which translates to

$${\mathcal{L}}_{ij}=\left\{\begin{array}{cc}1\hfill & i=j\hfill \\ -{\displaystyle \frac{1}{\sqrt{\mathrm{deg}(v_i)\mathrm{deg}(v_j)}}}\hfill & \{v_i,v_j\}\in E\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

Note 1. 

The normalized adjacency matrix for d-regular graphs, denoted by $\overline{A}$, is ${\displaystyle \frac{1}{d}}A$, and its normalized Laplacian is $\mathcal{L}=I-{\displaystyle \frac{1}{d}}A$.

We denote the eigenvalues of $\overline{A}$ by ${\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_n$ and the eigenvalues of $\mathcal{L}$ by ${\mu }_1\le {\mu }_2\cdots \le {\mu }_n$.

The following theorems concern the second-largest eigenvalue of $\overline{A}$.

Theorem 3. 

For every $d\in \mathbb{N}$, any d-regular graph of order n satisfies $\lambda (G)\ge {\displaystyle \frac{2\sqrt{d-1}}{d}}-o(1)$ when $\lambda (G)=max\{{\lambda }_2,|{\lambda }_n\left|\right\}$ [13].

Theorem 4. 

For every constant $d\in \mathbb{N}$, a random d-regular graph of order n satisfies with high probability that $\lambda \left(G\right)\le {\displaystyle \frac{2\sqrt{d-1}}{d}}+o\left(1\right)$ [13].

Theorem 5. 

Let G be a d-regular graph of order n, and let $X\subset V$. Then,

$$\left|e(X)-{\displaystyle \frac{d{\left|X\right|}^2}{n}}\right|\le d\lambda (G)\left|X\right|$$

where $e(X)$ is the number of edges in a subgraph induced by $X\subset V$. [14].

Proposition 1. 

Let X be an independent set of a d-regular graph G of order n. Then, $\left|X\right|\le \alpha (G)\le {\displaystyle \frac{\lambda (G)}{d}}n$.

Proof. 

X is an independent set; that is, $e(X)=0$. Thus, according to [Corollary 9.2.6] [7], we obtain

$${\displaystyle \frac{d{\left|X\right|}^2}{n}}\le \lambda (G)\left|X\right|.$$

Since this holds for all independent sets, the last equation also holds for $\alpha (G)$. □

Let G be a random d-regular graph of order n. The Vertex Expansion Ratio of G, denoted by ${\mathrm{\Psi }}_V$, is defined as

$${\mathrm{\Psi }}_V(G,k)=\underset{S\subset V,\left|S\right|\le k}{min}{\displaystyle \frac{\left|\partial S\right|}{\left|S\right|}}.$$

We also use another version of the vertex expansion:

$${\mathrm{\Psi }}_V^{\prime }=\underset{S\subset V,\left|S\right|qk}{min}{\displaystyle \frac{\left|N(S)\right|}{\left|S\right|}}$$

We have the following theorem:

Theorem 6. 

Let $d\ge 3$ be a fixed integer and let G be a random d-regular graph. Then, for every $ϵ>0$, there exists $\delta >0$ such that with high probability [15],

$$\begin{array}{c}\hfill {\mathrm{\Psi }}_V(G,\delta n)\ge d-2-ϵ;{\mathrm{\Psi }}_V^{\prime }(G,\delta n)\ge d-1-ϵ.\end{array}$$

3. Fragmentation of Random Graphs

We are interested in studying the behavior of the functions $m(\mathrm{\Gamma })$ and $M(\mathrm{\Gamma })$ from Definition 2 for general and random graphs.

3.1. Deterministic Results

Definition 3. 

A graph $G=(V,E)$ is a$(K,A)$ vertex expander if for every set $S\subset V$ such that $\left|S\right|\le K$, it holds that $\left|N(S)\right|\ge A·\left|S\right|$

Claim 1. 

If G is a $(K,A)$ vertex expander, then for each set $S\subset V$ with $\left|S\right|\le K$, it holds that

$$\left|\partial S\right|\ge (A-1)\left|S\right|.$$

Proof. 

By the definition of $\partial S$,

$$\left|\partial S\right|=\left|N(S)\backslash S\right|\ge \left|N(S)\right|-\left|S\right|\ge A·\left|S\right|-\left|S\right|.$$

□

Theorem 7. 

Let $G=(V,E)$ be a $(K,A)$ vertex expander with a maximum degree d. If S is a K-fragment of G, then

$${\displaystyle \frac{\left|S\right|}{n}}\ge {\displaystyle \frac{A-1}{d+A-1}}.$$

Proof. 

Let $C_1,\dots ,C_m$ be the components of $G\backslash S$. For each i, $\left|C_i\right|\le K$. Let $n=\left|V\right|$. We have $\left|{\bigcup }_{i-1}^m(C_i\cup \partial C_i)\right|\le n$. Since vertices in different components cannot be neighbors, we have $C_i\cap \partial C_j=\varnothing$ for all $i,j$ and $C_i\cap C_j=\varnothing$ for $i\ne j$. Thus, ${\sum }_{i=1}^m\left|C_i\right|+\left|{\bigcup }_{i=1}^m\partial C_i\right|\le n$.

Now, by Claim 1, $\left|\partial C_i\right|\ge (A-1)\left|C_i\right|$. Note that no vertex v can appear in $\partial C_i$ for more than d different $C_i$s. Therefore,

$$\left|\bigcup _{i=1}^m\partial C_i\right|\ge \sum _{i=1}^m\left|\partial C_i\right|/d\ge {\displaystyle \frac{A-1}{d}}\sum _{i=1}^m\left|C_i\right|$$

and

$$n\ge \left(1+{\displaystyle \frac{A-1}{d}}\right)\sum _{i=1}^m\left|C_i\right|={\displaystyle \frac{d+A-1}{d}}\sum _{i=1}^m\left|C_i\right|$$

By definition,

$$\bigcup _{i=1}^m\left(C_i\cup S\right)=V.$$

Thus,

$${\sigma }_f=1-{\displaystyle \frac{1}{n}}\sum _{i=1}^m\left|C_i\right|\ge 1-{\displaystyle \frac{d}{d+A-1}}={\displaystyle \frac{A-1}{d+A-1}}$$

□

Definition 4. 

A graph is$(a,b)$-tree-like if the induced subgraph on every subset $S\subset V$ of cardinality $\left|S\right|\le a$ can be made into a tree by removing at most b vertices.

Theorem 8. 

Let $G=(V,E)$ be an $(a,b)$-tree-like graph. If S is an a-fragment of G, then

$${\displaystyle \frac{\left|S\right|}{n}}\ge {\displaystyle \frac{a}{a-b}}\left(1-{\displaystyle \frac{2\alpha (G)}{n}}-b\left({\displaystyle \frac{2}{a}}+{\displaystyle \frac{1}{n}}\right)\right).$$

Proof. 

Denote the connected components of the graph $G\backslash S$ by $C_1,C_2,\dots ,C_m$, each of size at most a. Group the components into disjoint sets $A_1,\dots ,A_k$, where each $A_j={\bigcup }_{i\in B_j}{C}_i$ is of size at most a. The sets may be chosen such that all the sets $A_j$, except possibly one, have size at least ${\displaystyle \frac{a}{2}}$ (otherwise two small sets may be merged). Thus,

$$k\le ⌈{\displaystyle \frac{2(\left|V\right|-\left|S\right|)}{a}}⌉\le {\displaystyle \frac{2(n-\left|S\right|)}{a}}+1.$$

(1)

Removing at most b vertices from each $A_j$ leaves a forest. Color each tree in the forest properly with two colors. The vertices of the color with the larger cardinality form an independent set of the graph G and are thus of cardinality at most $\alpha (G)$. We have that the total number of vertices in the forest is at most $2\alpha (G)$. The total number of vertices removed to make the forest is at most $b\left({\displaystyle \frac{2(n-\left|S\right|)}{a}}+1\right)$. Therefore,

$$2\alpha (G)+b\left({\displaystyle \frac{2(n-\left|S\right|)}{a}}+1\right)\ge n-\left|S\right|.$$

Rearranging, we obtain

$$\left|S\right|\ge {\displaystyle \frac{a}{a-2b}}\left(n-2\alpha (G)-b\left({\displaystyle \frac{2n}{a}}+1\right)\right).$$

□

The next definition is similar to Definition 4, but it provides a cleaner result at the cost of a stronger assumption.

Definition 5. 

A partition P of a subset of the vertices of a graph G is called$(a,b)$-forest-like if the partition divides the vertices of G into sets of size at most a, and the graph induced by the partition can be made into a forest by removing at most b vertices.

Theorem 9. 

Let $G=(V,E)$ be a graph. If a set S is an a-fragment of G, and the partition into connected components of $G\backslash S$ forms an $(a,b)$-forest-like partition, then

$$\left|S\right|\ge n-2·\alpha (G)-b.$$

Proof. 

The graph $G\backslash S$ has components of order at most a. Removing at most b vertices, we obtain a forest. Assign two colors to each component of the forest. The color with the larger cardinality forms an independent set of the graph G and is thus of cardinality at most $\alpha (G)$. The forest is of size at most $2·\alpha (G)$. The total number of removed vertices required to make the graph into a forest after fragmentation is b. Therefore,

$$2·\alpha (G)+b\ge n-\left|S\right|$$

and then

$$\left|S\right|\ge n-2·\alpha (G)-b$$

□

The last lower bound compares nicely with the following trivial upper bound.

Fact 1. 

Let $\alpha (G)$ be the independence number of G. Then, there exists a set S that 1-fragments G such that 

$$\left|S\right|\le n-\alpha (G).$$

Remark 1. 

For every graph G of maximum degree Δ, $\chi (G)\le \mathrm{\Delta }+1$. Therefore, $\alpha (G)\ge n/(\mathrm{\Delta }+1)$. Hence,

$${\sigma }_f\le 1-{\displaystyle \frac{1}{\mathrm{\Delta }+1}}.$$

Our last deterministic result bounds the size of a fragmenting set (from above) using the size of a dominating set.

Lemma 2. 

Let G be a graph with maximum degree 3. If we remove a dominating set from G, then the remaining graph consists of a disjoint union of paths and cycles.

Proof. 

Every vertex outside of the dominating set Y has at least one neighbor in Y. Removing Y from G reduces the degree of every vertex by at least one so that every vertex in $G\backslash Y$ has a degree at most two, and this implies that the resulting graph is a union of disjoint paths and cycles. □

Theorem 10. 

Let $G=(V,E)$ be a 3-regular graph with n vertices, and assume that it has a dominating set of size y. Then, there is a set of size $y+2{\displaystyle \frac{n-y}{t+2}}$ that t-fragments G.

Proof. 

By definition, after removing Y we are left with a graph of maximum degree 2; that is, a collection of cycles and paths. Fragmenting a cycle requires at least as many vertices as fragmenting a path of the same length. t-fragmenting a cycle of length s requires $\lceil {\displaystyle \frac{s}{t+1}}\rceil$ vertices. The ratio ${\displaystyle \frac{\lceil \frac{s}{t+1}\rceil }{s}}$ attains its maximum at $s=t+2$, where we need to remove two vertices from every cycle (of which there are ${\displaystyle \frac{n-y}{t+2}}$). □

3.2. Results for Random Graphs

Let $G\sim G(n,d)$ or $G\sim G(n,p)$, where $p={\displaystyle \frac{c}{n}}$, $c>0$, and d are constants. Denote by S a fragmenting set of G. Our next goal is to prove that the partition of $G\backslash S$ is a $(\delta n,{\displaystyle \frac{ϵ}{3}}n)$-forest-like partition with high probability, where $\delta ,ϵ\to 0$. Then, we can use Theorem 9 to find a lower bound on S.

We use the following known claim as a tool in our argument.

Claim 2. 

Let $G\sim G(n,d)$ for constant $d\ge 3$ or $G\sim G(n,{\displaystyle \frac{c}{n}})$ for constant c, and fix $ϵ>0$. Then, there exists $\delta >0$ such that every vertex set A with cardinality at most $\delta n$ spans at most $(1+{\displaystyle \frac{ϵ}{3}})\left|A\right|$ edges [2].

Theorem 11. 

Let G be as in Claim 2. If S $\delta n$-fragments G, then, with high probability,

$${\displaystyle \frac{\left|S\right|}{n}}>1-{\displaystyle \frac{2\alpha (G)}{n}}-o(1)$$

Proof. 

Let P be the partition of $G\backslash S$ into the connected components whose order is at most $\delta n$. According to Claim 2, with high probability, we have to remove from each $A\in P$ at most ${\displaystyle \frac{ϵ}{3}}\left|A\right|+1$ vertices to turn $G[A]$ into a tree, since removing this many vertices is guaranteed to eliminate at least this many cycles. This implies that to turn an entire graph induced by the partition into a forest, we have to remove at most

$$\sum _{A\in P}\left({\displaystyle \frac{ϵ}{3}}\left|A\right|+1\right)={\displaystyle \frac{ϵ}{3}}\left(\sum _{A\in P}\left|A\right|\right)\le {\displaystyle \frac{ϵ}{3}}n+\left|P\right|$$

vertices with high probability. Thus,

$${\displaystyle \frac{\left|S\right|}{n}}\ge 1-{\displaystyle \frac{2\alpha (G)}{n}}-o(1).$$

□

Let $\mathrm{\Gamma }$ be $G(n,d)$ or $G(n,c/n)$. Denote by ${\alpha }_{\infty }(\mathrm{\Gamma })$ (the independence ratio) the value obtained with high probability as the limit ${\alpha }_{\infty }(\mathrm{\Gamma })={lim}_{n\to \infty }{\displaystyle \frac{\alpha (G)}{n}}$, where G is a random graph $G\sim \mathrm{\Gamma }$. Theorem 11 and Fact 1 provide both a lower and an upper bound.

Conclusion 2. 

We have 

$$1-2{\alpha }_{\infty }(G(n,d))-o(1)\le {\sigma }_f(G(n,d))\le 1-{\alpha }_{\infty }(G(n,d)),$$

and

$$1-2{\alpha }_{\infty }\left(G\left(n,{\displaystyle \frac{c}{n}}\right)\right)\le {\sigma }_f\left(G\left(n,{\displaystyle \frac{c}{n}}\right)\right)\le 1-{\alpha }_{\infty }\left(G\left(n,{\displaystyle \frac{c}{n}}\right)\right).$$

4. Fragmentation of $\mathit{G}\left(\mathit{n},{\displaystyle \frac{\mathit{c}}{\mathit{n}}}\right)$

In the previous section, we showed that if $G\sim G(n,{\displaystyle \frac{c}{n}})$ for constant c, or $G\sim G(n,d)$ for constant d, then, with high probability, a fragmentation coefficient ${\sigma }_f$ is bounded between

$$1-2{\alpha }_{\infty }\left(G\left(n,{\displaystyle \frac{c}{n}}\right)\right)-o(1)\mathrm{and}1-{\alpha }_{\infty }\left(G\left(n,{\displaystyle \frac{c}{n}}\right)\right).$$

Naturally, we are interested in closing this gap.

In this section, we find an improved lower bound for the size of the fragmenting set in the Erdős–Rényi model, which is valid when c is a large constant. We show that this lower bound is $\left(1-{\alpha }_{\infty }\left(G\left(n,{\displaystyle \frac{c}{n}}\right)\right)-o(1)\right)$. As a consequence, if $G\sim G(n,{\displaystyle \frac{c}{n}})$ for a sufficiently large but constant c, then, with high probability, the order of the graph remaining after fragmentation is $\alpha (G)(1+o(1))$, where $o(1)$ refers to a function that approaches zero as both n and c approach infinity. Hence, surprisingly, if one wants to remove vertices from $G(n,p=c/n)$ until all connected components are of size $o(n)$, one should not expect to do much better than leaving all components of size one.

Formally we want to prove the following theorem.

Theorem 12. 

Let $G\sim G(n,p)$, where $p={\displaystyle \frac{c}{n}}$ and c is a sufficiently large constant. With high probability, the order of the graph remaining after the removal of a fragmenting set is at most $\alpha (G)(1+o(1))$.

We have divided the proof into several lemmas.

Note 2. 

From now until the end of this section, fix c to be a sufficiently large constant, and let p be ${\displaystyle \frac{c}{n}}$.

Lemma 3. 

Let U be the set of vertices remaining after optimal fragmentation. Then, with high probability, in order to make $G[U]$ unicyclic, we need to remove at most $o(n)$ vertices.

Proof. 

This follows from the proof of Theorem 11 above, since by definition, $G\left[U\right]$ is composed of connected components of size $o(n)$. □

For the rest of this section, let m be the number of vertices remaining after optimal fragmentation. Our goal is to bound m from above.

Lemma 4. 

Let $A_K$ be the event in which a subset K of $G\sim G(n,p)$ of order k spans exactly k edges, and let $X_K$ be its characteristic random variable, i.e.,

$$X_K=\left\{\begin{array}{cc}1\hfill & \left|K\right|=k,\left|e(K)\right|=k\hfill \\ 0\hfill & \mathit{otherwise}\hfill \end{array}\right..$$

(2)

Let $X_k=\sum X_K$ be a random variable that counts the number of sets of order k that span exactly k edges. Then, for every $ϵ>0$, if $k>\alpha (G)(1+ϵ)$, one has $E[X_k]=o(1)$.

Proof. 

Recall that $p=c/n$. Then,

$$\begin{array}{cc}\hfill E\left[X_k\right]& =\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{\left(\genfrac{}{}{0pt}{}{k}{2}\right)}{k}}\right)p^k{(1-p)}^{\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2}}\right)-k}\le {\left({\displaystyle \frac{en}{k}}\right)}^k{\left({\displaystyle \frac{e\left(\genfrac{}{}{0pt}{}{k}{2}\right)}{k}}\right)}^k{p}^k{(1-p)}^{\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2}}\right)-k}\le \hfill \\ \hfill & \le {\left({\displaystyle \frac{en}{k}}\right)}^k{\left({\displaystyle \frac{k^{2}e}{2k}}\right)}^k{p}^k{e}^{-p\left[\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2}}\right)-k\right]}={\left({\displaystyle \frac{e^2{k}^{2}n}{2k^2}}\right)}^k{p}^k{e}^{-{\displaystyle \frac{pk(k-1)}{2}}+pk}=\hfill \\ \hfill & ={\left({\displaystyle \frac{e^{2}np{e}^p{e}^{\frac{-pk+p}{2}}}{2}}\right)}^k={\left({\displaystyle \frac{e^{2}n{e}^{-\frac{pk}{2}}{e}^{\frac{3p}{2}}}{2}}·{\displaystyle \frac{c}{n}}\right)}^k\approx {\left(l·c·e^{-{\displaystyle \frac{pk}{2}}}\right)}^k.\hfill \end{array}$$

Now,

$${\left(l·c·e^{-{\displaystyle \frac{pk}{2}}}\right)}^k<1⟺l·c·e^{-{\displaystyle \frac{pk}{2}}}<1⟺log(l·c·e^{-{\displaystyle \frac{pk}{2}}})<0⟺$$

$$log(l)+log(c)-{\displaystyle \frac{pk}{2}}<0⟺k>\left({\displaystyle \frac{2log(c)}{c}}+{\displaystyle \frac{2log(l)}{c}}\right)n$$

But according to Theorem 1, for a sufficiently large c,

$$\alpha (G)\approx {\displaystyle \frac{1}{c}}\left(2log(c)-loglog(c)+O(1)\right)n$$

which proves that for $k>\alpha (G)+n(1+ϵ)loglog(c)/c$, one has $E\left[X_k\right]=o(1)$. □

Lemma 5. 

Let $A_i$ be the event in which a subset K of order k of a random graph $G\sim G(n,p)$ spans exactly i edges, where $i\le k$, and let $X_{k,i}$ be a random variable that counts the number of such sets. That is, $X_{k,i}=\sum X_{k,T}$, where

$$X_{k,T}=\left\{\begin{array}{cc}1\hfill & T\in V,\left|T\right|=k,\left|e(T)\right|=i\hfill \\ 0\hfill & \mathit{otherwise}\hfill \end{array}\right.$$

Let $X=\sum X_{k,i}$ be a random variable that counts the number of subsets of G of order k with at most k edges. Then, $E\left[X\right]\to 0$ for $k>\alpha (G)$.

Proof. 

We fix k and omit it from the notation.

$$E\left[X_i\right]=\sum E\left[X_T\right]=\sum \left({\displaystyle \genfrac{}{}{0pt}{}{\left(\genfrac{}{}{0pt}{}{k}{2}\right)}{i}}\right)p^i{(1-p)}^{\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2}}\right)-i}$$

and then the expectation of X is

$$\begin{array}{cc}\hfill E\left[X\right]& =\sum _{i=0}^{k}E\left[X_i\right]=\sum _{i=0}^k\left({\displaystyle \genfrac{}{}{0pt}{}{\left(\genfrac{}{}{0pt}{}{k}{2}\right)}{i}}\right)\sum p^i{(1-p)}^{\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2}}\right)-i}=\hfill \\ \hfill & =\sum _{i=1}^k\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{\left(\genfrac{}{}{0pt}{}{k}{2}\right)}{i}}\right)p^i{(1-p)}^{\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2}}\right)-i}.\hfill \end{array}$$

(3)

Denote the summand i in Equation (3) by $a_i$. Thus, it is enough to show that for every $i<k$, one has $a_i\le q^{i-1}{a}_k$ for some $0<q<1$. Consider the quotient of $a_i$ and $a_{i+1}$ for $i<k$:

$$\begin{array}{cc}\hfill {\displaystyle \frac{a_i}{a_{i+1}}}& ={\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{\left(\genfrac{}{}{0pt}{}{k}{2}\right)}{i}\right)p^i{(1-p)}^{\left(\genfrac{}{}{0pt}{}{k}{2}\right)-i}}{\left(\genfrac{}{}{0pt}{}{\left(\genfrac{}{}{0pt}{}{k}{2}\right)}{i+1}\right)p^{i+1}{(1-p)}^{\left(\genfrac{}{}{0pt}{}{k}{2}\right)-i-1}}}={\displaystyle \frac{(i+1)!}{i!}}·{\displaystyle \frac{(\left(\genfrac{}{}{0pt}{}{k}{2}\right)-i-1)!}{(\left(\genfrac{}{}{0pt}{}{k}{2}\right)-i)!}}·{\displaystyle \frac{1-\frac{c}{n}}{\frac{c}{n}}}=\hfill \\ \hfill & ={\displaystyle \frac{i+1}{\left(\left(\genfrac{}{}{0pt}{}{k}{2}\right)-i\right)}}·{\displaystyle \frac{n-c}{c}}.\hfill \end{array}$$

Now, we aim to show that this quotient is less than 1:

$$\begin{array}{cc}\hfill {\displaystyle \frac{i+1}{\left(\left(\genfrac{}{}{0pt}{}{k}{2}\right)-i\right)}}·{\displaystyle \frac{n-c}{c}}& \le {\displaystyle \frac{k}{\left(\frac{k(k-1)}{2}-k\right)}}·{\displaystyle \frac{n-c}{c}}={\displaystyle \frac{2k}{\left(k(k-1)-2k\right)}}·{\displaystyle \frac{n-c}{c}}=\hfill \\ \hfill & ={\displaystyle \frac{2}{k-3}}·{\displaystyle \frac{n-c}{c}}\le {\displaystyle \frac{2}{\left(\frac{2log(c)}{c}n-3\right)}}·{\displaystyle \frac{n-c}{c}}=\hfill \\ \hfill & ={\displaystyle \frac{2}{2nlog(c)-3c}}·(n-c)={\displaystyle \frac{1}{nlog(c)-1.5c}}·(n-c).\hfill \end{array}$$

The second inequality holds because by assumption, $k>\alpha (G)\approx {\displaystyle \frac{2log(c)}{c}}n$.

Next,

$${\displaystyle \frac{1}{nlog(c)-1.5c}}·(n-c)<1⟺n-c<nlog(c)-1.5c⟺$$

$$⟺n<nlog(c)-0.5c⟺1<log(c)-{\displaystyle \frac{0.5c}{n}}$$

and the last inequality holds for sufficiently large values of n.

Denote by $t_{max}=sup{\displaystyle \frac{a_i}{a_{i+1}}}$. By induction, we have that for every $i<k$, $a_i\le t_{max}^{k-i}·a_k$, where

$$a_k=\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{\left(\genfrac{}{}{0pt}{}{k}{2}\right)}{k}}\right)p^k{(1-p)}^{\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2}}\right)-k}.$$

Therefore,

$$E\left[X\right]\le \sum _{i=1}^{k-1}{t}_{max}^{k-i}E\left[X_k\right]+E\left[X_k\right]=E\left[X_k\right]·\left(1+\sum _{i=0}^{k-1}{t}_{max}^i\right).$$

We already showed that $E\left[X_k\right]\to 0$, and it is clear that ${\sum }_{i=0}^k{t}_{max}^i$ converges to some finite constant when $n\to \infty$ because $t_{max}<1⟹E\left[X\right]\to 0$ when $n\to \infty$. □

Proof of Theorem 12. 

Recall that U is the set remaining after optimal fragmentation and m denotes its size. In order to turn $G[U]$ into a tree or a unicyclic graph, one needs to remove from U at most $o(n)$ vertices by Lemma 3. Denote the order of the graph remaining after this stage by k; that is, $l=k+o(n)$. Now, by Lemma 5, if $k>\alpha (G)$, then with high probability, there is no such set of order k that contains at most one cycle. This implies that necessarily $k\le \alpha (G)$ and

$$l=k+o(n)\le \alpha (G)+o(n)=\alpha (G)\left(1+{\displaystyle \frac{o(n)}{\alpha (G)}}\right)=\alpha (G)(1+o(1))$$

since $\alpha (G)$ is linear in n, and this completes the proof of Theorem 12. □

Conclusion 3. 

For a sufficiently large c, with high probability, the order of the fragmentation coefficient satisfies 

$${\sigma }_f\left(G\left(n,{\displaystyle \frac{c}{n}}\right)\right)=1-{\alpha }_{\infty }\left(G\left(n,{\displaystyle \frac{c}{n}}\right)\right)-o(1)$$

where $o(1)$ is a vanishing term as both n and c approach infinity.

Remark 2. 

According to Theorem 1, for a sufficiently large c, $\alpha (G)\approx {\displaystyle \frac{2log(c)}{c}}n$ with high probability. Thus, the order of the optimal fragmenting set of a random graph $G\sim G(n,{\displaystyle \frac{c}{n}})$ satisfies

$$1-{\displaystyle \frac{2log(c)}{c}}-o(1)\le {\sigma }_f\left(G\left(n,{\displaystyle \frac{c}{n}}\right)\right)\le 1-{\displaystyle \frac{2log(c)}{c}}+o(1)$$

with high probability.

5. Fragmentation of Regular Graphs

5.1. Highly Resilient Regular Graphs

In Conclusion 2, we saw that the fragmentation coefficient of a random d-regular graph G is bounded between two values:

$$1-2{\alpha }_{\infty }(G(n,d))-o(1)\le {\sigma }_f(G(n,d))\le 1-{\alpha }_{\infty }(G(n,d))$$

Recall that according to Theorem 2, for a sufficiently large d, $\alpha (G)\approx {\displaystyle \frac{2log(d)}{d}}n$. In conjunction with the results of Haxell et al. [6], this implies that

$$1-{\displaystyle \frac{2log(d)}{d}}-o(1)\le {\displaystyle \frac{\left|S\right|}{n}}\le 1-{\displaystyle \frac{2log(d)}{d}}+o(1),$$

where $o(1)$ represents a function that approaches zero as both n and d approach infinity.

We now show that a line graph $L(G)$ of a random regular graph G is asymptotically one of the hardest regular graphs to be fragmented, up to a constant factor in the number of undeleted nodes, i.e., there are two numbers $c_1$ and $c_2$ such that the fragmenting set S of $L(G)$ satisfies, with high probability,

$$1-{\displaystyle \frac{c_1}{d}}\le {\displaystyle \frac{\left|S\right|}{n}}\le 1-{\displaystyle \frac{c_2}{d}}$$

Let d be a large constant. We consider the order of the graph after fragmentation as a function of d, where n is assumed to go to infinity. We saw in Conclusion 1 that every d-regular graph on n vertices contains an independent set of size at least ${\displaystyle \frac{n}{d+1}}$. Removing everything but the largest independent set leaves us with a set of size at least ${\displaystyle \frac{n}{d+1}}$, which implies that the order of the set U remaining after fragmentation is $\left|U\right|\ge {\displaystyle \frac{n}{d+1}}$. Here, we show that this bound is asymptotically tight; that is, there are d-regular graphs for which the largest remaining graph after fragmentation is of size $\mathrm{\Theta }\left({\displaystyle \frac{n}{d}}\right)$.

Recall that the line graph of a regular graph is also regular.

Theorem 13. 

For a sufficiently large d, the order of the graph remaining after fragmenting the line graph of a random d-regular graph is, with high probability, $\mathrm{\Theta }\left({\displaystyle \frac{N}{D}}\right)$, where N is the order of the line graph of G and D is the degree of its vertices.

We use the following lemma.

Lemma 6. 

Let d be sufficiently large, and let G be a random d-regular graph. Then, for every $c\ge 2$, there exists $\delta =\delta \left(d,c\right)>0$ such that, with high probability, every set $E_0$ of $cn$ edges in G has a connected component of size at least $\delta n$.

Proof. 

Assume, in contrast, that for every $\delta$, there exists $c\ge 2$ and a set $E_0$ of edges such that $\left|E_0\right|\ge cn$, and that each of the connected components spanned by this set has size less than $\delta n$. Our purpose is to prove that, with high probability, this never happens.

Let $G_0=\left(\left[n\right],E_0\right)$ be a spanning subgraph of G; that is, with the same set of vertices $\left[n\right]$ and with $E_0$ as its set of edges. Fix $\delta >0$. Consider the densest connected component of $G_0$. Next, we show that its density is at least c, yet it is of order less than $\delta n$.

Denote the density of each connected component of $G_0$ by $c_i={\displaystyle \frac{\left|E_i\right|}{\left|V_i\right|}}$, where $G_i=(V_i,E_i)$ is a connected component of $G_0$. Then,

$$cn=\left|E_0\right|=\sum _i\left|E_i\right|=\sum _i{c}_i\left|V_i\right|$$

and division by n implies that

$$c=\sum _i{\displaystyle \frac{\left|V_i\right|}{n}}·c_i.$$

Thus, there must exist some $c_i\ge c$; otherwise,

$$\sum _i{\displaystyle \frac{\left|V_i\right|c_i}{n}}<\sum _i{\displaystyle \frac{\left|V_i\right|c}{n}}=\sum _i{\displaystyle \frac{\left|V_i\right|}{n}}·{\displaystyle \frac{\left|E_0\right|}{n}}={\displaystyle \frac{\left|E_0\right|}{n}}·{\displaystyle \frac{1}{n}}\sum _i\left|V_i\right|={\displaystyle \frac{\left|E_0\right|}{n}}=c$$

since ${\sum }_i\left|V_i\right|=n$, which is a contradiction.

By assumption, this connected component has sublinear size, and we saw in Claim 2 that, with high probability, every such component $V_i$ spans at most $\left(1+{\displaystyle \frac{ϵ}{3}}\right)\left|V_i\right|$ edges. Hence, the density of this connected component satisfies

$$c_i={\displaystyle \frac{\left|E_i\right|}{\left|V_i\right|}}\le {\displaystyle \frac{\left(1+\frac{ϵ}{3}\right)\left|V_i\right|}{\left|V_i\right|}}=\left(1+{\displaystyle \frac{ϵ}{3}}\right)$$

and we can always choose $ϵ<1$, since the above holds for every $ϵ>0$. Now,

$$2\le c\le c_i\le 1+{\displaystyle \frac{ϵ}{3}}<2$$

which is impossible. □

Remark 3. 

Actually, the proof above holds for $c>1$ since we can take $ϵ>0$ to be as small as desired.

Note 3. 

In the last claim, we proved that, with high probability, every subgraph spanned by a set of $cn$ edges for $c\ge 2$ has a connected component of linear size in n.

Proof of Theorem 13. 

Let $G\sim G(n,d)$ for a sufficiently large d, and let H be its line graph. H is a $(2d-2)$-regular graph of order ${\displaystyle \frac{nd}{2}}$. Denote $D=2d-2$ and $N={\displaystyle \frac{nd}{2}}$. Suppose that U is the set remaining after the optimal fragmentation of H. We have already seen that $\left|U\right|=\mathrm{\Omega }\left({\displaystyle \frac{N}{D}}\right)$, but it remains to show that $\left|U\right|=O\left({\displaystyle \frac{N}{D}}\right)$. Recall that every connected component of U is of size $o(N)$.

Note that the paths in G correspond to the paths in H because if $v_0,v_1,\dots v_m$ is a path in G, then there is a sequence of $m-1$ edges $e_1,e_2,\dots ,e_{m-1}$, which are vertices in H such that edge $e_i$ shares a vertex with edge $e_{i+1}$. This implies that vertex $e_i$ is a neighbor of vertex $e_{i+1}$ in H. Hence, the connected components in G are also preserved by the line graph transformation.

Recall that by Conclusion 1,

$$\left|U\right|\ge {\displaystyle \frac{N}{D+1}}={\displaystyle \frac{\frac{nd}{2}}{2d-1}}={\displaystyle \frac{d}{2(2d-1)}}n\approx {\displaystyle \frac{1}{4}}n$$

Now, we want to prove that $\left|U\right|$ cannot be more than $cn$ for $c\ge 2$, which means that it cannot be more than ${\displaystyle \frac{kN}{D+1}}$ for constant k. Assume the opposite. Let $c\ge 2$, and note that $cn$ vertices in H are $cn$ edges in G. According to Lemma 6, with high probability, every set of $cn$ edges of G, where $c\ge 2$ has a connected component of linear size in n. That is, there is some $\delta =\delta (c,d)>0$ such that every set of $cn$ edges in G has a connected component of size at least $\delta n$. This means that, with high probability, there is a connected component in H of linear size in N since $N={\displaystyle \frac{dn}{2}}$, which contradicts the assumption that every connected component of U must be of size $o(N)$.

Hence, $\left|U\right|=O\left({\displaystyle \frac{N}{D}}\right)$, implying that $\left|U\right|=\mathrm{\Theta }\left({\displaystyle \frac{N}{D}}\right)$. □

Conclusion 4. 

For any $ϵ>0$, there exists $d_0$ such that for any integer $d>d_0$, there exists a d-regular graph whose size after fragmentation is at least ${\displaystyle \frac{n}{d}}-ϵ·n$.

Proof. 

By Theorem 13, the fraction of vertices remaining after fragmenting the line graph of a random ${\displaystyle \frac{d+2}{2}}$-regular graph with ${\displaystyle \frac{2n}{d}}$ vertices is ${\displaystyle \frac{1}{d}}+o\left({\displaystyle \frac{1}{d}}\right)$. Thus, for any even sufficiently large d, the size after fragmentation is at least ${\displaystyle \frac{n}{d}}-ϵ·n$.

If d is odd, we construct the line graph of a random ${\displaystyle \frac{d+2}{2}}$-regular graph with ${\displaystyle \frac{2n}{d-1}}$ vertices. The fraction of vertices remaining after fragmenting this graph is ${\displaystyle \frac{1}{d-1}}+o\left({\displaystyle \frac{1}{d}}\right)={\displaystyle \frac{1}{d}}+o\left({\displaystyle \frac{1}{d}}\right)$ for a sufficiently large d. By Dirac’s theorem [16], if $n>2d$, the complement of the line graph contains a Hamilton cycle; thus, if n is even, it also contains a perfect matching. We add this matching to the line graph. Since adding edges can only increase the fragmentation set size, the conclusion is proven. □

Note that this conclusion implies that there are many graphs that are hard to fragment, as they do not arise as specific constructions but rather as line graphs of random graphs, which are quite abundant.

5.2. Spectral Bounds

In this section, we provide two lower bounds on the size of a fragmenting set of d-regular graphs obtained by considering concepts from spectral graph theory.

5.2.1. Vertex Expansion Lower Bound

Let $G\sim G(n,d)$, and denote by S a fragmenting set of G. We start by bounding the size of S using vertex expansion.

Claim 3. 

With high probability, S satisfies 

$$\left|S\right|\ge {\displaystyle \frac{d-2-ϵ}{2d-2}}n.$$

(4)

Proof. 

Recall that according to Theorem 6, we have that, with high probability, a random d-regular graph satisfies

$${\mathrm{\Psi }}_V^{\prime }(G,\delta n)\ge d-1-ϵ.$$

Hence, we know that a random graph G is a $\left(\delta n,d-1-ϵ\right)$-vertex expander. We can now use Theorem 7 and obtain

$${\displaystyle \frac{\left|S\right|}{n}}\ge {\displaystyle \frac{d-1-1-ϵ}{d+d-1-1+ϵ}}={\displaystyle \frac{d-2-ϵ}{2d-2-ϵ}}\ge {\displaystyle \frac{d-2-ϵ}{2d-2}}={\displaystyle \frac{d-2}{2d-2}}-o(1)$$

We can assume that $ϵ\to 0$ since the above holds for every $ϵ>0$. □

Thus, we have

Conclusion 5. 

$$c_f(G(n,d))\ge {\displaystyle \frac{d-2}{2d-2}}.$$

5.2.2. Fragmentation of Spectral Graphs

Our last result dealt with $(n,d,\lambda )$-graphs. Recall that

$$\lambda =\lambda (G)=max\{{\lambda }_2,\left|{\lambda }_n\right|\}.$$

Theorem 14. 

Let G be a random d-regular graph, and let S be an optimal fragmenting set. Then, with high probability,

$$\left|S\right|\ge (1-2\lambda /d)n.$$

Proof. 

We saw in Proposition 1 that $\alpha (G)\le {\displaystyle \frac{\lambda }{d}}n$, and by Theorem 11, with high probability, we have

$$\left|S\right|\ge n\left(1-{\displaystyle \frac{2\alpha (G)}{n}}-o(1)\right).$$

Thus, we obtain

$${\sigma }_f\ge 1-{\displaystyle \frac{2\lambda }{dn}}-o(1).$$

□

Conclusion 6. 

If G is a random d-regular graph, then, with high probability, 

$${\sigma }_f\ge 1-{\displaystyle \frac{4\sqrt{d-1}}{d^2}}-o(1)$$

(5)

Proof. 

The conclusion follows immediately from the previous conclusion, together with the known bound on $\lambda$ for random d-regular graphs (see, e.g., [13,15]). With high probability,

$$\lambda (G)\le {\displaystyle \frac{2\sqrt{d-1}}{d}}+o(1).$$

□

6. Discussion

In this study, we defined a parameter for typical graph fragmentation across different types of graphs. The findings and some previous results are summarized in

Table 1. Known bounds of fragmentation coefficients. Our contributions are denoted by *.

Bound	Formula	Model	Small $\mathit{c},\mathit{d}$	Large $\mathit{c},\mathit{d}$	Ref.
$m(\mathrm{\Gamma })$	${\displaystyle \frac{d-2}{2d-2}}-o(1)$	$G_{n,d}$	✓	Redundant	*
$m(\mathrm{\Gamma })$	$1-{\displaystyle \frac{4\sqrt{d-1}}{d}}-o(1)$	$G(n,d,\lambda )$		✓	*
$m(\mathrm{\Gamma })$	$n(1-{\displaystyle \frac{2\lambda }{n}}-o(1))$	$G(n,d,\lambda )$	✓	✓	*
$m(\mathrm{\Gamma })$	$1-{\displaystyle \frac{2logd}{d}}-o(1)$	$G_{n,d}$		✓	[6]
$m(\mathrm{\Gamma })$	$1-{\displaystyle \frac{2logc}{c}}-o(1)$	$G_{n,{\displaystyle \frac{c}{n}}}$		✓	*
$M(\mathrm{\Gamma })$	$1-{\displaystyle \frac{2logd}{d}}+o(1)$	$G_{n,d}$		✓	*
$M(\mathrm{\Gamma })$	$1-{\displaystyle \frac{2logc}{c}}+o(1)$	$G_{n,{\displaystyle \frac{c}{n}}}$		✓	*
$c_f\ge$	$1-\mathrm{\Theta }\left({\displaystyle \frac{1}{d}}\right)$	$\mathrm{avg}/\max \mathrm{degree}d$	✓	✓	[6]
$c_f\ge$	$1-\mathrm{\Theta }\left({\displaystyle \frac{1}{d}}\right)$	$L\left(G_{{\displaystyle \frac{2n}{d}},{\displaystyle \frac{d+2}{2}}}\right)$		✓	*
$c_f\ge$	${\displaystyle \frac{d-2}{2d-2}}-o(1)$	$G_{n,d}\mathrm{of}\mathrm{high}\mathrm{girth}$	✓	Redundant	[3]
$c_f\le$	${\displaystyle \frac{d-\frac{9}{4}}{d+1}}+O\left({\displaystyle \frac{1}{d^3}}\right)$	$\mathrm{avg}/\max \mathrm{degree}d$	✓	✓	[5]

.

The approximation of the maximum independent set has been studied in [17,18,19,20,21,22]. In Figure 1, we illustrate the different findings for random d-regular graphs. We present computational results for Conclusion 2, based on the latest findings in [22]. The bounds for the decycling number $\varphi$ are taken from [8], which were numerically estimated for several small values of d.