Impact of Auxiliary Information and Measurement Errors on Mean Estimation with Mixture Optional Enhanced Trust (MOET) Randomized Response Model

Abstract

Randomized response technique (RRT) surveys are designed to secure honest answers to sensitive questions. In this study, we consider the important issue of measurement error (ME). While non-response, a common culprit for survey inaccuracy, is a lesser issue in RRT studies because they are conducted through face-to-face interviews, measurement error is of particular significance. RRT models are generally more complex than other survey methods, sometimes requiring that respondents follow ordered instructions, draw cards from decks, and/or perform simple mathematical calculations. All of these steps can result in measurement errors, and when such error is high, estimation efficiency will suffer. In this study, we consider the impact of measurement error on a Mixture Optional Enhanced Trust (MOET) RRT model proposed in 2024, and we propose new estimators for this model that take measurement error into account. We also study the extent to which measurement error can be tolerated before it is so large that it overwhelms and undermines the benefit that RRT was implemented to yield in the first place (the reduction in or elimination of social desirability bias-related untruthfulness). We also draw attention to a surprising finding—that the presence of measurement error inadvertently serves to provide additional scrambling, thereby leading to an increase in privacy.

1. Introduction

When the subject of surveys is sensitive in nature (potentially embarrassing, shameful, or even illegal) respondents may not be truthful when they answer. Warner (1969) and Greenberg (1969) first pioneered models that provided some means through which respondents could hide their true responses to such sensitive questions, thereby removing their incentive to lie [1,2]. While these first models were binary in nature (are designed for questions with yes/no responses), there are also sensitive questions that are of a quantitative nature. While misrepresentation in responses to quantitative questions is less black and white, it is clear that a social desirability bias (SDB) impacts them too, and as Lanke (2017) described, causes respondents “to underreport socially undesirable attributes… and to over report more desirable attributes” [3]. Both Warner (1971) and Greenberg (1971) therefore followed up their models with new models that were applicable to sensitive questions with quantitative responses [4,5].

Following Warner’s and Greenberg’s inventions, many new RRT models were introduced, and they generally added ever greater levels of complexity. For instance, Pollock and Bek (1976), Eichhorn and Hayre (1983), and Diana, G and Perri (2011) all proposed models that included additive and/or multiplicative scrambling [6,7,8]. Perri (2008) combined Warner and Greenberg features into a single blank card model [9].

All of this complexity was intended to foster greater levels of scrambling and therefore to encourage more truthful RRT responses, but it came at a significant price: the potential for error. A flurry of research involving measurement error followed. Blattman et al. (2016) developed a survey validation technique that uses qualitative work to check for measurement error in potentially sensitive behaviors [10]. Sharma and Singh (2015) proposed the use of auxiliary information to improve efficiency, assuming that non-response and measurement error are present in both the study and auxiliary variables [11]. Khalil et al. (2018) proposed a generalized estimator in the presence of measurement error [12]. Makhdum et al. analyzed scenarios where non-response and measurement error are simultaneously present, and Singh and Vishwakarma (2019) proposed a method to measure the combined effect of measurement error and non-response when auxiliary information is used [13,14]. Priyanka et al. (2023) investigated the impact of measurement error in RRT successive sampling [15]. Beyond just accounting for ME, Audu et al. (2020) proposed a class of estimators that has superior efficiency when measurement errors are present [16].

In Section 2 of this study, we review the Mixture Optional Enhanced Trust (MOET) model proposed by Parker et al. (2024), as well as the ratio estimator for the MOET model proposed by Gupta et al. (2024); these will serve as the basis of this study [17,18]. Then, in Section 3, we derive basic and ratio estimators that reflect the impact of measurement error. In Section 4, we recognize that ME reduces efficiency, and study (1) the circumstances under which the ME resulting from the collection of auxiliary information is so large that it undermines the benefit of collecting such information, and (2) the circumstances under which ME is so large that it undermines the RRT’s overall benefit (the elimination of bias).

We then, in Section 5, turn our attention to an aspect of auxiliary information that has not been adequately explored. It is well known that auxiliary information can improve efficiency. However, auxiliary comes at a cost—its presence may reduce privacy. Indeed, if auxiliary information (represented by $X$) was perfectly correlated with the response to the sensitive question ($Y$), then knowledge of $X$ would lead directly to knowledge of $Y$. We explore this dynamic, and we also recognize that at the same time auxiliary information reduces privacy, measurement error inadvertently increases privacy. In Section 6, we provide simulations that validate the estimators developed in Section 3 and explore the behavior of these estimators.

2. MOET Model (2024)

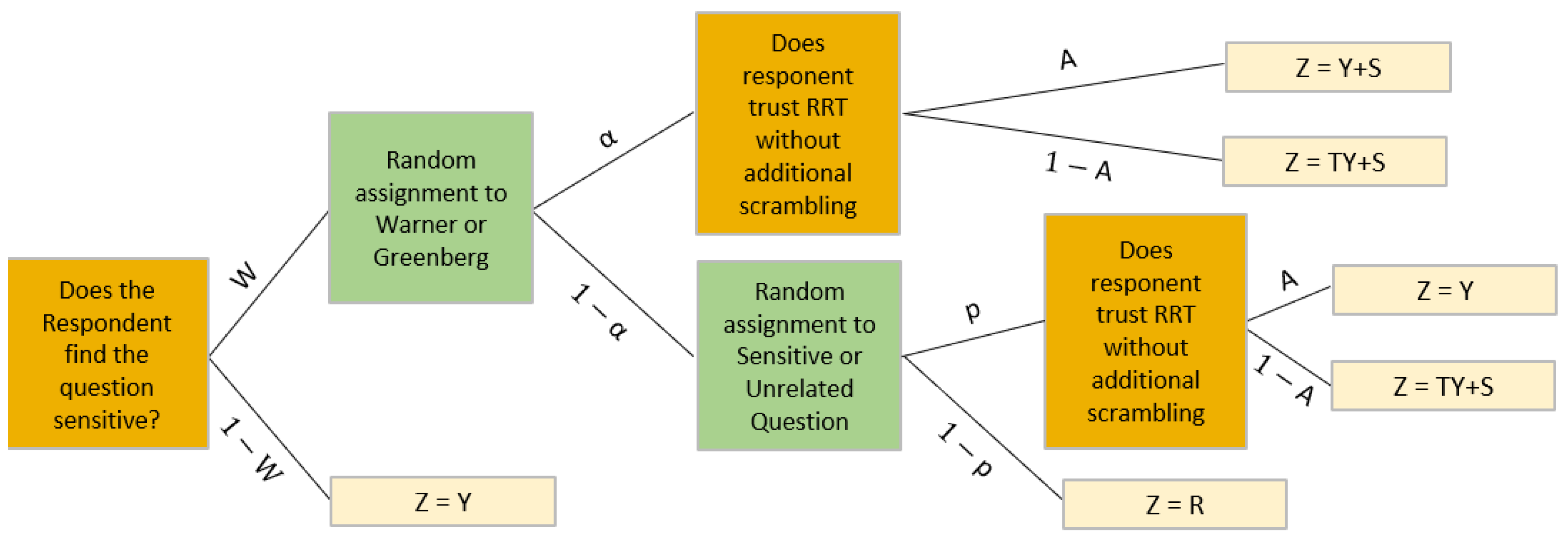
Here, we present the model that will serve as the basis of our study. The Mixture Optional Enhanced Trust (MOET) model was first proposed by Parker et al. (2024) [17], and features several recently innovated RRT features—mixture, optionality, and enhanced trust. Figure 1 provides a diagram of the model. In this section, we discuss certain common RRT manipulations that could trigger measurement error (ME) in RRT models like this one. Then, we discuss the basic and ratio mean estimators for this model, as proposed in earlier papers.

$$Z=\left\{\begin{array}{lll}Y+S& \mathrm{with} \mathrm{probability}& W\mathrm{\alpha }A\\ TY+S& \mathrm{with} \mathrm{probability}& W\left(1-A\right)\left(\mathrm{\alpha }+p-\mathrm{\alpha }p\right)\\ Y& \mathrm{with} \mathrm{probability}& W\left(1-\mathrm{\alpha }\right)pA+\left(1-W\right)\\ R& \mathrm{with} \mathrm{probability}& W\left(1-\mathrm{\alpha }\right)\left(1-p\right)\end{array}\right..$$

(1)

In the MOET model decision tree, two of the decisions (those involving α and $p$) must be made by a random process where the outcome is unknown to the researcher; therefore, the respondent themselves has to, in some sense, perform the randomization. This might be achieved by the respondent shuffling and picking a card from a deck. We mention this because although the process may be very simple, it none the less presents an opportunity for confusion and error. Note that ME includes any unintentional error (including confusion) that results in a recorded response being different from the respondent’s intended response. Additionally, some respondents will need to scramble their true responses by addition and/or multiplication ($Z=Y+S$ or $Z=TY+S$); again, these calculations must be performed by the respondent. There are many ways to keep these calculations simple (making it certain that $T$ and $S$ take on only positive whole-number values, providing a calculator or charts of computations to the respondent, etc.) but, nevertheless, the fact that calculations must be performed by the respondent presents the opportunity for ME.

MOET Parker Model Review [17]

We now review MOET model estimators. Detailed below are the basic mean estimator that Parker et al. (2024) proposed based on a split sample approach and an expression for the model’s efficiency (MSE), which will be used as a basis for comparison later in this study [17]. To distinguish it from the ratio estimator (which will also be considered in this study), we will call this mean estimator the basic mean estimator (or the basic estimator); the basic estimator along with its mean square error (MSE) is given in Equations (2) and (3).

$${\widehat{\mathrm{\mu }}}_Y={\displaystyle \frac{1-p_1}{p_2-p_1}}{\overline{Z}}_2-{\displaystyle \frac{1-p_2}{p_2-p_1}}{\overline{Z}}_1.$$

(2)

$$\mathrm{M}\mathrm{S}\mathrm{E}\left({\widehat{\mathrm{\mu }}}_Y\right)={\left({\displaystyle \frac{1-p_1}{p_2-p_1}}\right)}^2\mathrm{V}\mathrm{a}\mathrm{r}({\overline{Z}}_2)+{\left({\displaystyle \frac{1-p_2}{p_2-p_1}}\right)}^2\mathrm{V}\mathrm{a}\mathrm{r}({\overline{Z}}_1),$$

(3)

where

$$\begin{gathered} {\mathrm{V}\mathrm{a}\mathrm{r}(\overline{Z}}_i)={\displaystyle \frac{2}{n}}\left\{W\left[1-{\lambda }_i-A{\varphi }_i\right]{\mathrm{\sigma }}_S^2+\left[W\left(1-{\lambda }_i\right)\right(\left(1-A\right){\mathrm{\sigma }}_T^2+1)+1-W]\left({\mathrm{\sigma }}_Y^2+{\mathrm{\mu }}_Y^2\right)+W{\lambda }_i\left({\mathrm{\sigma }}_R^2+{\mathrm{\mu }}_R^2\right)-{\left[{\mathrm{\mu }}_Y+\left({\mathrm{\mu }}_R-{\mathrm{\mu }}_Y\right)W{\lambda }_i\right]}^2\right\}, \\ \begin{array}{l}{\lambda }_i=\left(1-\mathrm{\alpha }\right)\left(1-p_i\right), i=1,2,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\\ {\varphi }_i=p_i\left(1-\mathrm{\alpha }\right), i=1,2,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\\ p_1\ne p_2.\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\end{array} \end{gathered}$$

In Equations (2)–(6), the following symbols are used:

• $Y:$ The true response to the sensitive question. This random variable has mean ${\mu }_Y$ and variance ${\sigma }_Y^2$.
• $Z_i:$ The response collected from the respondent in the ith sub-sample, $i=\mathrm{1,2}$. This random variable has mean ${\mathrm{\mu }}_{Zi}$ and variance ${\sigma }_{Zi}^2$.
• $S:$ an additive scrambling variable with mean ${\mathrm{\mu }}_S=0$ and variance ${\sigma }_S^2$.
• $T:$ A multiplicative scrambling variable with mean ${\mathrm{\mu }}_T=1$ and variance ${\sigma }_T^2$. $T$ is independent of S and Y.
• $R:$ response to unrelated question with mean ${\mathrm{\mu }}_R$ and variance ${\sigma }_R^2$.
• $n:$ The sample size. In split sampling, $n$ is split into $n_1$ and $n_2$, where $n_1+n_2=n$.
• $p_i:$ the probability that an individual that has been assigned to the Greenberg sub-model within sub-sample $i$ is assigned the sensitive question, as opposed to the unrelated question.
• $A:$ the probability that a respondent will trust the RRT methodology without additional scrambling.
• $W:$ the sensitivity level of the sensitive question, that is, a proportion $(1-W)$ of the respondents do not consider the question sensitive and are willing to provide true responses without scrambling.
• $X:$ The auxiliary variable with known mean ${\mathrm{\mu }}_X$ and known variance ${\mathrm{\sigma }}_X^2$. This variable is known to have a strong positive correlation with $Y$.

The privacy provided by the MOET model is given by

$$\begin{gathered} {\mathsf{\nabla }}^a={\displaystyle \frac{1}{2}}\left\{2\mathrm{\alpha }A{\sigma }_S^2+\left({2-\lambda }_1-{\lambda }_2\right)\left(1-A\right)\left[\left({\mathrm{\sigma }}_Y^2+{\mu }_Y^2\right){\mathrm{\sigma }}_T^2+{\mathrm{\sigma }}_S^2\right] \\ \hspace{1em}\hspace{1em}\hspace{1em} \hspace{1em}\hspace{1em}\hspace{1em}+\left({\lambda }_1+{\lambda }_2\right)\left[{\mathrm{\sigma }}_Y^2+{\mathrm{\sigma }}_R^2+{\left({\mu }_Y-{\mu }_R\right)}^2\right]\right\}, \end{gathered}$$

(4)

where

$${\lambda }_1=\left(1-\mathrm{\alpha }\right)\left(1-p_1\right),$$

$${\lambda }_2=\left(1-\mathrm{\alpha }\right)\left(1-p_2\right),$$

$$p_1\ne p_2.$$

Gupta et al. further proposed a ratio estimator for the MOET model, consistent with standard ratio estimator formulation as represented by Thompson (2012) [18,19]. The estimator and an expression for the model’s efficiency (MSE) are given in Equations (5) and (6). These can be used when high-quality auxiliary information is available.

$${\widehat{\mathrm{\mu }}}_{YR}=\left[{\displaystyle \frac{1-p_1}{p_2-p_1}}{\overline{Z}}_2-{\displaystyle \frac{1-p_2}{p_2-p_1}}{\overline{Z}}_1\right]\left[{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{{\mathrm{\mu }}_X}{{\overline{x}}_1}}+{\displaystyle \frac{{\mathrm{\mu }}_X}{{\overline{x}}_2}}\right)\right].$$

(5)

$$\mathrm{M}\mathrm{S}\mathrm{E}\left({\widehat{\mu }}_{YR}\right)=\left[{{\left({\displaystyle \frac{1-p_1}{p_2-p_1}}\right)}^2\mathrm{V}\mathrm{a}\mathrm{r}(\overline{Z}}_2)+{ {\left({\displaystyle \frac{1-p_2}{p_2-p_1}}\right)}^2\mathrm{V}\mathrm{a}\mathrm{r}(\overline{Z}}_1)\right]+{\displaystyle \frac{1}{n}}{\left({\displaystyle \frac{{\mu }_Y}{{\mu }_X}}\right)}^2{\sigma }_X^2-{\displaystyle \frac{2}{n}}\left({\displaystyle \frac{{\mu }_Y}{{\mu }_X}}\right){\sigma }_{XY},$$

(6)

3. Reflecting Measurement Error in Our MOET Basic and Ratio Estimators

When variables are contaminated with measurement error, this will lead to less accurate estimates. To explore this, we will now propose basic and ratio estimators in the presence of measurement error.

3.1. Development of Basic Estimator Accounting for Measurement Error

The basic MOET mean estimator was given in Equation (2) previously. A new version of this estimator that accounts for measurement error can be represented as follows:

$${\widehat{\mu }}_{Y\left(ME\right)}={\displaystyle \frac{1-p_1}{p_2-p_1}}{\overline{z}}_2-{\displaystyle \frac{1-p_2}{p_2-p_1}}{\overline{z}}_1,$$

(7)

where

• ${\overline{z}}_i$ is the observed sample mean of split sample $i$;
• ${\overline{Z}}_i={\mathrm{\mu }}_{\mathrm{Z}\mathrm{i}}$ is the theoretical mean value of $Z$ in split sample $i$, with measurement error absent;
• ${\overline{Z}}_i^{\prime }={\overline{z}}_i-{\overline{Z}}_i$ is the mean effect of measurement error.

Equation (7) could equally be written as follows:

$${\widehat{\mu }}_{Y\left(ME\right)}={\displaystyle \frac{1-p_1}{p_2-p_1}}{\overline{Z}}_2-{\displaystyle \frac{1-p_2}{p_2-p_1}}{\overline{Z}}_1+{\displaystyle \frac{1-p_1}{p_2-p_1}}{\overline{Z}}_2^{\prime }-{\displaystyle \frac{1-p_2}{p_2-p_1}}{\overline{Z}}_1^{\prime }.$$

(8)

Since E(${\overline{Z}}_i^{\prime }$)$=0$, this estimator is obviously unbiased.

Turning our attention to the MSE/variance of this estimator, it is easy to see that

$${\widehat{\mu }}_{Y\left(ME\right)}={\mu }_Y+\left[{\displaystyle \frac{1-p_1}{p_2-p_1}}{\overline{Z}}_2^{\prime }-{\displaystyle \frac{1-p_2}{p_2-p_1}}{\overline{Z}}_1^{\prime }\right].$$

(9)

From this expression, one can directly conclude that

$$\mathrm{V}\mathrm{a}\mathrm{r}\left({\widehat{\mu }}_{Y\left(ME\right)}\right)=\mathrm{V}\mathrm{a}\mathrm{r}\left({\mu }_Y\right)+{\left({\displaystyle \frac{1-p_1}{p_2-p_1}}\right)}^2\mathrm{V}\mathrm{a}\mathrm{r}\left({\overline{Z}}_2^{\prime }\right)+{\left({\displaystyle \frac{1-p_2}{p_2-p_1}}\right)}^2\mathrm{V}\mathrm{a}\mathrm{r}\left({\overline{Z}}_1^{\prime }\right).$$

(10)

Since $Var\left({\mu }_Y\right)=0$, it follows that the variance of the basic estimator in the presence of measurement error can be written as follows:

$$\mathrm{V}\mathrm{a}\mathrm{r}({\widehat{\mu }}_{Y\left(ME\right)})={\left({\displaystyle \frac{1-p_1}{p_2-p_1}}\right)}^2\mathrm{V}\mathrm{a}\mathrm{r}\left({\overline{Z}}_2^{\prime }\right)+{\left({\displaystyle \frac{1-p_2}{p_2-p_1}}\right)}^2\mathrm{V}\mathrm{a}\mathrm{r}\left({\overline{Z}}_1^{\prime }\right).$$

(11)

We now let the random variable $U$represent the measurement error associated with $Z$, where $U$ and $Z$ are independent and $E\left(U\right)=0$. It follows from ${\overline{Z}}_i^{\prime }={\overline{Z}}_i+\overline{U}$ that

$$\mathrm{V}\mathrm{a}\mathrm{r}\left({\overline{Z}}_i^{\prime }\right)={\displaystyle \frac{{\mathrm{\sigma }}_{Zi}^2}{n_i}}+{\displaystyle \frac{{\mathrm{\sigma }}_U^2}{n_i}}.$$

(12)

Since MSE equals variance due to zero bias, we conclude for an equally split sample that

$$\mathrm{M}\mathrm{S}\mathrm{E}\left({\widehat{\mu }}_{Y\left(ME\right)}\right)={\displaystyle \frac{2}{n}}\left[{\left({\displaystyle \frac{1-p_2}{p_2-p_1}}\right)}^2\left({\mathrm{\sigma }}_{Z1}^2+{\mathrm{\sigma }}_U^2\right)+{\left({\displaystyle \frac{1-p_1}{p_2-p_1}}\right)}^2\left({\mathrm{\sigma }}_{Z2}^2+{\mathrm{\sigma }}_U^2\right)\right],$$

(13)

where

$$\begin{gathered} {\mathrm{\sigma }}_{Zi}^2=\left[W\left[1-{\lambda }_i-A{\varphi }_i\right]{\mathrm{\sigma }}_S^2+\left[W\left(1-{\lambda }_i\right)\left(\left(1-A\right){\mathrm{\sigma }}_T^2+1\right)+1-W\right]\left({\mathrm{\sigma }}_Y^2+{\mu }_Y^2\right)+W{\lambda }_i\left({\mathrm{\sigma }}_R^2+{\mu }_R^2\right) \\ -{\left[{\mu }_Y+\left({\mu }_R-{\mu }_Y\right)W{\lambda }_i\right]}^2\right],\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \end{gathered}$$

$${\lambda }_i=\left(1-\mathrm{\alpha }\right)\left(1-p_i\right), i=1, 2,$$

$${\varphi }_i=p_i\left(1-\mathrm{\alpha }\right), i=1, 2,$$

$$p_1\ne p_2.$$

Note that when ${\mathrm{\sigma }}_U^2=0$, this expression can be reduced to the familiar expression for the MSE of the MOET basic estimator, as shown in Equation (3). Therefore, we can rewrite Equation (13) as

$$\begin{gathered} \mathrm{M}\mathrm{S}\mathrm{E}\left({\widehat{\mu }}_{Y\left(ME\right)}\right)={\displaystyle \frac{2}{n}}\left[{\left({\displaystyle \frac{1-p_1}{p_2-p_1}}\right)}^2{\mathrm{\sigma }}_{Z2}^2+{\left({\displaystyle \frac{1-p_2}{p_2-p_1}}\right)}^2{\mathrm{\sigma }}_{Z1}^2\right] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle \frac{2}{n}}\left[{\left({\displaystyle \frac{1-p_1}{p_2-p_1}}\right)}^2+{\left({\displaystyle \frac{1-p_2}{p_2-p_1}}\right)}^2\right]{\mathrm{\sigma }}_U^2 \end{gathered}$$

(14)

This makes it clear that the ME impact on the MSE of the MOET model is independent of model parameters $A$, $W$, and α, as well as the means and variances of the MOET model random variables. While setting $p_1$ and $p_2$ strategically could limit the ME impact, this would be counterproductive, as these values are typically chosen to minimize the MSE associated with $Z_1$and $Z_2$ as per Parker, leading to a larger and more important impact [17].

3.2. Development of Ratio Estimator Reflecting Measurement Error

The ratio MOET mean estimator was shown previously in Equation (5). Its value will be affected not only by the error resulting from the collection of $Z$ values as above, but also by the error resulting from the collection of $\mathrm{X}$ values:

$${\widehat{\mu }}_{YR\left(ME\right)}={\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{1-p_1}{p_2-p_1}}{\overline{z}}_2-{\displaystyle \frac{1-p_2}{p_2-p_1}}{\overline{z}}_1\right]\left[\left({\displaystyle \frac{{\mathrm{\mu }}_{\mathrm{X}}}{{\mathrm{\mu }}_{\mathrm{X}}+{\overline{X}}_1^{\prime }}}\right)+\left({\displaystyle \frac{{\mathrm{\mu }}_X}{{\mathrm{\mu }}_{\mathrm{X}}+{\overline{X}}_2^{\prime }}}\right)\right].$$

(15)

The new variables relevant to this expression are as follows:

• ${\overline{x}}_i$ is the observed sample mean of observed $x$ values in split sample $i$;
• ${\overline{X}}_i={\mathrm{\mu }}_{\mathrm{X}}$ is the theoretical mean value of $X$ in split sample $i$, with an absent measurement error;
• ${\overline{X}}_i^{\prime }={\overline{x}}_i-{\overline{X}}_i$ is the mean effect of measurement associated with $X$.

$V$ is the random variable that represents the measurement error incurred while collecting auxiliary information ($X$), such that $x=X+V$, and $V$ is independent of $U$, $X$, and $Z$.

The mean estimate of the response to the sensitive question, reflecting measurement error, will be

$${\widehat{\mu }}_{YR\left(ME\right)}={\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{1-p_1}{p_2-p_1}}{\overline{z}}_2-{\displaystyle \frac{1-p_2}{p_2-p_1}}{\overline{z}}_1\right]\left[\left({\displaystyle \frac{{\mathrm{\mu }}_{\mathrm{X}}}{{\mathrm{\mu }}_{\mathrm{X}}+{\overline{X}}_1^{\prime }}}\right)+\left({\displaystyle \frac{{\mathrm{\mu }}_{\mathrm{X}}}{{\mathrm{\mu }}_{\mathrm{X}}+{\overline{X}}_2^{\prime }}}\right)\right].$$

(16)

Note that this estimator, like any ratio estimator, will be biased. However, the extent of the bias is not exaggerated by measurement error, which is assumed to have ${\mathrm{\mu }}_{\mathrm{U}}={\mathrm{\mu }}_{\mathrm{V}}=0$. The bias is as follows:

$$\mathrm{B}\mathrm{i}\mathrm{a}\mathrm{s}\left({\widehat{\mu }}_{YR\left(ME\right)}\right)={{\displaystyle \frac{2{\mathrm{\mu }}_{\mathrm{Y}}}{n}}\left({\displaystyle \frac{{\sigma }_X}{{\mathrm{\mu }}_{\mathrm{X}}}}\right)}^2-{\displaystyle \frac{{\sigma }_{XY}}{n{\mathrm{\mu }}_{\mathrm{X}}}}.$$

(17)

We now consider the efficiency of the measurement error-effected ratio estimator. An approximation for the MSE can be found based on first principles according to

$$\mathrm{M}\mathrm{S}\mathrm{E}\left({\widehat{\mu }}_{YR\left(ME\right)}\right)={\mathrm{E}\left({\widehat{\mu }}_{YR\left(ME\right)}-{\mu }_Y\right)}^2.$$

(18)

Following a second order Taylor expansion, we apply the following identities, whose derivations are summarized in Appendix A of this study:

• $$\mathrm{E}\left[{\overline{Z}}_i^{\prime }{\overline{Z}}_i^{\prime }\right]={\displaystyle \frac{1}{n_i}}\left({\sigma }_{Zi}^2+{\sigma }_U^2\right)$$

  (19)
• $$\mathrm{E}\left[{\overline{X}}_i^{\prime }{X}_i^{\prime }\right]={\displaystyle \frac{1}{n_i}}\left({\sigma }_X^2+{\sigma }_V^2\right)$$

  (20)
• $$\mathrm{E}\left[{\overline{X}}_i^{\prime }{\overline{Z}}_i^{\prime }\right]={\displaystyle \frac{1}{n_i}}[{\sigma }_{YX}-W(1-\alpha \left)\right(1-p_i\left)\left({\sigma }_{YX}+{\mathrm{\mu }}_R{\mathrm{\mu }}_X\right)\right]$$

  (21)

Applying these identities and assuming an equally split sample, this expression can be reduced to

$$\begin{array}{ll}\mathrm{M}\mathrm{S}\mathrm{E}\left({\widehat{\mu }}_{YR\left(ME\right)}\right)=& {\displaystyle \frac{{\mathrm{\mu }}_Y^2}{n{\mathrm{\mu }}_X^2}}\left({\sigma }_X^2+{\sigma }_V^2\right)\\ & +{\displaystyle \frac{2}{n}}\left[{\left({\displaystyle \frac{1-p_2}{p_2-p_1}}\right)}^2\left({\sigma }_{Z1}^2+{\sigma }_U^2\right)+{\left({\displaystyle \frac{1-p_1}{p_2-p_1}}\right)}^2\left({\sigma }_{Z2}^2+{\sigma }_U^2\right)\right]\\ & -{\displaystyle \frac{2{\mathrm{\mu }}_{\mathrm{Y}}{\sigma }_{YX}}{n{\mathrm{\mu }}_{\mathrm{X}}}},\end{array}$$

(22)

where

$$\begin{gathered} {\mathrm{\sigma }}_{Zi}^2=[W\left[1-{\lambda }_i-A{\varphi }_i\right]{\mathrm{\sigma }}_S^2+[W\left(1-{\lambda }_i\right)(\left(1-A\right){\mathrm{\sigma }}_T^2+1)+1-W]\left({\mathrm{\sigma }}_Y^2+{\mu }_Y^2\right)+W{\lambda }_i\left({\mathrm{\sigma }}_R^2+{\mu }_R^2\right) \\ -{\left[{\mu }_Y+\left({\mu }_R-{\mu }_Y\right)W{\lambda }_i\right]}^2],\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \end{gathered}$$

$${\lambda }_i=\left(1-\mathrm{\alpha }\right)\left(1-p_i\right), i=1, 2,$$

$${\varphi }_i=p_i\left(1-\mathrm{\alpha }\right), i=1, 2,$$

$$p_1\ne p_2.$$

Note that when ${\mathrm{\sigma }}_U^2=0$ and ${\mathrm{\sigma }}_V^2=0$, this expression can be reduced to the familiar expression for the MSE of the MOET ratio estimator ($\mathrm{M}\mathrm{S}\mathrm{E}\left({\widehat{\mu }}_{YR}\right)$), as shown in Equation (6).

As discussed above, the error associated with the measurement of $Z$, which is represented by the random variable $U$, will be independent of model parameters $A$, $W$, and α, as well as the means and variances of the MOET model random variables. It may seem that the story is different with respect to auxiliary information because $V$ reflects the error in measuring $X$, and according to Equation (22) the variance of $V$ impacts the ratio estimator’s MSE through the term ${\displaystyle \frac{{\mathrm{\mu }}_Y^2}{n{\mathrm{\mu }}_X^2}}{\sigma }_V^2$. But to the extent that the standard deviation of error in measuring $X$ correlates with the size of ${\mu }_X$ (which is expected), there will in fact be no measurement error impact on the ratio estimator MSE.

4. Impacts of Measurement Error

We have discussed the fact that RRT administrative complexities can heighten the advent of measurement error. In this section, we will study the size of measurement error impact on estimation in Section 4.1. Then, in Section 4.2, we will determine how significant ME would have to be to offset the value of using RRT in the first place.

4.1. Impact of Measurement Error on Estimator Efficiency

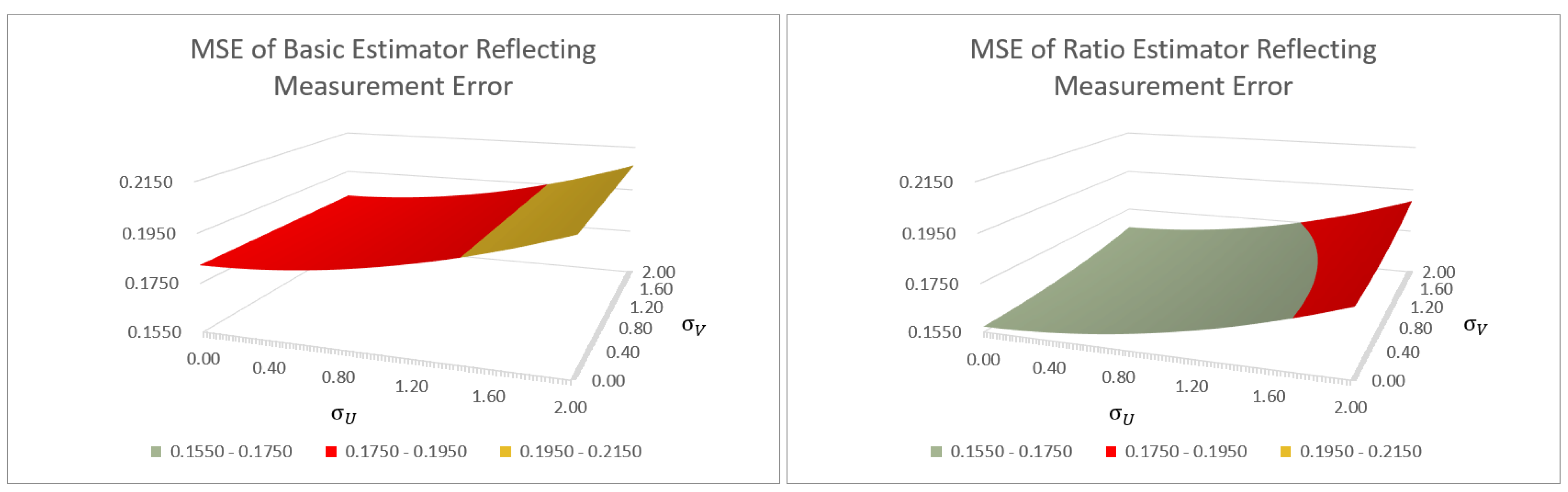
Measurement error will of course be more impactful on MSE when it is large. In Figure 2, we consider a scenario that is consistent with other RRT papers (see, for example, the scenarios assumed in Section 6 of Parker et al. (2024)), but with the addition of measurement error [17]. We consider both the error in measuring $Z$ (represented by the random variable $U$) and in measuring $X$ (represented by the random variable $V$). Figure 2 shows the MSE of the basic and ratio estimators across possible levels of measurement error, as represented by their standard deviations (each ranging from 0 to 2) in a standard scenario represented by the values listed immediately following the figure. Note that ${\sigma }_V$ is represented in the leftside graph to enable direct visual comparison between the two graphs, in spite of the fact that the leftside graph does not contain auxiliary information and therefore MSE does not vary across the ${\sigma }_V$ dimension.

The value of 2 was chosen as the upper limit for standard deviation (see Figure 2) to represent a high measurement error (a standard deviation of 2 implies that the measurement error equals 20% of the mean response value).

We make several observations. First, we see, not surprisingly, that as the measurement error rises, the estimator efficiency declines (MSE increases). We also see that the rate of increase in MSE for the ratio error (which is subject to two kinds of measurement errors) is steeper than that of the basic estimator. The highest MSE shown for the basic estimator (corresponding to ${\sigma }_U=2$) is 13.3% greater than the MSE observed when the measurement error is not accounted for. This can be thought of as the extent to which MSE would be under-represented if the measurement error was in fact at the ${\sigma }_U=2$ level but was not taken into account. In the righthand graph of Figure 2, we see that for the ratio estimator, the MSE rises both when ${\sigma }_U$ rises and when ${\sigma }_V$ rises, that is, MSE increases when there is significant error in the measurement of $Z$ and/or $X$. When there is high error in measuring both (corresponding to ${\sigma }_U={\sigma }_V=2$), then the MSE of the ratio estimator will be 20.6% greater than the MSE observed when the measurement error is not accounted for. But even with maximum measurement error, the MSE of the ratio estimator remains smaller than the MSE of the basic estimator, in this scenario where ${\rho }_{XY}=0.75$. The gain in efficiency realized by making use of auxiliary data is greater than the loss in efficiency attributable to the errors in measuring the data. While Figure 2 represents only one particular scenario, this key result can be generalized by solving the following inequality:

$$MSE\left({\widehat{\mu }}_{YR\left(ME\right)}\right)<MSE\left({\widehat{\mu }}_{Y\left(ME\right)}\right).$$

(23)

A comparison between Equations (13) and (22) makes it immediately clear that this inequality can be reduced to

$${\displaystyle \frac{{\mathrm{\mu }}_Y^2}{n{\mathrm{\mu }}_X^2}}\left({\sigma }_X^2+{\sigma }_V^2\right)<{\displaystyle \frac{2{\mathrm{\mu }}_{\mathrm{Y}}{\sigma }_{YX}}{n{\mathrm{\mu }}_{\mathrm{X}}}}.$$

(24)

Under the standard assumption that $\mathrm{C}\mathrm{V}\left(X\right)=\mathrm{C}\mathrm{V}\left(Y\right)$, the expression can then be simplified and restated as follows:

$${\displaystyle \frac{{\sigma }_V}{{\sigma }_X}}<\sqrt{2{\rho }_{YX}-1}, {\mathrm{\rho }}_{XY}>0.5.$$

(25)

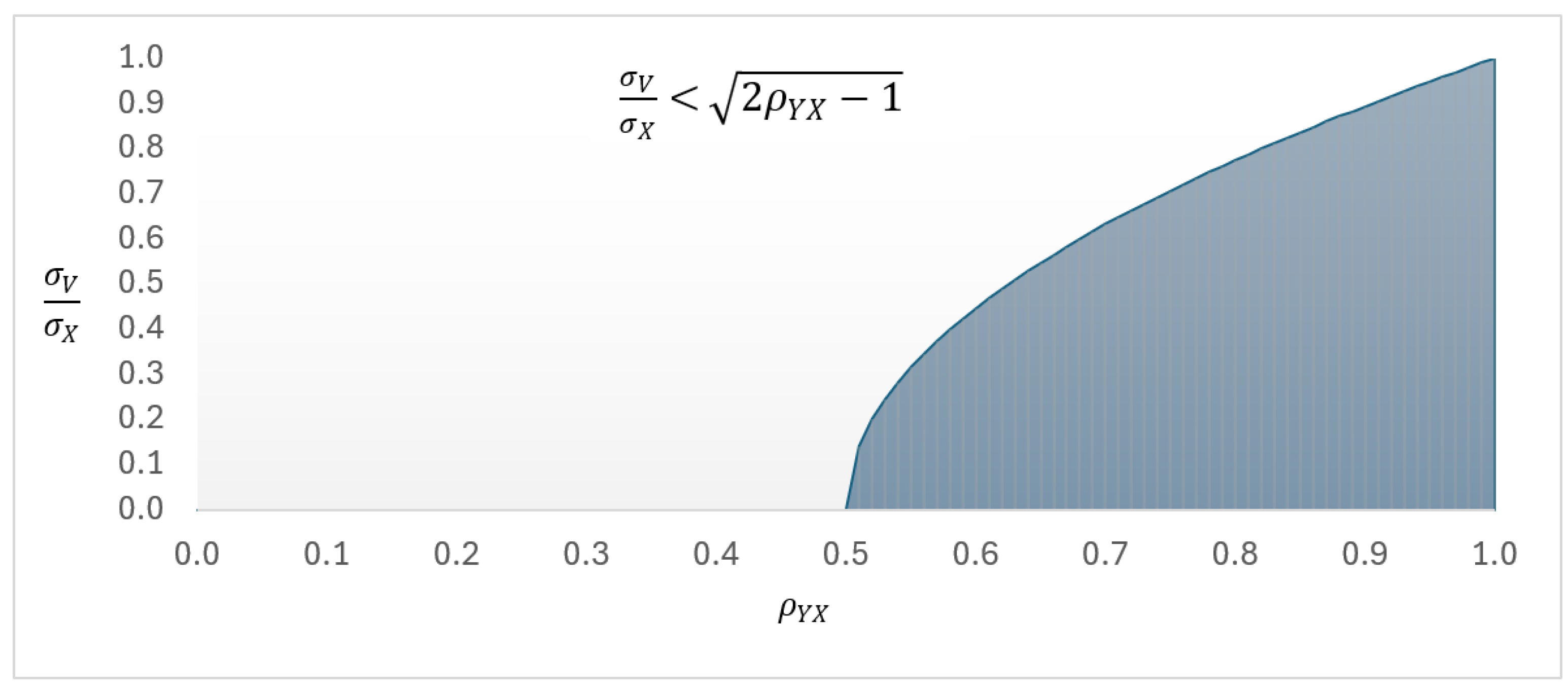
This condition is represented by the shaded region in Figure 3.

This figure shows us, for example, that if ${\rho }_{XY}=0.6$, then estimation will benefit from auxiliary information provided that the standard deviation attributable to ME is less than ~45% of the standard deviation associated with the auxiliary variable. In short, Equation (24) does not impose a restrictive condition, as ${\sigma }_X$ will generally be much larger than ${\sigma }_V$. In short, we can conclude that the specter of measurement error will infrequently discourage the use of well-correlated auxiliary information.

4.2. Measurement Error Impact on RRT Objective: Inducing Truthfulness

In this subsection, we study whether the benefit of RRT (removal of lying bias) outweighs its cost (addition of measurement error). Because RRT methods often require the respondent to consider whether they want to answer the sensitive question directly, to scramble their true response, to answer an unrelated question, to opt for additional levels of scrambling, and so on, the administration of RRT can result in elevated levels of measurement error.

For this reason, we now turn our focus to an important question: is there a point at which measurement error becomes so significant that it nullifies the RRT model’s ability to secure truthful responses efficiently? We develop a model to study this issue. The model relies on several key assumptions. The reasonableness of these assumptions will be discussed at the end of this subsection.

Our model is constructed as follows:

• We define a parameter $\mathrm{L}\mathrm{B}$ (lying bias), which represents the extent to which a group’s mean response will be impacted by untruthfulness, without some means of mitigation like RRT. As some questions are more sensitive than others, we will consider sensitive questions with 1%, 5%, and 10% lying bias (LB). For example, if the mean group response to a sensitive question had a +5% lying bias, and the true mean response to the sensitive question was 10, then a direct survey that employed no tactics to reduce the bias would see an average response of 10.5.
• We will model untruthfulness as a normal random variable $K$ with mean ${\mathrm{\mu }}_{\mathrm{k}}=LB\ast {\mathrm{\mu }}_{\mathrm{Y}}$ and standard deviation ${\mathrm{\sigma }}_{\mathrm{k}}={\displaystyle \frac{LB\ast {\mathrm{\mu }}_{\mathrm{Y}}}{2}}$. We choose this value of ${\mathrm{\sigma }}_{\mathrm{k}}$ because it fixes the range of lie-adjusted responses so that the lie-adjusted mean of ${\mathrm{\mu }}_{\mathrm{Y}}+{\mathrm{\mu }}_{\mathrm{k}},$ is precisely two standard deviations from the true mean ${\mathrm{\mu }}_{\mathrm{Y}}$, and therefore approximately 97.5% of lie-adjusted responses will be adjusted in the same direction as the assumed bias.
• We define $Y_{DS}$ as a random variable that reflects the responses that would be yielded by a survey soliciting direct responses to a sensitive question. Responses will equal truthful responses plus the impact of lying. Specifically,

●

$$Y_{DS}=Y+K.$$

(26)

●

$$Y_{DS}~N\left((1+\mathrm{L}\mathrm{B}){\mathrm{\mu }}_{\mathrm{Y}},\sqrt{{\mathrm{\sigma }}_Y^2+{\displaystyle \frac{LB*{\mathrm{\mu }}_{\mathrm{Y}}}{2}}}\right).$$

(27)

In various scenarios representing different levels of measurement error and lying bias, we want to calculate the probability that our basic MOET estimator outperforms estimation based on a direct survey (that will yield responses with some level of untruthfulness, but will not face material measurement error). Specifically, we calculate the probability that the MOET estimator will result in an estimate closer to the true value than the direct survey estimate will:

$$\mathrm{Pr}\left(\left|{\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}-{\mathrm{\mu }}_Y\right|<\left| {\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}-{\mathrm{\mu }}_Y\right|\right).$$

(28)

Using basic inequality identities, expression (28) can be represented as

$$\begin{gathered} 1-\mathrm{Pr}\left(-({\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}-{\mathrm{\mu }}_Y)<{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}-{\mathrm{\mu }}_Y<{\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}-{\mathrm{\mu }}_Y\right)-PR({\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}-{\mathrm{\mu }}_Y< \\ {\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}-{\mathrm{\mu }}_Y<-({\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}-{\mathrm{\mu }}_Y\left)\right), \end{gathered}$$

(29)

which can be rewritten as

$$\begin{gathered} 1-\mathrm{Pr}\left({\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}+{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}>2{\mathrm{\mu }}_Y, {{\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}-\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}>0\right)-\mathrm{P}\mathrm{r}({\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}+{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}< \\ 2{\mathrm{\mu }}_Y,{{\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}-\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}<0). \end{gathered}$$

(30)

To calculate the probabilities in the expression above, we need the distributions of $\left({\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}+{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}\right)$ and $\left({\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}-{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}\right)$. Recalling that ${\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}={\widehat{\mu }}_{\mathrm{Y}}+\overline{U}$ and ${\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}=\overline{Y}+\overline{K}$, we can write

$${\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}+{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}={\widehat{\mu }}_{\mathrm{Y}}+\overline{Y}+\overline{U}+\overline{K},$$

(31)

$${\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}-{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}={\widehat{\mu }}_{\mathrm{Y}}-\overline{Y}+\overline{U}-\overline{K}.$$

(32)

Before concerning ourselves with $\overline{U}$ and $\overline{K}$, we find the distributions of ${\widehat{\mu }}_{\mathrm{Y}}+\overline{Y}$ and ${\widehat{\mu }}_{\mathrm{Y}}-\overline{Y}$. As ${\widehat{\mu }}_{\mathrm{Y}}$ and $\overline{Y}$are both estimates of the quantity ${\mu }_{\mathrm{Y}}$ based on the same set of sampled $Y$ values, they are correlated. None the less, ${\widehat{\mu }}_{\mathrm{Y}}$ +/− $\overline{Y}$ have normal distributions as represented below:

$${\widehat{\mu }}_{\mathrm{Y}}+\overline{Y}~N\left(2{\mu }_{\mathrm{Y}},\sqrt{{\displaystyle \frac{2}{n}}{\left({\displaystyle \frac{1-p_1}{p_2-p_1}}\right)}^2{\mathrm{\sigma }}_{Z_2}^2+{\displaystyle \frac{2}{n}}{\left({\displaystyle \frac{1-p_2}{p_2-p_1}}\right)}^2{\mathrm{\sigma }}_{Z_1}^2+{\displaystyle \frac{1}{n}}{\mathrm{\sigma }}_Y^2+2{\rho }_{{\widehat{\mu }}_{\mathrm{Y}}+\overline{Y},{\widehat{\mu }}_{\mathrm{Y}}-\overline{Y}}\sqrt{{\displaystyle \frac{1}{n}}{\mathrm{\sigma }}_Y^2}\sqrt{{\displaystyle \frac{2}{n}}{\left({\displaystyle \frac{1-p_1}{p_2-p_1}}\right)}^2{\mathrm{\sigma }}_{Z_2}^2+{\displaystyle \frac{2}{n}}{\left({\displaystyle \frac{1-p_2}{p_2-p_1}}\right)}^2{\mathrm{\sigma }}_{Z_1}^2}}\right),$$

(33)

$${\widehat{\mu }}_{\mathrm{Y}}-\overline{Y}~N\left(0,\sqrt{{\displaystyle \frac{2}{n}}{\left({\displaystyle \frac{1-p_1}{p_2-p_1}}\right)}^2{\mathrm{\sigma }}_{Z_2}^2+{\displaystyle \frac{2}{n}}{\left({\displaystyle \frac{1-p_2}{p_2-p_1}}\right)}^2{\mathrm{\sigma }}_{Z_1}^2+{\displaystyle \frac{1}{n}}{\mathrm{\sigma }}_Y^2-2{\rho }_{{\widehat{\mu }}_{\mathrm{Y}}+\overline{Y},{\widehat{\mu }}_{\mathrm{Y}}-\overline{Y}}\sqrt{{\displaystyle \frac{1}{n}}{\mathrm{\sigma }}_Y^2}\sqrt{{\displaystyle \frac{2}{n}}{\left({\displaystyle \frac{1-p_1}{p_2-p_1}}\right)}^2{\mathrm{\sigma }}_{Z_2}^2+{\displaystyle \frac{2}{n}}{\left({\displaystyle \frac{1-p_2}{p_2-p_1}}\right)}^2{\mathrm{\sigma }}_{Z_1}^2}}\right).$$

(34)

$U$ and $K$ are normal and independent of each other and independent of both ${\widehat{\mu }}_{\mathrm{Y}}+\overline{Y}$ and ${\widehat{\mu }}_{\mathrm{Y}}-\overline{Y}$. We can therefore find the distributions of $\left({\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}+{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}\right)$ and $\left({\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}-{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}\right)$ shown in Equations (31) and (32). We conclude that

$${\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}+{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}~N\left(\left(2+LB\right){\mathrm{\mu }}_{\mathrm{Y}},\sqrt{{\displaystyle \frac{2}{n}}{\left({\displaystyle \frac{1-p_1}{p_2-p_1}}\right)}^2{\mathrm{\sigma }}_{Z_2}^2+{\displaystyle \frac{2}{n}}{\left({\displaystyle \frac{1-p_2}{p_2-p_1}}\right)}^2{\mathrm{\sigma }}_{Z_1}^2+{\displaystyle \frac{1}{n}}{\mathrm{\sigma }}_Y^2+2{\rho }_{{\widehat{\mu }}_{\mathrm{Y}}+\overline{Y},{\widehat{\mu }}_{\mathrm{Y}}-\overline{Y}}\sqrt{{\displaystyle \frac{1}{n}}{\mathrm{\sigma }}_Y^2}\sqrt{{\displaystyle \frac{2}{n}}{\left({\displaystyle \frac{1-p_1}{p_2-p_1}}\right)}^2{\mathrm{\sigma }}_{Z_2}^2+{\displaystyle \frac{2}{n}}{\left({\displaystyle \frac{1-p_2}{p_2-p_1}}\right)}^2{\mathrm{\sigma }}_{Z_1}^2}+{\displaystyle \frac{2}{n}}{\mathrm{\sigma }}_K^2+{\displaystyle \frac{2}{n}}{\mathrm{\sigma }}_U^2}\right),$$

(35)

$${\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}-{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}~N\left(-LB{\mathrm{\mu }}_{\mathrm{Y}},\sqrt{{\displaystyle \frac{2}{n}}{\left({\displaystyle \frac{1-p_1}{p_2-p_1}}\right)}^2{\mathrm{\sigma }}_{Z_2}^2+{\displaystyle \frac{2}{n}}{\left({\displaystyle \frac{1-p_2}{p_2-p_1}}\right)}^2{\mathrm{\sigma }}_{Z_1}^2+{\displaystyle \frac{1}{n}}{\mathrm{\sigma }}_Y^2-2{\rho }_{{\widehat{\mu }}_{\mathrm{Y}}+\overline{Y},{\widehat{\mu }}_{\mathrm{Y}}-\overline{Y}}\sqrt{{\displaystyle \frac{1}{n}}{\mathrm{\sigma }}_Y^2}\sqrt{{\displaystyle \frac{2}{n}}{\left({\displaystyle \frac{1-p_1}{p_2-p_1}}\right)}^2{\mathrm{\sigma }}_{Z_2}^2+{\displaystyle \frac{2}{n}}{\left({\displaystyle \frac{1-p_2}{p_2-p_1}}\right)}^2{\mathrm{\sigma }}_{Z_1}^2}+{\displaystyle \frac{2}{n}}{\mathrm{\sigma }}_K^2+{\displaystyle \frac{2}{n}}{\mathrm{\sigma }}_U^2}\right).$$

(36)

Written in more simplified terms,

$${\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}+{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}~N\left(\left(2+LB\right){\mathrm{\mu }}_{\mathrm{Y}},\sqrt{\mathrm{M}\mathrm{S}\mathrm{E}\left({\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}\right)+{\displaystyle \frac{1}{n}}{\mathrm{\sigma }}_Y^2+2{\rho }_{{\widehat{\mu }}_{\mathrm{Y}}+\overline{Y},{\widehat{\mu }}_{\mathrm{Y}}-\overline{Y}}\sqrt{{\displaystyle \frac{1}{n}}{\mathrm{\sigma }}_Y^2\mathrm{M}\mathrm{S}\mathrm{E}\left({\widehat{\mu }}_{\mathrm{Y}}\right)}+{\displaystyle \frac{2}{n}}{\mathrm{\sigma }}_K^2}\right),$$

(37)

$${\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}-{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}~N\left(-LB{\mathrm{\mu }}_{\mathrm{Y}},\sqrt{\mathrm{M}\mathrm{S}\mathrm{E}\left({\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}\right)+{\displaystyle \frac{1}{n}}{\mathrm{\sigma }}_Y^2-2{\rho }_{{\widehat{\mu }}_{\mathrm{Y}}+\overline{Y},{\widehat{\mu }}_{\mathrm{Y}}-\overline{Y}}\sqrt{{\displaystyle \frac{1}{n}}{\mathrm{\sigma }}_Y^2\mathrm{M}\mathrm{S}\mathrm{E}\left({\widehat{\mu }}_{\mathrm{Y}}\right)}+{\displaystyle \frac{2}{n}}{\mathrm{\sigma }}_K^2}\right).$$

(38)

The pair of random variables $\left({\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}+{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}\right)$ and $\left({\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}-{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}\right)$ is bivariate normal, so

$$\left({\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}+{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}},{\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}-{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}\right)~BVN\left({\mathrm{\mu }}_{{\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}+{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}},{\mathrm{\mu }}_{{\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}-{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}},{\mathrm{\sigma }}_{{\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}+{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}},{\mathrm{\sigma }}_{{\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}-{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}}, {\rho }_{{\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}+{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}},{\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}-{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}}\right),$$

(39)

where

$${\mathrm{\mu }}_{{\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}+{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}}=\left(2+LB\right){\mathrm{\mu }}_{\mathrm{Y}},$$

$${\mathrm{\mu }}_{{\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}-{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}}=-LB{\mathrm{\mu }}_{\mathrm{Y}},$$

$${\mathrm{\sigma }}_{{\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}+{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}}=\sqrt{\mathrm{M}\mathrm{S}\mathrm{E}\left({\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}\right)+{\displaystyle \frac{1}{n}}{\mathrm{\sigma }}_Y^2+2{\rho }_{{\widehat{\mu }}_{\mathrm{Y}}+\overline{Y},{\widehat{\mu }}_{\mathrm{Y}}-\overline{Y}}\sqrt{{\displaystyle \frac{1}{n}}{\mathrm{\sigma }}_Y^2\mathrm{M}\mathrm{S}\mathrm{E}\left({\widehat{\mu }}_{\mathrm{Y}}\right)}+{\displaystyle \frac{2}{n}}{\mathrm{\sigma }}_K^2},$$

$${\mathrm{\sigma }}_{{\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}-{\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}}=\sqrt{\mathrm{M}\mathrm{S}\mathrm{E}\left({\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}\right)+{\displaystyle \frac{1}{n}}{\mathrm{\sigma }}_Y^2-2{\rho }_{{\widehat{\mu }}_{\mathrm{Y}}+\overline{Y},{\widehat{\mu }}_{\mathrm{Y}}-\overline{Y}}\sqrt{{\displaystyle \frac{1}{n}}{\mathrm{\sigma }}_Y^2\mathrm{M}\mathrm{S}\mathrm{E}\left({\widehat{\mu }}_{\mathrm{Y}}\right)}+{\displaystyle \frac{2}{n}}{\mathrm{\sigma }}_K^2}.$$

With this joint distribution specified, Equation (28), which represents the probability that the basic estimator results in an estimate closer to the true value of ${\mathrm{\mu }}_Y$ than a direct survey would, can be studied.

Note that a similar theoretical expression to Equation (28), representing the probability that the ratio estimator would result in an estimate closer to the true value of ${\mathrm{\mu }}_Y$ than a direct survey would (i.e., $\mathrm{Pr}\left(\left|{\widehat{\mu }}_{\mathrm{Y}\mathrm{R}\left(\mathrm{M}\mathrm{E}\right)}-{\mathrm{\mu }}_Y\right|<\left| {\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}-{\mathrm{\mu }}_Y\right|\right)$), could not be derived because the distribution of the key quantity ${\widehat{\mu }}_{\mathrm{Y}\mathrm{R}\left(\mathrm{M}\mathrm{E}\right)}$ equals the ratio of two correlated normal variables, and this expression has no known distribution.

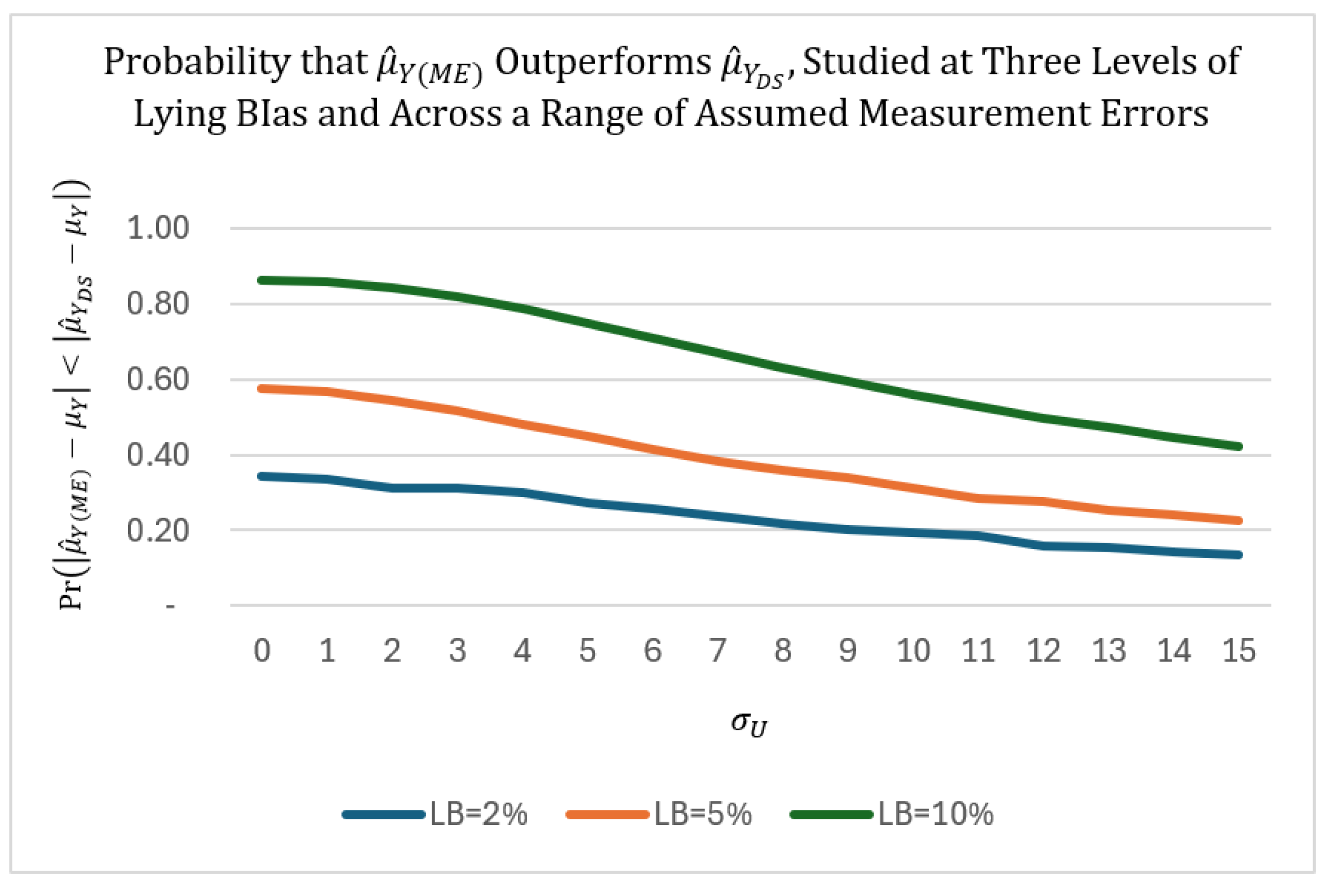
Figure 4 shows the probability that ${\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}$ will be closer to the true value ${\mu }_{\mathrm{Y}}$ than ${\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}$ is, over a range of measurement errors (${\mathrm{\sigma }}_U$) in a standard scenario represented by the values listed immediately following the figure. For illustrative purposes, we assume that the direct survey, which does not involve the administrative complexities inherent to RRT models, is not subject to measurement error. However, the direct survey will be impacted by untruthfulness (lying bias = LB). In contrast, the RRT model will eliminate untruthfulness but will be subject to measurement error. The probabilities represented in the figure are based on theoretical calculations that use empirical estimates for correlations; the calculated theoretical probabilities match empirical simulations closely.

As would be expected, when higher levels of untruthfulness are present and measurement error is low, the RRT-based estimate ${\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}$ will be dramatically more reliable than the direct survey estimate ${\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}$. For example, when there is no measurement error at all and respondents overreport their true responses by 10% (LB = +10%), ${\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}$ will yield an estimate closer to the true mean response than ${\widehat{\mu }}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}$ with 86% likelihood. Also, as expected, the superiority of ${\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}$ declines as the measurement error increases. But the most important observation we make is that the probability of MOET superiority deteriorates only gradually as ME rises. Therefore, for a given level of LB and sample size, small levels of ME do not excessively undermine MOET estimation. For example, when $\mathrm{L}\mathrm{B}=10\%$, ${\widehat{\mu }}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}$ will continue to be superior to ${\widehat{\mathrm{\mu }}}_{{\mathrm{Y}}_{\mathrm{D}\mathrm{S}}}$ (closer to the true value with more than 50% likelihood) except in implausible scenarios where ${\mathrm{\sigma }}_U>12$.

While our model is specific both in terms of assumptions and in terms of scenario, its conclusions are strong, as seen in Section 6. When LB is material and sample sizes are adequate, plausible levels of ME do not reduce MOET performance so drastically that its benefit (estimating truthful responses accurately) is thwarted.

5. Measurement Error Accentuates Privacy

Privacy is an absolutely critical element of all RRT methodologies. Lanke (1976) intimated that in fact the most important quality of an RRT model is the extent to which it “protect[s] the privacy of interviewees” [20]. Indeed, it is the fact that the respondent’s true response to a sensitive question is scrambled (as in Warner-type quantitative RRT models) or hidden among similar-looking answers to nonsensitive questions (as in Greenberg-type quantitative RRT models) that gives the respondent the confidence to respond truthfully, free from possible shame, embarrassment, or even legal repercussions. But the collection of auxiliary information may serve to undermine privacy, unmasking the respondent’s identity and revealing their true response to the sensitive question, thereby undercutting the very fundamentals of RRT. Arnab and Dorffner (2006) grappled with this issue, noting that “most surveys are complex” and that usually “information of more than one character is collected at a time. Some of them are of a confidential nature while the others are not” [21]. The collection of additional auxiliary information can importantly undermine privacy; at an extreme level, if auxiliary information was perfectly correlated with the response to the sensitive question, knowledge of $X$ would immediately lead to knowledge of $Y$.

Parker et al. (2024) pointed out that when auxiliary information ($X$) is collected, privacy can be represented as in [17]:

$$\mathsf{\nabla }\left(Y, X\right)=\left(1-\varphi \right)\mathsf{\nabla }\left(Y\right),$$

(40)

because $\mathsf{\nabla }\left(Y, X\right)$ is bound by 0 and $\mathsf{\nabla }\left(Y\right).$ $\mathsf{\nabla }\left(Y\right)$ and $\varphi$ are defined as follows:

• $\mathit{\nabla }\left(Y\right)$: privacy of the RRT model applied to the sensitive question whose true response is represented by the random variable $Y$.
• $\varphi$: percentage reduction in privacy associated with auxiliary data.

It follows that privacy loss due to auxiliary information is

$$\mathsf{\nabla }L=\mathsf{\nabla }\left(Y\right)-\mathsf{\nabla }\left(Y, X\right)=\varphi \mathsf{\nabla }\left(Y\right).$$

(41)

Using Yan et al.’s (2008) definition of privacy $\mathsf{\nabla }\left(Y\right)=\mathrm{E}\left[{\left(Z-Y\right)}^2\right]$, privacy in the presence of measurement error would be as follows [22]:

$${\mathsf{\nabla }}_{\left(ME\right)}\left(Y\right)=\mathrm{E}\left[{\left(Z+U-Y\right)}^2\right].$$

(42)

Recalling that $U$ is uncorrelated with $Z$ or $Y$, and that $\mathrm{E}\left[U\right]$ = 0, this expression can be simplified to

$${\mathsf{\nabla }}_{\left(ME\right)}\left(Y\right)=\mathrm{E}\left[Z^2\right]+\mathrm{E}\left[Y^2\right]-2\mathrm{E}\left[\mathrm{Z}\mathrm{Y}\right]+\mathrm{E}\left[U^2\right],$$

(43)

and can be further reduced to

$${\mathsf{\nabla }}_{\left(ME\right)}\left(Y\right)=\mathsf{\nabla }\left(Y\right)+{\sigma }_U^2.$$

(44)

Equation (44) makes it clear that privacy, surprisingly, improves as a result of measurement error. This is because measurement error inadvertently results in extra response scrambling.

When auxiliary information that reduces privacy is collected, privacy can be represented:

$${\mathsf{\nabla }}_{\left(ME\right)}\left(Y, X\right)=\left(1-\varphi \right)\mathsf{\nabla }\left(Y\right)+{\sigma }_U^2.$$

(45)

Note that auxiliary information will reduce the privacy resulting from RRT perturbation, but not the privacy resulting from measurement error. With this in mind, the privacy loss that occurs when ME is present will be the same as when ME is not present:

$${\mathsf{\nabla }L}_{\left(ME\right)}\left(Y, X\right)=\varphi \mathsf{\nabla }\left(Y\right).$$

(46)

For the MOET model, Parker et al. calculated privacy as

$$\begin{gathered} {\mathsf{\nabla }}^a={\displaystyle \frac{1}{2}}\left\{2\mathrm{\alpha }A{\sigma }_S^2+\left({2-\lambda }_1-{\lambda }_2\right)\left(1-A\right)\left[\left({\mathrm{\sigma }}_Y^2+{\mathrm{\mu }}_Y^2\right){\mathrm{\sigma }}_T^2+{\mathrm{\sigma }}_S^2\right] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\left({\lambda }_1+{\lambda }_2\right)\left[{\mathrm{\sigma }}_Y^2+{\mathrm{\sigma }}_R^2{\left({\mathrm{\mu }}_Y-{\mathrm{\mu }}_R\right)}^2\right]\right\}, \end{gathered}$$

(47)

where the superscript $a$ in the above expression reminds us that this measure has been adjusted to reflect the fact that optionality does not undermine privacy for the proportion of respondents $\left(1-W\right)$ who do not consider the sensitive question to be sensitive to them, as per Gupta et al. (2002) [23].

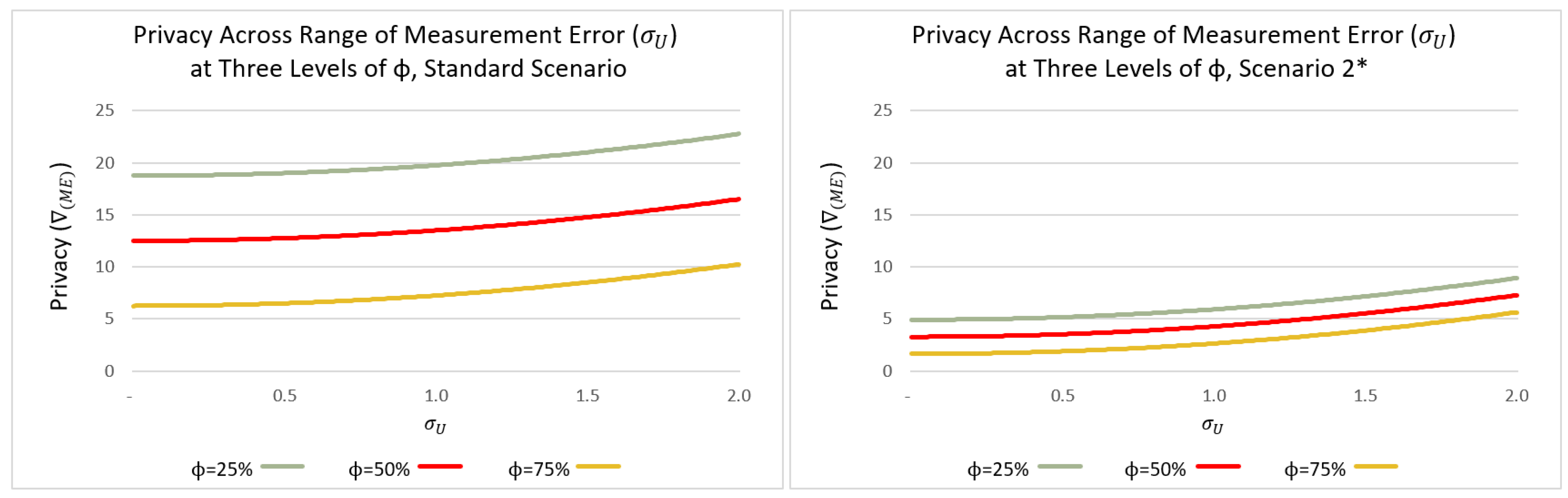
In Figure 5, we show the privacy that the MOET model provides when auxiliary information is collected, across a range of ME and at three different levels of privacy reduction due to auxiliary information ($\varphi$) in two reasonable scenarios, as represented by the values listed immediately following the figure.

The graph on the left represents the standard baseline scenario underlying the other graphs and figures throughout this study, with ${\mathrm{\sigma }}_Y={\mathrm{\sigma }}_X={\mathrm{\sigma }}_R=5$. In the standard scenario, privacy is higher by 21%, 32%, and 64% at ${\mathrm{\sigma }}_U=2$ than at ${\mathrm{\sigma }}_U=0$ at the three assumed levels of $\varphi$. The graph on the right represents another plausible scenario, in which the natural variability of $Y$ is smaller: ${\mathrm{\sigma }}_Y=2$. We also chose ${\mathrm{\sigma }}_X=2$ in this scenario because it is standard to assume $\mathrm{C}\mathrm{V}\left(X\right)=\mathrm{C}\mathrm{V}\left(Y\right)$, and we set ${\mathrm{\sigma }}_R=2$ because the parameters of the unrelated question should be similar to the parameters of the sensitive question. In this scenario, privacy is higher by 81%, 122%, and 234% at ${\mathrm{\sigma }}_U=2$ than at ${\mathrm{\sigma }}_U=0$ at the three assumed levels of $\varphi$. All of this is to say that ME provides an additional source of privacy to RRT models, especially when privacy is low.

ME decreases efficiency (increases MSE), as per Equations (13) and (22), but we have seen that ME also inadvertently increases privacy, as per Equations (44) and (45), that is, the same phenomenon (in this case, measurement error) causes one aspect of model quality (efficiency) to deteriorate while it causes the other (privacy) to improve. Singh et al. (2020) and other statisticians have faced this same problem of assessing overall model value when “level of [privacy] protection” and “efficient estimation” are competing considerations [24]. Gupta et al. (2018) offered a solution to this dilemma when they proposed a unified measure (UM) which enables the quantification of overall model quality, taking both efficiency and privacy into account [25]:

$${\delta }^a={\displaystyle \frac{\mathrm{M}\mathrm{S}\mathrm{E}\left({\widehat{\mathrm{\mu }}}_Y\right)}{{\mathsf{\nabla }}^a}}.$$

(48)

The superscript $a$ indicates that this measure has been adjusted to reflect Gupta et al.’s (2002) assertion that optionality does not reduce privacy for the proportion of respondents $\left(1-W\right)$ who do not consider the question to be sensitive [23]. Small values of UM reflect superior model performance. In Figure 6, we study UM across a range of ME values under three different privacy reduction assumptions in a standard scenario represented by the values listed immediately following the figure. We assume ${\mathrm{\sigma }}_U={\mathrm{\sigma }}_V$ across a range of 0 to 2; results are not sensitive to this assumption.

In our illustrative scenario, the ME impact on privacy (numerator) overpowers the ME impact on efficiency (denominator), so UM improves modestly as ME rises. This result can be generalized by calculating the relative change in UM when ME is present:

$$\Delta \left({\delta }^a\right)={\displaystyle \frac{{\delta }^a({\sigma }_U,{\sigma }_V)}{{\delta }^a({\sigma }_U={\sigma }_V=0)}}-1.$$

(49)

This expression equals

$$\Delta \left({\delta }^a\right)=\left({\displaystyle \frac{\mathsf{\nabla }\left(Y\right)-\varphi \mathsf{\nabla }\left(Y\right)}{\mathsf{\nabla }\left(Y\right)-\varphi \mathsf{\nabla }\left(Y\right)+{\sigma }_U^2}}\right){\displaystyle \frac{\frac{{\mathrm{\mu }}_Y^2}{n{\mathrm{\mu }}_X^2}{\sigma }_X^2+\frac{2}{n}\left[{\left(\frac{1-p_2}{p_2-p_1}\right)}^2{\sigma }_{Z1}^2+{\left(\frac{1-p_1}{p_2-p_1}\right)}^2{\sigma }_{Z2}^2\right]-\frac{2{\mathrm{\mu }}_{\mathrm{Y}}{\sigma }_{YX}}{n{\mathrm{\mu }}_{\mathrm{X}}}+\frac{2}{n}\left({\left(\frac{1-p_2}{p_2-p_1}\right)}^2+{\left(\frac{1-p_1}{p_2-p_1}\right)}^2\right){\sigma }_U^2+\frac{{\mathrm{\mu }}_Y^2}{n{\mathrm{\mu }}_X^2}{\sigma }_V^2}{\frac{{\mathrm{\mu }}_Y^2}{n{\mathrm{\mu }}_X^2}{\sigma }_X^2+\frac{2}{n}\left[{\left(\frac{1-p_2}{p_2-p_1}\right)}^2{\sigma }_{Z1}^2+{\left(\frac{1-p_1}{p_2-p_1}\right)}^2{\sigma }_{Z2}^2\right]-\frac{2{\mathrm{\mu }}_{\mathrm{Y}}{\sigma }_{YX}}{n{\mathrm{\mu }}_{\mathrm{X}}}}}-1.$$

(50)

But when $n$ is large, Equation (50) can be reduced to

$$\Delta \left({\delta }^a\right)=-{\left(1+{\displaystyle \frac{\left(1-\varphi \right)\mathsf{\nabla }\left(Y\right)}{{\sigma }_U^2}}\right)}^{-1}$$

(51)

The observation of this expression makes it clear that the change in UM will be negative when ME is introduced. Since small UM values indicate superior performance, this means that UM will in fact decrease (modestly) with a larger ME, if the sample size is large. Such a reduction will be the most significant when the adjusted privacy ($\left(1-\varphi \right)\mathsf{\nabla }\left(Y\right)$) is small. The major conclusion of this analysis is not that we expect UM gains from ME, but simply that we do not expect material UM deterioration as a result of ME.

6. Simulations

We show two tables of simulated values in this section. All tabular values represent model output that reflects the impact of measurement error on the MOET quantitative RRT model, and all simulations assume the same base parameter values, with minor deviations as noted. As a matter of full disclosure so that the values in the tables can be independently reproduced, scenario values are listed immediately preceding the tables. In both tables, the means of $Y$ and $X$ are set equal to 10 for convenience, as it is only their values relative to their standard deviations that matter. The standard deviations of $Y$ and $X$ are set equal to half of their means (5), as is consistent with other recent RRT studies such as Parker et al. (2024) [17]. The mean and variance of $R$ are set equal to the mean and variance of $Y$ because it is important that the unrelated question behaves similarly to the sensitive question. ${\mu }_S=0,{\mu }_T=1$, ${\sigma }_S=1, \mathrm{and} {\sigma }_T=1$ are standard choices for additive and multiplicative scrambling values, and the choices of ${\alpha =0.15,p}_1=0.85, \mathrm{a}\mathrm{n}\mathrm{d}{p}_2=0.15$ are chosen because they lead to high model efficiency, as per Parker et al. (2024) [17]. When not otherwise specified, $A$, $W$, and ${\mathrm{\rho }}_{XY}$ are set to the moderate values of $0.95$, $0.90$, and $0.75$, respectively. Each line of each table can be thought of as a unique scenario, based on a particular set of model parameters, and each scenario is run 10,000 times in R software version 4.3.1 to show the close match between simulated and theoretical values.

Table 1. Basic and ratio estimator performance reflecting measurement error. Scenario values: $A=0.95,W=0.90,{\alpha =0.15,p}_1=0.85,p_2=0.15,{\mu }_Y=10,{\mu }_X=10,{\mu }_R=10,{\mu }_S=0,{\mu }_T=1,{\mu }_U$ = 0, ${\mu }_V=0,{\sigma }_Y=5,{\sigma }_R=5,{\sigma }_S=1, \mathrm{and} {\sigma }_T=1$.

(A)
Parameters			Basic Estimator			Ratio Estimator
${\mathsf{\sigma }}_{\mathbf{U}}$	${\mathsf{\sigma }}_{\mathbf{V}}$	${\mathsf{\rho }}_{\mathbf{X}\mathbf{Y}}$	${{\widehat{\mathbf{\mu }}}_{\mathbf{Y}\left(\mathbf{M}\mathbf{E}\right)}}_{\mathbf{E}}$	${\mathbf{M}\mathbf{S}\mathbf{E}\left({\widehat{\mathbf{\mu }}}_{\mathbf{Y}\left(\mathbf{M}\mathbf{E}\right)}\right)}_{\mathbf{T}}$	${\mathbf{M}\mathbf{S}\mathbf{E}\left({\widehat{\mathbf{\mu }}}_{\mathbf{Y}\left(\mathbf{M}\mathbf{E}\right)}\right)}_{\mathbf{E}}$	${{\widehat{\mathbf{\mu }}}_{\mathbf{Y}\mathbf{R}\left(\mathbf{M}\mathbf{E}\right)}}_{\mathbf{T}}$	${{\widehat{\mathbf{\mu }}}_{\mathbf{Y}\mathbf{R}\left(\mathbf{M}\mathbf{E}\right)}}_{\mathbf{E}}$	${{\mathbf{B}\mathbf{i}\mathbf{a}\mathbf{s}(\widehat{\mathbf{\mu }}}_{\mathbf{Y}\mathbf{R}\left(\mathbf{M}\mathbf{E}\right)})}_{\mathbf{T}}$	${\mathbf{M}\mathbf{S}\mathbf{E}\left({\widehat{\mathbf{\mu }}}_{\mathbf{Y}\mathbf{R}\left(\mathbf{M}\mathbf{E}\right)}\right)}_{\mathbf{T}}$	${\mathbf{M}\mathbf{S}\mathbf{E}\left({\widehat{\mathbf{\mu }}}_{\mathbf{Y}\mathbf{R}\left(\mathbf{M}\mathbf{E}\right)}\right)}_{\mathbf{E}}$
0.00	0.00	0.95	10.0046	0.1823	0.1823	10.0053	10.0092	0.0053	0.1373	0.1381
0.50	0.50	0.95	10.0076	0.1838	0.1803	10.0053	10.0126	0.0053	0.1393	0.1404
1.00	1.00	0.95	10.0007	0.1884	0.1881	10.0053	10.0051	0.0053	0.1454	0.1464
1.50	1.50	0.95	9.9975	0.1960	0.1944	10.0053	10.0008	0.0053	0.1555	0.1546
2.00	2.00	0.95	10.0004	0.2066	0.2027	10.0053	10.0099	0.0053	0.1696	0.1663
0.00	0.00	0.75	10.0022	0.1823	0.1800	10.0063	10.0062	0.0063	0.1573	0.1567
0.50	0.50	0.75	9.9999	0.1838	0.1825	10.0063	10.0054	0.0063	0.1593	0.1571
1.00	1.00	0.75	9.9911	0.1884	0.1889	10.0063	9.9980	0.0063	0.1654	0.1649
1.50	1.50	0.75	9.9973	0.1960	0.1984	10.0063	10.0000	0.0063	0.1755	0.1781
2.00	2.00	0.75	9.9999	0.2066	0.2036	10.0063	10.0105	0.0063	0.1896	0.1893
0.00	0.00	0.50	9.9992	0.1823	0.1798	10.0075	10.0059	0.0075	0.1823	0.1816
0.50	0.50	0.50	10.0055	0.1838	0.1825	10.0075	10.0096	0.0075	0.1843	0.1852
1.00	1.00	0.50	10.0000	0.1884	0.1862	10.0075	10.0043	0.0075	0.1904	0.1926
1.50	1.50	0.50	9.9951	0.1960	0.1968	10.0075	10.0058	0.0075	0.2005	0.2047
2.00	2.00	0.50	10.0048	0.2066	0.2050	10.0075	10.0139	0.0075	0.2146	0.2125
(B)
Parameters			Basic Estimator			Ratio Estimator
${\mathit{\sigma }}_{\mathit{U}}$	${\mathit{\sigma }}_{\mathit{V}}$	${\mathrm{\rho }}_{\mathit{X}\mathit{Y}}$	${{\widehat{\mathit{\mu }}}_{\mathit{Y}\left(\mathit{M}\mathit{E}\right)}}_{\mathit{E}}$	${\mathbf{M}\mathbf{S}\mathbf{E}\left({\widehat{\mathit{\mu }}}_{\mathit{Y}\left(\mathit{M}\mathit{E}\right)}\right)}_{\mathit{T}}$	${\mathbf{M}\mathbf{S}\mathbf{E}\left({\widehat{\mathit{\mu }}}_{\mathit{Y}\left(\mathit{M}\mathit{E}\right)}\right)}_{\mathit{E}}$	${{\widehat{\mathit{\mu }}}_{\mathit{Y}\mathit{R}\left(\mathit{M}\mathit{E}\right)}}_{\mathit{T}}$	${{\widehat{\mathit{\mu }}}_{\mathit{Y}\mathit{R}\left(\mathit{M}\mathit{E}\right)}}_{\mathit{E}}$	${{\mathit{B}\mathit{i}\mathit{a}\mathit{s}(\widehat{\mathit{\mu }}}_{\mathit{Y}\mathit{R}\left(\mathit{M}\mathit{E}\right)})}_{\mathit{T}}$	${\mathbf{M}\mathbf{S}\mathbf{E}\left({\widehat{\mathit{\mu }}}_{\mathit{Y}\mathit{R}\left(\mathit{M}\mathit{E}\right)}\right)}_{\mathit{T}}$	${\mathbf{M}\mathbf{S}\mathbf{E}\left({\widehat{\mathit{\mu }}}_{\mathit{Y}\mathit{R}\left(\mathit{M}\mathit{E}\right)}\right)}_{\mathit{E}}$
0.00	0.50	0.95	10.0033	0.1823	0.1828	10.0053	10.0081	0.0053	0.1378	0.1424
0.50	0.50	0.95	9.9975	0.1838	0.1825	10.0053	10.0046	0.0053	0.1393	0.1394
1.00	0.50	0.95	10.0067	0.1884	0.1882	10.0053	10.0108	0.0053	0.1439	0.1450
1.50	0.50	0.95	10.0028	0.1960	0.1993	10.0053	10.0073	0.0053	0.1515	0.1536
2.00	0.50	0.95	10.0031	0.2066	0.2005	10.0053	10.0057	0.0053	0.1621	0.1572
0.00	0.50	0.75	9.9938	0.1823	0.1811	10.0063	10.0027	0.0063	0.1578	0.1581
0.50	0.50	0.75	10.0034	0.1838	0.1838	10.0063	10.0077	0.0063	0.1593	0.1621
1.00	0.50	0.75	9.9958	0.1884	0.1858	10.0063	10.0015	0.0063	0.1639	0.1619
1.50	0.50	0.75	9.9985	0.1960	0.1982	10.0063	10.0051	0.0063	0.1715	0.1728
2.00	0.50	0.75	10.0021	0.2066	0.2052	10.0063	10.0062	0.0063	0.1821	0.1810
0.00	0.50	0.50	9.9963	0.1823	0.1799	10.0075	10.0088	0.0075	0.1828	0.1813
0.50	0.50	0.50	10.0035	0.1838	0.1854	10.0075	10.0137	0.0075	0.1843	0.1870
1.00	0.50	0.50	9.9992	0.1884	0.1865	10.0075	10.0070	0.0075	0.1889	0.1897
1.50	0.50	0.50	10.0021	0.1960	0.1984	10.0075	10.0103	0.0075	0.1965	0.2001
2.00	0.50	0.50	10.0072	0.2066	0.2064	10.0075	10.0125	0.0075	0.2071	0.2064

is provided for two reasons. First, to exhibit the close match between theoretical and empirical values (denoted by subscripts T and E, respectively). Second, Table 1 is intended to show the behavior of the basic estimator and the ratio estimator across a range of assumed measurement errors (${\sigma }_U$ and ${\sigma }_V$ range from values of 0 to 2). We also show results across ${\mathrm{\rho }}_{XY}$ values because we want to witness the performance of the ratio estimator in comparison to the basic estimator, and the ratio estimator’s performance depends heavily on the correlation between auxiliary information ($X$) and the true response to the sensitive question ($Y$). We do not show results varying by $A$, $W$, and α, because, as noted in Section 3.1 and Section 3.2 (see Equations (13) and (22)), measurement error does not depend on these quantities.

Table 1 is split into sections (A) and (B), where Table 1A shows scenarios where the standard deviation of measurement error arising from the measurement of $Z$ and $X$ (represented by ${\sigma }_U$ and ${\sigma }_V$) rises in lockstep. Table 1B shows scenarios where ${\sigma }_V$ remains relatively low regardless of the value of ${\sigma }_U$. This represents the idea that the collection of RRT data, which is by nature complex, may result in more measurement error than the collection of auxiliary information.

It is clear throughout Table 1 that theoretical and empirical values match closely. For example, in the third row of the table, we see that the basic estimator ${{\widehat{\mu }}_{Y\left(ME\right)}}_E$ = 10.0007 is close to the theoretical value of 10.0000. Similarly, the theoretical and empirical values of $\mathrm{M}\mathrm{S}\mathrm{E}\left({\widehat{\mu }}_{Y\left(ME\right)}\right)$ for the basic estimator are 0.1884 and 0.1881. For the ratio estimator, the theoretical and empirical values of ${\widehat{\mu }}_{YR\left(ME\right)}$ are 10.0053 and 10.0051 and the theoretical and empirical values of $\mathrm{M}\mathrm{S}\mathrm{E}\left({\widehat{\mu }}_{YR\left(ME\right)}\right)$ are 0.1454 and 0.1464. In all cases, theoretical and empirical values match closely, implying that the theoretical results are validated by the simulations.

Analytically, we make several additional observations. We note that, as expected, when measurement error increases, MSE rises (i.e., efficiency declines). However, we also note that the rate of decline is greater for the ratio estimator than it is for the basic estimator, even in Table 1B where ${\sigma }_U$ is held constant. But because the ratio estimator is naturally more efficient when auxiliary data are of high quality, the ratio estimator generally remains more efficient than the basic estimator, even when high levels of measurement error are encountered. The only exceptions to this rule come when ${\mathrm{\rho }}_{XY}=0.5$. This consequence of low correlation was anticipated by Equation (25), as demonstrated in Figure 3. But in cases where correlation is low, the ratio estimator should typically not be used.

For each grouping of simulations (for example the first five rows of Table 1A), it is easy to think of the successive lines as representations of increasing levels of measurement error. However, it is more important to conceptualize this information in reverse. That is, if true measurement error is in reality ${\sigma }_U={\sigma }_V=2$ (as in line 5) but is not correctly recognized and accounted for (so, values are calculated based on ${\sigma }_U={\sigma }_V=0$, as in line 1), then the true level of MSE will be significantly understated. For example, the true MSE, when using the ratio estimator, would be 23.5% higher than it would appear to be if the measurement error was not taken into account (0.1696 versus 0.1373).

In

Table 2. Comparison between direct estimation reflecting lying bias and basic and ratio estimation reflecting measurement error. Scenario values: $A=0.95,W=0.90,{ \alpha =0.15,p}_1=0.85,{ p}_2=0.15,{ \mu }_Y$ = 10, ${ \mu }_X=10, {\mu }_R=10, {\mu }_S=0,{ \mu }_T=1,{ \mu }_U=0,{ \mu }_V=0,{\mathrm{\rho }}_{XY}=0.75,{ \sigma }_Y=5,{ \sigma }_R=5,{ \sigma }_S=1, \mathrm{and} {\sigma }_T=1$.

Parameters				Empirical Mean Estimates			$\mathbf{P}\mathbf{r}\left(\right|{\widehat{\mathit{\mu }}}_{\mathit{Y}\left(\mathit{M}\mathit{E}\right)}-{\mathit{\mu }}_{\mathit{Y}}|<|{{\widehat{\mathit{\mu }}}_{\mathit{Y}}}_{\mathit{D}\mathit{S}}-{\mathit{\mu }}_{\mathit{Y}}\left|\right)$		$\mathbf{P}\mathbf{r}\left(\right|{\widehat{\mathit{\mu }}}_{\mathit{Y}\mathit{R}\left(\mathit{M}\mathit{E}\right)}-{\mathit{\mu }}_{\mathit{Y}}|<|{{\widehat{\mathit{\mu }}}_{\mathit{Y}}}_{\mathit{D}\mathit{S}}-{\mathit{\mu }}_{\mathit{Y}}\left|\right)$
n	LB	${\mathit{\sigma }}_{\mathit{U}}$	${\mathit{\sigma }}_{\mathit{V}}$	${{\widehat{\mathit{\mu }}}_{\mathit{Y}}}_{\mathit{D}\mathit{S}}$	${\widehat{\mathit{\mu }}}_{\mathit{Y}\left(\mathit{M}\mathit{E}\right)}$	${\widehat{\mathit{\mu }}}_{\mathit{Y}\mathit{R}\left(\mathit{M}\mathit{E}\right)}$	Theoretical	Empirical	Empirical
50	2%	0.00	0.00	10.1910	9.9924	10.0652	0.30	0.30	0.35
50	2%	0.50	0.50	10.2143	10.0117	10.0642	0.30	0.30	0.34
50	2%	1.00	1.00	10.2049	9.9987	10.0549	0.29	0.28	0.33
50	2%	1.50	1.50	10.1896	9.9934	10.0748	0.30	0.29	0.32
50	2%	2.00	2.00	10.1855	10.0100	10.1045	0.29	0.29	0.32
50	5%	0.00	0.00	10.5000	9.9975	10.0715	0.37	0.37	0.39
50	5%	0.50	0.50	10.4987	9.9895	10.0622	0.35	0.36	0.39
50	5%	1.00	1.00	10.4987	10.0014	10.0689	0.36	0.36	0.39
50	5%	1.50	1.50	10.5131	9.9957	10.0670	0.35	0.36	0.38
50	5%	2.00	2.00	10.5009	9.9937	10.0686	0.35	0.35	0.36
50	10%	0.00	0.00	10.9945	9.9895	10.0640	0.53	0.53	0.54
50	10%	0.50	0.50	10.9951	9.9918	10.0686	0.53	0.53	0.55
50	10%	1.00	1.00	10.9976	9.9995	10.0676	0.52	0.52	0.53
50	10%	1.50	1.50	10.9999	9.9990	10.0737	0.51	0.52	0.52
50	10%	2.00	2.00	11.0059	10.0004	10.0808	0.50	0.51	0.51
250	2%	0.00	0.00	10.2012	9.9947	10.0043	0.34	0.35	0.39
250	2%	0.50	0.50	10.2025	10.0001	10.0109	0.34	0.34	0.38
250	2%	1.00	1.00	10.2062	10.0019	10.0088	0.34	0.34	0.38
250	2%	1.50	1.50	10.2023	10.0015	10.0185	0.34	0.34	0.37
250	2%	2.00	2.00	10.2031	9.9878	10.0055	0.33	0.33	0.35
250	5%	0.00	0.00	10.4958	9.9914	10.0082	0.57	0.57	0.58
250	5%	0.50	0.50	10.4984	9.9974	10.0134	0.57	0.56	0.57
250	5%	1.00	1.00	10.5026	9.9946	10.0051	0.57	0.57	0.58
250	5%	1.50	1.50	10.4927	9.9990	10.0162	0.56	0.56	0.57
250	5%	2.00	2.00	10.5008	10.0006	10.0151	0.54	0.54	0.55
250	10%	0.00	0.00	10.9928	9.9916	10.0106	0.86	0.86	0.88
250	10%	0.50	0.50	11.0043	10.0079	10.0162	0.86	0.86	0.88
250	10%	1.00	1.00	11.0062	10.0056	10.0156	0.86	0.86	0.87
250	10%	1.50	1.50	11.0018	9.9983	10.0108	0.85	0.85	0.86
250	10%	2.00	2.00	11.0006	9.9933	10.0097	0.84	0.84	0.84
500	2%	0.00	0.00	10.1990	10.0032	10.0085	0.40	0.40	0.43
500	2%	0.50	0.50	10.2021	10.0015	10.0062	0.40	0.40	0.43
500	2%	1.00	1.00	10.1988	9.9966	10.0065	0.40	0.40	0.43
500	2%	1.50	1.50	10.2064	10.0074	10.0106	0.39	0.39	0.42
500	2%	2.00	2.00	10.1954	9.9916	10.0011	0.38	0.38	0.40
500	5%	0.00	0.00	10.4988	10.0038	10.0126	0.72	0.72	0.73
500	5%	0.50	0.50	10.5008	10.0013	10.0058	0.72	0.73	0.74
500	5%	1.00	1.00	10.4998	10.0021	10.0084	0.72	0.71	0.72
500	5%	1.50	1.50	10.5024	9.9967	10.0044	0.71	0.71	0.71
500	5%	2.00	2.00	10.5018	10.0056	10.0122	0.69	0.70	0.70
500	10%	0.00	0.00	10.9976	9.9916	10.0014	0.95	0.95	0.97
500	10%	0.50	0.50	10.9961	9.9986	10.0085	0.95	0.95	0.97
500	10%	1.00	1.00	11.0034	10.0064	10.0121	0.95	0.96	0.97
500	10%	1.50	1.50	10.9980	9.9944	10.0044	0.95	0.95	0.96
500	10%	2.00	2.00	10.9973	9.9982	10.0083	0.95	0.95	0.96

(below), we study whether the benefit of RRT (removal of lying bias) outweighs its cost (addition of measurement error). To do this, we simulate two surveys—a direct survey which does not implement RRT or any other SDB-reduction mechanism, and an MOET RRT-based survey. We know that with RRT absent, the direct survey will be subject to lying bias, but will be simple to administer and therefore will provoke very little measurement error. In contrast, an RRT survey is administratively complex and will provoke significant measurement error but very little inaccuracy due to lying bias. Based on 10,000 iterations, we estimate the probability the RRT survey will result in a closer estimate of the mean response to the sensitive question by finding the proportion of iterations in which RRT estimates are closer to true values than direct survey estimates are. We compare results across three lying bias levels (2%, 5%, 10%) and across five levels of measurement error (0, 0.5, 1.0, 1.5, 2.0). We also study results across three different sample sizes (50, 250, 500). Note that, as discussed in Section 4.2, the distributions of $({\widehat{\mu }}_{YR\left(ME\right)}+{{\widehat{\mu }}_Y}_{DS})$ and (${\widehat{\mu }}_{YR\left(ME\right)}-{{\widehat{\mu }}_Y}_{DS}$) do not follow known distributions; therefore, no theoretical expression for $\mathrm{P}\mathrm{r}\left(\right|{\widehat{\mu }}_{YR\left(ME\right)}-{\mu }_Y|<|{{\widehat{\mu }}_Y}_{DS}-{\mu }_Y\left|\right)$ could be derived.

For the basic estimator, the probability that the MOET RRT model improves estimation ($\mathrm{P}\mathrm{r}\left(\right|{\widehat{\mu }}_{Y\left(ME\right)}-{\mu }_Y|<|{{\widehat{\mu }}_Y}_{DS}-{\mu }_Y\left|\right)$) is calculated on both a theoretical and empirical basis. Theoretical and empirical results match closely as seen in the eighth and ninth columns of the table, a fact which implies that the theoretical probability expressions shown in Equations (28)–(30) are correct and that the assumption of bivariate normality represented in Equation (39) is justified. Because the distribution underlying the ratio estimator could not be identified, only empirical estimates of $\mathrm{P}\mathrm{r}\left(\right|{\widehat{\mu }}_{YR\left(ME\right)}-{\mu }_Y|<|{{\widehat{\mu }}_Y}_{DS}-{\mu }_Y\left|\right)$ were calculated. As expected, in all cases, the ratio estimator’s performance was similar but superior to the basic estimator’s performance.

We note that there are three factors represented in the table that increase the probability that ${\widehat{\mu }}_{Y\left(ME\right)}$ and ${\widehat{\mu }}_{YR\left(ME\right)}$ will result in better estimates than ${\widehat{\mu }}_{DS}$: large sample sizes, high levels of lying bias, and low levels of measurement error. Indeed, when $n=50$, $\mathrm{L}\mathrm{B}=2\mathrm{\%}$, and ${\mathrm{\sigma }}_{\mathrm{U}}={\mathrm{\sigma }}_{\mathrm{U}}=2$, it is only 29% likely that ${\widehat{\mathrm{\mu }}}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}$ will be closer to ${\mathrm{\mu }}_{\mathrm{Y}}$ than ${\widehat{\mathrm{\mu }}}_{\mathrm{D}\mathrm{S}}$. But when $n=500$, $\mathrm{L}\mathrm{B}=10\mathrm{\%}$, and ${\mathrm{\sigma }}_{\mathrm{U}}={\mathrm{\sigma }}_{\mathrm{V}}=0$, the probability that ${\widehat{\mathrm{\mu }}}_{\mathrm{Y}\left(\mathrm{M}\mathrm{E}\right)}$ is closer to ${\mathrm{\mu }}_{\mathrm{Y}}$ than ${\widehat{\mathrm{\mu }}}_{\mathrm{D}\mathrm{S}}$ is 95%. Importantly to this study, measurement error is the least impactful of the three factors.

The tabular findings imply that the MOET model should not be used when the sample size is low and LB is expected to be small. However, the table also implies that MOET should definitely be used when the sample size is adequate and LB is expected to be significant (the exact circumstance that the RRT models were developed for). The table further indicates the important conclusion that while measurement error will reduce MOET performance, reasonable levels of measurement error should not impact a researcher’s decision to use or not use the model.

7. Conclusions

Measurement error is particularly important to RRT models because the administration of surveys based on these models is often complicated and can therefore lead to excess measurement error. In this study, we developed basic and ratio estimators that reflect measurement error for the recently proposed MOET RRT model by Parker et al. (2024) [17]. Using them, we identified circumstances where a failure to reflect ME could result in underestimating efficiency by more than 20%, confirming our expectation that the reflection of measurement error can be important. The accuracy of our new estimators was validated through simulation. Researchers should take standard precautions to avoid excessive measurement error, such as providing simple, clear instructions to respondents, providing only positive whole-number values as scrambling variables, and providing a calculator or charts of computations. And researchers would benefit from using the revised estimators proposed in this study to better quantify the efficiency of their estimations.

We further considered two important questions involving measurement error. The first involved determining if and when measurement error associated with the collection of auxiliary data was so high that it should not be collected. Equation (25) showed us that it would only be in unusual circumstances—such as when the correlation of auxiliary information with the sensitive question was low and the variance that comes from collecting auxiliary information (measurement error) was high relative to the variance inherent in the auxiliary information—that auxiliary information should not be collected. Of course, low correlation of auxiliary information with the sensitive question is a circumstance where ratio estimation is unlikely to be effective regardless of measurement error. Researchers should use Equation (25) to verify, according to a priory estimates of variance and correlation, that auxiliary information should be collected in their study.

Second, we considered whether measurement error might be so large that it undermined the MOET model’s ability to extract truthful answers to sensitive questions. Toward this objective, we derived relationships that allowed us to calculate the probability that an MOET estimate of the mean response to the sensitive question would be closer to the true response than an estimate based on a direct survey (which would be biased by untruthfulness). We concluded that the MOET model yielded superior estimates in spite of measurement error, provided that lying bias was significant and sample size was adequate. Finally, we recognized that while auxiliary information improves efficiency, it comes at a cost—it reduces privacy.