Polar Code BP Decoding Optimization for Green 6G Satellite Communication: A Geometry Perspective

Abstract

The rapid evolution of mega-constellation networks and 6G satellite communication systems has ushered in an era of ubiquitous connectivity, yet their sustainability is threatened by the energy-computation dilemma inherent in high-throughput data transmission. Polar codes, as a coding scheme capable of achieving Shannon’s limit, have emerged as one of the key candidate coding technologies for 6G networks. Despite the high parallelism and excellent performance of their Belief Propagation (BP) decoding algorithm, its drawbacks of numerous iterations and slow convergence can lead to higher energy consumption, impacting system energy efficiency and sustainability. Therefore, research on efficient early termination algorithms has become an important direction in polar code research. In this paper, based on information geometry theory, we propose a novel geometric framework for BP decoding of polar codes and design two early termination algorithms under this framework: an early termination algorithm based on Riemannian distance and an early termination algorithm based on divergence. These algorithms improve convergence speed by geometrically analyzing the changes in soft information during the BP decoding process. Simulation results indicate that, when $E_b/N_0$ is between 1.5 dB and 2.5 dB, compared to three classical early termination algorithms, the two early termination algorithms proposed in this paper reduce the number of iterations by 4.7–11% and 8.8–15.9%, respectively. Crucially, while this work is motivated by the unique demands of satellite networks, the geometric characterization of polar code BP decoding transcends specific applications. The proposed framework is inherently adaptable to any communication system requiring energy-efficient channel coding, including 6G terrestrial networks, Internet of Things (IoT) edge devices, and unmanned aerial vehicle (UAV) swarms, thereby bridging theoretical coding advances with real-world scalability challenges.

1. Introduction

Low-Earth Orbit (LEO) satellite communication systems are emerging as a vital component of future 6G networks, offering the potential for high-speed communication across the globe thanks to their low latency, high coverage, and robustness. However, with the expansion of LEO satellite communication systems and the development of mega-constellations, energy consumption has become a core challenge limiting their sustainable development. Satellites rely on limited solar power, and efficient energy utilization in communication links not only determines the lifespan and operational efficiency of satellites but also profoundly impacts the green development and long-term reliability of the entire constellation. Therefore, reducing energy consumption while ensuring communication performance has become a critical issue driving advancements in LEO satellite communication technology. This poses higher requirements for technologies such as signal processing, communication protocols, and channel coding within the 6G network architecture, while also presenting new research opportunities for achieving a sustainable 6G network architecture.

Among them, channel coding technology serves as the core of wireless communication systems, directly impacting the reliability and energy consumption performance of communication systems. In recent years, polar codes, as the first channel coding scheme theoretically proven to achieve Shannon’s limit [1], have not only been incorporated into the 5G standard but are also regarded as one of the important candidate coding technologies for 6G networks. Leveraging their soft-input soft-output (SISO) characteristics and high parallel decoding capability, the Belief Propagation (BP) decoding algorithm for polar codes excels in high-throughput communication scenarios [1,2,3]. However, a major drawback of BP decoding is its high number of iterations and slow convergence speed, requiring numerous iterations to complete decoding in low signal-to-noise ratio (SNR) communication environments. This not only consumes considerable decoding time but also occupies excessive hardware resources and incurs high energy consumption costs, contradicting the sustainability requirements of 6G networks. Therefore, developing efficient early termination algorithms to reduce BP decoding energy consumption and enhance energy efficiency and convergence speed has become one of the key focuses in polar code research.

To address the issues of high iteration counts and slow convergence speed in BP decoding algorithms, various early termination algorithms have been proposed. In summary, current early termination algorithms can be categorized into the following three approaches:

• The first approach involves designing a verification condition to judge the result of each iteration. If the condition is met, the iteration stops, and the current decoding result is output. For instance, the early termination criterion based on the G-matrix proposed in Ref. [4] determines whether to terminate early by comparing the estimated messages and codewords at the end of each BP decoding iteration. Ref. [5] improves upon the method in [4] by proposing the Bit Difference Ratio (BDR) criterion, which focuses on the number of differing bits between the estimated codeword and the codeword calculated based on the estimated messages. Ref. [6] introduces an early termination criterion based on the H-matrix, which has lower complexity compared to the G-matrix criterion in [4]. Ref. [7] incorporates Cyclic Redundancy Check (CRC) to more accurately perceive convergence properties. This approach draws inspiration from early termination algorithms for LDPC codes and belongs to the general idea of linear block code decoding. Its advantage lies in its simplicity and directness, while the disadvantage is that it does not incorporate the characteristics of polar codes.
• The second approach analyzes each information bit or frozen bit based on the characteristics of polarized channels and designs early termination algorithms according to their reliability. Ref. [8] points out that observing a group of information bits, known as the Worst of Information Bits (WIBs), can detect successful decoding. WIBs are bits transmitted through channels with higher error probabilities and thus require more decoding iterations for successful decoding compared to other bits. Additionally, Ref. [9] proposes an early termination criterion based on the bit error rate (BER) for frozen bits of polar codes. In Ref. [10], researchers suggest using optimal frozen bits to terminate decoding, as these partially frozen bits have lower average error probabilities. The advantage of this approach is that it leverages channel polarization theory and combines the characteristics of polar codes, while the disadvantage is that it does not incorporate the transmission of soft information for information nodes and does not utilize the advantages of BP decoding.
• The third approach leverages the SISO characteristics of polar code BP decoding to design early termination algorithms based on the Log-Likelihood Ratio (LLR). Since the BP decoding algorithm outputs soft information, the LLR of each information node represents the reliability of the information. Designing early termination algorithms by calculating the LLR exploits the advantages of polar code BP decoding algorithms. Ref. [4] proposes the min Log-Likelihood Ratio (minLLR) criterion, which was later simplified in subsequent research [11] with the decision condition that all LLR values are greater than a set threshold indicating successful decoding. Furthermore, in Ref. [7], an LLR magnitude-aided (LMA) early termination scheme based on the convergence properties of LLR messages is proposed, which terminates iterations early when the LLR of an information node remains unchanged for two consecutive times. Ref. [12] introduces a partial LLR-aided (PLA) early termination scheme, which terminates iterations early when the difference in LLR values of an information node over two consecutive times is less than a threshold. This approach fully exploits the characteristics of soft information transmission in polar code BP decoding, but existing algorithms directly use Euclidean distance to calculate LLR differences, lacking a mathematical analysis of LLR.

Moreover, some researchers have combined two of the above three approaches, as seen in [4,7,13]. Existing methods are typically designed based on empirical rules and lack support from a systematic theoretical framework, with the potential in the direction of early termination yet to be fully explored.

In recent years, information geometry theory has gradually emerged as a novel research tool in the field of channel coding and wireless communication [14,15]. This theory transforms complex communication problems into geometric optimization problems by mapping probability distribution functions to points on geometric manifolds, utilizing geometric tools such as metrics, curvature, and divergence for performance optimization [16]. This characteristic of information geometry provides a new perspective for optimizing the iterative process of polar code BP decoding, aiding in significantly reducing the number of iterations without sacrificing the bit error rate (BER), thereby achieving the goal of reducing energy consumption.

To better leverage the SISO characteristics of polar code BP decoding, this paper conducts a mathematical analysis of the changes in LLR values during the iterative process of polar code BP decoding and proposes a geometric framework for polar code BP decoding based on information geometry theory. This framework not only aids in intuitive understanding of iterative decoding but also facilitates the use of various geometric tools such as metrics, Riemannian distance, and divergence to address the issue of high iteration counts. Under this framework, this paper proposes two early termination algorithms for polar code BP decoding based on information geometry, which improve the convergence speed of polar code BP decoding without affecting the BER. These algorithms conduct a geometric analysis of the changes in soft information during the Belief Propagation decoding iterative process, effectively reducing energy consumption while significantly improving convergence speed. This not only underscores their broad application potential in green 6G satellite communications but also introduces a novel approach suitable for all resource-constrained scenarios in green communications, ranging from large-scale Internet of Things (IoT) deployments equipped with battery-limited sensors to unmanned aerial vehicle (UAV) communication networks.

The innovations of this paper are as follows:

• To mathematically analyze the changes in LLR values during the BP decoding process of polar codes, this paper utilizes mathematical tools—information geometry and modern differential geometry—to analyze the BP decoding algorithms of polar codes, establish a geometric framework for polar code BP decoding algorithms, and propose a theoretical explanation for polar code BP decoding algorithms. It maps information nodes to statistical manifolds, equates the probability information contained in nodes to points on manifolds, and represents the iterative process as finding convergence points on manifolds, providing an intuitive representation of the iterative process of polar code BP decoding algorithms. Under this framework, information geometry and modern differential geometry can be utilized to improve polar code BP decoding algorithms, providing new insights for research on polar code BP decoding algorithms.
• Addressing the issue of high iteration counts in BP decoding algorithms, this paper studies early termination algorithms for polar code BP decoding within the geometric framework. By calculating metrics, distance, and divergence in statistical manifolds, it optimizes existing algorithms and proposes early termination algorithms for polar code BP decoding based on Riemannian distance and divergence. These algorithms improve the convergence speed of polar code BP decoding without affecting the BER.

The remainder of this paper is organized as follows. Section 2 reviews the BP decoding process of polar codes. Section 3 introduces the BP decoding process of polar codes from an information geometry perspective. Section 4 proposes two early termination algorithms for polar code BP decoding based on information geometry. Section 5 presents simulation analysis. Section 6 concludes the paper and discusses future directions.The main symbols used in this paper are listed in Table 1.

Table 1. Summary of key symbols.

Symbol	Meaning
System Parameters
N	Code length
K	Information bits length
$E_b/N_0$	Energy-per-bit-to-noise power spectral density ratio
$I_{\max }$	Maximum number of iterations
Algorithmic Variables
$L_{i,j}$,$R_{i,j}$	Leftward LLR message at node $(i,j)$
$R_{i,j}$	Rightward LLR message at node $(i,j)$
${\xi }^t$	Leftward propagation vector at iteration t
${\zeta }^t$	Rightward propagation vector at iteration t
Geometric Framework
$\lambda$	Natural parameter of Bernoulli distribution
$G\left(\lambda \right)$	Metric matrix
${\eta }_L$	Soft information at leftmost bit nodes
${\theta }_R$	Soft information at rightmost bit nodes
$D(·)$	Riemannian distance or divergence measure
$I\left(\lambda \right)$	Fisher information matrix

  Note: LLR = Log-Likelihood Ratio.

2. BP Decoding Algorithm for Polar Codes

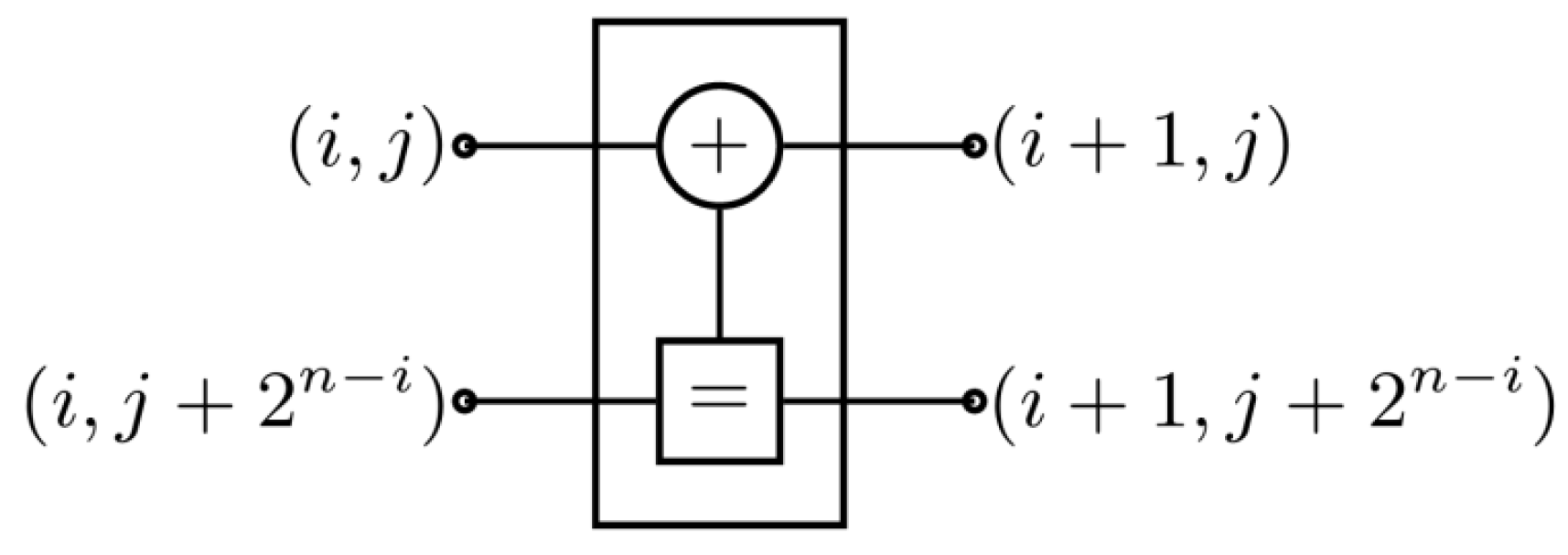
In the BP decoding algorithm, for a polar code with a code length of $N=2^n$, the factor graph of the polar code contains n stages and N levels, totaling $N(n+1)$ nodes, represented by ($i,j$) for the ith node at the jth stage. Each stage contains $N/2$ butterfly decoding units, and information propagates through the computing units, as shown in Figure 1. $L_{i,j}$ and $R_{i,j}$ denote the soft information for left-going and right-going messages, respectively, at node ($i,j$) on the factor graph, represented by Log-Likelihood Ratios (LLRs). According to reference [3], the information update process for a computing unit can be expressed as follows:

$$\left\{\begin{array}{cc}\hfill L_{i,j}^{t+1}& =f(L_{i+1,j}^t,L_{i+1,j+2^{n-1}}^t{R}_{i,j+2^{n-1}}^t)\hfill \\ \hfill L_{i,j+2^{n-1}}^{t+1}& =L_{i+1,j+2^{n-1}}^{t}f(L_{i+1,j}^t,R_{i,j}^t)\hfill \\ \hfill R_{i+1,j}^{t+1}& =f(R_{i,j}^t,L_{i+1,j+2^{n-1}}^t{R}_{i+1,j+2^{n-1}}^t)\hfill \\ \hfill R_{i+1,j+2^{n-1}}^{t+1}& =R_{i,j+2^{n-1}}^{t}f(R_{i,j}^t,L_{i+1,j}^t)\hfill \end{array}\right.$$

(1)

where

$$f(\alpha ,\beta )=ln\left({\displaystyle \frac{e^{\alpha +\beta }+1}{e^{\alpha }+e^{\beta }}}\right)\approx sign(\alpha ,\beta )min\left(\right|\alpha |,|\beta \left|\right)$$

(2)

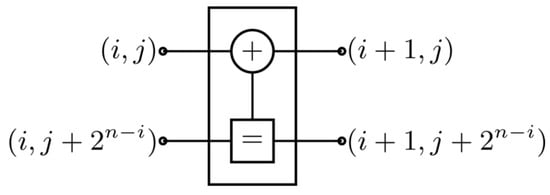
Figure 1. Minimal computational unit for BP decoding [3].

Equation (2) follows the min–sum approximation commonly used in BP decoding to reduce computational complexity [4].

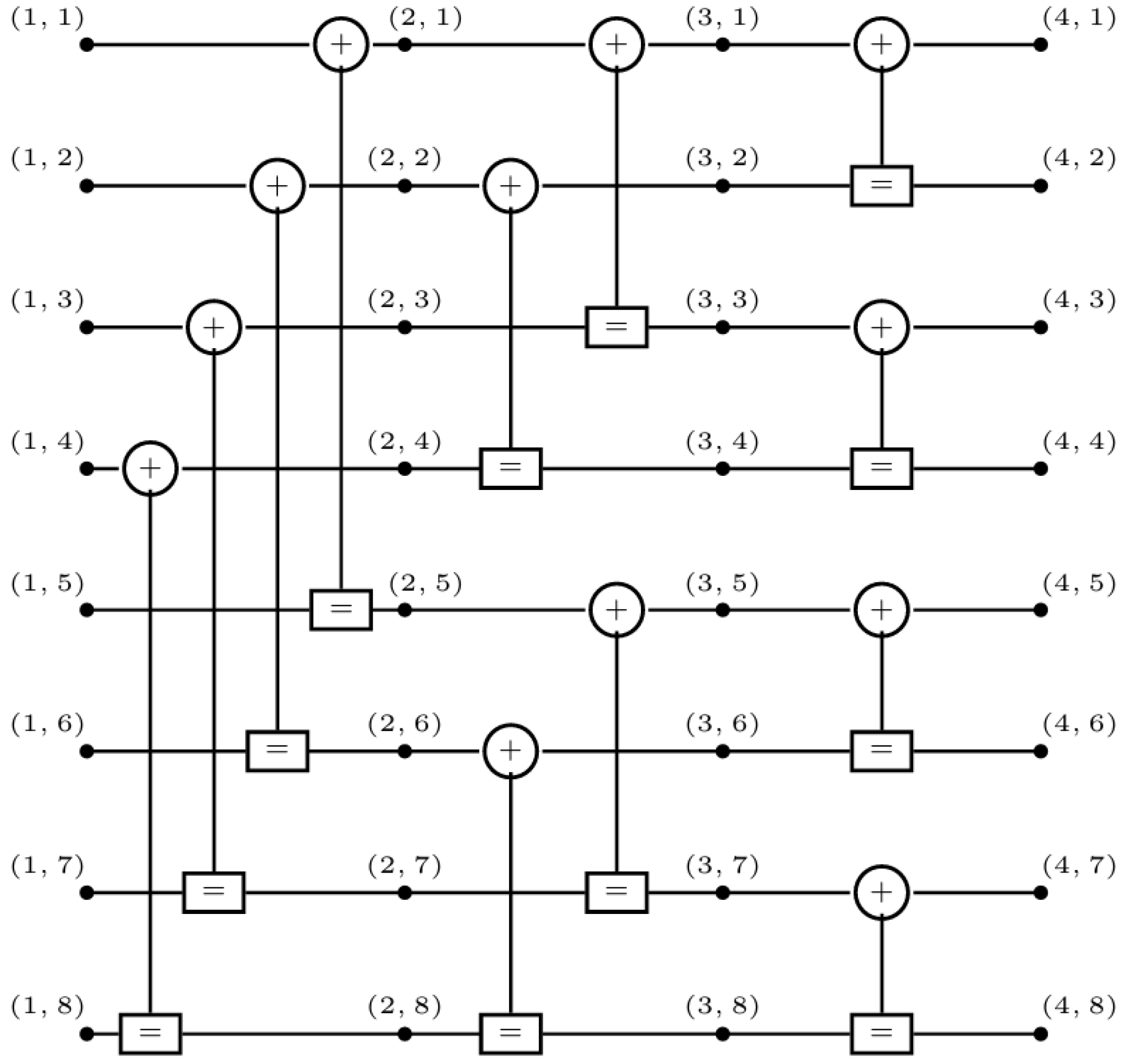
Figure 2 shows an example of a polar code factor graph with N = 8. From Equation (1), it can be seen that the iterative information of each intermediate node is determined by the iterative information of the remaining three nodes of the left and right butterfly decoders, where the node was located the previous time.

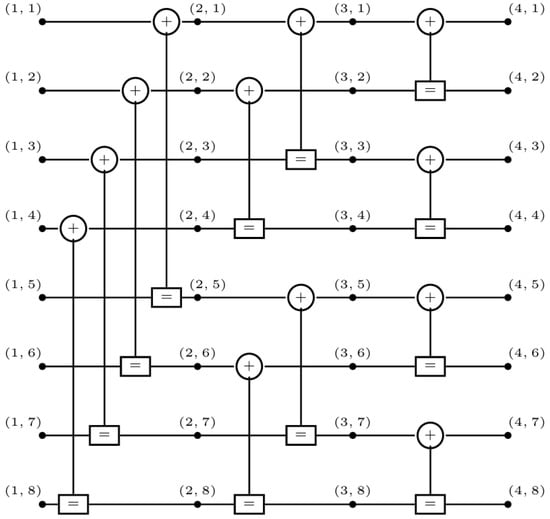
Figure 2. An example of a factor graph for a polar code with N = 8 [3].

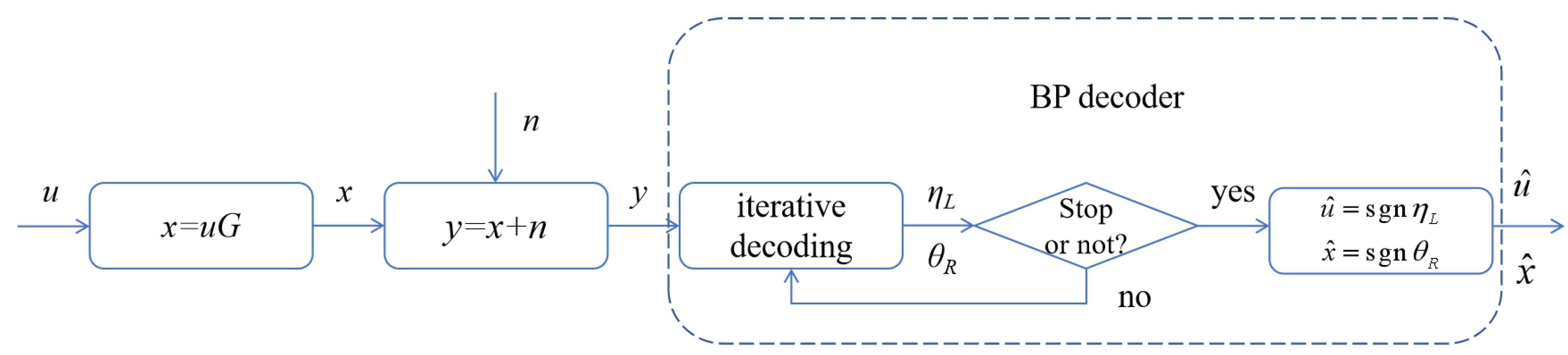
As shown in Figure 3, u represents the original codeword, G represents the generator matrix, x represents the codeword after encoding and transmission through the channel, and y represents the codeword sequence received at the receiver. ${\eta }_L$ denotes the soft information of the bit nodes at the leftmost side of the factor graph, which, after hard decision, becomes the decoded result. ${\theta }_R$ represents the soft information of the bits at the rightmost side of the factor graph, which, after hard decision, becomes $\widehat{x}$ (the predicted value of x).

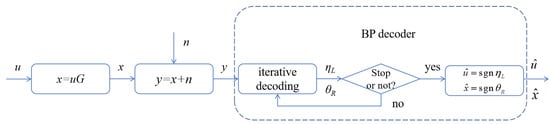
Figure 3. A schematic diagram of the BP decoding process for polar codes *.

* Note:

• When Erdal Arıkan introduced the BP decoding for polar codes, he did not specify a concrete stopping criterion. In practical applications, a maximum number of iterations is often set or one of the three approaches mentioned in the introduction is adopted to prematurely terminate the iterations.
• In the literature and practical applications, attention is often solely focused on $\widehat{u}$, while $\widehat{x}$ is overlooked. Ref. [4] points out that when the iterations are stopped, $\widehat{x}=\widehat{u}G$.

The process of polar code BP decoding is represented as Algorithm 1:

Algorithm 1 Polar Code BP Decoding

Require: Received signal vector y (length N), maximum iterations $I_{\max }$, frozen bit set $\mathcal{A}$ Ensure: Decoded result 1: for $i=1$ to N do 2:    Initialize $L_{i,n+1}=y_i$ 3:    for all j do 4:      Set $L_{i,j}=0$ and $R_{i,j}=0$ 5:    end for 6:    if $i\in \mathcal{A}$ then 7:      Set $R_{i,1}=+\infty$ {Indicate frozen bit position} 8:    end if 9: end for 10: for $\mathrm{iter}=1$ to $I_{\max }$ do 11:    for $j=1$ to N do 12:      Compute right-to-left messages based on Equation (1) 13:    end for 14:    for $j=1$ to N do 15:      Compute left-to-right messages based on Equation (1) 16:    end for 17:    if convergence criterion met (e.g., $L_{i,1}^{\mathrm{iter}}=L_{i,1}^{\mathrm{iter}+1}$ for all i) then 18:      Break 19:    end if 20: end for 21: Decision: Output decoded result based on final $L_{i,1}$ values

3. Information Geometry of BP Polar Decoding

3.1. Geometric Representation of Soft Information

The probability distribution of each codeword is a Bernoulli distribution, which we usually use as follows:

$$\left(\begin{array}{cc}0& 1\\ p& 1-p\end{array}\right).$$

(3)

The exponential deformation of Bernoulli distribution is defined as follows:

$$\begin{array}{c}p\left(x\right)=p^x{(1-p)}^{1-x}=exp[xlnx+(1-x)ln(1-p)].\hfill \end{array}$$

(4)

Let $\lambda =LLR=ln{\displaystyle \frac{p}{1-p}}$, and then $p={\displaystyle \frac{e^{\lambda }}{1+e^{\lambda }}}$; it follows that

$$\begin{array}{c}p(x;\lambda )=exp[xln\left({\displaystyle \frac{e^{\lambda }}{1+e^{\lambda }}}\right)+(1-x)ln\left(1-{\displaystyle \frac{e^{\lambda }}{1+e^{\lambda }}}\right)]\hfill \\ =exp[\lambda x-ln(1+e^{\lambda })].\hfill \end{array}$$

(5)

The statistical manifold on which the $LLR$ (Log-Likelihood Ratio) lies is

$$M=\{p(x;\lambda )=exp[\lambda x-ln(1+e^{\lambda })]\left|x\in \{0,1\},\right.\lambda \in R\}.$$

(6)

This is a one-dimensional manifold.

For a polar code with code length $(N,K)$, the output contains soft information for K information bits. As mentioned earlier, the soft information for one information bit can be represented as a point on a statistical manifold consisting of one-dimensional Bernoulli distributions. Therefore, the soft information for K information bits can be represented as a point on a K-dimensional statistical manifold, which is composed of the joint probability distribution of K one-dimensional Bernoulli distributions. The joint probability distribution can be expressed as

$$\begin{array}{c}p(x;\lambda )={\displaystyle \prod _i}exp[{\lambda }_{i}x-ln(1+e^{{\lambda }_i})]=exp[{\displaystyle \sum _i}{\lambda }_{i}x-{\displaystyle \sum _i}ln(1+e^{{\lambda }_i})]\hfill \end{array}.$$

(7)

In this formula, $\mathit{\lambda }=({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_K),i\in [1,K]$.

This K-dimensional statistical manifold can be represented as

$$M=\{p(x;\mathit{\lambda })=exp[\sum _i{\lambda }_{i}x-\sum _{i}ln(1+e^{{\lambda }_i})]\}.$$

(8)

Soft information is mapped to a point on a statistical manifold, whose value can be represented by the coordinates on the manifold, while the iterative process of soft information can be regarded as the movement of points on the statistical manifold. This geometric treatment brings the following three advantages:

• Intuitiveness: The geometric representation dynamically demonstrates the process of polar code BP decoding, providing a clear perspective for a deep understanding of the nature of decoding.
• Flexibility: The construction of the manifold can be flexibly adjusted according to research objectives. For example, when studying a particular information node, a two-dimensional manifold can be constructed through the Cartesian product, with left information and right information corresponding to different manifold coordinates, respectively. When studying the left information of N nodes, an N-dimensional manifold can be constructed, with each coordinate component representing the left information of one node.
• Practicality: Analyzing and optimizing characteristics such as metrics, curvature, and divergence on the manifold with geometric tools can effectively improve the convergence performance of decoding algorithms, providing powerful tool support for subsequent performance optimization.

3.2. Geometric Representation of Node Information

From a microscopic perspective, at time t, the left information of any node can be represented by the coordinate ${\lambda }_L^t$, and the manifold it resides on can be denoted as $M_1$; similarly, the right information can be represented by the coordinate ${\lambda }_R^t$, and the manifold it resides on can be denoted as $M_2$. Therefore, at time t, the coordinates of the node’s information on the manifold can be expressed as ${\lambda }^t({\lambda }_L^t,{\lambda }_R^t)$. By taking the Cartesian product of the manifold where the left information coordinate ${\lambda }_L^t$ resides and the manifold where the right information coordinate ${\lambda }_R^t$ resides, we obtain

$$M=M_1\times M_2,$$

(9)

which is a two-dimensional manifold with coordinates representing left information and right information, respectively.

For any node, its iterative information at any time can be represented by coordinates on M. In this way, the iterative process of the node’s information can be represented as the trajectory of a point moving on the manifold.

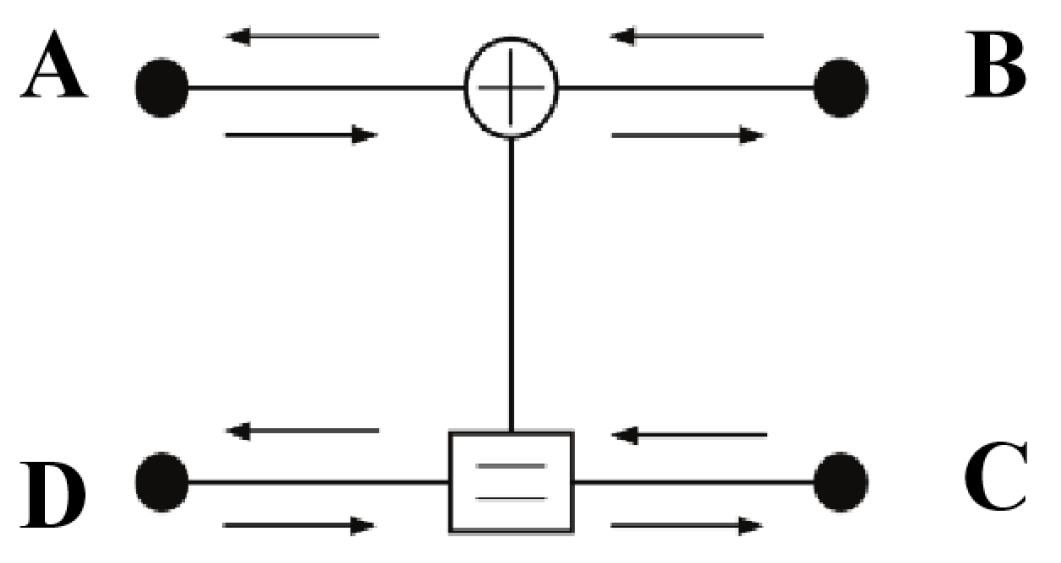
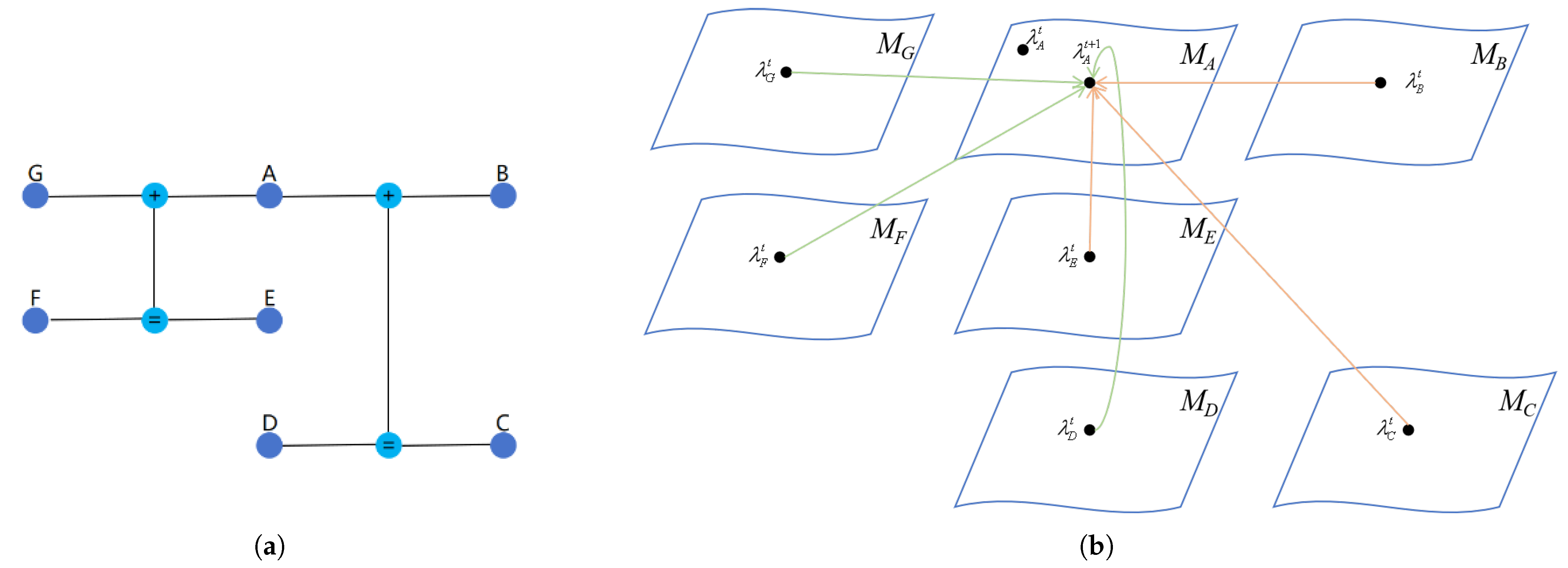
As shown in Figure 4, if four information nodes are represented as (A, B, C, D), then Equation (1) can be expressed as

$$\begin{array}{c}{\lambda }_{AL}^{t+1}=f({\lambda }_{BL}^t,{\lambda }_{DR}^t{\lambda }_{CL}^t)\hfill \\ {\lambda }_{DL}^{t+1}={\lambda }_{CL}^{t}f({\lambda }_{BL}^t,{\lambda }_{AR}^t)\hfill \\ {\lambda }_{BR}^{t+1}=f({\lambda }_{AR}^t,{\lambda }_{CL}^t{\lambda }_{DR}^t)\hfill \\ {\lambda }_{CR}^{t+1}={\lambda }_{DR}^{t}f({\lambda }_{AR}^t,{\lambda }_{BL}^t)\hfill \end{array}$$

(10)

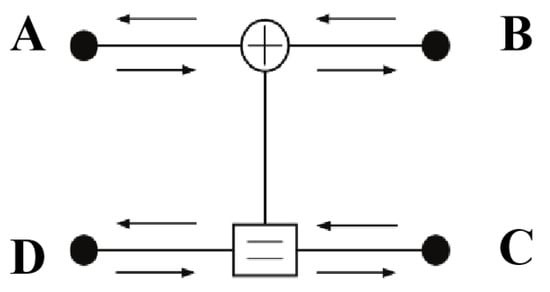
Figure 4. Another representation of the decoding unit.

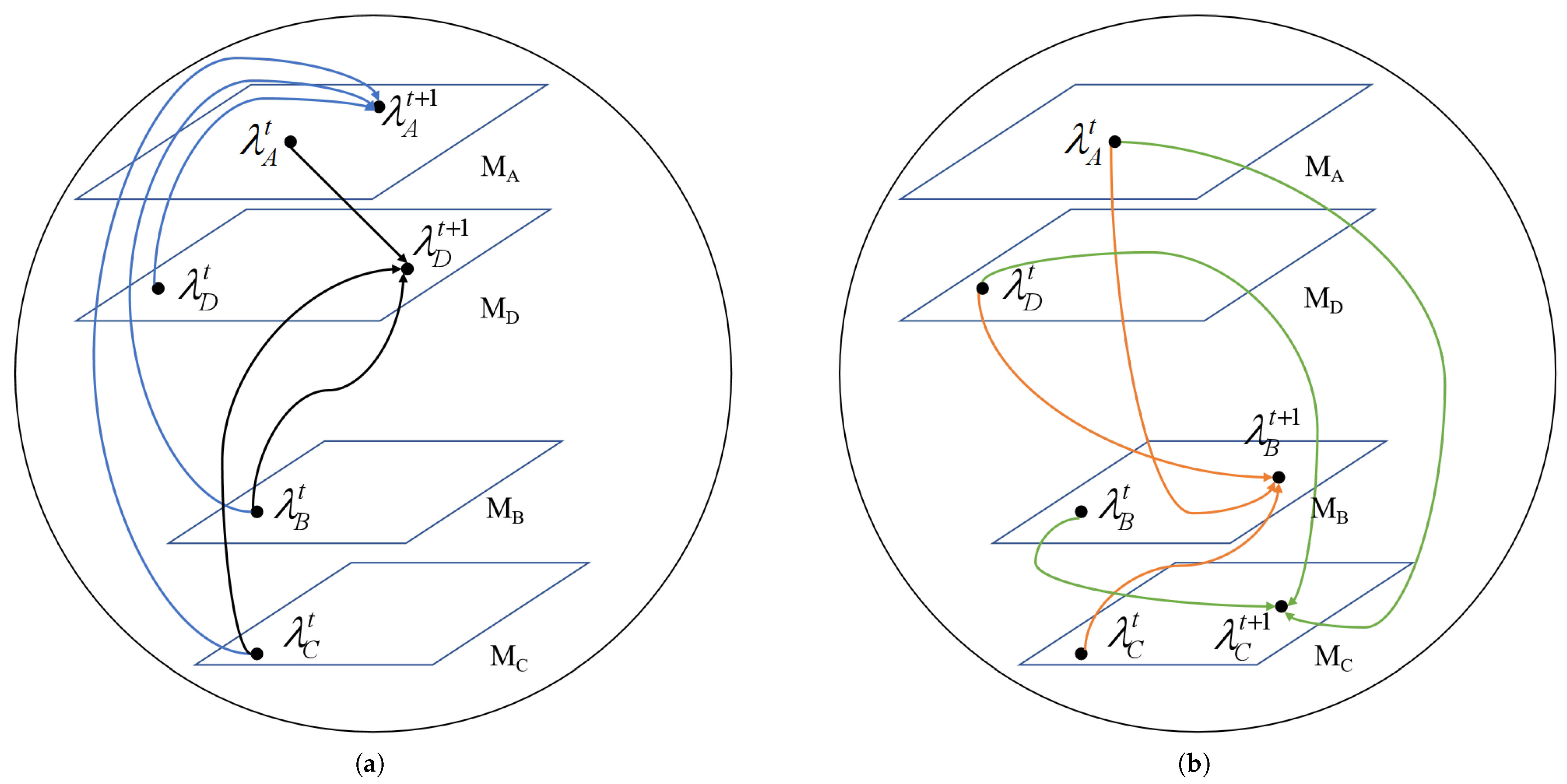
We correlate the four information nodes $(A,B,C,D)$ with the four statistical manifolds $(M_A,M_B,M_C,M_D)$. The probabilistic information embodied within these information nodes is equivalent to a point on the statistical manifold where the probability density function resides, thereby yielding four information points: ${\lambda }_A^t$, ${\lambda }_B^t$, ${\lambda }_C^t$, ${\lambda }_D^t$. The process of information transmission on the butterfly decoding unit can be represented by Figure 5.

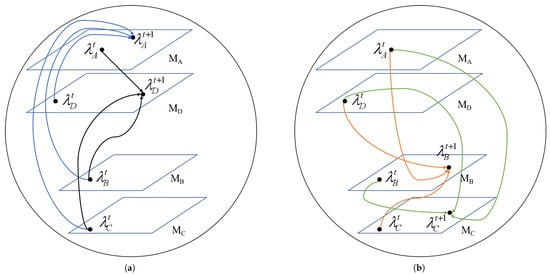
Figure 5. A schematic diagram of the iterative information process of a unit decoder from a geometric perspective. (a) A description of the schematic diagram of the left information iterative process. (b) A description of the schematic diagram of the right information iterative process.

For any intermediate node A, as shown in Figure 6a, its left information is determined by the information from the other three nodes $(B,C,D)$ in the butterfly decoder at the previous time step, and similarly, its right information is determined by the information from the other three nodes $(G,F,E)$ in another butterfly decoder at the previous time step. This information iteration is independent of the information of node A itself at the previous time step, and such information iteration can be termed as extrinsic information.

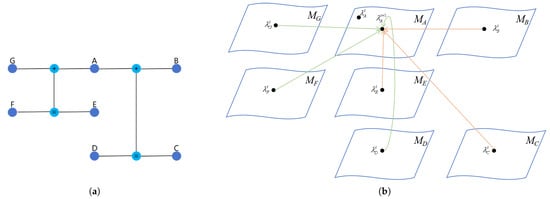
Figure 6. (a) The information carried by typical node A is related to six adjacent information nodes. (b) A schematic diagram of the information iteration process on typical node A from a geometric perspective.

From the perspective of information geometry, seven information nodes $(A,B,C,D$, $E,F,G)$ correspond to seven statistical manifolds $(M_A,M_B,M_C,M_D,M_E,M_F,M_G)$. The iterative process can be expressed as

$${\lambda }_A^{t+1}=g({\lambda }_{BL}^t,{\lambda }_{DR}^t,{\lambda }_{CL}^t,{\lambda }_{EL}^t,{\lambda }_{FR}^t,{\lambda }_{GR}^t),$$

(11)

or as

$${\lambda }_A^{t+1}=h({\lambda }_B^t,{\lambda }_D^t,{\lambda }_C^t,{\lambda }_E^t,{\lambda }_F^t,{\lambda }_G^t).$$

(12)

The information iteration process on node A is shown in Figure 6b, where the green arrows represent right information and the orange arrows represent left information.

3.3. Geometric Representation of Factor Graph Information

From the perspective of the factor graph, for a polar code with code length $(N,K)$, at time t, the information propagated leftwards contained in all nodes of the factor graph can be represented as an $N(n+1)$ vector ${\xi }_t$ as follows:

$${\xi }^t={\left({\lambda }_L^t\right)}_{N\times (n+1)}.$$

(13)

All possible probability distributions of the information transmitted to the left can form an $N(n+1)$-dimensional manifold $M_L$, where ${\xi }^t$ can be seen as a point on $M_L$. Among them, ${\eta }_L$ represents the soft information transmitted to the left of the leftmost bit node in the factor graph, and the manifold where ${\eta }_L$ is located is a K-dimensional submanifold of $M_L$, represented by Equation (8). ${\eta }_L$ is the projection of $\xi$ on this submanifold.

Similarly, at time t, the information propagated rightwards contained in all nodes of the factor graph can be represented as an $N(n+1)$ vector ${\zeta }_t$ as follows:

$${\zeta }^t={\left({\lambda }_R^t\right)}_{N\times (n+1)}.$$

(14)

All possible probability distributions of the information transmitted to the right can form an $N(n+1)$-dimensional manifold $M_R$, where ${\zeta }^t$ can be seen as a point on $M_R$. Among them, ${\theta }_R$ represents the soft information transmitted to the left of the leftmost bit node in the factor graph, and the manifold where ${\theta }_R$ is located is a N-dimensional submanifold of $M_R$. ${\eta }_L$ is the projection of $\zeta$ on this submanifold.

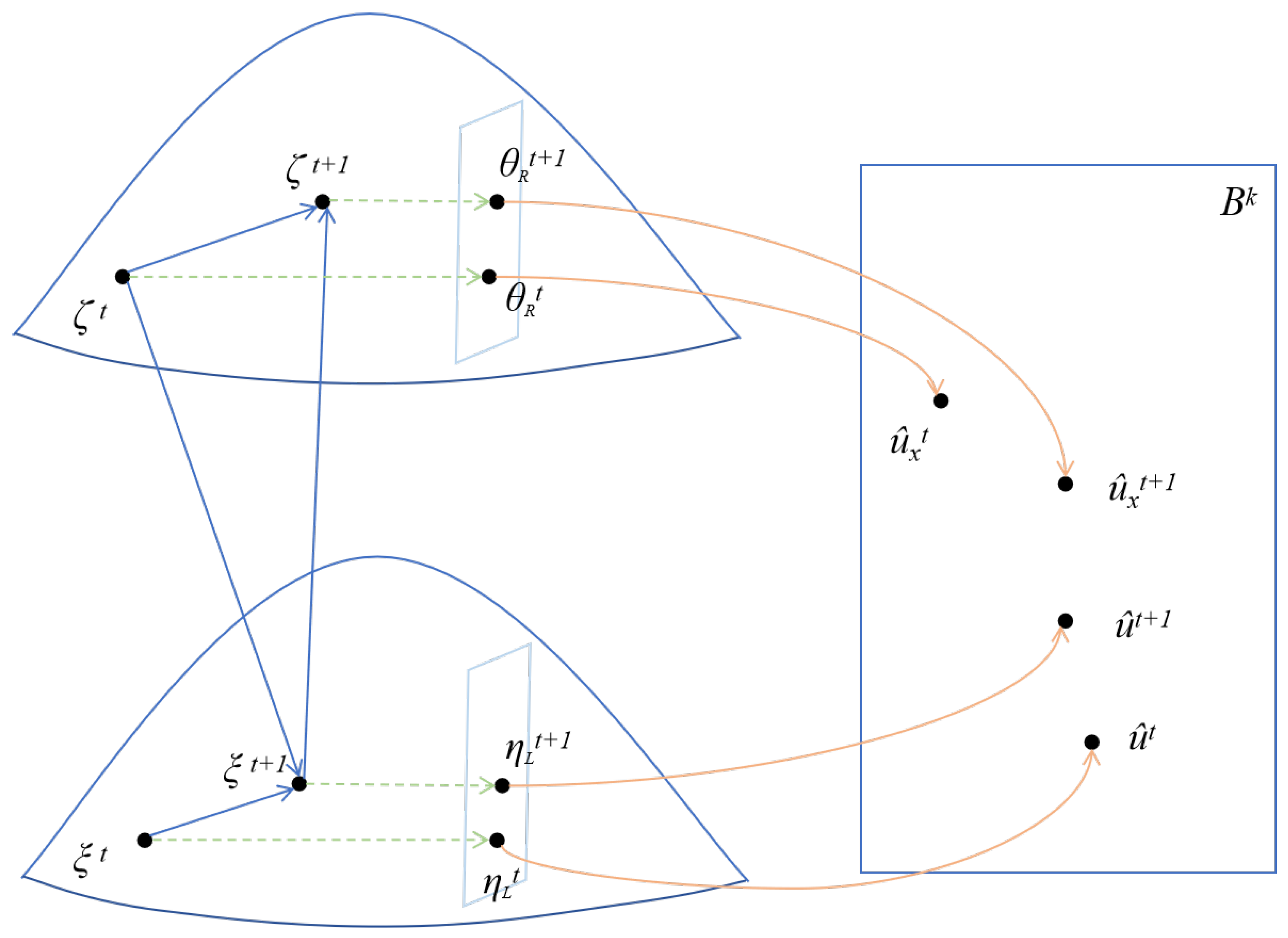
The parameter space of the codeword after hard judgment is K-dimensional Hamming space. The iterative process from a geometric perspective is shown in Figure 7:

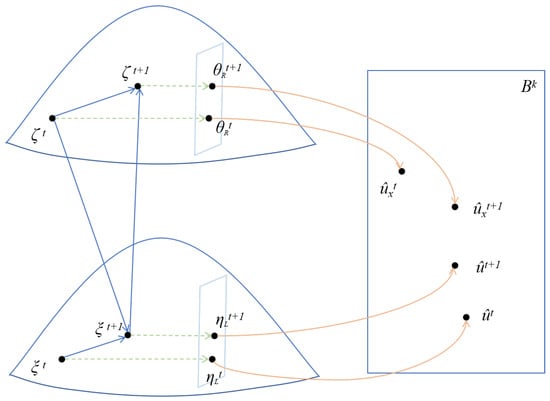
Figure 7. Polarization code BP decoding process from a geometric perspective.

Among them

$$\begin{array}{c}{\xi }^{t+1}={\mathrm{\Phi }}_L({\xi }^t,{\zeta }^t)\hfill \\ {\zeta }^{t+1}={\mathrm{\Phi }}_R({\zeta }^t,{\xi }^{t+1})\hfill \end{array}.$$

(15)

The process of hard judgment is

$$\begin{array}{c}{\widehat{u}}^t=\mathrm{sgn}{\eta }_L^t\hfill \\ {\widehat{u}}_x^t={\widehat{x}}^t{G}^{-1}\hfill \\ {\widehat{x}}^t=\mathrm{sgn}{\theta }_R^t\hfill \end{array}.$$

(16)

The iterative process of polar code BP decoding can be seen as the movement of $\xi$ and $\zeta$ on their respective manifolds. When decoding is complete, there is ${\xi }^t={\xi }^{t+1}$, ${\zeta }^t={\zeta }^{t+1},{\theta }_R^t={\theta }_R^{t+1},{\eta }_L^t={\eta }_L^{t+1},{\widehat{u}}^t={\widehat{u}}^{t+1},{\widehat{u}}_x^t={\widehat{u}}_x^{t+1},{\widehat{u}}^t={\widehat{u}}_x^t$.

The process of polar code BP decoding from a geometric perspective is represented as Algorithm 2:

Algorithm 2 Polar Code BP Decoding

Require: y: received signal vector (length N), maximum iteration number $I_{\max }$, frozen bits Ensure: decoded result $\widehat{u}$ 1: for $i=1$ to N do 2:    Initialize the coordinates of each node based on the received signal vector y and frozen bit positions 3: end for 4: for $iter=1$ to $I_{\max }$ do 5:    Left-to-right iteration: Update the coordinates of $\xi$ based on Equation (15) 6:    Right-to-left iteration: Update the coordinates of $\zeta$ based on Equation (15) 7:     if ${\xi }^t={\xi }^{t+1}$ and ${\zeta }^t={\zeta }^{t+1}$ then 8:      break 9:    end if 10: end for 11: Output: decoded result $\widehat{u}$

4. Early Stopping Based on Information Geometry

4.1. Algorithm Flow

In the process of polar code Belief Propagation (BP) decoding, the high number of iterations and significant computational load are crucial factors limiting decoding efficiency. Based on the geometric model for polar code BP decoding established in the previous section, this paper proposes an early convergence algorithm utilizing the geometric model. The objective is to prematurely terminate the decoding process by calculating the distance of soft information in differential geometric space, thereby enhancing decoding efficiency.

As mentioned in the previous section, when decoding concludes, we have ${\eta }_L^t={\eta }_L^{t+1}$. In fact, since ${\widehat{u}}^t=\mathrm{sgn}\left({\eta }_L^t\right)$, when the difference between ${\eta }_L^t$ and ${\eta }_L^{t+1}$ is sufficiently small, a correct decoding result can still be obtained. Therefore, the core of the algorithm lies in utilizing differential geometry theory to design a convergence threshold. This threshold, based on the non-Euclidean properties of soft information in geometric space, calculates the Riemannian distance or divergence to obtain a geometric distance, which is used to measure the minute differences in information updates during the iteration process. When the geometric distance of the soft information for the same information bit in two consecutive iterations is less than this threshold, the algorithm determines that the iteration has converged and prematurely terminates the decoding.

For Algorithm 3, during the implementation of the algorithm, the maximum number of iterations $I_{\max }$ is first set, and a convergence threshold eps is also established based on differential geometry principles. In the initialization stage, the Log-Likelihood Ratio (LLR) values for left-propagated soft information of the information nodes on the leftmost side of the factor graph required for decoding are prepared, and a geometric model is constructed to calculate the geometric distance between soft information.

During the iteration process, the algorithm updates the LLR values for each information bit one by one and calculates the geometric distance of the soft information between the current and previous iterations. If the geometric distance is less than the threshold eps, the iteration is deemed to have converged, and the iteration is terminated; if the number of iterations reaches $I_{\max }$ without convergence, the iteration is forcibly terminated.

Ultimately, the algorithm decides and outputs the decoding result based on the results of the final iteration. Since the threshold design is based on differential geometry principles, the algorithm achieves an improvement in decoding efficiency while ensuring decoding error correction performance.

Algorithm 3 Early Convergence Algorithm Based on Information Geometry

Require: Maximum number of iterations $I_{\max }$, Threshold eps Ensure: Decoding result 1: Initialize 2: for $t=1$ to $I_{\max }$ do 3:    for $j=1$ to N do 4:      Update LLR 5:    end for 6:    $\mathrm{covt}=\underset{i}{max}D[{\left({\eta }_L^t\right)}_i,{\left({\eta }_L^{t+1}\right)}_i]$ 7:    if $\mathrm{covt}<\mathrm{eps}$ then 8:      break 9:    end if 10: end for 11: Decide and output decoding result

4.2. Calculation of Geometric Distance

4.2.1. Riemann Distance

In this context, the Fisher Information Matrix degrades into the Fisher Information. According to reference [17], the Fisher Information is expressed as follows:

$$I\left(\lambda \right)=-E[{\displaystyle \frac{{\partial }^2}{\partial {\lambda }^2}}lnp(x;\lambda )].$$

(17)

E represents the expectation with respect to x.

Firstly, we calculate the first-order derivative:

$${\displaystyle \frac{\partial }{\partial \lambda }}lnp(x;\lambda )={\displaystyle \frac{\partial }{\partial \lambda }}[\lambda x-ln(1+e^{\lambda })]=x-{\displaystyle \frac{e^{\lambda }}{(1+e^{\lambda })}}.$$

(18)

The second-order derivative is

$${\displaystyle \frac{{\partial }^2}{\partial {\lambda }^2}}lnp(x;\lambda )={\displaystyle \frac{{\partial }^2}{\partial {\lambda }^2}}[\lambda x-ln(1+e^{\lambda })]=-{\displaystyle \frac{e^{\lambda }}{{(1+e^{\lambda })}^2}}.$$

(19)

The Fisher information matrix of a statistical manifold composed of Bernoulli distributions is

$$I\left(\lambda \right)=-E\left[{\displaystyle \frac{e^{\lambda }}{{(1+e^{\lambda })}^2}}\right]={\displaystyle \frac{e^{\lambda }}{{(1+e^{\lambda })}^2}}.$$

(20)

In this article, the inverse matrix of the Fisher information matrix is used as a metric for statistical manifolds, and the metric for statistical manifolds composed of Bernoulli distributions is defined as

$$G\left(\lambda \right)=I{\left(\lambda \right)}^{-1}={\displaystyle \frac{{(1+e^{\lambda })}^2}{e^{\lambda }}}.$$

(21)

In a one-dimensional Bernoulli distribution manifold, the Riemann distance can be approximated as follows:

$$D({\lambda }_1,{\lambda }_2)={\int }_{{\lambda }_1}^{{\lambda }_2}\sqrt{G\left(\lambda \right)}d\lambda ={\int }_{{\lambda }_1}^{{\lambda }_2}\sqrt{{\displaystyle \frac{{\left(1+e^{\lambda }\right)}^2}{e^{\lambda }}}}d\lambda .$$

(22)

First, calculate the indefinite integral as

$$\begin{array}{c}\int \sqrt{{\displaystyle \frac{{\left(1+e^{\lambda }\right)}^2}{e^{\lambda }}}}d\lambda =-2e^{-{\displaystyle \frac{1}{2}}\lambda }+2e^{{\displaystyle \frac{1}{2}}\lambda }\hfill \end{array}.$$

(23)

So, the Riemann distance of a one-dimensional Bernoulli distribution manifold can be expressed as

$$D({\lambda }_1,{\lambda }_2)=2\left|e^{{\displaystyle \frac{{\lambda }_2}{2}}}-e^{-{\displaystyle \frac{{\lambda }_2}{2}}}-e^{{\displaystyle \frac{{\lambda }_1}{2}}}+e^{-{\displaystyle \frac{{\lambda }_1}{2}}}\right|.$$

(24)

4.2.2. Divergence

In applications, divergence is also an important concept for describing the difference between two points on a manifold. The most widely used in statistical manifolds is Kullback–Leibler divergence (KL divergence). Using Riemann distance or divergence to calculate the difference between two probability distributions on a statistical manifold is a common method in information geometry.

The divergence formula on the manifold mentioned above is (see Appendix A for details) as follows:

$$\begin{array}{c}{D}_{KL}\left({\lambda }_1∥{\lambda }_2\right)={\displaystyle \sum _x}p(x;{\lambda }_1)log\frac{p(x;{\lambda }_1)}{p(x;{\lambda }_2)}\hfill \\ ={\displaystyle \sum _x}exp[{\lambda }_{1}x-ln(1+e^{{\lambda }_1})]log\frac{exp[{\lambda }_{1}x-ln(1+e^{{\lambda }_1})]}{exp[{\lambda }_{2}x-ln(1+e^{{\lambda }_2})]}\hfill \\ =({\lambda }_1-{\lambda }_2){\displaystyle \frac{e^{{\lambda }_1}}{1+e^{{\lambda }_1}}}-ln\left({\displaystyle \frac{1+e^{{\lambda }_1}}{1+e^{{\lambda }_2}}}\right)\hfill \end{array}.$$

(25)

The above two distance formulas are incorporated into the decoding algorithm framework, resulting in two polar code BP decoding algorithms based on information geometry: the BP polar decoding algorithm with early stopping based on Riemann distance (ESBP-R) and the BP polar decoding algorithm with early stopping based on divergence (ESBP-D).

5. Simulation Results and Comparisons

In this section, we compare the performances of the proposed early convergence algorithms, namely ESBP-R and ESBP-D, with several early convergence algorithms designed using LLR (Log-Likelihood Ratio) through simulations. These include the min Log-Likelihood Ratio (minLLR) algorithm proposed in reference [4], an LLR magnitude-aided (LMA) early convergence algorithm based on the convergence properties of LLR messages proposed in reference [7], and a partial LLR-aided (PLA) early convergence algorithm proposed in reference [12]. The performance metrics include the block error rate (BER) and the average number of iterations. The polar codes studied in the simulations have a code length of $N=1024$, an information bit length of $K=512$, a code rate of $r=0.5$, and a maximum number of iterations of 30. The channel is an Additive White Gaussian Noise (AWGN) channel, the polar code construction follows the Bhattacharyya parameter method as described in reference [1], and the modulation scheme is BPSK.

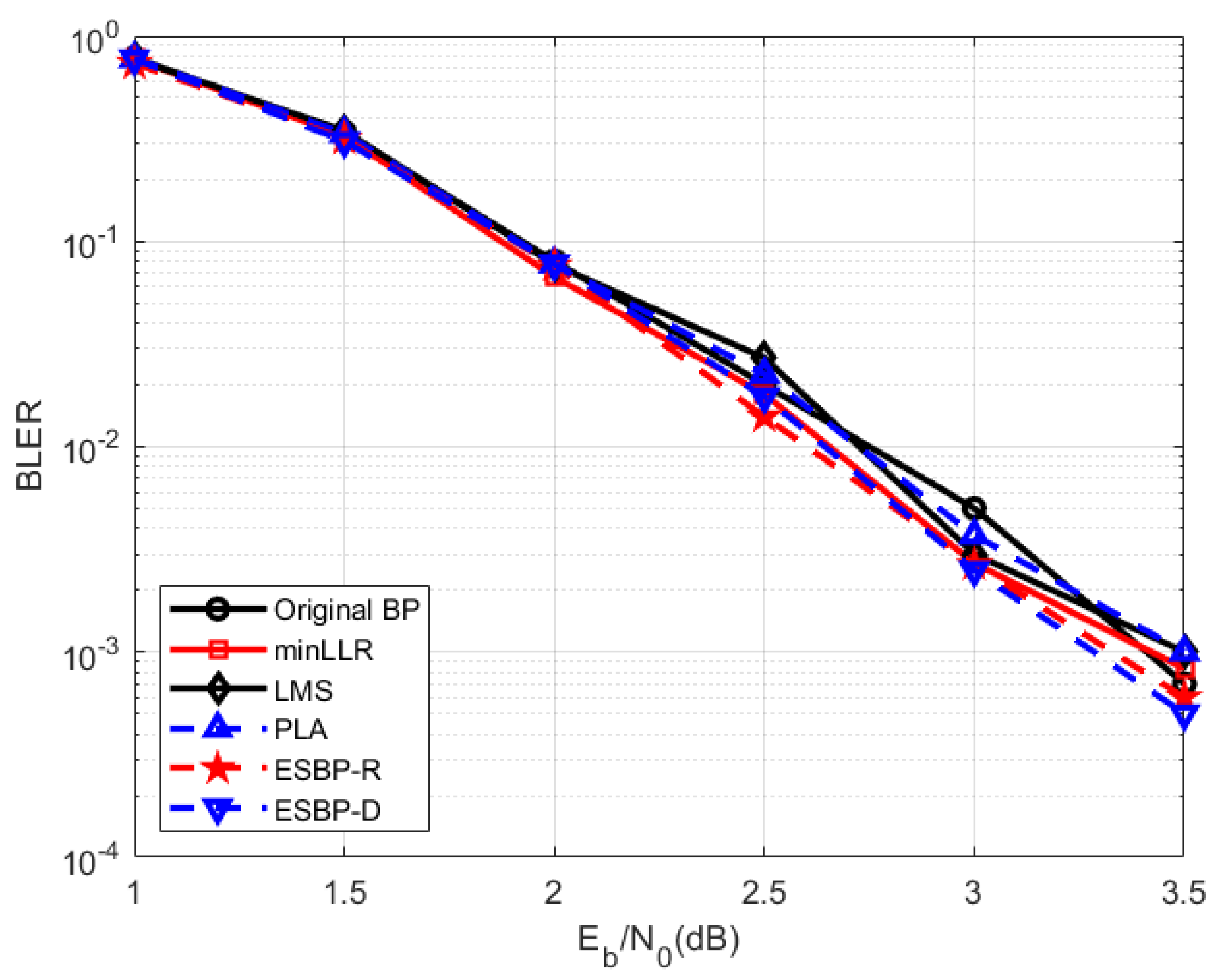
Figure 8 compares the block error rates of several decoding algorithms under three channel conditions. Figure 8 confirms that the two information geometry-based BP decoding algorithms for polar codes do not suffer from any loss in decoding performance.

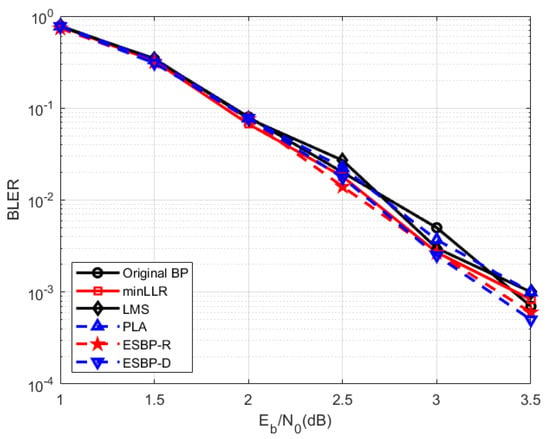
Figure 8. BLER performance for five polar codes with N = 1024 and K = 512. $E_b/N_0$ (energy-per-bit-to noise power spectral density ratio) measures the normalized signal quality.

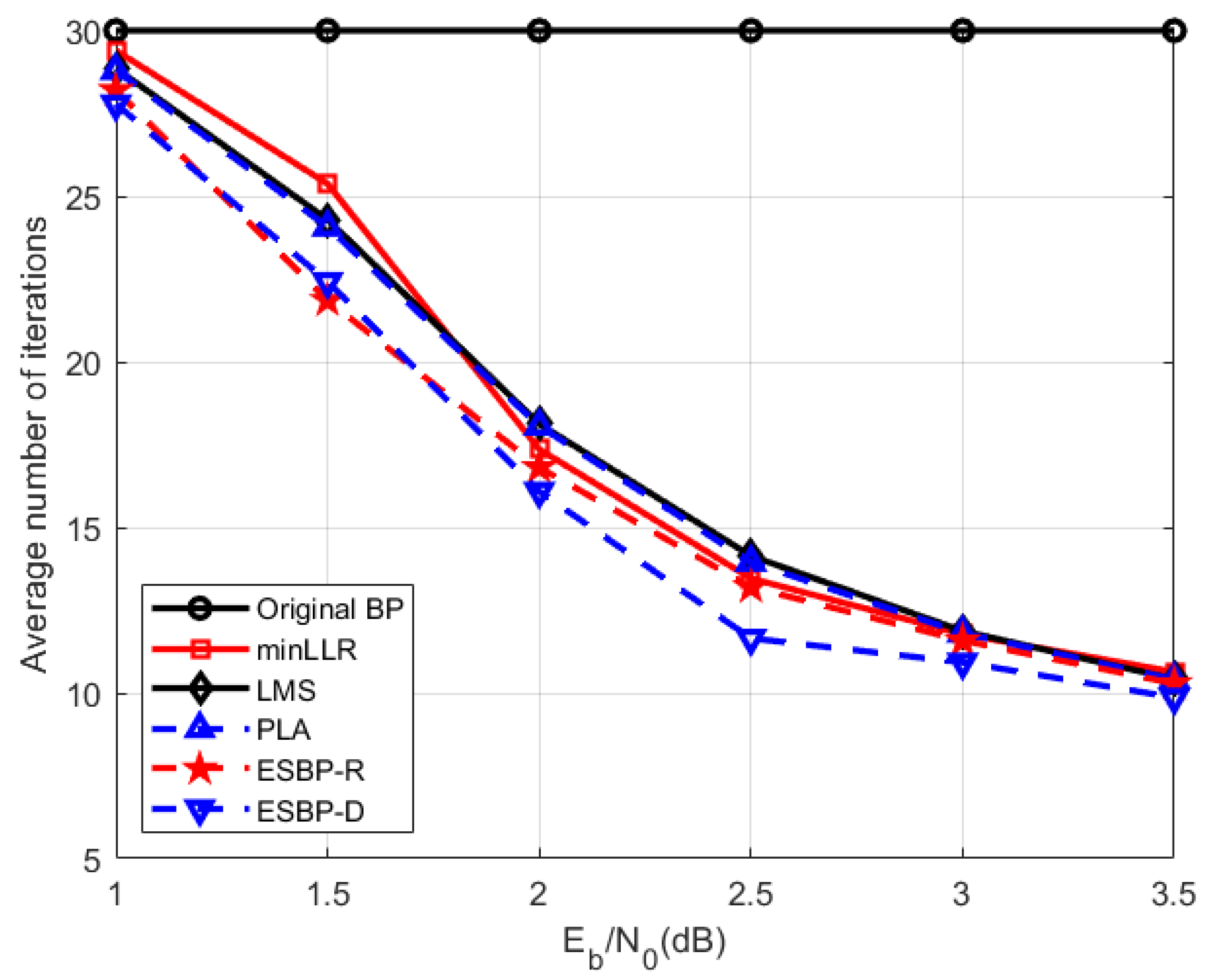
The average number of iterations is shown in Figure 9. Table 2 presents the ratios of iteration reductions achieved by several early convergence algorithms. Table 3 demonstrates that compared to the average number of iterations of the three existing early convergence algorithms designed based on LLR, ESBP-R reduces the number of iterations by 2–11%, and ESBP-D reduces it by 4–15%. Notably, at $E_b/N_0$ values ranging from 1.5 dB to 2.5 dB, ESBP-R and ESBP-D exhibit significant improvements in convergence speed.

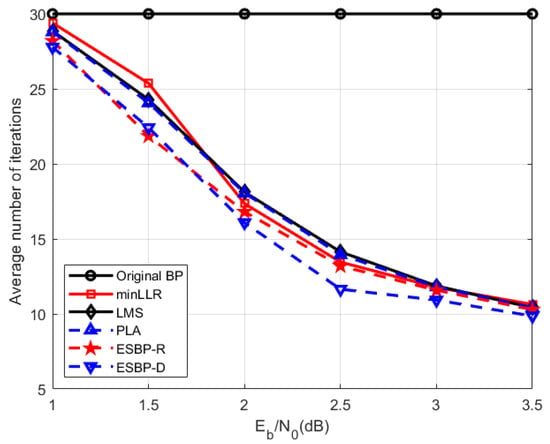
Figure 9. The average number of iterations corresponding to the simulation results in Figure 8.

Table 2. The ratio of the number of iterations reduced by several early convergence algorithms under different channel conditions.

${\mathit{E}}_{\mathit{b}}/{\mathit{N}}_0$	minLLR	LMS	PLA	ESBP-R	ESBP-D
1	2.01%	3.81%	4.01%	6.01%	7.39%
1.5	15.42%	19.03%	19.78%	27.15%	25.27%
2	42.14%	39.59%	39.81%	43.97%	46.38%
2.5	55.14%	52.87%	53.51%	56.01%	61.17%
3	60.74%	60.43%	60.63%	61.40%	63.59%
3.5	64.55%	65.28%	65.31%	65.71%	67.12%

Table 3. The ratio of reduced iteration times compared to three existing early convergence algorithms.

${\mathit{E}}_{\mathit{b}}/{\mathit{N}}_0$	ESBP-R	ESBP-D
1	2.8%	4.3%
1.5	11.0%	8.8%
2	5.8%	9.9%
2.5	4.7%	15.9%
3	2.0%	7.6%
3.5	2.0%	5.9%

Simulation results indicate that under various channel conditions, the two information geometry-based BP decoding algorithms for polar codes proposed in this paper, namely ESBP-R and ESBP-D, can terminate the decoding algorithm earlier than other methods, leading to a lower average number of iterations.

6. Conclusions

This paper addresses the issue of high energy consumption in the Belief Propagation (BP) decoding algorithm for polar codes in Low-Earth Orbit (LEO) satellite communication systems. A geometric framework for polar code BP decoding is established, and two early convergence algorithms for polar code BP decoding based on geometric distance are proposed. Simulation results demonstrate that both algorithms improve the convergence speed of polar code BP decoding without compromising the bit error rate. Our research provides a new theoretical interpretation and method for the BP decoding of polar codes, offering valuable insights for further enhancing the decoding performance of polar codes. It also presents fresh perspectives for achieving sustainable 6G network architectures and communications in all resource-constrained node scenarios.

Previous scholars have attempted to utilize geometry to study channel coding problems in Turbo codes and LDPC codes [14,18,19,20,21]. The geometric framework for polar code BP decoding proposed in this paper can be seen as a continuation of these studies. Through research on early convergence algorithms for polar code BP decoding, this paper validates the effectiveness of the geometric framework. Future work can leverage this geometric framework to improve optimization algorithms for polar code BP decoding and optimize the error correction performance of polar code BP decoding.