Shock Model of K/N: G Repairable Retrial System Based on Discrete PH Repair Time

Abstract

A discrete time modeling method is employed in this paper to analyze and evaluate the reliability of a discrete time K/N: G repairable retrial system with Bernoulli shocks and two-stage repair. Lifetime and shocks are two factors that lead to component failure, and both of them can lead to the simultaneous failure of multiple components. When the repairman is busy, the newly failed component enters retrial orbit and retries in accordance with the first-in-first-out (FIFO) rule to obtain the repair. The repairman provides two-stage repair for failed components, all of which require basic repair and some of which require optional repair. The discrete PH distribution controls the repair times for two stages. Based on discrete time stochastic model properties, priority rules are defined when multiple events occur simultaneously. The state transition probability matrix and state set analysis are used to evaluate the system performance indexes. Numerical experiments are used to illustrate the main performance indexes of the developed discrete time model, and the impact of each parameter variation on the system indexes is examined.

1. Introduction

The system will inevitably be subjected to shocks during operation, which may be caused by external friction, collision or over-pressure. The shock model was first proposed and studied by Esary et al. [1]. Subsequently, the shock model has been extensively studied. Shock models can be broadly categorized into four traditional types based on shock failure mechanisms: cumulative [2,3,4], run [5,6], $\delta$ [7,8] and extreme [9,10] shock models. In reliability design, redundancy technology is generally used to improve system reliability. Standby redundancy means that one or more online components work and the redundant components are used as standby components. The standby component replaces the failed component and starts working when an online working component fails. As a means of redundancy, the K/N structure can greatly improve system reliability, which is suitable for various fields such as electronics and military and aerospace design. Research on K/N systems has mainly focused on the assumption that the components have a continuous lifetime distribution [11,12,13,14,15,16].

Systems with discrete lifetime components are widely used in real-world production. For example, the service lifetime of a car tire is measured in kilometers or days and the lifetime of a switch is measured by the number of switches. In reliability studies of discrete time repairable systems, the geometric distribution is often used to model the event occurrence time. However, the disadvantage of applying a geometric distribution is that it reduces the applicability of the model. Once some random variables follow other distributions, it is difficult to analyze the stochastic model, especially to obtain specific analytical results. In view of this phenomenon, the PH distribution was proposed by Neuts, and the properties of the PH distribution and its application in queuing theory were discussed in [17]. In fact, the PH distribution is able to model systems with multiple performance stages in the form of well-structured matrices and is widely used in telecommunications, finance, reliability, biometrics and queuing theory. In addition, since the distribution obeyed by any non-negative random variable can be approximated by the PH distribution, the application of the PH distribution makes the model more general. In recent years, discrete time system models involving discrete PH distribution have been widely studied. Refs. [18,19,20] studied discrete time cold standby systems, in which the lifetime and repair time of the component are both discrete PH distributions. The reliability of the discrete time warm standby repairable system affected by external shocks has been studied in [21,22], where the shock arrival interval follows a discrete PH distribution. Ruiz-Castro and Li [23] conducted reliability modeling for a discrete time K/N: G system with R repairmen, in which component lifetime and repair time are subject to a discrete PH distribution. Based on the properties of the discrete PH distribution, Ruiz-Castro [24] analyzed the discrete time reliability model with preventive maintenance.

In recent years, retrial systems have been widely studied due to their applications in computer networks, telephone communication centers and industrial engineering. Almási et al. [25] studied repairable retrial queueing systems with an unreliable server. The finite-source retrial system with multiple servers and unreliable servers was studied by Gharbi and Ioualalen [26]. Boualem et al. [27] modeled and analyzed an M/G/1 retrial queuing system with vacation. Gao and Wang [28] studied the M/G/1 retrial queuing system with non-persistent customers. Peng et al. [29] considered an M/G/1 retrial G-queue with linear retrial policy, preemptive resume priority, collisions and server breakdowns. Kuo et al. [30] investigated a mixed standby retrial system and performed a cost–benefit ratio analysis for the system with and without retrial. The reliability model of retrial systems with warm standby components and imperfect coverage was studied by Yen and Wang [31]. Wang et al. [32] compared reliability indexes for four retrial systems with unreliable repair equipment and preventive maintenance. For more recent research on retrial systems, see [33,34,35,36].

In most repairable system reliability studies, it is generally assumed that the repairmen only perform one stage of repair on failed components. However, in order to meet different industrial needs, the repair strategy for failed components is diversifying beyond a single phase of repair. Two-stage repair is a common repair strategy with potential applications in communication networks, computer networks, manufacturing systems, and service industries. The early literature mainly focuses on queuing models with two-stage service from the perspective of queuing theory. For example, references [37,38,39] studied the M/G/1 queuing model with a second optional service. Wang and Zhao [40] proposed a discrete time retrial queuing system model with a second optional service and starting failures. Kumar and Jain [41] studied the unreliable queuing model with two-stage service and vacation, and used PSO and ABC optimization algorithms to determine the optimal service rate at optimum cost. Recently, the two-stage repair model from the perspective of system reliability has been studied in the following literature. A warm standby system with a second optional repair service was studied by Gao [42]; the system reliability indexes were solved based on the Laplace transform. Wang et al. [43] studied a linear continuous K/N: F system with vacation and two-stage repair, in which the two-stage repair times obeyed a continuous PH distribution.

Based on the current research status of the K/N: G system, it can be found that the research about the K/N: G system has the following limitations: (1) Shock models for K/N: G systems are generally studied in the continuous case. However, due to the internal structure of the system, working mode and monitoring methods, not all systems can be continuously monitored. (2) In the study of K/N: G system reliability, most K/N: G system models consider a single one-stage repair strategy. However, the case of repairmen providing multiple repair services of multi-stage for failed components is more realistic to research. In view of the above situation, we constructed a shock model of the K/N: G retrial system with two-stage repair in discrete time. The failure of components is influenced by external shocks and their lifetime, both of which might result in several components failing at once. For discrete time K/N: G retrial systems, Yu et al. [44] considered a model with single-stage repair and Bernoulli shocks, where repair time followed a geometric distribution. However, to meet different industrial needs, different repair strategies are often adopted, and additional tasks are assigned to repairmen to reduce the waste of resources. Therefore, based on this model, we extended the single-stage repair system to a two-stage repair system. Repair time was generalized from a geometric distribution to a discrete PH distribution to make the model more general. In addition, a discrete-time K/N: G system model is also discussed in [45], but there are still some significant differences from the model developed in this paper: (1) This paper considers the two-stage repair of repairmen, which was not considered in the work in [45]. (2) Extreme shock is considered in our model, while $\delta$-shock was considered in [45]. (3) This paper assumes that a discrete PH distribution dominates the repair time of the two stages, which is different from the geometric distribution of repair time in [45].

Based on the above motivation and comparative analysis, the main research work and contributions of this paper are as follows: (1) A shock model for a discrete time K/N: G repairable retrial system with a two-stage repair is proposed based on discrete time stochastic process theory. Both shock and lifetime could lead to simultaneous failure of multiple components. (2) The repairman provides two-stage repair for failed components: basic repair and optional repair. The repair time of both stages is subject to a discrete PH distribution. (3) The sequencing rules for multiple events occurring simultaneously are proposed. Reliability indexes for the system under transient-state and steady-state conditions are analyzed. The rest of this paper is organized as follows. In Section 2, detailed model assumptions and analysis are given. In Section 3, the steady-state and transient-state analyses of the model are performed, and a series of reliability indexes are obtained. The developed model is analyzed numerically in Section 4. Section 5 summarizes this paper.

2. System Model

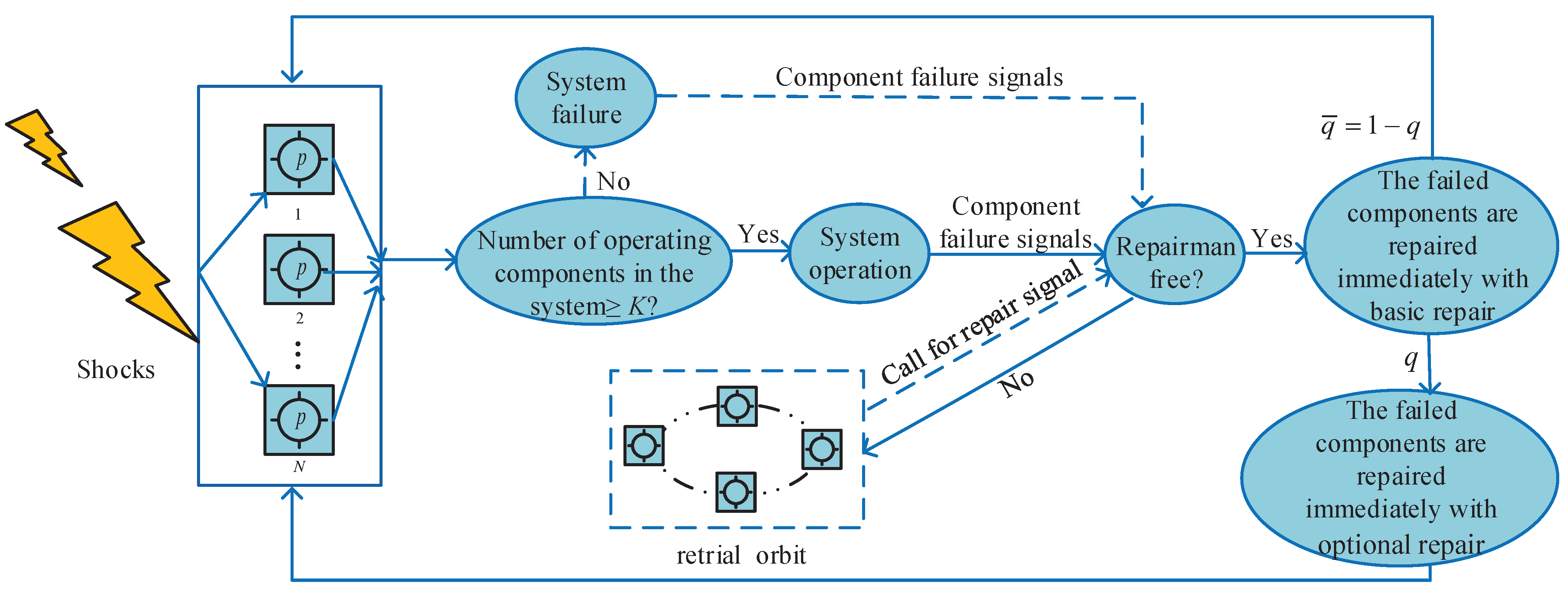
2.1. Model Description

The system consists of the same independent components; if which K or more components work, the system will work normally. At $\kappa$ = 0, all components are new and the repairman is in idle state. When the system is in a failed state, the normal components will still fail. In order to describe the system more intuitively, Figure 1 shows the specific operation principle of the system, and the specific assumptions are as follows:

(a)

Shock environment: The system suffers from Bernoulli shock currents (rate $\theta$), and the effect on components is independent. The failure threshold is a constant or a random variable, and the shock magnitude is a random variable. Component failure occurs at the time when the shock magnitude is more than the failure threshold.

(b)

Failure mechanism: The components fail due to two factors: external shocks and their lifetime. These two factors could lead to multiple component failures at once. The lifetime of the component is assumed to be geometrically distributed with parameter p. The impact of lifetime upon the components can be ignored when a shock arrives.

(c)

Repair mechanism: The failed component is repaired by a repairman who provides a two-stage repair service: basic repair and optional repair. After the completion of the basic repair, the component is repaired in an optional repair with probability q, or leaves the service desk with probability $\overline{q}=1-q$. Repair times for the two stages are different m-order discrete PH distributions, respectively expressed as $\left(\mathit{\alpha },\mathit{U}\right)$, $\mathit{\alpha }=\left({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_m\right)$, $\mathit{U}={\left(U_{ij}\right)}_{m\times m}\left(1\le i,j\le m\right)$, ${\mathit{U}}^0=\left(U_1^0,\cdots ,U_m^0\right)$ and $\left(\mathit{\beta },\mathit{V}\right),\mathit{\beta }=\left({\beta }_1,{\beta }_2,\cdots ,{\beta }_m\right)$, $\mathit{V}={\left(V_{ij}\right)}_{m\times m}\left(1\le i,j\le m\right),{\mathit{V}}^0=\left(V_1^0,\cdots ,V_m^0\right)$.

(d)

Retrial rule: When the repairman is busy, the newly failed component enters the retrial orbit and retries repeatedly to obtain repair according to FIFO rules. The retrial time is geometrically distributed with parameter $\gamma$.

(e)

Priority rule: (1) The following order of occurrence is specified when multiple events occur simultaneously: the component failure, the failed component retrial and the repair completion (any stage of repair). (2) The failure information of components is retrieved one by one when multiple components fail simultaneously, and the component retrieved first has priority for repair or joining the retrial orbit.

2.2. Discrete Time Markov Process

• System state analysis

Based on the model assumption, $\left\{L\left(\kappa \right),S\left(\kappa \right),\kappa =0,1,2,\cdots \right\}$ constitutes a discrete time Markov chain. Here,  

$L\left(\kappa \right)=\left\{\begin{array}{c}0,\mathrm{the}\mathrm{repairman}\mathrm{is}\mathrm{idle}\mathrm{at}\mathrm{time}\kappa ,\hfill \\ a_{l_1},\mathrm{the}\mathrm{repairman}\mathrm{is}\mathrm{in}\mathrm{phase}{l}_1\mathrm{for}\mathrm{the}\mathrm{basic}\mathrm{repair}\mathrm{at}\mathrm{time}\kappa ,l_1=1,2,\cdots ,m,\hfill \\ b_{l_2},\mathrm{the}\mathrm{repairman}\mathrm{is}\mathrm{in}\mathrm{phase}{l}_2\mathrm{for}\mathrm{the}\mathrm{optional}\mathrm{repair}\mathrm{at}\mathrm{time}\kappa ,l_2=1,2,\cdots ,m,\hfill \end{array}\right.$

and

$S\left(\kappa \right)=s$, if the retrial orbit has s components at time $\kappa$, $s=0,1,\cdots ,N-1$.

In order to simplify system state analysis, the system states are divided into N + 1 macro states based on the number of failed components. Then, the system state space $\mathsf{\Omega }=E_0\cup E_1\cup \cdots \cup E_N$, working state space $W=E_0\cup E_1\cup \cdots \cup E_{N-K}$ and failure state space $F=E_{N-K+1}\cup E_{N-K+2}\cup \cdots \cup E_N$, in which each macro state is described as follows:

(1)

$E_0=\left\{\left(0,0\right)\right\}$: there are no failed components in the system.

(2)

$E_s=\left\{\left(0,s\right),\left(a_{l_1},s-1\right),\left(b_{l_2},s-1\right),s=1,2,\cdots ,N-1,l_1,l_2=1,2,\cdots ,m\right\}$: there are s failed components in the system.

(3)

$E_N=\left\{\left(a_{l_1},N-1\right),\left(b_{l_2},N-1\right),l_1,l_2=1,2,\cdots ,m\right\}$: there are N failed components in the system.

• One-step transition probability

Based on assumption (a), the following two cases are considered.

Case I: the shock magnitude is a random variable X subject to an exponential distribution with parameter $\lambda$, and components have a constant failure threshold c.

Under these circumstances, we use $\epsilon$ and $\overline{\epsilon }$ to denote the probability that an individual component does not fail and fails when subjected to a shock, respectively; then, $\epsilon =1-\mathrm{P}\left\{X\ge c\right\}=1-{\mathrm{e}}^{-\lambda c}$ and $\overline{\epsilon }=\mathrm{P}\left\{X\ge c\right\}={\mathrm{e}}^{-\lambda c}$.

Case II: the shock magnitude is a random variable X subject to distribution $\phi$ and the failure threshold Y is subject to distribution $\xi$.

Under these circumstances, the probability that shocks lead to a single component failure is $P_x=\mathrm{P}(Y\le x)=\xi \left(x\right)$ when the shock magnitude value is x. Since X is a random variable, $\xi \left(X\right)$ is also a random variable on the interval [0,1]. Let $\widehat{X}=\xi \left(X\right)$ and we assume that the probability distribution function of $\widehat{X}$ is $\eta \left(\widehat{x}\right)$; then,

$$\eta \left(\widehat{x}\right)=\mathrm{P}\left(\widehat{X}\le \widehat{x}\right)=\mathrm{P}\left(\xi \left(X\right)\le \widehat{x}\right)=\mathrm{P}(X\le {\xi }^{-1}\left(\widehat{x}\right))=\phi ({\xi }^{-1}\left(\widehat{x}\right)).$$

Let ${\omega }_{a{a}^{\prime }}$$\left(a,a^{\prime }=0,1,\cdots ,N\right)$ denote the failure of $a^{\prime }-a$ components resulting from a shock, and ${\epsilon }_{a{a}^{\prime }}$ be the probability of occurrence of ${\omega }_{a{a}^{\prime }}$; then,

$${\epsilon }_{a{a}^{\prime }}={\int }_0^1\mathrm{P}\left({\omega }_{a{a}^{\prime }}|\widehat{X}=\widehat{x}\right)\mathrm{d}\eta \left(\widehat{x}\right)=C_{N-a}^{a^{\prime }-a}{\int }_0^1{\left(1-\widehat{x}\right)}^{N-a^{\prime }}{\widehat{x}}^{a^{\prime }-a}\mathrm{d}\eta \left(\widehat{x}\right).$$

Let $d_{\left(l,s\right),\left(l^{\prime },s^{\prime }\right)}$ denote the probability that the system transitions from state $(l,s)$ to $(l^{\prime },s^{\prime })$. Based on the probability discussion and analysis, one-step transition probabilities of system states under cases I and II are shown in

Table 1. One-step transition probabilities for case I.

State Transition	One-Step Transition Probability
$d_{\left(0,0\right),\left(0,0\right)}|d_{\left(0,s\right),\left(0,s\right)},s=1,2,\cdots ,N-1$	$\theta {\tau }^N+\overline{\theta }{\overline{p}}^N|\overline{\gamma }\left(\theta {\epsilon }^{N-s}\right.\left.+\overline{\theta }{\overline{p}}^{N-s}\right)$
$d_{\left(0,s\right),\left(a_{l_1},s+r-1\right)},s=0,1,\cdots ,N-1,l_1=1,2,\cdots ,m,r=1,2,\cdots ,N-s$	${\alpha }_{l_1}{C}_{N-s}^r\left(\theta {\epsilon }^{N-s-r}\right.\left.{\overline{\epsilon }}^r+\overline{\theta }{p}^r{\overline{p}}^{N-s-r}\right)$
$d_{\left(0,s\right),\left(a_{l_1},s-1\right)},s=1,2,\cdots ,N-1,l_1=1,2,\cdots ,m$	${\alpha }_{l_1}\gamma (\theta {\epsilon }^{N-s}+\overline{\theta }{\overline{p}}^{N-s})$
$d_{\left(a_{l_1},s\right),\left(0,s\right)}|d_{\left(a_{l_1},s\right),\left(a_{l_1^{\prime }},s\right)},s=0,1,\cdots ,N-1,l_1,l_1^{\prime }=1,2,\cdots ,m$	$U_{l_1}^0\overline{q}\left(\theta \right.\left.{\epsilon }^{N-s-1}+\overline{\theta }{\overline{p}}^{N-s-1}\right)|$
	$U_{l_1{l}_1^{\prime }}\left(\theta {\epsilon }^{N-s-1}+\overline{\theta }{\overline{p}}^{N-s-1}\right)$
$d_{\left(a_{l_1},s\right),\left(0,s+r\right)}|d_{\left(a_{l_1},s\right),\left(a_{l_1^{\prime }},s+r\right)},s=0,1,\cdots ,N-2,l_1,l_1^{\prime }=1,2,\cdots ,m,$	$U_{l_1}^0\overline{q}{C}_{N-s-1}^r\left(\theta \right.\left.{\epsilon }^{N-s-1-r}{\overline{\epsilon }}^r+\overline{\theta }{p}^r{\overline{p}}^{N-s-1-r}\right)|$
$r=1,2,\cdots ,N-s-1$	$U_{l_1{l}_1^{\prime }}{C}_{N-s-1}^r\left(\theta {\epsilon }^{N-s-1-r}{\overline{\epsilon }}^r+\overline{\theta }{p}^r{\overline{p}}^{N-s-1-r}\right)$
$d_{\left(a_{l_1},s\right),\left(b_{l_2},s\right)}|d_{\left(b_{l_2},s\right),\left(0,s\right)},s=0,1,\cdots ,N-1,l_1,l_2=1,2,\cdots ,m$	$U_{l_1}^{0}q{\beta }_{l_2}\left(\theta {\epsilon }^{N-s-1}+\overline{\theta }{\overline{p}}^{N-s-1}\right)|$
	$V_{l_2}^0\left(\theta {\epsilon }^{N-s-1}+\overline{\theta }{\overline{p}}^{N-s-1}\right)$
$d_{\left(a_{l_1},s\right),\left(b_{l_2},s+r\right)}|d_{\left(b_{l_2},s\right),\left(0,s+r\right)},s=0,1,\cdots ,N-2,l_1,l_2=1,2,\cdots ,m,$	$U_{l_1}^{0}q{\beta }_{l_2}{C}_{N-s-1}^r\left(\theta {\epsilon }^{N-s-1-r}{\overline{\epsilon }}^r+\overline{\theta }{p}^r{\overline{p}}^{N-s-1-r}\right)|$
$r=1,2,\cdots ,N-s-1$	$V_{l_2}^0{C}_{N-s-1}^r\left(\theta {\epsilon }^{N-s-1-r}{\overline{\epsilon }}^r+\overline{\theta }{p}^r{\overline{p}}^{N-s-1-r}\right)$
$d_{\left(b_{l_2},s\right),\left(b_{l_2^{\prime }},s\right)},s=0,1,\cdots ,N-1,l_2,l_2^{\prime }=1,2,\cdots ,m$	$V_{l_2{l}_2^{\prime }}\left(\theta {\epsilon }^{N-s-1}+\overline{\theta }{\overline{p}}^{N-s-1}\right)$
$d_{\left(b_{l_2},s\right),\left(b_{l_2^{\prime }},s+r\right)},s=0,1,\cdots ,N-2,l_2,l_2^{\prime }=1,2,\cdots ,m,$	$V_{l_2{l}_2^{\prime }}{C}_{N-s-1}^r\left(\theta {\epsilon }^{N-s-1-r}{\overline{\epsilon }}^r+\overline{\theta }{p}^r{\overline{p}}^{N-s-1-r}\right)$
$r=1,2,\cdots ,N-s-1$

and

Table 2. One-step transition probabilities for case II.

State Transition	One-Step Transition Probability
$d_{\left(0,0\right),\left(0,0\right)}|d_{\left(0,s\right),\left(0,s\right)},s=1,2,\cdots ,N-1$	$\theta {\epsilon }_{00}+\overline{\theta }{\overline{p}}^N|\overline{\gamma }\left(\theta {\epsilon }_{ss}\right.\left.+\overline{\theta }{\overline{p}}^{N-s}\right)$
$d_{\left(0,s\right),\left(a_{l_1},s+r-1\right)},s=0,1,\cdots ,N-1,l_1=1,2,\cdots ,m,r=1,2,\cdots ,N-s$	${\alpha }_{l_1}\left(\theta {\epsilon }_{s(s+r)}\right.\left.+C_{N-s}^r\overline{\theta }{p}^r{\overline{p}}^{N-s-r}\right)$
$d_{\left(0,s\right),\left(a_{l_1},s-1\right)},s=1,2,\cdots ,N-1,l_1=1,2,\cdots ,m$	${\alpha }_{l_1}\gamma (\theta {\epsilon }_{ss}+\overline{\theta }{\overline{p}}^{N-s})$
$d_{\left(a_{l_1},s\right),\left(0,s\right)}|d_{\left(a_{l_1},s\right),\left(a_{l_1^{\prime }},s\right)},s=0,1,\cdots ,N-1,l_1,l_1^{\prime }=1,2,\cdots ,m$	$U_{l_1}^0\overline{q}\left(\theta \right.\left.{\epsilon }_{\left(s+1\right)\left(s+1\right)}+\overline{\theta }{\overline{p}}^{N-s-1}\right)|$
	$U_{l_1{l}_1^{\prime }}\left(\theta {\epsilon }_{\left(s+1\right)\left(s+1\right)}+\overline{\theta }{\overline{p}}^{N-s-1}\right)$
$d_{\left(a_{l_1},s\right),\left(0,s+r\right)}|d_{\left(a_{l_1},s\right),\left(a_{l_1^{\prime }},s+r\right)},s=0,1,\cdots ,N-2,l_1,l_1^{\prime }=1,2,\cdots ,m,$	$U_{l_1}^0\overline{q}\left(\theta \right.\left.{\epsilon }_{\left(s+1\right)\left(s+r+1\right)}+C_{N-s-1}^r\overline{\theta }{p}^r{\overline{p}}^{N-s-1-r}\right)|$
$r=1,2,\cdots ,N-s-1$	$U_{l_1{l}_1^{\prime }}\left(\theta {\epsilon }_{\left(s+1\right)\left(s+r+1\right)}+C_{N-s-1}^r\overline{\theta }{p}^r{\overline{p}}^{N-s-1-r}\right)$
$d_{\left(a_{l_1},s\right),\left(b_{l_2},s\right)}|d_{\left(b_{l_2},s\right),\left(0,s\right)},s=0,1,\cdots ,N-1,l_1,l_2=1,2,\cdots ,m$	$U_{l_1}^{0}q{\beta }_{l_2}\left(\theta {\epsilon }_{\left(s+1\right)\left(s+1\right)}+\overline{\theta }{\overline{p}}^{N-s-1}\right)|$
	$V_{l_2}^0\left(\theta {\epsilon }_{\left(s+1\right)\left(s+1\right)}+\overline{\theta }{\overline{p}}^{N-s-1}\right)$
$d_{\left(a_{l_1},s\right),\left(b_{l_2},s+r\right)}|d_{\left(b_{l_2},s\right),\left(0,s+r\right)},s=0,1,\cdots ,N-2,l_1,l_2=1,2,\cdots ,m,$	$U_{l_1}^{0}q{\beta }_{l_2}\left(\theta {\epsilon }_{\left(s+1\right)\left(s+r+1\right)}+C_{N-s-1}^r\overline{\theta }{p}^r{\overline{p}}^{N-s-1-r}\right)|$
$r=1,2,\cdots ,N-s-1$	$V_{l_2}^0\left(\theta {\epsilon }_{\left(s+1\right)\left(s+r+1\right)}+C_{N-s-1}^r\overline{\theta }{p}^r{\overline{p}}^{N-s-1-r}\right)$
$d_{\left(b_{l_2},s\right),\left(b_{l_2^{\prime }},s\right)},s=0,1,\cdots ,N-1,l_2,l_2^{\prime }=1,2,\cdots ,m$	$V_{l_2{l}_2^{\prime }}\left(\theta {\epsilon }_{\left(s+1\right)\left(s+1\right)}+\overline{\theta }{\overline{p}}^{N-s-1}\right)$
$d_{\left(b_{l_2},s\right),\left(b_{l_2^{\prime }},s+r\right)},s=0,1,\cdots ,N-2,l_2,l_2^{\prime }=1,2,\cdots ,m,$	$V_{l_2{l}_2^{\prime }}\left(\theta {\epsilon }_{\left(s+1\right)\left(s+r+1\right)}+C_{N-s-1}^r\overline{\theta }{p}^r{\overline{p}}^{N-s-1-r}\right)$
$r=1,2,\cdots ,N-s-1$

, respectively.

2.3. Transition Probability Matrix

We divide the state of the system into working state set $W_0,W_1,W_2$ and failure state set $F_0,F_1,F_2$, and the states in each state set have the following arrangement:  

$W_0:\left\{\left(0,0\right),\left(0,1\right),\cdots ,\left(0,N-K\right)\right\}$, $W_1:\left\{w_{1,0},w_{1,1},\cdots ,w_{1,N-K-1}\right\}$,

$W_2:\left\{w_{2,0},w_{2,1},\cdots ,w_{2,N-K-1}\right\}$, $F_0:\left\{\left(0,N-K+1\right),\left(0,N-K+2\right),\cdots ,\left(0,N-1\right)\right\}$,

$F_1:\left\{f_{1,N-K},f_{1,N-K+1},\cdots ,f_{1,N-1}\right\}$, $F_2:\left\{f_{2,N-K},f_{2,N-K+1},\cdots ,f_{2,N-1}\right\}$,

where

$w_{1,s}=\left\{\left(a_1,s\right),\cdots ,\left(a_m,s\right)\right\}$, $w_{2,s}=\left\{\left(b_1,s\right),\cdots ,\left(b_m,s\right)\right\},s=0,1,\cdots ,N-K-1$,

$f_{1,s^{\prime }}=\left\{\left(a_1,s^{\prime }\right),\cdots ,\left(a_m,s^{\prime }\right)\right\}$, $f_{2,s^{\prime }}=\left\{\left(b_1,s^{\prime }\right),\cdots ,\left(b_m,s^{\prime }\right)\right\},$ $s^{\prime }=N-K,N-K+1,\cdots ,N-1$.

According to the above arrangement, one-step transition probability matrices of the states for cases I and II can be represented by the same block matrix L:

$$W_0{W}_1{W}_2{F}_0{F}_1{F}_2$$

$$\begin{array}{c}\mathit{L}=\begin{array}{c}{W}_0\\ W_1\\ W_2\\ F_0\\ F_1\\ F_2\end{array}{\left(\begin{array}{cccccc}{\mathit{L}}_{11}& {\mathit{L}}_{12}& {\mathit{L}}_{13}& {\mathit{L}}_{14}& {\mathit{L}}_{15}& {\mathit{L}}_{16}\\ {\mathit{L}}_{21}& {\mathit{L}}_{22}& {\mathit{L}}_{23}& {\mathit{L}}_{24}& {\mathit{L}}_{25}& {\mathit{L}}_{26}\\ {\mathit{L}}_{31}& {\mathit{L}}_{32}& {\mathit{L}}_{33}& {\mathit{L}}_{34}& {\mathit{L}}_{35}& {\mathit{L}}_{36}\\ {\mathit{L}}_{41}& {\mathit{L}}_{42}& {\mathit{L}}_{43}& {\mathit{L}}_{44}& {\mathit{L}}_{45}& {\mathit{L}}_{46}\\ {\mathit{L}}_{51}& {\mathit{L}}_{52}& {\mathit{L}}_{53}& {\mathit{L}}_{54}& {\mathit{L}}_{55}& {\mathit{L}}_{56}\\ {\mathit{L}}_{61}& {\mathit{L}}_{62}& {\mathit{L}}_{63}& {\mathit{L}}_{64}& {\mathit{L}}_{65}& {\mathit{L}}_{66}\end{array}\right)}_{\left(2m+1\right)N\times \left(2m+1\right)N}\hfill \end{array}.$$

The sub-blocks of L are shown in Appendix A.

3. Reliability Indexes

3.1. System Availability and Failure Condition Probability in Transient State

Let $p_{\left(l,s\right),\kappa }=\mathrm{P}\left\{L\left(\kappa \right)=l,S\left(\kappa \right)=s,\left(l,s\right)\in \mathsf{\Omega }\right\}$ be the probability that the system is in state $(l,s)$ at time $\kappa$, and

${\mathit{P}}_{\kappa }=\left({\mathit{P}}_{W_0,\kappa },{\mathit{P}}_{\left(a_{l_1},0\right),\kappa },\right.\cdots ,{\mathit{P}}_{\left(a_{l_1},N-K-1\right),\kappa },{\mathit{P}}_{\left(b_{l_2},0\right),\kappa },\cdots ,$

                              ${\mathit{P}}_{\left(b_{l_2},N-K-1\right),\kappa },{\mathit{P}}_{F_0,\kappa },{\mathit{P}}_{\left(a_{l_1},N-K\right),\kappa },\cdots ,$ $\left.{\mathit{P}}_{\left(a_{l_1},N-1\right),\kappa },{\mathit{P}}_{\left(b_{l_2},N-K\right),\kappa },\cdots ,{\mathit{P}}_{\left(b_{l_2},N-1\right),\kappa }\right)$

be the system state probability vector, where

${\mathit{P}}_{W_0,\kappa }=\left(p_{\left(0,0\right),\kappa },p_{\left(0,1\right),\kappa },\cdots ,\right.\left.p_{\left(0,N-K\right),\kappa }\right),{\mathit{P}}_{F_0,\kappa }=\left(p_{\left(0,N-K+1\right),\kappa },\right.\left.p_{\left(0,N-K+2\right),\kappa },\cdots ,p_{\left(0,N-1\right),\kappa }\right),$

${\mathit{P}}_{\left(a_{l_1},s\right),\kappa }=\left(p_{\left(a_1,s\right),\kappa },\right.\left.p_{\left(a_2,s\right),\kappa },\cdots ,p_{\left(a_m,s\right),\kappa }\right)$, $\left.{\mathit{P}}_{\left(b_{l_2},s\right),\kappa }=\left(p_{\left(b_1,s\right),\kappa },\right.p_{\left(b_2,s\right),\kappa },\cdots ,p_{\left(b_m,s\right),\kappa }\right),s=0,1,\cdots ,N-1$.

Then, the system state probability satisfies the following equations:

$$\begin{array}{cc}\hfill & \left\{\begin{array}{c}{\mathit{P}}_{\kappa }={\mathit{P}}_0{\mathit{L}}^{\kappa },\hfill \\ {\mathit{P}}_0={\left(1,0,\cdots ,0\right)}_{1\times \left(2m+1\right)N}.\hfill \end{array}\right.\hfill \end{array}$$

(1)

According to Equation (1), each state probability function in working state sets $W_0,W_1$ and $W_2$ can be expressed as

$$\begin{array}{c}\hfill p_{\left(0,s_1\right),\kappa }={\mathit{P}}_0{\mathit{L}}^{\kappa }{\mathit{\mu }}_{s_1+1},s_1=0,1,\cdots ,N-K,\end{array}$$

(2)

$$\begin{array}{c}\hfill p_{\left(a_{l_1},s_2\right),\kappa }={\mathit{P}}_0{\mathit{L}}^{\kappa }{\mathit{\mu }}_{\left(N-K+1\right)+m{s}_2+l_1},s_2=0,1,\cdots ,N-K-1,l_1=1,2,\cdots ,m,\end{array}$$

(3)

$$\begin{array}{c}\hfill p_{\left(b_{l_2},s_2\right),\kappa }={\mathit{P}}_0{\mathit{L}}^{\kappa }{\mathit{\mu }}_{(N-K+1)+m\left(N-K+s_2\right)+l_2},s_2=0,1,\cdots ,N-K-1,l_2=1,2,\cdots ,m,\end{array}$$

(4)

where

${\mathit{\mu }}_{s_1+1}={\left(0,\cdots ,0,1,0\cdots ,0\right)}_{1\times \left(2m+1\right)N}^{\mathtt{T}}$ with element 1 in row $s_1+1$,

${\mathit{\mu }}_{\left(N-K+1\right)+m{s}_2+l_1}={\left(0,\cdots ,0,1,0\cdots ,0\right)}_{1\times \left(2m+1\right)N}^{\mathtt{T}}$ with element 1 in row $(N-K+1)+m{s}_2+l_1$,

${\mathit{\mu }}_{(N-K+1)+m\left(N-K+s_2\right)+l_2}={\left(0,\cdots ,0,1,0\cdots ,0\right)}_{1\times \left(2m+1\right)N}^{\mathtt{T}}$ with element 1 in row $(N-K+1)+m(N-K+s_2)+l_2$.

Further, the following system reliability indexes can be obtained.

• The system transient-state availability $A\left(\kappa \right)$

Based on the above state probability function, we can obtain

$$\begin{array}{c}\hfill \begin{array}{c}A\left(\kappa \right)={\displaystyle \sum _{\left(l,s\right)\in W}}{p}_{\left(l,s\right),\kappa }\hfill \\ ={\displaystyle \sum _{s_1=0}^{N-K}}{p}_{\left(0,s_1\right),\kappa }+{\displaystyle \sum _{s_2=0}^{N-K-1}}\left({\displaystyle \sum _{l_1=1}^m}{p}_{\left(a_{l_1},s_2\right),\kappa }+{\displaystyle \sum _{l_2=1}^m}{p}_{\left(b_{l_2},s_2\right),\kappa }\right)\hfill \\ ={\displaystyle \sum _{s_1=0}^{N-K}}{\mathit{P}}_0{\mathit{L}}^{\kappa }{\mathit{\mu }}_{s_1+1}+{\displaystyle \sum _{s_2=0}^{N-K-1}}\left({\displaystyle \sum _{l_1=1}^m}{\mathit{P}}_0{\mathit{L}}^{\kappa }{\mathit{\mu }}_{\left(N-K+1\right)+m{s}_2+l_1}\right.\hfill \\ \left.+{\displaystyle \sum _{l_2=1}^m}{\mathit{P}}_0{\mathit{L}}^{\kappa }{\mathit{\mu }}_{(N-K+1)+m\left(N-K+s_2\right)+l_2}\right).\hfill \end{array}\end{array}$$

(5)

Furthermore, based on the above derivation and combined with mathematical computation software, the solution of $A\left(\kappa \right)$ can be realized by Algorithm 1.    

Algorithm 1: Solution of the system transient-state availability $A\left(\kappa \right)$

Input: N, K, m, $\kappa$, $\theta$, $\overline{\theta }$, $\gamma$, $\overline{\gamma }$, q, $\overline{q}$, $\mathit{\alpha }$, $\mathit{U}$, ${\mathit{U}}^0$, $\mathit{\beta }$, $\mathit{V}$, ${\mathit{V}}^0$ Output: System transient-state availability $A\left(\kappa \right)$ Procedure:   1: Given the the one-step transition probability matrix L and its block matrices;   2: Assign F as an identity matrix of order $(2m+1)N$;   3: Compute $\mathit{E}\leftarrow {\mathit{P}}_0\ast {\mathit{L}}^{\kappa }$;   4: Initialize $A\left(\kappa \right)\leftarrow 0$;   5: Step 1: Compute $A\left(\kappa 1\right)\leftarrow 0$;        for $s_1=0,\cdots ,N-K$ do             1.1.Update $p_{\left(0,s_1\right),\kappa }$ = $\mathit{E}\ast \mathit{F}\left(:,s_1+1\right)$;             1.2.Update $A\left(\kappa 1\right)=A\left(\kappa 1\right)+p_{\left(0,s_1\right),\kappa }$;        end   6: Step 2: Compute $A\left(\kappa 2\right)\leftarrow 0$;        for $s_2=0,\cdots ,N-K-1$ do              for $l_1=1,\cdots ,m$ do                    2.1.Update $p_{\left(a_{l_1},s_2\right),\kappa }=\mathit{E}\ast \mathit{F}\left(:,N-K+1+m\ast s_2+l_1\right)$;                    2.2.Update $A\left(\kappa 2\right)=A\left(\kappa 2\right)+p_{\left(a_{l_1},s_2\right),\kappa }$;              end         end   7: Step 3: Compute $A\left(\kappa 3\right)\leftarrow 0$;        for $s_2=0,\cdots ,N-K-1$ do              for $l_2=1,\cdots ,m$ do                    3.1.Update $p_{\left(b_{l_2},s_2\right),\kappa }=\mathit{E}\ast \mathit{F}\left(:,N-K+1+m\ast (N-K+s_2)+l_2\right)$;                    3.2.Update $A\left(\kappa 3\right)=A\left(\kappa 3\right)+p_{\left(b_{l_2},s_2\right),\kappa }$;              end        end   8: Final step: sum results. $A\left(\kappa \right)=A\left(\kappa 1\right)+A\left(\kappa 2\right)+A\left(\kappa 3\right)$.

• Failure conditional probability $M\left(\kappa \right)$ in transient state

When the system is in the working state at time $\kappa -1$, the probability of system failure at the next time $\kappa$ is called the failure conditional probability; then, we can obtain

$$\begin{array}{c}\hfill \begin{array}{c}M\left(\kappa \right)={\displaystyle \sum _{\left(l,s\right)\in W}}\left(p_{\left(l,s\right),\kappa -1}{\displaystyle \sum _{\left(l^{\prime },s^{\prime }\right)\in F}}{d}_{\left(l,s\right),\left(l^{\prime },s^{\prime }\right)}\right)\hfill \\ ={\displaystyle \sum _{s_1=0}^{N-K}}{p}_{\left(0,s_1\right),\kappa -1}\left({\mathit{\eta }}_{s_1+1}{\mathit{L}}_{15}{\mathit{e}}_{mK}\right)+{\displaystyle \sum _{s_2=0}^{N-K-1}}[{\displaystyle \sum _{l_1=1}^m}{p}_{\left(a_{l_1},s_2\right),\kappa -1}\left({\mathit{\eta }}_{m{s}_2+l_1}{\mathit{L}}_{24}{\mathit{e}}_{K-1}+{\mathit{\eta }}_{m{s}_2+l_1}\right.\hfill \\ \left.\times {\mathit{L}}_{25}{\mathit{e}}_{mK}+{\mathit{\eta }}_{m{s}_2+l_1}{\mathit{L}}_{26}{\mathit{e}}_{mK}\right)+{\displaystyle \sum _{l_2=1}^m}{p}_{\left(b_{l_2},s_2\right),\kappa -1}\left({\mathit{\eta }}_{m{s}_2+l_2}{\mathit{L}}_{34}{\mathit{e}}_{K-1}+{\mathit{\eta }}_{m{s}_2+l_2}{\mathit{L}}_{36}{\mathit{e}}_{mK}\right)]\hfill \\ ={\displaystyle \sum _{s_1=0}^{N-K}}{\mathit{P}}_0{\mathit{L}}^{\kappa -1}{\mathit{\mu }}_{s_1+1}\left({\mathit{\eta }}_{s_1+1}{\mathit{L}}_{15}{\mathit{e}}_{mK}\right)+{\displaystyle \sum _{s_2=0}^{N-K-1}}[{\displaystyle \sum _{l_1=1}^m}{\mathit{P}}_0{\mathit{L}}^{\kappa -1}{\mathit{\mu }}_{(N-K+1)+m{s}_2+l_1}\left({\mathit{\eta }}_{m{s}_2+l_1}\right.\hfill \\ \left.\times {\mathit{L}}_{24}{\mathit{e}}_{K-1}+{\mathit{\eta }}_{m{s}_2+l_1}{\mathit{L}}_{25}{\mathit{e}}_{mK}+{\mathit{\eta }}_{m{s}_2+l_1}{\mathit{L}}_{26}{\mathit{e}}_{mK}\right)+{\displaystyle \sum _{l_2=1}^m}{\mathit{P}}_0{\mathit{L}}^{\kappa -1}{\mathit{\mu }}_{(N-K+1)+m(N-K+s_2)+l_2}\hfill \\ \times \left({\mathit{\eta }}_{m{s}_2+l_2}{\mathit{L}}_{34}{\mathit{e}}_{K-1}\right.+\left.{\mathit{\eta }}_{m{s}_2+l_2}{\mathit{L}}_{36}{\mathit{e}}_{mK}\right)],\hfill \end{array}\end{array}$$

(6)

where ${\mathit{\eta }}_{s_1+1}={\left(0,\cdots ,0,1,0\cdots ,0\right)}_{1\times \left(N-K+1\right)}$ with element 1 in column $(s_1+1)$, ${\mathit{\eta }}_{m{s}_2+l_1}=\left(0,\cdots ,0,1,\right.$${\left.0\cdots ,0\right)}_{1\times m\left(N-K\right)}$ with element 1 in column $(m{s}_2+l_1)$, ${\mathit{\eta }}_{m{s}_2+l_2}=\left(0,\cdots ,0,1,0\cdots ,\right.$${\left.0\right)}_{1\times m\left(N-K\right)}$ with element 1 in column $(m{s}_2+l_2)$, ${\mathit{e}}_{K-1}=(1,1,\cdots ,1{)}_{1\times \left(K-1\right)}^{\mathtt{T}}$, ${\mathit{e}}_{mK}=(1,1,\cdots ,1{)}_{1\times mK}^{\mathtt{T}}$.

   In addition, based on the above derivation and combined with mathematical computation software, the solution of $M\left(\kappa \right)$ can be realized by Algorithm  2.

3.2. System Availability and Failure Condition Probability in Steady State

Let the probability of the system being in state $\left(l,s\right)\in \mathsf{\Omega }$ in steady state be $p_{l,s}$, and we denote steady-state probability vectors

$${\mathit{P}}_1={\left(p_{0,0},p_{0,1},\cdots ,p_{0,N-K}\right)}_{1\times \left(N-K+1\right)},$$

$${\mathit{P}}_2=({\mathit{P}}_{a_{l_1},0},{\mathit{P}}_{a_{l_1},1},\cdots ,{\mathit{P}}_{a_{l_1},N-K-1}{)}_{1\times m\left(N-K\right)},$$

$${\mathit{P}}_3=({\mathit{P}}_{b_{l_2},0},{\mathit{P}}_{b_{l_2},1},\cdots ,{\mathit{P}}_{b_{l_2},N-K-1}{)}_{1\times m\left(N-K\right)},$$

$${\mathit{P}}_4=(p_{0,N-K+1},p_{0,N-K+2},\cdots ,p_{0,N-1}{)}_{1\times \left(K-1\right)},$$

$${\mathit{P}}_5=({\mathit{P}}_{a_{l_1},N-K},{\mathit{P}}_{a_{l_1},N-K+1},\cdots ,{\mathit{P}}_{a_{l_1}},N-1{)}_{1\times mK}$$

$${\mathit{P}}_6=({\mathit{P}}_{b_{l_2},N-K},{\mathit{P}}_{b_{l_2},N-K+1},\cdots ,{\mathit{P}}_{b_{l_2},N-1}{)}_{1\times mK},$$

where ${\mathit{P}}_{a_{l_1},s}=\left(p_{a_1,s},p_{a_2,s},\cdots ,p_{a_m,s}\right),{\mathit{P}}_{b_{l_2},s}=\left(p_{b_1,s},p_{b_2,s},\cdots ,p_{b_m,s}\right),s=0,1,\cdots ,N-1.$

• System availability $A\left(\infty \right)$ in steady state

Based on the above steady-state probability vectors, we have

$$\begin{array}{c}A\left(\infty \right)={\mathit{P}}_1{\mathit{e}}_{N-K+1}+{\mathit{P}}_2{\mathit{e}}_{m\left(N-K\right)}+{\mathit{P}}_3{\mathit{e}}_{m\left(N-K\right)},\hfill \end{array}$$

(7)

where ${\mathit{e}}_{N-K-1}=(1,1,\cdots ,1{)}_{1\times \left(N-K-1\right)}^{\mathtt{T}}$, ${\mathit{e}}_{m\left(N-K\right)}=(1,1,\cdots ,1{)}_{1\times m\left(N-K\right)}^{\mathtt{T}}$.

• Failure condition probability M in steady state

Combined with the analysis in Section 3.1, the conditional probability of system failure under steady state can be represented as

$$\begin{array}{c}\hfill \begin{array}{c}M={\displaystyle \sum _{\left(l,s\right)\in W}}\left(p_{l,s}{\displaystyle \sum _{\left(l^{\prime },s^{\prime }\right)\in F}}{d}_{\left(l,s\right),\left(l^{\prime },s^{\prime }\right)}\right)\hfill \\ ={\displaystyle \sum _{s_1=0}^{N-K}}{p}_{0,s_1}\left({\mathbf{\eta }}_{s_1+1}{\mathit{L}}_{15}{\mathit{e}}_{mK}\right)+{\displaystyle \sum _{s_2=0}^{N-K-1}}[{\displaystyle \sum _{l_1=1}^m}{p}_{a_{l_1},s_2}\left({\mathbf{\eta }}_{m{s}_2+l_1}{\mathit{L}}_{24}{\mathit{e}}_{K-1}+{\mathbf{\eta }}_{m{s}_2+l_1}{\mathit{L}}_{25}{\mathit{e}}_{mK}\right.\hfill \\ \left.+{\mathbf{\eta }}_{m{s}_2+l_1}{\mathit{L}}_{26}{\mathit{e}}_{mK}\right)+{\displaystyle \sum _{l_2=1}^m}{p}_{b_{l_2},s_2}\left({\mathbf{\eta }}_{m{s}_2+l_2}{\mathit{L}}_{34}{\mathit{e}}_{K-1}+{\mathbf{\eta }}_{m{s}_2+l_2}{\mathit{L}}_{36}{\mathit{e}}_{mK}\right)].\hfill \end{array}\end{array}$$

(8)

Algorithm 2: Solution of the system failure conditional probability $M\left(\kappa \right)$

Input: N, K, m, $\kappa$, $\theta$, $\overline{\theta }$, $\gamma$, $\overline{\gamma }$, q, $\overline{q}$, $\mathit{\alpha }$, $\mathit{U}$, ${\mathit{U}}^0$, $\mathit{\beta }$, $\mathit{V}$, ${\mathit{V}}^0$ Output: Failure conditional probability $M\left(\kappa \right)$ in transient state   1: Given the the one-step transition probability matrix L and its block matrices;   2: Assign F, I and R as identity matrices of order $2(m+1)N$, $N-K+1$ and $m(N-K)$ respectively;   3: $\mathit{E}\leftarrow {\mathit{P}}_0\ast {\mathit{L}}^{\kappa }$;   4: $M\left(\kappa 1\right)\leftarrow 0$;        for $s_1=0,\cdots ,N-K$ do             $p_{\left(0,s_1\right),\kappa }$ = $\mathit{E}\ast \mathbf{F}\left(:,s_1+1\right)$;             $M=p_{\left(0,s_1\right),\kappa }\ast \mathit{I}\left(s_1+1,:\right)\ast {\mathit{L}}_{15}\ast {\mathit{e}}_{mK}$;             $M\left(\kappa 1\right)=M+M\left(\kappa 1\right)$;        end   5: $M\left(\kappa 2\right)\leftarrow 0$;        for $s_2=0,\cdots ,N-K-1$ do              for $l_1=1,\cdots ,m$ do                    $p_{\left(a_{l_1},s_2\right),\kappa }=\mathit{E}\ast \mathbf{F}\left(:,N-K+1+m\ast s_2+l_1\right)$;                    $M=p_{\left(a_{l_1},s_2\right),\kappa }\ast (\mathbf{R}\left(m\ast s_2+l_1,:\right)\ast {\mathit{L}}_{24}\ast {\mathit{e}}_{K-1}+\mathbf{R}\left(m\ast s_2+l_1,:\right)\ast {\mathit{L}}_{25}\ast {\mathit{e}}_{mK}$                             $+\mathbf{R}\left(m\ast s_2+l_1,:\right)\ast {\mathit{L}}_{26}\ast {\mathit{e}}_{mK})$;                    $M\left(\kappa 2\right)=M+M\left(\kappa 2\right)$;              end         end   6: $M\left(\kappa 3\right)\leftarrow 0$;        for $s_2=0,\cdots ,N-K-1$ do              for $l_2=1,\cdots ,m$ do                    $p_{\left(b_{l_2},s_2\right),\kappa }=\mathit{E}\ast \mathbf{F}\left(:,N-K+1+m\ast (N-K+s_2)+l_2\right)$;                    $M=p_{\left(b_{l_2},s_2\right),\kappa }\ast (\mathbf{R}\left(m\ast s_2+l_2,:\right)\ast {\mathit{L}}_{34}\ast {\mathit{e}}_{K-1}+\mathbf{R}\left(m\ast s_2+l_2,:\right)\ast {\mathit{L}}_{36}\ast {\mathit{e}}_{mK})$;                    $M\left(\kappa 3\right)=M+M\left(\kappa 3\right)$;              end        end   7: $M\left(\kappa \right)=M\left(\kappa 1\right)+M\left(\kappa 2\right)+M\left(\kappa 3\right)$.

• Steps for solving the steady-state probability vectors ${\mathit{P}}_1,{\mathit{P}}_2,{\mathit{P}}_3,{\mathit{P}}_4,{\mathit{P}}_5$ and ${\mathit{P}}_6$

(i)

Establishment of steady-state probability equation

Based on the discrete time analysis method, the following equations can be constructed:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathit{P}\mathit{L}=\mathit{P},\hfill \\ \mathit{P}{\mathit{e}}_{\left(2m+1\right)N}=1,\hfill \end{array}\right.\end{array}$$

(9)

where $\mathit{P}=\left({\mathit{P}}_1,\right.{\mathit{P}}_2,{\mathit{P}}_3,{\mathit{P}}_4,{\mathit{P}}_5,\left.{\mathit{P}}_6\right)$, ${\mathit{e}}_{\left(2m+1\right)N}=(1,1,\cdots ,1{)}_{1\times \left(2m+1\right)N}^{\mathtt{T}}$.

(ii)

Decomposition of steady-state probability equation

By substituting $\mathit{L}$ in Section 2.3 into Equation (9), we can obtain

$$\begin{array}{cc}\hfill & {\mathit{P}}_1{\mathit{L}}_{11}+{\mathit{P}}_2{\mathit{L}}_{21}+{\mathit{P}}_3{\mathit{L}}_{31}+{\mathit{P}}_5{\mathit{L}}_{51}+{\mathit{P}}_6{\mathit{L}}_{61}={\mathit{P}}_1,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & {\mathit{P}}_1{\mathit{L}}_{12}+{\mathit{P}}_2{\mathit{L}}_{22}={\mathit{P}}_2,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & {\mathit{P}}_2{\mathit{L}}_{23}+{\mathit{P}}_3{\mathit{L}}_{33}={\mathit{P}}_3,\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & {\mathit{P}}_2{\mathit{L}}_{24}+{\mathit{P}}_3{\mathit{L}}_{34}+{\mathit{P}}_4{\mathit{L}}_{44}+{\mathit{P}}_5{\mathit{L}}_{54}+{\mathit{P}}_6{\mathit{L}}_{64}={\mathit{P}}_4,\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & {\mathit{P}}_1{\mathit{L}}_{15}+{\mathit{P}}_2{\mathit{L}}_{25}+{\mathit{P}}_4{\mathit{L}}_{45}+{\mathit{P}}_5{\mathit{L}}_{55}={\mathit{P}}_5,\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & {\mathit{P}}_2{\mathit{L}}_{26}+{\mathit{P}}_3{\mathit{L}}_{36}+{\mathit{P}}_5{\mathit{L}}_{56}+{\mathit{P}}_6{\mathit{L}}_{66}={\mathit{P}}_6,\hfill \end{array}$$

(15)

$$\begin{array}{c}\hfill {\mathit{P}}_1{\mathit{e}}_{N-K+1}+{\mathit{P}}_2{\mathit{e}}_{m\left(N-K\right)}+{\mathit{P}}_3{\mathit{e}}_{m\left(N-K\right)}+{\mathit{P}}_4{\mathit{e}}_{K-1}+{\mathit{P}}_5{\mathit{e}}_{mK}+{\mathit{P}}_6{\mathit{e}}_{mK}=1,\end{array}$$

(16)

where ${\mathit{L}}_{11}$, ${\mathit{L}}_{22}$, ${\mathit{L}}_{33}$, ${\mathit{L}}_{44}$, ${\mathit{L}}_{55}$ and ${\mathit{L}}_{66}$ are non-singular matrices.

(iii)

Solution of the steady-state probability equation

By calculating Equations (11) and (12), we obtain

$$\begin{array}{c}{\mathit{P}}_2={\mathit{P}}_1{\mathit{L}}_{12}({\mathit{I}}_{m\left(N-K\right)}-{\mathit{L}}_{22}{)}^{-1},\hfill \end{array}$$

(17)

$$\begin{array}{c}{\mathit{P}}_3={\mathit{P}}_1{\mathit{L}}_{12}({\mathit{I}}_{m\left(N-K\right)}-{\mathit{L}}_{22}{)}^{-1}{\mathit{L}}_{23}({\mathit{I}}_{m\left(N-K\right)}-{\mathit{L}}_{33}{)}^{-1},\hfill \end{array}$$

(18)

where ${\mathit{I}}_{m(N-K)}$ is an $m(N-K)$-order identical matrix.

Bringing Equations (17), (18) into Equations (13)–(15), respectively, we obtain

$$\begin{array}{c}\hfill {\mathit{P}}_1\left[{\mathit{L}}_{12}{\left({\mathit{I}}_{m\left(N-K\right)}-{\mathit{L}}_{22}\right)}^{-1}{\mathit{L}}_{24}+{\mathit{A}}_1{\mathit{L}}_{34}\right]+{\mathit{P}}_4{\mathit{L}}_{44}+{\mathit{P}}_5{\mathit{L}}_{54}+{\mathit{P}}_6{\mathit{L}}_{64}={\mathit{P}}_4,\end{array}$$

(19)

$$\begin{array}{c}\hfill {\mathit{P}}_1\left[{\mathit{L}}_{15}+{\mathit{L}}_{12}{\left({\mathit{I}}_{m\left(N-K\right)}-{\mathit{L}}_{22}\right)}^{-1}{\mathit{L}}_{25}\right]+{\mathit{P}}_4{\mathit{L}}_{45}+{\mathit{P}}_5{\mathit{L}}_{55}={\mathit{P}}_5,\end{array}$$

(20)

$$\begin{array}{c}\hfill {\mathit{P}}_1\left[{\mathit{L}}_{12}{\left({\mathit{I}}_{m\left(N-K\right)}-{\mathit{L}}_{22}\right)}^{-1}{\mathit{L}}_{26}+{\mathit{A}}_1{\mathit{L}}_{36}\right]+{\mathit{P}}_5{\mathit{L}}_{56}+{\mathit{P}}_6{\mathit{L}}_{66}={\mathit{P}}_6,\end{array}$$

(21)

where ${\mathit{A}}_1={\mathit{L}}_{12}{\left({\mathit{I}}_{m\left(N-K\right)}-{\mathit{L}}_{22}\right)}^{-1}{\mathit{L}}_{23}{\left({\mathit{I}}_{m\left(N-K\right)}-{\mathit{L}}_{33}\right)}^{-1}$.  

By calculating Equations (19)–(21), we obtain

$$\begin{array}{c}\hfill {\mathit{P}}_4={\mathit{P}}_1{\mathit{C}}_1{{\mathit{C}}_2}^{-1},\end{array}$$

(22)

$$\begin{array}{c}\hfill {\mathit{P}}_5={\mathit{P}}_1\left[{\mathit{A}}_2+{\mathit{C}}_1{{\mathit{C}}_2}^{-1}{\mathit{L}}_{45}{\left({\mathit{I}}_{mK}-{\mathit{L}}_{55}\right)}^{-1}\right],\end{array}$$

(23)

$$\begin{array}{c}\hfill {\mathit{P}}_6={\mathit{P}}_1\left[{\mathit{B}}_1{\left({\mathit{I}}_{mK}-{\mathit{L}}_{66}\right)}^{-1}+{\mathit{C}}_1{{\mathit{C}}_2}^{-1}{\mathit{A}}_3\right],\end{array}$$

(24)

where

${\mathit{A}}_2={\mathit{L}}_{15}+{\mathit{L}}_{12}({\mathit{I}}_{m\left(N-K\right)}-{\mathit{L}}_{22}{)}^{-1}{\mathit{L}}_{25}{\left({\mathit{I}}_{mK}-{\mathit{L}}_{55}\right)}^{-1}$, 

${\mathit{A}}_3={\mathit{L}}_{45}{\left({\mathit{I}}_{mK}-{\mathit{L}}_{55}\right)}^{-1}{\mathit{L}}_{56}{\left({\mathit{I}}_{mK}-{\mathit{L}}_{66}\right)}^{-1}$,  

${\mathit{B}}_1={\mathit{L}}_{12}({\mathit{I}}_{m\left(N-K\right)}-{\mathit{L}}_{22}{)}^{-1}{\mathit{L}}_{26}+{\mathit{A}}_1{\mathit{L}}_{36}+{\mathit{A}}_2{\mathit{L}}_{56}$,  

${\mathit{C}}_1={\mathit{L}}_{12}({\mathit{I}}_{m\left(N-K\right)}-{\mathit{L}}_{22}{)}^{-1}{\mathit{L}}_{24}+{\mathit{A}}_1{\mathit{L}}_{34}+{\mathit{A}}_2{\mathit{L}}_{54}+{\mathit{B}}_1{\left({\mathit{I}}_{mK}-{\mathit{L}}_{66}\right)}^{-1}{\mathit{L}}_{64}$,  

${\mathit{C}}_2={\mathit{I}}_{K-1}-{\mathit{L}}_{44}-{\mathit{A}}_3{\mathit{L}}_{64}-{\mathit{L}}_{45}{\left({\mathit{I}}_{mK}-{\mathit{L}}_{55}\right)}^{-1}{\mathit{L}}_{54}$,  

${\mathit{I}}_{K-1}$ is an identical matrix of order $K-1$, and ${\mathit{I}}_{mK}$ is an identical matrix of order $mK$.

Then, by substituting Equations (17), (18) and Equations (22)–(24) into Equations (10) and (16), respectively, we can solve for ${\mathit{P}}_1$. By substituting ${\mathit{P}}_1$ back into Equations (17), (18) and Equations (22)–(24) to obtain ${\mathit{P}}_2$, ${\mathit{P}}_3$, ${\mathit{P}}_4$, ${\mathit{P}}_5$ and ${\mathit{P}}_6$.

Further, based on the above derivation and combined with mathematical computation software, the solution of steady-state probability vectors ${\mathit{P}}_1,{\mathit{P}}_2,{\mathit{P}}_3,{\mathit{P}}_4,{\mathit{P}}_5,{\mathit{P}}_6$, $A\left(\infty \right)$ and M can be realized by Algorithm 3.    

Algorithm 3: Solution of steady-state probability vectors ${\mathit{P}}_1,{\mathit{P}}_2,{\mathit{P}}_3,{\mathit{P}}_4,{\mathit{P}}_5,{\mathit{P}}_6$, $A(\infty )$ and M

Input: N, K, m, $\theta$, $\overline{\theta }$, $\gamma$, $\overline{\gamma }$, q, $\overline{q}$, $\mathit{\alpha }$, $\mathit{U}$, ${\mathit{U}}^0$, $\mathit{\beta }$, $\mathit{V}$, ${\mathit{V}}^0$ Output: ${\mathit{P}}_1,{\mathit{P}}_2,{\mathit{P}}_3,{\mathit{P}}_4,{\mathit{P}}_5,{\mathit{P}}_6$, $A(\infty )$, M   1: Obtain the one-step transition probability matrix L and its block matrices;       Obtain ${\mathit{P}}_i\left(i=2,3,4,5,6\right)$ with respect to ${\mathit{P}}_1$ by Equations (17), (18) and Equations (22)–(24),       and do the following   2: ${\mathit{E}}_2\leftarrow {\mathit{L}}_{12}\ast {\left({\mathit{I}}_{m\left(N-K\right)}-{\mathit{L}}_{22}\right)}^{-1}$;   3: ${\mathit{E}}_3\leftarrow {\mathit{L}}_{12}\ast {\left({\mathit{I}}_{m\left(N-K\right)}-{\mathit{L}}_{22}\right)}^{-1}\ast {\mathit{L}}_{23}\ast {\left({\mathit{I}}_{m\left(N-K\right)}-{\mathit{L}}_{33}\right)}^{-1}$;   4: ${\mathit{E}}_4\leftarrow {\mathit{C}}_1\ast {\mathit{C}}_2^{-1}$;   5: ${\mathit{E}}_5\leftarrow {\mathit{A}}_2+{\mathit{C}}_1\ast {{\mathit{C}}_2}^{-1}\ast {\mathit{L}}_{45}{\left({\mathit{I}}_{mK}-{\mathit{L}}_{55}\right)}^{-1}$;   6: ${\mathit{E}}_6\leftarrow {\mathit{B}}_1\ast {\left({\mathit{I}}_{mK}-{\mathit{L}}_{66}\right)}^{-1}+{\mathit{C}}_1\ast {{\mathit{C}}_2}^{-1}\ast {\mathit{A}}_3$;      Solve for ${\mathit{P}}_1$ based on Equations (10) and (16) ($\mathit{I}$ below represent an identity matrix of order       $(N-K+1)$)   7: $\mathbf{F}\leftarrow {\mathit{L}}_{11}+{\mathit{E}}_2\ast {\mathit{L}}_{21}+{\mathit{E}}_3\ast {\mathit{L}}_{31}+{\mathit{E}}_5\ast {\mathit{L}}_{51}+{\mathit{E}}_6\ast {\mathit{L}}_{61}-{\mathit{I}}_{N-K+1}$;   8: $\mathit{B}\leftarrow {\mathit{e}}_{N-K+1}+{\mathit{E}}_2\ast {\mathit{e}}_{m\left(N-K\right)}+{\mathit{E}}_3\ast {\mathit{e}}_{m\left(N-K\right)}+{\mathit{E}}_4\ast {\mathit{e}}_{K-1}+{\mathit{E}}_5\ast {\mathit{e}}_{mK}+{\mathit{E}}_6\ast {\mathit{e}}_{mK}$;   9: ${\mathbf{F}}_0\leftarrow \mathbf{F}\left(:,1:1:N-K\right)$;   10: $\mathit{D}=\left[\mathit{B},{\mathbf{F}}_0\right]$;   11: ${\mathit{P}}_1=\mathit{I}(1,:)/\mathit{D}$;         Substitute ${\mathit{P}}_1$ back into Equations (17), (18) and Equations (22)–(24) to solve ${\mathit{P}}_i\left(i=2,3,4,5,6\right)$   12: ${\mathit{P}}_2={\mathit{P}}_1\ast {\mathit{E}}_2$; ${\mathit{P}}_3={\mathit{P}}_1\ast {\mathit{E}}_3$; ${\mathit{P}}_4={\mathit{P}}_1\ast {\mathit{E}}_4$; ${\mathit{P}}_5={\mathit{P}}_1\ast {\mathit{E}}_5$; ${\mathit{P}}_6={\mathit{P}}_1\ast {\mathit{E}}_6$;         Calculate $A(\infty )$ based on Equation (7)   13: $A\left(\infty \right)={\mathit{P}}_1\ast {\mathit{e}}_{N-K+1}+{\mathit{P}}_2\ast {\mathit{e}}_{m\left(N-K\right)}+{\mathit{P}}_3\ast {\mathit{e}}_{m\left(N-K\right)}$;         Calculate $M(\infty )$ based on Equation (8)   14: $M_1\leftarrow 0$         for $i=1,\cdots ,N-K+1$ do                      $M={\mathit{P}}_1\left(i\right)\ast \mathit{I}\left(i,:\right)\ast {\mathit{L}}_{15}\ast {\mathit{e}}_{mK}$;                      $M_1=M+M_1;$         end   15: $M_2\leftarrow 0$;         for $i=1,\cdots ,m\ast (N-K)$ do                      $M={\mathit{P}}_2\left(i\right)\ast \left(\mathbf{R}\left(i,:\right)\ast {\mathit{L}}_{24}\ast {\mathit{e}}_{K-1}+\mathbf{R}\left(i,:\right)\ast {\mathit{L}}_{25}\ast {\mathit{e}}_{mK}+\mathbf{R}\left(i,:\right)\ast {\mathit{L}}_{26}\ast {\mathit{e}}_{mK}\right)$ $+{\mathit{P}}_3\left(i\right)\ast \left(\mathbf{R}\left(i,:\right)\ast {\mathit{L}}_{34}\ast {\mathit{e}}_{K-1}+\mathbf{R}\left(i,:\right)\ast {\mathit{L}}_{36}\ast {\mathit{e}}_{mK}\right)$;                      $M_2=M+M_2$;         end   16: $M\left(\infty \right)=M_1+M_2$;   17: return ${\mathit{P}}_1,{\mathit{P}}_2,{\mathit{P}}_3,{\mathit{P}}_4,{\mathit{P}}_5,{\mathit{P}}_6$, $A(\infty )$, M.

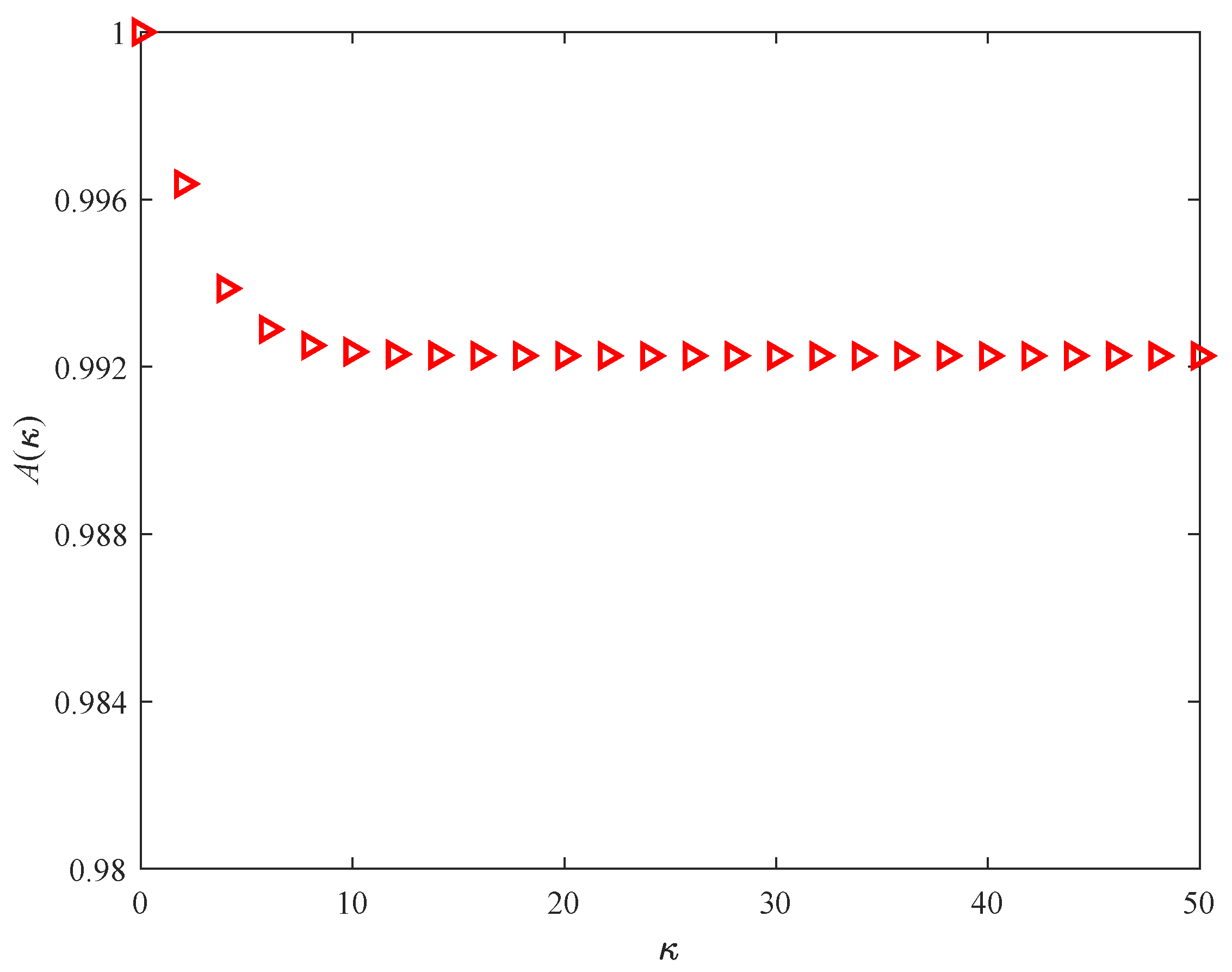
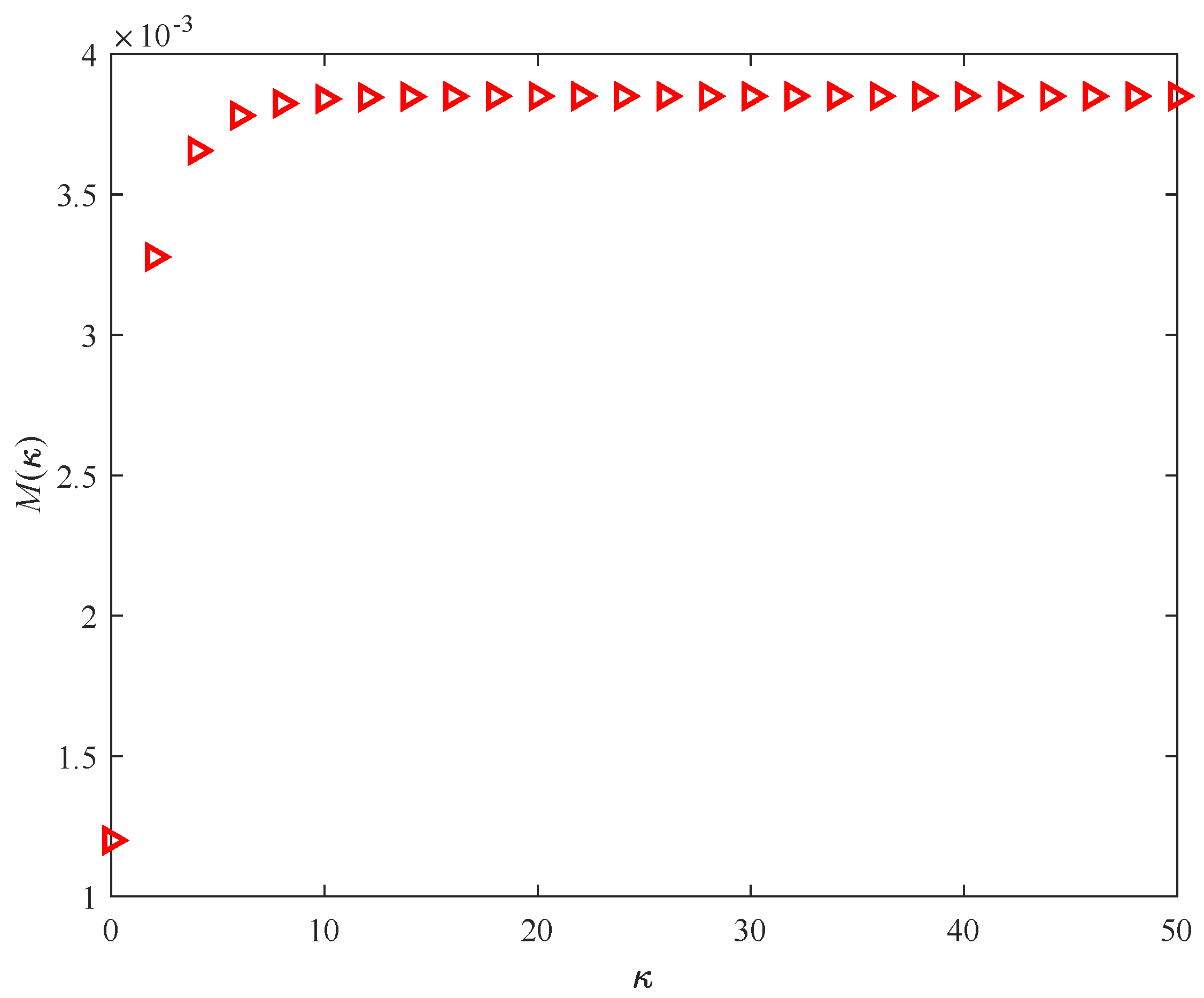
4. Numerical Example

A discrete time 2/3: G retrial system shock model based on two-stage repair is considered for two cases. Under case I, the parameters p = 0.02, $\theta$ = 0.01 and $\gamma$ = 0.9, q = 0.6 are the basic case, the components have a failure threshold with a value of 30 and the shock magnitude follows an exponential distribution, having a parameter of 0.1. Under case II, the parameters p = 0.02, $\theta$ = 0.01 and $\gamma$ = 0.9, q = 0.6 are the basic case, the distribution $\phi$ is the same as the distribution $\xi$, i.e., the $\widehat{X}$ follows a uniform distribution. Assuming that the two-stage repair time in both cases follows the two-order discrete PH distribution $\left(\mathit{\alpha },\mathit{U}\right)$ and $\left(\mathit{\beta },\mathit{V}\right)$, where $\mathit{\alpha }=\left(1,0\right)$, $\mathit{U}=\left(\begin{array}{cc}0.2& 0\\ 0.1& 0.5\end{array}\right)$, ${\mathit{U}}^0=\left(\begin{array}{c}0.8\\ 0.4\end{array}\right)$, $\mathit{\beta }=\left(1,0\right)$, $\mathit{V}=\left(\begin{array}{cc}0.25& 0.05\\ 0.5& 0.2\end{array}\right)$, ${\mathit{V}}^0=\left(\begin{array}{c}0.7\\ 0.3\end{array}\right)$.

Below, the system model is solved by mathematical computation software and some numerical experimental results are given.

Figure 2 and Figure 3 and

Table 3. Effect of p for $A\left(\kappa \right)$ and $M\left(\kappa \right)$ in case II.

Indexes	$\mathit{\kappa }$	p
		0.02	0.025	0.03	0.035
$A\left(\kappa \right)$	5	0.9765	0.9680	0.9596	0.9512
	10	0.9728	0.9630	0.9532	0.9436
	50	0.9724	0.9625	0.9527	0.9429
	100	0.9724	0.9625	0.9527	0.9429
	∞	0.9724	0.9625	0.9527	0.9429
$M\left(\kappa \right)$	5	0.0087	0.0112	0.0137	0.0161
	10	0.0090	0.0115	0.0140	0.0165
	50	0.0090	0.0116	0.0141	0.0165
	100	0.0090	0.0116	0.0141	0.0165
	∞	0.0090	0.0116	0.0141	0.0165

,

Table 4. Effect of $\theta$ for $A\left(\kappa \right)$ and $M\left(\kappa \right)$ in case II.

Indexes	$\mathit{\kappa }$	$\mathit{\theta }$
		0.01	0.015	0.02	0.025
$A\left(\kappa \right)$	5	0.9765	0.9680	0.9596	0.9512
	10	0.9728	0.9630	0.9532	0.9436
	50	0.9724	0.9625	0.9527	0.9429
	100	0.9724	0.9625	0.9527	0.9429
	∞	0.9724	0.9625	0.9527	0.9429
$M\left(\kappa \right)$	5	0.0087	0.0112	0.0137	0.0161
	10	0.0090	0.0115	0.0140	0.0165
	50	0.0090	0.0116	0.0141	0.0165
	100	0.0090	0.0116	0.0141	0.0165
	∞	0.0090	0.0116	0.0141	0.0165

and

Table 5. Effect of $\gamma$ for $A\left(\kappa \right)$ and $M\left(\kappa \right)$ in case II.

Indexes	$\mathit{\kappa }$	$\mathit{\gamma }$
		0.8	0.85	0.9	0.95
$A\left(\kappa \right)$	5	0.9763	0.9764	0.9765	0.9765
	10	0.9726	0.9725	0.9728	0.9730
	50	0.9718	0.9722	0.9724	0.9727
	100	0.9718	0.9722	0.9724	0.9727
	∞	0.9718	0.9722	0.9724	0.9727
$M\left(\kappa \right)$	5	0.00875	0.00874	0.00873	0.00872
	10	0.009018	0.009006	0.008986	0.008968
	50	0.009072	0.009044	0.009019	0.008997
	100	0.009072	0.009044	0.009019	0.008997
	∞	0.009072	0.009044	0.009019	0.008997

illustrate the influence of each parameter on $A\left(\kappa \right)$ and $M\left(\kappa \right)$ for two cases. Figure 2 and Figure 3 and Table 3, Table 4 and Table 5 show that as time $\kappa$ increases, $A\left(\kappa \right)$ gradually decreases and then tends to be stable; $M\left(\kappa \right)$ gradually increases and then stabilizes. $A\left(\kappa \right)$ decreases as p and $\theta$ increase, and increases as $\gamma$ increases. $M\left(\kappa \right)$ increases as p and $\theta$ increase and decreases with increasing $\gamma$. As p or $\theta$ increases, the system will be more likely to enter a failed state, which causes $A\left(\kappa \right)$ to decrease and $M\left(\kappa \right)$ to increase. As $\gamma$ increases, the number of failed components in retrial orbit decreases, which ensures that the system works smoothly for a longer period. This leads to an increase in $A\left(\kappa \right)$ and a decrease in $M\left(\kappa \right)$.

To further analyze the influence of N values on the system reliability indexes, we performed reliability analysis for a 10/N: G system in case I. The impact of various N for the system indexes is shown in

Table 6. 10/N: G system reliability indexes.

N	$\mathit{A}\left(\mathit{\infty }\right)$	M
10	0.5648	0.1045
15	0.9645	0.0080
20	0.9813	0.0042
25	0.982274	0.003987
30	0.982287	0.003984

. The result shows that (1) $A\left(\infty \right)$ increases with increasing N. M has the opposite conclusion. (2) It can be seen that adding standby components can significantly improve the system reliability in Table 6. However, when N is greater than 20, the method of adding standby components will no longer be efficient.

5. Conclusions

The reliability of some engineering systems needs to be assessed in discrete time, because of their internal structure and operating modes. In view of this, we proposed a shock model of a K/N: G repairable retrial system with two-stage repair in discrete time. The shock arrival interval, component lifetime and retrial time are assumed to be geometrically distributed, and the two-stage repair time is subject to a discrete PH distribution. In order to simplify the calculation and better display the results, the model analysis and main system reliability indexes were presented in matrix form. Based on the discrete time modeling method, the system’s steady-state availability was analyzed by the recurrence method. The transient-state availability and failure conditional probability were evaluated by matrix analysis and state set analysis. The developed system model was demonstrated through numerical experiments, and the variation of the system reliability indexes with the main parameters was analyzed. Additionally, the impact of various N on the system reliability indexes was given.

The reliability shock model developed in this paper has some limitations with respect to the complex and diverse system operation modes and environments. In the future, the model can be deepened in the following aspects: (1) Only one repairman was considered in this study, but in order to be more relevant to real industrial systems, the reliability evaluation of a K/N: G repairable retrial system with multiple repairmen can be considered under the discrete time assumption. (2) In order to model actual engineering systems as accurately as possible, interested scholars can extend this work to discrete time K/N: G repairable retrial systems with mixed standby components. (3) This study considered the extreme shock model and its other shock models can be applied to this model in subsequent studies. (4) The repair of certain components may be abandoned due to high repair costs or severe damage. The failure types of these components should be categorized as non-repairable. Therefore, discrete time K/N: G retrial systems with different failure types can be considered.