An Improved Analytical Approximation of the Bessel Function J2(x)
Abstract
1. Introduction
2. Theoretical Analysis
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Watson, G.N. A Treatise on the Theory of Bessel Functions; Cambridge University Press: Cambridge, UK, 1922. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Dover Publications: New York, NY, USA, 1964. [Google Scholar]
- Bowman, F. Introduction to Bessel Functions; Dover Publications: New York, NY, USA, 1958. [Google Scholar]
- Strutt, J.W. The Theory of Sound; Dover Publications: New York, NY, USA, 1945; Volume 2. [Google Scholar]
- Olver, F.W.J. Asymptotics and Special Functions; AK Peters/CRC Press: Wellesley, MA, USA, 1974. [Google Scholar]
- Baratella, P.; Garetto, M.; Vinardi, G. Approximation of the Bessel Function Jν(x) by Numerical Integration. J. Comput. Appl. Math. 1981, 7, 87–91. [Google Scholar] [CrossRef]
- Guerrero, A.L.; Martin, P. Higher Order Two-Point Quasi-Fractional Approximations to the Bessel Functions J0(x) and J1(x). J. Comput. Phys. 1988, 77, 276–281. [Google Scholar] [CrossRef]
- Maass, F.; Martin, P.; Olivares, J. Analytic Approximation to the Bessel Function J0(x). Comput. Appl. Math. 2020, 39, 222. [Google Scholar] [CrossRef]
- Molinari, L.G. A Note on Trigonometric Approximations of Bessel Functions of the First Kind, and Trigonometric Power Sums. Fundam. J. Math. Appl. 2022, 5, 266–272. [Google Scholar] [CrossRef]
- Maass, F.; Martin, P. Precise Analytic Approximations for the Bessel Function J1(x). Results Phys. 2018, 8, 1234–1238. [Google Scholar] [CrossRef]
- Maass, F.; Martin, P. A New Method to Obtain Analytic Approximations Applied to the J1(x) Function. J. Phys. Conf. Ser. 2018, 1043, 012002. [Google Scholar] [CrossRef]
- Millane, R.P.; Eads, J.L. Polynomial Approximations to Bessel Functions. IEEE Trans. Antennas Propag. 2003, 51, 1398–1400. [Google Scholar] [CrossRef]
- Harrison, J. Fast and Accurate Bessel Function Computation. In Proceedings of the 2009 19th IEEE Symposium on Computer Arithmetic, Portland, OR, USA, 8–10 June 2009; IEEE: New York, NY, USA, 2009; pp. 104–113. [Google Scholar]
- Yang, Z.H.; Chu, Y.M. On Approximating the Modified Bessel Function of the First Kind and Toader-Qi Mean. J. Inequal. Appl. 2016, 2016, 40. [Google Scholar] [CrossRef]
- Yang, Z.H.; Chu, Y.M. On Approximating the Modified Bessel Function of the Second Kind. J. Inequal. Appl. 2017, 2017, 41. [Google Scholar] [CrossRef] [PubMed]
- Cuyt, A.; Lee, W.; Wu, M. High Accuracy Trigonometric Approximations of the Real Bessel Functions of the First Kind. Comput. Math. Math. Phys. 2020, 60, 119–127. [Google Scholar] [CrossRef]
- Funes, J.O.; Kari, E.R.V.; Martin, P. The Modified Bessel Functions I3/4(x) and I−3/4(x) in Certain Fractional Differential Equations. J. Phys. Conf. Ser. 2021, 1730, 012065. [Google Scholar] [CrossRef]
- Martin, P.; Rojas, E.; Olivares, J.; Sotomayor, A. Quasi-Rational Analytic Approximation for the Modified Bessel Function I1(x) with High Accuracy. Symmetry 2021, 13, 741. [Google Scholar] [CrossRef]
- Blachman, N.M.; Mousavinezhad, S.H. Trigonometric approximations for Bessel functions. IEEE Trans. Aerosp. Electron. Syst. 1986, AES-22, 2–7. [Google Scholar] [CrossRef]
- Li, L.-L.; Li, F.; Gross, F.B. A new polynomial approximation for Jν Bessel functions. Appl. Math. Comput. 2006, 183, 1220–1225. [Google Scholar] [CrossRef]
- Krasikov, I. Approximations for the Bessel and Airy functions with an explicit error term. Lms J. Comput. Math. 2014, 17, 209–225. [Google Scholar] [CrossRef]
- Martin, P.; Ramos-Andrade, J.P.; Caro-Pérez, F.; Lastra, F. Accurate Analytical Approximation for the Bessel Function J2(x). Math. Comput. Appl. 2024, 29, 63. [Google Scholar] [CrossRef]


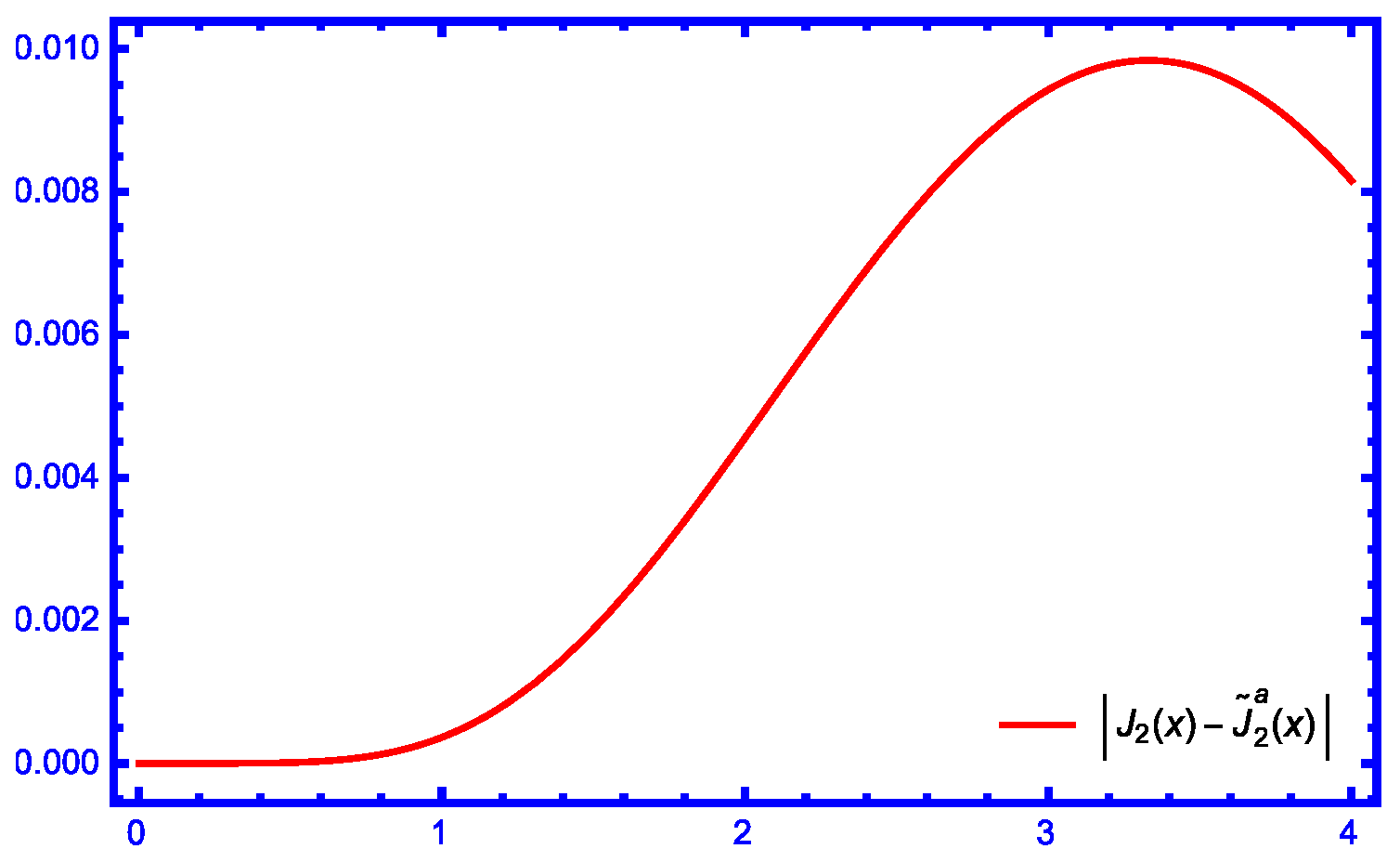



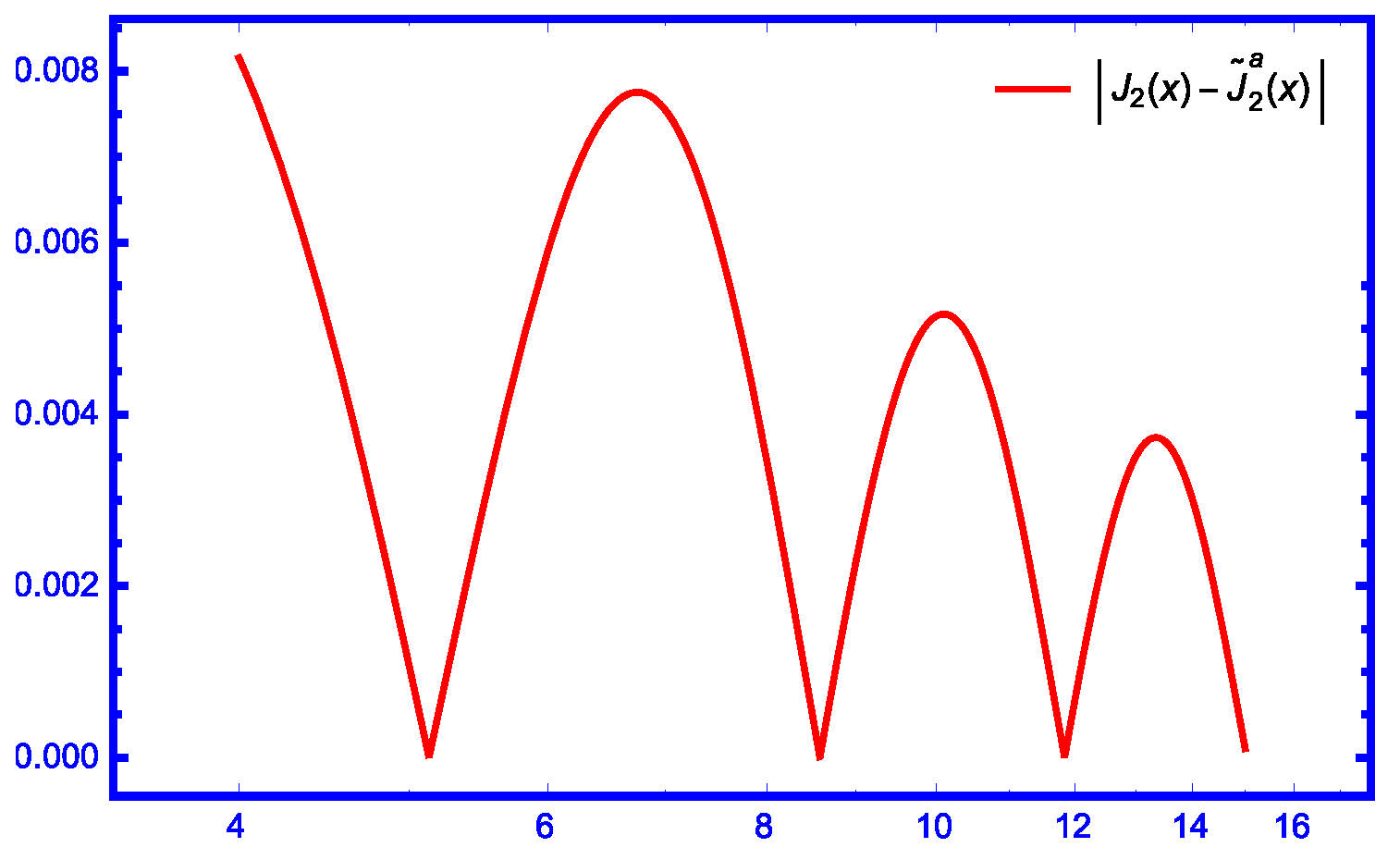
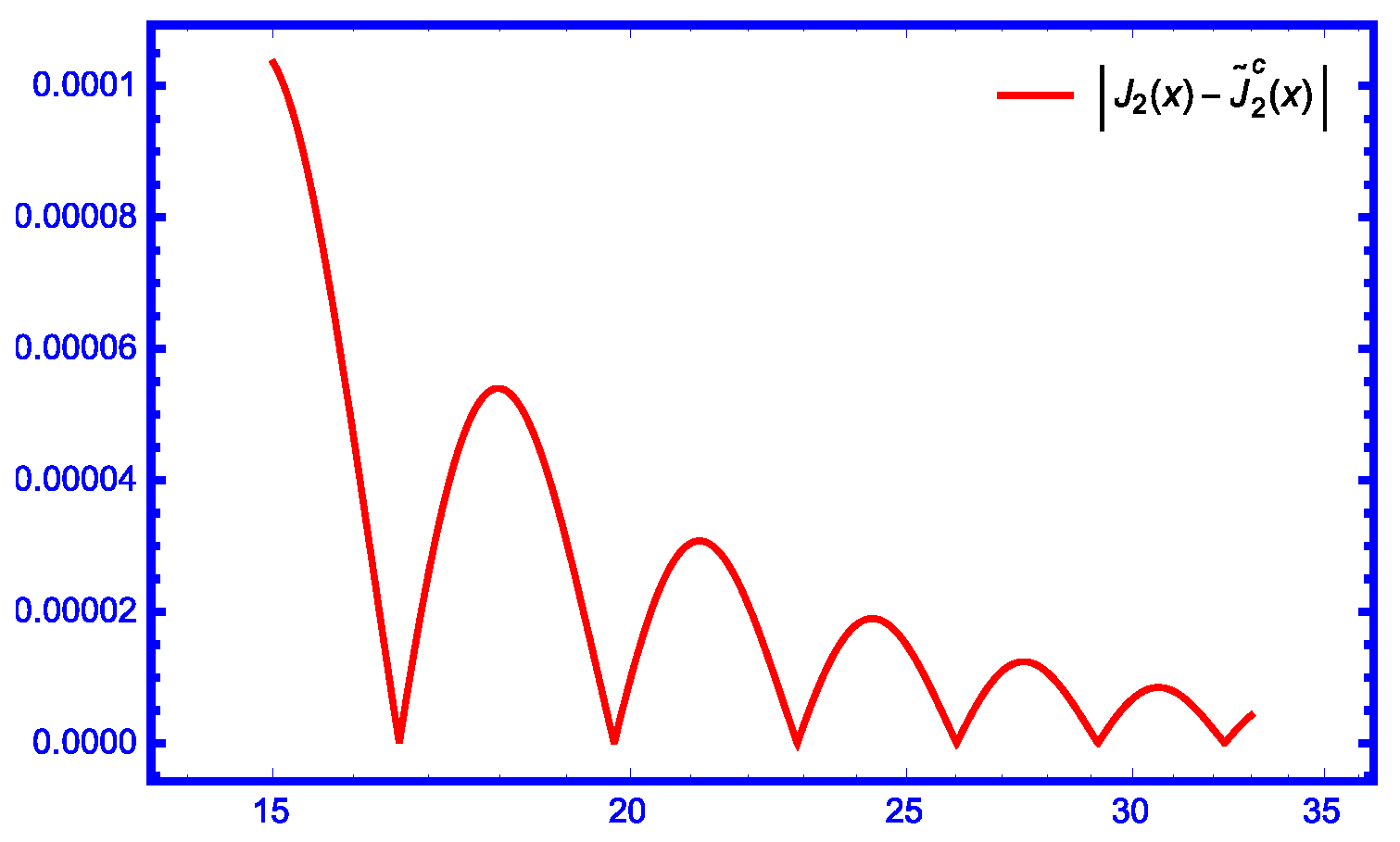


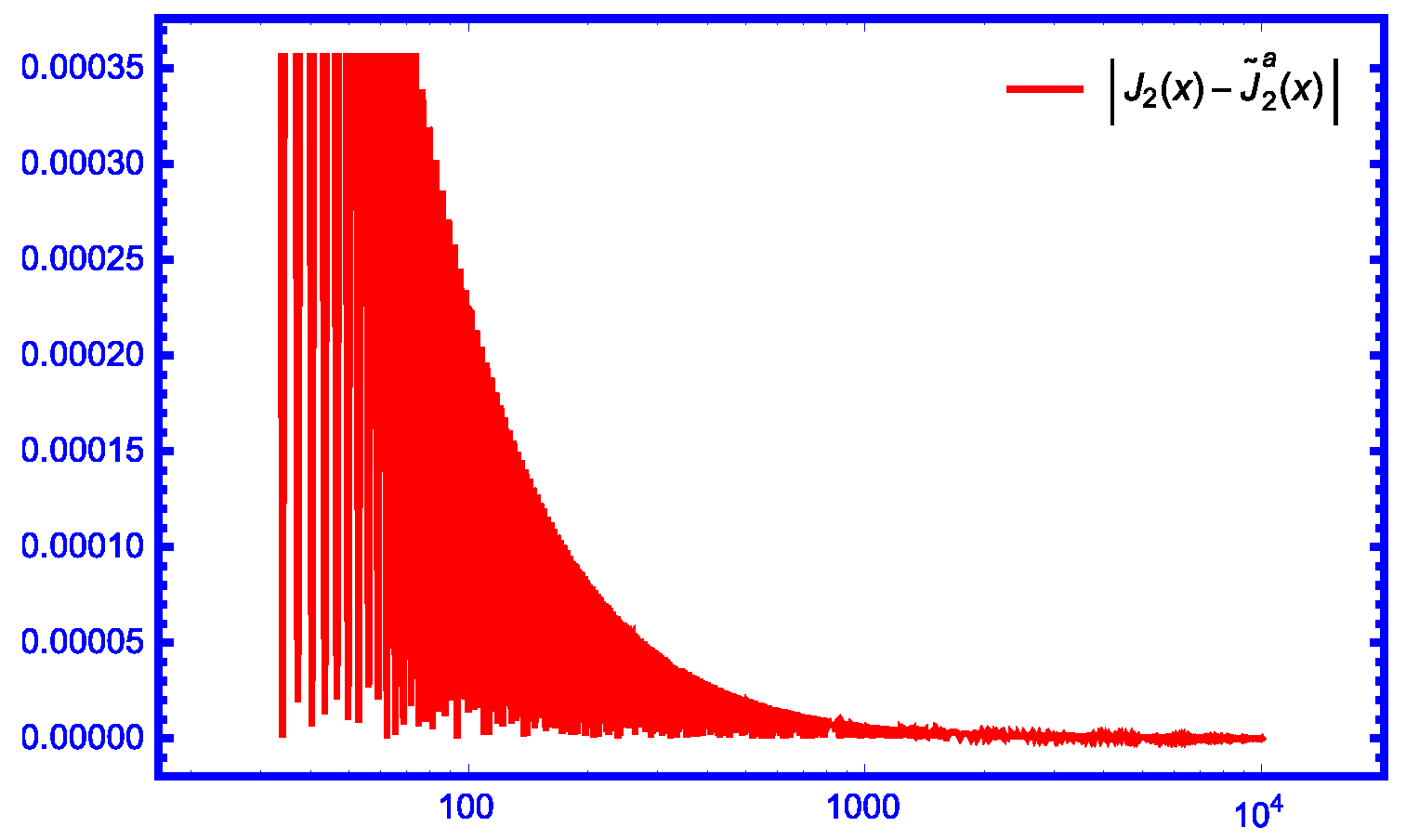
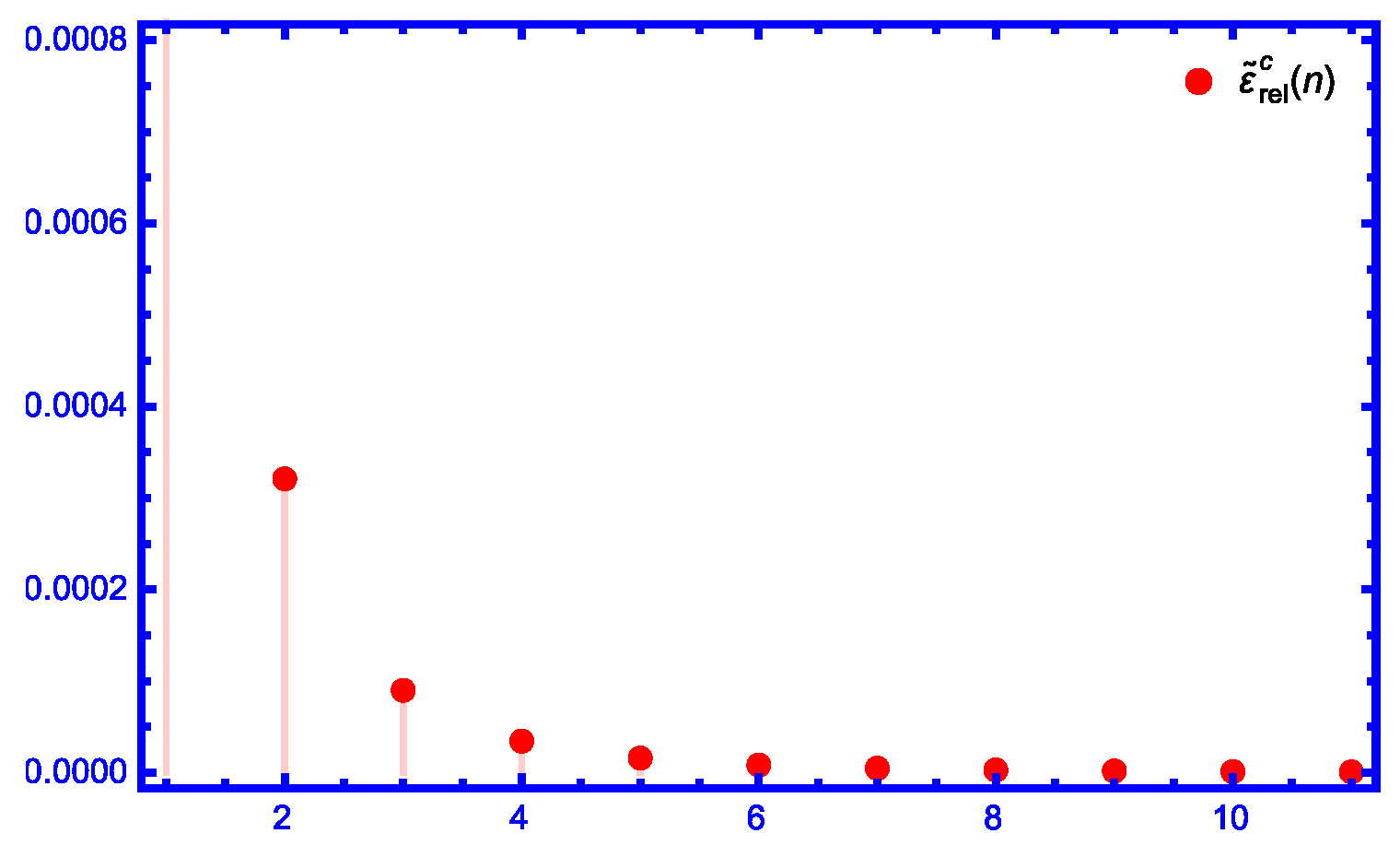
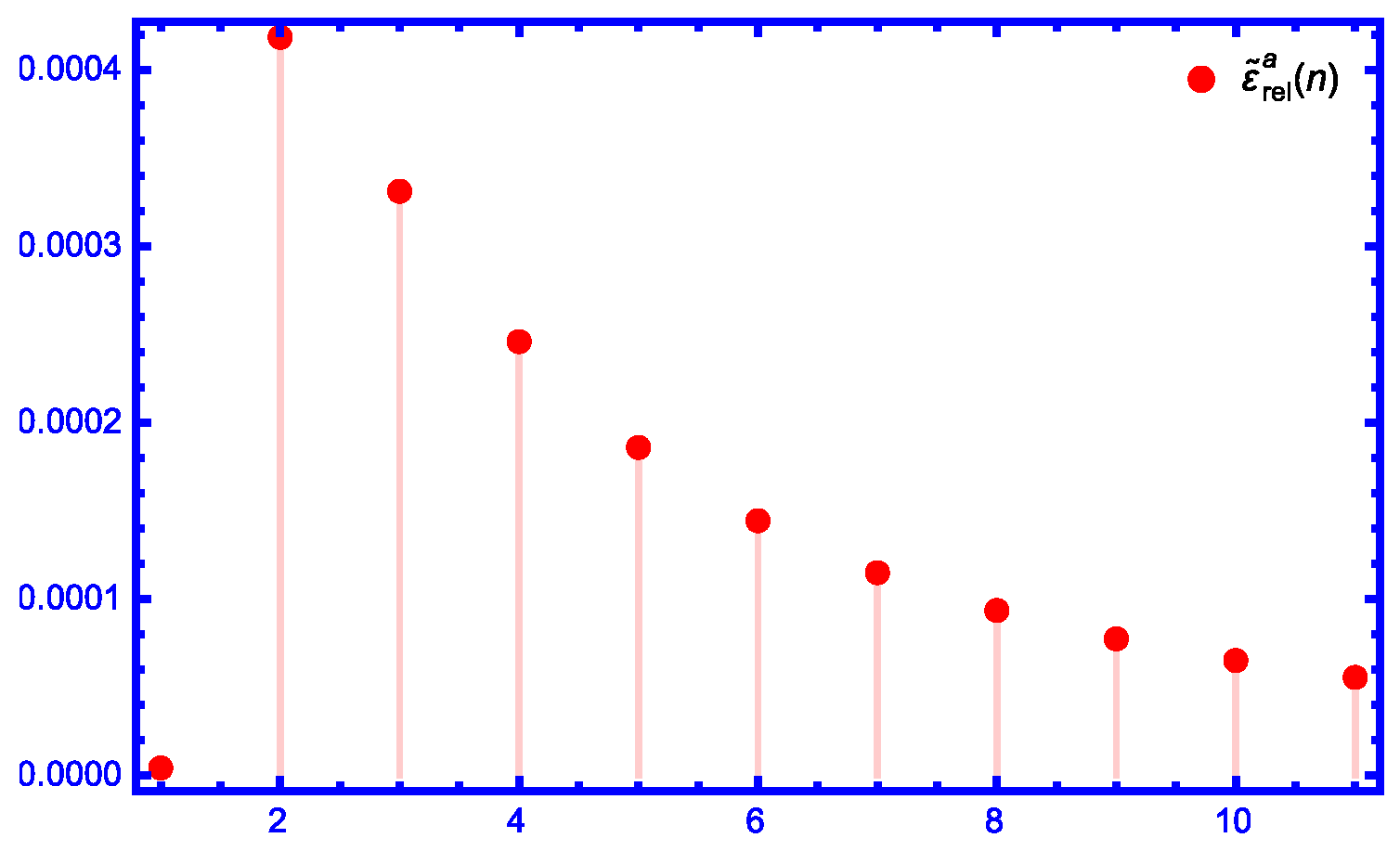
| Relative Error | Relative Error | |||
|---|---|---|---|---|
| Zeros of | Zeros of | Zeros of | of Zeros of | of Zeros of |
| 0.00219574 | ||||
| 0.000320998 | 0.000418401 | |||
| 0.0000900292 | 0.0003311 | |||
| 0.0000345615 | 0.000245909 | |||
| 0.0000160077 | 0.000185908 | |||
| 0.00014435 | ||||
| 0.000114911 | ||||
| 0.0000934664 | ||||
| 0.0000774272 | ||||
| 0.0000651459 | ||||
| 0.0000555473 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmoud, M.; Almuashi, H. An Improved Analytical Approximation of the Bessel Function J2(x). Axioms 2025, 14, 157. https://doi.org/10.3390/axioms14030157
Mahmoud M, Almuashi H. An Improved Analytical Approximation of the Bessel Function J2(x). Axioms. 2025; 14(3):157. https://doi.org/10.3390/axioms14030157
Chicago/Turabian StyleMahmoud, Mansour, and Hanan Almuashi. 2025. "An Improved Analytical Approximation of the Bessel Function J2(x)" Axioms 14, no. 3: 157. https://doi.org/10.3390/axioms14030157
APA StyleMahmoud, M., & Almuashi, H. (2025). An Improved Analytical Approximation of the Bessel Function J2(x). Axioms, 14(3), 157. https://doi.org/10.3390/axioms14030157






