On Some Unification Theorems: Yang–Baxter Systems; Johnson–Tzitzeica Theorem
Abstract
1. Introduction
2. Yang–Baxter Equations and Yang–Baxter Systems
3. Unifications Using Yang–Baxter Systems
4. On the Tzitzeica–Johnson Theorem
5. Conclusions and Further Comments
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, C.N. Some exact results for the many-body problem in one dimension with repulsive delta-function interaction. Phys. Rev. Lett. 1967, 19, 1312–1315. [Google Scholar] [CrossRef]
- Baxter, R.J. Exactly Solved Models in Statistical Mechanics; Academic Press: London, UK, 1982. [Google Scholar]
- Baxter, R.J. Partition function for the eight-vertex lattice model. Ann. Phys. 1972, 70, 193–228. [Google Scholar] [CrossRef]
- Nichita, F.F. (Ed.) Hopf Algebras, Quantum Groups and Yang-Baxter Equations; MDPI: Basel, Switzerland, 2019; ISBN 978-3-03897-325-6/978-3-03897-324-9. [Google Scholar]
- Kumar, A.; Mosic, D.; Stanimirovic, P.S.; Singh, G.; Kazakovtsev, L.A. Commuting Outer Inverse-Based Solutions to the Yang–Baxter-like Matrix Equation. Mathematics 2022, 10, 2738. [Google Scholar] [CrossRef]
- Andrusziewicz, R.R.; Smoktunowicz, A. The Yang–Baxter Matrix Equation for Involutions. Miskolc Math. Notes 2022, 23, 61–70. [Google Scholar] [CrossRef]
- Senturk, I.; Bozdan, E.N. Geometrical approach on set theoretical solutions of Yang–Baxter equation in Lie algebras. Malaya J. Mat. 2022, 10, 237–256. [Google Scholar]
- Kumar, A.; Cardoso, J.R.; Singh, G. Explicit Solutions of the Singular Yang–Baxter–like Matrix Equation and Their Numerical Computation. Mediterr. J. Math. 2022, 19, 85. [Google Scholar] [CrossRef]
- Dai, L.; Liang, M.; Shen, Y. Some Rank Formulas for the Yang-Baxter Matrix Equation AXA = XAX. Wuhan Univ. J. Nat. Sci. 2021, 26, 459–463. [Google Scholar] [CrossRef]
- Duplij, S.; Vogl, R. Polyadic Braid Operators and Higher Braiding Gates. Universe 2021, 7, 301. [Google Scholar] [CrossRef]
- Oner, T.; Katican, T.; Saeid, A.B. Yang–Baxter equation in median algebras. Rend. Circ. Mat. Palermo Ser. 2 2021, 70, 79–95. [Google Scholar] [CrossRef]
- Dimakis, A.; Müller-Hoissen, F. Tropical limit of matrix solitons and entwining Yang–Baxter maps. Lett. Math. Phys. 2020, 110, 3015–3051. [Google Scholar] [CrossRef]
- Turaev, V. The Yang-Baxter equation and invariants of links. Invent. Math. 1988, 92, 527–553. [Google Scholar] [CrossRef]
- Jones, V.F.R. A polynomial invariant for knots via von Neumann algebras. Bull. Am. Math. Soc. 1985, 12, 103–111. [Google Scholar] [CrossRef]
- Freyd, P.; Yetter, D.; Hoste, J.; Lickorish, W.B.R.; Millett, K.; Ocneanu, A. A new polynomial invariant of knots and links. Bull. Am. Math. Soc. 1985, 12, 239–246. [Google Scholar] [CrossRef]
- Przytycki, J.H.; Traczyk, P. Invariants of links of Conway type. Kobe J. Math. 1987, 4, 115–139. [Google Scholar]
- Kauffman, L.H. New invariants in the theory of knots. Astérisque 1988, 163–164, 137–219. [Google Scholar] [CrossRef]
- Nichita, F.F. Self-Inverse Yang-Baxter Operators from (Co)Algebra structures. J. Algebra 1999, 218, 738–759. [Google Scholar] [CrossRef]
- Massuyeau, G.; Nichita, F.F. Yang-Baxter operators arising from algebra structures and the Alexander polynomial of knots. Comm. Algebra 2005, 33, 2375–2385. [Google Scholar] [CrossRef]
- Morris, S.A. Pontryagin Duality and the Structure of Locally Compact Abelian Groups; Cambridge University Press: Cambridge, UK, 1977. [Google Scholar]
- Nichita, F.F.; Schack, S.D. The duality between algebras and coalgebras. Ann. Univ. Ferrara-Sez. VII-Sc. Mat. 2005, 51, 173–181. [Google Scholar] [CrossRef]
- Nichita, F.F.; Zielinski, B. The duality between corings and ring extensions. Axioms 2012, 1, 173–185. [Google Scholar] [CrossRef]
- Dǎscǎlescu, S.; Nichita, F.F. Yang-Baxter operators arising from (co)algebra structures. Comm. Algebra 1999, 27, 5833–5845. [Google Scholar] [CrossRef]
- Lebed, V. Braided Systems: A Unified Treatment of Algebraic Structures with Several Operations. Homol. Homotopy Appl. 2017, 19, 141–174. [Google Scholar] [CrossRef]
- Lebed, V. Homologies of algebraic structures via braidings and quantum shuffles. J. Algebra 2013, 391, 152–192. [Google Scholar] [CrossRef]
- Hlavaty, L.; Snobl, L. Solution of the Yang-Baxter system for quantum doubles. Int. J. Mod. Phys. 1999, A14, 3029–3058. [Google Scholar] [CrossRef]
- Nichita, F.F. Yang-Baxter systems, algebra factorizations and braided categories. Axioms 2013, 2, 437–442. [Google Scholar] [CrossRef]
- Majid, S.; Markl, M. Glueing operations for R-Matrices, quantum groups and link-invariants of Hecke type. Math. Proc. Camb. Philos. Soc. 1996, 119, 139–166. [Google Scholar] [CrossRef]
- Brzezinski, T.; Nichita, F.F. Yang-Baxter systems and entwined structures. Commun. Algebra 2005, 33, 1083–1093. [Google Scholar] [CrossRef]
- Țițeica, G. Wikipedia, the Free Encyclopedia. Available online: https://en.wikipedia.org/wiki/Gheorghe_%C8%9Ai%C8%9Beica (accessed on 19 January 2025).
- Anghel, N. A Generalization of the 5 RON Coin Tzitzeica’s Problem Gazeta Matematica B, Nr 11. 2012. Available online: http://ssmr.ro/gmb/201211 (accessed on 19 January 2025).
- Cook, C.D. Johnson Circle Theorem. 2012. Available online: https://www.johndcook.com/blog/2023/10/15/johnson-circle-theorem/ (accessed on 15 October 2023).
- Nichita, F.F. On the Johnson−Tzitzeica Theorem, Graph Theory, and Yang−Baxter Equations. Symmetry 2021, 13, 2070. [Google Scholar]
- Boskoff, W.G.; Barcanescu, S.; Bobe, A. On the non-generic Tzitzeica-Johnson’s Configuration. An. St. Univ. Ovidius Constanta 2012, 20, 21–26. [Google Scholar]
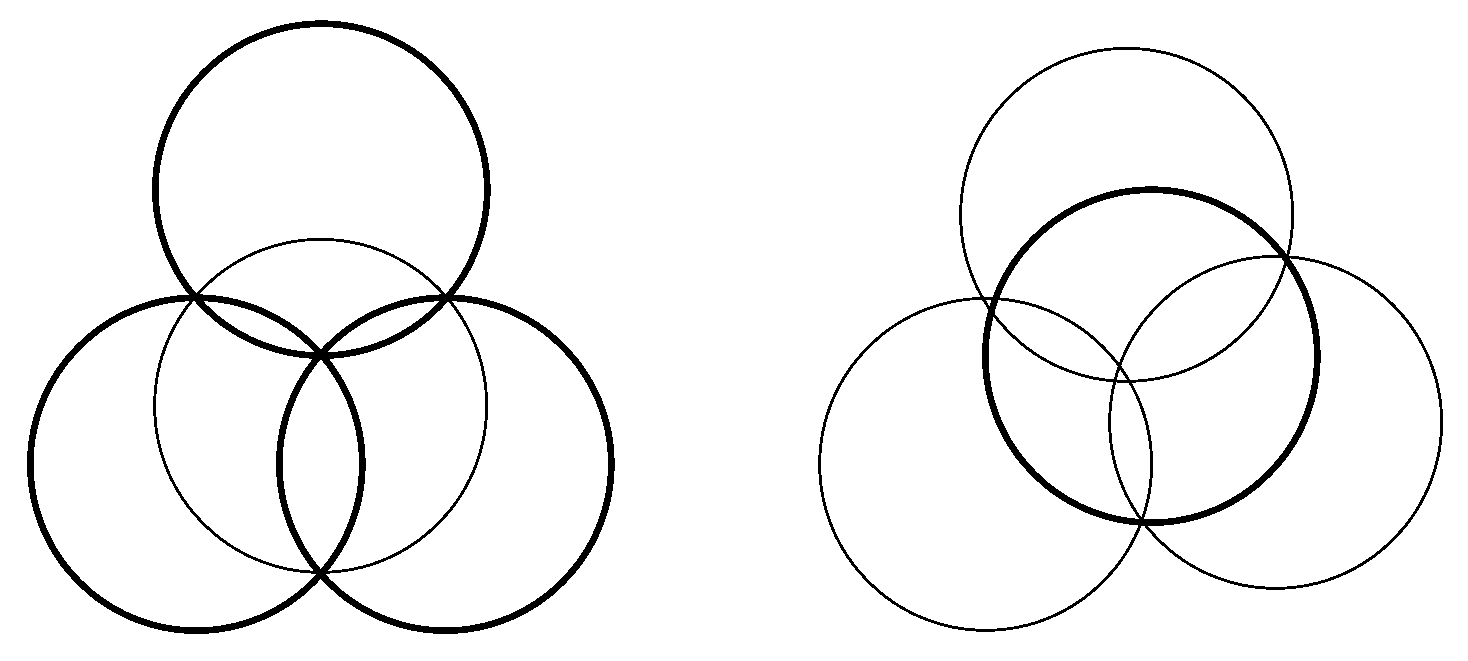
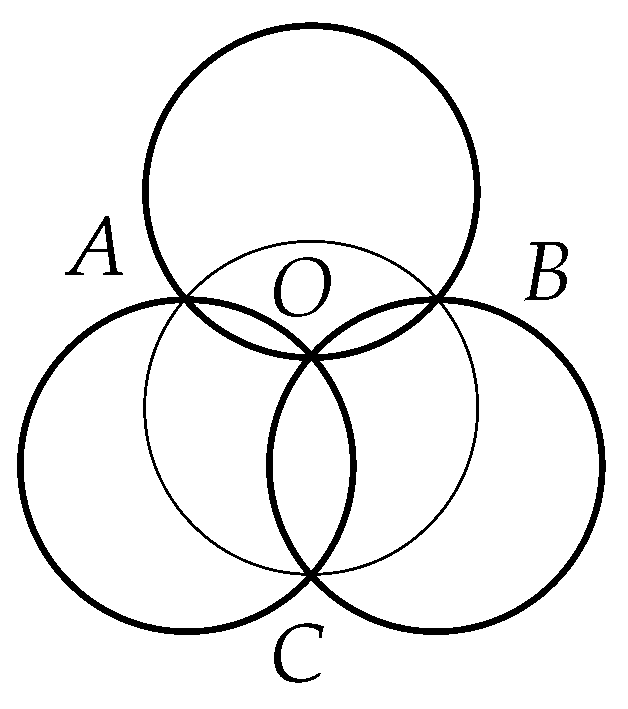
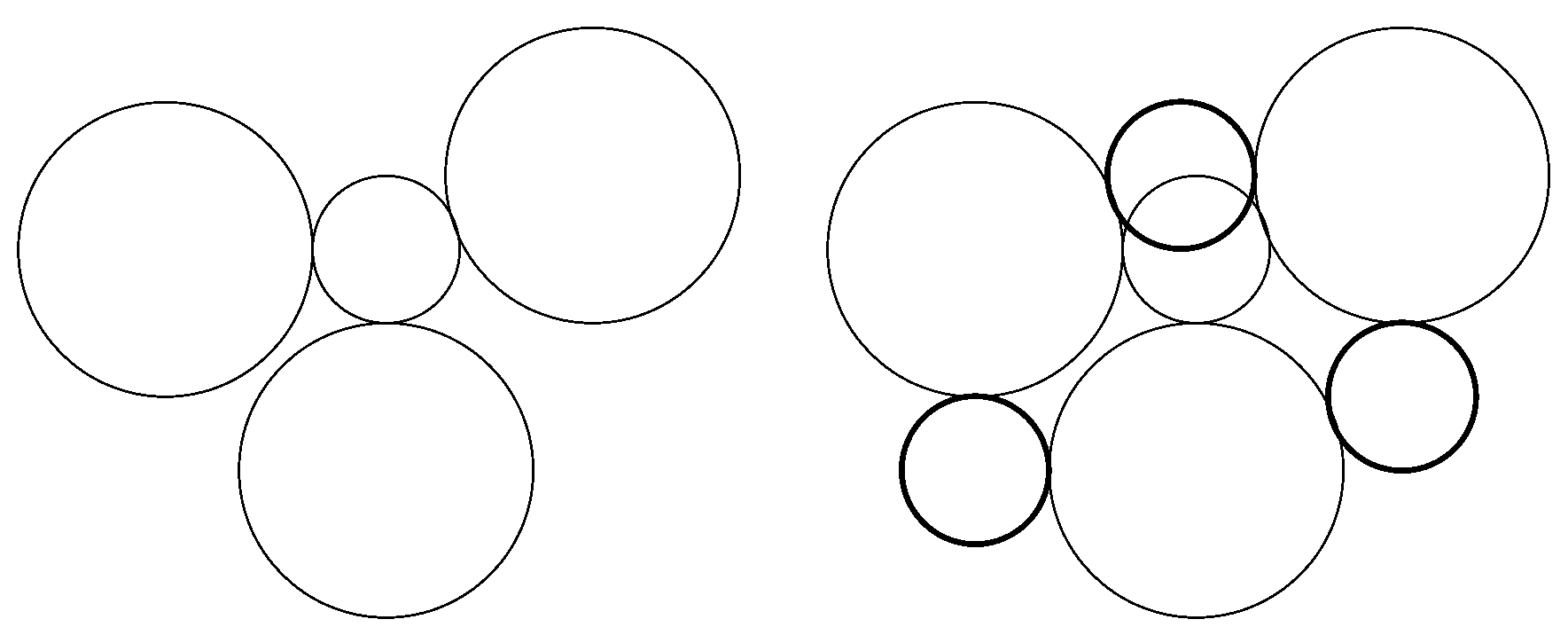
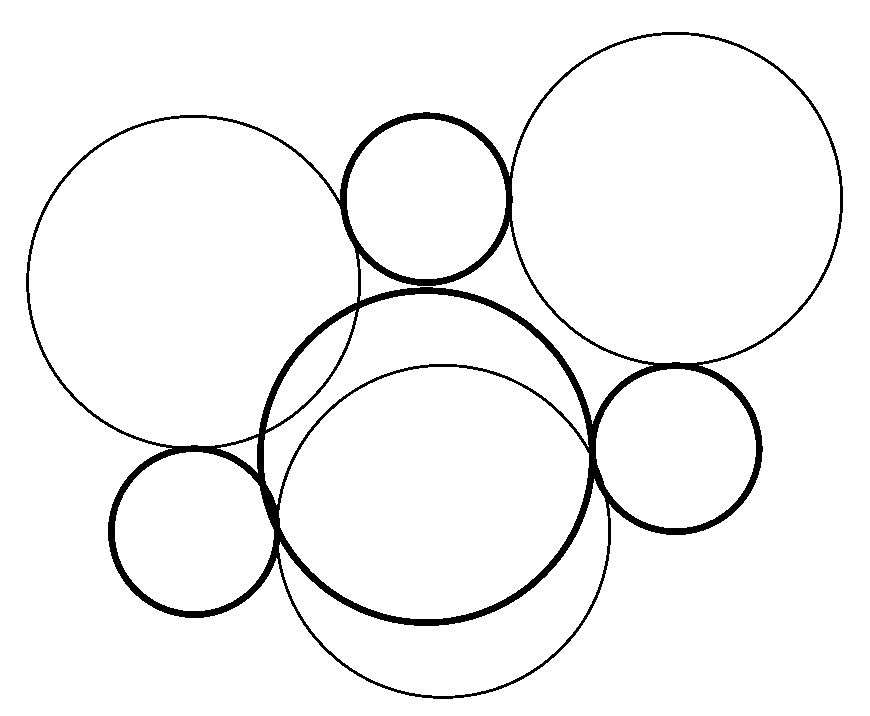

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nichita, F.F. On Some Unification Theorems: Yang–Baxter Systems; Johnson–Tzitzeica Theorem. Axioms 2025, 14, 156. https://doi.org/10.3390/axioms14030156
Nichita FF. On Some Unification Theorems: Yang–Baxter Systems; Johnson–Tzitzeica Theorem. Axioms. 2025; 14(3):156. https://doi.org/10.3390/axioms14030156
Chicago/Turabian StyleNichita, Florin Felix. 2025. "On Some Unification Theorems: Yang–Baxter Systems; Johnson–Tzitzeica Theorem" Axioms 14, no. 3: 156. https://doi.org/10.3390/axioms14030156
APA StyleNichita, F. F. (2025). On Some Unification Theorems: Yang–Baxter Systems; Johnson–Tzitzeica Theorem. Axioms, 14(3), 156. https://doi.org/10.3390/axioms14030156





