On Certain Analytic Functions Associated with Nephroid Function
Abstract
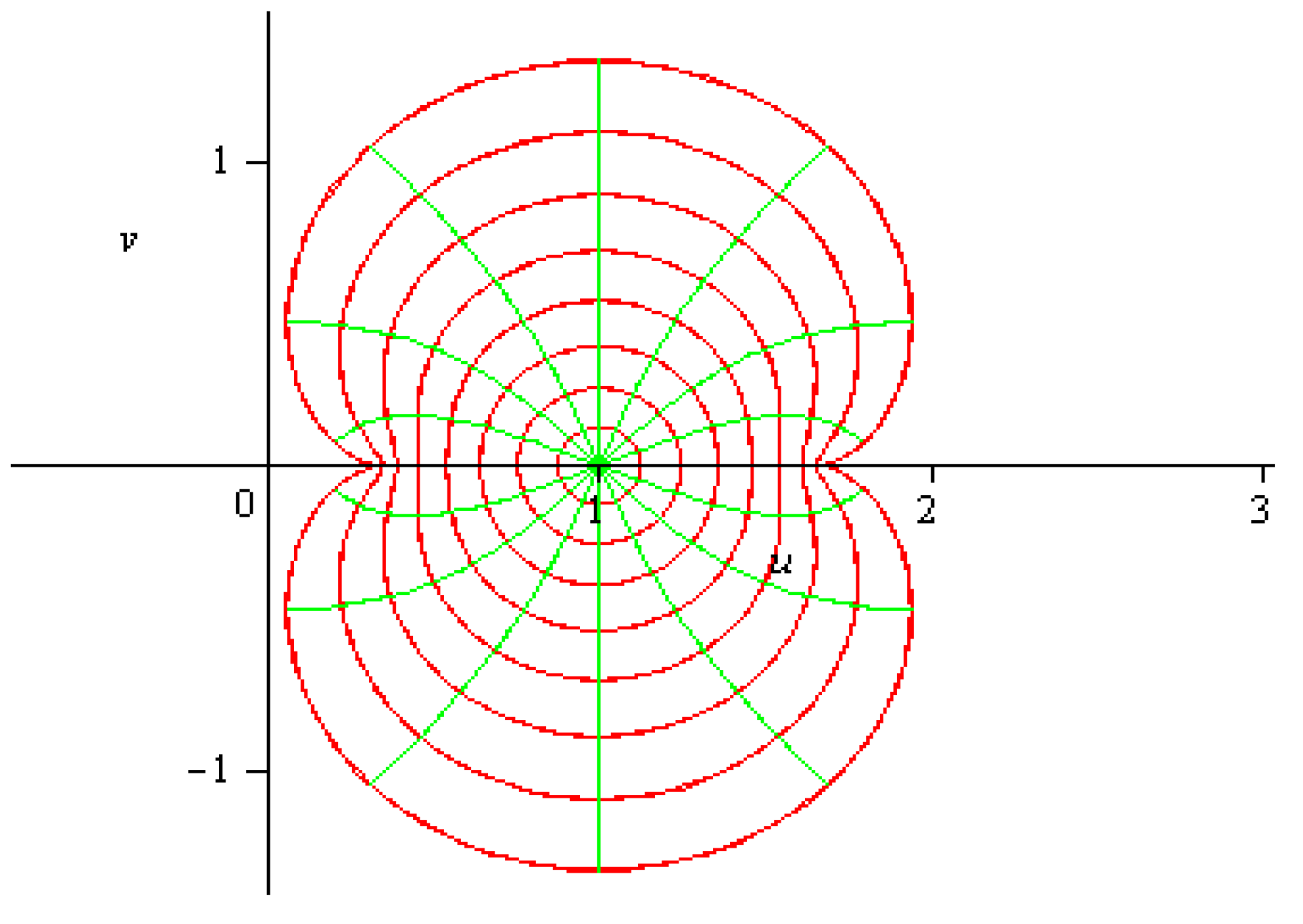
1. Introduction and Definitions
2. A Set of Lemmas
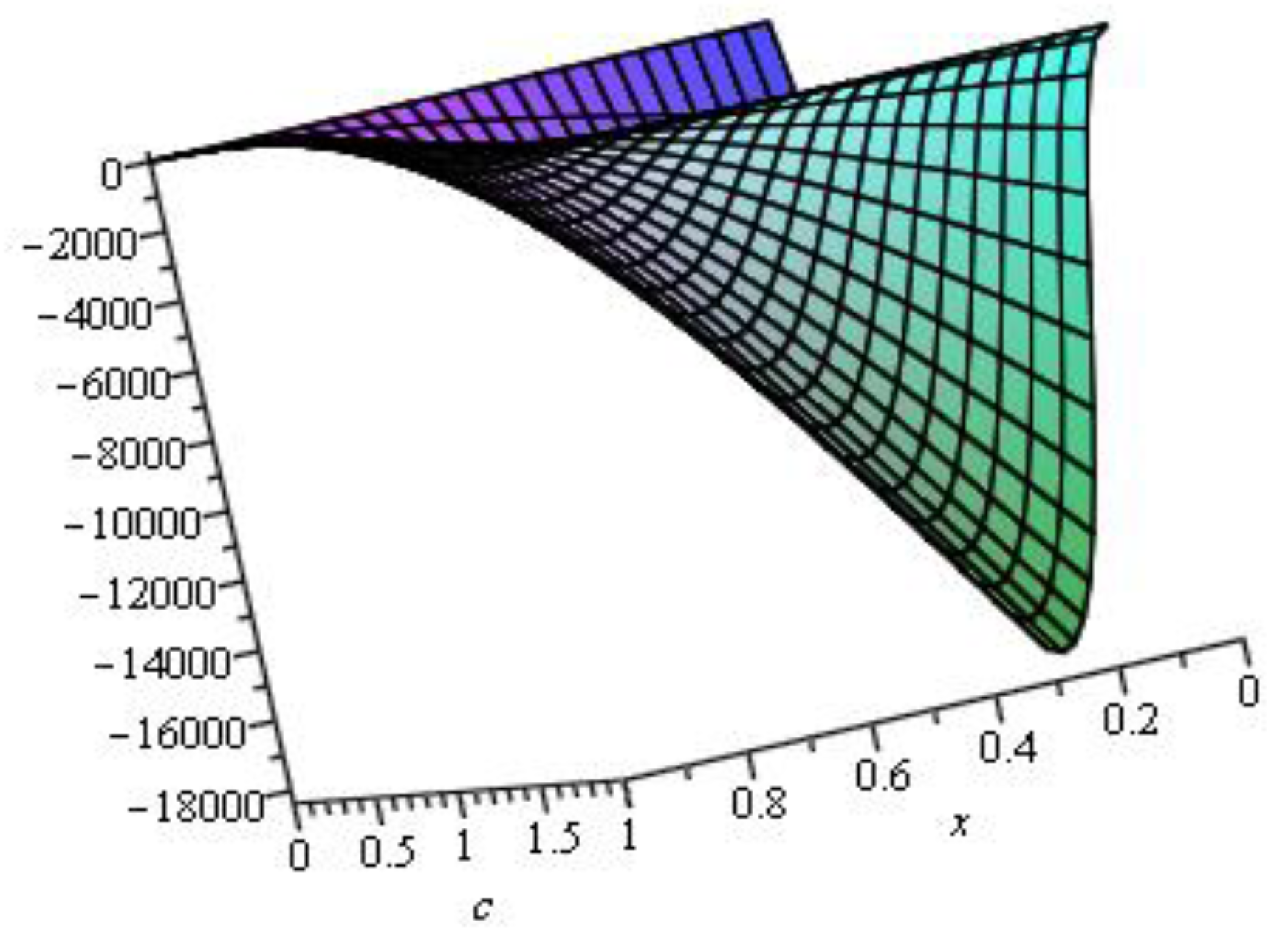
3. Third Hankel Determinant for the Class
4. Logarithmic Coefficient Inequalities for the Class
5. Hankel Determinant with Logarithmic Coefficients for the Class
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zaprawa, P. Third Hankel determinants for subclasses of univalent functions. Mediterr. J. Math. 2017, 14, 19. [Google Scholar] [CrossRef]
- Noonan, J.W.; Thomas, D.K. On the second Hankel determinant of mean p-valent functions. Trans. Am. Math. 1976, 223, 337–346. [Google Scholar] [CrossRef]
- Selvaraj, C.; Kumar, T.R.K. Second Hankel determinant for certain classes of analytic functions. Int. J. Appl. Math. 2015, 28, 37–50. [Google Scholar]
- Hayami, T.; Owa, S. Generalized Hankel determinant for certain classes. Int. J. Math. Anal. 2010, 4, 2573–2585. [Google Scholar]
- Liu, M.S.; Xu, J.F.; Yang, M. Upper bound of second Hankel determinant for certain subclasses of analytic functions. Abstr. Appl Anal. 2014, 2014, 603180. [Google Scholar] [CrossRef]
- Noonan, J.W.; Thomas, D.K. On the Hankel determinants of mean p-valent functions. Proc. Lond. Math. Soc. 1972, 3, 503–524. [Google Scholar] [CrossRef]
- Vamshee Krishna, D.; Ram Reddy, T. Hankel determinant for starlike and convex functions of order alpha. Tbil. Math. J. 2012, 5, 65–76. [Google Scholar]
- Libera, R.J.; Zlotkiewicz, E.J. Coefficient bounds for the inverse of a function with derivative in P. Proc. Am. Math. Soc. 1983, 87, 251–257. [Google Scholar] [CrossRef]
- Banga, S.; Kumar, S.S. The sharp bounds of the second and third Hankel determinants for the class SL*. Math. Slovaca 2020, 70, 849–862. [Google Scholar] [CrossRef]
- Kowalczyk, B.; Lecko, A.; Sim, Y.J. The sharp bound of the Hankel determinant of the third kind for convex functions. Bull. Aust. Math. Soc. 2018, 97, 435–445. [Google Scholar] [CrossRef]
- Kowalczyk, B.; Lecko, A.; Lecko, M.; Sim, Y.J. The sharp bound of the third Hankel determinant for some classes of analytic functions. Bull. Korean Math. Soc. 2018, 55, 1859–1868. [Google Scholar]
- Kwon, O.S.; Lecko, A.; Sim, Y.J. The bound of the Hankel determinant of the third kind for starlike functions. Bull. Malays. Math. Sci. Soc. 2019, 42, 767–780. [Google Scholar] [CrossRef]
- Riaz, A.; Raza, M.; Thomas, D.K. Hankel determinants for starlike and convex functions associated with sigmoid functions. Forum Math. 2021, 34, 137–156. [Google Scholar] [CrossRef]
- Zhang, H.-Y.; Tang, H.; Niu, X.-M. Third-order Hankel determinant for a certain class of analytic functions related with an exponential function. Symmetry 2018, 10, 501. [Google Scholar] [CrossRef]
- Pommerenke, C. On the coefficients and Hankel determinant of univalent functions. J. Lond. Math. Soc. 1966, 41, 111–122. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Ahmad, Q.Z.; Khan, N.; Khan, N.; Khan, B. Hankel and Toeplitz Determinants for a Subclass of q-Starlike Functions Associated with a General Conic Domain. Mathematics 2019, 7, 181. [Google Scholar] [CrossRef]
- Arif, M.; Raza, M.; Tang, H.; Hussain, S.; Khan, H. Hankel determinant of order three for familiar subsets of analytic functions related with sine function. Open Math. 2019, 17, 1615–1630. [Google Scholar] [CrossRef]
- Murugusundaramoorthy, G.; Bulboacă, T. Hankel Determinants for New Subclasses of Analytic Functions Related to a Shell Shaped Region. Mathematics 2020, 8, 1041. [Google Scholar] [CrossRef]
- Khan, B.; Aldawish, I.; Araci, S.; Khan, M.G. Third Hankel Determinant for the Logarithmic Coefficients of Starlike Functions Associated with Sine Function. Fractal Fract. 2022, 6, 261. [Google Scholar] [CrossRef]
- Raza, M.; Riaz, A.; Xin, Q.; Malik, S.N. Hankel Determinants and Coefficient Estimates for Starlike Functions Related to Symmetric Booth Lemniscate. Symmetry 2022, 14, 1366. [Google Scholar] [CrossRef]
- Riaz, A.; Raza, M.; Thomas, D.K. The Third Hankel determinant for starlike functions associated with sigmoid functions. Forum Math. 2022, 34, 137–156. [Google Scholar]
- Riaz, A.; Raza, M. Hankel determinants for starlike and convex functions associated with lune. Bull. Sci. MathéMatiques 2023, 187, 103289. [Google Scholar] [CrossRef]
- Riaz, A.; Raza, M.; Thomas, D.K. Hankel determinants for starlike and convex functions associated with a cardioid domain. Preprint 2022. [Google Scholar] [CrossRef]
- Cho, N.E.; Kowalczyk, B.; Kwon, O.S.; Lecko, A.; Sim, Y.J. On the third logarithmic coefficient in some subclasses of close-to-convex functions. Rev. R. Acad. Cienc. Exactas Fís. Nat. (Esp.) 2020, 114, 52. [Google Scholar] [CrossRef]
- Ali, M.F.; Vasudevarao, A. On logarithmic coefficients of some close-to-convex functions. Proc. Am. Math. Soc. 2018, 146, 1131–1142. [Google Scholar] [CrossRef]
- Pommerenke, C. Univalent Function; Vanderhoeck & Ruprecht: Göttingen, Germany, 1975. [Google Scholar]
- Carathéodory, C. Über den Variabilitätsbereich der Fourier’schen Konstanten von position harmonischen Funktionen. Rend. Circ. Mat. Palermo 1911, 32, 193–217. [Google Scholar] [CrossRef]
- Libera, R.J.; Złotkiewicz, E.J. Early coefficients of the inverse of a regular convex function. Proc. Am. Math. Soc. 1982, 85, 225–230. [Google Scholar] [CrossRef]
- Kwon, O.S.; Lecko, A.; Sim, Y.J. On the fourth coefficient of functions in the Carathéodory class. Comput. Methods Funct. Theory 2018, 18, 307–314. [Google Scholar] [CrossRef]
- Ravichandran, V.; Verma, S. Bound for the fifth coefficient of certain starlike functions. C. R. Math. Acad. Sci. Paris 2015, 353, 505–510. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, W.; Fayyaz, R.; Breaz, D.; Cotîrlă, L.-I. On Certain Analytic Functions Associated with Nephroid Function. Axioms 2025, 14, 136. https://doi.org/10.3390/axioms14020136
Ullah W, Fayyaz R, Breaz D, Cotîrlă L-I. On Certain Analytic Functions Associated with Nephroid Function. Axioms. 2025; 14(2):136. https://doi.org/10.3390/axioms14020136
Chicago/Turabian StyleUllah, Wahid, Rabia Fayyaz, Daniel Breaz, and Luminiţa-Ioana Cotîrlă. 2025. "On Certain Analytic Functions Associated with Nephroid Function" Axioms 14, no. 2: 136. https://doi.org/10.3390/axioms14020136
APA StyleUllah, W., Fayyaz, R., Breaz, D., & Cotîrlă, L.-I. (2025). On Certain Analytic Functions Associated with Nephroid Function. Axioms, 14(2), 136. https://doi.org/10.3390/axioms14020136







