Abstract
Fuzzy matrices play a crucial role in fuzzy logic and fuzzy systems. This paper investigates the problem of supervised learning fuzzy matrices through sample pairs of input–output fuzzy vectors, where the fuzzy matrix inference mechanism is based on the max–min composition method. We propose an optimization approach based on stochastic gradient descent (SGD), which defines an objective function by using the mean squared error and incorporates constraints on the matrix elements (ensuring they take values within the interval [0, 1]). To address the non-smoothness of the max–min composition rule, a modified smoothing function for max–min is employed, ensuring stability during optimization. The experimental results demonstrate that the proposed method achieves high learning accuracy and convergence across multiple randomly generated input–output vector samples.
Keywords:
fuzzy set; fuzzy matrix; supervised learning; stochastic gradient descent; decision making MSC:
15B15
1. Introduction
Fuzzy set theory, introduced by Zadeh in 1965 [1,2], has become a useful mathematical framework for handling uncertainty and imprecision in various scientific and engineering fields. It extends classical set theory by allowing the membership of elements in a set to be represented by degrees between 0 and 1, rather than just binary membership (0 or 1). This makes fuzzy set theory a powerful tool for modeling and reasoning under vagueness that is used in many real-world problems, including artificial intelligence [3,4], decision making [5,6], and data mining [7,8]. Within these fields, fuzzy matrices serve as a fundamental tool in fuzzy logic systems. They are typically employed to represent the relationships between various elements in a fuzzy system, where each element corresponds to a degree of membership or a fuzzy value. Fuzzy matrices can be used for tasks such as fuzzy inference, decision making, and optimization. The traditional approach to constructing fuzzy matrices has been largely dependent on expert knowledge, human intuition, and heuristic rules that reflect the domain-specific characteristics of the problem. For example, in applications like fuzzy model checking [9,10,11,12,13], the fuzzy matrix is often crafted manually, based on insights from experts in the respective field. However, this manual construction process is not without challenges: It is time-consuming, highly subjective, and tends toward inaccuracies, particularly in complex or unfamiliar domains. Moreover, expert knowledge may be scarce or unavailable, further complicating the construction of robust fuzzy systems.
As the field of data science has evolved, there has been a growing interest in using data-driven techniques to overcome the limitations of manual construction. The use of machine learning algorithms to automatically learn fuzzy matrices from data offers an alternative, allowing for the creation of more efficient and accurate fuzzy systems. This paradigm shift, from expert-driven to data-driven approaches, has the potential to significantly enhance the performance and applicability of fuzzy reasoning systems.
1.1. Motivations
The learning of fuzzy matrices has become a hot research topic, with applications emerging in various fields. For example, self-learning fuzzy discrete event systems based on external sensor variables [14,15] and self-learning modeling in possibility theory-based model checking [16] have been explored. These methods rely on supervised learning techniques, where input–output datasets are used to adjust the elements of the fuzzy matrix. One of the challenges in learning fuzzy matrices is dealing with non-smooth operations. In fuzzy reasoning systems, the max–min and max–product composition rules are the most commonly used inference mechanisms, involving taking the maximum of the minimum values between corresponding elements of the input and the matrix. This operation is non-differentiable, posing difficulties for various optimization methods. Previous work on learning fuzzy matrices has been based on the max–product composition method, which only requires smoothing the max operation. A substantial body of research has focused on methods for smoothing the max function [17,18]. However, the learning of fuzzy matrices for the max–min composition method has not been studied.
To fill this gap, we propose a supervised learning algorithm based on stochastic gradient descent (SGD) for learning fuzzy matrices in the max–min composition method. This algorithm optimizes a loss function that reflects the error between the predicted output and the target output based on input–output fuzzy vector pairs, allowing the fuzzy matrix to quickly converge to its true value. The simulation results show that the proposed learning algorithm exhibits good convergence performance toward the true value of the fuzzy matrix. The data-driven, automated process for learning fuzzy matrices will lead to more accurate, consistent, and scalable fuzzy systems, particularly in applications where expert knowledge is unavailable or difficult to obtain.
1.2. Structure of This Paper
The structure of this paper is as follows: Section 2 reviews the related theoretical foundations of the fuzzy matrix. Section 3 describes the proposed fuzzy matrix learning algorithm in detail. Section 4 presents the experimental setup. Section 5 shows the results and analysis. Section 6 concludes the paper and discusses potential future research directions.
2. Fuzzy Reasoning Model
Fuzzy reasoning models are widely used in situations where the relationships between variables are uncertain, imprecise, or vague. In many real-world applications, the exact values of input and output variables may not be known with certainty, and traditional binary logic is inadequate to handle the gradations of truth that exist in such systems. Fuzzy logic provides a more flexible framework, allowing for reasoning with degrees of truth rather than just true or false values. One of the key components of a fuzzy logic system is the fuzzy reasoning model, which helps infer outputs based on fuzzy inputs and predefined relationships. The model operates on fuzzy matrices, which represent the fuzzy relationships between input and output dimensions. By utilizing fuzzy inference rules, it can process uncertain or imprecise information and generate outputs that reflect the inherent vagueness of the system.
A fuzzy reasoning model is a fuzzy matrix P:
where each element represents the fuzzy relationship between the i-th input dimension and the j-th output dimension.
Given an input fuzzy vector s = , the output fuzzy vector is computed using the max–min composition rule (denoted by a symbol “∘”) as follows:
This formula indicates that for each output dimension j, the output is the maximum of the minimum values between the elements of the input vector and the corresponding elements of the fuzzy matrix . This method is a classic fuzzy reasoning method, widely used to make inferences under uncertainty and vagueness.
For example, let be an input fuzzy vector and P be a fuzzy matrix:
The is calculated as follows:
Thus, the resulting output vector .
This example illustrates how the max–min composition rule works: For each output dimension, the output value is determined by the maximum of the minimum values computed between the input vector and the corresponding column in the fuzzy matrix. This method is one of the fundamental techniques used in fuzzy reasoning and is particularly useful in situations where inputs are uncertain or imprecise, and we need to make decisions based on fuzzy relationships.
3. Learning Algorithm for Fuzzy Matrix
In real-world applications, is an unknown fuzzy inference model, and we only have input–output sample pairs to learn the unknown . The learned is then applied in the inference model: Given an input vector and , we obtain the output vector for decision making and control. In the simulation testing of this paper, to generalize our algorithm, we do not use actual datasets to obtain . Instead, we randomly generate a as the true , which is used to generate input–output vector sample pairs. These sample pairs are then used to supervise the learning of . The learned is compared with the randomly generated to verify the performance of the algorithm.
Suppose R sample pairs are available. We want to use them to learn all elements of the fuzzy matrix P based on max–min rules. Figure 1 shows the summary of learning algorithm for fuzzy matrix. To measure the discrepancy between the predicted value and the target value , we adopt the mean squared error (MSE) as the objective function. The objective function is optimized by calculating the average of the squared differences between the predicted and target values. Specifically, the loss function is defined as follows:
where is the predicted value obtained using the fuzzy matrix P and input fuzzy vector , and is the target value of the sample. By minimizing this loss function, we can learn the optimal fuzzy matrix P. Since P is a fuzzy matrix, parameters need to be learned by using objective function .
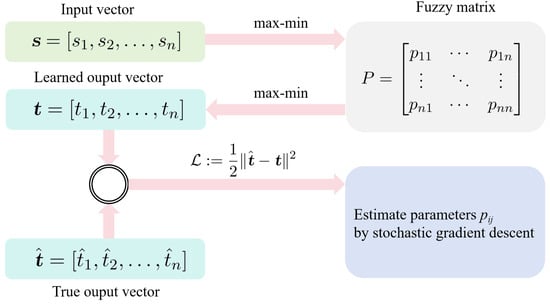
Figure 1.
Configuration of fuzzy matrix learning model.
Gradient Calculation and Optimization
Due to the non-smoothness of the fuzzy max–min composition operation, calculating the gradient of the elements of fuzzy matrix is more complex. To address this, we used a revised exponential penalty function to approximate the fuzzy max–min function in Equation (2) for the purpose of accurate learning, i.e.,
where constant is a hyperparameter determining the accuracy of approximation [19,20].
Figure 2 shows the approximation curves for , , and . In this case, the matrix P and the vector s are both randomly generated. As observed from the figure, the smaller the value of , the more accurate the approximation.
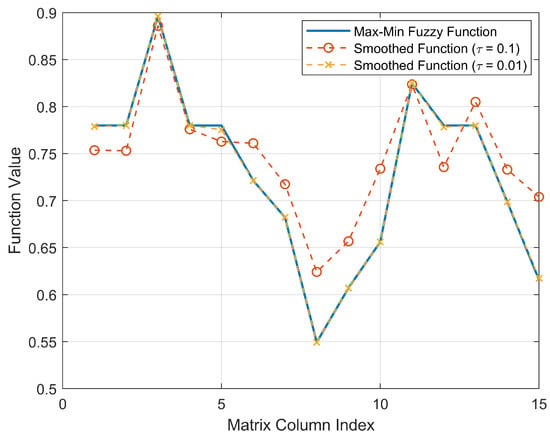
Figure 2.
Max–min fuzzy function vs smoothed approximation ().
This observation highlights the trade-off between computational complexity and approximation accuracy. A smaller often results in better precision but may require more computational effort to achieve convergence, as the optimization process becomes more sensitive to small changes in the parameters.
On the basis of the principle of gradient decent learning,
where is the learning rate, controlling the step size of each update. The superscript “new” is used to indicate the new value of the parameter after it has been updated in one iteration of learning.
To ensure that all elements of the matrix remain within the valid range for a fuzzy matrix, the fuzzy matrix P is projected onto the interval after each update; then, we have a new learning equation:
In this way, the fuzzy matrix P is progressively optimized to predict the output more accurately.
To compute the partial derivative of the function
with respect to . Rewriting the function, we define
then, the function becomes
Using the chain rule,
First, compute the derivative of :
For , only the term where depends on is used. Thus,
When , the contribution to is
where
Substitute this into the chain rule:
Simplify the following expression:
The complete learning algorithm workflow is as follows: Initialize the fuzzy matrix P with random values or 0.5. For each sample pair , compute the predicted value using the max–min composition rule. Compute the loss function and its gradient. Update P, and project it into the range . Repeat steps until the convergence condition is met.
4. Simulation Settings
The goal of the experimental section is to evaluate the performance of the proposed fuzzy matrix learning algorithm. In this section, we describe the experimental setup, including data generation, evaluation metrics, baseline methods, and results. We programmed a program in MATLAB (version 2021b) to achieve the learning algorithm and to generate the sample pairs required to evaluate the learning performance. We have made the MATLAB codes open source for this paper.
4.1. Data Generation
For the experiments, we generate R random sample pairs , where each input sample and its corresponding output are fuzzy vectors of size n, and their elements are drawn from the interval . The inputs are randomly generated as n-dimensional vectors, with each component sampled independently from an uniform distribution in . The output vectors are generated by applying a true fuzzy matrix to each input vector through the max–min composition rule described earlier: , i.e.,
where is a randomly generated fuzzy matrix, and the resulting output vectors represent the true output corresponding to each input vector . The number of samples R is varied to assess the impact of dataset size on the learning process.
4.2. Evaluation Metrics
To assess the performance of the proposed learning algorithm, we use two primary evaluation metrics:
- Mean Squared Error (MSE): The MSE is calculated between the predicted outputs and the true outputs over all samples. This metric quantifies the average squared difference between the predicted and target values and serves as a measure of the accuracy of the learned fuzzy matrix.
- Matrix Reconstruction Error (MRE): This metric evaluates how well the learned fuzzy matrix approximates the true fuzzy matrix . It is calculated as the Frobenius norm of the difference between the true matrix and the learned matrix:where represents the Frobenius norm, which sums the squared differences of all corresponding elements of the two matrices. Concretely, , where is the element in row i and column j of the matrix A. The smaller the value, the closer the learned matrix P is to the true matrix .
These metrics allow for a comprehensive assessment of both the accuracy of the output prediction and the quality of the learned fuzzy matrix.
5. Experimental Results and Analysis
The learning algorithms derived from the mentioned theories seem feasible but require computer simulations to evaluate their performance. Similar to other iterative optimization problems, the learning efficiency of the fuzzy matrix depends on various factors, including initial conditions, learning rates, sample sizes, and the number of epochs. The simulations conducted in this study are inherently abstract and not associated with any specific fuzzy system, yet they remain suitable for evaluating learning performance. Since this represents the inaugural proposal of a learning algorithm within the context of possibilistic model checking, conducting a comparative analysis is neither feasible nor supported. The results show the convergence behavior of the proposed algorithm. This indicates that the algorithm converges to a stable solution after a relatively small number of iterations, demonstrating the efficiency of the SGD approach.
5.1. Learning Performance Evaluation
We first choose to test the learning of a fuzzy matrix. Therefore, there are a total of nine parameters to be learned. The hyperparameter settings are as follows: number of samples , learning rate , and gradient approximation . A trial contains 50 training epochs.
Figure 3 illustrates the learning process of each element in the fuzzy matrix. The red dashed lines represent the true values, while the blue lines indicate the learning curves. It can be observed that regardless of the true values of the matrix, all elements converge to their true values within 20 epochs. Note that this performance is achieved using only 50 samples to learn nine parameters. In fact, the number of samples can be further reduced, but we did not explore this aspect in greater detail.
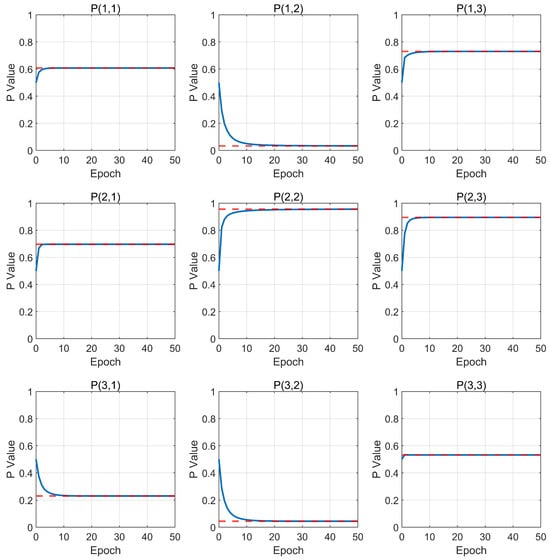
Figure 3.
Learning progress of fuzzy matrix.
At the end of learning, the learned fuzzy matrix is
and
Figure 4 shows the curve of the MSE as learning epochs. It can be observed that as the number of epochs increases, the MSE decreases rapidly. At the end of this particular trial, the MSE reached . The trial was completed in 0.67 s.
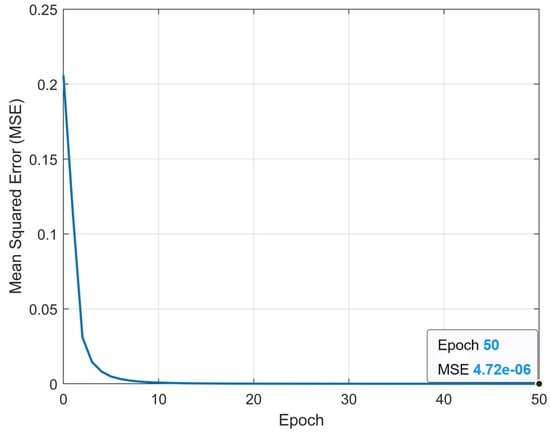
Figure 4.
Progressive decrease in the mean squared error.
Figure 5 shows the curve of the matrix reconstruction error as learning epochs. It can be observed that as the number of epochs increases, the matrix reconstruction error decreases rapidly. At the end of this particular trial, the MSE reached .
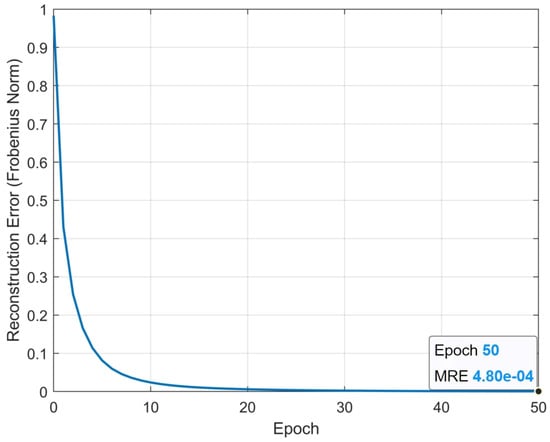
Figure 5.
Progressive decrease in the matrix reconstruction error.
We further explored the learning performance of the fuzzy matrix with the following parameter settings: learning , learning rate , and sample size . At the end of the learning process, the mean squared error (MSE) reached , and the MRE was 0.507827. The learning curves of the matrix are shown in Figure 6.
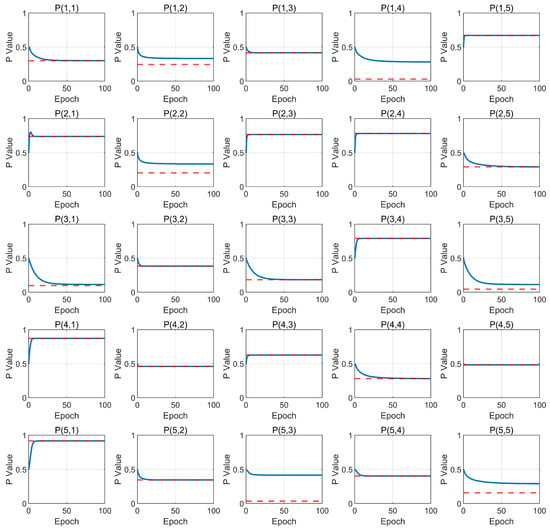
Figure 6.
Learning progress of fuzzy matrix.
From Figure 6, it can be observed that with the sample size fixed and the number of parameters to learn increasing to 25, the majority of parameters (20/25) quickly approach their true values. However, a few parameters fail to reach their true values, even when the MSE is sufficiently small and converged. This phenomenon is noteworthy and can be attributed to the fact that, under the max–min composition operation, the fuzzy matrix is not a one-to-one function but a one-to-many function. Consequently, a single set of samples may correspond to multiple optimal fuzzy matrices.
To address this issue, increasing the sample size can help reduce the parameter ambiguity. Subsequently, we further investigated the impact of different sample sizes on the reconstruction error of fuzzy matrices across varying dimensions. We plotted the 3D surfaces showing the variation of the mean squared error and reconstruction error with respect to the matrix dimension n ( and 20) and sample size R ( and 500), as shown in Figure 7 and Figure 8. Note that each data point represents a test set. The plane between data points is color-filled to better observe the trends between matrix dimensions, sample size, and MSE/MRE. The color blocks represent the predicted relationship plane, while the intersection lines between color blocks indicate the predicted relationship curves.
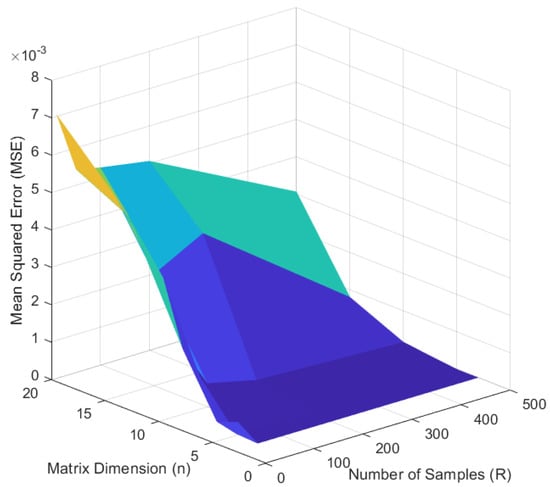
Figure 7.
The MSE varies with matrix dimension n and sample size R.
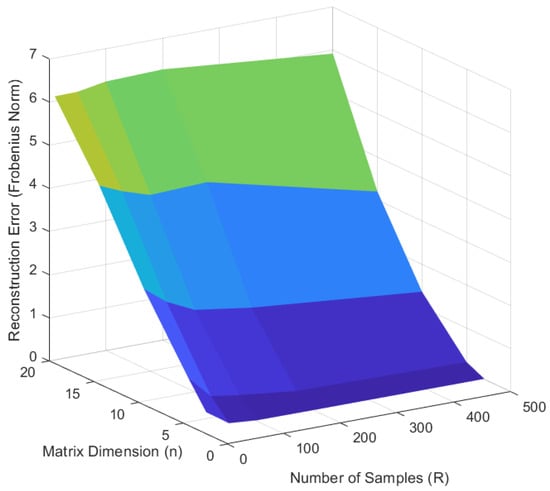
Figure 8.
The reconstruction error varies with matrix dimension n and sample size R.
From Figure 7, it can be observed that for fuzzy matrices of any dimension, the MSE decreases significantly as the sample size R increases. However, for the same sample size, higher-dimensional matrices (larger n) generally result in higher MSE values. Figure 8 illustrates the variation of the reconstruction error (Frobenius norm) with the matrix dimension n and sample size R. For lower-dimensional matrices, increasing the sample size R can substantially reduce the reconstruction error. However, for higher-dimensional matrices, significantly more samples are required to achieve a low reconstruction error; otherwise, the algorithm may experience a saturation effect.
We did not further investigate the specific number of samples required to noticeably reduce the reconstruction error when learning high-dimensional fuzzy matrices. as this goes beyond the scope of this study and is a time-consuming process.
In fact, Figure 7 and Figure 8 reflect the strong stability of the proposed learning algorithm. Figure 7 and Figure 8 illustrate the relationship between the number of samples, matrix dimensions, and MSE/MRE, respectively. It can be observed that for these tests, the proposed algorithm consistently exhibits a low MSE and MRE.
5.2. Robustness Test
To test the robustness of the proposed algorithm, we introduce varying levels of noise into the input data. Noise is added to the input vectors by randomly perturbing their elements with values drawn from a uniform distribution in the interval , where represents the noise level and and . The algorithm is then trained on this noisy data, and its performance is evaluated using the same metrics (MSE and MRE).
As shown in Figure 9 and Figure 10, even with a noise level of 0.1 (allowing an error of 0.1), the reconstruction error is only 0.035 at the end of the training. The MSE increases as the noise level increases. It is noteworthy that, at a noise level of 0.1, the final MSE is only 0.02. Therefore, the proposed algorithm exhibits strong stability and generalization capabilities under different noise levels. Even as the noise level increases, the algorithm maintains a low MSE and matrix reconstruction error, demonstrating its robustness to noisy data.
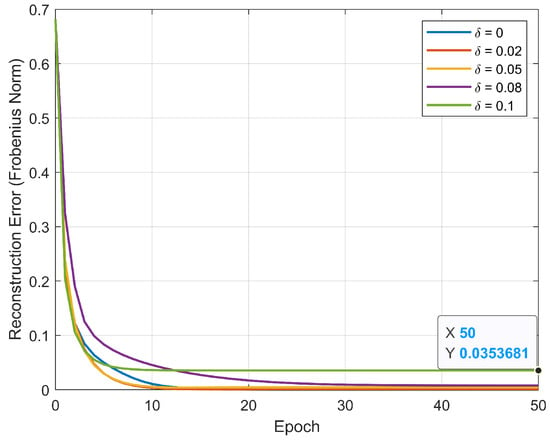
Figure 9.
MRE over epochs for different noise levels.
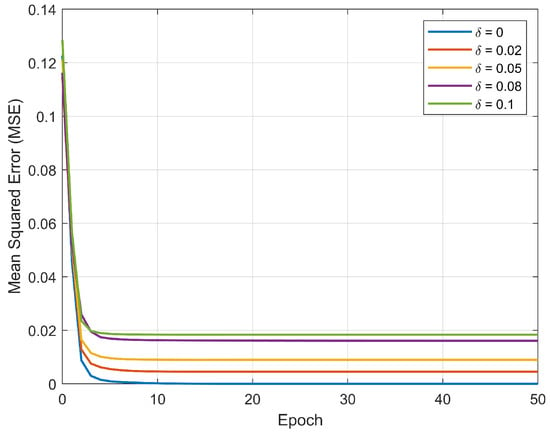
Figure 10.
MSE over epochs for different noise levels.
We did not pursue potentially better results, as the current results sufficiently validate the theoretical framework and demonstrate the learning performance of the proposed algorithms. The algorithm exhibits good convergence properties, robustness to noise, and strong generalization capabilities. It is worth noting that the learned model parameters are locally optimal rather than globally optimal. In fact, achieving optimal values (true values) for all parameters is highly challenging. Due to the nature of the max–min composition rule in fuzzy matrices, which is essentially a one-to-many function, the output is not unique. Therefore, under the max–min composition rule, multiple optimal fuzzy matrices can exist for the same set of samples. As a result, even if some parameters do not exactly reach their true values, we still consider the solution to be optimal.
The MATLAB program ran on a PC that was equipped with an Intel Xeon(R) E5-2680 v4 2.40 GHz CPU, 128 GB RAM, and the 64-bit Windows 10 operating system.
6. Conclusions
This paper proposes a stochastic gradient descent-based fuzzy matrix learning method using input–output vectors, filling the gap in fuzzy matrix learning under the max–min fuzzy composition rule. First, we introduce a smoothing function to approximate the max–min function. Then, based on the stochastic gradient descent optimization method, we derive the learning algorithm. Finally, we conduct a performance analysis of the proposed algorithm. The simulation results demonstrate that the learning algorithm achieves high accuracy and rapidly converges to its true values. Moreover, the algorithm exhibits strong robustness, as it can still quickly converge to values near the true ones under noise interference.
Future work will focus on three aspects: first, validation and application on real-world datasets, for example, applications in the control and decision making of fuzzy discrete event systems based on external variables [14,15], as well as self-learning modeling in possibilistic model checking [16]. Second, an important research direction is how input–output vectors can be obtained through external variables, for instance, connecting input-output vectors to external sensor variables using Gaussian membership functions, deriving the corresponding learning algorithm, and analyzing its learning performance. Additionally, extending this method to other fuzzy reasoning mechanisms is also an important research direction.
Author Contributions
Conceptualization, M.Y. and W.L.; methodology, M.Y., N.W., X.Y. and X.W.; formal analysis, M.Y. and W.L.; writing—original draft preparation, M.Y.; writing—review and editing, M.Y. and W.L.; visualization, M.Y., X.Y. and W.L.; project administration, M.Y.; funding acquisition, M.Y., N.W., X.Y. and X.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Shangluo University Key Disciplines Project under the discipline of Mathematics. The authors also acknowledge the financial support from the Shaanxi Provincial Natural Science Basic Research Program (No. 2024JC-YBMS-062). Additional funding was provided by the Shangluo University Foundation (Grant No. 20SKY021) and Shangluo University Foundation (Nos. 22SKY111, 23KYPY08).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The matlab codes of the study are openly available in https://www.alipan.com/s/qYveBYfAsQ6 (accessed on 25 December 2024).
Acknowledgments
The authors wish to express their gratitude to the anonymous referees for their valuable contributions in refining the presented ideas in this paper and enhancing the clarity of the presentation.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SGD | Stochastic gradient descent |
| MSE | Mean squared error |
| MRE | Matrix reconstruction error |
References
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1978, 1, 3–28. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Fuzzy set and possibility theory-based methods in artificial intelligence. Artif. Intell. 2003, 148, 1–9. [Google Scholar] [CrossRef]
- Pedrycz, W. An introduction to computing with fuzzy sets-analysis design and applications. IEEE ASSP Mag. 2021, 190, 79–93. [Google Scholar]
- Zimmermann, H.J. Fuzzy Sets, Decision Making, and Expert Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1987; Volume 10. [Google Scholar]
- Ferreira, M.A.D.d.O.; Ribeiro, L.C.; Schuffner, H.S.; Libório, M.P.; Ekel, P.I. Fuzzy-Set-Based Multi-Attribute Decision-Making, Its Computing Implementation, and Applications. Axioms 2024, 13, 142. [Google Scholar] [CrossRef]
- Hüllermeier, E. Fuzzy sets in machine learning and data mining. Appl. Soft Comput. 2011, 11, 1493–1505. [Google Scholar] [CrossRef]
- Miloudi, S.; Wang, Y.; Ding, W. An improved similarity-based clustering algorithm for multi-database mining. Entropy 2021, 23, 553. [Google Scholar] [CrossRef]
- Li, Y.; Liu, W.; Wang, J.; Yu, X.; Li, C. Model checking of possibilistic linear-time properties based on generalized possibilistic decision processes. IEEE Trans. Fuzzy Syst. 2023, 31, 3495–3506. [Google Scholar] [CrossRef]
- Liu, W.; Li, Y. Optimal strategy model checking in possibilistic decision processes. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 6620–6632. [Google Scholar] [CrossRef]
- Liu, W.; Wang, J.; He, Q.; Li, Y. Model checking computation tree logic over multi-valued decision processes and its reduction techniques. Chin. J. Electron. 2024, 33, 1399–1411. [Google Scholar] [CrossRef]
- Ma, Z.; Li, Z.; Li, W.; Gao, Y.; Li, X. Model checking fuzzy computation tree logic based on fuzzy decision processes with cost. Entropy 2022, 24, 1183. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Li, Y.; Geng, S.; Li, H. Fuzzy Computation Tree Temporal Logic with Quality Constraints and Its Model Checking. Axioms 2024, 13, 832. [Google Scholar] [CrossRef]
- Ying, H.; Lin, F. Self-learning fuzzy automaton with input and output fuzzy sets for system modelling. IEEE Trans. Emerg. Top. Comput. Intell. 2022, 7, 500–512. [Google Scholar] [CrossRef]
- Ying, H.; Lin, F. Discrete-Time Finite Fuzzy Markov Chains Realized through Supervised Learning Stochastic Fuzzy Discrete Event Systems. IEEE Trans. Fuzzy Syst. 2024, 32, 6088–6100. [Google Scholar] [CrossRef]
- Liu, W.; He, Q.; Li, Z.; Li, Y. Self-learning modeling in possibilistic model checking. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 264–278. [Google Scholar] [CrossRef]
- Bertsekas, D. Minimax methods based on approximation. In Proceedings 1976 John Hopkins Conference on Information Sciences and Systems; Johns Hopkins University: Baltimore, MD, USA, 1976. [Google Scholar]
- Xu, S. Smoothing method for minimax problems. Comput. Optim. Appl. 2001, 20, 267–279. [Google Scholar] [CrossRef]
- Tsoukalas, A.; Parpas, P.; Rustem, B. A smoothing algorithm for finite min–max–min problems. Optim. Lett. 2009, 3, 49–62. [Google Scholar] [CrossRef]
- Li, L.; Qiao, Z.; Liu, Y.; Chen, Y. A convergent smoothing algorithm for training max–min fuzzy neural networks. Neurocomputing 2017, 260, 404–410. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).