Spherical Fuzzy Credibility Dombi Aggregation Operators and Their Application in Artificial Intelligence
Abstract
1. Introduction
- In this paper, a new notion, spherical fuzzy credibility numbers (SFCNs), based on mixed information including spherical fuzzy values and its credibility value, is presented. This new idea promotes the rationality and validity of data.
- Using Dombi operation laws, we define new operation laws for spherical fuzzy credibility numbers.
- Based on the defined operation laws, some averaging and geometric aggregation operators are defined.
- With the help of the SFCDWA and SFCDWG operators that are built into SFCNs, together with their operational laws and score functions, one may use SFCN data to solve MADM issues with the useful mathematical tools.
- Using specified operators, a numerical example is solved.
- The research paper examines the benefits of the suggested data, emphasizing the discovered operators’ representations and the mathematical tool.
- A comparative examination of the proposed data is undertaken by contrasting them with certain pre-existing methods.
2. Preliminaries
- 1.
- if
- 2.
- if
- 3.
- If , then(i). If then(ii). If then
- 1.
- 2.
- iff
- 3.
- iff &
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
3. Spherical Fuzzy Credibility Dombi Aggregation Operators
3.1. Spherical Fuzzy Credibility Dombi Weighted Arithmetic Operators
3.2. Spherical Fuzzy Credibility Dombi Weighted Geometric Operators
3.3. Spherical Fuzzy Credibility Dombi Ordered Weighted Arithmetic Operators
3.4. Spherical Fuzzy Credibility Dombi Ordered Weighted Geometric Operators
4. Application to MADM with SFC Information
4.1. SFC Entropy Method
4.2. Algorithm for Solving MADAM Problem
4.3. Artificial Intelligence Symmetry Analysis Using the Proposed MADM
- : Extensibility: Aims to make AI models interpretable for better understanding;
- : Data Symmetry: Involves techniques for augmenting data;
- : Knowledge Representation: Focuses on symbolic AI methods;
- : Natural Language Processing (NLP): Concerned with understanding semantic symmetry in language;
- : Fairness and Bias: Addresses ensuring fairness in algorithms to avoid biased outcomes;
- : Algorithmic Symmetry: Deals with optimization algorithms and machine learning models.
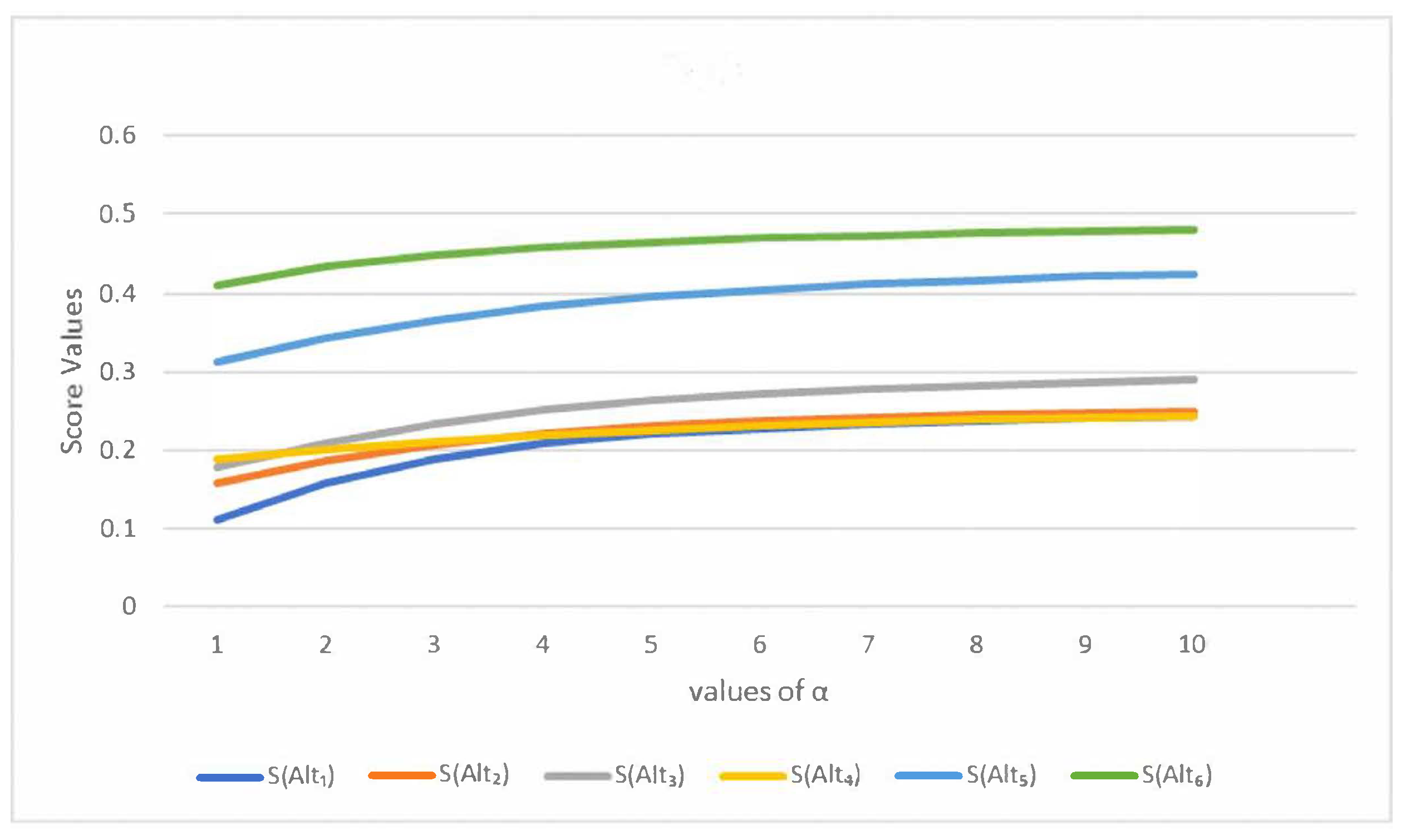
5. Analysis of the Effect of the Parameters on Decision Making
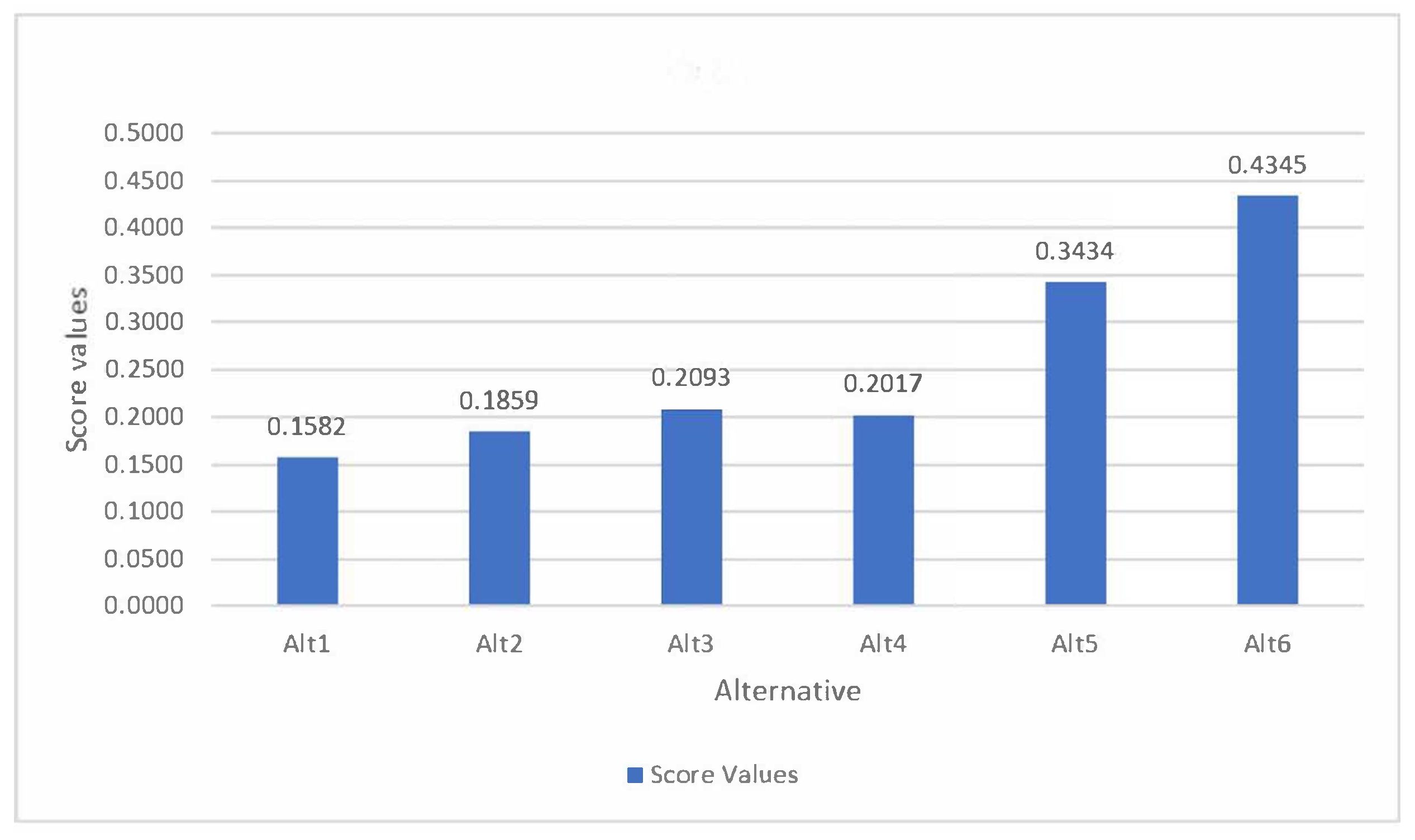
5.1. Decision Making with the SFCDWA Operator
5.2. Decision Making with the SFCFWG Operator
6. Comparison
- It is clear from Table 6 that the established spherical fuzzy credibility MADM technique based on the SFCDWA and SFCDWA operators and the standard spherical fuzzy MADM [33] approach based on the SFNWAA and SFNWAG operators have different ranking outcomes. According to the decision-making example’s final outcomes, , which corresponds to the proven spherical fuzzy credibility MADM strategy, and , which corresponds to the traditional spherical fuzzy MADM approach without the degrees of credibility, are the best options.
- It is evident from Table 6 that there is a difference in the ranking results between the established MADM method based on the SFCDWA and SFCDWA operators and the conventional spherical fuzzy MADM [47] approach based on the SFDWAA and SFDWAG operators. As per the decision-making example’s final results, , which aligns with the established spherical fuzzy credibility MADM approach, is the best alternative. On the other hand, , which is based on the SFDWAG operator, and , which is based on the SFDWAA operator, are the best alternatives, and they correspond to the traditional fuzzy MADM approach that lacks credibility.
- Table 6 make it clear that the established MADM method based on the SFCDWA and SFCDWA operators and the conventional spherical fuzzy MADM [48] approach based on the SFDPWAA and SFDPWAG operators have different ranking outcomes. According to the decision-making example’s final results, , which corresponds to the well-established SFC MADM approach, is the best option. Alternatively, , based on the SFDPWAA operator, and , based on the SFDPWAG operator, correspond to the traditional fuzzy MADM approach without the degrees of credibility.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chertok, M.; Keller, Y. Spectral symmetry analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1227–1238. [Google Scholar] [CrossRef]
- Parui, S.K.; Majumder, D.D. Symmetry analysis by computer. Pattern Recognit. 1983, 16, 63–67. [Google Scholar] [CrossRef]
- Belokoneva, E.L. Borate crystal chemistry in terms of the extended OD theory: Topology and symmetry analysis. Crystallogr. Rev. 2005, 11, 151–198. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy logic-a personal perspective. Fuzzy Sets Syst. 2015, 281, 4–20. [Google Scholar] [CrossRef]
- Zhang, S.; Hou, Y.; Zhang, S.; Zhang, M. Fuzzy control model and simulation for nonlinear supply chain system with lead times. Complexity 2017, 2017, 2017634. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, C.; Zhang, S.; Zhang, M. Discrete switched model and fuzzy robust control of dynamic supply chain network. Complexity 2018, 2018, 3495096. [Google Scholar] [CrossRef]
- Sarwar, M.; Li, T. Fuzzy fixed point results and applications to ordinary fuzzy differential equations in complex valued metric spaces. Hacet. J. Math. Stat. 2019, 48, 1712–1728. [Google Scholar] [CrossRef]
- Gao, M.; Zhang, L.; Qi, W.; Cao, J.; Cheng, J.; Kao, Y.; Wei, Y.; Yan, X. SMC for semi-Markov jump TS fuzzy systems with time delay. Appl. Math. Comput. 2020, 374, 125001. [Google Scholar]
- Xia, Y.; Wang, J.; Meng, B.; Chen, X. Further results on fuzzy sampled-data stabilization of chaotic nonlinear systems. Appl. Math. Comput. 2020, 379, 125225. [Google Scholar] [CrossRef]
- Lu, K.P.; Chang, S.T.; Yang, M.S. Change-point detection for shifts in control charts using fuzzy shift change-point algorithms. Comput. Ind. Eng. 2016, 93, 12–27. [Google Scholar] [CrossRef]
- Ruspini, E.H.; Bezdek, J.C.; Keller, J.M. Fuzzy clustering: A historical perspective. IEEE Comput. Intell. 2019, 14, 45–55. [Google Scholar] [CrossRef]
- Yang, M.S.; Sinaga, K.P. Collaborative feature-weighted multi-view fuzzy c-means clustering. Pattern Recognit. 2021, 119, 108064. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, P.; Zhang, M. Fuzzy emergency model and robust emergency strategy of supply chain system under random supply disruptions. Complexity 2019, 2019, 3092514. [Google Scholar] [CrossRef]
- Atanassov, K.T.; Atanassov, K.T. Intuitionistic Fuzzy Sets; Physica-Verlag HD: Heidelberg, Germany, 1999; pp. 1–137. [Google Scholar]
- Hwang, C.M.; Yang, M.S. New Construction for Similarity Measures between Intuitionistic Fuzzy Sets Based on Lower, Upper and Middle Fuzzy Sets. Int. J. Fuzzy Syst. 2013, 15, 359. [Google Scholar]
- Yang, M.S.; Hussain, Z.; Ali, M. Belief and plausibility measures on intuitionistic fuzzy sets with construction of belief-plausibility TOPSIS. Complexity 2020, 2020, 7849686. [Google Scholar] [CrossRef]
- Alkan, N.; Kahraman, C. Continuous intuitionistic fuzzy sets (CINFUS) and their AHP&TOPSIS extension: Research proposals evaluation for grant funding. Appl. Soft Comput. 2023, 145, 110579. [Google Scholar]
- Atanassov, K.T. Circular intuitionistic fuzzy sets. J. Intell. Fuzzy Syst. 2020, 39, 5981–5986. [Google Scholar] [CrossRef]
- Xu, C.; Wen, Y. New measure of circular intuitionistic fuzzy sets and its application in decision making. AIMS Math. 2023, 8, 24053–24074. [Google Scholar] [CrossRef]
- Alreshidi, N.A.; Shah, Z.; Khan, M.J. Similarity and entropy measures for circular intuitionistic fuzzy sets. Eng. Artif. Intell. 2024, 131, 107786. [Google Scholar] [CrossRef]
- Yager, R.R.; Abbasov, A.M. Pythagorean membership grades, complex numbers, and decision making. Int. J. Intell. Syst. 2013, 28, 436–452. [Google Scholar] [CrossRef]
- Meng, Z.; Lin, R.; Wu, B. Multi-criteria group decision making based on graph neural networks in Pythagorean fuzzy environment. Expert Syst. Appl. 2024, 242, 122803. [Google Scholar] [CrossRef]
- Akram, M.; Nawaz, H.S.; Deveci, M. Attribute reduction and information granulation in Pythagorean fuzzy formal contexts. Expert Syst. Appl. 2023, 222, 119794. [Google Scholar] [CrossRef]
- Salari, S.; Sadeghi-Yarandi, M.; Golbabaei, F. An integrated approach to occupational health risk assessment of manufacturing nanomaterials using Pythagorean Fuzzy AHP and Fuzzy Inference System. Sci. Rep. 2024, 14, 180. [Google Scholar] [CrossRef] [PubMed]
- Yager, R.R. Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 2016, 25, 1222–1230. [Google Scholar] [CrossRef]
- Liu, P.; Wang, P. Some q-rung orthopair fuzzy aggregation operators and their applications to multiple-attribute decision making. Int. J. Intell. Syst. 2018, 33, 259–280. [Google Scholar] [CrossRef]
- Yang, M.S.; Ali, Z.; Mahmood, T. Three-way decisions based on q-rung orthopair fuzzy 2-tuple linguistic sets with generalized Maclaurin symmetric mean operators. Mathematics 2021, 9, 1387. [Google Scholar] [CrossRef]
- Alcantud, J.C.R. Complemental fuzzy sets: A semantic justification of $ q $-rung orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 2023, 31, 4262–4270. [Google Scholar] [CrossRef]
- Cuong, B.C.; Kreinovich, V. Picture fuzzy sets-a new concept for computational intelligence problems. In Proceedings of the 2013 IEEE Third World Congress on Information and Communication Technologies (WICT 2013), Hanoi, Vietnam, 15–18 December 2013; pp. 1–6. [Google Scholar]
- Jana, C.; Senapati, T.; Pal, M.; Yager, R.R. Picture fuzzy Dombi aggregation operators: Application to MADM process. Appl. Soft Comput. 2019, 74, 99–109. [Google Scholar] [CrossRef]
- Singh, S.; Ganie, A.H. Applications of picture fuzzy similarity measures in pattern recognition, clustering, and MADM. Expert. Appl. 2021, 168, 114264. [Google Scholar] [CrossRef]
- Ganie, A.H.; Singh, S. An innovative picture fuzzy distance measure and novel multi-attribute decision-making method. Complex Intell. Syst. 2021, 7, 781–805. [Google Scholar] [CrossRef]
- Ashraf, S.; Abdullah, S.; Mahmood, T.; Ghani, F.; Mahmood, T. Spherical fuzzy sets and their applications in multi-attribute decision making problems. J. Intell. Fuzzy Syst. 2019, 36, 2829–2844. [Google Scholar] [CrossRef]
- Aydoğdu, A.; Gül, S. A novel entropy proposition for spherical fuzzy sets and its application in multiple attribute decision-making. Int. J. Intell. Syst. 2020, 35, 1354–1374. [Google Scholar] [CrossRef]
- Sarfraz, M.; Pamucar, D. A parametric similarity measure for spherical fuzzy sets and its applications in medical equipment selection. J. Eng. Manag. Syst. Eng. 2024, 3, 38–52. [Google Scholar] [CrossRef]
- Onar, S.C.; Kahraman, C.; Oztaysi, B. Multi-criteria spherical fuzzy regret based evaluation of healthcare equipment stocks. J. Intell. Fuzzy Syst. 2020, 39, 5987–5997. [Google Scholar] [CrossRef]
- Ye, J.; Song, J.; Du, S.; Yong, R. Weighted aggregation operators of fuzzy credibility numbers and their decision-making approach for slope design schemes. Comput. Appl. Math. 2021, 2021, 1–14. [Google Scholar] [CrossRef]
- Qiyas, M.; Madrar, T.; Khan, S.; Abdullah, S.; Botmart, T.; Jirawattanapaint, A. Decision support system based on fuzzy credibility Dombi aggregation operators and modified TOPSIS method. AIMS Math. 2022, 7, 19057–19082. [Google Scholar] [CrossRef]
- Midrar, T.; Khan, S.; Abdullah, S.; Botmart, T. Entropy based extended TOPOSIS method for MCDM problem with fuzzy credibility numbers. AIMS Math. 2022, 7, 17286–17312. [Google Scholar] [CrossRef]
- Yahya, M.; Abdullah, S.; Qiyas, M. Analysis of medical diagnosis based on fuzzy credibility Dombi Bonferroni mean operator. J. Ambient. Intell. Humaniz. Comput. 2023, 14, 12709–12724. [Google Scholar] [CrossRef]
- Qiyas, M.; Khan, N.; Naeem, M.; Abdullah, S. Intuitionistic fuzzy credibility Dombi aggregation operators and their application of railway train selection in Pakistan. AIMS Math. 2023, 8, 6520–6542. [Google Scholar] [CrossRef]
- Dombi, J. A general class of fuzzy operators, the DeMorgan class of fuzzy operators and fuzziness measures induced by fuzzy operators. Fuzzy Sets Syst. 1982, 8, 149–163. [Google Scholar] [CrossRef]
- Khan, A.A.; Ashraf, S.; Abdullah, S.; Qiyas, M.; Luo, J.; Khan, S.U. Pythagorean fuzzy Dombi aggregation operators and their application in decision support system. Symmetry 2019, 11, 383. [Google Scholar] [CrossRef]
- Jana, C.; Muhiuddin, G.; Pal, M. Some Dombi aggregation of Q-rung orthopair fuzzy numbers in multiple-attribute decision making. Int. J. Intell. Syst. 2019, 34, 3220–3240. [Google Scholar] [CrossRef]
- Du, W.S. More on Dombi operations and Dombi aggregation operators for q-rung orthopair fuzzy values. J. Intell. Fuzzy Syst. 2020, 39, 3715–3735. [Google Scholar] [CrossRef]
- Seikh, M.R.; Mandal, U. Intuitionistic fuzzy Dombi aggregation operators and their application to multiple attribute decision-making. Granul. Comput. 2021, 6, 473–488. [Google Scholar] [CrossRef]
- Ashraf, S.; Abdullah, S.; Mahmood, T. Spherical fuzzy Dombi aggregation operators and their application in group decision making problems. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 2731–2749. [Google Scholar] [CrossRef]
- Khan, Q.; Mahmood, T.; Ullah, K. Applications of improved spherical fuzzy Dombi aggregation operators in decision support system. Soft Comput. 2021, 25, 9097–9119. [Google Scholar] [CrossRef]


| Attributes | ||||
|---|---|---|---|---|
| SFCDWA Operator | SFCDWG Operator | |
|---|---|---|
| Ranking | ||||||
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 | ||||||
| 7 | ||||||
| 8 | ||||||
| 9 | ||||||
| 10 | ||||||
| Ranking order | ||||||
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 | ||||||
| 7 | ||||||
| 8 | ||||||
| 9 | ||||||
| 10 | ||||||
| Ranking order | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, N.; Qiyas, M.; Karabasevic, D.; Ramzan, M.; Ali, M.; Dugonjic, I.; Stanujkic, D. Spherical Fuzzy Credibility Dombi Aggregation Operators and Their Application in Artificial Intelligence. Axioms 2025, 14, 108. https://doi.org/10.3390/axioms14020108
Khan N, Qiyas M, Karabasevic D, Ramzan M, Ali M, Dugonjic I, Stanujkic D. Spherical Fuzzy Credibility Dombi Aggregation Operators and Their Application in Artificial Intelligence. Axioms. 2025; 14(2):108. https://doi.org/10.3390/axioms14020108
Chicago/Turabian StyleKhan, Neelam, Muhammad Qiyas, Darjan Karabasevic, Muhammad Ramzan, Mubashir Ali, Igor Dugonjic, and Dragisa Stanujkic. 2025. "Spherical Fuzzy Credibility Dombi Aggregation Operators and Their Application in Artificial Intelligence" Axioms 14, no. 2: 108. https://doi.org/10.3390/axioms14020108
APA StyleKhan, N., Qiyas, M., Karabasevic, D., Ramzan, M., Ali, M., Dugonjic, I., & Stanujkic, D. (2025). Spherical Fuzzy Credibility Dombi Aggregation Operators and Their Application in Artificial Intelligence. Axioms, 14(2), 108. https://doi.org/10.3390/axioms14020108








