Synchronization of Markovian Switching Stochastic Delayed Complex Dynamical Networks via Pinning Control

Abstract

This study examines the synchronization of Markovian switching stochastic delayed complex dynamical networks (MSSDCDNs). MSSDCDNs have general structures and coupling forms, which are influenced by Markovian switching, random disturbances, and time delays. Simultaneously, relevant controllers are incorporated into certain nodes. Utilizing the theory of stochastic differential equations, we establish adequate requirements to guarantee exponential synchronization in mean square inside the network by formulating suitable Lyapunov functions and employing general Itô formula and inequality approaches. Lastly, numerical examples and simulations are used to verify the validity of the derived theoretical results.

1. Introduction

In recent years, complex dynamic networks (CDNs) have become an important tool for modeling and analysis of many practical systems such as power systems, the Internet, biological networks, and social networks because they can truly reflect the interaction and information transmission between nodes [1,2,3,4]. In the CDNs, each node represents a specific entity or information, and the connection between nodes reveals the complex interaction mechanism within the system, which makes the network as a whole exhibit diverse and nonlinear dynamic behaviors. Therefore, in-depth study of the dynamic characteristics of this system not only has theoretical significance, but also has guiding value for engineering applications [5,6,7,8,9].

As a significant dynamic characteristic of CDNs, synchronization plays a key role in practical applications [10,11,12,13]. It is noteworthy that the concept of synchronization extends beyond complete agreement to include other collective phenomena such as anti-synchronization, where the states of nodes become diametrically opposed. Research on establishing global stability for such patterns, for instance in neural networks, provides valuable insights [14]. In practical applications, due to their complex structure and dynamic properties, most networks cannot spontaneously achieve synchronization. In order to solve this problem, various control strategies have emerged [15,16,17,18,19,20], including impulsive control strategies, asymptotical control strategies, event-triggered control strategies, and so on. However, due to the large number of nodes in complex dynamic networks, controlling them one by one will inevitably be costly. Fortunately, the pinning control strategy has been proposed as an efficient control strategy [21]. Because it only needs to control a small number of key nodes to realize the synchronization of the whole system, it has been widely studied [22,23]. For example, Yu et al. established a pinning synchronization criterion based on the Lyapunov method in a strongly connected network, and demonstrated that CDNs may be successfully synchronized by preferentially controlling tiny in-degree nodes [22]. Based on the spectral property of the minimum eigenvalue of the grounded Laplacian matrix, Liu et al. proposed a strategy to optimize the selection of control nodes, enhancing the synchronization robustness and convergence speed [23]. These studies provide a theoretical basis and practical guidance for the synchronization control of large-scale CDNs.

It is important to remember that random disturbance and temporal delays are important components that are typical of real systems. Due to the limitation of material transmission, communication delay, and transmission speed in information processing, the phenomenon of time delay inevitably occurs in various networks [24,25,26,27]. The analysis of systems with time delays has spurred the development of numerous advanced methodologies. Recent developments, for instance, include refined inequality techniques for stability analysis [25], innovative approaches to partitioning the delay interval to reduce conservatism [26], and the use of switched system models to study exponential stability and dissipativity [27]. At the same time, due to the influence of environmental noise, parameter uncertainty and external interference, the system is often accompanied by random disturbances [28,29,30,31]. The robustness of network dynamics against noise is a topic of significant interest, with recent studies highlighting how specific topological structures can offer inherent protection against disruptive fluctuations [29]. On the other hand, the topology of many real systems is not static, but changes over time. The Markovian switching model is widely used to describe the process of random switching between multiple finite states of the system structure, which has the characteristics of high modeling accuracy and strong practicability [32,33,34,35]. It is important to note that the Markovian switching is one of several mathematical frameworks used to capture the dynamics of time-varying networks. Other models, such as those considering mobility in heterogeneous environments or interactions based on spatial closeness, offer complementary perspectives on how network evolution impacts collective behavior [36,37].

Based on the above discussion, it is necessary to consider time delays, random disturbance, and Markovian switching factors in CDNs—that is, Markovian switching stochastic delayed complex dynamic networks (MSSDCDNs)—and study their external synchronization under pinning control. In contrast to the topological approach for robustness, this study employs a control–theoretic framework to actively suppress the negative effects of noise and delays. In this study, Lyapunov stability theory and stochastic differential system analysis method are used to design the corresponding control strategy based on state feedback to achieve stable external synchronization of the network in a random environment. By constructing the corresponding multistate Lyapunov function, a sufficient condition is derived to ensure the synchronization of the system in the mean square sense. This method framework provides a theoretical basis and practical insights for the study of MSSDCDNs. Furthermore, in comparison to prior research, the key contributions and innovations of this work are as follows:

• We establish a network model that considers time delays, random disturbance, and Markovian switching at the same time, so that the research results can better reflect the complexity in practical engineering.
• For the above MSSDCDNs, the corresponding control strategy is designed to apply control signals only at some nodes, and the sufficient conditions for the mean square exponential synchronization of the system are derived by using the Lyapunov–Krasovskii function, an inequality technique, and other mathematical tools.
• Some simulation experiments show the effectiveness and feasibility of the obtained theoretical results in the case of time delays, random disturbance, and Markovian switching mode.

The following sections of the article are structured accordingly. A brief synopsis of several preliminaries and model formulations is given in Section 2. The necessary conditions for MSSDCDNs synchronization are laid out in Section 3 through the application of the appropriate pinning control strategy and adaptive pinning control strategy, with the help of the Lyapunov method and inequality approach. To support our theoretical conclusions, examples are presented in Section 4. The findings are elaborated in Section 5.

Notation

In this study, we use some important mathematical symbols. The following are their definitions and brief descriptions. $\mathrm{Trace}\left(A\right)={\sum }_{i=1}^n{a}_{ii}$ is the definition of the trace of matrix $A={\left[a_{ij}\right]}_{n\times n}$. Suppose that ⊗ is the Kronecker product. Let ${\mathbb{R}}^n$ denote the n-dimensional real vector space, ${\mathbb{R}}^{N\times N}$ represent the set of all $N\times N$ real matrices, and ${\mathbb{R}}^{+}$ indicate the interval $[0,+\infty )$. $I_N$ represents a N-dimensional identity matrix. The transpose of matrix A is represented as $A^T$, whereas $A^{-1}$ denotes the inverse of matrix A. Let $A>0$ (or $A<0$) signify the positive (or negative) definiteness of the matrix A. The Euclidean norm of the vector $\gamma ={({\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n)}^T$ is defined as $\parallel \gamma \parallel ={\left({\sum }_{k=1}^n{\gamma }_k^2\right)}^{1/2}$. For the matrix $M\in {\mathbb{R}}^{N\times N}$, by removing any l row-column pairings (where $1\le l<N$), we define $M_l\in {\mathbb{R}}^{(N-l)\times (N-l)}$ as a sub-matrix of M. Let $(\Omega ,\mathcal{F},\mathbb{P})$ be a complete probability space. In addition to these symbols, any other specific symbols will be explained upon their first appearance according to the specific context, to ensure that each mathematical symbol and expression can be clearly understood in the appropriate context.

2. Preliminaries and Model Formulations

This study defines $\theta (·)$ as a right-continuous Markov chain on the probability space $(\Omega ,\mathcal{F},\mathbb{F},\mathbb{P})$, which assumes values in a finite state space $\mathbb{S}=\{1,2,\dots ,O\}$. The associated generator $\Gamma ={\left({\gamma }_{kh}\right)}_{O\times O}$ is defined as

$$\mathbb{P}\{\theta (t+\Delta )=h|\theta \left(t\right)=k\}=\left\{\begin{array}{cc}{\gamma }_{kh}\Delta +o(\Delta ),\hfill & \mathrm{if}k\ne h,\hfill \\ 1+{\gamma }_{kk}\Delta +o(\Delta ),\hfill & \mathrm{if}k=h,\hfill \end{array}\right.$$

where $\Delta >0$, ${\gamma }_{kh}\ge 0$ is the transition rate from k to h, while ${\gamma }_{kk}=-{\sum }_{k\ne h}{\gamma }_{kh}$. Therefore, we will discuss the synchronization problem of MSSDCDNs, which it aligns more closely with the reality structure. The structure is as below

$$\begin{array}{cc}\hfill d{x}_i\left(t\right)=& f_i(x_i\left(t\right),t,\theta \left(t\right))dt+{\displaystyle \sum _{j=1}^N}{G}_{ij}\left(\theta \left(t\right)\right)[c{H}_{ij}\left(x_j\left(t\right)\right)+c^{*}{F}_{ij}\left(x_j(t-{\tau }_j)\right)]dt\hfill \\ \hfill & +g_i\left(x_i(t-{\tau }_i),t,\theta \left(t\right)\right)dw\left(t\right),i=1,2,\dots ,N,\hfill \end{array}$$

(1)

where $x_i={\left(x_{i1},x_{i2},\dots ,x_{in}\right)}^T\in {\mathbb{R}}^n$ is the state vector of the ith node, $f_i\left(x_i,t\right):{\mathbb{R}}^n\times {\mathbb{R}}^{+}\to {\mathbb{R}}^n$ is the continuous vector function of ith node, the positive constant c and $c^{*}$ are the coupling strengths between nodes, $H_{ij}(·)$ and $F_{ij}(·):{\mathbb{R}}^n\to {\mathbb{R}}^n$ are the nonlinear coupling functions from the ith node to the jth node, the real numbers ${\tau }_j$ and ${\tau }_i>0$ represent the time delays, let $\tau =max\left({\tau }_i\right)$, and $g_i:{\mathbb{R}}^n\times {\mathbb{R}}^{+}\to {\mathbb{R}}^{n\times m}$ are Borel measurable functions, and $w\left(t\right)={(w_1\left(t\right),\dots ,w_m\left(t\right))}^T$ is Brownian motion, and we use $x_i\left(s\right)$, where $s\in [-\tau ,0]$, $x_i\left(s\right)\in C([-\tau ,0],{\mathbb{R}}^n)$ to represent the initial value, and $G\left(\theta \left(t\right)\right)={\left(G_{ij}\left(\theta \left(t\right)\right)\right)}_{N\times N}\in {\mathbb{R}}^{N\times N}$ is the state topological structure of the MSSDCDNs, where $G_{ij}\left(\theta \left(t\right)\right)$ are defined as follows: if the ith node is related to the jth node $(i\ne j)$, then $G_{ij}\left(\theta \left(t\right)\right)>0$; otherwise, $G_{ij}\left(\theta \left(t\right)\right)=0$; here, the coupling matrix G is not required to be symmetric; and the diagonal elements of G satisfies

$$G_{ii}\left(\theta \left(t\right)\right)=-\sum _{j=1,j\ne i}^N{G}_{ij}\left(\theta \left(t\right)\right)$$

(2)

In the following, we will consider the synchronization question of the SDCDNs (1). Suppose that we want to synchronize the nodes in the SDCDNs (1) to the corresponding nodes of the expected driving SDCDNs (3), described by

$$\begin{array}{cc}\hfill d{y}_i\left(t\right)=& f_i\left(y_i\left(t\right),t,\theta \left(t\right)\right)dt+{\displaystyle \sum _{j=1}^N}{G}_{ij}\left(\theta \left(t\right)\right)[c{H}_{ij}\left(y_j\left(t\right)\right)+c^{*}{F}_{ij}\left(y_j(t-{\tau }_j)\right)]dt\hfill \\ \hfill & +g_i\left(y_i(t-{\tau }_i),t,\theta \left(t\right)\right)dw\left(t\right),i=1,2,\dots ,N,\hfill \end{array}$$

(3)

where $y_i={\left(y_{i1},y_{i2},\dots ,y_{in}\right)}^T\in {\mathbb{R}}^n$.

To realize the synchronization of the SDCDNs (1), controllers will be added to certain nodes; the controlled MSSDCDNs can be described as

$$\begin{array}{cc}\hfill d{x}_i\left(t\right)=& f_i\left(x_i\left(t\right),t,\theta \left(t\right)\right)dt+{\displaystyle \sum _{j=1}^N}{G}_{ij}\left(\theta \left(t\right)\right)[c{H}_{ij}\left(x_j\left(t\right)\right)+c^{*}{F}_{ij}\left(x_j(t-{\tau }_j)\right)]dt\hfill \\ \hfill & +u_{i}dt+g_i\left(x_i(t-{\tau }_i),t,\theta \left(t\right)\right)dw\left(t\right),i=1,2,\dots ,N,\hfill \end{array}$$

(4)

where $u_i$ is the n-dimensional controller, which will be designed in the following.

Next, we will consider the synchronization problem of SDCDNs (4). Let $e_i\left(t\right)=x_i\left(t\right)-y_i\left(t\right)$, and subtracting control system (3) from control system (4), we can get the error dynamic Equation:

$$\begin{array}{cc}\hfill d{e}_i\left(t\right)=& \left(f_i\left(x_i\left(t\right),t,\theta \left(t\right)\right)-f_i\left(y_i\left(t\right),t,\theta \left(t\right)\right)\right)dt\hfill \\ \hfill & +{\displaystyle \sum _{j=1}^N}{G}_{ij}\left(\theta \left(t\right)\right)[c{H}_{ij}\left(x_j\left(t\right)\right)-H_{ij}\left(y_j\left(t\right)\right)+c^{*}{F}_{ij}\left(x_j(t-{\tau }_j)\right)-F_{ij}\left(y_j(t-{\tau }_j)\right)+u_i]dt\hfill \\ \hfill & +[g_i\left(x_i(t-{\tau }_i),t,\theta \left(t\right)\right)-g_i\left(y_i(t-{\tau }_i),t,\theta \left(t\right)\right)]dw\left(t\right),i=1,2,\dots ,N,\hfill \end{array}$$

(5)

If $r\left(t\right)=k\in \mathbb{S}$. Let $F_i(x_i,t,k)=f_i(e_i,t,k)-f_i(y_i,t,k),H_{ij}\left(e_j\left(t\right)\right)=H_{ij}\left(x_j\left(t\right)\right)-H_{ij}\left(y_j\left(t\right)\right),F_{ij}\left(e_j(t-{\tau }_j)\right)=F_{ij}\left(x_j(t-{\tau }_j)\right)-F_{ij}\left(y_j(t-{\tau }_j)\right),g_i(e_i(t-{\tau }_i),t,k)=g_i(x_i(t-{\tau }_i),t,k)-g_i(y_i(t-{\tau }_i),t,k)$; then, for $V(e_i,t,k)\in C^{2,1}({\mathbb{R}}^n\times {\mathbb{R}}_{+}\times \mathbb{S};{\mathbb{R}}_{+})$, define a differential operator $\mathcal{L}V(e_i,t,k)$ associated with Equation (5) by

$$\begin{array}{cc}\hfill \mathcal{L}V(e_i,t,k)\triangleq & \sum _{h=1}^O{\gamma }_{kh}V(e_i,t,h)+{\displaystyle \frac{\partial V(e_i,t,k)}{\partial t}}\hfill \\ & +{\displaystyle \frac{\partial V(e_i,t,k)}{\partial e_i}}\left[F_i(e_i,t,k)+\sum _{j=1}^N{G}_{ij}\left(k\right)(c{H}_{ij}\left(e_j\left(t\right)\right)+c^{*}{F}_{ij}\left(e_j(t-{\tau }_j)\right))+u_i\right]\hfill \\ & +{\displaystyle \frac{1}{2}}\mathrm{Trace}\left\{{\left[g_i(e_i(t-{\tau }_i),t,k)\right]}^T{\displaystyle \frac{{\partial }^2{V}_i(e_i,t,k)}{\partial e_i^2}}\left[g_i(e_i(t-{\tau }_i),t,k)\right]\right\},\hfill \end{array}$$

where

$${\displaystyle \frac{\partial V_i(e_i,t,k)}{\partial e_i}}=\left({\displaystyle \frac{\partial V_i(e_i,t,k)}{\partial e_i^{\left(1\right)}}},\dots ,{\displaystyle \frac{\partial V_i(e_i,t,k)}{\partial e_i^{\left(n\right)}}}\right),{\displaystyle \frac{{\partial }^2{V}_i(e_i,t,k)}{\partial e_i^2}}={\left({\displaystyle \frac{{\partial }^2{V}_i(e_i,t,k)}{\partial e_i^{\left(k\right)}\partial e_i^{\left(h\right)}}}\right)}_{n\times n}.$$

Remark 1.

In this paper, for MSSCDNs (1), we consider the influence of multiple factors, in which the coupling term considers the more general form of nonlinear coupling, and characterizes the existence and non-existence of time delay, respectively, and introduces the influence of random interference. However, it should be pointed out that for more general cases, the time delay may be time-varying, and the random disturbance may also be diverse. We hope that, in the future research, we can fully consider the influence of these factors.

To get the results of the paper, the following assumptions and lemmas and definition are needed:

Assumption 1.

Assume that the functions $f_i(·)$ and $F_{ij}(·)$ are bounded, and there has Lipschitz constants $l_{f\left(k\right)}$ and ${\beta }_{ij}$:

$$\begin{array}{cc}\hfill \left|\right|f_i\left(x,t,k\right)-f_i\left(y,t,k\right)\left|\right|& \le l_{f\left(k\right)}\left|\right|x-y\left|\right|,\hfill \\ \hfill \left|\right|F_{ij}\left(x\right)-F_{ij}\left(y\right)\left|\right|& \le {\beta }_{ij}\left|\right|x-y\left|\right|,\hfill \end{array}$$

(6)

Assumption 2.

Assume that it has constants ${\alpha }_{ij}^{\left(1\right)}$ and ${\alpha }_{ij}^{\left(2\right)}>0$, such that, for any $\sigma ,\beta \in \mathbb{R}$, the nonlinear function $H_{ij}(·)$ has

$${\alpha }_{ij}^{\left(1\right)}\le {\displaystyle \frac{H_{ij}\left(\sigma \right)-H_{ij}\left(\beta \right)}{\sigma -\beta }}\le {\alpha }_{ij}^{\left(2\right)}$$

(7)

Assumption 3.

Assume that the noise intensity function vector ${\sigma }_i(·):{\mathbb{R}}^n\times {\mathbb{R}}^{+}\to {\mathbb{R}}^{n\times m}$ adhere to the Lipschitz condition, meaning there exists a constant $q_i$, such that:

$$trace{\left[{\sigma }_i(x_i\left(t\right),t)-{\sigma }_i(y_i\left(t\right),t)\right]}^T\left[{\sigma }_i(x_i\left(t\right),t)-{\sigma }_i(y_i\left(t\right),t)\right]\le q_i\left|\right|(x_i\left(t\right)-y_i\left(t\right)){\left|\right|}^2$$

(8)

Lemma 1

([38]). For any symmetric positive matrix $P\in R^n\times R^n$$x,y\in R^n$, it has

$$\pm 2x^{T}y\le x^{T}Px+y^T{P}^{-1}y$$

(9)

Lemma 2

([39]). Let $V\in C^{2,1}({\mathbb{R}}^n\times {\mathbb{R}}_{+}\times \mathbb{S},{\mathbb{R}}_{+})$ and $0\le {\tau }_1\le {\tau }_2$ be bounded stopping times. When $V\left(x\right(t),t,r(t\left)\right)$ is bounded for $t\in [{\tau }_1,{\tau }_2]$ with probability 1, it has

$$EV(x\left({\tau }_2\right),{\tau }_2,r\left({\tau }_2\right))=EV(x\left({\tau }_1\right),{\tau }_1,r\left({\tau }_1\right))+E{\int }_{{\tau }_1}^{{\tau }_2}\mathcal{L}V(x\left(s\right),s,r\left(s\right))ds.$$

Lemma 3

([22]). The following linear matrix inequality (LMI)

$$\left(\begin{array}{cc}\mathcal{A}\left(ϵ\right)& \mathcal{B}\left(ϵ\right)\\ {\mathcal{B}}^T\left(ϵ\right)& \mathcal{C}\left(ϵ\right)\end{array}\right)>0$$

where $\mathcal{A}\left(ϵ\right)={\mathcal{A}}^T\left(ϵ\right)$, $\mathcal{C}\left(ϵ\right)={\mathcal{C}}^T\left(ϵ\right)$ is equivalent to one of the following conditions:

$\left(i\right)$

$\mathcal{A}\left(ϵ\right)>0,and\mathcal{C}\left(ϵ\right)-{\mathcal{B}}^T\left(ϵ\right){\mathcal{A}\left(ϵ\right)}^{-1}\mathcal{B}\left(ϵ\right)>0$

$\left(ii\right)$

$\mathcal{C}\left(ϵ\right)>0,and\mathcal{A}\left(ϵ\right)-\mathcal{B}\left(ϵ\right){\mathcal{C}\left(ϵ\right)}^{-1}{\mathcal{B}}^T\left(ϵ\right)>0$

Lemma 4

([40]). Supposing that matrix $\mathcal{H}=\left({\mathcal{H}}_{ij}\right)\in {\mathbb{R}}^{n\times n}$ satisfies ${\mathcal{H}}_{ij}={\mathcal{H}}_{ji}$ and ${\mathcal{H}}_{ii}=-{\sum }_{j=1,i\ne j}^n{\mathcal{H}}_{ij}$, $i,j=1,2,\dots ,n$, and for any vectors $\sigma ={({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_n)}^T$, $\beta ={({\beta }_1,{\beta }_2,\dots ,{\beta }_n)}^T$, it has

$${\sigma }^T\mathcal{H}\beta =\sum _{i=1}^n\sum _{j=1}^n{\sigma }_i{\mathcal{H}}_{ij}{\beta }_j=-\sum _{j>i}{\mathcal{H}}_{ij}({\sigma }_i-{\sigma }_j)({\beta }_i-{\beta }_j)$$

(10)

Definition 1.

The response MSSDCDNs (1) and the drive MSSDCDNs (3) achieve mean square exponential synchronization. If there are constants $M>0$, $u>0$, such that for any initial condition $e_i\left(s\right)\in C([-\tau ,0];{\mathbb{R}}^n)$, the state vector satisfies the following conditions

$$\mathbb{E}\left\{\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)\right\}\le M{e}^{-ut}E\left\{\underset{s\in [-\tau ,0]}{max}\sum _{i=1}^N{e}_i^T\left(s\right)e_i\left(s\right)\right\}i=1,2,\dots ,N,$$

(11)

where $e_i=x_i-y_i$.

3. Main Results

This section examines the synchronization criteria for MSSDCDNs.

3.1. On Synchronization Criteria of SDCDNs via Pinning Control

To achieve synchronization between the response MSSDCDNs (1) and the drive MSSDCDNs (3), we develop the appropriate pinning controller. The arrangement is as follows:

$$\begin{array}{c}\hfill u_i\left(t\right)=\left\{\begin{array}{cc}-c{d}_i(x_i\left(t\right)-y_i\left(t\right)),\hfill & i=1,2,\dots ,l,\hfill \\ 0,\hfill & i=l+1,\dots ,N,\hfill \end{array}\right.\end{array}$$

(12)

where $d_i>0$ is the control gain.

Remark 2.

Here, we assume that control is applied to the first l nodes, which is still satisfied in practical applications. Moreover, we hope to obtain a global control gain $d_i$ to deal with the influence of Markov jump, so that the obtained results are more general.

Theorem 1.

Assume that Assumptions 1 and 2 hold and the pinning controller $u_i$ is designed in (12), the response MSSDCDNs (1) and the drive MSSDCDNs (3) achieve mean square exponential synchronization if the following condition is satisfied:

$$({\displaystyle \frac{1}{2}}u{q}^{\left(k\right)}+l_{f\left(k\right)}{q}^{\left(k\right)}+w+c^{*}m{q}^{\left(k\right)}+\sum _{h=1}^o{\gamma }_{kh}{q}^{\left(h\right)})I_N+c\alpha q^{\left(k\right)}{\displaystyle \frac{G{\left(k\right)}^T+G\left(k\right)}{2}}-c{q}^{\left(k\right)}D<0$$

(13)

where $w=max\{e^{u{\tau }_i}{q}^{\left(k\right)}{\displaystyle \frac{p_{\left(k\right)}+c^{*}N{\beta }^{2}m\left(k\right)}{2}}\}$, $\alpha =\underset{i,j=1,2,\dots ,N}{min}\left\{{\alpha }_{ij}^{\left(1\right)}\right\}$, and $\beta =\underset{i,j=1,2,\dots ,N}{max}\left\{{\beta }_{ij}\right\}$, $D=diag(d_1,\dots ,d_l,0,\dots ,0)\in {\mathbb{R}}^{N\times N}$.

Proof of Theorem 1.

We can get the error dynamic equation:

$$\begin{array}{cc}\hfill d{e}_i\left(t\right)=& f_i(e_i\left(t\right),t,k)dt+{\displaystyle \sum _{j=1}^N}{G}_{ij}\left(k\right)[c{H}_{ij}\left(e_j\left(t\right)\right)+c^{*}{F}_{ij}\left(e_j(t-{\tau }_j)\right)-c{d}_i{e}_i\left(t\right)]dt\hfill \\ \hfill & +g_i\left(e_i(t-{\tau }_i),t,k\right)dw\left(t\right),i=1,2,\dots ,l,\hfill \\ \hfill d{e}_i\left(t\right)=& f_i(e_i\left(t\right),t,k)dt+{\displaystyle \sum _{j=1}^N}{G}_{ij}\left(k\right)[c{H}_{ij}\left(e_j\left(t\right)\right)+c^{*}{F}_{ij}\left(e_j(t-{\tau }_j)\right)]dt\hfill \\ \hfill & +g_i\left(e_i(t-{\tau }_i),t,k\right)dw\left(t\right),i=l+1,2,\dots ,N.\hfill \end{array}$$

(14)

Consider the Lyapunov functional:

$$V\left(e\left(t\right),t,k\right)={\displaystyle \frac{1}{2}}{q}^{\left(k\right)}{e}^{ut}\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)+w\sum _{i=1}^N{\int }_{t-{\tau }_i}^t{e}^{u\sigma }{e}_i^T\left(\sigma \right)e_i\left(\sigma \right)d\sigma ,$$

(15)

where $e\left(t\right)={\left(e_1^T\left(t\right),e_2^T\left(t\right),\dots ,e_N^T\left(t\right)\right)}^T$.

The derivative of $V\left(e\right(t),t)$ along the trajectory of error dynamic Equation (14) is expressed as:

$$\begin{array}{cc}\hfill \mathcal{L}V\left(e\left(t\right),t,k\right)=& {\displaystyle \frac{1}{2}}u{q}^{\left(k\right)}{e}^{ut}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)+q^{\left(k\right)}{e}^{ut}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)[f_i(e_i\left(t\right),t,k)\hfill \\ \hfill & +{\displaystyle \sum _{j=1}^N}{G}_{ij}\left(k\right)(c{H}_{ij}\left(e_j\left(t\right)\right)+c^{*}{F}_{ij}\left(e_j(t-{\tau }_j)\right)-c{d}_i{e}_i\left(t\right)]\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{q}^{\left(k\right)}{e}^{ut}{\displaystyle \sum _{i=1}^N}trace[g_i{(e_i(t-{\tau }_i),t,k)}^T(g_i(e_i(t-{\tau }_i),t,k)]\hfill \\ \hfill & +\left[w{e}^{ut}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)-{\displaystyle \frac{w}{max\left\{e^{u{\tau }_i}\right\}}}{e}^{ut}{\displaystyle \sum _{i=1}^N}{e}_i^T(t-{\tau }_i)e_i(t-{\tau }_i)\right]dt\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\displaystyle \sum _{h=1}^o}{\gamma }_{kh}{q}^{\left(h\right)}{e}^{ut}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right).\hfill \end{array}$$

(16)

According to all assumptions and Lemma 4, the following can be obtained:

$$\begin{array}{c}\hfill {\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)f_i(e_i\left(t\right),t,k)\le l_f\left(k\right){\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)\\ \hfill c{\displaystyle \sum _{j=1}^N}{G}_{ij}\left(k\right)H_{ij}\left(e_j\left(t\right)\right)\le c{\displaystyle \sum _{j=1}^N}{G}_{ij}\left(k\right)\left(\alpha e_j\left(t\right)\right),\end{array}$$

(17)

and

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{i=1}^N}trace\left[g_i{(e_i(t-{\tau }_i),t,k)}^T{g}_i(x_i(t-{\tau }_i),t,k)\right]\hfill \\ \hfill & \le p_{\left(k\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T(t-{\tau }_i)e_i(t-{\tau }_i),`\hfill \end{array}$$

(18)

where $p_{\left(k\right)}=max\left\{p_{i\left(k\right)}\right\},i=1,2,\dots ,N.$

In summary, Equation (16) can be simplified as:

$$\begin{array}{cc}\hfill \mathcal{L}V\left(e\right(t),t,k)\le & e^{ut}[{\displaystyle \frac{1}{2}}u{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)+l_{f\left(k\right)}{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)\hfill \\ \hfill & +c\alpha q^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right){\displaystyle \sum _{j=1}^N}{G}_{ij}\left(k\right)e_j\left(t\right)+c^{*}{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right){\displaystyle \sum _{j=1}^N}{G}_{ij}\left(k\right)F_{ij}\left(e_j(t-{\tau }_j)\right)\hfill \\ \hfill & -c{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{d}_i{e}_i^T\left(t\right)e_i\left(t\right)+{\displaystyle \frac{p_{\left(k\right)}{q}^{\left(k\right)}}{2}}{\displaystyle \sum _{i=1}^N}{e}_i^T(t-{\tau }_i)e_i(t-{\tau }_i)]\hfill \\ \hfill & +\left[w{e}^{ut}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)-{\displaystyle \frac{w}{max\left\{e^{u{\tau }_i}\right\}}}{e}^{ut}{\displaystyle \sum _{i=1}^N}{e}_i^T(t-{\tau }_i)e_i(t-{\tau }_i)\right]dt\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\displaystyle \sum _{h=1}^o}{\gamma }_{kh}{q}^{\left(h\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)\hfill \\ \hfill =& e^{ut}[({\displaystyle \frac{1}{2}}u{q}^{\left(k\right)}+l_{f\left(k\right)}{q}^{\left(k\right)}){\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)+{\displaystyle \frac{1}{2}}{\displaystyle \sum _{h=1}^o}{\gamma }_{kh}{q}^{\left(h\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)\hfill \\ \hfill & +c\alpha q^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right){\displaystyle \sum _{j=1}^N}{G}_{ij}\left(k\right)e_j\left(t\right)-c{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{d}_i{e}_i^T\left(t\right)e_i\left(t\right)\hfill \\ \hfill & +c^{*}{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right){\displaystyle \sum _{j=1}^N}{G}_{ij}\left(k\right)F_{ij}\left(e_j(t-{\tau }_j)\right)+{\displaystyle \frac{p_{\left(k\right)}{q}^{\left(k\right)}}{2}}{\displaystyle \sum _{i=1}^N}{e}_i^T(t-{\tau }_i)e_i(t-{\tau }_i)]\hfill \\ \hfill & +\left[w{e}^{ut}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)-{\displaystyle \frac{w}{max\left\{e^{u{\tau }_i}\right\}}}{e}^{ut}{\displaystyle \sum _{i=1}^N}{e}_i^T(t-{\tau }_i)e_i(t-{\tau }_i)\right]dt.\hfill \end{array}$$

(19)

Based on Lemma 1, we can derive:

$$\begin{array}{cc}\hfill & q^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right){\displaystyle \sum _{j=1}^N}{G}_{ij}\left(k\right)F_{ij}\left(e_j(t-{\tau }_j)\right)\hfill \\ \hfill & =q^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}{G}_{ij}\left(k\right)e_i^T\left(t\right)F_{ij}\left(e_j(t-{\tau }_j)\right)\hfill \\ \hfill & \le {\displaystyle \frac{1}{2}}{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)|{\displaystyle \sum _{j=1}^N}{G}_{ij}\left(k\right)|e_i\left(t\right)+{\displaystyle \frac{1}{2}}{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{F}_{ij}^T\left(e_j(t-{\tau }_j)\right)|{\displaystyle \sum _{j=1}^N}{G}_{ij}\left(k\right)|F_{ij}\left(e_j(t-{\tau }_j)\right)\hfill \\ \hfill & \le m\left(k\right)q^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)+{\displaystyle \frac{N{\beta }^{2}m\left(k\right)}{2}}{\displaystyle \sum _{i=1}^N}{e}_i^T(t-{\tau }_i)e_i(t-{\tau }_i).\hfill \end{array}$$

(20)

Combining the above inequalities, we can get:

$$\begin{array}{cc}\hfill \mathcal{L}V\left(e\right(t),t,k)\le & e^{ut}[({\displaystyle \frac{1}{2}}u+l_{f\left(k\right)}+c^{*}m)q^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)\hfill \\ \hfill & +{\displaystyle \sum _{h=1}^o}{\gamma }_{kh}{q}^{\left(h\right)}{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)+c\alpha q^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right){\displaystyle \sum _{j=1}^N}{G}_{ij}\left(k\right)e_j\left(t\right)\hfill \\ \hfill & -c{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{d}_i{e}_i^T\left(t\right)e_i\left(t\right)+{\displaystyle \frac{p_{\left(k\right)}+c^{*}N{\beta }^{2}m}{2}}{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T(t-{\tau }_i)e_i(t-{\tau }_i)]\hfill \\ \hfill & +\left[w{e}^{ut}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)-{\displaystyle \frac{w}{max\left\{e^{u{\tau }_i}\right\}}}{e}^{ut}{\displaystyle \sum _{i=1}^N}{e}_i^T(t-{\tau }_i)e_i(t-{\tau }_i)\right]\hfill \\ \hfill \le & e^{ut}({\displaystyle \frac{1}{2}}u{q}^{\left(k\right)}+l_{f\left(k\right)}{q}^{\left(k\right)}+w+c^{*}m{q}^{\left(k\right)}+{\displaystyle \sum _{h=1}^o}{\gamma }_{kh}{q}^{\left(h\right)}){\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)\hfill \\ \hfill & +c\alpha {\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right){\displaystyle \sum _{j=1}^N}{G}_{ij}\left(k\right)e_j\left(t\right)-c{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{d}_i{e}_i^T\left(t\right)e_i\left(t\right)\hfill \\ \hfill =& e^{ut}\left[e^T\left(t\right)\right\{(({\displaystyle \frac{1}{2}}u{q}^{\left(k\right)}+l_{f\left(k\right)}{q}^{\left(k\right)}+w+c^{*}m{q}^{\left(k\right)}+{\displaystyle \sum _{h=1}^o}{\gamma }_{kh}{q}^{\left(h\right)})I_N\hfill \\ \hfill & +c\alpha q^{\left(k\right)}{\displaystyle \frac{G{\left(k\right)}^T+G\left(k\right)}{2}}-c{q}^{\left(k\right)}D)\otimes I_n\}]e\left(t\right).\hfill \end{array}$$

(21)

Let $M_{\left(k\right)}=(({\displaystyle \frac{1}{2}}u{q}^{\left(k\right)}+l_{f\left(k\right)}{q}^{\left(k\right)}+w+c^{*}m{q}^{\left(k\right)}+{\sum }_{h=1}^o{\gamma }_{kh}{q}^{(h)})I_N+c\alpha q^{\left(k\right)}{\displaystyle \frac{G{\left(k\right)}^T+G\left(k\right)}{2}}-c{q}^{\left(k\right)}D)=\left(\begin{array}{cc}{A}_{\left(k\right)}-\tilde{D}& B_{\left(k\right)}\\ B_{\left(k\right)}^T& M_{\left(k\right)l}\end{array}\right)$, where $\tilde{D}=diag(d_1,d_2,\dots ,d_l).$ Furthermore, according to theorem Condition (13) if $M_{\left(k\right)l}<0$, one can choose $\tilde{D}>{\lambda }_{max}(A_{\left(k\right)}-B_{\left(k\right)}{M_{\left(k\right)l}}^{-1}{B}_{\left(k\right)}^T)I_l$; then, according to Lemma 3, $M_{\left(k\right)}<0$ is obtained.

Therefore, taking the expectation of Inequality (21), we can get:

$$\begin{array}{c}\hfill \mathcal{L}V\left(e\right(t),t,k)\le 0\end{array}$$

(22)

with Lemma 2, it has

$$\begin{array}{cc}\hfill E\left\{V\right(e\left(t\right),t,k\left)\right\}& =E\left\{V\right(e\left(0\right),0,k\left)\right\}\hfill \\ \hfill & +E{\int }_0^t\mathcal{L}V(e\left(s\right),s,k)ds\hfill \\ \hfill & \le E\left\{V\right(e\left(0\right),0,k\left)\right\}.\hfill \end{array}$$

(23)

Considering the specific Lyapunov functional $V\left(e\right(t),t,k)$ and Inequality (23)

$$\begin{array}{c}\hfill E\{{\displaystyle \frac{1}{2}}{e}^{ut}{q}^{\left(k\right)}\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)\}\le E\left\{V(e\left(t\right),t,k)\right\}\le E\left\{V(e\left(0\right),0,k)\right\},\end{array}$$

(24)

and

$$\begin{array}{cc}\hfill E\{V(e\left(0\right),0,k\left)\right\}& =E\{{\displaystyle \frac{1}{2}}{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(0\right)e_i\left(0\right)+w{\displaystyle \sum _{i=1}^N}{\int }_{-{\tau }_i}^0{e}^{u\sigma }{e}_i^T\left(\sigma \right)e_i\left(\sigma \right)d\sigma \}\hfill \\ \hfill & \le E\{{\displaystyle \frac{1}{2}}{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(0\right)e_i\left(0\right)+w\tau \underset{s\in [-\tau ,0]}{max}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(s\right)e_i\left(s\right)\},\hfill \end{array}$$

(25)

where $\tau =max\left\{{\tau }_i\right\}$.

Combining the inequalities, we can get:

$$\begin{array}{cc}\hfill & E\{{\displaystyle \frac{1}{2}}{e}^{ut}min\left\{q^{\left(k\right)}\right\}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)\}\hfill \\ \hfill & \le E\{{\displaystyle \frac{1}{2}}max\left\{q^{\left(k\right)}\right\}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(0\right)e_i\left(0\right)+w\tau \underset{s\in [-\tau ,0]}{max}{\displaystyle \sum _{i=1}^N},e_i^T\left(s\right)e_i\left(s\right)\}\hfill \end{array}$$

(26)

Simplified we can obtain

$$\begin{array}{c}\hfill E\{\sum _{i=1}^N{e}_i^T\left(t\right)e\left(t\right)\}\le M{e}^{-ut}E\left\{\underset{s\in [-\tau ,0]}{max}\sum _{i=1}^N{e}_i^T\left(s\right)e_i\left(s\right)\right\},\end{array}$$

(27)

where $M={\displaystyle \frac{2w\tau +max\left\{q^{\left(k\right)}\right\}}{min\left\{q^{\left(k\right)}\right\}}}$.

Therefore, the synchronization criterion described in Definition 1 is satisfied. In other words, the response MSSDCDNs (1) and the drive MSSDCDNs (3) achieve mean square exponential synchronization. □

Remark 3.

In Theorem 1, we effectively derive the conditions for mean square exponential synchronization by fixing the control gain. However, in practical applications, this may be greater than the actual required value, which may cause unnecessary cost waste. Therefore, we hope to solve this problem by dynamically adjusting the control gain.

3.2. Global Synchronization Criteria with Adaptive Control Approach

Theorem 2.

Assume that all assumptions and lemmas hold; then, the response MSSDCDNs (1) and the drive MSSDCDNs (3) can achieve mean square exponential synchronization under linear adaptive pinning control law:

$$\begin{array}{c}\hfill u_i\left(t\right)=\left\{\begin{array}{cc}-c{d}_i\left(t\right)(x_i\left(t\right)-y_i\left(t\right)),\hfill & i=1,2,\dots ,l,\hfill \\ 0,\hfill & i=l+1,\dots ,N,\hfill \end{array}\right.\end{array}$$

(28)

where $d_i\left(t\right)$ is the control gain varying with time and ${\dot{d}}_i\left(t\right)=a_i{q}^{\left(k\right)}{e}^{ut}{e_i\left(t\right)}^T{e}_i\left(t\right)$, $a_i$ are positive constants.

Proof of Theorem 2.

One considers the controlled network that the controllers are selected by adaptive control approach:

$$\begin{array}{cc}\hfill d{e}_i\left(t\right)=& f_i(e_i\left(t\right),t,k)dt+\sum _{j=1}^N{G}_{ij}\left(k\right)[c{H}_{ij}\left(e_j\left(t\right)\right)+c^{*}{F}_{ij}\left(e_j(t-{\tau }_j)\right)-c{d}_i\left(t\right)e_i\left(t\right)]dt\hfill \\ \hfill & +g_i\left(e_i(t-{\tau }_i),t,k\right)dw\left(t\right),i=1,2,\dots ,l,\hfill \\ \hfill d{e}_i\left(t\right)=& f_i(e_i\left(t\right),t,k)dt+\sum _{j=1}^N{G}_{ij}\left(k\right)[c{H}_{ij}\left(e_j\left(t\right)\right)+c^{*}{F}_{ij}\left(e_j(t-{\tau }_j)\right)]dt\hfill \\ \hfill & +g_i\left(e_i(t-{\tau }_i),t,k\right)dw\left(t\right),i=l+1,2,\dots ,N.\hfill \end{array}$$

(29)

Consider the Lyapunov functional candidate

$$V\left(e\left(t\right),t,k\right)={\displaystyle \frac{1}{2}}{q}^{\left(k\right)}{e}^{ut}\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)+w\sum _{i=1}^N{\int }_{t-{\tau }_i}^t{e}^{u\sigma }{e}_i^T\left(\sigma \right)e_i\left(\sigma \right)d\sigma +\sum _{i=1}^l{\displaystyle \frac{c}{2a_i}}{(d_i\left(t\right)-d)}^2,$$

(30)

where d is a positive constant to be determined below.

The derivative of $V\left(e\right(t),t)$ along the trajectory of error dynamic Equation (29) is expressed as:

$$\begin{array}{cc}\hfill \mathcal{L}V\left(e\left(t\right),t\right)& ={\displaystyle \frac{1}{2}}u{q}^{\left(k\right)}{e}^{ut}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)+q^{\left(k\right)}{e}^{ut}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)[f_i(e_i\left(t\right),t,k)\hfill \\ \hfill & +{\displaystyle \sum _{j=1}^N}{G}_{ij}\left(k\right)(c{H}_{ij}\left(e_j\left(t\right)\right)+c^{*}{F}_{ij}\left(e_j(t-{\tau }_j)\right)-c{d}_i\left(t\right)e_i\left(t\right)]\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}trace[g_i{(e_i(t-{\tau }_i),t,k)}^T(g_i(e_i(t-{\tau }_i),t,k)]\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\displaystyle \sum _{h=1}^o}{\gamma }_{kh}{q}^{\left(h\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)+c{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}(d_i\left(t\right)-d)e_i^T\left(t\right)e_i\left(t\right)\hfill \\ \hfill & +w{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)-{\displaystyle \frac{w}{max\left\{e^{u{\tau }_i}\right\}}}{\displaystyle \sum _{i=1}^N}{e}_i^T(t-{\tau }_i)e_i(t-{\tau }_i)\hfill \\ \hfill & \le e^{ut}[{\displaystyle \frac{1}{2}}u{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)+l_{f\left(k\right)}{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)\hfill \\ \hfill & +c\alpha q^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right){\displaystyle \sum _{j=1}^N}{G}_{ij}{e}_j\left(t\right)+c^{*}{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right){\displaystyle \sum _{j=1}^N}{G}_{ij}{F}_{ij}\left(e_j(t-{\tau }_j)\right)\hfill \\ \hfill & -c{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{d}_i\left(t\right)e_i^T\left(t\right)e_i\left(t\right)+{\displaystyle \frac{p_{\left(k\right)}{q}^{\left(k\right)}}{2}}{\displaystyle \sum _{i=1}^N}{e}_i^T(t-{\tau }_i)e_i(t-{\tau }_i)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\displaystyle \sum _{h=1}^o}{\gamma }_{kh}{q}^{\left(h\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)+w{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)\hfill \\ \hfill & -{\displaystyle \frac{w}{max\left\{e^{u{\tau }_i}\right\}}}{\displaystyle \sum _{i=1}^N}{e}_i^T(t-{\tau }_i)e_i(t-{\tau }_i)+c{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}(d_i\left(t\right)-d)e_i^T\left(t\right)e_i\left(t\right)]\hfill \\ \hfill \le & e^{ut}\left[e^T\left(t\right)\right\{(({\displaystyle \frac{1}{2}}u{q}^{\left(k\right)}+l_{f\left(k\right)}{q}^{\left(k\right)}+w+c^{*}m{q}^{\left(k\right)}+{\displaystyle \sum _{h=1}^o}{\gamma }_{kh}{q}^{\left(h\right)})I_N\hfill \\ \hfill & +c\alpha q^{\left(k\right)}{\displaystyle \frac{G{\left(k\right)}^T+G\left(k\right)}{2}}-cd{q}^{\left(k\right)}{\tilde{I}}_N)\otimes I_n\}e\left(t\right)]dt,\hfill \end{array}$$

(31)

where ${\tilde{I}}_N=diag(1,\dots ,1,0,\dots ,0)$.

It follows that $M_l\le 0$, and by choosing $d>{\lambda }_{max}(A-B{\tilde{M}}^{-1}{B}^T)$, we can get:

$$\begin{array}{c}\hfill \mathcal{L}V\left(e\right(t),t,k)\le 0\end{array}$$

(32)

with Lemma 2, we get

$$\begin{array}{c}\hfill E\left\{V\right(e\left(t\right),t,k\left)\right\}\le E\left\{V\right(e\left(0\right),0,k\left)\right\}.\end{array}$$

(33)

Considering the specific Lyapunov functional $V\left(e\right(t),t,k)$ and Inequality (33)

$$\begin{array}{c}\hfill E\{{\displaystyle \frac{1}{2}}{e}^{ut}{q}^{\left(k\right)}\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)\}\le E\left\{V(e\left(t\right),t,k)\right\}\le E\left\{V(e\left(0\right),0,k)\right\}\end{array}$$

(34)

and

$$\begin{array}{cc}\hfill E\left\{V\right(e\left(0\right),0,k\left)\right\}& =E\{{\displaystyle \frac{1}{2}}{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(0\right)e_i\left(0\right)+w{\displaystyle \sum _{i=1}^N}{\int }_{-{\tau }_i}^0{e}^{u\sigma }{e}_i^T\left(\sigma \right)e_i\left(\sigma \right)d\sigma +{\displaystyle \sum _{i=1}^l}{\displaystyle \frac{c{d}^2}{2a_i}}\}\hfill \\ \hfill & \le E\{{\displaystyle \frac{1}{2}}{q}^{\left(k\right)}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(0\right)e_i\left(0\right)+w\tau \underset{s\in [-\tau ,0]}{max}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(s\right)e_i\left(s\right)+{\displaystyle \sum _{i=1}^l}{\displaystyle \frac{c{d}^2}{2a_i}}\},\hfill \end{array}$$

(35)

where $\tau =max\left\{{\tau }_i\right\}$.

Combining the inequalities, we can get:

$$\begin{array}{cc}\hfill & E\{{\displaystyle \frac{1}{2}}{e}^{ut}min\left\{q^{\left(k\right)}\right\}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(t\right)e_i\left(t\right)\}\hfill \\ \hfill & \le E\{{\displaystyle \frac{1}{2}}max\left\{q^{\left(k\right)}\right\}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(0\right)e_i\left(0\right)+w\tau \underset{s\in [-\tau ,0]}{max}{\displaystyle \sum _{i=1}^N}{e}_i^T\left(s\right)e_i\left(s\right)+{\displaystyle \sum _{i=1}^l}{\displaystyle \frac{c{d}^2}{2a_i}}\}.\hfill \end{array}$$

(36)

Simplified, we can obtain

$$\begin{array}{c}\hfill E\{\sum _{i=1}^N{e}_i^T\left(t\right)e\left(t\right)\}\le M{e}^{-ut},\end{array}$$

(37)

where $M={\displaystyle \frac{max\left\{q^{\left(k\right)}\right\}{\sum }_{i=1}^N{e}_i^T\left(0\right)e_i\left(0\right)+2w\tau \underset{s\in [-\tau ,0]}{max}{\sum }_{i=1}^N{e}_i^T\left(s\right)e_i\left(s\right)+{\sum }_{i=1}^l\frac{c{d}^2}{a_i}}{min\left\{q^{\left(k\right)}\right\}}}$.

The response MSSDCDNs (1) and the drive MSSDCDNs (3) achieve mean square exponential synchronization. □

Remark 4.

Regarding the comparison with existing results, it is noteworthy that the network model established in this paper comprehensively integrates multiple practical factors, including Markovian switching topology, stochastic disturbances, and time-varying delays. Precisely because of this more realistic and complex modeling approach, the synchronization criteria we derive, while appearing in a specific form, inherently possess a broader scope of application. They are designed to ensure synchronization under the simultaneous influence of these coupled factors, which many existing works do not fully address. Therefore, the primary advantage of our results lies in their wider applicability to complex real-world scenarios, rather than in a direct comparison of conservatism with results derived for simpler models.

4. Simulation Examples

This section provides examples of numerical simulations to illustrate the utility and feasibility of our developed results.

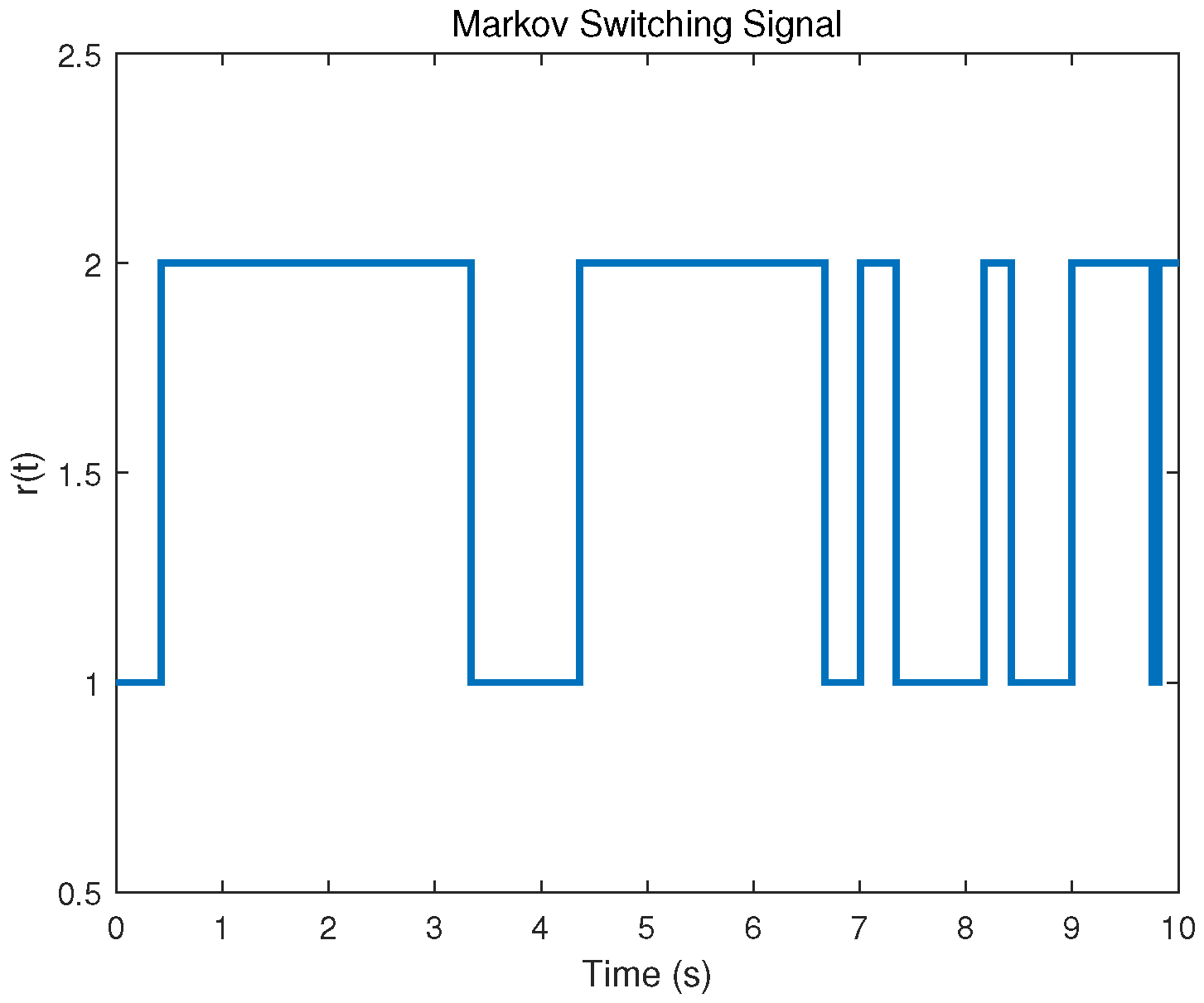
4.1. Synchronization of SDCDNs via Feedback Pinning Control

We consider the controlled MSSDCDNs (4) with ten nodes:

$$\begin{array}{cc}\hfill d{x}_i\left(t\right)=& f_i\left(x_i\left(t\right),t,\theta \left(t\right)\right)dt+{\displaystyle \sum _{j=1}^{10}}{G}_{ij}\left(\theta \left(t\right)\right)[c{H}_{ij}\left(x_j\left(t\right)\right)+c^{*}{F}_{ij}\left(x_j(t-{\tau }_j)\right)]dt\hfill \\ \hfill & +u_{i}dt+g_i\left(x_i(t-{\tau }_i),t,\theta \left(t\right)\right)dw\left(t\right),i=1,2,\dots ,10,\hfill \end{array}$$

(38)

where $x_i\left(t\right)={(x_{i1}\left(t\right),x_{i2}\left(t\right),x_{i3}\left(t\right))}^T\in {\mathbb{R}}^3$.

Let $\theta \left(t\right)$ be a right continuous Markov chain with state space $\mathbb{S}=\{1,2\}$, and its generating matrix is

$$\Gamma ={\left(\gamma \right)}_{2\times 2}=\left[\begin{array}{cc}-3& 3\\ 1& -1\end{array}\right].$$

For convenience, we let nonlinear functions $H_{ij}\left(x_j\left(t\right)\right)=4x_j+sin\left(x_j\left(t\right)\right),F_{ij}\left(x_j(t-{\tau }_j)\right)=0.2tanh\left(x_j\left(t\right)\right)$. For $r\left(t\right)=1$, we select $f_i(x_i\left(t\right),t,1)=-W_1{x}_i+Y_{1}f\left(x_i\left(t\right)\right)$, and $g_i\left(x_i(t-{\tau }_i),t,1\right)=0.1e^{-0.1t}{x}_i(t-{\tau }_i)$. For $r\left(t\right)=2$, we select $f_i(x_i\left(t\right),t,2)=-W_2{x}_i+Y_{2}f\left(x_i\left(t\right)\right),$ and $g_i\left(x_i(t-{\tau }_i),t,2\right)=0.2e^{-0.1t}{x}_i(t-{\tau }_i)$. Where $W_1=I_3,W_2=1.2I_3.$ and $f\left(x_i\left(t\right)\right)=\left(\right|x_i\left(t\right)+1|-|x_i\left(t\right)-1\left|\right)/2$.

$$Y_1=Y_2=\left[\begin{array}{ccc}1.25& -3.2& -3.2\\ -3.2& 1.1& -4.4\\ -3.2& 4.4& 1\end{array}\right].$$

The coupled configuration matrix $G\left(r\right(t\left)\right)$ of the MSSDCDNs (1) can be obtained as follows:

$$\mathbf{G}\left(1\right)=\left[\begin{array}{cccccccccc}-1& 0& 0& 0& 0& 0& 0& 0& 1& 0\\ 0& -1& 0& 0& 0& 0& 1& 0& 0& 0\\ 1& 0& -2& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 1& -1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& -1& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& -1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& -1& 1& 0& 0\\ 1& 1& 0& 0& 0& 0& 0& -3& 0& 1\\ 0& 1& 0& 0& 0& 0& 0& 1& -2& 0\\ 1& 0& 0& 0& 0& 1& 0& 0& 0& -2\end{array}\right],$$

$$\mathbf{G}\left(2\right)=\left[\begin{array}{cccccccccc}-1& 0& 0& 0& 0& 0& 0& 0& 1& 0\\ 0& -1& 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& -1& 1& 0& 0& 0& 0& 0& 0\\ 1& 0& 0& -2& 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& -1& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& -1& 0& 1& 0& 0\\ 1& 0& 1& 1& 0& 0& -3& 0& 0& 0\\ 1& 1& 0& 1& 0& 0& 0& -3& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 1& -2& 0\\ 0& 0& 1& 0& 0& 0& 1& 0& 0& -2\end{array}\right].$$

The relevant parameters are given as $q^{\left(k\right)}=1$, and time delay ${\tau }_j=0.1$$\left(j=1,2,\dots ,10\right)$, the coupling strength $c=6$, $c^{*}=0.2$, and the parameters $u=0.1,m\left(k\right)=3,p_{\left(k\right)}=0.04$. By calculation, we can get the Lipschitz parameters $l_{f\left(k\right)}=5,\alpha =3,\beta =0.2$. Select the top 3 nodes for control, that is, $l=3$, and the fixed control gain $q_i=7,i=1,2,3$. It is a simple exercise to demonstrate that all conditions in Theorem 1 are fulfilled. To illustrate the behavior of the system and the effectiveness of our control strategy, we have plotted the synchronization errors for each component of the system over time, where we suppose that the initial

$$\begin{array}{cc}\hfill & x_1\left(s\right)={(0.34,1.78,0.56)}^T,x_2\left(s\right)={(1.90,0.23,1.56)}^T,x_3\left(s\right)={(0.67,1.23,0.89)}^T,\hfill \\ \hfill & x_4\left(s\right)={(1.45,0.78,1.23)}^T,x_5\left(s\right)={(0.12,1.56,0.90)}^T,x_6\left(s\right)={(1.78,0.34,1.67)}^T,\hfill \\ \hfill & x_7\left(s\right)={(0.56,1.89,0.23)}^T,x_8\left(s\right)={(1.23,0.67,1.45)}^T,x_9\left(s\right)={(0.78,1.01,0.56)}^T,\hfill \\ \hfill & x_{10}\left(s\right)={(1.56,0.89,1.78)}^T,s\in [-0.1,0],\hfill \\ \hfill & y_1\left(s\right)={(1.34,1.78,1.56)}^T,y_2\left(s\right)={(1.90,1.23,1.56)}^T,y_3\left(s\right)={(1.67,1.12,1.89)}^T,\hfill \\ \hfill & y_4\left(s\right)={(1.45,1.78,1.23)}^T,y_5\left(s\right)={(1.12,1.56,1.90)}^T,y_6\left(s\right)={(1.78,1.34,1.67)}^T,\hfill \\ \hfill & y_7\left(s\right)={(1.56,1.89,1.23)}^T,y_8\left(s\right)={(1.12,1.67,1.45)}^T,y_9\left(s\right)={(1.78,1.01,1.56)}^T,\hfill \\ \hfill & y_{10}\left(s\right)={(1.56,1.89,1.78)}^T,s\in [-0.1,0].\hfill \end{array}$$

The numerical simulation results shown in Figure 1 and Markovian switching simulation in Figure 2.

Here, Figure 1a represents the state errors of the first component of the MSSDCDNs nodes, Figure 1b represents the state errors of the second component of the nodes, and Figure 1c represents the state errors of the third component of the nodes. From the three-dimensional state errors trajectory of the nodes in Figure 1, Under the control strategy, the state errors tends to zero, indicating that synchronization is achieved.

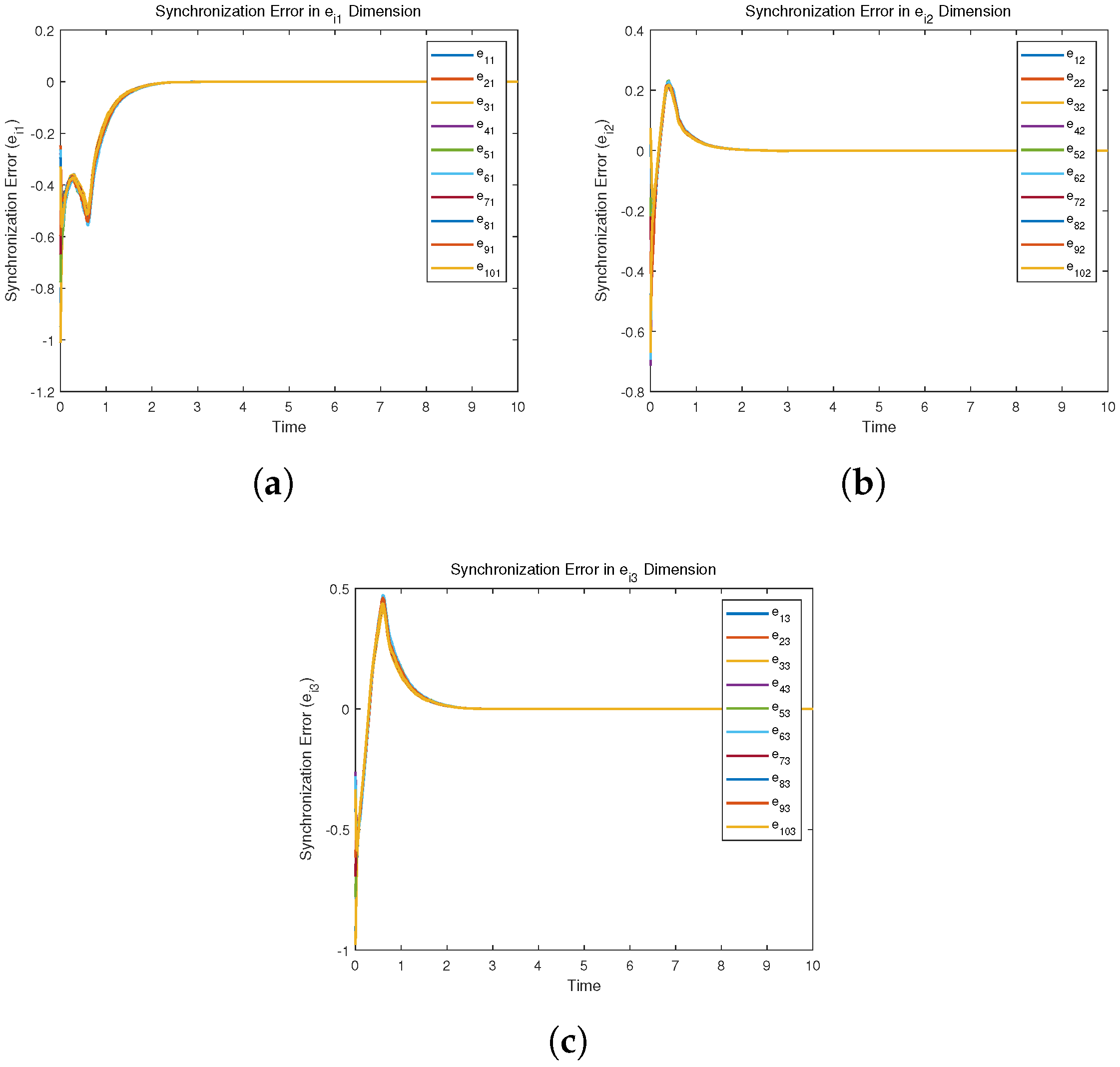
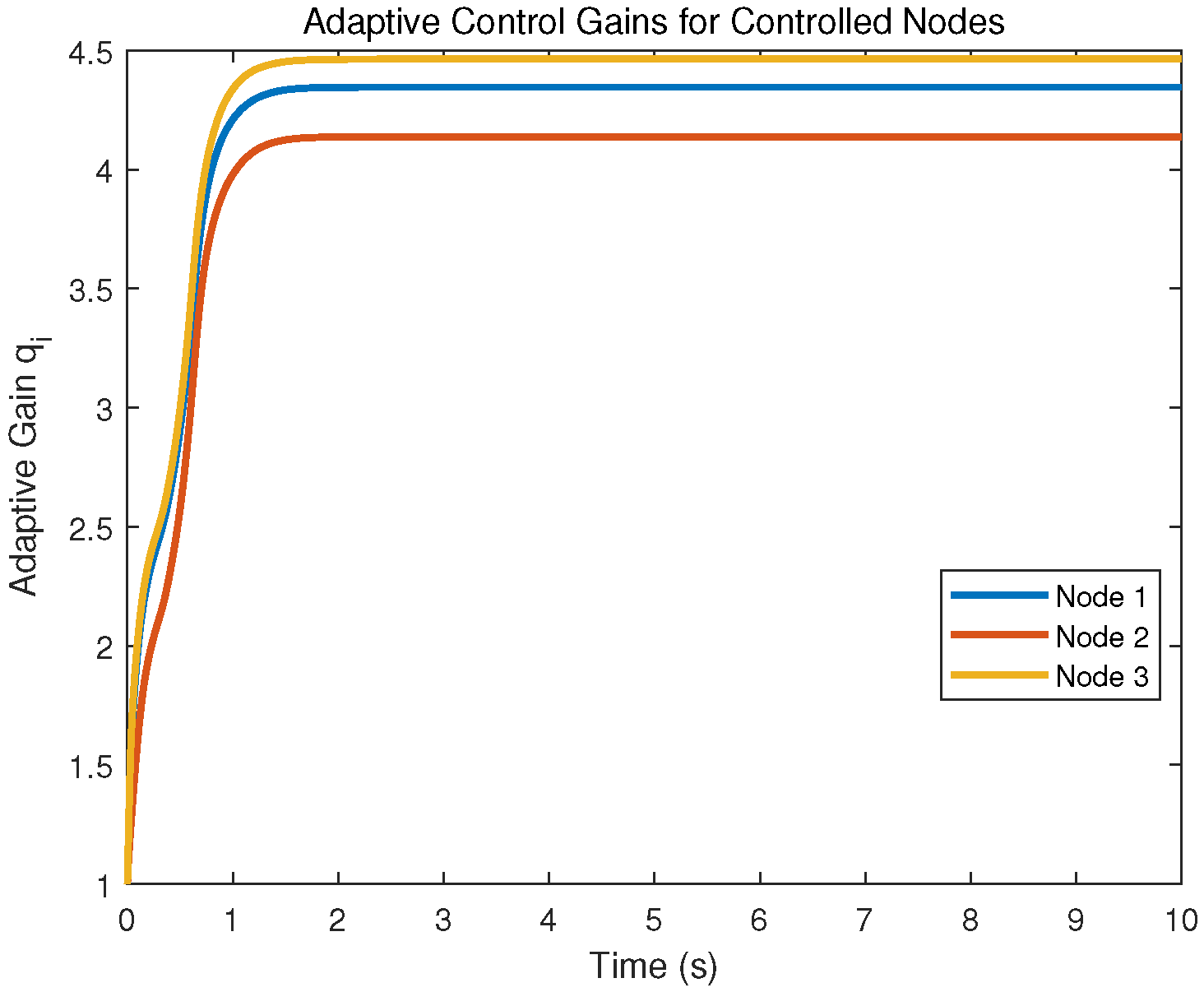
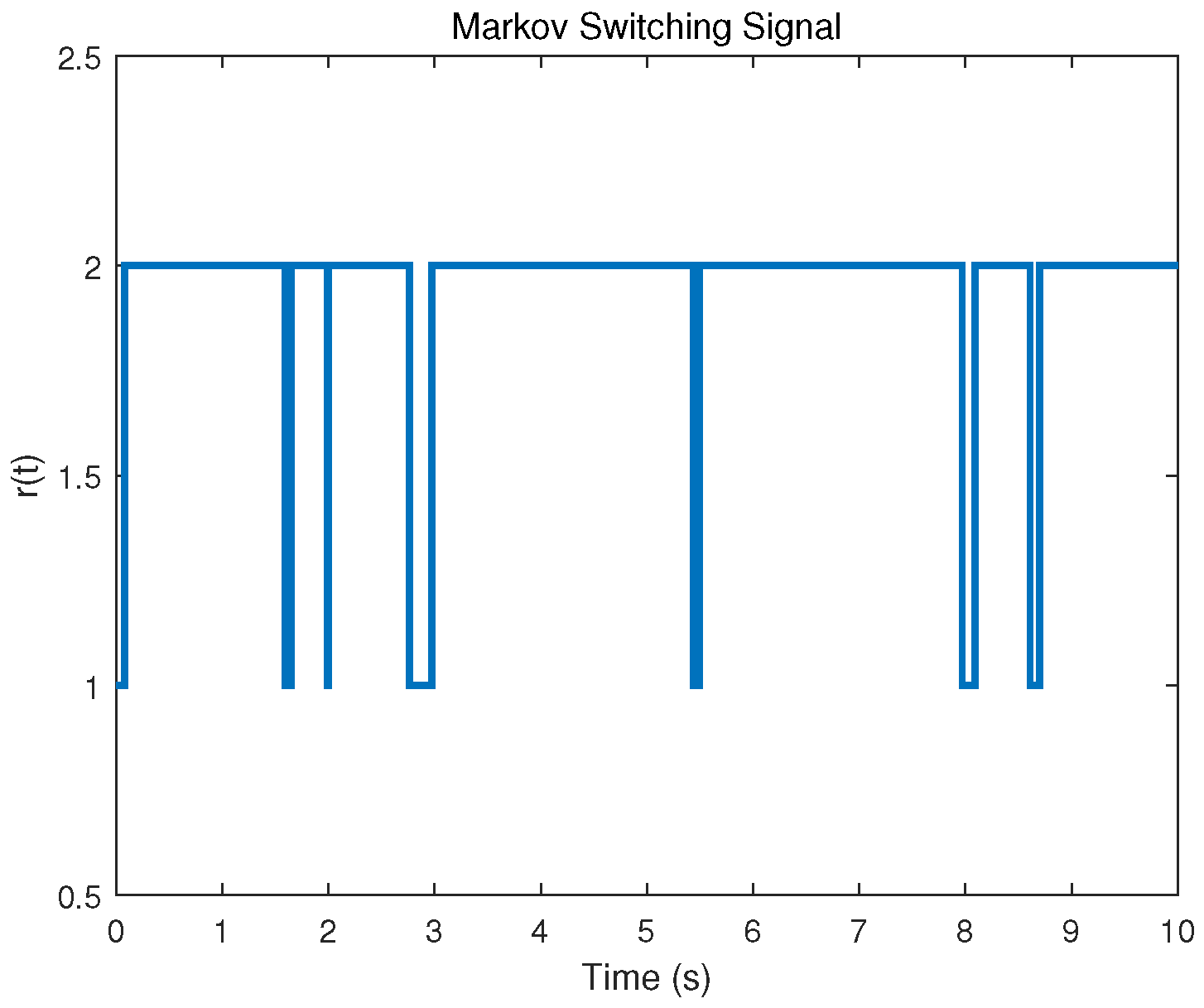
4.2. Synchronization of SDCDNs via Adaptive Pinning Control

Furthermore, we choose the adaptive pinning control Strategy (28) in Theorem 2. Furthermore, in order to better compare with the results of Theorem 1, for the MSSDCDNs (4), we choose the same parameters and initial values as the above example. Similarly, we also choose the first four nodes to control and the gain constant $a_i=0.1$, $d_i\left(t\right)=0$, $i=1,2,3,4,t\in [-0.1,0]$. We can get the synchronization error image of the MSSDCDNs (4) with adaptive pinning control in Figure 3.

From the state error trajectories of the three nodes in Figure 3, it can be seen that under the adaptive pinning control strategy, the error tends to zero indicating that synchronization is achieved and Figure 4 is the control gains change image; Figure 5 shows the Markovian switching simulation.

5. Conclusions

The synchronization issue of a class of MSSDCDNs is examined in this study. Aiming to address practical factors, such as Markovian switching, uncertain disturbance, and communication delay in the system, a network model closer to reality is constructed. On this basis, two kinds of pinning control strategies are designed: one is fixed gain pinning control strategy, and the other is adaptive gain pinning control strategy. In order to guarantee that the network reaches exponential synchronization in the mean square sense, adequate requirements are derived by building a multistate Lyapunov function using the Itô formula and inequality techniques. The simulation results show that under the two control strategies, the designed controller can effectively drive the network state to be synchronized, which proves the theoretical correctness and engineering feasibility of the proposed method. However, there are still some shortcomings in this paper. For example, in practice, the network may face more complex delays and more random perturbations, such as impulse perturbations, levy noise, etc. In the future, we intend to study the scenario of facing these factors at the same time.