Inequalities Including Fractional Integral Operators of General Riemann–Liouville for an Abstract Convex Function and Their Applications
Abstract
1. Introduction
2. Preliminaries
2.1. Fractional Integral Types
2.2. –Convexity
2.3. Hermite–Hadamard Inequalities for –Convex Functions
| 1 | 2 | 1.21895 | 1.32843 |
| 1 | 3 | 1.39872 | 1.59808 |
| 2 | 3 | 1.57848 | 1.66062 |
| 2 | 4 | 1.72386 | 1.87868 |
| 1 | 4 | 1.55556 | 1.83333 |
| 1 | 2 | 0.88622 | 0.97412 |
| 1 | 3 | 2.82435 | 3.28512 |
| 2 | 3 | 1.16367 | 1.22877 |
| 2 | 4 | 3.54491 | 3.89651 |
| 1 | 4 | 5.70375 | 6.89725 |
| 1 | 2 | 0.948196 | 1.03062 |
| 1 | 3 | 3.1316 | 3.5473 |
| 2 | 3 | 1.2114 | 1.27412 |
| 2 | 4 | 3.79278 | 4.12248 |
| 1 | 4 | 6.46893 | 7.51674 |
3. Hermite–Hadamard Type Inequalities Involving Generalized Riemann–Liouville Fractional Integral Operators
4. Inequalities Involving Different Types of the Fractional Integral Operators
| 1 | 2 | 1.5 | 1.63242 |
| 1 | 3 | 4 | 4.54714 |
| 2 | 3 | 2.5 | 2.62931 |
| 2 | 4 | 6 | 6.52969 |
| 1 | 4 | 7.5 | 8.75817 |
| 1 | 2 | 1.48645 | 1.62742 |
| 1 | 3 | 12.9618 | 15.1384 |
| 2 | 3 | 1.9982 | 2.09967 |
| 2 | 4 | 16.8173 | 18.4121 |
| 1 | 4 | 55.1634 | 57.6667 |
| 1 | 2 | 1.76097 | 1.86193 |
| 1 | 3 | 16.81 | 18.3444 |
| 2 | 3 | 2.20966 | 2.27913 |
| 2 | 4 | 19.9231 | 21.1438 |
| 1 | 4 | 64.6095 | 71.6667 |

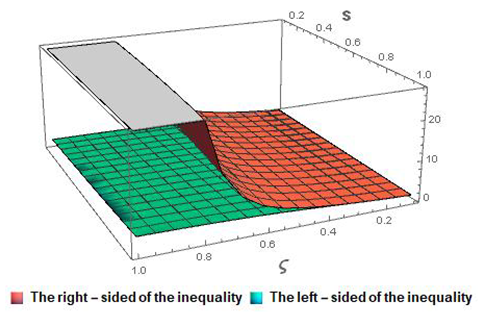
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Katugampola Udita, N. A New Approach to Generalized Fractional Derivatives. Bull. Math. Anal. Appl. 2014, 6, 1–15. [Google Scholar]
- Sarikaya, M.Z.; Yildirim, H. On generalization of the Riesz potential. Indian J. Math. Math. Sci. 2007, 3, 231–235. [Google Scholar]
- Budak, H.; Kara, H.; Hezenci, F.; Sarıkaya, M.Z. New parameterized inequalities for twice differentiable functions. Filomat 2023, 37, 3737–3753. [Google Scholar] [CrossRef]
- Sarikaya, M.Z.; Ertugral, F. On the generalized Hermite–Hadamard inequalities. Ann. Univ. Craiova–Math. Comput. Sci. Ser. 2020, 47, 193–213. [Google Scholar]
- Soontharanon, J.; Ali, M.A.; Budak, H.; Kosem, P.; Nonlaopon, K.; Sitthiwirattham, T. Some new generalized fractional Newton’s type inequalities for convex functions. J. Funct. Spaces 2022, 1, 6261970. [Google Scholar] [CrossRef]
- Yildirim, H. On generalization of the quasi homogeneous Riesz potential. Turk. J. Math. 2005, 29, 381–387. [Google Scholar]
- Yildiz, C.; Rahman, G.; Cotirla, L.I. On Further Inequalities for Convex Functions via Generalized Weighted–Type Fractional Operators. Fractal Fract. 2023, 7, 513. [Google Scholar] [CrossRef]
- Valdés, J.E.N.; Rabossi, F.; Samaniego, A.D. Convex functions: Ariadne’s thread or Charlotte’s Spiderweb? Adv. Math. Models Appl. 2020, 5, 176–191. [Google Scholar]
- Adilov, G.; Rubinov, A.M. –convex sets and functions. Numer. Funct. Anal. Optim. 2006, 27, 237–257. [Google Scholar] [CrossRef]
- Eken, Z.; Sezer, S.; Tinaztepe, G.; Adilov, G. s–Convex functions in the fourth sense and some of their properties. Konuralp J. Math. 2021, 9, 260–267. [Google Scholar]
- Kemali, S.; Sezer, S.; Tinaztepe, G.; Adilov, G. s–convex functions in the third sense. Korean J. Math. 2021, 29, 593–602. [Google Scholar] [CrossRef]
- Liu, Z. A note on Ostrowski type inequalities related to some s–convex functions in the second sense. Bull. Korean Math. Soc. 2012, 49, 775–785. [Google Scholar] [CrossRef]
- Sezer, S.; Eken, Z.; Tinaztepe, G.; Adilov, G. p–Convex functions and some of their properties. Numer. Funct. Anal. Optim. 2021, 42, 443–459. [Google Scholar] [CrossRef]
- Adilov, G.; Yesilce, I. –convex Functions. J. Convex Anal. 2017, 24, 505–517. [Google Scholar]
- Adilov, G.; Yesilce, I. –convex Sets and –measurable Maps. Numer. Funct. Anal. Optim. 2017, 33, 131–141. [Google Scholar] [CrossRef]
- Adilov, G.; Yesilce, I. On Generalization of the Concept of Convexity. Hacet. J. Math. Stat. 2017, 41, 723–730. [Google Scholar]
- Briec, W.; Liang, Q.B. On Some Semilattice Structures for Production Technologies. Eur. J. Oper. Res. 2011, 215, 740–749. [Google Scholar] [CrossRef]
- Kemali, S.; Yesilce, I.; Adilov, G. –convexity, –convexity, and Their Comparison. Numer. Funct. Anal. Optim. 2015, 36, 133–146. [Google Scholar] [CrossRef]
- Tinaztepe, G.; Yesilce, I.; Adilov, G. Separation of –convex Sets by –measurable Maps. J. Convex Anal. 2014, 21, 571–580. [Google Scholar]
- Dragomir, S.S.; Pearce, C.E.M. Selected Topics on Hermite–Hadamard Inequalities and Applications; RGMIA Monographs: Melbourne, Australia, 2000. [Google Scholar]
- Eken, Z.; Sezer, S. The Popoviciu Type Inequalities For s–Convex Functions in the Third Sense. Math. Inequalities Appl. 2023, 26, 769–782. [Google Scholar] [CrossRef]
- Tinaztepe, G.; Sezer, S.; Eken, Z.; Evcan, S.S. The Ostrowski inequality for s–convex functions in the third sense. AIMS Math. 2022, 7, 5605–5615. [Google Scholar] [CrossRef]
- Hadamard, J. Etude sur les proprietes des fonctions entieres et en particulier d’une fonction consideree par Riemann. J. Des Math. Pures Appl. 1893, 58, 171–215. [Google Scholar]
- Hermite, C. Sur deux limites d’une integrale define. Mathesis 1883, 3, 82. [Google Scholar]
- Niculescu, C.P.; Persson, L.-E. Old and New on the Hermite–Hadamard Inequality. Real Anal. Exch. 2003, 29, 663–685. [Google Scholar] [CrossRef]
- Yesilce, I. Inequalities for B–convex functions via generalized fractional integral. J. Inequalities Appl. 2019, 1, 194. [Google Scholar] [CrossRef]
- Eken, Z.; Kemali, S.; Tinaztepe, G.; Adilov, G. The Hermite–Hadamard inequalities for p–convex functions. Hacet. J. Math. Stat. 2021, 50, 1268–1279. [Google Scholar] [CrossRef]
- Yesilce, I.; Adilov, G. Hermite–Hadamard Inequalities for –convex and –convex Functions. Int. J. Nonlinear Anal. Appl. 2017, 8, 225–233. [Google Scholar] [CrossRef]
- Dahmani, Z. On Minkowski and Hermite–Hadamard Integral Inequalities via Fractional Integration. Ann. Funct. Anal. 2010, 1, 51–58. [Google Scholar] [CrossRef]
- Sarikaya, M.Z.; Set, E.; Yaldiz, H.; Basak, N. Hermite–Hadamard’s Inequalities for Fractional Integrals and Related Fractional Inequalities. Math. Comput. Model. 2013, 57, 2403–2407. [Google Scholar] [CrossRef]
- Yesilce, I.; Adilov, G. Hermite–Hadamard type inequalities for –convex functions involving generalized fractional integral operators. Filomat 2018, 32, 6457–6464. [Google Scholar] [CrossRef]
- Yesilce, I. Some Inequalities for –convex Functions via Fractional Integral Operator. TWMS J. Appl. Eng. Math. 2019, 9, 620–625. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables; Courier Corporation: San Francisco, CA, USA, 1965. [Google Scholar]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, 2nd ed.; John Wiley and Sons: Hoboken, NJ, USA, 1994. [Google Scholar]
- Press, W.H.; William, H.; Teukolsky, S.A.; Saul, A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Arfken, G.B.; Weber, H.J. Mathematical Methods for Physicists, 6th ed.; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Kilbas, A.A.; Marichev, O.I.; Samko, S.G. Fractional Integrals and Derivatives. Theory and Applications; Gordon and Breach: Newark, NY, USA, 1993. [Google Scholar]
- Romero, L.G.; Luque, L.L.; Dorrego, G.A.; Cerutti, R.A. On the k–Riemann–Liouville fractional derivative. Int. J. Contemp. Math. Sci. 2013, 8, 41–51. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Ahmad, B.; Alsaedi, A.; Kirane, M.; Torebek, B.T. Hermite–Hadamard, Hermite–Hadamard–Fejér, Dragomir–Agarwal and Pachpatte type inequalities for convex functions via new fractional integrals. J. Comput. Appl. Math. 2019, 353, 120–129. [Google Scholar] [CrossRef]
- Valdés, J.E.N. Some integral inequalities in the framework of generalized k–proportional fractional integral operators with general kernel. Honam Math. J. 2021, 43, 587–596. [Google Scholar] [CrossRef]
- Liu, F.; Li, J. Analytical Properties and Hermite–Hadamard Type Inequalities Derived from Multiplicative Generalized Proportionalσ–Riemann–Liouville Fractional Integrals. Symmetry 2025, 17, 702. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yesilce Isik, I. Inequalities Including Fractional Integral Operators of General Riemann–Liouville for an Abstract Convex Function and Their Applications. Axioms 2025, 14, 816. https://doi.org/10.3390/axioms14110816
Yesilce Isik I. Inequalities Including Fractional Integral Operators of General Riemann–Liouville for an Abstract Convex Function and Their Applications. Axioms. 2025; 14(11):816. https://doi.org/10.3390/axioms14110816
Chicago/Turabian StyleYesilce Isik, Ilknur. 2025. "Inequalities Including Fractional Integral Operators of General Riemann–Liouville for an Abstract Convex Function and Their Applications" Axioms 14, no. 11: 816. https://doi.org/10.3390/axioms14110816
APA StyleYesilce Isik, I. (2025). Inequalities Including Fractional Integral Operators of General Riemann–Liouville for an Abstract Convex Function and Their Applications. Axioms, 14(11), 816. https://doi.org/10.3390/axioms14110816





