Inequalities Including Fractional Integral Operators of General Riemann–Liouville for an Abstract Convex Function and Their Applications

Abstract

An abstract convexity type is ${\mathbb{B}}^{-1}$–convexity. For ${\mathbb{B}}^{-1}$–convex functions, the Hermite–Hadamard inequality was previously found. Recently, however, new and more popular types of fractional integral operators have been developed. This paper’s goal is to demonstrate the Hermite–Hadamard inequality using additional, more general kinds of fractional integral operators. The generalization of the results are proven with the additional theorems. It is shown that the old fractional Hermite–Hadamard inequalities for ${\mathbb{B}}^{-1}$–convex functions can be obtained from the new inequalities given in this paper. Additionally, applications for each results are presented with tables and graphs. The inequalities for incomplete gamma function are proved and presented with graphs.

1. Introduction

Fractional calculus has a long history and has recently attracted renewed attention due to applications in engineering and applied sciences [1]. Various and more general fractional operators have been defined. Furthermore, it is used in electrical transmission, networks, numerical calculations, quantum theory, physics, wave phenomena, etc. One of the main fractional integral operators is known as Riemann–Liouville fractional operator. Afterwards, some new fractional operators are developed and some of the operators are generalized. Generally, the definition of fractional integrals is determined by the field of application. There are generalized Riemann–Liouville fractional integral operators related to Riesz potential studied in [2]. This is mentioned in numerous articles [3,4,5,6]. Also, it is modified by putting a weight function in the kernel of the integral [7]. The generalization of the operator is achieved from its definition. In this paper, this fractional integral operator is used to generalize the inequalities.

Convexity is a fascinating field in mathematics in recent times. It has a wide range of applications such that inequalities, optimal and economic problems [8]. In this way, it is generalized to different abstract convexity types, with p–convexity, s–convexities in first, second, third and fourth types, and $\mathbb{B}$–convexity and ${\mathbb{B}}^{-1}$–convexity being some of the abstract convexity types [9,10,11,12,13]. In this paper, ${\mathbb{B}}^{-1}$–convex functions are studied [14,15,16,17,18,19].

Inequalities are used in mathematics and various fields of science. They provide boundaries for the value of the functions and related problems. Convexity is used in a huge number of inequalities [20,21,22]. Hermite–Hadamard inequality is the most popular one [20,23,24,25,26]. It is about some kinds of means of the convex functions. It is studied by numerous scientists for convex functions [4,25,27,28]. Additionally, it is applied for enormously abstract convex functions [29,30]. For ${\mathbb{B}}^{-1}$–convex functions, Hermite–Hadamard inequalities were proved in [28]. The miscellaneous fractional types of the inequality are worked in [31,32]. In this article, the most general one is achieved.

Convexity has numerous applications via inequalities. In this paper, the inequalities provide some useful evaluations for the incomplete gamma functions. The incomplete gamma function constitutes a fundamental mathematical tool in the analysis of statistical distributions and various applied domains. It is prominently utilized in the evaluation of cumulative distribution functions (CDFs) of the gamma and chi-square distributions, wherein it serves as a core analytical component [33,34]. Moreover, it arises naturally in the context of Poisson processes, particularly in the computation of tail probabilities. From a numerical analysis perspective, the function is extensively employed to derive analytical approximations for integrals that lack closed-form solutions [35]. In machine learning and Bayesian inference, the incomplete gamma function plays a crucial role in the normalization of gamma prior distributions and in probabilistic computations involving marginal likelihoods [36]. Beyond statistics, it finds broad applicability in physics and engineering—especially in quantum mechanics, statistical thermodynamics, and signal processing—where it is instrumental in the generalization of special functions and the analytical treatment of integral expressions [37].

In this paper, the fractional integral operators are introduced firstly. ${\mathbb{B}}^{-1}$–convex is reminded, then the old inequalities for ${\mathbb{B}}^{-1}$–convex functions are exhibited, followed by an illustration of the ${\mathbb{B}}^{-1}$–convex function and the function’s applications for the previous inequalities with tables. The Hermite–Hadamard inequalities are proved using generalized Riemann–Liouville fractional operators in Section 3. In Section 4, specific inequalities are illustrated using different fractional operators, and tables and graphs are included to illustrate each result. Some inequalities for incomplete gamma function are demonstrated and shown using graphs.

2. Preliminaries

In this section, some required definition and theorems are given. The section is divided into three subsections. In first one, definitions and relations of fractional operators are expressed. Then, the definitions of ${\mathbb{B}}^{-1}$–convex set and function are introduced. The Hermite–Hadamard inequalities for ${\mathbb{B}}^{-1}$–convex functions via different integrals are represented in the third subsection.

2.1. Fractional Integral Types

When the fractional integral inequalities of Hermite–Hadamard type for ${\mathbb{B}}^{-1}$–convex functions are represented, some kind of fractional integrals which are defined as follows are used. To provide the most general fractional operator used in this article, we first need to define the following function.

Let us define a function $\kappa :\left[0,\infty \right)\to \left[0,\infty \right)$ satisfying the following conditions:

$$\begin{array}{c}\hfill \kappa \left(0\right)=0\end{array}$$

(1)

$$\begin{array}{c}\hfill {\int }_0^1{\displaystyle \frac{\kappa \left(\vartheta \right)}{\vartheta }}d\vartheta <\infty \end{array}$$

(2)

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{A_1}}\le {\displaystyle \frac{\kappa \left(s\right)}{\kappa \left(r\right)}}\le A_{2}for{\displaystyle \frac{1}{2}}\le {\displaystyle \frac{s}{r}}\le 2\end{array}$$

(3)

$$\begin{array}{c}\hfill {\displaystyle \frac{\kappa \left(r\right)}{r^2}}\le A_2{\displaystyle \frac{\kappa \left(s\right)}{s^2}}fors\le r\end{array}$$

(4)

$$\begin{array}{c}\hfill \left|{\displaystyle \frac{\kappa \left(r\right)}{r^2}}-{\displaystyle \frac{\kappa \left(s\right)}{s^2}}\right|\le A_3\left|r-s\right|{\displaystyle \frac{\kappa \left(r\right)}{r^2}}for{\displaystyle \frac{1}{2}}\le {\displaystyle \frac{s}{r}}\le 2\end{array}$$

(5)

where $A_1,A_2,A_3>0$ are independent of $r,s>0$. See [2]. In [6], it is called the generalization of the quasi-homogeneous Riesz potential. One can consult [4] for further information of function $\kappa$.

Let $f:\left[\rho ,\sigma \right]\to \mathbb{R}$ be a given function, where $0\le \rho <\sigma <+\infty$ and $f\in L_1\left[\rho ,\sigma \right]$ through the subsection. Also, $\mathsf{\Gamma }\left(\varsigma \right)$ is the Gamma function.

Definition 1 

([7]). The left-sided generalized Riemann–Liouville fractional integral of f is defined by

$${}_{{\rho }^{+}}I_{\kappa }f\left(\varpi \right)={\int }_{\rho }^{\varpi }{\displaystyle \frac{\kappa \left(\varpi -\vartheta \right)}{\varpi -\vartheta }}f\left(\vartheta \right)d\vartheta ,\varpi >\rho$$

(6)

provided that the integral exists. The right-sided generalized Riemann–Liouville fractional integral of f is defined by

$${}_{{\sigma }^{-}}I_{\kappa }f\left(\varpi \right)={\int }_{\varpi }^{\sigma }{\displaystyle \frac{\kappa \left(\vartheta -\varpi \right)}{\vartheta -\varpi }}f\left(\vartheta \right)d\vartheta ,\varpi <\sigma$$

(7)

provided that the integral exists.

These generalized Riemann–Liouville fractional integral operators include various kinds of the fractional operators as follows.

– If $\kappa \left(\vartheta \right)=\vartheta$ is taken, then the operators (6) and (7) reduce to the Riemann integral.

– If $\kappa \left(\vartheta \right)={\displaystyle \frac{{\vartheta }^{\varsigma }}{\mathsf{\Gamma }\left(\varsigma \right)}}$ is taken, the operators (6) and (7) reduce to the Riemann–Liouville fractional integral.

Definition 2 

([38]). The left-sided Riemann–Liouville integral $J_{{\rho }^{+}}^{\varsigma }f$ and the right-sided Riemann–Liouville integral $J_{{\sigma }^{-}}^{\varsigma }f$ of order $\varsigma >0$ are defined by

$$J_{{\rho }^{+}}^{\varsigma }f\left(\varpi \right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\varsigma \right)}}{\int }_{\rho }^{\varpi }{\left(\varpi -\vartheta \right)}^{\varsigma -1}f\left(\vartheta \right)d\vartheta ,\varpi >\rho$$

(8)

and

$$J_{{\sigma }^{-}}^{\varsigma }f\left(\varpi \right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\varsigma \right)}}{\int }_{\varpi }^{\sigma }{\left(\vartheta -\varpi \right)}^{\varsigma -1}f\left(\vartheta \right)d\vartheta ,\varpi <\sigma$$

(9)

respectively.

– If $\kappa \left(\vartheta \right)={\displaystyle \frac{1}{k{\mathsf{\Gamma }}_k\left(\varsigma \right)}}{\vartheta }^{{\displaystyle \frac{\varsigma }{k}}}$ is taken, the operators (6) and (7) reduce to the k–Riemann–Liouville fractional integral which is the special form of the Riemann–Liouville fractional operator.

Definition 3 

([39]). The left-sided k–Riemann–Liouville integral $J_{{\rho }^{+},k}^{\varsigma }f$ and the right-sided k–Riemann–Liouville integral $J_{{\sigma }^{-},k}^{\varsigma }f$ of order $\varsigma >0$ are defined by

$$J_{{\rho }^{+},k}^{\varsigma }f\left(\varpi \right)={\displaystyle \frac{1}{k{\mathsf{\Gamma }}_k\left(\varsigma \right)}}{\int }_{\rho }^{\varpi }{\left(\varpi -\vartheta \right)}^{{\displaystyle \frac{\varsigma }{k}}-1}f\left(\vartheta \right)d\vartheta ,\varpi >\rho$$

(10)

and

$$J_{{\sigma }^{-},k}^{\varsigma }f\left(\varpi \right)={\displaystyle \frac{1}{k{\mathsf{\Gamma }}_k\left(\varsigma \right)}}{\int }_{\varpi }^{\sigma }{\left(\vartheta -\varpi \right)}^{{\displaystyle \frac{\varsigma }{k}}-1}f\left(\vartheta \right)d\vartheta ,\varpi <\sigma$$

(11)

respectively. Here,

$${\mathsf{\Gamma }}_k\left(\varsigma \right)={\int }_0^{\infty }{\vartheta }^{\varsigma -1}{e}^{-{\displaystyle \frac{{\vartheta }^k}{k}}}d\vartheta$$

is k–gamma function.

– If $\kappa \left(\vartheta \right)=\vartheta {\left(\varpi -\vartheta \right)}^{\varsigma -1}$ is taken, the operators (6) reduce to the conformable operator.

Definition 4 

([40]). The conformable operator $J_{\rho }^{\varsigma }f$ of order $\varsigma \in \left(0,1\right)$ is defined by

$$J_{\rho }^{\varsigma }f\left(\varpi \right)={\int }_{\rho }^{\varpi }{\vartheta }^{\varsigma -1}f\left(\vartheta \right)d\vartheta ,\varpi >\rho$$

(12)

– If

$$\kappa \left(\vartheta \right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\varsigma \right)}}{\displaystyle \frac{{\left[\left(log\varpi -log\left(\varpi -\vartheta \right)\right)\right]}^{\varsigma -1}}{\varpi -\vartheta }}$$

and

$$\kappa \left(\vartheta \right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\varsigma \right)}}\vartheta {\displaystyle \frac{{\left[\left(log\left(\vartheta -\varpi \right)-log\varpi \right)\right]}^{\varsigma -1}}{\vartheta -\varpi }}$$

are taken, the operators (6) and (7) reduce to the right-sided and left-sided Hadamard fractional integrals.

Definition 5 

([38]). The left-sided Hadamard fractional integral $J_{{\rho }^{+}}^{\varsigma }$ of order $\varsigma >0$ of f is defined by

$$J_{{\rho }^{+}}^{\varsigma }f\left(\varpi \right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\varsigma \right)}}{\int }_{\rho }^{\varpi }{\left(ln{\displaystyle \frac{\varpi }{\vartheta }}\right)}^{\varsigma -1}{\displaystyle \frac{f\left(\vartheta \right)}{\vartheta }}d\vartheta ,\varpi >\rho$$

(13)

provided that the integral exists. The right-sided Hadamard fractional integral $J_{{\sigma }^{-}}^{\varsigma }$ of order $\varsigma >0$ of f is defined by

$$J_{{\sigma }^{-}}^{\varsigma }f\left(\varpi \right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\varsigma \right)}}{\int }_{\varpi }^{\sigma }{\left(ln{\displaystyle \frac{\vartheta }{\varpi }}\right)}^{\varsigma -1}{\displaystyle \frac{f\left(\vartheta \right)}{\vartheta }}d\vartheta ,\varpi <\sigma$$

(14)

provided that the integral exists.

– If $\kappa \left(\vartheta \right)={\displaystyle \frac{\vartheta }{\varsigma }}exp\left(-{\displaystyle \frac{1-\varsigma }{\varsigma }}\vartheta \right)$ is taken, the operators (6) and (7) reduce to the right-sided and left-sided fractional integral operators with exponential kernel.

Definition 6 

([41]). The left-sided integral operators with exponential kernel $I_{{\rho }^{+}}^{\varsigma }f$ and the right-sided integral operators with exponential kernel $I_{{\sigma }^{-}}^{\varsigma }f$ of order $\varsigma \in \left(0,1\right)$ are defined by

$$I_{{\rho }^{+}}^{\varsigma }f\left(\varpi \right)={\displaystyle \frac{1}{\varsigma }}{\int }_{\rho }^{\varpi }exp\left(-{\displaystyle \frac{1-\varsigma }{\varsigma }}\left(\varpi -\vartheta \right)\right)f\left(\vartheta \right)d\vartheta ,\varpi >\rho$$

(15)

and

$$I_{{\sigma }^{-}}^{\varsigma }f\left(\varpi \right)={\displaystyle \frac{1}{\varsigma }}{\int }_{\varpi }^{\sigma }exp\left(-{\displaystyle \frac{1-\varsigma }{\varsigma }}\left(\vartheta -\varpi \right)\right)f\left(\vartheta \right)d\vartheta ,\varpi <\sigma$$

(16)

respectively.

2.2. ${\mathbb{B}}^{-1}$–Convexity

For $r\in {\mathbb{Z}}^{-}$, where ${\mathbb{Z}}^{-}=\left\{a\left|a\in \mathbb{Z},a<0\right.\right\}$, the map $\varpi \to {\theta }_r\left(\varpi \right)={\varpi }^{2r+1}$ is a homeomorphism from ${\mathbb{R}}_{*}=\mathbb{R}\setminus \left\{0\right\}$ to itself; $\varpi =({\varpi }_1,{\varpi }_2,\dots ,{\varpi }_n)\to {\mathsf{\Theta }}_r\left(\varpi \right)=({\theta }_r\left({\varpi }_1\right),{\theta }_r\left({\varpi }_2\right),\dots ,{\theta }_r\left({\varpi }_n\right))$ is a homeomorphism from ${\mathbb{R}}_{*}^n$ to itself.

Definition 7 

([15]). A subset U of ${\mathbb{R}}_{*}^n$ is ${\mathbb{B}}^{-1}$–convex if for all finite subset $A\subset U$ the ${\mathbb{B}}^{-1}$–polytope $C{o}^{-\infty }\left(A\right)={lim}_{r\to -\infty }C{o}^r\left(A\right)={lim}_{r\to -\infty }\left\{{\mathsf{\Theta }}_r^{-1}\left({\displaystyle \sum _{i=1}^m}{t}_i{\mathsf{\Theta }}_r\left({\varpi }_i\right)\right):{\varpi }_i\in A,t_i\ge 0,{\displaystyle \sum _{i=1}^m}{t}_i=1\right\}$ is contained in U.

Here, the limit of the set is the upper limit of the sequence of sets in the Painleve–Kuratowski sense.

In ${\mathbb{R}}_{++}^n$, the following theorem for ${\mathbb{B}}^{-1}$–convex sets can be given [15].

Theorem 1. 

A subset U of ${\mathbb{R}}_{++}^n$ is ${\mathbb{B}}^{-1}$–convex if and only if for all $\varpi ,y\in U$ and all $\lambda \in \left[1,\infty \right)$ one has $\lambda \varpi \wedge y\in U$.

We denote by ${\wedge }_{i=1}^m{x}^{\left(i\right)}$ the greatest lower bound with respect to the coordinate-wise order relation of $x^{\left(1\right)},x^{\left(2\right)},\dots ,x^{\left(m\right)}\in {\mathbb{R}}_{++}^n$, that is

$${\wedge }_{i=1}^m{x}^{\left(i\right)}=\left(min\left\{x_1^{\left(1\right)},x_1^{\left(2\right)},\dots ,x_1^{\left(m\right)}\right\},\dots ,min\left\{x_n^{\left(1\right)},x_n^{\left(2\right)},\dots ,x_n^{\left(m\right)}\right\}\right)$$

where $x_j^{\left(i\right)}$ denotes jth coordinate of the point $x^{\left(i\right)}$.

Remark 1. 

From Theorem 1, ${\mathbb{B}}^{-1}$–convex sets in $\left(0,+\infty \right)$ are positive intervals.

Definition 8 

([18]). A function $f:U\subset {\mathbb{R}}_{*}^n\to {\mathbb{R}}_{*}$ is called a ${\mathbb{B}}^{-1}$–convex function if $ep{i}^{*}\left(f\right)=\left\{\left(\varpi ,\beta \right)\left|\varpi \in U,\beta \in {\mathbb{R}}_{*},\beta \ge f\left(\varpi \right)\right.\right\}$ is a ${\mathbb{B}}^{-1}$–convex set.

The following fundamental theorem which provides a sufficient and necessary condition for ${\mathbb{B}}^{-1}$–convex functions in ${\mathbb{R}}_{++}^n$ can be given [18].

Theorem 2. 

The function $f:U\subset {\mathbb{R}}_{++}^n\to \left(0,+\infty \right)$ is ${\mathbb{B}}^{-1}$–convex if and only if the set U is ${\mathbb{B}}^{-1}$–convex and one has the inequality

$$f\left(\lambda \varpi \wedge y\right)\le \lambda f\left(\varpi \right)\wedge f\left(y\right)$$

(17)

for all $\varpi ,y\in U$ and all $\lambda \in \left[1,+\infty \right)$.

Example 1. 

The function $f:\left[\rho ,\sigma \right]\subset \left(0,+\infty \right)\to \left(0,+\infty \right)$, $f\left(\varpi \right)={\varpi }^s$, $0<s<1$ is ${\mathbb{B}}^{-1}$–convex.

The function f holds the inequality (17). Indeed, if $\lambda \varpi \wedge y=\lambda \varpi$, then $f\left(\lambda \varpi \wedge y\right)=f\left(\lambda \varpi \right)={\left(\lambda \varpi \right)}^s\le \lambda {\varpi }^s$ is obtained. Since ${\left(\lambda \varpi \right)}^s\le y^s$, one has

$$f\left(\lambda \varpi \wedge y\right)={\left(\lambda \varpi \right)}^s\le \lambda {\varpi }^s\wedge y^s=\lambda f\left(\varpi \right)\wedge f\left(y\right).$$

On the other hand, if $\lambda \varpi \wedge y=y$, it is simple to demonstrate the validity of the inequality for the ${\mathbb{B}}^{-1}$–convex function.

The function $f\left(\varpi \right)={\varpi }^s$, $0<s<1$ in the example above is not a convex function; namely, the ${\mathbb{B}}^{-1}$–convexity also examines the class of non-convex functions. Additionally, the detailed analysis of the ${\mathbb{B}}^{-1}$–convex functions, with examples, was ascertainable in [14]. For example, $f:{\mathbb{R}}_{++}^n\to {\mathbb{R}}_{+}$ is the Cobb–Douglas function, namely $f\left(z_1,z_2,\dots ,z_n\right)={\prod }_{i=1}^n{z}_i^{s_i}$. For $s_i\ge 0\left(\forall i=1,2,\dots ,n\right)$ such that ${\sum }_{i=1}^n{s}_i\le 1$, the function f is ${\mathbb{B}}^{-1}$–convex.

2.3. Hermite–Hadamard Inequalities for ${\mathbb{B}}^{-1}$–Convex Functions

The following theorem that yields the Hermite–Hadamard inequality involving classic integral for ${\mathbb{B}}^{-1}$–convex functions is dedicated in [28]. Let $f:\left[\rho ,\sigma \right]\to \mathbb{R}$ be a given function, where $0<\rho <\sigma <+\infty$ and $f\in L_1\left[\rho ,\sigma \right]$ through the paper. Additionally, the “min” is used instead of “∧” when studying with the functions of one variable.

Theorem 3. 

Let $f:\left[\rho ,\sigma \right]\subset \left(0,+\infty \right)⟶\left(0,+\infty \right)$ be a ${\mathbb{B}}^{-1}$–convex function. Then, the inequality

$${\displaystyle \frac{1}{\sigma -\rho }}{\int }_{\rho }^{\sigma }f\left(\vartheta \right)d\vartheta \le \left\{\begin{array}{cc}{\displaystyle \frac{f\left(\rho \right)\left(\rho +\sigma \right)}{2\rho }},\hfill & {\displaystyle \frac{\sigma }{\rho }}\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}\hfill \\ {\displaystyle \frac{2\sigma f\left(\rho \right)f\left(\sigma \right)-\rho \left[{\left(f\left(\rho \right)\right)}^2+{\left(f\left(\sigma \right)\right)}^2\right]}{2\left(\sigma -\rho \right)f\left(\rho \right)}},\hfill & 1\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}<{\displaystyle \frac{\sigma }{\rho }}.\hfill \end{array}\right.$$

(18)

is valid.

Example 2. 

The inequality of Hermite–Hadamard for the ${\mathbb{B}}^{-1}$–convex function $f\left(\varpi \right)=\sqrt{\varpi }$ ($s={\displaystyle \frac{1}{2}}$ in example 1) can be calculated for different values of the variables. The table about the results is given as follows. The results show the availability of the inequality. Additionally, the right side of the inequality in the following table is ${\displaystyle \frac{2\sigma f\left(\rho \right)f\left(\sigma \right)-\rho \left[{\left(f\left(\rho \right)\right)}^2+{\left(f\left(\sigma \right)\right)}^2\right]}{2\left(\sigma -\rho \right)f\left(\rho \right)}}$, because of the $1\le {\displaystyle \frac{\sqrt{\sigma }}{\sqrt{\rho }}}<{\displaystyle \frac{\sigma }{\rho }}$.

$\rho$	$\sigma$	${\displaystyle \frac{1}{\sigma -\rho }}{\int }_{\rho }^{\sigma }f\left(\vartheta \right)d\vartheta$	${\displaystyle \frac{2\sigma f\left(\rho \right)f\left(\sigma \right)-\rho \left[{\left(f\left(\rho \right)\right)}^2+{\left(f\left(\sigma \right)\right)}^2\right]}{2\left(\sigma -\rho \right)f\left(\rho \right)}}$
1	2	1.21895	1.32843
1	3	1.39872	1.59808
2	3	1.57848	1.66062
2	4	1.72386	1.87868
1	4	1.55556	1.83333

The Riemann–Liouville fractional Hermite–Hadamard inequalities for ${\mathbb{B}}^{-1}$–convex functions which were given with the following theorems for left-sided integral and right-sided integral were proved in [32], respectively.

Theorem 4. 

Let $f:\left[\rho ,\sigma \right]\subset \left(0,+\infty \right)\to \left(0,+\infty \right)$ and $f\in L_1\left[\rho ,\sigma \right]$. If the function f is ${\mathbb{B}}^{-1}$–convex function on $\left[\rho ,\sigma \right]$, then the inequality

$$J_{{\rho }^{+}}^{\varsigma }f\left(\sigma \right)\le \left\{\begin{array}{cc}{\displaystyle \frac{f\left(\rho \right){\left(\sigma -\rho \right)}^{\varsigma }\left(\varsigma \rho +\sigma \right)}{\rho \mathsf{\Gamma }\left(\varsigma +2\right)}},\hfill & {\displaystyle \frac{\sigma }{\rho }}\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}\hfill \\ {\displaystyle \frac{{\left(f\left(\rho \right)\right)}^{\varsigma +1}{\left(\sigma -\rho \right)}^{\varsigma }\left(\varsigma \rho +\sigma \right)-{\left(\sigma f\left(\rho \right)-\rho f\left(\sigma \right)\right)}^{\varsigma +1}}{\rho {\left(f\left(\rho \right)\right)}^{\varsigma }\mathsf{\Gamma }\left(\varsigma +2\right)}},\hfill & 1\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}<{\displaystyle \frac{\sigma }{\rho }}\hfill \end{array}\right.$$

(19)

is valid. Here, $\varsigma >0$.

Example 3. 

The Hermite–Hadamard inequality including left-sided Riemann–Liouville fractional for the ${\mathbb{B}}^{-1}$–convex function $f\left(\varpi \right)=\sqrt{\varpi }$ is calculated for different values of the variables. The table about the results is given as follows. The results show the validity of the inequality. The right side of the inequality in the following table is the second equation, because of the $1\le {\displaystyle \frac{\sqrt{\sigma }}{\sqrt{\rho }}}<{\displaystyle \frac{\sigma }{\rho }}$. Here, $\varsigma ={\displaystyle \frac{3}{2}}$ is taken.

$\rho$	$\sigma$	$J_{{\rho }^{+}}^{\varsigma }f\left(\sigma \right)$	${\displaystyle \frac{{\left(f\left(\rho \right)\right)}^{\varsigma +1}{\left(\sigma -\rho \right)}^{\varsigma }\left(\varsigma \rho +\sigma \right)-{\left(\sigma f\left(\rho \right)-\rho f\left(\sigma \right)\right)}^{\varsigma +1}}{\rho {\left(f\left(\rho \right)\right)}^{\varsigma }\mathsf{\Gamma }\left(\varsigma +2\right)}}$
1	2	0.88622	0.97412
1	3	2.82435	3.28512
2	3	1.16367	1.22877
2	4	3.54491	3.89651
1	4	5.70375	6.89725

Theorem 5. 

Let $f:\left[\rho ,\sigma \right]\subset \left(0,+\infty \right)\to \left(0,+\infty \right)$ and $f\in L_1\left[\rho ,\sigma \right]$. If f is a ${\mathbb{B}}^{-1}$–convex function on $\left[\rho ,\sigma \right]$; then, the following inequality holds:

$$J_{{\sigma }^{-}}^{\varsigma }f\left(\rho \right)\le \left\{\begin{array}{cc}{\displaystyle \frac{f\left(\rho \right){\left(\sigma -\rho \right)}^{\varsigma }\left(\varsigma \sigma +\rho \right)}{\rho \mathsf{\Gamma }\left(\varsigma +2\right)}},\hfill & {\displaystyle \frac{\sigma }{\rho }}\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}\hfill \\ {\displaystyle \frac{\rho \left(\varsigma +1\right){\left(f\left(\rho \right)\right)}^{\varsigma }f\left(\sigma \right){\left(\sigma -\rho \right)}^{\varsigma }-{\left(\rho f\left(\sigma \right)-\rho f\left(\rho \right)\right)}^{\varsigma +1}}{\rho {\left(f\left(\rho \right)\right)}^{\varsigma }\mathsf{\Gamma }\left(\varsigma +2\right)}},\hfill & 1\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}<{\displaystyle \frac{\sigma }{\rho }}\hfill \end{array}\right.$$

(20)

with $\varsigma >0$.

Example 4. 

Under the same conditions of the Example 3, the Hermite–Hadamard inequality including right-sided Riemann–Liouville fractional for the ${\mathbb{B}}^{-1}$–convex function $f\left(\varpi \right)=\sqrt{\varpi }$ is given for some discrete values in the following table.

$\rho$	$\sigma$	$J_{{\sigma }^{-}}^{\varsigma }f\left(\rho \right)$	${\displaystyle \frac{\rho \left(\varsigma +1\right){\left(f\left(\rho \right)\right)}^{\varsigma }f\left(\sigma \right){\left(\sigma -\rho \right)}^{\varsigma }-{\left(\rho f\left(\sigma \right)-\rho f\left(\rho \right)\right)}^{\varsigma +1}}{\rho {\left(f\left(\rho \right)\right)}^{\varsigma }\mathsf{\Gamma }\left(\varsigma +2\right)}}$
1	2	0.948196	1.03062
1	3	3.1316	3.5473
2	3	1.2114	1.27412
2	4	3.79278	4.12248
1	4	6.46893	7.51674

3. Hermite–Hadamard Type Inequalities Involving Generalized Riemann–Liouville Fractional Integral Operators

In this section, the inequalities for ${\mathbb{B}}^{-1}$–convex functions are proved which are the most general inequalities ever. The generalizations of the inequalities are shown via the generalization of the fractional operators.

Theorem 6. 

Let $f:\left[\rho ,\sigma \right]\to \left(0,+\infty \right)$ be a ${\mathbb{B}}^{-1}$–convex function and $f\in L_1\left[\rho ,\sigma \right]$; then, the following fractional integral inequalities hold:

$${}_{{\rho }^{+}}I_{\kappa }f\left(\sigma \right)\le \left\{\begin{array}{cc}{\displaystyle \frac{f\left(\rho \right)}{\rho }}{\int }_{\rho }^{\sigma }{\displaystyle \frac{\kappa \left(\sigma -\vartheta \right)}{\sigma -\vartheta }}\vartheta d\vartheta ,\hfill & 1<{\displaystyle \frac{\sigma }{\rho }}\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}\hfill \\ {\displaystyle \frac{f\left(\rho \right)}{\rho }}{\int }_{\rho }^{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}{\displaystyle \frac{\kappa \left(\sigma -\vartheta \right)}{\sigma -\vartheta }}\vartheta d\vartheta +f\left(\sigma \right){\int }_{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}^{\sigma }{\displaystyle \frac{\kappa \left(\sigma -\vartheta \right)}{\sigma -\vartheta }}d\vartheta ,\hfill & 1\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}<{\displaystyle \frac{\sigma }{\rho }}.\hfill \end{array}\right.$$

(21)

Proof. 

The function f is a ${\mathbb{B}}^{-1}$–convex function; thus, the inequality (17) is valid for all $\lambda \in \left[1,+\infty \right)$ and $0<\rho <\sigma <+\infty$. Both sides of the (17) multiply with the coefficient ${\displaystyle \frac{\kappa \left(\sigma -min\left\{\lambda \rho ,\sigma \right\}\right)}{\sigma -\lambda \rho }}$, and since $\kappa \left(0\right)=0$ and the properties (1) of the $\kappa$, the following are valid. Firstly, the left-sided of the inequality is

$$\begin{array}{cc}\hfill {\int }_1^{+\infty }& {\displaystyle \frac{\kappa \left(\sigma -min\left\{\lambda \rho ,\sigma \right\}\right)}{\sigma -\lambda \rho }}f\left(min\left\{\lambda \rho ,\sigma \right\}\right)d\lambda ={\int }_1^{{\displaystyle \frac{\sigma }{\rho }}}{\displaystyle \frac{\kappa \left(\sigma -\lambda \rho \right)}{\sigma -\lambda \rho }}f\left(\lambda \rho \right)d\lambda \hfill \\ \hfill & ={\int }_{\rho }^{\sigma }{\displaystyle \frac{\kappa \left(\sigma -\vartheta \right)}{\sigma -\vartheta }}f\left(\vartheta \right){\displaystyle \frac{1}{\rho }}d\vartheta ={\displaystyle \frac{1}{\rho }}{\int }_{\rho }^{\sigma }{\displaystyle \frac{\kappa \left(\sigma -\vartheta \right)}{\sigma -\vartheta }}f\left(\vartheta \right)d\vartheta ={\displaystyle \frac{1}{\rho }}\rho +I_{\kappa }f\left(\sigma \right).\hfill \end{array}$$

The right side of the inequality should be examined in two cases. In the first case, $1<{\displaystyle \frac{\sigma }{\rho }}\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}$ is analyzed, then

$$\begin{array}{ccc}\hfill {\int }_1^{+\infty }{\displaystyle \frac{\kappa \left(\sigma -min\left\{\lambda \rho ,\sigma \right\}\right)}{\sigma -\lambda \rho }}min\left\{\lambda f\left(\rho \right),f\left(\sigma \right)\right\}d\lambda & =& {\int }_1^{{\displaystyle \frac{\sigma }{\rho }}}{\displaystyle \frac{\kappa \left(\sigma -\lambda \rho \right)}{\sigma -\lambda \rho }}\lambda f\left(\rho \right)d\lambda \hfill \\ & =& {\displaystyle \frac{f\left(\rho \right)}{{\rho }^2}}{\int }_{\rho }^{\sigma }{\displaystyle \frac{\kappa \left(\sigma -\vartheta \right)}{\sigma -\vartheta }}\vartheta d\vartheta \hfill \end{array}$$

is obtained. In the $1\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}<{\displaystyle \frac{\sigma }{\rho }}$ case, the equation

$$\begin{array}{ccc}\hfill {\int }_1^{+\infty }{\displaystyle \frac{\kappa \left(\sigma -min\left\{\lambda \rho ,\sigma \right\}\right)}{\sigma -\lambda \rho }}& & min\left\{\lambda f\left(\rho \right),f\left(\sigma \right)\right\}d\lambda \hfill \\ & =& {\int }_1^{{\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}}{\displaystyle \frac{\kappa \left(\sigma -\lambda \rho \right)}{\sigma -\lambda \rho }}\lambda f\left(\rho \right)d\lambda +{\int }_{{\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}}^{{\displaystyle \frac{\sigma }{\rho }}}{\displaystyle \frac{\kappa \left(\sigma -\lambda \rho \right)}{\sigma -\lambda \rho }}f\left(\sigma \right)d\lambda \hfill \\ & =& {\int }_{\rho }^{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}{\displaystyle \frac{\kappa \left(\sigma -\vartheta \right)}{\sigma -\vartheta }}f\left(\rho \right){\displaystyle \frac{\vartheta }{\rho }}{\displaystyle \frac{1}{\rho }}d\vartheta +{\int }_{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}^{\sigma }{\displaystyle \frac{\kappa \left(\sigma -\vartheta \right)}{\sigma -\vartheta }}f\left(\sigma \right){\displaystyle \frac{1}{\rho }}d\vartheta \hfill \\ & =& {\displaystyle \frac{f\left(\rho \right)}{{\rho }^2}}{\int }_{\rho }^{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}{\displaystyle \frac{\kappa \left(\sigma -\vartheta \right)}{\sigma -\vartheta }}\vartheta d\vartheta +{\displaystyle \frac{f\left(\sigma \right)}{\rho }}{\int }_{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}^{\sigma }{\displaystyle \frac{\kappa \left(\sigma -\vartheta \right)}{\sigma -\vartheta }}d\vartheta \hfill \end{array}$$

is handled. Therefore, the inequality (21) is obtained. □

Theorem 7. 

Let $f:\left[\rho ,\sigma \right]\to \left(0,+\infty \right)$ be a ${\mathbb{B}}^{-1}$–convex function and $f\in L_1\left[\rho ,\sigma \right]$; then, the following right Riemann–Liouville fractional integral inequalities hold:

$${}_{{\sigma }^{-}}I_{\kappa }f\left(\rho \right)\le \left\{\begin{array}{cc}{\displaystyle \frac{f\left(\rho \right)}{\rho }}{\int }_{\rho }^{\sigma }{\displaystyle \frac{\kappa \left(\vartheta -\rho \right)}{\vartheta -\rho }}\vartheta d\vartheta ,\hfill & 1<{\displaystyle \frac{\sigma }{\rho }}\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}\hfill \\ {\displaystyle \frac{f\left(\rho \right)}{\rho }}{\int }_{\rho }^{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}{\displaystyle \frac{\kappa \left(\vartheta -\rho \right)}{\vartheta -\rho }}\vartheta d\vartheta +f\left(\sigma \right){\int }_{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}^{\sigma }{\displaystyle \frac{\kappa \left(\vartheta -\rho \right)}{\vartheta -\rho }}d\vartheta ,\hfill & 1\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}<{\displaystyle \frac{\sigma }{\rho }}.\hfill \end{array}\right.$$

(22)

Proof. 

Since the function $f:\left[\rho ,\sigma \right]\to \left(0,+\infty \right)$ is ${\mathbb{B}}^{-1}$–convex function, the following inequality is provided:

$$f\left(min\left\{\lambda \rho ,\sigma \right\}\right)\le min\left\{\lambda f\left(\rho \right),f\left(\sigma \right)\right\}$$

(23)

for all $\lambda \in \left[1,+\infty \right)$. In order to obtain the inequality (22), both sides of (23) is multiplied by ${\displaystyle \frac{\kappa \left(min\left\{\lambda \rho ,\sigma \right\}-\rho \right)}{min\left\{\lambda \rho ,\sigma \right\}-\rho }}$. The integral should be considered in $[1,{\displaystyle \frac{\sigma }{\rho }}]$ in order to ensure the result is finite [28]. Here, let us consider the properties (1) of the $\kappa$.

Initially, the left side of the inequality is

$$\begin{array}{ccc}\hfill {\int }_1^{{\displaystyle \frac{\sigma }{\rho }}}{\displaystyle \frac{\kappa \left(min\left\{\lambda \rho ,\sigma \right\}-\rho \right)}{min\left\{\lambda \rho ,\sigma \right\}-\rho }}f\left(min\left\{\lambda \rho ,\sigma \right\}\right)d\lambda & =& {\int }_1^{{\displaystyle \frac{\sigma }{\rho }}}{\displaystyle \frac{\kappa \left(\lambda \rho -\rho \right)}{\lambda \rho -\rho }}f\left(\lambda \rho \right)d\lambda \hfill \\ & =& {\displaystyle \frac{1}{\rho }}{\int }_{\rho }^{\sigma }{\displaystyle \frac{\kappa \left(\vartheta -\rho \right)}{\vartheta -\rho }}f\left(\vartheta \right)d\vartheta ={\displaystyle \frac{1}{\rho }}{}_{{\sigma }^{-}}I_{\kappa }f\left(\rho \right).\hfill \end{array}$$

Two different cases can be discussed for the right side of the inequality. The case of $1<{\displaystyle \frac{\sigma }{\rho }}\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}$ is the first case. Thus, in this circumstance, the following calculations are made:

$${\int }_1^{{\displaystyle \frac{\sigma }{\rho }}}{\displaystyle \frac{\kappa \left(min\left\{\lambda \rho ,\sigma \right\}-\rho \right)}{min\left\{\lambda \rho ,\sigma \right\}-\rho }}min\left\{\lambda f\left(\rho \right),f\left(\sigma \right)\right\}d\lambda ={\int }_1^{{\displaystyle \frac{\sigma }{\rho }}}{\displaystyle \frac{\kappa \left(\lambda \rho -\rho \right)}{\lambda \rho -\rho }}\lambda f\left(\rho \right)d\lambda ={\displaystyle \frac{f\left(\rho \right)}{{\rho }^2}}{\int }_{\rho }^{\sigma }{\displaystyle \frac{\kappa \left(\vartheta -\rho \right)}{\vartheta -\rho }}\vartheta d\vartheta .$$

The second case is $1\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}<{\displaystyle \frac{\sigma }{\rho }}$. In this condition, the integral is

$$\begin{array}{ccc}\hfill {\int }_1^{{\displaystyle \frac{\sigma }{\rho }}}{\displaystyle \frac{\kappa \left(\lambda \rho -\rho \right)}{\lambda \rho -\rho }}min\left\{\lambda f\left(\rho \right),f\left(\sigma \right)\right\}d\lambda & =& {\int }_1^{{\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}}{\displaystyle \frac{\kappa \left(\lambda \rho -\rho \right)}{\lambda \rho -\rho }}\lambda f\left(\rho \right)d\lambda +{\int }_{{\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}}^{{\displaystyle \frac{\sigma }{\rho }}}{\displaystyle \frac{\kappa \left(\lambda \rho -\rho \right)}{\lambda \rho -\rho }}f\left(\sigma \right)d\lambda \hfill \\ & =& f\left(\rho \right){\int }_{\rho }^{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}{\displaystyle \frac{\kappa \left(\vartheta -\rho \right)}{\vartheta -\rho }}{\displaystyle \frac{\vartheta }{\rho }}{\displaystyle \frac{1}{\rho }}d\vartheta +f\left(\sigma \right){\int }_{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}^{\sigma }{\displaystyle \frac{\kappa \left(\vartheta -\rho \right)}{\vartheta -\rho }}{\displaystyle \frac{1}{\rho }}d\vartheta \hfill \\ & =& {\displaystyle \frac{f\left(\rho \right)}{{\rho }^2}}{\int }_{\rho }^{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}{\displaystyle \frac{\kappa \left(\vartheta -\rho \right)}{\vartheta -\rho }}\vartheta d\vartheta +{\displaystyle \frac{f\left(\sigma \right)}{\rho }}{\int }_{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}^{\sigma }{\displaystyle \frac{\kappa \left(\vartheta -\rho \right)}{\vartheta -\rho }}d\vartheta .\hfill \end{array}$$

After accounting for all these, the inequality (22) is obtained. □

Theorems 6 and 7 include the most general inequalities for ${\mathbb{B}}^{-1}$–convex functions. This is proved with the aid of the properties of the generalized Riemann–Liouville fractional integral operators. If the function $\kappa$ is considered as in the definition of the fractional operator, the following conclusions can be attained.

Corollary 1. 

The classical Hermite–Hadamard inequality for ${\mathbb{B}}^{-1}$–convex function is derived by the inequalities (21) and (22).

Proof. 

If the function $\kappa$ is $\kappa \left(\varpi \right)=\varpi$, then the inequalities (21) and (22) yield the inequality (18). □

Corollary 2. 

The Hermite–Hadamard inequalities via Riemann–Liouville fractional integral operators given with the (19) and (20) can be acquired from the inequalities (21) and (22), respectively.

Proof. 

The generalized fractional integral operators give the Riemann–Liouville fractional integrals if the function $\kappa$ is $\kappa \left(\varpi \right)={\displaystyle \frac{{\varpi }^{\varsigma }}{\mathsf{\Gamma }\left(\varsigma \right)}}$. Thereby, the inequalities (19) and (20) are achieved by Theorems 6 and 7. □

4. Inequalities Involving Different Types of the Fractional Integral Operators

In this section, some inequalities via different types fractional integral operators and their applications are demonstrated. The first inequality is with regard to conformable fractional integral operator. The Hermite–Hadamard inequality including conformable fractional integral operator for ${\mathbb{B}}^{-1}$–convex function is provided below.

Theorem 8. 

Let $f:\left[\rho ,\sigma \right]\to \left(0,+\infty \right)$ be a ${\mathbb{B}}^{-1}$–convex function and $f\in L_1\left[\rho ,\sigma \right]$; then, the following conformable integral inequalities hold:

$$J_{\rho }^{\varsigma }f\left(\sigma \right)\le \left\{\begin{array}{cc}{\displaystyle \frac{f\left(\rho \right)}{\rho }}{\displaystyle \frac{{\sigma }^{\varsigma +1}-{\rho }^{\varsigma +1}}{\varsigma +1}},\hfill & 1<{\displaystyle \frac{\sigma }{\rho }}\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}\hfill \\ {\displaystyle \frac{{\sigma }^{\varsigma }\left(\varsigma +1\right){\left(f\left(\rho \right)\right)}^{\varsigma }f\left(\sigma \right)-{\rho }^{\varsigma }\left(\varsigma {\left(f\left(\rho \right)\right)}^{\varsigma +1}+{\left(f\left(\sigma \right)\right)}^{\varsigma +1}\right)}{\varsigma \left(\varsigma +1\right){\left(f\left(\rho \right)\right)}^{\varsigma }}},\hfill & 1\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}<{\displaystyle \frac{\sigma }{\rho }}.\hfill \end{array}\right.$$

(24)

Proof. 

In the inequality (6), the function $\kappa \left(\varpi \right)=\varpi {\left(\sigma -\varpi \right)}^{\varsigma -1}$ is placed, and the following are obtained, respectively:

$${\displaystyle \frac{f\left(\rho \right)}{\rho }}{\int }_{\rho }^{\sigma }{\displaystyle \frac{\kappa \left(\sigma -\vartheta \right)}{\sigma -\vartheta }}\vartheta d\vartheta ={\displaystyle \frac{f\left(\rho \right)}{\rho }}{\int }_{\rho }^{\sigma }{\vartheta }^{\varsigma }d\vartheta ={\displaystyle \frac{f\left(\rho \right)}{\rho }}{\displaystyle \frac{{\sigma }^{\varsigma +1}-{\rho }^{\varsigma +1}}{\varsigma +1}}$$

and

$$\begin{array}{ccc}& {\displaystyle \frac{f\left(\rho \right)}{\rho }}& {\int }_{\rho }^{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}{\displaystyle \frac{\kappa \left(\sigma -\vartheta \right)}{\sigma -\vartheta }}\vartheta d\vartheta +f\left(\sigma \right){\int }_{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}^{\sigma }{\displaystyle \frac{\kappa \left(\sigma -\vartheta \right)}{\sigma -\vartheta }}d\vartheta \hfill \\ & =& {\displaystyle \frac{f\left(\rho \right)}{\rho }}{\int }_{\rho }^{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}{\vartheta }^{\varsigma }d\vartheta +f\left(\sigma \right){\int }_{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}^{\sigma }{\vartheta }^{\varsigma -1}d\vartheta \hfill \\ & =& {\displaystyle \frac{f\left(\rho \right)}{\rho \left(\varsigma +1\right)}}{\displaystyle \frac{{\rho }^{\varsigma +1}{\left(f\left(\sigma \right)\right)}^{\varsigma +1}-{\rho }^{\varsigma +1}{\left(f\left(\rho \right)\right)}^{\varsigma +1}}{{\left(f\left(\rho \right)\right)}^{\varsigma +1}}}+{\displaystyle \frac{f\left(\sigma \right)}{\varsigma }}{\displaystyle \frac{{\sigma }^{\varsigma }{\left(f\left(\rho \right)\right)}^{\varsigma }-{\rho }^{\varsigma }{\left(f\left(\sigma \right)\right)}^{\varsigma }}{{\left(f\left(\rho \right)\right)}^{\varsigma }}}\hfill \\ & =& {\displaystyle \frac{{\sigma }^{\varsigma }\left(\varsigma +1\right){\left(f\left(\rho \right)\right)}^{\varsigma }f\left(\sigma \right)-{\rho }^{\varsigma }\left(\varsigma {\left(f\left(\rho \right)\right)}^{\varsigma +1}+{\left(f\left(\sigma \right)\right)}^{\varsigma +1}\right)}{\varsigma \left(\varsigma +1\right){\left(f\left(\rho \right)\right)}^{\varsigma }}}.\hfill \end{array}$$

□

An example for the inequality (24) is given as follows.

Example 5. 

The Hermite–Hadamard inequality including conformable integral for the ${\mathbb{B}}^{-1}$–convex function $f\left(\varpi \right)=\sqrt{\varpi }$ is given for some values within the following table. Indeed, the results give the effectiveness of the inequality (24). ($\varsigma ={\displaystyle \frac{3}{2}}$)

$\rho$	$\sigma$	$J_{\rho }^{\varsigma }f\left(\sigma \right)$	${\displaystyle \frac{{\sigma }^{\varsigma }\left(\varsigma +1\right){\left(f\left(\rho \right)\right)}^{\varsigma }f\left(\sigma \right)-{\rho }^{\varsigma }\left(\varsigma {\left(f\left(\rho \right)\right)}^{\varsigma +1}+{\left(f\left(\sigma \right)\right)}^{\varsigma +1}\right)}{\varsigma \left(\varsigma +1\right){\left(f\left(\rho \right)\right)}^{\varsigma }}}$
1	2	1.5	1.63242
1	3	4	4.54714
2	3	2.5	2.62931
2	4	6	6.52969
1	4	7.5	8.75817

The Hermite–Hadamard inequalities including k–Riemann–Liouville fractional integral operators for ${\mathbb{B}}^{-1}$–convex function are proven below.

Theorem 9. 

Let $f:\left[\rho ,\sigma \right]\to {\mathbb{R}}_{++}$ be a ${\mathbb{B}}^{-1}$–convex function, $k>0$ and $f\in L_1\left[\rho ,\sigma \right]$; then, the following k–Riemann–Liouville fractional integral inequalities hold:

$$J_{{\rho }^{+};k}^{\varsigma }f\left(\sigma \right)\le \left\{\begin{array}{cc}{\displaystyle \frac{f\left(\rho \right){\left(\sigma -\rho \right)}^{\frac{\varsigma }{k}}\left(k\sigma +\varsigma \rho \right)}{\rho {\mathsf{\Gamma }}_k\left(\varsigma +2k\right)}},\hfill & 1<{\displaystyle \frac{\sigma }{\rho }}\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}\hfill \\ {\displaystyle \frac{{\left(f\left(\rho \right)\right)}^{\frac{\varsigma }{k}+1}{\left(\sigma -\rho \right)}^{\frac{\varsigma }{k}}\left(k\sigma +\varsigma \rho \right)-k{\left(\sigma f\left(\rho \right)-\rho f\left(\sigma \right)\right)}^{\frac{\varsigma }{k}+1}}{\rho {\mathsf{\Gamma }}_k\left(\varsigma +2k\right){\left(f\left(\rho \right)\right)}^{\frac{\varsigma }{k}}}},\hfill & 1\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}<{\displaystyle \frac{\sigma }{\rho }}.\hfill \end{array}\right.$$

(25)

Proof. 

For the function $\kappa \left(\vartheta \right)={\displaystyle \frac{1}{k{\mathsf{\Gamma }}_k\left(\varsigma \right)}}{\vartheta }^{{\displaystyle \frac{\varsigma }{k}}}$, the inequality (6) gives

$$\begin{array}{ccc}\hfill {\displaystyle \frac{f\left(\rho \right)}{\rho }}{\int }_{\rho }^{\sigma }{\displaystyle \frac{\kappa \left(\sigma -\vartheta \right)}{\sigma -\vartheta }}\vartheta d\vartheta ={\displaystyle \frac{f\left(\rho \right)}{\rho k{\mathsf{\Gamma }}_k\left(\varsigma \right)}}{\int }_{\rho }^{\sigma }{\left(\sigma -\vartheta \right)}^{{\displaystyle \frac{\varsigma }{k}}-1}\vartheta d\vartheta & =& {\displaystyle \frac{f\left(\rho \right){\left(\sigma -\rho \right)}^{\frac{\varsigma }{k}}}{\rho k{\mathsf{\Gamma }}_k\left(\varsigma \right)}}\left[{\displaystyle \frac{k\sigma }{\varsigma }}-{\displaystyle \frac{k\sigma -k\rho }{\varsigma +k}}\right]\hfill \\ & =& {\displaystyle \frac{f\left(\rho \right){\left(\sigma -\rho \right)}^{\frac{\varsigma }{k}}\left(k\sigma +\varsigma \rho \right)}{\rho \varsigma \left(\varsigma +k\right){\mathsf{\Gamma }}_k\left(\varsigma \right)}}\hfill \end{array}$$

to the case $1<{\displaystyle \frac{\sigma }{\rho }}\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}$. Here, ${\mathsf{\Gamma }}_k\left(\varsigma +k\right)=\varsigma {\mathsf{\Gamma }}_k\left(\varsigma \right)$; therefore, the desired equality is attained.

To the case of $1\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}<{\displaystyle \frac{\sigma }{\rho }}$, the equation is

$$\begin{array}{cc}\hfill {\displaystyle \frac{f\left(\rho \right)}{\rho }}& {\int }_{\rho }^{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}{\displaystyle \frac{\kappa \left(\sigma -\vartheta \right)}{\sigma -\vartheta }}\vartheta d\vartheta +f\left(\sigma \right){\int }_{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}^{\sigma }{\displaystyle \frac{\kappa \left(\sigma -\vartheta \right)}{\sigma -\vartheta }}d\vartheta \hfill \\ \hfill & ={\displaystyle \frac{f\left(\rho \right)}{\rho k{\mathsf{\Gamma }}_k\left(\varsigma \right)}}{\int }_{\rho }^{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}{\left(\sigma -\vartheta \right)}^{{\displaystyle \frac{\varsigma }{k}}-1}\vartheta d\vartheta +{\displaystyle \frac{f\left(\sigma \right)}{k{\mathsf{\Gamma }}_k\left(\varsigma \right)}}{\int }_{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}^{\sigma }{\left(\sigma -\vartheta \right)}^{{\displaystyle \frac{\varsigma }{k}}-1}d\vartheta \hfill \\ \hfill & =-{\displaystyle \frac{\sigma f\left(\rho \right)}{\rho \varsigma {\mathsf{\Gamma }}_k\left(\varsigma \right)}}\left[{\left({\displaystyle \frac{\sigma f\left(\rho \right)-\rho f\left(\sigma \right)}{f\left(\rho \right)}}\right)}^{{\displaystyle \frac{\varsigma }{k}}}-{\left(\sigma -\rho \right)}^{{\displaystyle \frac{\varsigma }{k}}}\right]\hfill \\ \hfill & +{\displaystyle \frac{f\left(\rho \right)}{\rho \left(\varsigma +k\right){\mathsf{\Gamma }}_k\left(\varsigma \right)}}\left[{\left({\displaystyle \frac{\sigma f\left(\rho \right)-\rho f\left(\sigma \right)}{f\left(\rho \right)}}\right)}^{{\displaystyle \frac{\varsigma }{k}}+1}+{\left(\sigma -\rho \right)}^{{\displaystyle \frac{\varsigma }{k}}+1}\right]\hfill \\ \hfill & +{\displaystyle \frac{f\left(\sigma \right)}{\varsigma {\mathsf{\Gamma }}_k\left(\varsigma \right)}}{\left({\displaystyle \frac{\sigma f\left(\rho \right)-\rho f\left(\sigma \right)}{f\left(\rho \right)}}\right)}^{{\displaystyle \frac{\varsigma }{k}}}\hfill \\ \hfill & ={\displaystyle \frac{{\left(\sigma f\left(\rho \right)-\rho f\left(\sigma \right)\right)}^{\frac{\varsigma }{k}}}{{\mathsf{\Gamma }}_k\left(\varsigma \right){\left(f\left(\rho \right)\right)}^{\frac{\varsigma }{k}}}}\left[-{\displaystyle \frac{\sigma f\left(\rho \right)}{\rho \varsigma }}+{\displaystyle \frac{\sigma f\left(\rho \right)-\rho f\left(\sigma \right)}{\rho \left(\varsigma +k\right)}}+{\displaystyle \frac{f\left(\sigma \right)}{\varsigma }}\right]+{\displaystyle \frac{f\left(\rho \right){\left(\sigma -\rho \right)}^{\frac{\varsigma }{k}}}{\rho {\mathsf{\Gamma }}_k\left(\varsigma \right)}}\left[{\displaystyle \frac{\sigma }{\varsigma }}-{\displaystyle \frac{\sigma -\rho }{\varsigma +k}}\right]\hfill \\ \hfill & ={\displaystyle \frac{{\left(f\left(\rho \right)\right)}^{\frac{\varsigma }{k}+1}{\left(\sigma -\rho \right)}^{\frac{\varsigma }{k}}\left(k\sigma +\varsigma \rho \right)-k{\left(\sigma f\left(\rho \right)-\rho \left(\sigma \right)\right)}^{\frac{\varsigma }{k}+1}}{\rho {\mathsf{\Gamma }}_k\left(\varsigma +2k\right){\left(f\left(\rho \right)\right)}^{\frac{\varsigma }{k}}}}.\hfill \end{array}$$

Therefore, the proof is completed. □

Example 6. 

Let $f\left(\varpi \right)=\sqrt{\varpi }$, $\varsigma ={\displaystyle \frac{3}{2}}$ and $k={\displaystyle \frac{1}{2}}$. The function f is ${\mathbb{B}}^{-1}$–convex function; thus, the Hermite–Hadamard inequality including k–Riemann–Liouville fractional integral can be calculated as follows.

$\rho$	$\sigma$	$J_{{\rho }^{+};k}^{\varsigma }f\left(\sigma \right)$	${\displaystyle \frac{{\left(f\left(\rho \right)\right)}^{\frac{\varsigma }{k}+1}{\left(\sigma -\rho \right)}^{\frac{\varsigma }{k}}\left(k\sigma +\varsigma \rho \right)-k{\left(\sigma f\left(\rho \right)-\rho f\left(\sigma \right)\right)}^{\frac{\varsigma }{k}+1}}{\rho {\mathsf{\Gamma }}_k\left(\varsigma +2k\right){\left(f\left(\rho \right)\right)}^{\frac{\varsigma }{k}}}}$
1	2	1.48645	1.62742
1	3	12.9618	15.1384
2	3	1.9982	2.09967
2	4	16.8173	18.4121
1	4	55.1634	57.6667

Theorem 10. 

Let $f:\left[\rho ,\sigma \right]\to {\mathbb{R}}_{++}$ be a ${\mathbb{B}}^{-1}$–convex function, $k>0$ and $f\in L_1\left[\rho ,\sigma \right]$; then, the following k–Riemann–Liouville fractional integral inequality holds:

$$J_{{\sigma }^{-};k}^{\varsigma }f\left(\rho \right)\le \left\{\begin{array}{cc}{\displaystyle \frac{f\left(\rho \right){\left(\sigma -\rho \right)}^{\frac{\varsigma }{k}}\left(k\rho +\varsigma \sigma \right)}{\rho {\mathsf{\Gamma }}_k\left(\varsigma +2k\right)}},\hfill & 1<{\displaystyle \frac{\sigma }{\rho }}\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}\hfill \\ {\displaystyle \frac{{\left(f\left(\rho \right)\right)}^{\frac{\varsigma }{k}}{\left(\sigma -\rho \right)}^{\frac{\varsigma }{k}}\left(k+\varsigma \right)f\left(\sigma \right)-k{\rho }^{\frac{\varsigma }{k}}{\left(f\left(\sigma \right)-f\left(\rho \right)\right)}^{\frac{\varsigma }{k}}}{{\mathsf{\Gamma }}_k\left(\varsigma +2k\right){\left(f\left(\rho \right)\right)}^{\frac{\varsigma }{k}}}},\hfill & 1\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}<{\displaystyle \frac{\sigma }{\rho }}.\hfill \end{array}\right.$$

(26)

Proof. 

The function $\kappa$ is ${\displaystyle \frac{1}{k{\mathsf{\Gamma }}_k\left(\varsigma \right)}}{\vartheta }^{{\displaystyle \frac{\varsigma }{k}}}$; thus, the inequality (22) transforms into following for the case $1<{\displaystyle \frac{\sigma }{\rho }}\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}$

$$\begin{array}{ccc}\hfill {\displaystyle \frac{f\left(\rho \right)}{\rho }}{\int }_{\rho }^{\sigma }{\displaystyle \frac{\kappa \left(\vartheta -\rho \right)}{\vartheta -\rho }}\vartheta d\vartheta ={\displaystyle \frac{f\left(\rho \right)}{\rho k{\mathsf{\Gamma }}_k\left(\varsigma \right)}}{\int }_{\rho }^{\sigma }{\left(\vartheta -\rho \right)}^{{\displaystyle \frac{\varsigma }{k}}-1}\vartheta d\vartheta & =& {\displaystyle \frac{f\left(\rho \right){\left(\sigma -\rho \right)}^{\frac{\varsigma }{k}}}{\rho {\mathsf{\Gamma }}_k\left(\varsigma \right)}}\left({\displaystyle \frac{\sigma -\rho }{\varsigma +k}}+{\displaystyle \frac{\rho }{\varsigma }}\right)\hfill \\ & =& {\displaystyle \frac{f\left(\rho \right){\left(\sigma -\rho \right)}^{\frac{\varsigma }{k}}\left(k\rho +\varsigma \sigma \right)}{\rho {\mathsf{\Gamma }}_k\left(\varsigma +2k\right)}}\hfill \end{array}$$

and for the case of $1\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}<{\displaystyle \frac{\sigma }{\rho }}$

$$\begin{array}{cc}\hfill {\displaystyle \frac{f\left(\rho \right)}{\rho }}& {\int }_{\rho }^{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}{\displaystyle \frac{\kappa \left(\vartheta -\rho \right)}{\vartheta -\rho }}\vartheta d\vartheta +f\left(\sigma \right){\int }_{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}^{\sigma }{\displaystyle \frac{\kappa \left(\vartheta -\rho \right)}{\vartheta -\rho }}d\vartheta \hfill \\ \hfill & ={\displaystyle \frac{f\left(\rho \right)}{\rho k{\mathsf{\Gamma }}_k\left(\varsigma \right)}}{\int }_{\rho }^{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}{\left(\vartheta -\rho \right)}^{{\displaystyle \frac{\varsigma }{k}}-1}\vartheta d\vartheta +{\displaystyle \frac{f\left(\sigma \right)}{k{\mathsf{\Gamma }}_k\left(\varsigma \right)}}{\int }_{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}^{\sigma }{\left(\vartheta -\rho \right)}^{{\displaystyle \frac{\varsigma }{k}}-1}d\vartheta \hfill \\ \hfill & ={\displaystyle \frac{f\left(\rho \right)}{\rho {\mathsf{\Gamma }}_k\left(\varsigma \right)}}\left[{\displaystyle \frac{{\left(\rho f\left(\sigma \right)-\rho f\left(\rho \right)\right)}^{\frac{\varsigma }{k}+1}}{\left(\varsigma +k\right){\left(f\left(\rho \right)\right)}^{\frac{\varsigma }{k}+1}}}+{\displaystyle \frac{\rho {\left(\rho f\left(\sigma \right)-\rho f\left(\rho \right)\right)}^{\frac{\varsigma }{k}}}{\varsigma {\left(f\left(\rho \right)\right)}^{\frac{\varsigma }{k}}}}\right]\hfill \\ \hfill & +{\displaystyle \frac{f\left(\sigma \right)}{\varsigma {\mathsf{\Gamma }}_k\left(\varsigma \right)}}\left({\left(\sigma -\rho \right)}^{{\displaystyle \frac{\varsigma }{k}}}-{\displaystyle \frac{{\left(\rho f\left(\sigma \right)-\rho f\left(\rho \right)\right)}^{\frac{\varsigma }{k}}}{{\left(f\left(\rho \right)\right)}^{\frac{\varsigma }{k}}}}\right)\hfill \\ \hfill & ={\displaystyle \frac{{\left(\rho f\left(\sigma \right)-\rho f\left(\rho \right)\right)}^{\frac{\varsigma }{k}}}{\varsigma {\mathsf{\Gamma }}_k\left(\varsigma \right){\left(f\left(\rho \right)\right)}^{\frac{\varsigma }{k}}}}\left[{\displaystyle \frac{\varsigma f\left(\sigma \right)+kf\left(\rho \right)}{\varsigma +k}}-f\left(\sigma \right)\right]+{\displaystyle \frac{f\left(\sigma \right){\left(\sigma -\rho \right)}^{\frac{\varsigma }{k}}}{\varsigma {\mathsf{\Gamma }}_k\left(\varsigma \right)}}\hfill \\ \hfill & ={\displaystyle \frac{{\left(f\left(\rho \right)\right)}^{\frac{\varsigma }{k}}{\left(\sigma -\rho \right)}^{\frac{\varsigma }{k}}\left(k+\varsigma \right)f\left(\sigma \right)-k{\rho }^{\frac{\varsigma }{k}}{\left(f\left(\sigma \right)-f\left(\rho \right)\right)}^{\frac{\varsigma }{k}}}{{\mathsf{\Gamma }}_k\left(\varsigma +2k\right){\left(f\left(\rho \right)\right)}^{\frac{\varsigma }{k}}}}.\hfill \end{array}$$

Taking all these calculations into account, the inequality (26) is achieved. □

Example 7. 

Let $f\left(\varpi \right)=\sqrt{\varpi }$, $\varsigma ={\displaystyle \frac{3}{2}}$ and $k={\displaystyle \frac{1}{2}}$. The function f is ${\mathbb{B}}^{-1}$–convex function; thus, the Hermite–Hadamard inequality including k–Riemann–Liouville fractional integral can be calculated. The outcomes of the calculations are given with the table as follows.

$\rho$	$\sigma$	$J_{{\sigma }^{-};k}^{\varsigma }f\left(\rho \right)$	${\displaystyle \frac{{\left(f\left(\rho \right)\right)}^{\frac{\varsigma }{k}}{\left(\sigma -\rho \right)}^{\frac{\varsigma }{k}}\left(k+\varsigma \right)f\left(\sigma \right)-k{\rho }^{\frac{\varsigma }{k}}{\left(f\left(\sigma \right)-f\left(\rho \right)\right)}^{\frac{\varsigma }{k}}}{{\mathsf{\Gamma }}_k\left(\varsigma +2k\right){\left(f\left(\rho \right)\right)}^{\frac{\varsigma }{k}}}}$
1	2	1.76097	1.86193
1	3	16.81	18.3444
2	3	2.20966	2.27913
2	4	19.9231	21.1438
1	4	64.6095	71.6667

The Hermite–Hadamard inequalities including right-sided and left-sided exponential kernel fractional integral operators are provided with the following theorems. Then, two examples of the theorems are presented with graphics.

Theorem 11. 

Let $f:\left[\rho ,\sigma \right]\to {\mathbb{R}}_{++}$ be a ${\mathbb{B}}^{-1}$–convex function, $0<\varsigma <1$ and $f\in L_1\left[\rho ,\sigma \right]$; then, the following fractional integral with exponential kernel inequalities hold:

$$I_{{\rho }^{+}}^{\varsigma }f\left(\sigma \right)\le \left\{\begin{array}{cc}{\displaystyle \frac{f\left(\rho \right)\left(\varsigma \sigma +\varsigma -1\right)+f\left(\rho \right)e^{\frac{1-\varsigma }{\varsigma }\left(\rho -\sigma \right)}\left(1-\varsigma -\varsigma \rho \right)}{\varsigma \left(1-\varsigma \right)\rho }},\hfill & 1<{\displaystyle \frac{\sigma }{\rho }}\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}\hfill \\ {\displaystyle \frac{f\left(\rho \right)\left(\varsigma \rho -\rho -\varsigma \right)e^{-\frac{1-\varsigma }{\varsigma }\left(\sigma -\rho \right)}+\varsigma f\left(\rho \right)e^{-\frac{1-\varsigma }{\varsigma }\left(\sigma -\frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}\right)}+\rho \left(1-\varsigma \right)f\left(\sigma \right)}{\rho {\left(1-\varsigma \right)}^2}},\hfill & 1\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}<{\displaystyle \frac{\sigma }{\rho }}.\hfill \end{array}\right.$$

(27)

Proof. 

The generalized Riemann–Liouville fractional integral operator gives the fractional operator including exponential kernel when the function $\kappa \left(\vartheta \right)={\displaystyle \frac{\vartheta }{\varsigma }}exp\left(-{\displaystyle \frac{1-\varsigma }{\varsigma }}\vartheta \right)$. If the function $\kappa$ is substituted in the inequality (21), it is

$$\begin{array}{cc}\hfill {\displaystyle \frac{f\left(\rho \right)}{\rho }}{\int }_{\rho }^{\sigma }{\displaystyle \frac{\kappa \left(\sigma -\vartheta \right)}{\sigma -\vartheta }}\vartheta d\vartheta & ={\displaystyle \frac{f\left(\rho \right)}{\rho \varsigma }}{\int }_{\rho }^{\sigma }{e}^{-{\displaystyle \frac{1-\varsigma }{\varsigma }}\left(\sigma -\vartheta \right)}\vartheta d\vartheta ={\displaystyle \frac{f\left(\rho \right)}{\rho \varsigma e^{\frac{1-\varsigma }{\varsigma }\sigma }}}{\int }_{\rho }^{\sigma }{e}^{{\displaystyle \frac{1-\varsigma }{\varsigma }}\vartheta }\vartheta d\vartheta \hfill \\ \hfill & ={\displaystyle \frac{f\left(\rho \right)}{\rho \varsigma e^{\frac{1-\varsigma }{\varsigma }\sigma }}}\left[e^{{\displaystyle \frac{1-\varsigma }{\varsigma }}\sigma }\left({\displaystyle \frac{\sigma \varsigma -1+\varsigma }{1-\varsigma }}\right)+e^{{\displaystyle \frac{1-\varsigma }{\varsigma }}\rho }\left({\displaystyle \frac{1-\varsigma -\rho \varsigma }{1-\varsigma }}\right)\right]\hfill \\ \hfill & ={\displaystyle \frac{f\left(\rho \right)\left(\varsigma \sigma +\varsigma -1\right)+f\left(\rho \right)e^{\frac{1-\varsigma }{\varsigma }\left(\rho -\sigma \right)}\left(1-\varsigma -\varsigma \rho \right)}{\varsigma \left(1-\varsigma \right)\rho }}.\hfill \end{array}$$

The same process is applied for the condition $1\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}<{\displaystyle \frac{\sigma }{\rho }}$, and one has

$$\begin{array}{cc}\hfill {\displaystyle \frac{f\left(\rho \right)}{\rho }}& {\int }_{\rho }^{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}{\displaystyle \frac{\kappa \left(\sigma -\vartheta \right)}{\sigma -\vartheta }}\vartheta d\vartheta +f\left(\sigma \right){\int }_{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}^{\sigma }{\displaystyle \frac{\kappa \left(\sigma -\vartheta \right)}{\sigma -\vartheta }}d\vartheta \hfill \\ \hfill & ={\displaystyle \frac{f\left(\rho \right)}{\rho \varsigma }}{\int }_{\rho }^{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}{e}^{-{\displaystyle \frac{1-\varsigma }{\varsigma }}\left(\sigma -\vartheta \right)}\vartheta d\vartheta +{\displaystyle \frac{f\left(\sigma \right)}{\varsigma }}{\int }_{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}^{\sigma }{e}^{-{\displaystyle \frac{1-\varsigma }{\varsigma }}\left(\sigma -\vartheta \right)}d\vartheta \hfill \\ \hfill & ={\displaystyle \frac{f\left(\rho \right)}{1-\varsigma }}{e}^{-{\displaystyle \frac{1-\varsigma }{\varsigma }}\left(\sigma -\rho \right)}\left[-1-{\displaystyle \frac{\varsigma }{\rho \left(1-\varsigma \right)}}\right]-{\displaystyle \frac{\varsigma f\left(\rho \right)}{\rho {\left(1-\varsigma \right)}^2}}{e}^{-{\displaystyle \frac{1-\varsigma }{\varsigma }}\left(\sigma -{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}\right)}+{\displaystyle \frac{f\left(\sigma \right)}{1-\varsigma }}\hfill \\ \hfill & ={\displaystyle \frac{f\left(\rho \right)\left(\varsigma \rho -\rho -\varsigma \right)e^{-\frac{1-\varsigma }{\varsigma }\left(\sigma -\rho \right)}+\varsigma f\left(\rho \right)e^{-\frac{1-\varsigma }{\varsigma }\left(\sigma -\frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}\right)}+\rho \left(1-\varsigma \right)f\left(\sigma \right)}{\rho {\left(1-\varsigma \right)}^2}}.\hfill \end{array}$$

Thus, in relation to the two obtained results mentioned above, the inequality (27) is derived. □

The application of the inequality (27) for the ${\mathbb{B}}^{-1}$–convex function $f\left(\varpi \right)={\varpi }^s,0<s<1$ yields an inequality for the incomplete gamma function. The example about the result is presented as follows. Here, the incomplete gamma function is

$$\gamma \left(s,\varpi \right)={\int }_0^{\varpi }{\vartheta }^{s-1}{e}^{-\vartheta }d\vartheta .$$

(28)

Example 8. 

The function $f\left(\varpi \right)={\varpi }^s,0<s<1$ is a ${\mathbb{B}}^{-1}$–convex function from Example 1; hence, the inequality (27) is achieved. Indeed, the left side of the inequality is

$$\begin{array}{ccc}\hfill I_{{\rho }^{+}}^{\varsigma }f\left(\sigma \right)& =& {\displaystyle \frac{1}{\varsigma }}{\int }_{\rho }^{\sigma }exp\left(-{\displaystyle \frac{1-\varsigma }{\varsigma }}\left(\sigma -\vartheta \right)\right){\vartheta }^{s}d\vartheta \hfill \\ & =& {\displaystyle \frac{1}{1-\varsigma }}\left[{\left({\displaystyle \frac{\varsigma }{\varsigma -1}}\right)}^s{e}^{{\displaystyle \frac{\left(\varsigma -1\right)\sigma }{\varsigma }}}\left[\gamma \left(s+1,{\displaystyle \frac{\left(\varsigma -1\right)\sigma }{\varsigma }}\right)-\gamma \left(s+1,{\displaystyle \frac{\left(\varsigma -1\right)\rho }{\varsigma }}\right)\right]\right].\hfill \end{array}$$

The right side of the inequality is

$$\begin{array}{ccc}& & {\displaystyle \frac{f\left(\rho \right)\left(\varsigma \rho -\rho -\varsigma \right)e^{-\frac{1-\varsigma }{\varsigma }\left(\sigma -\rho \right)}+\varsigma f\left(\rho \right)e^{-\frac{1-\varsigma }{\varsigma }\left(\sigma -\frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}\right)}+\rho \left(1-\varsigma \right)f\left(\sigma \right)}{\rho {\left(1-\varsigma \right)}^2}}\hfill \\ & & ={\displaystyle \frac{\varsigma {\rho }^s{e}^{\frac{\left(\varsigma -1\right)\sigma }{\varsigma }}\left[\rho e^{\frac{\left(1-\varsigma \right)\rho }{\varsigma }}+e^{\frac{\left(1-\varsigma \right)}{\varsigma }\frac{{\sigma }^s}{{\rho }^{s-1}}}\right]-\left({\rho }^{s+1}+{\rho }^s\varsigma \right)e^{\frac{\left(\varsigma -1\right)}{\varsigma }\left(\sigma -\rho \right)}+\left(1-\varsigma \right)\rho {\sigma }^s}{{\left(1-\varsigma \right)}^2\rho }}.\hfill \end{array}$$

From above calculations, it has

$$\begin{array}{ccc}& {\displaystyle \frac{1}{1-\varsigma }}& \left[{\left({\displaystyle \frac{\varsigma }{\varsigma -1}}\right)}^s{e}^{{\displaystyle \frac{\left(\varsigma -1\right)\sigma }{\varsigma }}}\left[\gamma \left(s+1,{\displaystyle \frac{\left(\varsigma -1\right)\sigma }{\varsigma }}\right)-\gamma \left(s+1,{\displaystyle \frac{\left(\varsigma -1\right)\rho }{\varsigma }}\right)\right]\right]\hfill \\ & & \le {\displaystyle \frac{\varsigma {\rho }^s{e}^{\frac{\left(\varsigma -1\right)\sigma }{\varsigma }}\left[\rho e^{\frac{\left(1-\varsigma \right)\rho }{\varsigma }}+e^{\frac{\left(1-\varsigma \right)}{\varsigma }\frac{{\sigma }^s}{{\rho }^{s-1}}}\right]-\left({\rho }^{s+1}+{\rho }^s\varsigma \right)e^{\frac{\left(\varsigma -1\right)}{\varsigma }\left(\sigma -\rho \right)}+\left(1-\varsigma \right)\rho {\sigma }^s}{{\left(1-\varsigma \right)}^2\rho }}\hfill \\ & \gamma & \left(s+1,{\displaystyle \frac{\left(\varsigma -1\right)\sigma }{\varsigma }}\right)-\gamma \left(s+1,{\displaystyle \frac{\left(\varsigma -1\right)\rho }{\varsigma }}\right)\hfill \\ & & \le {\displaystyle \frac{\varsigma {\left(\varsigma -1\right)}^s{\rho }^s{e}^{\frac{\left(\varsigma -1\right)\sigma }{\varsigma }}\left[\rho e^{\frac{\left(1-\varsigma \right)\rho }{\varsigma }}+e^{\frac{\left(1-\varsigma \right)}{\varsigma }\frac{{\sigma }^s}{{\rho }^{s-1}}}\right]-{\left(\varsigma -1\right)}^s\left({\rho }^{s+1}+{\rho }^s\varsigma \right)e^{\frac{\left(\varsigma -1\right)}{\varsigma }\left(\sigma -\rho \right)}+{\left(\varsigma -1\right)}^s\left(1-\varsigma \right)\rho {\sigma }^s}{{\varsigma }^s\left(1-\varsigma \right)\rho e^{\frac{\left(\varsigma -1\right)\sigma }{\varsigma }}}}\hfill \end{array}$$

If $\rho =1,\sigma =3$ and $0<s<1,0<\varsigma <1$, then the above inequality is graphed as follows.

Theorem 12. 

Let $f:\left[\rho ,\sigma \right]\to {\mathbb{R}}_{++}$ be a ${\mathbb{B}}^{-1}$–convex function, $0<\varsigma <1$ and $f\in L_1\left[\rho ,\sigma \right]$; then, the following fractional integral with exponential kernel inequality holds:

$$I_{{\sigma }^{-}}^{\varsigma }f\left(\rho \right)\le \left\{\begin{array}{cc}{\displaystyle \frac{f\left(\rho \right)e^{\frac{1-\varsigma }{\varsigma }\left(\rho -\sigma \right)}\left(\sigma \varsigma -\sigma -\varsigma \right)-f\left(\rho \right)\left(\rho \varsigma -\rho -\varsigma \right)}{\rho {\left(\varsigma -1\right)}^2}},\hfill & 1<{\displaystyle \frac{\sigma }{\rho }}\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}\hfill \\ {\displaystyle \frac{\varsigma f\left(\rho \right)e^{\frac{1-\varsigma }{\varsigma }\left(\frac{\rho f\left(\rho \right)-\rho f\left(\sigma \right)}{f\left(\rho \right)}\right)}-\left(\rho \varsigma -\rho -\varsigma \right)f\left(\rho \right)+\rho \left(\varsigma -1\right)f\left(\sigma \right)e^{\frac{1-\varsigma }{\varsigma }\left(\rho -\sigma \right)}}{\rho {\left(\varsigma -1\right)}^2}},\hfill & 1\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}<{\displaystyle \frac{\sigma }{\rho }}.\hfill \end{array}\right.$$

(29)

Proof. 

When the same method is followed as above theorem, for the condition $1<{\displaystyle \frac{\sigma }{\rho }}\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}$, it has

$$\begin{array}{cc}\hfill {\displaystyle \frac{f\left(\rho \right)}{\rho }}{\int }_{\rho }^{\sigma }{\displaystyle \frac{\kappa \left(\vartheta -\rho \right)}{\vartheta -\rho }}\vartheta d\vartheta & ={\displaystyle \frac{f\left(\rho \right)}{\rho \varsigma }}{\int }_{\rho }^{\sigma }{e}^{-{\displaystyle \frac{1-\varsigma }{\varsigma }}\left(\vartheta -\rho \right)}\vartheta d\vartheta ={\displaystyle \frac{f\left(\rho \right)e^{\frac{1-\varsigma }{\varsigma }\rho }}{\rho \varsigma }}{\int }_{\rho }^{\sigma }t{e}^{-{\displaystyle \frac{1-\varsigma }{\varsigma }}\vartheta }d\vartheta \hfill \\ \hfill & ={\displaystyle \frac{f\left(\rho \right)e^{\frac{1-\varsigma }{\varsigma }\rho }}{\rho \left(\varsigma -1\right)}}\left(\sigma e^{-{\displaystyle \frac{1-\varsigma }{\varsigma }}\sigma }-\rho e^{-{\displaystyle \frac{1-\varsigma }{\varsigma }}\rho }\right)-{\displaystyle \frac{\varsigma f\left(\rho \right)e^{\frac{1-\varsigma }{\varsigma }\rho }}{\rho {\left(\varsigma -1\right)}^2}}\left(e^{-{\displaystyle \frac{1-\varsigma }{\varsigma }}\sigma }-e^{-{\displaystyle \frac{1-\varsigma }{\varsigma }}\rho }\right)\hfill \\ \hfill & ={\displaystyle \frac{f\left(\rho \right)e^{\frac{1-\varsigma }{\varsigma }\left(\rho -\sigma \right)}\left(\sigma \varsigma -\sigma -\varsigma \right)-f\left(\rho \right)\left(\rho \varsigma -\rho -\varsigma \right)}{\rho {\left(\varsigma -1\right)}^2}}.\hfill \end{array}$$

In the second condition $1\le {\displaystyle \frac{f\left(\sigma \right)}{f\left(\rho \right)}}<{\displaystyle \frac{\sigma }{\rho }}$, the equation is

$$\begin{array}{cc}\hfill {\displaystyle \frac{f\left(\rho \right)}{\rho }}& {\int }_{\rho }^{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}{\displaystyle \frac{\kappa \left(\vartheta -\rho \right)}{\vartheta -\rho }}\vartheta d\vartheta +f\left(\sigma \right){\int }_{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}^{\sigma }{\displaystyle \frac{\kappa \left(\vartheta -\rho \right)}{\vartheta -\rho }}d\vartheta \hfill \\ \hfill & ={\displaystyle \frac{f\left(\rho \right)e^{\frac{1-\varsigma }{\varsigma }\rho }}{\rho \varsigma }}{\int }_{\rho }^{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}\vartheta e^{-{\displaystyle \frac{1-\varsigma }{\varsigma }}\vartheta }d\vartheta +{\displaystyle \frac{f\left(\sigma \right)e^{\frac{1-\varsigma }{\varsigma }\rho }}{\varsigma }}{\int }_{{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}^{\sigma }{e}^{-{\displaystyle \frac{1-\varsigma }{\varsigma }}\vartheta }d\vartheta \hfill \\ \hfill & ={\displaystyle \frac{f\left(\rho \right)e^{\frac{1-\varsigma }{\varsigma }\rho }}{\rho \left(\varsigma -1\right)}}\left[e^{-{\displaystyle \frac{1-\varsigma }{\varsigma }}{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}\left({\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}-{\displaystyle \frac{\varsigma }{\varsigma -1}}\right)-e^{-{\displaystyle \frac{1-\varsigma }{\varsigma }}\rho }\left(\rho -{\displaystyle \frac{\varsigma }{\varsigma -1}}\right)\right]\hfill \\ \hfill & +{\displaystyle \frac{f\left(\sigma \right)e^{\frac{1-\varsigma }{\varsigma }\rho }}{\varsigma -1}}\left(e^{-{\displaystyle \frac{1-\varsigma }{\varsigma }}\sigma }-e^{-{\displaystyle \frac{1-\varsigma }{\varsigma }}{\displaystyle \frac{\rho f\left(\sigma \right)}{f\left(\rho \right)}}}\right)\hfill \\ \hfill & ={\displaystyle \frac{\varsigma f\left(\rho \right)e^{\frac{1-\varsigma }{\varsigma }\left(\frac{\rho f\left(\rho \right)-\rho f\left(\sigma \right)}{f\left(\rho \right)}\right)}-\left(\rho \varsigma -\rho -\varsigma \right)f\left(\rho \right)+\rho \left(\varsigma -1\right)f\left(\sigma \right)e^{\frac{1-\varsigma }{\varsigma }\left(\rho -\sigma \right)}}{\rho {\left(\varsigma -1\right)}^2}}.\hfill \end{array}$$

Consequently, the proof is accomplished. □

Example 9. 

The inequality (29) is valid for the ${\mathbb{B}}^{-1}$–convex function $f\left(\varpi \right)={\varpi }^s,0<s<1$. Indeed, the left side of the (29) is

$$\begin{array}{ccc}\hfill I_{{\sigma }^{-}}^{\varsigma }f\left(\rho \right)& =& {\displaystyle \frac{1}{\varsigma }}{\int }_{\rho }^{\sigma }exp\left(-{\displaystyle \frac{1-\varsigma }{\varsigma }}\left(\vartheta -\rho \right)\right){\vartheta }^{s}d\vartheta \hfill \\ & =& {\displaystyle \frac{1}{1-\varsigma }}\left[{\left({\displaystyle \frac{\varsigma }{1-\varsigma }}\right)}^s{e}^{{\displaystyle \frac{\left(1-\varsigma \right)\rho }{\varsigma }}}\left[\gamma \left(s+1,{\displaystyle \frac{\left(1-\varsigma \right)\rho }{\varsigma }}\right)-\gamma \left(s+1,{\displaystyle \frac{\left(1-\varsigma \right)\sigma }{\varsigma }}\right)\right]\right].\hfill \end{array}$$

The right side of the (29) is

$$\begin{array}{ccc}& & {\displaystyle \frac{\varsigma f\left(\rho \right)e^{\frac{1-\varsigma }{\varsigma }\left(\frac{\rho f\left(\rho \right)-\rho f\left(\sigma \right)}{f\left(\rho \right)}\right)}-\left(\rho \varsigma -\rho -\varsigma \right)f\left(\rho \right)+\rho \left(\varsigma -1\right)f\left(\sigma \right)e^{\frac{1-\varsigma }{\varsigma }\left(\rho -\sigma \right)}}{\rho {\left(\varsigma -1\right)}^2}}\hfill \\ & & ={\displaystyle \frac{\varsigma {\rho }^s{e}^{\frac{1-\varsigma }{\varsigma }\left(\rho -\frac{{\sigma }^s}{{\rho }^{s-1}}\right)}-\left(\rho \varsigma -\rho -\varsigma \right){\rho }^s+\rho \left(\varsigma -1\right){\sigma }^s{e}^{\frac{1-\varsigma }{\varsigma }\left(\rho -\sigma \right)}}{\rho {\left(\varsigma -1\right)}^2}}.\hfill \end{array}$$

From above, one has

$$\begin{array}{ccc}\hfill & {\displaystyle \frac{1}{1-\varsigma }}& \left[{\left({\displaystyle \frac{\varsigma }{1-\varsigma }}\right)}^s{e}^{{\displaystyle \frac{\left(1-\varsigma \right)\rho }{\varsigma }}}\left[\gamma \left(s+1,{\displaystyle \frac{\left(1-\varsigma \right)\rho }{\varsigma }}\right)-\gamma \left(s+1,{\displaystyle \frac{\left(1-\varsigma \right)\sigma }{\varsigma }}\right)\right]\right]\hfill \\ & & \le {\displaystyle \frac{\varsigma {\rho }^s{e}^{\frac{1-\varsigma }{\varsigma }\left(\rho -\frac{{\sigma }^s}{{\rho }^{s-1}}\right)}-\left(\rho \varsigma -\rho -\varsigma \right){\rho }^s+\rho \left(\varsigma -1\right){\sigma }^s{e}^{\frac{1-\varsigma }{\varsigma }\left(\rho -\sigma \right)}}{\rho {\left(\varsigma -1\right)}^2}}\hfill \\ & \gamma & \left(s+1,{\displaystyle \frac{\left(1-\varsigma \right)\rho }{\varsigma }}\right)-\gamma \left(s+1,{\displaystyle \frac{\left(1-\varsigma \right)\sigma }{\varsigma }}\right)\hfill \\ & & \le {\displaystyle \frac{\varsigma {\left(1-\varsigma \right)}^{s-1}{\rho }^s{e}^{\frac{1-\varsigma }{\varsigma }\left(\rho -\frac{{\sigma }^s}{{\rho }^{s-1}}\right)}-{\left(1-\varsigma \right)}^{s-1}\left(\rho \varsigma -\rho -\varsigma \right){\rho }^s-\rho {\left(1-\varsigma \right)}^s{\sigma }^s{e}^{\frac{1-\varsigma }{\varsigma }\left(\rho -\sigma \right)}}{\rho {\varsigma }^s{e}^{\frac{1-\varsigma }{\varsigma }\rho }}}.\hfill \end{array}$$

(30)

If $\rho =1,\sigma =3$ and $0<s<1,0<\varsigma <1$, then the inequality (30) is graphed as follows.

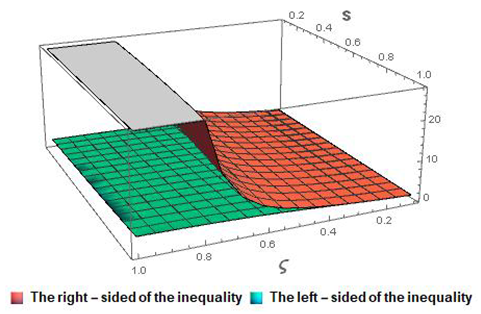
5. Conclusions

In the article, new general fractional inequalities have been proven for ${\mathbb{B}}^{-1}$–convex functions. The generalization of the inequalities have been demonstrated with the corollaries of the main theorems and the theorems in Section 4 also. It is shown that the old fractional Hermite–Hadamard inequalities for ${\mathbb{B}}^{-1}$–convex functions can be obtained from the new inequalities given in this paper. There are numerical examples for the fractional inequalities, and the validity of these inequalities have been established. Additionally, when two variables are released, two examples with graphs demonstrate the precision of the inequality using a fractional integral with an exponential kernel. Consequently, for the first time, numerical and graphical examples have been provided in research on ${\mathbb{B}}^{-1}$–convexity.

The future works about inequalities could be studied for different types of inequalities such as Ostrowski, Gauss–Jacobi, etc. Furthermore, because the fractional calculus has been expanding so quickly, a variety of fractional differential operators may be employed in the new inequalities. For example, the fractional operators in [42,43] could be used. Other kinds of abstract convexity could be examined in the forthcoming papers; however, the paper has been about the ${\mathbb{B}}^{-1}$–convexity.