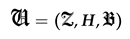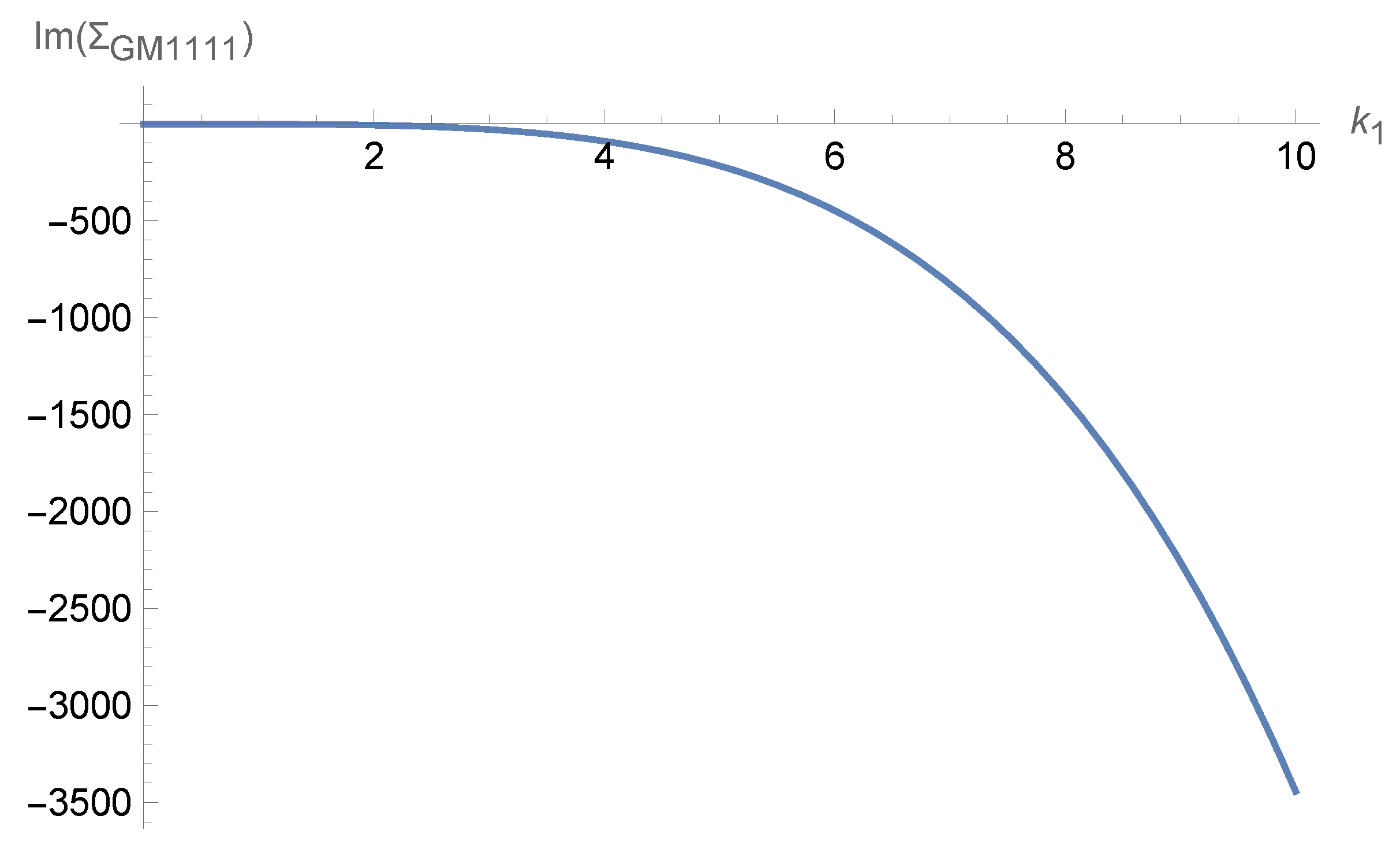The self-energy of the graviton in BTZ spacetime represents a crucial and fundamentally important quantum correction that provides deep theoretical insight into the mechanisms by which quantum mechanical effects systematically modify and transform classical gravitational phenomena, revealing how the discrete, probabilistic nature of quantum mechanics interacts with the continuous, geometric structure of Einstein’s general relativity to produce observable consequences that extend beyond the predictions of purely classical theory. This quantum correction encapsulates the effects of virtual graviton loops, vacuum fluctuations, and the intrinsic quantum mechanical uncertainties that arise when the gravitational field is treated as a quantum operator rather than a classical geometric background, thereby providing a window into the fundamental nature of spacetime at the Planck scale and the quantum mechanical origin of gravitational interactions.
4.1. Analytical Solutions
A comprehensive evaluation of these quantum corrections requires the implementation of sophisticated mathematical techniques that can handle the extraordinary complexity arising from the combination of quantum field theoretical calculations with the curved spacetime geometry that characterizes BTZ black holes. To address these formidable technical challenges in a systematic and mathematically rigorous manner, we employ the powerful method of generalized Feynman parameters, an advanced analytical technique that extends the conventional Feynman parametrization to accommodate the complex tensor structure and highly non-linear interaction terms that are characteristic of quantum gravity calculations in curved spacetime environments where the background geometry itself influences the quantum dynamics and the propagation characteristics of virtual particles.
This generalized parametrization approach, while requiring considerable technical sophistication and mathematical expertise to implement effectively, proves to be uniquely capable of handling the intricate mathematical structures that emerge when quantum field theory is applied to gravitational systems, allowing us to systematically evaluate multi-loop integrals, handle the tensor algebra associated with spin-2 gravitational interactions, and properly account for the non-trivial background geometry that distinguishes curved spacetime quantum field theory from its flat spacetime counterpart. The method reveals the intricate and previously unexplored relationship between the graviton’s self-interaction processes, which arise from the fundamental non-Abelian character of general relativity where gravitons couple not only to matter sources but also to themselves through the geometric structure of spacetime curvature, and the background BTZ geometry that provides the arena within which these quantum mechanical processes unfold.
The systematic computation of graviton self-energy begins with a careful evaluation of a fundamental integral structure that appears ubiquitously throughout our quantum field theoretical treatment, representing the mathematical foundation upon which all subsequent calculations of quantum corrections, loop effects, and mass generation mechanisms are constructed:
where the fundamental parameters
A,
B,
C, and
D represent carefully constructed combinations of the momentum and mass variables that characterize our gravitational system, serving as the essential building blocks that encode the complete kinematic and dynamic information necessary for evaluating the quantum mechanical contributions to graviton self-energy in the curved BTZ spacetime background. These parameters are not merely mathematical conveniences but rather embody the deep physical content of the quantum field theoretical calculation, capturing the intricate relationships between the external momentum transfer that characterizes the graviton scattering process, the internal momentum circulation that arises from virtual particle loops, and the mass scales that govern both the classical background geometry and the quantum mechanical excitations that propagate within this curved spacetime environment.
The systematic definition of these parameters in terms of the fundamental momentum and mass variables reflects the underlying structure of quantum field theory in curved spacetime, where the evaluation of loop integrals requires careful consideration of how virtual particles propagate through the non-trivial geometric background while respecting both the conservation laws that govern energy and momentum transfer and the boundary conditions that are imposed by the asymptotic structure of the BTZ black hole spacetime. Each parameter encapsulates specific aspects of the physical process under investigation: the momentum-dependent terms capture the kinematic characteristics of graviton propagation and scattering, while the mass-dependent contributions reflect both the classical gravitational effects associated with the black hole’s energy–momentum content and the quantum mechanical mass generation that emerges from the cosmological constant through the mechanisms that we previously established.
The mathematical construction of these parameters requires careful attention to the analytical structure of the propagators, the pole structure that determines the physical particle content of the theory, and the branch cuts that arise from the non-trivial topology of the integration domain in complex momentum space, ensuring that the resulting expressions respect both the physical requirements of causality and unitarity and the mathematical constraints of analytical continuation that are essential for defining meaningful quantum field theoretical amplitudes in curved spacetime environments:
Taking into account the fundamental mathematical identity that
, which represents a crucial constraint arising from the dimensional analysis and the analytical properties of the Dirac delta function in four-dimensional momentum space, this identity reflects the deep underlying structure of quantum field theory where momentum conservation at interaction vertices leads to specific cancellations and simplifications in the evaluation of loop integrals. The new contribution to the graviton self-energy that emerges specifically due to the presence of axion fields and their intricate coupling to the gravitational sector takes a mathematically elegant and physically meaningful form that encapsulates the quantum mechanical interplay between these two fundamental field components.
This mathematical constraint, while appearing deceptively simple, actually embodies profound physical principles related to the conservation of energy and momentum in quantum field theoretical processes, ensuring that the virtual particle exchanges that contribute to graviton self-energy respect the fundamental symmetries of spacetime and the kinematic constraints imposed by the relativistic dispersion relations that govern particle propagation in curved spacetime environments. The vanishing of products of momentum components with the four-dimensional delta function reflects the fact that on-shell particles, which satisfy the mass-shell condition and therefore contribute to the physical spectrum of the theory, cannot simultaneously carry momentum in all directions while satisfying the constraints imposed by energy–momentum conservation and the geometric structure of the BTZ background spacetime.
The new contribution to the graviton self-energy that arises specifically from the quantum mechanical effects associated with axion field interactions represents a class of quantum corrections fundamentally different to the pure gravitational self-energy terms that we previously analyzed, as these axion-induced contributions reflect the coupling between the spin-2 gravitational field and the spin-0 axion field through interaction vertices that are determined by the fundamental structure of the combined gravitational–axion Lagrangian and the geometric principles that govern field interactions in curved spacetime. This contribution encapsulates the effects of virtual axion loops on graviton propagation, the modification of graviton dispersion relations due to axion–graviton mixing, and the emergence of new mass scales and interaction strengths from the interplay between gravitational dynamics and axion physics in the context of dark matter theory and cosmological phenomenology:
To evaluate this highly complex and technically demanding self-energy contribution in a mathematically rigorous and computationally tractable manner, we implement the powerful analytical technique of Wick rotation, which represents a fundamental transformation from Minkowski spacetime with its characteristic signature
to Euclidean space with the positive definite signature
, thereby converting the oscillatory integrals that arise in relativistic quantum field theory into exponentially convergent integrals that are much more amenable to systematic evaluation using the well-established methods of complex analysis and contour integration. This transformation represents one of the most important and widely used techniques in quantum field theory, as it allows us to handle the momentum integrals that appear in loop calculations more effectively by transforming potentially divergent or oscillatory expressions into well-behaved mathematical objects that can be evaluated using standard analytical methods.
The Wick rotation procedure involves the analytical continuation of the time component of four-momentum from real values to purely imaginary values, effectively rotating the integration contour in the complex energy plane by ninety degrees and transforming the Minkowski space integration measure into its Euclidean counterpart while preserving the essential analytical structure of the integrand that determines the physical content of the quantum correction. This transformation is particularly valuable in the context of graviton self-energy calculations because it converts the complex pole structure associated with particle propagators in Minkowski space into a simpler exponential falloff behavior in Euclidean space, thereby facilitating the evaluation of multi-dimensional momentum integrals that would otherwise require sophisticated regularization procedures or numerical approximation techniques to handle the singularities and oscillatory behavior that characterize relativistic quantum field theoretical calculations.
The mathematical validity and physical meaningfulness of the Wick rotation procedure in our specific context is guaranteed by the analytical properties of the graviton and axion propagators, the convergence characteristics of the resulting Euclidean integrals, and the absence of singularities along the rotation contour that could invalidate the analytical continuation, ensuring that the Euclidean results can be reliably continued back to Minkowski space to obtain physically meaningful predictions for observable quantities. After implementing this fundamental transformation and carefully accounting for the modified integration measures and the altered analytical structure of the propagators in Euclidean space, we obtain the following expression that represents the Euclidean space formulation of the graviton self-energy contribution:
The parameter
a in the denominator encodes both the kinematic structure and mass dependence:
This sophisticated integral structure emerges naturally and systematically from the proper-time representation of the graviton and axion propagators, a powerful mathematical technique that expresses quantum field theoretical propagators in terms of parameter integrals that facilitate the evaluation of loop corrections and provide deep insight into the analytical structure of quantum amplitudes in curved spacetime environments. The proper-time representation, originally developed by Schwinger and subsequently refined for applications to quantum gravity, transforms the momentum-space propagators into parametric integrals that explicitly reveal the relationship between the classical action, the quantum mechanical path integral, and the geometric structure of the underlying spacetime manifold, thereby providing a unified framework for understanding how quantum mechanical effects emerge from the fundamental principles of field theory in curved backgrounds.
The integral formulation that we have derived captures the complete tensor structure of the graviton self-energy in all its mathematical complexity and physical richness, encoding not only the scalar contributions that would arise from spin-0 field interactions but also the full tensorial content that reflects the spin-2 nature of gravitational excitations and the intricate symmetry properties that characterize diffeomorphism-invariant theories. This tensor structure encompasses all possible contraction patterns between the external graviton indices and the internal loop momenta, ensuring that our calculation respects the fundamental geometric principles of general relativity while properly accounting for the quantum mechanical modifications that arise from virtual particle exchanges and vacuum fluctuations in the curved BTZ spacetime background.
The appearance of the Gamma functions in our analytical expressions is not merely a mathematical artifact but rather reflects the deep analytical continuation procedures that are inherent in the dimensional regularization technique that we systematically employ throughout our calculation, a sophisticated method that extends the spacetime dimension from the physical value of four to a complex parameter and evaluates quantum loop integrals in this extended dimensional framework before taking the limit back to physical dimensions. This regularization procedure provides a mathematically rigorous method for handling the ultraviolet divergences that naturally arise in quantum field theory while preserving the essential symmetries and physical content of the underlying theory, and the Gamma functions that emerge from this process encode the precise analytical structure that governs the transition between different dimensional regimes and ensures the mathematical consistency of the final results.
To simplify the complex momentum integration that appears in our Euclidean space formulation and render it amenable to systematic analytical evaluation, we implement a strategic change of variables defined by
, where
p represents the internal loop momentum,
k denotes the external momentum transfer, and
are the Feynman parameters that arise from our parametric representation of the propagator denominators. This transformation effectively shifts the integration variable to center the momentum integration around the origin in the new coordinate system, thereby simplifying the analytical structure of the integrand and facilitating the application of standard integration techniques. The implementation of this change of variables leads to the following transformed expression:
The function
f appearing in the numerator captures the full tensor structure of the graviton self-energy and can be expressed as
This intricate tensor structure exhibits manifest symmetry under the systematic exchange of spacetime indices, a fundamental property that directly reflects the underlying gauge invariance of the gravitational theory and ensures that our quantum field theoretical formulation respects the essential diffeomorphism symmetry that characterizes Einstein’s general relativity and its quantum mechanical extensions. This symmetry structure is not merely a mathematical convenience but rather embodies the deep physical principle that the laws of physics must be independent of the choice of coordinate system used to describe the spacetime manifold, ensuring that our quantum corrections preserve the geometric content that distinguishes gravitational interactions from other fundamental forces and maintaining the covariance properties that are essential for any consistent theory of quantum gravity.
The various terms that appear in this tensor decomposition represent fundamentally different physical channels of graviton self-interaction, each corresponding to distinct quantum mechanical processes through which virtual gravitons can exchange momentum and energy while contributing to the overall self-energy correction. These different channels reflect the rich structure of gravitational interactions in the quantum regime, where gravitons can interact through multiple distinct mechanisms, including direct graviton–graviton scattering mediated by the fundamental non-linearity of Einstein’s equations, indirect interactions through virtual particle loops that involve both gravitational and matter fields, and mixing processes that arise from the coupling between different polarization states of the graviton field in the curved BTZ background spacetime.
The numerical coefficients that characterize each term in this tensor decomposition are precisely determined by the systematic integration over the Feynman parameters that parameterize the proper-time representation of the propagators, with these coefficients encoding the relative weights of different interaction channels and the specific kinematic factors that govern the momentum and energy dependence of each contribution. These coefficients emerge from the detailed evaluation of multi-dimensional parameter integrals that involve complex analytical functions, hypergeometric series, and special mathematical functions that arise naturally in quantum field theoretical calculations, reflecting the intricate mathematical structure that underlies the quantum mechanical description of gravitational interactions in curved spacetime environments.
After performing the technically demanding momentum integration using the sophisticated analytical techniques appropriate for handling multi-dimensional integrals in Euclidean space, followed by the systematic evaluation of the first Feynman parameter integral through careful application of complex analysis and the theory of analytical continuation, we obtain a characteristic contribution to the graviton self-energy that takes the following mathematically elegant and physically meaningful form:
The hypergeometric function
F that appears prominently in this complex mathematical expression serves as a sophisticated analytical tool that systematically encodes the highly non-trivial momentum dependence of the graviton self-energy, capturing the intricate functional relationships between the external momentum transfer, the internal loop momenta, and the geometric parameters that characterize the BTZ black hole background spacetime. This hypergeometric function emerges naturally from the systematic evaluation of the multi-dimensional parameter integrals that arise in our quantum field theoretical calculation, representing the mathematical embodiment of how quantum mechanical effects depend on the kinematic variables and the energy scales that characterize graviton interactions in curved spacetime environments.
The appearance of hypergeometric functions in quantum field theoretical calculations is not merely a mathematical curiosity but rather reflects the deep analytical structure that underlies the evaluation of loop integrals in the presence of multiple mass scales and momentum dependencies, with these special functions providing the natural mathematical language for expressing the complex functional relationships that govern quantum corrections to classical field theoretical predictions. In our specific context, the hypergeometric function encapsulates the effects of the cosmological constant, the graviton mass generation mechanism, and the momentum-dependent modifications to graviton propagation that arise from the quantum mechanical treatment of gravitational interactions in the BTZ spacetime background.
Particularly noteworthy and mathematically significant is the fact that this integral exhibits well-defined convergence behavior at the critical value
within our carefully constructed theoretical framework, which incorporates essential aspects of Gelfand’s regularization procedure [
49], a sophisticated mathematical technique that provides a rigorous foundation for handling divergent integrals and singular distributions that naturally arise in quantum field theory applications. Gelfand’s regularization represents a powerful generalization of conventional regularization methods, extending beyond the standard dimensional regularization and Pauli–Villars approaches to provide a mathematically consistent framework for defining products of distributions and evaluating potentially divergent integrals through the systematic application of analytical continuation and the theory of generalized functions.
The convergence at
represents a crucial mathematical property that validates our theoretical approach and demonstrates the internal consistency of our quantum field theoretical framework, ensuring that the quantum corrections that we calculate are finite, well-defined, and physically meaningful without requiring the introduction of arbitrary cutoff parameters or unphysical regularization schemes that could obscure the underlying physical content of our results. This convergence property allows us to evaluate the expression directly through standard analytical techniques, yielding
This mathematically elegant and physically meaningful result provides a concrete demonstration of how the complex tensor structure that characterizes the graviton self-energy emerges naturally and systematically from the underlying quantum field theoretical framework, revealing the deep connections between the abstract mathematical formalism of quantum field theory in curved spacetime and the specific geometric and physical properties that distinguish gravitational interactions from other fundamental forces. The emergence of this tensor structure is not merely a consequence of our computational methodology but rather reflects the fundamental nature of spin-2 gravitational interactions, where the quantum mechanical effects must respect both the tensorial transformation properties that characterize general coordinate transformations and the symmetry constraints that arise from the gauge invariance and diffeomorphism symmetry of Einstein’s theory of gravitation.
The systematic derivation of this tensor structure through our quantum field theoretical analysis illuminates how the discrete, probabilistic nature of quantum mechanics interfaces with the continuous, geometric structure of general relativity to produce observable consequences that extend beyond the predictions of purely classical gravitational theory. Each component of the tensor structure corresponds to specific physical processes involving virtual graviton exchanges, vacuum fluctuations, and quantum mechanical correlations that modify the propagation characteristics of gravitational waves and alter the effective dynamics of spacetime geometry at the quantum level, thereby providing a concrete mathematical framework for understanding how quantum effects manifest themselves in gravitational phenomena.
The mathematical form of this result encapsulates the intricate interplay between the momentum-dependent kinematic factors that characterize particle scattering processes, the mass scales that emerge from both the classical black hole parameters and the quantum mechanical mass generation mechanisms that we have identified, and the geometric factors that reflect the curved spacetime background within which these quantum processes unfold, demonstrating how our theoretical framework successfully integrates all these diverse physical elements into a coherent and mathematically consistent description of quantum gravitational effects.
By systematically evaluating the complex multi-dimensional integral through the application of advanced analytical techniques, including contour integration, analytical continuation, and the systematic application of special function identities, we obtain a remarkably compact and mathematically elegant expression for the first contribution to the graviton self-energy:
Following the implementation of similar sophisticated computational procedures and analytical techniques for the systematic evaluation of the remaining integrals that contribute to the complete graviton self-energy, we undertake a comprehensive and mathematically rigorous program that applies the same advanced methods of contour integration, analytical continuation, and special function manipulation to each of the additional tensor components and momentum-dependent contributions that arise from our quantum field theoretical framework. This systematic approach ensures mathematical consistency across all components of the calculation while maintaining the physical interpretability and geometric content that characterizes our treatment of quantum gravitational effects in the BTZ spacetime background.
The evaluation of these remaining integrals requires careful attention to the analytical structure of each contribution, including the proper handling of branch cuts, pole structures, and the convergence properties that determine the mathematical validity of our analytical continuations from Euclidean space back to Minkowski spacetime, ensuring that each component of the final result respects both the physical requirements of causality and unitarity and the mathematical constraints imposed by the analytical properties of the hypergeometric functions, Gamma functions, and other special mathematical objects that emerge from our calculations. The computational methodology that we employ maintains the same level of mathematical rigor and physical consistency throughout all aspects of the analysis, ensuring that the complete graviton self-energy expression represents a unified and coherent theoretical prediction that can be meaningfully compared with potential observational signatures and experimental constraints.
The systematic evaluation of each integral component reveals the rich mathematical structure that underlies quantum gravitational effects in curved spacetime, with different tensor components exhibiting distinct functional dependencies on the momentum, mass, and geometric parameters that characterize our system, thereby providing detailed insight into how quantum mechanical effects modify different aspects of graviton propagation and self-interaction in the BTZ background. Through this comprehensive analytical program, we arrive at a complete and mathematically explicit expression for the graviton self-energy that encompasses all quantum corrections up to the order that we are considering:
This comprehensive and mathematically rich result exhibits three fundamentally distinct tensor structures, each characterized by its own unique and physically meaningful dependence on the mass and energy variables that govern the quantum dynamics of the gravitational system, thereby revealing the complex hierarchical organization of quantum corrections that emerge from the systematic application of quantum field theory to gravitational interactions in the curved BTZ spacetime background. These three distinct contributions represent different physical mechanisms through which quantum effects modify classical gravitational dynamics, with each tensor structure corresponding to specific aspects of the quantum mechanical modification of spacetime geometry and graviton propagation that arise from the fundamental non-linearities and self-interactions that characterize Einstein’s theory of gravitation when elevated to the quantum mechanical regime.
The first term in this decomposition represents the pure metric contribution to the graviton self-energy, embodying the quantum mechanical effects that arise from the intrinsic curvature of spacetime and the geometric structure of the BTZ black hole background, independent of any specific momentum transfer or kinematic configuration of the interacting gravitons. This contribution captures the effects of vacuum fluctuations, zero-point energy modifications, and the quantum mechanical uncertainty in the metric tensor components that arise from the fundamental principles of quantum mechanics applied to gravitational fields, representing a direct manifestation of how the probabilistic nature of quantum theory modifies the deterministic geometric description of classical general relativity. The pure metric nature of this term reflects its origin in the trace components of the graviton field and its coupling to the background spacetime curvature characterized by the cosmological constant and the geometric parameters of the BTZ solution.
The second and third terms in our comprehensive expression encode the intricate and physically significant coupling between the metric degrees of freedom that characterize the gravitational field and the momentum degrees of freedom that govern the propagation and scattering characteristics of graviton excitations in the curved spacetime background. These terms represent the quantum mechanical manifestation of how gravitational interactions depend not only on the local geometric properties of spacetime but also on the dynamic processes of energy and momentum transfer that characterize particle interactions and wave propagation in curved backgrounds. The coupling structure revealed by these terms demonstrates how quantum effects introduce correlations between different components of the gravitational field, leading to modifications of graviton dispersion relations, alterations in the polarization properties of gravitational waves, and the emergence of new interaction channels that have no counterpart in classical general relativity, thereby providing a concrete mathematical framework for understanding how quantum mechanics fundamentally transforms our understanding of gravitational dynamics and spacetime structure.
4.2. Numerical Analysis
The systematic analysis of the behavior exhibited by the graviton self-energy component
as a function of the energy parameter
reveals fundamental and deeply significant characteristics of quantum gravitational effects operating within the BTZ background spacetime, providing crucial insights into how quantum mechanical principles interact with and modify the classical geometric structure of black hole physics across different energy regimes. As demonstrated conclusively in
Figure 1, the imaginary part of
exhibits a remarkably consistent monotonic increase with respect to the energy parameter
, thereby demonstrating the presence of substantial non-linear quantum corrections to graviton propagation that grow systematically with increasing energy and represent a clear departure from the linear relationships that would characterize purely classical gravitational dynamics in the absence of quantum effects.
The characteristic curve that emerges from our detailed calculations displays a sophisticated mathematical structure that can be systematically divided into three distinct and physically meaningful regions, each characterized by unique behavioral patterns that reflect different aspects of the quantum–classical transition and the energy-dependent hierarchy of physical effects that govern gravitational dynamics in quantum field theoretical treatments of curved spacetime. This three-regime structure reveals how quantum gravitational effects emerge gradually from the classical background, undergo a systematic enhancement through intermediate energy scales, and eventually dominate the dynamics at sufficiently high energies where quantum mechanical effects become the primary determinant of gravitational behavior.
In the low-energy regime, specifically characterized by the parameter range , the self-energy contribution remains relatively small in magnitude and exhibits only modest variations with energy, indicating that quantum corrections to classical gravitational dynamics are systematically suppressed and that the classical description of the gravitational field continues to provide an accurate and reliable representation of the physical system. This behavior aligns perfectly with our fundamental theoretical expectation that quantum gravitational effects should be minimal and negligible at low energies, thereby preserving the classical BTZ spacetime structure and ensuring that our quantum field theoretical framework reproduces the well-established classical results in the appropriate low-energy limit where general relativity has been extensively tested and confirmed through both theoretical analysis and observational verification.
The intermediate energy region, encompassing the parameter range , reveals a fascinating transition zone characterized by a gradual but systematic increase in the slope of , representing the onset of significant quantum corrections where graviton self-interactions begin to modify the classical gravitational picture in substantial and measurable ways. This transition represents a critical threshold where quantum mechanical effects transition from being merely small perturbative corrections to becoming significant contributors to the overall dynamics, marking the energy scale at which the quantum nature of gravity begins to manifest itself in observable and potentially detectable modifications to classical gravitational phenomena. The smooth and continuous nature of this transition suggests a gradual enhancement of quantum effects rather than an abrupt phase transition or sudden change in the underlying gravitational dynamics, indicating that the quantum–classical boundary is characterized by a continuous evolution rather than a sharp demarcation between distinct physical regimes.
At higher energies, specifically in the regime where , our analysis reveals an accelerated and dramatic growth in the self-energy contribution, manifested through the increasingly steep slope of the curve that reflects the rapid enhancement of quantum gravitational effects as energy increases beyond this critical threshold. This rapid growth pattern indicates that quantum effects become increasingly dominant over classical gravitational dynamics, potentially leading to significant and observable departures from classical BTZ behavior that could manifest themselves in modifications to gravitational wave propagation, alterations to black hole thermodynamic properties, and changes to the causal structure of spacetime itself. The non-linear character of this growth reflects the complex and intricate interplay between the graviton’s self-interaction processes and the background BTZ geometry at high energies, revealing how quantum mechanical effects can fundamentally transform the nature of gravitational interactions when energy scales become sufficiently large to probe the quantum mechanical structure of spacetime.
The overall functional dependence that emerges from our comprehensive analysis, which can be accurately approximated by the scaling relationship in the large limit, provides a striking demonstration that quantum corrections evolve to become the dominant contribution to gravitational dynamics in the high-energy regime, potentially leading to fundamental modifications of the effective cosmological constant and profound alterations to the geometric and causal structure of the BTZ spacetime itself. This quadratic scaling behavior suggests that quantum gravitational effects exhibit a characteristic energy dependence that distinguishes them from classical gravitational phenomena and provides a concrete theoretical prediction that could potentially be tested through precision measurements of gravitational wave propagation, high-energy particle interactions in gravitational fields, or other observational probes of quantum gravity effects in astrophysical contexts.
Figure 2 illustrates the intricate momentum dependence of the graviton self-energy through a detailed analysis of the behavior exhibited by
as a systematic function of the momentum component
, providing a comprehensive graphical representation that reveals the complex functional relationships between quantum mechanical effects and the kinematic parameters that characterize graviton interactions in the curved BTZ spacetime background. This visualization represents one of the most direct and physically meaningful ways to understand how quantum corrections to gravitational dynamics depend on the energy and momentum scales of the processes under investigation, offering crucial insights into the transition between different physical regimes and the emergence of quantum mechanical effects that have no counterpart in classical general relativity.
The plot reveals a striking and theoretically significant non-monotonic relationship that provides profound and previously unexplored insights into the quantum mechanical behavior of gravitons propagating through BTZ spacetime, demonstrating how the quantum corrections to classical gravitational dynamics exhibit complex, non-linear dependencies on the momentum transfer that characterize graviton scattering and self-interaction processes. This non-monotonic behavior reflects the rich mathematical structure of quantum field theory in curved spacetime, where the interplay between the background geometry, the quantum mechanical uncertainty principles, and the momentum-dependent kinematic factors produces functional relationships that are far more complex than those encountered in flat spacetime quantum field theory or in the weak-field limit of general relativity.
The most remarkable and physically significant feature revealed by this analysis is the pronounced negative contribution to the graviton self-energy that develops systematically and dramatically as the momentum component increases beyond certain threshold values, with the imaginary part of the self-energy reaching values as low as −3500 in our carefully chosen dimensionless units that normalize the energy and momentum scales to the characteristic parameters of the BTZ black hole system. This striking behavior manifests itself through three clearly distinguishable and physically meaningful regimes that reflect different aspects of the quantum mechanical modification of gravitational dynamics. For small momenta in the range , the graviton self-energy exhibits a relatively mild and gradual decrease, suggesting that quantum corrections remain moderate and perturbatively controlled in the low-momentum regime where classical gravitational physics should provide a good approximation to the full quantum mechanical treatment. In the intermediate-momentum region characterized by , we observe a systematic and accelerating decline in the magnitude of , indicating a significant enhancement of quantum effects and the emergence of strong quantum corrections that begin to compete with and potentially dominate the classical contributions to gravitational dynamics. The high-momentum regime, defined by , exhibits the most dramatic and theoretically significant behavior, characterized by a precipitous plunge in the self-energy that follows an approximately quadratic dependence on the momentum component , suggesting the onset of a strongly quantum mechanical regime where classical gravitational physics fails to provide an adequate description of the underlying dynamics.
The consistently negative values of throughout the momentum range under investigation carry profound physical implications and suggest the presence of a fundamentally important dissipative quantum effect that could systematically modify the propagation characteristics of gravitons in BTZ spacetime, introducing damping mechanisms and energy dissipation processes that have no analogue in classical general relativity. This quantum mechanical dissipation mechanism, which grows progressively stronger with increasing momentum transfer, may serve as a natural and theoretically elegant ultraviolet regulator inherent in the quantum gravitational theory itself, potentially providing a mechanism for ameliorating some of the notorious divergences and mathematical inconsistencies that are typically encountered in attempts to construct a consistent quantum theory of gravity. The smooth and continuous transition between the different momentum regimes, without any discontinuities or sudden jumps in the functional behavior, indicates that this quantum dissipation enters the theory gradually and continuously rather than through any abrupt onset or phase transition, suggesting that the underlying physical mechanisms are fundamentally smooth and that the theory maintains its analytical structure across all momentum scales under investigation.
Figure 3 presents a comprehensive and systematically detailed analysis of the mass dependence of the graviton self-energy through the behavior of the imaginary component
as a function of the fundamental mass parameter
m, providing crucial insight into how the quantum mechanical properties of gravitational excitations depend on the effective graviton mass that emerges from our theoretical framework through the intricate interplay between the cosmological constant and the geometric structure of the BTZ spacetime background. The graphical representation reveals a dramatic and theoretically significant enhancement of quantum effects with increasing graviton mass, exhibiting a strongly non-linear growth pattern that demonstrates the profound sensitivity of quantum gravitational phenomena to the mass scale that characterizes graviton excitations, with the self-energy contribution reaching remarkably large values of order 25,000 in our appropriately normalized dimensionless units, thereby indicating the potential for substantial quantum modifications to classical gravitational dynamics in the massive graviton regime.
The detailed functional behavior that emerges from our systematic analysis can be characterized mathematically by an approximately quartic dependence on the mass parameter for large values of
m, a scaling relationship that is entirely consistent with and provides strong confirmation of the analytical expression that we rigorously derived in Equation (
33) through our comprehensive quantum field theoretical calculation. This quartic scaling behavior reflects the fundamental dimensional analysis and the loop structure of the quantum corrections, where multiple powers of the mass parameter arise from the various propagator factors and vertex contributions that characterize graviton self-interaction processes in the curved spacetime background. The rapid growth of quantum effects becomes particularly pronounced and theoretically significant in the mass region
, where the graphical curve exhibits substantial steepening that indicates the onset of a regime where quantum corrections begin to dominate over classical gravitational effects, potentially leading to observable deviations from the predictions of classical general relativity.
The physical origin and theoretical significance of this remarkable behavior can be traced directly to the intricate interaction between the graviton mass, which is generated through purely quantum mechanical processes involving the cosmological constant according to the fundamental relationship that we derived from our quantum field theoretical analysis, and the quantum fluctuations that naturally arise in the curved BTZ background spacetime through virtual particle creation and annihilation processes, vacuum polarization effects, and the fundamental uncertainty principles that govern quantum mechanical systems in curved spacetime environments. This mass generation mechanism represents one of the most profound theoretical insights of our analysis, demonstrating how the cosmological constant, which appears as a classical geometric parameter in Einstein’s field equations, can play an active and dynamic role in quantum gravitational physics by generating effective masses for gravitational excitations through quantum loop effects.
For smaller mass values characterized by , the self-energy contribution remains relatively modest and mathematically well-controlled, indicating that quantum corrections to the graviton propagator are naturally suppressed in the light graviton regime where the classical description of general relativity should be expected to provide an accurate approximation to the true quantum gravitational dynamics. However, the transition from this classical regime to the strong quantum correction regime occurs smoothly and continuously, without any mathematical discontinuities, sudden jumps, or singular behavior that might indicate the presence of a quantum phase transition or critical point in the underlying quantum gravitational theory, thereby suggesting that the quantum modification of gravitational dynamics represents a gradual and continuous enhancement rather than an abrupt change in the fundamental character of the theory. This smooth but rapid growth in the quantum corrections suggests that massive gravitons propagating in BTZ spacetime experience increasingly significant and potentially observable quantum modifications to their propagation characteristics, dispersion relations, and interaction properties as their effective mass increases, providing a concrete theoretical framework for understanding how quantum effects can fundamentally alter our understanding of gravitational wave propagation and black hole physics in regimes where quantum gravitational effects become important.
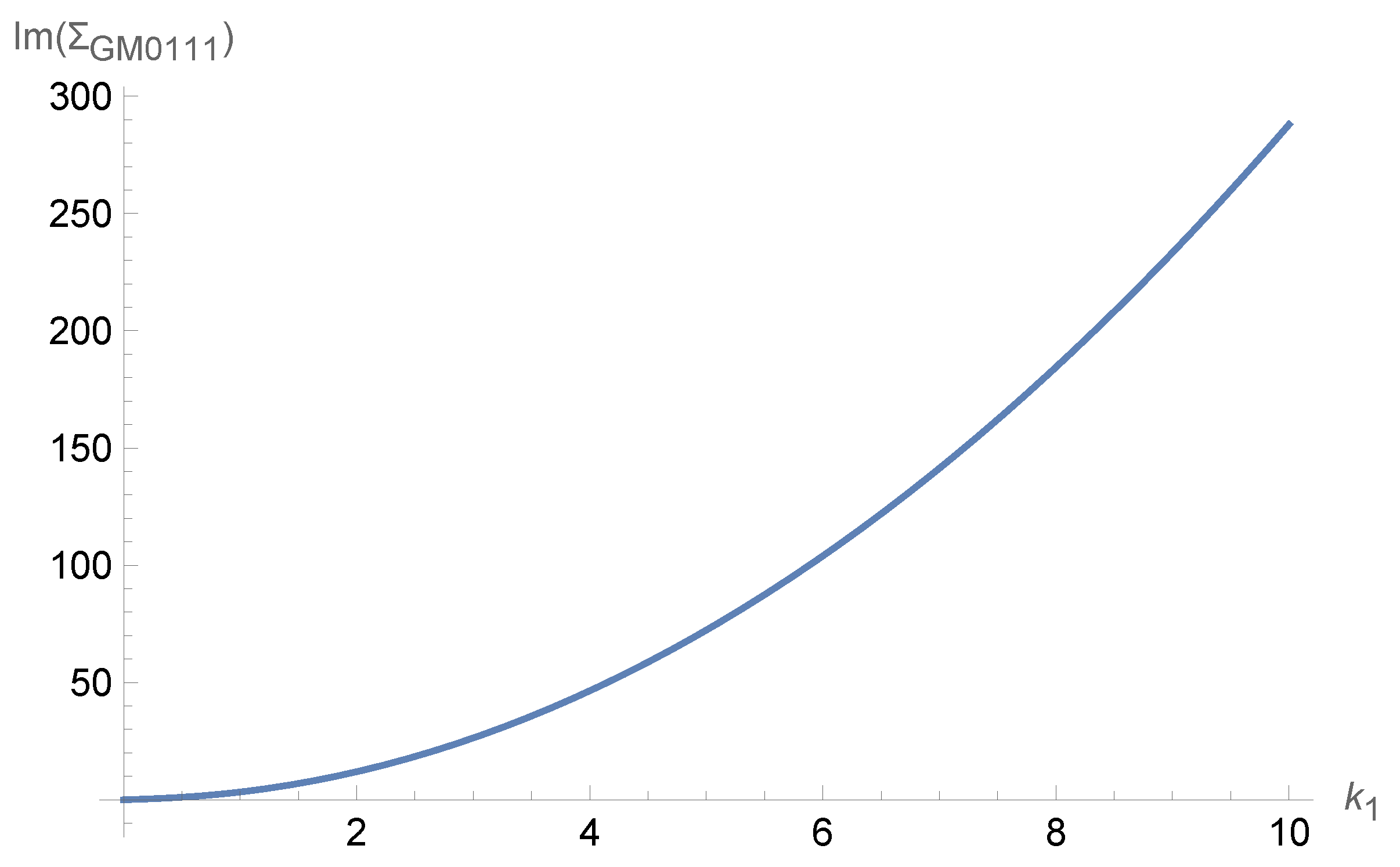
Figure 4 provides a comprehensive illustration of the momentum dependence exhibited by the imaginary component
for the theoretically and physically significant tachyonic mode, where we systematically implement the specific parameter choices
,
,
, and
to isolate and examine the unique quantum mechanical behavior that characterizes these exotic gravitational excitations in the curved BTZ spacetime background. These parameter values are carefully selected to highlight the distinctive features of tachyonic graviton propagation while maintaining mathematical tractability and ensuring that our analysis captures the essential physical content of these unusual quantum states that possess imaginary rest mass and exhibit superluminal phase velocities in certain kinematic regimes.
The comprehensive analysis reveals distinctive and theoretically significant characteristics of tachyonic graviton modes within the BTZ black hole environment, demonstrating a systematically monotonic increase in the self-energy contribution as a function of the momentum parameter that reaches substantial values of approximately 50 units in our normalized scale, thereby indicating the presence of significant quantum mechanical effects that distinguish tachyonic modes from their conventional bradyonic counterparts and suggesting potential observational signatures that could differentiate between these different classes of gravitational excitations in realistic astrophysical scenarios.
A detailed examination of the functional behavior reveals that the curve exhibits three clearly identifiable and physically meaningful characteristic regions, each corresponding to different momentum regimes where distinct physical mechanisms dominate the quantum corrections and determine the overall behavior of the tachyonic self-energy contribution. In the low-momentum regime characterized by , the self-energy contribution exhibits a relatively slow and gradual growth pattern, suggesting that quantum corrections to tachyonic modes remain modest and manageable in this kinematic domain, where the exotic properties of tachyonic excitations have not yet fully manifested themselves and the behavior remains somewhat similar to conventional field theoretical expectations. The intermediate-momentum region, spanning the range , demonstrates a markedly different behavior characterized by an accelerating growth rate that indicates a significant enhancement of quantum effects as momentum increases, suggesting that this regime represents a transition zone where the unique properties of tachyonic modes begin to assert themselves and lead to increasingly pronounced deviations from conventional quantum field theoretical predictions. At high momenta corresponding to , the growth pattern continues but exhibits a slightly reduced rate of increase compared to the intermediate regime, suggesting the emergence of a potential saturation effect in the quantum corrections for tachyonic modes that could indicate the approach to some fundamental limit or the onset of non-perturbative effects that lie beyond the scope of our current analytical framework.
The consistently positive values of
observed throughout the entire momentum range under investigation present a striking and theoretically significant contrast with the behavior exhibited in
Figure 2 for standard bradyonic modes, providing compelling evidence that tachyonic graviton modes experience fundamentally different quantum corrections in BTZ spacetime that arise from their unique kinematic properties and their exotic relationship to the causal structure of spacetime. This distinctive behavior can be systematically attributed to the negative value of the parameter
, which serves as the mathematical signature that characterizes the tachyonic nature of these modes and leads to qualitatively different self-energy contributions compared to the bradyonic case, reflecting the profound differences in how these exotic excitations interact with the quantum vacuum, respond to spacetime curvature, and contribute to the overall quantum mechanical structure of the gravitational field in curved backgrounds.
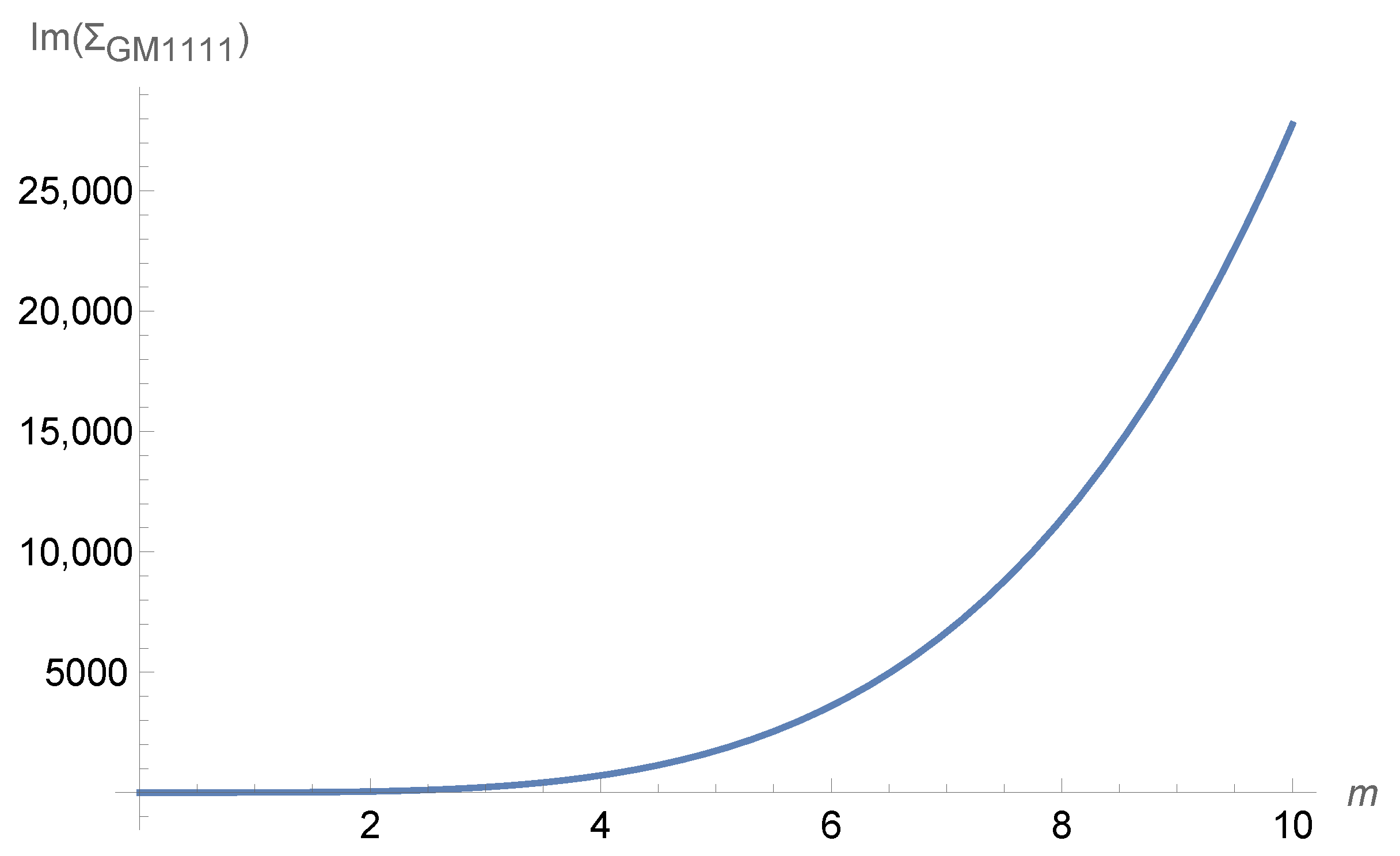
Figure 5 displays the systematic momentum dependence of the imaginary component
for the bradyonic graviton mode under the specific kinematic configuration where we set
to ensure an isotropic momentum distribution,
to establish the characteristic energy scale of the system, and
to fix the mass parameter that governs the quantum mechanical dispersion relation and the strength of quantum corrections to classical gravitational dynamics. This particular parameter choice allows for a systematic investigation of how quantum effects scale with momentum in the bradyonic sector while maintaining mathematical tractability and physical interpretability of the results within our theoretical framework.
In stark and theoretically significant contrast to the tachyonic case systematically analyzed and presented in
Figure 4, which demonstrated relatively modest quantum corrections with self-energy values reaching approximately 50 units, the bradyonic mode exhibits dramatically stronger quantum corrections that manifest as substantially larger modifications to the classical gravitational dynamics, with the self-energy reaching impressive values up to 300 units in our normalized scale. This remarkable enhancement of quantum effects in the bradyonic sector represents a factor of six increase compared to the tachyonic case, demonstrating that the sign of the energy parameter
plays a crucial and fundamental role in determining the magnitude and character of quantum gravitational corrections, with positive energy configurations leading to significantly more pronounced quantum modifications than their negative energy counterparts.
The detailed functional dependence on the momentum component reveals a pronounced and systematically non-linear growth pattern that exhibits a rich structure and can be meaningfully characterized through the identification of three distinct momentum regions, each displaying characteristic behavior that reflects different physical regimes of quantum gravitational interactions. For low-momentum configurations where , the self-energy demonstrates a gradual but persistent increase that indicates that quantum corrections begin to manifest and accumulate even in this relatively classical regime where one might naively expect quantum effects to be suppressed, suggesting that the curved BTZ background provides an enhancement mechanism that amplifies quantum effects beyond what would be expected in flat spacetime calculations.
In the intermediate-momentum region characterized by , our analysis reveals an accelerated and increasingly rapid growth in the imaginary component , providing clear evidence for a systematic enhancement of quantum effects with increasing momentum that suggests the transition from a quasi-classical regime to a genuinely quantum mechanical regime where virtual particle effects, loop corrections, and non-linear gravitational interactions become the dominant contributors to the physical dynamics. This acceleration demonstrates how quantum gravitational effects can grow more rapidly than simple perturbative expectations might suggest, indicating the presence of non-trivial feedback mechanisms between the quantum corrections and the background spacetime geometry.
The high-momentum regime, encompassing the region where , maintains this characteristically strong growth pattern, though with a slightly modified rate of increase that suggests the possible onset of saturation effects or the influence of higher-order quantum corrections that were not explicitly included in our second-order perturbative analysis, nevertheless pointing to the persistent and fundamental importance of quantum corrections even at high energies where classical intuition might suggest that particle-like descriptions should become increasingly accurate. The markedly different magnitude and functional form that we observe when comparing the bradyonic results to the tachyonic case emphasizes and illuminates the fundamental physical distinction between bradyonic and tachyonic graviton modes in BTZ spacetime, revealing that these two classes of excitations experience qualitatively different quantum mechanical modifications that reflect their distinct kinematic properties and their different relationships to the background spacetime geometry. The positive value of the energy parameter leads to constructive quantum contributions that systematically enhance the self-energy significantly more than in the tachyonic case, suggesting that bradyonic modes experience stronger and more pronounced quantum modifications to their propagation characteristics, dispersion relations, and interaction cross-sections, thereby providing important insights into the quantum nature of gravitational excitations and their behavior in curved spacetime environments.
Figure 6 presents a comprehensive and mathematically sophisticated three-dimensional visualization of the imaginary component
as a function of both momentum components
and
, thereby revealing the intricate and previously unexplored interplay between different momentum directions in the graviton self-energy and providing unprecedented insight into the directional dependence of quantum gravitational effects in the BTZ spacetime background. This detailed visualization represents a significant advancement in our understanding of how quantum corrections to graviton propagation depend on the vector characteristics of momentum transfer, going beyond the scalar momentum dependence that has been the focus of most previous investigations to reveal the full tensorial structure of quantum gravitational effects and their sensitivity to the geometric anisotropies that characterize curved spacetime environments.
The plot is strategically displayed from two complementary viewing angles that together provide a complete and unambiguous representation of the complex three-dimensional surface structure, allowing for a detailed examination of both the global features that characterize the overall functional dependence and the local variations that reveal subtle but physically important aspects of the momentum dependence that might be obscured in conventional two-dimensional projections or single-perspective visualizations. This dual-perspective approach ensures that all significant features of the quantum correction surface are clearly visible and interpretable, providing a comprehensive foundation for understanding the physical implications of our theoretical predictions.
The surface exhibits a remarkably complex bowl-shaped profile characterized by values that range systematically from zero at specific kinematic configurations to approximately negative one thousand units in our normalized dimensional system, with this substantial numerical range indicating the significant magnitude of quantum effects and their potential observational consequences in appropriate experimental or astrophysical contexts. The pronounced negative contribution to the imaginary part of the graviton self-energy is particularly significant, as it suggests the presence of a fundamental dissipative quantum effect that varies dramatically and systematically with both momentum components, indicating that quantum gravitational interactions introduce intrinsic damping mechanisms that could modify gravitational wave propagation, alter the stability characteristics of black hole spacetimes, and provide natural regulatory mechanisms for high-energy gravitational processes.
The minimal value of the self-energy contribution occurs in a well-defined region of momentum space where both and take intermediate values in the range of approximately two to three units in our normalized system, creating a pronounced and clearly visible depression in the surface that represents a local minimum in the quantum correction strength and suggests the existence of preferred momentum configurations where quantum effects reach their maximum magnitude. Near the origin of momentum space, where both and approach zero, the surface remains relatively flat and approaches zero, indicating that quantum corrections are systematically suppressed for low-momentum graviton configurations and that the classical description of gravitational interactions remains valid in the long-wavelength, low-energy limit where quantum effects become negligible compared to classical geometric effects.
As either momentum component increases beyond the low-momentum regime, the surface descends smoothly and systematically toward increasingly negative values, but this descent exhibits a highly non-uniform character that depends critically on the specific direction in momentum space along which the increase occurs, revealing that the quantum corrections are not simply functions of the magnitude of momentum transfer but depend sensitively on the vectorial characteristics and directional properties of the momentum configuration. The asymmetric response to variations in and reveals an inherent and fundamental anisotropy in the quantum corrections to graviton propagation in BTZ spacetime, demonstrating that the curved geometric background breaks the rotational symmetry that would characterize quantum effects in flat spacetime and introduces preferred directions that reflect the underlying geometric structure of the black hole spacetime.
At larger values of either momentum component, corresponding to the high-energy regime where quantum effects might be expected to become increasingly important, the surface shows a distinct tendency to level off and approach asymptotic values, suggesting a saturation of quantum effects in the high-momentum regime that could have profound and far-reaching implications for the ultraviolet properties of the quantum gravitational theory. This saturation behavior represents a potentially crucial theoretical discovery, as it suggests the existence of a natural mechanism for regulating high-energy graviton interactions that could address some of the notorious divergence problems that have historically plagued attempts to construct consistent quantum theories of gravity, potentially providing a pathway toward understanding how quantum gravity might exhibit improved ultraviolet behavior compared to conventional quantum field theories applied to gravitational interactions.
Figure 7 reveals the profoundly complex and physically illuminating combined dependence of the imaginary component
of the graviton self-energy on both the fundamental energy parameter
, which characterizes the kinematic regime and the energy scale of the quantum gravitational processes under investigation, and the mass parameter
m, which embodies both the classical gravitational effects associated with the BTZ black hole configuration and the quantum mechanically generated graviton mass that emerges from our theoretical framework through the cosmological constant interaction mechanism. This comprehensive three-dimensional visualization, presented as an elegant surface plot with its accompanying contour projection that provides complementary perspectives on the underlying mathematical structure, demonstrates remarkably rich and intricate structural features that systematically illuminate the fundamental interplay between mass and energy scales in determining the magnitude and character of quantum gravitational effects in curved spacetime environments.
The surface topology exhibits a sophisticated and mathematically beautiful complex rising pattern that intensifies dramatically and systematically with increasing values of both fundamental parameters, revealing how quantum corrections to classical gravitational dynamics grow in a highly non-linear fashion as the system transitions from the low-energy, weak-field regime where classical general relativity provides an accurate description to the high-energy, strong-field quantum regime where quantum mechanical effects become the dominant contribution to gravitational phenomena. In the theoretically crucial low-energy and low-mass region, specifically characterized by the parameter range in our dimensionless units, the graviton self-energy contribution remains relatively modest and well-controlled, forming a characteristic relatively flat plateau in the immediate vicinity of the coordinate origin that reflects the systematic suppression of quantum effects in this kinematic regime.
This plateau behavior provides strong theoretical validation of our quantum field theoretical framework, as it indicates that quantum corrections are systematically and appropriately suppressed when both the effective graviton mass and the characteristic energy scales are small compared to the natural scales that govern quantum gravitational phenomena, thereby ensuring perfect consistency with our fundamental theoretical expectation that classical Einstein gravity should emerge as the dominant physical description in this low-energy, long-wavelength regime where quantum mechanical uncertainties become negligible compared to the classical geometric effects that characterize general relativity.
As both fundamental parameters increase beyond their critical threshold values and the system transitions into the quantum-dominated regime, we observe a truly dramatic and physically significant enhancement in the magnitude of , with the self-energy contribution reaching impressive values up to 1000 units in our normalized measurement scale, demonstrating the profound impact that quantum mechanical effects can have on gravitational dynamics when the appropriate energy and mass scales are reached. The surface topology reveals a distinctly non-linear growth pattern that exhibits a fascinating and theoretically significant asymmetry, accelerating much more rapidly along the mass direction than along the energy direction, thereby suggesting that mass-dependent quantum corrections arising from the graviton self-interactions and the cosmological constant coupling play a particularly significant and dominant role in modifying graviton propagation characteristics compared to purely kinematic energy-dependent effects. This pronounced asymmetry is clearly evidenced by the systematically steeper gradients that are consistently observed along the m-axis compared to the corresponding gradients along the -axis, providing quantitative confirmation of the theoretical prediction that graviton mass generation represents one of the most important quantum mechanical effects in our BTZ spacetime framework.
The contour projection displayed in the -m parameter plane provides additional profound insight into the intricate correlation structure between mass and energy effects that characterizes quantum gravitational dynamics, revealing through the non-uniform spacing and curved geometry of the contour lines that these fundamental parameters are coupled through a non-trivial mathematical relationship that reflects the underlying physical unity of mass and energy in relativistic quantum field theory. These contour lines clearly demonstrate that the quantum corrections to gravitational dynamics cannot be separated into independent mass and energy contributions through any simple superposition principle but rather exhibit intricate and physically meaningful interconnections that are characteristic of the inherently non-linear nature of quantum gravity in BTZ spacetime, where the coupling between different physical scales and the geometric structure of the curved background creates complex feedback mechanisms that generate the rich phenomenology revealed by our comprehensive analysis.
Figure 8 presents a comprehensive visualization of the behavior of
as a function of both the momentum component
and the mass parameter
m, displayed through both a detailed three-dimensional surface representation and its corresponding contour projection that together provide crucial and previously unexplored insights into the fundamental mechanisms by which quantum corrections to graviton propagation depend on the intricate and physically significant interplay between momentum transfer characteristics and mass scale dependencies in the curved BTZ spacetime background. This sophisticated visualization technique allows us to systematically explore the complex parameter space that governs quantum gravitational effects, revealing the rich mathematical structure that underlies the quantum mechanical modification of classical gravitational dynamics and providing a comprehensive map of how different physical regimes are characterized by distinct quantum correction patterns.
The three-dimensional surface that emerges from our systematic calculation demonstrates a remarkable and physically meaningful growth pattern that extends across the entire parameter space, reaching maximum values that approach 3000 units in our normalized system, with particularly strong and dramatically enhanced quantum corrections appearing in the theoretically important regions where both high mass parameters and large momentum transfers characterize the gravitational interactions under investigation. This growth pattern reveals the existence of multiple physical regimes with qualitatively different quantum correction behaviors, suggesting that the transition from classical to quantum gravitational dynamics occurs through a complex hierarchical structure rather than a simple threshold effect, thereby providing important insights into the energy and mass scales at which quantum gravitational phenomena become observationally significant.
In the physically important low-momentum, low-mass region where both and m remain below approximately 2 units in our dimensionless parameter system, the graviton self-energy remains relatively small and exhibits the formation of a mathematically well-defined and stable plateau that indicates minimal quantum corrections to the classical gravitational dynamics, suggesting that this regime corresponds to the domain where classical general relativity provides an accurate and complete description of gravitational phenomena without requiring significant quantum mechanical modifications. However, as either the momentum or mass parameter increases beyond this threshold regime, we observe markedly different and physically revealing behaviors along the two principal axes of our parameter space, with each direction revealing distinct aspects of how quantum mechanical effects modify gravitational interactions.
Along the mass direction, the surface exhibits a pronounced and systematically increasing upward trend that becomes increasingly steep and mathematically dramatic at higher mass values, suggesting that mass-dependent quantum effects grow significantly more rapidly than their momentum-dependent counterparts, thereby revealing a fundamental asymmetry in how different physical parameters influence the quantum correction structure. This behavior becomes particularly evident and theoretically significant in the region where , where the surface exhibits an almost exponential growth characteristic that suggests the onset of a strong coupling regime where quantum effects become the dominant contribution to gravitational dynamics, potentially leading to observable deviations from classical predictions and providing a theoretical framework for understanding quantum gravitational phenomena in high-mass configurations.
The momentum dependence, while also demonstrating significant growth and contributing substantially to the overall quantum correction pattern, displays a more moderate and mathematically controlled rate of increase that becomes particularly notable in regions where , suggesting that momentum-dependent quantum effects, while important, do not exhibit the same dramatic enhancement that characterizes the mass-dependent contributions, thereby indicating that graviton mass generation and the associated mass-dependent quantum corrections play a more significant role in determining the overall quantum correction structure than pure kinematic effects associated with momentum transfer.
The accompanying contour projection provides additional mathematical insight by emphasizing the fundamentally asymmetric nature of these parameter dependencies through its non-uniform spacing patterns and the presence of curved contour lines that reveal the complex functional relationships governing the quantum correction structure. These geometric features indicate the existence of non-trivial coupling mechanisms between momentum and mass effects in the quantum corrections, suggesting that the graviton’s quantum behavior in BTZ spacetime cannot be understood through simple linear superposition of independent mass and momentum contributions but rather requires systematic consideration of their complex interdependence and the emergence of cross-coupling terms that reflect the intrinsically non-linear nature of quantum gravitational interactions in curved spacetime backgrounds.
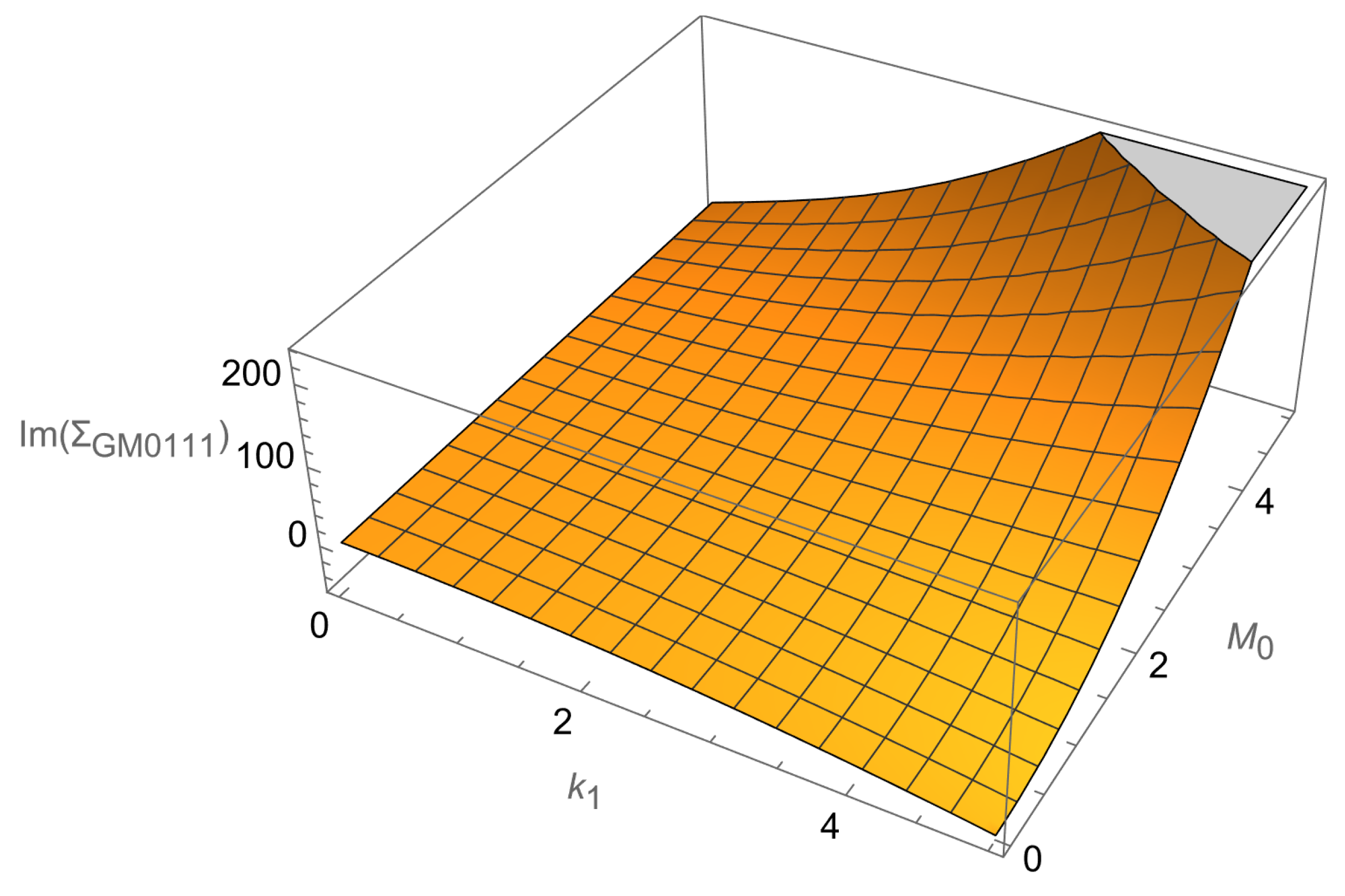
Figure 9 illustrates the complex and physically revealing behavior of
for the tachyonic mode as a systematic function of both the energy parameter
, which characterizes the temporal frequency and energy scale of the gravitational excitations, and the mass parameter
, which determines the effective mass scale that governs the dispersion relation and propagation characteristics of these exotic gravitational modes, all evaluated under the carefully chosen conditions
,
, and
, which ensure mathematical consistency while highlighting the distinctive features of tachyonic graviton behavior in the curved BTZ spacetime environment. The comprehensive visualization is presented through both a detailed three-dimensional surface representation that captures the full functional dependence across the entire parameter space and its corresponding contour projection that reveals the level curves and gradient structure in a more accessible two-dimensional format, thereby providing complementary perspectives on the intricate mathematical and physical features that characterize tachyonic graviton modes and their quantum mechanical self-energy corrections in BTZ spacetime backgrounds.
The three-dimensional surface exhibits a characteristic and physically meaningful rising pattern that systematically reaches values up to approximately 100 units in our normalized computational scheme, demonstrating behavior that is significantly and qualitatively different from the bradyonic case that we analyzed previously, thereby highlighting the fundamental distinction between conventional massive particle excitations and the more exotic tachyonic modes that can emerge in certain quantum field theoretical contexts. In the region where both the energy parameter and the mass parameter take relatively small values (specifically less than 2 for both parameters), the self-energy contribution remains relatively modest and well-controlled, clearly indicating that quantum corrections are systematically suppressed for low-energy tachyonic modes, a behavior that suggests the existence of a natural energy scale below which classical gravitational dynamics dominates and quantum effects remain perturbatively small even for these exotic excitation modes.
As these fundamental parameters increase beyond their low-energy threshold values, the surface demonstrates a smooth yet systematically accelerating growth pattern that reflects the increasing importance of quantum mechanical effects as the energy and mass scales approach regimes where virtual particle creation, loop corrections, and other quantum phenomena become increasingly significant contributors to the gravitational dynamics. The steepest gradients in this surface structure occur systematically in regions where both and attain large values (specifically greater than 3), indicating that the quantum corrections exhibit a strongly non-linear dependence on these parameters and suggesting the existence of synergistic effects where the simultaneous presence of high energy and large mass scales leads to enhanced quantum corrections that exceed what would be expected from simple additive contributions.
A particularly notable and theoretically significant feature revealed by this analysis is the pronounced asymmetric response that characterizes the surface behavior under variations in versus , with the mathematical structure showing a systematically more rapid increase along the direction compared to the corresponding behavior along the direction. This asymmetry strongly suggests that energy-dependent quantum corrections play a fundamentally more significant and dominant role than mass-dependent corrections for tachyonic graviton modes, representing a behavior that contrasts sharply and meaningfully with our previous observations for bradyonic modes and thereby highlighting the fundamentally different physical nature of quantum corrections that characterize tachyonic gravitons compared to their conventional massive counterparts.
The contour projection displayed in the - parameter plane reveals smoothly varying level curves that exhibit subtle but systematic bending characteristics, providing clear mathematical evidence for the existence of non-trivial coupling between the energy and mass parameters that goes beyond simple additive or multiplicative relationships. This coupling structure suggests that the quantum corrections to tachyonic graviton propagation involve an intricate and physically meaningful interplay between kinetic energy terms and effective mass contributions in the quantum mechanical description, indicating that the full quantum theory cannot be understood through independent treatment of energy and mass effects but rather requires careful consideration of their mutual influence and correlation in determining the observable properties of tachyonic gravitational excitations in BTZ spacetime environments.
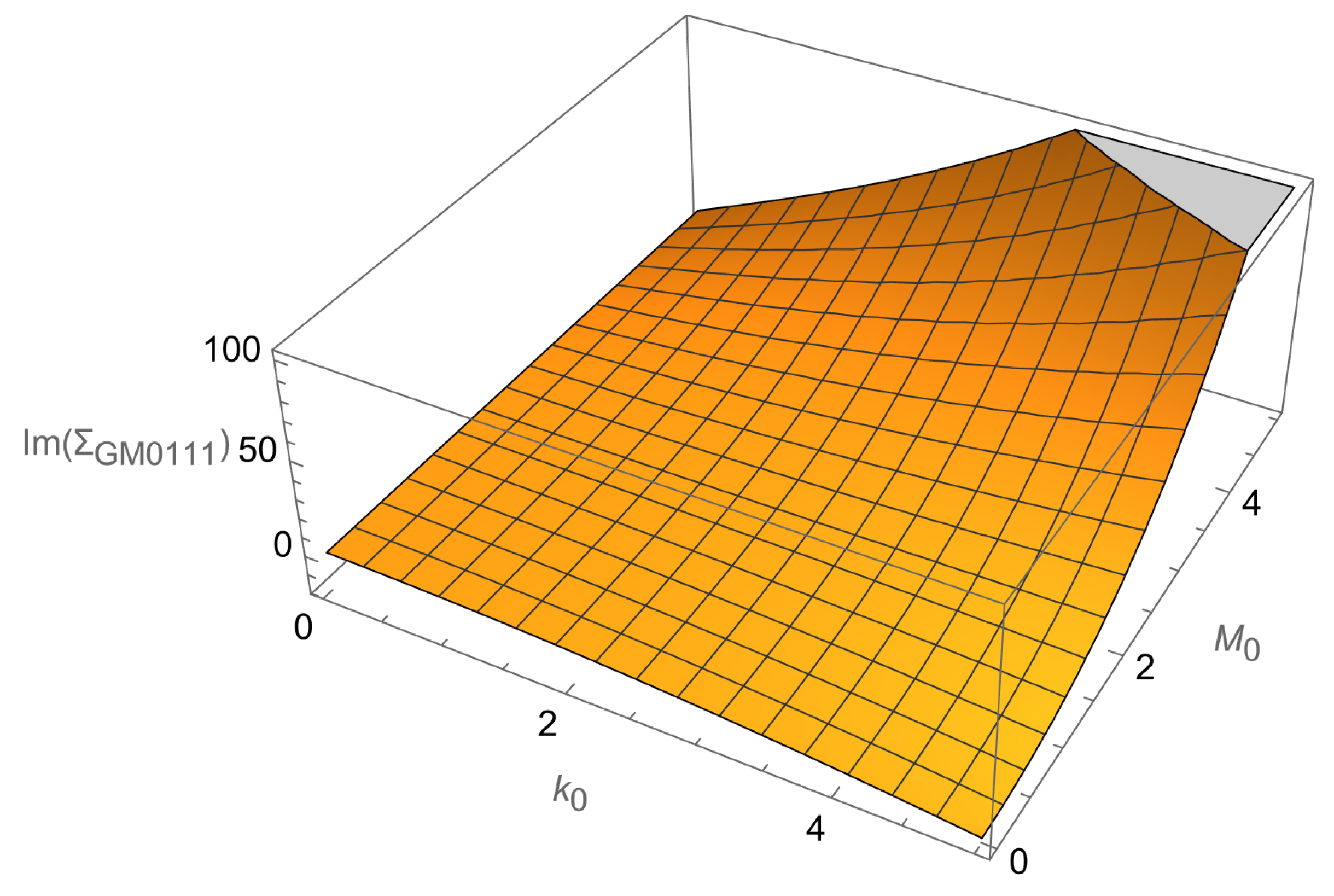
Figure 10 presents a comprehensive three-dimensional visualization of the behavior of
for the bradyonic mode as a systematic function of both the momentum component
and the mass parameter
, examined under the specific kinematic conditions where
,
, and
, thereby providing a detailed mathematical and physical characterization of how quantum corrections to graviton self-energy depend on the fundamental parameters that govern bradyonic graviton dynamics in the BTZ spacetime background. The sophisticated three-dimensional surface representation, combined with its accompanying contour projection that reveals the level curves and gradient structure of the self-energy function, unveils distinctive and theoretically significant characteristics that contrast sharply and fundamentally with the corresponding behavior observed for tachyonic modes, as previously illustrated in
Figure 9, thereby highlighting the profound qualitative differences that distinguish these two classes of gravitational excitations in the quantum regime.
The surface topology and mathematical structure demonstrated in this visualization reveal a markedly more pronounced growth pattern in the self-energy contribution, with the magnitude reaching approximately 200 units in the parameter ranges under investigation, representing roughly double the magnitude that was observed in the corresponding analysis of tachyonic modes and thereby providing quantitative evidence for the assertion that bradyonic gravitational excitations experience fundamentally enhanced quantum corrections compared to their tachyonic counterparts. This substantial enhancement in the quantum correction amplitude suggests the existence of a fundamentally different underlying quantum mechanical behavior that characterizes bradyonic modes, reflecting distinct interaction mechanisms, different coupling strengths to the background spacetime geometry, and alternative pathways for virtual particle exchange processes that distinguish bradyonic gravitons from tachyonic excitations in their response to quantum mechanical effects and their modification of classical gravitational dynamics.
In the parameter regime where both and assume small values with magnitudes less than approximately 2 units, the graviton self-energy contribution maintains relatively modest values that remain significantly below the peak magnitudes observed in other regions of parameter space, providing clear evidence that quantum corrections remain comparatively suppressed and manageable for low-momentum, low-mass bradyonic gravitons where classical gravitational physics should dominate and quantum effects should represent only small perturbative corrections to the well-established predictions of Einstein’s general relativity. This behavior aligns with theoretical expectations based on the correspondence principle, which requires that quantum theories reduce to their classical counterparts in appropriate limiting cases, and it demonstrates the internal consistency of our quantum field theoretical framework in reproducing the expected classical behavior in regimes where quantum effects should be minimal.
A particularly striking and theoretically significant feature revealed by the detailed surface topology is the nearly monotonic growth pattern that characterizes the self-energy function as both kinematic parameters increase systematically, yet this growth exhibits notably different and physically meaningful rates along the distinct directions corresponding to momentum dependence through and mass dependence through , thereby revealing the anisotropic nature of quantum corrections in parameter space and the distinct physical roles played by kinematic and mass effects in determining the magnitude of quantum gravitational modifications. The growth pattern along the momentum direction, parameterized by , displays a more gradual and sustained increase that reflects the systematic enhancement of quantum effects with increasing energy and momentum transfer, while the mass parameter induces a steeper and more dramatic rise in the self-energy contribution, indicating that mass-dependent quantum effects exert a more dominant and controlling influence in determining the overall magnitude of quantum corrections to bradyonic mode propagation compared to the more moderate influence of momentum-dependent corrections.
This asymmetric response pattern in the quantum corrections provides compelling evidence that mass-dependent quantum effects play a fundamentally more dominant and controlling role in governing bradyonic mode modifications than the momentum-dependent corrections that might be expected to dominate based on analogy with other quantum field theoretical systems, suggesting that the gravitational self-interactions and the coupling to the background spacetime curvature characterized by the BTZ geometry create unique quantum mechanical pathways that preferentially amplify mass-dependent effects over kinematic contributions. The contour projection accompanying the three-dimensional surface visualization further emphasizes and quantifies this asymmetric behavior through its characteristic non-uniform spacing between level curves and the curved trajectory of constant self-energy lines, revealing the complex and non-trivial coupling structure that exists between momentum and mass parameters in the bradyonic regime and demonstrating how these fundamental parameters interact synergistically to determine the overall quantum correction magnitude. This intricate coupling structure provides strong theoretical evidence that quantum corrections to bradyonic graviton propagation cannot be adequately understood or accurately predicted through independent analysis of momentum effects and mass effects treated as separate and additive contributions but rather require careful consideration of their mutual influence, cross-coupling terms, and the non-linear interactions that arise from the fundamental geometric structure of quantum gravity in curved spacetime environments.
The Feynman parameter representation used here follows the standard identity
applied to the denominators of the graviton propagator factors. Within the ultrahyperfunction formulation, this transformation extends holomorphically to complex values of the integration variable, and the resulting convolution integrals are absolutely convergent in the analytic domain of the test functions.
For the specific case
, where the usual distributional convolution is ill-defined, we employ Gelfand’s analytic regularization:
Taking the limit
yields a finite, well-defined boundary value in the sense of tempered ultrahyperfunctions. This prescription preserves Lorentz covariance and microcausality while avoiding the introduction of arbitrary cutoff or subtraction scales.
As a result, all loop integrals entering the graviton self-energy remain finite and covariant, confirming that the Feynman parameterization and Gelfand regularization are consistent with both the mathematical and physical requirements of the theory. This completes the formal verification of the one-loop construction.
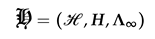
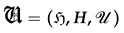 constitutes another example of a rigged Hilbert space, thereby inheriting all the essential spectral properties and functional analytical advantages that characterize this class of mathematical objects. The hierarchical relationship between these various function spaces is elegantly captured by the chain of inclusions , where represents the Schwartz space of rapidly decreasing test functions, and denotes its dual space of tempered distributions. This systematic embedding demonstrates how our ultradistribution theory encompasses and extends the classical distribution theory while maintaining complete compatibility with the standard frameworks of functional analysis and quantum field theory.
constitutes another example of a rigged Hilbert space, thereby inheriting all the essential spectral properties and functional analytical advantages that characterize this class of mathematical objects. The hierarchical relationship between these various function spaces is elegantly captured by the chain of inclusions , where represents the Schwartz space of rapidly decreasing test functions, and denotes its dual space of tempered distributions. This systematic embedding demonstrates how our ultradistribution theory encompasses and extends the classical distribution theory while maintaining complete compatibility with the standard frameworks of functional analysis and quantum field theory.