Structural Optimization of Cryogenic Gas Liquefaction Based on Exergetic Principles—The Linde–Hampson Cycle
Abstract
1. Introduction
2. The Cryogenic Liquefaction Linde–Hampson Cycle with a Single Throttling
2.1. System Configuration of the Single Throttling Scheme
2.2. Mathematical Modeling of the Single-Stage System Operation
2.2.1. Energy Analysis of the Single-Stage System
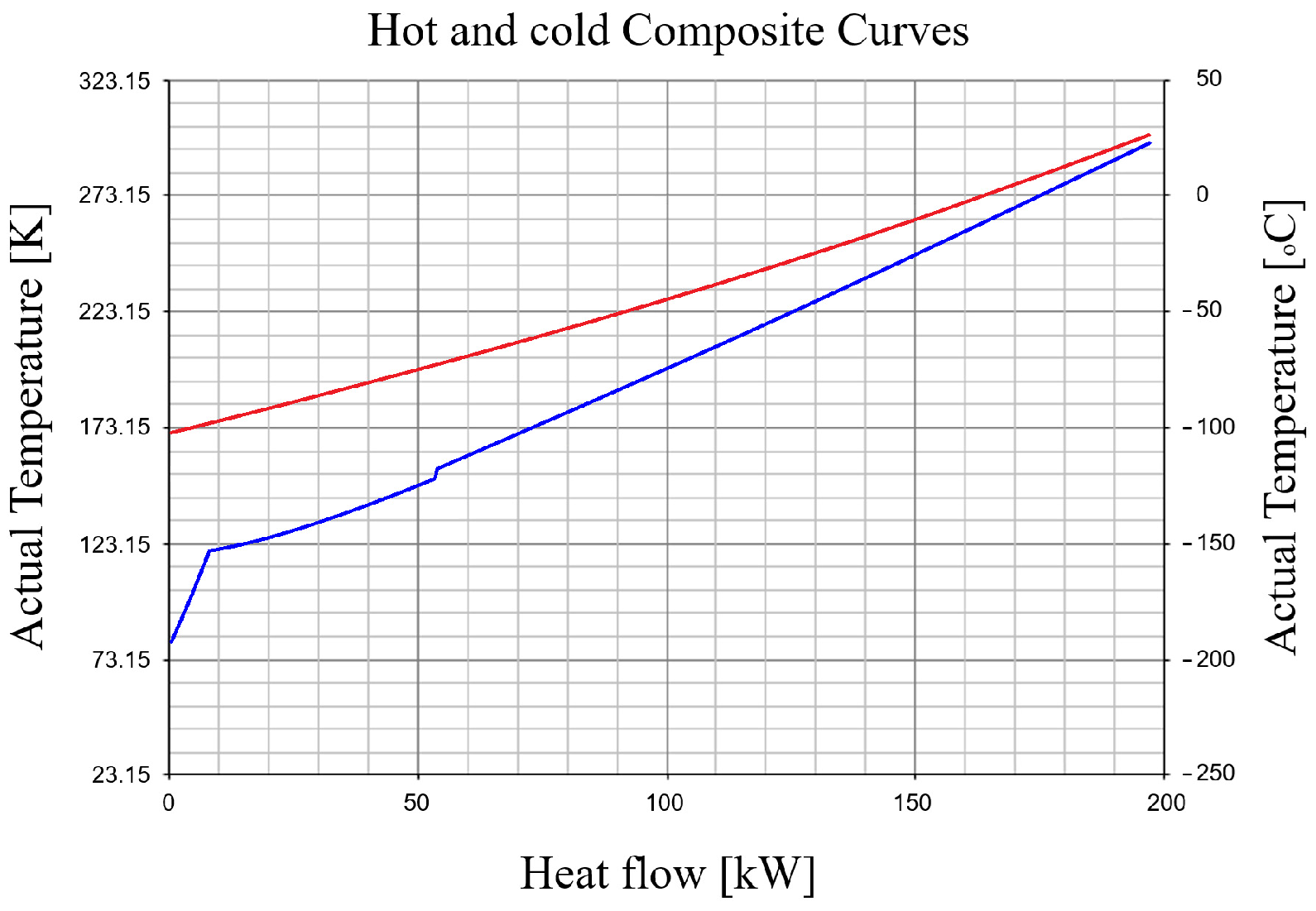
2.2.2. Determination of the Minimum Temperature Difference ∆Tmin in the Recuperative Heat Exchanger
2.2.3. Exergy Analysis of the Cryogenic Linde–Hampson Cycle with a Single Throttling
2.2.4. Results of the Exergy Analysis of the Cryogenic Linde–Hampson Cycle with a Single Throttling
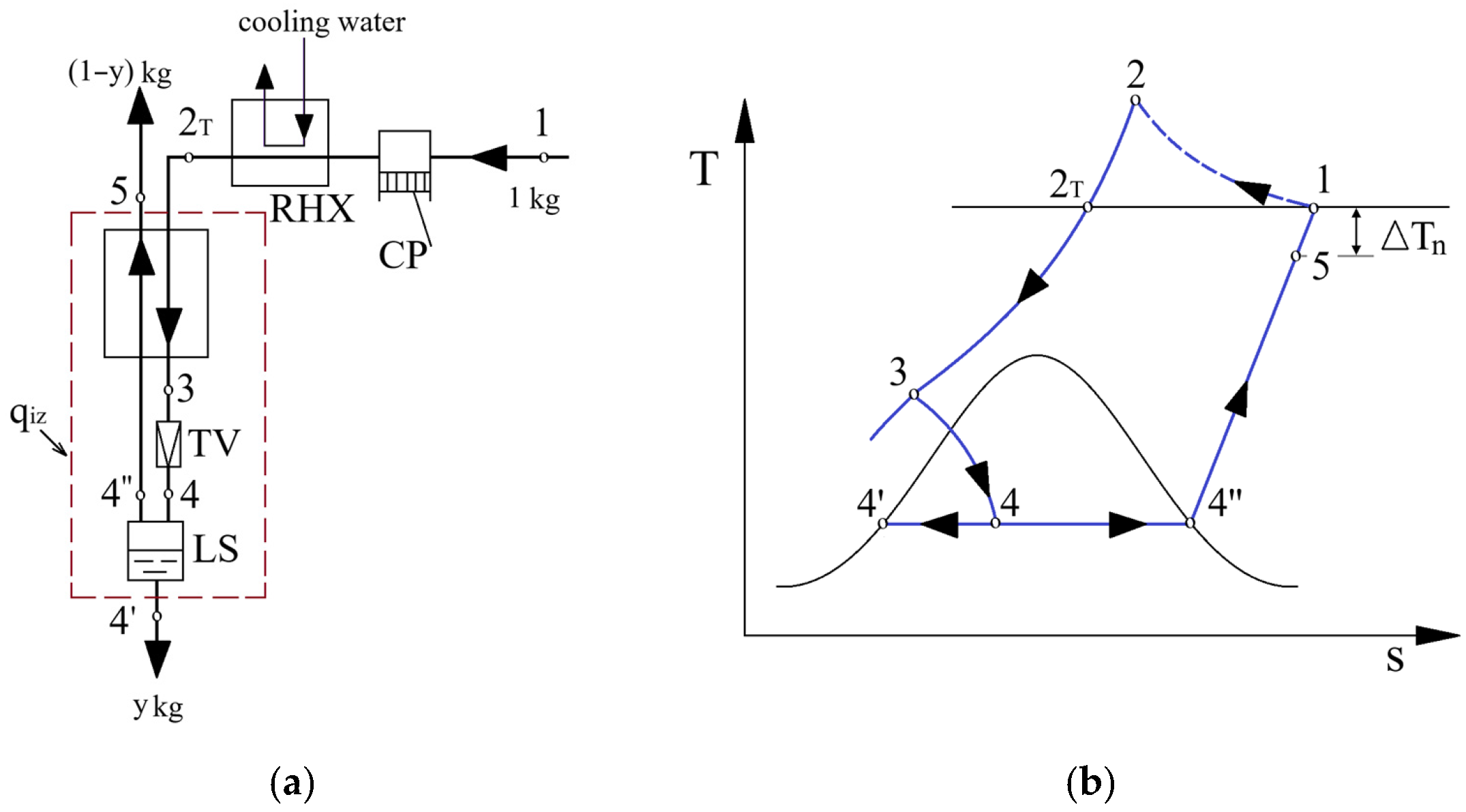
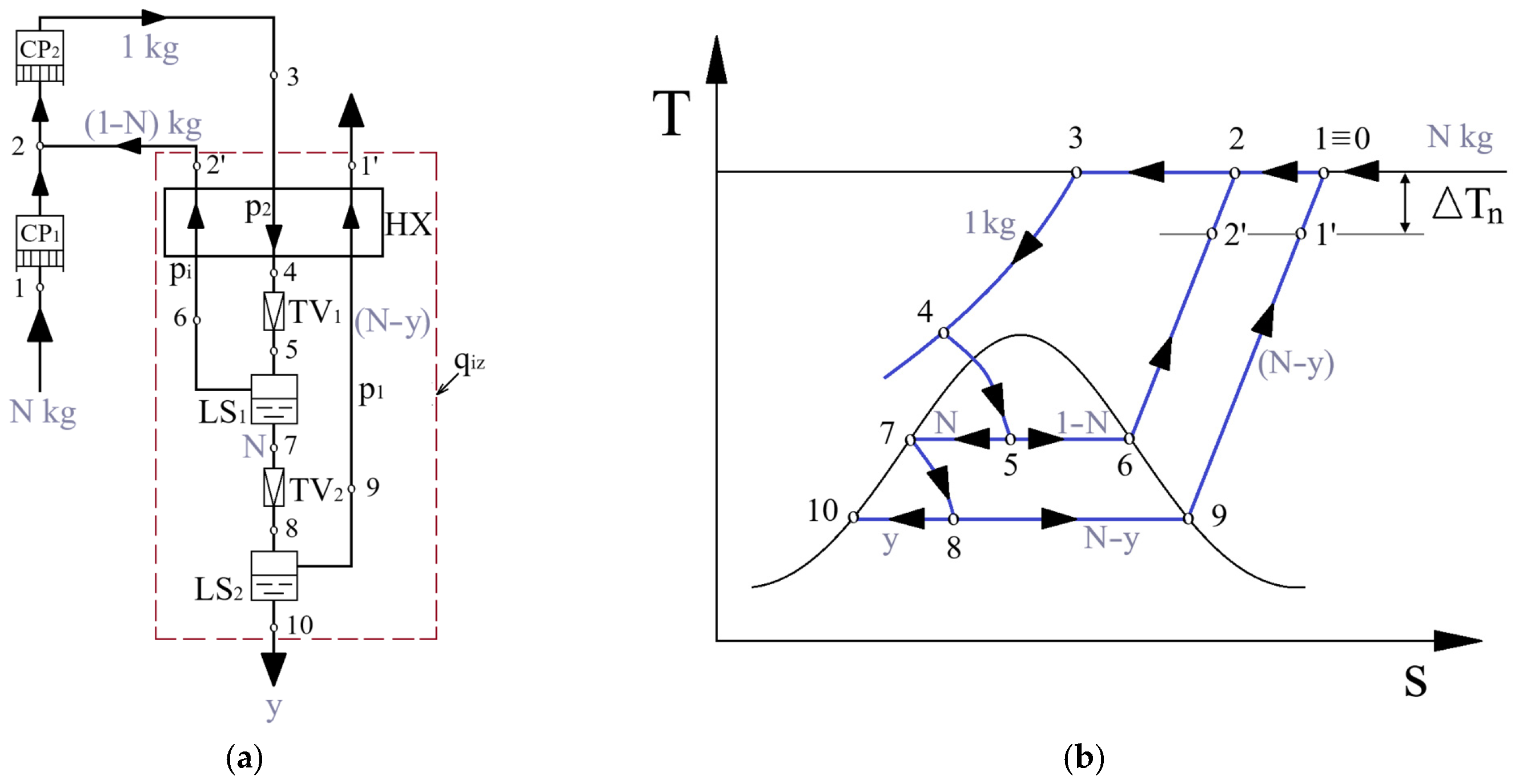
3. Cryogenic Liquefaction Linde–Hampson Cycle with Two Throttling Stages
3.1. System Configuration of the Two-Stage Throttling Scheme
3.2. Mathematical Modeling of the Two-Stage System Operation
3.2.1. Energy Analysis of the Two-Stage System
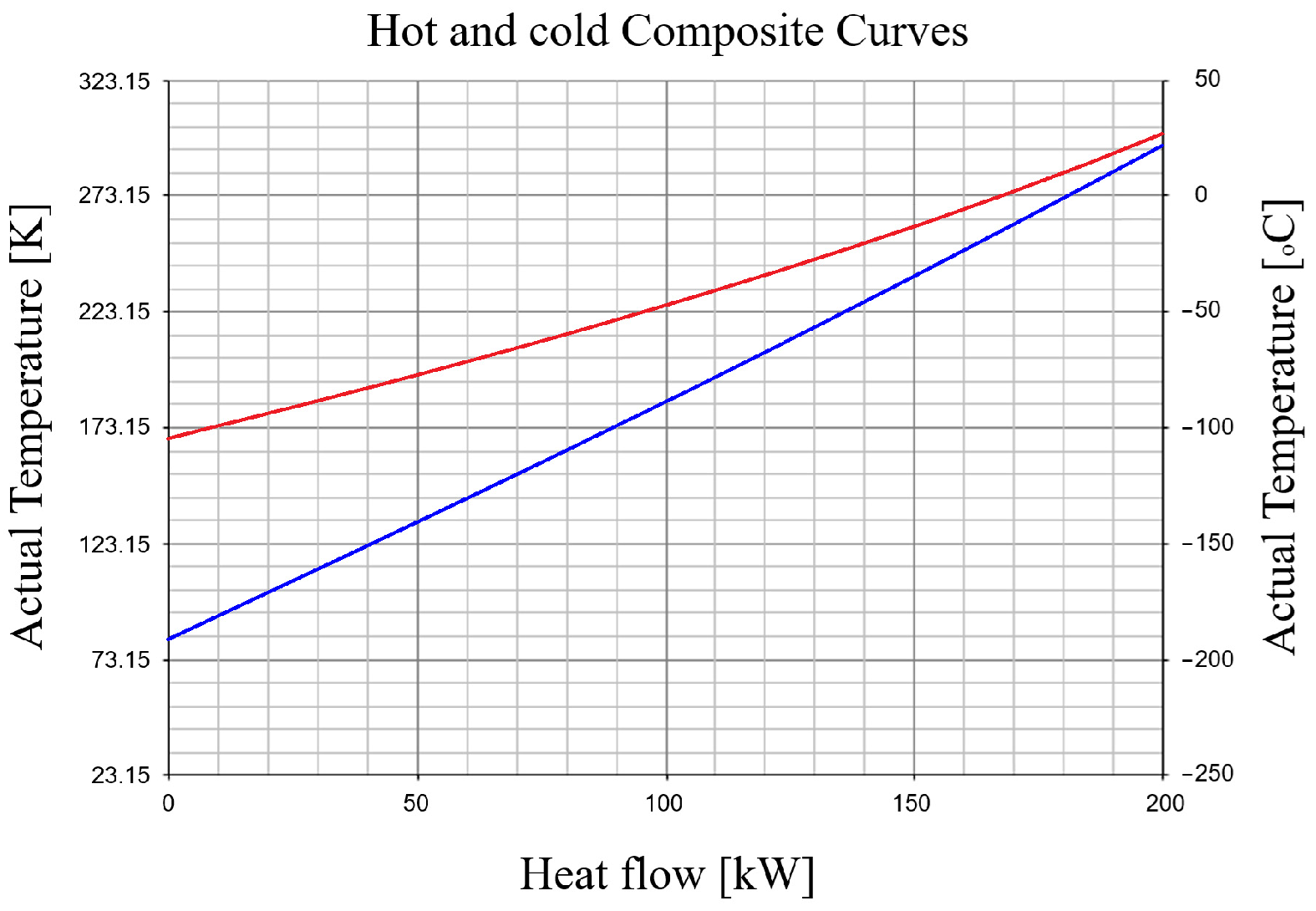
3.2.2. Temperature Distribution in the Recuperative Heat Exchanger
3.2.3. Exergy Analysis of the Linde–Hampson Liquefaction Cycle with Two Throttling Stages
3.2.4. Results of the Energy and Exergy Analysis of the Cryogenic Linde–Hampson Cycle with Two Throttling Stages
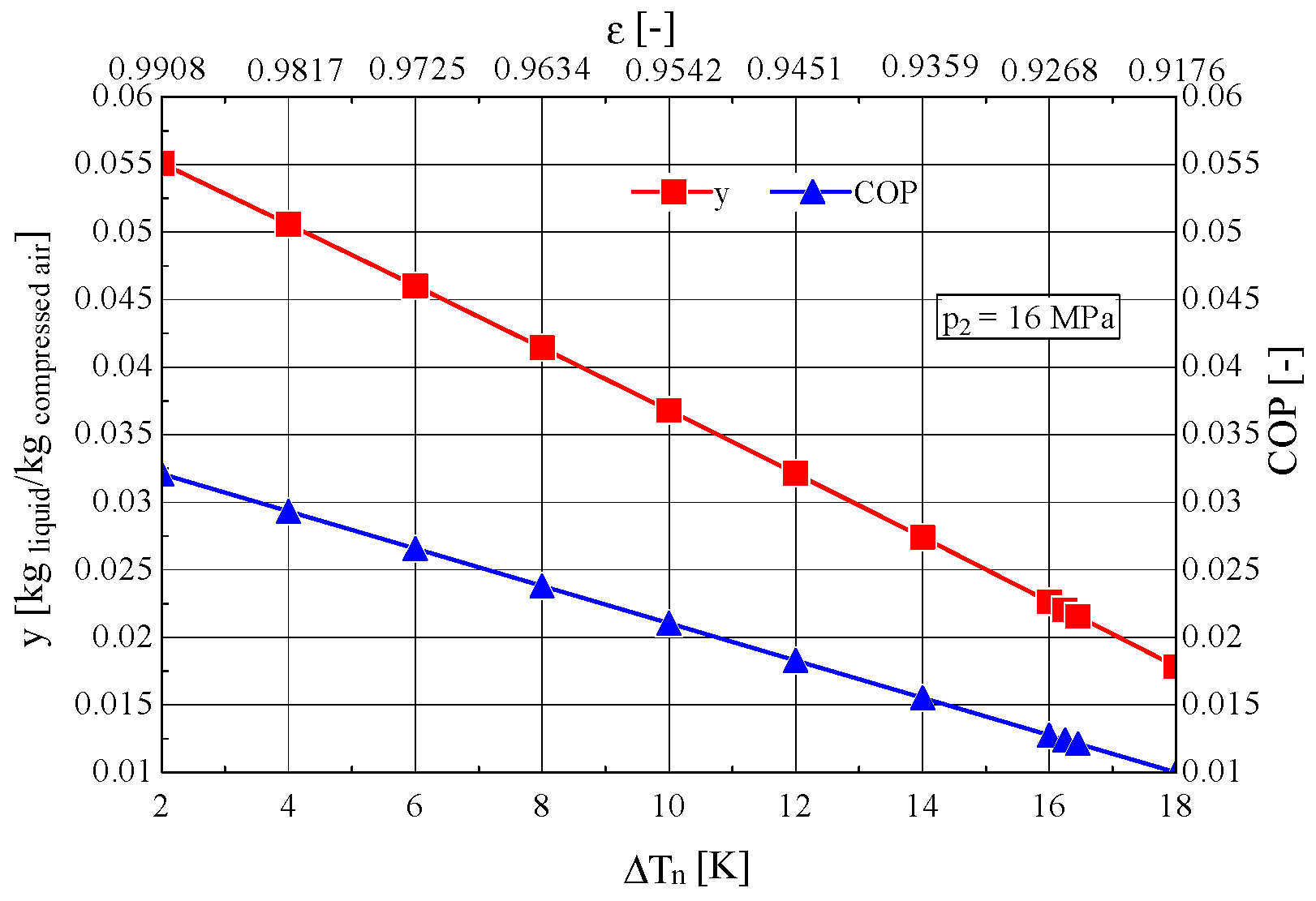
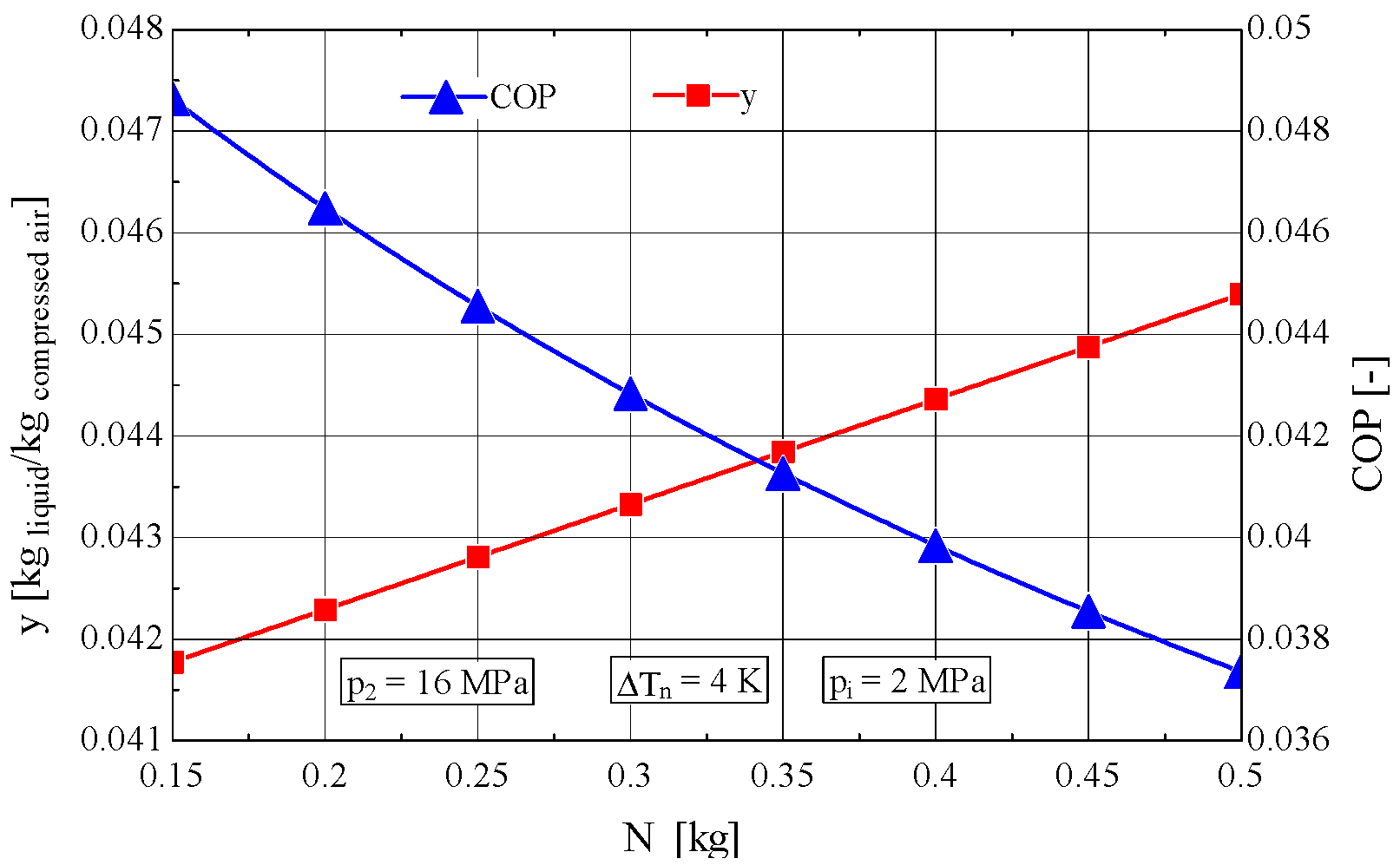
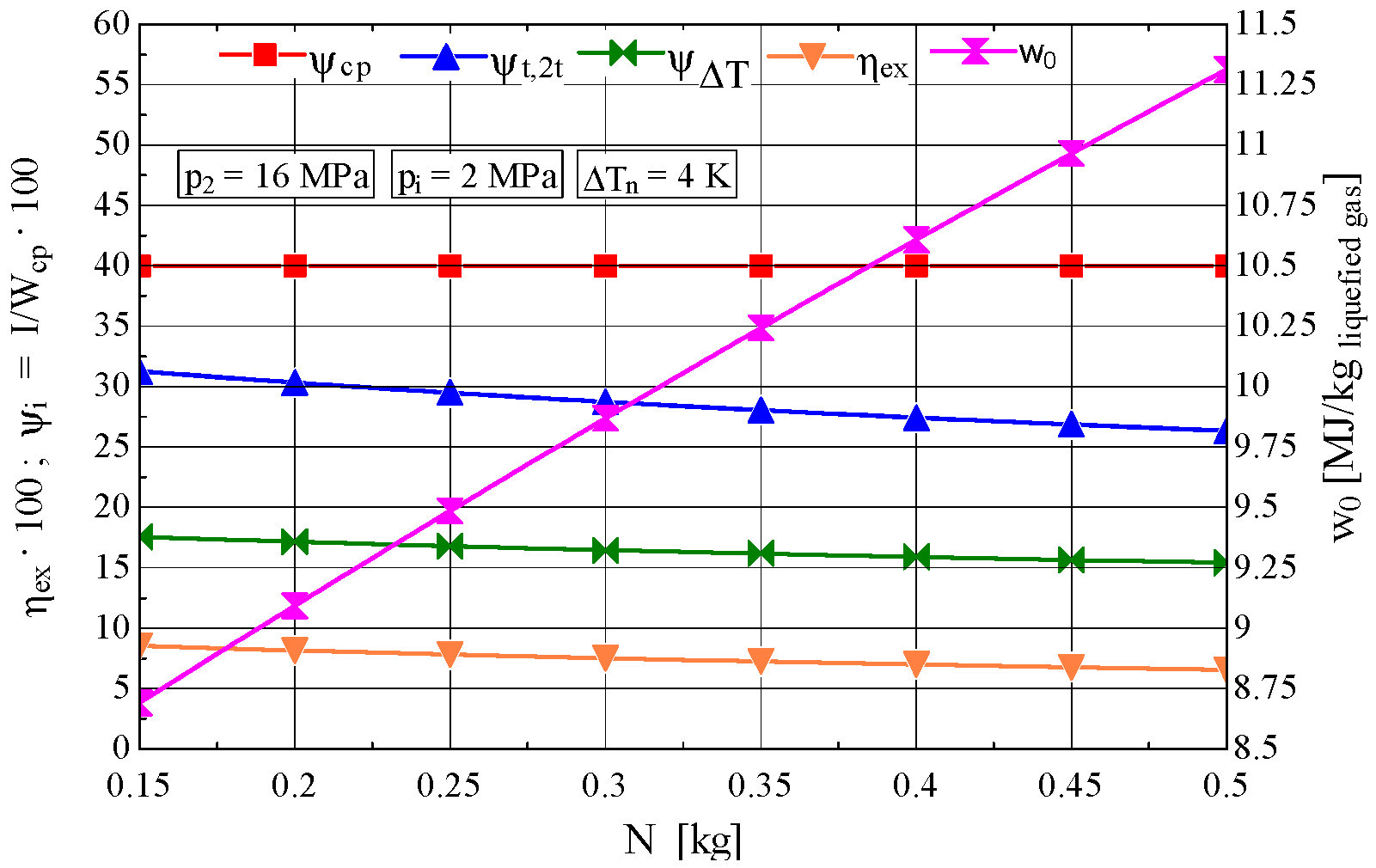
4. Determination of the Optimal Mass Velocity Ratio Between the Forward and Returning Streams of the Recuperative Heat Exchanger
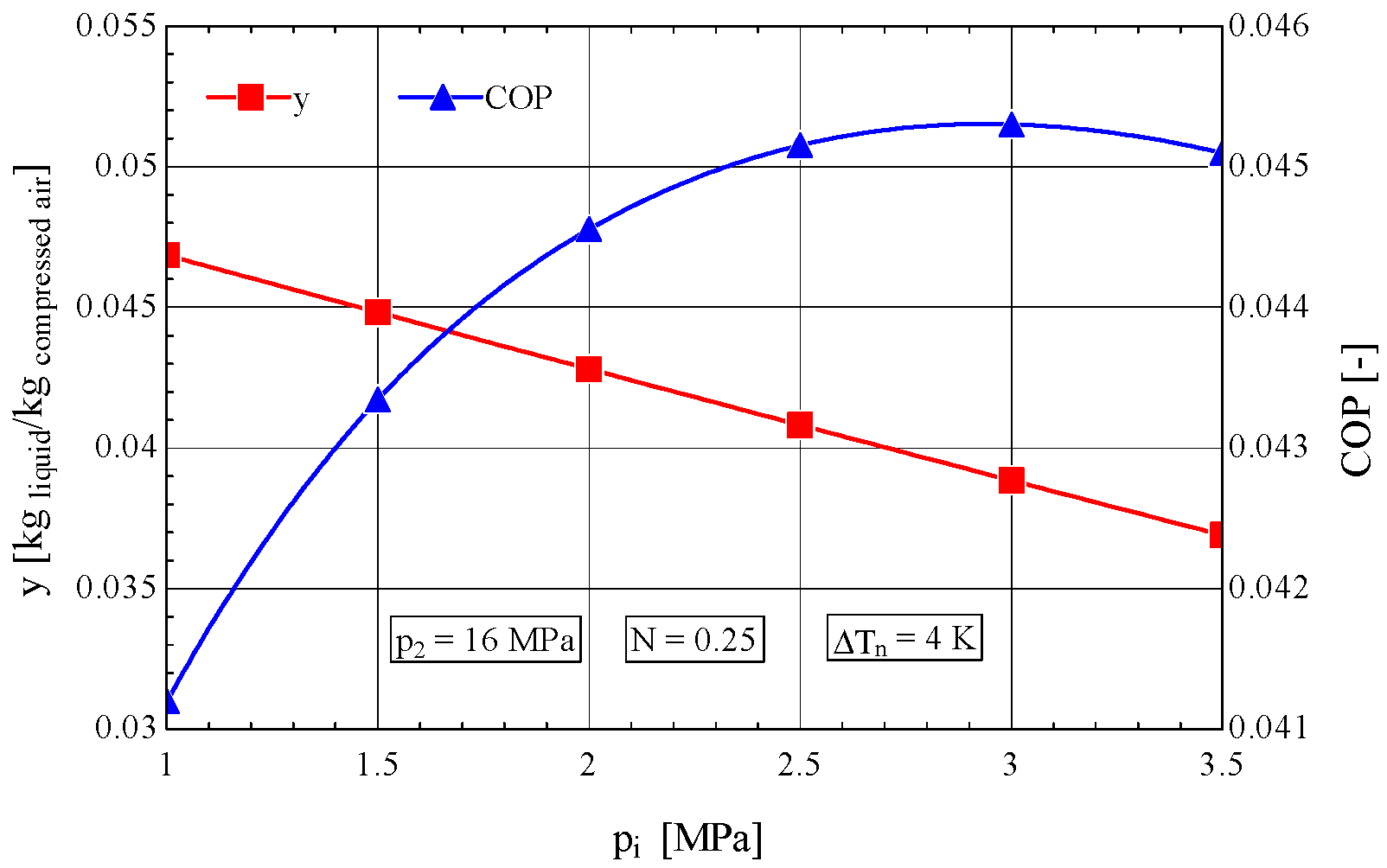
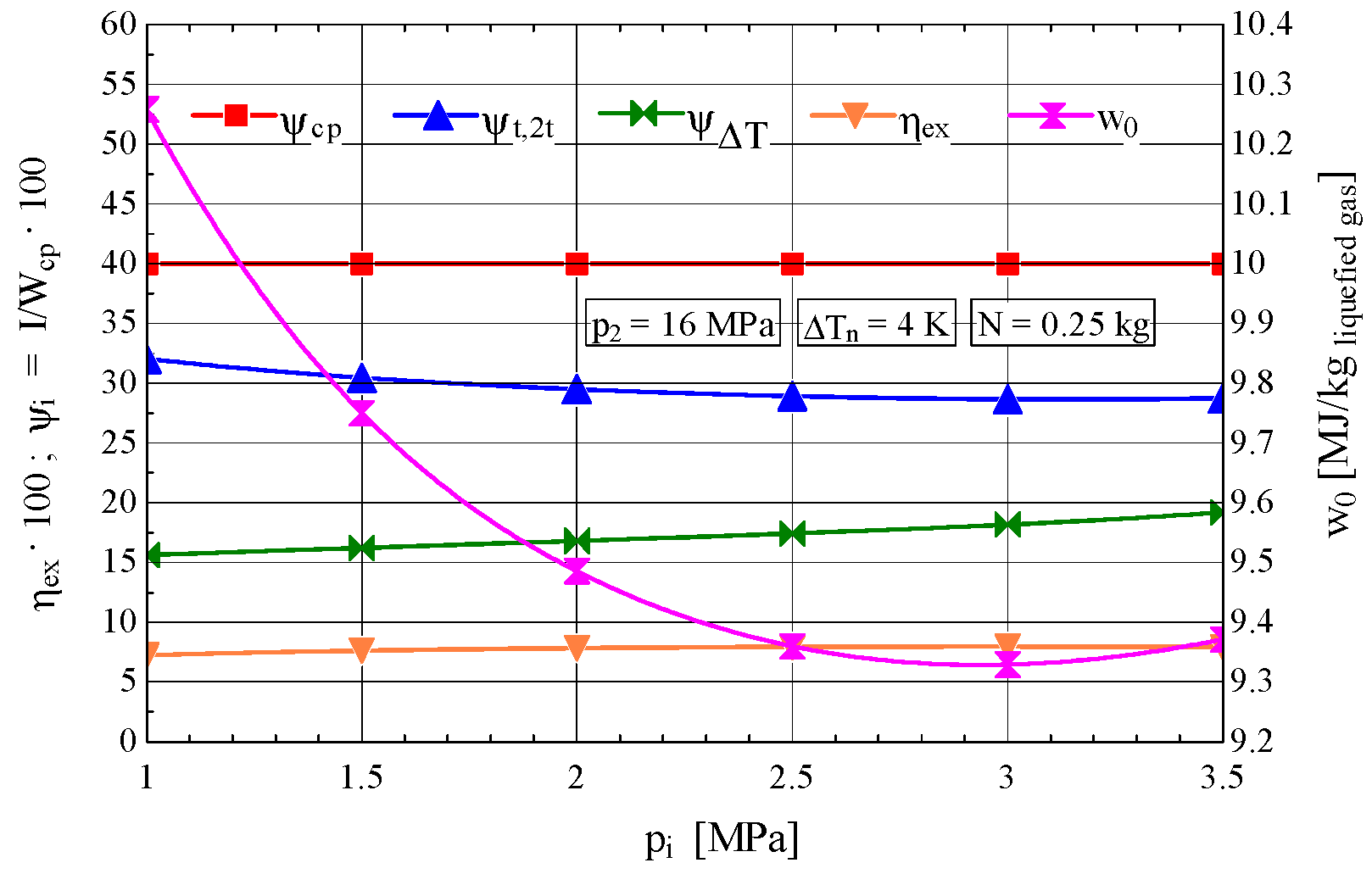
4.1. Construction of the Objective Function to Be Extremized
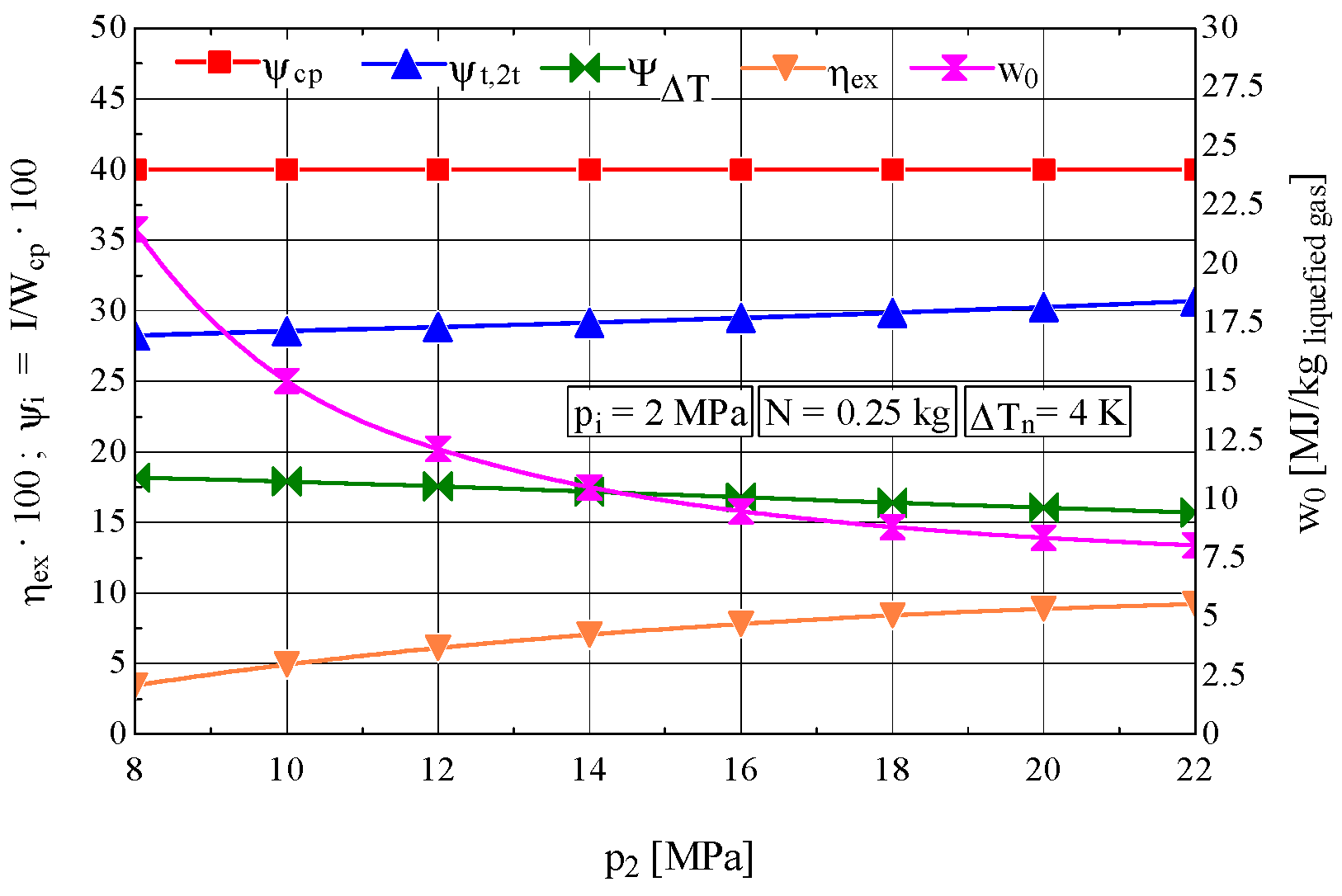
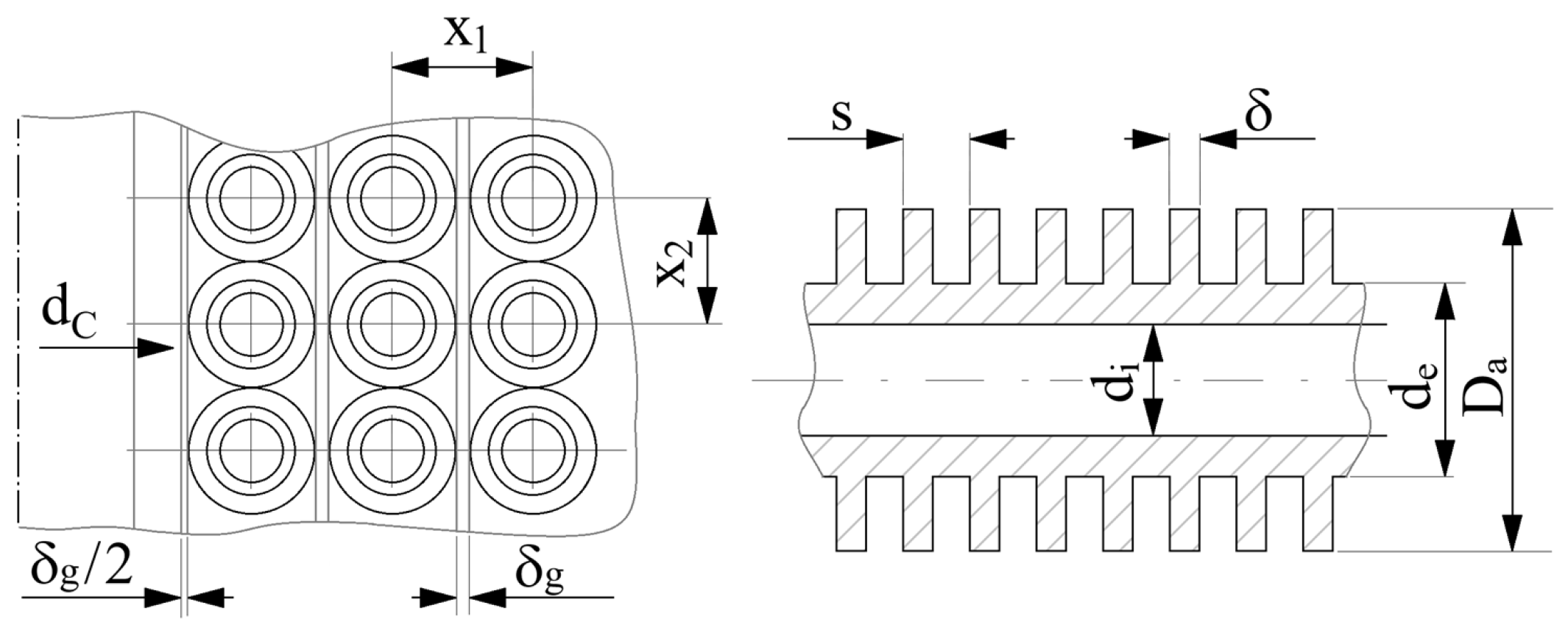
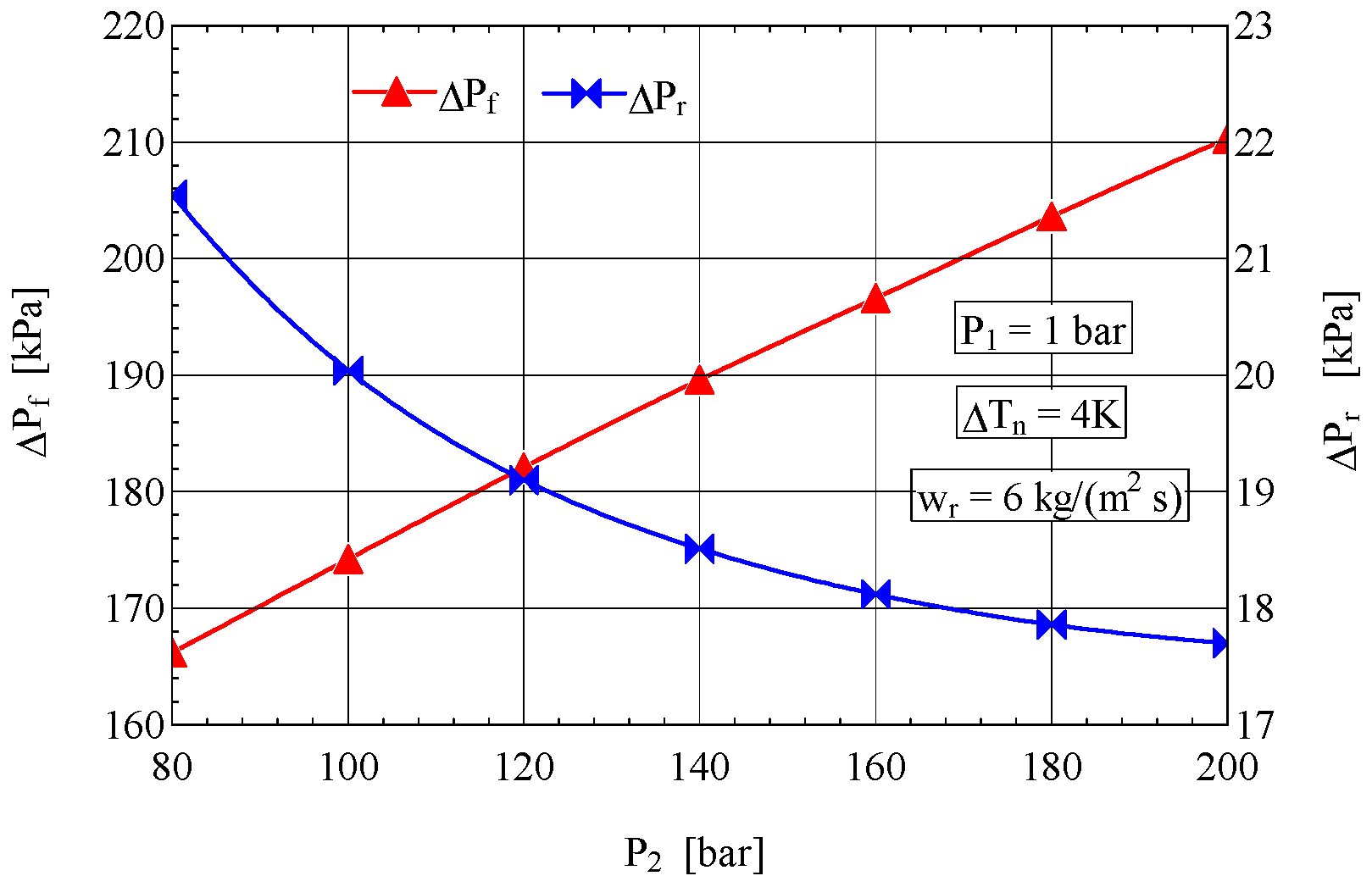
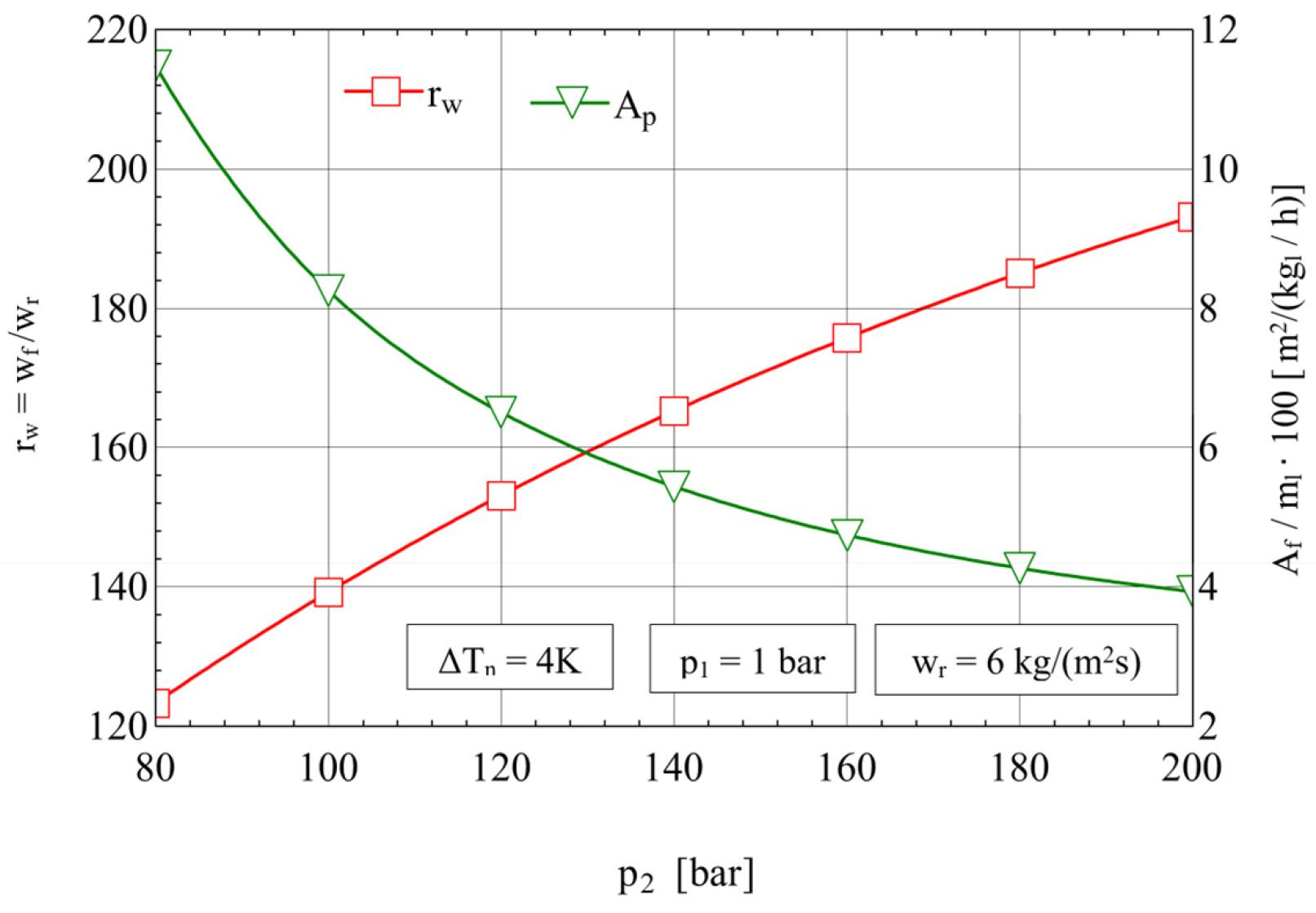
4.2. Analysis of the Influence of the Compression Pressure p2 on the Design and Functional Parameters of the Recuperative Heat Exchanger
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| ASU | air separation unit |
| COP | coefficient of performance |
| HX | Heat Exchanger |
| LAES | liquid air energy storage |
| LS | liquid separator |
| ORC | Organic Rankine Cycle |
| RHX | recuperative heat exchanger |
| TV | throttling valve |
| Latin Letters | |
| A | heat exchange area, m2 |
| C | heat capacity, kW/K |
| CP | compressor |
| cp | mass heat capacity, kJ/kg/K |
| Ex | exergy, kJ |
| e, ex | mass exergy kJ/kg |
| mechanical exergy, kJ | |
| thermal exergy, kJ | |
| f | friction factor |
| h | mass enthalpy, kJ/kg, convective heat transfer coefficient, W/m2/K |
| I | exergy destruction due to internal irreversibility, kJ |
| k | conductive heat transfer coefficient, W/m/K |
| L | length of a tube, m, current of exergy loss, kW |
| mass flow rate, kg/s | |
| N | fraction of gas separated as liquid after the first throttling, kg |
| n | number of tubes in the flow direction |
| number of rows of the serpentine tubes | |
| number of tubes | |
| p | pressure, Pa |
| current of heat, W | |
| specific cooling capacity of the gas, kJ/kg | |
| heat penetration due to imperfect insulation, kJ/kg compressed gas | |
| cooling loss due to temperature difference at the hot end of the heat exchanger, kJ/kg | |
| R | particular constant of gases, J/kg/K |
| Re | Reynolds number |
| Nu | Nusselt number |
| Pr | Prandtl |
| ratio of convective heat transfer coefficients from the forward and return gas streams | |
| ratio of the mass velocities from the forward and return gas streams | |
| s | mass entropy, kJ/kg/K |
| T | temperature, K |
| U | overall heat transfer coefficient, W/m2/K |
| v | specific volume m3/kg |
| W | work kJ |
| w | specific mechanical work, kJ/kg, mass velocity of the gas stream, kg/m2/s |
| mechanical work consumption to obtain 1 kg of liquefied gas, kJ/kg liquid | |
| y | fraction of liquefied gas, kg liquid/kg compressed gas |
| Subscripts | |
| 0 | environment, in equilibrium with the environment |
| 1t | single-throttling Linde–Hampson cycle |
| 2t | double-throttling Linde–Hampson cycle |
| c | cold |
| cp | compressor |
| e | exit |
| ex | exergetic |
| f | forward gas stream |
| gen | generated |
| h | hot |
| i | inlet, summation index. |
| id | ideal |
| iz | insulation |
| L | loss |
| m | mean |
| max | maximum |
| min | minimum |
| pressure drop | |
| P | Pinch |
| Q | heat |
| r | return gas stream |
| t | throttle |
| temperature difference at the hot end of the heat exchanger | |
| Superscript | |
| f | forward gas stream |
| r | return gas stream |
| cp | compression |
| opt | optim |
| TM | thermo-mechanical |
| Greek Symbol | |
| difference | |
| compressor isothermal efficiency | |
| exergetic efficiency | |
| ε | heat exchanger efficiency |
| the ratio between the finned external surface area and the internal surface area of the tube | |
| coefficient accounting for the curvature of the serpentine tubes | |
| Ψ | share of an exergetic loss or destruction in the fuel consumption |
| exergetic factor of temperature |
References
- European Commision. Energy, Climate Change and Environment. Available online: https://energy.ec.europa.eu/topics_en (accessed on 29 August 2025).
- International Energy Agency (IEA). Energy Efficiency 2023. Available online: https://www.iea.org/reports/energy-efficiency-2023 (accessed on 29 August 2025).
- European Commision. “Fit for 55”: Delivering the EU’s 2030 Climate Target on the Way to Climate Neutrality. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:52021DC0550 (accessed on 29 August 2025).
- Cong, L.; Li, X. Reduced-Order Modeling and Control of Heat-Integrated Air Separation Column Based on Nonlinear Wave Theory. Processes 2023, 11, 2918. [Google Scholar] [CrossRef]
- Bucșa, S.; Serban, A.; Balan, M.; Ionita, C.; Nastase, G.; Dobre, C.; Dobrovicescu, A. Exergetic Analysis of a Cryogenic Air Separation Unit. Entropy 2022, 24, 272. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Li, J.; Li, X.; Sun, H. State-of-the-Art Development about Cryogenic Technologies to Support Space-Based Infrared Detection. Chin. J. Aeronaut. 2023, 36, 32–52. [Google Scholar] [CrossRef]
- Tariq, M.; Siddhantakar, A.; Sherman, J.D.; Cimprich, A.; Young, S.B. Life Cycle Assessment of Medical Oxygen. J. Clean. Prod. 2024, 444, 141126. [Google Scholar] [CrossRef]
- Choe, C.; Haider, J.; Lim, H. Carbon Capture and Liquefaction from Methane Steam Reforming Unit: 4E’s Analysis (Energy, Exergy, Economic, and Environmental). Appl. Energy 2023, 332, 120545. [Google Scholar] [CrossRef]
- Percembli, A.A.; Dupuy, A.; Grosu, L.; Dima, D.; Dobrovicescu, A. Exergetic Analysis and Design of a Mechanical Compression Stage—Application for a Cryogenic Air Separation Plant. Entropy 2025, 27, 532. [Google Scholar] [CrossRef] [PubMed]
- Hamayun, M.H.; Ramzan, N.; Hussain, M.; Faheem, M. Evaluation of Two-Column Air Separation Processes Based on Exergy Analysis. Energies 2020, 13, 6361. [Google Scholar] [CrossRef]
- Dzido, A.; Krawczyk, P.; Wołowicz, M.; Badyda, K. Comparison of Advanced Air Liquefaction Systems in Liquid Air Energy Storage Applications. Renew Energy 2022, 184, 727–739. [Google Scholar] [CrossRef]
- Kılıç, M.; Altun, A.F. Comprehensive Thermodynamic Performance Evaluation of Various Gas Liquefaction Cycles for Cryogenic Energy Storage. Sustainability 2023, 15, 16906. [Google Scholar] [CrossRef]
- Khoshgoftar Manesh, M.H.; Ghorbani, B. Energy and Exergy Analyses of an Innovative Energy Storage Configuration Using Liquid Air Integrated with Linde-Hampson Liquefaction System, Molten Carbonate Fuel Cell, and Organic Rankine Cycle. J. Energy Storage 2022, 47, 103676. [Google Scholar] [CrossRef]
- Incer-Valverde, J.; Hamdy, S.; Morosuk, T.; Tsatsaronis, G. Improvement Perspectives of Cryogenics-Based Energy Storage. Renew Energy 2021, 169, 629–640. [Google Scholar] [CrossRef]
- He, T.; Lin, W. Design and Optimization of Nitrogen Expansion Liquefaction Processes Integrated with Ethane Separation for High Ethane-Content Natural Gas. Appl. Therm. Eng. 2020, 173, 115272. [Google Scholar] [CrossRef]
- Khosravi, S.; Khoshbakhti Saray, R.; Neshat, E.; Arabkoohsar, A. Towards an Environmentally Friendly Power and Hydrogen Co-Generation System: Integration of Solar-Based Sorption Enhanced Gasification with in-Situ CO2 Capture and Liquefaction Process. Chemosphere 2023, 343, 140226. [Google Scholar] [CrossRef] [PubMed]
- Amirhaeri, Y.; Hadavi, H.; Kasaeian, A. Exergy and Energy Analysis of a Hybrid Natural Gas/Hydrogen Liquefaction Cycle Combined with Methanol Production Plant. Energy Convers. Manag. 2024, 299, 117834. [Google Scholar] [CrossRef]
- Berstad, D.; Skaugen, G.; Wilhelmsen, Ø. Dissecting the Exergy Balance of a Hydrogen Liquefier: Analysis of a Scaled-up Claude Hydrogen Liquefier with Mixed Refrigerant Pre-Cooling. Int. J. Hydrogen Energy 2021, 46, 8014–8029. [Google Scholar] [CrossRef]
- Yilmaz, F.; Ozturk, M.; Selbas, R. Development and Assessment of a Newly Developed Renewable Energy-Based Hybrid System with Liquid Hydrogen Storage for Sustainable Development. Int. J. Hydrogen Energy 2024, 56, 406–417. [Google Scholar] [CrossRef]
- Chen, F.; Morosuk, T. Exergetic and Economic Evaluation of CO2 Liquefaction Processes. Energies 2021, 14, 7174. [Google Scholar] [CrossRef]
- Kays, W.M.; London, A.L. Compact Heat Exchangers, 3rd ed.; Krieger Publishing Company: Malabar, FL, USA, 1998; ISBN 1-57524-060-2. [Google Scholar]
- Kamp, I.C. Pinch Analysis and Process Integration: A User Guide on Process Integration for the Efficient Use of Energy, 2nd ed.; Butterworth-Heinemann: Burlington, MA, USA, 2007; ISBN 0-7506-8260-4. [Google Scholar]
- Moran, M.J.; Shapiro, H.N.; Boettner, D.D.; Bailey, M.B. Fundamentals of Engineering Thermodynamics, 9th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2018; ISBN 1119391768. [Google Scholar]
- Barron, R.F.; Nellis, G.F. Cryogenic Heat Transfer, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2016; ISBN 9781315373430. [Google Scholar]
- Stamatescu, C.; Peculea, M.; Radcenco, V.; Porneală, S.; Barbu, H. Technical Cryogenics; Bucharest Technical Publishing House: Bucharest, Romania, 1982. (In Romanian) [Google Scholar]
- White, F.M. Fluid Mechanics, 7th ed.; McGraw Hill: New York, NY, USA, 2011; pp. 356–396. [Google Scholar]
- Zukauskas, A.; Ulinskas, R. Heat Transfer in Tube Banks in Crossflow; Hemisphere Publishing Corporation: New York, NY, USA, 1988; pp. 20–21. ISBN 0-89116-685-8. [Google Scholar]
- Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 8th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2017; pp. 496–497. ISBN 978-1-119-32042-5. [Google Scholar]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urduza, D.C.; Grosu, L.; Percembli, A.A.; Șerban, A.; Dobrovicescu, A. Structural Optimization of Cryogenic Gas Liquefaction Based on Exergetic Principles—The Linde–Hampson Cycle. Axioms 2025, 14, 785. https://doi.org/10.3390/axioms14110785
Urduza DC, Grosu L, Percembli AA, Șerban A, Dobrovicescu A. Structural Optimization of Cryogenic Gas Liquefaction Based on Exergetic Principles—The Linde–Hampson Cycle. Axioms. 2025; 14(11):785. https://doi.org/10.3390/axioms14110785
Chicago/Turabian StyleUrduza, Dănuț Cristian, Lavinia Grosu, Adalia Andreea Percembli (Chelmuș), Alexandru Șerban, and Alexandru Dobrovicescu. 2025. "Structural Optimization of Cryogenic Gas Liquefaction Based on Exergetic Principles—The Linde–Hampson Cycle" Axioms 14, no. 11: 785. https://doi.org/10.3390/axioms14110785
APA StyleUrduza, D. C., Grosu, L., Percembli, A. A., Șerban, A., & Dobrovicescu, A. (2025). Structural Optimization of Cryogenic Gas Liquefaction Based on Exergetic Principles—The Linde–Hampson Cycle. Axioms, 14(11), 785. https://doi.org/10.3390/axioms14110785






