Embedding Vacuum Fluctuations in the Dirac Equation: On the Neutrino Electric Millicharge and Magnetic Moment

Abstract

An extension of the Dirac equation for an initially massless particle carrying an electric charge, assumed to be embedded via minimal coupling into an external fluctuating electromagnetic four-potential of the vacuum, is suggested. We conjecture that appropriate averages of the four-vector can lead to observable quantities, such as a particle mass in its rest frame. The conditions on the potential mean values to become gauge-invariant are obtained. The mass is found to be proportional to the magnitude of the charge times the associated mean Lorentz scalar of the four-potential, and the relation holds for both spacelike and timelike types of four-vectors. For the latter, the extended Dirac equation violates Lorentz covariance, but the violation can be argued to occur within a time scale allowed by the uncertainty principle. For larger times, the particle has acquired a mass and Lorentz covariance is restored. This mathematical scenario is applied to acquire estimates of the neutrino millicharge and magnetic moment, in good agreement with the present upper bounds obtained experimentally. The issue of unstable particle decay is considered by focusing, for illustration, on the main decay channels of the selected particles. From the lifetime of the $\tau$ lepton, a lower bound of the effective neutrino mass is predicted, which can be tested in future experiments.

1. Introduction

Following Heisenberg’s formulation of matrix mechanics in 1925, the publication of the non-relativistic Schrödinger equation in 1926, and its relativistic counterpart, the Klein–Gordon equation, published independently by Klein and Gordon later that year, signaled a decisive step in the advent of modern quantum mechanics and marked a breakthrough in our understanding of matter at atomic length scales.

The Schrödinger equation is a partial differential equation that is first-order in time and second-order in the spatial coordinates. In contrast, the Klein–Gordon (KG) equation arises from the Lorentz-invariant relation for the four-momentum,

$$P^{\nu }{P}_{\nu }=E^2-p^2{c}^2=m^2{c}^4$$

upon applying the operator substitutions [1],

$$E\to i\hslash {\partial }_t,\overrightarrow{p}\to -i\hslash \overrightarrow{\nabla },$$

which yield a differential equation second order in both time and space, consistent with special relativity. Both equations act on a scalar wavefunction and therefore describe a quantum particle without spin.

In 1927, Pauli extended the Schrödinger equation to spin-½ particles, introducing a two-component spinor wavefunction. The spinor accounts for the two possible spin projections, $S_z=\pm \hslash /2$. While successful in describing spin non-relativistically, Pauli’s formulation was still incompatible with special relativity, motivating Dirac’s search for a fully relativistic equation for spin-½ particles.

In 1928, Dirac published a new relativistic equation, requiring it to be first-order in all four space–time coordinates. Formally, such an equation can be obtained by linearizing the Klein–Gordon equation (see e.g., [2]), so that the Dirac operator $H_{\mathrm{D}}$ satisfies

$$H_{\mathrm{D}}^2\equiv H_{\mathrm{KG}}.$$

The resulting Dirac equation introduces a four-component spinor wavefunction. Two components describe the electron’s spin projections, while the additional two account for the corresponding antiparticle states, later identified as the positron.

Remarkably, the Dirac equation, when coupled to the electromagnetic (EM) field, reduces to the Pauli equation in the non-relativistic limit, with the electron gyromagnetic factor taking the value $g_s=2$ in the absence of radiative corrections. This factor enters the definition of the electron magnetic moment, ${\mu }_e$, in terms of its spin $S=\hslash /2$,

$${\mu }_e=-g_s{\displaystyle \frac{e}{2m_{e}c}}S=-g_s{\mu }_{\mathrm{B}}{\displaystyle \frac{S}{\hslash }}=-{\mu }_{\mathrm{B}},$$

(1)

where the electron charge is $-e$, $e>0$ denoting the elementary charge, and ${\mu }_{\mathrm{B}}=e\hslash /\left(2m_{e}c\right)$ is the Bohr magneton (in Gaussian units). For comparison, a classical rotating charged body yields $g_s=1$. The Dirac equation is strongly supported by its successful prediction of the hydrogen atom fine structure [1,2] and constitutes a cornerstone of the Standard Model (SM) [3].

The Dirac equation describes all known spin-½ massive particles, often referred to as Dirac particles, such as the electron (e), the unstable leptons—the muon ($\mu$) and tau ($\tau$)—and the six quark flavors. An open and actively debated issue concerns the nature of the three neutrinos (${\nu }_e$, ${\nu }_{\mu }$ and ${\nu }_{\tau }$), which complete the lepton family. There is still no conclusive proof whether neutrinos are Dirac or Majorana particles. In the Dirac case, neutrinos and antineutrinos are distinct states, potentially allowing for electromagnetic properties such as a magnetic moment or even a tiny electric charge. In the Majorana scenario, by contrast, particle and antiparticle are identical. The following selected works provide a broad, though not exhaustive, overview of the present constraints on the neutrino electric charge and magnetic moment reported in recent years.

Laboratory experiments provide experimental bounds on the neutrino electric charge and magnetic moment, which have been discussed in [4,5,6,7,8,9]: In [4] (2016), the authors obtained an estimation of the electron neutrino electric millicharge, $\left|\mathfrak{q}\right|\lesssim 1.5 · {10}^{-12}e$, by comparing the neutrino magnetic moment and millicharge contributions to the total cross-section at the electron recoil energy threshold obtained from the GEMMA experiment. This limit is more stringent than the previous one obtained in [5] (2007) which was based on the TEXONO [6] (2003) reactor experiment data.

In [7] (2022), using data from the CONUS experiment, the authors report an upper limit on the electron neutrino magnetic moment, ${\mu }_{\nu }<7.5 · {10}^{-11}{\mu }_{\mathrm{B}}$ (90% confidence level (CL)), from which they derive an effective neutrino millicharge, $\left|\mathfrak{q}\right|<3.3 · {10}^{-12}e$. The experiment employs germanium detectors, where electron antineutrinos are emitted from the 3.9 GW_th reactor core of the Brokdorf Nuclear Power Plant (Germany).

In [8] (2023), using elastic electron neutrino scattering results from the LUX-ZEPLIN experiment, the authors obtain upper bounds for the electron neutrino magnetic moment and the associated neutrino millicharge, yielding ${\mu }_{\nu }<1.1 · {10}^{-11}{\mu }_{\mathrm{B}}$ (90% CL), and $\left|\mathfrak{q}\right|<1.5 · {10}^{-13}e$ (90% CL), respectively. The former can be compared with the results estimated from the XENONnT experiment [9], yielding ${\mu }_{\nu }<6.4 · {10}^{-12}{\mu }_{\mathrm{B}}$. The XENONnT bounds are flavor-independent ’effective upper bounds’, based on a single parameter assumed to be the same for all neutrino flavors (${\nu }_e$, ${\nu }_{\mu }$, ${\nu }_{\tau }$) reaching the detector.

Theoretical bounds have been studied in [10,11,12,13]: In [10] (2014), using the neutrino magnetic moment bound obtained from the GEMMA experiment, the authors obtain an order-of-magnitude estimate for the upper bound on the neutrino electric millicharge, $\left|\mathfrak{q}\right|<1.5 · {10}^{-12}e$. They also predict a more stringent upper bound, $\left|\mathfrak{q}\right|<1.8 · {10}^{-13}e$, which could be tested in future experiments.

In [11], the authors review the theory and phenomenology of neutrino EM interactions, providing tools to probe physics beyond the SM. They derive the general structure of Dirac and Majorana neutrino interactions in the one-photon approximation, discuss their effects in terrestrial and astrophysical environments, and present experimental bounds compared with predictions from beyond-SM theories. Notably, they also estimate a possible value of the neutrino charge radius, $R_{\nu }\sim 4 · {10}^{-17}$ m.

In [12] (2016), the authors examine the role that a nonzero neutrino millicharge can play in astrophysical contexts. Their results rely on the fact that, in such environments, EM interactions of the neutrino millicharge with strong electromagnetic fields, together with weak interactions of neutrinos with dense background matter, can give rise to novel phenomena accessible to astrophysical observations. Remarkably, they obtain a new limit on the neutrino millicharge, $\left|\mathfrak{q}\right|<1.3 · {10}^{-19}e$, representing one of the most stringent astrophysical constraints to date.

In [13] (2020), the authors explore extensions of the SM in which neutrinos can acquire tiny electric charges. They review theoretical scenarios permitting such charges, confront them with observational limits, and derive new direct upper bounds for muon and tau neutrinos. They further establish a flavor-universal lower bound from the weak gravity conjecture and an astrophysical upper bound from magnetar observations, yielding constraints in the range $\left|\mathfrak{q}\right|<{10}^{-14}e$ down to $\left|\mathfrak{q}\right|<{10}^{-21}e$.

In this paper, we aim to obtain estimates of the neutrino charge and magnetic moment consistent with their presently known upper bounds, without entering into the issue of neutrino ’left-handedness’. To achieve our main goal, we discuss an extension of the Dirac equation for an initially massless particle carrying an electric charge $\mathfrak{q}$, assumed to be embedded in an external fluctuating EM potential of the vacuum characterized by an ensemble of states ${\left\{A^{\nu }\right\}}_{\mathrm{vac}}$, where $A^{\nu }=(\varphi ,\overrightarrow{A})$ (in Gaussian units). The four-potential components are assumed to be independent of time and spatial coordinates for each value of $A^{\nu }$ in the ensemble. Based on the following

$$\mathrm{CONJECTURE}:{\langle A^{\nu }\rangle }_{\mathrm{vac}}=0,{\langle A^{\nu }{A}_{\nu }\rangle }_{\mathrm{vac}}\ne 0,$$

determining the behavior of the first two moments of the vacuum four-potential, we prove the result,

$$m_{\mathfrak{q}}{c}^2=\left|\mathfrak{q}\right||{\langle {\varphi }^2\rangle }_{\mathrm{vac}}-\langle |\overrightarrow{A}{|}^2{{\rangle }_{\mathrm{vac}}|}^{1/2},$$

where $m_{\mathfrak{q}}$ is the effective mass acquired by the particle, valid for both spacelike and timelike four-vectors ${\left\{A^{\nu }\right\}}_{\mathrm{vac}}$. In addition, the conditions for the invariance under gauge transformations, $A^{\prime \nu }=A^{\nu }+{\partial }^{\nu }\psi$,

$${\langle A^{\prime \nu }{A}_{\nu }^{\prime }\rangle }_{\mathrm{vac}}={\langle A^{\nu }{A}_{\nu }\rangle }_{\mathrm{vac}},$$

are obtained, suggesting that the vacuum EM potential-induced mass, $m_{\mathfrak{q}}{c}^2$, becomes a Lorentz scalar in those cases. Finally, we use these theoretical results to show that the neutrino charge, $\mathfrak{q}$, and magnetic moment, ${\mu }_{\mathfrak{q}}$, are given by the following expressions:

$${\displaystyle \frac{\mathfrak{q}}{e}}={\left({\displaystyle \frac{m_{\mathfrak{q}}}{m_e}}\right)}^3,{\displaystyle \frac{{\mu }_{\mathfrak{q}}}{{\mu }_{\mathrm{B}}}}={\left({\displaystyle \frac{m_{\mathfrak{q}}}{m_e}}\right)}^2\to {\displaystyle \frac{{\mu }_{\mathfrak{q}}}{{\mu }_{\mathrm{B}}}}={\left({\displaystyle \frac{\mathfrak{q}}{e}}\right)}^{2/3},$$

yielding values consistent with the experimental bounds. Additional arguments are presented indicating that the present mass mechanism does not challenge the prevailing paradigm of particle physics; rather, it outlines a mathematical scenario consistent with established physical laws.

The paper is organized as follows. In Section 2, we review the Dirac equation for free particles. In Section 3, we consider the Dirac equation by adding, using minimal coupling, an EM four-potential assumed to be independent of time and spatial coordinates. In Section 4, the problem of generating a finite particle mass from the $\mathfrak{q}$–$A_{\mathrm{vac}}^{\nu }$ coupling is discussed. In Section 5, we develop models for the neutrino charge and magnetic moment. The section ends with a brief summary on unstable particle decays from which we extract a lower bound for the effective neutrino mass. Finally, Section 6 contains a summary of the results and the concluding remarks.

2. Dirac Equation for Free Particles: The Mass

We present a brief discussion of the Dirac equation and its solutions in a few cases relevant to the main theme of the paper. To this end, we introduce the necessary quantities and definitions, with particular attention to the notation employed. In this work, we use the spacetime metric with signature $(1,-1,-1,-1)$.

2.1. Generalities and Notation

We start by considering the Dirac equation for a free particle of mass m, described by a four-spinor $\psi \left(x\right)$ at the contravariant four-vector position $x^{\nu }=(ct,\overrightarrow{x})$, where the index $\nu =0$ denotes time and $\nu =1,2,3$ (also indicated by the italic letter j) correspond to the three spatial coordinates, which is given by

$$E\psi \left(x\right)=\left(\sum _{j=1}^3{\alpha }^j{p}_{j}c+{\alpha }^{0}m{c}^2\right)\psi \left(x\right),$$

(2)

where $E=i\hslash c\partial /{\partial }_{ct}$ is the energy operator and $\overrightarrow{p}=-i\hslash \overrightarrow{\nabla }$ is the linear momentum operator. The four $4\times 4$ matrices ${\alpha }^{\nu }$ are assumed to be given in the Pauli representation in terms of the following $2\times 2$ matrices:

$${\sigma }_0=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right),{\sigma }_1=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right),{\sigma }_2=\left(\begin{array}{cc}0& -i\\ i& 0\end{array}\right),{\sigma }_3=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right),$$

(3)

according to

$${\alpha }^0=\left(\begin{array}{cc}{\sigma }_0& \mathbf{0}\\ \mathbf{0}& -{\sigma }_0\end{array}\right)\mathrm{and}{\alpha }^j=\left(\begin{array}{cc}\mathbf{0}& {\sigma }_j\\ {\sigma }_j& \mathbf{0}\end{array}\right)\mathrm{for}j=(1,2,3).$$

(4)

In the latter, $\mathbf{0}$ denotes the $2\times 2$ null matrix. The matrices ${\alpha }^{\nu }$ ensure that (2) is consistent with the Klein–Gordon equation, a necessary condition for any relativistic wave equation. Equation (2) can be rewritten using the covariant four-gradient, ${\partial }_{\nu }=\left(\frac{\partial }{\partial ct},\overrightarrow{\nabla }\right)$, to obtain

$$i\hslash c{\partial }_0\psi \left(x\right)=\left(-i\hslash c\sum _{j=1}^3{\alpha }^j{\partial }_j+{\alpha }^{0}m{c}^2\right)\psi \left(x\right),$$

(5)

which can be brought into covariant form by multiplying from the left by ${\alpha }^0$ and introducing the Dirac matrices ${\gamma }^{\nu }$, defined as

$${\gamma }^{\nu }={\alpha }^0{\alpha }^{\nu }=\left(\begin{array}{cc}\mathbf{0}& {\sigma }_{\nu }\\ -{\sigma }_{\nu }& \mathbf{0}\end{array}\right),\mathrm{for}\nu =(1,2,3),$$

(6)

and ${\gamma }^0={\alpha }^0$. Noting that ${\left({\alpha }^0\right)}^2=\mathbb{I}$, where $\mathbb{I}$ is the 4 × 4 identity matrix, we get

$$i{\gamma }^{\nu }{\partial }_{\nu }\psi \left(x\right)=q_0\mathbb{I}\psi \left(x\right)=q_0\psi \left(x\right),$$

(7)

where $q_0=m{c}^2/\hslash c=1/{ƛ}_0$; i.e., ${ƛ}_0=\hslash c/m{c}^2$ is the reduced Compton wavelength. Equation (7) constitutes a system of four differential equations for the four components of the spinor $\psi \left(x\right)$.

2.2. Solution of the Dirac Equation for Free Particles

Let us briefly review the properties of the solution $\psi \left(x\right)$ to Equation (7). In general, it can be written as

$$\psi \left(x\right)=A_{\beta }exp(-i{k}^{\nu }{x}_{\nu })U\left(k\right),$$

(8)

where $A_{\beta }$ is a volume-normalization factor that also depends on the relative speed V of the particle with respect to the observer, $V=\beta c=c^{2}k/\omega$ (related to the group velocity; see below), and accounts for Lorentz contraction. Here, $k^{\nu }=(\omega /c,\overrightarrow{k})$ is the contravariant four-wavevector, $U\left(k\right)$ is a four-spinor, and the minus sign in the exponential is conventional.

2.2.1. Normalization of $\psi \left(x\right)$

We assume that $\psi \left(x\right)$ is normalized within a volume $V_0$ in the particle’s rest frame. Thus,

$${\int }_{V_0}{d}^{\left(3\right)}x{\left|\psi \left(x\right)\right|}^2=A_0^2{V}_0{U}^{†}\left(k\right)U\left(k\right)=1.$$

(9)

Since we require normalized spinors, $U^{†}\left(k\right)U\left(k\right)=1$, it follows that

$$A_0^2=V_0^{-1}.$$

(10)

For a particle moving with speed V, the normalization condition becomes

$${\int }_{V_{\beta }}{d}^{\left(3\right)}{x}^{\prime }{\left|\psi \left(x^{\prime }\right)\right|}^2=A_{\beta }^2{V}_{\beta }=1,$$

(11)

where, due to Lorentz contraction, $V_{\beta }=\sqrt{1-{\beta }^2}{V}_0$, with $\beta =V/c$. From Equations (10) and (11) we then obtain

$$A_{\beta }^2=\gamma V_0^{-1}.$$

(12)

where $\gamma =1/\sqrt{1-{\beta }^2}$ is the Lorentz factor.

2.2.2. The Lorentz Scalar ${\varphi }_s$

Next, let us consider the exponential factor in Equation (8), $exp(-i{\varphi }_s)$, which depends on the Lorentz scalar, ${\varphi }_s=k^{\nu }{x}_{\nu }=k^0{x}_0-\overrightarrow{k}·\overrightarrow{x}$. Using $k^0=\omega /c$, we obtain,

$${\varphi }_s=\omega t-\overrightarrow{k}·\overrightarrow{x}.$$

(13)

Setting ${\varphi }_s=\mathrm{const}$ and differentiating with respect to t gives the phase velocity ${\overrightarrow{v}}_p$, which satisfies $\overrightarrow{k}·{\overrightarrow{v}}_p=\omega$. The propagation of the wave packet is determined by the group velocity ${\overrightarrow{v}}_g$, obtained from

$${\overrightarrow{\nabla }}_k{\varphi }_s={\overrightarrow{\nabla }}_k\omega t-\overrightarrow{x}.$$

Setting ${\overrightarrow{\nabla }}_k{\varphi }_s=0$ yields ${\overrightarrow{v}}_g={\overrightarrow{\nabla }}_k\omega$. As shown in Section 2.2.3, for a Dirac particle (as well as for a Klein–Gordon one) $\omega$ satisfies the dispersion relation

$$\omega =\pm c\sqrt{k^2+q_0^2},$$

(14)

which admits both positive and negative solutions. Differentiating with respect to k gives ${\overrightarrow{\nabla }}_k\omega =c^2\overrightarrow{k}/\omega$. Hence, the equation of motion is

$$\overrightarrow{x}=c^2{\displaystyle \frac{\overrightarrow{k}}{\omega }}t={\overrightarrow{v}}_{g}t,\mathrm{with}{\overrightarrow{v}}_g=c^2{\displaystyle \frac{\overrightarrow{k}}{\omega }}.$$

(15)

The group velocity can also be expressed as ${\overrightarrow{v}}_g=c^2\overrightarrow{p}/\hslash \omega$, where $\overrightarrow{p}$ is the linear momentum. Finally, we note that $\omega$ is related to the total energy by $E=\hslash \omega$, which naturally raises the issue of interpreting negative energies.

Finally, let us briefly discuss the behavior of ${\overrightarrow{v}}_g$ in the two limiting cases, $k\ll q_0$ and $k\gg q_0$. Using Equation (14), we find

$${\overrightarrow{v}}_g\simeq (\pm )\left\{\begin{array}{cc}\hslash \overrightarrow{k}/m,\hfill & \mathrm{when}k\ll q_0,\hfill \\ c\widehat{k}(1-q_0^2/2k^2),\hfill & \mathrm{when}k\gg q_0,\hfill \end{array}\right.$$

(16)

where the (±) sign corresponds to a wave propagating in the same or opposite direction to the momentum vector $\overrightarrow{k}$. The phase velocity behaves analogously, satisfying $\overrightarrow{k}·{\overrightarrow{v}}_p=\omega$.

2.2.3. The Spinors $U\left(k\right)$

We now turn to the problem of determining the spinors $U\left(k\right)$ from Equation (8) by solving Equation (7). The action of the differential operator on $\psi \left(x\right)$ gives

$$i{\gamma }^{\nu }{\partial }_{\nu }\psi \left(x\right)=\left({\displaystyle \frac{\omega }{c}}{\gamma }^0-\sum _{j=1}^3{\gamma }^j{k}_j\right)A_{\beta }{e}^{-i{\varphi }_s}U\left(k\right)=A_{\beta }{e}^{-i{\varphi }_s}{\mathcal{M}}_{\mathrm{free}}U\left(k\right),$$

(17)

where the matrix ${\mathcal{M}}_{\mathrm{free}}$ is defined as

$${\mathcal{M}}_{\mathrm{free}}=\left(\begin{array}{cccc}\omega /c& 0& -k_z& -k_{-}\\ 0& \omega /c& -k_{+}& k_z\\ k_z& k_{-}& -\omega /c& 0\\ k_{+}& -k_z& 0& -\omega /c\end{array}\right),$$

(18)

where $k_{\pm }=k_x\pm i{k}_y$. Substituting this into Equation (7), we solve the eigenvector equations

$$\left({\mathcal{M}}_{\mathrm{free}}-q_0\mathbb{I}\right)U_{\lambda }\left(k\right)=0,\lambda =(1,2,3,4),$$

(19)

with eigenvalues $\omega$ determined from

$${\Delta }_{\mathrm{free}}=det({\mathcal{M}}_{\mathrm{free}}-q_0\mathbb{I})=0.$$

Evaluating the determinant gives

$${\Delta }_{\mathrm{free}}={[{(\omega /c)}^2-k^2-q_0^2]}^2=0,$$

(20)

which yields Equation (14), with two positive-frequency solutions, ${\omega }_{1,2}=+{\omega }_0$, and two negative-frequency solutions, ${\omega }_{3,4}=-{\omega }_0$, where

$${\omega }_0=+c\sqrt{k^2+q_0^2}.$$

(21)

The corresponding system of equations for the components of $U_{\lambda }\left(k\right)$ in Equation (19) becomes

$$\begin{array}{ccc}\hfill (\omega /c-q_0)U_{\lambda ,1}-k_z{U}_{\lambda ,3}-k_{-}{U}_{\lambda ,4}& & =0,\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill (\omega /c-q_0)U_{\lambda ,2}-k_{+}{U}_{\lambda ,3}+k_z{U}_{\lambda ,4}& & =0,\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill k_z{U}_{\lambda ,1}+k_{-}{U}_{\lambda ,2}-(\omega /c+q_0)U_{\lambda ,3}& & =0,\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill k_{+}{U}_{\lambda ,1}-k_z{U}_{\lambda ,2}-(\omega /c+q_0)U_{\lambda ,4}& & =0.\hfill \end{array}$$

(25)

(1)

Positive-frequency solutions ${\omega }_{1,2}={\omega }_{+}=+{\omega }_0$: $U_{1,2}$.

To solve Equations (22)–(25), let us define ${\omega }_{1+}={\omega }_{+}+q_{0}c$, and express the components $U_{\lambda ,3}$ and $U_{\lambda ,4}$ in terms of $U_{\lambda ,1}$ and $U_{\lambda ,2}$, as follows:

$$\begin{array}{ccc}\hfill U_{\lambda ,3}& & =(k_{z}c/{\omega }_{1+})U_{\lambda ,1}+(k_{-}c/{\omega }_{1+})U_{\lambda ,2},\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill U_{\lambda ,4}& & =(k_{+}c/{\omega }_{1+})U_{\lambda ,1}-(k_{z}c/{\omega }_{1+})U_{\lambda ,2}.\hfill \end{array}$$

(27)

Substituting these expressions back into Equations (22) and (23), we find

$$({\omega }_{+}-q_{0}c)U_{\lambda ,1}=(k_z^{2}c/{\omega }_{1+}+k_{+}{k}_{-}c/{\omega }_{1+})U_{\lambda ,1}+(k_z{k}_{-}c/{\omega }_{1+}-k_z{k}_{-}c/{\omega }_{1+})U_{\lambda ,2},$$

and

$$({\omega }_{+}-q_{0}c)U_{\lambda ,2}=(k_z{k}_{+}c/{\omega }_{1+}-k_z{k}_{+}c/{\omega }_{1+})U_{\lambda ,1}+(k_z^{2}c/{\omega }_{1+}+k_{+}{k}_{-}c/{\omega }_{1+})U_{\lambda ,2}.$$

Now, noting that $k_z^2+k_{+}{k}_{-}=k^2$ and that the off-diagonal terms vanish, we have two independent solutions: $(U_{11}=1,U_{12}=0)$, and $(U_{21}=0,U_{22}=1)$. Using these forms, the remaining components are given by

$$(U_{13}=k_{z}c/{\omega }_{1+},U_{14}=k_{+}c/{\omega }_{1+}),\mathrm{and}(U_{23}=k_{-}c/{\omega }_{1+},U_{24}=-k_{z}c/{\omega }_{1+}),$$

while the normalization condition can be obtained by noting that

$$U_1^{†}{U}_1\to 1+(k_z^2+k_{-}{k}_{+})c^2/{\omega }_{1+}^2=2{\omega }_{+}/{\omega }_{1+}.$$

Thus, the first two normalized spinors are given by

$$U_1=A_{k+}\left(\begin{array}{c}1\\ 0\\ k_{z}c/{\omega }_{1+}\\ k_{+}c/{\omega }_{1+}\end{array}\right),U_2=A_{k+}\left(\begin{array}{c}0\\ 1\\ k_{-}c/{\omega }_{1+}\\ -k_{z}c/{\omega }_{1+}\end{array}\right),$$

(28)

where $A_{k+}={\left({\omega }_{1+}/2{\omega }_{+}\right)}^{1/2}$. It can also be verified that the latter are orthogonal, i.e., $U_1^{†}·U_2=(k_z{k}_{-}-k_{+}^{*}{k}_z)c/{\omega }_{1+}=0$. Note also that for non-relativistic particles, $k\ll q_0$, the 3rd and 4th components of the spinors behave as $kc/{\omega }_{1+}\lesssim \hslash k/mc\simeq v_g/c\ll 1$. In particular, in the rest frame, $U_1^{†}=\sqrt{1/2}(1,0,0,0)$ and $U_1^{†}=\sqrt{1/2}(0,1,0,0)$.

(2)

Negative-frequency solutions ${\omega }_{3,4}={\omega }_{-}=-{\omega }_0$: $U_{3,4}$.

In this case, we write $U_{\lambda ,1}$ and $U_{\lambda ,2}$ in terms of $U_{\lambda ,3}$ and $U_{\lambda ,4}$ from Equations (22) and (23), and using ${\omega }_{1-}={\omega }_{-}-q_{0}c$, we obtain

$$\begin{array}{ccc}\hfill U_{\lambda ,1}& & =(k_{z}c/{\omega }_{1-})U_{\lambda ,3}+(k_{-}c/{\omega }_{1-})U_{\lambda ,4},\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill U_{\lambda ,2}& & =(k_{+}c/{\omega }_{1-})U_{\lambda ,3}-(k_{z}c/{\omega }_{1-})U_{\lambda ,4}.\hfill \end{array}$$

(30)

Similarly to above, the two independent solutions are ($U_{33}=1,U_{34}=0$), and ($U_{43}=0$, $U_{44}=1$), and the corresponding normalized spinors are given by

$$U_3=A_{k-}\left(\begin{array}{c}{k}_{z}c/{\omega }_{1-}\\ k_{+}c/{\omega }_{1-}\\ 1\\ 0\end{array}\right),U_4=A_{k-}\left(\begin{array}{c}{k}_{-}c/{\omega }_{1-}\\ -k_{z}c/{\omega }_{1-}\\ 0\\ 1\end{array}\right).$$

(31)

where $A_{k-}={\left({\omega }_{1-}/2{\omega }_{-}\right)}^{1/2}$. Note that the equality $A_{k+}=A_{k-}$ holds.

Similarly as for positive-frequency spinors, in the rest frame one has $U_3^{†}=\sqrt{1/2}(0,0,1,0)$ and $U_4^{†}=\sqrt{1/2}(0,0,0,1)$. Again, one can immediately verify that $U_3$ and $U_4$ are orthogonal to each other. Furthermore, the above spinors are also orthogonal to their positive-frequency counterparts, i.e.,

$$\begin{array}{ccc}\hfill U_1^{†}·U_3& & \to (1/{\omega }_{1-}+1/{\omega }_{1+})k_{z}c=0,\hfill \\ \hfill U_1^{†}·U_4& & \to (1/{\omega }_{1-}+1/{\omega }_{1+})k_{-}c=0,\hfill \\ \hfill U_2^{†}·U_3& & \to (1/{\omega }_{1-}+1/{\omega }_{1+})k_{+}c=0,\hfill \\ \hfill U_2^{†}·U_4& & \to (1/{\omega }_{1-}+1/{\omega }_{1+})(-)k_{z}c=0,\hfill \end{array}$$

where we have used the fact that ${\omega }_{1-}+{\omega }_{1+}=0$.

For completeness, Appendix A discusses properties and results concerning the current operator associated with Dirac wave packets. For illustration, we consider the cases of a single spinor, two spinors with the same energy, two spinors with different energies, and spinors at rest. This appendix complements known results in the literature and is intended to help the reader become acquainted with the interesting behavior of Dirac particles.

3. Dirac Equation in a Constant EM Four-Potential: The Electric Charge

We next consider the Dirac equation for a particle of charge $\mathfrak{q}$ in the presence of an electromagnetic contravariant four-potential $A^{\nu }=(\varphi ,\overrightarrow{A})$ (in Gaussian units), where $\nu =(0,1,2,3)$. Here, we assume $A^{\nu }$ to be independent of both space and time coordinates. An application of this simplified model will be elaborated in Section 4. The resulting Dirac equation can be expressed in terms of its free-particle form, Equation (2), by implementing the minimal-coupling substitutions,

$$E\to E-\mathfrak{q}\varphi =i\hslash {\partial }_t-\mathfrak{q}\varphi ,\overrightarrow{p}\to \overrightarrow{p}-\mathfrak{q}\overrightarrow{A}/c=-i\hslash \overrightarrow{\nabla }-\mathfrak{q}\overrightarrow{A}/c.$$

Here, $\overrightarrow{p}=-i\hslash \overrightarrow{\nabla }$ denotes the canonical (conjugate) momentum operator, while

$${\overrightarrow{p}}_{\mathrm{kin}}=-i\hslash \overrightarrow{\nabla }-\mathfrak{q}\overrightarrow{A}/c$$

is the kinetic momentum operator. Substituting these definitions into Equation (2), one obtains

$$(i\hslash c{\partial }_0-\mathfrak{q}\varphi )\psi \left(x\right)=\left(\sum _{j=1}^3{\alpha }^j(-i\hslash c{\partial }_j+\mathfrak{q}{A}_j)+{\alpha }^{0}m{c}^2\right)\psi \left(x\right),$$

(32)

where we have used the covariant four-gradient expression for $p_j$ (see Section 2.1) and the fact that $A_{\nu }=(\varphi ,-\overrightarrow{A})$.

Multiplying Equation (32) by ${\alpha }^0$ from the left, and using the result ${\alpha }_0^2=\mathbb{I}$ together with the Dirac matrices ${\gamma }^{\nu }$, we obtain

$$\left[{\gamma }^0\left(i{\partial }_0-\phi \right)+\sum _{j=1}^3{\gamma }^j\left(i{\partial }_j-{\mathcal{A}}_j\right)\right]\psi \left(x\right)=q_0\mathbb{I}\psi \left(x\right),$$

(33)

where $\phi =\mathfrak{q}\varphi /\hslash c={\mathcal{A}}_0$ and ${\mathcal{A}}_j=\mathfrak{q}{A}_j/\hslash c$ form the covariant four-vector ${\mathcal{A}}_{\nu }=(\varphi ,-\overrightarrow{A})\mathfrak{q}/\hslash c$. As a result, Equation (33) can be written in manifestly covariant form as follows:

$${\gamma }^{\nu }(i{\partial }_{\nu }-{\mathcal{A}}_{\nu })\psi \left(x\right)=q_0\mathbb{I}\psi \left(x\right)=q_0\psi \left(x\right).$$

(34)

Now, using the Ansatz $\psi \left(x\right)=A_{\beta }{e}^{-i\left(k^{\nu }{x}_{\nu }\right)}U\left(k\right)$ (Equation (8)), we can write Equation (33) in eigenvector form,

$$\left({\mathcal{M}}_{\mathrm{free}}+{\mathcal{M}}_{\mathrm{em}}-q_0\mathbb{I}\right)U_{\lambda }\left(k\right)=0,\lambda =(1,2,3,4),$$

(35)

where ${\mathcal{M}}_{\mathrm{free}}$ is given in Equation (18) and, following our assumption of constant $A^{\nu }$, we obtain

$${\mathcal{M}}_{\mathrm{em}}=\left(\begin{array}{cccc}-\phi & 0& -{\mathcal{A}}_z& -{\mathcal{A}}_{-}\\ 0& -\phi & -{\mathcal{A}}_{+}& {\mathcal{A}}_z\\ {\mathcal{A}}_z& {\mathcal{A}}_{-}& \phi & 0\\ {\mathcal{A}}_{+}& -{\mathcal{A}}_z& 0& \phi \end{array}\right),$$

(36)

with ${\mathcal{A}}_{\pm }={\mathcal{A}}_x\pm i{\mathcal{A}}_y$. The sum ${\mathcal{M}}_{\mathrm{free}}+{\mathcal{M}}_{\mathrm{em}}$ is then given by

$${\mathcal{M}}_{\mathrm{free}}+{\mathcal{M}}_{\mathrm{em}}=\left(\begin{array}{cccc}\omega /c-\phi & 0& -k_z-{\mathcal{A}}_z& -k_{-}-{\mathcal{A}}_{-}\\ 0& \omega /c-\phi & -k_{+}-{\mathcal{A}}_{+}& k_z+{\mathcal{A}}_z\\ k_z+{\mathcal{A}}_z& k_{-}+{\mathcal{A}}_{-}& -\omega /c+\phi & 0\\ k_{+}+{\mathcal{A}}_{+}& -k_z-{\mathcal{A}}_z& 0& -\omega /c+\phi \end{array}\right),$$

(37)

and the eigenvalues are obtained as the four roots of the determinant,

$$det({\mathcal{M}}_{\mathrm{free}}+{\mathcal{M}}_{\mathrm{em}}-q_0\mathbb{I})=0,$$

which is a function of ($\omega /c-\phi$) and ($\overrightarrow{k}+\overrightarrow{\mathcal{A}}$). It can be written in the compact form

$${\left[{\left({\displaystyle \frac{\omega }{c}}-\phi \right)}^2-{(\overrightarrow{k}+\overrightarrow{\mathcal{A}})}^2-q_0^2\right]}^2=0,$$

(38)

that reduces to Equation (20) for vanishing vector potential ${\mathcal{A}}_{\nu }$. The four solutions are grouped into pairs, ${\omega }_{1,2}={\omega }_{\mathfrak{q}+}$ and ${\omega }_{3,4}={\omega }_{\mathfrak{q}-}$, which can be written in terms of the components of ${\mathcal{A}}_{\nu }$ according to

$${\displaystyle \frac{{\omega }_{\mathfrak{q}\pm }}{c}}={\displaystyle \frac{\mathfrak{q}}{\hslash c}}\varphi \pm \sqrt{k^2-{\displaystyle \frac{2\mathfrak{q}}{\hslash c}}\overrightarrow{k}·\overrightarrow{A}+{\displaystyle \frac{{\mathfrak{q}}^2}{{\hslash }^2{c}^2}}{\left|A\right|}^2+q_0^2}.$$

(39)

This result is consistent with the classical one, valid for constant $A^{\nu }$, obtained by multiplying (39) by $\hslash c$ and making the replacements $E=\hslash \omega$, $\overrightarrow{P}=\hslash \overrightarrow{k}$, which yields (see, e.g., [14], p. 606)

$$E=\mathfrak{q}\varphi +\sqrt{{(\overrightarrow{P}c-\mathfrak{q}\overrightarrow{A})}^2+m^2{c}^4},$$

where only the positive root is retained in the classical picture, $\overrightarrow{P}$ denotes the canonically conjugate momentum of the charged particle and $\overrightarrow{p}=\overrightarrow{P}-\mathfrak{q}\overrightarrow{A}/c$ is the kinetic momentum.

Finally, from Equations (18), (35) and (36) one can obtain the following system of equations for the spinors:

$$\begin{array}{ccc}\hfill (\omega /c-\phi -q_0)U_{\lambda ,1}-{\kappa }_z{U}_{\lambda ,3}-{\kappa }_{-}{U}_{\lambda ,4}& & =0,\hfill \end{array}$$

(40)

$$\begin{array}{ccc}\hfill (\omega /c-\phi -q_0)U_{\lambda ,2}-{\kappa }_{+}{U}_{\lambda ,3}+{\kappa }_z{U}_{\lambda ,4}& & =0,\hfill \end{array}$$

(41)

$$\begin{array}{ccc}\hfill {\kappa }_z{U}_{\lambda ,1}+{\kappa }_{-}{U}_{\lambda ,2}-(\omega /c-\phi +q_0)U_{\lambda ,3}& & =0,\hfill \end{array}$$

(42)

$$\begin{array}{ccc}\hfill {\kappa }_{+}{U}_{\lambda ,1}-{\kappa }_z{U}_{\lambda ,2}-(\omega /c-\phi +q_0)U_{\lambda ,4}& & =0,\hfill \end{array}$$

(43)

where $\overrightarrow{\kappa }=\overrightarrow{k}-\mathfrak{q}\overrightarrow{A}/\hslash c$, and ${\kappa }_{\pm }={\kappa }_x\pm i{\kappa }_y$, corresponding to a kinetic momentum $\overrightarrow{p}=\hslash \overrightarrow{\kappa }$. Interestingly, Equations (40)–(43) have the same form as Equations (22)–(25), if in the latter we make the substitutions, $\omega /c\to \omega /c-\phi$ and $\overrightarrow{k}\to \overrightarrow{\kappa }$. Then, the expressions for the corresponding spinors can be taken from Equations (28) for the positive sign in Equation (39), and from Equations (31) for the negative one. For completeness, we explicitly report the spinor expressions below.

(1)

Positive-sign solutions ${\omega }_{1,2}={\omega }_{\mathfrak{q}+}$: $U_{1,2}$.

$$U_1=A_{k+}\left(\begin{array}{c}1\\ 0\\ {\kappa }_{z}c/{\omega }_{1+}\\ {\kappa }_{+}c/{\omega }_{1+}\end{array}\right),U_2=A_{k+}\left(\begin{array}{c}0\\ 1\\ {\kappa }_{-}c/{\omega }_{1+}\\ -{\kappa }_{z}c/{\omega }_{1+}\end{array}\right),$$

(44)

where ${\omega }_{1+}={\omega }_{\mathfrak{q}+}-c\phi +q_{0}c$, and

$$A_{k+}^2={\displaystyle \frac{{\omega }_{1+}}{2({\omega }_{\mathfrak{q}+}-c\phi )}}.$$

(45)

(2)

Negative-sign solutions ${\omega }_{3,4}={\omega }_{\mathfrak{q}-}$: $U_{3,4}$.

$$U_3=A_{k-}\left(\begin{array}{c}{\kappa }_{z}c/{\omega }_{1-}\\ {\kappa }_{+}c/{\omega }_{1-}\\ 1\\ 0\end{array}\right),U_4=A_{k-}\left(\begin{array}{c}{\kappa }_{-}c/{\omega }_{1-}\\ -{\kappa }_{z}c/{\omega }_{1-}\\ 0\\ 1\end{array}\right).$$

(46)

where ${\omega }_{1-}={\omega }_{\mathfrak{q}-}-c\phi -q_{0}c$, and

$$A_{k-}^2={\displaystyle \frac{{\omega }_{1-}}{2({\omega }_{\mathfrak{q}-}-c\phi )}}.$$

(47)

Finally, we note that the equality $A_{k+}=A_{k-}$ is also obeyed in this case, and the new spinors remain orthogonal, a result which follows from the relation, ${\omega }_{1-}+{\omega }_{1+}=0$, which holds in this case too.

4. Dirac Equation Embedded in Vacuum EM Potential Fluctuations: The Emergence of Mass

Let us consider the problem of a charged, massless particle and ask whether, within an extended Dirac framework, a mechanism exists that can endow the particle with a finite mass. The model we propose couples the particle charge $\mathfrak{q}$ to vacuum EM four-potential fluctuations (to be specified) and aims to suggest a possible route for the emergence of mass. Our approach, largely phenomenological, is not intended to challenge the prevailing paradigm of particle physics but rather to outline a mathematical scenario consistent with established physical laws. While each key assumption is justified as rigorously as possible, open questions remain regarding their practical implementation.

The basic idea is that the point charge is embedded in a fluctuating EM potential $A^{\nu }$, whose properties may differ significantly from those of a free field, since they act locally and may exhibit specific features. Justifying such behavior would require detailed knowledge of the vacuum structure, which lies beyond the scope of this work. Here, we limit ourselves to providing predictions that may, a posteriori, either support or rule out the model. In our framework, the vector $A^{\nu }\in {\left\{A^{\nu }\right\}}_{\mathrm{vac}}$ is conjectured to obey the following expectation values:

$${\langle A^{\nu }\rangle }_{\mathrm{vac}}=0,{\langle A^{\nu }{A}_{\nu }\rangle }_{\mathrm{vac}}\ne 0,$$

(48)

where the averages are performed over the ensemble ${\left\{A^{\nu }\right\}}_{\mathrm{vac}}$. Specifically, we assume that each $A^{\nu }$ remains constant, i.e., independent of spacetime coordinates, within a finite proper time interval $\Delta s_{\mathrm{vac}}/c>0$. This assumption can be seen as a zeroth-order approximation of the four-potential valid on small length scales. It has two important merits: first, it allows for an exact simple solution of the Dirac Equation (35) since the vector potential does not depend on the coordinates, and second, it ensures the absence of local electric and magnetic fields in vacuum. Under these conditions, the results of Section 3 can be applied to obtain the eigenvalues in Equation (38), from which the vacuum average ${\langle \dots \rangle }_{\mathrm{vac}}$ can be formally calculated. The condition ${\langle A^{\nu }\rangle }_{\mathrm{vac}}=0$ is consistent with time-reversal symmetry, while the requirement ${\langle A^{\nu }{A}_{\nu }\rangle }_{\mathrm{vac}}\ne 0$ provides the mechanism we seek.

However, to be physically acceptable, such EM fluctuations must remain invariant under gauge transformations—a property that the vector potential $A^{\nu }$ does not generally possess. Only the electromagnetic field tensor $F^{\mu \nu }$ is gauge-invariant, which ensures the invariance of both the electric and magnetic fields. Therefore, to make use of ${\langle A^{\nu }{A}_{\nu }\rangle }_{\mathrm{vac}}$, we must determine the conditions that gauge transformations must satisfy for this quantity to remain invariant. These conditions are discussed in Appendix B.

There is a further issue related to the form of the vacuum potential $A^{\nu }$; that is, it can have either a spacelike or a timelike character. In the following, we consider the two cases separately.

4.1. The Vacuum EM Potential Fluctuations: Spacelike Four-Potential

We begin with Equation (38), setting $q_0=0$ in accordance with the assumption of a massless particle. We then evaluate the equation for the two distinct roots by taking the vacuum average,

$$\langle {\left(\omega /c-\phi \right)}^2-{(\overrightarrow{k}+\overrightarrow{\mathcal{A}})}^2{\rangle }_{\mathrm{vac}}=0.$$

(49)

By expanding the squares we then obtain

$${\displaystyle \frac{{\omega }^2}{c^2}}-2{\displaystyle \frac{\omega }{c}}{\langle \phi \rangle }_{\mathrm{vac}}+{\langle {\phi }^2\rangle }_{\mathrm{vac}}-[k^2+2\overrightarrow{k}·{\langle \overrightarrow{\mathcal{A}}\rangle }_{\mathrm{vac}}+\langle |\overrightarrow{\mathcal{A}}{|}^2{\rangle }_{\mathrm{vac}}]=0.$$

(50)

Since by assumption the mean values vanish, we end up with

$${\displaystyle \frac{{\omega }^2}{c^2}}=k^2-{\langle {\phi }^2\rangle }_{\mathrm{vac}}+\langle |\overrightarrow{\mathcal{A}}{{|}^2\rangle }_{\mathrm{vac}}.$$

(51)

Assuming a spacelike four-vector, i.e., $\langle |\overrightarrow{{\mathcal{A}}_{\mathrm{v}}}{{|}^2\rangle }_{\mathrm{vac}}>{\langle {\phi }_{\mathrm{v}}^2\rangle }_{\mathrm{vac}}$, we obtain

$$\begin{array}{cc}\hfill {\hslash }^2{\omega }^2& ={(\hslash k)}^2{c}^2+{\mathfrak{q}}^2\left(\langle |\overrightarrow{A}{{|}^2\rangle }_{\mathrm{vac}}-{\langle {\varphi }^2\rangle }_{\mathrm{vac}}\right)\hfill \end{array}$$

(52)

$$\begin{array}{cc}\hfill & \equiv {(\hslash k)}^2{c}^2+m_{\mathfrak{q}}^2{c}^4,\hfill \end{array}$$

(53)

where the effective mass of the charged particle, $m_{\mathfrak{q}}$, is given by

$$m_{\mathfrak{q}}{c}^2=\left|\mathfrak{q}\right|{\left[\langle |\overrightarrow{A}{{|}^2\rangle }_{\mathrm{vac}}-{\langle {\varphi }^2\rangle }_{\mathrm{vac}}\right]}^{1/2}.$$

(54)

We expect that EM potential fluctuations act within a time scale $\Delta t_{\mathrm{vac}}$ allowed by the uncertainty principle, i.e.,

$$\Delta t_{\mathrm{vac}}\sim {\displaystyle \frac{\hslash }{2m_{\mathfrak{q}}{c}^2}},$$

(55)

after which the particle has acquired a finite mass $m_{\mathfrak{q}}$ (see Section 5.2). Note that the distance covered by a photon within this time is basically given by the reduced Compton wavelength, $c\Delta t_{\mathrm{vac}}\simeq (1/2)\hslash c/m_{\mathfrak{q}}{c}^2$ (see discussion below Equation (7)). We can identify this length with the proper interval $\Delta s_{\mathrm{vac}}$.

4.2. The Vacuum EM Potential Fluctuations: Timelike Four-Potential

To find the equivalent of Equation (54) for a timelike potential $A^{\nu }$, we need to modify the Dirac Equation (34), now written in terms of a new vector, ${\mathcal{A}}_{\nu }^{\prime }$, as follows:

$${\gamma }^{\nu }(i{\partial }_{\nu }-{\mathcal{A}}_{\nu }^{\prime })\psi \left(x\right)=q_0\mathbb{I}\psi \left(x\right)=q_0\psi \left(x\right).$$

(56)

The basic idea behind the new four-potential consists in assuming that the coupling constant, $\mathfrak{q}$, takes the value $\mathfrak{q}$ for the first two components of the four-spinor, and $-\mathfrak{q}$ for the third and fourth ones, while for the standard coupling it takes the same value $\mathfrak{q}$ for all four components. To take this change of sign into account we define

$${\mathcal{A}}_{\nu }^{\prime }={\gamma }^0{\mathcal{A}}_{\nu }.$$

(57)

Unfortunately, this choice violates the Lorentz covariance of the Dirac equation. One way to bypass this restriction consists in accepting the violation provided that it occurs within the time scale, $\Delta t_{\mathrm{vac}}$ (Equation (55)). In other words, the assumption of constant $A^{\nu }$ (valid for both spacelike and timelike potentials) and the violation of Lorentz covariance for eventual timelike EM potentials are permissible within the time scale $\Delta t_{\mathrm{vac}}$. For both types of EM potentials, we interpret $\Delta t_{\mathrm{vac}}$ as the time it takes the vacuum to provide a charge with a proper mass (see the discussion in Section 5.2).

We proceed next with the mathematical aspects of the modified Dirac equation by discussing in sufficient detail the new algebra involved. The only matrix in (34) affected by the substitution Equation (56) is ${\mathcal{M}}_{\mathrm{em}}$, which becomes ${\mathcal{M}}_{\mathrm{vac}}$ given by

$${\mathcal{M}}_{\mathrm{vac}}=\left(\begin{array}{cccc}-\phi & 0& {\mathcal{A}}_z& {\mathcal{A}}_{-}\\ 0& -\phi & {\mathcal{A}}_{+}& -{\mathcal{A}}_z\\ {\mathcal{A}}_z& {\mathcal{A}}_{-}& -\phi & 0\\ {\mathcal{A}}_{+}& -{\mathcal{A}}_z& 0& -\phi \end{array}\right),$$

(58)

where the diagonal elements are equal to $-\phi$, and the off-diagonal blocks carry the same sign. Then, the sum ${\mathcal{M}}_{\mathrm{free}}+{\mathcal{M}}_{\mathrm{vac}}$ becomes

$${\mathcal{M}}_{\mathrm{free}}+{\mathcal{M}}_{\mathrm{vac}}=\left(\begin{array}{cccc}\omega /c-\phi & 0& -k_z+{\mathcal{A}}_z& -k_{-}+{\mathcal{A}}_{-}\\ 0& \omega /c-\phi & -k_{+}+{\mathcal{A}}_{+}& k_z-{\mathcal{A}}_z\\ k_z+{\mathcal{A}}_z& k_{-}+{\mathcal{A}}_{-}& -(\omega /c+\phi )& 0\\ k_{+}+{\mathcal{A}}_{+}& -(k_z+{\mathcal{A}}_z)& 0& -(\omega /c+\phi )\end{array}\right),$$

(59)

The resulting determinant ${\Delta }_{\mathrm{vac}}$ can be written, upon averaging over vacuum fluctuations, in the compact form (see Appendix C for details and Equations (A39) and (A40)),

$${\langle {\Delta }_{\mathrm{vac}}\rangle }_{\mathrm{vac}}={\left([{\omega }^2/c^2-{\langle {\phi }^2\rangle }_{\mathrm{vac}}]-[k^2-{\langle {\overrightarrow{\mathcal{A}}}^2\rangle }_{\mathrm{vac}}]\right)}^2.$$

Setting ${\langle {\Delta }_{\mathrm{vac}}\rangle }_{\mathrm{vac}}=0$, the frequencies $\omega$ are given by

$${\displaystyle \frac{{\omega }^2}{c^2}}=k^2+{〈{\phi }^2〉}_{\mathrm{vac}}-\langle {\overrightarrow{\mathcal{A}}}^2\rangle \mathrm{vac}.$$

(60)

In the case of a timelike four-vector, i.e., ${\langle {\phi }_{\mathrm{v}}^2\rangle }_{\mathrm{vac}}>\langle |\overrightarrow{{\mathcal{A}}_{\mathrm{v}}}{{|}^2\rangle }_{\mathrm{vac}}$, we obtain

$$\begin{array}{cc}\hfill {\hslash }^2{\omega }^2& ={(\hslash k)}^2{c}^2+{\mathfrak{q}}^2\left({\langle {\varphi }^2\rangle }_{\mathrm{vac}}-\langle |\overrightarrow{A}{{|}^2\rangle }_{\mathrm{vac}}\right)\hfill \end{array}$$

(61)

$$\begin{array}{cc}\hfill & \equiv {(\hslash k)}^2{c}^2+m_{\mathfrak{q}}^2{c}^4,\hfill \end{array}$$

(62)

where the effective mass of the charged particle, $m_{\mathfrak{q}}$, is now given by

$$m_{\mathfrak{q}}{c}^2=\left|\mathfrak{q}\right|{\left[{\langle {\varphi }^2\rangle }_{\mathrm{vac}}-\langle |\overrightarrow{A}{{|}^2\rangle }_{\mathrm{vac}}\right]}^{1/2}.$$

(63)

4.3. The Emergence of Mass for a Charged Particle Coupled to Vacuum EM Potential Fluctuations

We have shown that coupling an otherwise massless charge $\mathfrak{q}$ to electromagnetic vacuum fluctuations, represented by a fluctuating four-potential $A^{\nu }$ with expectation values given in Equation (48), can generate a finite particle mass $m_{\mathfrak{q}}$, regardless of whether $A^{\nu }$ is spacelike or timelike. This result relies on two main assumptions: (i) the potential $A^{\nu }$ is constant, and (ii) it acts within the proper time $\Delta t_{\mathrm{vac}}\sim \hslash /2m_{\mathfrak{q}}{c}^2$, during which the mass is generated. In addition, they allow for a Lorentz covariance violation in the possible case of timelike potentials.

Furthermore, the interactions of the charge with the vacuum potential fluctuations are encoded in the effective mass, such that at larger time scales the resulting charged massive object can be treated as a free charged particle. In this scenario, the results discussed in Section 2 apply. However, in order to treat neutrinos using free Dirac spinors, the issue of their left-handedness needs to be specifically added to the formalism (see the introduction of Section 5).

A general expression for the mass can then be written in the form

$$m_{\mathfrak{q}}{c}^2=\left|\mathfrak{q}\right||{\langle {\varphi }^2\rangle }_{\mathrm{vac}}-\langle |\overrightarrow{A}{|}^2{{\rangle }_{\mathrm{vac}}|}^{1/2},$$

(64)

valid for both spacelike and timelike four-vectors. In the following, we simplify the notation by defining

$${\overline{A}}_{\mathfrak{q}}\equiv |{\langle {\varphi }^2\rangle }_{\mathrm{vac}}-\langle |\overrightarrow{A}{|}^2{{\rangle }_{\mathrm{vac}}|}^{1/2},$$

(65)

which stresses the fact that the amplitude of vacuum fluctuations may depend on the magnitude of $\mathfrak{q}$. After (64) and (65) we thus have

$$\mathfrak{q}{\overline{A}}_{\mathfrak{q}}=m_{\mathfrak{q}}{c}^2,$$

(66)

where, without loss of generality, we take $\mathfrak{q}>0$. The unit of charge is denoted simply as e (≃$4.8 · {10}^{-10}$ esu in Gaussian units). The issue of a spatial extension of the charge, being either a point-like or a finite one, is addressed in the following section.

5. The Vacuum EM Fluctuations for Generating Mass: Leptons

For the lepton family (e, $\mu$, $\tau$), we use the notation ${\overline{A}}_e$, which takes the same value for all three members since they carry the same electric charge. In specific cases, we may denote the charge as $e^{-}$ (<0) or $e^{+}$ (>0) to distinguish between negatively and positively charged particles.

Since ${\overline{A}}_e$ is independent of lepton flavor, the amount of mass acquired through the vacuum mechanism is the same for all three charged leptons. For simplicity, and to avoid introducing additional parameters into this model, we assume that the electron obtains essentially all of its mass from vacuum fluctuations. In this framework, the $\mu$ and $\tau$ leptons would receive at most $m_e{c}^2$, i.e., $0.511\times {10}^6$ eV of their rest mass. For the heavier leptons, however, this contribution represents only a negligible fraction of their total masses, indicating that an alternative mechanism—such as the Higgs mechanism—is required to account for the deficit.

Our assumption regarding the electron mass is consistent with the fact that the Yukawa coupling for a lepton ℓ, $y_{\ell }=\sqrt{2}{m}_{\ell }{c}^2/v_{\mathrm{H}}$, with $v_{\mathrm{H}}\simeq 246.22$ GeV, takes a comparatively small value for the electron relative to the other two charged leptons. In what follows, we focus on the possibility that neutrinos can be treated as charged Dirac particles, with their charge denoted by $\mathfrak{q}$. Our conjecture regarding the Dirac nature of neutrinos is consistent with the results of the GERDA experiment [15], which was designed to detect possible neutrinoless double-beta decay, a signal of the Majorana neutral nature of neutrinos (see also [16]). No evidence for the $0\nu \beta \beta$ decay of $\begin{array}{c}\hfill {}^{76}\mathrm{Ge}\end{array}$ to the ground state of $\begin{array}{c}\hfill {}^{76}\mathrm{Se}\end{array}$ has been found, corresponding to an effective Majorana neutrino mass $m_0\lesssim (79$–$180)$ meV.

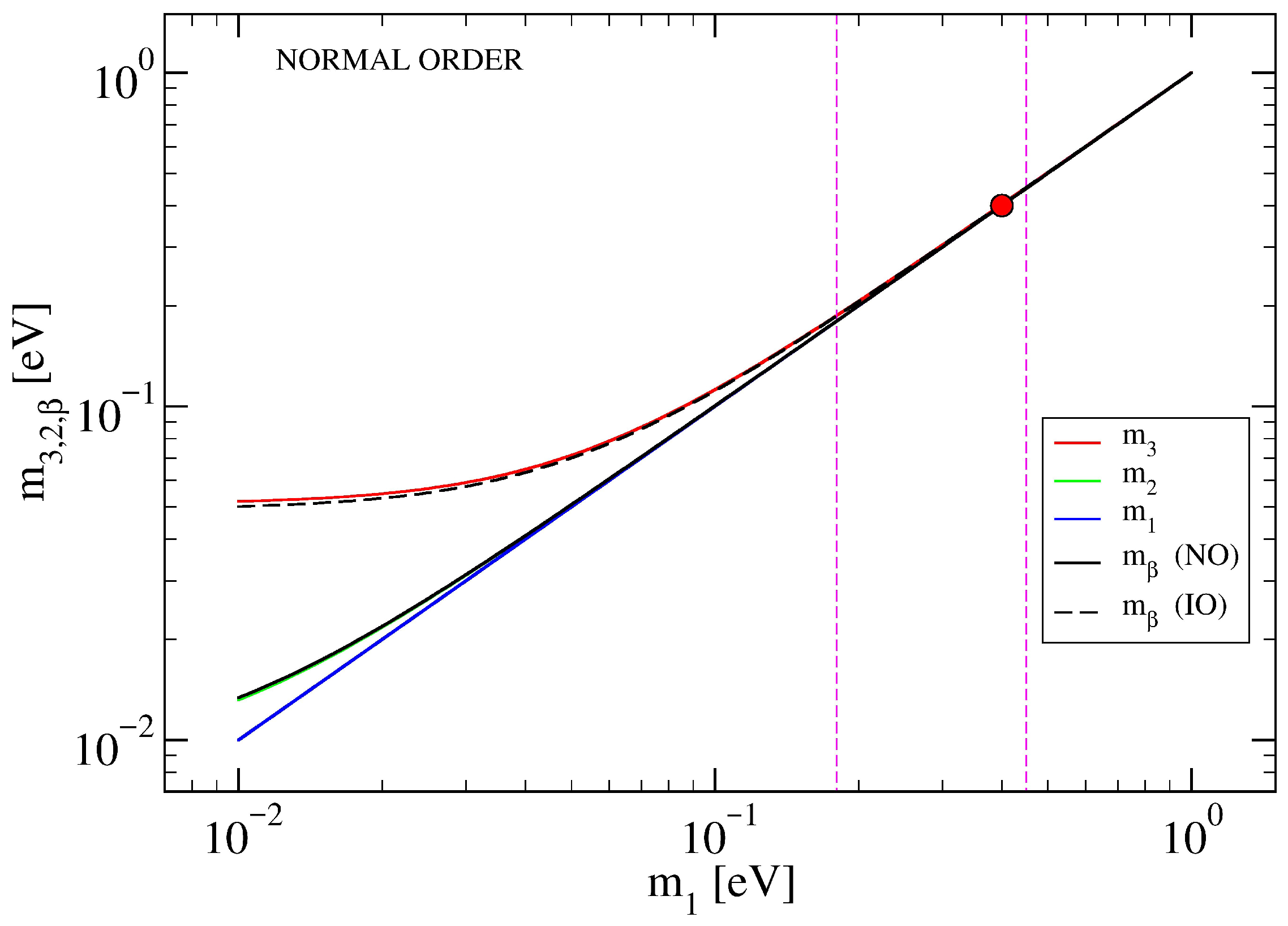
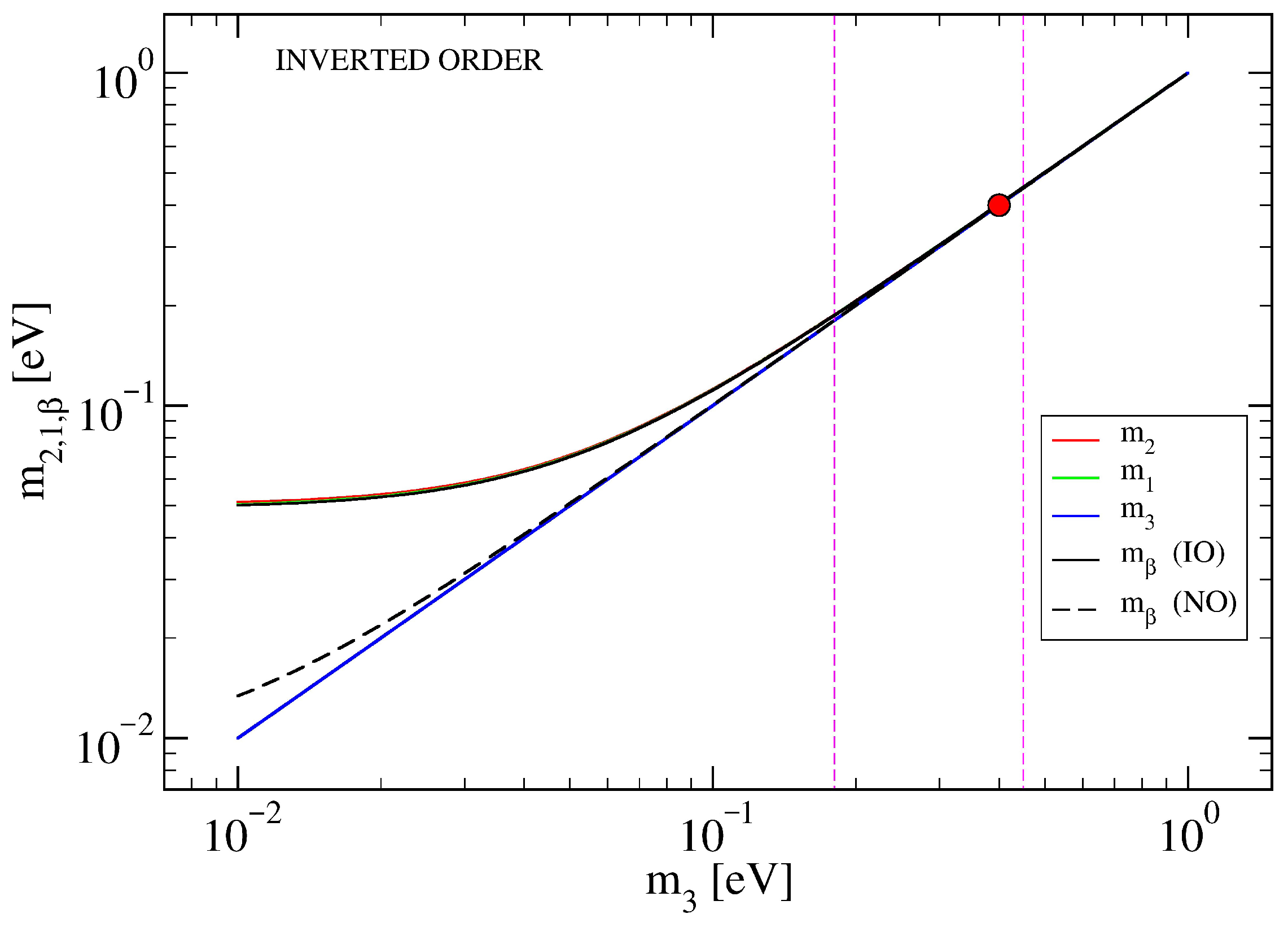
Here, we attempt to estimate a realistic value for the neutrino charge. For simplicity, we restrict our analysis to the electron neutrino and assume that its entire mass arises from the coupling of its charge $\mathfrak{q}$ to the vacuum amplitude fluctuations ${\overline{A}}_{\mathfrak{q}}$. This choice is dictated by the fact that neutrinos appear to have different masses (see Appendix D for more details), which would in turn require introducing three distinct charges. A detailed treatment of the flavor scenario therefore lies beyond the scope of our simplified approach, but it could be pursued once the absolute masses of all three neutrinos become available. In addition, our model allows, as it stands, for both left- and right-handed neutrinos.

5.1. Modeling the Neutrino Electric Charge and Magnetic Moment

It is generally accepted that neutrinos possess a finite mass, although the exact ordering of the flavor mass hierarchy remains uncertain. For our purposes, we base our approach on the recent experimental results of the KATRIN collaboration [17] (2025), which provide the following constraint on the effective electron antineutrino mass:

$$m_{\mathfrak{q}}{c}^2<0.45\mathrm{eV}(90\%\mathrm{CL}).$$

(67)

For practical reasons, we assume the value $m_{\mathfrak{q}}{c}^2=0.40$ eV to obtain first estimates (see Appendix D). Later, we suggest a lower bound for the mass, yielding $m_{\mathfrak{q}}{c}^2>7$ meV. We present results for different masses to obtain a more complete and useful picture.

The basic quantities to build a model of the neutrino electric charge, and its associated magnetic moment, are given by the relations

$$e{\overline{A}}_e=m_e{c}^2\mathrm{and}\mathfrak{q}{\overline{A}}_{\mathfrak{q}}=m_{\mathfrak{q}}{c}^2,$$

(68)

from which we obtain

$${\overline{A}}_{\mathfrak{q}}={\displaystyle \frac{1}{\beta }}{\displaystyle \frac{m_{\mathfrak{q}}{c}^2}{m_e{c}^2}}{\overline{A}}_e,\mathrm{with}\beta ={\displaystyle \frac{\mathfrak{q}}{e}}.$$

(69)

Our final goal is to find a direct relationship between $\beta$ and the mass ratio. To achieve this, we suggest that the four-potential magnitudes, ${\overline{A}}_{\mathfrak{q}}$ and ${\overline{A}}_e$, may depend on the ’spatial extension’ of the respective electric charges, in terms of, say, charge radii $R_{\mathfrak{q}}$’s, consistent with the idea that vacuum fluctuations are coupled to the electric charge and thus adjust their amplitudes accordingly. The way this happens must be derived from additional information on the behavior of ${\overline{A}}_{\mathfrak{q},e}$. Fortunately, the precise values of the electric charge radii are not explicitly needed, but their very existence is formally required to complete the picture. This particular feature leaves open the possibility that $R_{\mathfrak{q}}$ could be interpreted as an effective length scale which is quantum-mechanically associated with a finite charge distribution. We expect that the charge radii be smaller than the respective Compton wavelengths.

In view of the above discussion, we assume that the four-potential magnitude, generically denoted as ${\overline{A}}_{\mathfrak{q}}$, obeys the empirical scaling law

$${\overline{A}}_{\mathfrak{q}}=A_0{\left({\displaystyle \frac{R_0}{R_{\mathfrak{q}}}}\right)}^{\gamma },$$

(70)

that is, the smaller the radius $R_{\mathfrak{q}}$, the larger the field magnitude ${\overline{A}}_{\mathfrak{q}}$ will be. The quantity $R_0$ is an auxiliary length introduced to allow the exponent $\gamma$ to be fractional. We will show that $\gamma$ may indeed vary in the range $1<\gamma <3$ to be consistent with the experimental data. However, the quantities $A_0$ and $R_0$ disappear when we take the ratio between potential amplitudes.

Moreover, when considering a finite spatial extension of a charge distribution, we assume that the different charges, $\mathfrak{q}$ and e, differ only in their radii, thus keeping the charge density constant. This suggests that the mechanism responsible for charge localization is a property of the vacuum, independent of the total amount of charge involved. The way charge becomes quantized remains to be understood—a problem that goes beyond our current theoretical resources. Therefore, the condition of a constant charge density,

$${\displaystyle \frac{\mathfrak{q}}{R_{\mathfrak{q}}^3}}={\displaystyle \frac{e}{R_e^3}},$$

translates into the following relation:

$$R_{\mathfrak{q}}={\beta }^{1/3}{R}_e.$$

(71)

Now we can use Equations (70) and (71) into Equation (69) to obtain

$$\beta ={\displaystyle \frac{\mathfrak{q}}{e}}={\left({\displaystyle \frac{m_{\mathfrak{q}}{c}^2}{m_e{c}^2}}\right)}^{3/(3-\gamma )}.$$

(72)

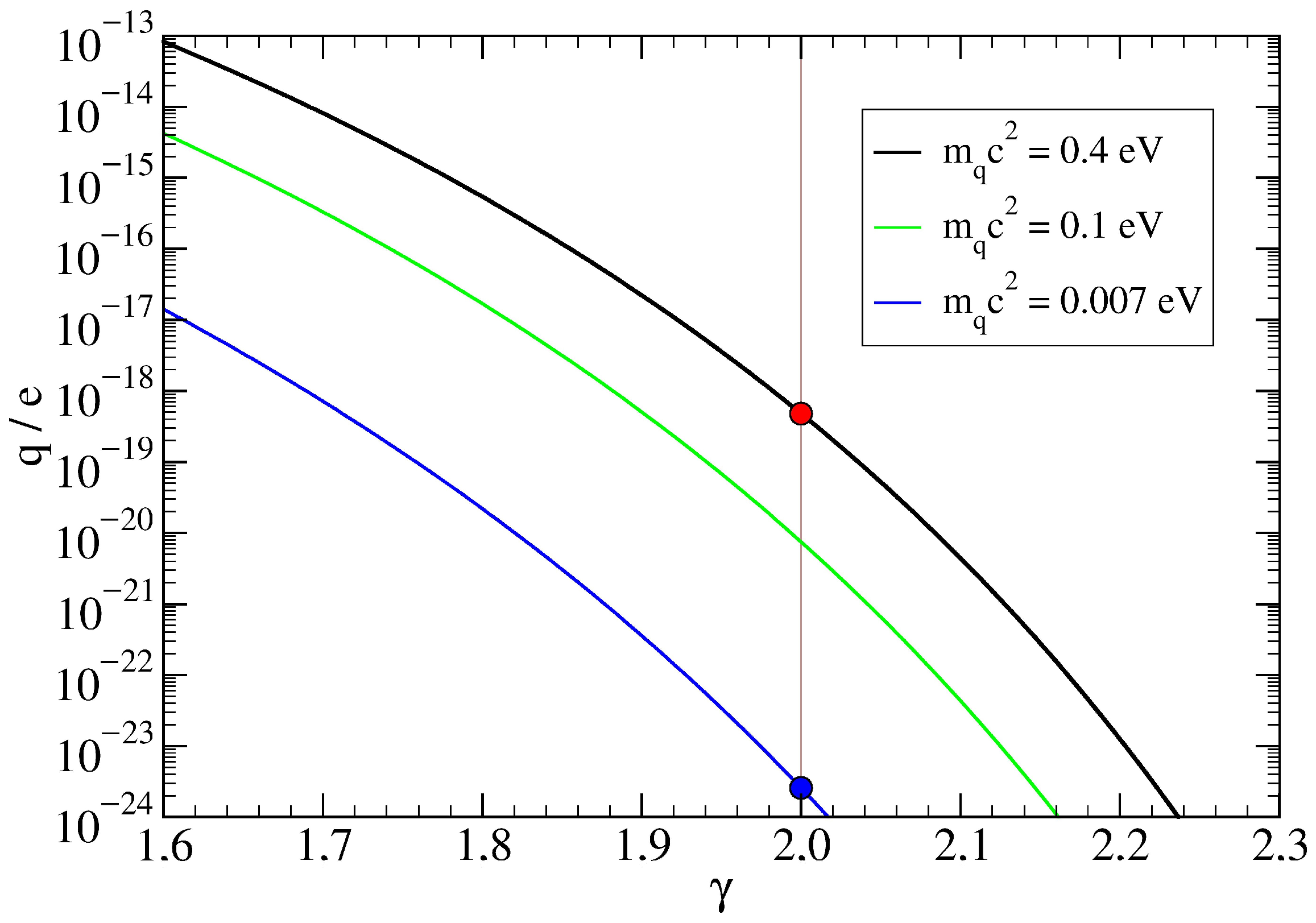
For illustration, this relation is plotted in Figure 1 for three selected values of $m_{\mathfrak{q}}{c}^2\le 0.4$ eV. As is apparent, the relevant range of the exponent $\gamma$ is rather narrow, roughly $1.6<\gamma <2.3$. The lowest mass value 7 meV will be justified in Section 5.2. In the figure, we highlight the integer value $\gamma =2$, which acquires a special meaning as discussed next.

If we take $\gamma =2$ in Equation (70), we find the simpler relation,

$${\overline{A}}_{\mathfrak{q}}{R}_{\mathfrak{q}}^2=A_e{R}_e^2=\mathrm{const},$$

(73)

which reminds us of a conservation law, similar to mass conservation in classical fluid dynamics, where the exponent $\gamma =2$ has the meaning of a spatial dimension $d=2$, corresponding to a standard Euclidean surface. From this observation, we can interpret fractional values of $\gamma$ as a fractal dimension, $\gamma \equiv d_f$, where $1<d_f<3$. Note that the extreme case $d_f=3$ yields a vanishing neutrino charge, while the one-dimensional case, $d_f=1$, would yield too-large neutrino charges, which are unrealistic. In keeping with such an intuitive interpretation, we assume in the following that $\gamma =2$ represents the physics of mass generation most realistically and accurately, so that

$${\displaystyle \frac{\mathfrak{q}}{e}}={\left({\displaystyle \frac{m_{\mathfrak{q}}{c}^2}{m_e{c}^2}}\right)}^3,$$

(74)

yields our ’simplest’ estimation for the neutrino electric charge. However, in certain extensions of the model, it is possible, at least speculatively, to consider fractal formulations describing a conservation law across fractal interfaces.

In Figure 2, we plot the ratio $\mathfrak{q}/e$ as a function of neutrino mass, $m_{\mathfrak{q}}{c}^2$, for the relevant case $\gamma =2$. As one can see, the predicted charge ratios are consistent with the presently available experimental data (see Section 1).

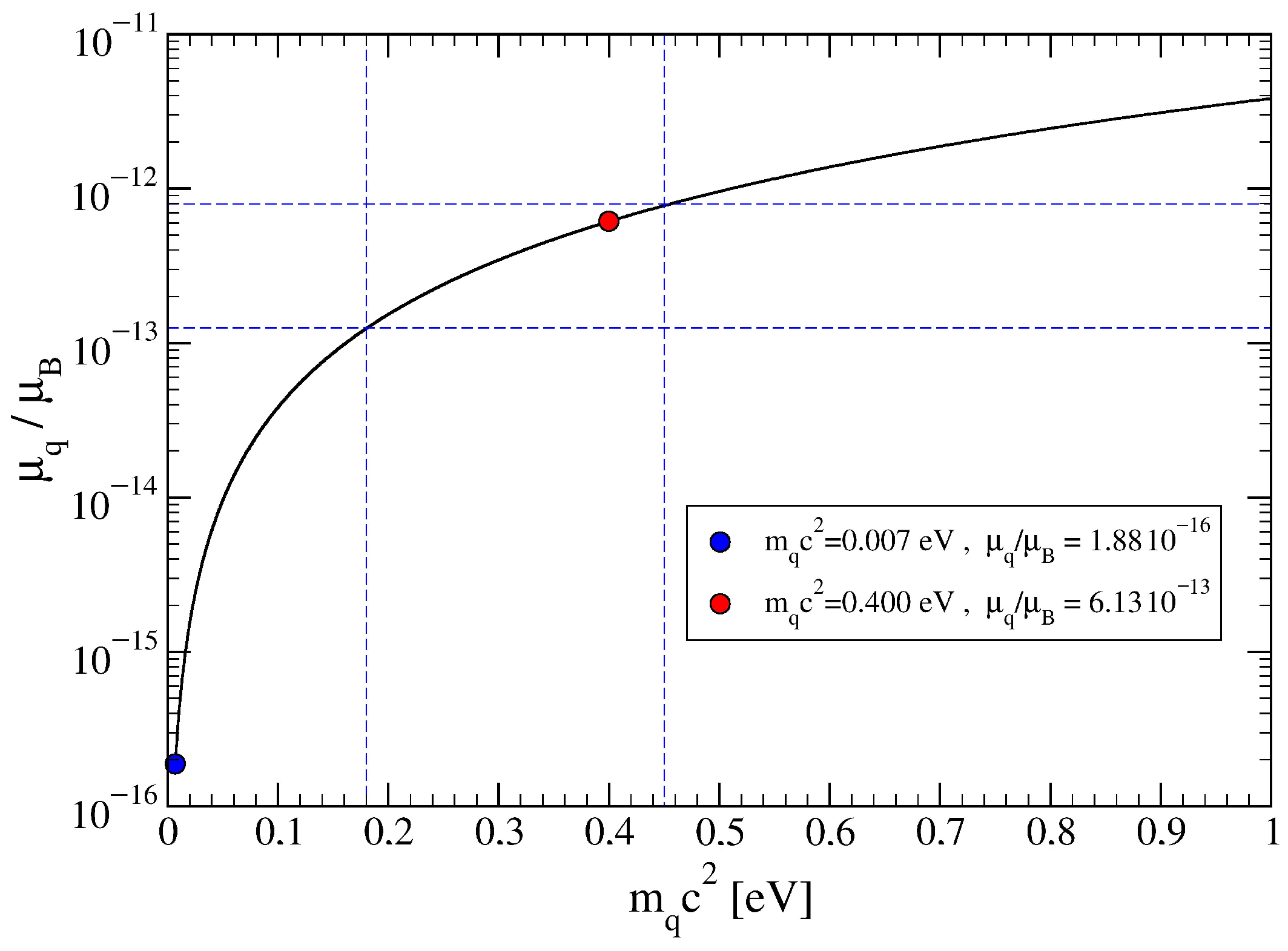
Finally, to estimate the Dirac neutrino magnetic moment, ${\mu }_{\mathfrak{q}}$, we assume that it follows the same relation as the Dirac electron magnetic moment with gyromagnetic factor $g_s=2$ as in Equation (1), namely

$${\mu }_{\mathfrak{q}}={\displaystyle \frac{1}{2}}{\displaystyle \frac{\mathfrak{q}\hslash c}{m_{\mathfrak{q}}{c}^2}}={\displaystyle \frac{\mathfrak{q}}{e}}\left({\displaystyle \frac{m_e{c}^2}{m_{\mathfrak{q}}{c}^2}}\right){\mu }_{\mathrm{B}},$$

(75)

Using Equation (74), we find our final result,

$${\displaystyle \frac{{\mu }_{\mathfrak{q}}}{{\mu }_{\mathrm{B}}}}={\left({\displaystyle \frac{m_{\mathfrak{q}}{c}^2}{m_e{c}^2}}\right)}^2.$$

(76)

In Figure 3, we plot the ratio, ${\mu }_{\mathfrak{q}}/{\mu }_{\mathrm{B}}$, as a function of neutrino mass using Equation (76). Also in this case the predicted values for the magnetic moment ratio are consistent with the available experimental data.

5.2. Particle Decays and Minimum Neutrino Mass

The issue of particle decay is central to estimating the minimum neutrino mass allowed by the present model. To illustrate the main idea, we compare our considerations with available experimental data on particle decays [3]. The relevant cases are summarized in

Table 1. Unstable particle (1st column) and its creation time [s] (2nd column). The 3rd column reports the unstable particle lifetime $T_p$ [s], and the 4th column the main decay channel. The 5th column reports the ’creation’ times for each daughter particle (p). The creation time, $t_c$, is assumed to be given by $t_c=\hslash /2m_p{c}^2$ (see text). For neutrinos we have taken the mass value 0.4 eV for illustration. We have included the neutral Higgs boson for comparison.

Unstable Particle	Creation Time [s]	Lifetime [s]	Decay Channel	Daughter Particle Creation Times [s]
neutron	$2.2\times {10}^{-24}$	$\simeq 611$	$p^{+}+e^{-}+{\overline{\nu }}_e$	$2.2\times {10}^{-24}$, $4.1\times {10}^{-21}$, $5.2\times {10}^{-15}$
${\mu }^{-}$	$2.0\times {10}^{-23}$	$2.2\times {10}^{-6}$	$e^{-}+{\overline{\nu }}_e+{\nu }_{\mu }$	$4.1\times {10}^{-21}$, $5.2\times {10}^{-15}$, $5.2\times {10}^{-15}$
${\tau }^{-}$	$1.2\times {10}^{-24}$	$2.9\times {10}^{-13}$	$e^{-}+{\overline{\nu }}_e+{\nu }_{\tau }$	$4.1\times {10}^{-21}$, $5.2\times {10}^{-15}$, $5.2\times {10}^{-15}$
Higgs boson	$1.7\times {10}^{-26}$	$1.6\times {10}^{-22}$	$\overline{b}+b$	$4.9\times {10}^{-25}$, $4.9\times {10}^{-25}$
top quark	$1.2\times {10}^{-26}$	$5\times {10}^{-25}$	$W^{+}+b$	$2.6\times {10}^{-26}$, $4.9\times {10}^{-25}$

, which reports data for the neutron (the slowest known particle decay), the unstable leptons, and the top quark (the fastest known decay). In the comparison below we have implicitly assumed that the time scales for the Higgs mechanism and the present model to generate a finite mass are of similar order of magnitude. This remains to be understood.

According to our discussion leading to Equation (55), we interpret $\Delta t_{\mathrm{vac}}$ as the time required to vacuum EM potential fluctuations to provide a mass $m_p$ to a charge. We denote this proper time as the creation time, $t_c=\hslash /2m_p{c}^2$ (see Table 1). In the case of an unstable particle, we conjecture that the creation time must be shorter than the particle’s lifetime, $T_p$, i.e., $t_c<T_p$, for its formation to occur. We have not found exceptions to this rule (see the second and third columns of Table 1).

A natural question is whether this rule also applies to the daughter particles produced in the decay of an unstable parent with lifetime $T_p$. The main decay channels for the parent examples are listed in the fourth column of Table 1, and they indicate that the creation-time rule holds for parent–daughter decays as well (see fifth column). In the following, we discuss various aspects of the cases presented in Table 1.

In the case of the neutron, charge conservation implies that its electric charge must equal the electron antineutrino millicharge (provided that $p^{+}+e^{-}=0$). This issue has been addressed in the literature, where recent reviews cover both experimental results [18] and theoretical arguments [19]. In general, the upper bounds for the neutron millicharge obtained in experiments are smaller than those discussed above for neutrinos. The observed discrepancies remain unresolved, and further investigation will be required to clarify their origin.

Regarding the unstable leptons, the $\tau$ presents the shortest lifetime, $T_{\tau }\simeq 3 · {10}^{-13}$ s. Among the decay products, there is always a $\tau$-neutrino present, due to flavor conservation, and in the case of Table 1 an electron antineutrino ${\overline{\nu }}_e$. This fact is very illuminating, since in order to make the decays possible, the neutrinos (according to our simple model) must be created sufficiently fast, imposing the condition that their effective mass should be larger than the lower-bound mass cutoff,

$$m_{\mathfrak{q}}{c}^2>{\displaystyle \frac{\hslash }{2T_{\tau }}}\simeq 0.007\mathrm{eV}.$$

This is the value we have referred to in our previous discussions.

Furthermore, the $\tau$ lifetime is the shortest one among all known decays, except for those of the intermediate bosons, the Higgs boson, and the heavy quarks [3]. In the case of the top quark, $t\to W^{+}+b$, for instance, we observe that the creation time for the b quark (4.2 GeV) is slightly shorter than the top quark lifetime $T_t$ (see Table 1), making the decay possible.

6. Concluding Remarks

We have discussed an extension of the Dirac equation for an initially massless particle carrying an electric charge $\mathfrak{q}$, assumed to be embedded in an external fluctuating EM potential of the vacuum, characterized by an ensemble of states ${\left\{A^{\nu }\right\}}_{\mathrm{vac}}$, where $A^{\nu }=(\varphi ,\overrightarrow{A})$ (in Gaussian units). The solution of the equation is obtained in the case that the four-potential components are independent of time and spatial coordinates, valid for each value of $A^{\nu }$ in the ensemble. We conjecture that in order to lead to observable quantities, the fields must obey the following conditions:

$${\langle A^{\nu }\rangle }_{\mathrm{vac}}=0,{\langle A^{\nu }{A}_{\nu }\rangle }_{\mathrm{vac}}\ne 0.$$

In addition, we show that $A^{\nu }$ may indeed become gauge-invariant in an average sense, such that ${\langle A^{\prime \nu }{A}_{\nu }^{\prime }\rangle }_{\mathrm{vac}}={\langle A^{\nu }{A}_{\nu }\rangle }_{\mathrm{vac}}$ is obeyed in the case of a massless field describing the gauge transformations. As a result, we show that a finite mass can be attributed to the electric charge, which is given by

$$m_{\mathfrak{q}}{c}^2=\left|\mathfrak{q}\right||{\langle {\varphi }^2\rangle }_{\mathrm{vac}}-\langle |\overrightarrow{A}{|}^2{{\rangle }_{\mathrm{vac}}|}^{1/2},$$

valid for both spacelike and timelike vector fields. The proposed mass mechanism, assumed to act within a finite time scale $t_c=\hslash /\left(2m_{\mathfrak{q}}c\right)$ consistent with the uncertainty principle, allows a Lorentz covariance violation required to extend the mass result to timelike vacuum potentials.

Using the above expression for the generated mass, we estimate both the electric charge, $\mathfrak{q}$, and magnetic moment, ${\mu }_{\mathfrak{q}}$, of a generic neutrino. The above mass–charge relation is written compactly as $\mathfrak{q}{\overline{A}}_{\mathfrak{q}}=m_{\mathfrak{q}}{c}^2$, which becomes the cornerstone of the present approach. In order to proceed further, these unknown quantities are expressed relative to the electron properties, used as reference. Hence, we assume that a similar relation, $e{\overline{A}}_e=m_e{c}^2$, can be applied to the electron. After introducing additional features, such as a scaling behavior of ${\overline{A}}_{\mathfrak{q}}$ with a length scale describing the spatial distribution of the elementary charge $\mathfrak{q}$, we derive our main results, namely

$${\displaystyle \frac{\mathfrak{q}}{e}}={\left({\displaystyle \frac{m_{\mathfrak{q}}}{m_e}}\right)}^3,{\displaystyle \frac{{\mu }_{\mathfrak{q}}}{{\mu }_{\mathrm{B}}}}={\left({\displaystyle \frac{m_{\mathfrak{q}}}{m_e}}\right)}^2\to {\displaystyle \frac{{\mu }_{\mathfrak{q}}}{{\mu }_{\mathrm{B}}}}={\left({\displaystyle \frac{\mathfrak{q}}{e}}\right)}^{2/3},$$

(77)

yielding the correct order of magnitude as compared with the experimental upper bounds. The resulting scaling relation (77), ${\mu }_{\mathfrak{q}}\sim {\mathfrak{q}}^{2/3}$, can be seen as a reference feature of neutrino EM properties and can be put to the test when upper bounds are determined. Significant deviations from this rule might indicate a failure of the present approach. However, if the above values for the electric millicharge and magnetic moment are confirmed by experiments, one may expect that neutrinos behave as charged Dirac particles. Furthermore, the issue of neutrino (antineutrino) left (right) handedness remains unresolved within this model. Further theoretical ideas need to be explored to obtain some insight into this unique feature of neutrinos [20].

We have also discussed examples of unstable particles by considering their main decay channels. We postulate that the time $t_c$, defined in relation to the applicability of the present mass scenario, admits a rather important interpretation in terms of the time required to ’dress’ a charge $\mathfrak{q}$ with a mass $m_{\mathfrak{q}}$. This ’creation’ time is argued to be shorter than the unstable particle lifetime, $T_p$. From this relation, confirmed in the cases considered, we derive a lower bound for the effective neutrino mass, where $T_{\tau }\simeq 2.9 · {10}^{-13}$ s is the $\tau$ lepton lifetime, namely $m_{\mathfrak{q}}{c}^2>\hslash /\left(2T_{\tau }\right)\simeq 7$ meV, a prediction which may be tested in future experiments.

Among the open questions not addressed here, which may be studied in future works, are the way our assumed stochastic vector potential connects to the QED vacuum and whether the obtained neutrino mass, charge, and magnetic moment satisfy Ward identities. In addition, the connections to the Schwinger–Dyson equation approach, stochastic quantization concepts, and background-field methods remain to be understood.