An Efficient Temporal Two-Mesh Compact ADI Method for Nonlinear Schrödinger Equations with Error Analysis

Abstract

In this article, we present an efficient numerical strategy for the two-dimensional nonlinear Schrödinger equation, focusing on its development and analysis. Our approach begins with proposing a nonlinear, energy-conservative, fourth-order, compact, alternating-direction, implicit (ADI) scheme. To boost efficiency when solving the associated nonlinear system, we then implement this scheme using a temporal two-mesh (TTM) algorithm. Under discretization with coarse time step ${\tau }_C$, fine time step ${\tau }_F$, and spatial mesh size h, the numerical scheme exhibits a convergence rate of order $\mathcal{O}({\tau }_C^4+{\tau }_F^2+h^4)$ in both the discrete $L_2$-norm and $H_1$-norm. To facilitate the convergence analysis under fine time discretization, we propose a novel technique along with several supporting lemmas that enable the estimation of the discrete $L_4$-norm error term over the temporal coarse mesh. Numerical experiments are then performed to validate the theoretical results and demonstrate the effectiveness of the proposed algorithm. The numerical results show that the new algorithm produces highly accurate results and preserves the conservation laws of mass and energy. Compared with the fully nonlinear compact ADI scheme, it reduces computational time while maintaining accuracy.

1. Introduction

The nonlinear Schrödinger (NLS) equation is a key mathematical model for problems arising in various fields of physics, including nonlinear optics, plasma physics, and quantum mechanics. In this article, we consider the following model of the two-dimensional (2D) NLS problem:

$$\left\{\begin{array}{l}-i{\displaystyle \frac{\partial u}{\partial t}}=\Delta u+\beta {|u|}^{2}u+\nu \left(\mathbf{x}\right)u,(\mathbf{x},t)\in \Omega \times (0,T],\\ u(\mathbf{x},0)=\phi \left(\mathbf{x}\right),\mathbf{x}\in \Omega \cup \partial \Omega ,\\ u(\mathbf{x},t)=\psi (\mathbf{x},t),(\mathbf{x},t)\in \partial \Omega \times [0,T],\end{array}\right.$$

(1)

where $\mathbf{x}=(x,y)$ and  $\Omega =(a_1,b_1)\times (a_2,b_2)$ denote a bounded domain in ${\mathbb{R}}^2$ with boundary $\partial \Omega$. Here, $\Delta$ represents the Laplacian operator acting on spatial variables. The unknown function $u(\mathbf{x},t)$ is a complex-valued wave function. $\phi \left(\mathbf{x}\right)$ and $\psi (\mathbf{x},t)$ are sufficiently smooth functions. The trapping potential $\nu \left(\mathbf{x}\right)$ is real-valued, non-negative, and bounded on $\Omega$. In Equation (1), the real constant parameter $\beta \ne 0$ characterizes the strength of local interactions between particles: positive values of $\beta$ correspond to focusing effects, while negative values lead to defocusing behavior. The model (1) conserves the total mass and energy such that

$$\mathbf{Q}\left(u(·,t)\right):={\int }_{\Omega }{|u(\mathbf{x},t)|}^2\mathrm{d}\mathbf{x}\equiv \mathbf{Q}\left(u(·,0)\right),t>0,$$

and

$$\mathbf{E}\left(u(·,t)\right):={\int }_{\Omega }\left({|\nabla u|}^2-{\nu \left(\mathbf{x}\right)|u|}^2-{\displaystyle \frac{\beta }{2}}{|u|}^4\right)\mathrm{d}\mathbf{x}\equiv \mathbf{E}\left(u(·,0)\right),t>0,$$

respectively.

For analytical studies including the derivation, well-posedness, and dynamical properties of the NLS equation, one can refer to [1,2,3,4] and the references therein. For numerical studies, different efficient and accurate numerical methods including the finite difference method [5,6,7,8,9,10], finite element method [11,12,13,14], spectral method [15,16], discontinuous Galerkin method [17], virtual element method [18], Runge–Kutta or Crank–Nicolson pseudo-spectral method [19,20], and meshless method [21] have been developed for the NLS equation. Naturally, each method possesses both advantages and disadvantages. For numerical comparisons between different numerical methods for solving the NLS equation, we refer readers to [22,23,24] and the references therein.

In recent years, significant efforts have been directed toward advancing high-order, compact, alternating-direction, implicit (HOC-ADI) methods to solve the multidimensional (i.e., $d=2,3$) NLS equation, aiming to achieve high spatial accuracy while tackling its inherent multidimensional complexity. Studies [25,26,27,28,29] focus on developing HOC-ADI methods for solving multidimensional NLS equations while utilizing linear Fourier analysis to prove their unconditional stability. Nevertheless, rigorous analyses of error estimates for HOC-ADI schemes solving multidimensional NLS equations have yielded limited results. Gao and Xie [30] proposed a fourth-order compact ADI scheme for a two-dimensional NLS equation and used an induction argument to prove convergence in the discrete $L_2$-norm under a CFL-type condition. Wang and Guo et al. [31] analyzed a fourth-order compact scheme for the two-dimensional NLS equation, establishing error estimates in the $L_2$-norm without restrictions on the mesh ratio via discrete interpolation inequalities and Sobolev embedding theorems. Later, by introducing a ‘lifting’ technique and cut-off function technique, Wang and Zhao [32] conducted further studies on the unconditional global $L_{\infty }$-convergence of two fourth-order compact schemes for multidimensional NLS equations. Chen et al. [33] developed a three-level compact ADI scheme to solve the two-dimensional coupled NLS system, proving unconditional convergence in the $L_{\infty }$-norm with temporal order two and spatial order four via mathematical induction. For further details on the HOC-ADI method applied to coupled NLS systems, refer to the references cited in [33]. Additionally, other types of high-order methods exist; see [34] and the references therein. However, the aforementioned HOC difference methods are fully implicit and require solving a nonlinear system at each time step using a nonlinear iterative method, which can be time-consuming. Therefore, to efficiently handle the nonlinearity, most schemes for solving the NLS equation use a linearized extrapolation technique [30] or a split-step (time-splitting) method [5,9,22,24,25,35].

Alternatively, the two-grid method, initially introduced by Xu [36], represents another efficient approach for handling nonlinear problems. The two-grid algorithm first addresses the complex problem on a coarser grid to obtain an initial approximation. This coarse solution then acts as the starting point for a single Newton iteration applied to a finer grid, where it solves a linearized or symmetric positive-definite system. Due to its simplicity and computational efficiency, this method has become increasingly popular for solving the NLS equation in recent years. In [37,38,39,40,41], several two-grid (mixed) finite element (FE) schemes were proposed for solving the NLS equation, and their optimal-order error estimates were analyzed. Two-grid schemes based on finite volume (Zhang et al. [42]) and finite element methods (Chen et al. [43]) were proposed, with thorough convergence analyses supporting their accuracy. The work of Wang et al. [44] established global $H_1$-norm superconvergence for two-grid finite element approximations of the NLS equation. However, implementing two-grid FE methods often demands sophisticated mesh generation techniques, thereby increasing computational complexity and practical implementation challenges.

Instead, the two-grid FD method simplifies temporal and spatial discretization, making scheme construction more straightforward and calculations more convenient. This renders it more suitable for rapid solving and real-time applications. A spatial two-grid finite difference (FD) scheme for NLS equations is constructed by Ignat et al. in [45], where the equations on the fine grid are linearized but not decoupled. Following the idea of [46], we developed a new temporal two-mesh (TTM) fourth-order compact difference scheme for one-dimensional NLS equations in [47]. The novelty lies in using the fine mesh solution, once obtained, as the initial guess for the linear system. This strategy effectively improves the accuracy of the final numerical solutions. Wang et al. [48] introduced an innovative TTM fitted scheme for the one-dimensional time-fractional NLS equation with nonsmooth solutions and proved its convergence in an $L_2$-norm of order $\mathcal{O}({\tau }_F^2+{\tau }_C^4+h^2)$. Here, ${\tau }_C$ is the coarse time step, ${\tau }_F$ is the fine time step, and h is the spatial mesh size. Typically, convergence analyses of TTM schemes in much of the literature rely heavily on the mathematical induction and the error bound for ${\parallel u^n-U_C^n\parallel }_4^4$, with the latter derived from an optimal error estimate on the coarse time mesh in the discrete $L^{\infty }$-norm. Here,  $u^n$ denotes the exact solution at $t=t_n$, while $U_C^n$ represents its approximation on the temporal coarse mesh. However, in two or three dimensions, obtaining an $L^{\infty }$-norm error bound remains challenging. To the best of our knowledge, few studies on TTM compact ADI methods have been published for the multidimensional NLS equations thus far.

Overall, the main goal of this article is to construct new efficient fourth-order compact ADI algorithms for solving the two-dimensional NLS Equation (1) and provide an alternative approach for proving error estimates in both the global discrete $L_2$-norm and $H_1$-norm. The proposed algorithm consists of three steps: (1) A nonlinear compact ADI scheme is first established on the time coarse mesh. Since the computational scale of this nonlinear model is relatively small, it is solved via an iterative method. (2) Using solutions from Step 1, Lagrangian linear interpolation generates rough approximations on the fine temporal mesh. (3) One Newton iteration refines the nonlinear term on the fine temporal mesh, yielding a linear ADI system whose solution provides the final numerical results. Therefore, unlike Refs. [37,38,39,40,41,42,43,44], where spatial two-grid algorithms are coupled with finite (volume) element methods, our article develops a temporal two-mesh algorithm based on the compact ADI method. Furthermore, compared to prior temporal two-mesh approaches [46,47,48], we specifically study the fourth-order compact ADI variant for the two-dimensional NLS equation and prove its error estimates on the fine mesh by introducing novel techniques and key lemmas. Notably, our proof strategy differs significantly from those proposed in [46,47,48]. The main contributions or contents of this article are as follows:

• In order to handle the nonlinearity, we adopt the temporal two-mesh technique, which is similar to the two-grid method but focuses specifically on splitting the time domain into coarse and fine grids. Meanwhile, the ADI technique is applied, respectively, to the nonlinear and linear schemes, decomposing multidimensional problems into sequences of independent one-dimensional subproblems.
• To deal with the discrete $L_4$-norm error term ${\parallel u^n-U_C^n\parallel }_4^4$, we introduce a discrete version of the Sobolev inequality [31,49,50] and apply the standard energy method to provide a detailed estimate for this term. Here, $u^n$ denotes the exact solution at $t=t_n$, while $U_C^n$ represents its approximation on the coarse temporal mesh. Notably, our proof avoids the need for a separate, complex derivation of an optimal error estimate in the discrete maximum norm on the coarse temporal mesh.
• We prove convergence results with an order of $\mathcal{O}({\tau }_C^4+{\tau }_F^2+h^4)$ in both the discrete $L_2$-norm and $H_1$-norm. Here, ${\tau }_C$ and ${\tau }_F$ denote the coarse and fine time steps, respectively, and h is the spatial step size. Additionally, the discrete conservation laws of the proposed scheme are analyzed on the coarse temporal mesh.
• We perform several numerical tests on the focusing and defocusing models to simulate long-term dynamics and blow-up solutions, thereby demonstrating the computational efficiency of our proposed algorithm.These tests confirm that the algorithm produces highly accurate results, conserves discrete mass and energy, and reduces CPU usage.

The rest of this article is organized as follows: In Section 2, some notations are introduced and a temporal two-mesh compact ADI scheme is proposed. In Section 3, some basic lemmas are introduced or proven. In Section 4, discrete conservation laws of the proposed scheme are discussed and an a priori estimate is obtained, then the convergence is proven based on this estimation. Numerical results are reported in Section 5, and some brief conclusions are given in Section 6. Throughout this paper, the symbol C is used to denote a generic positive constant.

2. Notations and the TTM Compact ADI Scheme

For a positive integer $\mathcal{N}$, let ${\tau }_F={\displaystyle \frac{T}{\mathcal{N}}}$ and $t_n=n{\tau }_F(n=0,1,\cdots ,\mathcal{N})$. The time domain $[0,T]$ is covered by the fine mesh ${\Omega }_{\tau }^F=\{t_n|0\le n\le \mathcal{N}\}$. Similarly, for positive integers s and N, let ${\tau }_C={\displaystyle \frac{T}{N}}$ and $t_{ps}=p{\tau }_C(0\le p\le N).$ The coarse mesh is  ${\Omega }_{\tau }^C=\{t_{ps}|0\le p\le N\}$, where $\mathcal{N}=sN(2\le s\le {\displaystyle \frac{1}{{\tau }_C}})$ and $t_{ps}=(p·s){\tau }_F.$ Given a time mesh function $w=\{w^n|0\le n\le \mathcal{N}\}$ on ${\Omega }_{\tau }^F$, we denote

$${\partial }_t{w}^n={\displaystyle \frac{w^{n+1}-w^n}{{\tau }_F}},w^{n+1/2}={\displaystyle \frac{1}{2}}\left(w^{n+1}+w^n\right).$$

Similar notations can also be defined on the coarse mesh ${\Omega }_{\tau }^C$.

For spatial approximation, let $h_x={\displaystyle \frac{b_1-a_1}{J_x}}$ and $h_y={\displaystyle \frac{b_2-a_2}{J_y}}$ be spatial step sizes, where $J_x$ and $J_y$ are given positive integers. Denote ${\Omega }_h={\overline{\Omega }}_h\cap \Omega ,\partial {\Omega }_h={\overline{\Omega }}_h\cap \partial \Omega$, and $h=max\{h_x,h_y\}$, where ${\overline{\Omega }}_h=\{(x_j,y_k)|x_j=a_1+j{h}_x,0\le j\le J_x;y_k=a_2+k{h}_y,0\le k\le J_y\}$. Given a grid function $v=\{v_{jk}|(x_j,y_k)\in {\Omega }_h\}$ denote

$$\begin{array}{c}{\partial }_x{v}_{jk}={\displaystyle \frac{v_{j+1,k}-v_{jk}}{h_x}},{\delta }_x^2{v}_{jk}={\displaystyle \frac{v_{j+1,k}-2v_{jk}+v_{j-1,k}}{h_x^2}},\hfill \\ {\mathcal{A}}_x{v}_{jk}=\left(1+{\displaystyle \frac{h_x^2}{12}}{\delta }_x^2\right)v_{jk}={\displaystyle \frac{1}{12}}\left(v_{j-1,k}+10v_{jk}+v_{j+1,k}\right).\hfill \end{array}$$

The notations ${\partial }_y{v}_{jk},{\delta }_y^2{v}_{jk}$, and ${\mathcal{A}}_y{v}_{jk}$ are defined similarly. In addition, for the discretization of the second-order derivatives ${\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}$ and ${\displaystyle \frac{{\partial }^{2}u}{\partial y^2}}$, we introduce the following lemma.

Lemma 1

(Ref. [49,51]). Let the function $g\left(x\right)\in C^6[0,1]$ and $\zeta \left(\lambda \right)=5{(1-\lambda )}^3-3{(1-\lambda )}^5$. Then it holds that for $1\le j\le J_x-1$,

$${\mathcal{A}}_x{g}^{″}\left(x_j\right)={\delta }_x^{2}g\left(x_j\right)+{\displaystyle \frac{h_x^4}{36}}{\int }_0^1\left[g^{\left(6\right)}(x_j-\lambda h_x)+g^{\left(6\right)}(x_j+\lambda h_x)\right]\zeta \left(\lambda \right)\mathrm{d}\lambda .$$

Let $H_0\left({\Omega }_h\right)$ be the space of grid functions v defined on ${\overline{\Omega }}_h$ with boundary conditions $v=0$ on $\partial {\Omega }_h$. Define the discrete inner products and norms via

$$\begin{array}{c}(v,w)=\sum _{j=1}^{J_x-1}\sum _{k=1}^{J_y-1}{v}_{jk}{\overline{w}}_{jk}{h}_x{h}_y,{(v,w)}_l=\sum _{j=0}^{J_x-1}\sum _{k=0}^{J_y-1}{v}_{jk}{\overline{w}}_{jk}{h}_x{h}_y,\hfill \\ {(v,w)}_{l_x}=\sum _{j=0}^{J_x-1}\sum _{k=1}^{J_y-1}{v}_{jk}{\overline{w}}_{jk}{h}_x{h}_y,{(v,w)}_{l_y}=\sum _{j=1}^{J_x-1}\sum _{k=0}^{J_y-1}{v}_{ij}{\overline{w}}_{jk}{h}_x{h}_y,\hfill \end{array}$$

$$\begin{array}{c}\parallel v\parallel =\sqrt{(v,w)},{\parallel v\parallel }_{xy}=\sqrt{{(v,v)}_l},{\parallel v\parallel }_x=\sqrt{{(v,v)}_{l_x}},{\parallel v\parallel }_y=\sqrt{{(v,v)}_{l_y}},\hfill \\ {\parallel v\parallel }_{\infty }=\underset{j,k}{max}\left|v_{jk}\right|,{\parallel {\nabla }_{h}v\parallel }^2={\parallel {\partial }_{x}v\parallel }_x^2+{\parallel {\partial }_{y}v\parallel }_y^2,{\parallel v\parallel }_1^2={\parallel v\parallel }^2+{\parallel {\nabla }_{h}v\parallel }^2,\hfill \end{array}$$

where ${\overline{w}}_{jk}$ denotes the complex conjugate of $w_{jk}$. We also define the discrete $L^p(2<p<\infty )$ norm as

$${\parallel v\parallel }_p={\left(\sum _{j=1}^{J_x-1}\sum _{k=1}^{J_y-1}{|v_{jk}|}^p{h}_x{h}_y\right)}^{1/p}.$$

Considering Equation (1) at the point $(x_j,y_k,t_{n+1/2})$ with $t_{n+1/2}={\displaystyle \frac{1}{2}}(t_{n+1}+t_n)$, we have

$$-i{\partial }_t{u}_{jk}^n={\left({\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}\right)}_{jk}^{n+1/2}+{\left({\displaystyle \frac{{\partial }^{2}u}{\partial y^2}}\right)}_{jk}^{n+1/2}+\beta {\left({|u|}^2\right)}_{jk}^{n+1/2}{u}_{jk}^{n+1/2}+{\nu }_{jk}{u}_{jk}^{n+1/2}+r_{1jk}^n,$$

(2)

where

$$\begin{array}{cc}\hfill r_{1jk}^n& =i{\displaystyle \frac{\partial u}{\partial t}}(x_j,y_k,t_{n+1/2})-i{\partial }_t{u}_{jk}^n+\nu (x_j,y_k)u(x_j,y_k,t_{n+1/2})-{\nu }_{jk}{u}_{jk}^{n+1/2}\hfill \\ & +{\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}(x_j,y_k,t_{n+1/2})-{\left({\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}\right)}_{jk}^{n+1/2}+{\displaystyle \frac{{\partial }^{2}u}{\partial y^2}}(x_j,y_k,t_{n+1/2})-{\left({\displaystyle \frac{{\partial }^{2}u}{\partial y^2}}\right)}_{jk}^{n+1/2}\hfill \\ & +\beta \left[{\left|u(x_j,y_k,t_{n+1/2})\right|}^{2}u(x_j,y_k,t_{n+1/2})-{\left({|u|}^2\right)}_{jk}^{n+1/2}{u}_{jk}^{n+1/2}\right],\hfill \end{array}$$

and $u_{jk}^n=u(x_j,y_k,t_n),{\nu }_{jk}=\nu (x_j,y_k),$ and $u_{jk}^{n+1/2}={\displaystyle \frac{1}{2}}\left(u_{jk}^{n+1}+u_{jk}^n\right)$.

Using the operator ${\mathcal{A}}_x{\mathcal{A}}_y$ on both sides of Equation (2) and applying Lemma 1, we obtain

$$\begin{array}{cc}\hfill -i{\mathcal{A}}_x{\mathcal{A}}_y{\partial }_t{u}_{jk}^n& ={\mathcal{A}}_y{\delta }_x^2{u}_{jk}^{n+1/2}+{\mathcal{A}}_x{\delta }_y^2{u}_{jk}^{n+1/2}\hfill \\ \hfill & +{\mathcal{A}}_x{\mathcal{A}}_y\left[\beta {\left({|u|}^2\right)}_{jk}^{n+1/2}{u}_{jk}^{n+1/2}+{\nu }_{jk}{u}_{jk}^{n+1/2}\right]+r_{2jk}^n,\hfill \end{array}$$

(3)

where $r_{2jk}^n={\mathcal{A}}_x{\mathcal{A}}_y{r}_{1jk}^n+{\displaystyle \frac{h_x^4}{36}} {\int }_0^1{\mathcal{A}}_y\left[{\displaystyle \frac{{\partial }^{6}u}{\partial x^6}}(x_j-\lambda h_x,y_k,t_{n+1/2})+{\displaystyle \frac{{\partial }^{6}u}{\partial x^6}}(x_j+\lambda h_x,y_k,t_{n+1/2})\right]$$\zeta \left(\lambda \right)\mathrm{d}\lambda +$ ${\displaystyle \frac{h_y^4}{36}}{\int }_0^1{\mathcal{A}}_x\left[{\displaystyle \frac{{\partial }^{6}u}{\partial y^6}}(x_j,y_k-\lambda h_y,t_{n+1/2})+{\displaystyle \frac{{\partial }^{6}u}{\partial y^6}}(x_j,y_k+\lambda h_y,t_{n+1/2})\right]\zeta \left(\lambda \right)\mathrm{d}\lambda$.

Using Taylor expansion and based on the assumption $u(\mathbf{x},t)\in C^{6,4}\left(\Omega ,(0,T]\right)$, there exits a positive constant C such that

$$|r_{1jk}^n|\le C{\tau }^2,|r_{2jk}^n|\le C({\tau }^2+h_x^4+h_y^4),(x_j,y_k)\in {\Omega }_h,$$

(4)

where $\tau$ can be either ${\tau }_C$ or ${\tau }_F$.

In order to construct the ADI scheme, we first rewrite Equation (3) as follows:

$$\begin{array}{cc}\hfill -i({\mathcal{A}}_x{\mathcal{A}}_y-{\displaystyle \frac{i\tau }{2}}{\mathcal{A}}_y{\delta }_x^2& -{\displaystyle \frac{i\tau }{2}}{\mathcal{A}}_x{\delta }_y^2){\partial }_t{u}_{jk}^n={\mathcal{A}}_y{\delta }_x^2{u}_{jk}^n+{\mathcal{A}}_x{\delta }_y^2{u}_{jk}^n\hfill \\ \hfill & +{\mathcal{A}}_x{\mathcal{A}}_y\left[\beta {\left({|u|}^2\right)}_{jk}^{n+1/2}{u}_{jk}^{n+1/2}+{\nu }_{jk}{u}_{jk}^{n+1/2}\right]+r_{2jk}^n.\hfill \end{array}$$

(5)

Then, adding a small term ${\displaystyle \frac{i{\tau }^2}{4}}{\delta }_x^2{\delta }_y^2{\partial }_t{u}_{jk}^n$ on both sides of Equation (5), we have

$$\begin{array}{cc}\hfill -i\left({\mathcal{A}}_x-{\displaystyle \frac{i\tau }{2}}{\delta }_x^2\right)& \left({\mathcal{A}}_y-{\displaystyle \frac{i\tau }{2}}{\delta }_y^2\right){\partial }_t{u}_{jk}^n={\mathcal{A}}_y{\delta }_x^2{u}_{jk}^n+{\mathcal{A}}_x{\delta }_y^2{u}_{jk}^n\hfill \\ & +{\mathcal{A}}_x{\mathcal{A}}_y\left[\beta {\left({|u|}^2\right)}_{jk}^{n+1/2}{u}_{jk}^{n+1/2}+{\nu }_{jk}{u}_{jk}^{n+1/2}\right]+r_{jk}^n,\hfill \end{array}$$

(6)

where the truncation error $r_{jk}^n=r_{2jk}^n+{\displaystyle \frac{i{\tau }^2}{4}}{\delta }_x^2{\delta }_y^2{\partial }_t{u}_{jk}^n$. Together with the fact that $|{\displaystyle \frac{{\tau }^2}{4}}{\delta }_x^2{\delta }_y^2{\partial }_t{u}_{jk}^n|$$\le C{\tau }^2$, we obtain

$$|r_{jk}^n|\le C({\tau }^2+h_x^4+h_y^4),(x_j,y_k)\in {\Omega }_h.$$

(7)

Based on Equation (6), a temporal two-mesh compact difference scheme is constructed as follows.

Step 1: For $p=0,1,\cdots ,N-1$, solve the following nonlinear system to find $U_{C,jk}^{ps}=V_{C,jk}^{ps}+i{W}_{C,jk}^{ps}$ on the temporal coarse mesh, such that

$$\left\{\begin{array}{c}-i\left({\mathcal{A}}_x-{\displaystyle \frac{i{\tau }_C}{2}}{\delta }_x^2\right)\left({\mathcal{A}}_y-{\displaystyle \frac{i{\tau }_C}{2}}{\delta }_y^2\right){\partial }_t{U}_{C,jk}^{ps}={\mathcal{A}}_y{\delta }_x^2{U}_{C,jk}^{ps}+{\mathcal{A}}_x{\delta }_y^2{U}_{C,jk}^{ps}+{\mathcal{A}}_x{\mathcal{A}}_y{F}_C^{(p+1/2)s},\hfill \\ U_{C,jk}^{ps}={\psi }_{jk}^{ps},0\le p\le N,(x_j,y_k)\in \partial {\Omega }_h,\hfill \\ U_{C,jk}^0=\phi (x_j,y_k),(x_j,y_k)\in {\overline{\Omega }}_h,\hfill \end{array}\right.$$

(8)

where $V_{C,jk}^{ps}$ and $W_{C,jk}^{ps}$ denote the real part and imaginary part of the complex number $U_{C,jk}^{ps}$, and $F_C^{(p+1/2)s}=\beta {\left({\left|U_C\right|}^2\right)}_{jk}^{(p+1/2)s}{U}_{C,jk}^{(p+1/2)s}+{\nu }_{jk}{U}_{C,jk}^{(p+1/2)s}.$

Step 2: Based on the solutions $U_{C,jk}^{ps}$ obtained in Step 1, we use Lagrange’s linear interpolation formula to compute $U_{C,jk}^n(n=1,2,\cdots ,\mathcal{N})$. That is, at time levels $t_{ps-l}(l=0,1,\cdots ,s;p=1,2,\cdots ,N;ps-l=n)$, we have

$$\begin{array}{cc}\hfill U_{C,jk}^n=U_{C,jk}^{ps-l}& ={\displaystyle \frac{t_{ps-l}-t_{ps}}{t_{(p-1)s}-t_{ps}}}{U}_{C,jk}^{(p-1)s}+{\displaystyle \frac{t_{ps-l}-t_{(p-1)s}}{t_{ps}-t_{(p-1)s}}}{U}_{C,jk}^{ps}\hfill \\ & ={\displaystyle \frac{l}{s}}{U}_{C,jk}^{(p-1)s}+(1-{\displaystyle \frac{l}{s}})U_{C,jk}^{ps}.\hfill \end{array}$$

(9)

Step 3: According to the solution $U_{C,jk}^{n+1}$ obtained in Step 2, we construct the following linearized system on the fine temporal mesh to solve  $U_{F,jk}^n=V_{F,jk}^n+i{W}_{F,jk}^n$, such that

$$\left\{\begin{array}{c}-i\left({\mathcal{A}}_x-{\displaystyle \frac{i{\tau }_F}{2}}{\delta }_x^2\right)\left({\mathcal{A}}_y-{\displaystyle \frac{i{\tau }_F}{2}}{\delta }_y^2\right){\partial }_t{U}_{F,jk}^n={\mathcal{A}}_y{\delta }_x^2{U}_{F,jk}^n+{\mathcal{A}}_x{\delta }_y^2{U}_{F,jk}^n+{\mathcal{A}}_x{\mathcal{A}}_y{F}^{n+1/2},\hfill \\ U_{F,jk}^n={\psi }_{jk}^n,0\le n\le \mathcal{N},(x_j,y_k)\in \partial {\Omega }_h,\hfill \\ U_{F,jk}^0=\phi (x_j,y_k),(x_j,y_k)\in {\overline{\Omega }}_h,\hfill \end{array}\right.$$

(10)

where $V_{F,jk}^{ps}$ and $W_{F,jk}^{ps}$ denote the real part and imaginary part of the complex number $U_{F,jk}^{ps}$,  $F^{n+1/2}={\tilde{F}}^{n+1/2}+i{\widehat{F}}^{n+1/2}$, and

$$\begin{array}{c}{\tilde{F}}^{n+1/2}=g_R^C+g_{R,v}^C·\left(E\left(V_{F,jk}^n\right)-V_{C,jk}^{n+1/2}\right)+g_{R,w}^C·\left(E\left(W_{F,jk}^n\right)-W_{C,jk}^{n+1/2}\right),\hfill \\ {\widehat{F}}^{n+1/2}=g_I^C+g_{I,v}^C·\left(E\left(V_{F,jk}^n\right)-V_{C,jk}^{n+1/2}\right)+g_{I,w}^C·\left(E\left(W_{F,jk}^n\right)-W_{C,jk}^{n+1/2}\right).\hfill \end{array}$$

(11)

Here, the extrapolation operator $E\left(v^n\right)$ is defined by

$$E\left(v^n\right)=\left\{\begin{array}{c}{v}^0+{\displaystyle \frac{i{\tau }_F}{2}}\left[\Delta v^0+\beta \left(|v^0{|}^2\right)v^0+\nu v^0\right],n=0,\hfill \\ {\displaystyle \frac{3v^n-v^{n-1}}{2}},n=1,2,\cdots ,\mathcal{N}-1.\hfill \end{array}\right.$$

(12)

If we consider two functions $g_R(v,w)=\beta (v^2+w^2)v+\nu v$ and $g_I(v,w)=\beta (v^2+w^2)w+\nu w$, the symbols are defined by

$$\begin{array}{c}{g}_R^C=g_R(V_{C,jk}^{n+1/2},W_{C,jk}^{n+1/2}),g_I^C=g_I(V_{C,jk}^{n+1/2},W_{C,jk}^{n+1/2}),\hfill \\ g_{R,v}^C=g_{R,v}(V_{C,jk}^{n+1/2},W_{C,jk}^{n+1/2})={\displaystyle \frac{\partial g_R}{\partial v}}(V_{C,jk}^{n+1/2},W_{C,jk}^{n+1/2}),\hfill \\ g_{R,w}^C=g_{R,w}(V_{C,jk}^{n+1/2},W_{C,jk}^{n+1/2})={\displaystyle \frac{\partial g_R}{\partial w}}(V_{C,jk}^{n+1/2},W_{C,jk}^{n+1/2}).\hfill \end{array}$$

(13)

The definitions of symbols $g_{I,v}^C$ and $g_{I,w}^C$ are similar to those of  $g_{R,v}^C$ and $g_{R,w}^C$.

Finally, introducing the intermediate variables $U_C^{\ast ps}$ and $U_F^{\ast n}$, respectively, the temporal two-mesh compact ADI scheme is constructed as follows.

Step 1: For $p=0,1,\cdots ,N-1$, $U_C^{ps}$ is determined by solving the following two sets of one-dimensional problems:

$$\left\{\begin{array}{c}-i\left({\mathcal{A}}_x-{\displaystyle \frac{i{\tau }_C}{2}}{\delta }_x^2\right)U_C^{\ast ps}={\mathcal{A}}_y{\delta }_x^2{U}_{C,jk}^{ps}+{\mathcal{A}}_x{\delta }_y^2{U}_{C,jk}^{ps}+{\mathcal{A}}_x{\mathcal{A}}_y{F}_C^{(p+1/2)s},\hfill \\ \left({\mathcal{A}}_y-{\displaystyle \frac{i{\tau }_C}{2}}{\delta }_y^2\right){\partial }_t{U}_{C,jk}^{ps}=U_C^{\ast ps},\hfill \end{array}\right.$$

(14)

where the initial and boundary conditions are

$$\left\{\begin{array}{c}{U}_C^{\ast ps}=\left({\mathcal{A}}_y-{\displaystyle \frac{i{\tau }_C}{2}}{\delta }_y^2\right){\partial }_t{\psi }_{jk}^{ps},j=0,J_x,k=1,\cdots ,J_y-1,\hfill \\ U_{C,jk}^{ps}={\psi }_{jk}^{ps},0\le p\le N,(x_j,y_k)\in \partial {\Omega }_h,\hfill \\ U_{C,jk}^0=\phi (x_j,y_k),(x_j,y_k)\in {\overline{\Omega }}_h.\hfill \end{array}\right.$$

Step 2: Step 2 is the same as Equation (9).

Step 3: For $n=0,1,\cdots ,\mathcal{N}-1$, $U_F^n$ is determined by solving the following two sets of independent one-dimensional problems:

$$\left\{\begin{array}{c}-i\left({\mathcal{A}}_x-{\displaystyle \frac{i{\tau }_F}{2}}{\delta }_x^2\right)U_F^{\ast n}={\mathcal{A}}_y{\delta }_x^2{U}_{F,jk}^n+{\mathcal{L}}_x{\delta }_y^2{U}_{F,jk}^n+{\mathcal{A}}_x{\mathcal{A}}_y{F}^{n+1/2},\hfill \\ \left({\mathcal{A}}_y-{\displaystyle \frac{i{\tau }_F}{2}}{\delta }_y^2\right){\partial }_t{U}_{F,jk}^n=U_F^{\ast n},\hfill \end{array}\right.$$

(15)

where the initial and boundary conditions are

$$\left\{\begin{array}{c}{U}_F^{\ast n}=\left({\mathcal{A}}_y-{\displaystyle \frac{i{\tau }_F}{2}}{\delta }_y^2\right){\partial }_t{\psi }_{jk}^n,j=0,J_x,k=1,\cdots ,J_y-1,\hfill \\ U_{F,jk}^n={\psi }_{jk}^n,0\le n\le \mathcal{N},(x_j,y_k)\in \partial {\Omega }_h,\hfill \\ U_{F,jk}^0=\phi (x_j,y_k),(x_j,y_k)\in {\overline{\Omega }}_h.\hfill \end{array}\right.$$

3. Some Basic Lemmas

We give some auxiliary lemmas which will be used later.

Lemma 2

(Ref. [30]). For any grid functions $v,w\in H_0\left({\Omega }_h\right)$, there are

$$\begin{array}{c}({\delta }_x^{2}v,w)=-{({\partial }_{x}v,{\partial }_{x}w)}_{l_x},({\delta }_y^{2}v,w)=-{({\partial }_{y}v,{\partial }_{y}w)}_{l_y},\hfill \\ ({\delta }_x^2{\delta }_y^{2}v,w)={({\partial }_x{\partial }_{y}v,{\partial }_x{\partial }_{y}w)}_l.\hfill \end{array}$$

Lemma 3

(Ref. [30]). For any grid function $v\in H_0\left({\Omega }_h\right)$, it holds that

$$\begin{array}{c}\parallel {\partial }_x{v\parallel }_x^2\le {\displaystyle \frac{4}{h_x^2}}{\parallel v\parallel }^2,\parallel {\partial }_y{v\parallel }_y^2\le {\displaystyle \frac{4}{h_y^2}}{\parallel v\parallel }^2,\hfill \\ \parallel {\partial }_x{\partial }_y{v\parallel }_{xy}^2\le {\displaystyle \frac{16}{h_x^2{h}_y^2}}{\parallel v\parallel }^2,{\parallel v\parallel }_{\infty }^2\le {\displaystyle \frac{1}{h_x{h}_y}}{\parallel v\parallel }^2.\hfill \end{array}$$

Lemma 4

(Ref. [31,49,50]). For any grid function u defined on and ${\overline{\Omega }}_h$, it holds that

$$\begin{array}{c}\hfill {\parallel u\parallel }_p\le {\parallel u\parallel }^{{\displaystyle \frac{2}{p}}}{\left(C_p{|u|}_1+{\displaystyle \frac{1}{\ell }}\parallel u\parallel \right)}^{1-{\displaystyle \frac{2}{p}}},2\le p<\infty ,\end{array}$$

where $C_p=max\{2\sqrt{2},{\displaystyle \frac{p}{\sqrt{2}}}\},\ell =min\{b_1-a_1,b_2-a_2\}$.

To prove the convergence of the proposed scheme, we provide some key matrices and their associated properties (such as eigenvalues) below. By convention, the symbol $\tau$ in the equations below represents either ${\tau }_C$ (coarse time step) or ${\tau }_F$ (fine time step).

Let ${\mathit{A}}_x$ and ${\mathit{B}}_x$ be two $(J_x-1)\times (J_x-1)$ symmetric matrices defined by

$${\mathit{A}}_x={\displaystyle \frac{1}{12}}\left[\begin{array}{ccccc}10& 1& 0& \cdots & 0\\ 1& 10& 1& \ddots & ⋮\\ 0& \ddots & \ddots & \ddots & 0\\ ⋮& \ddots & 1& 10& 1\\ 0& \cdots & 0& 1& 10\end{array}\right],{\mathit{B}}_x=\left[\begin{array}{ccccc}-2& 1& 0& \cdots & 0\\ 1& -2& 1& \ddots & ⋮\\ 0& \ddots & \ddots & \ddots & 0\\ ⋮& \ddots & 1& -2& 1\\ 0& \cdots & 0& 1& -2\end{array}\right].$$

Matrices  ${\mathit{A}}_y$ and ${\mathit{B}}_y$ denote  $(J_y-1)\times (J_y-1)$ symmetric matrices with the same entries as  ${\mathit{A}}_x$ and ${\mathit{B}}_x$, respectively. The eigenvalues of  ${\mathit{A}}_x$ (or ${\mathit{A}}_y$ ) are given in the form

$${\lambda }_j={\displaystyle \frac{5}{6}}+{\displaystyle \frac{1}{6}}cos{\displaystyle \frac{k\pi }{J}},k=1,2,\cdots ,J-1,J=J_x-1(\mathrm{or}{J}_y-1),$$

(16)

which implies that ${\displaystyle \frac{2}{3}}\le {\lambda }_j\le 1$. This indicates that the matrices ${\mathit{A}}_x$ and ${\mathit{A}}_y$ are positive-definite and invertible. The eigenvalues of  ${\mathit{B}}_x$ (or ${\mathit{B}}_y$) are given in the form

$${\mu }_j=-2+2cos{\displaystyle \frac{k\pi }{J}},k=1,2,\cdots ,J-1,J=J_x-1(\mathrm{or}{J}_y-1),$$

(17)

and then $-4\le {\mu }_j<0$.

Furthermore, we denote

$$\begin{array}{c}{\mathit{M}}_x={\mathit{A}}_x^{-1},{\mathit{M}}_y={\mathit{A}}_y^{-1},\hfill \\ \mathit{M}={\mathit{M}}_y\otimes {\mathit{M}}_x,{\mathit{H}}_x={\mathit{I}}_y\otimes {\mathit{M}}_x,{\mathit{H}}_y={\mathit{M}}_y\otimes {\mathit{I}}_x,\hfill \end{array}$$

(18)

where ${\mathit{I}}_x$ and ${\mathit{I}}_y$ are $(J_x-1)\times (J_x-1)$-order and  $(J_y-1)\times (J_y-1)$-order unitary matrices, respectively. From our knowledge of matrices, we know that ${\mathit{M}}_x,{\mathit{M}}_y,\mathit{M},{\mathit{H}}_x$, and ${\mathit{H}}_y$ are also real, positive-definite, and symmetric, respectively. And two discrete norms are introduced as follows:

$${||v||}_H={\left[({\mathit{H}}_{x}v,v)+({\mathit{H}}_{y}v,v)\right]}^{{\displaystyle \frac{1}{2}}},{\parallel v\parallel }_M={(\mathit{M}v,v)}^{{\displaystyle \frac{1}{2}}},$$

(19)

where the any grid function is $v={(v_{1,1},v_{2,1},\cdots ,v_{J-1,1},\cdots ,v_{1,J-1},v_{2,J-1},\cdots ,v_{J-1,J-1})}^T$.

Lemma 5

(Ref. [31]). For any grid function v defined on ${\overline{\Omega }}_h$, there are

$$\sqrt{2}\parallel v\parallel \le {||v||}_H\le \sqrt{3}\parallel v\parallel ,\parallel v\parallel \le {\parallel v\parallel }_M\le {\displaystyle \frac{3}{2}}\parallel v\parallel .$$

Lemma 6

(Ref. [31]). For any grid function $U^n\in H_0\left({\Omega }_h\right),n=0,1,\cdots ,\mathcal{N}-1$, there are

$$\begin{array}{c}\mathrm{Im}\left({\mathbf{H}}_x{\delta }_x^2{U}^{n+1/2}+{\mathbf{H}}_y{\delta }_y^2{U}^{n+1/2},U^{n+1/2}\right)=0,\hfill \\ \mathrm{Re}\left({\mathbf{H}}_x{\delta }_x^2{U}^{n+1/2}+{\mathbf{H}}_y{\delta }_y^2{U}^{n+1/2},{\partial }_t{U}^n\right)=-{\displaystyle \frac{1}{2\tau }}\left({||{\nabla }_h{U}^{n+1}||}_H^2-{||{\nabla }_h{U}^n||}_H^2\right),\hfill \end{array}$$

where $“\mathrm{Im}\left(s\right)”$ and $“\mathrm{Re}\left(s\right)”$ mean taking the imaginary part and the real part of a complex number s, respectively.

Lemma 7.

For any grid function u defined on ${\overline{\Omega }}_h$, there are

$${\mathbf{M}}_x{\delta }_x^{2}u={\delta }_x^2\left({\mathbf{M}}_{x}u\right),{\mathbf{M}}_y{\delta }_y^{2}u={\delta }_y^2\left({\mathbf{M}}_{y}u\right),u={(u_1,u_2,\cdots ,u_{J_x-1})}^T.$$

(20)

Proof. 

For the  k-th entry of the vector ${\mathit{M}}_{x}u$, there is

$${\left({\mathit{M}}_{x}u\right)}_k=\sum _{s=1}^{J_x-1}{m}_{ks}{u}_s;$$

then

$${\delta }_x^2{\left({\mathit{M}}_{x}u\right)}_k=\sum _{s=1}^{J_x-1}{m}_{ks}{\delta }_x^2{u}_s.$$

(21)

On the other hand,

$${\left({\mathit{M}}_x{\delta }_x^{2}u\right)}_k=\sum _{s=1}^{J_x-1}{m}_{ks}{\left({\delta }_x^{2}u\right)}_s=\sum _{s=1}^{J_x-1}{m}_{ks}{\delta }_x^2{u}_s,$$

(22)

which implies that ${\mathit{M}}_x{\delta }_x^{2}u={\delta }_x^2\left({\mathit{M}}_{x}u\right)$. Furthermore, based on (20), we will have ${\mathit{M}}_x{\mathit{B}}_x={\mathit{B}}_x{\mathit{M}}_x$. Similarly,  ${\mathit{M}}_y{\delta }_y^{2}u={\delta }_y^2\left({\mathit{M}}_{y}u\right)$ can also be proven, and this completes the proof.    □

Lemma 8.

For any two grid functions u and v defined on ${\overline{\Omega }}_h$, there are

$$(\mathbf{M}{\delta }_x^2{\delta }_y^{2}u,v)=(u,\mathbf{M}{\delta }_x^2{\delta }_y^{2}v),(\mathbf{M}{\delta }_x^2{\delta }_y^{2}u,u)\le {\displaystyle \frac{36}{h_x^2{h}_y^2}}{\parallel u\parallel }^2.$$

(23)

Proof. 

We choose $J=J_x=J_y$ for simplification. Let the discrete functions $v_{j,k}$ in vector form be written as

$$v={(v_{1,1},v_{2,1},\cdots ,v_{J-1,1},\cdots ,v_{1,J-1},v_{2,J-1},\cdots ,v_{J-1,J-1})}^T,$$

and the matrix form of

$$\mathit{M}{\delta }_x^2{\delta }_y^{2}u={\displaystyle \frac{1}{h_x^2{h}_y^2}}\mathit{M}\mathit{B}u,$$

where $\mathit{M}={\mathit{M}}_y\otimes {\mathit{M}}_x$ and $\mathit{B}={\mathit{B}}_y\otimes {\mathit{B}}_x$.

Using properties of the Kroneker product and Lemma 7, we have

$$\begin{array}{cc}\hfill {\left(\mathit{M}\mathit{B}\right)}^T& ={\left(({\mathit{M}}_y\otimes {\mathit{M}}_x)({\mathit{B}}_y\otimes {\mathit{B}}_x)\right)}^T={\left(\left({\mathit{M}}_y{\mathit{B}}_y\right)\otimes \left({\mathit{M}}_x{\mathit{B}}_x\right)\right)}^T\hfill \\ & =\left({\mathit{B}}_y^T{\mathit{M}}_y^T\right)\otimes \left({\mathit{B}}_x^T{\mathit{M}}_x^T\right)=\left({\mathit{B}}_y{\mathit{M}}_y\right)\otimes \left({\mathit{B}}_x{\mathit{M}}_x\right)\hfill \\ & =\left({\mathit{M}}_y{\mathit{B}}_y\right)\otimes \left({\mathit{M}}_x{\mathit{B}}_x\right)\hfill \\ & =({\mathit{M}}_y\otimes {\mathit{M}}_x)({\mathit{B}}_y\otimes {\mathit{B}}_x)=\mathit{M}\mathit{B},\hfill \end{array}$$

which implies that $(\mathit{M}{\delta }_x^2{\delta }_y^{2}u,v)=(u,\mathit{M}{\delta }_x^2{\delta }_y^{2}v)$.

Furthermore, from (16)–(18), we have that the eigenvalues of $\mathit{M}$ and $\mathit{B}$ satisfy

$$1\le {\gamma }_j\le {\displaystyle \frac{9}{4}},0<{\delta }_j\le 16,j=1,2,\cdots ,(J_x-1)\times (J_y-1).$$

(24)

This implies that

$$\parallel \mathit{M}\mathit{B}\parallel =\rho \left(\mathit{M}\mathit{B}\right)\le 36.$$

(25)

Then, we obtain

$$(\mathit{M}{\delta }_x^2{\delta }_y^{2}u,u)={\displaystyle \frac{1}{h_x^2{h}_y^2}}(\mathit{M}\mathit{B}u,u)\le {\parallel \mathit{M}\mathit{B}\parallel \parallel u\parallel }^2\le {\displaystyle \frac{36}{h_x^2{h}_y^2}}{\parallel u\parallel }^2.$$

This completes the proof.    □

Lemma 9.

Suppose that the exact solution $u(\mathbf{x},t)\in C^{6,4}\left(\Omega ,(0,T]\right)$, and

$$\begin{array}{cc}\hfill & \underset{\mathbf{x}\in \Omega ,0\le t\le T}{max}|u(\mathbf{x},t)|\le C_u,\underset{\mathbf{x}\in \Omega ,0\le t\le T}{max}|u_{tt}(\mathbf{x},t)|\le C_1,\hfill \\ \hfill & \underset{\mathbf{x}\in \Omega ,0\le t\le T}{max}|\nabla u(\mathbf{x},t)|\le C_2,\underset{\mathbf{x}\in \Omega ,0\le t\le T}{max}|\nabla u_{tt}(\mathbf{x},t)|\le C_3.\hfill \end{array}$$

(26)

Then it holds that

$$\parallel {\nabla }_h{u}^n\parallel \le C,\parallel {\nabla }_h{u}_{tt}^n\parallel \le C,n=0,1,\cdots ,\mathcal{N},$$

(27)

where $C_u$ and $C_i(i=1,2,3)$ are known positive constants, $\nabla u={({\displaystyle \frac{\partial u}{\partial x}},{\displaystyle \frac{\partial u}{\partial y}})}^T,$ and $u_{tt}={\displaystyle \frac{{\partial }^{2}u}{\partial t^2}}$.

Proof. 

To estimate $\parallel {\nabla }_h{u}^n\parallel$, it is sufficient to give the estimates of ${\partial }_x{u}^n$ and ${\partial }_y{u}^n$. Notice that

$$\begin{array}{c}\hfill {\parallel {\partial }_x{u}^n\parallel }_x^2\le h_x{h}_y\sum _{j=0}^{J_x-1}\sum _{k=1}^{J_y-1}{|{\partial }_x{u}_{jk}^n|}^2\le h_x{h}_y\sum _{j=0}^{J_x-1}\sum _{k=1}^{J_y-1}{\left|{\displaystyle \frac{\partial u}{\partial x}}({\zeta }_j,y_k,t_n)\right|}^2\le |\Omega |C_2^2,\end{array}$$

(28)

where $|\Omega |$ represents the area of $\Omega$. Similarly,  ${\parallel {\partial }_y{u}^n\parallel }_x^2\le |\Omega |C_2^2.$ Then, $\parallel {\nabla }_h{u}^n\parallel \le C.$

In the same way as above, one can prove the inequality $\parallel {\nabla }_h{u}_{tt}^n\parallel \le C$, and this completes the proof.    □

4. Numerical Analysis of the TTM Compact ADI Scheme

For the sake of convenience and without loss of generality, we consider the homogeneous Dirichlet boundary condition in the following theoretical analysis. When $v=u(\mathbf{x},t)-\psi (\mathbf{x},t)$, problem (1) can be rewritten as

$$\left\{\begin{array}{c}-i{\displaystyle \frac{\partial v}{\partial t}}=\Delta v+F\left(v\right),(\mathbf{x},t)\in \Omega \times (0,T],\hfill \\ v(\mathbf{x},0)=\phi \left(\mathbf{x}\right)-\psi (\mathbf{x},0),\mathbf{x}\in \Omega \cup \partial \Omega ,\hfill \\ u(\mathbf{x},t)=0,(\mathbf{x},t)\in \partial \Omega \times [0,T],\hfill \end{array}\right.$$

where $F\left(v\right)={\beta |v+\psi |}^2(v+\psi )+\nu (v+\psi )+i{\displaystyle \frac{\partial \psi }{\partial t}}+\Delta \psi$.

Furthermore, in the numerical analysis, the subindex $“j,k”$ is omitted and Equation (6) is rewritten as follows:

$$\begin{array}{cc}\hfill -i{\partial }_t{u}^n+{\displaystyle \frac{i{\tau }^2}{4}}{\mathcal{A}}_x^{-1}{\mathcal{A}}_y^{-1}{\delta }_x^2{\delta }_y^2{\partial }_t{u}^n& ={\mathcal{A}}_x^{-1}{\delta }_x^2{u}^{n+1/2}+{\mathcal{A}}_y^{-1}{\delta }_y^2{u}^{n+1/2}\hfill \\ & +\beta {\left({|u|}^2\right)}^{n+1/2}{u}^{n+1/2}+\nu u^{n+1/2}+{\mathcal{A}}_x^{-1}{\mathcal{A}}_y^{-1}{r}^n,\hfill \end{array}$$

(29)

Equation (8) can also be written as

$$-i{\partial }_t{U}_C^{ps}+{\displaystyle \frac{i{\tau }^2}{4}}{\mathcal{A}}_x^{-1}{\mathcal{A}}_y^{-1}{\delta }_x^2{\delta }_y^2{\partial }_t{U}_C^{ps}={\mathcal{A}}_x^{-1}{\delta }_x^2{U}_C^{(p+1/2)s}+{\mathcal{A}}_y^{-1}{\delta }_y^2{U}_C^{(p+1/2)s}+F_C^{(p+1/2)s}.$$

(30)

Then, using the Kronecker product, the matrix form of Equation (29) can be written as

$$\begin{array}{cc}\hfill -i{\partial }_t{u}^n+{\displaystyle \frac{i{\tau }^2}{4}}\mathit{M}{\delta }_x^2{\delta }_y^2{\partial }_t{u}^n& ={\mathit{H}}_x{\delta }_x^2{u}^{n+1/2}+{\mathit{H}}_y{\delta }_y^2{u}^{n+1/2}\hfill \\ \hfill & +\beta {\left({|u|}^2\right)}^{n+1/2}{u}^{n+1/2}+\nu u^{n+1/2}+\mathit{M}{r}^n,\hfill \end{array}$$

(31)

and the matrix form of Equation (30) is written as

$$-i{\partial }_t{U}_C^{ps}+{\displaystyle \frac{i{\tau }_C^2}{4}}\mathit{M}{\delta }_x^2{\delta }_y^2{\partial }_t{U}_C^{ps}={\mathit{H}}_x{\delta }_x^2{U}_C^{(p+1/2)s}+{\mathit{H}}_y{\delta }_y^2{U}_C^{(p+1/2)s}+F_C^{(p+1/2)s}.$$

(32)

Similarly, the matrix form of Equation (10) can also be rewritten as

$$-i{\partial }_t{U}_F^n+{\displaystyle \frac{i{\tau }_F^2}{4}}\mathit{M}{\delta }_x^2{\delta }_y^2{\partial }_t{U}_F^n={\mathit{H}}_x{\delta }_x^2{U}_F^{n+1/2}+{\mathit{H}}_y{\delta }_y^2{U}_F^{n+1/2}+F^{n+1/2}.$$

(33)

Remark 1.

Equation (8) is suitable for computation during implementation. However, since the nonlinear terms in Equation (8) are distributed across different grids in a certain proportion, it is not suitable for theoretical analysis. Thus, in the numerical analysis, we will use the equivalent form of Equation (32).

4.1. Conservation

Theorem 1.

Scheme (8) is conservative in the following sense:

$${\mathcal{Q}}^{ps}={\mathcal{Q}}^0,{\mathcal{E}}^{ps}={\mathcal{E}}^0,p=0,1,\cdots ,N,$$

(34)

where

$${\mathcal{Q}}^{ps}={\parallel U_C^{ps}\parallel }^2-{\displaystyle \frac{{\tau }_C^2}{4}}{\parallel {\partial }_x{\partial }_y{U}_C^{ps}\parallel }_M^2,{\mathcal{E}}^{ps}={||{\nabla }_h{U}_C^{ps}||}_H^2-{\displaystyle \frac{\beta }{2}}{\parallel U_C^{ps}\parallel }_4^4-(\nu U_C^{ps},U_C^{ps}),$$

and ${\mathcal{Q}}^0$ and ${\mathcal{E}}^0$ are the mass with a small negative term ${\displaystyle \frac{{\tau }_C^2}{4}}{\parallel {\partial }_x{\partial }_y\phi \parallel }_M^2$ and the energy in the discrete sense.

Proof. 

Doing the inner product of (32) with $2U_C^{(p+1/2)s}$, and taking the imaginary part, we get

$${\parallel U_C^{(p+1)s}\parallel }^2-{\displaystyle \frac{{\tau }_C^2}{4}}{\parallel {\partial }_x{\partial }_y{U}_C^{(p+1)s}\parallel }_M^2={\parallel U_C^{ps}\parallel }^2-{\displaystyle \frac{{\tau }_C^2}{4}}{\parallel {\partial }_x{\partial }_y{U}_C^{ps}\parallel }_M^2,$$

(35)

where Lemmas 6 and 8 were used.

By computing the inner product of (32) with ${\partial }_t{U}_C^{ps}$ and taking the real part, we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{2{\tau }_C}}\left[\right(||{\nabla }_h{U}_C^{(p+1)s}{||}_H^2& -{\displaystyle \frac{\beta }{2}}{\parallel U_C^{(p+1)s}\parallel }_4^4-(\nu U_C^{(p+1)s},U_C^{(p+1)s}))\hfill \\ \hfill & -\left(||{\nabla }_h{U}_C^{ps}{||}_H^2-{\displaystyle \frac{\beta }{2}}{\parallel U_C^{ps}\parallel }_4^4-(\nu U_C^{ps},U_C^{ps})\right)]=0,\hfill \end{array}$$

(36)

where Lemma 6 is used. This gives (34) and completes the proof.    □

Remark 2.

The addition of the term ${\displaystyle \frac{i{\tau }^2}{4}}{\delta }_x^2{\delta }_y^2{\partial }_t{u}_{jk}^n$ to both sides of Equation (5) for the purpose of building an ADI scheme introduces an extra term, ${\displaystyle \frac{{\tau }_C^2}{4}}{\parallel {\partial }_x{\partial }_y{U}_C^{ps}\parallel }_M^2$, into the discrete mass ${\mathcal{Q}}^{ps}$.

4.2. A Priori Estimate

Theorem 2.

Let $U_C$ be the coarse solution obtained from schemes (8) and (9). If $\sigma ={\displaystyle \frac{{\tau }_C^2}{h_x^2{h}_y^2}}<{\displaystyle \frac{1}{9}}$ and we assume that one of the following two conditions is satisfied,

$$\begin{array}{cc}\hfill & \left(a\right)\phi \in H_p^2(\Omega ),\beta <0,\hfill \\ \hfill & \left(b\right)\phi \in H_p^2(\Omega ),{\parallel \phi \parallel }^2\le {\displaystyle \frac{(2-\tilde{\epsilon })(1-9\sigma )}{4(1+\epsilon )\beta }},\beta >0,\hfill \end{array}$$

then there exits a constant C such that

$$\parallel U_C^n\parallel \le C\parallel \phi \parallel ,\parallel {\nabla }_h{U}_C^n\parallel \le C,n=0,1,\cdots ,\mathcal{N}.$$

(37)

Proof. 

The proof contains two cases. (I)  For the case of $n=ps,(k=1,\cdots ,N)$, using Lemma 8 and assuming that $\sigma ={\displaystyle \frac{{\tau }_C^2}{h_x^2{h}_y^2}}<{\displaystyle \frac{1}{9}}$, we obtain from (34) that

$$\parallel U_C^n\parallel \le {\displaystyle \frac{1}{\sqrt{1-9\sigma }}}\parallel \phi \parallel .$$

(38)

Analogous to the process of (35), taking the inner product of (32) with $2\nu U_C^{(p+1/2)s}$ and taking the imaginary part, we obtain

$$(\nu U_C^{ps},U_C^{ps})-(\nu \phi ,\phi )={\displaystyle \frac{{\tau }_C^2}{4}}(\mathit{M}{\delta }_x^2{\delta }_y^2{U}_C^{ps},\nu U_C^{ps})-{\displaystyle \frac{{\tau }_C^2}{4}}(\mathit{M}{\delta }_x^2{\delta }_y^2\phi ,\nu \phi ),$$

(39)

and for the case of $n=ps$, combining (36) and (39), we have

$$\begin{array}{cc}\hfill ||{\nabla }_h{U}_C^n{||}_H^2& -{\displaystyle \frac{\beta }{2}}\parallel U_C^n{\parallel }_4^4=||{\nabla }_h\phi {||}_H^2-{\displaystyle \frac{\beta }{2}}{\parallel \phi \parallel }_4^4\hfill \\ \hfill & +{\displaystyle \frac{{\tau }_C^2}{4}}\left\{(\mathit{M}{\delta }_x^2{\delta }_y^2{U}_C^n,\nu U_C^n)-(\mathit{M}{\delta }_x^2{\delta }_y^2\phi ,\nu \phi )\right\}.\hfill \end{array}$$

(40)

Then, under condition (a), applying Lemma 8 and (38), we obtain

$$\begin{array}{cc}\hfill ||{\nabla }_h{U}_C^n{||}_H^2& \le ||{\nabla }_h\phi {||}_H^2-{\displaystyle \frac{\beta }{2}}{\parallel \phi \parallel }_4^4+{\displaystyle \frac{{\nu }_{max}\sigma }{4}}\left\{\parallel U_C^n{\parallel }^2+{\parallel \phi \parallel }^2\right\}\hfill \\ \hfill & \le ||{\nabla }_h\phi {||}_H^2-{\displaystyle \frac{\beta }{2}}{\parallel \phi \parallel }_4^4+{\displaystyle \frac{{\nu }_{max}\sigma (2-9\sigma )}{4(1-9\sigma )}}{\parallel \phi \parallel }^2,\hfill \end{array}$$

(41)

where the assumption $0\le \nu \le {\nu }_{max}$ is used.

Under condition (b), applying Lemma 4 and (38), we obtain

$$\begin{array}{cc}\hfill \parallel U_C^n{\parallel }_4^4& \le \parallel U^n{\parallel }^2{\left(2\parallel {\nabla }_h{U}_C^n\parallel +{\displaystyle \frac{1}{\ell }}\parallel U_C^n\parallel \right)}^2\hfill \\ \hfill & \le \parallel U^n{\parallel }^2\left(4(1+\epsilon )\parallel {\nabla }_h{U}_C^n{\parallel }^2+(1+{\epsilon }^{-1}){\displaystyle \frac{1}{\ell }}{\parallel U_C^n\parallel }^2\right)\hfill \\ \hfill & \le 4(1+\epsilon ){\displaystyle \frac{1}{1-9\sigma }}{\parallel \phi \parallel }^2\parallel {\nabla }_h{U}_C^n{\parallel }^2+(1+{ϵ}^{-1}){\displaystyle \frac{1}{\ell }}{\parallel U_C^n\parallel }^4\hfill \\ \hfill & \le {\displaystyle \frac{2}{\beta }}\parallel {\nabla }_h{U}_C^n{\parallel }^2-{\displaystyle \frac{\tilde{\epsilon }}{\beta }}\parallel {\nabla }_h{U}_C^n{\parallel }^2+(1+{ϵ}^{-1}){\displaystyle \frac{1}{\ell }}{\parallel U_C^n\parallel }^4,\hfill \end{array}$$

(42)

where $\epsilon$ and $\tilde{\epsilon }$ are two positive numbers that can be arbitrarily small. This together with (41) and Lemmas 4 and 5 gives

$$(1+{\displaystyle \frac{\tilde{\epsilon }}{2}})\parallel {\nabla }_h{U}_C^n{\parallel }^2\le (2+{\displaystyle \frac{\tilde{\epsilon }}{2}})\parallel {\nabla }_h{\phi \parallel }^2+{\displaystyle \frac{{\nu }_{max}\sigma (2-9\sigma )}{4(1-9\sigma )}}{\parallel \phi \parallel }^2.$$

(43)

(II) For the case of $n=ps-l,(l=0,1,\cdots ,s;p=1,2,\cdots ,N)$, combining (9) with (38) and (43), respectively, we have

$$\begin{array}{cc}\hfill & \parallel U_C^n\parallel =\parallel U_C^{ps-l}\parallel \le {\displaystyle \frac{l}{s}}\parallel U_C^{(p-1)s}\parallel +(1-{\displaystyle \frac{l}{s}})\parallel U_C^{ps}\parallel \le {\displaystyle \frac{1}{\sqrt{1-9\sigma }}}\parallel \phi \parallel ,\hfill \\ \hfill & (1+{\displaystyle \frac{\tilde{\epsilon }}{2}})\parallel {\nabla }_h{U}_C^n{\parallel }^2=(1+{\displaystyle \frac{\tilde{\epsilon }}{2}})\parallel {\nabla }_h{U}_C^{ps-l}\parallel \le (2+{\displaystyle \frac{\tilde{\epsilon }}{2}})\parallel {\nabla }_h{\phi \parallel }^2+{\displaystyle \frac{{\nu }_{max}\sigma (2-9\sigma )}{4(1-9\sigma )}}{\parallel \phi \parallel }^2.\hfill \end{array}$$

(44)

Synthesizing the above two cases, one can obtain the result of Theorem 2, and this completes the proof.    □

4.3. Convergence

First, consider the error analysis on the coarse temporal mesh. Denote $e_C^n=u^n-U_C^n,$ with $1\le n\le \mathcal{N}$. Subtracting Equation (32) from Equation (31) yields the following error equation:

$$\begin{array}{c}\hfill -i{\partial }_t{e}_C^n+{\displaystyle \frac{i{\tau }_C^2}{4}}\mathit{M}{\delta }_x^2{\delta }_y^2{\partial }_t{e}_C^n={\mathit{H}}_x{\delta }_x^2{e}_C^{n+1/2}+{\mathit{H}}_y{\delta }_y^2{e}_C^{n+1/2}+\beta {\mathcal{G}}^n+\nu e_C^{n+1/2}+\mathit{M}{r}^n,\end{array}$$

(45)

where

$$\begin{array}{cc}\hfill {\mathcal{G}}^n& ={\left({|u|}^2\right)}^{n+1/2}{u}^{n+1/2}-{\left(|U_C{|}^2\right)}^{n+1/2}{U}_C^{n+1/2}\hfill \\ & ={\displaystyle \frac{1}{2}}\left(|u^n{|}^2+|u^{n+1}{|}^2-|U_C^n{|}^2-{|U_C^{n+1}|}^2\right)u^{n+1/2}\hfill \\ & +{\displaystyle \frac{1}{2}}\left(|U_C^n{|}^2+{|U_C^{n+1}|}^2\right)e_C^{n+1/2}={\theta }^{n+1/2}+{\xi }^{n+1/2}.\hfill \end{array}$$

(46)

Theorem 3.

Suppose that the initial condition φ is satisfied the assumptions (a) and (b), and assume that the exact solution $u^n\in C^6(\Omega ),$ $\sigma ={\displaystyle \frac{{\tau }_C^2}{h_x^2{h}_y^2}}<{\displaystyle \frac{1}{9}}$, and ${\tau }_C<{\displaystyle \frac{35}{36C}}$. Then

$$\parallel u^n-U_C^n\parallel \le C({\tau }_C^2+h^4),1\le n\le \mathcal{N},$$

(47)

where the positive constant C only depends on the norms of $u(\mathbf{x},t),u_{tt}(\mathbf{x},t),\nabla u(\mathbf{x},t),$ and $\nabla u_{tt}(\mathbf{x},t)$.

Proof. 

The proof contains two cases. (I)  For the case of $n=ps,(k=1,\cdots ,N)$, computing the inner product of (45) with $2e_C^{n+1/2}$ and then taking the imaginary part, we obtain

$$-{\partial }_t\parallel e_C^n{\parallel }^2+{\displaystyle \frac{{\tau }_C^2}{4}}{\partial }_t{\parallel {\partial }_x{\partial }_y{e}_C^n\parallel }_M^2=2\beta \mathrm{Im}({\mathcal{G}}^n,e_C^{n+1/2})+2\mathrm{Im}(\mathit{M}{r}^n,e_C^{n+1/2}),$$

(48)

where Lemma 6 is used. Note that $|U_C^n|\le |u^n|+|e_C^n|\le C_u+|e_C^n|$, so we obtain

$$\begin{array}{cc}\hfill |{\theta }^{n+1/2}|& \le \left\{\left(|u^n|+|U_C^n|\right)|e_C^n|+\left(|u^{n+1}|+|U_C^{n+1}|\right)|e_C^{n+1}|\right\}|u^{n+1/2}|\hfill \\ \hfill & \le \left\{\left(2|u^n|+|e_C^n|\right)|e_C^n|+\left(2|u^{n+1}|+|e_C^{n+1}|\right)|e_C^{n+1}|\right\}|u^{n+1/2}|\hfill \\ \hfill & \le 2C_u^2\left(|e_C^n|+|e_C^{n+1}|\right)+C_u\left(|e_C^n{|}^2+{|e_C^{n+1}|}^2\right).\hfill \end{array}$$

(49)

Applying the Cauchy–Schwartz inequality, we obtain

$$\begin{array}{cc}\hfill & |2\beta \mathrm{Im}({\mathcal{G}}^n,e_C^{n+1/2})|=|2\beta \mathrm{Im}({\theta }^{n+1},e_C^{n+1/2})|\hfill \\ \hfill & \le 2|\beta |h_x{h}_y\sum _{j=1}^{J_x-1}\sum _{k=1}^{J_y-1}\left\{2C_u^2\left(|e_{C,jk}^n|+|e_{C,jk}^{n+1}|\right)+C_u\left(|e_{C,jk}^n{|}^2+{|e_{C,jk}^{n+1}|}^2\right)\right\}|e_{C,jk}^{n+1/2}|\hfill \\ \hfill & \le C{C}_u^2\left(\parallel e_C^n{\parallel }^2+\parallel e_C^{n+1}{\parallel }^2+2{\parallel e_C^{n+1/2}\parallel }^2\right)+C{C}_u\left(\parallel e_C^n{\parallel }_4^2\parallel e_C^{n+1/2}\parallel +\parallel e_C^{n+1}{\parallel }_4^2\parallel e_C^{n+1/2}\parallel \right),\hfill \end{array}$$

(50)

and

$$2|\mathrm{Im}(\mathit{M}{r}^n,e_C^{n+1/2})|\le {\displaystyle \frac{9}{4}}\parallel r^n{\parallel }^2+{\parallel e_C^{n+1/2}\parallel }^2.$$

(51)

Then, from (48)–(51), we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\tau }_C}}\{{\parallel e_C^{n+1}\parallel }^2& -\parallel e_C^n{\parallel }^2\}-{\displaystyle \frac{{\tau }_C}{4}}\left\{(\mathit{M}{\delta }_x^2{\delta }_y^2{e}_C^{n+1},e_C^{n+1})-(\mathit{M}{\delta }_x^2{\delta }_y^2{e}_C^n,e_C^n)\right\}\hfill \\ \hfill & \le {\displaystyle \frac{9}{4}}\parallel r^n{\parallel }^2+C\left\{\parallel e_C^n{\parallel }^2+{\parallel e_C^{n+1}\parallel }^2\right\}+2C_u\left(\parallel e_C^n{\parallel }_4^2+{\parallel e_C^{n+1}\parallel }_4^2\right)\parallel e_C^{n+1/2}\parallel .\hfill \end{array}$$

(52)

Additionally, when $\sigma ={\displaystyle \frac{{\tau }_C^2}{h_x^2{h}_y^2}}<{\displaystyle \frac{1}{9}}$, Theorem 2, Lemma 9, and (26) give that

$$\begin{array}{cc}\hfill & \parallel e_C^n\parallel \le \parallel u^n\parallel +\parallel U_C^n\parallel \le \sqrt{max\{b_1-a_1,b_2-a_2\}}{C}_u+C,\hfill \\ \hfill & \parallel {\nabla }_h{e}_C^n\parallel \le \parallel {\nabla }_h{u}^n\parallel +\parallel {\nabla }_h{U}_C^n\parallel \le C,\hfill \end{array}$$

(53)

and then according to Lemma 4, we have

$$\left(\parallel e_C^n{\parallel }_4^2+{\parallel e_C^{n+1}\parallel }_4^2\right)\parallel e_C^{n+1/2}\parallel \le C\left\{\parallel e_C^n{\parallel }^2+{\parallel e_C^{n+1}\parallel }^2\right\}.$$

(54)

Summing up the inequality (52), using Lemma 8, and noting that $e_C^0=0$, we obtain

$$\begin{array}{cc}\hfill \alpha \parallel e_C^{n+1}{\parallel }^2& \le {\tau }_C\sum _{s=0}^n{\displaystyle \frac{9}{4}}\parallel r^s{\parallel }^2+C{\tau }_C\sum _{s=0}^n\parallel e_C^s{\parallel }^2+C{\tau }_C{\parallel e_C^{n+1}\parallel }^2,\hfill \end{array}$$

(55)

where $\alpha =1-{\displaystyle \frac{\sigma }{4}}$ and the condition  $\sigma <{\displaystyle \frac{1}{9}}$ yields $\alpha >0$. By taking ${\tau }_C<{\displaystyle \frac{35}{36C}}$ and applying the discrete Gronwall’s inequality, we then have

$$\parallel u^n-U_C^n\parallel \le C({\tau }_C^2+h^4).$$

(56)

(II) For the case of $n=ps-l,(l=0,1,\cdots ,s;p=1,2,\cdots ,N)$, based on Lagrange’s interpolation formula, we obtain

$$\begin{array}{cc}\hfill u^{ps-l}& ={\displaystyle \frac{t_{ps-l}-t_{ps}}{t_{(p-1)s}-t_{ps}}}{u}^{(p-1)s}+{\displaystyle \frac{t_{ps-l}-t_{(p-1)s}}{t_{ps}-t_{(p-1)s}}}{u}^{ps}={\displaystyle \frac{l}{s}}{u}^{(p-1)s}+(1-{\displaystyle \frac{l}{s}})u^{ps}\hfill \\ \hfill & +{\displaystyle \frac{u_{tt}\left(\eta \right)}{2}}(t-t_{(p-1)s})(t-t_{ps}),\eta \in (t_{(p-1)s},t_{ps}).\hfill \end{array}$$

(57)

Subtracting  (9) from (57) and using (56) and the triangle inequality, we obtain

$$\begin{array}{c}\hfill \parallel e_C^{ps-l}\parallel \le {\displaystyle \frac{l}{s}}\parallel e_C^{(p-1)s}\parallel +(1-{\displaystyle \frac{l}{s}})\parallel e_C^{ps}\parallel +{\tau }_C^2\parallel {\displaystyle \frac{u_{tt}\left(\eta \right)}{2}}\parallel \le C({\tau }_C^2+h^4).\end{array}$$

(58)

Finally, synthesizing (56) and (58), we complete the proof.    □

Theorem 4.

Suppose that the initial condition φ is satisfied the assumptions (a) and (b), and assume that the exact solution $u^n\in C^6(\Omega ),$ $\sigma ={\displaystyle \frac{{\tau }_C^2}{h_x^2{h}_y^2}}<{\displaystyle \frac{1}{9}}$, and ${\tau }_C<{\displaystyle \frac{35}{36C}}$. Then,

$$\parallel {\nabla }_h{e}_C^n\parallel \le C({\tau }_C^2+h^4),1\le n\le \mathcal{N}.$$

(59)

Furthermore,

$$\parallel u^n-U_C^n{\parallel }_1\le C({\tau }_C^2+h^4),1\le n\le \mathcal{N},$$

(60)

where the positive constant C only depends on the norms of $u(\mathbf{x},t),u_{tt}(\mathbf{x},t),\nabla u(\mathbf{x},t)$, and $\nabla u_{tt}(\mathbf{x},t)$.

Proof. 

The proof contains two cases. (I)  For the case of $n=ps,(p=0,\cdots ,N-1)$, computing the inner product of (45) with $2e_C^{(p+1/2)s}$ and taking the real part, we obtain

$$\begin{array}{cc}\hfill ||{\nabla }_h{e}_C^{(p+1/2)s}{||}_H^2+2\beta \mathrm{Re}({\mathcal{G}}^n,e_C^{(p+1/2)s})+& 2\mathrm{Re}(\nu e_C^{(p+1/2)s},e_C^{(p+1/2)s})\hfill \\ \hfill & +2\mathrm{Re}(\mathit{M}{r}^{ps},e_C^{(p+1/2)s})=0.\hfill \end{array}$$

(61)

Analogous to the proof of (50), applying (53) and (54), we have

$$|2\beta \mathrm{Re}({\theta }^{(p+1/2)s},e_C^{(p+1/2)s})|\le C\{\parallel e_C^{ps}{\parallel }^2+{\parallel e_C^{(p+1)s}\parallel }^2\}.$$

(62)

Using the Cauchy–Schwartz inequality, we obtain

$$\begin{array}{cc}\hfill |2\beta \mathrm{Re}({\xi }^{(p+1/2)s},e_C^{(p+1/2)s})|& \le 2|\beta |h_x{h}_y\sum _{j=1}^{J_x-1}\sum _{k=1}^{J_y-1}\left(|U_{C,jk}^{ps}{|}^2+{|U_{C,jk}^{(p+1)s}|}^2\right){|e_{C,jk}^{(p+1/2)s}|}^2\hfill \\ \hfill & \le C{C}_u^2{\parallel e_C^{(p+1/2)s}\parallel }^2,\hfill \end{array}$$

(63)

and

$$\begin{array}{cc}\hfill & 2|\mathrm{Re}(\mathit{M}{r}^{ps},e_C^{(p+1/2)s})|\le {\displaystyle \frac{9}{4}}\parallel r^{ps}{\parallel }^2+{\parallel e_C^{(p+1/2)s}\parallel }^2,\hfill \\ \hfill & 2|\mathrm{Re}(\nu e_C^{(p+1/2)s},e_C^{(p+1/2)s})|\le C{\nu }_{max}{\parallel e_C^{(p+1/2)s}\parallel }^2.\hfill \end{array}$$

(64)

Then, combining (47) with (61)–(64), we have

$$\begin{array}{cc}\hfill 2\parallel {\nabla }_h{e}_C^{(p+1/2)s}{\parallel }^2& \le ||{\nabla }_h{e}_C^{(p+1/2)s}{||}_H^2\le \left|2\beta \mathrm{Re}({\mathcal{G}}^{ps},e_C^{(p+1/2)s})\right|\hfill \\ \hfill & +\left|2\mathrm{Re}(\nu e_C^{(p+1/2)s},e_C^{(p+1/2)s})\right|+\left|2\mathrm{Re}(\mathit{M}{r}^{ps},e_C^{(p+1/2)s})\right|\hfill \end{array}$$

(65)

$$\begin{array}{cc}\hfill & \le C\{\parallel e_C^{ps}{\parallel }^2+{\parallel e_C^{(p+1)s}\parallel }^2\}+{\parallel r^{ps}\parallel }^2\le C({\tau }_C^4+h^8),\hfill \end{array}$$

where Lemma 5 is used.

Based on (65), we then use the mathematical induction method to prove the error estimate of $\parallel {\nabla }_h{e}_C^{ps}\parallel ,(p=1,2,\cdots ,N)$. Due to the fact that $e_C^0=0$, from (65) with $p=0$, we obtain

$$\parallel {\nabla }_h{e}_C^s\parallel =\parallel {\nabla }_h{e}_C^{s/2}\parallel \le C({\tau }_C^2+h^4).$$

(66)

Therefore, the conclusion is valid for $p=0$. Now suppose (59) is valid for $0\le p\le m$, and then we prove that (59) is valid for $p=m+1$.

Applying (65) and the triangle inequality, we have

$$\parallel {\nabla }_h{e}_C^{(m+1)s}\parallel \le 2\parallel {\nabla }_h{e}_C^{(m+1/2)s}\parallel +\parallel {\nabla }_h{e}_C^{ms}\parallel \le C({\tau }_C^2+h^4).$$

(67)

(II)  For the case of $n=ps-l,(l=0,1,\cdots ,s;p=1,2,\cdots ,N)$, subtracting (9) from (57), and using (27), (67), and triangle inequality, we obtain

$$\begin{array}{c}\hfill \parallel {\nabla }_h{e}_C^{ps-l}\parallel \le {\displaystyle \frac{l}{s}}\parallel {\nabla }_h{e}_C^{(p-1)s}\parallel +(1-{\displaystyle \frac{l}{s}})\parallel {\nabla }_h{e}_C^{ps}\parallel +{\tau }_C^2\parallel {\displaystyle \frac{{\nabla }_h{u}^{″}\left(\eta \right)}{2}}\parallel \le C({\tau }_C^2+h^4).\end{array}$$

(68)

Finally, synthesizing (67) and (68) gives us (59). Furthermore, the discrete $H^1$-norm error estimate (60) can be proven by combining (59) and (47). This complete the proof.    □

Next, consider the error analysis of the fine temporal mesh. Denote

$$\begin{array}{c}{u}^n=v^n+i{w}^n,U_C^n=V_C^n+i{W}_C^n,U_F^n=V_F^n+i{W}_F^n,\hfill \\ e_F^n=u^n-U_F^n,e_C^n=u^n-U_C^n,1\le n\le \mathcal{N},\hfill \\ e_F^n=e_{R,F}^n+i{e}_{I,F}^n,e_C^n=e_{R,C}^n+i{e}_{I,C}^n,1\le n\le \mathcal{N}.\hfill \end{array}$$

Here, we also use the symbols $g_R,g_I,{\tilde{F}}^{n+1/2},{\widehat{F}}^{n+1/2},g_R^C,g_I^C,g_{R,v}^C,g_{R,w}^C,g_{I,v}^C,g_{I,w}^C$, and $E\left(v^n\right)$ in the following part, whose definitions have already been given in (11)–( 13), respectively.

Subtracting Equation (33) from Equation (31) yields the following error equation:

$$\begin{array}{c}\hfill -i{\partial }_t{e}_F^n+{\displaystyle \frac{i{\tau }_F^2}{4}}\mathit{M}{\delta }_x^2{\delta }_y^2{\partial }_t{e}_F^n={\mathit{H}}_x{\delta }_x^2{e}_F^{n+1/2}+{\mathit{H}}_y{\delta }_y^2{e}_F^{n+1/2}+{\mathcal{S}}^n+\mathit{M}{r}^n,\end{array}$$

(69)

where

$$\begin{array}{c}\hfill {\mathcal{S}}^n=\left(g_R(v^{n+1/2},w^{n+1/2})-{\tilde{F}}^{n+1/2}\right)+i\left(g_I(v^{n+1/2},w^{n+1/2})-{\widehat{F}}^{n+1/2}\right).\end{array}$$

(70)

Notice that

$$\begin{array}{cc}\hfill g_R(v^{n+1/2},w^{n+1/2})& -{\tilde{F}}^{n+1/2}=g_{R,v}^C·\left[v^{n+1/2}-E\left(V_F^n\right)\right]+g_{R,w}^C·\left[w^{n+1/2}-E\left(W_F^n\right)\right]\hfill \\ & +{\displaystyle \frac{1}{2}}{g}_{R,vv}·{\left[v^{n+1/2}-V_C^{n+1/2}\right]}^2+{\displaystyle \frac{1}{2}}{g}_{R,ww}·{\left[w^{n+1/2}-W_C^{n+1/2}\right]}^2\hfill \\ & +g_{R,vw}·\left[(v^{n+1/2}-V_C^{n+1/2})(w^{n+1/2}-W_C^{n+1/2})\right],\hfill \\ \hfill g_I(v^{n+1/2},w^{n+1/2})& -{\widehat{F}}^{n+1/2}=g_{I,v}^C·\left[v^{n+1/2}-E\left(V_F^n\right)\right]+g_{I,w}^C·\left[w^{n+1/2}-E\left(W_F^n\right)\right]\hfill \\ & +{\displaystyle \frac{1}{2}}{g}_{I,vv}·{\left[v^{n+1/2}-V_C^{n+1/2}\right]}^2+{\displaystyle \frac{1}{2}}{g}_{I,ww}·{\left[w^{n+1/2}-W_C^{n+1/2}\right]}^2\hfill \\ & +g_{I,vw}·\left[(v^{n+1/2}-V_C^{n+1/2})(w^{n+1/2}-W_C^{n+1/2})\right],\hfill \end{array}$$

(71)

where the second-derivative terms $g_{R,vv}=6\beta {\zeta }_1,g_{R,ww}=2\beta {\zeta }_1,g_{R,vw}=2\beta {\eta }_1$, and $g_{I,vv}=2\beta {\eta }_2,g_{I,ww}=6\beta {\eta }_2,g_{I,vw}=2\beta {\zeta }_2$, in which the point $({\eta }_j,{\zeta }_j)$ lies on the line segment between the points $(v^{n+1/2},w^{n+1/2})$ and $(V_C^{n+1/2},W_C^{n+1/2})$, and the second-order Taylor expansion of functions $g_R(v,w)$ and $g_I(v,w)$ about the point $(V_C^{n+1/2},W_C^{n+1/2})$ were used, respectively.

Theorem 5.

Suppose that the initial condition φ is satisfied the assumptions (a) and (b), and assume that the exact solution $u^n\in C^6(\Omega ),$ $\sigma ={\displaystyle \frac{{\tau }_C^2}{h_x^2{h}_y^2}}<{\displaystyle \frac{1}{9}}$, and ${\tau }_F<{\displaystyle \frac{35}{36C}}$. Then,

$$\parallel u^n-U_F^n\parallel \le C({\tau }_C^4+{\tau }_F^2+h^4),1\le n\le \mathcal{N},$$

(72)

where the positive constant C only depends on the norms of $u(\mathbf{x},t),u_{tt}(\mathbf{x},t),\nabla u(\mathbf{x},t),$ and $\nabla u_{tt}(\mathbf{x},t)$.

Proof. 

Computing the inner product of (69) with $2e_F^{n+1/2}$ and taking the imaginary part, we obtain

$$\begin{array}{cc}\hfill -{\partial }_t{\parallel e_F^n\parallel }^2& +{\displaystyle \frac{{\tau }_F^2}{4}}{\partial }_t{\parallel {\partial }_x{\partial }_y{e}_F^n\parallel }_M^2=\{\left(g_R(v^{n+1/2},w^{n+1/2})-{\tilde{F}}^{n+1/2},2e_{I,F}^{n+1/2}\right)\hfill \\ \hfill & +\left(g_I(v^{n+1/2},w^{n+1/2})-{\widehat{F}}^{n+1/2},2e_{R,F}^{n+1/2}\right)\}+\mathrm{Im}(\mathbb{M}{r}^n,2e_F^{n+1/2}),\hfill \end{array}$$

(73)

where Lemma 6 is used.

According to the smoothness assumption of the exact solution and the inequality $\sigma <{\displaystyle \frac{1}{9}}$, we have

$$\begin{array}{cc}\hfill & \parallel e_C^n{\parallel }_{\infty }\le h^{-1}\parallel e_C^n\parallel \le C{h}^3\le 1,1\le n\le \mathcal{N},\hfill \\ \hfill & \parallel U_C^n{\parallel }_{\infty }\le \parallel e_C^n{\parallel }_{\infty }+{\parallel u^n\parallel }_{\infty }\le C_u+1,1\le n\le \mathcal{N}.\hfill \end{array}$$

(74)

Then it follows that

$$\begin{array}{cc}\hfill & \parallel g_{R,v}^C{\parallel }_{\infty }\le C{(C_u+1)}^2+{\nu }_{max},{\parallel g_{R,w}^C\parallel }_{\infty }\le C{(C_u+1)}^2+{\nu }_{max},\hfill \\ \hfill & \parallel g_{R,vv}{\parallel }_{\infty }\le C(C_u+1),\parallel g_{R,ww}{\parallel }_{\infty }\le C(C_u+1),{\parallel g_{R,vw}\parallel }_{\infty }\le C(C_u+1).\hfill \end{array}$$

(75)

Similar bounds for $g_{I,v}^C,g_{I,w}^C,g_{I,vv},g_{I,vw},$ and $g_{I,ww}$ can also be obtained in the same way as above.

Using the Cauchy–Schwartz inequality and (75), we obtain

$$\begin{array}{cc}\hfill & \left|\left(g_{R,v}^C·\left[v^{n+1/2}-E\left(V_F^n\right)\right],2e_{I,F}^{n+1/2}\right)\right|\le C\left\{\parallel {\displaystyle \frac{3e_{R,F}^n-e_{R,F}^{n-1}}{2}}{\parallel }^2+{\parallel 2e_{I,F}^{n+1/2}\parallel }^2\right\}+O\left({\tau }_F^4\right),\hfill \\ \hfill & \left|\left(g_{R,w}^C·\left[w^{n+1/2}-E\left(W_F^n\right)\right],2e_{I,F}^{n+1/2}\right)\right|\le C\left\{\parallel {\displaystyle \frac{3e_{I,F}^n-e_{I,F}^{n-1}}{2}}{\parallel }^2+{\parallel 2e_{I,F}^{n+1/2}\parallel }^2\right\}+O\left({\tau }_F^4\right),\hfill \\ \hfill & \left|\left({\displaystyle \frac{1}{2}}{g}_{R,vv}{\left[e_{R,C}^{n+1/2}\right]}^2+{\displaystyle \frac{1}{2}}{g}_{R,ww}·{\left[e_{I,C}^{n+1/2}\right]}^2+g_{R,vw}·\left[e_{R,C}^{n+1/2}{e}_{I,C}^{n+1/2}\right],2e_{I,F}^{n+1/2}\right)\right|\hfill \\ \hfill & \le C\left\{{\displaystyle \frac{1}{2}}\parallel {\left(e_{R,C}^{n+1/2}\right)}^2{\parallel }^2+\parallel e_{R,C}^{n+1/2}{e}_{I,C}^{n+1/2}{\parallel }^2+{\displaystyle \frac{1}{2}}\parallel {\left(e_{I,C}^{n+1/2}\right)}^2{\parallel }^2+{\parallel 2e_{I,F}^{n+1/2}\parallel }^2\right\}.\hfill \end{array}$$

(76)

It follows that

$$\begin{array}{cc}\hfill & \left|\left(g_R(v^{n+1/2},w^{n+1/2})-{\tilde{F}}^{n+1/2},2e_{I,F}^{n+1/2}\right)\right|\hfill \\ \hfill & \le C\left\{\parallel {\displaystyle \frac{3e_F^n-e_F^{n-1}}{2}}{\parallel }^2+3\parallel 2e_{I,F}^{n+1/2}{\parallel }^2+{\parallel e_C^{n+1/2}\parallel }_4^4\right\}+O\left({\tau }_F^4\right).\hfill \end{array}$$

(77)

Similarly,

$$\begin{array}{cc}\hfill & \left|\left(g_I(v^{n+1/2},w^{n+1/2})-{\widehat{F}}^{n+1/2},2e_{R,F}^{n+1/2}\right)\right|\hfill \\ \hfill & \le C\left\{\parallel {\displaystyle \frac{3e_F^n-e_F^{n-1}}{2}}{\parallel }^2+3\parallel 2e_{R,F}^{n+1/2}{\parallel }^2+{\parallel e_C^{n+1/2}\parallel }_4^4\right\}+O\left({\tau }_F^4\right).\hfill \end{array}$$

(78)

Substituting  (77) and (78) into (73) yields

$$\begin{array}{cc}\hfill \parallel e_F^{n+1}{\parallel }^2-{\displaystyle \frac{{\tau }_F^2}{4}}{\parallel {\partial }_x{\partial }_y{e}_F^{n+1}\parallel }_M^2& \le \parallel e_F^n{\parallel }^2-{\displaystyle \frac{{\tau }_F^2}{4}}\parallel {\partial }_x{\partial }_y{e}_F^n{\parallel }_M^2+C{\tau }_F\{\parallel e_F^{n-1}{\parallel }^2+7{\parallel e_F^n\parallel }^2\hfill \\ \hfill & +4\parallel e_F^{n+1}{\parallel }^2+{\parallel e_C^{n+1/2}\parallel }_4^4\}+O({\tau }_F^4+h^8).\hfill \end{array}$$

(79)

Summing up (79) for n from 1 to m then replacing m by n and using Lemma 8, we obtain

$$\begin{array}{cc}\hfill \alpha \parallel e_F^{n+1}{\parallel }^2& \le \parallel e_F^1{\parallel }^2-{\displaystyle \frac{{\tau }_F^2}{4}}\parallel {\partial }_x{\partial }_y{e}_F^1{\parallel }_M^2+C{\tau }_F\sum _{s=0}^n{\parallel e_C^s\parallel }_4^4\hfill \\ \hfill & +C{\tau }_F\sum _{s=0}^n\parallel e_F^s{\parallel }^2+C{\tau }_F{\parallel e_F^{n+1}\parallel }^2+O({\tau }_F^4+h^8),\hfill \end{array}$$

(80)

where $\alpha =1-{\displaystyle \frac{\sigma }{4}},$ and $\sigma <{\displaystyle \frac{1}{9}}$ yields $\alpha >0$.

Next, we will give the error estimate of $\parallel e_C^n{\parallel }_4^4$. Using Lemma 4, (47) and (59),we have

$$\parallel e_C^n{\parallel }_4^4\le {\parallel e_C^n\parallel }^2{\left(C_p\parallel {\nabla }_h{e}_C^n\parallel +{\displaystyle \frac{1}{\ell }}\parallel e_C^n\parallel \right)}^2\le C({\tau }_C^8+h^{16}).$$

(81)

In addition, noting that $v^{1/2}-E\left(v_F^0\right)=O\left({\tau }_F^2\right)$, for $n=0$, cf. (77) and (78),

$$\begin{array}{cc}\hfill \left|\left(g_R(v^{1/2},w^{1/2})-{\tilde{F}}^{1/2},2e_{I,F}^{1/2}\right)\right|+& \left|\left(g_I(v^{1/2},w^{1/2})-{\widehat{F}}^{1/2},2e_{R,F}^{1/2}\right)\right|\hfill \\ \hfill & \le C\left\{3\parallel 2e_F^{1/2}{\parallel }^2+{\parallel e_C^{1/2}\parallel }_4^4\right\}+O\left({\tau }_F^4\right).\hfill \end{array}$$

(82)

Then for $n=0$, noting that $e_C^0=0$ and substituting (82) into (73) at $n=0$, we obtain, cf. (79),

$$\begin{array}{cc}\hfill \parallel e_F^1{\parallel }^2-{\displaystyle \frac{{\tau }_F^2}{4}}{\parallel {\partial }_x{\partial }_y{e}_F^1\parallel }_M^2& \le C{\tau }_F\left\{{\displaystyle \frac{9}{4}}\parallel r^0{\parallel }^2+3\parallel e_F^1{\parallel }^2+{\parallel e_C^{1/2}\parallel }_4^4\right\}+O\left({\tau }_F^4\right).\hfill \end{array}$$

(83)

Finally, combining (80), (81), and (83) yields

$$\parallel e_F^{n+1}{\parallel }^2\le C{\tau }_F\sum _{s=0}^n{\parallel e_F^s\parallel }^2+O({\tau }_F^4+{\tau }_C^8+h^8),$$

(84)

By taking ${\tau }_F<{\displaystyle \frac{35}{36C}}$ and applying the discrete Gronwall’s inequality, we then obtain

$$\parallel u^n-U_F^n\parallel \le C({\tau }_C^4+{\tau }_F^2+h^4).$$

(85)

This completes the proof.    □

Through a similar proof of Theorem 4, we can also obtain the following results.

Theorem 6.

Suppose that the initial condition φ is satisfied the assumptions (a) and (b), and assume that the exact solution $u^n\in C^6(\Omega ),$ $\sigma ={\displaystyle \frac{{\tau }_C^2}{h_x^2{h}_y^2}}<{\displaystyle \frac{1}{9}}$, and ${\tau }_F<{\displaystyle \frac{35}{36C}}$. Then,

$$\parallel {\nabla }_h{e}_F^n\parallel \le C({\tau }_C^4+{\tau }_F^2+h^4),1\le n\le \mathcal{N}.$$

(86)

Furthermore,

$$\parallel u^n-U_F^n{\parallel }_1\le C({\tau }_C^4+{\tau }_F^2+h^4),1\le n\le \mathcal{N},$$

(87)

where the positive constant C only depends on the norms of $u(\mathbf{x},t),u_{tt}(\mathbf{x},t),\nabla u(\mathbf{x},t),$ and $\nabla u_{tt}(\mathbf{x},t)$.

Remark 3.

To construct the ADI scheme, we add the term ${\displaystyle \frac{i{\tau }^2}{4}}{\delta }_x^2{\delta }_y^2{\partial }_t{u}_{jk}^n$ to both sides of Equation (5). This modification imposes a mesh ratio condition, $\sigma ={\displaystyle \frac{{\tau }_C^2}{h_x^2{h}_y^2}}<{\displaystyle \frac{1}{9}}$, which is necessary for Theorems 3–6. Crucially, this constraint can be eliminated by adopting a temporal two-mesh scheme that does not rely on the ADI method.

5. Numerical Examples

In this section, we present several numerical tests to verify our theoretical analysis regarding the convergence order and discrete conservation laws. These experiments were performed using MATLAB R2019b on a computer equipped with an Intel Core i7 processor and 8 GB of RAM. To solve the resulting nonlinear system (14), an iterative algorithm was implemented as described below.

$$\left\{\begin{array}{c}\left(a\right)-i\left({\mathcal{A}}_x-{\displaystyle \frac{i{\tau }_C}{2}}{\delta }_x^2\right)U_C^{\ast ps}={\mathcal{A}}_y{\delta }_x^2{U}_C^{ps}+{\mathcal{A}}_x{\delta }_y^2{U}_C^{ps}+{\mathcal{A}}_x{\mathcal{A}}_y{F}_{C(\ell )}^{(p+1/2)s},\hfill \\ \left(b\right)\left({\mathcal{A}}_y-{\displaystyle \frac{i{\tau }_C}{2}}{\delta }_y^2\right)U_{C(\ell +1)}^{(p+1)s}=\left({\mathcal{A}}_y-{\displaystyle \frac{i{\tau }_C}{2}}{\delta }_y^2\right)U_C^{ps}+{\tau }_C{U}_C^{\ast ps},\ell =0,1,\cdots ,\hfill \end{array}\right.$$

(88)

where $F_{C(\ell )}^{(p+1/2)s}=\left\{{\displaystyle \frac{\beta }{4}}\left(|U_{C(\ell )}^{(p+1)s}{|}^2+{|U_C^{ps}|}^2\right)+{\displaystyle \frac{\nu }{2}}\right\}\left(U_{C(\ell )}^{(p+1)s}+U_C^{ps}\right)$ and $U_{C\left(0\right)}^{(p+1)s}=U_C^{ps}$, with $\parallel U_{C(\ell +1)}^{(p+1)s}-U_{C(\ell )}^{(p+1)s}{\parallel }_{\infty }\le {10}^{-6}$. The implementation of the iterative algorithm (88) is shown in Algorithm 1.

Let $e_{L_2}(h,\tau )$ and $e_{H_1}(h,\tau )$ denote the errors $\parallel e^N\parallel$ and $\parallel e^N{\parallel }_1$, respectively, with time step $\tau$ and mesh size h. The spatial convergence rates in the discrete $L_2$-norm and $H_1$-norm are computed by

$${\mathrm{rate}}_{L_2}^S={\displaystyle \frac{\log \left(e_{L_2}(h_1,\tau )/e_{L_2}(h_2,\tau )\right)}{\log \left(h_1/h_2\right)}},{\mathrm{rate}}_{H_1}^S={\displaystyle \frac{\log \left(e_{H_1}(h_1,\tau )/e_{H_1}(h_2,\tau )\right)}{\log \left(h_1/h_2\right)}},$$

respectively. The temporal convergence rates in the discrete $L_2$-norm and $H_1$-norm are computed by

$${\mathrm{rate}}_{L_2}^T={\displaystyle \frac{\log \left(e_{L_2}(h,{\tau }_1)/e_{L_2}(h,{\tau }_2)\right)}{\log \left({\tau }_1/{\tau }_2\right)}},{\mathrm{rate}}_{H_1}^T={\displaystyle \frac{\log \left(e_{H_1}(h,{\tau }_1)/e_{H_1}(h,{\tau }_2)\right)}{\log \left({\tau }_1/{\tau }_2\right)}},$$

respectively. Furthermore, to numerically investigate the conversation laws of our scheme, we consider the numerically invariant mass $\mathcal{Q}$ and energy $\mathcal{E}$, computed by

$$\begin{array}{c}{\mathcal{Q}}^n=\sum _{j=0}^{J_x}\sum _{k=0}^{J_y}{|U_{jk}^n|}^2{h}_x{h}_y,\hfill \\ {\mathcal{E}}^n=\sum _{j=0}^{J_x-1}\sum _{k=1}^{J_y-1}|{\partial }_x{U}_{jk}^n{|}^2{h}_x{h}_y+\sum _{j=1}^{J_x-1}\sum _{k=0}^{J_y-1}{|{\partial }_y{U}_{jk}^n|}^2{h}_x{h}_y\hfill \\ -\sum _{j=0}^{J_x}\sum _{k=0}^{J_y}{\nu }_{jk}|U_{jk}^n{|}^2{h}_x{h}_y-{\displaystyle \frac{\beta }{2}}\sum _{j=0}^{J_x}\sum _{k=0}^{J_y}{|U_{jk}^n|}^4{h}_x{h}_y\hfill \end{array}$$

Using the first two examples with exact solutions, we assessed the accuracy and convergence rate of the TTM compact ADI scheme (14) and (15) for solving the NLS problem (1). These results were then compared with those from the fully nonlinear (FN) compact ADI scheme (14) on the fine temporal mesh.

Algorithm 1 Implementation of the iterative algorithm (88)

Require:  positive constants $N,J_x,J_y,\beta ,\nu ,s$, temporal step size $\tau$, spatial step sizes $h_x,h_y$, maximum iteration limit $I{t}_{Max}$; Ensure:  Updates the numerical solutions: ${\mathbf{U}}_C^{ps}=\left(U_{C,jk}^{ps}\right)$ for $j=0,1,\cdots ,J_x;k=0,1,\cdots ,J_y$ and $p=1,\cdots ,N$; 1: Compute initial condition ${\mathbf{U}}_C^0=\left(U_{C,jk}^0\right)$ for $j=0,\cdots J_x$ and $k=0,\cdots J_y$; 2: Generate the corresponding matrices ${\mathit{A}}_x,{\mathit{A}}_y,{\mathit{B}}_x,{\mathit{B}}_y$; 3: for p from 0 to $N-1$ do 4:     Set provisional update guess: ${\mathbf{U}}_g={\mathbf{U}}_{current}$; iteration counter: $\ell =1$; 5:     while $\ell <I{t}_{Max}$ do 6:         Assemble the matrix ${\mathbf{F}}_{C(\ell )}^{(p+1/2)s}$ with entries dependent on ${\mathbf{U}}_C^{ps}=\left(U_{C,jk}^{ps}\right)$ and ${\mathbf{U}}_g=\left(U_{g,jk}\right)$ for $j=0,1,\cdots ,J_x$ and $k=0,1,\cdots ,J_y$; 7:         Assemble the matrix ${\mathbf{G}}_{x(\ell )}^{ps}$ with entries dependent on the boundary conditions $U_{C,jk}^{ps}$ and $U_{g,jk}$ for $j=0,J_x$ and $k=0,1,\cdots ,J_y$; 8:         Assemble the coefficient matrix and the right-hand side matrix, cf. (88(a)); 9:         Get the intermediate solution ${\mathbf{U}}_C^{\ast ps}$ from $$\begin{array}{cc}\hfill -i\left({\mathit{A}}_x-6i{\displaystyle \frac{\tau }{h_x^2}}{\mathit{B}}_x\right){\mathbf{U}}_C^{\ast ps}=& {\displaystyle \frac{1}{2}}\left({\displaystyle \frac{1}{h_x}}{\mathit{B}}_x{\mathbf{U}}_C^{ps}{\mathit{A}}_y+{\displaystyle \frac{1}{h_y}}{\mathit{A}}_x{\mathbf{U}}_C^{ps}{\mathit{B}}_y\right)\hfill \\ & +{\displaystyle \frac{1}{12}}{\mathit{A}}_x{\mathbf{F}}_{C(\ell )}^{(p+1/2)s}{\mathit{A}}_y+{\mathbf{G}}_{x(\ell )}^{ps}.\hfill \end{array}$$ 10:         Assemble the matrix ${\mathbf{G}}_{y(\ell )}^{ps}$ with entries dependent on the boundary conditions $U_{C,jk}^{ps}$ and ${\mathbf{U}}_{C,jk}^{\ast ps}$ for $k=0,J_y$ and $j=0,1,\cdots ,J_x$; 11:         Assemble the coefficient matrix and the right-hand side matrix, cf. (88(b)); 12:         Get the new proposed update guess ${\mathbf{U}}_{g-new}$ from $${\mathbf{U}}_{g-new}\left({\mathit{A}}_y-6i{\displaystyle \frac{\tau }{h_y^2}}{\mathit{B}}_y\right)={\mathbf{U}}_C^{ps}\left({\mathit{A}}_y-6i{\displaystyle \frac{\tau }{h_y^2}}{\mathit{B}}_y\right)+12\tau {\mathbf{U}}_C^{\ast ps}+{\mathbf{G}}_{y(\ell )}^{ps}.$$ 13:         if  $\parallel {\mathbf{U}}_{g-new}-{\mathbf{U}}_g{\parallel }_{\infty }\le {10}^{-6}$ then 14:            Store converged solution: ${\mathbf{U}}_C^{(p+1)s}={\mathbf{U}}_{g-new}$; Set $p=p+1$; 15:            Go to Step 4; 16:         else 17:            Update guess for next iteration: ${\mathbf{U}}_g={\mathbf{U}}_{g-new}$; Set $\ell =\ell +1$; 18:            Go to Step 5; 19:         end if 20:     end while 21: end for

Example 1.

Taking the coefficients in (1) as $\beta =-1$, with the potential function given as $\nu (x,y)=1+{sin}^2\left(x\right){sin}^2\left(y\right)$ in the domain $\Omega =[0,2\pi )\times [0,2\pi )$, the exact solution is given by

$$u(x,y,t)=sin\left(x\right)sin\left(y\right)exp(-it),(x,y)\in \Omega ,t\in [0,1].$$

The initial condition and the Dirichlet boundary condition can be immediately taken as $\psi =sin\left(x\right)sin\left(y\right)$ and $\phi =0$, respectively.

To validate the theoretical second-order temporal convergence rate $\mathcal{O}\left({\tau }^2\right)$, we conducted experiments with a fixed spatial mesh size, $h={\displaystyle \frac{\pi }{256}}$. The temporal step sizes were varied following the relation ${\tau }_F={\tau }_C^2$. At the final time $T=1.0$,

Table 1. Temporal errors and convergence rates in computing Example 1 at time $T=1.0$ with different time steps under mesh size $h={\displaystyle \frac{\pi }{256}}$.

$\mathrm{TTM}$	${\tau }_C$	${\tau }_F$	$e_{L_2}(h,\tau )$	${\mathrm{rate}}_{L_2}^T$	$e_{H_1}(h,\tau )$	${\mathrm{rate}}_{H_1}^T$	$\mathrm{CPU}\left(s\right)$
	$0.1$	$0.01$	$2.04691627877232\times {10}^{-5}$		$4.80052533295909\times {10}^{-5}$		10.17
	$0.05$	$0.0025$	$1.31374279417345\times {10}^{-6}$	1.9809	$3.07223340113465\times {10}^{-6}$	1.9829	33.76
	$0.025$	$0.000625$	$8.22001605493149\times {10}^{-8}$	1.9992	$1.92517116674512\times {10}^{-7}$	1.9981	121.91
	$0.02$	$0.0004$	$3.34072217225511\times {10}^{-8}$	2.0175	$7.8538497358386\times {10}^{-8}$	2.0090	208.73
$\mathrm{FN}$	${\tau }_C$	${\tau }_F$	$e_{L_2}(h,\tau )$	${\mathrm{rate}}_{L_2}^T$	$e_{H_1}(h,\tau )$	${\mathrm{rate}}_{H_1}^T$	$\mathrm{CPU}\left(s\right)$
	$0.1$	$0.01$	$5.23590848670945\times {10}^{-5}$		$9.06882158527494\times {10}^{-5}$		20.75
	$0.05$	$0.0025$	$3.27146472201406\times {10}^{-6}$	2.0002	$5.66631976433781\times {10}^{-6}$	2.0002	63.38
	$0.025$	$0.000625$	$2.03930530805114\times {10}^{-7}$	2.0019	$3.53216564364463\times {10}^{-7}$	2.0019	322.06
	$0.02$	$0.0004$	$8.31798410070326\times {10}^{-8}$	2.0094	$1.44071108372991\times {10}^{-7}$	2.0094	395.41

reports the observed errors, estimated convergence orders, and execution times (CPU) for both the TTM scheme and the FN scheme. Similarly, to confirm the fourth-order spatial convergence $\mathcal{O}\left(h^4\right)$, another set of tests was performed using a very small fixed time step (${\tau }_C^2={\tau }_F=0.000016$) while systematically refining the spatial grid. These results are summarized in

Table 2. Spatial errors and convergence rates in computing Example 1 at time $T=1.0$ with different mesh sizes under time step ${\tau }_C^2={\tau }_F=0.000016$.

$\mathrm{TTM}$	h	$e_{L_2}(h,\tau )$	${\mathrm{rate}}_{L_2}^s$	$e_{H_1}(h,\tau )$	${\mathrm{rate}}_{H_1}^s$	$\mathrm{CPU}\left(s\right)$
	${\displaystyle \frac{\pi }{4}}$	$1.019422047375990\times {10}^{-2}$		$1.735798393573050\times {10}^{-2}$		4.09
	${\displaystyle \frac{\pi }{8}}$	$6.263668308446760\times {10}^{-4}$	4.0246	$8.829806045219760\times {10}^{-4}$	4.2971	7.12
	${\displaystyle \frac{\pi }{16}}$	$3.89717441058798\times {10}^{-5}$	4.0065	$4.7704910561724\times {10}^{-5}$	4.2102	14.72
	${\displaystyle \frac{\pi }{32}}$	$2.43290094091532\times {10}^{-6}$	4.0017	$2.88797385411899\times {10}^{-6}$	4.0460	38.09
$\mathrm{FN}$	h	$e_{L_2}(h,\tau )$	${\mathrm{rate}}_{L_2}^S$	$e_{H_1}(h,\tau )$	${\mathrm{rate}}_{H_1}^S$	$\mathrm{CPU}\left(s\right)$
	${\displaystyle \frac{\pi }{4}}$	$1.019422040479520\times {10}^{-2}$		$1.735798381830240\times {10}^{-2}$		24.16
	${\displaystyle \frac{\pi }{8}}$	$6.263667610924430\times {10}^{-4}$	4.0248	$8.829805061830120\times {10}^{-4}$	4.2971	29.74
	${\displaystyle \frac{\pi }{16}}$	$3.89716742746788\times {10}^{-5}$	4.0066	$4.77048250772759\times {10}^{-5}$	4.2102	41.62
	${\displaystyle \frac{\pi }{32}}$	$2.43283109355201\times {10}^{-6}$	4.0018	$2.88788385855894\times {10}^{-6}$	4.0461	73.40

.

From Table 1 and Table 2, one can find that

(i)

The errors produced by both methods exhibit similar magnitudes when assessed under discrete norms. Specifically, under both the discrete $L_2$-norm and $H_1$-norm, the observed convergence rates are approximately second-order in time and fourth-order in space. These findings validate the theoretical accuracy established in Theorems 5 and 6.

(ii)

As shown by the CPU time comparison, the proposed TTM scheme requires less computation time than the FN scheme. This demonstrates that the TTM scheme is computationally more efficient than the fully nonlinear implicit scheme.

Moreover, Figure 1 illustrates the evolution of the two invariants, the mass (${\mathcal{Q}}^n$) and energy (${\mathcal{E}}^n$), which appear to remain constant over time. This figure clearly shows that the proposed TTM method preserves the discrete analogues of the mass and energy conservation laws.

Example 2

(Ref. [31]). Consider Equation (1) with $\beta =-2$ and potential function $\nu =0$, which generates a progressive plane wave solution:

$$u(x,y,t)=Aexp\left(i(k_{1}x+k_{2}y-\omega t)\right),\omega =k_1^2+k_2^2-\beta {|A|}^2,(x,y)\in [0,2\pi )\times [0,2\pi ).$$

The initial data is evaluated by taking $t=0$ from the exact solution and the $(2\pi ,2\pi )$-periodic condition is used.

In the first case, we examine the numerical accuracy by setting $A=1$ and $k_1=k_2=1$. Similarly to Example 1,

Table 3. Temporal errors and convergence rates in computing Example 2 at time $T=1.0$ with different time steps under mesh size $h={\displaystyle \frac{\pi }{256}}$.

$\mathrm{TTM}$	${\tau }_C$	${\tau }_F$	$e_{L_2}(h,\tau )$	${\mathrm{rate}}_{L_2}^T$	$e_{H_1}(h,\tau )$	${\mathrm{rate}}_{H_1}^T$	$\mathrm{CPU}\left(s\right)$
	$0.1$	$0.01$	$1.765857913021030\times {10}^{-2}$		$3.056554834501620\times {10}^{-2}$		13.41
	$0.05$	$0.0025$	$1.108781959642190\times {10}^{-3}$	1.9967	$1.919210392955970\times {10}^{-3}$	1.9967	37.00
	$0.025$	$0.000625$	$6.93878915803477\times {10}^{-5}$	1.9991	$1.201047343059710\times {10}^{-4}$	1.9991	126.96
	$0.02$	$0.0004$	$2.84251749447057\times {10}^{-5}$	1.9997	$4.92016403237431\times {10}^{-5}$	1.9997	234.72
$\mathrm{FN}$	${\tau }_C$	${\tau }_F$	$e_{L_2}(h,\tau )$	${\mathrm{rate}}_{L_2}^T$	$e_{H_1}(h,\tau )$	${\mathrm{rate}}_{H_1}^T$	$\mathrm{CPU}\left(s\right)$
	$0.1$	$0.01$	$2.727462315909150\times {10}^{-3}$		$4.721012979663230\times {10}^{-3}$		34.97
	$0.05$	$0.0025$	$1.705098091257620\times {10}^{-4}$	1.9998	$2.951384579526420\times {10}^{-4}$	1.9998	93.04
	$0.025$	$0.000625$	$1.06575920739157\times {10}^{-5}$	2.0000	$1.84474154677304\times {10}^{-5}$	2.0000	376.31
	$0.02$	$0.0004$	$4.37570436465692\times {10}^{-6}$	1.9947	$7.57398442503598\times {10}^{-6}$	1.9947	434.23

and

Table 4. Spatial errors and convergence rates in computing Example 2 at time $T=1.0$ with different mesh sizes under time step ${\tau }_C^2={\tau }_F=0.000016$.

$\mathrm{TTM}$	h	$e_{L_2}(h,\tau )$	${\mathrm{rate}}_{L_2}^s$	$e_{H_1}(h,\tau )$	${\mathrm{rate}}_{H_1}^s$	$\mathrm{CPU}\left(s\right)$
	${\displaystyle \frac{\pi }{4}}$	$2.293694969988050\times {10}^{-2}$		$3.760716300166500\times {10}^{-2}$		4.50
	${\displaystyle \frac{\pi }{8}}$	$1.330985616172760\times {10}^{-3}$	4.1071	$1.848653917863150\times {10}^{-3}$	4.3465	8.24
	${\displaystyle \frac{\pi }{16}}$	$8.03365561602388\times {10}^{-5}$	4.0503	$9.78423013132799\times {10}^{-5}$	4.2399	17.53
	${\displaystyle \frac{\pi }{32}}$	$4.89991801158601\times {10}^{-6}$	4.0352	$5.46940621343395\times {10}^{-6}$	4.1610	46.94
$\mathrm{FN}$	h	$e_{L_2}(h,\tau )$	${\mathrm{rate}}_{L_2}^S$	$e_{H_1}(h,\tau )$	${\mathrm{rate}}_{H_1}^S$	$\mathrm{CPU}\left(s\right)$
	${\displaystyle \frac{\pi }{4}}$	$2.293698233680740\times {10}^{-2}$		$3.760721651280360\times {10}^{-2}$		23.94
	${\displaystyle \frac{\pi }{8}}$	$1.331016520946440\times {10}^{-3}$	4.1071	$1.848696842578590\times {10}^{-3}$	4.3464	31.19
	${\displaystyle \frac{\pi }{16}}$	$8.0366554724327\times {10}^{-5}$	4.0498	$9.78788367102812\times {10}^{-5}$	4.2394	47.48
	${\displaystyle \frac{\pi }{32}}$	$4.92942819847463\times {10}^{-6}$	4.0271	$5.50234618081315\times {10}^{-6}$	4.1529	89.57

present the errors, convergence orders, and CPU times for both methods applied for temporal and spatial discretization. The data in Table 3 and Table 4 show that both methods exhibit nearly second-order convergence in time and nearly fourth-order convergence in space. However, the proposed TTM scheme requires less computational time than the FN scheme. These numerical results are consistent with the error estimates provided in Theorems 5 and 6.

In the second case, we examine the simulation effect of the TTM compact ADI method on long-term behavior in capturing high-frequency waves by letting $A=1$ and $k_1=k_2=4$ at $T=10$ and $A=1$ and $k_1=k_2=8$ at $t=4$, respectively. Given a spatial step size $h=\pi /30$ and temporal step sizes $20{\tau }_C={\tau }_F=0.00005$, we compute the numerical approximations for the wave solution $U^n(x,\pi ,t)$. For the parameters $A=1$ and $k_1=k_2=4$, Figure 2 displays the real parts of both the numerical and exact solutions at times $t=1.0,4.0,7.0$ and $t=10.0$. Similarly, Figure 3 shows the results for the parameters $A=1$ and $k_1=k_2=8$ at times $t=2.0$ and $t=4.0$. Invariants ${\mathcal{Q}}^n$ and ${\mathcal{E}}^n$ for both wave types are tracked in Figure 4 and Figure 5, respectively. These results demonstrate that the proposed method reliably preserves discrete conservation laws and maintains accuracy over extended simulations.

In the next two examples, we aim to investigate the simulation performance of the TTM compact ADI method in solving problems lacking exact solutions.

Example 3

(Ref. [25]). Consider the Gross–Pitaevskii equation

$$i{u}_t=-{\displaystyle \frac{1}{2}}\Delta u+\nu (x,y)u+2{|u|}^{2}u,(x,y)\in \Omega =[-4,4]\times [-4,4],$$

(89)

with trapping potential $\nu (x,y)=-{\displaystyle \frac{x^2+2y^2}{2}}$, the initial condition

$$u(x,y,0)={\displaystyle \frac{\sqrt[4]{2}}{\sqrt{2\pi }}}exp\left(-{\displaystyle \frac{x^2+2y^2}{2}}\right),$$

and homogeneous boundary conditions on $\partial \Omega$.

The numerical experiment is performed from $t=0$ to $t=40$ with $5{\tau }_C={\tau }_F=0.0004$ and $h=0.1$. Figure 6 exhibits the contour plots of the wave solution for Example 3 at different times, and the numerical residuals of mass and energy are displayed in Figure 7. From these figures, we observe that the mass is preserved well, while the energy fluctuates quasi-periodically within a small range throughout the simulation. These observations are consistent with the results reported in [25].

Example 4

(Refs. [30,31,32]). Consider the focusing NLS equation

$$i{u}_t+\Delta u+\beta {|u|}^{2}u=0,$$

(90)

with a singular solution (when $\beta =1$). Here, we consider the initial condition

$$u(x,t)=(1+sin(x\left)\right)(2+sin(y\left)\right),$$

and the $(2\pi ,2\pi )$-periodic boundary condition in the domain $\Omega =[0,2\pi )\times [0,2\pi )$.

The focusing NLS Equation (90), widely studied in the literature, exhibits a blow-up solution at finite time $t=0.108$. To investigate this phenomenon, we apply the proposed TTM method to compute its numerical solution from $t=0$ to $t=0.15$, using parameters $20{\tau }_C={\tau }_F=0.00001$ and $h=\pi /140$. Figure 8 presents the profiles and contour plots of the modulus of numerical solutions for Example 4 at times $t=0.0,0.104,0.108,$ and $0.12$. The corresponding numerical mass and energy conservation is displayed in Figure 9.

These figures reveal the following phenomena:

(i)

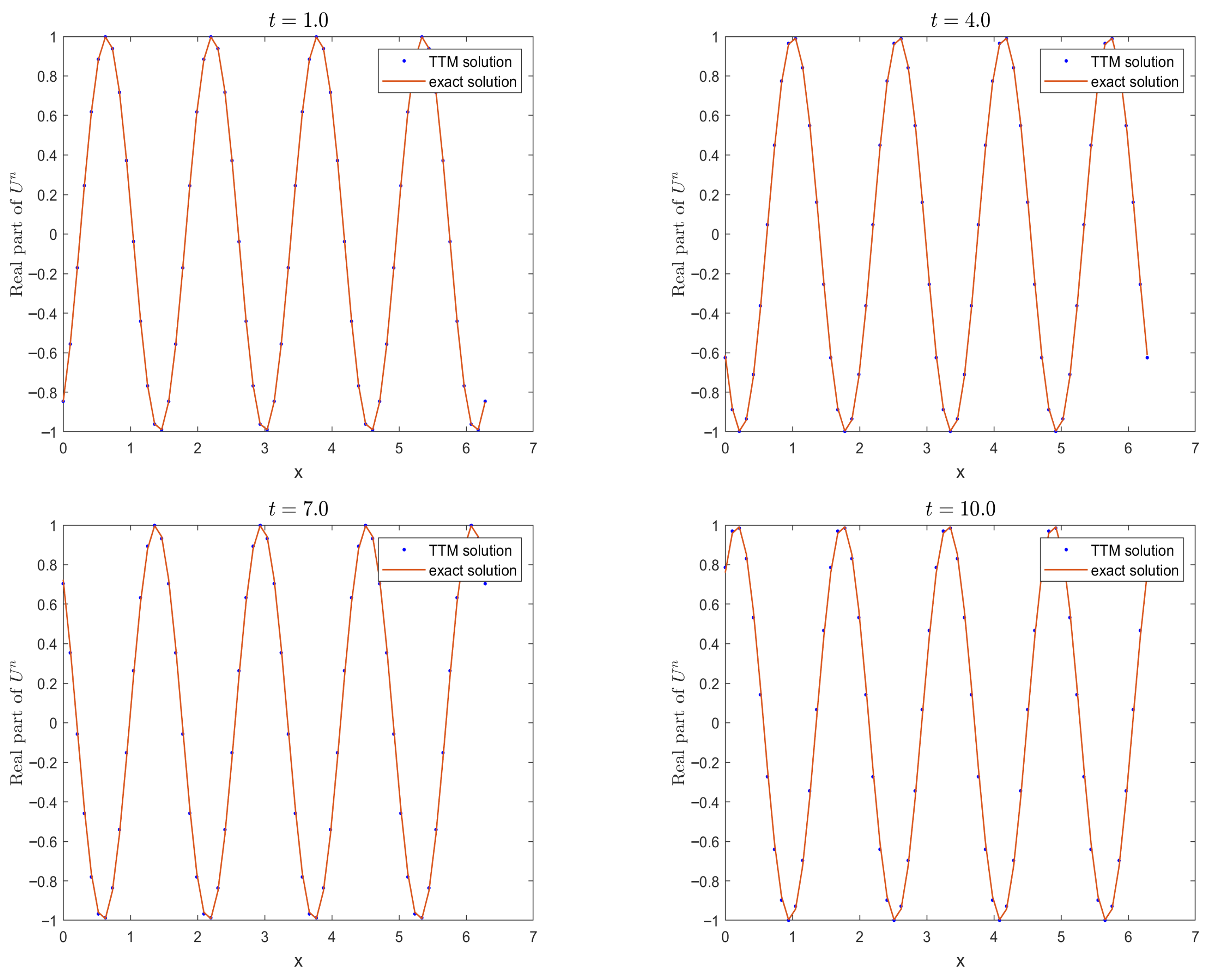
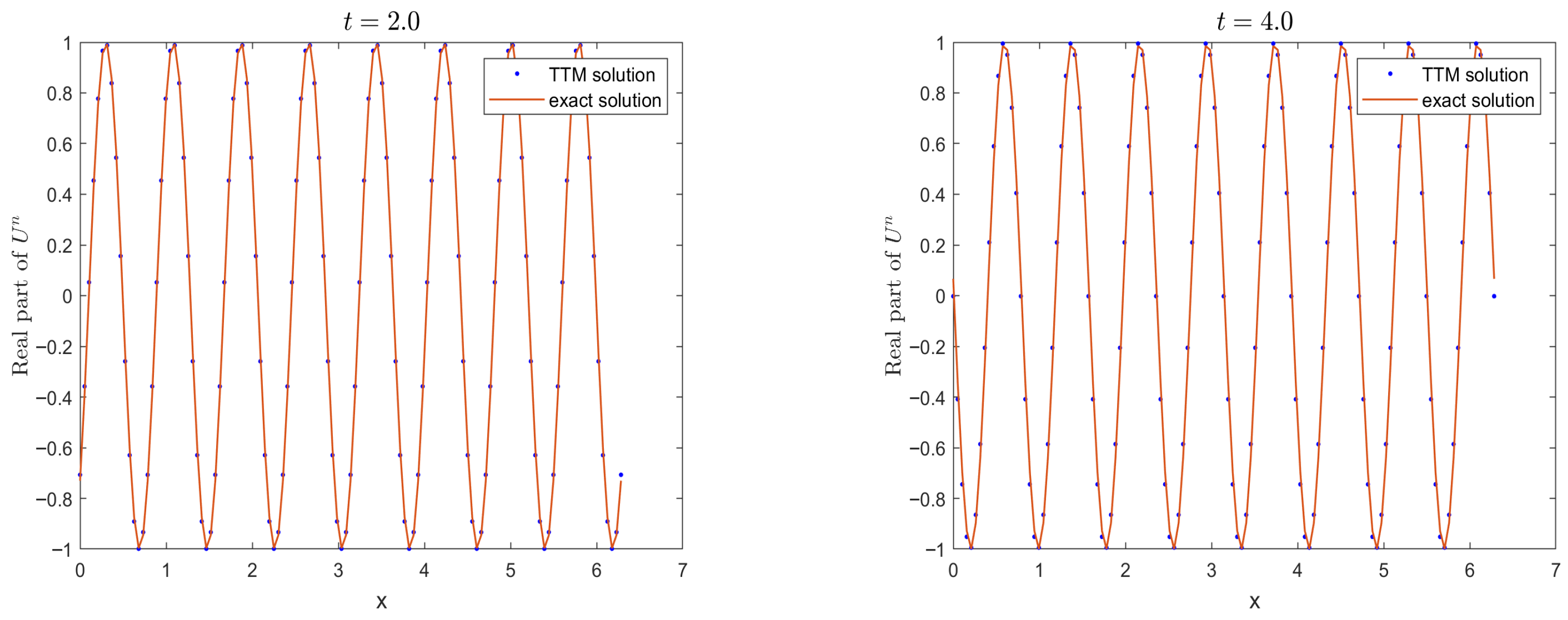
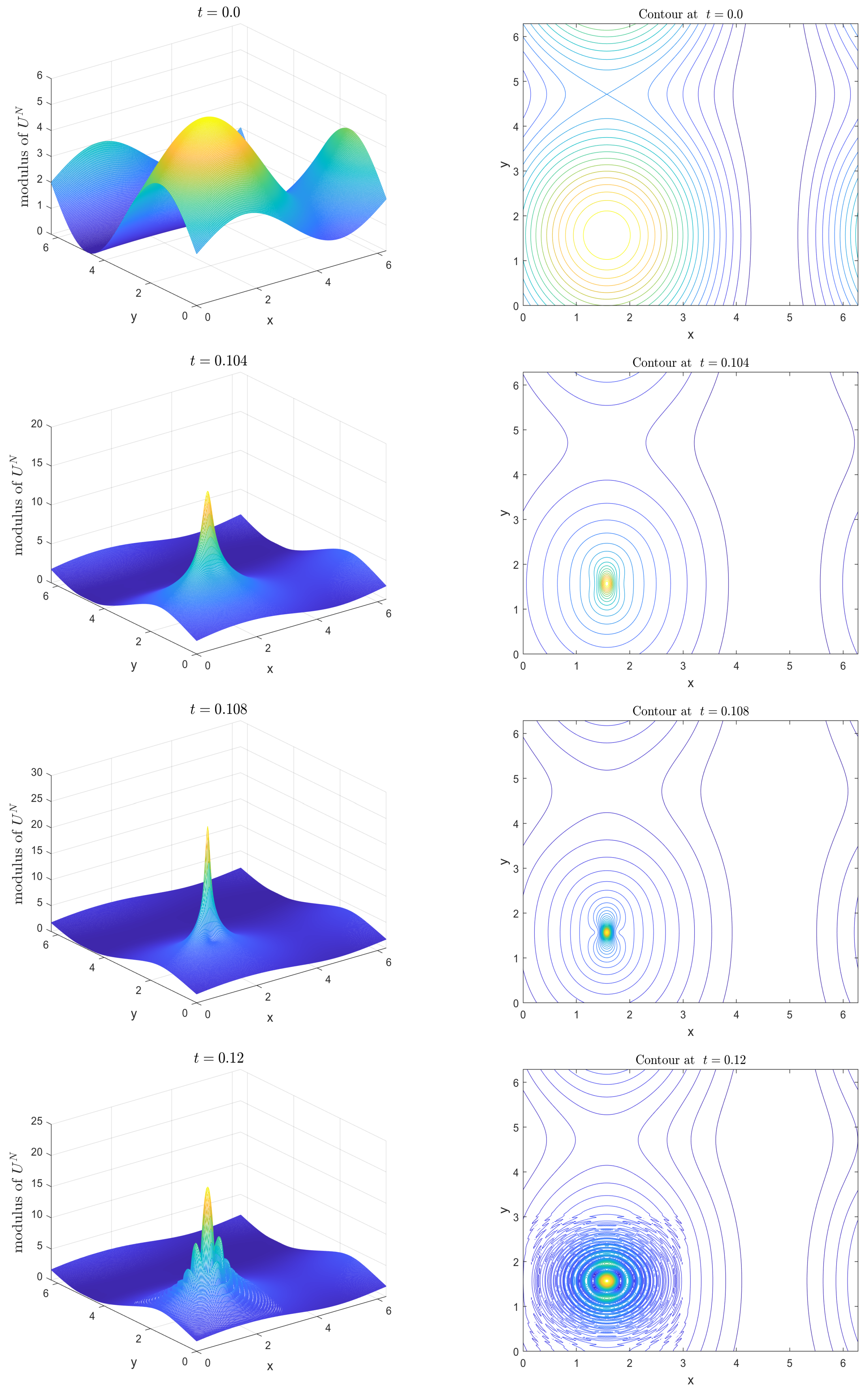
Strong singular solutions emerge at $t=0.104$ and $t=0.108$, while multiple waveforms appear at $t=0.12$.

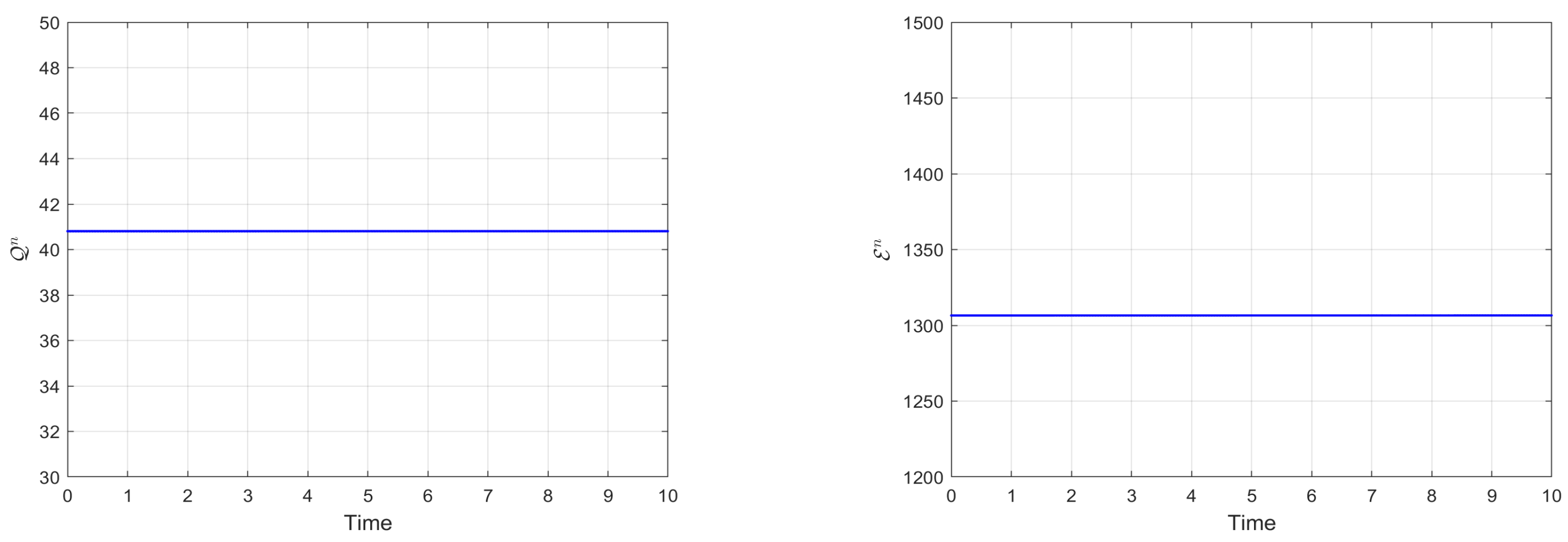
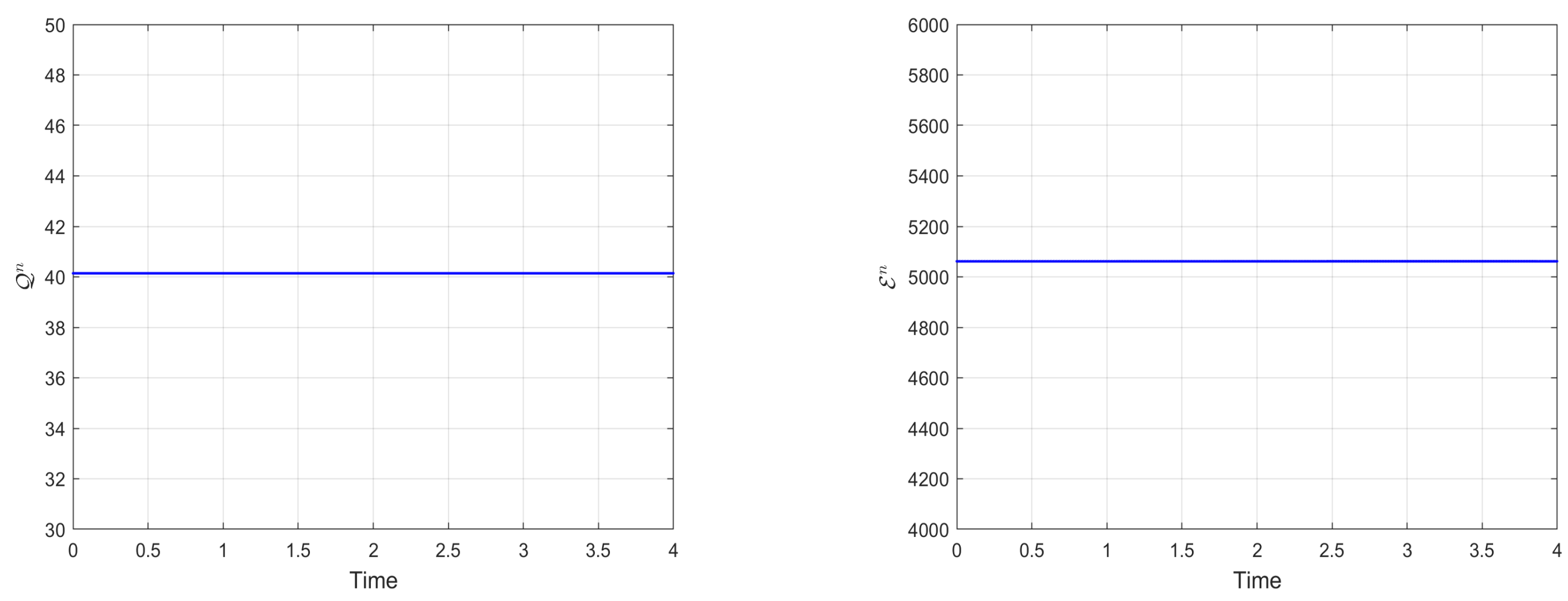
(ii)

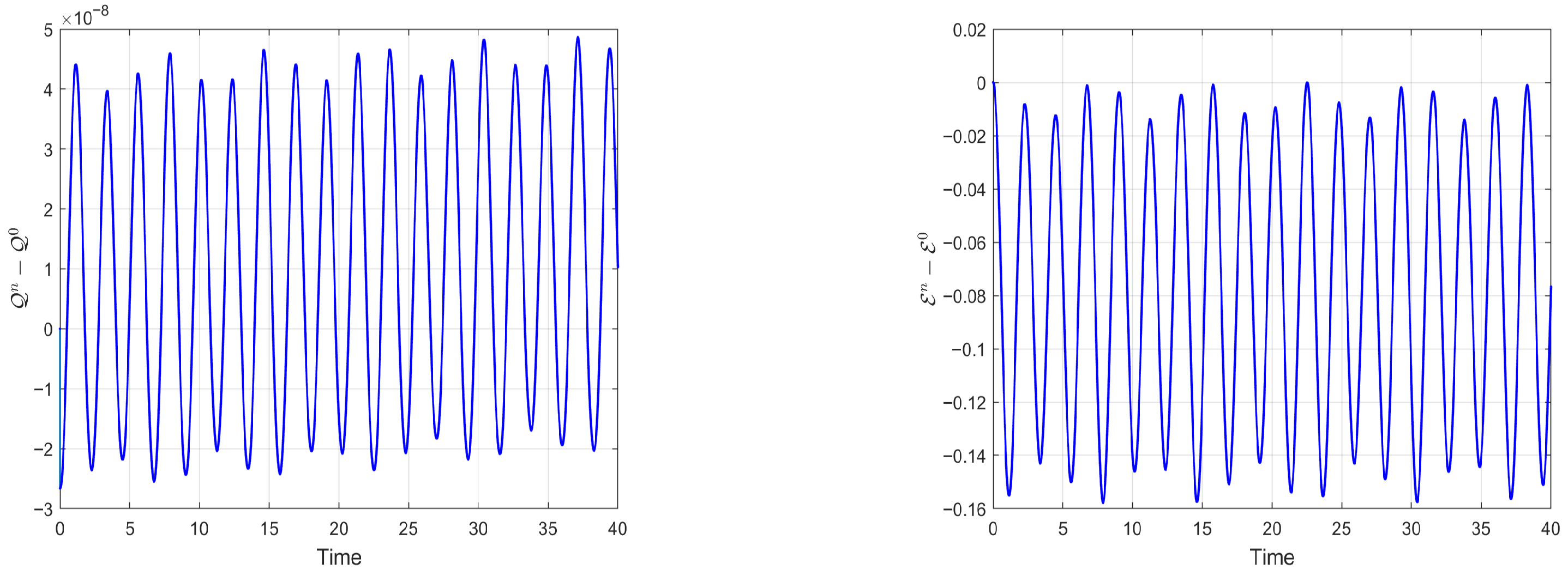
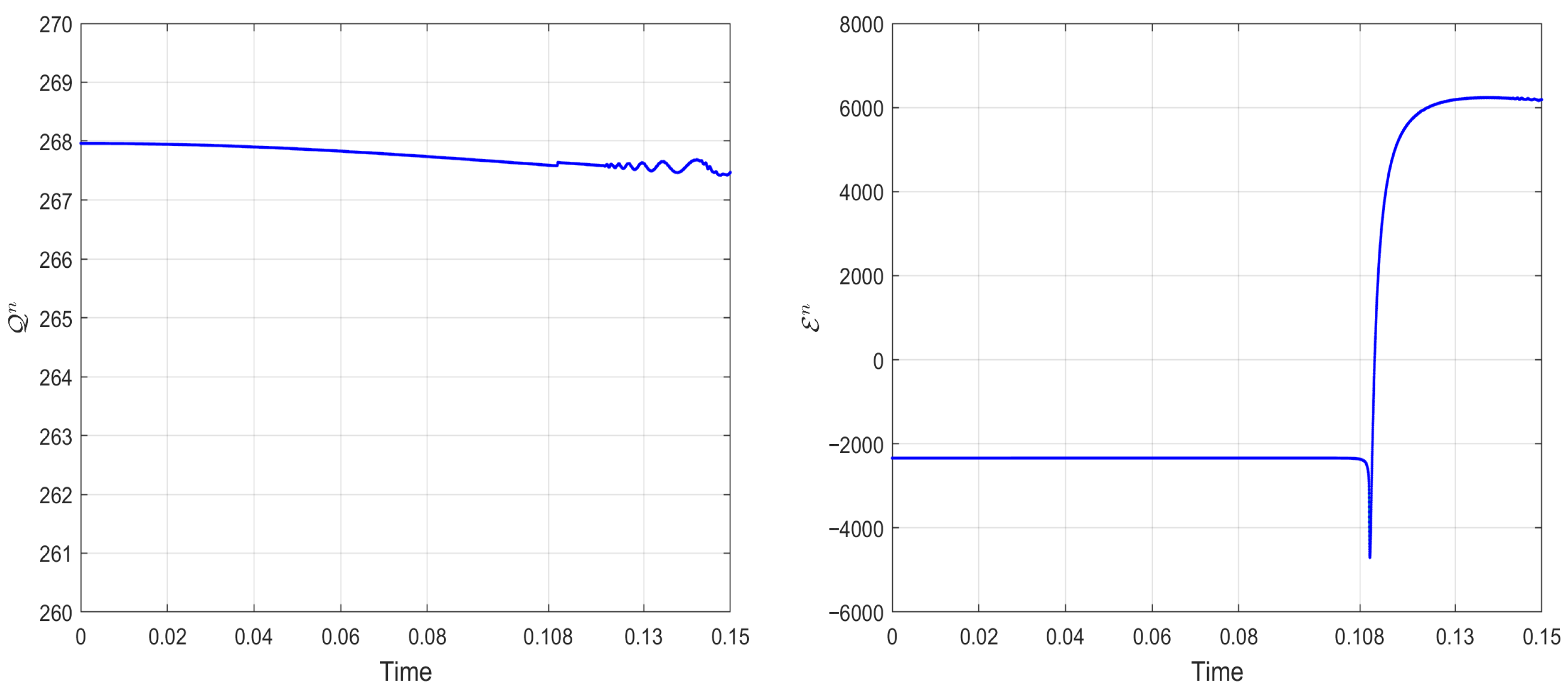
Until $t=0.108$, the numerical mass ${\mathcal{Q}}^n$ and energy ${\mathcal{E}}^n$ showed minimal variation. Beyond $t=0.108$, however, conservation laws were no longer maintained for either quantity.

The above two phenomena may result from the emergence of blow-up solutions after a finite time. Specifically, the solution starts to blow up at $t=0.018$, and the number of waves increases as time progresses. These observations align well with findings reported in [30,31,32].

6. Conclusions

This article proposes a temporal two-mesh scheme based on the fourth-order compact ADI method to efficiently solve the two-dimensional NLS equation. Under this framework, the temporal two-mesh technique treats the nonlinearity, whereas the ADI method resolves the challenges inherent in multiple dimensions. We derive detailed theoretical analyses encompassing discrete conservation laws and optimal error estimates in both the discrete $L_2$-norm and $H_1$-norm. The theoretical analyses, including discrete conservation laws and optimal error estimates in both the discrete $L_2$-norm and $H_1$-norm, are given in detail. To confirm our theoretical results and illustrate the algorithm’s computational efficiency, we conduct numerical experiments for both focusing and defocusing models. The numerical results demonstrate that the proposed TTM compact ADI method enhances computational efficiency while maintaining accuracy comparable to the fully nonlinear compact ADI method. Future work will extend this TTM compact ADI framework to three-dimensional fractional differential equations and coupled NLS systems.