Finite Time Stability and Optimal Control for Stochastic Dynamical Systems

Abstract

In real-world applications, finite time convergence to a desired Lyapunov stable equilibrium is often necessary. This notion of stability is known as finite time stability and refers to systems in which the state trajectory reaches an equilibrium in finite time. This paper explores the notion of finite time stability in probability within the context of nonlinear stochastic dynamical systems. Specifically, we introduce sufficient conditions based on Lyapunov methods, utilizing Lyapunov functions that satisfy scalar differential inequalities involving fractional powers for guaranteeing finite time stability in probability. Then, we address the finite time optimal control problem by developing a framework for designing optimal feedback control laws that achieve finite time stochastic stability of the closed-loop system using a Lyapunov function that also serves as the solution to the steady-state stochastic Hamilton–Jacobi–Bellman equation.

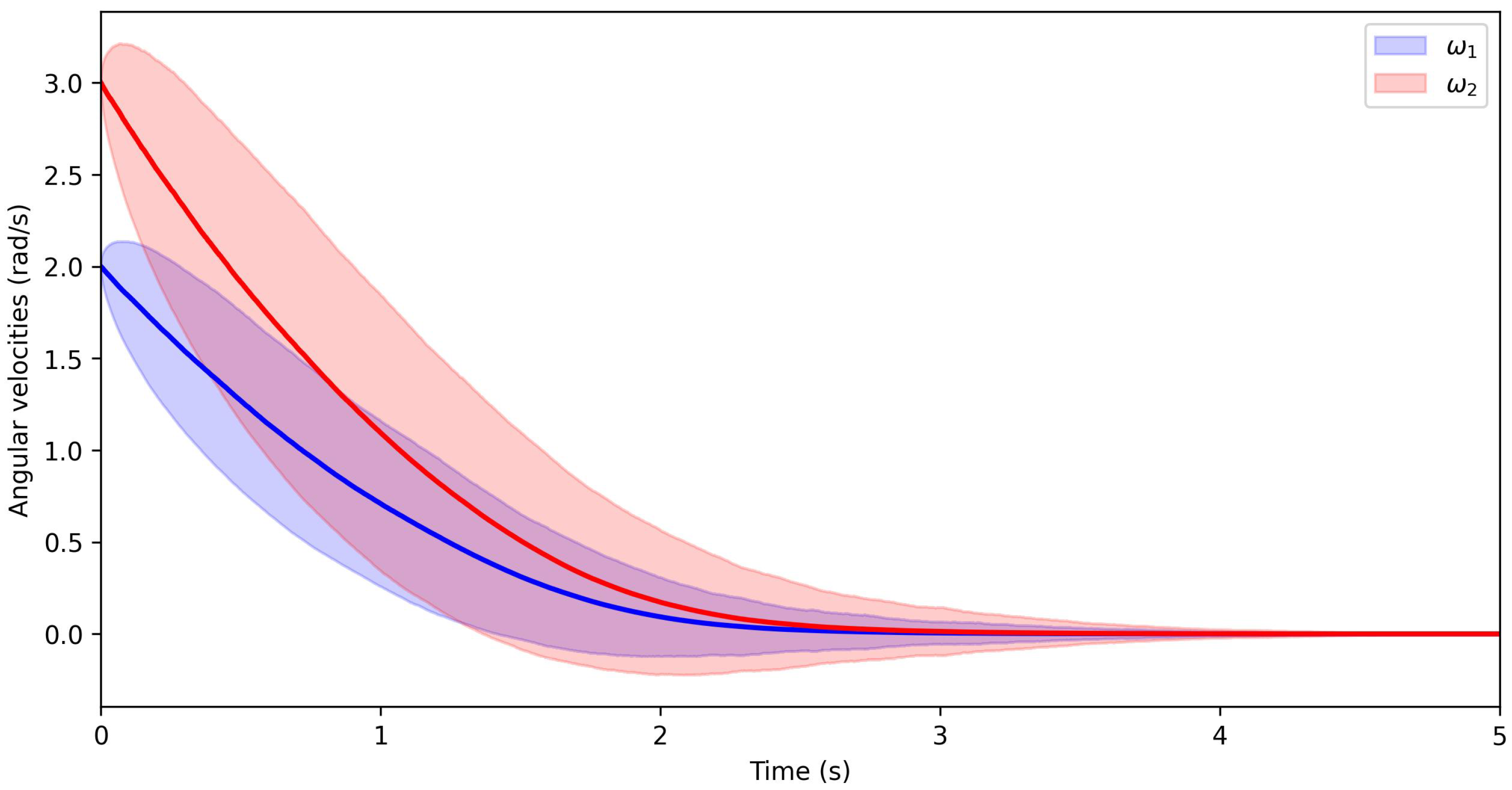
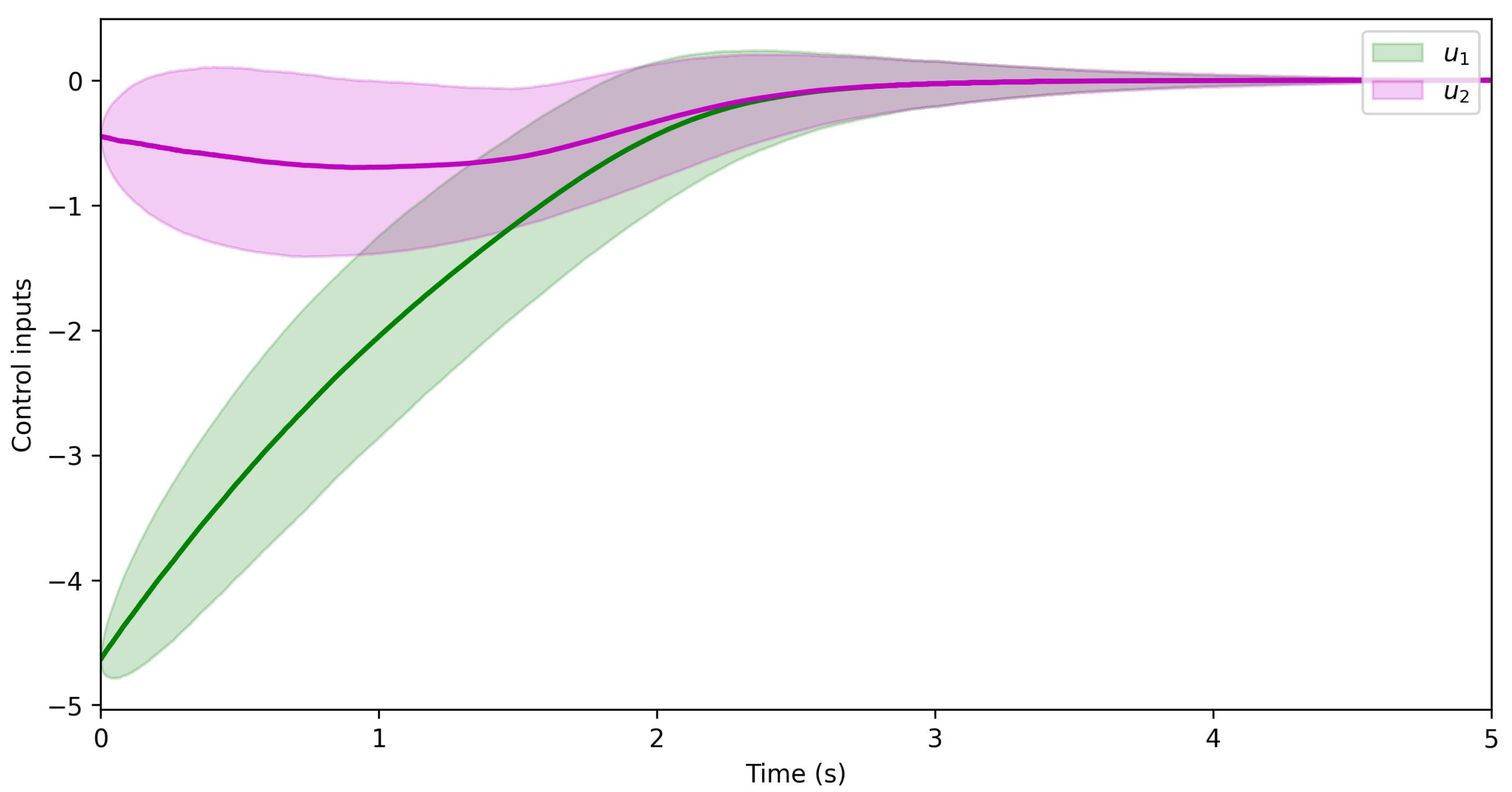
1. Introduction

The classical notions of asymptotic and exponential stability in dynamical systems theory involve system trajectories approaching a Lyapunov stable equilibrium state over an infinite time horizon. However, in many engineering and scientific applications, it is necessary for the system to reach a stable equilibrium within finite time rather than asymptotically. Achieving finite time stability in deterministic systems requires the closed-loop system dynamics to be non-Lipschitz, which can result in nonuniqueness of solutions in backward time. Nonetheless, it is possible to preserve forward time uniqueness of solutions for finite time convergent systems.

Sufficient conditions for forward time uniqueness in deterministic systems without assumption of the Lipschitz continuity of the system dynamics are given in [1]. For stochastic systems, refs. [2,3,4] provide criteria that guarantee the forward time uniqueness of solutions without requiring Lipschitz continuity. These works also show that if the dynamics are continuous and forward time uniqueness holds, then the system trajectories are almost surely continuous with respect to the system initial conditions, even in the absence of the Lipschitz continuity of the drift and diffusion functions characterizing the stochastic dynamical system.

The concept of finite time stability, that is, convergence of the system trajectories to a Lyapunov stable equilibrium in finite time, was first introduced by Roxin [5] and further developed in [6,7] for time-invariant deterministic systems, as well as in [8,9,10] for time-varying deterministic systems. In particular, Lyapunov and converse Lyapunov theorems for finite time stability were established using Lyapunov functions that satisfy scalar differential inequalities with fractional powers, and it was shown that the regularity of the Lyapunov function depends on the properties of the settling time function, which characterizes the finite time convergence behavior of the system.

Even though extensions of finite time stability for stochastic systems have been addressed in the literature [11,12,13,14], several of these results contain errors. Specifically, as pointed out in [15], several definitions and the main result in [11] are incorrect. Moreover, the authors in [13] used the results of [11] to develop partial-state stabilization in finite time, propagating the errors of [11] in their work, whereas the proof of the main theorem of [12] used Jensen’s inequality incorrectly, thus invalidating their result. And finally, ref. [14] failed to provide a bound on the expectation of the settling time function, which is crucial in providing a complete theory for finite time stability and stabilization for stochastic dynamical systems.

In this paper, we correct these oversights to present a self-contained theory for finite time stability in probability and build upon the framework established in [16,17] to address the problem of optimal finite time stabilization for stochastic nonlinear systems. Specifically, we ensure finite time stability in probability for the closed-loop system using a Lyapunov function that satisfies a scalar differential inequality that involves fractional powers. This Lyapunov function is shown to correspond to the steady-state solution of the stochastic Hamilton–Jacobi–Bellman equation, ensuring both finite time stability in probability and optimal performance. Finally, we also develop connections of our approach to inverse optimal control [18,19] by constructing a family of finite time stabilizing stochastic feedback laws that minimize a derived cost functional.

2. Mathematical Preliminaries

We will start by reviewing some basic results on nonlinear stochastic dynamical systems [20,21,22,23]. First, however, we require some notations and definitions. The notation, definitions, and mathematical preliminaries in this section are adopted from [17]. A probability space is a mathematical construct that provides a model for a random experiment and consists of the triple $(\Omega ,\mathcal{F},\mathbb{P})$. The sample space $\Omega$ is the set of all possible outcomes of the experiment. The event space $\mathcal{F}$ is a collection of subsets of the sample space, where each subset represents an event. The event space $\mathcal{F}$ has the algebraic structure of a σ-algebra. The pair $(\Omega ,\mathcal{F})$ is a measurable space, and the function $\mathbb{P}$ defines a probability measure on the $\sigma$-algebra $\mathcal{F}$, assigning a probability to each event in the event space $\mathcal{F}$. A complete probability space is one in which the $\sigma$-algebra $\mathcal{F}$ includes all the subsets of sets with a probability measure zero.

A Borel set is a set in a topological space that is derived from open (or closed) sets through the repeated operation of countable unions, countable intersections, and relative complements. The Borel σ-algebra on $\mathcal{A}$, denoted by $\mathfrak{B}\left(\mathcal{A}\right)$, is the smallest $\sigma$-algebra containing all the open sets in $\mathcal{A}$. An ${\mathbb{R}}^n$-valued random vector x is a measurable function $x:\Omega \to {\mathbb{R}}^n$, that is, for every Borel set $B\in \mathfrak{B}\left({\mathbb{R}}^n\right)$, its preimage is $x^{-1}\left(B\right)=\left\{\omega \in \Omega :x\left(\omega \right)\in B\right\}\in \mathcal{F}$. A random variable is a scalar random vector. In general, given a random vector x and a $\sigma$-algebra $\mathcal{E}$, we say that x is $\mathcal{E}$-measurable if $x^{-1}\left(B\right)\in \mathcal{E}$ for all $B\in \mathfrak{B}\left({\mathbb{R}}^n\right)$. Given an integrable random vector x and a sub-$\sigma$-algebra $\mathcal{E}\subseteq \mathcal{F}$, $\mathbb{E}\left[x\right]$ and $\mathbb{E}\left[x\right|\mathcal{E}]$ denote, respectively, the expectation of the random vector x and the conditional expectation of x given $\mathcal{E}$ under the probability measure $\mathbb{P}$.

A continuous-time stochastic process $x\left(t\right):t\ge 0$ is a collection of random vectors defined on the probability space $(\Omega ,\mathcal{F},\mathbb{P})$, and it is indexed by the set of nonnegative real numbers ${\overline{\mathbb{R}}}_{+}$ that are greater than or equal to 0. Occasionally, we write $x(t,\omega )$ for $x\left(t\right)$ to denote the explicit dependence of the random variable $x\left(t\right)$ on the outcome $\omega \in \Omega$. For every fixed time $t\ge 0$, the random variable $\omega \mapsto x(t,\omega )$ assigns a vector to every outcome $\omega \in \Omega$, and for every fixed $\omega \in \Omega$, the mapping $t\mapsto x(t,\omega )$ generates a sample path (or sample trajectory) of the stochastic process $x(·)$, where, for convenience, we write $x(·)$ to denote the stochastic process $\left\{x\right(t):t\ge 0\}$.

A (continuous-time) filtration $\{{\mathcal{F}}_t:t\ge 0\}$ on $(\Omega ,\mathcal{F},\mathbb{P})$ is a collection of sub-$\sigma$-fields of $\mathcal{F}$, and it is indexed by ${\overline{\mathbb{R}}}_{+}$, such that ${\mathcal{F}}_s\subseteq {\mathcal{F}}_t$, $0\le s\le t$. A filtration is complete if every ${\mathcal{F}}_t$ contains the set of all sets that are contained in a $\mathbb{P}$-null set. The stochastic process $x(·)$ is progressively measurable with respect to $\{{\mathcal{F}}_t:t\ge 0\}$ if, for every $t\ge 0$, the map $(s,\omega )\mapsto x(s,\omega )$ defined on $[0,t]\times \Omega$ is $\mathfrak{B}\left([0,t]\right)\times {\mathcal{F}}_t$-measurable. The stochastic process $x(·)$ is said to be adapted with respect to $\{{\mathcal{F}}_t:t\ge 0\}$, or it is simply ${\mathcal{F}}_t$-adapted if $x\left(t\right)$ is ${\mathcal{F}}_t$-measurable for every $t\ge 0$. An adapted stochastic process with right continuous (or left continuous) sample paths is progressively measurable [24].

The stochastic process $V\left(t\right):t\ge 0$, where $V\left(t\right),t\ge 0$, is a random variable, is a martingale with respect to the filtration $\{{\mathcal{F}}_t:t\ge 0\}$ if it is ${\mathcal{F}}_t$-adapted, $\mathbb{E}\left[\right|V\left(t\right)\left|\right]<\infty ,t\ge 0$, and $\mathbb{E}\left[V\left(t\right)\right|{\mathcal{F}}_s]=V\left(s\right),0\le s<t$. If we replace the equality in $\mathbb{E}\left[V\left(t\right)\right|{\mathcal{F}}_s]=V\left(s\right)$ with “≤” (respectively, “≥”), then $V(·)$ is a supermartingale (respectively, submartingale). A random variable $\tau :\Omega \to {\overline{\mathbb{R}}}_{+}\cup \infty$ is called a stopping time of the filtration $\{{\mathcal{F}}_t:t\ge 0\}$ if $\{\omega \in \Omega :\tau (\omega )\le t\}\in {\mathcal{F}}_t$ for all $t\ge 0$. A stopping time $\tau$ is a bounded stopping time if the event $\{\tau \le M\}$, where $M\ge 0$ is a constant, has a probability of one. (For an additional discussion on stochastic processes, filtrations, martingales, and stopping times, see [24]).

In this paper, we consider stochastic dynamical systems $\mathcal{G}$ of the form

$$\begin{array}{cc}\hfill \mathrm{d}x\left(t\right)& =f\left(x\left(t\right)\right)\mathrm{d}t+D\left(x\left(t\right)\right)\mathrm{d}w\left(t\right),x\left(0\right)=x_0,t\ge 0,\hfill \end{array}$$

(1)

where (1) is a stochastic differential equation. The stochastic process $x(·)$ represents the system state, $x_0$ is a random system initial condition vector, and $w(·)$ is a d-dimensional Brownian motion process. For every $t\ge 0$, the random variable $x\left(t\right)$ takes values in the state space ${\mathbb{R}}^n$. The Borel measurable mappings $f:{\mathbb{R}}^n\to {\mathbb{R}}^n$ and $D:{\mathbb{R}}^n\to {\mathbb{R}}^{n\times d}$ satisfy $f\left(0\right)=0$ and $D\left(0\right)=0$, and they are known as the system drift and diffusion functions. The stochastic differential equation (1) is interpreted as a way of expressing the integral equation

$$\begin{array}{cc}\hfill x\left(t\right)& =x\left(0\right)+{\int }_0^{t}f\left(x\left(s\right)\right)\mathrm{d}s+{\int }_0^{t}D\left(x\left(s\right)\right)\mathrm{d}w\left(s\right),x\left(0\right)=x_0,t\ge 0,\hfill \end{array}$$

(2)

where the first integral in (2) is a Lebesgue integral and the second is an Itô integral [25].

Let $(\Omega ,\mathcal{F},\{{\mathcal{F}}_t:t\ge 0\},\mathbb{P})$ be a fixed complete filtered probability space, $w(·)$ be a ${\mathcal{F}}_t$-adapted Brownian motion, and $x_0$ be a ${\mathcal{F}}_0$-measurable initial condition. A solution to (1) is an ${\mathbb{R}}^n$-valued ${\mathcal{F}}_t$-adapted process $x(·)$ with continuous sample paths such that the integrals in (2) exist and (2) holds almost surely for all $t\ge 0$. For a Brownian motion disturbance and initial condition given in a prescribed probability space, the solution to (2) is known as a strong solution [26]. In this paper, we focus on strong solutions, and we will simply use the term “solution” to refer to a strong solution. A solution to (1) is unique if for any two solutions $x_1(·)$ and $x_2(·)$ that satisfy (1), $x_1\left(t\right)=x_2\left(t\right)$ for all $t\ge 0$ almost surely.

For a stochastic system of the form given by (1) with solution $x(·)$, the (infinitesimal) generator $\mathcal{A}$ of $x(·)$ is an operator acting on the function $V:{\mathbb{R}}^n\to \mathbb{R}$, and it is defined as ([22])

$$\mathcal{A}V\left(x\right)=\underset{t\to 0^{+}}{lim}{\displaystyle \frac{{\mathbb{E}}^x\left[V\left(x\left(t\right)\right)\right]-V\left(x\right)}{t}},x\in {\mathbb{R}}^n,$$

(3)

where ${\mathbb{E}}^x[·]$ denotes the expectation given that x is a fixed point in ${\mathbb{R}}^n$. The set of functions $V:{\mathbb{R}}^n\to \mathbb{R}$ for which the limit in (3) exists is denoted by ${\mathcal{D}}_{\mathcal{A}}$. If $V\in {\mathrm{C}}^2\left({\mathbb{R}}^n\right)$ has compact support, where ${\mathrm{C}}^r\left({\mathbb{R}}^n\right)$ denotes the space of functions with r-continuous derivatives, then $V\in {\mathcal{D}}_{\mathcal{A}}$ and $\mathcal{A}V\left(x\right)=\mathcal{L}V\left(x\right)$, where

$$\mathcal{L}V\left(x\right)\triangleq V^{\prime }\left(x\right)f\left(x\right)+\frac{1}{2}\mathrm{tr}\left[D^{\mathrm{T}}\left(x\right)V^{\prime \prime }\left(x\right)D\left(x\right)\right],x\in {\mathbb{R}}^n,$$

(4)

$V^{\prime }\left(x\right)\triangleq \frac{\partial V}{\partial x}\left(x\right)$, and $V^{\prime \prime }\left(x\right)\triangleq \frac{{\partial }^{2}V}{\partial x^2}\left(x\right)$ [22]. Note that the differential operator $\mathcal{L}$ introduced in (4) is defined for every $V\in {\mathrm{C}}^2\left({\mathbb{R}}^n\right)$, and it is characterized by the system drift and diffusion functions. With a minor abuse in terminology, we will refer to the differential operator $\mathcal{L}$ as the (infinitesimal) generator of the system $\mathcal{G}$.

If $V\in {\mathrm{C}}^2\left({\mathbb{R}}^n\right)$, then it follows from Itô’s formula [26] that the stochastic process $\left\{V\right(x\left(t\right)):t\ge 0\}$ satisfies

$$V\left(x\left(t\right)\right)=V\left(x\left(0\right)\right)+{\int }_0^t\mathcal{L}V\left(x\left(s\right)\right)\mathrm{d}s+{\int }_0^t{V}^{\prime }\left(x\left(s\right)\right)D\left(x\left(s\right)\right)\mathrm{d}w\left(s\right),t\ge 0.$$

(5)

If the terms appearing in (5) are integrable and the Itô integral in (5) is a martingale, then it follows from (5) that

$$\begin{array}{c}\hfill \mathbb{E}\left[V\left(x\left(t\right)\right)\right]=\mathbb{E}\left[V\left(x\left(0\right)\right)\right]+\mathbb{E}\left[{\int }_0^t\mathcal{L}V\left(x\left(s\right)\right)\mathrm{d}s\right],t\ge 0.\end{array}$$

(6)

A more general version of (6) that holds for t is replaced by a stopping time $\tau$ is known as Dynkin’s formula [22].

We say that a function $g:{\mathbb{R}}^n\to \mathbb{R}$ is of polynomial growth if there exist positive constants C and m such that

$$\left|g\left(x\right)\right|\le C(1+{\left|\right|x\left|\right|}^m),x\in {\mathbb{R}}^n.$$

(7)

For $V\in {\mathrm{C}}^r\left({\mathbb{R}}^n\right),r\in \mathbb{N}$, where $\mathbb{N}$ denotes the set of natural numbers, we write $V\in {\mathrm{C}}_{\mathrm{p}}^r\left({\mathbb{R}}^n\right)$ if V and all its partial derivatives up to order r are of polynomial growth. As shown in [27], $V\in {\mathrm{C}}_{\mathrm{p}}^r\left({\mathbb{R}}^n\right)$ is a sufficient condition for the integrability of the terms in (5). In this case, it can be shown that (3) implies (4). In this paper, we assume all Lyapunov functions V are of polynomial growth with $r=1$.

Given a function $V:{\mathbb{R}}^n\to \mathbb{R}$, we say that V is positive definite with respect to $x_{\mathrm{e}}\in {\mathbb{R}}^n$ if $V\left(x_{\mathrm{e}}\right)=0$ and $V\left(x\right)>0,x\in {\mathbb{R}}^n,x\ne x_{\mathrm{e}}$. If $x_{\mathrm{e}}=0$, then V is positive definite with respect to the origin, or V is simply positive definite. Moreover, we say a function V is nonnegative definite if $V\left(x\right)\ge 0,x\in {\mathbb{R}}^n$. We say that V is negative definite if $-V$ is positive definite. In addition, we say that V is radially unbounded if ${lim}_{x\to \infty }V\left(x\right)=\infty$.

As discussed in the introduction, in order to achieve convergence in finite time for stochastic dynamical systems, the drift and diffusion functions characterizing the system dynamics need to be non-Lipschitzian giving rise to nonuniqueness of solutions in backward time ([20], Lemma 5.3). Uniqueness of solutions in forward time, however, can be preserved in the case of finite time convergence. The next result establishes the existence and uniqueness of solutions for the stochastic differential equation (1) with non-Lipchitzian drift and diffusion functions. For the statement of this result, ${\mathcal{B}}_{\delta }\left(x_{\mathrm{e}}\right),\delta >0$, denotes the open ball centered at $x_{\mathrm{e}}$ with radius $\delta$ in the Euclidean norm.

Theorem 1

([4]). Consider the nonlinear stochastic dynamical system (1) with initial condition $x_0$ such that $\mathbb{E}\left[{x_0}^p\right]<\infty ,p\in \mathbb{N}$, and assume that the following conditions hold:

(i)

Continuity. $f:{\mathbb{R}}^n\to {\mathbb{R}}^n$ and $D:{\mathbb{R}}^n\to {\mathbb{R}}^{n\times d}$ are continuous.

(ii)

Linear growth. There exists a constant $K>0$ such that, for all $x\in {\mathbb{R}}^n$,

$$\left|\right|f\left(x\right)\left|\right|+\left|\right|D\left(x\right)\left|\right|\le K(1+|\left|x\right|\left|\right).$$

(8)

(iii)

For every $q\in \mathbb{N}$, there exist a strictly increasing, continuous, and concave function $g_q:[0,\infty )\to [0,\infty )$, as well as a constant $c_q\ge 0$ such that, for all $x,y\in {\mathcal{B}}_q\left(0\right)$,

$${\int }_0^{\infty }{\displaystyle \frac{\mathrm{d}\sigma }{g_q\left(\sigma \right)}}=\infty$$

and

$$2{(x-y)}^{\mathrm{T}}{[f\left(x\right)-f\left(y\right)]+\parallel D\left(x\right)-D\left(y\right)\parallel }^2\le c_q{g}_q{(\parallel x-y\parallel }^2).$$

(9)

Then, there exists a unique solution to (1). Furthermore,

$$\mathbb{E}\left[{\left(\underset{0\le s\le t}{sup}\left|\right|x\left(s\right)\left|\right|\right)}^p\right]<\infty ,t\ge 0,p\in \mathbb{N}.$$

(10)

Assumption 1.

For the remainder of this paper, we assume that the conditions for existence and uniqueness given in Theorem 1 are satisfied for system (1).

3. Finite Time Stability for Stochastic Dynamical Systems

In this section, we introduce the notion of finite time stability in probability and present sufficient conditions for finite time stability of (1) using a Lyapunov function that satisfies a scalar differential inequality involving fractional powers. First, however, we require some additional definitions and results. We denote the solution $\left\{x\right(t):t\ge 0\}$ to (1) with the initial condition $x\left(0\right)=x$ at time t by $s(t,x,\omega )$, and we define $s_t\triangleq s(t,·,\omega ):{\mathbb{R}}^n\to {\mathbb{R}}^n$ and $s^x\triangleq s(·,x,·):{\overline{\mathbb{R}}}_{+}\times \Omega \to {\mathbb{R}}^n$, with $s^x$ denoting the sample trajectory of (1). Thus, for every $x\in {\mathbb{R}}^n$, there exists a trajectory defined for all $t\ge 0$ and $\omega \in \Omega$ satisfying the dynamical process (1) with initial condition $x\left(0\right)=x_0$. For simplicity of exposition, we write $s(t,x)$ for $s(t,x,\omega )$ and $s^x\left(t\right)$ for $s^x(t,\omega )$ omitting their dependence on $\omega$.

The following definitions introduce the notions of a stochastic settling time and finite time stability in probability for stochastic dynamical systems. Here, we assume that the initial condition $x_0$ is a constant, and hence, whenever we write $x_0\in {\mathbb{R}}^n$, we mean that $x_0$ is a constant vector. In this case, we will find it convenient to introduce the notation ${\mathbb{P}}^{x_0}[·]$ and ${\mathbb{E}}^{x_0}[·]$ to denote the probability and expected value, respectively, given that the initial condition $x\left(0\right)$ is the fixed point $x_0\in {\mathbb{R}}^n$ almost surely.

Definition 1.

Consider the nonlinear stochastic dynamical system given by (1). The stochastic settling time $T:{\mathbb{R}}^n\times \Omega \to \{{\overline{\mathbb{R}}}_{+}\cup \infty \}$ is a stopping time with respect to $\{{\mathcal{F}}_t:t\ge 0\}$, and is defined as

$$T(x,\omega )\triangleq inf\{t\ge 0:s(t,x,\omega )=0\}.$$

(11)

Note that if $s(t,x,\omega )\ne 0,t\ge 0$, then $T(x,\omega )=+\infty$. For simplicity of exposition, we write $T\left(x\right)$ for $T(x,\omega )$, omitting its dependence on $\omega$.

Definition 2.

Consider the nonlinear stochastic dynamical system given by (1) and let $T:{\mathbb{R}}^n\to \{{\overline{\mathbb{R}}}_{+}\cup \infty \}$ be as in Definition 1, then the zero solution $x(·)\equiv 0$ to (1) is finite time stable in probability if the following statements hold:

(i)

The zero solution $x(·)\equiv 0$ to (1) is Lyapunov stable in probability, that is, for every $\epsilon >0$, we have

$$\underset{x_0\to 0}{lim}{\mathbb{P}}^{x_0}\left(\underset{t\ge 0}{sup}\parallel x\left(t\right)\parallel >\epsilon \right)=0$$

(12)

or, equivalently, for every $\epsilon >0$ and $\rho \in (0,1),$ there exists $\delta =\delta (\rho ,\epsilon )>0$ such that, for all $x_0\in {\mathcal{B}}_{\delta }\left(0\right)$,

$${\mathbb{P}}^{x_0}\left(\underset{t\ge 0}{sup}\parallel x\left(t\right)\parallel >\epsilon \right)\le \rho .$$

(13)

(ii)

For every $\rho \in (0,1)$, there exists $\delta =\delta \left(\rho \right)>0$ such that if $x_0\in {\mathcal{B}}_{\delta }\left(0\right)$, then

$${\mathbb{P}}^{x_0}(T\left(x_0\right)<\infty )\ge 1-\rho .$$

(14)

• The zero solution $x(·)\equiv 0$ to (1) is globally finite time stable in probability if ${\mathbb{P}}^{x_0}(T\left(x_0\right)<\infty )=1$ for all $x_0\in {\mathbb{R}}^n$.

Proposition 1.

Consider the nonlinear stochastic dynamical system (1). Assume that the zero solution $x(·)\equiv 0$ to (1) is globally finite time stable in probability. Let $T:{\mathbb{R}}^n\to [0,\infty )$ be as in Definition 1, then, for all $x_0\in {\mathbb{R}}^n$,

$${\mathbb{P}}^{x_0}\left(\underset{t\ge T\left(x_0\right)}{sup}\parallel s(t,x_0)\parallel =0\right)=1.$$

(15)

Proof. 

Since (1) is globally finite time stable, $T(x_0,\omega )<\infty$ and $x(T(x_0,\omega ),\omega )=0$ for all $x_0\in {\mathbb{R}}^n$ and almost all $\omega \in \Omega$. Defining $\tilde{x}:{\overline{\mathbb{R}}}_{+}\times \Omega \to {\mathbb{R}}^n$ as

$$\tilde{x}(t,\omega )\triangleq \left\{\begin{array}{c}x(t,\omega ),t\le T(x_0,\omega ),\hfill \\ 0,t>T(x_0,\omega ),\hfill \end{array}\right.$$

and using the fact that $x(t,\omega )$ is sample continuous in t, it follows that

$$\underset{t\to T{(x_0,\omega )}^{-}}{lim}\tilde{x}(t,\omega )=\tilde{x}(T(x_0,\omega ),\omega )=0=\underset{t\to T{(x_0,\omega )}^{+}}{lim}\tilde{x}(t,\omega ),$$

which implies $\tilde{x}(t,\omega )$ is sample continuous in t. Since $x(t,\omega )$ is ${\mathcal{F}}_t$-adapted, it follows that $\tilde{x}(t,\omega )$ is ${\mathcal{F}}_t$-adapted. Clearly, $\tilde{x}(t,\omega )$ satisfies (2) for all $t\le T(x_0,\omega )$.

Next, using the fact that $f\left(0\right)=0$ and $D\left(0\right)=0$, it follows that, for all $t>T(x_0,\omega )$,

$$\begin{array}{cc}\hfill x_0+{\int }_0^{t}f\left(\tilde{x}(s,\omega )\right)\mathrm{d}s+{\int }_0^{t}D\left(\tilde{x}(s,\omega )\right)\mathrm{d}w\left(s\right)& =\tilde{x}(T(x_0,\omega ),\omega )+{\int }_{T(x_0,\omega )}^{t}f\left(\tilde{x}(s,\omega )\right)\mathrm{d}s\hfill \\ \hfill & +{\int }_{T(x_0,\omega )}^{t}D\left(\tilde{x}(s,\omega )\right)\mathrm{d}w\left(s\right)\hfill \\ \hfill & =\tilde{x}(T(x_0,\omega ),\omega )\hfill \\ \hfill & =0\hfill \\ \hfill & =\tilde{x}(t,\omega ),\hfill \end{array}$$

and hence, it follows that (2) is satisfied for all $t\ge 0$. Now, since the solution to (1) is unique, $\tilde{x}(t,\omega )$ is the only solution to (1) with $x\left(0\right)=x_0$. Finally, the result follows by noting that this holds for almost all $\omega \in \Omega$. □

Proposition 1 implies that, for every $\epsilon >0$ and $\rho \in (0,1)$, there exists $\delta =\delta (\rho ,\epsilon )>0$ such that, for all $x_0\in {\mathcal{B}}_{\delta }\left(0\right)$,

$${\mathbb{P}}^{x_0}\left(\underset{t\ge 0}{sup}\parallel x\left(t\right)\parallel >\epsilon \right)\le \rho$$

(16)

and

$${\mathbb{P}}^{x_0}\left(\underset{0\le t\le T\left(x_0\right)}{sup}\parallel x\left(t\right)\parallel >\epsilon \right)\le \rho ,$$

(17)

which are equivalent. Hence, it follows from Proposition 1 that if the zero solution $x(·)\equiv 0$ to (1) is globally finite time stable in probability, then it is globally asymptotically stable in probability. Thus, global finite time stability in probability is a stronger notion than global asymptotic stability in probability.

The following theorem based on the results appearing in [14,28] gives sufficient conditions for stochastic finite time stability using a Lyapunov function involving a scalar differential inequality. For completeness, we give a self-contained proof of this result as it forms the foundation for all later developments in this paper. For the statement of this theorem, ${\mathbb{1}}_{\left\{\mathcal{A}\right\}}$ denotes the indicator function of the set $\mathcal{A}$, that is,

$${\mathbb{1}}_{\left\{\mathcal{A}\right\}}\left(x\right)=\left\{\begin{array}{c}1,\mathrm{if}x\in \mathcal{A},\hfill \\ 0,\mathrm{if}x\notin \mathcal{A}.\hfill \end{array}\right.$$

Theorem 2.

Let $\mathcal{D}\subseteq {\mathbb{R}}^n$ be an open subset containing the origin. Consider the nonlinear stochastic dynamical system (1) and assume that there exist a two-times continuously differentiable function $V:\mathcal{D}\to \mathbb{R}$ and constants $a>0$ and $\alpha \in (0,1)$ such that

$$\begin{array}{cc}\hfill V\left(0\right)& =0,\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill V\left(x\right)& >0,x\in \mathcal{D},x\ne 0,\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill \mathcal{L}V\left(x\right)& \le -a{\left(V\left(x\right)\right)}^{\alpha },x\in \mathcal{D}.\hfill \end{array}$$

(20)

Then, the zero solution $x(·)\equiv 0$ to (1) is finite time stable in probability. If, in addition, $\mathcal{D}={\mathbb{R}}^n$, V is radially unbounded, and (19) and (20) hold on ${\mathbb{R}}^n\setminus \left\{0\right\}$, then the zero solution $x(·)\equiv 0$ to (1) is globally finite time stable in probability. Moreover, there exists a stochastic settling time $T:{\mathbb{R}}^n\to [0,\infty )$ such that

$${\mathbb{E}}^{x_0}\left[T\left(x_0\right)\right]\le {\displaystyle \frac{V{\left(x_0\right)}^{1-\alpha }}{a(1-\alpha )}},x_0\in {\mathbb{R}}^n.$$

(21)

Proof. 

Conditions (18)–(20) imply Lyapunov stability in probability by Theorem 2 of [17]. Thus, for every $\epsilon >0$ and $\rho \in (0,1)$ such that ${\overline{\mathcal{B}}}_{\epsilon }\left(0\right)\subseteq \mathcal{D}$, there exists $\delta =\delta (\rho ,\epsilon )>0$ such that, for all $x_0\in {\mathcal{B}}_{\delta }\left(0\right)$,

$${\mathbb{P}}^{x_0}\left(\underset{t\ge 0}{sup}\parallel x\left(t\right)\parallel >\epsilon \right)\le \rho .$$

(22)

Next, note that finite time stability in probability holds trivially for $x_0=0$. For all $x_0\in {\mathcal{B}}_{\delta }\left(0\right)\setminus \left\{0\right\}$, define the stopping times ${\tau }_{\epsilon }\triangleq inf\{t\ge 0:\parallel s(t,x_0)\parallel >\epsilon \}$, ${\tau }_k\triangleq inf\{t\ge 0:\parallel s(t,x_0)||\le {\displaystyle \frac{1}{k}}\}$, ${\tau }_k\left(t\right)\triangleq min\{t,{\tau }_k\}$, and ${\tau }_{k,\epsilon }\left(t\right)\triangleq min\{t,{\tau }_k,{\tau }_{\epsilon }\}$, where $k\in \mathbb{N}$, $k\ge K$ and $||x_0\parallel >{\displaystyle \frac{1}{K}}$.

Since $V{\left(x\right)}^{1-\alpha }$ is two-times continuously differentiable for all $x\in {\mathbb{R}}^n$ such that $\parallel x\parallel >{\displaystyle \frac{1}{K}}$, it follows from Itô’s formula [22] that, for all $t\ge 0$ and $k\ge K$,

$$\begin{array}{cc}\hfill V{\left(x\left({\tau }_{k,\epsilon }\left(t\right)\right)\right)}^{1-\alpha }& =V{\left(x_0\right)}^{1-\alpha }+{\int }_0^{{\tau }_{k,\epsilon }\left(t\right)}(1-\alpha )V{\left(x\left(s\right)\right)}^{-\alpha }{V}^{\prime }\left(x\left(s\right)\right)f\left(x\left(s\right)\right)\mathrm{d}s\hfill \\ \hfill & +{\int }_0^{{\tau }_{k,\epsilon }\left(t\right)}{\displaystyle \frac{1}{2}}\mathrm{tr}\left[D^{\mathrm{T}}\left(x\left(s\right)\right)\right(-\alpha (1-\alpha )V{\left(x\left(s\right)\right)}^{-\alpha -1}{V}^{\prime \mathrm{T}}\left(x\left(s\right)\right)V^{\prime }\left(x\left(s\right)\right)\hfill \\ \hfill & +(1-\alpha )V{\left(x\left(s\right)\right)}^{-\alpha }{V}^{\prime \prime }\left(x\left(s\right)\right)\left)D\left(x\left(s\right)\right)\right]\mathrm{d}s\hfill \\ \hfill & +{\int }_0^t{\mathbb{1}}_{\{s\le {\tau }_k\}}{\mathbb{1}}_{\{s\le {\tau }_{\epsilon }\}}(1-\alpha )V{\left(x\left(s\right)\right)}^{-\alpha }{V}^{\prime }\left(x\left(s\right)\right)D\left(x\left(s\right)\right)\mathrm{d}w\left(s\right).\hfill \end{array}$$

(23)

The process $(t,\omega )\to {\mathbb{1}}_{\{t\le {\tau }_k\}}{\mathbb{1}}_{\{t\le {\tau }_{\epsilon }\}}(1-\alpha )V{\left(x\left(t\right)\right)}^{-\alpha }{V}^{\prime }\left(x\left(t\right)\right)D\left(x\left(t\right)\right)$ is $\mathcal{B}[0,\infty )\times \mathcal{F}$-measurable and ${\mathcal{F}}_t$-adapted due to the measurability of the mappings involved and the properties of the processes $x(·)$. Now, since V is continuously differentiable and D is continuous, it follows that, for all $t\ge 0$ and $k\ge K$,

$$\begin{array}{cc}\hfill {\mathbb{E}}^{x_0}[{\int }_0^t{\mathbb{1}}_{\{s\le {\tau }_k\}}{\mathbb{1}}_{\{s\le {\tau }_{\epsilon }\}}{(1-\alpha )}^2& {\parallel V\left(x\left(s\right)\right)}^{-\alpha }{V}^{\prime }{\left(x\left(s\right)\right)D\left(x\left(s\right)\right)\parallel }^2\mathrm{d}s]\hfill \\ \hfill & \le {(1-\alpha )}^2\underset{{\displaystyle \frac{1}{k}}\le \parallel x\parallel \le \epsilon }{max}{\{\parallel V\left(x\right)}^{-\alpha }{V}^{\prime }\left(x\right)D\left(x\right){\parallel }^2\}t\hfill \\ \hfill & <\infty ,\hfill \end{array}$$

(24)

and hence, by Corollary 3.2.6 of [22], the Itô integral in (23) is a martingale. Now, (23) and the properties of the expectation of a martingale yield

$$\begin{array}{cc}\hfill {\mathbb{E}}^{x_0}\left[V{\left(x\left({\tau }_{k,\epsilon }\left(t\right)\right)\right)}^{1-\alpha }\right]& =V{\left(x_0\right)}^{1-\alpha }+{\mathbb{E}}^{x_0}\left[{\int }_0^{{\tau }_{k,\epsilon }\left(t\right)}(1-\alpha )V{\left(x\left(s\right)\right)}^{-\alpha }\right(V^{\prime }\left(x\left(s\right)\right)f\left(x\left(s\right)\right)\hfill \\ & +{\displaystyle \frac{1}{2}}\mathrm{tr}{D}^{\mathrm{T}}\left(x\left(s\right)\right)V^{\prime \prime }\left(x\left(s\right)\right)D\left(x\left(s\right)\right)\left)\mathrm{d}s\right]\hfill \\ & -{\mathbb{E}}^{x_0}\left[{\int }_0^{{\tau }_{k,\epsilon }\left(t\right)}V{\left(x\right)}^{-\alpha -1}\alpha (1-\alpha )\mathrm{tr}\right(D^{\mathrm{T}}\left(x\left(s\right)\right)V^{\prime \mathrm{T}}\left(x\left(s\right)\right)\hfill \end{array}$$

$$\begin{array}{c}\hfill ·V^{\prime }\left(x\left(s\right)\right)D\left(x\left(s\right)\right)\left)\mathrm{d}s\right]\\ \le V{\left(x_0\right)}^{1-\alpha }+{\mathbb{E}}^{x_0}\left[{\int }_0^{{\tau }_{k,\epsilon }\left(t\right)}(1-\alpha )V{\left(x\left(s\right)\right)}^{-\alpha }\mathcal{L}V\left(x\left(s\right)\right)\mathrm{d}s\right].\hfill \end{array}$$

(25)

Note that the expectations in (25) are well defined because ${\tau }_{k,\epsilon }\left(t\right)$ is a stopping time for exiting the bounded set ${\mathcal{S}}_k\triangleq \{x\in {\mathbb{R}}^n:{\displaystyle \frac{1}{k}}<\parallel x\parallel \le \epsilon \}$ and the integrands are continuous in ${\mathcal{S}}_k$.

Next, it follows from (19), (20), and (25) that

$$\begin{array}{cc}\hfill V{\left(x_0\right)}^{1-\alpha }& \ge {\mathbb{E}}^{x_0}\left[{\int }_0^{{\tau }_{k,\epsilon }\left(t\right)}a(1-\alpha )\right]\hfill \\ \hfill & =a(1-\alpha ){\mathbb{E}}^{x_0}\left[{\tau }_{k,\epsilon }\left(t\right)\right]\hfill \\ \hfill & \ge a(1-\alpha ){\mathbb{E}}^{x_0}\left[{\mathbb{1}}_{\{{\tau }_{\epsilon }=\infty \}}{\tau }_k\left(t\right)\right].\hfill \end{array}$$

(26)

Since (26) holds for all $t\ge 0$, it also holds for $t=k\ge K$, implying that

$${\mathbb{E}}^{x_0}\left[{\mathbb{1}}_{\{{\tau }_{\epsilon }=\infty \}}{\tau }_k\left(k\right)\right]\le {\displaystyle \frac{V{\left(x_0\right)}^{1-\alpha }}{a(1-\alpha )}},k\ge K.$$

We claim that

$$\underset{k\to \infty }{lim}{\tau }_k\left(k\right){\mathbb{1}}_{\{{\tau }_{\epsilon }=\infty \}}=T\left(x_0\right){\mathbb{1}}_{\{{\tau }_{\epsilon }=\infty \}}.$$

(27)

To see this, note that, since the stopping times ${\tau }_k$ are increasing with k, ${lim}_{k\to \infty }{\tau }_k$ exists or is infinite for almost all $\omega \in \Omega$. Next, since $x(·)$ is sample continuous, ${\tau }_k\le T\left(x_0\right)$ for all $k\ge K$, which yields

$$\underset{k\to \infty }{lim}{\tau }_k\le T\left(x_0\right).$$

(28)

Now, for almost all $\omega \in \{{\tau }_{\epsilon }<\infty \}$, (27) holds trivially; moreover, for some $\overline{\omega }\in \{{\tau }_{\epsilon }=\infty \}$, if ${lim}_{k\to \infty }{\tau }_k\left(\overline{\omega }\right)=\infty$, then (28) implies (27). Alternatively, if ${lim}_{k\to \infty }{\tau }_k\left(\overline{\omega }\right)<\infty$, then assume that, ad absurdum, ${lim}_{k\to \infty }{\tau }_k\left(\overline{\omega }\right)<T(x_0,\overline{\omega })$. It follows from the definition of ${\tau }_k$ that

$$\parallel s({\tau }_k\left(\overline{\omega }\right),x_0,\overline{\omega })\parallel \le {\displaystyle \frac{1}{k}},k\ge K,$$

which implies

$$\underset{k\to \infty }{lim}\parallel s({\tau }_k\left(\overline{\omega }\right),x_0,\overline{\omega })\parallel =0.$$

Next, since $s(t,x,\omega )$ is sample continuous in t, we conclude

$$∥s\left(\underset{k\to \infty }{lim}{\tau }_k\left(\overline{\omega }\right),x_0,\overline{\omega }\right)∥=0,$$

which contradicts ${lim}_{k\to \infty }{\tau }_k\left(\overline{\omega }\right)<T(x_0,\overline{\omega })$, and hence, (27) holds for almost all $\omega \in \Omega$.

Now, it follows from Fatou’s lemma [29] that

$${\mathbb{E}}^{x_0}\left[{\mathbb{1}}_{\{{\tau }_{\epsilon }=\infty \}}T\left(x_0\right)\right]\le {\displaystyle \frac{V{\left(x_0\right)}^{1-\alpha }}{a(1-\alpha )}},$$

(29)

which implies that

$$\begin{array}{c}\hfill \mathbb{P}(T\left(x_0\right)<\infty )\ge \mathbb{P}({\tau }_{\epsilon }=\infty )\ge 1-\rho ,\end{array}$$

(30)

proving finite time stability in probability.

To show global finite time stability in probability, for every $x_0\in {\mathbb{R}}^n$, define the stopping times ${\tau }_l\triangleq inf\{t\ge 0:\parallel s(t,x_0)\parallel \notin (1/l,l)\}$ and ${\tau }_l\left(t\right)\triangleq min\{t,{\tau }_l\}$, where $l\in \mathbb{N}$ and $l\ge L$, such that $\parallel x_0\parallel \in (1/L,L)$. Using a similar argument as the one used to obtain (26) with ${\tau }_{k,\epsilon }\left(t\right)$, replacing ${\tau }_l\left(t\right)$ yields

$${\mathbb{E}}^{x_0}\left[{\tau }_l\left(t\right)\right]\le {\displaystyle \frac{V{\left(x_0\right)}^{1-\alpha }}{a(1-\alpha )}},t\ge 0.$$

(31)

Since (31) holds for all $t\ge 0$, it also holds for $t=l\ge L$, which implies

$${\mathbb{E}}^{x_0}\left[{\tau }_l\left(l\right)\right]\le {\displaystyle \frac{V{\left(x_0\right)}^{1-\alpha }}{a(1-\alpha )}},l\ge L.$$

Next, we claim that

$$\underset{l\to \infty }{lim}{\tau }_l\left(l\right)=T\left(x_0\right).$$

(32)

Since the stopping times ${\tau }_l$ are increasing with l, ${lim}_{l\to \infty }{\tau }_l$ exists or is infinite for almost all $\omega \in \Omega$. Now, using an analogous argument as the one used to obtain (28) gives

$$\underset{l\to \infty }{lim}{\tau }_l\le T\left(x_0\right).$$

(33)

Next, for almost all $\omega \in \{{lim}_{l\to \infty }{\tau }_l=\infty \}$, (33) implies (32). Alternatively, for some $\overline{\omega }\in \{{lim}_{l\to \infty }{\tau }_l<\infty \}$, assume that, ad absurdum, ${lim}_{l\to \infty }{\tau }_l\left(\overline{\omega }\right)<T(x_0,\overline{\omega })$. Since (18)−(20) hold and V is radially unbounded, ${lim}_{t\to \infty }\parallel x(t,\overline{\omega })\parallel =0$ applies by Theorem 2 of [17]. Thus, there exists $M(x_0,\overline{\omega })>0$ such that $\parallel x(t,\overline{\omega })\parallel \le M(x_0,\overline{\omega })$ for all $t\ge 0$, and hence,

$$\parallel s({\tau }_l\left(\overline{\omega }\right),x_0,\overline{\omega })\parallel \le {\displaystyle \frac{1}{l}},l>max\{L,M(x_0,\overline{\omega })\},$$

which implies

$$\underset{l\to \infty }{lim}\parallel s({\tau }_l\left(\overline{\omega }\right),x_0,\overline{\omega })\parallel =0.$$

Now, since $s(t,x,\omega )$ is sample continuous in t, we conclude

$$∥s\left(\underset{l\to \infty }{lim}{\tau }_l\left(\overline{\omega }\right),x_0,\overline{\omega }\right)∥=0,$$

which contradicts ${lim}_{l\to \infty }{\tau }_l\left(\overline{\omega }\right)<T(x_0,\overline{\omega })$, and hence, (32) holds for almost all $\omega \in \Omega$.

Finally, it follows from Fatou’s lemma [29] that

$${\mathbb{E}}^{x_0}\left[T\left(x_0\right)\right]\le {\displaystyle \frac{V{\left(x_0\right)}^{1-\alpha }}{a(1-\alpha )}},$$

(34)

and hence,

$$\mathbb{P}(T\left(x_0\right)<\infty )=1,$$

(35)

which proves global finite time stability in probability. □

4. Stochastic Optimal Finite Time Stabilization

In the first part of this section, we provide connections between the Lyapunov functions and nonquadratic cost evaluation. Specifically, we consider the problem of evaluating a nonlinear–nonquadratic performance measure that depends on the solution of the stochastic nonlinear dynamical system given by (1). In particular, we show that the nonlinear–nonquadratic performance measure

$$J\left(x_0\right)\triangleq {\mathbb{E}}^{x_0}\left[{\int }_0^{\infty }L\left(x\left(t\right)\right)\mathrm{d}t\right],$$

(36)

where $L:{\mathbb{R}}^n\to \mathbb{R}$ and $x\left(t\right)$, $t\ge 0$, satisfies (1) with $x\left(0\right)=x_0$, can be evaluated in a convenient form so long as (1) is related to an underlying Lyapunov function that proves finite time stability in the probability of (1).

The following theorem generalizes Theorem 6 of [17] to finite time stability.

Theorem 3.

Consider the nonlinear stochastic dynamical system given by (1) with the nonlinear–nonquadratic performance measure (36), where $x(·)$ is the solution to (1). Furthermore, assume that there exist a two-times continuously differentiable radially unbounded function $V\in {\mathrm{C}}_{\mathrm{p}}^1\left({\mathbb{R}}^n\right)$ and constants $a>0$ and $\alpha \in (0,1)$ such that

$$\begin{array}{cc}\hfill V\left(0\right)& =0,\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill V\left(x\right)& >0,x\in {\mathbb{R}}^n,x\ne 0,\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill \mathcal{L}V\left(x\right)& \le -a{\left(V\left(x\right)\right)}^{\alpha },x\in {\mathbb{R}}^n,\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill \mathcal{L}{V}^p\left(x\right)& \le 0,x\in {\mathbb{R}}^n,\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill L\left(x\right)+\mathcal{L}V\left(x\right)& =0,x\in {\mathbb{R}}^n,\hfill \end{array}$$

(41)

where $p>1$. Then, the zero solution $x(·)\equiv 0$ to (1) is globally finite time stable in probability. Moreover, there exists a stochastic settling time $T:{\mathbb{R}}^n\to [0,\infty )$ such that

$${\mathbb{E}}^{x_0}\left[T\left(x_0\right)\right]\le {\displaystyle \frac{V{\left(x_0\right)}^{1-\alpha }}{a(1-\alpha )}},x_0\in {\mathbb{R}}^n,$$

(42)

and

$$J\left(x_0\right)=V\left(x_0\right).$$

(43)

Proof. 

Global finite time stability in probability along with the existence of a stochastic settling time $T:{\mathbb{R}}^n\to [0,\infty )$ such that (42) holds are a direct consequence of (37)–(39) and V being radially unbounded by Theorem 2. Using the fact that V is continuous and $\mathbb{E}\left[T\left(x_0\right)\right]<\infty$ yields

$$\underset{t\to \infty }{lim}V\left(x\left(t\right)\right)=0$$

(44)

almost surely.

Next, we show that the stochastic process $\{{\int }_0^t{V}^{\prime }\left(x\left(s\right)\right)D\left(x\left(s\right)\right)\mathrm{d}w\left(s\right):t\ge 0\}$ is a martingale. To see this, first note that the process $(t,\omega )\mapsto V^{\prime }\left(x\left(t\right)\right)D\left(x\left(t\right)\right)$ is $\mathcal{B}[0,\infty ]\times \mathcal{F}$-measurable and ${\mathcal{F}}_t$-adapted because of the measurability of the mappings involved and the properties of the process $x(·)$. Now, using Tonelli’s theorem [29] it follows that, for all $t\ge 0$,

$$\begin{array}{cc}\hfill \mathbb{E}\left[{\int }_0^t{\parallel V^{\prime }\left(x\left(s\right)\right)D\left(x\left(s\right)\right)\parallel }^2\mathrm{d}s\right]& ={\int }_0^t\mathbb{E}\left[\parallel V^{\prime }{\left(x\left(s\right)\right)D\left(x\left(s\right)\right)\parallel }^2\right]\mathrm{d}s\hfill \\ \hfill & \le {\int }_0^t\mathbb{E}\left[\alpha (1+{x\left(s\right)}^{\beta })\right]\mathrm{d}s\hfill \\ \hfill & \le {\int }_0^t\alpha \left(1+\mathbb{E}\left[{\left(\underset{0\le s\le t}{sup}\left|\right|x\left(s\right)\left|\right|\right)}^{\beta }\right]\right)\mathrm{d}s\hfill \\ \hfill & <\infty ,\hfill \end{array}$$

(45)

for some positive constants $\alpha$ and $\beta$, and hence, by Corollary 3.2.6 of [22] the Itô integral

$${\int }_0^t{V}^{\prime }\left(x\left(s\right)\right)D(x\left(s\right),u\left(s\right))\mathrm{d}w\left(s\right),t\ge 0,$$

is a martingale. To arrive at (45) we used the fact that $V\in {\mathrm{C}}_{\mathrm{p}}^1\left({\mathbb{R}}^n\right)$, the linear growth condition (8), and the finiteness of the expected value of the supremum of the moments of the system state (10). Note that the supremum in (45) exists because of the continuity of the sample paths of $x(·)$.

Next, the measurability of the solution of (1) implies that $V\left(x\right(t\left)\right)$ is ${\mathcal{F}}_t$-adapted and $\mathbb{E}\left[V\right(x\left(t\right)\left)\right]$ exists since $V\in {\mathrm{C}}_{\mathrm{p}}^1\left({\mathbb{R}}^n\right)$ and (10) holds. Now, using Itô’s formula [22] and (39) we have, for every $t>s\ge 0$ and almost every $\omega \in \Omega$,

$$\begin{array}{c}\hfill \mathbb{E}\left[V\left(x\left(t\right)\right)\right|{\mathcal{F}}_s]\le V\left(x\left(s\right)\right)+\mathbb{E}\left[{\int }_s^t{V}^{\prime }\left(x\left(r\right)\right)D\left(x\left(r\right)\right)\mathrm{d}w\left(r\right)|{\mathcal{F}}_s\right].\end{array}$$

(46)

Since the Itô integral in (46) is a martingale, (46) implies

$$\mathbb{E}\left[V\left(x\left(t\right)\right)\right|{\mathcal{F}}_s]\le V\left(x\left(s\right)\right),t>s\ge 0,$$

(47)

which shows that the process $\left\{V\right(x\left(t\right)):t\ge 0\}$ is a nonnegative supermartingale. An analogous argument implies that the process $\{V^p\left(x\left(t\right)\right):t\ge 0\}$ is also a nonnegative supermartingale for any $p>1$.

Next, using the fact that supermartingales have decreasing expectations gives

$$\underset{t\ge 0}{sup}{\mathbb{E}}^{x_0}\left[V^p\left(x\left(t\right)\right)\right]\le {\mathbb{E}}^{x_0}\left[V^p\left(x_0\right)\right]=V^p\left(x_0\right)<\infty ,$$

(48)

which shows that the stochastic process $\left\{V\right(x\left(t\right)):t\ge 0\}$ is uniformly integrable [22] (p. 323). Thus, by Doob’s martingale convergence theorem [22], $V\left(x\right(t\left)\right)$ converges in ${\mathcal{L}}_1$, and hence,

$$\underset{t\to \infty }{lim}{\mathbb{E}}^{x_0}\left[V\left(x\left(t\right)\right)\right]={\mathbb{E}}^{x_0}\left[\underset{t\to \infty }{lim}V\left(x\left(t\right)\right)\right]=0.$$

(49)

Furthermore, it follows from (41) and Itô’s formula that, for all $t\ge 0$,

$$\begin{array}{cc}\hfill {\int }_0^{t}L\left(x\left(s\right)\right)\mathrm{d}s=& {\int }_0^t-\mathcal{L}V\left(x\left(s\right)\right)\mathrm{d}s\hfill \\ \hfill =& V\left(x_0\right)-V\left(x\left(t\right)\right)+{\int }_0^t{V}^{\prime }\left(x\left(s\right)\right)D\left(x\left(s\right)\right)\mathrm{d}w\left(s\right).\hfill \end{array}$$

(50)

Taking the expected value operator on both sides of (50) and using the martingale property of the stochastic integral in (50) yields

$${\mathbb{E}}^{x_0}\left[{\int }_0^{t}L\left(x\left(s\right)\right)\mathrm{d}s\right]=V\left(x_0\right)-{\mathbb{E}}^{x_0}\left[V\left(x\left(t\right)\right)\right].$$

(51)

Now, taking the limit as $t\to \infty$ and using (49) yields

$$\underset{t\to \infty }{lim}{\mathbb{E}}^{x_0}\left[{\int }_0^{t}L\left(x\left(s\right)\right)\mathrm{d}s\right]=V\left(x_0\right)-\underset{t\to \infty }{lim}{\mathbb{E}}^{x_0}\left[V\left(x\left(t\right)\right)\right]=V\left(x_0\right).$$

Finally, note that

$$\begin{array}{c}\hfill J\left(x_0\right)={\mathbb{E}}^{x_0}\left[\underset{t\to \infty }{lim}{\int }_0^{t}L\left(x\left(s\right)\right)\mathrm{d}s\right]=\underset{t\to \infty }{lim}{\mathbb{E}}^{x_0}\left[{\int }_0^{t}L\left(x\left(s\right)\right)\mathrm{d}s\right]=V\left(x_0\right),\end{array}$$

(52)

where the interchanging of the limit with the expectation operator in the second equality in (52) follows from the Lebesgue monotone convergence theorem [30] by noting that, by (39) and (41), $L\left(x\right)\ge 0,x\in {\mathbb{R}}^n$, and hence, ${\int }_0^{t}L\left(x\left(s\right)\right)\mathrm{d}s,t\ge 0$, is monotone increasing, and thus, converges pointwise to ${lim}_{t\to \infty }{\int }_0^{t}L\left(x\left(s\right)\right)\mathrm{d}s$. □

Next, we use the framework developed in Theorem 3 to obtain a characterization of the stochastic optimal feedback controllers that guarantee closed-loop, finite time stabilization in probability. Specifically, sufficient conditions for optimality are given in a form that corresponds to a steady-state version of the stochastic Hamilton–Jacobi–Bellman equation. To address the problem of characterizing finite time stabilizing feedback controllers, consider the nonlinear controlled stochastic dynamical system

$$\begin{array}{cc}\hfill \mathrm{d}x\left(t\right)=F\left(x\right(t),u(t\left)\right)\mathrm{d}t+D\left(x\right(t),u(t\left)\right)\mathrm{d}w\left(t\right),& x\left(0\right)=x_0,u(·)\in \mathcal{U},t\ge 0,\hfill \end{array}$$

(53)

where the stochastic process $u(·)$ represents the controller input, and $\mathcal{U}$ is the set of admissible control inputs. For every $t\ge 0$, the random variables $x\left(t\right)$ and $u\left(t\right)$ take values in the state space ${\mathbb{R}}^n$ and the control space ${\mathbb{R}}^m$, respectively. The mappings $F:{\mathbb{R}}^n\times {\mathbb{R}}^m\to {\mathbb{R}}^n$ and $D:{\mathbb{R}}^n\times {\mathbb{R}}^m\to {\mathbb{R}}^{n\times d}$ satisfy (8) and (9), with $f\left(x\right)=F(x,u)$ and $D\left(x\right)=D(x,u)$, uniformly in u, and $F(0,0)=0$ and $D(0,0)=0$.

We assume that every $u(·)\in \mathcal{U}$ is an ${\mathbb{R}}^m$-valued Markov control process. An input process $u(·)$ is a Markov control process if there exists a function $\varphi :{\overline{\mathbb{R}}}_{+}\times {\mathbb{R}}^n\to {\mathbb{R}}^m$ such that $u\left(t\right)=\varphi (t,x(t\left)\right),t\ge 0$. Note that the class of Markov controls encompasses both time-varying inputs (i.e., possibly open-loop control input processes) and state-dependent inputs (i.e., possibly a state feedback control input$u\left(t\right)=\varphi \left(x\right(t\left)\right)$, where $\varphi :{\mathbb{R}}^n\to {\mathbb{R}}^m$ is a feedback control law). Note that, given the feedback control law $\varphi$, the closed-loop system (53) takes the form

$$\begin{array}{cc}\hfill \mathrm{d}x\left(t\right)=F\left(x\right(t),\varphi (x\left(t\right)\left)\right)\mathrm{d}t+D\left(x\right(t),& \varphi \left(x\left(t\right)\right))\mathrm{d}w\left(t\right),x\left(0\right)=x_0.t\ge 0.\hfill \end{array}$$

(54)

The following theorem generalizes Theorem 7 of [17] to optimal finite time stabilization.

Theorem 4.

Consider the nonlinear stochastic dynamical system given by (53) with nonlinear-nonquadratic performance measure

$$J(x_0,u(·))\triangleq {\mathbb{E}}^{x_0}\left[{\int }_0^{\infty }L(x\left(t\right),u\left(t\right))\mathrm{d}t\right],$$

(55)

where $x(·)$ is the solution to (53) with control input $u(·)$. Furthermore, assume that there exist a two-times continuously differentiable function $V\in {\mathrm{C}}_{\mathrm{p}}^1\left({\mathbb{R}}^n\right)$, constants $a>0$ and $\alpha \in (0,1)$, and a feedback control law $\varphi :{\mathbb{R}}^n\to {\mathbb{R}}^m$ such that

$$\begin{array}{cc}\hfill V\left(0\right)& =0,\hfill \end{array}$$

(56)

$$\begin{array}{cc}\hfill V\left(x\right)& >0,x\in {\mathbb{R}}^n,x\ne 0,\hfill \end{array}$$

(57)

$$\begin{array}{cc}\hfill \varphi \left(0\right)& =0,\hfill \end{array}$$

(58)

$$\begin{array}{cc}\hfill \mathcal{L}V(x,\varphi (x\left)\right)& \le -a{\left(V\left(x\right)\right)}^{\alpha },x\in {\mathbb{R}}^n,\hfill \end{array}$$

(59)

$$\begin{array}{cc}\hfill \mathcal{L}{V}^p(x,\varphi \left(x\right))& \le 0,x\in {\mathbb{R}}^n,\hfill \end{array}$$

(60)

$$\begin{array}{cc}\hfill H(x,\varphi (x\left)\right)& =0,x\in {\mathbb{R}}^n,\hfill \end{array}$$

(61)

$$\begin{array}{cc}\hfill H(x,u)& \ge 0,x\in {\mathbb{R}}^n,u\in {\mathbb{R}}^m,\hfill \end{array}$$

(62)

where $p>1$ and

$$\begin{array}{c}\hfill H(x,u)\triangleq L(x,u)+\mathcal{L}V(x,u).\end{array}$$

(63)

Then, with the feedback control law $u(·)=\varphi \left(x\right(·\left)\right)$, the closed-loop system (54) is globally finite time stable in probability. Moreover, there exists a stochastic settling time $T:{\mathbb{R}}^n\to [0,\infty )$ such that

$${\mathbb{E}}^{x_0}\left[T\left(x_0\right)\right]\le {\displaystyle \frac{V{\left(x_0\right)}^{1-\alpha }}{a(1-\alpha )}},x_0\in {\mathbb{R}}^n,$$

(64)

and

$$J(x_0,\varphi \left(x(·)\right))=V\left(x_0\right),x_0\in {\mathbb{R}}^n.$$

(65)

In addition, the feedback control law $u(·)=\varphi \left(x\right(·\left)\right)$ minimizes (55)in the sense that

$$\begin{array}{c}\hfill J(x_0,\varphi \left(x(·)\right))=\underset{u(·)\in \mathcal{S}\left(x_0\right)}{min}J(x_0,u(·)),\end{array}$$

(66)

where $\mathcal{S}\left(x_0\right)$ denotes the set of controllers given by

$$\begin{array}{cc}\hfill \mathcal{S}\left(x_0\right)\triangleq \{& u(·):u(·)\in \mathcal{U}\mathit{and}x(·)\mathit{\text{given by}} \text{(53)} \mathit{\text{is such that}}\hfill \\ \hfill & {\mathbb{E}}^{x_0}\left[{\int }_0^{\infty }\left|L\left(x\right(t),u(t\left)\right)\right|\mathrm{d}t\right]<\infty \mathrm{and}\underset{t\to \infty }{lim}{\mathbb{E}}^{x_0}\left[V\left(x\left(t\right)\right)\right]=0\},\hfill \end{array}$$

(67)

where $x_0\in {\mathbb{R}}^n$ and $u(·)=\varphi \left(x(·)\right)\in \mathcal{S}\left(x_0\right)$.

Proof. 

Global finite time stability in probability along with the existence of a stochastic settling time $T:{\mathbb{R}}^n\to [0,\infty )$ such that (64) holds are a direct consequence of (56)−(59) by applying Theorem 2 to the closed-loop system (54).

To show that $u(·)=\varphi \left(x(·)\right)\in \mathcal{S}\left(x_0\right)$, note that since $\varphi$ is Borel measurable, $\varphi \left(x\right(·\left)\right)$ is ${\mathcal{F}}_t$-progressively measurable and (59) and (61) imply that

$$L(x,\varphi \left(x\right))\ge 0,x\in {\mathbb{R}}^n.$$

Thus,

$$\begin{array}{cc}\hfill J(x_0,\varphi \left(x(·)\right))& ={\mathbb{E}}^{x_0}\left[{\int }_0^{\infty }L(x\left(t\right),\varphi \left(x\left(t\right)\right))\mathrm{d}t\right]\hfill \\ \hfill & ={\mathbb{E}}^{x_0}\left[{\int }_0^{\infty }\left|L(x\left(t\right),\varphi \left(x\left(t\right)\right))\right|\mathrm{d}t\right]\hfill \\ \hfill & =V\left(x_0\right)\hfill \\ \hfill & <\infty .\hfill \end{array}$$

(68)

Now, using an analogous argument as in the proof of Theorem 3, it follows that

$$\underset{t\to \infty }{lim}{\mathbb{E}}^{x_0}\left[V\left(x\left(t\right)\right)\right]=0$$

for $u(·)=\varphi \left(x\right(·\left)\right)$, and hence, $u(·)=\varphi \left(x(·)\right)\in \mathcal{S}\left(x_0\right)$.

Next, let $u(·)\in \mathcal{S}\left(x_0\right)$, and note that, by Itô’s lemma [22],

$$\begin{array}{cc}\hfill V\left(x\right(t\left)\right)=& V\left(x\left(0\right)\right)+{\int }_0^t\mathcal{L}V(x\left(s\right),u\left(s\right))\mathrm{d}s\hfill \end{array}$$

$$\begin{array}{c}\hfill +{\int }_0^t{V}^{\prime }\left(x\left(s\right)\right)D(x\left(s\right),u\left(s\right))\mathrm{d}w\left(s\right).\end{array}$$

(69)

It now follows using an analogous argument as the one in the proof of Theorem 3 that the stochastic integral in (69) is a martingale, and hence,

$$\begin{array}{cc}\hfill {\mathbb{E}}^{x_0}\left[V\left(x\left(t\right)\right)\right]& =V\left(x_0\right)+{\mathbb{E}}^{x_0}\left[{\int }_0^t\mathcal{L}V(x\left(s\right),u\left(s\right))\mathrm{d}s\right],\hfill \end{array}$$

(70)

where ${\mathbb{E}}^{x_0}\left[V\left(x\left(t\right)\right)\right]$ exists since $V\in {\mathrm{C}}_{\mathrm{p}}^1\left({\mathbb{R}}^n\right)$ and (10) holds. Next, taking the limit as $t\to \infty$ yields

$$\begin{array}{cc}\hfill \underset{t\to \infty }{lim}{\mathbb{E}}^{x_0}\left[V\left(x\left(t\right)\right)\right]& =V\left(x_0\right)+\underset{t\to \infty }{lim}{\mathbb{E}}^{x_0}\left[{\int }_0^t\mathcal{L}V(x\left(s\right),u\left(s\right))\mathrm{d}s\right].\hfill \end{array}$$

(71)

Since $u(·)\in \mathcal{S}\left(x_0\right)$, the control law satisfies ${lim}_{t\to \infty }{\mathbb{E}}^{x_0}\left[V\left(x\left(t\right)\right)\right]=0$, and hence, it follows from (71) that

$$\begin{array}{c}\hfill V\left(x_0\right)=-\underset{t\to \infty }{lim}{\mathbb{E}}^{x_0}\left[{\int }_0^t\mathcal{L}V(x\left(s\right),u\left(s\right))\mathrm{d}s\right].\end{array}$$

(72)

Now, combining (62) and (72) yields

$$\begin{array}{c}\hfill V\left(x_0\right)\le \underset{t\to \infty }{lim}{\mathbb{E}}^{x_0}\left[{\int }_0^{t}L(x\left(s\right),u\left(s\right))\mathrm{d}s\right].\end{array}$$

(73)

Next, note that, for every $t\ge 0$,

$$\begin{array}{cc}\hfill |{\int }_0^{t}L(x\left(s\right),u\left(s\right))\mathrm{d}s|& \le {\int }_0^t\left|L\left(x\right(s),u(s\left)\right)\right|\mathrm{d}s\le {\int }_0^{\infty }\left|L\left(x\right(s),u(s\left)\right)\right|\mathrm{d}s,\hfill \end{array}$$

(74)

and, since $u(·)\in \mathcal{S}\left(x_0\right)$, ${\mathbb{E}}^{x_0}\left[{\int }_0^{\infty }\left|L\left(x\right(s),u(s\left)\right)\right|\mathrm{d}s\right]<\infty$. Thus, it follows from the dominated convergence theorem [31] that

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}{\mathbb{E}}^{x_0}\left[{\int }_0^{t}L(x\left(s\right),u\left(s\right))\mathrm{d}s\right]={\mathbb{E}}^{x_0}\left[{\int }_0^{\infty }L(x\left(s\right),u\left(s\right))\mathrm{d}s\right].\end{array}$$

(75)

Finally, combining (65), (73), and (75) yields

$$\begin{array}{c}\hfill V\left(x_0\right)=J(x_0,\varphi \left(x(·)\right))\le J(x_0,u(·)),\end{array}$$

(76)

which proves (66). □

Observe that (61) represents the steady-state form of the stochastic Hamilton–Jacobi–Bellman equation. To see this, recall that the general form of the stochastic Hamilton–Jacobi–Bellman equation is given by

$${\displaystyle \frac{\partial V}{\partial t}}(t,x)+\underset{u\in {\mathbb{R}}^m}{min}\left[L(t,x,u)+\mathcal{L}V(t,x,u)\right]=0,t\ge 0,x\in {\mathbb{R}}^n,$$

(77)

which serves as the fundamental condition for optimal control in stochastic, time-dependent systems over either finite or infinite horizons [21]. When the system is time-invariant and considered over an infinite time horizon, the value function becomes stationary, that is, $V(t,x)=V\left(x\right)$; as a result, (77) simplifies to (61) and (62). These equations ensure optimality within the class of admissible control policies $\mathcal{S}\left(x_0\right)$. Notably, it is not necessary to explicitly characterize this admissible set $\mathcal{S}\left(x_0\right)$, and the optimal feedback control law $u=\varphi \left(x\right)$ is independent of the specific initial state $x_0$.

To guarantee that the closed-loop system given by (54) is globally finite time stable in probability, Theorem 4 requires that the value function V satisfy Conditions (56), (57), and (59). These requirements ensure that V serves as a Lyapunov function for the closed-loop system. However, these Lyapunov conditions are not necessary for establishing optimality. In particular, if V is twice continuously differentiable and $V\in {\mathrm{C}}_{\mathrm{p}}^1\left({\mathbb{R}}^n\right)$, and if the control signal $u(·)=\varphi \left(x\right(·\left)\right)$ lies in the admissible set $\mathcal{S}\left(x_0\right)$, then satisfaction of (61) and (62) leads to the fulfillment of (65) and (66). It is also crucial to emphasize that, in contrast to the deterministic framework [16], p. 857, establishing optimality in the stochastic setting necessitates an additional condition, namely the transversality condition ${lim}_{t\to \infty }{\mathbb{E}}^{x_0}\left[V\left(x\left(t\right)\right)\right]=0$ as stated in (67). (For more detailed discussions on this requirement, the reader is referred to [32], p. 323, [33], p. 125, and [34], p. 139.)

5. Inverse Optimal Stochastic Control for Nonlinear Affine Systems

In this section, we specialize Theorem 4 to nonlinear stochastic dynamical systems that are affine in control. We develop nonlinear feedback controllers that aim to minimize a nonlinear and nonquadratic performance criterion. This is achieved by selecting control laws such that the infinitesimal generator of a Lyapunov function for the closed-loop system satisfies (59) while providing sufficient conditions for the existence of solutions to the stochastic Hamilton–Jacobi–Bellman equation. As a result, we obtain a family of globally finite time stabilizing (in probability) controllers, each of which are parameterized by the cost functional being optimized.

The feedback control laws introduced here are derived from an inverse optimal stochastic control problem [16,18,19,35,36,37,38,39]. Instead of solving the stochastic steady-state Hamilton–Jacobi–Bellman equation directly for a given cost functional—an often complex task for higher dimensional systems—we define a family of stochastically finite time stabilizing controllers that optimize a derived cost functional. This approach offers flexibility in shaping the control laws. The performance integrand explicitly depends on the nonlinear system dynamics, the Lyapunov function for the closed-loop system, and the finite time stabilizing control laws. The coupling between these elements is governed by the stochastic Hamilton–Jacobi–Bellman equation. By adjusting the parameters in both the Lyapunov function and the performance criterion, this framework allows for the design of a class of globally finite time stabilizing (in probability) controllers that can meet specific performance and response requirements for the closed-loop system.

Consider the nonlinear affine in the control stochastic dynamical system given by

$$\begin{array}{ccc}\hfill \mathrm{d}x\left(t\right)=\left[f\left(x\right(t\left)\right)+G\left(x\right(t\left)\right)u\left(t\right)\right]\mathrm{d}t+D\left(x\left(t\right)\right)\mathrm{d}w\left(t\right),& x\left(0\right)=x_0,u(·)\in \mathcal{U},\hfill & \hfill t\ge 0,\end{array}$$

(78)

where, for every $t\ge 0$, the random variables $x\left(t\right)$ and $u\left(t\right)$ take values in the state space ${\mathbb{R}}^n$ and the control space ${\mathbb{R}}^m$, respectively. The mappings $f:{\mathbb{R}}^n\to {\mathbb{R}}^n$, $G:{\mathbb{R}}^n\to {\mathbb{R}}^{n\times m}$, and $D:{\mathbb{R}}^n\to {\mathbb{R}}^{n\times d}$ satisfy (8) and (9), with $f\left(x\right)=f\left(x\right)+G\left(x\right)u$ uniformly in u. Furthermore, we consider performance integrands $L(x,u)$ of the form

$$\begin{array}{c}\hfill L(x,u)\triangleq L_1\left(x\right)+L_2\left(x\right)u+u^{\mathrm{T}}{R}_2\left(x\right)u,\end{array}$$

(79)

where $L_1:{\mathbb{R}}^n\to \mathbb{R},L_2:{\mathbb{R}}^n\to {\mathbb{R}}^{1\times m}$, and $R_2:{\mathbb{R}}^n\to {\mathbb{R}}^{m\times m}$ with $R_2\left(x\right)>0$, $x\in {\mathbb{R}}^n$, such that (55) becomes

$$\begin{array}{cc}\hfill J(x_0,u(·))={\mathbb{E}}^{x_0}[{\int }_0^{\infty }[L_1\left(x\left(t\right)\right)+& L_2\left(x\left(t\right)\right)u\left(t\right)+u^{\mathrm{T}}\left(t\right)R_2\left(x\left(t\right)\right)u\left(t\right)\left]\mathrm{d}t\right].\hfill \end{array}$$

(80)

Theorem 5.

Consider the nonlinear stochastic dynamical system given by (78) with performance functional (80). Assume that there exist a two-times continuously differentiable function $V\in {\mathrm{C}}_{\mathrm{p}}^1\left({\mathbb{R}}^n\right)$, constants $a>0$ and $\alpha \in (0,1)$, and a function $L_2:{\mathbb{R}}^n\times {\mathbb{R}}^{n_2}\to {\mathbb{R}}^{1\times m}$ such that

$$\begin{array}{c}V\left(0\right)=0,\end{array}$$

(81)

$$\begin{array}{c}V\left(x\right)>0,x\in {\mathbb{R}}^n,x\ne 0,\end{array}$$

(82)

$$L_2\left(0\right)=0,$$

(83)

$$V^{\prime }\left(x\right)\left[f\left(x\right)-{\displaystyle \frac{1}{2}}G\left(x\right)R_2^{-1}\left(x\right)L_2^{\mathrm{T}}\left(x\right)-{\displaystyle \frac{1}{2}}G\left(x\right)R_2^{-1}\left(x\right)G^{\mathrm{T}}\left(x\right)V^{\prime \mathrm{T}}\left(x\right)\right]$$

$$\begin{array}{c}+{\displaystyle \frac{1}{2}}\mathrm{tr}{D}^{\mathrm{T}}\left(x\right)V^{\prime \prime }\left(x\right)D\left(x\right)\le -a{\left(V\left(x\right)\right)}^{\alpha },x\in {\mathbb{R}}^n.\end{array}$$

(84)

Then the closed-loop system

$$\begin{array}{cc}\hfill \mathrm{d}x\left(t\right)& =\left[f\left(x\right(t\left)\right)+G\left(x\right(t\left)\right)\varphi \left(x\right(t\left)\right)\right]\mathrm{d}t+D\left(x\left(t\right)\right)\mathrm{d}w\left(t\right),x\left(0\right)=x_0,t\ge 0,\hfill \end{array}$$

(85)

is globally finite time stable in probability with feedback control law

$$\varphi \left(x\right)=-{\displaystyle \frac{1}{2}}{R}_2^{-1}\left(x\right){[V^{\prime }\left(x\right)G\left(x\right)+L_2\left(x\right)]}^{\mathrm{T}}.$$

(86)

Moreover, there exists a stochastic settling time $T:{\mathbb{R}}^n\to [0,\infty )$ such that

$${\mathbb{E}}^{x_0}\left[T\left(x_0\right)\right]\le {\displaystyle \frac{V{\left(x_0\right)}^{1-\alpha }}{a(1-\alpha )}},x_0\in {\mathbb{R}}^n.$$

(87)

Furthermore, if

$$\mathcal{L}{V}^p(x,\varphi \left(x\right))\le 0,x\in {\mathbb{R}}^n,$$

(88)

where $p>1$, then the performance functional (80), with

$$\begin{array}{cc}\hfill L_1\left(x\right)=& {\varphi }^{\mathrm{T}}\left(x\right)R_2\left(x\right)\varphi \left(x\right)-V^{\prime }\left(x\right)f\left(x\right)-{\displaystyle \frac{1}{2}}\mathrm{tr}{D}^{\mathrm{T}}\left(x\right)V^{\prime \prime }\left(x\right)D\left(x\right),\hfill \end{array}$$

(89)

is minimized in the sense of (66) and (65) holds.

Proof. 

The result is a direct consequence of Theorem 4 with $F(x,u)=f\left(x\right)+G\left(x\right)u$, $D(x,u)=D\left(x\right)$, and $L(x,u)=L_1\left(x\right)+L_2\left(x\right)u+u^{\mathrm{T}}{R}_2\left(x\right)u$. Specifically, with (79), we have

$$\begin{array}{cc}\hfill H(x,u)=& L_1\left(x\right)+L_2\left(x\right)u+u^{\mathrm{T}}{R}_2\left(x\right)u+V^{\prime }\left(x\right)[f\left(x\right)+G\left(x\right)u]+{\displaystyle \frac{1}{2}}\mathrm{tr}{D}^{\mathrm{T}}\left(x\right)V^{\prime \prime }\left(x\right)D\left(x\right).\hfill \end{array}$$

Now, (86) is obtained by setting ${\displaystyle \frac{\partial H}{\partial u}}=0$. With (86), it follows that (84) implies (59).

Next, since V is twice continuously differentiable and $x=0$ is a local minimizer of V, it follows that $V^{\prime }\left(0\right)=0$; hence, since by (83) $L_2\left(0\right)=0$, it follows that $\varphi \left(0\right)=0$, which implies (58). Next, with $L_1\left(x\right)$ given by (89), $\varphi \left(x\right)$ is given by (86) and (61) holds. Since $H(x,u)=H(x,u)-H(x,\varphi \left(x\right))={[u-\varphi \left(x\right)]}^{\mathrm{T}}{R}_2\left(x\right)[u-\varphi \left(x\right)]$ and $R_2\left(x\right)$ is positive definite for all $x\in {\mathbb{R}}^n$, then (62) holds. The result now follows from Theorem 4. □

Remark 1.

It is important to note that the inverse optimal control design approach provides a framework for constructing the Lyapunov function for the closed-loop system that serves as an optimal value function and, as shown in [16,18,39], achieves desired stability margins. Specifically, nonlinear inverse optimal controllers that minimize a meaningful (in the terminology of [18,39]) nonlinear–nonquadratic performance criterion involving a nonlinear–nonquadratic, nonnegative–definite function of the state and a quadratic positive–definite function of the feedback control are shown to possess gain and sector margin guarantees to input nonlinearities in the conic sector $(1/2,\infty )$.

Example 1.

Consider the axisymmetric spacecraft with stochastic disturbances given by [40] (p. 753)

$$\begin{array}{cc}\hfill \mathrm{d}{\omega }_1\left(t\right)& =[I_{23}{\omega }_3{\omega }_2\left(t\right)+u_1\left(t\right)]\mathrm{d}t+\sigma {\omega }_1\left(t\right)\mathrm{d}{w}_1\left(t\right),{\omega }_1\left(0\right)={\omega }_{10},t\ge 0,\hfill \end{array}$$

(90)

$$\begin{array}{cc}\hfill \mathrm{d}{\omega }_2\left(t\right)& =[-I_{23}{\omega }_3{\omega }_1\left(t\right)+u_2\left(t\right)]\mathrm{d}t+\sigma {\omega }_2\left(t\right)\mathrm{d}{w}_2\left(t\right),{\omega }_2\left(0\right)={\omega }_{20},\hfill \end{array}$$

(91)

where $I_{23}\triangleq {\displaystyle \frac{I_3-I_2}{I_1}}$, $I_1$, $I_2$, and $I_3$ are the principal moments of inertia of the spacecraft such that $0<I_1=I_2<I_3$, ${\omega }_1(·)$, ${\omega }_2(·)$, and ${\omega }_3\in \mathbb{R}$ are the angular velocities of the spacecraft in the body frame; $u_1$ and $u_2$ are spacecraft control moments; $w_1(·)$ and $w_2(·)$ are standard Wiener processes capturing perturbations in the system dynamics; and $\sigma \in \mathbb{R}$.

For this example, we seek state feedback control laws ${[u_1,u_2]}^{\mathrm{T}}=\varphi \left(x\right)$, where $x={[x_1,x_2]}^{\mathrm{T}}={[{\omega }_1,{\omega }_2]}^{\mathrm{T}}$, such that the performance measure

$$\begin{array}{cc}\hfill J(x_0,u(·))& ={\mathbb{E}}^{x_0}[{\int }_0^{\infty }[L_1\left(x\left(t\right)\right)+2[I_{23}{\omega }_3{\omega }_2\left(t\right)+{\sigma }^2{\omega }_1\left(t\right)]u_1\left(t\right)\hfill \\ \hfill & +[-I_{23}{\omega }_3{\omega }_1\left(t\right)+{\sigma }^2{\omega }_2\left(t\right)]u_2\left(t\right)+u_1^2\left(t\right)+u_2^2\left(t\right)\left]\mathrm{d}t\right]\hfill \end{array}$$

(92)

is minimized in the sense of (66). Note that, in this case, $R_2\left(x\right)=I_2$ and

$$L_2\left(x\right)=2[I_{23}{\omega }_3{\omega }_2+{\sigma }^2{\omega }_1,-I_{23}{\omega }_3{\omega }_1+{\sigma }^2{\omega }_2].$$

Here, we apply Theorem 5 to find an inverse optimal feedback controller such that the spacecraft (90) and (91) is globally finite time stable in probability and (92) is minimized. To accomplish this, consider the Lyapunov function candidate given by

$$V\left(x\right)=\mu {({\omega }_1^2+{\omega }_2^2)}^{{\displaystyle \frac{2}{3}}},$$

(93)

where $\mu >0$. Note $V\left(x\right)$ satisfies (81) and (82). Furthermore, note that

$$\begin{array}{cc}\hfill \mathcal{L}V(x,\varphi (x\left)\right)& =V^{\prime }\left(x\right)\left[f\left(x\right)-{\displaystyle \frac{1}{2}}G\left(x\right)R_2^{-1}\left(x\right)L_2^{\mathrm{T}}\left(x\right)-{\displaystyle \frac{1}{2}}G\left(x\right)R_2^{-1}\left(x\right)G^{\mathrm{T}}\left(x\right)V^{\prime \mathrm{T}}\left(x\right)\right]\hfill \\ & +{\displaystyle \frac{1}{2}}\mathrm{tr}{D}^{\mathrm{T}}\left(x\right)V^{\prime \prime }\left(x\right)D\left(x\right)\hfill \\ \hfill & ={\displaystyle \frac{4\mu }{3}}{({\omega }_1^2+{\omega }_2^2)}^{-{\displaystyle \frac{1}{3}}}[{\omega }_1,{\omega }_2]\left\{-\left[\begin{array}{c}{\sigma }^2{\omega }_1\\ {\sigma }^2{\omega }_2\end{array}\right]-\left[\begin{array}{c}{\displaystyle \frac{2\mu }{3}}{({\omega }_1^2+{\omega }_2^2)}^{-{\displaystyle \frac{1}{3}}}{\omega }_1\\ {\displaystyle \frac{2\mu }{3}}{({\omega }_1^2+{\omega }_2^2)}^{-{\displaystyle \frac{1}{3}}}{\omega }_2\end{array}\right]\right\}\hfill \\ \hfill & +{\displaystyle \frac{2\mu }{9}}{\sigma }^2{({\omega }_1^2+{\omega }_2^2)}^{{\displaystyle \frac{2}{3}}}\hfill \\ \hfill & =-{\displaystyle \frac{8{\mu }^2}{9}}{({\omega }_1^2+{\omega }_2^2)}^{{\displaystyle \frac{1}{3}}}-{\displaystyle \frac{10\mu }{9}}{\sigma }^2{({\omega }_1^2+{\omega }_2^2)}^{{\displaystyle \frac{2}{3}}}\hfill \\ \hfill & \le -{\displaystyle \frac{8{\mu }^2}{9}}{({\omega }_1^2+{\omega }_2^2)}^{{\displaystyle \frac{1}{3}}}\hfill \\ \hfill & =-{\displaystyle \frac{8{\mu }^{\frac{3}{2}}}{9}}{\left(V\left(x\right)\right)}^{{\displaystyle \frac{1}{2}}},x\in {\mathbb{R}}^2,\hfill \end{array}$$

which shows that (84) is satisfied. Hence, it follows from Theorem 5 that the zero solution $x(·)\equiv 0$ of the closed-loop system (90) and (91) is globally finite time stable in probability with the feedback control law given by

$$\begin{array}{c}\hfill \varphi \left(x\right)=-{\displaystyle \frac{1}{2}}{R}_2^{-1}\left(x\right){[V^{\prime }\left(x\right)G\left(x\right)+L_2\left(x\right)]}^{\mathrm{T}}=\left[\begin{array}{c}-{\displaystyle \frac{2\mu }{3}}{\left({\omega }_1^2+{\omega }_2^2\right)}^{-{\displaystyle \frac{1}{3}}}{\omega }_1-I_{23}{\omega }_3{\omega }_2-{\sigma }^2{\omega }_1\\ -{\displaystyle \frac{2\mu }{3}}{\left({\omega }_1^2+{\omega }_2^2\right)}^{-{\displaystyle \frac{1}{3}}}{\omega }_2+I_{23}{\omega }_3{\omega }_1-{\sigma }^2{\omega }_2\end{array}\right].\end{array}$$

(94)

Next, note that

$$\begin{array}{cc}\hfill \mathcal{L}{V}^{{\displaystyle \frac{3}{2}}}(x,\varphi \left(x\right))& =[2{\omega }_1,2{\omega }_2]\left[\begin{array}{c}{I}_{23}{\omega }_3{\omega }_1\\ -I_{23}{\omega }_3{\omega }_1\end{array}\right]\hfill \\ \hfill & +[2{\omega }_1,2{\omega }_2]\left[\begin{array}{c}-{\displaystyle \frac{2\mu }{3}}{({\omega }_1^2+{\omega }_2^2)}^{-{\displaystyle \frac{1}{3}}}{\omega }_1-I_{23}{\omega }_3{\omega }_2-{\sigma }^2{\omega }_1\\ -{\displaystyle \frac{2\mu }{3}}{({\omega }_1^2+{\omega }_2^2)}^{-{\displaystyle \frac{1}{3}}}{\omega }_2+I_{23}{\omega }_3{\omega }_1-{\sigma }^2{\omega }_2\end{array}\right]\hfill \\ \hfill & +{\sigma }^2{\omega }_1^2+{\sigma }^2{\omega }_2^2\hfill \\ \hfill & =-{\displaystyle \frac{4\mu }{3}}{({\omega }_1^2+{\omega }_2^2)}^{-{\displaystyle \frac{1}{3}}}{\omega }_1^2-{\displaystyle \frac{4\mu }{3}}{({\omega }_1^2+{\omega }_2^2)}^{-{\displaystyle \frac{1}{3}}}{\omega }_2^2-{\sigma }^2{\omega }_1^2-{\sigma }^2{\omega }_2^2\hfill \\ \hfill & \le 0,x\in {\mathbb{R}}^2,\hfill \end{array}$$

which shows that (88) is satisfied with $p={\displaystyle \frac{3}{2}}$. Hence, it follows from Theorem 5 that the performance functional (92), with

$$\begin{array}{cc}\hfill L_1\left(x\right)& ={\varphi }^{\mathrm{T}}\left(x\right)R_2\left(x\right)\varphi \left(x\right)-V^{\prime }\left(x\right)f\left(x\right)-{\displaystyle \frac{1}{2}}tr{D}^{\mathrm{T}}\left(x\right)V^{\prime \prime }\left(x\right)D\left(x\right)\hfill \\ \hfill & ={\left({\displaystyle \frac{2\mu }{3}}{({\omega }_1^2+{\omega }_2^2)}^{-{\displaystyle \frac{1}{3}}}{\omega }_1+I_{23}{\omega }_3{\omega }_2+{\sigma }^2{\omega }_1\right)}^2\hfill \\ \hfill & +{\left({\displaystyle \frac{2\mu }{3}}{({\omega }_1^2+{\omega }_2^2)}^{-{\displaystyle \frac{1}{3}}}{\omega }_2-I_{23}{\omega }_3{\omega }_1+{\sigma }^2{\omega }_2\right)}^2+{\displaystyle \frac{2\mu }{9}}{\sigma }^2{({\omega }_1^2+{\omega }_2^2)}^{{\displaystyle \frac{2}{3}}}\hfill \end{array}$$

(95)

is minimized in the sense of (66).

For $x_0={[2,3]}^{\mathrm{T}},I_{23}=1,{\omega }_3=1,\mu =2,$ and $\sigma =0.5$, Figure 1 and Figure 2 show the mean along with one standard deviation (shaded area) of the closed-loop system states along with the control inputs for ${10}^4$ sample paths.

Figure 1. System states versus time for Example 1. The bold lines show the average states over ${10}^4$ sample paths, whereas the shaded area shows a one standard deviation from the average.

Figure 2. Control inputs versus time for Example 1. The bold lines show the average states over ${10}^4$ sample paths, whereas the shaded area shows a one standard deviation from the average.

6. Conclusions

In this paper, we formulated an optimal control problem for finite time stochastic stabilization and derived sufficient conditions for designing a nonlinear feedback controller that ensures finite time stability in probability of the closed-loop system. The approach is based on a steady-state, stochastic Hamilton–Jacobi–Bellman framework, where the notion of optimality is associated with a Lyapunov function that satisfies a scalar differential inequality involving fractional powers. Furthermore, we developed inverse optimal feedback controllers for affine nonlinear stochastic systems. In future research, we will extend this framework to develop finite time stability in probability for semi-Markov jump systems [41], as well as for Itô diffusion processes with Markovian switching [42]. In addition, we will address the problem of fixed time optimal stabilization, as well as develop extensions to hybrid stochastic finite time and fixed time optimal control.