First and Second Moments of Spherical Distributions That Are Relevant for Biological Applications

Abstract

Spherical distributions, in particular, the von Mises–Fisher distribution, are often used to analyze directional data. The first and second moments of these distributions are of central interest, as they describe mean orientations as well as anisotropic diffusion tensors. Finding these moments often requires a numerical approximation of complex trigonometric integrals. Instead, we apply the divergence theorem on suitable domains to derive explicit forms of the first and second moments for n-dimensional von Mises–Fisher and peanut distributions. Based on these new formulas, we characterize some meaningful characteristics of these distributions: fractional anisotropy and the anisotropy ratio. We find, surprisingly, that the peanut distribution has an upper bound on anisotropy, while the von-Mises Fisher distribution has no such bound. As a side benefit, we find different forms of some identities for Bessel functions.

1. Introduction

Spherical distributions are of special importance when working with directional data [1]. They are used to represent orientation of objects or individuals and identify movement directions. Recently, spherical distributions have been particularly important in the modelling of directed motion in biology. Examples in ecology that have been modelled include the directed motion of wolves along seismic lines [2], the orientation of sea turtles along geomagnetic lines [3], hilltopping of butterflies [4], and migration of whales [5]. Examples of directed cell movement include the movement of melanoma cells [6], spread of glioma in the brain [7], oriented motion of cells on microfabricated structures [8], and directed motion of immune cells [9].

Mathematically, a spherical distribution is a probability distribution on the unit sphere ${\mathbb{S}}^{n-1}$ in ${\mathbb{R}}^n$, where $n>0$ denotes the space dimension. We usually denote it as $q\left(\theta \right)$, $\theta \in {\mathbb{S}}^{n-1}$ with the basic properties

$$q\left(\theta \right)\ge 0,\mathrm{f}\mathrm{o}\mathrm{r} \mathrm{a}\mathrm{l}\mathrm{l} \theta \in {\mathbb{S}}^{n-1},\mathrm{a}\mathrm{n}\mathrm{d}{\int }_{{\mathbb{S}}^{n-1}}q\left(\theta \right)d\theta =1.$$

(1)

For application to glioma, three spherical distributions have been proposed (we give explicit definitions later): the von Mises distribution (5) (also called von Mises–Fisher for higher dimensions), the peanut distribution (6), and the ordinary distribution function (ODF) (7) [7,10,11,12]. The von Mises distribution has been used in a model that was fit to data for 10 patients diagnosed with glioma in [7], while the ODF has been used for a theoretical model for glioma growth incorporating the effect from endothelial cells as well as the acidity from the environment in [12]. Here, we focus on the peanut and von Mises distributions. We generalize the distributions to any space dimensions $n>0$ and we compute new formulas for the expectation and variance–covariance matrices for these distributions. We also applied the method to the ODF distribution, but, unfortunately, we did not obtain an explicit formula for the second moment of the ODF distribution. Other important spherical distributions are the Bingham, the Fisher–Bingham, and the Kent distributions. These have not been used extensively in biological modelling; hence, we discuss them only briefly in the conclusion section.

1.1. Anisotropic Transport Equations

The popular use of spherical distributions in ecology and cell biology relies on the modelling of movement data with transport equations. In this short subsection, we recall some of the essential steps of this framework, to set the stage for the following calculations. Among the above applications, let us choose the example of wolf movement along seismic lines. The arguments for the other applications (glioma, immune cells, sea turtles, whales) are very similar.

Seismic lines are clear-cut lines in the Northern Canadian forests, which are cut by oil exploration companies to search for oil and gas [13]. Wolves in these forests can use these lines to migrate further than normal and increase their hunting success. Needless to say, this has a severe ecological impact. Using GPS data on wolf movement, it was shown by McKenzie et al. [2,14] that the directional orientation of wolves near seismic lines follows a von Mises distribution. Let us call it $q(x,\theta )$, $\theta \in {\mathbb{S}}^{n-1}$.

To formulate a mathematical model for the wolf movement, we introduce a wolf density $p(t,x,\theta )$ that depends on time t, location x, and orientation $\theta$ and consider the anisotropic transport equation

$$p_t+s\theta ·\nabla p=\mu \left(q(x,\theta ){\int }_{{\mathbb{S}}^{n-1}}p(t,x,{\theta }^{\prime })d{\theta }^{\prime }-p\right).$$

(2)

Here $\mu$ is a rate of change of direction and s is an average speed. The arguments of $p(t,x,\theta )$ have been suppressed in three of the terms.

The analysis of these types of models is well established, many papers are available [15,16,17] and we will not recall any details here. However, we will discuss the important parabolic scaling. Parabolic scaling is a scaling transformation of the transport Equation (2) into macroscopic time and space scales. It can be shown that, to leading order the integrated particle density

$$P(t,x)={\int }_{{\mathbb{S}}^{n-1}}p(t,x,\theta )d\theta$$

satisfies an advection diffusion equation

$$P_t(t,x)+\nabla ·\left(\mathbf{b}\left(x\right)P(t,x)\right)=\nabla {\nabla }^T:\left(\mathbb{D}\left(x\right)P(t,x)\right),$$

(3)

where the drift velocity and the diffusion coefficient are proportional to the first and second moments of $q\left(\theta \right)$:

$$\mathbf{b}\left(x\right)=s{\int }_{{\mathbb{S}}^{n-1}}\theta q(x,\theta )d\theta ,\mathbb{D}\left(x\right)=\frac{s^2}{\mu }{\int }_{{\mathbb{S}}^{n-1}}\theta {\theta }^{T}q(x,\theta )d\theta .$$

(4)

Hence, very clearly, knowledge of the first and second moments of $q\left(\theta \right)$ is essential here.

In the application to wolf data, the distribution $q(x,\theta )$ encodes the directional network of seismic lines in the environment [2,14]. In the case of sea turtles, $q(x,\theta )$ describes the orientation towards the target site [3]. Applied to glioma data, $q(x,\theta )$ is informed from an MRI imaging technique called diffusion tensor imaging (DTI) [7,12,18,19,20] (see also Section 5 for a simplified example).

Hillen et al. [10] calculated the explicit forms of the expectation and the variance–covariance matrix for the von Mises–Fisher distribution in two and three dimensions. It appears that the use of the divergence theorem in suitable domains was the key to obtaining the explicit formulas for the moments of these distributions.

1.2. Outline of the Paper

Here, we extend that methodology to higher dimensions. The advantage of knowing the explicit form of the moments for spherical distributions is that one can easily calculate the expectation and variance–covariance matrix without having to do the integrals numerically; hence, significantly reducing the computational cost for large dimensions. We find explicit forms for n-dimensional von Mises–Fisher and peanut distributions which, to our knowledge, are new formulas.

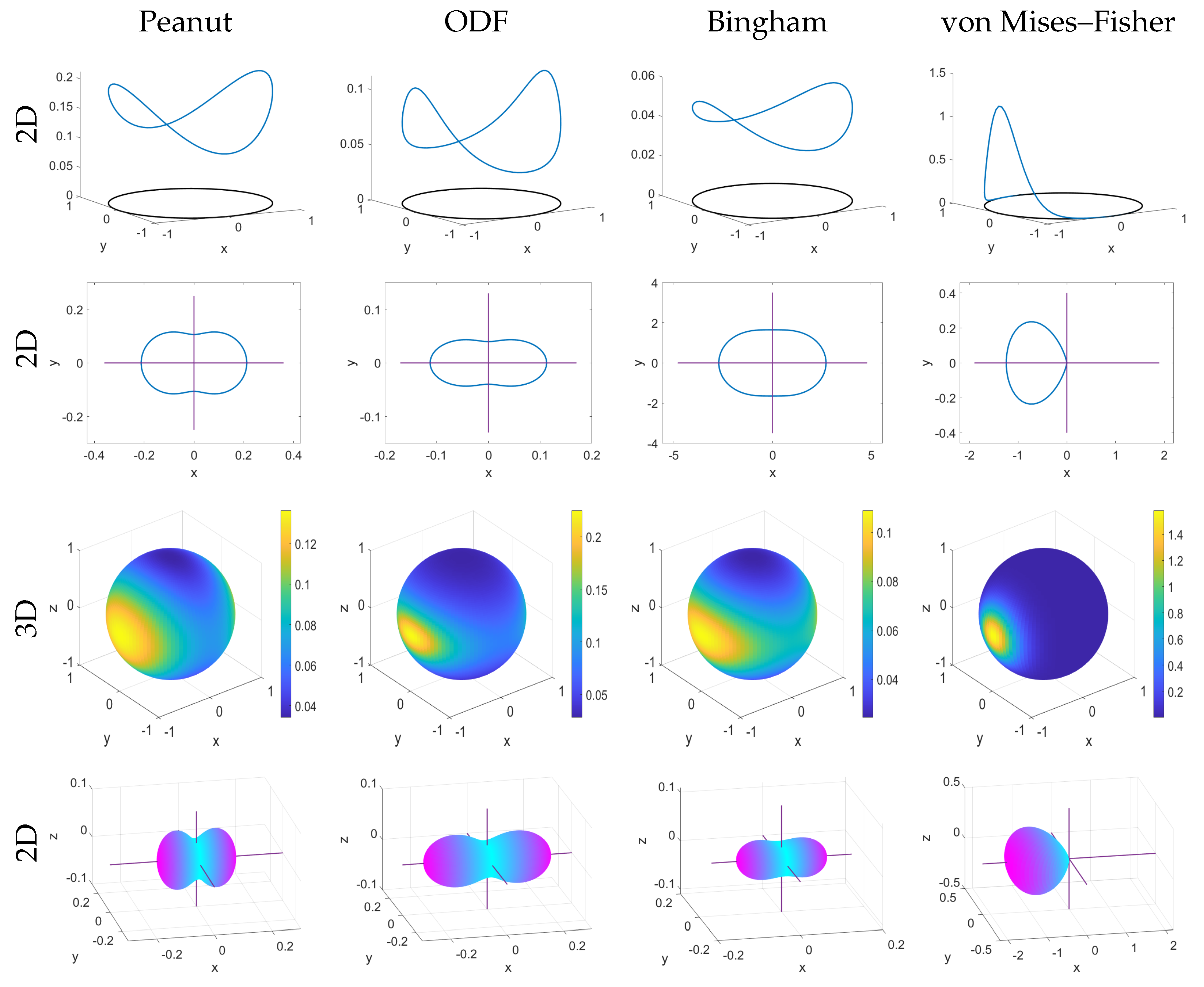
In addition, we consider the level of anisotropies that arise from these different formulations (peanut, ODF, von Mises–Fisher). The anisotropy is a measure of the distortion of the distribution in certain directions. It can be easily visualized by plotting level sets of the corresponding distributions $q\left(\theta \right)=const$ (see Figure 1). To measure the anisotropy, we first compute the eigenvalues of the corresponding variance–covariance matrices, and then compute the fractional anisotropy ($\mathsf{FA}$) and the maximal eigenvalue ratio R. We find that peanut distribution has a limit to how much anisotropy it can account for, however the von Mises–Fisher does not have such a limitation, showing that the von Mises–Fisher is the better choice for capturing anisotropy. Please note that, here, we focus on theoretical results, specific applications are treated in the cited literature [2,3,7,14,17].

Figure 1. Illustration of the spherical distributions in 2D and 3D (first and third rows, respectively) as well as their diffusion peanuts in 2D and 3D (second and last row, respectively). For the peanut, ODF, and Bingham distributions, ${\mathbb{D}}_W$ was taken to be a diagonal matrix with $1,0.5$, and $1,0.5,0.25$ on the main diagonal for 2D and 3D, respectively. For the Bingham distribution, $\Delta =0.75$. For von Mises–Fisher, $k=10$ and the preferred direction u was set to $(-1,0)$ and $(-1,0,0)$ for 2D and 3D, respectively. Note here that the peanut and ODF are symmetric ($q(-\theta )=q\left(\theta \right)$), whereas von Mises−Fisher is asymmetric.

1.3. Definitions of Some Spherical Distributions

In this section, we give the explicit definitions of the spherical distributions that we will work with. We use given parameters where $k>0$ is a concentration parameter, $u\in {\mathbb{R}}^n$ is a given vector, and $A\in {\mathbb{R}}^{n\times n}$ is a given positive definite matrix. In the case of glioma modelling, A is estimated from the diffusion tensor data (see Section 5).

• The n-dimensional von Mises–Fisher distribution is defined as [10]

  $$q\left(\theta \right)=\frac{k^{\frac{n}{2}-1}}{{\left(2\pi \right)}^{\frac{n}{2}}{I}_{\frac{n}{2}-1}\left(k\right)}{e}^{k\theta ·u}$$

  (5)

  where $\theta \in {\mathbb{S}}^{n-1}$ and $I_p\left(k\right)$ with $p\in \mathbb{C}$ defines the modified Bessel function of the first kind of order p, k is the concentration parameter, and $u\in {\mathbb{S}}^{n-1}$ defines the likeliest direction of the distribution. Here, we employ a formulation that uses Bessel functions. An alternative definition uses the Gamma function and can be found in Appendix A.1.
• The n-dimensional peanut distribution is defined as [11]

  $$q\left(\theta \right)=\frac{n}{|{\mathbb{S}}^{n-1}|tr\left(A\right)}{\theta }^{T}A\theta$$

  (6)

  where $tr\left(A\right)$ denotes the trace of A, $\theta \in {\mathbb{S}}^{n-1}$, and $|{\mathbb{S}}^{n-1}|$ is the surface area of an $n-1$ dimensional sphere.
• The n-dimensional ODF distribution is defined as [12,21]

  $$q\left(\theta \right)=\frac{1}{{4\pi \left|A\right|}^{\frac{1}{2}}{\left({\theta }^T{A}^{-1}\theta \right)}^{\frac{3}{2}}},$$

  (7)

  where $\theta$ and A hold the same definitions as in the peanut distribution defined above. In (7), $A^{-1}$ denotes the inverse of A and $\left|A\right|=detA$.
• We only briefly discuss the Bingham distribution [1,22], which is defined as

  $$q\left(\theta \right)=\frac{1}{\sqrt{{\left|A\right|(4\pi \Delta )}^3}}{e}^{\frac{-{\theta }^T{A}^{-1}\theta }{4\Delta }}$$

  (8)

  where $\theta$, A, $\left|A\right|$ hold the same definitions as above and $\Delta$ is the diffusion time.
• The Fisher–Bingham distribution [1] is defined as

  $$q\left(\theta \right)=\frac{1}{a(k,A)}{e}^{k{u}^T\theta +{\theta }^{T}A\theta }$$

  (9)

  where k is a concentration parameter and u is the mean direction and $a(k,A)$ is a normalization constant. In the case of a diagonal matrix A, the Fisher–Bingham distribution is also known as Kent distribution [1,23].

We show the 2D and 3D versions of the peanut, ODF, Bingham, and von Mises–Fisher distributions in Figure 1.

1.4. Definitions of First and Second Moments

Since we will be calculating the first and second moments of the spherical distributions in n dimensions to obtain the expectation and the variance–covariance matrix, we provide the explicit definitions here. In general, the expectation [10] is defined as

$$\mathsf{E}\left[q\right]={\int }_{{\mathbb{S}}^{n-1}}\theta q\left(\theta \right)d\theta$$

(10)

and variance–covariance matrix [10] is defined as

$$\mathsf{Var}\left[q\right]={\int }_{{\mathbb{S}}^{n-1}}\theta {\theta }^{T}q\left(\theta \right)d\theta -\mathsf{E}\left[q\right]\mathsf{E}{\left[q\right]}^T.$$

(11)

Here, $a{b}^T$ for $a,b\in {\mathbb{R}}^n$ denotes the tensor product between matrices. For simplicity of notation, we give names to the zeroth, first, and second moment. The zeroth moment is defined by

$${\mathsf{M}}^0\left[q\left(\theta \right)\right]={\int }_{{\mathbb{S}}^{n-1}}q\left(\theta \right)d\theta ,$$

(12)

the first moment is defined by

$${\mathsf{M}}^1\left[q\left(\theta \right)\right]={\int }_{{\mathbb{S}}^{n-1}}\theta q\left(\theta \right)d\theta =\mathsf{E}\left[q\left(\theta \right)\right]$$

(13)

and the second moment is defined by

$${\mathsf{M}}^2\left[q\left(\theta \right)\right]={\int }_{{\mathbb{S}}^{n-1}}\theta {\theta }^{T}q\left(\theta \right)d\theta .$$

(14)

2. First and Second Moments of von Mises–Fisher Distributions

In this section, we calculate the first and second moments of the general n-dimensional von Mises–Fisher distributions (5), in order to get general formulas for expectation and the variance–covariance matrix for these distributions.

For simplicity of notation, sums over crossed repeated indices are understood as in tensor calculus [10]

$$a^i{b}_i=\sum _{i=1}^n{a}^i{b}_i.$$

(15)

We also recommend referring to Appendix A.2, Appendix A.4 and Appendix A.5 for the basic properties of Bessel functions, definitions of ${\mathbb{B}}_1\left(0\right)$ and ${\mathbb{S}}^{n-1}$, as well as formulas that are used in the preceeding calculations.

Theorem 1. 

Consider the von Mises–Fisher distribution (5) in any dimension n. The expectation and variance–covariance matrix are

$$\begin{array}{ccc}\hfill \mathsf{E}\left[q\right]& =& \frac{I_{\frac{n}{2}}\left(k\right)}{I_{\frac{n}{2}-1}\left(k\right)}u,\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill \mathsf{Var}\left[q\right]& =& \frac{I_{\frac{n}{2}}\left(k\right)}{k{I}_{\frac{n}{2}-1}\left(k\right)}\mathbb{I}+\left[\frac{I_{\frac{n}{2}+1}\left(k\right)}{I_{\frac{n}{2}-1}\left(k\right)}-{\left(\frac{I_{\frac{n}{2}}\left(k\right)}{I_{\frac{n}{2}-1}\left(k\right)}\right)}^2\right]u{u}^T.\hfill \end{array}$$

(17)

Proof. 

Expectation: We abbreviate the normalization constant in (5) as

$$c=\frac{k^{\frac{n}{2}-1}}{{\left(2\pi \right)}^{\frac{n}{2}}{I}_{\frac{n}{2}-1}\left(k\right)}.$$

(18)

Following a similar procedure as in [10] we calculate the expectation. Let $b\in {\mathbb{R}}^n$ be an arbitrary vector, then, using (5) we obtain

$$\begin{array}{c}\hfill b·\frac{1}{c}\mathsf{E}\left[q\right]=b·{\int }_{{\mathbb{S}}^{n-1}}\theta e^{k\theta u}d\theta ={\int }_{{\mathbb{S}}^{n-1}}{\theta }^j{b}_j{e}^{k{\theta }_l{u}^l}d\theta ,\end{array}$$

(19)

where we use the summation convention (15). Note, that $\theta$ is a unit vector and also the outside normal vector at $\theta$ on ${\mathbb{S}}^{n-1}$. Hence, we apply the divergence theorem on ${\mathbb{S}}^{n-1}$ and continue the calculation as follows

$$\begin{array}{cc}\hfill {\int }_{{\mathbb{S}}^{n-1}}{\theta }^j{b}_j{e}^{k{\theta }_l{u}^l}d\theta & ={\int }_{{\mathbb{B}}_1\left(0\right)}\frac{\partial }{\partial v^j}{b}_j{e}^{k{v}_l{u}^l}dv\hfill \\ \hfill & =b·uk{\int }_{{\mathbb{B}}_1\left(0\right)}{e}^{kvu}dv\hfill \\ \hfill & =b·uk{\int }_0^1{\int }_{{\mathbb{S}}^{n-1}}{e}^{krvu}{r}^{n-1}dvdr\hfill \\ \hfill & =b·u\frac{{\left(2\pi \right)}^{\frac{n}{2}}}{k^{\frac{n}{2}-2}}{\int }_0^1{r}^{\frac{n}{2}}{I}_{\frac{n}{2}-1}\left(rk\right)dr,\hfill \end{array}$$

(20)

where, in the third equivalence, we divide the integral on a ball into radial and angular components, and in the last step we applied (1).

Making use of the Bessel identities (A5) and (A6), we rewrite the term within the integral, that is

$$\begin{array}{c}\hfill r^{\frac{n}{2}}{I}_{\frac{n}{2}-1}\left(rk\right)=r^{\frac{n}{2}}{i}^{-\frac{n}{2}+1}{J}_{\frac{n}{2}-1}\left(irk\right)=\frac{i^{-n}}{k^{\frac{n}{2}+1}}\frac{d}{dr}{\left(irk\right)}^{\frac{n}{2}}{J}_{\frac{n}{2}}\left(irk\right).\end{array}$$

(21)

Using (21), we simplify further and apply the fundamental theorem of calculus to obtain

$$b·u\frac{{\left(2\pi \right)}^{\frac{n}{2}}}{k^{\frac{n}{2}-2}}{\int }_0^1{r}^{\frac{n}{2}}{I}_{\frac{n}{2}-1}\left(rk\right)dr=b·u\frac{{\left(2\pi \right)}^{\frac{n}{2}}}{k^{\frac{n}{2}-1}}{i}^{-\frac{n}{2}}{J}_{\frac{n}{2}}\left(ik\right)=b·u\frac{{\left(2\pi \right)}^{\frac{n}{2}}}{k^{\frac{n}{2}-1}}{I}_{\frac{n}{2}}\left(k\right).$$

(22)

Therefore, we find that

$$b·\frac{1}{c}\mathsf{E}\left[q\right]=b·u\frac{{\left(2\pi \right)}^{\frac{n}{2}}}{k^{\frac{n}{2}-1}}{I}_{\frac{n}{2}}\left(k\right).$$

After simplifying, and noting that b is an arbitrary vector, it follows that

$$\mathsf{E}\left[q\right]=\frac{I_{\frac{n}{2}}\left(k\right)}{I_{\frac{n}{2}-1}\left(k\right)}u.$$

(23)

Note that, from this calculation, we also obtain the following useful formula

$${\int }_{{\mathbb{B}}_1\left(0\right)}{e}^{kvu}dv=\frac{{\left(2\pi \right)}^{\frac{n}{2}}}{k^{\frac{n}{2}}}{I}_{\frac{n}{2}}\left(k\right),$$

(24)

by equating the right-hand term of the fourth equivalence in (20) with the right-hand term in the last equivalence of (22).

Second moment: We now calculate the second moment as well as the variance–covariance matrix for the von Mises–Fisher distribution (5).

Since the expectation for (5) is nonzero, we directly calculate the second term in the variance–covariance matrix formula (11). Using (23), it is simply

$$\mathsf{E}\left[q\right]\mathsf{E}{\left[q\right]}^T={\left(\frac{I_{\frac{n}{2}}\left(k\right)}{I_{\frac{n}{2}-1}\left(k\right)}\right)}^{2}u{u}^T.$$

(25)

Now, we calculate the first term in the variance–covariance matrix formula (11), which is the second moment, by following the approach in [10].

Let c be defined by (18) and $a,b\in {\mathbb{R}}^n$. Again, we use the fact that $\theta$ is the outside normal vector at $\theta$ on ${\mathbb{S}}^{n-1}$ to apply the divergence theorem. Thus, we obtain

$$\begin{array}{cc}\hfill a^T{\int }_{{\mathbb{S}}^{n-1}}\theta {\theta }^{T}q\left(\theta \right)d\theta b& =c{\int }_{{\mathbb{S}}^{n-1}}{a}_j{\theta }^j{b}_m{\theta }^m{e}^{k{\theta }^l{u}_l}d\theta \hfill \\ \hfill & =c{\int }_{{\mathbb{S}}^{n-1}}{\theta }^j\left(a_j{b}_m{\theta }^m{e}^{k{\theta }^l{u}_l}\right)d\theta \hfill \\ \hfill & =c{\int }_{{\mathbb{B}}_1\left(0\right)}\frac{\partial }{\partial v^j}\left(a_j{b}_m{v}^m{e}^{k{v}^l{u}_l}\right)dv\hfill \\ \hfill & =c\left(a^{T}b{\int }_{{\mathbb{B}}_1\left(0\right)}{e}^{kvu}dv+k{a}^{T}ub·{\int }_{{\mathbb{B}}_1\left(0\right)}v{e}^{kvu}dv\right).\hfill \end{array}$$

The first integral is solved in (24). We calculate the integral in the second term as

$${\int }_{{\mathbb{B}}_1\left(0\right)}v{e}^{kvu}dv={\int }_0^1{r}^n{\int }_{{\mathbb{S}}^{n-1}}v{e}^{kr\theta u}dvdr=\frac{{\left(2\pi \right)}^{\frac{n}{2}}}{k^{\frac{n}{2}-1}}u{\int }_0^1{r}^{\frac{n}{2}+1}{I}_{\frac{n}{2}}\left(rk\right)dr$$

by applying (1) at the second equivalence.

By using the Bessel identities (A5) and (A6), we can rewrite the term in the integral as

$$r^{\frac{n}{2}+1}{I}_{\frac{n}{2}}\left(rk\right)=r^{\frac{n}{2}+1}{i}^{-\frac{n}{2}}{J}_{\frac{n}{2}}\left(irk\right)=\frac{i^{-n-2}}{k^{\frac{n}{2}+2}}\frac{d}{dr}{\left(irk\right)}^{\frac{n}{2}+1}{J}_{\frac{n}{2}+1}\left(irk\right).$$

(26)

Using (26) and (A5), we obtain

$$\frac{{\left(2\pi \right)}^{\frac{n}{2}}}{k^{\frac{n}{2}-1}}u{\int }_0^1{r}^{\frac{n}{2}+1}{I}_{\frac{n}{2}}\left(rk\right)dr=\frac{{\left(2\pi \right)}^{\frac{n}{2}}{i}^{-\frac{n}{2}-1}}{k^{\frac{n}{2}}}u{J}_{\frac{n}{2}+1}\left(ik\right)=\frac{{\left(2\pi \right)}^{\frac{n}{2}}}{k^{\frac{n}{2}}}u{I}_{\frac{n}{2}+1}\left(k\right).$$

(27)

Thus,

$${\int }_{{\mathbb{B}}_1\left(0\right)}v{e}^{kvu}dv=\frac{{\left(2\pi \right)}^{\frac{n}{2}}}{k^{\frac{n}{2}}}u{I}_{\frac{n}{2}+1}\left(k\right).$$

(28)

Using (22) and (28), we find that

$${\int }_{{\mathbb{S}}^{n-1}}\theta {\theta }^{T}q\left(\theta \right)d\theta =\frac{I_{\frac{n}{2}}}{k{I}_{\frac{n}{2}-1}}\mathbb{I}+\frac{I_{\frac{n}{2}+1}}{I_{\frac{n}{2}-1}}u{u}^T,$$

(29)

since $a,b$ are arbitrary.

Substituting (25) and (29) into the variance formula (11), we obtain

$$\mathsf{Var}\left[q\right]=\frac{I_{\frac{n}{2}}\left(k\right)}{k{I}_{\frac{n}{2}-1}\left(k\right)}\mathbb{I}+\frac{I_{\frac{n}{2}+1}\left(k\right)}{I_{\frac{n}{2}-1}\left(k\right)}u{u}^T-{\left(\frac{I_{\frac{n}{2}}\left(k\right)}{I_{\frac{n}{2}-1}\left(k\right)}\right)}^{2}u{u}^T.$$

(30)

□

Corollary 1. 

Consider the bimodal von Mises–Fisher distribution

$$q\left(\theta \right)=\frac{k^{\frac{n}{2}-1}}{2{\left(2\pi \right)}^{\frac{n}{2}}{I}_{\frac{n}{2}-1}\left(k\right)}(e^{k\theta ·u}+e^{-k\theta ·u}).$$

(31)

The expectation and the variance–covariance matrix for (31) is given by

$$\begin{array}{ccc}\hfill \mathsf{E}\left[q\right]& =& 0,\hfill \\ \hfill \mathsf{Var}\left[q\right]& =& \frac{I_{\frac{n}{2}}\left(k\right)}{k{I}_{\frac{n}{2}-1}\left(k\right)}\mathbb{I}+\frac{I_{\frac{n}{2}+1}\left(k\right)}{I_{\frac{n}{2}-1}\left(k\right)}u{u}^T.\hfill \end{array}$$

(32)

Proof. 

We can rewrite (31) as

$$q\left(\theta \right)=\frac{1}{2}{q}_u\left(\theta \right)+\frac{1}{2}{q}_{-u}\left(\theta \right)$$

(33)

where $q_u\left(\theta \right)$ is defined by (5) and $q_{-u}\left(\theta \right)$ is also defined by (5), but with u replaced by $-u$. Using this, we can calculate the expectation and the variance–covariance matrix using the results in Theorem 1. The expectation is calculated as follows

$$E\left[q\right]=\frac{1}{2}E\left[q_u\right]+\frac{1}{2}E\left[q_{-u}\right]=\frac{I_{\frac{n}{2}}\left(k\right)}{2I_{\frac{n}{2}-1}\left(k\right)}u-\frac{I_{\frac{n}{2}}\left(k\right)}{2I_{\frac{n}{2}-1}\left(k\right)}u=0.$$

(34)

Since the expectation is 0, the variance–covariance matrix is given by its second moment. Therefore, using (29), we obtain

$$\begin{array}{cc}\hfill Var\left[q\right]& =\frac{1}{2}\left[\frac{I_{\frac{n}{2}}}{k{I}_{\frac{n}{2}-1}}\mathbb{I}+\frac{I_{\frac{n}{2}+1}}{I_{\frac{n}{2}-1}}u{u}^T\right]+\frac{1}{2}\left[\frac{I_{\frac{n}{2}}}{k{I}_{\frac{n}{2}-1}}\mathbb{I}+\frac{I_{\frac{n}{2}+1}}{I_{\frac{n}{2}-1}}(-u){(-u)}^T\right]\hfill \\ \hfill & =\frac{I_{\frac{n}{2}}}{k{I}_{\frac{n}{2}-1}}\mathbb{I}+\frac{I_{\frac{n}{2}+1}}{I_{\frac{n}{2}-1}}u{u}^T.\hfill \end{array}$$

(35)

□

Example for $n=2$: The von Mises–Fisher distribution in two dimensions is called the von Mises distribution. It has been used in various applications that we mentioned above. Hence, here, we recall the result for the bimodal von Mises distribution in two dimensions [10]:

$$\begin{array}{ccc}\hfill \mathsf{E}\left[q\right]& =& 0,\hfill \\ \hfill \mathsf{Var}\left[q\right]& =& \frac{I_1\left(k\right)}{k{I}_0\left(k\right)}\mathbb{I}+\frac{I_2\left(k\right)}{I_0\left(k\right)}u{u}^T.\hfill \end{array}$$

(36)

Example for $n=3$: It is interesting to consider the important case of the von Mises distribution (5) for $n=3$. For $n=3$, we find

$$\begin{array}{ccc}\hfill \mathsf{E}\left[q\right]& =& \frac{I_{\frac{3}{2}}\left(k\right)}{I_{\frac{1}{2}}\left(k\right)}u,\hfill \\ \hfill \mathsf{Var}\left[q\right]& =& \frac{I_{\frac{3}{2}}\left(k\right)}{k{I}_{\frac{1}{2}}\left(k\right)}\mathbb{I}+\left[\frac{I_{\frac{5}{2}}\left(k\right)}{I_{\frac{1}{2}}\left(k\right)}-{\left(\frac{I_{\frac{3}{2}}\left(k\right)}{I_{\frac{1}{2}}\left(k\right)}\right)}^2\right]u{u}^T.\hfill \end{array}$$

In [10], these terms were found as

$$\begin{array}{ccc}\hfill \mathsf{E}\left[q\right]& =& \left(cothk-\frac{1}{k}\right)u,\hfill \\ \hfill \mathsf{Var}\left[q\right]& =& \left(\frac{cothk}{k}-\frac{1}{k^2}\right)\mathbb{I}+\left[1-\frac{cothk}{k}+\frac{2}{k^2}-{coth}^{2}k\right]u{u}^T.\hfill \end{array}$$

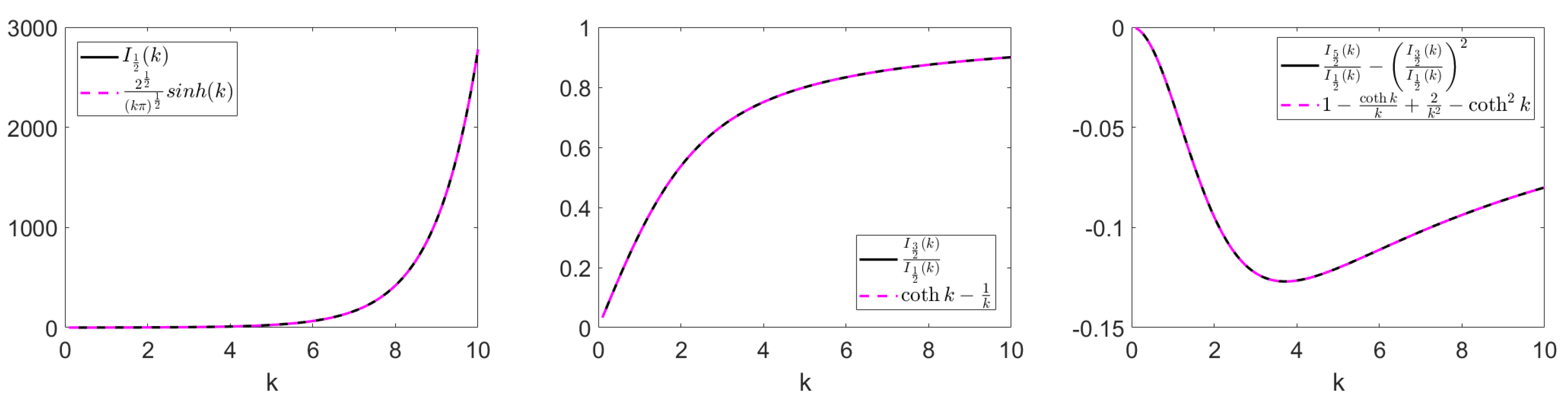
Hence, we can compare the coefficients and find three new identities for Bessel functions:

$$\begin{array}{ccc}\hfill \frac{I_{\frac{3}{2}}\left(k\right)}{I_{\frac{1}{2}}\left(k\right)}& =& cothk-\frac{1}{k},\hfill \end{array}$$

(37)

$$\begin{array}{ccc}\hfill \frac{I_{\frac{3}{2}}\left(k\right)}{k{I}_{\frac{1}{2}}\left(k\right)}& =& \frac{cothk}{k}-\frac{1}{k^2},\hfill \end{array}$$

(38)

$$\begin{array}{ccc}\hfill \frac{I_{\frac{5}{2}}\left(k\right)}{I_{\frac{1}{2}}\left(k\right)}-{\left(\frac{I_{\frac{3}{2}}\left(k\right)}{I_{\frac{1}{2}}\left(k\right)}\right)}^2& =& 1-\frac{cothk}{k}+\frac{2}{k^2}-{coth}^{2}k.\hfill \end{array}$$

(39)

Note that (37) is equivalent with (38) for $k\ne 0$. These formulas can also be derived by using the trigonometric form of Bessel function identities for $I_{\frac{1}{2}}$, $I_{\frac{3}{2}}$, $I_{\frac{5}{2}}$ defined in [24], where

$$I_{\frac{1}{2}}\left(k\right)=\frac{2^{\frac{1}{2}}}{{\left(k\pi \right)}^{\frac{1}{2}}}sinhk.$$

(40)

We confirm that the above identities hold numerically in Figure 2.

Figure 2. The black curve in the left, middle, and left images illustrates the left−hand side of the Equations (40), (37), and (39). The dashed pink curve in the left, middle, and left images illustrates the right-hand side of the Equations (40), (37), and (39). The images show numerical agreement between both sides of the equivalences (40), (37), and (39).

Summary of Section 2

In this section, we computed the first and second moments of the von Mises–Fisher distribution (5) in the proof of Theorem 1 to obtain the explicit forms of the expectation and variance–covariance matrix for n dimensions. To our knowledge, these formulas for the expectation and the variance–covariance matrix in the general dimension n are new. Corollary 1 provides a method on how to generalize the explicit formulas in Theorem 1 to obtain the analytical form of the expectation and variance–covariance matrix for mixed modal von Mises–Fisher distributions, where we used the bimodal von Mises–Fisher distribution as an example. In this section, we also find new versions of Bessel function identities as a side result.

3. First and Second Moment of Peanut Distribution

We first note that the peanut distribution (6), the ODF (7), and the Bingham distribution (8) are all of the form

$$q\left(\theta \right)=F\left({\theta }^{T}A\theta \right),$$

with an appropriate function F, where A is a given matrix. In the case of ODF, we actually use $A^{-1}$, but the structure is the same. Due to symmetry in $\theta$, the first moment equals zero:

Lemma 1. 

If A is a given matrix and q is of the form $q\left(\theta \right)=F\left({\theta }^{T}A\theta \right)$, then $\mathsf{E}\left[q\right]=0$. Moreover, all odd moments are zero too.

Proof. 

Let ${\theta }_1$ denote the first coordinate of $\theta$ in ${\mathbb{R}}^n$. We split the sphere ${\mathbb{S}}^{n-1}$ according to the positive and negative ${\theta }_1$ component, obtaining two hemispheres:

$$S^{+}:=\{\theta \in {\mathbb{S}}^{n-1}:{\theta }_1\ge 0\}\mathrm{a}\mathrm{n}\mathrm{d} S^{-}:=\{\theta \in {\mathbb{S}}^{n-1}:{\theta }_1<0\}.$$

This allows us to exploit symmetry to get the following result

$$\begin{array}{ccc}\hfill \mathsf{E}\left[q\right]& =& {\int }_{S^{+}}\theta F\left({\theta }^{T}A\theta \right)d\theta +{\int }_{S^{-}}\theta F\left({\theta }^{T}A\theta \right)d\theta \hfill \\ & =& {\int }_{S^{+}}\theta F\left({\theta }^{T}A\theta \right)d\theta +{\int }_{S^{+}}-\theta F\left((-{\theta }^T)A(-\theta )\right)d\theta \hfill \\ & =& 0.\hfill \end{array}$$

□

• For the second moment, we consider each distribution separately.

3.1. Second Moment of the Peanut Distribution

Here, we calculate the variance–covariance matrix for the peanut distribution (6). Note that, since $\mathsf{E}\left[q\right]=0$, the variance–covariance matrix is simply the second moment of (6), that is

$$\begin{array}{c}\hfill \mathsf{Var}\left[q\right]={\int }_{{\mathbb{S}}^{n-1}}\theta {\theta }^{T}q\left(\theta \right)d\theta .\end{array}$$

(41)

With this, we can formulate our result, which to our knowledge is a new formula for the variance–covariance matrix of the peanut distribution (6) in n dimensions.

Theorem 2. 

Consider the peanut distribution (6). Then

$$\begin{array}{ccc}\hfill \mathsf{E}\left[q\right]& =& 0,\hfill \end{array}$$

(42)

$$\begin{array}{ccc}\hfill \mathsf{Var}\left[q\right]& =& \frac{1}{(n+2)}\mathbb{I}+\frac{1}{(n+2)tr\left(A\right)}(A+A^T).\hfill \end{array}$$

(43)

Proof. 

We have seen in Lemma 1 that $\mathsf{E}\left(q\right)=0$. For simplicity, we define the coefficient in (6) as

$$c=\frac{n}{|{\mathbb{S}}^{n-1}|tr\left(A\right)}.$$

(44)

To compute the second moment, we multiply $\mathsf{Var}\left[q\right]$ by two arbitrary vectors $a,b\in {\mathbb{R}}^n$ in order to obtain a scalar value. Then, we use the fact that $\theta$ is the outside normal vector at $\theta$ on ${\mathbb{S}}^{n-1}$ to apply the divergence theorem. Using (6) and (44), we obtain the following result

$$\begin{array}{cc}\hfill a^T\left(\mathsf{Var}\left[q\right]\right)b& ={\int }_{{\mathbb{S}}^{n-1}}{a}^T\theta {\theta }^{T}q\left(\theta \right)bd\theta \hfill \\ \hfill & =c{\int }_{{\mathbb{S}}^{n-1}}{a}_i{\theta }^i{b}_j{\theta }^j{\theta }^{T}A\theta d\theta \hfill \\ \hfill & =c{\int }_{{\mathbb{B}}_1\left(0\right)}\frac{\partial }{\partial v_i}\left(a_i{b}_j{v}^j{v}^{T}Av\right)dv\hfill \\ \hfill & =a^T\left(c{\int }_{{\mathbb{B}}_1\left(0\right)}{v}^{T}Avdv\right)b+a^T\left(c{\int }_{{\mathbb{B}}_1\left(0\right)}(A+A^T)v{v}^{T}dv\right)b,\hfill \end{array}$$

where, in the third equivalence, the divergence theorem was applied and, in the last equivalence, the product rule was used.

Next, we simplify the final two terms in the above calculation. The first term simplifies as

$$\begin{array}{cc}\hfill a^T\left(c{\int }_{{\mathbb{B}}_1\left(0\right)}{v}^{T}Avdv\right)b& =a^T\left(c{\int }_0^1{r}^{n+1}{\int }_{{\mathbb{S}}^{n-1}}{\theta }^{T}A\theta d\theta \right)b\hfill \\ \hfill & =\frac{a^{T}b}{n+2},\hfill \end{array}$$

(45)

since ${\int }_{{\mathbb{S}}^{n-1}}q\left(\theta \right)d\theta =1$, implying that ${\int }_{{\mathbb{S}}^{n-1}}{\theta }^{T}A\theta d\theta =1/c.$ For the second term, we set

$$J=A+A^T$$

and simplify

$$\begin{array}{cc}\hfill a^T\left(c{\int }_{{\mathbb{B}}_1\left(0\right)}Jv{v}^{T}dv\right)b& =c{\int }_0^1{r}^{n+1}dr{\int }_{{\mathbb{S}}^{n-1}}{\theta }_j{a}^i{J}_{ij}{\theta }^m{b}_{m}d\theta \hfill \\ \hfill & =\frac{c}{n+2}{\int }_{{\mathbb{B}}_1\left(0\right)}\frac{\partial }{\partial w_j}\left(a^i{J}_{ij}{w}^m{b}_m\right)dw\hfill \\ \hfill & =\frac{c}{n+2}{a}^i{J}_{ij}{\int }_{{\mathbb{B}}_1\left(0\right)}\frac{\partial }{\partial w_j}{w}^m{b}_{m}dw\hfill \\ \hfill & =\frac{c}{n+2}{a}^i{J}_{ij}{b}_j\left|{\mathbb{B}}_1\left(0\right)\right|\hfill \\ \hfill & =\frac{1}{(n+2)tr\left(A\right)}{a}^{T}Jb.\hfill \end{array}$$

(46)

In the above calculation, the divergence theorem was applied at the second equivalence and the last equivalence made use of (A10).

Therefore, since $a,b\in {\mathbb{R}}^n$ are arbitrary, it follows that

$$\mathsf{Var}\left[q\right]=\frac{1}{(n+2)}\mathbb{I}+\frac{1}{(n+2)tr\left(A\right)}(A+A^T).$$

□

3.2. Summary of Section 3

In this section, we computed the first and second moments of the peanut distribution (6) to obtain explicit forms for the expectation and variance–covariance matrix in Theorem 6. To our knowledge, the analytical formulas for expectation and variance–covariance matrix for the peanut distribution are new. We also showed that spherical distributions in the form $q\left(\theta \right)=F\left({\theta }^{T}A\theta \right)$ have $E\left[q\right]=0$. We applied the same method for the ODF and the Bingham distributions, but unfortunately, no closed-form expressions could be derived.

4. Eigenvalues and Anisotropy

When spherical distributions are used in diffusion models, the variance–covariance matrix describes the anisotropic movement of the random walkers [17]. The level of anisotropy can be measured by the eigenvalues of the diffusion tensor and by the fractional anisotropy ($\mathsf{FA}$) [7]. The fractional anisotropy $\mathsf{FA}$ is an index between 0 and 1, where 0 is the case of full radial symmetry giving isotropy and 1 is the case of extreme anisotropic alignment to a particular direction. Another indicator of anisotropy is the ratio R of the largest to the smallest eigenvalue of the diffusion tensor. This quantity ranges between 1 (isotropic) to ∞ (maximal anisotropic).

Note that the fractional anisotropy and the anisotropy ratio are only used for symmetric distributions of the form $q(-\theta )=q\left(\theta \right)$. In this case, $\mathsf{E}\left[q\right]=0$ and

$$\mathsf{Var}\left[q\right]={\int }_{{\mathbb{S}}^{n-1}}\theta {\theta }^{T}q\left(\theta \right)d\theta .$$

Hence, the following applies to the peanut distribution and to the bimodal von Mises Fisher distribution (31). The ODF and the Bingham distributions are also symmetric, but since we do not have explicit forms of the second moments, we cannot compute their anisotropy values for general dimensions.

Recall that, in (4), we identified the diffusion tensor as

$$\mathbb{D}=\frac{s^2}{\mu }\mathsf{Var}\left[q\right],$$

(47)

where s is the speed and $\mu$ is the turning rate of a cell or individual. Hence, the eigenvalues of $\mathbb{D}$ are scaled versions of the eigenvalues of ${\mathsf{Var}}_q$.

The fractional anisotropy (FA) formulas are defined separately for two and three dimensions and we summarize them in the following definition.

Definition 1. 

1. 

The fractional anisotropy in two dimensions is given by

$${\mathsf{FA}}_2=\sqrt{\frac{2[{({\lambda }_1-\overline{\lambda })}^2+{({\lambda }_2-\overline{\lambda })}^2]}{{\lambda }_1^2+{\lambda }_2^2}},$$

(48)

where ${\lambda }_1,{\lambda }_2$ are the eigenvalues of a two-dimensional tensor and $\overline{\lambda }$ is the average of the two eigenvalues [7].

2. 

The fractional anisotropy in three dimensions is given by

$${\mathsf{FA}}_3=\sqrt{\frac{3[{({\lambda }_1-\overline{\lambda })}^2+{({\lambda }_2-\overline{\lambda })}^2+{({\lambda }_3-\overline{\lambda })}^2]}{2({\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2)}},$$

(49)

where ${\lambda }_1,{\lambda }_2,{\lambda }_3$ are the eigenvalues of a three-dimensional tensor and $\overline{\lambda }$ is the average of the three eigenvalues [7].

3. 

The anisotropy ratio R is defined as

$$R=\frac{max\left\{eigenvalues of \mathbb{D}\right\}}{min\left\{eigenvalues of \mathbb{D}\right\}}.$$

(50)

Theorem 3. 

Given a symmetric, positive definite matrix A with eigenvalue and eigenvector pairs $({\widehat{\lambda }}_i,{\widehat{v}}_i)$, $i=1,\dots ,n$, the diffusion tensor arising from the peanut distribution (6) is

$$\mathbb{D}=\frac{s^2}{\mu (n+2)}\mathbb{I}+\frac{2s^2}{\mu (n+2)tr\left(A\right)}A.$$

(51)

The diffusion tensor (51) has the eigenvalues

$${\lambda }_n=\frac{s^2}{\mu (n+2)}\left(1+\frac{2{\widehat{\lambda }}_n}{tr\left(A\right)}\right).$$

The fractional anisotropies and the ratio of eigenvalues are bounded where

$$\begin{array}{cc}\hfill 0\le {\mathsf{FA}}_2& =2|{\widehat{\lambda }}_1-{\widehat{\lambda }}_2|\sqrt{\frac{1}{{(tr\left(A\right)+2{\widehat{\lambda }}_1)}^2+{(tr\left(A\right)+2{\widehat{\lambda }}_2)}^2}}\le \frac{2}{\sqrt{10}},\hfill \end{array}$$

(52)

$$\begin{array}{cc}\hfill 0\le {\mathsf{FA}}_3& =\sqrt{\frac{2[{(2{\widehat{\lambda }}_1+{\widehat{\lambda }}_2-{\widehat{\lambda }}_3)}^2+{(2{\widehat{\lambda }}_2-{\widehat{\lambda }}_1-{\widehat{\lambda }}_3)}^2+{(2{\widehat{\lambda }}_3-{\widehat{\lambda }}_1-{\widehat{\lambda }}_2)}^2]}{3[{(tr\left(A\right)+2{\widehat{\lambda }}_1)}^2+{(tr\left(A\right)+2{\widehat{\lambda }}_2)}^2+{(tr\left(A\right)+2{\widehat{\lambda }}_3)}^2]}}\le \frac{2}{\sqrt{11}},\hfill \end{array}$$

(53)

$$\begin{array}{cc}\hfill 1\le R& =\frac{tr\left(A\right)+2max\left({\widehat{\lambda }}_n\right)}{tr\left(A\right)+2min\left({\widehat{\lambda }}_n\right)}\le 3.\hfill \end{array}$$

(54)

Proof. 

To compute the eigenvalues, we multiply both sides of (51) by the eigenvector ${\widehat{v}}_n$ of A and obtain

$$\mathbb{D}{\widehat{v}}_n=\frac{s^2}{\mu (n+2)}{\widehat{v}}_n+\frac{2s^2}{\mu (n+2)tr\left(A\right)}{\widehat{\lambda }}_n{\widehat{v}}_n=\frac{s^2}{\mu (n+2)}\left(1+\frac{2{\widehat{\lambda }}_n}{tr\left(A\right)}\right){\widehat{v}}_n.$$

The formulas for the fractional anisotropy follow directly, by substituting the eigenvalues of (51) into (48) and (49), respectively. The upper bound follows from taking ${\lambda }_1\to \infty$. For the ratio R, we write

$$R=\frac{{\widehat{\lambda }}_1+{\sum }_{i=2}^{n-1}{\widehat{\lambda }}_i+3{\widehat{\lambda }}_n}{3{\widehat{\lambda }}_1+{\sum }_{i=2}^{n-1}{\widehat{\lambda }}_i+{\widehat{\lambda }}_n}\le \frac{9{\widehat{\lambda }}_1+3{\sum }_{i=2}^{n-1}{\widehat{\lambda }}_i+3{\widehat{\lambda }}_n}{3{\widehat{\lambda }}_i+{\sum }_{i=2}^{n-1}{\widehat{\lambda }}_i+{\widehat{\lambda }}_n}\le 3.$$

where the maximum eigenvalue and minimum eigenvalues of A are denoted by ${\widehat{\lambda }}_n$ and ${\widehat{\lambda }}_1$, respectively. All other eigenvalues are called ${\widehat{\lambda }}_i$ and the trace becomes the sum of the eigenvalues. □

It is very surprising to see that the anisotropy ratio is bounded by a finite value of 3 in any space dimension, and the fractional anisotropies are uniformly bounded by a value less than 1. This means the peanut distribution does not allow for arbitrary anisotropies, and for that reason it is of limited use in the modelling of biological movement data.

Next, we consider the anisotropy of the bimodal von Mises–Fisher distribution (31).

Theorem 4. 

Let $u\in {\mathbb{S}}^{n-1}$ be a given direction and k the concentration parameter. The diffusion tensor arising from the bimodal von Mises–Fisher distribution (31) is of the form

$$\mathbb{D}=\alpha \left(k\right)\mathbb{I}+\beta \left(k\right)u{u}^T,where\alpha \left(k\right)=\frac{s^2{I}_{\frac{n}{2}}\left(k\right)}{\mu k{I}_{\frac{n}{2}-1}\left(k\right)}and\beta \left(k\right)=\frac{s^2{I}_{\frac{n}{2}+1}\left(k\right)}{\mu I_{\frac{n}{2}-1}\left(k\right)}.$$

(55)

The diffusion tensor (55) has eigenvalues

$${\lambda }_1=\alpha +\beta ,\begin{array}{c}\hfill and{\lambda }_2,\dots ,{\lambda }_n=\alpha .\end{array}$$

The anisotropies and the ratio of the eigenvalues satisfy

$$\begin{array}{ccc}\hfill 0\le {\mathsf{FA}}_2& =& \left|\beta \right|\sqrt{\frac{1}{{(\alpha +\beta )}^2+{\alpha }^2}}=\sqrt{\frac{1}{{(\frac{\alpha }{\beta }+1)}^2+{\left(\frac{\alpha }{\beta }\right)}^2}}\le 1\hfill \\ \hfill 0\le {\mathsf{FA}}_3& =& \left|\beta \right|\sqrt{\frac{1}{{(\alpha +\beta )}^2+2{\alpha }^2}}=\sqrt{\frac{1}{{(\frac{\alpha }{\beta }+1)}^2+2{\left(\frac{\alpha }{\beta }\right)}^2}}\le 1\hfill \\ \hfill 1\le R& =& 1+\frac{\beta }{\alpha }\le \infty .\hfill \end{array}$$

Proof. 

To compute the eigenvalues for (55), we first take the vector u and show that it is indeed an eigenvector of (55), since

$$\mathbb{D}u=\alpha u+\beta u{u}^{T}u=(\alpha +\beta )u.$$

(56)

Hence, ${\lambda }_1=\alpha +\beta$. Now, we take any $u^{\perp }\in {\mathbb{S}}^{n-1}$ (where $u^T{u}^{\perp }=0$) and show that it is an eigenvector of (55) as well, since

$$\mathbb{D}{u}^{\perp }=\alpha u^{\perp }+\beta u{u}^T{u}^{\perp }=\alpha u^{\perp }.$$

(57)

Thus, $u^{\perp }\in {\mathbb{S}}^{n-1}$ is an eigenvector with an eigenvalue $\lambda =\alpha$. Since we can define $n-1$ perpendicular vectors, we conclude that ${\lambda }_2,\dots ,{\lambda }_n=\alpha .$

The formulas for the anisotropies and for R follow from substituting the determined eigenvalues into the definitions. To determine the upper bounds for the formulas, we compute the limits of $\alpha \left(k\right)$ and $\beta \left(k\right)$. We start with the isotropic case of $k\to 0$. We apply the expansion of Bessel functions as shown in (A4)

$$\begin{array}{ccc}\hfill \underset{k\to 0}{lim}\alpha \left(k\right)& =\frac{s^2}{\mu }\underset{k\to 0}{lim}\frac{\frac{1}{\mathsf{\Gamma }(\frac{n}{2}+1)2^{\frac{n}{2}}}{k}^{\frac{n}{2}}+\frac{1}{\mathsf{\Gamma }(\frac{n}{2}+2)2^{\frac{n}{2}+2}}{k}^{\frac{n}{2}+2}+\dots }{k\left[\frac{1}{\mathsf{\Gamma }\left(\frac{n}{2}\right)2^{\frac{n}{2}-1}}{k}^{\frac{n}{2}-1}+\frac{1}{\mathsf{\Gamma }(\frac{n}{2}+1)2^{\frac{n}{2}+1}}{k}^{\frac{n}{2}+1}+\dots \right]}\hfill & \hfill =\frac{s^2}{\mu n}.\end{array}$$

(58)

and

$$\begin{array}{ccc}\hfill \underset{k\to 0}{lim}\beta \left(k\right)& =\frac{s^2}{\mu }\underset{k\to 0}{lim}\frac{\frac{1}{\mathsf{\Gamma }(\frac{n}{2}+2)2^{\frac{n}{2}+1}}{k}^{\frac{n}{2}+1}+\frac{1}{\mathsf{\Gamma }(\frac{n}{2}+3)2^{\frac{n}{2}+3}}{k}^{\frac{n}{2}+3}+\dots }{\frac{1}{\mathsf{\Gamma }\left(\frac{n}{2}\right)2^{\frac{n}{2}-1}}{k}^{\frac{n}{2}-1}+\frac{1}{\mathsf{\Gamma }(\frac{n}{2}+1)2^{\frac{n}{2}+1}}{k}^{\frac{n}{2}+1}+\dots }\hfill & \hfill =0.\end{array}$$

(59)

To evaluate the limit as $k\to \infty$, we apply the expansion (A7) for large k to obtain

$$\begin{array}{cc}\hfill \underset{k\to \infty }{lim}\alpha \left(k\right)& =\frac{s^2}{\mu }\underset{k\to \infty }{lim}\frac{\frac{e^k}{\sqrt{2\pi k}}[1-\frac{1}{8k}(4{\left(\frac{n}{2}\right)}^2-1)+\dots ]}{k\frac{e^k}{\sqrt{2\pi k}}[1-\frac{1}{8k}(4{(\frac{n}{2}-1)}^2-1)+\dots ]}=0,\hfill \end{array}$$

(60)

and

$$\begin{array}{cc}\hfill \underset{k\to \infty }{lim}\beta \left(k\right)& =\frac{s^2}{\mu }\underset{k\to \infty }{lim}\frac{\frac{e^k}{\sqrt{2\pi k}}[1-\frac{1}{8k}(4{(\frac{n}{2}+1)}^2-1)+\dots ]}{\frac{e^k}{\sqrt{2\pi k}}[1-\frac{1}{8k}(4{(\frac{n}{2}-1)}^2-1)+\dots ]}=1.\hfill \end{array}$$

(61)

Now, we compute the bounds for the ratio $R\left(k\right)$. We see that if $k\to 0$, $R\left(k\right)\to 1$ by the above calculations. Further, $R\left(k\right)\to \infty$ as $k\to \infty$, since

$$\underset{k\to \infty }{lim}\frac{\beta \left(k\right)}{\alpha \left(k\right)}=\underset{k\to \infty }{lim}\frac{k{I}_{\frac{n}{2}+1}}{I_{\frac{n}{2}}}=\underset{k\to \infty }{lim}\frac{k\frac{e^k}{\sqrt{2\pi k}}[1-\frac{1}{8k}(4{(\frac{n}{2}+1)}^2-1)+\dots ]}{\frac{e^k}{\sqrt{2\pi k}}[1-\frac{1}{8k}(4{\left(\frac{n}{2}\right)}^2-1)+\dots ]}=\infty .$$

(62)

And finally,

$$\underset{k\to \infty }{lim}\frac{\alpha \left(k\right)}{\beta \left(k\right)}=\underset{k\to \infty }{lim}\frac{I_{\frac{n}{2}}}{k{I}_{\frac{n}{2}+1}}=\underset{k\to \infty }{lim}\frac{\frac{e^k}{\sqrt{2\pi k}}[1-\frac{1}{8k}(4{\left(\frac{n}{2}\right)}^2-1)+\dots ]}{k\frac{e^k}{\sqrt{2\pi k}}[1-\frac{1}{8k}(4{(\frac{n}{2}+1)}^2-1)+\dots ]}=0.$$

(63)

So, ${\mathsf{FA}}_2\to 0$ and ${\mathsf{FA}}_3\to 0$ as $k\to 0$. Further, ${\mathsf{FA}}_2\to 1$ and ${\mathsf{FA}}_3\to 1$ as $k\to \infty$. □

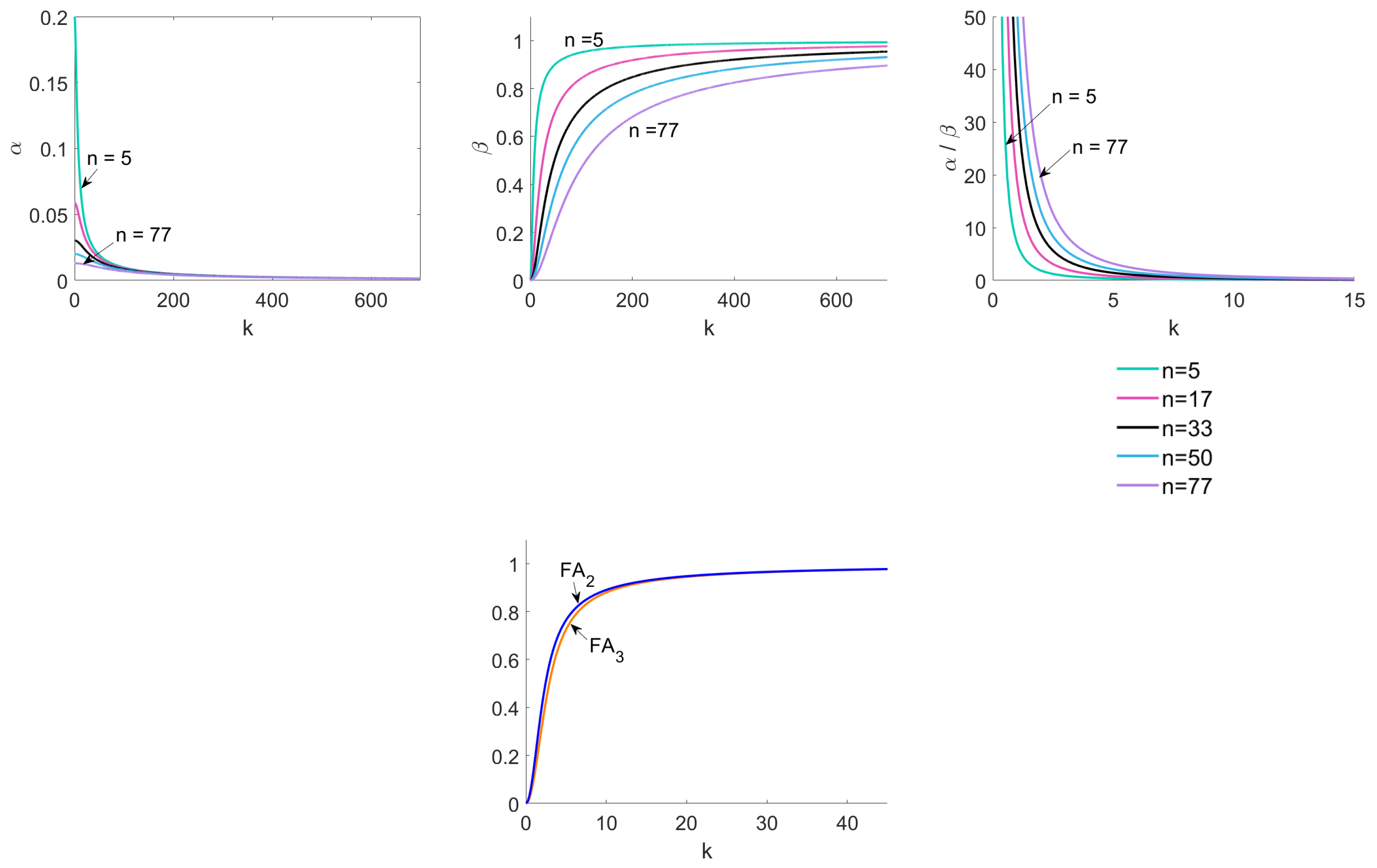
In Figure 3, we confirm our calculations numerically. We plot $\alpha \left(k\right)$, $\beta \left(k\right)$, $\frac{\alpha \left(k\right)}{\beta \left(k\right)}$, $F{A}_2\left(k\right)$, $F{A}_3\left(k\right)$ with respect to k and illustrate that they converge to the limits computed above. Note that, for some images in Figure 3, we truncated the intervals to see the functions more clearly.

Figure 3. The top row illustrates $\alpha \left(k\right)\to 0$, $\beta \left(k\right)\to 1$, and $\frac{\alpha \left(k\right)}{\beta \left(k\right)}\to 0$ as $k\to \infty$ for $n=5,17,33,50,77$ (see Theorem 4 for explicit forms of $\alpha \left(k\right)$ and $\beta \left(k\right)$). The bottom image illustrates $F{A}_2\left(k\right)\to 1$ and $F{A}_3\left(k\right)\to 1$ as $k\to \infty$ for dimensions $n=2$ and $n=3$, respectively. In the bottom figure, the blue curve is $F{A}_2\left(k\right)$ and the orange curve is $F{A}_3\left(k\right)$ (see Theorem 4 for the definitions of $F{A}_2$ and $F{A}_3$). All images relate to the bimodal von Mises–Fisher distribution.

Summary

In this section, we computed the eigenvalues for the peanut (6) and the bimodal von Mises–Fisher distributions (31) for their respective diffusion tensors in Theorems 3 and 4. We also found explicit versions of the $F{A}_2$ and $F{A}_3$ formulas as well as the R ratio in Theorems 3 and 4. The $F{A}_2$, $F{A}_3$, and R formulas for the peanut distribution have been shown to be bounded, unlike for the von Mises–Fisher distribution.

5. An Illustrative Example of Glioma Spread

To illustrate the main results, we consider a glioma spread model in a simplified scenario. Glioma are highly aggressive brain tumors which invade into healthy tissue guided by white matter fibre tracks [25]. This process has been successfully modelled using Fisher–KPP-type equations (see model (66) below) [7,26,27]. The underlying anisotropy of white matter tracks can be measured through diffusion tensor MRI (DTI) [18,28,29], and this is where we start our illustrative example. We consider a two-dimensional domain and assume that a diffusion tensor is measured as

$$A:=\left(\begin{array}{cc}1& 0\\ 0& 0.01\end{array}\right).$$

This indicates a strong bias in the x direction and much less movement in the y direction. The measurements of DTI record the movement of water molecules [18,29], which we need to transfer into a movement model for cancer cells. We do this using the transport equation approach mention in Section 1.1 and the peanut distribution and the bimodal von Mises distributions, respectively. Both methods will give us an effective diffusion tensor for the glioma cells.

We also assume, for simplification, that movement speed and turning rate are normalized such that $s^2/\mu =1$.

Taking A from above, with $trA=1.01$, we compute the two-dimensional diffusion tensor of the peanut distribution (51) as

$${\mathbb{D}}_{Peanut}=\frac{1}{4}\mathbb{I}+\frac{2}{4\left(1.01\right)}A=\left(\begin{array}{cc}0.745& 0\\ 0& 0.255\end{array}\right).$$

(64)

To compute the corresponding diffusion tensor for the bimodal von Mises distribution (55) for $n=2$, we need the dominant eigenvector u and the concentration parameter k. In [7], the model was fit to glioma patient data and it was found that the concentration parameter k is about 3–5 times the fractional anisotropy of the patients DTI data. Hence, here, we assume

$$k=5{\mathsf{FA}}_2\left(A\right)=5\sqrt{2}=7.07.$$

The dominant direction is $u={(1,0)}^T$. Then, from (36) we find

$${\mathbb{D}}_{vonMises}=\left(\begin{array}{cc}\frac{I_1\left(k\right)}{k{I}_0\left(k\right)}+\frac{I_2\left(k\right)}{I_0\left(k\right)}& 0\\ 0& \frac{I_1\left(k\right)}{k{I}_0\left(k\right)}\end{array}\right)=\left(\begin{array}{cc}0.869& 0\\ 0& 0.131\end{array}\right).$$

(65)

We see immediately that the von Mises tensor is more anisotropic than the peanut tensor above.

We now take these two diffusion tensors, (64) and (65), and an isotropic tensor, ${\mathbb{D}}_{iso}=\mathrm{diag}(0.5,0.5)$, for comparison and solve the corresponding anisotropic glioma model [7]

$$P_t=\nabla \nabla :\left(\mathbb{D}P\right)+rP(1-P)$$

(66)

on a square domain with no-flux boundary conditions. Here $P(x,t)$ describes the glioma cell density as a function of space and time and r is the maximal cancer growth rate. We choose $r=0.1$ and we initialize the simulation with a small cancer seed in the middle of the domain. In Figure 4, we show the initial condition and the model results after 40 time units. We see that the von Mises distribution is able to describe a stronger directional bias as compared to the peanut. Note that, for this example, A does not change with space and remains constant at any given spatial point, meaning that this example is applicable to a small region in the tissue, such as a small section of a white matter tract in the brain. For larger domains, like the entire brain, $A\left(x\right)$ depends on space, and a more detailed modelling is needed. This was done, for example, in [7,11,20].

Figure 4. Initial condition and simulations of glioma spread of model (66) at time $t=40$ on a $[0,60]\times [0,60]$ square domain, using three different diffusion tensors, the isotropic tensor, the peanut, and the bimodal von Mises. Here, blue indicates maximum tumor density, while white indicates healthy tissue.

6. Discussion

The standard way to compute moments of spherical distributions would be to use polar coordinates and engage in a series of trigonometric integrations. While this is often possible in two and three dimensions, it gets tedious, or impossible, in higher dimensions. Here, we present an alternative method that can be used in any space dimension. This method was first used in [10] in two and three dimensions. It uses the divergence theorem on the unit ball to transform and simplify the integrals as much as possible. As a result, we obtain explicit formulas for the variance–covariance matrices of the n-dimensional von Mises–Fisher distribution (Theorem 1) and the n-dimensional peanut distribution (Theorem 2) as new results. The formulas derived in Theorems 1 and 2 involve Bessel functions, which are standard functions in any software package. Hence, the numerical implementation of these formulas is straightforward. We tried to apply the method for computing the first and second moments of other spherical distributions such as the ordinary distribution function (ODF) (7) and the Bingham distribution (8), which, unfortunately, did not lead to closed form expressions. However, because Bingham and ODF distributions are symmetric, we do show that their expectation is zero. We also note that, based on our experience, Bingham and Kent distributions have not been used in the biological context yet. They seem to be more relevant in geophysical applications [30]. Hence, they are not the main focus of our paper.

Once the variance–covariance matrices were established, we considered levels of anisotropy as measured through the fractional anisotropies and the ratio of maximal over minimal eigenvalues. Surprisingly, the anisotropy of the peanut distribution is bounded away from 1 (Theorem 3) making it problematic to use in modelling. The anisotropy of the von Mises–Fisher distribution covers the entire range from isotropic to fully anisotropic (Theorem 4), and seems to have no restriction if used for modelling.

Using the explicit formulas derived here will significantly decrease the computation time in problems having a large amount of data that require a higher-dimensional von Mises–Fisher distribution [31] and decrease the computation time when simulating the transport equations (partial differential equations) that utilize the biological movement data [3,4,7]. Moreover, the formulas derived for the generalized von Mises–Fisher distribution can be easily extended to compute the expectation and variance covariance matrices of mixed von Mises–Fisher distributions by substituting the appropriate directional vectors and adding up the terms.

As we compute the higher dimensional integrals, we showcase a geometric interpretation of these integrals and the use of the divergence theorem. Hence, we combine the theory of distributions with calculus in a new way. Besides our explicit formulas, we believe our approach can open the door for further computations of explicit formulas for expectation, variance, and even higher moments of spherical distributions and enable further applications in biology.

Appendix A.1. Derivation of the von Mises–Fisher Distribution

In [1], the von Mises–Fisher distribution is defined as the probability density

$$f(u;\mu ,k)={\left(\frac{k}{2}\right)}^{\frac{n}{2}-1}\frac{1}{\mathsf{\Gamma }\left(\frac{n}{2}\right)I_{\frac{n}{2}-1}\left(k\right)}{e}^{k\theta u}$$

(A1)

with respect to the uniform distribution on ${\mathbb{S}}^{n-1}$. The parameters in $f(u;\mu ,k)$ have the same interpretation as in (5). If we use the standard Lebesgue measure on ${\mathbb{S}}^{n-1}$, we divide (A1) by $|{\mathbb{S}}^{n-1}|$, and obtain the probability density (5). We can see this by the following calculation

$$q\left(\theta \right)=\frac{1}{|{\mathbb{S}}^{n-1}|}{\left(\frac{k}{2}\right)}^{\frac{n}{2}-1}\frac{1}{\mathsf{\Gamma }\left(\frac{n}{2}\right)I_{\frac{n}{2}-1}\left(k\right)}{e}^{k\theta u}=\frac{k^{\frac{n}{2}-1}}{{\left(2\pi \right)}^{\frac{n}{2}}{I}_{\frac{n}{2}-1}\left(k\right)}{e}^{k\theta u}$$

(A2)

where we made use of (A8) and (A9).

Appendix A.2. Modified Bessel Functions of First Kind

The von Mises–Fisher distribution (5) has a modified Bessel function of first kind appearing in the normalization factor. Here, we state the definitions of the Bessel function of first kind $J_p\left(x\right)$ and the modified Bessel function of first kind $I_p\left(x\right)$ of order p ($p,x\in \mathbb{C}$) as well as list some useful identities.

The Bessel function and modified Bessel function of first kind can be defined as follows [32]

$$J_p\left(x\right)=\sum _{m=0}^{\infty }\frac{{(-1)}^m}{m!\mathsf{\Gamma }(p+m+1)}{\left(\frac{x}{2}\right)}^{2m+p},$$

(A3)

$$I_p\left(x\right)=\sum _{m=0}^{\infty }\frac{1}{m!\mathsf{\Gamma }(p+m+1)}{\left(\frac{x}{2}\right)}^{2m+p},$$

(A4)

where $p\in \mathbb{C}$, $x\in \mathbb{C}$.

Bessel functions have many identities [24]. We will use the following ones often in our calculations

$$I_p\left(x\right)=i^{-p}{J}_p\left(ix\right),$$

(A5)

$$\frac{d}{dx}\left(x^p{J}_p\left(x\right)\right)=x^p{J}_{p-1}\left(x\right),$$

(A6)

where $p\in \mathbb{R}$. See Appendix A.3 for the proofs of these identities.

We will also make use of the following expansion for large $x\in \mathbb{R}$, $x>0$ [33]

$$I_p\left(x\right)\sim \frac{e^x}{\sqrt{2\pi x}}\left(1+\sum _{n=0}^{\infty }\frac{{(-1)}^n}{n!{\left(8x\right)}^n}\left(\prod _{m=1}^{n}4p^2-{(2m-1)}^2\right)\right).$$

(A7)

for fractional and integer orders p.

Appendix A.3. Bessel Function Identities Proofs

Identity (A5) follows through the following calculation

$$i^{-p}{J}_p\left(ix\right)=\sum _{m=0}^{\infty }\frac{{(-1)}^m}{m!\mathsf{\Gamma }(p+m+1)}{i}^{2m}{\left(\frac{x}{2}\right)}^{2m+p}=\sum _{m=0}^{\infty }\frac{1}{m!\mathsf{\Gamma }(p+m+1)}{\left(\frac{x}{2}\right)}^{2m+p}=I_p\left(x\right)$$

since $i^{2m}={\left(i^2\right)}^m={(-1)}^m$.

To prove (A6), we compute

$$\begin{array}{cc}\hfill \frac{d}{dx}{x}^p{J}_p\left(x\right)& =\frac{d}{dx}\left(\sum _{m=0}^{\infty }\frac{{(-1)}^m}{m!\mathsf{\Gamma }(m+p+1)}{\left(\frac{x}{2}\right)}^{2p+2m}{2}^p\right)\hfill \\ \hfill & =\sum _{m=0}^{\infty }\frac{{(-1)}^m(2p+2m)}{m!\mathsf{\Gamma }(m+p+1)}{\left(\frac{x}{2}\right)}^{2p+2m-1}{2}^{p-1}\hfill \\ \hfill & =x^p\sum _{m=0}^{\infty }\frac{{(-1)}^m(p+m)}{m!\mathsf{\Gamma }(m+p+1)}{\left(\frac{x}{2}\right)}^{p+2m-1}\hfill \\ \hfill & =x^p\sum _{m=0}^{\infty }\frac{{(-1)}^m}{m!\mathsf{\Gamma }(m+p)}{\left(\frac{x}{2}\right)}^{p+2m-1}\hfill \\ \hfill & =x^p{J}_{p-1}\left(x\right)\hfill \end{array}$$

where the exchange of integration and summation operators is justified since the sum is absolutely convergent by ratio test, and in the fourth equivalence (A9) was used.

Appendix A.4. n-Ball and (n − 1)-Sphere

The surface area of an n-sphere, $|{\mathbb{S}}^{n-1}|$, and the volume of an n-ball, $|{\mathbb{B}}^n|$, appear often in our calculations. Here, we recall these formulas explicitly [34]

$$|{\mathbb{S}}^{n-1}|=\frac{2{\pi }^{\frac{n}{2}}}{\mathsf{\Gamma }\left(\frac{n}{2}\right)},|{\mathbb{B}}_1\left(0\right)|=|{\mathbb{B}}^n|=\frac{{\pi }^{\frac{n}{2}}}{\mathsf{\Gamma }(\frac{n}{2}+1)},$$

(A8)

where $\mathsf{\Gamma }\left(x\right)$ is the gamma function. See [34] for more details as to how the formulas in (A8) were derived.

The gamma function has the following identity [35], which we will use often

$$\mathsf{\Gamma }(x+1)=x\mathsf{\Gamma }\left(x\right).$$

(A9)

Using (A9) it is easy to see that

$$\frac{n|{\mathbb{B}}_1\left(0\right)|}{|{\mathbb{S}}^{n-1}|}=1.$$

(A10)

Appendix A.5. Matrix Derivative

We denote by $D_v$ an operator that performs the gradient with respect to $v\in {\mathbb{R}}^n$, that is, $D_{v}w={(w_{v_1},w_{v_2},\dots ,w_{v_n})}^T$. It follows that

$$D_x\left(x^{T}Ax\right)=Ax+A^{T}x$$

(A11)

where $A\in {\mathbb{R}}^{n\times n}.$ The identity (A11) can be computed as follows. Since

$$x^{T}Ax=\sum _{i=1}^n\sum _{j=1}^n{x}_i{A}_{ij}{x}_j$$

(A12)

and

$$\begin{array}{cc}\hfill \frac{d{x}^{T}Ax}{d{x}_k}& =\sum _{i=1}^n\frac{d{x}_i}{d{x}_k}\sum _{j=1}^n{A}_{ij}{x}_j+\sum _{i=1}^n{x}_i\sum _{j=1}^n{A}_{ij}\frac{d{x}_j}{d{x}_k}\hfill \\ \hfill & =\sum _{j=1}^n{A}_{kj}{x}_j+\sum _{i=1}^n{x}_i{A}_{ik}\hfill \end{array}$$

it follows that

$$D_x{x}^{T}Ax=\left(\begin{array}{c}\frac{d{x}^{T}Ax}{d{x}_1}\\ \frac{d{x}^{T}Ax}{d{x}_2}\\ ⋮\\ \frac{d{x}^{T}Ax}{d{x}_2}\end{array}\right)=\left(\begin{array}{c}\sum _{j=1}^n{A}_{1j}{x}_j+\sum _{i=1}^n{x}_i{A}_{i1}\\ \sum _{j=1}^n{A}_{2j}{x}_j+\sum _{i=1}^n{x}_i{A}_{i2}\\ ⋮\\ \sum _{j=1}^n{A}_{nj}{x}_j+\sum _{i=1}^n{x}_i{A}_{in}\end{array}\right)=Ax+A^{T}x.$$

(A13)