Modeling and Transmission Dynamics of a Stochastic Fractional Delay Cervical Cancer Model with Efficient Numerical Analysis
Abstract
1. Introduction
2. Preliminaries
3. Main Results
3.1. Existence and Uniqueness
3.2. Positivity and Boundedness
3.3. Model Equilibria and Reproduction Number
3.4. Local Stability
3.5. Global Stability
3.6. Sensitivity Analysis
4. Numerical Simulations
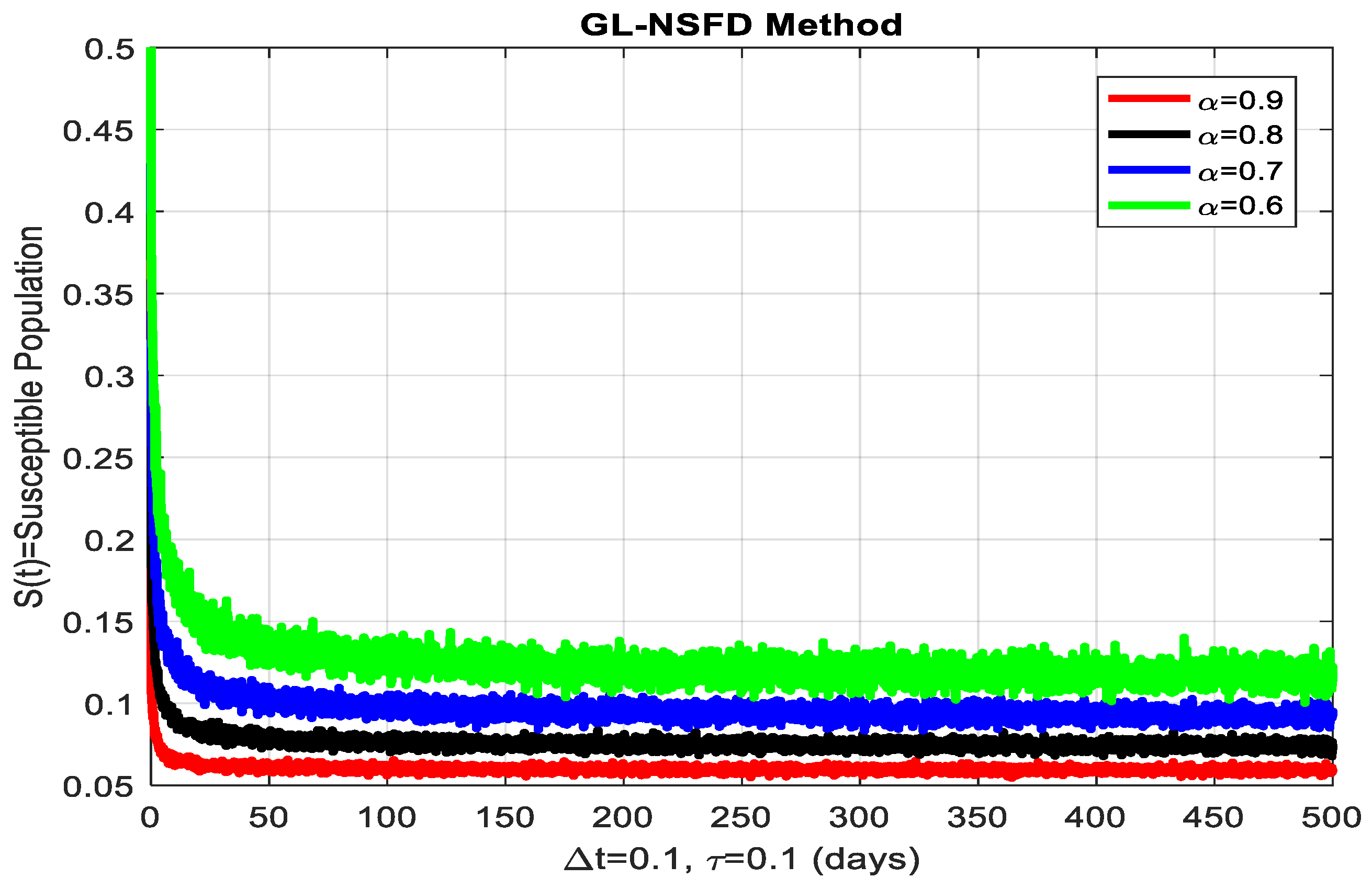
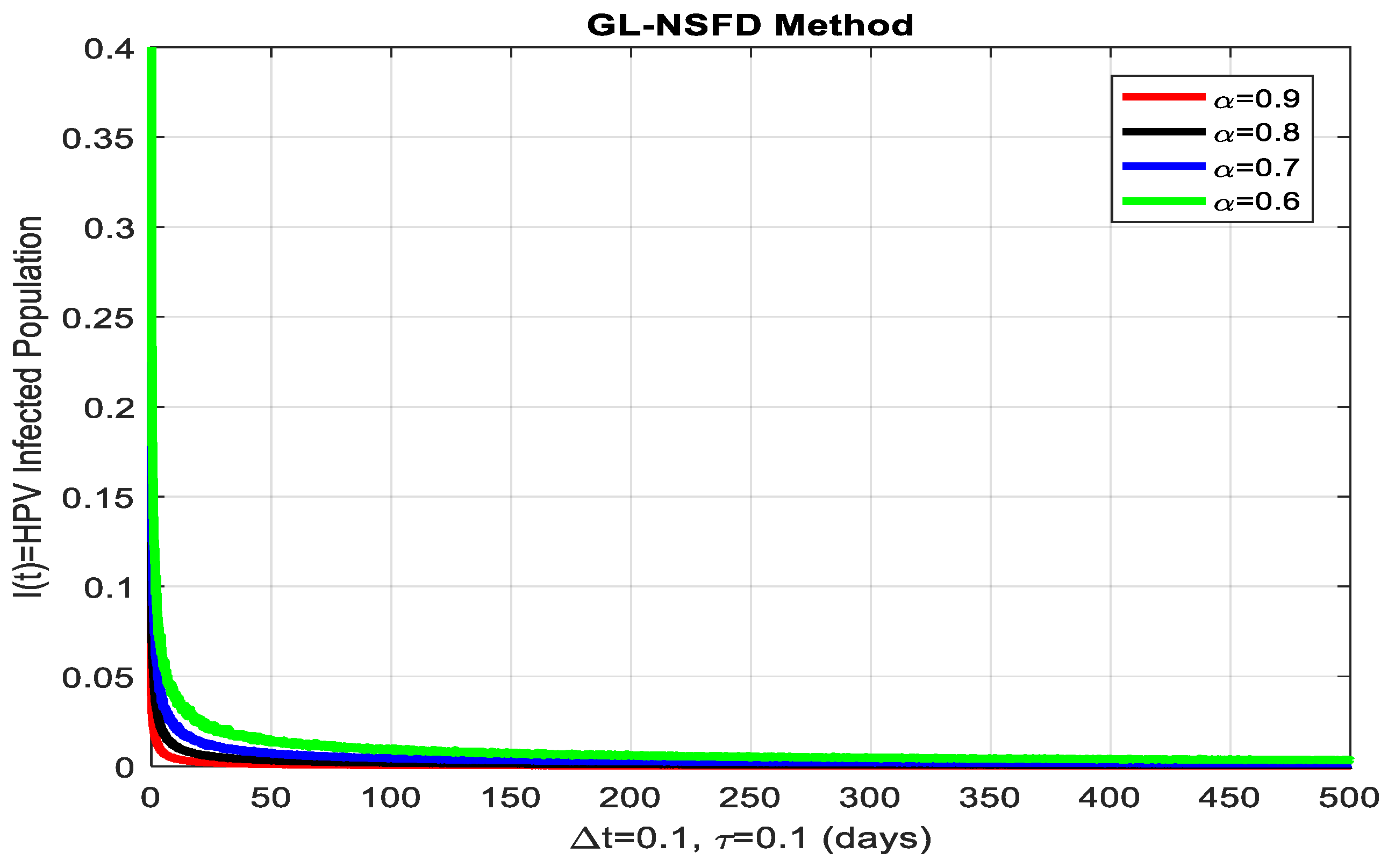
4.1. Non-Standard Finite Difference (NSFD) Scheme
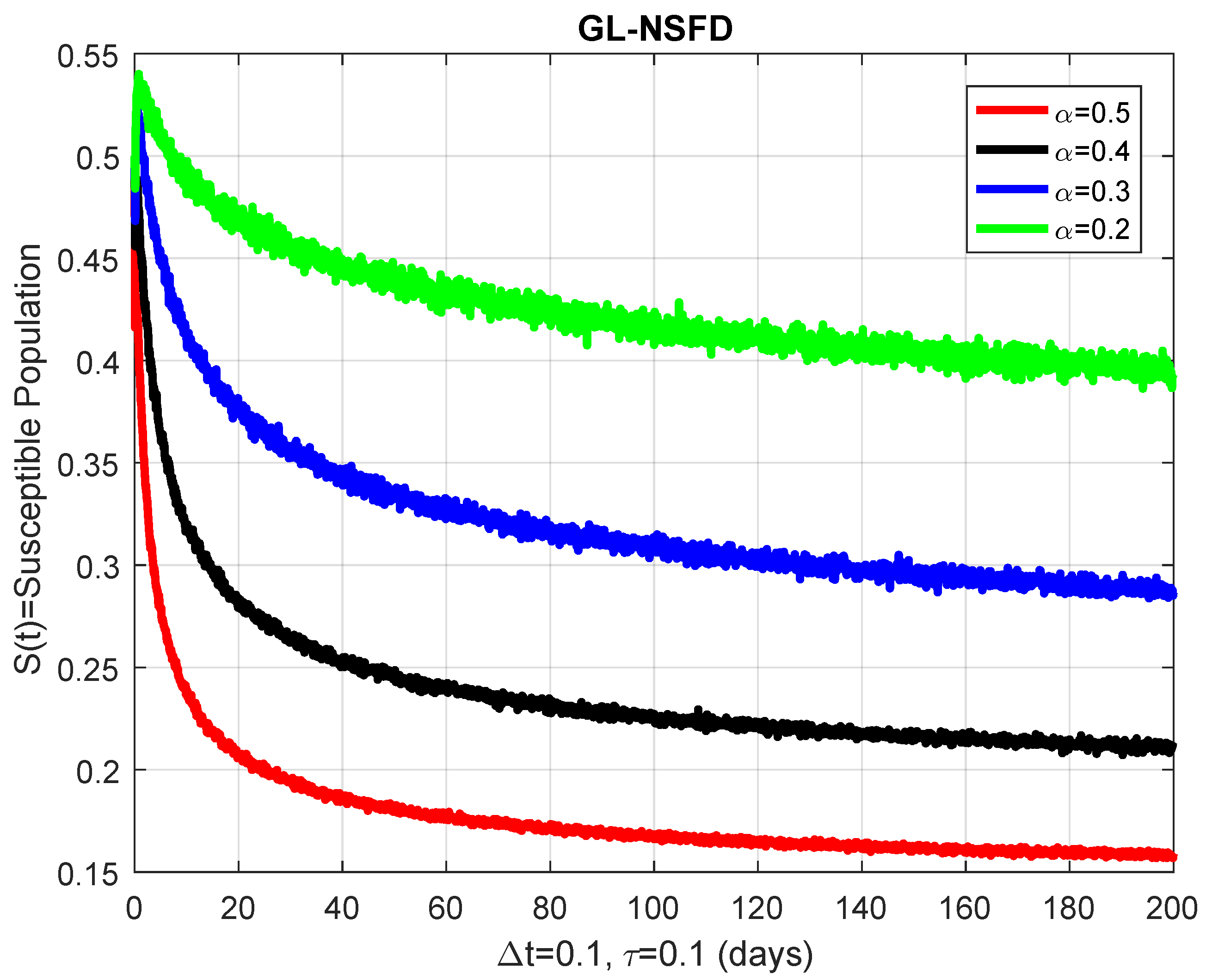
4.2. Graphical Simulation
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ali, J.; Ciancio, A.; Khan, K.A.; Raza, N.; Baskonus, H.M.; Luqman, M.; Khan, Z.U. Evolutionary Safe Padé Approximation Scheme for Dynamical Study of Nonlinear Cervical Human Papilloma Virus Infection Model. CMES-Comput. Model. Eng. Sci. 2024, 140, 3. [Google Scholar] [CrossRef]
- Tivde, T.; Ameh, E.O.; Gweryina, R.I. On the Sensitivity Analysis of a Mathematical Model of the Transmission Dynamics and Control of Cervical Cancer Disease for Optimal Human Health. GSJ 2024, 12, 3. [Google Scholar]
- Liu, C.; Liu, H.; Zhu, X.; Lin, X. Sensitivity Analysis and Numerical Simulation of a Human Papillomavirus Infection Model. In Proceedings of the Third International Conference on Biomedical and Intelligent Systems (IC-BIS 2024), Nanchang, China, 26–28 April 2024; SPIE: Bellingham, WA, USA, 2024; Volume 13208, pp. 398–405. [Google Scholar]
- Bahi, M.C.; Bahramand, S.; Jan, R.; Boulaaras, S.; Ahmad, H.; Guefaifia, R. Fractional View Analysis of Sexual Transmitted Human Papilloma Virus Infection for Public Health. Sci. Rep. 2024, 14, 3048. [Google Scholar] [CrossRef]
- Rajan, P.K.; Kuppusamy, M.; Yusuf, A. A Fractional-Order Modeling of Human Papillomavirus Transmission and Cervical Cancer. Model. Earth Syst. Environ. 2024, 10, 1337–1357. [Google Scholar] [CrossRef]
- Rajan, P.K.; Kuppusamy, M. A Fractional Order Human Papillomavirus Model with Caputo Derivative. J. Anal. 2024, 32, 2135–2156. [Google Scholar] [CrossRef]
- Kim, M.; Kim, E. Effective Vaccination Strategies for Human Papillomavirus (HPV) Infection and Cervical Cancer Based on the Mathematical Model with a Stochastic Process. J. Med. Virol. 2024, 96, e29558. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Sawleshwarkar, S.; Piraveenan, M. Computational Approaches of Modelling Human Papillomavirus Transmission and Prevention Strategies: A Systematic Review. J. Biol. Dyn. 2025, 19, 2436376. [Google Scholar] [CrossRef]
- Boudreau, M.C.; Cohen, J.A.; Hébert-Dufresne, L. Within-Host Infection Dynamics with Master Equations and the Method of Moments: A Case Study of Human Papillomavirus in the Epithelium. arXiv 2024, arXiv:2408.05298. [Google Scholar] [CrossRef]
- Cameron, R.L.; Palmer, T.J.; Cuschieri, K.; Kavanagh, K.; Roy, K. Assessing Real World Vaccine Effectiveness: A Review of Scotland’s Approach to Monitoring Human Papillomavirus (HPV) Vaccine Impact on HPV Infection and Cervical Disease. Vaccine 2024, 42, 126177. [Google Scholar] [CrossRef]
- Phongsamart, W.; Lou, P.J.; Sukarom, I.; Wu, Y.H.; Zaidi, O.; Du, F.; Simon, A.; Bernauer, M. Integrative Literature Review on Human Papillomavirus Vaccination Recommendations in National Immunization Programs in Select Areas in the Asia-Pacific Region. Hum. Vaccines Immunother. 2024, 20, 2362449. [Google Scholar] [CrossRef]
- Zhao, C.; Zhao, Y.; Li, J.; Li, M.; Shi, Y.; Wei, L. Opportunities and Challenges for Human Papillomavirus Vaccination in China. Hum. Vaccines Immunother. 2024, 20, 2329450. [Google Scholar] [CrossRef] [PubMed]
- Sadeghi, F.; Mostaghimi, T.; Taheri, M.; Yazdani, S.; Javadian, M.; Ranaee, M.; Ghorbani, H.; Bouzari, Z.; Sadeghi, F. Investigating the Role of Epstein-Barr Virus and Human Papillomavirus Types 16 and 18 Co-Infections in Cervical Disease of Iranian Women. Front. Oncol. 2024, 14, 1331862. [Google Scholar] [CrossRef]
- Wang, J.; Elfström, K.M.; Dillner, J. Human Papillomavirus-Based Cervical Screening and Long-Term Cervical Cancer Risk: A Randomised Health-Care Policy Trial in Sweden. Lancet Public Health 2024, 9, e886–e895. [Google Scholar] [CrossRef]
- Setayeshi, S.; Hasanzadeh, A.; Yahyapour, Y.; Alizadeh, A.; Ghorbani, H.; Nokhostin, F.; Bagheri, M.; Sadeghi, F. Evaluation of Human Papillomavirus Type 16 Viral Load and Genome Physical Status in Iranian Women with Cervical Disease. Mol. Biol. Rep. 2024, 51, 411. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, Z. ab0996 Human Papillomavirus Vaccination Awareness in Chinese Autoimmune Inflammatory Rheumatic Diseases: A Large Real-World Survey. Ann. Rheum. Dis. 2024, 83, 1814–1815. [Google Scholar] [CrossRef]
- Tobaiqy, M.; MacLure, K. A Systematic Review of Human Papillomavirus Vaccination Challenges and Strategies to Enhance Uptake. Vaccines 2024, 12, 746. [Google Scholar] [CrossRef] [PubMed]
- Del Prete, R.; Nesta, D.; Triggiano, F.; Lorusso, M.; Garzone, S.; Vitulano, L.; Denicolò, S.; Indraccolo, F.; Mastria, M.; Ronga, L.; et al. Human Papillomavirus Carcinogenicity and the Need of New Perspectives: Thoughts from a Retrospective Analysis on Human Papillomavirus Outcomes Conducted at the Hospital University of Bari, Apulia, Italy, between 2011 and 2022. Diagnostics 2024, 14, 968. [Google Scholar] [CrossRef]
- Baandrup, L.; Maltesen, T.; Dehlendorff, C.; Kjaer, S.K. Human Papillomavirus Vaccination and Anal High-Grade Precancerous Lesions and Cancer—A Real-World Effectiveness Study. JNCI J. Natl. Cancer Inst. 2024, 116, 283–287. [Google Scholar] [CrossRef]
- Burger, E.A.; Laprise, J.F.; Portnoy, A.; Spencer, J.C.; Sy, S.; Regan, M.C.; Kim, J.J. Population-Level Health Impact of Hypothetical Waning 1-Dose Human Papillomavirus Vaccination and 2-Dose Mitigation Strategies in a High Cervical Cancer Burden Setting. JNCI Monogr. 2024, 67, 379–386. [Google Scholar] [CrossRef] [PubMed]
- Albadarneh, R.B.; Batiha, I.; Alomari, A.K.; Tahat, N. Numerical Approach for Approximating the Caputo Fractional-Order Derivative Operator. AIMS Math. 2021, 6, 12743–12756. [Google Scholar] [CrossRef]
- Hethcote, H.W. The Mathematics of Infectious Diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Lakshmikantham, V.; Leela, S. Differential and Integral Inequalities: Theory and Applications, Volume I: Ordinary Differential Equations; Academic Press: New York, NY, USA, 1969. [Google Scholar]
- Mickens, R.E. Nonstandard Finite Difference Models of Differential Equations; World Scientific: Singapore, 1993. [Google Scholar]
- Arenas, A.J.; Gonzalez-Parra, G.; Chen-Charpentier, B.M. Construction of Nonstandard Finite Difference Schemes for the SI and SIR Epidemic Models of Fractional Order. Math. Comput. Simul. 2016, 121, 48–63. [Google Scholar] [CrossRef]
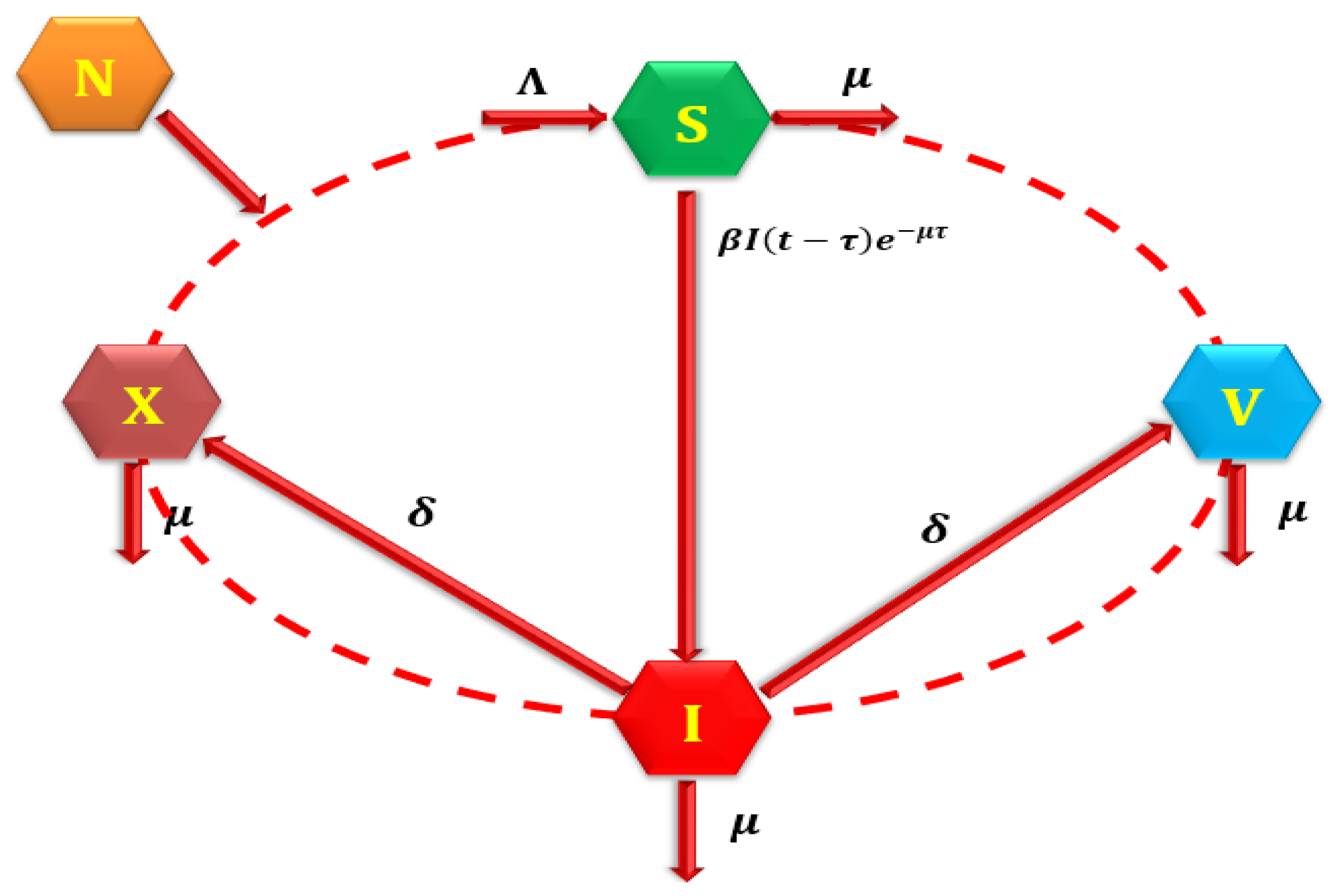
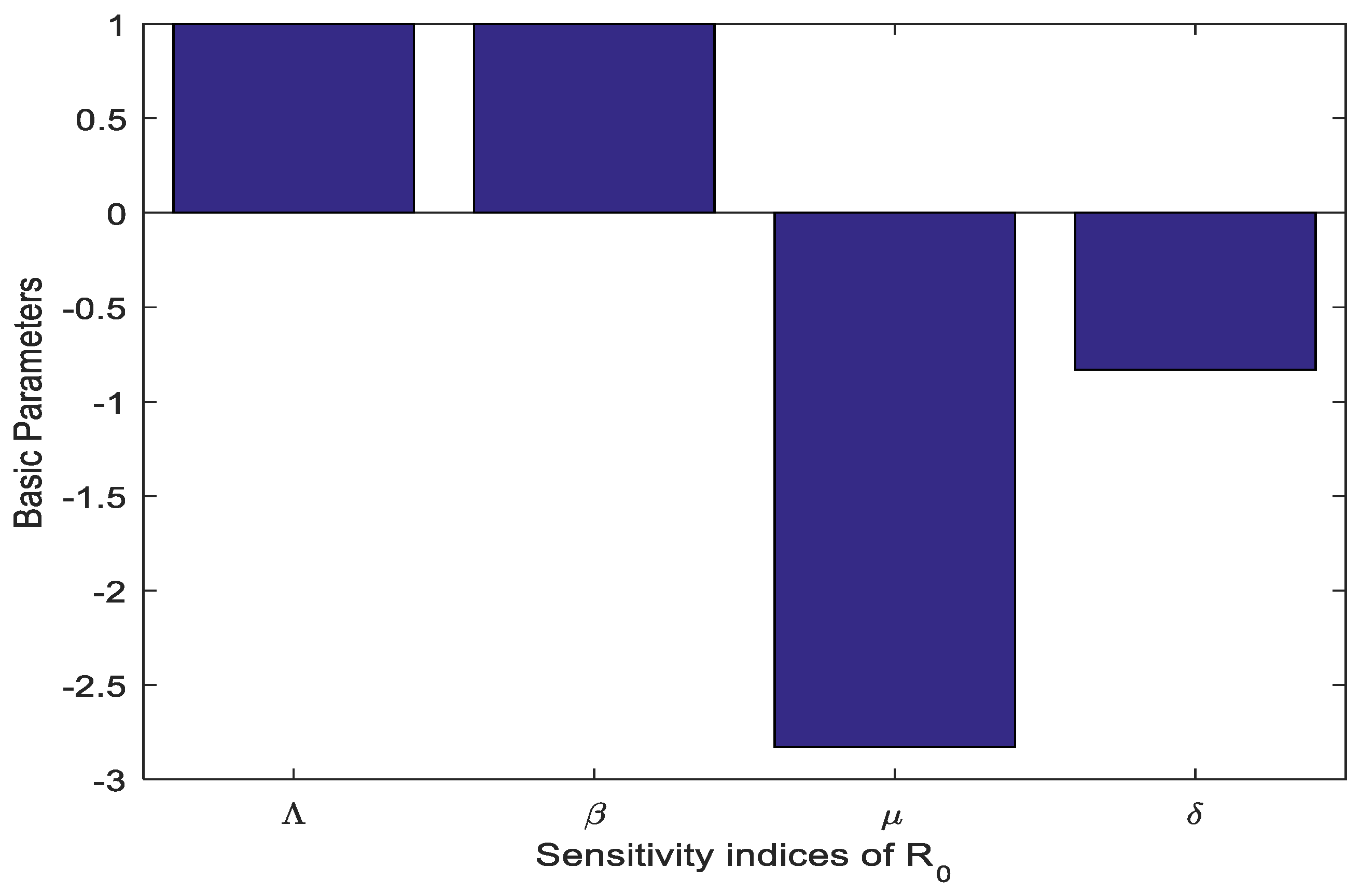



| Parameters | Signs | Values |
|---|---|---|
| Positive | 1.0 | |
| Positive | 1.0 | |
| Negative | −0.83 | |
| Negative | −2.83 |
| Parameter | Description | Value | Range | Justification |
|---|---|---|---|---|
| Recruitment rate | 0.5 | [0.3, 0.7] | Estimated to reflect moderate population inflow | |
| HPV transmission rate | 1.6 | [1.0, 2.5] | Based on contact rate and infection probability [1] | |
| Natural death rate | 0.5 | [0.4, 0.6] | Assumed average human mortality per time unit | |
| Progression rate to cervical cancer | 0.7 | [0.5, 1.0] | Assumed based on typical HPV-to-CCE progression | |
| Fractional effect/intervention | [0, 1] | Estimated to model intervention or memory effects |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shafique, U.; Raza, A.; Torres, D.F.M.; Abd Elwahab, M.E.; Mohsin, M. Modeling and Transmission Dynamics of a Stochastic Fractional Delay Cervical Cancer Model with Efficient Numerical Analysis. Axioms 2025, 14, 742. https://doi.org/10.3390/axioms14100742
Shafique U, Raza A, Torres DFM, Abd Elwahab ME, Mohsin M. Modeling and Transmission Dynamics of a Stochastic Fractional Delay Cervical Cancer Model with Efficient Numerical Analysis. Axioms. 2025; 14(10):742. https://doi.org/10.3390/axioms14100742
Chicago/Turabian StyleShafique, Umar, Ali Raza, Delfim F. M. Torres, Maysaa Elmahi Abd Elwahab, and Muhammad Mohsin. 2025. "Modeling and Transmission Dynamics of a Stochastic Fractional Delay Cervical Cancer Model with Efficient Numerical Analysis" Axioms 14, no. 10: 742. https://doi.org/10.3390/axioms14100742
APA StyleShafique, U., Raza, A., Torres, D. F. M., Abd Elwahab, M. E., & Mohsin, M. (2025). Modeling and Transmission Dynamics of a Stochastic Fractional Delay Cervical Cancer Model with Efficient Numerical Analysis. Axioms, 14(10), 742. https://doi.org/10.3390/axioms14100742







