Sensitivity Analysis of Eigenvalues for PDNT Toeplitz Matrices
Abstract
1. Introduction
2. Main Concepts and Definitions
3. Eigenvalue Sensitivity
3.1. Individual Eigenvalue Condition Numbers
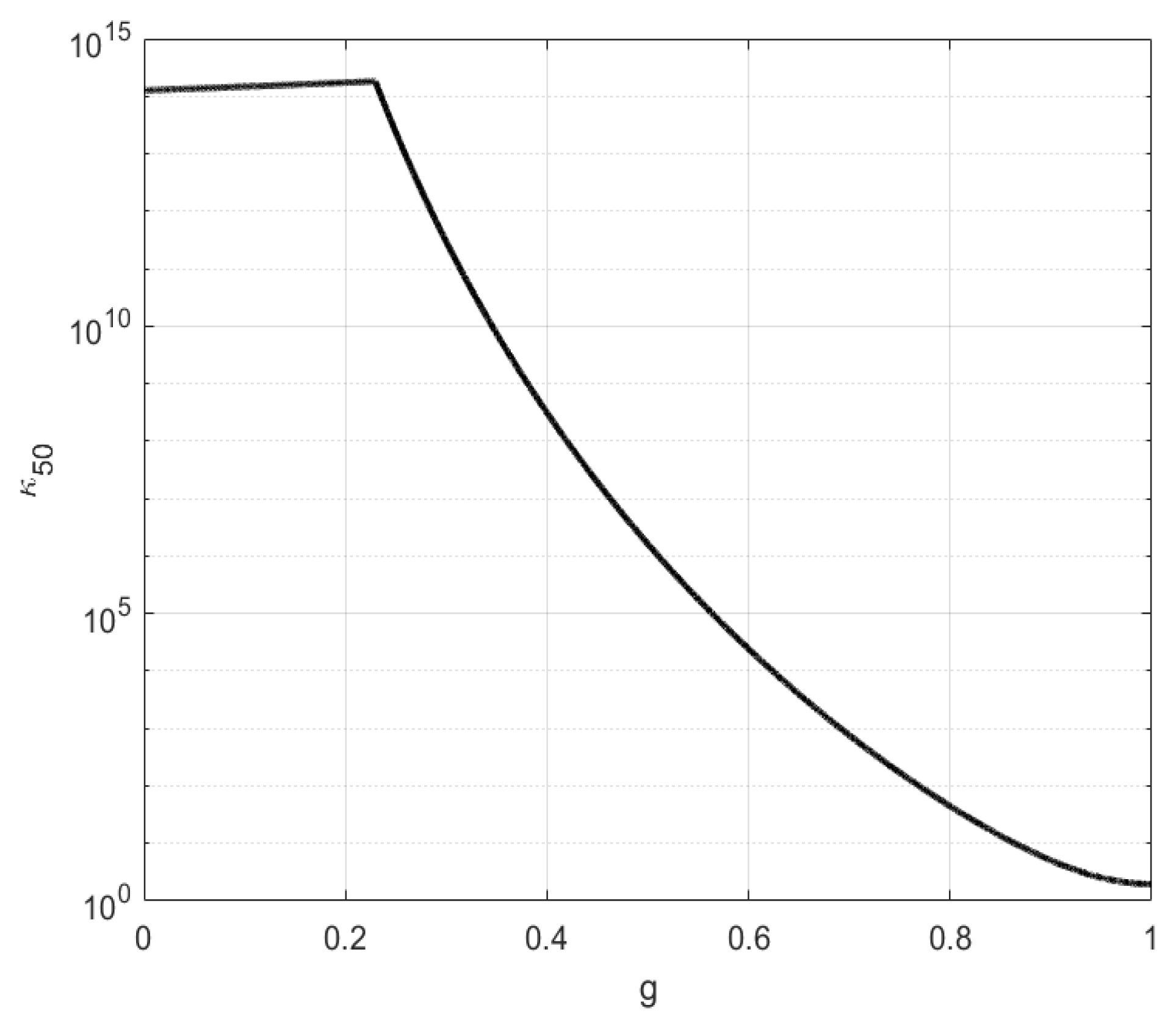
3.2. The Global Eigenvalue Condition Number
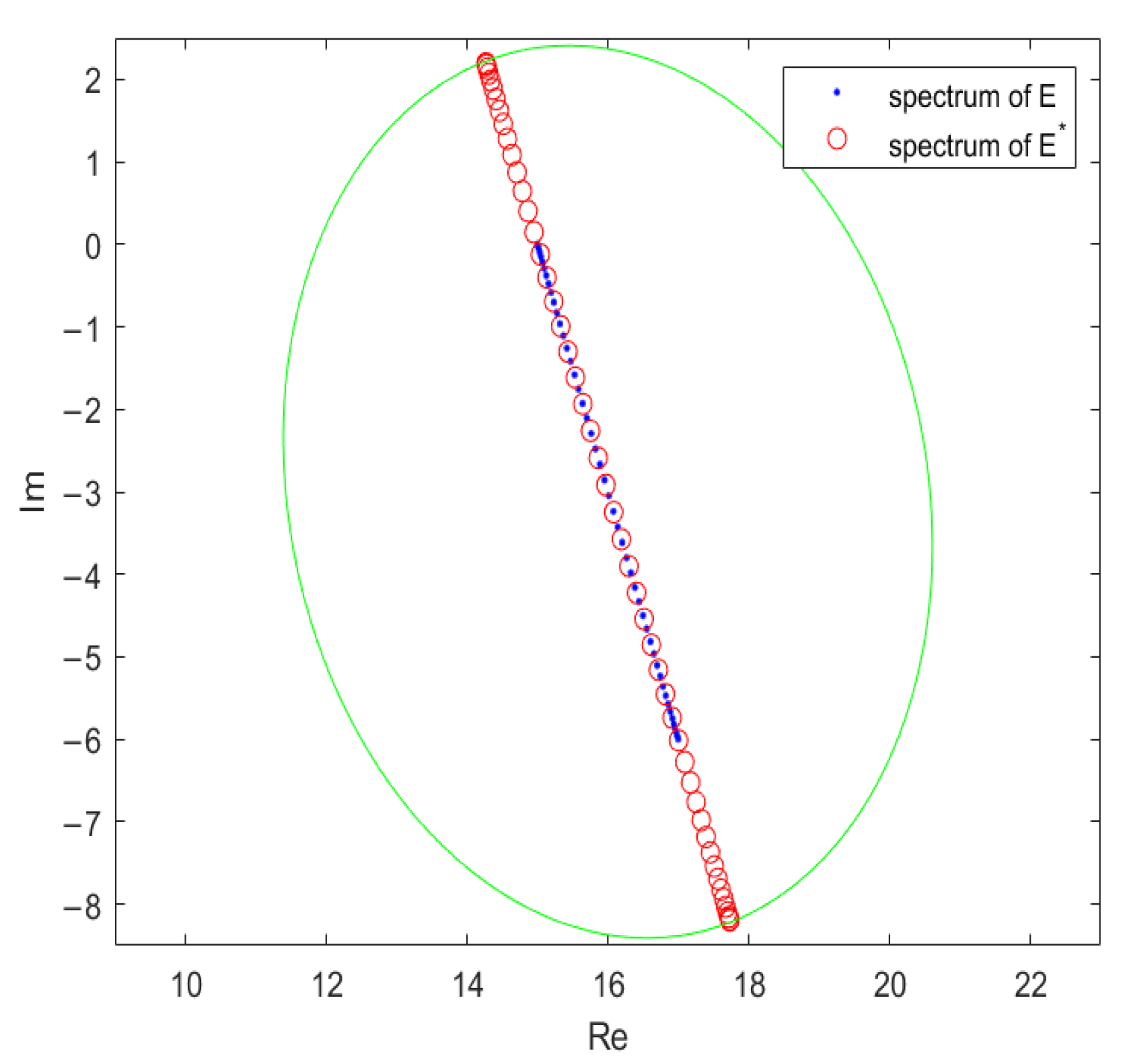
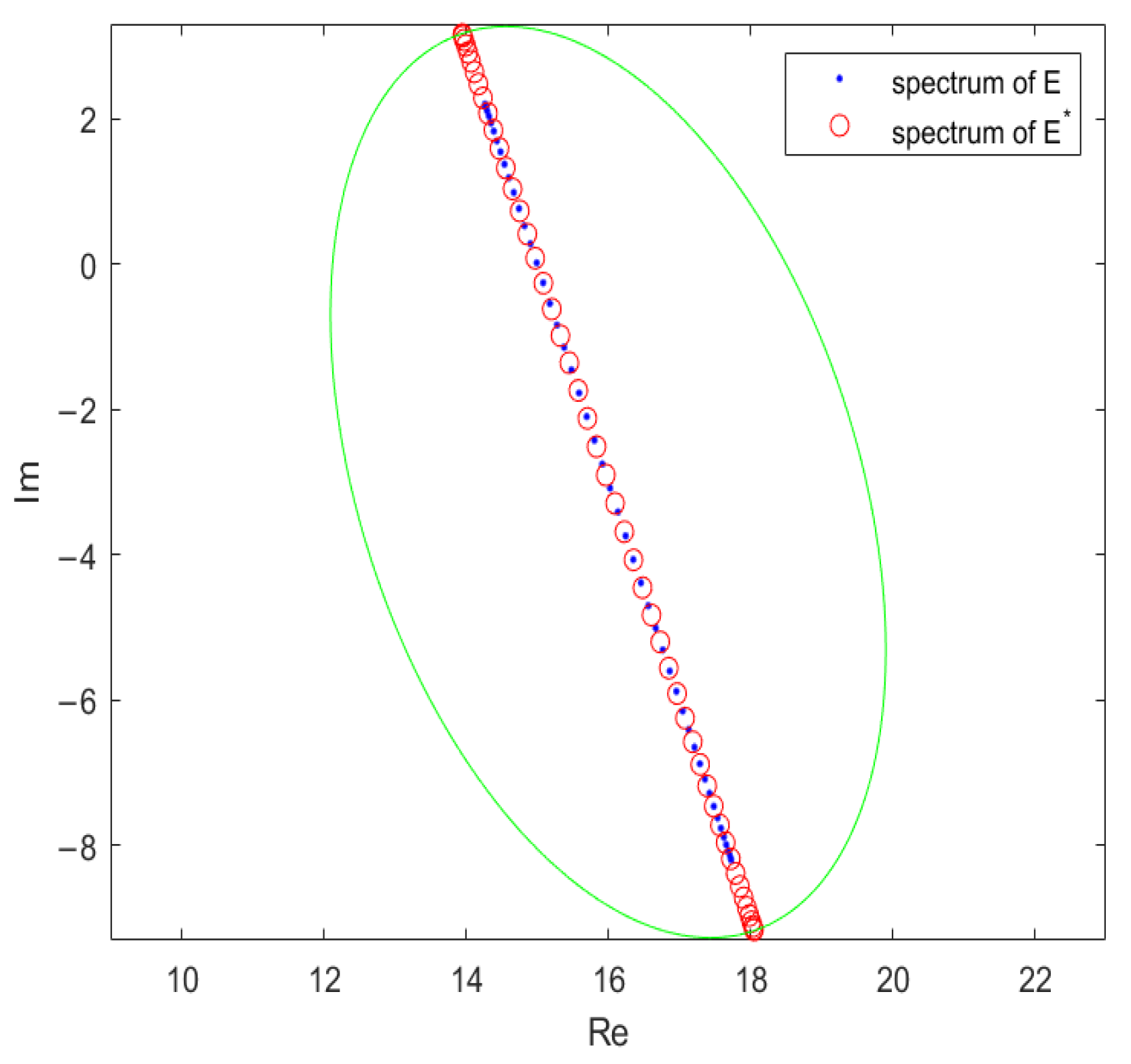
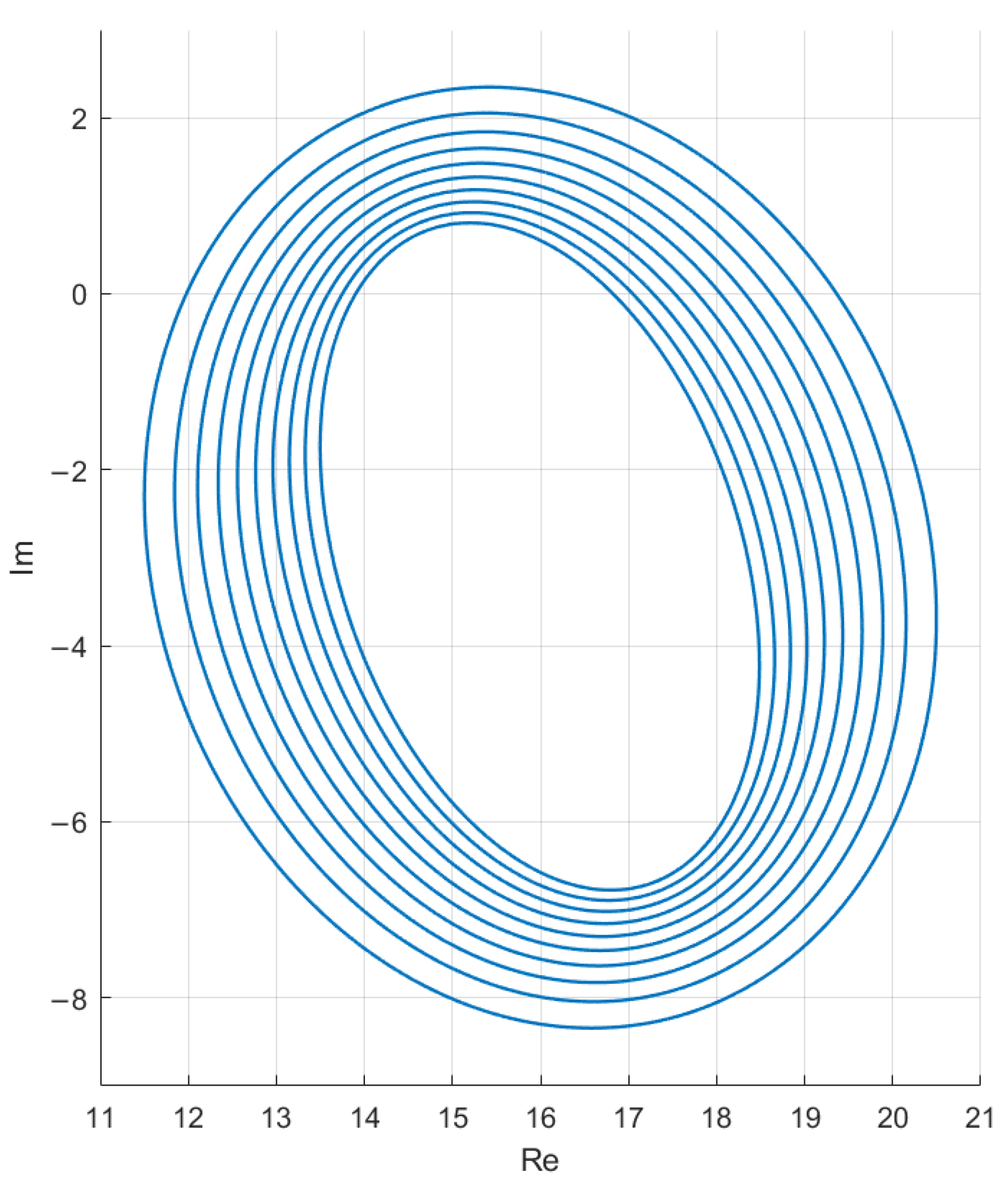
3.3. The -Pseudospectrum
3.4. Structured Perturbations
4. Examples of Eigenvalue Sensitivity
5. Inverse Problems for
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, Z.L.; Chu, H.X.; Miao, Q.Y.; Jiang, Z.W. Structured distance to normality of Dirichlet–Neumann tridiagonal Toeplitz matrices. Axioms 2025, 14, 609. [Google Scholar] [CrossRef]
- Jiang, X.Y.; Zhang, G.J.; Zheng, Y.P.; Jiang, Z.L. Explicit potential function and fast algorithm for computing potentials in α × β conic surface resistor network. Expert Syst. Appl. 2024, 238, 122157. [Google Scholar] [CrossRef]
- Yue, C.M.; Xu, Y.F.; Song, Z.D.; Weng, H.M.; Lu, Y.M.; Fang, C.; Dai, X. Symmetry-enforced chiral hinge states and surface quantum anomalous Hall effect in the magnetic axion insulator Bi2−xSmxSe3. Nat. Phys. 2019, 15, 577–581. [Google Scholar] [CrossRef]
- Schneider, B.I.; Gharibnejad, H. Numerical methods every atomic and molecular theorist should know. Nat. Rev. Phys. 2020, 2, 89–102. [Google Scholar] [CrossRef]
- Diele, F.; Lopez, L. The use of the factorization of five-diagonal matrices by tridiagonal Toeplitz matrices. Appl. Math. Lett. 1998, 11, 61–69. [Google Scholar] [CrossRef]
- Fischer, D.; Golub, G.; Hald, O.; Leiva, C.; Widlund, O. On Fourier-Toeplitz methods for separable elliptic problems. Math. Comput. 1974, 28, 349–368. [Google Scholar] [CrossRef]
- Willms, A.R. Analytic results for the eigenvalues of certain tridiagonal matrices. SIAM J. Matrix Anal. Appl. 2008, 30, 639–656. [Google Scholar] [CrossRef]
- Yueh, W.C.; Cheng, S.S. Explicit eigenvalues and inverses of tridiagonal Toeplitz matrices with four perturbed corners. ANZIAM J. 2008, 49, 361–387. [Google Scholar] [CrossRef]
- Luati, A.; Proietti, T. On the spectral properties of matrices associated with trend filters. Econom. Theory 2010, 26, 1247–1261. [Google Scholar] [CrossRef]
- Hansen, P.C. Rank-Deficient and Discrete Ill-Posed Problems: Numerical Aspects of Linear Inversion; SIAM: Philadelphia, PA, USA, 1998. [Google Scholar]
- Reichel, L.; Ye, Q. Simple square smoothing regularization operators. Electron. Trans. Numer. Anal. 2009, 33, 63–83. [Google Scholar]
- Jia, J.; Li, S. On the inverse and determinant of general bordered tridiagonal matrices. Comput. Math. Appl. 2015, 69, 503–509. [Google Scholar] [CrossRef]
- Sogabe, T. New algorithms for solving periodic tridiagonal and periodic pentadiagonal linear systems. Appl. Math. Comput. 2008, 202, 850–856. [Google Scholar] [CrossRef]
- Du, L.; Sogabe, T.; Zhang, S.L. A fast algorithm for solving tridiagonal quasi-Toeplitz linear systems. Appl. Math. Lett. 2018, 75, 74–81. [Google Scholar] [CrossRef]
- Liu, Z.; Li, S.; Yin, Y.; Zhang, Y. Fast solvers for tridiagonal Toeplitz linear systems. Comput. Appl. Math. 2020, 39, 315. [Google Scholar] [CrossRef]
- Fonseca, C.M.D. On the eigenvalues of some tridiagonal matrices. J. Comput. Appl. Math. 2007, 200, 283–286. [Google Scholar] [CrossRef]
- Wang, J.; Zheng, Y.P.; Jiang, Z.L. Norm equalities and inequalities for tridiagonal perturbed Toeplitz operator matrices. J. Appl. Anal. Comput. 2023, 13, 671–683. [Google Scholar] [CrossRef]
- Fu, Y.; Jiang, X.Y.; Jiang, Z.L.; Jhang, S. Properties of a class of perturbed Toeplitz periodic tridiagonal matrices. Comput. Appl. Math. 2020, 39, 146. [Google Scholar] [CrossRef]
- Fu, Y.; Jiang, X.Y.; Jiang, Z.L.; Jhang, S. Inverses and eigenpairs of tridiagonal Toeplitz matrix with opposite-bordered rows. J. Appl. Anal. Comput. 2020, 10, 1599–1613. [Google Scholar] [CrossRef]
- Wei, Y.; Zheng, Y.P.; Jiang, Z.L.; Shon, S. The inverses and eigenpairs of tridiagonal Toeplitz matrices with perturbed rows. J. Appl. Math. Comput. 2022, 68, 623–636. [Google Scholar] [CrossRef]
- Wei, Y.L.; Jiang, X.Y.; Jiang, Z.L.; Shon, S. On inverses and eigenpairs of periodic tridiagonal Toeplitz matrices with perturbed corners. J. Appl. Anal. Comput. 2020, 10, 178–191. [Google Scholar] [CrossRef]
- Noschese, S.; Pasquini, L.; Reichel, L. Tridiagonal Toeplitz matrices: Properties and novel applications. Numer. Linear Algebra Appl. 2013, 20, 302–326. [Google Scholar] [CrossRef]
- Bebiano, N.; Furtado, S. Structured distance to normality of tridiagonal matrices. Linear Algebra Appl. 2018, 552, 239–255. [Google Scholar] [CrossRef]
- Demmel, J. Nearest Defective Matrices and the Geometry of Ill-Conditioning; Oxford University Press: New York, NY, USA, 1990. [Google Scholar]
- Böttcher, A.; Grudsky, S.M. Spectral Properties of Banded Toeplitz Matrices; SIAM: Philadelphia, PA, USA, 2005. [Google Scholar]
- Reichel, L.; Trefethen, L.N. Eigenvalues and pseudo-eigenvalues of Toeplitz matrices. Linear Algebra Appl. 1992, 162, 153–185. [Google Scholar] [CrossRef]
- Trefethen, L.N.; Embree, M. Spectra and Pseudospectra: The Behavior of Nonnormal Matrices and Operators; Princeton University Press: Princeton, NJ, USA, 2005. [Google Scholar]
- Arnold, M.; Datta, B.N. Single-input eigenvalue assignment algorithms: A close look. SIAM J. Matrix Anal. Appl. 1998, 19, 444–467. [Google Scholar] [CrossRef]
- Datta, B. An algorithm to assign eigenvalues in a Hessenberg matrix: Single input case. IEEE Trans. Autom. Control 1987, 32, 414–417. [Google Scholar] [CrossRef]
- Datta, B.N.; Lin, W.-W.; Wang, J.-N. Robust partial pole assignment for vibrating systems with aerodynamic effects. IEEE Trans. Autom. Control 2006, 51, 1979–1984. [Google Scholar] [CrossRef]
- Datta, B.N.; Sokolov, V. A solution of the affine quadratic inverse eigenvalue problem. Linear Algebra Appl. 2011, 434, 1745–1760. [Google Scholar] [CrossRef]
- Golub, G.H.; Wilkinson, J.H. Ill-conditioned eigensystems and the computation of the Jordan canonical form. SIAM Rev. 1976, 18, 578–619. [Google Scholar] [CrossRef]
- Wilkinson, J.H. The Algebraic Eigenvalue Problem; Oxford University Press: Oxford, UK, 1965. [Google Scholar]
- Wilkinson, J.H. Sensitivity of eigenvalues II. Utilitas Math. 1986, 30, 243–286. [Google Scholar]
- Stewart, G.W. Matrix Perturbation Theory; Academic Press: New York, NY, USA, 1990. [Google Scholar]
- Karow, M.; Kressner, D.; Tisseur, F. Structured eigenvalue condition numbers. SIAM J. Matrix Anal. Appl. 2006, 28, 1052–1068. [Google Scholar] [CrossRef]
- Noschese, S.; Pasquini, L. Eigenvalue condition numbers: Zero-structured versus traditional. J. Comput. Appl. Math. 2006, 185, 174–189. [Google Scholar] [CrossRef]
- Noschese, S.; Pasquini, L. Eigenvalue patterned condition numbers: Toeplitz and Hankel cases. J. Comput. Appl. Math. 2007, 206, 615–624. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.; Chu, H.; Miao, Q.; Jiang, Z. Sensitivity Analysis of Eigenvalues for PDNT Toeplitz Matrices. Axioms 2025, 14, 739. https://doi.org/10.3390/axioms14100739
Jiang Z, Chu H, Miao Q, Jiang Z. Sensitivity Analysis of Eigenvalues for PDNT Toeplitz Matrices. Axioms. 2025; 14(10):739. https://doi.org/10.3390/axioms14100739
Chicago/Turabian StyleJiang, Zhaolin, Hongxiao Chu, Qiaoyun Miao, and Ziwu Jiang. 2025. "Sensitivity Analysis of Eigenvalues for PDNT Toeplitz Matrices" Axioms 14, no. 10: 739. https://doi.org/10.3390/axioms14100739
APA StyleJiang, Z., Chu, H., Miao, Q., & Jiang, Z. (2025). Sensitivity Analysis of Eigenvalues for PDNT Toeplitz Matrices. Axioms, 14(10), 739. https://doi.org/10.3390/axioms14100739




