A Quintic Spline-Based Computational Method for Solving Singularly Perturbed Periodic Boundary Value Problems
Abstract
1. Introduction
2. Maximum Principle and Stability Result
3. Discretization of the Problem
3.1. Shishkin Mesh
3.2. Derivation of the Difference Scheme
4. Error Estimate
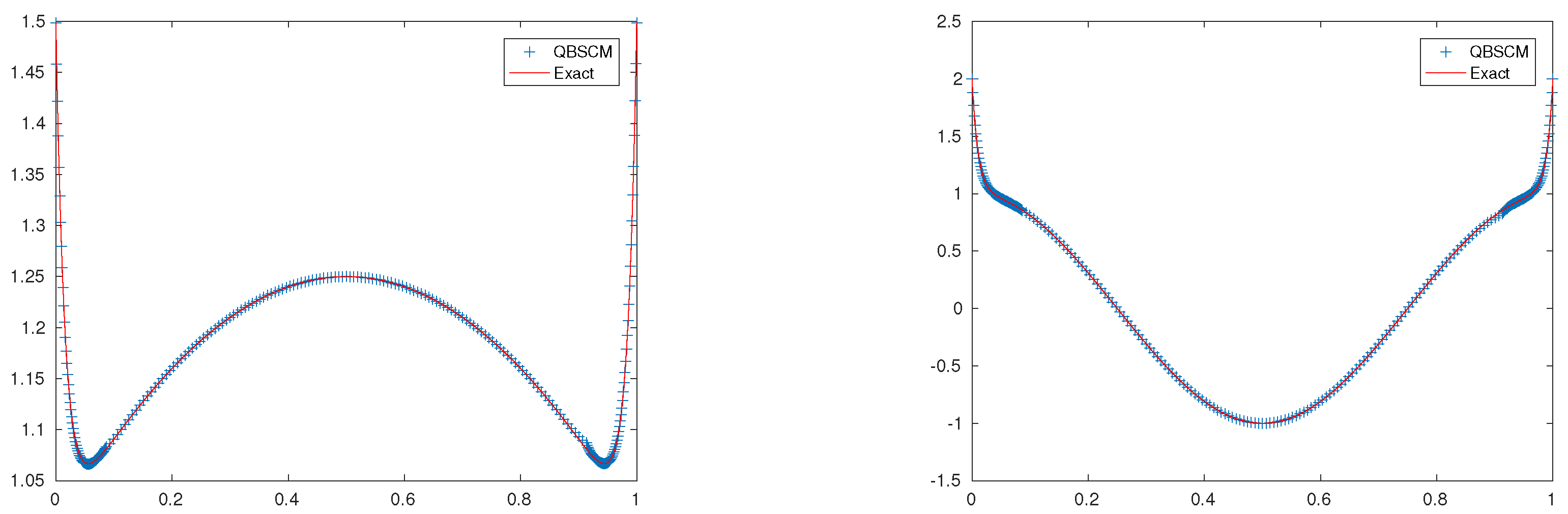
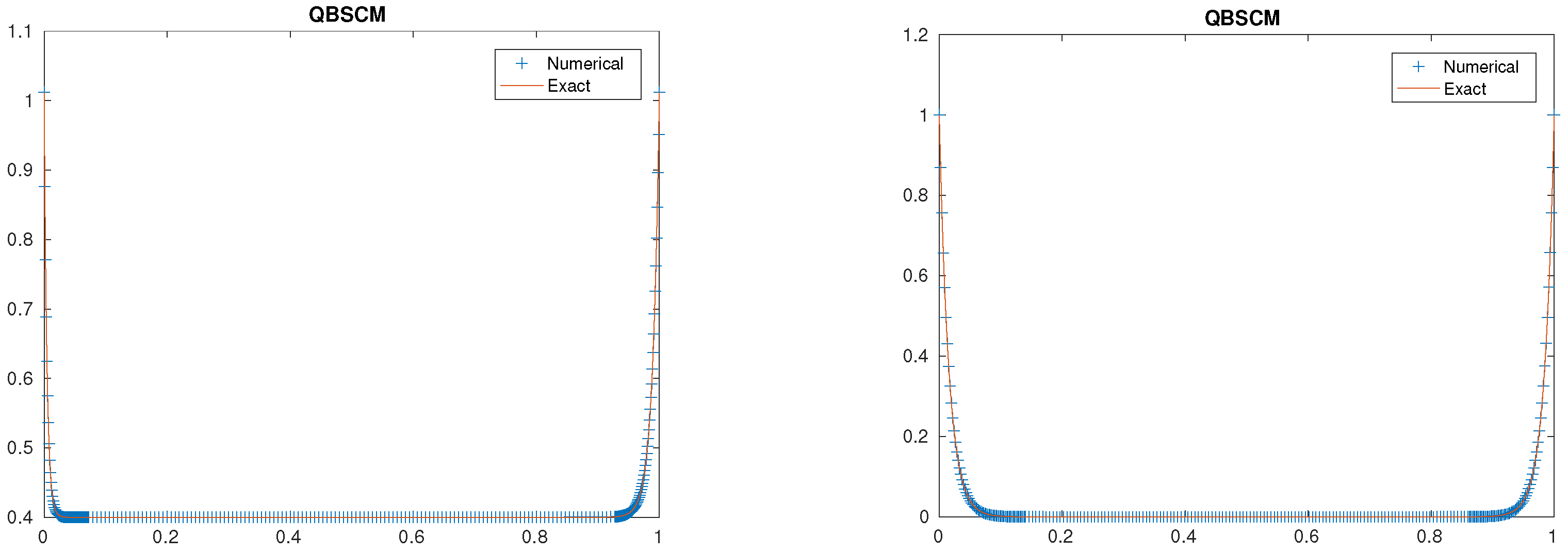
5. Numerical Experiments
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SPPBVP | Singularly perturbed periodic boundary value problem |
| QBSCM | Quintic B-spline collocation method |
References
- Miller, J.J.H.; O’Riordan, E.; Shishkin, G.I. Fitted Numerical Methods for Singular Perturbation Problems: Error Estimates in the Maximum Norm for Linear Problems in One and Two Dimensions; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2012. [Google Scholar]
- Farrell, P.A.; Hegarty, A.F.; Miller, J.J.H.; O’Riordan, E.; Shishkin, G.I. Robust Computational Techniques for Boundary Layers; Chapman and Hall/CRC: Boca Ration, FL, USA, USA, 2000. [Google Scholar]
- Roos, H.G.; Stynes, M.; Tobiska, L. Robust Numerical Methods for Singularly Perturbed Differential Equations, Computational Mathematics; Springer: Berlin, Germany, 2008. [Google Scholar]
- Kumar, D. A collocation method for singularly perturbed differential-difference turning point problems exhibiting boundary/interior layers. J. Differ. Equ. Appl. 2018, 24, 1847–1870. [Google Scholar] [CrossRef]
- Puvaneswari, A. Valanarasu, T; Ramesh Babu, A. A System of Singularly Perturbed Periodic Boundary Value Problem: Hybrid Difference Scheme. Int. J. Appl. Comput. Math. 2020, 6, 86. [Google Scholar] [CrossRef]
- Raja, V.; Geetha, N.; Mahendran, R.; Senthilkumar, L.S. Numerical solution for third order singularly perturbed turning point problems with integral boundary condition. J. Appl. Math. Comput. 2024, 1–21. [Google Scholar] [CrossRef]
- Chandru, M.; Shanthi, V. A boundary value technique for singularly perturbed boundary value problem of reaction-diffusion with non-smooth data. J. Eng. Sci. Technol. Spec. Issue ICMTEA2013 Conf. 2014, 32–45. [Google Scholar]
- Amiraliyev, G.M.; Duru, H. A uniformly convergence difference method for the periodical boundary value problem. Int. J. Comput. Math. Appl. 2003, 46, 695–703. [Google Scholar] [CrossRef]
- Cen, Z. Uniformly convergent second-order difference scheme for a singularly perturbed periodical boundary value problem. Int. J. Comput. Math. 2011, 88, 196–206. [Google Scholar] [CrossRef]
- Puvaneswari, A.; Ramesh Babu, A.; Valanarasu, T. Cubic spline scheme on variable mesh for singularly perturbed periodical boundary value problem. Novi Sad J. Math. 2020, 50, 157–172. [Google Scholar]
- Kadalbajoo, M.K.; Patidar, K.C. A survey of numerical techniques for solving singularly perturbed ordinary differential equations. Appl. Math. Comput. 2002, 130, 457–510. [Google Scholar] [CrossRef]
- Lang, F.G.; Xu, X.P. Quintic B-spline collocation method for second order mixed boundary value problem. Comput. Phys. Commun. 2012, 183, 913–921. [Google Scholar] [CrossRef]
- Singh, S.; Kumar, D.; Shanthi, V. Uniformly convergent scheme for fourth-order singularly perturbed convection-diffusion ODE. Appl. Numer. Math. 2023, 186, 334–357. [Google Scholar] [CrossRef]
- Singh, S.; Kumar, D. Spline-based parameter-uniform scheme for fourth-order singularly perturbed differential equations. J. Math. Chem. 2022, 60, 1872–1902. [Google Scholar] [CrossRef]
- Yousaf, M.Z.; Srivastava, H.M.; Abbas, M.; Nazir, T.; Mohammed, P.O.; Vivas-Cortez, M.; Chorfi, N. A Novel quintic B-spline technique for numerical solutions of the fourth-order singular singularly-perturbed problems. Symmetry 2023, 15, 1929. [Google Scholar] [CrossRef]
- Viswanadham, K.K.; Krishna, P.M. Quintic B-Spline Galerkin method for fifth order boundary value problems. ARPN J. Eng. Appl. Sci. 2010, 5, 74–77. [Google Scholar]
- Mishra, H.K.; Lodhi, R.K. Two-parameter singular perturbation boundary value problems via quintic B-spline method. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2022, 92, 541–553. [Google Scholar] [CrossRef]
- Micula, G. Handbook of Splines; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999. [Google Scholar]
- Kumar, D. A parameter-uniform method for singularly perturbed turning point problems exhibiting interior or twin boundary layers. Int. J. Comput. Math. 2019, 96, 865–882. [Google Scholar] [CrossRef]
- Kadalbajoo, M.K.; Yadaw, A.S.; Kumar, D. Comparative study of singularly perturbed two-point BVPs via: Fitted mesh finite difference method, B-spline collocation method. Appl. Math. Comput. 2008, 204, 713–725. [Google Scholar]
- Puvaneswari, A.; Valanarasu, T. Spline approximation methods for second order singularly perturbed convection-diffusion equation with integral boundary condition. Indian J. Pure Appl. Math. 2024, 1–12. [Google Scholar] [CrossRef]
- Chandru, M.; Shanthi, V. An asymptotic numerical method for singularly perturbed fourth order ODE of convection-diffusion type turning point problem. Neural Parallel Sci. Comput. 2016, 24, 473–488. [Google Scholar]
- De Boor, C. A Practical Guide to Splines; Springer: New York, NY, USA, 1978. [Google Scholar]
- Hall, C.A. On error bounds for spline interpolation. J. Approx. Theory I 1968, 209–218. [Google Scholar] [CrossRef]
- Kadalbajoo, M.K.; Patidar, K.C. ε-Uniform fitted mesh finite difference methods for general singular perturbation problems. Appl. Math. Comput. 2006, 179, 248–266. [Google Scholar]
- Chandru, M.; Shanthi, V. A Schwarz method for fourth-order singularly perturbed reaction-diffusion problem with discontinuous source term. J. Appl. Math. Inform. 2016, 34, 495–508. [Google Scholar] [CrossRef]


| Number of mesh points N | ||||||
| 32 | 64 | 128 | 256 | 512 | 1024 | |
| Hybrid difference scheme in [9] | ||||||
| 1.4252 | 1.5069 | 1.5742 | 1.6308 | 1.6768 | — | |
| Cubic spline scheme [10] | ||||||
| 1.6586 | 2.0695 | 2.1964 | 2.1806 | 2.1247 | — | |
| QBSCM | ||||||
| 2.8496 | 3.0996 | 3.2110 | 3.5799 | 3.8775 | — | |
| Number of mesh points N | ||||||
| 32 | 64 | 128 | 256 | 512 | 1024 | |
| Hybrid difference scheme in [9] | ||||||
| 1.3332 | 1.4901 | 1.6686 | 1.6986 | 1.7072 | — | |
| Cubic spline scheme [10] | ||||||
| 2.3179 | 1.9180 | 1.9701 | 2.0010 | 2.0189 | — | |
| QBSCM | ||||||
| 2.8963 | 3.1109 | 3.3837 | 3.5052 | 3.7471 | — | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arumugam, P.; Thynesh, V.; Muthusamy, C.; Ramos, H. A Quintic Spline-Based Computational Method for Solving Singularly Perturbed Periodic Boundary Value Problems. Axioms 2025, 14, 73. https://doi.org/10.3390/axioms14010073
Arumugam P, Thynesh V, Muthusamy C, Ramos H. A Quintic Spline-Based Computational Method for Solving Singularly Perturbed Periodic Boundary Value Problems. Axioms. 2025; 14(1):73. https://doi.org/10.3390/axioms14010073
Chicago/Turabian StyleArumugam, Puvaneswari, Valanarasu Thynesh, Chandru Muthusamy, and Higinio Ramos. 2025. "A Quintic Spline-Based Computational Method for Solving Singularly Perturbed Periodic Boundary Value Problems" Axioms 14, no. 1: 73. https://doi.org/10.3390/axioms14010073
APA StyleArumugam, P., Thynesh, V., Muthusamy, C., & Ramos, H. (2025). A Quintic Spline-Based Computational Method for Solving Singularly Perturbed Periodic Boundary Value Problems. Axioms, 14(1), 73. https://doi.org/10.3390/axioms14010073








