On Analytical Continuation of the Horn’s Hypergeometric Functions H3 and Their Ratios
Abstract
1. Introduction
2. Domains of Analytical Extension
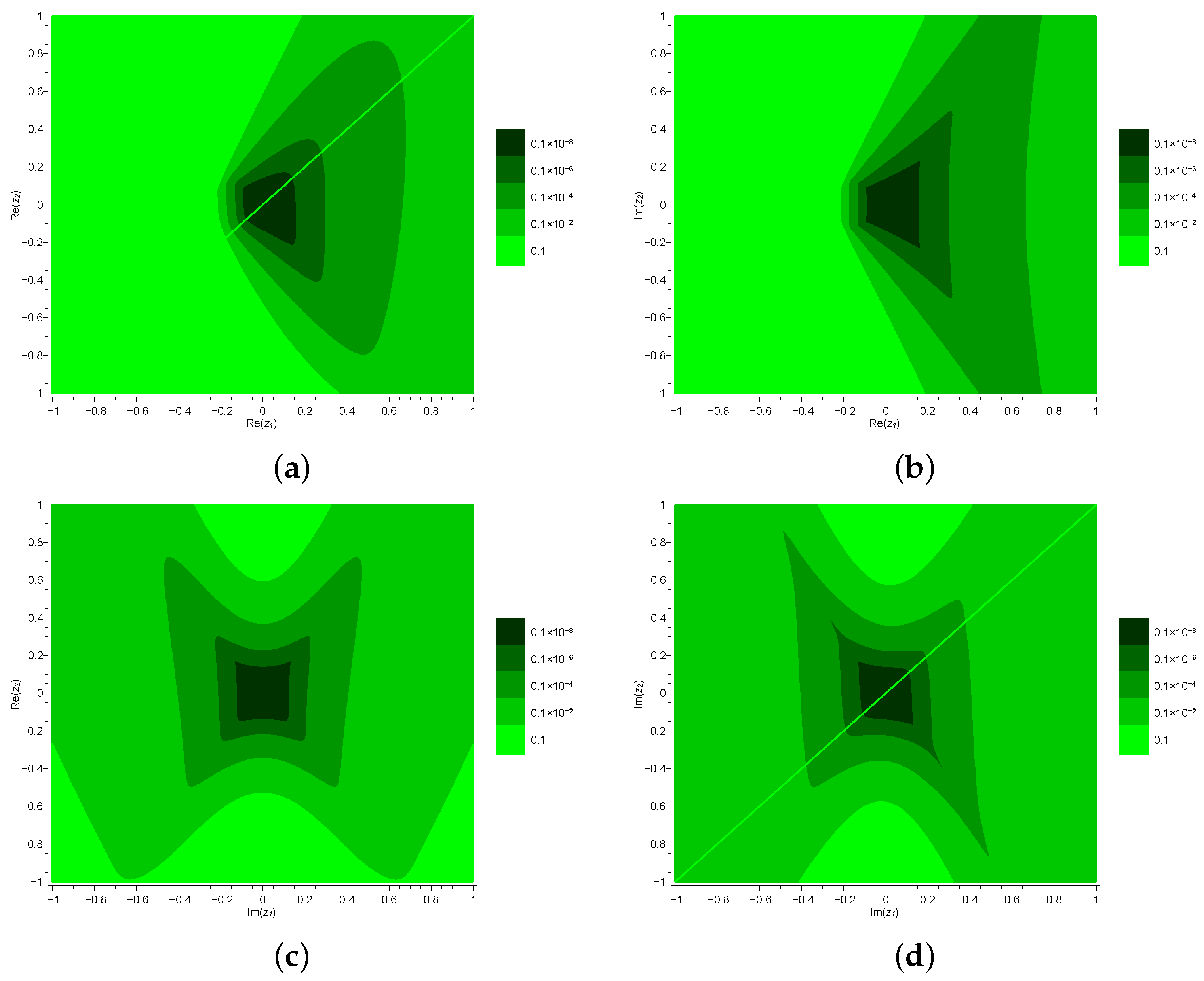
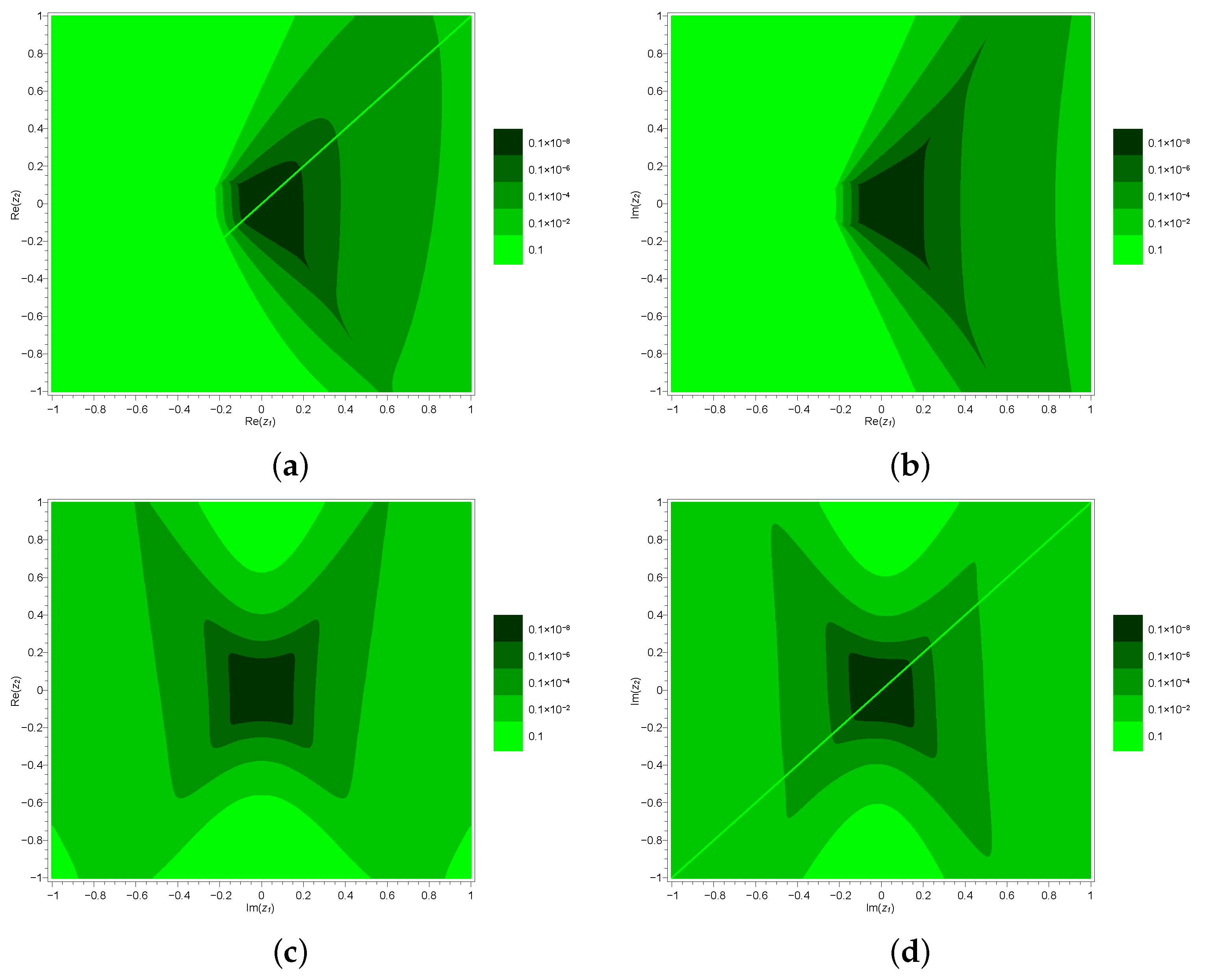
3. Applications
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bailey, W.N. Generalised Hypergeometric Series; Cambridge University Press: Cambridge, UK, 1935. [Google Scholar]
- Choi, J. Recent advances in special functions and their applications. Symmetry 2023, 15, 2159. [Google Scholar] [CrossRef]
- Exton, H. Multiple Hypergeometric Functions and Applications; Horwood, E., Ed.; Halsted Press: Chichester, UK, 1976. [Google Scholar]
- Hang, P.-C.h.; Luo, M.-J. Asymptotics of Saran’s hypergeometric function FK. J. Math. Anal. Appl. 2025, 541, 128707. [Google Scholar] [CrossRef]
- Seaborn, J.B. Hypergeometric Functions and Their Applications. Springer: New York, NY, USA, 1991. [Google Scholar]
- Srivastava, H.M.; Karlsson, P.W. Multiple Gaussian Hypergeometric Series; Horwood, E., Ed.; Halsted Press: Chichester, UK, 1985. [Google Scholar]
- Gauss, C.F. Disquisitiones generales circa seriem infinitam . In Commentationes Societatis Regiae Scientiarum Gottingensis Recentiores; Classis Mathematicae, 1812; H. Dieterich: Gottingae, Germany, 1813; Volume 2, pp. 3–46. [Google Scholar]
- Riemann, B. Sullo svolgimento del quoziente di due serie ipergeometriche in frazione continua infinita. In Gesammelte Werke; Teubner: Leipzig, Germany, 1876; pp. 400–406. [Google Scholar]
- Thomé, L.W. Ueber die Kettenbriichentwicklung des Gausschen Quotienten…. J. Reine Angew. 1867, 67, 299–309. [Google Scholar]
- Van Vleck, E.V. On the convergence of the continued fraction of Gauss and other continued fractions. Ann. Math. 1901–1902, 3, 1–18. [Google Scholar] [CrossRef]
- Wall, H.S. Analytic Theory of Continued Fractions; D. Van Nostrand Co.: New York, NY, USA, 1948. [Google Scholar]
- Cuyt, A.A.M.; Petersen, V.; Verdonk, B.; Waadeland, H.; Jones, W.B. Handbook of Continued Fractions for Special Functions; Springer: Dordrecht, The Netherlands, 2008. [Google Scholar]
- Jones, W.B.; Thron, W.J. Continued Fractions: Analytic Theory and Applications; Addison-Wesley Pub. Co.: Reading, MA, USA, 1980. [Google Scholar]
- Lorentzen, L.; Waadeland, H. Continued Fractions—Volume 1: Convergence Theory, 2nd ed.; Atlantis Press: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Bodnarchuk, P.I.; Skorobogatko, V.Y. Branched Continued Fractions and Their Applications; Naukova Dumka: Kyiv, Ukraine, 1974. (In Ukrainian) [Google Scholar]
- Antonova, T.; Dmytryshyn, R.; Goran, V. On the analytic continuation of Lauricella-Saran hypergeometric function FK(a1, a2, b1, b2; a1, b2, c3; z). Mathematics 2023, 11, 4487. [Google Scholar] [CrossRef]
- Antonova, T.; Dmytryshyn, R.; Sharyn, S. Branched continued fraction representations of ratios of Horn’s confluent function H6. Constr. Math. Anal. 2023, 6, 22–37. [Google Scholar] [CrossRef]
- Bodnar, D.I.; Bodnar, O.S.; Bilanyk, I.B. A truncation error bound for branched continued fractions of the special form on subsets of angular domains. Carpathian Math. Publ. 2023, 15, 437–448. [Google Scholar] [CrossRef]
- Bodnar, D.I. Expansion of a ratio of hypergeometric functions of two variables in branching continued fractions. J. Math. Sci. 1993, 64, 1155–1158. [Google Scholar] [CrossRef]
- Cuyt, A.; Verdonk, B. A review of branched continued fraction theory for the construction of multivariate rational approximants. Appl. Numer. Math. 1988, 4, 263–271. [Google Scholar] [CrossRef]
- Dmytryshyn, R.I. The two-dimensional g-fraction with independent variables for double power series. J. Approx. Theory 2012, 164, 1520–1539. [Google Scholar] [CrossRef][Green Version]
- Hladun, V.R.; Bodnar, D.I.; Rusyn, R.S. Convergence sets and relative stability to perturbations of a branched continued fraction with positive elements. Carpathian Math. Publ. 2024, 16, 16–31. [Google Scholar] [CrossRef]
- Hladun, V.R.; Dmytryshyn, M.V.; Kravtsiv, V.V.; Rusyn, R.S. Numerical stability of the branched continued fraction expansions of the ratios of Horn’s confluent hypergeometric functions H6. Math. Model. Comput. 2024, 11, 1152–1166. [Google Scholar] [CrossRef]
- Hladun, V.; Kravtsiv, V.; Dmytryshyn, M.; Rusyn, R. On numerical stability of continued fractions. Mat. Stud. 2024, 62, 168–183. [Google Scholar] [CrossRef]
- Hoyenko, N.P.; Hladun, V.R.; Manzij, O.S. On the infinite remains of the Nörlund branched continued fraction for Appell hypergeometric functions. Carpathian Math. Publ. 2014, 6, 11–25. (In Ukrainian) [Google Scholar] [CrossRef]
- Petreolle, M.; Sokal, A.D.; Zhu, B.X. Lattice paths and branched continued fractions: An infinite sequence of generalizations of the Stieltjes-Rogers and Thron-Rogers polynomials, with coefficientwise Hankel-total positivity. arXiv 2020, arXiv:1807.03271v2. [Google Scholar] [CrossRef]
- Horn, J. Hypergeometrische Funktionen zweier Veränderlichen. Math. Ann. 1931, 105, 381–407. [Google Scholar] [CrossRef]
- Antonova, T.; Dmytryshyn, R.; Kravtsiv, V. Branched continued fraction expansions of Horn’s hypergeometric function H3 ratios. Mathematics 2021, 9, 148. [Google Scholar] [CrossRef]
- Antonova, T.M. On convergence of branched continued fraction expansions of Horn’s hypergeometric function H3 ratios. Carpathian Math. Publ. 2021, 13, 642–650. [Google Scholar] [CrossRef]
- Dmytryshyn, R.; Antonova, T.; Dmytryshyn, M. On the analytic extension of the Horn’s confluent function H6 on domain in the space C2. Constr. Math. Anal. 2024, 7, 11–26. [Google Scholar] [CrossRef]
- Dmytryshyn, R.; Lutsiv, I.-A.; Dmytryshyn, M. On the analytic extension of the Horn’s hypergeometric function H4. Carpathian Math. Publ. 2024, 16, 32–39. [Google Scholar] [CrossRef]
- Hladun, V.; Rusyn, R.; Dmytryshyn, M. On the analytic extension of three ratios of Horn’s confluent hypergeometric function H7. Res. Math. 2024, 32, 60–70. [Google Scholar] [CrossRef]
- Bodnar, D.I.; Bodnar, O.S.; Dmytryshyn, M.V.; Popov, M.M.; Martsinkiv, M.V.; Salamakha, O.B. Research on the convergence of some types of functional branched continued fractions. Carpathian Math. Publ. 2024, 16, 448–460. [Google Scholar] [CrossRef]
- Bodnar, D.I. Branched Continued Fractions; Naukova Dumka: Kyiv, Ukraine, 1986. (In Russian) [Google Scholar]
- Brychkov, Y.A.; Savischenko, N.V. On some formulas for the Horn functions H3(a, b; c; w, z), H6(c)(a; c; w, z) and Humbert function Φ3(b; c; w, z). Integral Transforms Spec. Funct. 2021, 32, 661–676. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dmytryshyn, R.; Antonova, T.; Hladun, S. On Analytical Continuation of the Horn’s Hypergeometric Functions H3 and Their Ratios. Axioms 2025, 14, 67. https://doi.org/10.3390/axioms14010067
Dmytryshyn R, Antonova T, Hladun S. On Analytical Continuation of the Horn’s Hypergeometric Functions H3 and Their Ratios. Axioms. 2025; 14(1):67. https://doi.org/10.3390/axioms14010067
Chicago/Turabian StyleDmytryshyn, Roman, Tamara Antonova, and Sofiia Hladun. 2025. "On Analytical Continuation of the Horn’s Hypergeometric Functions H3 and Their Ratios" Axioms 14, no. 1: 67. https://doi.org/10.3390/axioms14010067
APA StyleDmytryshyn, R., Antonova, T., & Hladun, S. (2025). On Analytical Continuation of the Horn’s Hypergeometric Functions H3 and Their Ratios. Axioms, 14(1), 67. https://doi.org/10.3390/axioms14010067








