Fractal Continuum Maxwell Creep Model
Abstract
1. Introduction
2. Generalization of the Maxwell Model from Conventional to Fractal Calculus
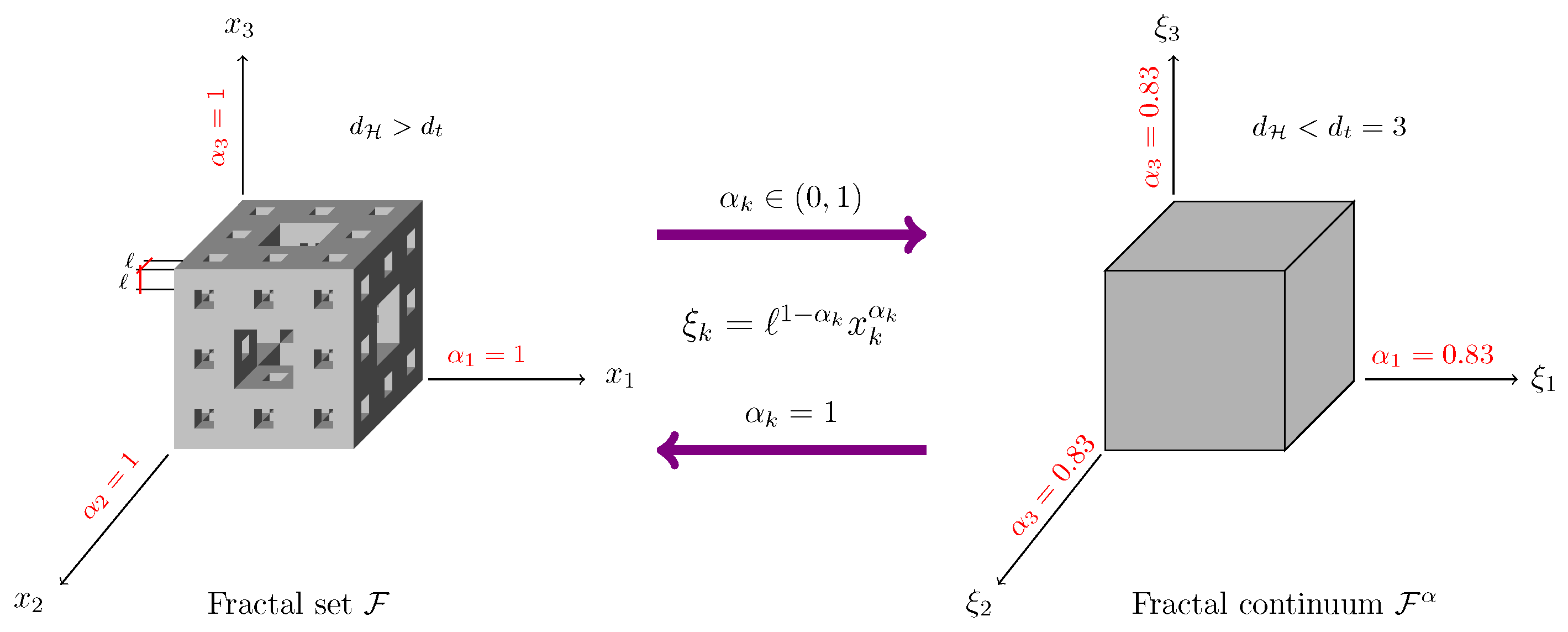
2.1. Balankin’s Approach
2.2. Fractal Continuum Maxwell Creep Model
3. Study of the Fractal Continuum Maxwell Model in Specimen Sierpinski’s Carpets Type
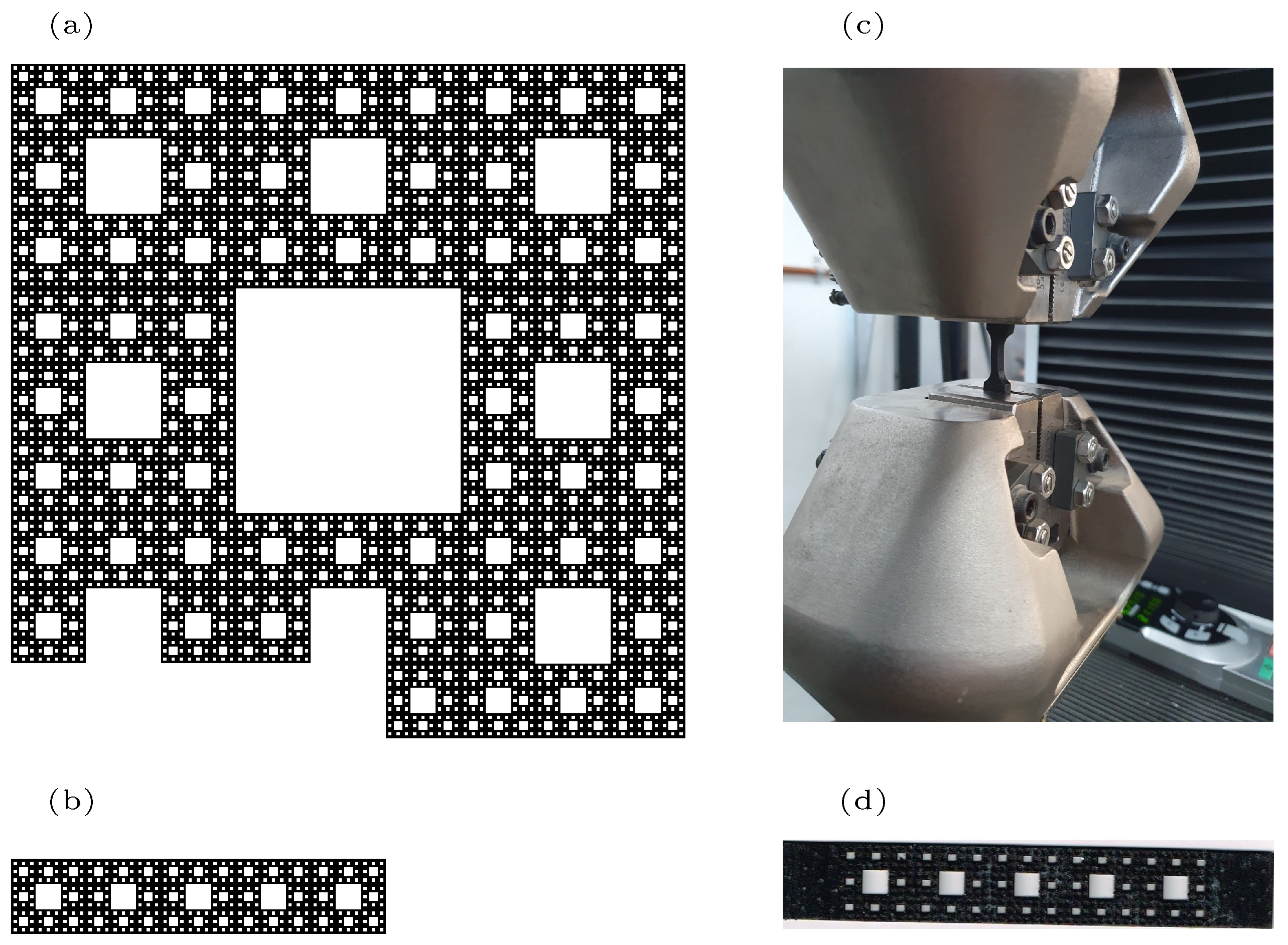
3.1. Sierpinski’s Carpets
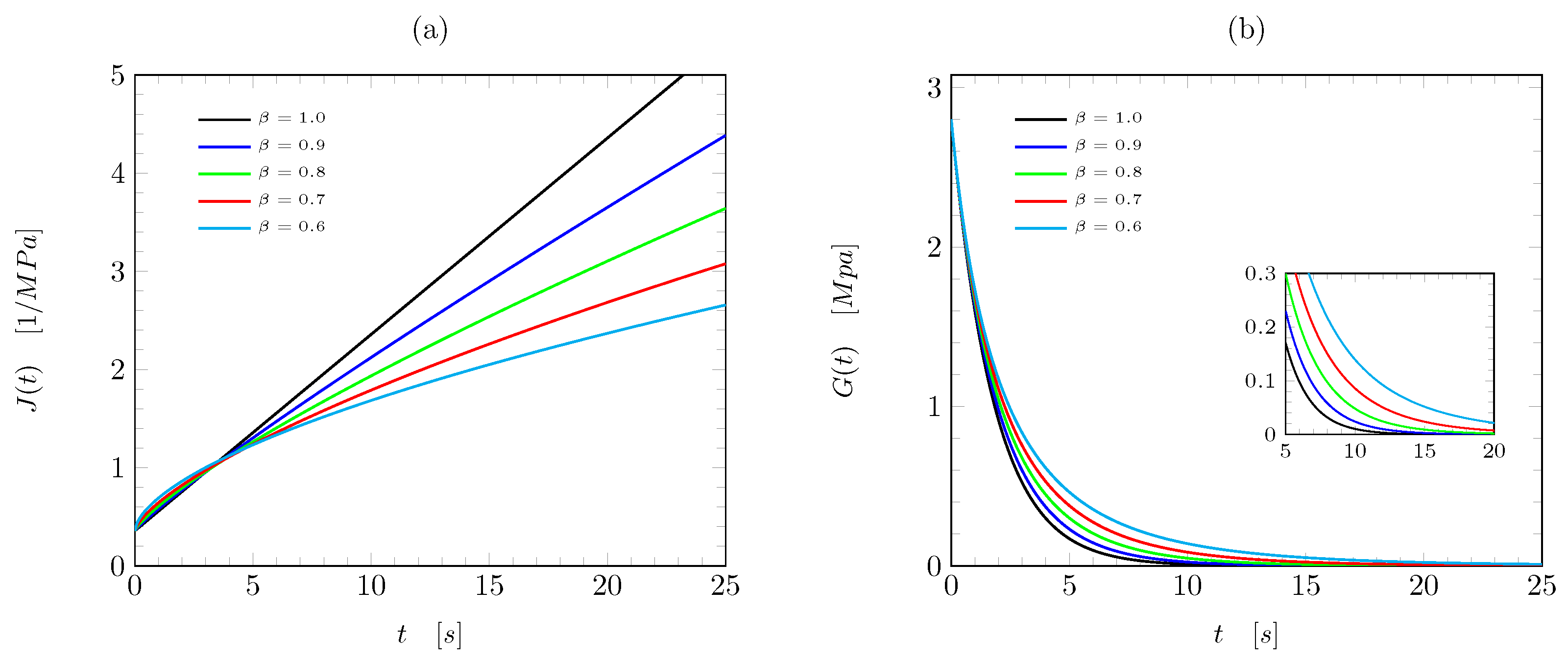
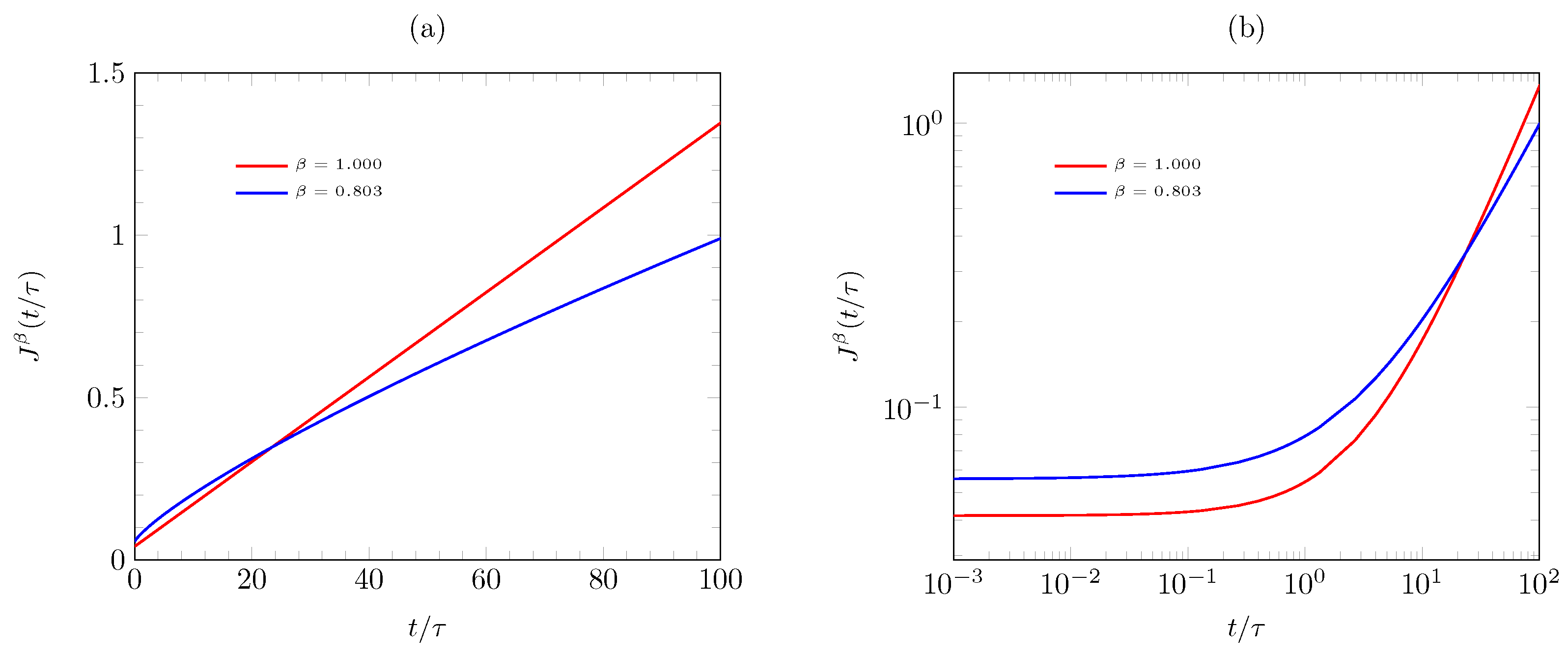
3.2. Theoretical Applications
4. Analysis and Discussion of Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Daghigh, V.; Edalati, H.; Daghigh, H.; Belk, D.M.; Nikbin, K. Time-dependent creep analysis of ultra-high-temperature functionally graded rotating disks of variable thickness. Forces Mech. 2023, 13, 100235. [Google Scholar] [CrossRef]
- Seddighi, H.; Ghannad, M.; Loghman, A.; Zamani Nejad, M. Creep analysis of a cylinder subjected to 2D thermoelasticity loads and boundary conditions with inner heat generation source. Forces Mech. 2024, 15, 100271. [Google Scholar] [CrossRef]
- Kumar, N.; Alen, S.; Mehrotra, P.; Yadav, S. An improved dislocation density reliant model to address the creep deformation of reduced activation ferritic martensitic steel. Forces Mech. 2022, 9, 100117. [Google Scholar] [CrossRef]
- Hiemer, S.; Moretti, P.; Zapperi, S.; Zaiser, M. Predicting creep failure by machine learning—Which features matter? Forces Mech. 2022, 9, 100141. [Google Scholar] [CrossRef]
- Findley, W.; Lai, J.; Onaran, K. Creep and Relaxation of Nonlinear Viscoelastic Materials: With an Introduction to Linear Viscoelasticity; Dover Civil and Mechanical Engineering: Dover, UK, 1989. [Google Scholar]
- Farfan-Cabrera, L.; Pascual-Francisco, J. An Experimental Methodological Approach for Obtaining Viscoelastic Poisson’s Ratio of Elastomers from Creep Strain DIC-Based Measurements. Exp. Mech. 2022, 62, 287–297. [Google Scholar] [CrossRef]
- Pascual-Francisco, J.; Susarrey-Huerta, O.; Farfan-Cabrera, L.; Flores-Hernández, R. Creep Properties of a Viscoelastic 3D Printed Sierpinski Carpet-Based Fractal. Fractal Fract. 2023, 7, 568. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; World Scientific: Singapore, 2022. [Google Scholar]
- Scott Blair, G. Analytical and Integrative Aspects of the Stress-Strain-Time Problem. J. Sci. Instrum. 1944, 21, 80. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Yin, B.; Luo, W. A Nonlinear Fractional Viscoelastic-Plastic Creep Model of Asphalt Mixture. Polymers 2021, 13, 1278. [Google Scholar] [CrossRef]
- Ribeiro, J.G.T.; de Castro, J.T.P.; Meggiolaro, M.A. Modeling concrete and polymer creep using fractional calculus. J. Mater. Res. Technol. 2021, 12, 1184–1193. [Google Scholar] [CrossRef]
- Bouras, Y.; Vrcelj, Z. Fractional and fractal derivative-based creep models for concrete under constant and time-varying loading. Constr. Build. Mater. 2023, 367, 130324. [Google Scholar] [CrossRef]
- Garra, R.; Mainardi, F.; Spada, G. A generalization of the Lomnitz logarithmic creep law via Hadamard fractional calculus. Chaos Solitons Fractals 2017, 102, 333–338. [Google Scholar] [CrossRef]
- Giusti, A.; Colombaro, I.; Garra, R.; Garrappa, R.; Mentrelli, A. On variable-order fractional linear viscoelasticity. Fract. Calc. Appl. Anal. 2024, 27, 1564–1578. [Google Scholar] [CrossRef]
- Cai, W.; Chen, W.; Xu, W. Characterizing the creep of viscoelastic materials by fractal derivative models. Int. J. Non-Linear Mech. 2016, 87, 58–63. [Google Scholar] [CrossRef]
- Wang, R.; Zhuo, Z.; Zhou, H.; Liu, J. A fractal derivative constitutive model for three stages in granite creep. Results Phys. 2017, 7, 2632–2638. [Google Scholar] [CrossRef]
- Yin, Q.; Dai, J.; Dai, G.; Gong, W.; Zhang, F.; Zhu, M. Study on Creep Behavior of Silty Clay Based on Fractal Derivative. Appl. Sci. 2022, 12, 8327. [Google Scholar] [CrossRef]
- Chen, W. Time-space fabric underlying anomalous diffusion. Chaos Soliton Fractals 2006, 28, 923–929. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, X.; Korosak, D. Investigation on Fractional and Fractal Derivative Relaxation-Oscillation Models. Int. J. Nonlinear Sci. Numer. Simul. 2010, 11, 3–9. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1982. [Google Scholar]
- Falconer, K. Fractal Geometry: Mathematical Foundations and Applications; John Wiley and Sons, Ltd.: Chichester, UK, 2014. [Google Scholar]
- Husain, A.; Nanda, M.; Chowdary, M.; Sajid, M. Fractals: An Eclectic Survey, Part-I. Fractal Fract. 2022, 6, 89. [Google Scholar] [CrossRef]
- Husain, A.; Nanda, M.; Chowdary, M.; Sajid, M. Fractals: An Eclectic Survey, Part-II. Fractal Fract. 2022, 6, 379. [Google Scholar] [CrossRef]
- Balankin, A.S. Fractional space approach to studies of physical phenomena on fractals and in confined low-dimensional systems. Chaos Solitons Fractals 2020, 132, 109572. [Google Scholar] [CrossRef]
- Patino-Ortiz, J.; Patino-Ortiz, M.; Martínez-Cruz, M.A.; Balankin, A. A Brief Survey of Paradigmatic Fractals from a Topological Perspective. Fractal Fract. 2023, 7, 597. [Google Scholar] [CrossRef]
- Balka, R.; Buczolich, Z.; Elekes, M. A new fractal dimension: The topological Hausdorff dimension. Adv. Math. 2015, 274, 881–927. [Google Scholar] [CrossRef]
- Balankin, A.; Patino, J.; Patino, M. Inherent features of fractal sets and key attributes of fractal models. Fractals 2022, 30, 2250082. [Google Scholar] [CrossRef]
- Mosco, U. Invariant field metrics and dynamical scalings on fractals. Phys. Rev. Lett. 1997, 79, 4067–4070. [Google Scholar] [CrossRef]
- Havlin, S.; Ben-Avraham, D. Diffusion in disordered media. Phi 2002, 52, 187–292. [Google Scholar] [CrossRef]
- Balankin, A.S.; Elizarraraz, B.E. Hydrodynamics of fractal continuum flow. Phys. Rev. E 2012, 85, 025302(R). [Google Scholar] [CrossRef]
- Balankin, A.S.; Elizarraraz, B.E. Map of fluid flow in fractal porous medium into fractal continuum flow. Phys. Rev. E 2012, 85, 056314. [Google Scholar] [CrossRef]
- Balankin, A.S.; Elizarraraz, B.E. Reply to “Comment on ‘Hydrodynamics of fractal continuum flow’ and ‘Map of fluid flow in fractal porous medium into fractal continuum flow’”. Phys. Rev. E 2013, 88, 057002. [Google Scholar] [CrossRef]
- Balankin, A.S. A continuum framework for mechanics of fractal materials I: From fractional space to continuum with fractal metric. Eur. Phys. J. 2015, 88, 90. [Google Scholar] [CrossRef]
- Balankin, A.S. Effective degrees of freedom of a random walk on a fractal. Phys. Rev. E 2015, 92, 062146. [Google Scholar] [CrossRef]
- Balankin, A.S.; Mena, B.; Patino, J.; Morales, D. Electromagnetic fields in fractal continua. Phys. Lett. A 2013, 377, 783–788. [Google Scholar] [CrossRef]
- Balankin, A.S. A continuum framework for mechanics of fractal materials II: Elastic stress fields ahead of cracks in a fractal medium. Eur. Phys. J. 2015, 88, 91. [Google Scholar] [CrossRef]
- Samayoa, D.; Damián, L.; Kriyvko, A. Map of bending problem for self-similar beams into fractal continuum using Euler-Bernoulli principle. Fractal Fract. 2022, 6, 230. [Google Scholar] [CrossRef]
- Samayoa, D.; Kriyvko, A.; Velázquez, G.; Mollinedo, H. Fractal Continuum Calculus of Functions on Euler-Bernoulli Beam. Fractal Fract. 2022, 6, 552. [Google Scholar] [CrossRef]
- Samayoa, D.; Alcántara, A.; Mollinedo, H.; Barrera-Lao, F.; Torres-SanMighel, C. Fractal Continuum Mapping Applied to Timoshenko Beams. Mathematics 2023, 11, 3492. [Google Scholar] [CrossRef]
- Damián-Adame, L.; Gutiérrez-Torres, C.C.; Figueroa-Espinoza, B.; Barbosa-Saldaña, J.G.; Jiménez-Bernal, J.A. A Mechanical Picture of Fractal Darcy’s Law. Fractal Fract. 2023, 7, 639. [Google Scholar] [CrossRef]
- Cristea, L.L.; Steinsky, B. Connected generalised Sierpinski carpets. Topol. Its Appl. 2010, 157, 1157–1162. [Google Scholar] [CrossRef]
- Cristea, L. A geometric property of the Sierpiński carpet. Quaest. Math. 2005, 28, 251–262. [Google Scholar] [CrossRef]
- Balankin, A.S. The topological Hausdorff dimension and transport properties of Sierpinski carpets. Phys. Lett. A 2017, 381, 2801–2808. [Google Scholar] [CrossRef]
- Rieth, M. A comprising steady-state creep model for the austenitic AISI 316 L(N) steel. J. Nucl. Mater. 2007, 367–370, 915–919. [Google Scholar] [CrossRef]
- Pineda León, E.; Samayoa Ochoa, D.; Rodríguez-Castellanos, A.; Aliabadi, M.; Avalos Gauna, E.; Olivera-Villaseñor, E. Creeping analysis with variable temperature applying the boundary element method. Eng. Anal. Bound. Elem. 2012, 36, 1715–1720. [Google Scholar] [CrossRef]
- Liu, W.; Zhou, H.; Zhang, S.; Jiang, S.; Yang, L. A nonlinear creep model for surrounding rocks of tunnels based on kinetic energy theorem. J. Rock Mech. Geotech. Eng. 2023, 15, 363–374. [Google Scholar] [CrossRef]
- Reyes de Luna, E.; Kryvko, A. Pascual-Francisco, J.; Hernández, I.; Samayoa, D. Generalized Kelvin–Voigt Creep Model in Fractal Space–Time. Mathematics 2024, 12, 3099. [Google Scholar] [CrossRef]
- Myers, D.; De Iaco, S.; Posa, D.; De Cesare, L. Space-time radial basis functions. Comput. Math. Appl. 2002, 43, 539–549. [Google Scholar] [CrossRef]
- Hamaidi, M.; Naji, A.; Charafi, A. Space–time localized radial basis function collocation method for solving parabolic and hyperbolic equations. Eng. Anal. Bound. Elem. 2016, 67, 152–163. [Google Scholar] [CrossRef]
- Noorizadegan, A.; Chen, C.S.; Young, D.; Chen, C. Effective condition number for the selection of the RBF shape parameter with the fictitious point method. Appl. Numer. Math. 2022, 178, 280–295. [Google Scholar] [CrossRef]
- Amir Noorizadegan, D.L.Y.; Chen, C.S. Space–time method for analyzing transient heat conduction in functionally graded materials. Numer. Heat Transf. Part B Fundam. 2024, 85, 828–841. [Google Scholar] [CrossRef]
- Davey, K.; Rasgado, M. Analytical solutions for vibrating fractal composite rods and beams. Appl. Math. Model. 2011, 35, 1194–1209. [Google Scholar] [CrossRef]
| ℓ | i | ||||||
|---|---|---|---|---|---|---|---|
| 0 | 3 | 3 | 3 | 3 | 1 | ||
| 2 | 1.715 | 1.715 | 1.588 | 1 | 1.841 |
| Tensile Strength (MPa) | |
|---|---|
| Percent elongation at break | |
| Young modulus (MPa) | |
| Nominal strain at break |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kryvko, A.; Gutiérrez-Torres, C.d.C.; Jiménez-Bernal, J.A.; Susarrey-Huerta, O.; Reyes de Luna, E.; Samayoa, D. Fractal Continuum Maxwell Creep Model. Axioms 2025, 14, 33. https://doi.org/10.3390/axioms14010033
Kryvko A, Gutiérrez-Torres CdC, Jiménez-Bernal JA, Susarrey-Huerta O, Reyes de Luna E, Samayoa D. Fractal Continuum Maxwell Creep Model. Axioms. 2025; 14(1):33. https://doi.org/10.3390/axioms14010033
Chicago/Turabian StyleKryvko, Andriy, Claudia del C. Gutiérrez-Torres, José Alfredo Jiménez-Bernal, Orlando Susarrey-Huerta, Eduardo Reyes de Luna, and Didier Samayoa. 2025. "Fractal Continuum Maxwell Creep Model" Axioms 14, no. 1: 33. https://doi.org/10.3390/axioms14010033
APA StyleKryvko, A., Gutiérrez-Torres, C. d. C., Jiménez-Bernal, J. A., Susarrey-Huerta, O., Reyes de Luna, E., & Samayoa, D. (2025). Fractal Continuum Maxwell Creep Model. Axioms, 14(1), 33. https://doi.org/10.3390/axioms14010033








