Abstract
In the framework of linear viscoelasticity, the authors have previously calculated a novel inverse Laplace transform involving the Mittag–Leffler function in order to calculate the relaxation modulus in the Andrade model. Here, we generalize this result, calculating the inverse Laplace transform of a given function by using two different approaches: the Bromwich integral and the decomposition of in simple fractions. From both calculations, we obtain a set of novel Laplace and Stieltjes transforms.
MSC:
44Axx; 44A10; 33E12
1. Introduction and Preliminaries
A great variety of applications of integral transforms is well known in the existing literature. Among these applications, we can find that different integral transforms are an effective tool for the solution of ordinary differential equations, partial differential equations, integral equations, and boundary-value problems [1]. The Laplace transform occupies a prominent place among the integral transforms. This transform simplifies differentiation and integration in the time domain by converting them into multiplication and division in the Laplace domain. This makes it widely useful for solving linear differential equations and dynamical systems. There is pervasive literature about the Laplace transform [2,3], as well as an extensive compendium of direct [4] and inverse Laplace transform tables [5].
However, the Stieltjes transform and its applications are not so popular within the integral transforms realm. Also, the compendia of tables are not so extensive ([6], Chapter XIV). However, it is worth noting that the Stieltjes transform is connected with the moment problem for the semi-infinite interval [7] and, consequently, with specific continued fractions.
Next, we set the notation for the Laplace and Stieltjes transforms.
Definition 1.
The Laplace transform of a function , defined for all real non-negative arguments , is a function of the complex variable s, defined as [2]
whenever the improper integral given in (1) exists.
Definition 2.
The Stieltjes transform of a function is defined as ([8], Equation 1.14.47)
If is piecewise continuous on and the integral (2) converges, then we can write the Stieltjes transform as an iterated Laplace transform. Indeed, according to [9], we can formally write
since
Under suitable conditions, the inverse Stieltjes transform can be obtained by Titchmarsh’s formula ([2], Section 3.3):
It is worth noting that this inversion formula is used to calculate the time-spectral functions from the knowledge of the creep and relaxation functions in linear viscoelasticity ([10], Section 2.7). However, Titchmarsh’s formula cannot be applied for all rheological models [11]; thus, the enhancement of Stieltjes transformation tables is quite valuable.
The departure point of this note is to calculate the inverse Laplace transform of the following function in the Laplace domain:
from two different approaches. The first one decomposes in simple fractions for rational , and the second one calculates the inverse Laplace transform of for real , applying the Bromwich formula. From the results of both approaches, we calculate some new Laplace and Stieltjes transforms.
It is worth noting that the authors have calculated the inverse Laplace transform of (5) for the particular case and rational in the framework of linear viscoelasticity [10] in order to calculate the relaxation modulus in the Andrade model [12,13].
This paper is organized as follows. In Section 2 and Section 3, we calculate the inverse Laplace transform of (5) for rational and real , respectively. From both calculations, we derive the main results of the paper in terms of two novel integral transforms: one as a Laplace transform and another one as a Stieltjes transform in Section 4. Also in Section 4, we consider some interesting particular cases of these novel integral transforms. Finally, we collect our conclusions in Section 5.
2. Inverse Laplace Transform for Rational-Valued
Consider the case , and perform the change ,
If has n non-repeated roots , , we can recast (6) as ([14], Equation 17:13:10)
thus,
Apply the inverse Laplace transform formula ([14], Equation 45:14:4):
to (8), where denotes the two-parameter Mittag–Leffler function [15], i.e.,
in order to obtain
i.e.,
where denotes the n different roots of the polynomial,
3. Inverse Laplace Transform for Real-Valued
The inverse Laplace transform can be calculated by using the Bromwich formula ([2], Equation 3.4.2), also known as Fourier–Mellin inversion formula ([3], Equation 4.3),
where . According to the Cauchy’s residue theorem ([16], Section 70), if C is a closed integration contour, and the function is analytic in the interior of C, then
Note that
is an analytic function . In order to prove this, consider the function , and calculate the roots of taking :
Note that , and recall that and , ; thus,
Also,
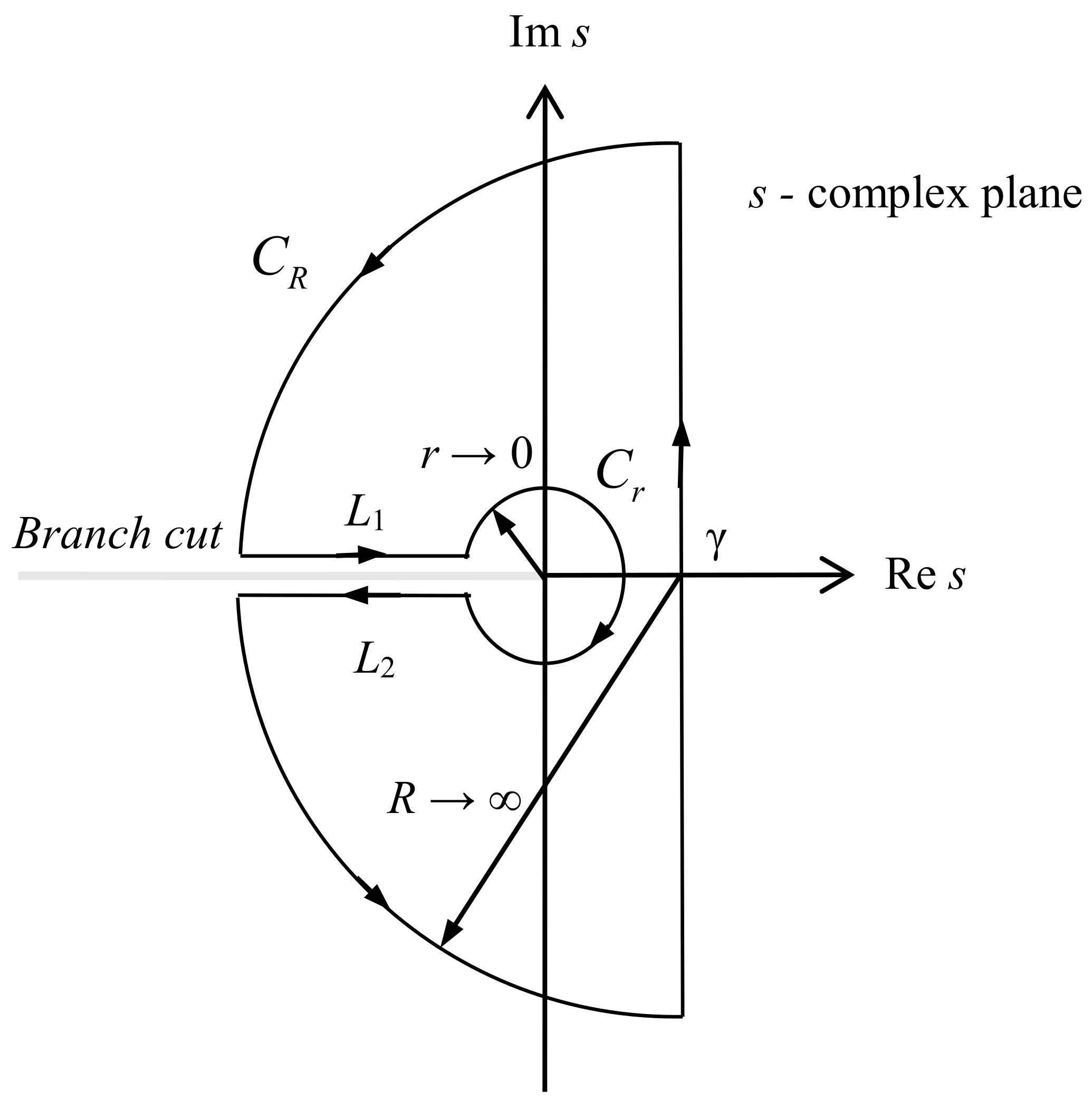
Therefore, the roots of , if any, should lie at origin or on the negative real semi-axis, i.e., on the branch cut of . Consequently, if we take the integration contour path C given in Figure 1, we obtain
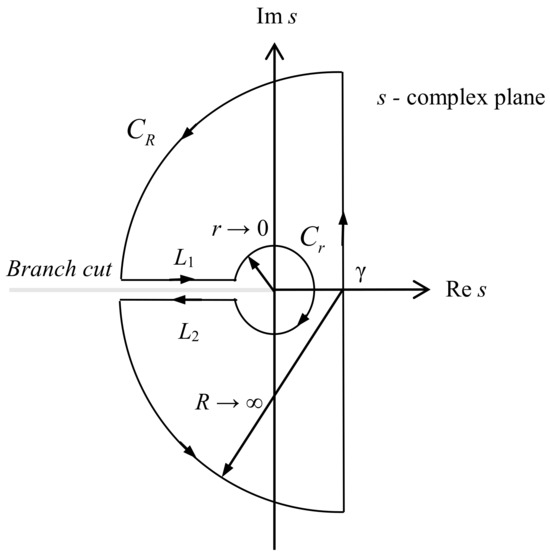
Figure 1.
Integration contour path.
Now, split the integration path C as indicated in Figure 1:
Thus, according to (14) and (22), by taking limits, we obtain
In order to calculate the integrals given in (23), we present the following lemmas below.
Lemma 1.
For , the following limit holds true:
Proof.
Following the proof of Jordan’s lemma ([16], Section 81), take for ,
Therefore,
Perform the change of variables to obtain
Consequently,
and the proof is completed. □
Lemma 2.
For , the following limit holds true:
Proof.
Take for ; thus, for , we have
as we aim to prove. □
4. Main Results and Particular Cases
Theorem 1.
For , , , and with , the following Laplace transform holds true:
where denotes the n different roots of the polynomial,
Theorem 2.
For , , , and , the following Stieltjes transform holds true:
Proof.
4.1. Particular Cases
4.1.1. Laplace Transform
- 1.
- Consider and . Taking , , , and with in (40), we arrive atwhich is an alternative form of the following result given in [4] (Equation 2.1.3(6)) for (see Appendix A for the equivalence):where denotes the upper incomplete gamma function ([14], Equation 45:3:2).
- 2.
- Consider , and . Taking , , , and with in (40), we arrive at
- 3.
- Consider , , , and . Taking , , and in (40), we arrive at
- 4.
- Consider , and . Taking , , , and in (40), we arrive at
4.1.2. Stieltjes Transform
5. Conclusions
We have calculated two novel formulas of integral transforms, one corresponding to a Laplace transform and the other one to a Stieltjes transform. For this purpose, we have calculated the inverse Laplace transform of the function given in (5) by calculating the Bromwich integral for , as well as decomposing in simple fractions, and then calculating the inverse Laplace transform term by term. On the one hand, the calculation of the Bromwich integral has been expressed in terms of a Laplace transform, which has allowed us to obtain a new formula for the Stieltjes transform, i.e., (41). On the other hand, since the decomposition of in simple fractions is only possible for rational , the novel Laplace transform obtained in (40) depends on two parameters , with .
It is worth pointing out why the Mittag–Leffler function arises in Theorem 1. The Mittag–Leffler function is a beneficial particular function in fractional calculus, up to the point that it is called the queen function of fractional calculus [17]. Therefore, it is not surprising that the Mittag–Leffler function arises in solving the relaxation modulus in the Andrade model within the theory of linear viscoelasticity, because this theory is related to fractional calculus [10].
We have also calculated a set of integral transform formulas in Section 4.1, taking particular values for the parameters in the novel Laplace and Stieltjes transforms obtained (i.e., Theorems 1 and 2). The formula given in (43) is also given in the existing literature, but with a completely different expression, i.e., (44). As a consistency test, we have calculated the equivalence between both expressions in Appendix A. In addition to this analytical test, we have numerically checked the main results in Theorems 1 and 2, and the other particular cases given in Section 4.1 with MATHEMATICA. This MATHEMATICA code is available at https://shorturl.at/j5HCm (accessed on 23 August 2024).
Finally, in a future work, the authors would like to extend the analytical method described in this paper to solve fractional differential equations arising in Physical Sciences, usually solved using numerical methods ([18], Chapter 8).
Author Contributions
Conceptualization, J.L.G.-S. and A.A.; Validation, J.L.G.-S.; Formal analysis, J.L.G.-S.; Investigation, A.A.; Writing—original draft, J.L.G.-S.; Writing—review & editing, A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors would like to acknowledge Francesco Mainardi and Giorgio Spada from University of Bologna for introducing us to this line of research.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Proof of the Equivalence of Formulas
Lemma A1.
The following identity involving Mittag–Leffler functions holds true:
Proof.
According to the definition of the Mittag–Leffler function (10), and by splitting the sum in odd and even terms, we have
as we aim to prove. □
Theorem A1.
For and the following identity holds true:
Proof.
First, consider the expansion given in [14] (Equation 46:6:2):
where denotes the lower incomplete gamma function and denotes the Pochhammer symbol. Using the factorial property of the gamma function ([14], Equation 43:5:3), , and the definition of the Mittag–Leffler function (10), is easy to prove from (A4) that
Therefore, using (A5), and the property ([14], Equation 45:1:2),
we write the left hand side (LHS) of (A3) as
Now, we apply the reflection formula ([14], Equation 43:5:1),
for with to obtain
Also, for , note that
Finally, apply (A1) to complete the proof. □
References
- Davies, B. Integral Transforms and Their Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 41. [Google Scholar]
- Apelblat, A. Laplace Transforms and Their Applications; Mathematics Research Developments Series; Nova Science Publishers: Hauppauge, NY, USA, 2012. [Google Scholar]
- Schiff, J.L. The Laplace Transform: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series: Direct Laplace Transforms; CRC Press: Boca Raton, FL, USA, 1986; Volume 4. [Google Scholar]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series: Inverse Laplace Transforms; CRC Press: Boca Raton, FL, USA, 1986; Volume 5. [Google Scholar]
- Erdélyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F. Tables of Integral Transforms; McGraw-Hill: New York, NY, USA, 1954; Volume II. [Google Scholar]
- Shohat, J.; Tamarkin, J. The Problem of Moments; American Mathematical Society: Providence, RI, USA, 1943. [Google Scholar]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Widder, D.V. The Stieltjes transform. Trans. Am. Math. Soc. 1938, 43, 7–60. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; World Scientific: Singapore, 2022. [Google Scholar]
- Mainardi, F.; Masina, E.; González-Santander, J.L. A note on the Lambert W function: Bernstein and Stieltjes properties for a creep model in Linear Viscoelasticity. Symmetry 2023, 15, 1654. [Google Scholar] [CrossRef]
- González-Santander, J.L.; Spada, G.; Mainardi, F.; Apelblat, A. Calculation of the relaxation modulus in the Andrade model by using the Laplace transform. Fractal Fract. 2024, 8, 439. [Google Scholar] [CrossRef]
- Cosorzi, A.; Mellini, D.; González-Santander, J.; Spada, G. On the Love numbers of an Andrade planet. Earth Space Sci. 2024, 11, e2024EA003779. [Google Scholar] [CrossRef]
- Oldham, K.B.; Myland, J.; Spanier, J. An Atlas of Functions: With Equator, the Atlas Function Calculator; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Mittag-Leffler functions and their applications. J. Appl. Math. 2011, 2011, 298628. [Google Scholar] [CrossRef]
- Brown, J.W.; Churchill, R.V. Complex Variables and Applications; McGraw-Hill: New York, NY, USA, 2009. [Google Scholar]
- Mainardi, F. Why the Mittag-Leffler function can be considered the queen function of the fractional calculus? Entropy 2020, 22, 1359. [Google Scholar] [CrossRef] [PubMed]
- Podlubny, I. Fractional Differential Equations; Acedemic Press: Cambridge, MA, USA, 1998. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).