1. Introduction
Distance functions, or metrics, are always a fascinating topic in research due to their diverse and intuitive applications [
1,
2]. In this article, we investigate the relationship between linear dependence and metrics. For each metric
d with a finite domain size, say
n, it can be represented (or the nodes relabeled) by
metric matrices (or
). Because the simultaneous exchange of any two rows and the exchange of any two columns does not change the value of the determinants, i.e.,
for all
, it is sufficient to study one representation. Here,
denotes the set of all 4-by-4 real matrices where the diagonal elements are 0 and the off-diagonal elements are all positive real numbers.
Definition 1.
Officially, we should probably call these matrices ‘distance matrices’. However, in order not to confuse them with the typical Eulidean Distance Matrix (or EDM) [
3,
4] based on square distances, we simply call our simple distance-based matrices metric matrices. In this paper, we study and characterize the necessary and sufficient conditions for the dependence and independence of
. First, we provide the necessary conditions for the linear dependence of a metric matrix. These conditions are mainly found in Lemma 1. Then, we show that any metric matrix containing at least one real triangular triplet would not satisfy the necessary conditions, as shown in Claims 1 and 3. This leads directly to the further characterization of the necessary condition, as shown in Claims 2 and 4 and summarized in Lemma 2 and 3. We then show the sufficient conditions for linear dependence by constructing three sets of disjoint dependence metric matrices:
, and
, respectively defined in Definitions 2, 4, and 5. We show that these categorized metric matrices fully characterize the dependent metric matrices in
via Theorem 1, Corollary 1, and Lemma 4. The entire theorems, associated presentations, and derivations are presented in
Section 2. Applications of these theorems are presented in
Section 3 and
Section 4.
2. Theories and Derivations
Lemma 1 (Necessary conditions)
. If and , thenor Proof. Let , where □
Because
is invertible (thus,
), we have
, i.e.,
i.e.,
where
. Therefore,
Claim 1. Ifwhere for all and , then . Proof. Assume
. From the premise, we have
;
;
;
, where
if
and
, otherwise
. These results lead to
Now, we can divide both sides of Equations (
1)–(4) by
, and
, respectively, yielding
Multiplying Equation (
5) by
and (6) by
yields
Substituting Equations (
9) and (10) into (3) and (4), respectively, yields
where
if
and
otherwise, and where
if
and
otherwise. Furthermore, the equations can be simplified as follows:
i.e.,
, i.e.,
, as
. This yields a contradiction; hence,
. □
Remark 1. In order to save space for our expositions, this claim and the following claims, lemmas, theorems, etc., are not expressed in the traditional way. In principle, to capture the conditions for the premises of the triangle inequlaity, we need batches of premises. Instead, we use the notation ⊛ together withto denote all remaining cases (except the premise with the equations based on triangle equality: ). In other words, this claim or the following similar statements deal with uniform triangle equality cases. Strictly speaking, if we adopt the traditional representation we would have fifteen claims for this claim alone; thus, we use the notation ⊛ to save space. Another advantage of our presentation is it keeps the derivations as concise as possible and makes it easier for readers to check the validity of the statements. Claim 2. If , then and .
Proof. Per Claim 1, if we have
, then
i.e.,
and
, i.e.,
and
. □
Lemma 2. iff ; ; .
Proof. Per Claim 2, and , i.e., . Because , it follows that . From the property , we have . On the other hand, if ; ; , then . □
Claim 3. Ifwhere for all , and , then . Proof. Assume
. From the premise, we have
;
;
;
, where
if
and
, otherwise
. These results lead to
In fact, the notation
is meant to represent the equation
if and only if
and
. Now, we can divide both sides of Equations (
11)–(14) by
and
, respectively, to yield
Multiplying Equation (
15) by
and (16) by
yields
Substituting Equations (
19) and (20) into (13) and (14), respectively, yields
where
if
, otherwise
and where
if
, otherwise
. Furthermore, the equations can be simplified as follows:
i.e.,
Multiplying Equation (
21) with (22) together yields
, where
if
and
otherwise. In fact, the notation
is meant to represent the equation
if and only if
and
and
. Hence,
, as
. This yields a contradiction; hence,
. □
Claim 4. If , then Proof. This follows immediately from Claim 3. □
Lemma 3. iff ; ; .
Proof. Without loss of generality, per Claim 4, let us assume
and
; then, we can identify Equations (
15) and (18) with
Subtracting Equation (24) from (
23) yields
Then, we argue
; if
, then per Claim 4 we have
. Thusm
, i.e.,
, which is not possible. Hence,
; thus, per Equation (
27),
, i.e.,
Substituting Equation (
28) into either Equation (
23), (24), (25), or (26), we have
From Equations (
28) and (
29), we have
, i.e.,
, i.e.,
and
. Thus, from the premise,
. Per Claim 4, we know that
; hence, we have
. □
Based on the above-mentioned theorems, claims, etc., we can identify the dependence metric matrices as follows.
Definition 2. (First-type dependence metric matrices)
Definition 3. (Second-type dependence metric matrices)
.
Definition 4. (First subtype of second-type dependence metric matrices)
.
Definition 5. (Second subtype of second-type dependence metric matrices)
.
Definition 6. .
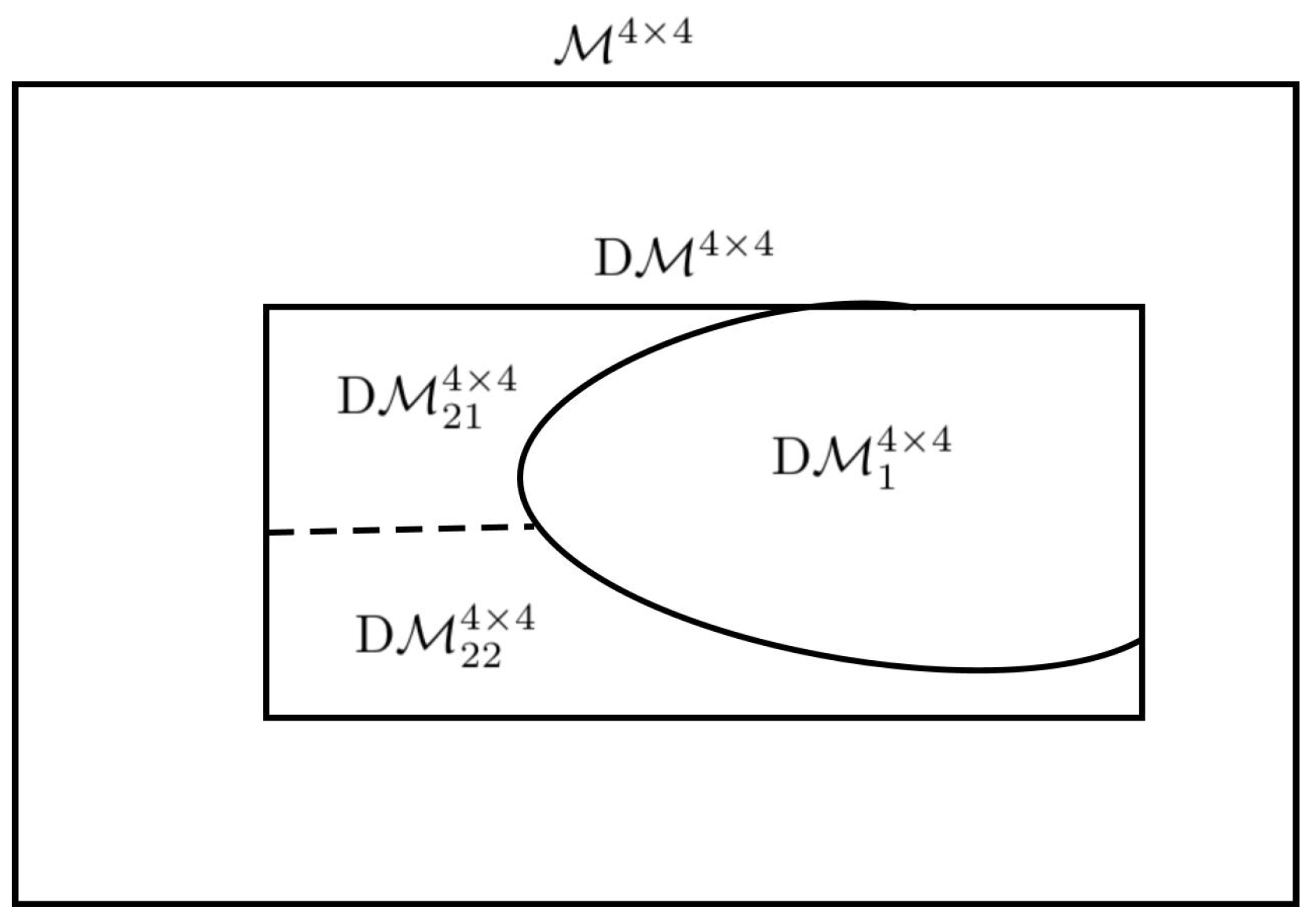
Observing that and . We show that these definitions are sufficient to characterize the set of dependence and independence metric matrices.
Theorem 1. is the maximal set of all the linearly dependent 4-by-4 metric matrices.
Proof. The result follows immediately from Lemmas 1–3. □
Corollary 1. is the maximal set of all the linearly independent 4-by-4 metric matrices.
Theorem 2. For all pairs with and :
- 1.
is closed under positive linear combinations, i.e., if , then .
- 2.
is closed under positive linear combinations.
- 3.
is closed under positive linear combinations.
Proof. The first statement is trivial. Here, we prove the second and third statements. Let
, let
be an arbitrary pair such that
and
, and let
; then,
furthermore,
Hence, we have shown that . A similar proof applies to the third statement. □
Example 1. If , , and , then , and .
The completely characterization of the above relation can be seen in
Figure 1:
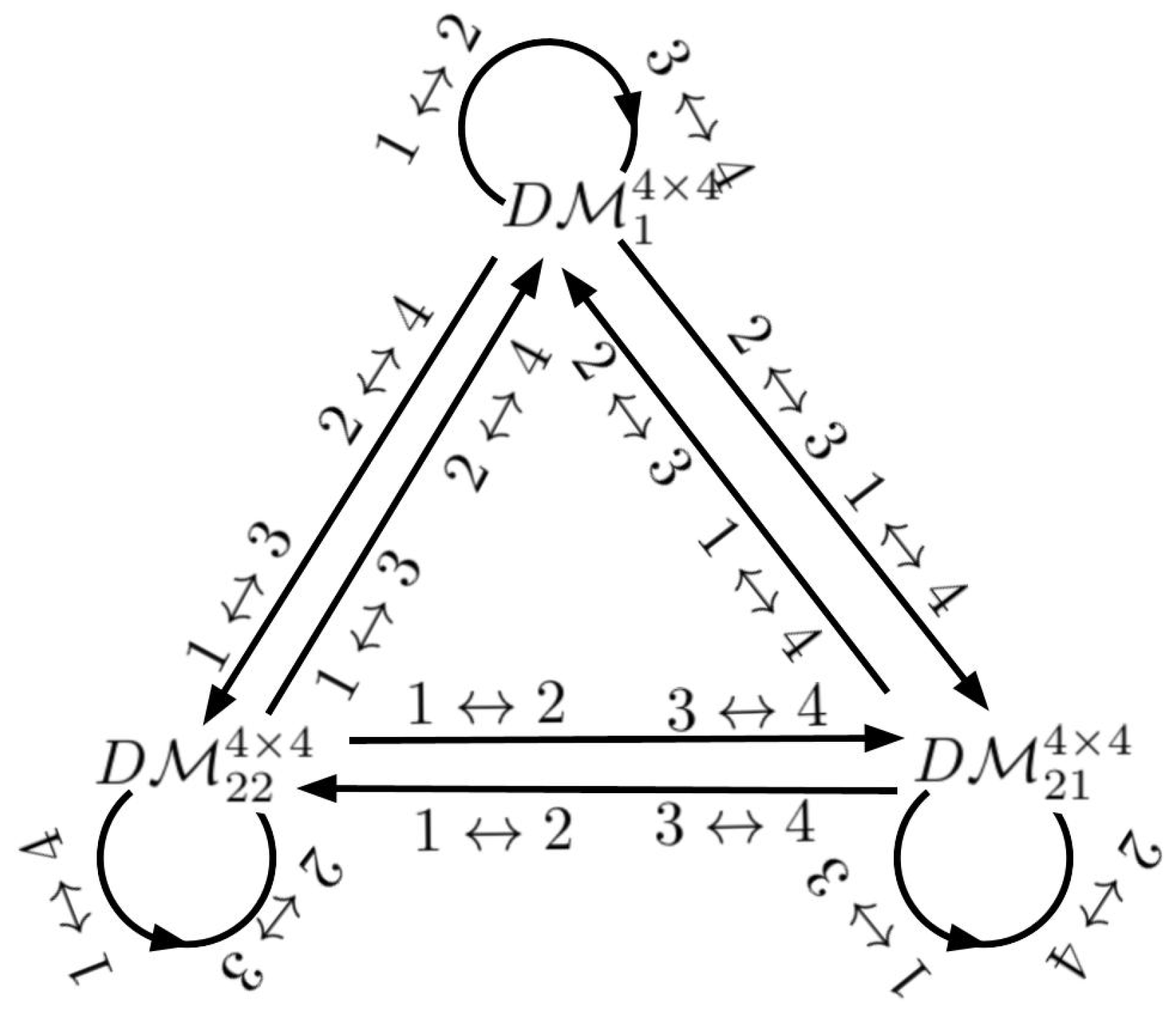
Let be arbitrary, and let denote the metric matrix after swapping the i-th and j-th rows and the i-th and j-th columns of K.
Claim 5. - 1.
If , then ; ; .
- 2.
If , then ; ; ;
- 3.
If , then ; ; .
Proof. Let be arbitrary. Then, only swap and in K, i.e., . Furthermore, and . Similarly, and . Now, let be arbitrary, where . Then, and ; similarly, , and . Lastly, let be arbitrary, where ; then, , as does . Moreover, , as does . Lastly, , as does . □
These results are encapsulated in
Figure 2.
Lemma 4. is closed under the relabeling of the four nodes.
Proof. Let N denote the set , and let T denote the set of all the bijective functions from N to N. Then, there are bijective functions in T, or , where is associated with the identity function. Each can be regarded as several transformations (each of which is a simultaneous exchanges of i-th and j-th rows and columns), starting from l; then, per Claim 5, the result follows immediately. □
Before we proceed to the application of our results, let us summarize the derived results in this article. It is quite obvious that all metric matrices consisting of three points, i.e., 3-by-3 matrices, are all linearly independent. Intuitively (based on Euclidean distance), all metric matrices consisting of four points or more would be linearly independent. In this article, we show that this is not the case. We partition the set of all 4-by-4 metric matrices, or
(see Definition 1), into the set of all dependent metric matrices, or
(see Definition 6) and the set of all independent metric matrices (or
). We further partition
into
(see Definition 2) and
(see Definition 3). Finally, we partition
into
(see Definition 4) and
(see Definition 5). These partitions (see
Figure 1) can be listed as follows:
,
,
.
3. Application One
Now that we have completed the characterization of dependence and independence metric matrices, we can define their deviation.
Definition 7 (Deviation from dependence)
. Define by In addition, we can also find some other applications. Let d denote a metric over a finite set consisting of four distinct points, and let denote its associated metric matrix.
Claim 6. For any arbitrary distinct real numbers , it is the case that , where derives a linearly independent metric matrix.
Proof. Let
denote
, i.e.,
, and let
denote the associated metric matrix with metric
d. If
is not independent, then
, i.e.,
, i.e.,
From Equations (
30) and (31), we have
. On the other hand, from Equations (32) and (33) we have
. This obviously contradicts the linear order of
. □
Similarly, we can investigate the dependence and independence of
p-order Minkowski distance functions
, where
. Minkowski distance functions have diverse applications in AI, data science [
5,
6], and machine learning-based subjects [
7]. Let distinct
, and
be arbitrary; then,
. Suppose there exists
such that
, i.e.,
or
, or
. We can show that
cannot be true. Let
and
; then,
i.e., (by norms)
which is true only if
, i.e., if
and
are collinear and if
lies between
and
. Similarly,
, i.e.,
which is true only if
, i.e., if
and
are collinear and if
lies between
and
. This, together with
and
being collinear and
lying strictly between
and
, implies
, which contradicts the fact that
. Hence, it is impossible to have
. By the same arguments, we find that it is impossible to have
or
, i.e.,
, an independent metric matrix.
Example 2. ; then, , where denotes the k-th element of vector . After a sequence of computations, we obtain and i.e., , i.e., is an independent metric matrix.
Lemma 5. , or precisely , is linearly independent for all .
4. Application Two
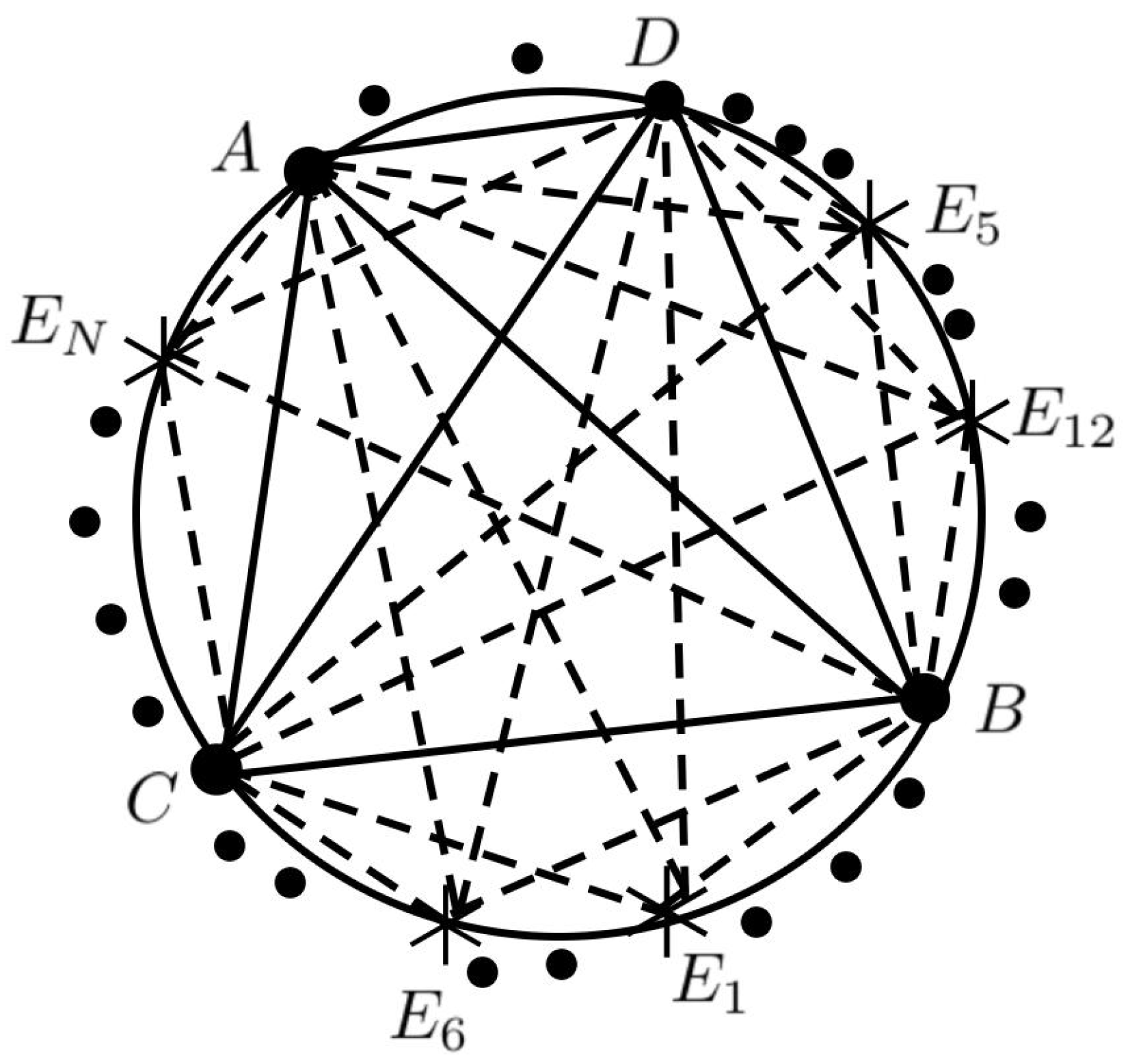
Claim 7. Any associated metric matrices with four concyclic points are linearly independent.
Proof. Let
be four arbitrary points on a given circle, as shown in
Figure 3. Per Ptolemy’s Theorem [
8], the lengths of edges abide by
Let
; if
, then per Lemma 1 we have
Comparing Equation (
34) with (
35), we have
, which is a contradiction. Therefore,
, i.e.,
could serve as a basis for other points on the circumsphere of the given circle. □
Based on Claim 7, we can analyze a dataset. Given a dataset , we can compute each distance column matrix . Then, the set of distances (or coordinates) between the dataset and the four representative points can be calculated as . This set provides us with some information about the dataset in terms of the distances between representative points.
Example 3. Given a 2D unit circle with origin and eight uniformly sampled points , are respectively associated with , while , , , are respectively associated with . After a series of calculations, the following results are obtained:
; . Hence, the distances between and the basis can be represented by