Abstract
In the realm of management decision-making, the selection of green suppliers has long been a complex issue. Companies must take a holistic approach, evaluating potential suppliers based on their capabilities, economic viability, and environmental impact. The decision-making process, fraught with intricacies and uncertainties, urgently demands the development of a scientifically sound and efficient method for guidance. Since the concept of Fermatean fuzzy sets (FFSs) was proposed, it has been proved to be an effective tool for solving multi-attribute decision-making (MADM) problems in complicated realistic situations. And the Power Bonferroni mean (PBM) operator, combining the strengths of the power average (PA) and Bonferroni mean (BM), excels in considering attribute interactions for a thorough evaluation. To ensure a comprehensive and sufficient evaluation framework for supplier selection, this paper introduces innovative aggregation operators that extend the PBM and integrate probabilistic information into Fermatean hesitant fuzzy sets (FHFSs) and Fermatean probabilistic hesitant fuzzy sets (FPHFSs). It successively proposes the Fermatean hesitant fuzzy power Bonferroni mean (FHFPBM), Fermatean hesitant fuzzy weighted power Bonferroni mean (FHFWPBM), and Fermatean hesitant fuzzy probabilistic weighted power Bonferroni mean (FHFPWPBM) operators, examining their key properties like idempotency, boundedness, and permutation invariance. By further integrating PBM with probabilistic information into FPHFSs, three new Fermatean probabilistic hesitant fuzzy power Bonferroni aggregation operators are developed: the Fermatean probabilistic hesitant fuzzy power Bonferroni mean (FPHFPBM), Fermatean probabilistic hesitant fuzzy weighted power Bonferroni mean (FPHFWPBM), and Fermatean probabilistic hesitant fuzzy probabilistic weighted power Bonferroni mean (FPHFPWPBM). Subsequently, a MADM method based on these operators is constructed. Finally, a numerical example concerning the selection of green suppliers is presented to demonstrate the applicability and effectiveness of this method using the FPHFPWPBM operator.
Keywords:
Fermatean probabilistic hesitant fuzzy set; power Bonferroni mean operators; probabilistic information; multi-attribute decision-making MSC:
03B52; 03E72; 94D05
1. Introduction
Multi-attribute decision-making (MADM) is frequently utilized to effectively rank or select one or more alternatives from a discrete set of candidate schemes in the presence of multiple, usually conflicting, criteria or attributes [1]. As human economies and societies rapidly evolve, the complexity of decision-making problems has escalated, compounded by the proliferation of data in everyday production and life. The presence of inaccurate and incomplete information, coupled with the subjective ambiguity and cognitive constraints of decision-makers, frequently renders existing MADM methods inadequate for practical needs. Consequently, considerable efforts have been continuously made towards developing more effective approaches to mitigate the impact of subjectivity and uncertainty on the decision-making process [2]. In an idealized decision-making situation, the decision results are usually presented in the form of a precise numerical value or a set of specific orders. However, the reality is that the decision results often fall within a range of vague values, and there may be many potential outcomes of ranking. In response, Zadeh [3] raised the concept of fuzzy set (FS), allowing the evaluation results to be intermediate between several fuzzy numbers. Subsequent related studies have continuously enriched the FS theory and provided some effective methods for dealing with complex decision-making problems under uncertain circumstances.
Having recognized the inadequacy of FS containing only membership degree in evaluating the information, Atanassov [4] proposed intuitionistic fuzzy set (IFS) by adding non-membership degree to represent the negation degree of a certain attribute. Compared with the FS, the IFS can better describe the completeness and accuracy of decision information and reflect the degree of support, opposition, and neutrality of decision-makers. Numerous works have shed light on the capability of IFSs to navigate the challenges of uncertainty and fuzziness [5,6,7,8,9,10], including aggregation operators [5,6], distance measures [7], correlation coefficients [8], and the application of MADM methods in IFS [9,10]. With the increasing complexity of practical decision problems, the condition of IFSs on the sum of membership and non-membership degrees not greater than 1 gradually shows an inadequacy in data aggregation. Thus, Yager [11] proposed Pythagorean fuzzy set (PFS), which broadens the condition to allow the sum of membership and non-membership degrees greater than 1 with the sum of square less than or equal to 1, so it has a stronger ability to describe fuzzy phenomena than FS and IFS. PFS has been widely studied since it was proposed, mainly focusing on the application of information aggregation operator [12,13], information measure including distance, similarity and entropy measure [14,15,16], and combination with MADM methods [17,18]. Subsequently, to encompass a wider array of scenarios, Yager [19] extended the framework of PFSs, introducing a novel concept known as “q-rung orthopair fuzzy sets” (q-ROFSs), where the sum of qth power of the membership and non-membership is constrained such that with . Obviously, q-ROFSs offer a broader spectrum of fuzzy information, making them a more versatile and suitable approach for addressing unpredictable situations. In recent years, the concept of q-ROFSs has garnered growing scholarly attention, thereby broadening its applications in the realms of information integration and decision-making [20,21,22]. Specifically, in order to address decision situations with more huge and complicated information, Senapati and Yager [23] adopted a similar approach and proposed Fermatean fuzzy set (FFS), further extending the condition that allow the sum of squares of membership and non-membership degrees greater than 1 with the sum of cubic less than or equal to 1. Obviously, compared to IFS and PFS, the FFS can help decision-makers describe complex information under uncertain environments more adequately. In recent years, the research on FFS has emerged and scholars have conducted extensive research on relevant aspects including information aggregation operators [24,25,26], information measures [27,28], and extensions of FFSs [29,30].
To accommodate the indecision between multiple evaluation values that often occurs in actual decision-making situation, Torra [31] suggested the concept of hesitant fuzzy set (HFS). Compared to the single value of the membership degrees in FS, the HFS allows membership degrees to be multiple values, which can better describe the hesitation of decision-makers. As a prominent tool for depicting hesitancy in decision-making processes, scholars have constantly enriched the extensions of HFSs, such as interval-valued hesitant fuzzy set (IVHFS) [32], intuitionistic hesitant fuzzy set (IHFS) [33], Pythagorean hesitant fuzzy set (PyHFS) [34], and Fermatean hesitant fuzzy set (FHFS) [35]. Combining the advantages of FFS and HFS, FHFS is acknowledged as an excellent tool for information integration in fuzzy environments, thus attracting a large number of scholars to conduct research on it. Lai et al. [36] introduced the concept of hesitant Fermatean fuzzy sets (HFFSs) and advanced the CoCoSo method by integrating aggregation operators and information measures specific to HFFSs. Mishra et al. [37] brought forth the notion of interval-valued hesitant Fermatean fuzzy sets (IVHFFSs), enhancing the COPRAS method with IVHFF information. Liu and Luo [38] utilized the probabilistic hesitant Fermatean fuzzy set to illustrate the comprehensive evaluation information. Ruan et al. [39] explored a Fermatean hesitant fuzzy information aggregation method by combining the FHFSs with Heronian mean (HM) operators.
Although HFS can reflect the decision-maker’s hesitancy, it ignores the decision-maker’s preferences for different values within each membership degree. To address this, Xu et al. [40] introduced concept of probabilistic hesitant fuzzy set (PHFS) and its basic operational rules. By adding probabilities to each membership degree, the PHFS can effectively address the issues of individual expert preferences and the number of experts in the decision-making process. Therefore, since the definition of PHFS, it has achieved a series of research results in the field of MADM. Scholars have successively investigated probabilistic linguistic term set (PLTS) [41], probabilistic interval-valued hesitant fuzzy set (PIVHFS) [42], probabilistic interval-valued intuitionistic hesitant fuzzy set [43], and probabilistic interval-valued Fermatean hesitant fuzzy set (PIVFHFS) [44]. Combining the advantages of q-ROFSs and PHFSs, Ren et al. [45] proposed the concept of q-rung orthopair probabilistic hesitant fuzzy rough sets (q-ROPHFSs), which provides a more comprehensive framework for modeling complex and nuanced uncertainties. Chen et al. [46] improved the algorithms for q-ROPHFS by introducing the Schweizer-Sklar T-norm and developed a MADM model based on the newly proposed q-rung orthopair probabilistic hesitant fuzzy Schweizer-Sklar power weighted Hamy mean operator, enhancing the computational efficiency of the information aggregation operator within q-ROPHFS framework. Chen et al. [47] also explored the application of the q-rung orthopair probability hesitant fuzzy GRA-TOPSIS as a modeling tool for assessing airspace operation effectiveness. Additionally, Attaullah et al. [48] introduced the concept of q-rung orthopair probabilistic hesitant fuzzy rough set (q-ROPHFRS) by integrating rough set with q-ROPHFS and successfully applied it in a numerical case study regarding the selection of medical oxygen suppliers for hospitals. In recent years, as scholars have been enriching the research on q-ROPHFSs, the study of the specific fuzzy set paradigms associated with it has also been continuously evolving, i.e., Pythagorean probabilistic hesitant fuzzy set (PyPHFS) [49], and Fermatean probabilistic hesitant fuzzy set (FPHFS) [50]. Among them, the FPHFS, by integrating probabilistic information into Fermatean Hesitant Fuzzy Sets, is capable of more fully expressing the uncertainty of information and the hesitancy of decision-makers. For example, there is a Fermatean probabilistic hesitant fuzzy number within a FPHFS used to denote the evaluation results for an element x regarding the attribute “good quality” by a group of experts. Obviously, we can consider that in the evaluation results given by the experts, for the membership degree, 30% show 0.4 and 70% show 0.6; for the non-membership degree, 40% show 0.2, and the remaining 60% show 0.3. Compared to the single numerical evaluation results in FFS, the multiple values contained in FPHFS can reflect the decision-makers’ hesitancy; whereas in the FHFS, the possibility of evaluation values is assumed to be uniform by default, the FPHFS retain the probability of the evaluation values, thereby better reflecting the decision-makers’ risk preferences.
In actual decision-making, various evaluation attributes may not be completely independent but may have varying degrees of correlation, such as complementary, redundant, and preference relationships, etc. Considering the interplay between evaluation attributes can directly affect the accuracy and rationality of decision outcomes, Yager [51] proposed the power average (PA) operator. This operator adjusts the weights of assessment values that deviate significantly from the overall information by calculating the support degree, effectively overcoming the impact of information interrelation on decision outcomes. The PA operator provides more information and versatility for the aggregation of information, which has attracted widespread attention and in-depth research from subsequent scholars. On the basis of the PA operator, Xu and Yager [52] integrated the geometric mean (GM) operator into it, developing the power geometric (PG) operator, weighted power geometric (WPG) operator, and power ordered weighted geometric (POWG) operator. Zhang [53] extended the PA operator to the hesitant fuzzy environment and defined the hesitant fuzzy power average (HFPA) operator and the hesitant fuzzy power geometric (HFPG) operator. By generalizing the PA operator to the intuitive fuzzy environment, Xu [54,55] proposed a series of novel intuitionistic fuzzy power aggregation operators and interval-valued intuitionistic fuzzy power aggregation operators. He et al. [56] applied the PA operator to the Pythagorean fuzzy environment, defining several Pythagorean fuzzy power average aggregation operators and developed a decision-making method based on the proposed operators.
Another operator that considers the mutual influence between input variables for data aggregation is the Bonferroni mean (BM) operator. Yager [57] was the first to provide an interpretation of the BM operator, emphasizing that it can capture the interrelationship between criteria, which has laid a theoretical foundation for its decision-making applications. Beliakov et al. [58] extended Yager’s results by proposing the generalized extensions of the BM operator. Shortly after, Xu [59] extended the BM operator to the decision-making environment with interval numbers, and proposed the intuitionistic fuzzy Bonferroni mean (IFBM) operator and the weighted intuitionistic fuzzy Bonferroni mean (WIFBM) operator along with Yager [60]. To integrate and capitalize on the strengths of the PA and BM operators, He et al. [61] combined the PA operator with the BM operator to propose the Power Bonferroni Mean (PBM) operator. Subsequently, the PBM operator was extended to various fuzzy environments, including intuitionistic fuzzy sets [62], interval-valued intuitionistic fuzzy sets [63], and linguistic intuitionistic fuzzy sets [64]. Luo et al. [65] extended the PBM operator to the Pythagorean fuzzy environment, proposing a series of Pythagorean fuzzy power Bonferroni aggregation operators. Furthermore, by integrating the PBM operator and the FFS information, Ruan et al. [66] introduced the Fermatean fuzzy power Bonferroni mean (FFPBM) and Fermatean fuzzy weighted power Bonferroni mean (FFWPBM) operators, thereby enriching the MADM methods. However, there is currently a scarcity of research on the extension and application of the PBM operator in FHFSs and FPHFSs, indicating that research in this field holds considerable potential for future exploration.
As environmental awareness increases and businesses pursue sustainable development, green supply chain management has become an important component of corporate competitiveness. At the same time, with the significant impact of the concept of sustainable development on business and marketing, the selection of green suppliers is increasingly critical for effective green supply chain management, garnering attention from both researchers and practitioners [67,68]. To select the appropriate green suppliers, companies need to consider various dimensions involving economic, environmental, and social aspects during the evaluation and decision-making process, making the green supplier selection a typical multi-attribute decision-making (MADM) problem [69]. In recent years, scholars have introduced MADM methods and attempted to build various decision models to explore how to effectively carry out the selection of green suppliers. Deng et al. [70] developed the D-AHP method, extending the classical analytic hierarchy process (AHP) method to incorporate so-called D numbers for uncertain information, and applied it to supplier selection. Boran ey al. [71] proposed a TOPSIS method combined with intuitionistic fuzzy set to select appropriate supplier in group decision making environment. Qu et al. [67] developed a framework combining fuzzy TOPSIS and ELECTRE approaches to screen appropriate green chain suppliers, validating its feasibility with a case study of a Chinese internet company. It is worth noting that the selection of green suppliers often faces inaccurate or incomplete information in uncertain environments, and the potential interplay between different evaluation criteria may also have a significant impact on the decision outcomes. However, existing methodologies for green supplier selection seldom account for the interrelationships among attributes, and they inadequately address the fuzziness and randomness inherent in evaluation data. This limitation hampers their applicability to the supplier selection problem within dynamic and complex contexts. In real-world decision-making, to enhance the quality of decision outcomes, decision-makers must not only consider the potential interrelationships between attributes but also account for the fuzziness of evaluation data, the hesitancy of decision-makers, as well as the randomness arising in uncertain environments especially, which is typically expressed through probabilistic information. Consequently, this paper endeavors to extend the PBM operator to the extensions of FFS, introducing a novel MADM method that incorporates attribute interrelationships and complex probabilistic information, which is expected to serve as a robust framework to address the intricacies of green supplier selection.
This MADM method will be developed through a structured process. Initially, we consider integrating the PBM operator and probabilistic information into FHFSs, innovatively proposing relevant Fermatean hesitant fuzzy power Bonferroni aggregation operators, i.e., the Fermatean hesitant fuzzy power Bonferroni mean (FHFPBM), Fermatean hesitant fuzzy weighted power Bonferroni mean (FHFWPBM) and Fermatean hesitant fuzzy probabilistic weighted power Bonferroni mean (FHFPWPBM) operators. These operators can not only effectively combine evaluation information with attribute interrelations and random properties in complex fuzzy environments, but also reflect the hesitancy in the decision-makers’ psychology. Subsequently, following a similar approach, we further extends the PBM operator and probabilistic information to FPHFSs, presenting relevant Fermatean probabilistic hesitant fuzzy power Bonferroni aggregation operators including the Fermatean probabilistic hesitant fuzzy power Bonferroni mean (FPHFPBM), Fermatean probabilistic hesitant fuzzy weighted power Bonferroni mean (FPHFWPBM) and Fermatean probabilistic hesitant fuzzy probabilistic weighted power Bonferroni mean (FPHFPWPBM) operators. It should be noted that the proposed FPHFPWPBM operator, due to the inclusion of external weighted probabilistic information and internal probabilistic information within the fuzzy sets, can fully capture the stochastic nature of the evaluation data and be better adapted to the generally complex situations in modern decision-making. Ultimately, a novel MADM method is constructed based on the FPHFPWPBM operator that uniquely encapsulates dual probabilistic characteristics of evaluation data, thereby be well-suited for application in the case study of green supplier selection.
Thus, the main contributions of this paper can be summarized as follows: (1) The PBM operator has been extended to the Fermatean hesitant fuzzy environment and the Fermatean probabilistic hesitant fuzzy environment, respectively, with corresponding aggregation operators being proposed and named as FHFPBM. FHFWPBM, FHFPWPBM and FPHFPBM. FPHFWPBM, FPHFPWPBM operators. (2) The probabilistic information is incorporated into these proposed aggregation operators, among which the FHFPWPBM operator takes into account the influence of positional weights and external probabilistic information (such as the degree of expert familiarity) during the attribute weighting process, while the FPHFPWPBM operator further considers the probabilistic information inherent in the evaluation data itself, making the decision-making more closely aligned with real-world conditions. (3) A novel Fermatean probabilistic hesitant fuzzy MADM method combining the PBM operator with probabilistic information has been developed, and its scientific validity and practicality have been substantiated through a numerical case study concerning the selection of green suppliers. This further enriches the field of Fermatean probabilistic hesitant fuzzy aggregation operators and expands the application domain of the PBM operator.
The remainder of this work is organized as follows. Section 2 provides a brief review of the basic concepts and operational rules concerning FFS, FHFS, FPHFS, and the PBM operator. Section 3 and Section 4 develop the Fermatean hesitant fuzzy power Bonferroni aggregation operators and the Fermatean probabilistic hesitant fuzzy power Bonferroni aggregation operators, respectively. Section 5 introduces a multi-attribute decision-making method based on the FPHFPWPBM operator and applies it to a numerical case study on green supplier selection. And this paper ends in Section 6 with some conclusions.
2. Preliminaries
2.1. Fermatean Fuzzy Set (FFS)
Definition 1 [23].
Let be a nonempty set. A Fermatean fuzzy set on is defined as:
where is the membership degree and is the non-membership degree of each element , satisfying the condition . The indeterminacy degree of each element in is .
Definition 2 [23].
Let , , and be three Fermatean fuzzy numbers (FFNs). Some basic operations are defined as follows:
- (1)
- ;
- (2)
- ;
- (3)
- , ;
- (4)
- , if and only if .
Definition 3 [23].
Let , , and be three FFNs. Several basic operations between them are given as follows:
- (1)
- ;
- (2)
- ;
- (3)
- , ;
- (4)
- , .
2.2. Fermatean Hesitant Fuzzy Set (FHFS)
Torra [31] proposed the concept of hesitant fuzzy set (HFS), which allows the membership of each element belonging to a set to be represented as multiple possible values between 0 and 1.
Definition 4 [35].
Let be a fixed set. A hesitant fuzzy set (HFS) on is a structure of the following form:
where is the set of several values belonging to , denoting some possible membership degrees of the element to the set .
Definition 5 [35].
Let be a universe of discourse. A Fermatean hesitant fuzzy set (FHFS) on can be defined as follows:
where and are nonempty finite subsets on , and respectively represent the set of all the possible membership and non-membership degrees of each element. , , the condition holds for each element on . For , is named as a Fermatean hesitant fuzzy number (FHFN). For convenience, we denote it as and as all Fermatean hesitant fuzzy numbers.
Definition 6 [35].
Let , , and be three FHFNs, and , then
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- .
2.3. Fermatean Probabilistic Hesitant Fuzzy Set (FPHFS)
Definition 7 [50].
Let be a fixed non-empty set. A Fermatean probabilistic hesitant fuzzy set (FPHFS) on is presented as:
where and are both non-empty finite sets on , representing all possible membership and non-membership degrees of the element to the FPHFS respectively, and satisfying the condition and , , , . and respectively denotes all the set of probabilities corresponding to the possible membership and non-membership, under the condition that with and , where and respectively represents the cardinal number of the set and . For ease, the Fermatean Probabilistic Hesitant Fuzzy Number (FPHFN) is symbolized by the pair .
In addition, it means that the probabilistic information is complete when and , while there is some unknown probabilistic information when or . In this case, the FPHFN is labeled as the weak Fermatean Probabilistic Hesitant Fuzzy Number, which can be corrected to the complete FPHFN by the following formula:
Definition 8 [50].
Let and be two FPHFNs, the fundamental operational laws are defined as:
- (1)
- ;
- (2)
- ;
- (3)
- .
Definition 9 [50].
Let and be two FPHFNs and , then their operations are articulated as follows:
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- .
Definition 10 [50].
Let be a FPHFN, and denote the number of elements in the set and , respectively. Then, the score function and accuracy function of are defined as follows:
Theorem 1
[50]. Let and be two FPHFNs, then
- (1)
- If , then ;
- (2)
- If , then ;
- (3)
- If , then
- (i)
- If , then ;
- (ii)
- If , then .
Given that the membership and non-membership are both information determined by the decision-maker and the accuracy function also represents the decision-maker’s certain information, this paper proposes a function of indeterminacy degree based on the accuracy function of Definition 10 and the research results by Liang et al. [72] as follows.
Theorem 2
[72]. Let be a FPHFN, the degree of indeterminacy of is
When analyzing the comparison of FHFNs, we encounter that the number of their corresponding element may not be equal. To deal with this situation, we utilize the normalization method proposed by Zhu et al. [73] which is shown as follows.
Definition 11 [73].
Let be a FPHFN. and are the added membership degree and the non-membership degree, respectively. and are the maximum and the minimum elements of , respectively. and are the maximum and the minimum elements of , respectively. is a parameter representing the decision maker’s risk preference. Then we can obtain three special cases of the preference of the decision maker:
- (1)
- When the value of is 1, the optimistic decision maker may add the maximum membership degree and the maximum non-membership degree .
- (2)
- When the value of is 0.5, the neutral decision maker may add the membership degree of and the non-membership degree of .
- (3)
- When the value of is 0, the pessimist decision maker may add the minimum membership degree and the minimum non-membership degree .
For unification, the set elements are added by default from a pessimistic perspective, and represented by simplified symbols, and the elements in the set of membership, non-membership and indeterminacy are arranged in ascending order in this paper. Additionally, to preserve the original probabilistic distribution, the probability of the original elements is redistributed equally among themselves and the newly added elements, ensuring that the addition of new elements does not alter the existing probabilities.
Example 1.
Let , be two FPHFN, which are set as
To reflect the fuzzy information completely, we add the indeterminacy degree based on Equation (8) respectively, namely
Then we can obtain
After adding the minimum elements from a pessimistic perspective respectively, the two FPHFNs are normalized as
Definition 12 [66].
Let and be two FPHFNs, the support degree between them can be expressed as:
where represents the distance beween the two FHFNs and , defined as follows:
where and , and are the smallest values of the membership degrees of , and are the smallest values of the non-membership degrees of , and denotes the indeterminacy degree of .
2.4. Power Bonferroni Mean (PBM) Operator
Definition 13 [51].
Let be a set of real numbers, power average (PA) operator can be defined as the following form:
where , denoting the support degree between and .
Definition 14 [57].
Let be a set of real numbers and . The parameters and they are not both zero simultaneously, then the Bonferroni mean (BM) operator can be shown as the following form:
Definition 15 [61].
Let be a set of real numbers and , the parameters and they are not both zero simultaneously. A power Bonferroni mean (PBM) operator holds the following form:
3. Fermatean Hesitant Fuzzy Power Bonferroni Aggregation Operators
In this section, we shall discuss several Fermatean hesitant fuzzy power Bonferroni aggregation operators and their classic properties.
Definition 16.
Suppose that and they are not both zero simultaneously, and is a set of FHFNs. The Fermatean hesitant fuzzy power Bonferroni mean (FHFPBM) operator is a mapping such that
where , and indicates the support degree between Fermatean hesitant fuzzy sets and .
Theorem 3.
Let be a collection of FHFNs, the parameters and they cannot be both zero simultaneously. The result obtained after the aggregation of FHFPBM operator is still FHFNs, and
where and are the smallest values of the membership degrees of the FHFNs and , respectively. And and are the smallest values of non-membership degrees of and , respectively. and , where
and
denote the number of elements contained in the membership and non-membership degrees of each FHFN, respectively.
Proof.
Let , then Equations (14) and (15) can be simplified as the following forms, respectively:
According to the operational rules of FHFNs in Definition 6, it is easy to obtain
and
Then
Hence
Since , and , it can be derived as
and
Therefore, the Theorem 3 has been proved according to the above. □
In addition, the FHFPBM operator owns several properties such as idempotency, boundedness and permutation invariance, which will be discussed in detail as follows.
Property 1 (Idempotency).
Let be a set of FHFNs. If , then
Property 2 (Boundedness).
Let be a Fermatean hesitant fuzzy set, then
Property 3 (Permutation invariance).
Let be a set of FHFNs. If is any permutation of , then
Given that the indicators of decision-making are usually assigned unequal weights in real life, this section further propose Fermatean hesitant fuzzy weighted power Bonferroni mean (FHFWPBM) operator, which takes the weights of indicators into account and is shown as follows.
Definition 17.
Let be a set of FHFNs, and , and can not both be zero simultaneously. The Fermatean hesitant fuzzy weighted power Bonferroni mean (FHFWPBM) operator is a mapping such that
where
is the weighting vector of
,
,
, and
. represents the support degree between
and
.
Theorem 4.
Let be a collection of FHFNs, the parameters and they cannot be both zero simultaneously. The result obtained after the aggregation of FHFWPBM operator is still FHFNs, and
where
and
are the
smallest values of the membership degrees of the FHFNs
and
, respectively. And
and
are the
smallest values of non-membership degrees of
and
, respectively.
and
, where
and
denote the number of elements contained in the membership and non-membership degrees of each FHFN, respectively.
The proving process of Theorem 4 is similar to the proof of Theorem 3 which is shown before. And the FHFWPBM operator has excellent properties such as idempotency, boundedness and permutation invariance, which are omitted here.
Definition 18.
Let ( and cannot both be zero simultaneously), and be a Fermatean hesitant fuzzy set. A Fermatean hesitant fuzzy probabilistic weighted power Bonferroni mean (FHFPWPBM) operator for is a mapping such that
where
represents the comprehensive weighted probability,
with
. is the weighting vector of
,
,
, and
is the probabilistic vector with
and
. Suppose
is the
largest element of
, then
denotes the probability corresponding to
. , where
representing the support degree between
and
.
Particularly, when , the FHFPWPBM operator degenerates to the FHFWPBM operator. When , the FHFPWPBM operator degenerates to the Fermatean hesitant fuzzy probabilistic power Bonferroni mean (FHFPPBM) operator. And a numerical example is provided below to specify the process of obtaining the comprehensive weighted probability .
Example 2.
Given three FHFNs: , , and . The weighting vector is and the probabilistic vector is , .
First, let’s calculate the score of each FHFN and sort them according to their score values. Since
we have
Then the ordered probability are
Consequently, the comprehensive weighted probability of each one can be calculated as
Theorem 5.
Let be a collection of FHFNs with a corresponding probabilistic vector and its weight vector is . The parameters and they cannot be both zero simultaneously. The result obtained after the aggregation of FHFPWPBM operator is still FHFNs.
where
represents the comprehensive weighted probability combining the weight vector
and probabilistic vector
by
with
,
is the probability corresponding to
that denotes the
largest element of
. And
and
are the
smallest values of the membership degrees of the FHFNs
and
, respectively. Similarly,
and
are the
smallest values of non-membership degrees of
and
, respectively.
and
, where
and
represent the number of components contained in the membership and non-membership degrees of each FHFN, respectively.
4. Fermatean Probabilistic Hesitant Fuzzy Power Bonferroni Aggregation Operators
With the increasing uncertainty and complexity of the evaluation information in real decision-making problems, the FPHFSs, which can better describe the probabilistic information than FHFSs during decision-making process, deserve to be introduced for handling MADM problems. Therefore, in order to better characterize the randomness of information evaluation results and maximize the completeness and accuracy of the information integration, a series of Fermatean probabilistic hesitant fuzzy power Bonferroni aggregation operators will be presented next, including the Fermatean probabilistic hesitant fuzzy power Bonferroni mean (FPHFPBM) operator, the Fermatean probabilistic hesitant fuzzy weighted power Bonferroni mean (FPHFPWPBM) operator and the Fermatean probabilistic hesitant fuzzy probabilistic weighted power Bonferroni mean (FPHFPWPBM) operator. And the excellent properties of each are investigated as well.
Definition 19.
Suppose that and they are not both zero simultaneously, and is a set of FPHFNs. The Fermatean probabilistic hesitant fuzzy power Bonferroni mean (FPHFPBM) operator is a mapping such that
where
, and
indicates the support degree between the FPHFNs
and
.
Theorem 6.
Let be a collection of FPHFNs, the parameters and they cannot be both zero simultaneously. The result obtained after the aggregation of FPHFPBM operator is still FPHFNs, and
where
and
are the
smallest values of the membership degrees of
and
, respectively. And
and
are the
smallest values of non-membership degrees of
and
, respectively.
and
, where
and
denote the number of elements contained in the membership and non-membership degrees of each FPHFN, respectively.
Proof.
Let , , then Equations (25) and (26) can be simplified as the following forms, respectively:
According to the operational rules of FPHFNs in Definition 9, it can be derived that
and
Then
Hence
Since , and , it is easy to obtain that
and
Also, given that , , it is evident that
Therefore, the Theorem 6 has been proved according to the above. □
In addition, the FPHFPBM operator owns several properties such as idempotency, boundedness and permutation invariance, which will be discussed in detail as follows.
Property 4 (Idempotency).
Let be a set of FPHFNs. If , then
Property 5 (Boundedness).
Let be a Fermatean probabilistic hesitant fuzzy set, then
Property 6 (Permutation invariance).
Let be a set of FPHFNs. If is any permutation of , then
Definition 20.
Let be a set of FPHFNs, and , and can not both be zero simultaneously. The Fermatean probabilistic hesitant fuzzy weighted power Bonferroni mean (FPHFWPBM) operator is a mapping such that
where
is the weighting vector of
,
,
, and
. represents the support degree between
and
.
Theorem 7.
Let be a set of FPHFNs, the parameters and they cannot be both zero simultaneously. The result obtained after the aggregation of FPHFWPBM operator is still FPHFNs, and
The proving process of Theorem 7 is similar to the proof of Theorem 3 which is shown before. And the FPHFWPBM operator has excellent properties such as idempotency, boundedness and permutation invariance, which are omitted here.
Definition 21.
Let ( and cannot both be zero simultaneously), and be a Fermatean probabilistic hesitant fuzzy set. A Fermatean probabilistic hesitant fuzzy probabilistic weighted power Bonferroni mean (FPHFPWPBM) operator for is a mapping such that
where
. represents the support degree between
and
. with
, and
is the ordered probability related to
, which is the
largest element of
.
Definition 22.
Let be a set of FPHFNs, and ( and cannot both be zero simultaneously), then
where
with
,
is the weighting vector of
with
,
, and
is the probabilistic vector with
,
. is the ordered probability associated with
which denotes the
largest element of
. and
are the
smallest values of the membership degrees of
and
, respectively. And
and
are the
smallest values of non-membership degrees of
and
, respectively.
and
, where
and
denote the number of elements contained in the membership and non-membership degrees of each FPHFN, respectively.
The proposed FPHFPWPBM operator innovatively combines the PBM operator and probabilistic information for incorporating the weight allocation under the Fermatean probabilistic hesitant fuzzy environment. It extends the traditional Fermatean hesitant fuzzy aggregation operators to the Fermatean hesitant fuzzy power Bonferroni aggregation operators with dual-probabilistic information, which can certainly provide a novel technique and method to deal with more complex MADM problems with uncertain information.
5. Application of the FPHFPWPBM Operator in Green Supplier Selection
5.1. Decision-Making Process
Suppose that the expert group is currently planning to hold a specific discussion on a multi-attribute decision-making (MADM) issue. Let be a set of alternatives and be a collection of attributes. is the weighting vector corresponding to each attribute such that and . is a set of Fermatean probabilistic hesitant fuzzy numbers, where denotes the evaluation value of alternative with respect to attribute , and represent the probabilities attached to each element in the membership and non-membership degrees, respectively. Then, the Fermatean probabilistic hesitant fuzzy decision matrix is obtained. In light of this issue this paper proposes a Fermatean probabilistic hesitant fuzzy MADM method based on FPHFPWPBM operator, and the specific steps are as follows:
Step 1. Relevant experts are invited to give evaluation information for each alternative and a Fermatean probabilistic hesitant fuzzy decision matrix is established. Then judge whether the matrix is normalized or not. If it is not normalized, normalize it according to the following Formula.
Step 2. Add constant elements to make the cardinal numbers of the FPHFSs under each alternative equal and the processed Fermatean probabilistic hesitant fuzzy decision matrix is obtained. From a pessimistic perspective, the smallest elements are added to the set to equalize the cardinal numbers. And the probability values attached to the newly added elements are assigned based on the criteria outlined in Definition 11.
Step 3. Calculate the support degree between varibles.
Step 4. Calculate the corresponding support degree connected to FPHFN based on the comprehensive weighted probability , and further obtain the support degree index of the variables.
Step 5. Use the definition of FPHFPWPBM operator to aggregate the attribute value corresponding to each alternative so as to obtain the comprehensive attribute value of scheme .
Step 6. The score function (Formula (4)) and accuracy function (Formula (5)) are used to sort the comprehensive attribute values, and then the best scheme is selected based on the sorting results.
Given that the probability values contained in might be so tiny, it is advisable to cope with the probability values by the following Formula (40), which can help to facilitate the numerical calculation without affecting the score results. Then the comprehensive attribute value used to calculate the final scores are obtained. The detailed flowchart of this method is shown in Figure 1.
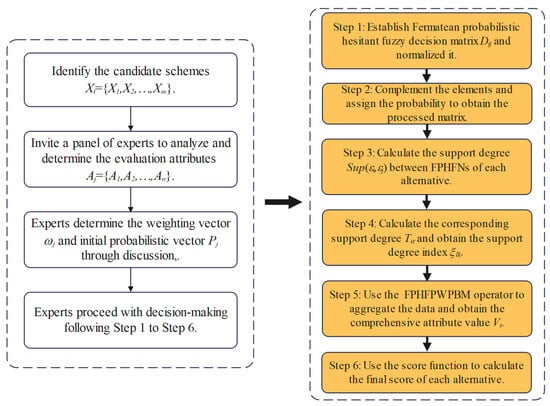
Figure 1.
The flow chart of the proposed method.
5.2. Numerical Example
With the continuous development of the economy and society, and the increasingly severe global environmental issues, more and more countries and regions have begun to advocate for green and low-carbon production and lifestyles. The demand for sustainable products among consumers has gradually increased. In order to better win consumers’ favor for green products, more and more enterprises are beginning to transition towards green and low-carbon practices. Green supply chain management has now become an important way for enterprises to enhance competitiveness and achieve sustainable development [74].
First proposed in 1996, the concept of green supply chain management refers to a supply chain system that meets environmental protection requirements throughout the entire life cycle of a product from initial design to recycling and disposal, so as to realize the dual unity of economic benefits and environmental benefits. Now widely applied in various fields such as manufacturing, automotive industry, construction industry and service industry, the key link of Green supply chain management is the selection of green suppliers [75]. By choosing green suppliers that are compatible with their development strategies and production programme, the core enterprises can guide the green behaviors of upstream and downstream enterprises, help them to achieve environmental goals, improve economic performance, and thus improve the green and sustainability of the entire supply chain network. Therefore, it is particularly important for green enterprises to establish and implement scientific, reasonable, and effective evaluation and selection methods for green suppliers, which has become a common challenge faced in the process of enterprise development. In recent years, under the background of proposal of the “dual carbon goals” in China, many enterprises have begun to get involved in the evaluation and selection of green suppliers [76]. In July 2024, the State Council of China proposed to accelerate the comprehensive green transformation of economic and social development, and to promote the green and low-carbon transformation and upgrading of traditional industries, thereby clarifying the direction for green supply chain management. In pursuit of sustainable development, supply chain enterprises must fully consider the green development capabilities of their supply chain when assessing potential suppliers. The assessment content often involves a rigorous comparative analysis of key attributes, such as the supplier’s product quality, price performance, and service level.
Suppose that a new energy vehicle manufacturer is looking for the best auto parts suppliers that can meet the development needs of the enterprise in order to produce better cars and meet the requirements of green production. After the investigation and screening of the parts suppliers on the market, the manufacturer initially identify four candidate suppliers . To further select the suitable suppliers, the manufacturer decides to organize an expert panel to carry out relevant evaluation. After clarifying the evaluation criteria and objectives for the selection of green suppliers, the manufacturing company invited a panel of 11 experts with relevant professional backgrounds and experience. These experts, including renowned scholars and practitioners, have extensive experience in technological innovation and supply chain management. By collecting pertinent information, they provided a detailed explanation of the development status and evaluation objectives of the candidate companies. Through in-depth discussions and opinion exchanges, the panel have reached a consensus on the four foundational evaluation indicators as follows, informed by their collective and integrated assessment.
: Product quality.
Product factors serve as tangible indicators of a supplier’s green innovation capabilities and are of significant importance for the market operations of upstream and downstream enterprises as well as for the stable development of a green supply chain. Product quality is a critical indicator, reflecting not only the supplier’s quality assurance system but also their capability to manufacture specific low-carbon, eco-friendly products that align with green demand. Existing research has found that the product quality and delivery compliance of suppliers are particularly significant for the manufacturing industry in emerging economies [77], which indicates a direction for systematic improvement in supply chain systems.
: Price performance.
When selecting suppliers, companies must consider their product offerings, carbon emissions, transportation, recycling, and other aspects of price performance. Stable, good, and competitive pricing is an important factor in ensuring corporate profits and supply chain performance. Shah et al. [78] has demonstrated, through the construction of a mathematical model, that the green efforts incorporated in products have a significant impact on corporate pricing decisions, which in turn can regulate the sales performance of the products. Therefore, the pricing performance of suitable green suppliers should be congruent with the corporate objectives of green development.
: Service capability.
In the context of fierce market competition, suppliers with a high level of service are increasingly favored. Typically, the degree of management involvement, service attitude, timeliness of delivery, and market responsiveness are critical indicators for assessing the excellence of a supplier’s comprehensive service capabilities. Wang et al. [79] consider the service level to be a key element affecting logistics quality in their construction of evaluation indicators for green suppliers. Consequently, enterprises must meticulously assess the service capabilities of potential suppliers in their selection process.
: Social responsibility.
To select green suppliers for sustainable development, companies should consider their social responsibility performance, including but not limited to environmental responsibilities, employee rights protection, and social ethical responsibilities.These factors not only affect the company’s environmental performance and green innovation capabilities but can also have a significant impact on the company’s economic benefits and social reputation. Moreover, governance mechanisms of social responsibility based on supplier selection and supplier development have a positive impact on the supply chain core enterprise’s social and environmental performance [80].
After determining the evaluation indicators, the panel of experts, through extensive discussion, unanimously decide that the associated weighting vector is . Now the experts are invited to conduct an anonymous evaluation of each alternative in the form of Fermatean hesitant fuzzy numbers, where the repeated membership and non-membership degrees are considered only once in order to ensure the scientificity and rationality of the decision results. And the familiarity of these experts with each evaluation attribute is regarded as the initial probabilistic vector . Then a Fermatean probabilistic hesitant fuzzy decision matrix is established and shown as Table 1, where denotes a Fermatean probabilistic hesitant fuzzy set. Each of the four candidate suppliers is evaluated and the optimal one is selected according to the evaluation information and specific decision-making steps given as follows.

Table 1.
The Fermatean probabilistic hesitant fuzzy decision matrix.
Step 1. Judge whether the established Fermatean probabilistic hesitant fuzzy decision matrix needs to be normalized or not. Since the attribute : Cost price belongs to the cost-type attribute while other three indicators are all benefit-type attributes, it is only necessary to normalize based on Formula (36) and the normalized matrix is shown as Table 2.

Table 2.
The normalized Fermatean probabilistic hesitant fuzzy decision matrix.
Step 2. Supplement elements of the FPHFNs with smaller from a pessimistic perspective, namely adding minimal elements to the certain sets. Then the processed Fermatean probabilistic hesitant fuzzy decision matrix which is shown as Table 3 can be obtained.

Table 3.
The processed Fermatean hesitant fuzzy decision matrix.
Step 3. Calculate the support degree among the four attributes for each alternative to derive the corresponding support matrix as follows:
Step 4. Calculate the support degree between overall variables based on the comprehensive weighted probability and further figure out the support degree index of the variables, where can be calculated for the following results according to the given weighting vector and initial probabilistic vector . And the value of is assumed to be 0.6.
For example, the score values of in Table 3 are calculated and sorted as follows: . Then, calculate the value of the probability according to the ordering of :, , , . The rest of the can be calculated by the same principle.
Step 5. Use the proposed FPHFPWPBM operator to aggregate the corresponding attribute values of each alternative. Then the comprehensive attribute values regarding alternatives are calculated as the following results. In particular, for a convenient calculation, we let the parameters and , thereby the results are obtained as follows:
Step 6. Use the score function to calculate the final scores of corresponding comprehensive attribute values respectively, which will serve as the basis for ranking the alternatives.
Based on the score values above, it is clear that . Therefore, the sorting of the four candidate suppliers should be , which indicates that is the optimal choice.
5.3. Sensitivity Analysis
The above results are obtained under the assumption that the parameter . To observe the variation of the optimal alternative under different parameter values, without loss of generality, we assign different values of 0.3, 0.7, 1.5, 2.4, 3, 5, 10 to both and . And the specific sorting results calculated with FHFPWPBM operator are shown in Table 4 below.

Table 4.
Sorting results calculated with FPHFPWPBM operator when p, q are equal.
Figure 2 below clearly illustrates the score values and their trend of change for each alternative as the equal values of parameters and vary.

Figure 2.
The score for each alternative when p, q are equal.
According to the results shown in Table 4 and Figure 2, it can be observed that the ranking of the schemes changes slightly with the variation in parameter values when . Specifically, when the parameters and are assigned less than 1.5, the sorting results remain as . However, when both and are set equal to 1.5, the ranking changes with and exchanging priority. Moreover, starting from , the ordering results consistently show as the parameter values increase, demonstrating the stability and reliability of the MADM method based on the FPHFPWPBM operator. Further analysis finds that the comprehensive score of each alternative will decrease as the parameters and increase, which may be a result of the change in risk preference of the decision-makers in different contexts. Therefore, decision-makers can choose the appropriate parameters and according to their risk preference during the decision-making process.
The following Figure 3 further clarifies the sensitivity of the score values of each scheme to the variation of parameter values when and are equal.
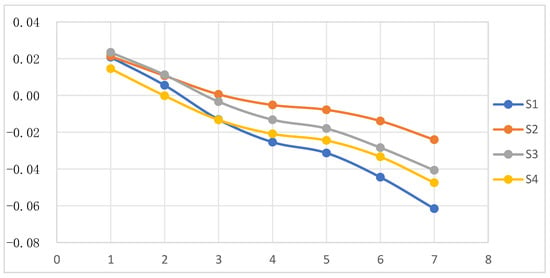
Figure 3.
The parameter sensitivity of the score values for each alternative when p, q are equal.
From Figure 3, it can be observed that when the parameter values are increased synchronously from 1 to 7, exhibits the greatest change, followed in order by , and . This indicates that alternative is the most sensitive to the parameter changes in this range, while is the least sensitive among the options presented. This indicates to a certain extent that, compared to other candidate schemes, is more significantly affected by parameter changes, and therefore decision-makers may need to optimize their decisions based on their specific preferences.
In addition, since the above results are calculated when parameters and are assigned the same value, we are completely interested in taking results with different values when and are not equal. Table 5 below shows the comprehensive score and sorting results in that case.

Table 5.
Sorting results calculated with FPHFPWPBM operator when p, q are not equal.
Similarly, the following Figure 4 depicts the value and change trend of the score for each alternative when the parameters and are not equal and their value changes.

Figure 4.
The score for each alternative when p, q are not equal.
As it can be seen from the Table 5 and Figure 4, the values of parameters and will affect the scoring results and ranking of each alternative in the case where they are not equal. To be precise, the score value of each scheme will decrease as and increase. And when the parameters and are set at a relatively low level, for example, and , remains the optimal alternative according to the ranking results. Nevertheless, when and are taken at a relatively high level, for example, and , the optimal alternative changes to and the ranking remains stable as even as and increase. In a word, according to the ranking results above, the optimal scheme is when and take values at a lower level, while becomes the best option when the parameters take values at a higher level. Therefore, in the practical application of this MADM method, the decision-makers are advised to assign the parameters and based on the degree of their risk aversion, and the values are advised to be assigned at not less than 3 to ensure the reliability and practicality of the decision-making results.
Next, to further clarify the sensitivity of each scheme’s score to parameter value changes when p and q are not equal, a radar chart is used for description, and the results are shown in Figure 5 below.
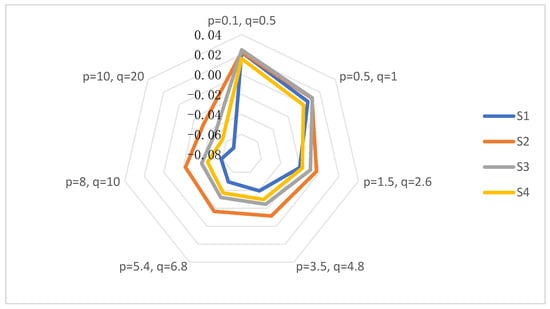
Figure 5.
The parameter sensitivity of the score values for each alternative when p, q are not equal.
Furthermore, Figure 5 illustrates the impact of the simultaneous change in parameters and on the score values of each alternative. It can be observed that, as the parameter values increase from small to large, the score values of all schemes correspondingly decrease, depicted graphically by the inward movement of the scores. Among the alternatives, exhibits the largest absolute decrease in score, while shows the smallest. and demonstrate intermediate levels of change, positioned between the extremes of the above two. This suggests that the variations in parameter values exert the most pronounced impact on , with subsequent notable effects on and , and the least influence on . Consequently, we can infer that the alternative exhibits the highest sensitivity to parameter value fluctuations, whereas appears to be a more robust option across various scenarios with varying parameter values, which is similar to the situation when parameters and are equal.
In summary, decision makers can adjust the parameter value of and according to risk preferences in the decision-making process of using this MADM method with FPHFPWPBM operator, so as to enhance the fairness, impartiality and objectivity of decision results.
5.4. Comparative Analysis
In order to further verify the scientificity and effectiveness of the MADM method with FHFPOWPBM operator proposed in this paper, a series of related aggregation operators will be used for the comparative analysis. First of all, the FHFWPBM, FHFPWPBM and FPHFWPBM operators, as presented above, will be applied for aggregating the evaluation data from the aforementioned numerical example to explore the impact of different and varying degrees of probabilistic information, taking into account the correlation of attributes. Then several Fermatean hesitant fuzzy aggregation operators involving ordered weighted average (OWA) method presented by Ruan et al. [78], including the FHFPA, FHFOWA, FHFPOWA and the GFHFPOWA operators, are used to perform a comparative analysis. In addition, two types of Fermatean probabilistic hesitant fuzzy aggregation operators mentioned by Qahtan et al. [46] are also included in the consideration.
Table 6 below compares the differences in the properties of these operators to more clearly describe their respective characteristics. In this context, the external probabilistic information refers to the probability involved in the weight allocation process (such as the probability indicating the level of expert familiarity), while the internal probabilistic information refers to the probability carried by the evaluation data itself (such as the frequency with which a value appears in the evaluation data). It can be observed that the four operators proposed in this paper for comparative analysis all take into account attribute correlation. However, the FPHFPWPBM operator, additionally, considers dual probabilistic information (that is, internal and external probabilistic information). In contrast, the other operators used for comparison do not take into account attribute correlation. Specifically, the operators proposed by Ruan et al. [81] do not involve internal probabilistic information, and those introduced by Qahtan et al. [50] do not involve external probabilistic information.

Table 6.
Comparison with existing operators, in which “+” indicates compliance with the characteristic, and “−” indicates non-compliance with the characteristic.
Subsequently, these operators are individually adopted to aggregate the evaluation data from the numerical example. To facilitate computation, the parameters of these comparison operators are uniformly set to 1. The results of the comparative analysis are shown in Table 7 below.

Table 7.
Comparison of the ranking results for different operators.
From the results above, it can be easily find that the optimal choice of sorting results is either or , which is consistent with the results of the parameter analysis, indicating that the MADM method proposed in this paper has a certain degree of stability and reliability. Specifically, when considering the correlation of attributes, the optimal scheme obtained by the FPHFPWPBM operator is while other operators including the FHFWPBM, FHFPWPBM and FPHFWPBM operators yield . This is primarily due to the different probabilistic information and the extent to which it is considered. For instance, the FHFWPBM operator only takes into account the hesitancy of the evaluation data and the interaction between attributes. The FHFPWPBM operator incorporates external probabilistic information for ordered weighting on top of the FHFWPBM. Meanwhile, the FPHFWPBM operator considers the internal probabilistic information of the evaluation data on the basis of the FHFWPBM. Different from the others, the FPHFPWPBM operator incorporates dual probabilistic information on the basis of the FHFWPBM operator, which means it not only includes the external probabilities in the weighting process but also takes into account the probabilistic information inherent in the evaluation data itself. As a result, the sorting result of the FPHFPWPBM operator is likely to be more objective, accurate and comprehensive compared to the other three operators.
Then, let’s pay attention to several other Fermatean hesitant fuzzy aggregation operators and Fermatean probabilistic hesitant fuzzy aggregation operators that involve the OWA method. The OWA operators primarily integrates information through the method of arithmetic averaging, which can effectively reflect the concentration of a set of data and are widely applied to traditional weighted decision-making problems. The new series of operators proposed in this paper also involve weighted averaging, hence it is necessary to conduct a comparative analysis among them. From Table 6, we can observe that the ranking results of the FHFPA, FHFOWA, FHFPOWA and the GFHFPOWA operators are consistently , but the FPHFAM and FPHFWM operators yield the optimal option as , although there is a slight difference in the ranking of the schemes between the two. Obviously, the sorting result of the FPHFPWPBM operator is more closely aligned with that of the FPHFAM and FPHFWM operators, which indicates the consistency of the Fermatean probabilistic hesitant fuzzy aggregation operators when considering the internal probabilistic information of the data. In contrast, the Fermatean hesitant fuzzy aggregation operators only consider external weighted probabilities at most, thus it is reasonable that there are differences in the ranking results. Therefore, the information integration result of the FPHFPWPBM operator may be more convincing and representative when dealing with more complex MADM problems in real life.
6. Conclusions
This paper develops a novel MADM method which combines the PBM operator theory and probabilistic information under Fermatean hesitant fuzzy environment and Fermatean probabilistic hesitant fuzzy environment, along with newly proposed Fermatean hesitant fuzzy power Bonferroni aggregation operators and Fermatean probabilistic hesitant fuzzy power Bonferroni aggregation operators. Firstly, given that the PBM operator is recognized for its ability to mitigate the effects of inappropriate aggregation values and for considering the interaction between evaluation attributes during decision-making process, we propose several Fermatean hesitant fuzzy power Bonferroni aggregation operators to further expand the application of the PBM operator in FHFS, including the FHFPBM, FHFWPBM and FHFPWPBM operators. Among them, the FHFPWPBM operator not only develops a combination of PBM operator and FHFS, but takes into account the weighted probability of combining degrees of expert familiarity and attribute weights, assisting in managing complex decision-making problems characterized by inaccuracy and uncertainty.
In real decision-making, as the probability value is an effective way to describe information uncertainty, it is essential to pay attention to the probabilistic information in the study of MADM methods. Accordingly, we introduce the PBM operator into FPHFS by presenting several Fermatean probabilistic hesitant fuzzy power Bonferroni aggregation operators, including the FPHFPBM, FPHFWPBM and FPHFPWPBM operators. In particular, the FPHFPWPBM operator, further developed from the FHFPWPBM operator, incorporates dual probabilistic information. One is the aforementioned external weighted probability, and the other is the internal probability value attached to the evaluation data itself. It undoubtedly indicates that the information integration result of the FPHFPWPBM operator not only considers the correlation between evaluation attributes, but also better reflects the stochastic nature in the data evaluation process, effectively quantifying the importance of attributes. Then a new MADM method is proposed based on these operators. Finally, this method is applied to a numerical example about a manufacturer enterprise selecting the most suitable green supplier. Furthermore, the scientificity and practicability of this method are demonstrated and verified through the parameter analysis and comparative analysis of the information integration results.
In conclusion, this paper creatively proposes a series of aggregation operators by introducing PBM operator and probabilistic information into FHFSs and FPHFSs, and constructs a new MADM method based on these operators, which provides a new technique and path for solving complex and uncertain decision-making problems in real life. Future research is expected to expand the PBM operator to more complex fuzzy environment such as interval-valued Fermatean hesitant fuzzy environment and probabilistic interval-valued Fermatean hesitant fuzzy environment, so as to further enrich the information aggregation operator under the theoretical system of Fermatean fuzzy information. Moreover, it is valuable to consider the application of the proposed method in different practical domains or scenarios, such as venture capital proposal evaluation, product scheme selection, quality assessment in talent recruitment, among others.
Author Contributions
Conceptualization, C.R. and L.Y.; Methodology, C.R. and L.Y.; Validation, C.R. and L.Y.; Writing-original draft preparation, C.R. and L.Y.; Writing-review and editing, C.R. and L.Y.; Project assessment, C.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Guangdong Provincial Philosophy and Social Science Planning Project (No GD23XGL012) and the Innovative Team Project of Guangdong Universities (No 2019WCXTD008).
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
List of Main Abbreviations:
| Sr.NO | Complete Word | Abbreviation |
| 1 | Multi-attribute decision-making | MADM |
| 2 | Fuzzy set | FS |
| 3 | Intuitionistic fuzzy set | IFS |
| 4 | Pythagorean fuzzy set | PFS |
| 5 | Fermatean fuzzy set | FFS |
| 6 | q-Rung orthopair fuzzy set | q-ROFS |
| 7 | Hesitant fuzzy set | HFS |
| 8 | Interval-valued hesitant fuzzy set | IVHFS |
| 9 | Intuitionistic hesitant fuzzy set | IHFS |
| 10 | Pythagorean hesitant fuzzy set | PyHFS |
| 11 | Fermatean hesitant fuzzy set | FHFS |
| 12 | Interval-valued hesitant Fermatean fuzzy set | IVHFFS |
| 13 | Probabilistic hesitant fuzzy set | PHFS |
| 14 | Probabilistic linguistic term set | PLTS |
| 15 | Probabilistic interval-valued hesitant fuzzy set | PIVHFS |
| 16 | Probabilistic interval-valued Fermatean hesitant fuzzy set | PIVFHFS |
| 17 | q-Rung orthopair probabilistic hesitant fuzzy rough set | q-ROPHFS |
| 18 | q-Rung orthopair probabilistic hesitant fuzzy rough set | q-ROPHFRS |
| 19 | Pythagorean probabilistic hesitant fuzzy set | PyPHFS |
| 20 | Fermatean probabilistic hesitant fuzzy set | FPHFS |
| 21 | Power average | PA |
| 22 | Bonferroni mean | BM |
| 23 | Power Bonferroni Mean | PBM |
| 24 | Fermatean fuzzy power Bonferroni mean | FFPBM |
| 25 | Fermatean fuzzy weighted power Bonferroni mean | FFWPBM |
| 26 | Fermatean hesitant fuzzy power Bonferroni mean | FHFPBM |
| 27 | Fermatean hesitant fuzzy weighted power Bonferroni mean | FHFWPBM |
| 28 | Fermatean hesitant fuzzy probabilistic weighted power Bonferroni mean | FHFPWPBM |
| 29 | Fermatean probabilistic hesitant fuzzy power Bonferroni mean | FPHFPBM |
| 30 | Fermatean probabilistic hesitant fuzzy weightedpower Bonferroni mean | FPHFWPBM |
| 31 | Fermatean probabilistic hesitant fuzzy probabilistic weighted power Bonferroni mean | FPHFPWPBM |
| 32 | Ordered weighted average | OWA |
| 33 | Fermatean probabilistic hesitant fuzzy average mean | FPHFAM |
| 34 | Fermatean probabilistic hesitant fuzzy weighted average | FPHFWA |
References
- Yeh, C.-H. A Problem-based Selection of Multi-attribute Decision-making Methods. Int. Trans. Oper. Res. 2022, 9, 169–181. [Google Scholar] [CrossRef]
- Dyer, J.S.; Fishburn, P.C.; Steuer, R.E.; Wallenius, J.; Zionts, S. Multiple criteria decision making, multiattribute utility theory: The next ten years. Manag. Sci. 1992, 38, 645–653. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Zou, X.Y.; Chen, S.M.; Fan, K.Y. Multiple attribute decision making using improved intuitionistic fuzzy weighted geometric operators of intuitionistic fuzzy values. Inf. Sci. 2020, 535, 242–253. [Google Scholar] [CrossRef]
- Yang, W.; Jhang, S.T.; Shi, S.G.; Ma, Z.M. Aggregating intuitionistic fuzzy preference relations with symmetrical intuitionistic fuzzy Bonferroni mean operators in group decision making. Int. J. Fuzzy Syst. 2021, 23, 455–473. [Google Scholar] [CrossRef]
- Mahanta, J.; Panda, S. A novel distance measure for intuitionistic fuzzy sets with diverse applications. Int. J. Intell. Syst. 2021, 36, 615–627. [Google Scholar] [CrossRef]
- Singh, S.; Sharma, S.; Lalotra, S. Generalized correlation coefficients of intuitionistic fuzzy sets with application to MAGDM and clustering analysis. Int. J. Fuzzy Syst. 2020, 22, 1582–1595. [Google Scholar] [CrossRef]
- Zhang, Z. Interval-Valued Intuitionistic Hesitant Fuzzy Aggregation Operators and Their Application in Group Decision-Making. J. Appl. Math. 2013, 2013, 1–33. [Google Scholar] [CrossRef]
- Joshi, D.; Kumar, S. Interval-valued Intuitionistic HesitantFuzzy Choquet Integral Based TOPSIS Method for Multi-criteria Group Decision Making. Eur. J. Oper. Res. 2016, 248, 183–191. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean membership grades in multicriteria decision making. IEEE Trans. Fuzzy Syst. 2013, 22, 958–965. [Google Scholar] [CrossRef]
- Haktanır, E. Interval valued pythagorean fuzzy aggregation operators based malcolm baldrige national quality award assessment. J. Intell. Fuzzy Syst. 2020, 39, 6431–6441. [Google Scholar] [CrossRef]
- Mu, Z.; Zeng, S.; Wang, P. Novel approach to multi-attribute group decision-making based on interval-valued Pythagorean fuzzy power Maclaurin symmetric mean operator. Comput. Ind. Eng. 2021, 155, 107049. [Google Scholar] [CrossRef]
- Pan, L.; Deng, Y.; Cheong, K.H. Quaternion model of Pythagorean fuzzy sets and its distance measure. Expert Syst. Appl. 2023, 213, 119222. [Google Scholar] [CrossRef]
- Ejegwa, P.A. Distance and similarity measures for Pythagorean fuzzy sets. Granul. Comput. 2020, 5, 225–238. [Google Scholar] [CrossRef]
- Kumar, K.; Chen, S.M. Group decision making based on entropy measure of Pythagorean fuzzy sets and Pythagorean fuzzy weighted arithmetic mean aggregation operator of Pythagorean fuzzy numbers. Inf. Sci. 2023, 624, 361–377. [Google Scholar] [CrossRef]
- Yanmaz, O.; Turgut, Y.; Can, E.N.; Kahraman, C. Interval-valued Pythagorean fuzzy EDAS method: An application to car selection problem. J. Intell. Fuzzy Syst. 2020, 38, 4061–4077. [Google Scholar] [CrossRef]
- Biswas, A.; Sarkar, B. Pythagorean fuzzy TOPSIS for multicriteria group decision-making with unknown weight information through entropy measure. Int. J. Intell. Syst. 2019, 34, 1108–1128. [Google Scholar] [CrossRef]
- Yager, R.R. Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 2016, 25, 1222–1230. [Google Scholar] [CrossRef]
- Liu, D.; Peng, D.; Liu, Z. The distance measures between q-rung orthopair hesitant fuzzy sets and their application in multiple criteria decision making. Int. J. Intell. Syst. 2019, 34, 2104–2121. [Google Scholar] [CrossRef]
- Khan, M.R.; Wang, H.; Ullah, K.; Karamti, H. Construction Material Selection by Using Multi-Attribute Decision Making Based on q-Rung Orthopair Fuzzy Aczel–Alsina Aggregation Operators. Appl. Sci. 2022, 12, 8537. [Google Scholar] [CrossRef]
- Khan, M.R.; Ullah, K.; Karamti, H.; Khan, Q.; Mahmood, T. Multi-attribute group decision-making based on q-rung orthopair fuzzy Aczel–Alsina power aggregation operators. Eng. Appl. Artif. Intell. 2023, 126, 106629. [Google Scholar] [CrossRef]
- Senapati, T.; Yager, R.R. Fermatean fuzzy sets. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 663–674. [Google Scholar] [CrossRef]
- Seikh, M.R.; Mandal, U. Interval-valued Fermatean fuzzy Dombi aggregation operators and SWARA based PROMETHEE II method to bio-medical waste management. Expert Syst. Appl. 2023, 226, 120082. [Google Scholar] [CrossRef]
- Barokab, O.M.; Khan, A.; Khan, S.A.; Jun, Y.B.; Rushdi, A.M.A. University’s recruitment process using Fermatean fuzzy Einstein prioritized aggregation operators. J. Intell. Fuzzy Syst. 2023, 45, 3985–4008. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R. Fermatean fuzzy Einstein aggregation operators-based MULTIMOORA method for electric vehicle charging station selection. Expert Syst. Appl. 2021, 182, 115267. [Google Scholar] [CrossRef]
- Ganie, A.H. Multicriteria decision-making based on distance measures and knowledge measures of Fermatean fuzzy sets. Granul. Comput. 2022, 7, 979–998. [Google Scholar] [CrossRef]
- Deng, Z.; Wang, J. New distance measure for Fermatean fuzzy sets and its application. Int. J. Intell. Syst. 2022, 37, 1903–1930. [Google Scholar] [CrossRef]
- Attaullah; Rehman, N.; Khan, A.; Santos-García, G. Fermatean hesitant fuzzy rough aggregation operators and their applications in multiple criteria group decision-making. Sci. Rep. 2023, 13, 6676. [Google Scholar] [CrossRef]
- Gül, S. Fermatean fuzzy set extensions of SAW, ARAS, and VIKOR with applications in COVID-19 testing laboratory selection problem. Expert Syst. 2021, 38, e12769. [Google Scholar] [CrossRef]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Bahram, F. Information measures for hesitant fuzzy sets and interval-valued hesitant fuzzy sets. Inf. Sci. 2013, 240, 129–144. [Google Scholar]
- Chen, X.; Suo, C.; Li, Y. Distance measures on intuitionistic hesitant fuzzy set and its application in decision-making. Comput. Appl. Math. 2021, 40, 84. [Google Scholar] [CrossRef]
- Sajjad Ali Khan, M.; Ali, A.; Abdullah, S.; Amin, F.; Hussain, F. New extension of TOPSIS method based on Pythagorean hesitant fuzzy sets with incomplete weight information. J. Intell. Fuzzy Syst. 2018, 35, 5435–5448. [Google Scholar] [CrossRef]
- Ruan, C.Y.; Chen, X.J.; Gong, S.C.; Ali, S.; Almutairi, B. A decision-making framework based on the Fermatean hesitant fuzzy distance measure and TOPSIS. AIMS Math. 2024, 9, 2722–2755. [Google Scholar] [CrossRef]
- Lai, H.; Liao, H.; Long, Y.; Zavadskas, E.K. A hesitant Fermatean fuzzy CoCoSo method for group decision-making and an application to blockchain platform evaluation. Int. J. Fuzzy Syst. 2022, 24, 2643–2661. [Google Scholar] [CrossRef]
- Mishra, A.R.; Chen, S.M.; Rani, P. Multiattribute decision making based on Fermatean hesitant fuzzy sets and modified VIKOR method. Inf. Sci. 2022, 607, 1532–1549. [Google Scholar] [CrossRef]
- Liu, J.; Luo, S.H. Probabilistic hesitant Fermatean fuzzy extension MULTIMOORA method for evaluation of regional green restoration level. Control Decis. 2022, 37, 1–10. [Google Scholar]
- Ruan, C.Y.; Chen, X.J.; Han, L.N. Fermatean Hesitant Fuzzy Prioritized Heronian Mean Operator and Its Application in Multi-Attribute Decision Making. Comput. Mater. Contin. 2023, 75, 3203–3222. [Google Scholar] [CrossRef]
- Xu, Z.; Zhou, W. Consensus building with a group of decision makers under the hesitant probabilistic fuzzy environment. Fuzzy Optim. Decis. Mak. 2017, 16, 481–503. [Google Scholar] [CrossRef]
- Pang, Q.; Xu, Z.S.; Wang, H. Probabilistic linguistic term sets in multi-attribute group decision making. Inf. Sci. 2016, 369, 128–143. [Google Scholar] [CrossRef]
- He, Y.; Xu, Z.S.; Jiang, W.L. Probabilistic interval reference ordering sets in multi-criteria group decision making. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2017, 25, 189–212. [Google Scholar] [CrossRef]
- Zhai, Y.; Xu, Z.; Liao, H. Measures of probabilistic interval-valued intuitionistic hesitant fuzzy sets and the application in reducing excessive medical examinations. IEEE Trans. Fuzzy Syst. 2017, 26, 1651–1670. [Google Scholar] [CrossRef]
- Ruan, C.; Chen, X. Probabilistic Interval-Valued Fermatean Hesitant Fuzzy Set and Its Application to Multi-Attribute Decision Making. Axioms 2023, 12, 979. [Google Scholar] [CrossRef]
- Ren, Y.; Yuan, X.; Zhao, X.; Yu, B. Calculation and Aggregation of Q-rung Orthopair Probabilistic Hesitant Fuzzy Information. In Proceedings of the 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 March 2021. [Google Scholar]
- Chen, Z.; Shen, D.; Yu, F.; Tang, X.; Zhang, Z. Multi-attribute decision-making method based on q-rung orthopair probabilistic hesitant fuzzy schweizer-sklar power weighted hamy mean operator. PLoS ONE 2023, 18, e0266779. [Google Scholar] [CrossRef]
- Chen, Z.; Shen, D.; Ren, Y.; Yu, F.; Yuan, X. Airspace Operation Effectiveness Evaluation Based on q-Rung Orthopair Probabilistic Hesitant Fuzzy GRA and TOPSIS. Symmetry 2022, 14, 242. [Google Scholar] [CrossRef]
- Attaullah; Ashraf, S.; Rehman, N.; Khan, A. q-Rung Orthopair Probabilistic Hesitant Fuzzy Rough Aggregation Information and Their Application in Decision Making. Int. J. Fuzzy Syst. 2023, 25, 2067–2080. [CrossRef]
- Bushra, B.; Mumtaz, A.; Saleem, A.; Shahzaib, A.; Ronnason, C. Entropy Based Pythagorean Probabilistic Hesitant Fuzzy Decision Making Technique and Its Application for Fog-Haze Factor Assessment Problem. Entropy 2020, 22, 318. [Google Scholar] [CrossRef]
- Qahtan, S.; Alsattar, H.A.; Zaidan, A.A.; Deveci, M.; Pamucar, D.; Delen, D.; Pedrycz, W. Evaluation of agriculture-food 4.0 supply chain approaches using Fermatean probabilistic hesitant-fuzzy sets based decision making model. Appl. Soft Comput. 2023, 138, 110170. [Google Scholar] [CrossRef]
- Yager, R.R. The power average operator. IEEE Trans. Syst. Man Cybern. 2001, 31, 724–731. [Google Scholar] [CrossRef]
- Xu, Z.; Yager, R.R. Power-geometric operators and their use in group decision making. IEEE Trans. Fuzzy Syst. 2010, 18, 94–105. [Google Scholar]
- Zhang, Z. Hesitant fuzzy Power aggregation operators and their application to multiple attribute group decision making. Inf. Sci. 2013, 234, 150–181. [Google Scholar] [CrossRef]
- Xu, Z.S. Approaches to multiple attribute group decision making based on intuitionistic fuzzy power aggregation operators. Knowl.-Based Syst. 2011, 24, 749–760. [Google Scholar] [CrossRef]
- Xu, Z.S.; Cai, X.Q. Uncertain power average operator average operators for aggregating interval fuzzy decision and negotiation. Group Decis. Negot. 2012, 21, 381–397. [Google Scholar] [CrossRef]
- He, X.; Du, Y.X.; Liu, W.F. Pythagorean Fuzzy Power Average Operators. Fuzzy Syst. Math. 2016, 30, 116–124. [Google Scholar]
- Yager, R.R. On generalized Bonferroni mean operators for multi-criteria aggregation. Int. J. Approx. Reason. 2009, 50, 1279–1286. [Google Scholar] [CrossRef]
- Beliakov, G.; James, S.; Mordelva, J. Generalized Bonferroni mean operators in multi-criteria aggregation. Fuzzy Sets Syst. 2010, 161, 2227–2242. [Google Scholar] [CrossRef]
- Xu, Z.S. Uncertain Bonferroni means operators. Int. J. Intell. Syst. 2010, 3, 761–769. [Google Scholar]
- Xu, Z.S.; Yager, R.R. Intuitionistic fuzzy Bonferroni means. IEEE Trans. Syst. Man Cybern. B Cybern. 2011, 41, 568–578. [Google Scholar]
- He, Y.; He, Z.; Wang, G.; Chen, H. Hesitant fuzzy power Bonferroni means and their application to multiple attribute decision making. IEEE Trans. Fuzzy Syst. 2015, 23, 1655–1668. [Google Scholar] [CrossRef]
- He, Y.D.; He, Z.; Jin, C.; Chen, H.Y. Intuitionistic fuzzy power geometric Bonferroni means and their application to multiple attribute group decision making. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2015, 23, 285–315. [Google Scholar] [CrossRef]
- Liu, P.; Li, H. Interval-Valued Intuitionistic Fuzzy Power Bonferroni Aggregation Operators and Their Application to Group Decision Making. Cogn. Comput. 2017, 9, 494–512. [Google Scholar] [CrossRef]
- Liu, P.; Liu, X. Multi-attribute group decision making methods based on linguistic intuitionistic fuzzy power Bonferroni mean operators. Complexity 2017, 2017, 1–15. [Google Scholar]
- Luo, D.; Zeng, S. Pythagorean Fuzzy Power Bonferroni Aggregation Operators and Their Application in Decision Making. Comput. Eng. Appl. 2020, 56, 58–65. [Google Scholar]
- Ruan, C.; Chen, X.; Zeng, S.; Ali, S.; Almutairi, B. Fermatean fuzzy power Bonferroni aggregation operators and their applications to multi-attribute decision-making. Soft Comput. 2024, 28, 191–203. [Google Scholar] [CrossRef]
- Qu, G.; Zhang, Z.; Qu, W.; Xu, Z. Green Supplier Selection Based on Green Practices Evaluated Using Fuzzy Approaches of TOPSIS and ELECTRE with a Case Study in a Chinese Internet Company. Int. J. Environ. Res. Public Health 2020, 17, 3268. [Google Scholar] [CrossRef]
- Konys, A. Green Supplier Selection Criteria: From a Literature Review to a Comprehensive Knowledge Base. Sustainability 2019, 11, 4208. [Google Scholar] [CrossRef]
- Qian, Y.; Hou, F. An approach for green supplier selection in the automobile manufacturing industry. Kybernetes 2016, 45, 571–588. [Google Scholar]
- Deng, X.; Hu, Y.; Deng, Y.; Mahadevan, S. Supplier selection using AHP methodology extended by D numbers. Expert Syst. Appl. 2014, 41, 156–167. [Google Scholar] [CrossRef]
- Boran, F.E.; Genç, S.; Kurt, M.; Akay, D. A multi-criteria intuitionistic fuzzy group decision making for supplier selection with TOPSIS method. Expert Syst. Appl. 2009, 36, 11363–11368. [Google Scholar] [CrossRef]
- Liang, D.; Xu, Z. The new extension of TOPSIS method for multiple criteria decision making with hesitant Pythagorean fuzzy sets. Appl. Soft Comput. 2017, 60, 167–179. [Google Scholar] [CrossRef]
- Zhu, B.; Xu, Z.; Xia, M. Dual Hesitant Fuzzy Sets. J. Appl. Math. 2012, 2012, 1–13. [Google Scholar] [CrossRef]
- Srivastava, S. Green Supply Chain Management: A State-of-The-Art Literature Review. Int. J. Manag. Rev. 2007, 9, 53–80. [Google Scholar] [CrossRef]
- Gupta, S.; Soni, U.; Kumar, G. Green supplier selection using multi-criterion decision making under fuzzy environment: A case study in automotive industry. Comput. Ind. Eng. 2019, 136, 663–680. [Google Scholar] [CrossRef]
- Wang, S.; Ji, Y.; Wahab, M.I.M.; Xu, D.; Zhou, C. A New Decision Framework of Online Multi-Attribute Reverse Auctions for Green Supplier Selection under Mixed Uncertainty. Sustainability 2022, 14, 16879. [Google Scholar] [CrossRef]
- Kumar Kar, A.; K. Pani, A. Exploring the importance of different supplier selection criteria. Manag. Res. Rev. 2014, 37, 89–105. [Google Scholar] [CrossRef]
- Shah, N.; Shah, P.; Patel, M. Pricing Decisions with Effect of Advertisement and Greening Efforts for a Greengocer. Sustainability 2022, 14, 13807. [Google Scholar] [CrossRef]
- Wang, K.-Q.; Liu, H.-C.; Liu, L.; Huang, J. Green Supplier Evaluation and Selection Using Cloud Model Theory and the QUALIFLEX Method. Sustainability 2017, 9, 688. [Google Scholar] [CrossRef]
- Yadlapalli, A.; Rahman, S.; Gunasekaran, A. Socially responsible governance mechanisms for manufacturing firms in apparel supply chains. Int. J. Prod. Econ. 2017, 196, 135–149. [Google Scholar] [CrossRef]
- Ruan, C.; Chen, X.; Yan, L. Fermatean hesitant fuzzy multi-attribute decision-making method with probabilistic information and its application. Axioms 2024, 13, 456. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).