Abstract
Planetary gear transmission mechanisms (PGTMs) are widely used in mechanical transmission systems due to their compact structure and high transmission efficiency. To implement the reliability design and optimization of a PGTM, a novel multi-objective dynamic reliability optimization approach is proposed. First, a multi-objective reliability optimization model is established. Furthermore, considering the strength degradation of gears during service, a dynamic reliability analysis is conducted based on the theory of nonlinear fatigue damage accumulation. In addition, to improve computing efficiency, a random forest surrogate model based on the particle swarm optimization algorithm is proposed. Finally, an adaptive multi-objective evolutionary algorithm based on decomposition (AMOEA/D) is designed to optimize the mechanism, along with an adaptive neighborhood updating strategy and a hybrid crossover operator. The feasibility and superiority of the proposed approach are verified through an NGW planetary gear reducer. The results show that the proposed surrogate model can reduce the calculation cost and has high accuracy. The AMOEA/D algorithm can improve transmission efficiency, reduce gear volume and ensure reliability at the same time. It can provide guidance for actual gear production.
MSC:
90B25
1. Introduction
The planetary gear transmission mechanism (PGTM) is a commonly used type of transmission device that consists of multiple planet gears. It achieves transmission through the combination of a sun gear and a ring gear. Due to its advantages such as high efficiency, large load-bearing capacity, compact structure, and smooth operation, the PGTM finds wide applications in aerospace [1], engineering machinery [2], automotive [3], wind power [4], etc. As an integral component of the transmission system, the performance of the PGTM directly impacts the overall system performance. The PGTM endures high loads and torques in harsh operating conditions that involve high speed, high temperature, and high pressure [2]. Any failure in the PGTM can disrupt normal operations. Therefore, it is of great significance to study the reliability design and optimization of the PGTM.
Recently, the design optimization of planetary gears focuses on achieving a light weight and improving transmission efficiency. For example, Kalmaganbetov et al. [5] developed a set of optimization procedures to design a compact electric vehicle transmission system, and achieved the minimum gearbox volume while ensuring transmission efficiency. Troha et al. [6] proposed a multi-criterion optimization method for a two-load two-speed planetary gear train, aiming at minimizing quality and production costs. In addition, to improve the service life, the reliability analysis of gears has been widely studied. For instance, Dong et al. [4] proposed a method for analyzing gear contact fatigue and established a limit state equation. Additionally, they resolved the reliability function of gear contact fatigue by utilizing the proposed approach. Similarly, Cui et al. [2] performed a reliability analysis and optimization of planetary gears based on the stress–strength interference model and a genetic algorithm. Unfortunately, certain issues within the reliability analysis of gears still warrant further investigation. While the stress–strength interference model conveniently computes the failure rate of gears, it fundamentally addresses static load and static strength issues. In the actual service life of gears, the strength continuously degenerates with increasing service time. However, previous studies have not adequately accounted for the strength degradation process of gears. Therefore, this study emphasizes the dynamic reliability analysis of a PGTM.
The reliability design and optimization approach has been widely employed for assessing the reliability of structures. However, its computational workload can be significant, leading researchers to propose various models to solve this problem. Common methods include Monte Carlo simulation [7], first-order reliability analysis [8], second-order reliability analysis [9], the performance measure method [10], and multidisciplinary design optimization [11,12]. Among these methods, Monte Carlo simulation is widely implemented due to its ease of use and avoidance of the complex process of constructing functional functions. For instance, Yang et al. [13] adopted the traditional double-loop Monte Carlo method to analyze system reliability. Similarly, Sun et al. [14] applied fault tree analysis to establish a fault tree diagram for a recreational vehicle reducer and predicted its reliability using the Monte Carlo simulation method.
A common feature of the aforementioned simulation methods is that they are computationally expensive in practical applications. As a result, surrogate models have gained popularity in reliability modeling. A good surrogate model provides results that are very close to the original model, while significantly reducing the computational burden. Commonly used surrogate models include the Kriging model [15], Response Surface [16], Artificial Neural Networks [17], Support Vector Machines [18], and Polynomial Chaos Expansion [19]. For instance, Yi et al. [20] optimized wind turbine gearboxes using a full second-order polynomial response surface method and implemented a screening algorithm to search the solution space for gear optimization. Cui et al. [2] used the Kriging model to reduce the computational cost. Although the reliability optimization problem of gears has been widely researched, the accuracy of surrogate models has not been analyzed and verified by aforementioned studies. Further research and improvements are necessary.
The reliability design and optimization approach to gears is a combination of the reliability analysis theory and a mathematical planning method [2]. In the optimization design, the design parameters of gears are taken as random variables, while the reliability and other objectives are taken as objective functions. Subsequently, the reliability of the gear is calculated through reliability analysis, and the optimal design parameters are obtained by running optimization technology. In general, it is a combination of reliability analysis and structural optimization. Recently, intelligent optimization algorithms have shown remarkable performance in the optimization of structures. For instance, Mendi et al. [21] used the genetic algorithm to optimize spur gears and obtained the minimum volume design that can withstand system loads. Similarly, Savsani et al. [22] used the particle swarm optimization and simulated annealing algorithms to optimize the design of multi-stage spur gears. Dixit and Kulkarni [23] used the genetic algorithm for multi-objective optimization in the design of a pair of spur gears. Wang et al. [24] proposed an improved bare-bones multi-objective particle swarm algorithm to solve the multi-objective size optimization problems with nonlinearity and constraints in structural design and optimization.
The reliability optimization design problem of gears is usually a complex multi-objective problem with nonlinear constraints. First, the computational cost of using Monte Carlo simulation to evaluate reliability is huge. Therefore, it is necessary to propose an efficient surrogate model to balance precision and efficiency. Second, previous studies typically used a weighted approach to convert multi-objective optimization problems into single-objective optimization problems [2,25], resulting in the loss of trade-off relationships and information between different objectives. To address these issues, this study proposes a particle swarm optimization-based random forest model (PSO-RF) and an adaptive multi-objective evolutionary algorithm based on decomposition (AMOEA/D) for optimizing a PGTM. The main contributions are as follows:
- A multi-objective reliability optimization model is established with the objectives of maximizing transmission efficiency and reliability and minimizing volume.
- To conduct the dynamic reliability analysis, the residual strength is calculated based on the theory of nonlinear fatigue damage accumulation, and dynamic reliability is analyzed using the Monte Carlo simulation method.
- To improve calculation efficiency and accuracy, the PSO-RF surrogate model is established, and the cross-validation method is used to evaluate the accuracy.
- An AMOEA/D algorithm is proposed with an adaptive neighborhood updating strategy and a hybrid crossover operator to solve the multi-objective reliability optimization model.
The rest of this study is organized as follows. Section 2 describes the research motivation and establishes a multi-objective reliability optimization model. Section 3 describes the PSO-RF surrogate model. Section 4 designs an AMOEA/D algorithm to optimize the PGTM. Section 5 conducts a case study based on an NGW planetary gear reducer. Section 6 provides the conclusion and directions future work.
2. Problem Description and Model Construction
2.1. Research Motivation
As illustrated in Figure 1, a PGTM comprises several planetary gears, a sun gear, and a ring gear, with numerous design parameters. The dynamic reliability design optimization of the PGTM involves two parts: reliability analysis and parameter optimization. The reliability analysis is carried out by calculating the stress and strength of the gear, and considering the strength degradation of the gear during service. Dynamic reliability refers to the reliability of the gear that gradually changes as the strength deteriorates. Unlike static reliability, dynamic reliability emphasizes how the system changes over time. Due to the complex computational process in reliability analysis, a surrogate model should be proposed. Because the accuracy of the surrogate model directly affects the system reliability evaluation, if the prediction is not accurate enough, it will result in inaccurate optimal parameters. Therefore, the establishment of a high-precision surrogate model is of great importance. In addition, as the optimization of this mechanism involves numerous design variables, nonlinear constraints, and multiple objectives, a multi-objective algorithm that can achieve global optimization and deal with multiple variables and constraints needs to be proposed.
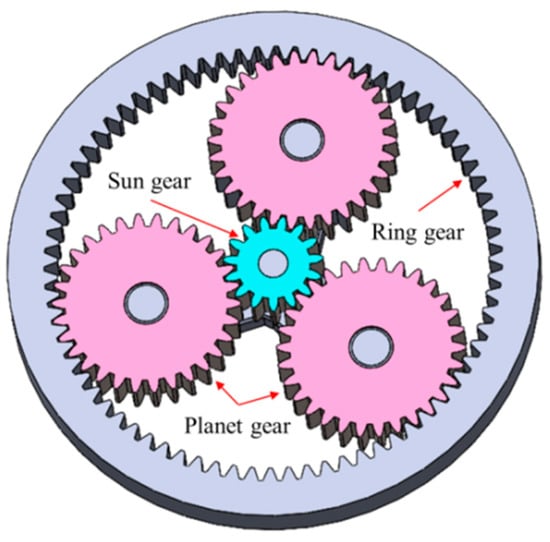
Figure 1.
Example of planetary gear transmission system.
2.2. Model Construction
2.2.1. Notations
To improve the readability, Table 1 provides the parameters related to the PGTM and the variables involved in the model.

Table 1.
Notations.
2.2.2. Multi-Objective Reliability Optimization Model
The PGTM contains many design parameters. Only optimizing the tooth number, modulus, and tooth width will lead to incomplete performance optimization. Additionally, it is necessary to consider the correlation between variables when selecting design variables. For example, the tooth number of the sun gear affects the planetary gears and ring gear. Thus, the optimized design variables are shown in Equation (1).
The transmission efficiency of the gear directly affects the performance of the whole system, and the high efficiency of the gear can reduce the energy loss. The lightweight design of the gear can reduce the cost and improve the portability of the gear. In addition, the reliability of the gear is directly related to the maintenance cost and service life of the equipment, and the optimization considering reliability can improve the durability of the gear. Therefore, to ensure reliability while achieving goals such as a compact structure and high transmission efficiency, a multi-objective reliability optimization model is established with the objectives of minimizing the volume and maximizing the transmission efficiency and reliability, i.e.,
In this study, a multi-objective optimization algorithm is employed, and the Chebyshev function is used to evaluate the quality of the solutions. The proposed method is suitable for multi-objective minimization problems. Equation (2) calculates the volume. To facilitate the optimization algorithm and ensure the rationality of the problem, the complements of reliability and transmission efficiency are taken as the optimization objectives, transforming the problem into a minimization problem. As shown in Equations (3) and (4), the complement of transmission efficiency is taken as the objective function, and the smaller the value, the higher the transmission efficiency of the gear. In Equation (5), the reliability complement, that is, the failure rate, is taken as the objective function to achieve reliability optimization. This approach redefines the objective function but does not compromise the rationality of the problem. Equation (6) represents the objective function of the optimization model.
The constraints that the model needs to satisfy are as follows:
Equations (7)–(10) describe the gear meshing conditions. Among them, Equation (7) is the transmission ratio condition, Equation (8) is the concentricity constraint, Equation (9) is the installation condition, and Equation (10) is the adjacency condition. Equations (11) and (12) represent the constraints on the profile shift factor, Equation (13) indicates the module constraint, and Equation (14) shows the constraint on the tooth number of the sun gear. Equations (15)–(17) represent the constraints on the helix angle and meshing angles, and Equation (18) imposes constraints on the factor of tooth width.
The model involves numerous design variables which restrict each other. Moreover, there is a beneficial inverse relationship between the reliability, transmission efficiency, and volume objectives. In addition, the relationship between the design parameters and the performance of the transmission mechanism is usually nonlinear. In summary, the model has the characteristics of being multi-variable and multi-objective and having nonlinear constraints, so the optimization problem has high complexity, which brings difficulty to the solution.
2.2.3. Dynamic Reliability Calculation
According to the structural characteristics of planetary gears, the main reliability values of a PGTM include the following:
- The reliability of tooth surface contact fatigue strength between three planetary gears and the sun gear , and .
- The reliability of tooth root bending fatigue strength of three planetary gears and the sun gear , and .
In the stress–strength interference model, it is believed that the reliability of components in mechanical products depends on the relationship between strength and stress. When the strength exceeds the stress, the parts work normally. When the strength is less than the stress, failure occurs. The conditions for ensuring the reliability of the mechanism are shown in Constraint (19).
- Reliability of tooth contact fatigue strength
When calculating the reliability of tooth surface contact fatigue strength, destructive pitting is considered the limit state of the tooth surface [26]. The tooth surface contact stress can be calculated by Equation (20):
The allowable contact stress on the tooth surface is calculated by Equation (21).
- b.
- Reliability of tooth root bending fatigue strength
The reliable condition for the bending fatigue strength of the tooth root is that the bending strength is greater than the bending stress. The tooth root bending stress can be calculated by Equation (22) [27].
The allowable tooth root bending stress can be calculated by Equation (23).
Based on Equations (19)–(22), the mean value, factor of variation, and standard deviation of the stress and strength can be calculated so that the stress distribution function can be determined.
- c.
- Dynamic reliability calculation
The gear transmission system is subjected to dynamic loads, and internal damage will continue to accumulate, resulting in the performance and strength of the components gradually decreasing over time. The reliability also declines with the degradation of strength, so it is defined as the dynamic reliability. In this study, the residual strength of the gears is analyzed based on the theory of nonlinear fatigue damage accumulation [28]. The dynamic reliability considering strength degradation is expressed by Equation (24).
The strength degradation model based on the theory of nonlinear fatigue damage accumulation is represented by Equations (25) and (26). Due to the different frequencies of various components in a mechanical system, the number of load cycles can be converted into service time .
where represents the residual strength; represents the static strength at the initial moment. represents the peak value of the cyclic stress. represents the fatigue life, represents the stress amplitude, represents the mean stress, and represents the material constant.
The residual strength of the gear can be determined using Equations (25) and (26). Based on actual experimental tests on the gear, it is found that the stress follows a log-normal distribution. With the residual strength and stress distribution taken into account, the dynamic reliability analysis can be conducted. According to the obtained residual strength and dynamic stress, the reliability can be calculated using the Monte Carlo simulation method. The flowchart of the Monte Carlo simulation method is shown in Figure 2.
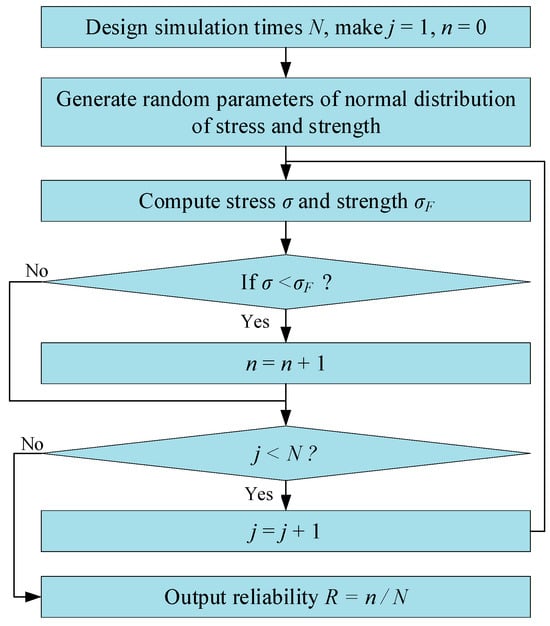
Figure 2.
Monte Carlo simulation method.
The main steps of the Monte Carlo simulation method are as follows:
Step 1: set the simulation number = 10,000, and initialize the parameter as 1 and failure times as 0.
Step 2: calculate the gear tooth surface contact stress, root bending stress, and strength based on Section 2.2.3.
Step 3: if the stress exceeds the strength, increment by 1.
Step 4: Check if the simulation termination condition is met, i.e., . If true, output the failure rate . Otherwise, repeat Steps 2–3 in a loop.
Repeat the simulation three times and take the average value as the result.
3. PSO-RF-Based Surrogate Model
3.1. Framework of PSO-RF
When analyzing reliability using the Monte Carlo simulation method, the calculation accuracy heavily relies on the number of simulations. However, conducting a large number of simulations can significantly decrease efficiency. To address this problem, a surrogate model is established. While a random forest model exhibits better generalization performance and robustness compared to a single decision tree, optimizing its hyperparameters may enhance its predictive performance. In this study, the particle swarm optimization algorithm is employed to optimize the hyperparameters of the random forest model. The particle swarm optimization algorithm is an efficient and easy-to-implement global optimization algorithm and can be used for hyperparameter optimization in machine learning algorithms [29]. The flowchart of the PSO-RF algorithm is shown in Figure 3.
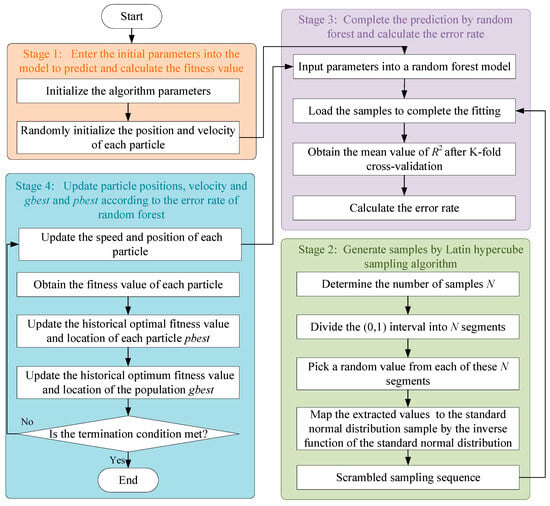
Figure 3.
Flowchart of PSO-RF algorithm.
The random forest model consists of four main parameters: the number of trees , the maximum tree depth , the minimum samples to split a node , and the minimum samples in a leaf .
The detailed steps of optimizing the random forest algorithm using the particle swarm optimization algorithm are as follows:
Step 1: initialize parameters.
Step 2: Initialize the positions and velocities of each particle. Input the initial population (values of random forest parameters) into the random forest model for prediction.
Step 3: generate samples by using the Latin hypercube sampling method [30] to make predictions.
Step 4: calculate the error rate based on K-fold cross-validation as the fitness value for the particle swarm algorithm.
Step 5: Obtain the fitness values of each particle. Find the optimal hyperparameters of the random forest algorithm based on the particle swarm optimization algorithm.
3.2. Random Forest Model
As shown in Figure 4, the random forest model [31] is an ensemble learning method based on decision trees. Where green points indicate the path predicted by the model, and the blue indicates the path that was not selected. The main idea is to construct multiple decision trees and use a voting method to classify or predict each sample, thereby improving the accuracy and generalization ability of the model.
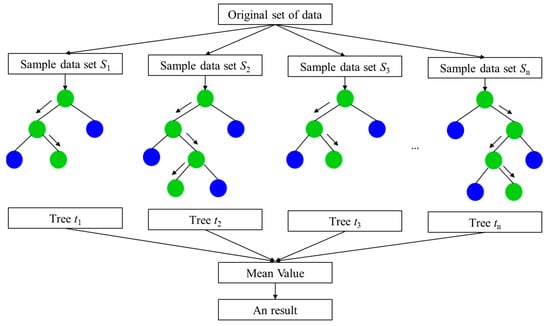
Figure 4.
Random forest model.
The modeling steps of the random forest model are as follows:
Step 1: randomly select a subset from the training data set and randomly select some feature attributes.
Step 2: build a decision tree model using the subset and feature attributes for training.
Step 3: repeat the above two steps until the specified number of decision trees are built.
Step 4: When unknown data are input, each decision tree will be predicted. Based on the prediction results of the decision trees, take the average value of the decision trees as the final prediction result.
3.3. Particle Swarm Optimization Algorithm
The particle swarm optimization algorithm [32] is a type of swarm intelligence algorithm that simulates the foraging behavior of birds to search for solutions. The basic principle assumes the existence of a food source (i.e., the optimal solution to an optimization problem) within a given region. The task of the swarm is to find this food source. The detailed steps of the particle swarm optimization which are shown in Stage 4 in Figure 3 are as follows:
Step 1: Initialize the parameters, including the swarm size, the number of iterations, the inertia weight, the learning factors, etc. Initialize the positions and velocities of each particle. Here, the positions of the particles correspond to the values of the hyperparameters for the random forest model.
Step 2: perform K-fold cross-validation to calculate the error rate for each set of hyperparameters, which will be used as the fitness value for each particle.
Step 3: determine the initial individual best solution and the global best solution for the swarm.
Step 4: update the positions and velocities of each particle based on the individual and global best solutions.
Step 5: calculate the fitness value for the newly generated particles.
Step 6: Check if the termination condition is met. If yes, output the optimal hyperparameters; if not, go back to Step 4 and repeat the process.
4. AMOEA/D Algorithm
4.1. Framework of AMOEA/D Algorithm
Multi-objective evolutionary algorithms based on decomposition (MOEA/D) have been widely applied to multi-objective optimization problems due to their strong search capability, high robustness, and scalability [33,34,35]. However, the basic MOEA/D algorithm has the following shortcomings when dealing with multi-objective optimization: poor population diversity and a tendency to become stuck in local optima. To address these issues, the following strategies are proposed to improve the MOEA/D algorithm.
First, a hybrid crossover operator is introduced to improve the population diversity and the algorithm’s search capability. This operator combines different crossover operators to generate diverse offsprings. By incorporating various crossover operators, it enhances the exploration of the solution space. Second, an adaptive neighborhood updating strategy is proposed to avoid being trapped in local optima.
The overall flowchart of the algorithm is shown in Figure 5. The detailed steps of the AMOEA/D algorithm are as follows:
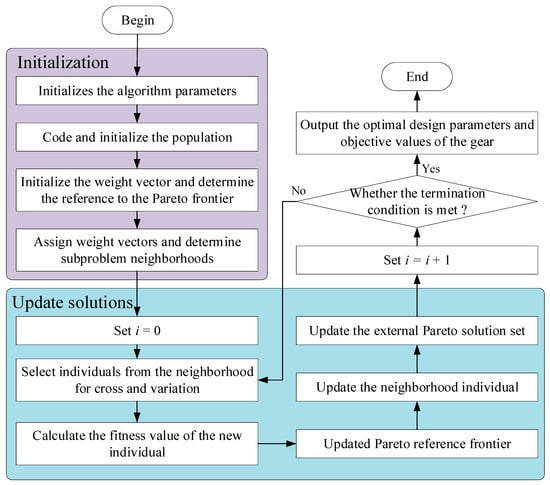
Figure 5.
Flowchart of AMOEA/D algorithm.
Initialization:
Step 1: initialize the algorithm parameters, including population size NP, termination condition I, crossover probability pc, mutation probability pm, neighborhood updating factor, etc.
Step 2: set the initial external solution set as an empty set, used to store the Pareto solutions.
Step 3: Calculate the Euclidean distance between any two weight vectors to determine the neighbors for each weight vector. For each weight vector , its T neighbors are denoted as , where are weight vectors of .
Step 4: randomly initialize the population and calculate the fitness values of the initial population.
Step 5: Initialize the reference point as a target value reference. In the modeling process, convert the model into a minimization problem model, so the initial reference point is set as
Updating solutions:
Step 6: select two optimal individuals from the neighborhood solutions and generate new solutions through crossover and mutation operators.
Step 7: update the new solutions using the Chebyshev aggregation function.
Step 8: Update the neighborhood solutions based on the adaptive neighborhood update strategy. Use the Chebyshev function to judge the superiority or inferiority of a solution.
Step 9: Update the external solution set , remove the solutions that are dominated by the new solutions, and add the new solutions in the . If the new solutions do not dominate any solution in , they are not updated.
Step 10: Check if the termination condition is met. If it is met, output the external solution set . Otherwise, continue with Steps 6–9.
4.2. Encode and Initialize Population
As shown in Figure 6, chromosomes are generated using real-number encoding, where each gene in the chromosome represents a value for the macroscopic parameters of the PGTM.

Figure 6.
Example of chromosome.
Considering that random initialization can lead to the poor uniformity of solutions, the initial population is generated using the Latin hypercube sampling method. Latin hypercube sampling ensures that the sampled points are uniformly distributed within each small interval [30].
4.3. Genetic Operators
4.3.1. Hybrid Crossover Operator
To facilitate diverse populations and expand the solution space, a hybrid crossover operator has been designed, which incorporates uniform crossover and multi-point crossover. By combining these techniques, the diversity within the population is enhanced, allowing for a more comprehensive exploration of the solution space.
As shown in Figure 7, the detailed process of the hybrid crossover operator is as follows: A random number is generated between 0 and 1. If , the uniform crossover is performed, otherwise the two-point crossover is executed. The steps for the uniform crossover are as follows:
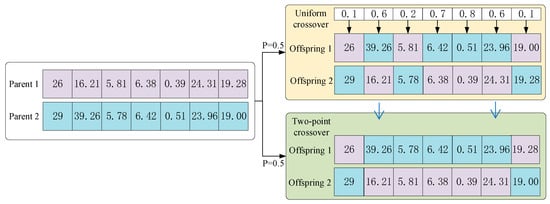
Figure 7.
Example of crossover operator.
Step 1: generate a random number between 0 and 1.
Step 2: If > , swap the genes between Parent 1 and Parent 2. Otherwise, do not perform any swapping.
Step 3: repeat the process until the entire chromosome is traversed.
The steps of the two-point crossover are as follows:
Step 1: randomly select two points on the chromosome as the starting and ending positions for the gene segment to be exchanged.
Step 2: swap the gene segment selected in Step 1 between Parent 1 and Parent 2 to generate Offspring 1 and Offspring 2.
4.3.2. Mutation Operator
Indeed, for optimization problems related to gear systems where each gene in the chromosome represents different parameters of the gears, random gene swapping in single-point or multi-point mutations may lead to infeasible solutions. To address this issue, a non-uniform mutation operator has been designed.
Figure 8 shows the steps for the uniform mutation operator.
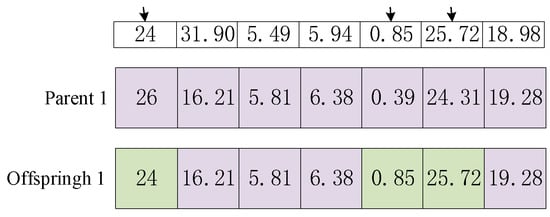
Figure 8.
Example of mutation operator.
Step 1: randomly generate a set of design parameters that satisfy the constraints.
Step 2: randomly select between 1 and points, where is the length of the chromosome.
Step 3: update the genes in Parent 1 using the generated design parameters at the selected points to create an offspring individual.
By introducing the uniform mutation operator, the algorithm can explore the solution space more effectively, avoiding premature convergence. This helps to improve the overall optimization results for gear-related problems.
4.4. Aggregate Function
The MOEA/D algorithm uses aggregation functions to distinguish the quality of solutions. Commonly used aggregation functions include the weighted aggregation function, Chebyshev aggregation function, and boundary intersection aggregation function. Among them, the Chebyshev aggregation function is a nonlinear aggregation method that restricts the convergence acceptance area in high-dimensional problems, which can ensure the convergence of the population.
Equation (27) is the Chebyshev aggregation function. Here, is the weight vector of the i-th objective, and is the reference point for the objective function.
4.5. Adaptive Neighborhood Updating Strategy
To improve the population diversity, an adaptive neighborhood updating strategy is proposed by modifying the strategy proposed in [34]. The steps of this strategy are as follows.
Step 1: calculate the number of neighbors to be updated according to Equation (28).
where is the number of neighbors, is the current iteration, is the maximal iterations, and is a control parameter ( [0, 1)).
Step 2: find the most suitable subproblem for ; the subproblem is defined as the most suitable subproblem if it satisfies Equation (27).
Step 3: Update the neighbors of the individual . For each solution from the neighborhood of , replace with if dominates .
5. Case Study
All of the algorithms were compiled and run in the 12th Gen Intel(R) Core(TM) i7-12700 F 2.10 GHz CPU, 16.00 GB RAM, Win10 64-bit operating system, Python programming language, and Pycharm programming environment. An NGW planetary reducer was selected to verify the effectiveness of the proposed approach, and the basic parameter design is shown in Table 2.

Table 2.
Basic parameter design of NGW planetary reducer.
5.1. Parametric Orthogonal Test
To determine the parameters of the AMOEA/D algorithm, a parameter orthogonal experiment is designed. The key parameters that need to be determined for the AMOEA/D algorithm include the neighborhood size , adjustment parameter , crossover probability and mutation probability .
The comprehensive values are taken as the reference values [35]; the average value of the reference value at each level of each factor is calculated, and the corresponding level of the minimum value is selected for each factor. According to the results in Table 3, the values of each parameter were determined as follows: , , , and .

Table 3.
Parametric orthogonal test.
5.2. Dynamic Reliability Analysis
To verify the effectiveness of the proposed algorithm for dynamic reliability optimization, numerical experiments are designed. The strength degradation processes of gear tooth contact fatigue and tooth root bending fatigue are analyzed.
Figure 9 is the degradation process of tooth contact and bending fatigue strength. The contact fatigue strength of the sun gear degrades faster than that of the planetary gear (see Figure 9a), while the bending fatigue strength shows the opposite trend (see Figure 9b). The gear strength exhibits steady degradation in the early and middle stages, followed by rapid degradation in the final stage, which is consistent with the characteristic of “sudden death” in metal materials.
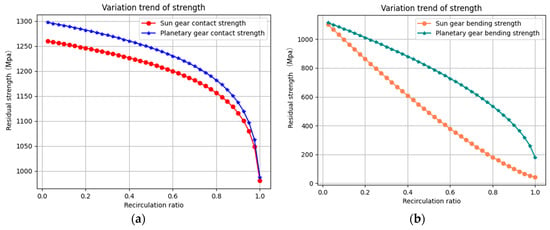
Figure 9.
Process of strength degradation. (a) Degradation of tooth contact fatigue strength. (b) Degradation of tooth bending fatigue strength.
As shown in Figure 10, the reliability of the system decreases slowly in the early stage of operation and rapidly in the later stage. The planetary gears have relatively high reliability and maintain stability before and after operation. Due to the high rotation speed of the sun gear and the large number of load cycles it experiences, the reliability of the sun gear is relatively low. This indicates that the sun gear is a weak link in the transmission system and should be given special attention during the design process.
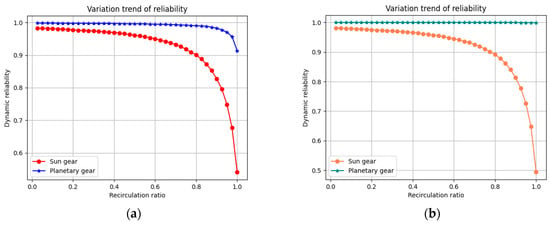
Figure 10.
Dynamic reliability after optimization. (a) Dynamic reliability of tooth surface contact. (b) Dynamic reliability of tooth root bending.
5.3. Comparison Experiment of PSO-RF Surrogate Model with Other Models
The hyperparameters of the random forest model are optimized by the particle swarm optimization algorithm, which are shown in Table 4. The Latin hypercube sampling method is used to extract 1000 samples, of which 80% are training sets and 20% are test sets.

Table 4.
Hyperparameters of random forest model.
To verify the accuracy of the PSO-RF surrogate model, the following commonly used structural reliability models were selected for comparison.
Kriging model: the Kriging model [2] is an interpolation method based on the Gaussian process, suitable for establishing nonlinear relationships between the input and output.
XGBoost: XGBoost [37] is an ensemble learning algorithm which uses gradient boosting trees. It performs well in terms of prediction accuracy and generalization ability.
Basic random forest model [31]: this is a traditional random forest model without PSO optimization which trains and predicts decision trees by randomly selecting features and samples.
- Correlation analysis
The correlation analysis characterizes the strength of the relationship between variables. In Figure 11, each value represents the degree of correlation between the corresponding variables. The closer the value is to 1 or −1, the higher the correlation between the variables, indicating a strong linear relationship. If the value is close to 0, it indicates a weak correlation. Based on the results in Figure 11, it can be observed that there is no significant correlation among the seven design variables. Therefore, the optimization can be focused on these seven variables. The gear parameters that have a significant impact on the reliability prediction results are the number of teeth, tooth width, and normal module.
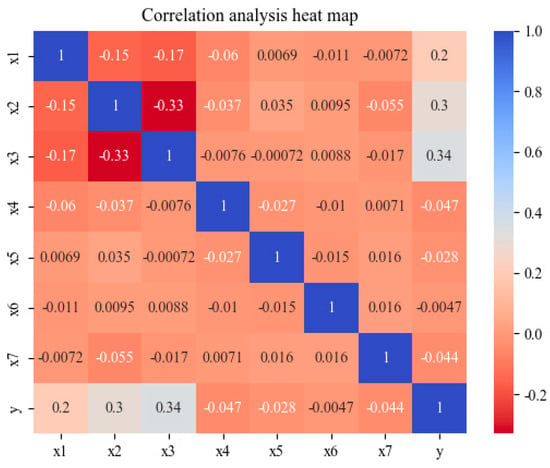
Figure 11.
Correlation analysis heat map.
- b.
- Comparison of four models
Figure 12 presents the comparison results of four different surrogate models, with the blue curve representing the observed values. Figure 12a–d show the fitting results of the PSO-RF model, random forest model, Kriging model, and XGBoost model, respectively. It can be observed that the results of the PSO-RF model are the closest match to the observed values.
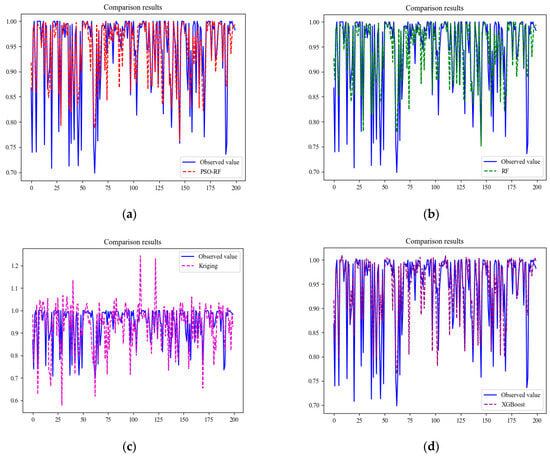
Figure 12.
Comparison results of four surrogate models. (a) Fitting results of PSO-RF. (b) Fitting results of RF. (c) Fitting results of Kriging. (d) Fitting results of XGBoost.
To visually assess the performance of the algorithms, the following metrics were calculated [38]. Among them, the Mean Squared Error (MSE) in Equation (29) is a commonly used measure to evaluate the difference between model predictions and actual observations. A smaller MSE indicates a smaller difference, indicating a better fit of the model. Based on Equation (30), the Mean Absolute Error (MAE) is obtained. A smaller MAE indicates a better fit of the model. in Equation (31) represents the proportion of the variability in the dependent variable that can be explained by the model, indicating the degree of fit of the model to the data. A higher value indicates that the model can better explain the variability in the dependent variable. The explainable variance indicator (Evar) measures the similarity between the dispersion of all predicted values and the dispersion of the samples themselves, which can be calculated by Equation (32). A higher value indicates a closer match between the dispersion of predicted and sample values.
As shown in Table 5, the PSO-RF model performs the best in the four mentioned metrics, making it more suitable as a surrogate model for constructing a multi-objective reliability optimization model for the PGTM.

Table 5.
Indicators of four surrogate models.
5.4. Comparison Experiments of AMOEA/D with Other State-of-the-Art Multi-Objective Meta-Heuristics
To verify the performance of the AMOEA/D algorithm, the following numerical experiments are conducted. According to previous studies, the differential evolution algorithm and decomposition-based multi-objective evolution algorithms have a stable performance in multi-objective optimization problems, especially for discrete problems. When exploring Pareto solutions, they have a better development performance and convergence performance. Therefore, we choose the basic MOEA/D [33] and the differential evolution algorithm (DE), which performs well in multi-objective optimization problems [39], as comparisons.
Figure 13 presents box plots of the three algorithms in terms of volume, transmission efficiency, and reliability metrics. Please refer to Figure 13a to understand the box diagram. Regarding the volume metric, the AMOEA/D algorithm exhibits a lower median position (see Figure 13a), indicating that the overall solutions obtained are significantly superior to those of the DE algorithm and MOEA/D algorithm. In terms of transmission efficiency, the AMOEA/D algorithm achieves the highest median value (see Figure 13b), indicating the overall optimality of the solutions obtained, followed by the DE algorithm and then the MOEA/D algorithm. In the case of reliability, the AMOEA/D algorithm demonstrates a clear advantage, as the obtained reliability is closest to 1 (see Figure 13a). The MOEA/D algorithm ranks second, while the DE algorithm performs the poorest.
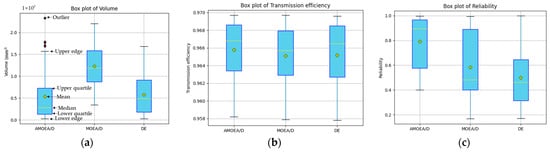
Figure 13.
Box plots of three objectives. (a) Box plot of volume. (b) Box plot of transmission efficiency. (c) Box plot of reliability.
We take one solution from the Pareto frontier and compare it with the results of the conventional design. The design variables and objective values are shown in Table 6. With reliability ensured not to be lower than that of the conventional design, the volume is reduced by 28.97% and the transmission efficiency is improved by 1.10%.

Table 6.
Optimization results.
6. Conclusions and Future Work
In this study, a reliability design and optimization approach for a PGTM is proposed. To ensure the reliability of the PGTM while achieving a light weight and high transmission efficiency, a multi-objective reliability optimization model is established. Considering that the strength of gears is not a constant during service, the residual strength is analyzed based on the stress–strength interference model and the theory of nonlinear fatigue damage accumulation. And the Monte Carlo simulation method is adopted to calculate the dynamic reliability. Subsequently, due to the massive computational requirements of the Monte Carlo simulation method, the random forest model is employed to construct a surrogate model. At the same time, the particle swarm optimization algorithm is used to optimize the hyperparameters of the random forest model. Furthermore, the AMOEA/D algorithm is proposed to take into account the optimization of the three objectives and provides guidance for the actual design. Finally, taking an NGW-type planetary gear reducer as an example, the effectiveness of the proposed approach is verified. The conclusion demonstrates that the PSO-RF surrogate model has higher accuracy than other commonly used models. After optimization using AMOEA/D, the volume is reduced by 28.97% and the transmission efficiency is improved by 1.10%, while ensuring reliability.
To the best of our knowledge, this is the first study to conduct dynamic reliability analysis on a PGTM and use a multi-objective algorithm to optimize volume, transmission efficiency, and reliability. However, there are still some shortcomings in this study, such as the lack of analysis and calculation of dynamic loads under actual working conditions. Future research will consider making improvements in terms of these aspects. For example, the dynamic stress of the gear during operation can be simulated by finite element analysis. Then, statistical methods such as rain flow counting can be used to analyze load spectrum data.
Author Contributions
Conceptualization, S.T. and X.Y. (Xiaoyan Yan); methodology, X.Y. (Xiaoyan Yan); investigation, S.T. and X.Y. (Xiaoyan Yan); writing—original draft preparation, X.Y. (Xiaoyan Yan); writing—review and editing, L.Y. and X.Y. (Xianmiao Yang); funding acquisition, S.T. and L.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China under grants 52005032 and 72271025, the Key Research and Development Program of Zhejiang Province 2022C01010, and the Guangdong Basic and Applied Basic Research Foundation under grants 2023A1515011532 and 2024A1515010132).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- Li, M.; Luo, Y.; Qu, L.; Xie, L.; Zhao, B. Influence of ring gear flexibility on the fatigue reliability of planetary gear systems in heavy helicopters. Mech. Mach. Theory 2024, 191, 105520. [Google Scholar] [CrossRef]
- Cui, D.; Wang, G.; Lu, Y.; Sun, K. Reliability design and optimization of the planetary gear by a GA based on the DEM and Kriging model. Reliab. Eng. Syst. Saf. 2020, 203, 107074. [Google Scholar] [CrossRef]
- Liu, C.; Yang, C.; Zhao, Y.; Luo, J.; Chen, X. Dynamic modeling and analysis of high-speed flexible planetary gear transmission systems. Alex. Eng. J. 2023, 80, 444–464. [Google Scholar] [CrossRef]
- Dong, W.; Nejad, A.R.; Moan, T.; Gao, Z. Structural reliability analysis of contact fatigue design of gears in wind turbine drivetrains. J. Loss Prev. Process Ind. 2020, 65, 104115. [Google Scholar] [CrossRef]
- Kalmaganbetov, S.; Isametova, M.; Troha, S.; Vrcan, Ž.; Marković, K.; Marinkovic, D. Selection of Optimal Planetary Transmission for Light Electric Vehicle Main Gearbox. J. Appl. Comput. Mech. 2024, in press. [Google Scholar] [CrossRef]
- Troha, S.; Vrcan, Ž.; Karaivanov, D.; Isametova, M. The selection of optimal reversible two-speed planetary gear trains for machine tool gearboxes. FU Mech. Eng. 2020, 18, 121. [Google Scholar] [CrossRef]
- Lee, I.; Choi, K.K.; Du, L.; Gorsich, D. Dimension reduction method for reliability-based robust design optimization. Comput. Struct. 2008, 86, 1550–1562. [Google Scholar] [CrossRef]
- Dersjö, T.; Olsson, M. Reliability Based Design Optimization Using a Single Constraint Approximation Point. J. Mech. Des. 2011, 133, 031006. [Google Scholar] [CrossRef]
- Kiureghian, A.D.; Stefano, M.D. Efficient Algorithm for Second-Order Reliability Analysis. J. Eng. Mech. 1991, 117, 2904–2923. [Google Scholar] [CrossRef]
- Youn, B.D.; Choi, K.K.; Du, L. Enriched Performance Measure Approach for Reliability-Based Design Optimization. AIAA J. 2005, 43, 874–884. [Google Scholar] [CrossRef]
- Wang, L.; Ren, Q.; Ma, Y.; Wu, D. Optimal Maintenance Design-Oriented Nonprobabilistic Reliability Methodology for Existing Structures Under Static and Dynamic Mixed Uncertainties. IEEE Trans. Reliab. 2019, 68, 496–513. [Google Scholar] [CrossRef]
- Wang, L.; Xiong, C. A novel methodology of sequential optimization and non-probabilistic time-dependent reliability analysis for multidisciplinary systems. Aerosp. Sci. Technol. 2019, 94, 105389. [Google Scholar] [CrossRef]
- Yang, L.; He, K.; Guo, Y. Reliability analysis of a nonlinear rotor/stator contact system in the presence of aleatory and epistemic uncertainty. J. Mech. Sci. Technol. 2018, 32, 4089–4101. [Google Scholar] [CrossRef]
- Sun, Y.G.; Yu, G.B.; Zhang, J.; Wang, F.; Sun, Y.Q.; Chen, J.H. Reliability Prediction of RV Reducer Based on Fault Tree and Monte-Carlo Simulation. Appl. Mech. Mater. 2013, 274, 663–666. [Google Scholar] [CrossRef]
- Wang, D.; Qiu, H.; Gao, L.; Xu, D.; Jiang, C. Time-dependent system reliability analysis using adaptive single-loop Kriging with probability of rejecting classification. Struct. Multidiscip. Optim. 2023, 66, 186. [Google Scholar] [CrossRef]
- Zeng, H.; Wang, L.; Sun, H.; Wang, T.; Gao, Q. Optimized design of straight bevel gear tooth root transition surface. Struct. Multidiscip. Optim. 2022, 65, 36. [Google Scholar] [CrossRef]
- Karunanithi, N.; Whitley, D.; Malaiya, Y.K. Using neural networks in reliability prediction. IEEE Softw. 1992, 9, 53–59. [Google Scholar] [CrossRef]
- Bourinet, J.-M.; Deheeger, F.; Lemaire, M. Assessing small failure probabilities by combined subset simulation and Support Vector Machines. Struct. Saf. 2011, 33, 343–353. [Google Scholar] [CrossRef]
- Cheng, K.; Lu, Z. Sparse polynomial chaos expansion based on D-MORPH regression. Appl. Math. Comput. 2018, 323, 17–30. [Google Scholar] [CrossRef]
- Yi, P.X.; Dong, L.J.; Chen, Y.X. The Multi-Objective Optimization of the Planet Carrier in Wind Turbine Gearbox. Appl. Mech. Mater. 2012, 184–185, 565–569. [Google Scholar] [CrossRef]
- Mendi, F.; Başkal, T.; Boran, K.; Boran, F.E. Optimization of module, shaft diameter and rolling bearing for spur gear through genetic algorithm. Expert Syst. Appl. 2010, 37, 8058–8064. [Google Scholar] [CrossRef]
- Savsani, V.; Rao, R.V.; Vakharia, D.P. Optimal weight design of a gear train using particle swarm optimization and simulated annealing algorithms. Mech. Mach. Theory 2010, 45, 531–541. [Google Scholar] [CrossRef]
- Dixit, Y.; Kulkarni, M.S. Multi-objective optimization with solution ranking for design of spur gear pair considering multiple failure modes. Tribol. Int. 2023, 180, 108284. [Google Scholar] [CrossRef]
- Wang, Z.H.; Yang, G.B.; Sun, Y.X.; Li, Y.X.; Wu, F.H. An Improved Bare-Bones Particle Swarm Algorithm for Multi-Objective Optimization with Application to the Engineering Structures. FU Mech. Eng. 2023. Available online: https://casopisi.junis.ni.ac.rs/index.php/FUMechEng/article/view/10976 (accessed on 5 July 2024).
- Zhang, G.; Wang, G.; Li, X.; Ren, Y. Global optimization of reliability design for large ball mill gear transmission based on the Kriging model and genetic algorithm. Mech. Mach. Theory 2013, 69, 321–336. [Google Scholar] [CrossRef]
- ISO 6336-2:2019; Calculation of Load Capacity of Spur and Helical Gears—Part 2: Calculation of Surface Durability (Pitting). International Organization for Standardization: Geneva, Switzerland, 2019.
- ISO 6336-3:2019; Calculation of Load Capacity of Spur and Helical Gears—Part 3: Calculation of Tooth Bending Strength. International Organization for Standardization: Geneva, Switzerland, 2019.
- Huffman, P.J.; Beckman, S.P. A non-linear damage accumulation fatigue model for predicting strain life at variable amplitude loadings based on constant amplitude fatigue data. Int. J. Fatigue 2013, 48, 165–169. [Google Scholar] [CrossRef]
- Bai, B.; Zhang, J.; Wu, X.; Wei Zhu, G.; Li, X. Reliability prediction-based improved dynamic weight particle swarm optimization and back propagation neural network in engineering systems. Expert Syst. Appl. 2021, 177, 114952. [Google Scholar] [CrossRef]
- Shields, M.D.; Zhang, J. The generalization of Latin hypercube sampling. Reliab. Eng. Syst. Saf. 2016, 148, 96–108. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hou, P.; Hu, W.; Soltani, M.; Chen, Z. Optimized Placement of Wind Turbines in Large-Scale Offshore Wind Farm Using Particle Swarm Optimization Algorithm. IEEE Trans. Sustain. Energy 2015, 6, 1272–1282. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Q.; Zhou, A.; Gong, M.; Jiao, L. Adaptive Replacement Strategies for MOEA/D. IEEE Trans. Cybern. 2016, 46, 474–486. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Yan, X.; Wang, L. Optimizing job release and scheduling jointly in a reentrant hybrid flow shop. Expert Syst. Appl. 2022, 209, 118278. [Google Scholar] [CrossRef]
- ISO 1328-1:2013(E); Cylindrical Gears—ISO System of Flank Tolerance Classification—Part 1: Definitions and Allowable Values of Deviations Relevant to Flanks of Gear Teeth. International Organization for Standardization: Geneva, Switzerland, 2013.
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: San Francisco, CA, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).