Critical Permeability from Resummation

Abstract

Special calculation methods are presented for critical indices and amplitudes for the permeability of thin wavy channels dependent on the waviness. The effective permeability and wetted perimeter of the two-dimensional random percolating media are considered as well. A special mathematical framework is developed to characterize the dependencies on porosities, critical points, and indices. Various approximation techniques are applied without involving popular lubrication approximation in any sense. In particular, the Borel summation technique is applied to the effective polynomial approximations with or without optimization. Minimal difference and minimal derivative optimal conditions are adapted to calculations of critical indices and amplitudes for the effective permeability of thin wavy channels. Critical indices, amplitudes, and thresholds are obtained for the effective permeability and wetted perimeter of the two-dimensional percolating random media. Closed-form expressions for all porosities, critical points, and indices are calculated from the polynomial approximations for the first time.

1. Introduction

Let the function $\Phi \left(x\right)$ of a real variable $x\in \left[0,\infty \right)$ be defined as the solution to some physical problem. The positive variable $x>0$ can represent the porosity or concentration of particles. Let $\Phi \left(x\right)$ exhibit a critical behavior, as follows:

$$\Phi \left(x\right)\simeq A{(x_c-x)}^{\alpha },\mathrm{as}x\to x_c-0.$$

(1)

In Formula (1), $\alpha$ stands for a critical index and A denotes critical amplitude at a finite critical point $x_c$. Critical phenomena formalized by some power law in the form (1) (or (5)), are widespread [1,2,3,4], ranging from hydrodynamics to quantum field theory. It is both vital and challenging to explain related critical indices theoretically. Moreover, quite recently, it was documented that certain types of critical states, characterized by standard critical indices, persist in brain functioning [5]. The criticality in brain activity could also be self-organized [6].

The index $\alpha$ could consist of negative or positive real numbers. The values of critical points may be known from some sources. The main problem consists of finding index $\alpha$. By solving the problem of the index, one can approach the problem of finding the amplitude, A. When required, we also have to calculate the positions of critical points, $x_c$.

In many cases, it is possible to develop some kind of perturbation theory for the sought-after quantity, $\Phi \left(x\right)$. For a smooth function, $\Phi \left(x\right)$, the asymptotic power series [7,8], i.e.,

$$\Phi \left(x\right)\sim \sum _{n=0}^{\infty }{c}_n{x}^n,$$

(2)

can be found after laborious analytical, numerical, and symbolic computations [9,10]. To make the problem even more difficult, typically, one can obtain only a few terms from expansion (2) at small variables, as follows:

$$\Phi \left(x\right)\simeq {\Phi }_k\left(x\right),\mathrm{as}x\to 0,$$

(3)

where

$${\Phi }_k\left(x\right)=1+\sum _{n=1}^k{c}_n{x}^n.$$

(4)

In order to extrapolate expansion (4) outside of the region of numerical convergence, we construct some analytical expressions, the so-called approximants. The approximants are asymptotically equivalent to the truncated series (4). The approximants generate an additional infinite number of coefficients, approximating unknown exact coefficients. By means of proper approximants, one can also construct an interpolation formula that includes both limits of (1) and (4).

We outline below the main tenets of the optimal summations to be used in the current paper following a recent paper, Ref. [11]. In order to find proper approximants and optimizations for the most difficult problem of extrapolation, we suggest going through the following steps:

Firstly, the initial truncated series is to be transformed and a new transformed truncated series is to be considered. We believe that the new series is more amenable to resummation than the original. Already at this stage, some free parameters could be introduced, aimed at controlling convergence at the final stage.

Secondly, to the transformed series, we apply some proper approximants. The approximants are expected to be defined naturally for any k. In addition, the approximants should possess a power law behavior in the region of interest. The approximants should also be transparent enough to allow for some analytical approach to optimization at the last stage.

Thirdly, the application of self-similarity with accompanying dynamic equations formulated in the space of approximations leads to self-similar iterated root approximants [11]. Compact expressions for the critical amplitudes can be found. By solving the problem of critical amplitudes, one also solves the problem of critical indices with a $DLog$ transformation formally setting an auxiliary index to $-1$.

Fourthly, the final critical amplitude formulae can be factored in. There are two explicitly written multipliers arising from the approximants and the inverse transformation. Therefore, it could be treated analytically.

Fifthly, in order to find concrete values of the control parameters introduced in the first stage, additional conditions could be imposed. We employ the optimization conditions with respect to the critical amplitude. One can consider two equivalent optimization conditions: the minimal difference condition and the minimal derivative condition. Satisfying both conditions separately, we find several solutions for the control parameters. These optimization conditions are considered equivalent and treated together by calculating the average and variance of all solutions with equal weight.

The Padé approximants, $P_{n,m}$, are simply the ratio of two polynomials, $P_n\left(x\right)$ and $Q_m\left(x\right)$, of orders n and m, respectively [12,13,14,15]. The poles of Padé approximants provide the position of a critical point $x_c$. Extrapolating to infinity using standard Padé approximants invariably yields an integer number. However, solutions to many problems exhibit irrational functional behaviors. Such behaviors cannot be properly described by the standard rational Padé approximants. To overcome the problem and produce the irrational $\alpha$, one can turn to the different approximants, such as roots, factors, iterated roots, corrected Padé, additive, $DLog$-additive, etc. [9,10].

In another situation when a function at $x\to \infty$ behaves as a power law, i.e.,

$$\Phi \left(x\right)\simeq A{x}^{\alpha },$$

(5)

the index $\alpha$ is represented formally by the following limit:

$$\alpha =\underset{x\to \infty }{lim}x\psi \left(x\right),$$

(6)

where

$$\psi \left(x\right)={\partial }_{x}log\left(\Phi \left(x\right)\right),$$

(7)

is the $DLog$ transformation of the original $\Phi \left(x\right)$. The small-variable expansion of the function $\psi \left(x\right)$ can be found from the original expansion for $\Phi \left(x\right)$. It can be resumed by means of some approximants. Only the non-diagonal $P_{n,n+1}\left(x\right)$ approximants give the finite critical index $\alpha$.

Instead of Padé, one can use different approximants, such as iterated roots behaving as $x^{-1}$ as $x\to \infty$ [9,10]. It is worthwhile to stress that the critical index in the $DLog$ formulation appears as the amplitude in the asymptotic behavior of the $DLog$ transform. Thus, if we can master the calculation of the critical amplitudes, the same or similar method can be transferred directly or with minor modifications to the calculation of the critical indices.

If the value of the threshold is known in advance but the index is unknown, we can reuse the very same formulas for the case of asymptotic behavior (5). One can apply the following transformation:

$$y={\displaystyle \frac{x}{x_c-x}}\iff x={\displaystyle \frac{y{x}_c}{y+1}},$$

(8)

to the original expansions (3) and (4).

In a recent paper [11], multiple examples were presented and various methods were applied to the critical amplitude calculations. But the central problem of finding critical indices from truncated expansions (4) was not addressed. In the current paper, we fill this gap by calculating critical indices for several examples. We also explain and apply several methods for critical index calculations.

Thus, we apply the different methods for critical index calculations to several problems involving rather long truncations for the effective permeability and wetted perimeter. The examples deserve consideration due to their merit. Some of them are difficult for various Padé techniques and require extra optimization efforts.

The first group of problems consists of calculating the critical indices for the effective permeability of Darcy flow in thin wavy channels. Various approximation techniques, such as $DLog$ Padé, Borel summation, optimization, optimal iterated roots, etc., will be applied depending on the context.

For the second group of problems, which includes studying the effective permeability and wetted perimeter of two-dimensional random media as functions of porosity, we will apply different methods to calculate critical indices for both permeability and the wetted perimeter. We also calculate the threshold by means of the Padé approximants and explore closed-form expressions for arbitrary porosities.

We employ two distinct approaches to optimize critical amplitudes for calculating the critical indices. In the optimization technique employed in Section 2.2, the critical index by itself plays the role of the control parameter. In the optimization technique considered in Section 2.4, the control of convergence is achieved by finding an optimal number of iterations for the Borel transformation [11,16].

2. Permeability of Thin Wavy Channels

The flow of a viscous fluid through a channel is described by Darcy’s law [17]. Darcy’s law describes a linear relation. It connects the pressure gradient and the average component of the velocity along the pressure gradient [17]. The proportionality coefficient in Darcy’s law stands for permeability K.

The classical Poiseuille flow unfolds in channels according to Darcy’s law. The channel is bounded by two parallel planes separated by a distance, $2b$. The flow is generated by an average pressure gradient. The velocity profile is parabolic for small Reynolds numbers. When the channel is wavy and Reynolds numbers are not small, some additional terms appear in the Darcy relation.

The formally small non-dimensional “waviness” parameter $ϵ\ge 0$ quantifies the geometric perturbations around the flow inside a straight channel. The Poiseuille flow is considered the zero approximation [18]; around this, a perturbation theory in the waviness parameter $ϵ$ has been developed [19]. Rather long and numerically accurate expansions for permeability in Stokes flow through a wavy channel have been established in [19]. The cases of two-dimensional and three-dimensional wavy walls were considered.

The flow of a viscous fluid through a channel is considered for small Reynolds numbers. The fluid flow is governed by the Stokes equations. The solution for the velocity is found from the Stokes equations. It is sought within the class of periodic functions [19].

The primary quantity of interest is permeability $K=K\left(ϵ\right)$. It is defined as the ratio of the dimensional permeability and permeability of the Poiseuille flow in the channel bounded by two parallel planes under a pressure gradient. For the Poiseuille flow, permeability degenerates to a single parabolic term, which is simply equal to the following: ${\displaystyle \frac{b^2}{3}}$.

The formulae developed in Ref. [19] determine the coefficients of a truncated Taylor series expansion for permeability, resulting in a Taylor polynomial of the order k, in a form analogous to expansion (4). The Taylor truncated series is divergent for larger $ϵ$.

For larger $ϵ$, the so-called lubrication approximation is considered. The lubrication approximation of Ref. [17] is motivated by the case of two cylinders of different radii. The flow is studied when the cylinders are almost in contact with one another. For equal radii of cylinders, the flow rate is proportional to the pressure variation. The permeability $K_l$ emerges as the coefficient of proportionality in the formula, which links the flow rate and pressure variation. $K_l$ could be expressed through the gap between the cylinders. In turn, the gap is expressed through b and $ϵ$. As $ϵ\to {ϵ}_c=1$, the power law (10) emerges [17].

2.1. Symmetric Sinusoidal Two-Dimensional Channel

The flow within the bounded two-dimensional wavy channel with upper and lower walls, which can touch and fully block the flow, is modeled analytically by some adequate formulas studied in Ref. [19]. The expansion for permeability can be found in Ref. [19] as the function of power of the “waviness” parameter $ϵ$, as follows:

$$\begin{array}{ccc}{K}_{30}\left(ϵ\right)=\hfill & \hfill & \\ 1-3.14963{ϵ}^2+4.08109{ϵ}^4-3.48479{ϵ}^6+2.93797{ϵ}^8-2.56771{ϵ}^{10}+\hfill \\ 2.21983{ϵ}^{12}-1.93018{ϵ}^{14}+1.67294{ϵ}^{16}-1.45302{ϵ}^{18}+1.26017{ϵ}^{20}-\hfill \\ 1.09411{ϵ}^{22}+0.949113{ϵ}^{24}-0.823912{ϵ}^{26}+0.714804{ϵ}^{28}-0.620463{ϵ}^{30}\hfill \\ +O\left({ϵ}^{32}\right),\hfill \end{array}$$

(9)

for $b=0.5$.

For larger $ϵ$, a lubrication approximation $K_l$ for the permeability, i.e.,

$$K_l\simeq {\displaystyle \frac{8\sqrt{2}{b}^2}{9\pi }}\times {(1-ϵ)}^{5/2},ϵ\to {ϵ}_c=1,$$

(10)

was considered in [17]. For comparison with general expression (1), one can easily identify the values of the critical index, amplitude, and threshold. However, the lubrication approximation does fail quantitatively as explained in [10,17,19]. The main reason for that is that the velocity is assumed to have a parabolic profile.

We completely avoid any lubrication approximation below. However, the emergence of expression (9) and power law (10) suggest the potential for the widespread application of ideas and methods from the theory of critical phenomena [9] to the problems of hydrodynamics in wavy channels [10]. Various resummation techniques allow us to enter the critical region based on the information extracted from expansion (9) and avoid lubrication approximation altogether.

Let us calculate the index and amplitude for the critical behavior written in general form, as follows:

$$K\left(ϵ\right)\simeq A{({ϵ}_c-ϵ)}^{\varkappa },\mathrm{as}ϵ\to {ϵ}_c-0.$$

(11)

Here, we consider the case with the unknown index and amplitude. But the threshold is known and ${ϵ}_c=1$.

Let us first apply the transformation of the type of (8), modified slightly to the following form, i.e.,

$$y={\displaystyle \frac{{ϵ}^2}{1-{ϵ}^2}}\iff {ϵ}^2={\displaystyle \frac{y}{y+1}},$$

(12)

to the truncation (9) and find the new, transformed expansion $M_1\left(y\right)$. Such a truncated series, after undergoing a $DLog$ transformation, is transformed into another series $M\left(y\right)$. From the latter series, one can finally obtain the sought-after critical index in the form of a sequence of approximate values, as follows:

$${\varkappa }_n=-\underset{y\to \infty }{lim}\left(yPadeApproximant[M\left[y\right],n,n+1]\right),$$

(13)

with $n=0,1\dots k-1$. where $n=0,1\dots ,n_{max}$ is a non-negative integer. In the case of an odd k, ${(2n+1)}_{max}=k$. When k is even, ${(2n+1)}_{max}=k-1$.

The approximations for the critical index generated by the sequence of Padé approximants by means of Formula (13) are shown as follows:

$${\varkappa }_1=2.49873,{\varkappa }_2=2.49676,{\varkappa }_3=2.49941,{\varkappa }_4=2.4977,$$

$${\varkappa }_5=2.49769,{\varkappa }_6=2.49827.$$

The sequence points to the value of $5/2$ for the sought-after critical index. The results agree with estimates from the optimization technique that will be presented later. The procedure shows very fast numerical convergence. Even the appearance of defects—or closely positioned poles and zeros—in the Padé approximants, does not significantly influence accuracy [14].

In place of the Padé approximation, we can apply the so-called iterated roots [10]:

$${\mathcal{R}}_n^{\ast }\left(y\right)={\left({\left({\left({(1+{\mathcal{B}}_{1}y)}^2+{\mathcal{B}}_2{y}^2\right)}^{3/2}+{\mathcal{B}}_3{y}^3\right)}^{4/3}+\dots +{\mathcal{B}}_k{y}^k\right)}^{\alpha /k}.$$

Of course, only the approximants with auxiliary $\alpha =-1/k,$ behaving as $y^{-1}$ as $y\to \infty$, are relevant [10]. The parameters ${\mathcal{B}}_j$ will be found from asymptotic equivalence with relevant truncation. A general type, known as the self-similar root approximant [20], has a more general form and can be useful for calculating the correction-to-scaling indices [10].

For the critical index, we simply have a formula analogous to Formula (13), i.e.,

$${\varkappa }_n=-\underset{y\to \infty }{lim}\left(y{\mathcal{R}}_n^{\ast }\left(y\right)\right),$$

(14)

for $n=1,2\dots k-1$. The sought-after index at infinity simply follows from the latter formula with iterated roots calculated for the very same $M\left(y\right)$. Thus, from Formula (14), we calculate the following:

$${\varkappa }_1=2.18445,{\varkappa }_2=2.49515,{\varkappa }_3=2.52705,{\varkappa }_4=2.49609,$$

$${\varkappa }_5=2.48791,{\varkappa }_6=2.49851,{\varkappa }_7=2.50319,{\varkappa }_8=2.49995,$$

$${\varkappa }_9=2.49793,{\varkappa }_{10}=2.49947,{\varkappa }_{11}=2.50099.$$

The last number in the sequence agrees well with calculations of $\varkappa$ performed in [10].

Consider the channel bounded by the wavy surfaces with the parameter, $b=0.25$ [19], so that the Taylor expansion for permeability is given as follows:

$$\begin{array}{c}K\left(ϵ\right)=\hfill \\ 1-3.03748{ϵ}^2+3.54570{ϵ}^4-2.33505{ϵ}^6+1.35447{ϵ}^8-0.83303{ϵ}^{10}\hfill \\ +0.49762{ϵ}^{12}-0.30350{ϵ}^{14}+0.18185{ϵ}^{16}-0.11083{ϵ}^{18}+0.06636{ϵ}^{20}\hfill \\ -0.04051{ϵ}^{22}+0.02419{ϵ}^{24}-0.01483{ϵ}^{26}+0.00880{ϵ}^{28}-0.00544{ϵ}^{30}+\hfill \\ O\left({ϵ}^{32}\right).\hfill \end{array}$$

(15)

Applying Formula (13), we found the following estimates:

$${\varkappa }_1=2.49996,{\varkappa }_2=2.49994,{\varkappa }_3=2.50077,{\varkappa }_4=2.50074,$$

$${\varkappa }_5=2.50457,{\varkappa }_6=2.50016.$$

The procedure shows very fast numerical convergence. Even the appearance of defects—or closely positioned poles and zeros—in the Padé approximants does not significantly influence accuracy [14].

Alternatively, one can apply iterated roots and Formula (14) with the following results:

$${\varkappa }_1=2.34165,{\varkappa }_2=2.50182,{\varkappa }_3=2.50587,{\varkappa }_4=2.49962,$$

$${\varkappa }_5=2.49925,{\varkappa }_6=2.50033,{\varkappa }_7=2.50056,{\varkappa }_8=2.50051,$$

$${\varkappa }_9=2.50057,{\varkappa }_{10}=2.5007,{\varkappa }_{11}=2.50084.$$

The last number in the sequence agrees well with calculations of $\varkappa$ performed in [10].

2.2. Critical Index as the Optimization Parameter

Let us consider the case involving two-dimensional channels explained in Section 2.1. Permeability, in this case, behaves critically as expressed by Formula (11). By changing the variables according to (12), one can move the critical point “under the carpet” and deal with the power law in the form of (5). In the present paper, we analyze the numerical convergence of root approximants in high orders, up to the 20th order inclusively. We consider the two cases of permeability $K\left(ϵ\right)$, with the truncations (9) and (15), already employed above in Section 2.1.

The root approximants expressed in general form were derived rigorously in Ref. [20]. However, from a technical standpoint, it is difficult to explicitly find all the control parameters. Some simplified approximants of the same kind—but with fewer parameters—could be more convenient for optimization procedures. Concretely, we construct the iterated root approximants [9], as follows:

$${\mathcal{R}}_k^{\ast }(y,\alpha )={\left({\left({\left({(1+{\mathcal{B}}_{1}y)}^2+{\mathcal{B}}_2{y}^2\right)}^{3/2}+{\mathcal{B}}_3{y}^3\right)}^{4/3}+\dots +{\mathcal{B}}_k{y}^k\right)}^{\alpha /k}.$$

(16)

The internal amplitudes ${\mathcal{B}}_j={\mathcal{B}}_j\left(\alpha \right)$ depend on the sought-after critical index. They can be explicitly obtained from their asymptotic equivalence with the expansions, while $\alpha$ is found from the optimal conditions. The approximate expression for the permeability shows the desirable power-law asymptotic forms, i.e.,

$${\mathcal{R}}_k^{\ast }(y,\alpha )\simeq A_k{y}^{{\alpha }_k},asy\to \infty .$$

(17)

as well as critical amplitudes, i.e.,

$$A_k={\left({\left({({\mathcal{B}}_1^2+{\mathcal{B}}_2)}^{3/2}+{\mathcal{B}}_3\right)}^{4/3}+\dots +{\mathcal{B}}_k\right)}^{{\alpha }_k/k},$$

(18)

These are expressed explicitly as a function of the approximate ${\alpha }_k$. To define the approximate critical index ${\alpha }_k$, we analyze the optimization conditions as follows:

$${\Delta }_{kn}=0,$$

(19)

with ${\Delta }_{kn}\left({\alpha }_k\right)=A_k\left({\alpha }_k\right)-A_n\left({\alpha }_k\right)$. When the optimization problem is solved, we arrive at the optimal iterated roots with the optimal $\alpha$. The results for the two most natural sequences in the case of $b={\displaystyle \frac{1}{2}}$ are shown in

Table 1. The walls of the channel can touch (expansion (9)). Critical indices for the permeability ${\varkappa }_k$ are obtained from the optimization conditions (19).

${\mathit{\varkappa }}_{\mathit{k}}$	${\mathbf{\Delta }}_{\mathit{k}\mathbf{,}\mathit{k}\mathbf{+}\mathbf{1}}\mathbf{\left(}{\mathit{\varkappa }}_{\mathit{k}}\mathbf{\right)}\mathbf{=}\mathbf{0}$	${\mathbf{\Delta }}_{\mathit{k}\mathbf{10}}\mathbf{\left(}{\mathit{\varkappa }}_{\mathit{k}}\mathbf{\right)}\mathbf{=}\mathbf{0}$
${\varkappa }_1$	2.18445	2.40709
${\varkappa }_2$	2.68311	2.517
${\varkappa }_3$	2.48138	2.49348
${\varkappa }_4$	2.49096	2.49759
${\varkappa }_5$	2.5012	2.49976
${\varkappa }_6$	2.49935	2.49928
${\varkappa }_7$	2.49861	2.49925
${\varkappa }_8$	2.49949	2.49963
${\varkappa }_9$	2.49978	2.49978

. In the case of $b={\displaystyle \frac{1}{4}}$, similar results are presented in

Table 2. Walls of the channel can touch (expansion (15)). Critical indices ${\varkappa }_k$ are found in the optimization conditions (19).

${\mathit{\varkappa }}_{\mathit{k}}$	${\mathbf{\Delta }}_{\mathit{k}\mathbf{,}\mathit{k}\mathbf{+}\mathbf{1}}\mathbf{\left(}{\mathit{\varkappa }}_{\mathit{k}}\mathbf{\right)}\mathbf{=}\mathbf{0}$	${\mathbf{\Delta }}_{\mathit{k}\mathbf{10}}\mathbf{\left(}{\mathit{\varkappa }}_{\mathit{k}}\mathbf{\right)}\mathbf{=}\mathbf{0}$
${\varkappa }_1$	2.34165	2.4571
${\varkappa }_2$	2.52463	2.50468
${\varkappa }_3$	2.4976	2.49957
${\varkappa }_4$	2.49941	2.50017
${\varkappa }_5$	2.50028	2.5004
${\varkappa }_6$	2.50032	2.50044
${\varkappa }_7$	2.50041	2.5005
${\varkappa }_8$	2.50051	2.50055
${\varkappa }_9$	2.5006	2.5006

.

The $DLog$ Padé and iterated root methods discussed above bring convergent sequences for the permeability index $\varkappa$ as well. With $\varkappa =5/2$, we calculate amplitude A by means of odd and even Padé and odd and even Padé–Borel techniques [21]. The four methods produce very close results for A in the range from $3.77$ (even Padé–Borel) to $3.773$ (odd Padé).

Our current estimates of the critical indices and amplitudes support the conclusions on their values made in Ref. [10]. The optimization technique employed earlier in this section is rather unique. The critical index is interpreted as a control parameter [1,10], beyond its conventional role of quantifying an asymptotic power law. Advantageously, no other artificial control parameters are required. Yet, a different way to introduce controls that can be considered as “natural” is explored below in Section 2.4.

The closed-form expressions for the permeability of wavy channels for arbitrary $ϵ$ were derived [10]. Moreover, the case of a symmetric sinusoidal three-dimensional channel was discussed in [10], and a novel sub-critical index for the permeability was calculated.

2.3. Parallel Sinusoidal Two-Dimensional Channel

Consider the case when the walls forming the channel cannot touch, ensuring that the channel is bounded by surfaces with simple expressions given explicitly in [10,19]. The permeability of Darcy’s flow undergoes only a non-critical transition [20]. It decays according to a power law as $ϵ$ becomes large. Our primary interest here is to find the characteristics of this asymptotic power law, expressed in the form of (5).

The following truncation for the permeability was calculated up to $O\left({ϵ}^{32}\right)$, as follows:

$$\begin{array}{c}{K}_{30}\left(ϵ\right)=\hfill \\ 1-2.53686\times {10}^{-1}{ϵ}^2+4.28907\times {10}^{-2}{ϵ}^4-5.46188\times {10}^{-3}{ϵ}^6\hfill \\ +4.54695\times {10}^{-4}{ϵ}^8+9.0656\times {10}^{-6}{ϵ}^{10}-1.41572\times {10}^{-5}{ϵ}^{12}+3.76584\times {10}^{-6}{ϵ}^{14}\hfill \\ -6.72021\times {10}^{-7}{ϵ}^{16}+7.58331\times {10}^{-8}{ϵ}^{18}+2.34495\times {10}^{-9}{ϵ}^{20}-4.59993\times {10}^{-9}{ϵ}^{22}\hfill \\ +1.88446\times {10}^{-9}{ϵ}^{24}-8.6005\times {10}^{-11}{ϵ}^{26}+3.34156\times {10}^{-9}{ϵ}^{28}+1.63748\times {10}^{-9}{ϵ}^{30}.\hfill \end{array}$$

(20)

In order to extrapolate $K\left(ϵ\right)$ for each relevant $ϵ$, one can apply the Padé approximation to the polynomial (20). For this purpose, the Padé approximant $K_{10,20}\left(ϵ\right)$ was advanced in [19]. It behaves as $K_{10,20}\left(ϵ\right)\sim {ϵ}^{-10}$, as $ϵ\to \infty$. Based on such results, we hypothesize that the permeability decays according to

$$K\left(ϵ\right)\simeq A{ϵ}^{\varkappa },$$

as $ϵ\to \infty$, with the critical index $\varkappa$ and amplitude A to be found from the expansion (20).

From the small-variable expansion (20), using the new variable $y={ϵ}^2$, and after the $DLog$ transformation, as explained in Section 1, we can find the effective critical exponent as follows:

$${\varkappa }_n=\underset{y\to \infty }{lim}\left(y{P}_{n,n+1}\left(y\right)\right).$$

(21)

The limit (21) can be computed, depending on the order n, so that

$${\varkappa }_1=-4.32262,{\varkappa }_2=-4.3622,{\varkappa }_3=-4.01855,$$

$${\varkappa }_4=-3.79527,{\varkappa }_5=-3.96512,{\varkappa }_6=-4.01319.$$

The procedure shows reasonable numerical convergence. However, the appearance of defects—or closely positioned poles and zeros—in the Padé approximants appears to slow down the convergence [14]. The last number in the sequence agrees well with calculations of $\varkappa$ performed in [10].

2.4. Critical Index from Optimal Borel Summation

In order to obtain control over the convergence of the estimates for the critical indices produced by the Borel-type summation, one can apply the iterative Borel summation [7]. It amounts to the following transformation, i.e.,

$$B_k(x,p)=\sum _{n=0}^k{\displaystyle \frac{a_n}{{\left(\Gamma (1+n)\right)}^p}}{x}^n,$$

(22)

of the original series, where p is the control parameter that generalizes a discrete number of iterations, with the subsequent inverse transformation [11,16]. The transformation (22) and corresponding inverse transformation can be performed analytically in the case of $x\to \infty$ [11,16]. The sought-after critical amplitude, i.e.,

$$A_k\left(p\right)=C_k\left(p\right){\left(\Gamma \left(1+\alpha \right)\right)}^p,$$

(23)

is given explicitly in analytical form [11,16], and it appears to be dependent on the control parameter, which could be found from additional optimal conditions. Here, the marginal amplitude $C_k\left(p\right)$ is given in the form analogous to (18).

The celebrated Borel summation method [22,23] follows from the above formulas as $p=1$. The inverse Borel transformation:

$${\Phi }_k^{\ast }\left(x\right)={\int }_0^{\infty }{e}^{-t}{B}_k^{\ast }(tx,1)dt,$$

(24)

and the calculation of $B^{\ast }$ can be made concrete with iterated roots given in the form analogous to (16) and applied to the transformed $B_k(x,1)$. There are multiple works employing different versions of the Borel summation and alike, such as [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40], but none of them allow for straightforward analytical calculations in the critical regime.

Most significantly, the resultant (24) reduces to the power law, as follows:

$${\Phi }_k^{\ast }\left(x\right)\simeq A_k{x}^{\alpha },$$

(25)

where $A_k=A_k\left(1\right)$ in the asymptotic regime $x\to \infty$. And the critical amplitude can be expressed analytically [11,16], as follows:

$$A_k=C_k\Gamma (1+\alpha ),$$

(26)

where $C_k=C_k\left(1\right)$.

The critical exponent can be expressed by the Formulas (6) and (7) as a $DLog$ function. Now, we would like to apply the Borel summation to ${\psi }_k\left(x\right)$, which behaves as $x^{-1}$ at a large x. And the amplitude in such an asymptotic formula is supposed to give the critical index. However, the relevant case of the critical index equal to $-1$ appears to be divergent, as can be seen from Formula (26) for amplitudes derived from the Borel summation.

In order to avoid the divergence of amplitudes, it is possible to consider an inverse of the $DLog$ function, $\psi {\left(x\right)}^{-1}$, which grows linearly on x at a large x with some proportionality coefficient $\gamma$. With such a behavior, there is no divergence in the formulas for critical amplitudes and the critical indices. After the Borel summation procedure is applied to $\gamma$, one can find the resumed ${\gamma }^{\ast }.$ Then, ${\displaystyle \frac{1}{{\gamma }^{\ast }}}\equiv {\alpha }^{\ast },$ where ${\alpha }^{\ast }$ gives the sought-after critical index $\alpha$.

Let us first examine the results obtained from the Borel summation method described above. After completing calculations for $p=1$, we arrive at the following sequence of the approximate values for the index $\varkappa$:

$${\varkappa }_1=-6.00767,{\varkappa }_2=-4.28957,{\varkappa }_3=-4.16382,{\varkappa }_4=-4.10622,$$

$${\varkappa }_5=-4.09231,{\varkappa }_6=-4.08109,{\varkappa }_7=-4.07667,{\varkappa }_8=-4.06716,$$

$${\varkappa }_9=-4.0557,{\varkappa }_{10}=-4.03978,{\varkappa }_{11}=-4.02216.$$

The Borel summation presented above is non-parametric and the accuracy can be controlled only through the addition of more terms to the expansion. Such an accuracy-through-order approach is very costly. Moreover, very often, only a few terms are available.

Let us now proceed with the realization of a scheme with control. To this end, we introduce the following differences:

$${\Delta }_{k,k+1}\left(p\right)=A_{k+1}\left(p\right)-A_k\left(p\right).$$

(27)

The control parameters, $p_k$, can be found from the following minimal difference conditions:

$$\mid {\Delta }_{k,k+1}\left(p_k\right)\mid ={\min }_p\mid {\Delta }_{k,k+1}\left(p\right)\mid ,$$

(28)

with $k=1,2,3,\dots$ Most often, but not always, the control parameter is found from the following condition:

$$A_{k+1}\left(p\right)-A_k\left(p\right)=0.$$

(29)

For instance, in the 11-th order of perturbation theory, we arrive at the following equation:

$$\mid {\Delta }_{10,11}\left(p_k\right)\mid ={\min }_p\mid {\Delta }_{10,11}\left(p\right)\mid ,$$

(30)

where the difference, i.e., ${\Delta }_{10,11}=A_{11}\left(p_{10}\right)-A_{10}\left(p_{10}\right)$ can be expressed analytically.

Equation (30) possesses three close solutions, i.e.,

$$p^{\left(1\right)}=0.7077650163419956,$$

$$p^{\left(2\right)}=1.268482421995318,$$

$$p^{\left(3\right)}=1.5015134416931766,$$

which are not very different from unity, so that one can also find three close estimates for the index:

$${\displaystyle \frac{{\varkappa }_{11}^{\left(1\right)}}{2}}=1/A_{11}\left(p^{\left(1\right)}\right)=-1.99152,$$

$${\displaystyle \frac{{\varkappa }_{11}^{\left(2\right)}}{2}}=1/A_{11}\left(p^{\left(2\right)}\right)=-2.01917,$$

$${\displaystyle \frac{{\varkappa }_{11}^{\left(3\right)}}{2}}=1/A_{11}\left(p^{\left(3\right)}\right)=-2.0003.$$

Their average gives ${\varkappa }^{\ast }=-4.007\pm 0.023$ as the estimate for the critical index $\varkappa$.

One can also find the control parameter, p, from the minimal derivative condition, by finding ${\min }_p\mid {\displaystyle \frac{d{A}_k\left(p\right)}{dp}}\mid$. Or, we can simply require the following:

$${\displaystyle \frac{d{A}_k\left(p\right)}{dp}}=0.$$

(31)

The minimal differences and minimal derivative conditions are equivalent and should be treated together without giving a priori preference to any of them. From Equation (31), with $k=11$, one finds the following three solutions:

$$p^{\left(4\right)}=0.7494099141198123,$$

$$p^{\left(5\right)}=1.1835142307326223,$$

$$p^{\left(6\right)}=1.870676961956001,$$

and

$${\displaystyle \frac{{\varkappa }_{11}^{\left(4\right)}}{2}}=1/A_{11}\left(p^{\left(4\right)}\right)=-1.99036,$$

$${\displaystyle \frac{{\varkappa }_{11}^{\left(5\right)}}{2}}=1/A_{11}\left(p^{\left(5\right)}\right)=-2.02132,$$

$${\displaystyle \frac{{\varkappa }_{11}^{\left(6\right)}}{2}}=1/A_{11}\left(p^{\left(7\right)}\right)=-1.98145.$$

By averaging all the solutions, we find ${\varkappa }^{\ast }=-4.001\pm 0.03.$

Also, the well-known Mittag–Leffler summation [23,40,41,42] could be applied to introduce control parameters into Borel transformations even when $p=1$. Optimal conditions employed in such a case are analogous to the Equations (28) and (31), and can be written by a simple change of notations. In our particular case, there is a single solution to the minimal-difference equation and three solutions to the minimal derivatives condition. By averaging all the solutions, we find ${\varkappa }^{\ast }=-3.997\pm 0.027.$

With the conjectured critical index $\varkappa =-4$, we can calculate the critical amplitude A directly, by means of odd and even Padé and odd and even Padé–Borel techniques [21]. The four methods produce the results for A in the range from $42.88$ (even Padé–Borel) to $43.22$ (even Padé).

With conjectured critical index $\varkappa =-4$, we can apply the same optimization techniques to calculate the amplitude A. The following optimal parameters,

$$p^{\left(1\right)}=0.5919588538453786,p^{\left(2\right)}=0.8669880637988079,p^{\left(3\right)}=0.8669880637988079,$$

are found from the minimal difference condition. The following estimates for the amplitudes (after inversion) readily follow

$$A^{\left(1\right)}={\displaystyle \frac{1}{A_{11}\left(p^{\left(1\right)}\right)}}=43.0971,A^{\left(2\right)}={\displaystyle \frac{1}{A_{11}\left(p^{\left(2\right)}\right)}}=42.8136,A^{\left(3\right)}={\displaystyle \frac{1}{A_{11}\left(p^{\left(3\right)}\right)}}=44.8234.$$

The following optimal parameters

$$p^{\left(4\right)}=0.5179511020261915,p^{\left(5\right)}=1.2560338100049357,$$

are found from the minimal derivative condition. The following estimates readily follow

$$A^{\left(4\right)}={\displaystyle \frac{1}{A_{11}\left(p^{\left(4\right)}\right)}}=43.1165,A^{\left(5\right)}={\displaystyle \frac{1}{A_{11}\left(p^{\left(5\right)}\right)}}=42.5459.$$

By averaging all the solutions, we find for the critical amplitude, A, the following estimate, $A^{\ast }=43.2793\pm 0.7999.$

With the conjectured critical index, we can also calculate the critical amplitude by means of odd and even Padé and odd and even Padé–Borel techniques [21]. The four methods produce the results for A in the range from $42.88$ (even Padé–Borel) to $43.22$ (even Padé), corresponding with the results from the optimization procedure.

3. Permeability and the Wetted Perimeter of Random Media

Adler numerically solved the Stokes hydrodynamic problem for a two-dimensional random medium generated by a site percolation [43]. Numerically, he found permeability $\mathcal{K}\left(\epsilon \right)$ and the wetted perimeter $\mathcal{P}\left(\epsilon \right)$ of this porous medium dependent on porosity $\epsilon$.

Based on the expectations from the underlying site percolation problem, one can hypothesize that the two macroscopic quantities in the high-porosity limit behave critically, as follows:

$$\mathcal{K}\left(\epsilon \right)\sim {({\epsilon }_c-\epsilon )}^{\alpha },\mathrm{as}\epsilon \to {\epsilon }_c-0,$$

(32)

and

$$\mathcal{P}\left(\epsilon \right)\sim {({\epsilon }_c-\epsilon )}^{\beta },\mathrm{as}\epsilon \to {\epsilon }_c-0.$$

(33)

Also, one can expect that ${\epsilon }_c$ is nothing else but the threshold for site percolation, i.e., ${\epsilon }_c=1-0.4073=0.5927$ [44,45,46]. Below, we intend to evaluate the threshold, ${\epsilon }_c$, as well as the critical indices, $\alpha$, $\beta$, directly from the approximating polynomials of [43].

Indeed, for low and moderate porosities, the polynomial ${\mathcal{K}}_{26}$ in powers of porosity $\epsilon$ for the permeability $\mathcal{K}\left(\epsilon \right)$ of random two-dimensional percolating media was obtained in [43], as follows:

$$\begin{array}{c}{\mathcal{K}}_{26}\left(\epsilon \right)=\hfill \\ 0.034861\epsilon +0.088186{\epsilon }^2+0.086946{\epsilon }^3+0.207506{\epsilon }^4+0.162461{\epsilon }^5+0.21551{\epsilon }^6+\hfill \\ 0.21598{\epsilon }^7+0.35215{\epsilon }^8-9317.72{\epsilon }^9+97461.1{\epsilon }^{10}-484084{\epsilon }^{11}+1.50809\times {10}^6{\epsilon }^{12}-\hfill \\ 3.28782\times {10}^6{\epsilon }^{13}+5.30752\times {10}^6{\epsilon }^{14}-6.55349\times {10}^6{\epsilon }^{15}+6.30861\times {10}^6{\epsilon }^{16}-\hfill \\ 4.78387\times {10}^6{\epsilon }^{17}+2.86871\times {10}^6{\epsilon }^{18}-1.35795\times {10}^6{\epsilon }^{19}+\mathrm{503,701}{\epsilon }^{20}-\mathrm{144,403}{\epsilon }^{21}+\hfill \\ \mathrm{31,299.8}{\epsilon }^{22}-4957.39{\epsilon }^{23}+542.976{\epsilon }^{24}-37.1486{\epsilon }^{25}+1.2247{\epsilon }^{26};\hfill \end{array}$$

(34)

Diagonal Padé approximants [12,14] produce several sensible estimates for the critical point ${\epsilon }_c$ with the approximations ${\mathcal{K}}_{2,2}$, ${\mathcal{K}}_{3,3}$, ${\mathcal{K}}_{5,5}$, and ${\mathcal{K}}_{6,6}$. The lowest estimate, $0.63009$, is produced by ${\mathcal{K}}_{5,5}$, while the largest estimate, $0.644874$, is found from ${\mathcal{K}}_{2,2}$.

The Padé approximant for the following permeability is as follows:

$$\begin{array}{c}{\mathcal{K}}_{7,1}\left(\epsilon \right)={\displaystyle \frac{0.0830455\epsilon (0.656544-\epsilon )(\epsilon +0.427161)\left({\epsilon }^2-0.375392\epsilon +0.635935\right)\left({\epsilon }^2+0.969452\epsilon +1.44358\right)}{0.613318-\epsilon }},\hfill \end{array}$$

(35)

could be chosen because it provides the approximate threshold of $0.613318$, which is rather close to the numerically exact threshold for the site percolation [44,45,46].

Applying the method of $DLog$-Padé approximations [12,14], we obtain the following Padé approximant with qualitatively correct critical behavior:

$$\begin{array}{c}{k}_{4,5}\left(\epsilon \right)={\displaystyle \frac{0.506127(\epsilon -0.0340985)(\epsilon +0.979687)\left({\epsilon }^2+0.0321024\epsilon +0.000793327\right)}{(0.623605-\epsilon )(\epsilon -0.0340988)(\epsilon +0.314322)\left({\epsilon }^2+0.0321025\epsilon +0.000793322\right)}},\hfill \end{array}$$

(36)

which leads to the qualitatively correct critical behavior of the ensuing expression for the following permeability:

$$\mathcal{K}\left(\epsilon \right)=0.034861\epsilon exp\left({\int }_0^{\epsilon }{k}_{4,5}(\Omega )d\Omega \right).$$

(37)

The latter formula leads to the closed-form expression of the permeability, as follows:

$$\begin{array}{c}\mathcal{K}\left(\epsilon \right)={\displaystyle \frac{0.0351048\epsilon {(\epsilon +0.314322)}^{0.359046}{e}^{6.{66155757749385}^{-7}{tan}^{-1}(43.2063\epsilon +0.693515)}}{{(\epsilon (\epsilon +0.0321025)+0.000793322)}^{4.{076554101311368}^{-8}}{(0.623605-\epsilon )}^{0.865172}}},\hfill \end{array}$$

(38)

with a reasonable threshold value of $0.623605$. During the integration, we simply discarded the defect [12,14] appearing on the expression (36). Formula (38) is practically indistinguishable from the results of numerical integration in (37) with the complete expression (36). From Formula (38), one can deduce the power law (32) with the critical index $\alpha =-0.86517$. The divergent behavior of permeability was also implied in Adler’s paper [43].

The application of the optimization method explained in Section 2.2 gives slightly higher results, $\alpha =-1.05417$. The Borel summation of the 11th order gives a close result, $\alpha =-1.06017$. Optimization with respect to the parameter, p, as explained in Section 2.4, again gives a close result,

$$\alpha =-1.05897\pm 0.0039.$$

In the two-dimensional case, one would expect that $\alpha \approx 1.3$ based on the results of lattice percolation problems [47]. However, in the continuous percolation problems, the critical indices for conductivity can be lower [9], covering the whole spectrum from $1/2$ to $1.3$.

One can easily reconstruct the corresponding results for the iterated roots employed during the optimization process, as described in Section 2.2, e.g., at the 10th order, the behavior of the optimal iterated root

$$R_{10}^{\ast }\left(\epsilon \right)={\mathcal{B}}_{0}y\left(\epsilon \right){\left({\left({\left(1+{\mathcal{B}}_{1}y\left(\epsilon \right)\right)}^2+{\mathcal{B}}_{2}y{\left(\epsilon \right)}^2\right)}^{3/2}+\dots +{\mathcal{B}}_{10}y{\left(\epsilon \right)}^{10}\right)}^{a/10},$$

is deduced from Formulas (8) and (16), with the parameter $a=0.05417$, and the amplitudes

$${\mathcal{B}}_0=0.0206621,{\mathcal{B}}_1=9.21878,{\mathcal{B}}_2=38.9346,{\mathcal{B}}_3=443.469,$$

$${\mathcal{B}}_4=4787.57,{\mathcal{B}}_5=56779.2,{\mathcal{B}}_6=620514,{\mathcal{B}}_7=6.9263\ast {10}^6,$$

$${\mathcal{B}}_8=6.73286\ast {10}^7,{\mathcal{B}}_9=5.18816\ast {10}^8,{\mathcal{B}}_{10}=-0.212085.$$

Now, we find the sought-after critical index $\alpha =-(1+a)=-1.05417$.

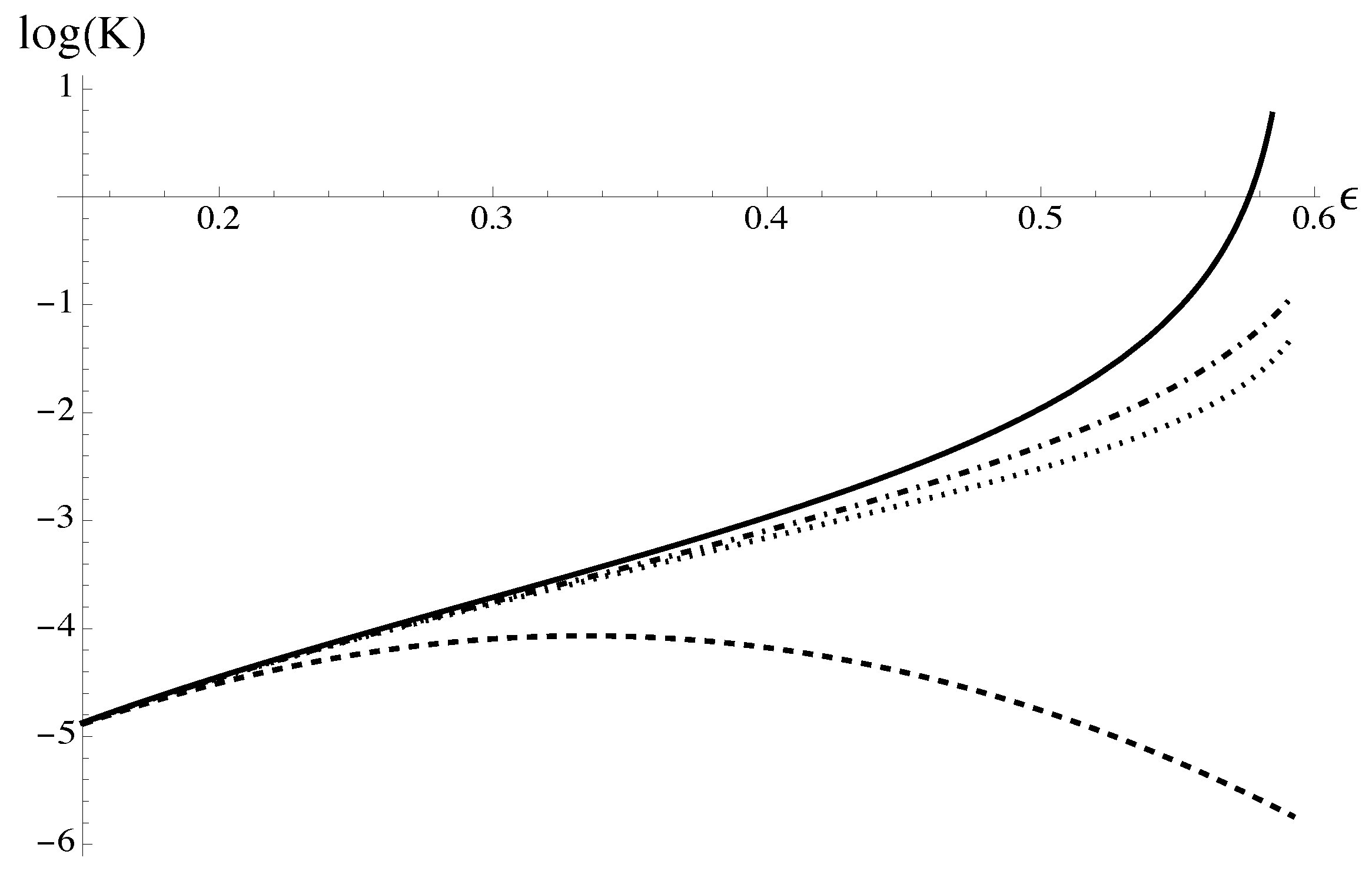
The formula for $R_{10}^{\ast }$ is illustrated in Figure 1. The Padé approximation (35) and $DLog$-Padé approximation (38) are shown in Figure 1, compared to the polynomial approximation (34).

For the wetted perimeter of random two-dimensional media, another approximating polynomial, ${\mathcal{P}}_{26}$, in powers of porosity was obtained in [43], as follows:

$$\begin{array}{c}{\mathcal{P}}_{26}\left(\epsilon \right)=\hfill \\ 4\epsilon -4{\epsilon }^2-\mathrm{189,720}{\epsilon }^9+\mathrm{2,069,112}{\epsilon }^{10}-\mathrm{10,640,008}{\epsilon }^{11}+\mathrm{34,174,868}{\epsilon }^{12}-\mathrm{76,610,308}{\epsilon }^{13}\hfill \\ +\mathrm{126,928,128}{\epsilon }^{14}-\mathrm{160,615,112}{\epsilon }^{15}+\mathrm{158,242,656}{\epsilon }^{16}-\mathrm{122,651,992}{\epsilon }^{17}+\mathrm{75,071,548}{\epsilon }^{18}-\hfill \\ \mathrm{36,216,312}{\epsilon }^{19}+\mathrm{13,668,504}{\epsilon }^{20}-\mathrm{3,980,704}{\epsilon }^{21}+\mathrm{875,292}{\epsilon }^{22}-\mathrm{140,496}{\epsilon }^{23}+\mathrm{15,588}{\epsilon }^{24}-\hfill \\ 1080{\epsilon }^{25}+36{\epsilon }^{26}.\hfill \end{array}$$

(39)

The two following approximants give the threshold values close to the threshold for site percolation, i.e.,

$$\begin{array}{c}{\mathcal{P}}_{13,8}\left(\epsilon \right)=7.27602\times {10}^{54}(0.594711-\epsilon )\times \hfill \\ {\displaystyle \frac{\epsilon (\epsilon +0.204917)\left({\epsilon }^2-1.16927\epsilon +0.371507\right)}{\left(2.93807\times {10}^{12}{\epsilon }^2-4.58365\times {10}^{11}\epsilon +1.95686\times {10}^{12}\right)\left(2.93807\times {10}^{12}{\epsilon }^2+1.79451\times {10}^{12}\epsilon +1.72157\times {10}^{12}\right)}}\times \hfill \\ {\displaystyle \frac{\left({\epsilon }^2-1.12637\epsilon +0.455706\right)\left({\epsilon }^2-0.245625\epsilon +0.0877446\right)\left({\epsilon }^2+0.126756\epsilon +0.0560204\right)\left({\epsilon }^2+0.339376\epsilon +0.0449487\right)}{\left(2.93807\times {10}^{12}{\epsilon }^2+3.34602\times {10}^{12}\epsilon +1.59693\times {10}^{12}\right)\left(2.93807\times {10}^{12}{\epsilon }^2+4.14558\times {10}^{12}\epsilon +1.54129\times {10}^{12}\right)}},\hfill \end{array}$$

(40)

with the threshold at $0.594711$. And

$$\begin{array}{c}{\mathcal{P}}_{9,11}\left(\epsilon \right)=4.{378332}^{-38}(0.596454-\epsilon )\times \hfill \\ {\displaystyle \frac{\epsilon (\epsilon +0.204841)\left(3.52328\times {10}^{12}{\epsilon }^2-8.61385\times {10}^{11}\epsilon +3.08931\times {10}^{11}\right)}{(\epsilon +0.304116)\left({\epsilon }^2-0.584636\epsilon +0.232772\right)}}\times \hfill \\ {\displaystyle \frac{\left(3.52328\times {10}^{12}{\epsilon }^2+4.45417\times {10}^{11}\epsilon +1.97294\times {10}^{11}\right)\left(3.52328\times {10}^{12}{\epsilon }^2+1.19636\times {10}^{12}\epsilon +1.58475\times {10}^{11}\right)}{\left({\epsilon }^2-0.14438\epsilon +0.152743\right)\left({\epsilon }^2+0.179688\epsilon +0.120501\right)\left({\epsilon }^2+0.417562\epsilon +0.10402\right)\left({\epsilon }^2+0.561096\epsilon +0.0953101\right)}},\hfill \end{array}$$

(41)

with the threshold at $0.596454$.

Many Padé approximants, such as ${\mathcal{P}}_{11,10}$, ${\mathcal{P}}_{11,11}$, ${\mathcal{P}}_{9,12}$, ${\mathcal{P}}_{15,6}$, ${\mathcal{P}}_{15,7}$, ${\mathcal{P}}_{17,5}$, and ${\mathcal{P}}_{19,3}$ all produce rather good results for the threshold. The lower bound, $0.586438$, comes from ${\mathcal{P}}_{15,6}$, while the upper bound, $0.62884$, is from ${\mathcal{P}}_{11,11}$. Note that, in the case of the wetted perimeter, we resorted to studying the whole table of the Padé approximants, not only of the diagonal sequences as is typically recommended [12,14]. Although the diagonal sequence turned out to not be informative, we managed to find a grouping of approximants with close thresholds for the number of terms $k=20,21,22$.

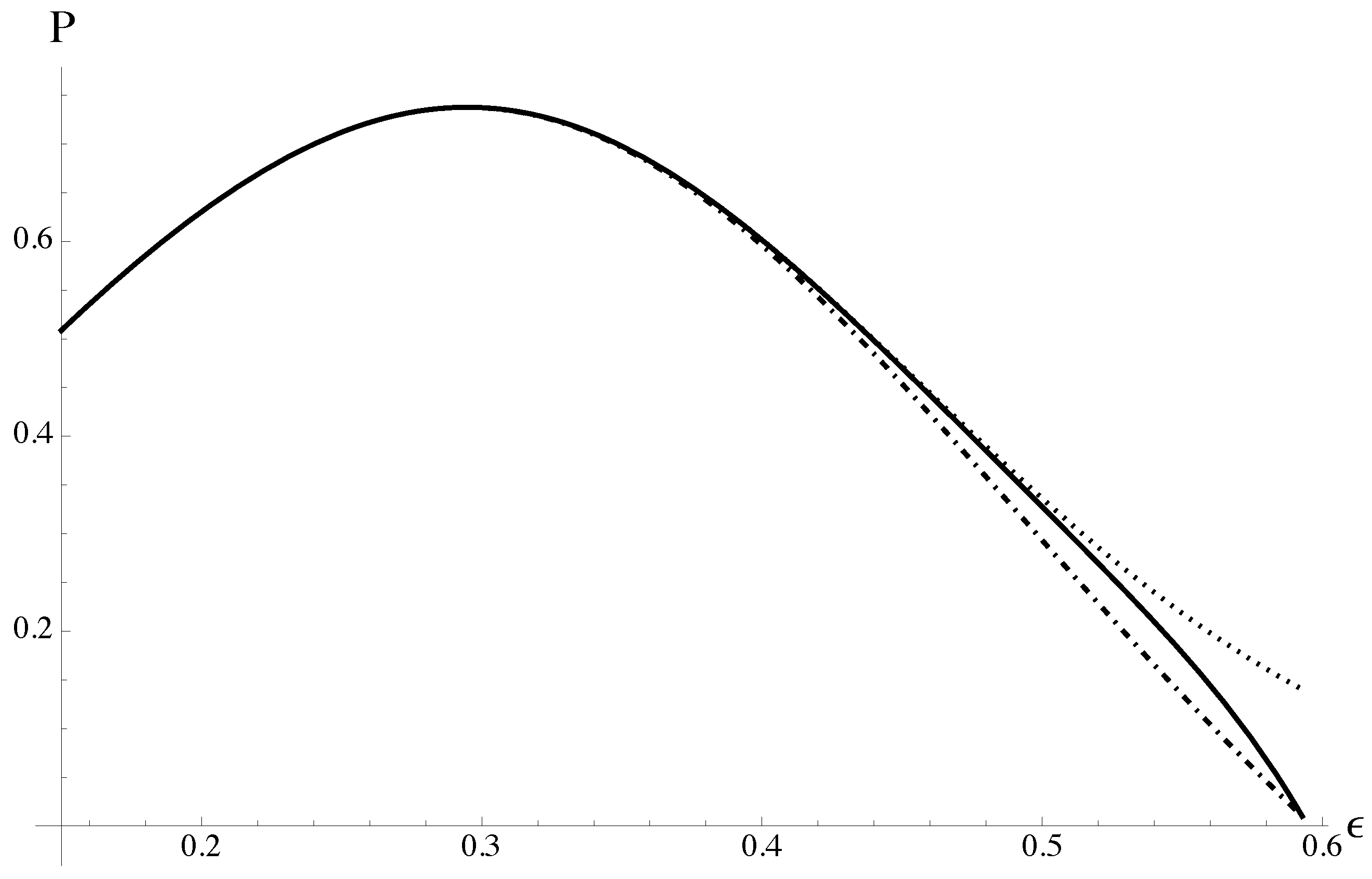
In Figure 2, the Padé approximants (40) and (41) are shown and compared with the polynomial approximation (39). The approximant (40) agrees with the polynomial up to $\epsilon <0.5$, in accordance with expectations of [43].

After the $DLog$ transformation and in the variables analogous to (8), we arrive at the relevant Padé approximant, as follows:

$$\begin{array}{c}{p}_{9,10}\left(z\right)=-1.29505{\displaystyle \frac{(z+0.194875)}{(z+0.256911)}}\times \hfill \\ {\displaystyle \frac{\left(z^2-0.33957z+0.270362\right)\left(z^2+0.196832z+0.0759378\right)\left(z^2+0.350562z+0.0444925\right)\left(z^2+11.7475z+69.3493\right)}{(z+0.987107)(z+2.16222)(z+7.00743)\left(z^2+0.101906z+0.299004\right)\left(z^2+0.387962z+0.116118\right)\left(z^2+0.487195z+0.0752418\right)}},\hfill \end{array}$$

(42)

where $z=z\left(\epsilon \right)={\displaystyle \frac{\epsilon }{{\epsilon }_c-\epsilon }}$, and  ${\epsilon }_c=0.5927$. The former expression leads to the formula for the wetted perimeter, as follows:

$$\mathcal{P}\left(\epsilon \right)=2.3708z\left(\epsilon \right)exp\left({\int }_0^{{\displaystyle \frac{\epsilon }{{\epsilon }_c-\epsilon }}}{p}_{9,10}(\Omega )d\Omega \right).$$

(43)

The latter formula can, in principle, lead to the closed-form expression, but it is going to be too cumbersome to be useful. Therefore, we compute the integral (43) numerically. From Formulas (42) and (43), one can deduce the power law (33), with the critical index $\beta =0.29505$.

The application of the optimization method explained in Section 2.2 yields a slightly smaller result at the 7th order, with $\beta =0.15263$. The Borel summation in the 6th order produces a close result, $\beta =0.20411$. Optimization with respect to the parameter p, as explained in Section 2.4, in the 11th order, also produces a close result, $\beta =0.21682$.

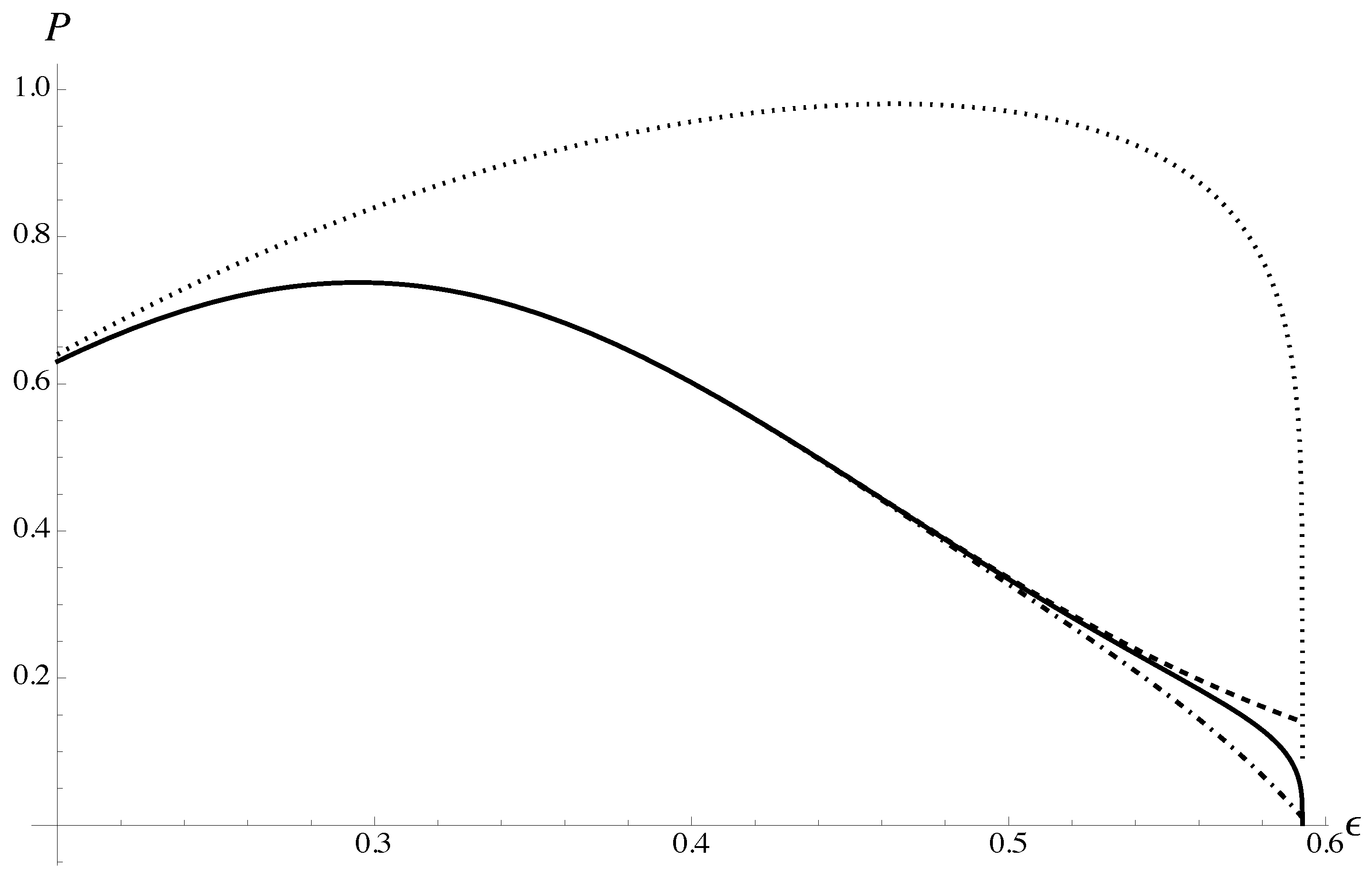
One can easily reconstruct the corresponding iterated roots employed during optimization, as described in Section 2.2; e.g., in the 6th order, the optimal iterated root $R_6^{\ast }$ (44) is illustrated in Figure 3. The Padé approximation (40), and $DLog$-Padé approximation (43) are shown and compared to the polynomial approximation (39).

$$\begin{array}{c}{R}_6^{\ast }\left(\epsilon \right)={\displaystyle \frac{\epsilon }{(0.5927-\epsilon )}}\times \hfill \\ {\displaystyle \frac{2.3708}{{\left(\frac{0.258435{\epsilon }^6}{{(\epsilon -0.5927)}^6}+{\left({\left(\frac{0.363971{\epsilon }^4}{{(\epsilon -0.5927)}^4}+{\left({\left(\frac{0.463888{\epsilon }^2+0.452579\epsilon +0.351293}{{(\epsilon -0.5927)}^2}\right)}^{3/2}-\frac{0.356937{\epsilon }^3}{{(\epsilon -0.5927)}^3}\right)}^{4/3}\right)}^{5/4}-\frac{0.365166{\epsilon }^5}{{(\epsilon -0.5927)}^5}\right)}^{6/5}\right)}^{0.192105}}}.\hfill \end{array}$$

(44)

4. Concluding Remarks and Discussion

Our current estimates of the critical indices and amplitudes for Darcy flow in thin wavy channels corroborate the values made in Ref. [10]. We suggest various approximation techniques that do not involve the lubrication approximation for calculating the critical indices and amplitudes. The polynomial expressions derived for the effective properties at small values of waviness appear to be rather informative about the critical properties as well. The $DLog$ Padé method seemed to apply to all cases of criticality studied above. More sophisticated methods such as Borel summation with or without optimization, $DLog$ iterated roots, etc., are useful as well, particularly when the $DLog$ Padé method is unstable.

We also conclude that polynomial approximations in Ref. [43] contain information about the percolation threshold, which is located close to the known threshold for site percolation in 2D. The concrete values for the latter can be most effectively found via non-diagonal Padé approximants. Various methods were used to calculate critical indices for permeability and the wetted perimeter. In the former case, the index $\alpha \approx -1.06$ is found, while in the latter, the small novel index $\beta \approx 0.2$–$0.3$ is anticipated.

Reasonably compact formulae valid for all $\epsilon$ are presented for the effective permeability and wetted perimeter. In the case of permeability, the formulae deviate significantly from the polynomial approximation, while for the wetted perimeter, the results are fairly close to the polynomial, except for the region close to the threshold.

The methodological universality of critical phenomena across various systems [48] appears to be supported here by the examples of permeability behavior. Multiple examples of resummation methods applied to various effective transport properties can be found in [9,10,48]. More examples of their application to physical problems could be found in [11].

Remarkably, while obtaining an approximate solution, information about the critical regime is inadvertently embedded into the coefficients of the expansion for small $ϵ$. Such an effect is not possible to control or induce purposely, yet the information can still be recovered by means of various analytical techniques of varying sophistication.

There are two approaches to address the problem of non-uniqueness of solutions encountered during the course of solving actual optimal conditions. The first approach requires considering all possible solutions to the optimization problem and selecting or creating a unique representative according to some plausible selection criteria or averaging scheme. The second approach, as suggested in [49,50,51,52], requires such a definition of the optimization problem so that the solution appears to always be unique.

The optimization technique employed in Section 2.2 is unique since the critical index by itself plays the role of a control parameter [1,10]. In Section 2.4, we considered another optimization with respect to the large-variable amplitude $A_k\left(p\right)$, where p is the number of iterations. In the latter case, we employ two optimization conditions: the minimal difference condition, i.e., $A_{k+1}\left(p\right)-A_k\left(p\right)=0,$ and the minimal derivative condition, i.e., ${\displaystyle \frac{d{A}_k\left(p\right)}{dp}}=0.$ Solving both equations separately, we obtain several solutions to the control parameters, all of which we enumerate as $p^{\left(j\right)}$, with $j=1,2,\dots$. These optimization conditions are considered equivalent and are treated together. Apart from calculating the average and variance of all solutions, one can try some different approaches by imposing plausible measures designed to select the solution.

For instance, the so-called lasso measures [49,50] could be applied such that the solution to the optimization problem minimizes the sum of the Borel-transformed coefficients. The close condition is the minimization of the sum of the relative values of the transformed and original coefficients, as described in the generalized Tikhonov regularization [51,52]. The generalization of the lasso selection criteria could be introduced to ensure that the unique solution deviates minimally from the one with Borel-transformed coefficients. Yet another generalization of the lasso calls for a preferred solution to deviate minimally from the solution with original coefficients. In the second approach, one introduces a cost functional $F\left(p\right)$. The functional is a combination of the minimal-difference and minimal-derivative conditions, plus a ridge-type penalty term introduced to select the unique solution that deviates minimally from the pure Borel solution, $F\left(p\right)=|A_{k+1}\left(p\right)-A_k{\left(p\right)|}^2+{\left|{\displaystyle \frac{d{A}_k\left(p\right)}{dp}}\right|}^2+{(p-1)}^2$. The optimal control parameter is supposed to minimize the cost functional. The two approaches sketched above will be compared in a separate paper.

Finally, we highlight that differences of the type (19) and of the type (27) look very similar and could lead to even more general types of optimization. For instance, one could optimize Borel-type approximations with respect to the critical index as an optimization parameter, while the number of iterations is fixed. Or, one can form and analyze differences in amplitudes, either with or without Borel-type transformations.