Optimal Investment Strategy for DC Pension Plan with Stochastic Salary and Value at Risk Constraint in Stochastic Volatility Model
Abstract
1. Introduction
2. Model and Assumptions
2.1. Financial Market
2.2. Wealth Process
3. Optimal Strategy without Dynamic VaR Constraint
4. Optimal Strategy with Dynamic VaR Constraint
4.1. Dynamic VaR, CVaR and wcCVaR
- (1)
- ;
- (2)
- satisfies ;
- (3)
- the Equation (5) has a pathwise unique solution .
4.2. Optimal Investment Strategy with Dynamic VaR Constraint
- (a)
- If
- (b)
- If
- (c)
- If
5. Analysis of the Results and Numerical Illustration
5.1. Parameter Value
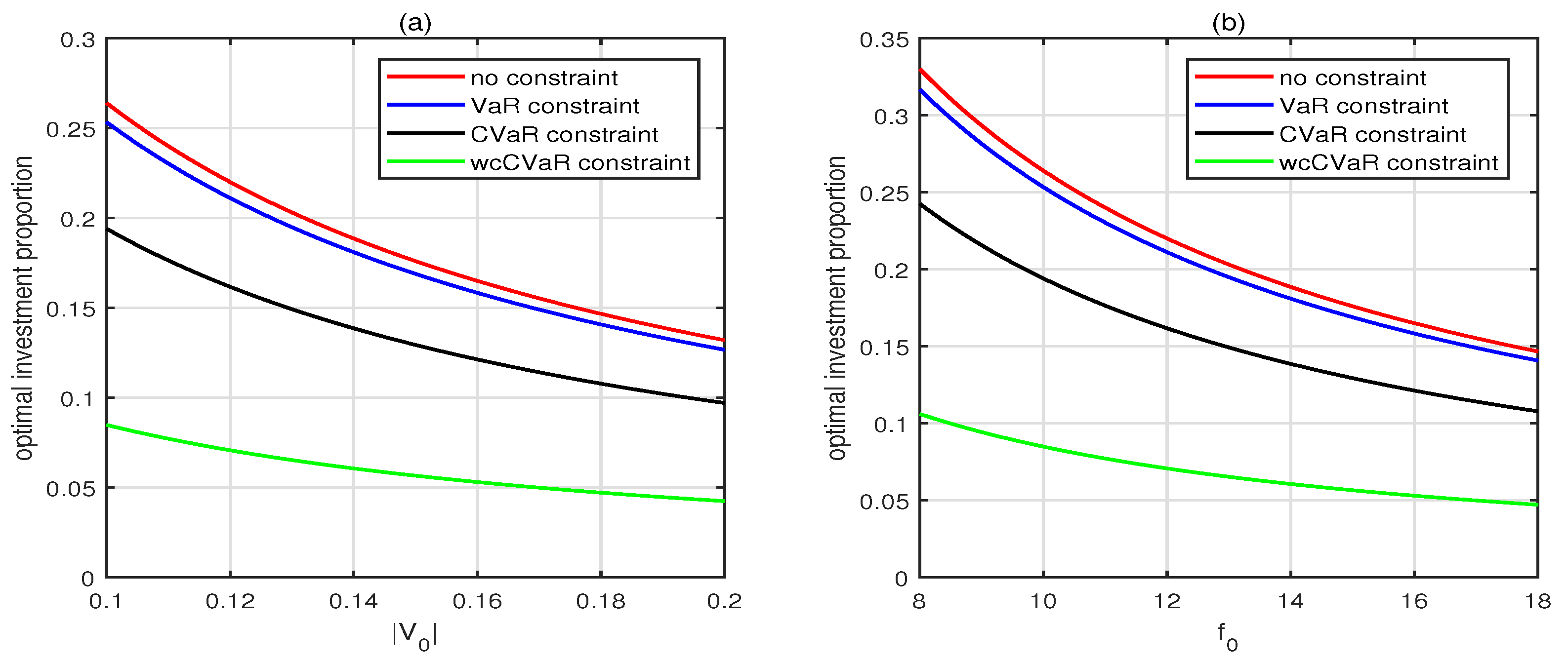
5.2. Optimal Investment Strategy without VaR Constraint
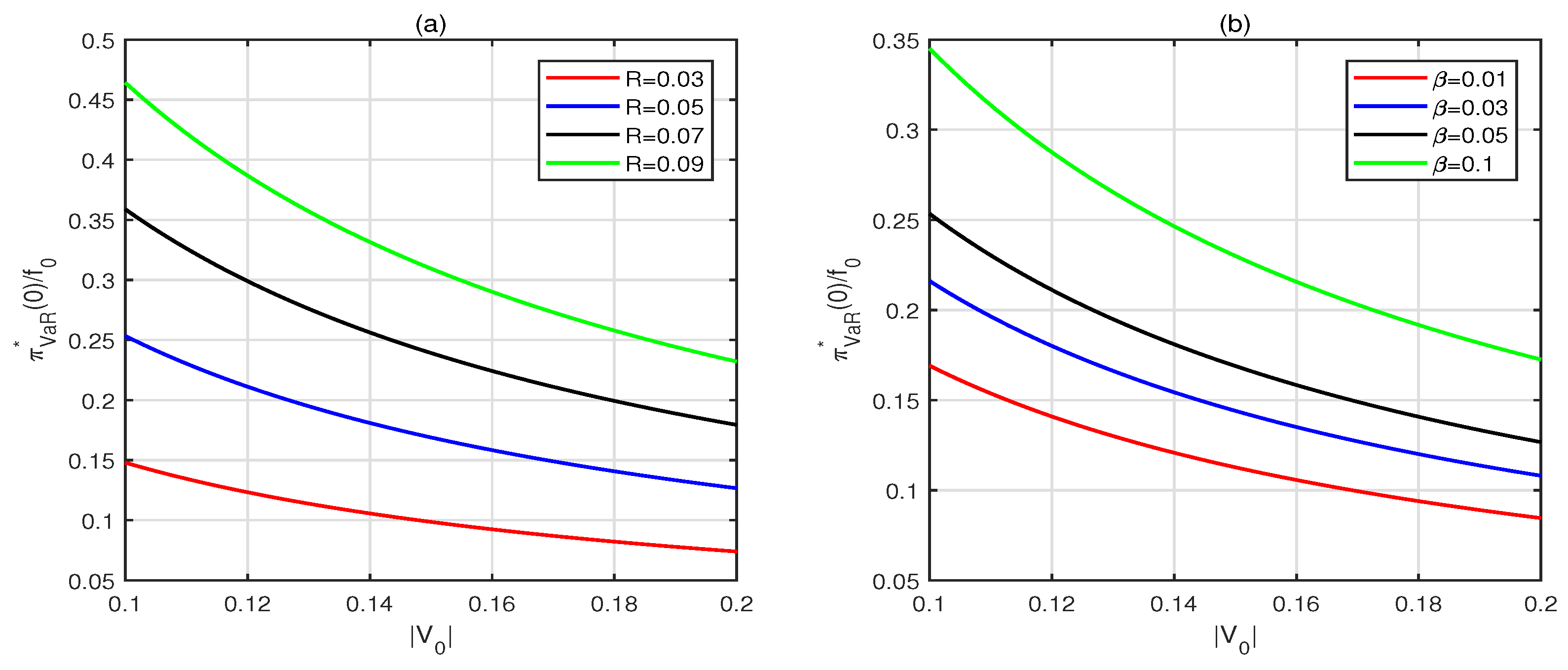
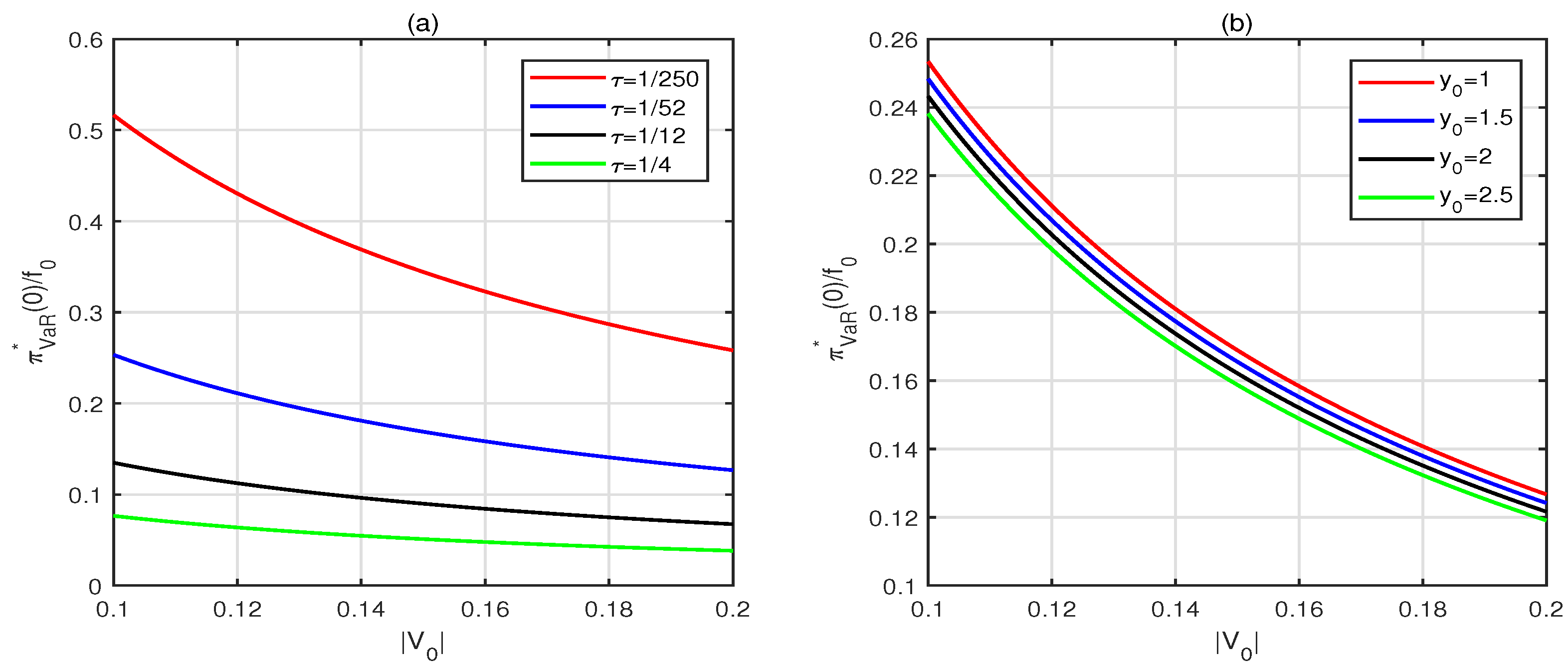
5.3. Optimal Investment Strategy with VaR Constraint
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Lemma 1
Appendix B. Proof of Lemma 2
- (1)
- If , . Thus,
- (2)
- If , the left part of the first inequality in Equation (A15) is a quadratic function of which forms an upward-opening parabola. Moreover, we obtain . According to the properties of quadratic functions, we know the quadratic equation has two distinct real rootsHence, . Then, we have
- (3)
Appendix C. Proof of Theorem 1
- (1)
- If , then ;
- (2)
- If , then
- (3)
- If , then .
- (i)
- For ,
- (a)
- If , then is optimal investment strategy. Under these conditions, the VaR constraint does not work. From the Section 3, we can obtain .
- (b)
- If , then we substitute into the Formula (A20). On one hand, given that the utility function adopted is an exponential utility, the optimal value function is concave relative to pension fund wealth, i.e., . Therefore, we have . This leads to . On the another hand, we deduce due to . From this, we can easily determine that . Consequently, is identified as the Kuhn-Tucker (K-T) point. Thus .
- (c)
- If , then we put into the Formula (A20). For one thing, since , it follows that . Thus, . For another thing, we find that due to . From this, we can conclude that . Consequently, is identified as the Kuhn-Tucker (K-T) point. Thus .
- (ii)
- For ,
- (a)
- If , then is optimal investment strategy. We easily obtain .
- (b)
- If , similar to (i), we can obtain .
References
- Boulier, J.; Huang, S.; Taillard, G. Optimal management under stochastic interest rates: The case of a protected defined contribution pension fund. Insur. Math. Econ. 2001, 28, 173–189. [Google Scholar] [CrossRef]
- Haberman, S.; Vigna, E. Optimal investment strategies and risk measures in defined contribution pension schemes. Insur. Math. Econ. 2002, 31, 35–69. [Google Scholar] [CrossRef]
- Cairns, A.; Blake, D.; Dowd, K. Stochastic lifestyling: Optimal dynamic asset allocation for defined contribution pension plans. J. Econ. Dyn. Control 2006, 30, 843–877. [Google Scholar] [CrossRef]
- Guan, G.; Liang, Z. Mean-variance efficiency of DC pension plan under stochastic interest rate and mean-reverting returns. Insur. Math. Econ. 2015, 61, 99–109. [Google Scholar] [CrossRef]
- Wu, H.; Zeng, Y. Equilibrium investment strategy for defined-contribution pension schemes with generalized mean-variance criterion and mortality risk. Insur. Math. Econ. 2015, 64, 396–408. [Google Scholar] [CrossRef]
- Sun, J.; Li, Y.; Zhang, L. Robust portfolio choice for a defined contribution pension plan with stochastic income and interest rate. Commun. Stat.-Theory Methods 2018, 47, 4106–4130. [Google Scholar] [CrossRef]
- Bian, L.; Li, Z.; Yao, H. Pre-commitment and equilibrium investment strategies for the DC pension plan with regime switching and a return of premiums clause. Insur. Math. Econ. 2018, 81, 78–94. [Google Scholar] [CrossRef]
- Wang, P.; Shen, Y.; Zhang, L.; Kang, Y. Equilibrium investment strategy for a DC pension plan with learning about stock return predictability. Insur. Math. Econ. 2021, 100, 384–407. [Google Scholar] [CrossRef]
- Zhang, Y. Optimal DC pension investment with square-root factor processes under stochastic income and inflation risks. Optimization 2023, 72, 2951–2988. [Google Scholar] [CrossRef]
- Ng, K.; Chong, W. Optimal investment in defined contribution pension schemes with forward utility preferences. Insur. Math. Econ. 2024, 114, 192–211. [Google Scholar] [CrossRef]
- Guan, G.; Liang, Z. Optimal management of DC pension plan under loss aversion and Value-at-Risk constraints. Insur. Math. Econ. 2016, 69, 224–237. [Google Scholar] [CrossRef]
- Yan, M.; Cao, Z.; Wang, T.; Zhang, S. Robust optimal investment strategy of DC pension plans with stochastic salary and a return of premiums clause. Commun. Stat.-Theory Methods 2021, 51, 7980–8011. [Google Scholar] [CrossRef]
- Chang, H.; Li, J.; Zhao, H. Robust optimal strategies of DC pension plans with stochastic volatility and stochastic income under mean-variance criteria. J. Ind. Manag. Optim. 2022, 18, 1393–1423. [Google Scholar] [CrossRef]
- Gao, J. Optimal portfolios for DC pension plans under a CEV model. Insur. Math. Econ. 2009, 44, 479–490. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, X.; Zhang, J. Optimal investment strategy for DC pension plan with deposit loan spread under the CEV model. Axioms 2022, 11, 382. [Google Scholar] [CrossRef]
- Zhao, H.; Rong, X. Portfolio selection problem with multiple risky assets under the constant elasticity of variance model. Insur. Math. Econ. 2012, 50, 179–190. [Google Scholar] [CrossRef]
- Guan, G.; Liang, Z. Optimal management of DC pension plan in a stochastic interest rate and stochastic volatility framework. Insur. Math. Econ. 2014, 57, 58–66. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, H.; Rong, X. Optimal investment strategy for a DC pension plan with mispricing under the Heston model. Commun. Stat.-Theory Methods 2020, 49, 3168–3183. [Google Scholar] [CrossRef]
- He, X.; Zhu, S. An alternative form to calibrate the correlated Stein-Stein option pricing model. Comput. Appl. Math. 2019, 38, 68. [Google Scholar] [CrossRef]
- Lin, S.; Lin, X.; He, X. Analytically pricing European options with a two-factor Stein-Stein model. J. Comput. Appl. Math. 2024, 440, 115662. [Google Scholar] [CrossRef]
- Artzner, P.; Delbaen, F.; Eber, J.M.; Heath, D. Coherent measures of risk. Math. Financ. 1999, 9, 203–228. [Google Scholar] [CrossRef]
- Basak, S.; Shapiro, A. Value-at-risk-based risk management: Optimal policies and asset prices. Rev. Financ. Stud. 2001, 14, 371–405. [Google Scholar] [CrossRef]
- Čerbáková, J. Worst-case VaR and CVaR. In Operations Research Proceedings; Springer: Berlin/Heidelberg, Germany, 2006; Volume 2005. [Google Scholar]
- Natarajan, K.; Pachamanova, D.; Sim, M. Constructing risk measures from uncertainty sets. Oper. Res. 2009, 57, 1129–1141. [Google Scholar] [CrossRef]
- Yiu, K. Optimal portfolios under a value-at-risk constraint. J. Econ. Dyn. Control 2004, 28, 1317–1334. [Google Scholar] [CrossRef]
- Cuoco, D.; He, H.; Isaenko, S. Optimal dynamic trading strategies with risk limits. Oper. Res. 2008, 56, 358–368. [Google Scholar] [CrossRef]
- Zhang, N.; Jin, Z.; Li, S.; Chen, P. Optimal reinsurance under dynamic VaR constraint. Insur. Math. Econ. 2016, 71, 232–243. [Google Scholar] [CrossRef]
- Zhang, Q.; Gao, Y. Portfolio selection based on a benchmark process with dynamic value-at-risk constraints. J. Comput. Appl. Math. 2017, 313, 440–447. [Google Scholar] [CrossRef]
- Dong, Y.; Tang, C.; Hua, C. Optimal investment of DC pension plan under a joint VaR-ES constraint. AIMS Math. 2024, 9, 2084–2104. [Google Scholar] [CrossRef]
- Deelstra, G.; Grasselli, M.; Koehl, P.F. Optimal investment strategies in the presence of a minimum guarantee. Insur. Math. Econ. 2003, 33, 189–207. [Google Scholar] [CrossRef]
- Zhang, C.; Rong, X.; Zhao, H.; Hou, R. Optimal investment for the defined-contribution pension with stochastic salary under a CEV model. Appl. Math.-A J. Chin. Univ. 2013, 28, 187–203. [Google Scholar] [CrossRef]
- Li, D.; Rong, X.; Zhao, H. Time-consistent investment strategy for DC pension plan with stochastic salary under CEV model. J. Syst. Sci. Complex. 2016, 29, 428–454. [Google Scholar] [CrossRef]
- Zeng, Y.; Li, D.; Chen, Z.; Yang, Z. Ambiguity aversion and optimal derivative-based pension investment with stochastic income and volatility. J. Econ. Dyn. Control 2018, 88, 70–103. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Huang, Y.; Zhou, J. Optimal portfolios for the DC pension fund with mispricing under the HARA utility framework. J. Ind. Manag. Optim. 2023, 19, 1262–1281. [Google Scholar] [CrossRef]
- Pirvu, T. Portfolio optimization under the value-at-risk constraint. Quant. Financ. 2007, 7, 125–136. [Google Scholar] [CrossRef]
- Zhu, S.; Fukushima, M. Worst-case conditional value-at-risk with application to robust portfolio management. Oper. Res. 2009, 57, 1155–1168. [Google Scholar] [CrossRef]
- Chen, S.; Li, Z.; Li, K. Optimal investment–reinsurance policy for an insurance company with VaR constraint. Insur. Math. Econ. 2010, 47, 144–153. [Google Scholar] [CrossRef]


| p | R | m | T | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 0.1 | 1 | 0.05 | 2 | 0.02 | 0.1 | 0.05 | 0.05 | 5 | 10 | 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Zhang, H.; Wang, Y.; Huang, Y. Optimal Investment Strategy for DC Pension Plan with Stochastic Salary and Value at Risk Constraint in Stochastic Volatility Model. Axioms 2024, 13, 543. https://doi.org/10.3390/axioms13080543
Liu Z, Zhang H, Wang Y, Huang Y. Optimal Investment Strategy for DC Pension Plan with Stochastic Salary and Value at Risk Constraint in Stochastic Volatility Model. Axioms. 2024; 13(8):543. https://doi.org/10.3390/axioms13080543
Chicago/Turabian StyleLiu, Zilan, Huanying Zhang, Yijun Wang, and Ya Huang. 2024. "Optimal Investment Strategy for DC Pension Plan with Stochastic Salary and Value at Risk Constraint in Stochastic Volatility Model" Axioms 13, no. 8: 543. https://doi.org/10.3390/axioms13080543
APA StyleLiu, Z., Zhang, H., Wang, Y., & Huang, Y. (2024). Optimal Investment Strategy for DC Pension Plan with Stochastic Salary and Value at Risk Constraint in Stochastic Volatility Model. Axioms, 13(8), 543. https://doi.org/10.3390/axioms13080543





