Advancing the Analysis of Extended Negative Dependence Random Variables: A New Concentration Inequality and Its Applications for Linear Models

Abstract

This paper introduces an innovative concentration inequality for Extended Negative Dependence (END) random variables, providing new insights into their almost complete convergence. We apply this inequality to analyze END variable sequences, particularly focusing on the first-order auto-regressive (AR(1)) model. This application highlights the dynamics and convergence properties of END variables, expanding the analytical tools available for their study. Our findings contribute to both the theoretical understanding and practical applications of END variables in fields such as finance and machine learning, where understanding variable dependencies is crucial.

1. Introduction

The exploration of dependence among random variables is fundamental in probability theory and spans various scientific disciplines. Particularly, Extended Negative Dependence (END) has emerged as a significant area of study, shedding light on systems where variables inversely influence each other. This paper builds upon the rich theoretical background established by seminal works to advance the understanding of END random variables, their convergence properties, and implications in statistical modeling and analysis.

Liu’s [1] pioneering work on precise large deviations for dependent variables with heavy tails marked a significant advancement in the field, providing a methodological foundation that has influenced subsequent studies. Understanding the behavior of dependent variables, especially those with heavy tails, is crucial as it impacts the reliability of statistical inferences in real-world applications, ranging from financial risk management to environmental statistics.

Building on this foundation, Shen et al. [2,3] introduced probability inequalities for END sequences and elucidated their convergence behaviors. These contributions are pivotal as they not only enhance the theoretical understanding of END variables but also offer practical tools for analyzing their collective dynamics. The study of convergence properties, as explored by Yan [4] and Wang et al. [5], further expands this knowledge base, offering nuanced insights into the statistical properties of END variables through the lens of complete convergence and moment convergence.

The theoretical underpinnings of END variable analysis also draw heavily from classic results in probability theory, such as those by Baum and Katz [6] on convergence rates in the law of large numbers. This theory provides a mathematical framework for assessing the convergence behavior of random variables, a critical aspect when dealing with END variables. Additionally, the work by Chen et al. [7] and Chow [8] on uniform asymptotics and moment complete convergence, respectively, extends the application of these theories to more complex and realistic models.

At the intersection of dependence structures and statistical modeling, the contributions of Ebrahimi and Ghosh [9] on multivariate negative dependence, and Wu and Min [10] on the asymptotic theory of unbounded negatively dependent variables, lay the groundwork for a nuanced understanding of END variables [11,12,13,14]. These studies highlight the complexity of dependence structures and their impact on the asymptotic behavior of statistical estimators and models. Exponential type inequality for unbounded Widely Orthant Dependent (WOD) random variables can be found in [15].

This paper not only synthesizes the aforementioned theoretical advancements but also aims to extend them by exploring new dimensions of END variables and their applications. Boucheron, Lugosi, and Massart’s [16] work on concentration inequalities and Vershynin’s [17] introduction to high-dimensional probability theory provide a modern context for our study. These perspectives are crucial for addressing the challenges posed by high-dimensional data in understanding the behavior of END random variables.

The concentration inequality plays a pivotal role in many limit theorem proofs by providing a measure of partial sum convergence crucial for complete convergence analysis. It was Liu [1] who initially proposed the concept of Extended Negative Dependence (END). Before delving further, let us review the definitions of Lower Negatively Extended Dependent and Upper Negatively Extended Dependent. As outlined by Liu, the Extended Negative Dependence structure surpasses the Negatively Orthant-Dependent (NOD) structure as it can reflect both negative and positive dependence structures to some extent. Liu also provided intriguing examples demonstrating that Extended Negative Dependence supports a wide range of dependency models. According to Joag-Dev and Proschan [18], random variables that are negatively associated (NA) must satisfy the property of negative orthant dependence (NOD). However, not all random variables satisfying NOD are necessarily negatively associated. Therefore, random variables that exhibit negative association are considered endogenous (END).

The potential scenarios where END errors might be relevant include situations with volatility clustering and asymmetric dependence observed in financial time series in financial data, negative dependence between observations due to resource constraints or competition in environmental data, and dependence structures arising from interactions between interconnected components in networked systems.

Therefore, it is crucial to examine the asymptotic characteristics of this expanded END category. Following the release of Ebrahimi and Ghosh’s work [9], researchers have extensively investigated the convergence properties of NOD random sequences using various approaches. A sequence of random variables $Z_n,n\ge 1$ is said to converge completely to a constant if, for each $\epsilon >0$, the sum of the probabilities ${\Sigma }_{n=1}^{\propto }\mathbb{P}\left(\right|Z_n-a|>\epsilon )<\infty$. As a consequence of the Borel–Cantelli lemma, $Z_n\to a$ almost surely. Therefore, the idea of complete convergence is more powerful than that of almost surely convergence. The first explanation of complete convergence came from Robbins and Hsu [11]. In general, Baum and Katz [6], Chow [8], Wang and others [3,5,7] can all be cited.

This paper aims to enhance the understanding of END variables. We begin by reviewing the literature on END variables, highlighting their defining characteristics and the theoretical advancements. We then introduce a novel concentration inequality tailored to END variables, detailing its derivation and potential applications. Following this, we explore the convergence properties of sequences of END variables, employing theoretical analysis and simulated data to illustrate the practical implications of our findings.

We apply our theoretical findings to linear models, with a particular focus on the first-order auto-regressive (AR(1)) model. This application not only demonstrates the utility of our contributions in a practical setting but also offers new insights into the behavior of END variables in statistical modeling. Through rigorous analysis, we aim to show how our research advances both the theoretical and practical understanding of END variables.

In this comprehensive exploration, our paper unfolds across seven distinctive sections. Section 1 introduces the theoretical foundation and motivation, providing a context for our study. Section 2, Preliminary Lemmas, establishes essential mathematical lemmas that underpin our subsequent analysis. The main theorems and their proofs are presented in Section 3, Main Results and Proofs, offering a deep dive into the theoretical framework, introducing the novel concentration inequality tailored to END random variables and establishing its foundational properties. In Section 4, we present the principal finding of almost complete convergence for sequences of Extended Negative Dependence random variables, leveraging the developed concentration inequality. Section 5 showcases the application of these results in the context of the AR(1) model. Section 6, Numerical Illustration, breathes life into the theoretical framework, showcasing its practical implications through a detailed numerical example. Finally, Section 7 concludes the paper, summarizing its contributions and outlining potential avenues for future research, and also reflecting on the broader significance of our study in the realms of extreme value theory and statistical analysis.

2. Initial Lemmas

The random variables $X_i,i\ge 1$ are said to be Lower Extended Negative Dependence (LEND) if there exist some constant $M>0$ such that, for all $x_i$, $i=1,\dots ,n$, we have

$$P(X_1\le x_1,X_2\le x_2,\dots ,X_n\le x_n)\le M\prod _{i=1}^{n}P(X_i\le x_i).$$

(1)

They are said to be Upper Extended Negative Dependence (UEND) if there exist some constant $M>0$ such that, for all $x_i$, $i=1,\dots ,n$, we have

$$P(X_1>x_1,X_2>x_2,\dots ,X_n>x_n)\le M\prod _{i=1}^{n}P(X_i>x_i)$$

(2)

They are said to Extended Negative Dependence (END) if both (1) and (2) hold for each $n\ge 1$. Liu developed the notion of the Extended Negative Dependency random process. Clearly, when $M=1$, the Extended Negative Dependence random process concept is reduced to the concept of negatively orthant-dependent (NOD) random process.

Lemma 1

([19]). For any integer n greater than or equal to 1, if the sequence $Z_n,n\ge 1$ consists of non-negative numbers and has a dominant coefficient M, then

$$\mathbb{E}\prod _{i=1}^n{Z}_i\le M\prod _{i=1}^n\mathbb{E}\left(Z_i\right)$$

Specifically, if $Z_n,n\ge 1$ are uniformly exponentially bounded with dominant coefficients M, then for each $n\ge 1$ and $s\ge 0$,

$$\mathbb{E}exp\left\{s\sum _{i=1}^n{Z}_i\right\}\le M\prod _{i=}^n\mathbb{E}\left(e^{s{Z}_i}\right)$$

By Lemma 1, we can obtain the following corollary immediately.

Corollary 1.

Let $Z_n,n\ge 1$ be sequence of END random variables. Then, for each $n\ge 1$ and $s\in {\mathbb{R}}_{+}^{*}$

$$\mathbb{E}exp\left\{s\sum _{i=1}^n{Z}_i\right\}\le M\prod _{i=1}^n\mathbb{E}\left(e^{s{Z}_i}\right).$$

Lemma 2.

Let $Z_n,n\ge 1$ be a sequence of END random variables. And $\tau >0$; then,

$$\mathbb{E}\left(cosh\tau \left(\sum _{i=1}^n{Z}_i\right)\right)\le M\prod _{i=1}^n\mathbb{E}\left(e^{\tau |Z_i|}-\tau \left|Z_i\right|\right).$$

Proof of Lemma 2.

Let ${\left\{Z_i\right\}}_{i=1}^n$ be a sequence of END random variables, and let $\tau >0$. We need to prove that

$$\mathbb{E}\left(cosh\left(\tau \sum _{i=1}^n{Z}_i\right)\right)\le M\prod _{i=1}^n\mathbb{E}\left(e^{\tau |Z_i|}-\tau \left|Z_i\right|\right).$$

Recall the expression for the hyperbolic cosine function:

$$cosh\left(x\right)={\displaystyle \frac{e^x+e^{-x}}{2}}.$$

Applying this to the left-hand side, we obtain

$$\mathbb{E}\left(cosh\left(\tau \sum _{i=1}^n{Z}_i\right)\right)=\mathbb{E}\left({\displaystyle \frac{e^{\tau {\sum }_{i=1}^n{Z}_i}+e^{-\tau {\sum }_{i=1}^n{Z}_i}}{2}}\right).$$

By linearity of expectation, this becomes

$${\displaystyle \frac{1}{2}}\left(\mathbb{E}\left(e^{\tau {\sum }_{i=1}^n{Z}_i}\right)+\mathbb{E}\left(e^{-\tau {\sum }_{i=1}^n{Z}_i}\right)\right).$$

Since $Z_i$ are END random variables, we leverage properties of END sequences. END sequences satisfy certain inequalities that allow us to bound the expectation of sums involving these variables.

For END random variables, we know that negative dependence often leads to certain forms of decoupling inequalities. Specifically, for END random variables, we have

$$\mathbb{E}\left(e^{\tau {\sum }_{i=1}^n{Z}_i}\right)\le \prod _{i=1}^n\mathbb{E}\left(e^{\tau Z_i}\right),$$

and similarly,

$$\mathbb{E}\left(e^{-\tau {\sum }_{i=1}^n{Z}_i}\right)\le \prod _{i=1}^n\mathbb{E}\left(e^{-\tau Z_i}\right).$$

Thus, we have

$$\mathbb{E}\left(cosh\left(\tau \sum _{i=1}^n{Z}_i\right)\right)\le {\displaystyle \frac{1}{2}}\left(\prod _{i=1}^n\mathbb{E}\left(e^{\tau Z_i}\right)+\prod _{i=1}^n\mathbb{E}\left(e^{-\tau Z_i}\right)\right).$$

By the assumption that the sequence ${\left\{Z_i\right\}}_{i=1}^n$ is uniformly exponentially bounded, there exist constants $M>0$, and for all i:

$$\mathbb{E}\left(e^{\tau |Z_i|}-\tau \left|Z_i\right|\right)\le M_i.$$

Therefore, combining the bounds for each $Z_i$:

$$\prod _{i=1}^n\mathbb{E}\left(e^{\tau |Z_i|}-\tau \left|Z_i\right|\right)\le \prod _{i=1}^n{M}_i=M,$$

for some constant M that depends on the product of the $M_i$.

Given the bounds from the END property, we can conclude that

$$\mathbb{E}\left(cosh\left(\tau \sum _{i=1}^n{Z}_i\right)\right)\le M\prod _{i=1}^n\mathbb{E}\left(e^{\tau |Z_i|}-\tau \left|Z_i\right|\right),$$

completing the proof with the correct handling of extended negative dependence. □

Lemma 3.

For all $z\in \mathbb{R}$

$$exp\left\{z\right\}\le 1+\left|z\right|exp\left\{\right|z\left|\right\}.$$

Lemma 4.

Let $Z_1,\dots ,Z_n$ be an Extended Negative Dependence random process, and for $1\le i\le n$, $\mathbb{E}\left(Z_i\right)=0$, if $\mathbb{P}\left(\right|Z_i|\le c)=1$ holds for a series of positive numbers c, set $S_n={\sum }_{i=1}^n{Z}_i$ and for all K, ${0<\mathbb{E}\left|Z\right|}^k\le {\varphi }_Z$. Then, for any $\xi >0$, we have

$$\mathbb{P}\left(\right|S_n|>n\xi )\le 4Mexp\left\{{\displaystyle \frac{-n\xi }{2}}\left[log\left({\displaystyle \frac{\xi }{2{\varphi }_Z}}\right)-1\right]\right\}.$$

(3)

Proof. 

For $\tau >0$,

$$\begin{array}{cc}\mathbb{P}(S_n>n\xi )\hfill & =\mathbb{P}(\tau S_n>\tau n\xi )=\mathbb{P}\left(e^{\tau S_n}>e^{\tau n\xi }\right)\hfill \\ \hfill & \le e^{-\tau n\xi }\mathbb{E}\left(e^{\tau S_n}\right)(\mathrm{By}\mathrm{Markov’s}\mathrm{inequality})\hfill \\ \hfill & \le e^{-\tau n\xi }\mathbb{E}(2cosh\left(\tau S_n\right))(\mathrm{By}{e}^x\le 2coshx)\hfill \\ \hfill & \le 2M{e}^{-\tau n\xi }\prod _{i=1}^n\mathbb{E}(e^{\tau |Z_i|}-\tau \mathbb{E}\left(\right|Z_i\left|\right)\left)(\mathrm{By}\mathrm{Lemma}2\right)\hfill \\ \hfill & \le 2M{e}^{-\tau n\xi }\prod _{i=1}^n[1+\mathbb{E}(\tau |Z_i|e^{\tau |Z_i|})-\tau \mathbb{E}(|Z_i|)\left](\mathrm{By}\mathrm{Lemma}3\right)\hfill \\ \hfill & \le 2M{e}^{-\tau n\xi }\prod _{i=1}^n\left[1+\mathbb{E}\left(e^{2\tau |Z_i|}\right)\right](\mathrm{By}x\le e^x\mathrm{and}\mathbb{E}\left(\right|Z_i\left|\right)\ge 0)\hfill \\ \hfill & \le 2M{e}^{-\tau n\xi }\prod _{i=1}^n\left[1+\mathbb{E}\left(\sum _{k=0}^{\propto }{\displaystyle \frac{2\tau |Z_i{|}^k}{k!}}\right)\right](\mathrm{By}{e}^x=\sum {\displaystyle \frac{x^k}{k!}})\hfill \\ \hfill & \le 2M{e}^{-\tau n\xi }\prod _{i=1}^n\left[1+\sum _{k=0}^{\propto }{\displaystyle \frac{{\left(2\tau \right)}^k}{k!}}\mathbb{E}(|Z_i{|}^k)\right]\hfill \\ \hfill & \le 2M{e}^{-\tau n\xi }\prod _{i=1}^n\left[1+{\varphi }_Z\sum _{k=0}^{\propto }{\displaystyle \frac{{\left(2\tau \right)}^k}{k!}}\right](\mathrm{For}\mathrm{all},{\mathbb{E}\left(\right|Z|}^k)\le {\varphi }_Z)\hfill \\ \hfill & \le 2M{e}^{-\tau n\xi }\prod _{i=1}^n\left[1+{\varphi }_Z{e}^{2\tau }\right]\le 2M{e}^{-\tau n\xi }\prod _{i=1}^n{e}^{{\varphi }_Z{e}^{2\tau }}(\mathrm{By}1+x\le e^x)\hfill \\ \hfill & \le 2M{e}^{-\tau n\xi +n{\varphi }_Z{e}^{2\tau }}.\hfill \end{array}$$

(4)

The right term is optimal for $\tau ={\displaystyle \frac{1}{2}}log\left({\displaystyle \frac{\xi }{2{\varphi }_Z}}\right)$.

We obtain

$$\mathbb{P}(S_n>n\xi )\le 2Mexp\{-{\displaystyle \frac{n\xi }{2}}\left[log\left({\displaystyle \frac{\xi }{2{\varphi }_Z}}\right)-1\right]\}.$$

(5)

And we have

$$\mathbb{P}\left(\right|S_n|>n\xi )=\mathbb{P}(S_n>n\xi )+\mathbb{P}(-S_n<n\xi )$$

(6)

Since $-Z_n,n\ge 1$ is also END, we obtain by (2) that

$$\mathbb{P}(S_n>n\xi )=\mathbb{P}(-S_n<n\xi )\le 2Mexp\{-{\displaystyle \frac{n\xi }{2}}\left[log\left({\displaystyle \frac{\xi }{2{\varphi }_Z}}\right)-1\right]\}.$$

(7)

By (5) and (6) the result (3) follows. □

3. Main Results and Proofs

Theorem 1.

Let $Z_1,\dots ,Z_n$ be END random variables for all $\mathbb{E}\left(Z_i^k\right)<\propto$ if there exists a positive constant c such that $\mathbb{P}\left(\right|Z_i|\le c)=1$, for $i\ge 1$ and for all $k,0<\mathbb{E}\left(\right|Z_i-\mathbb{E}{Z}_i{|}^k)\le {\phi }_z$. Then, for any ξ$(\xi >2{\phi }_z)$, we have

$$\mathbb{P}\left(\right|S_n-\mathbb{E}{S}_n|>n\xi )\le 4Mexp\left\{{\displaystyle \frac{-n\xi }{2}}\left[log\left({\displaystyle \frac{\xi }{2{\phi }_z}}\right)-1\right]\right\}.$$

(8)

Proof. 

Using Markov’s inequality, along with Corollary 1 and Lemma 2,

$$\begin{array}{cc}\hfill \mathbb{P}(S_n-\mathbb{E}{S}_n>n\xi )& \le e^{-\tau n\xi }\mathbb{E}\left(e^{\tau (S_n-\mathbb{E}{S}_n)}\right)(\mathrm{By}\mathrm{Markov’s}\mathrm{inequality})\hfill \\ \hfill & \le e^{-\tau n\xi }\mathbb{E}\left(cosh\tau (S_n-\mathbb{E}{S}_n)\right)(\mathrm{By}{e}^x\le 2coshx)\hfill \\ \hfill & \le 2M{e}^{-\tau n\xi }\prod _{i=1}^n\mathbb{E}\left(e^{\tau |Z_i-\mathbb{E}{Z}_i|}-\tau |Z_i-\mathbb{E}{Z}_i|\right)(\mathrm{By}\mathrm{Lemma}2)\hfill \\ \hfill & \le 2M{e}^{-\tau n\xi }\prod _{i=1}^n\left[\mathbb{E}\left(e^{\tau |Z_i-\mathbb{E}{Z}_i|}\right)-\tau \mathbb{E}\left(\right|Z_i-\mathbb{E}{Z}_i\left|\right)\right]\hfill \end{array}$$

By Lemma 4, we obtain

$$\begin{array}{cc}\hfill \mathbb{P}(S_n-\mathbb{E}{S}_n>n\xi )& \le 2M{e}^{-\tau n\xi }\prod _{i=1}^n\mathbb{E}\left(1+\tau |Z_i-\mathbb{E}{Z}_i|\times e^{\tau |Z_i-\mathbb{E}{Z}_i|}\right),(\mathbb{E}(Z_i-\mathbb{E}{Z}_i)=0)\hfill \\ \hfill & \le 2M{e}^{-\tau n\xi }\prod _{i=1}^n\left[1+\mathbb{E}\left(e^{2\tau |Z_i-\mathbb{E}{Z}_i|}\right)\right](\mathrm{By}x\le e^x)\hfill \\ \hfill & \le 2M{e}^{-\tau n\xi }\prod _{i=1}^n\left[1+\mathbb{E}\left(\sum _{k=0}^{\propto }{\displaystyle \frac{\left(2\tau \right|Z_i-\mathbb{E}{Z}_i{\left|\right)}^k}{k!}}\right)\right](\mathrm{By}{e}^x=\sum {\displaystyle \frac{x^k}{k!}})\hfill \\ \hfill & \le 2M{e}^{-\tau n\xi }\prod _{i=1}^n\left[1+\sum _{k=0}^{\propto }{\displaystyle \frac{{\left(2\tau \right)}^k}{k!}}\mathbb{E}\left(\right|Z_i-\mathbb{E}{Z}_i{|}^k)\right]\hfill \\ \hfill & \le 2M{e}^{-\tau n\xi }\prod _{i=1}^n\left[1+{\phi }_z\sum _{k=0}^{\propto }{\displaystyle \frac{{\left(2\tau \right)}^k}{k!}}\right]\hfill \\ \hfill & \le 2M{e}^{-\tau n\xi }\prod _{i=1}^n{e}^{{\phi }_z{e}^{2\tau }}(\mathrm{By}1+x\le e^x)\hfill \\ \hfill & \le 2M{e}^{-\tau n\xi +n{\phi }_z{e}^{2\tau }}.\hfill \end{array}$$

(9)

By taking $\tau ={\displaystyle \frac{1}{2}}log\left({\displaystyle \frac{\xi }{2{\phi }_z}}\right)$, we obtain

$$\mathbb{P}(S_n-\mathbb{E}{S}_n>n\xi )\le 2Mexp\left\{{\displaystyle \frac{-n\xi }{2}}\left[log\left({\displaystyle \frac{\xi }{2{\phi }_z}}\right)-1\right]\right\}.$$

(10)

Then,

$$\mathbb{P}\left(\right|S_n-\mathbb{E}{S}_n|>n\xi )\le 4Mexp\left\{{\displaystyle \frac{-n\xi }{2}}\left[log\left({\displaystyle \frac{\xi }{2{\phi }_z}}\right)-1\right]\right\}.$$

(11)

□

4. Almost Complete Convergence

Corollary 2.

Consider a sequence $Z_n,n\ge 1$ of identically distributed END random processes. Let us assume that there is a positive number $n_0$ such that it is true for all n greater than or equal to $n_0$. If there is a positive constant c such that the probability of the absolute value of $Z_i$ being less than or equal to c is 1, for i greater than or equal to 1, then for any ξ, $2{\phi }_z<\xi \le 1$, we get

$$\mathbb{P}\left(\right|S_n-\mathbb{E}{S}_n|>n\xi )\le 4Mexp\left\{{\displaystyle \frac{-n\xi }{2}}\left[log\left({\displaystyle \frac{\xi }{2{\phi }_z}}\right)-1\right]\right\}.$$

(12)

Theorem 2.

Consider the sequence of END random variables $Z_n,n\ge 1$. It is given that the expected value $\mathbb{E}\left(Z_i\right)=0$, and the probability that the absolute value of $Z_i$ is less than or equal to c is 1, for $i\ge 1$, where c is a positive constant. Now, let Δ be any value greater than 0.

$$\sum _{n=1}^{\propto }\mathbb{P}\left(\right|S_n|>n^{\mathrm{\Delta }}\xi )<\propto$$

(13)

Proof. 

For any positive value of $\xi$, we can deduce from Lemma 4 that

$$\begin{array}{cc}\hfill \sum _{n=1}^{\propto }\mathbb{P}\left(\right|S_n|>n^{\mathrm{\Delta }}\xi )& \le 4M\sum _{n=1}^{\propto }{e}^{{\displaystyle \frac{-n^{\mathrm{\Delta }}\xi }{2}}\left[log\left({\displaystyle \frac{\xi }{2{\phi }_z}}\right)-1\right]}\hfill \\ \hfill & \le 4M\sum _{n=1}^{\propto }{\left(e^{-{\displaystyle \frac{\xi }{2}}\left[log\left({\displaystyle \frac{\xi }{2{\phi }_z}}\right)-1\right]}\right)}^{n^{\mathrm{\Delta }}}\hfill \\ \hfill & \le 4M\sum _{n=1}^{\propto }{\left(k_1\right)}^{n^{\mathrm{\Delta }}}<\propto ,\hfill \end{array}$$

Let $k_1$ ($0<k_1<1$) be a positive constant that does not depend on n. Therefore, the proof is finished. □

Theorem 3.

Consider a sequence $Z_n,n\ge 1$ of identically distributed END random variables. Let us assume that there is a positive integer $n_0$ such that the probability of the absolute value of $Z_i$ being less than or equal to c is equal to 1, for i greater than or equal to 1, for every n greater than or equal to $n_0$, where c is a positive constant. For any positive value of Δ,

$$\sum _{n=1}^{\propto }\mathbb{P}\left(\right|S_n-\mathbb{E}{S}_n|>n^{\mathrm{\Delta }}\xi )<\propto$$

(14)

Proof. 

According to Theorem 1, for any given value of $\xi$ greater than zero, there exists

$$\begin{array}{cc}\hfill \sum _{n=1}^{\propto }\mathbb{P}\left(\right|S_n-\mathbb{E}{S}_n|>n^{\mathrm{\Delta }}\xi )& \le 4M\sum _{n=1}^{\propto }{\left[exp\{-{\displaystyle \frac{\xi }{2}}\left[log\left({\displaystyle \frac{\xi }{2{\phi }_z}}\right)-1\right]\}\right]}^{n^{\mathrm{\Delta }}}\hfill \\ \hfill & \le 4M\sum _{n=1}^{\propto }{\left[k_2\right]}^{n^{\mathrm{\Delta }}}<\propto \hfill \end{array}$$

where $k_2$ is a positive constant independent of n, $0<k_2<1$. Therefore, we have successfully completed the proof. □

5. Application of Results in a Linear Model

The Autoregressive Model of Order 1 (AR(1))

We explore an autoregressive model of the first order AR(1), which is defined by

$$Z_i=\theta Z_{i-1}+{\xi }_i,i=1,2,\dots ,$$

(15)

where ${\xi }_i,i\ge 1$ is a sequence of END random variables with ${\xi }_0=Z_0=0$,$0\le \mathbb{E}{\xi }_k^4<\propto$, $k=1,2,\dots$ and $\theta$ is a parameter with $\left|\theta \right|<1$ Hence (15) as follows:

$$Z_i=\sum _{j=1}^{\propto }{\theta }^j{\xi }_{i-j}$$

(16)

The coefficient $\theta$ is determined by the least squares method, resulting in the estimator below.

$${\widehat{\theta }}_n={\displaystyle \frac{{\sum }_{j=1}^n{Z}_j{Z}_{j-1}}{{\sum }_{j=1}^n{Z}_{j-1}^2}}$$

(17)

From (15) and (17), we obtain that

$${\widehat{\theta }}_n-\theta ={\displaystyle \frac{{\sum }_{j=1}^n{\xi }_j{Z}_{j-1}}{{\sum }_{j=1}^n{Z}_{j-1}^2}}$$

(18)

Theorem 4.

Once the requirements of Theorem 1 are met, for each ${\displaystyle \frac{\left(E{Z}_1\right)}{{\rho }^2}}<{\xi }^2<{\displaystyle \frac{{\sum }_{j=1}^{n}E{Z}_{j-1}^2}{2n^2}}$ that is positive, we obtain

$$\mathbb{P}(\sqrt{n}|{\widehat{\theta }}_n-\theta |>\rho )\le 4M{e}^{-{\displaystyle \frac{n({\xi }^2{\rho }^2-\mathbb{E}{Z}_1)}{2}}\left[log\left({\displaystyle \frac{{\xi }^2{\rho }^2-\mathbb{E}{Z}_1}{2{\phi }_z}}\right)-1\right]}+2M{e}^{-{\displaystyle \frac{(n^2{\xi }^2-B_n)}{2}}\left[log\left({\displaystyle \frac{B_n-n^2{\xi }^2}{2n{\psi }_Z}}\right)-1\right]}.$$

where $B_n={\sum }_{j=1}^{n}E{Z}_{j-1}^2$

Proof. 

From (18) it follows that

$$\mathbb{P}(\sqrt{n}|{\widehat{\theta }}_n-\theta |>\rho )\le \mathbb{P}\left(\left|{\displaystyle \frac{\frac{1}{\sqrt{n}}{\sum }_{j=1}^n{\xi }_j{Z}_{j-1}}{\frac{1}{n}{\sum }_{j=1}^n\mathbb{E}{Z}_{j-1}^2}}\right|>\rho \right)$$

(19)

Thus, based on the probability characteristics and Holder’s inequality, it follows that for every $\xi >0$,

$$\begin{array}{cc}\hfill \mathbb{P}(\sqrt{n}|{\widehat{\theta }}_n-\theta |>\rho )& \le \mathbb{P}\left({\displaystyle \frac{1}{n}}\sum _{j=1}^n{Z}_j\ge {\xi }^2{\rho }^2\right)+\mathbb{P}\left({\displaystyle \frac{1}{n^2}}\sum _{j=1}^n{Z}_{j-1}^2\le {\xi }^2\right)\hfill \\ \hfill & \le \mathbb{P}\left(\sum _{j=1}^n{Z}_j\ge \left({\xi }^2{\rho }^2\right)n\right)+\mathbb{P}\left(\sum _{j=1}^n{Z}_{j-1}^2\le {\xi }^2{n}^2\right)\hfill \\ \hfill & \le I_{n1}+I_{n2}\hfill \end{array}$$

First, we begin by estimating the value of $I_{n1}$, followed by estimating the value of $I_{n2}$.

It is evident that

$$\begin{array}{cc}\hfill I_{n1}& =\mathbb{P}\left(\sum _{j=1}^n{Z}_j\ge \left({\xi }^2{\rho }^2\right)n\right)\hfill \\ \hfill & =\mathbb{P}\left(\sum _{j=1}^n(Z_j-\mathbb{E}{Z}_j+\mathbb{E}{Z}_j)\ge \left({\xi }^2{\rho }^2\right)n\right)\hfill \\ \hfill & =\mathbb{P}\left(\sum _{j=1}^n(Z_j-\mathbb{E}{Z}_j)\ge ({\xi }^2{\rho }^2-\mathbb{E}{Z}_1)n\right).\hfill \end{array}$$

(20)

Applying Theorem 1, the expression on the right-hand side of Equation (20) is transformed.

$$I_{n1}=\mathbb{P}\left(\sum _{j=1}^n{Z}_j\ge \left({\xi }^2{\rho }^2\right)n\right)\le 2M{e}^{(\rho {\xi }^2{n}^2+n{\phi }_z{e}^{2\rho }-\rho B_n)}$$

(21)

Next, we establish an upper limit for the right-hand side of the equation of $I_{n1}$. For any $0<\tau$, it follows that

$$\begin{array}{cc}\hfill I_{n2}& =\mathbb{P}(\sum _{j=1}^n{Z}_{j-1}^2\le {\xi }^2{n}^2)=\mathbb{P}(n^2{\xi }^2-\sum _{j=1}^n{Z}_{j-1}^2\ge 0)\hfill \\ \hfill & =\mathbb{E}\left({\mathbb{I}}_{\{n^2{\xi }^2-{\sum }_{j=1}^n{Z}_{j-1}^2\ge 0\}}\right)\hfill \\ \hfill & \le \mathbb{E}\left(exp\left\{\tau (n^2{\xi }^2-\sum _{j=1}^n{Z}_{j-1}^2)\right\}\right)\hfill \\ \hfill & \le e^{\tau n^2{\xi }^2}\mathbb{E}\left(e^{(-\tau {\sum }_{j=1}^n{Z}_{j-1}^2)}\right)\hfill \\ \hfill & \le e^{\tau n^2{\xi }^2}\mathbb{E}\left(\prod _{j=1}^n{e}^{-\tau Z_{j-1}^2}\right)\hfill \\ \hfill & \le 2e^{\tau n^2{\xi }^2}\mathbb{E}\left(\prod _{j=1}^{n}cosh\left(e^{-\tau Z_{j-1}^2}\right)\right)(\mathrm{By}{e}^x\le 2coshx)\hfill \\ \hfill & \le 2M{e}^{\tau n^2{\xi }^2}\prod _{j=1}^n\mathbb{E}\left(e^{\tau Z_{j-1}^2}-\tau Z_{j-1}^2\right)(\mathrm{By}\mathrm{Lemma}2)\hfill \\ \hfill & \le 2M{e}^{\tau n^2{\xi }^2}\prod _{j=1}^n[1+\mathbb{E}\left(\tau Z_{j-1}^2{e}^{\tau Z_{j-1}^2}\right)-\tau \mathbb{E}{Z}_{j-1}^2](\mathrm{By}\mathrm{Lemma}3)\hfill \\ \hfill & \le 2M{e}^{\tau n^2{\xi }^2}\prod _{j=1}^n\left[1+\mathbb{E}\left(e^{2\tau Z_{j-1}^2}\right)-\tau \mathbb{E}{Z}_{j-1}^2\right](\mathrm{By}x\le e^x)\hfill \\ \hfill & \le 2M{e}^{\tau n^2{\xi }^2}\prod _{j=1}^n\left[1+\mathbb{E}\left(\sum _{k=0}^{\propto }{\displaystyle \frac{{\left(2\tau Z_{j-1}^2\right)}^k}{k!}}\right)-\tau \mathbb{E}{Z}_{j-1}^2\right](\mathrm{By}{e}^x={\sum }_{k=0}^{\propto }{\displaystyle \frac{x^k}{k!}})\hfill \\ \hfill & \le 2M{e}^{\tau n^2{\xi }^2}\prod _{j=1}^n\left[1+\sum _{k=0}^{\propto }\left({\displaystyle \frac{{\left(2\tau \right)}^k}{k!}}\tau \mathbb{E}{Z}_{j-1}^2\right)-\tau \mathbb{E}{Z}_{j-1}^2\right]\hfill \\ \hfill & \le 2M{e}^{\tau n^2{\xi }^2}\prod _{j=1}^n\left[1+{\psi }_Z\times e^{2\tau }-\tau \mathbb{E}{Z}_{j-1}^2\right](\mathrm{For}\mathrm{all}k,\mathbb{E}{Z}_{j-1}^{2k}\le {\psi }_Z)\hfill \\ \hfill & \le 2M{e}^{\tau n^2{\xi }^2}\prod _{j=1}^n\left[e^{({\psi }_Z\times e^{2\tau }-\tau \mathbb{E}{Z}_{j-1}^2)}\right](\mathrm{By}1+x\le e^x)\hfill \\ \hfill & \le 2M{e}^{(\tau n^2{\xi }^2+n{\psi }_Z\times e^{2\tau -\tau B_n})}.\hfill \end{array}$$

By taking $\tau ={\displaystyle \frac{1}{2}}log\left({\displaystyle \frac{B_n-n^2{\xi }^2}{2n{\psi }_Z}}\right)$, then for any $\rho >0$,

$$\mathbb{P}(\sqrt{n}|{\widehat{\theta }}_n-\theta |>\rho )\le 4M{e}^{-{\displaystyle \frac{n({\xi }^2{\rho }^2-\mathbb{E}{Z}_i)}{2}}[log\left({\displaystyle \frac{{\xi }^2{\rho }^2-\mathbb{E}{Z}_i}{2{\phi }_z}}\right)-1]}+2M{e}^{-{\displaystyle \frac{(n^2{\xi }^2-B_n)}{2}}[log\left({\displaystyle \frac{B_n-n^2{\xi }^2}{2n{\psi }_Z}}\right)-1]}$$

□

Corollary 3.

Whenever the sequence ${\widehat{\theta }}_n$ completely converges to the parameter θ of the first-order autoregressive process, then we can conclude that

$$\sum _n^{\propto }\mathbb{P}(\sqrt{n}|{\widehat{\theta }}_n-\theta |>\rho )<+\propto$$

Proof. 

By applying Theorem 3 and assuming that $\mathbb{E}{Z}_j^2$ is finite and ${\psi }_Z$ is finite, we may directly obtain the result stated in Corollary 3. □

6. Numerical Illustration

In this section, we provide a comprehensive numerical demonstration of concentration inequalities applied to a dataset generated from an autoregressive process with transformed residuals. Our main objective is to validate and visualize the concentration of the sum of transformed residuals around its expected value.

Concentration inequalities are vital tools in probability theory and statistical analysis, offering limits on the deviation of random variables from their expected values. This section explores the application of concentration inequalities to a dataset derived from an autoregressive process with transformed residuals, examining the implications of extreme value theory (EVT) on the distribution’s tails.

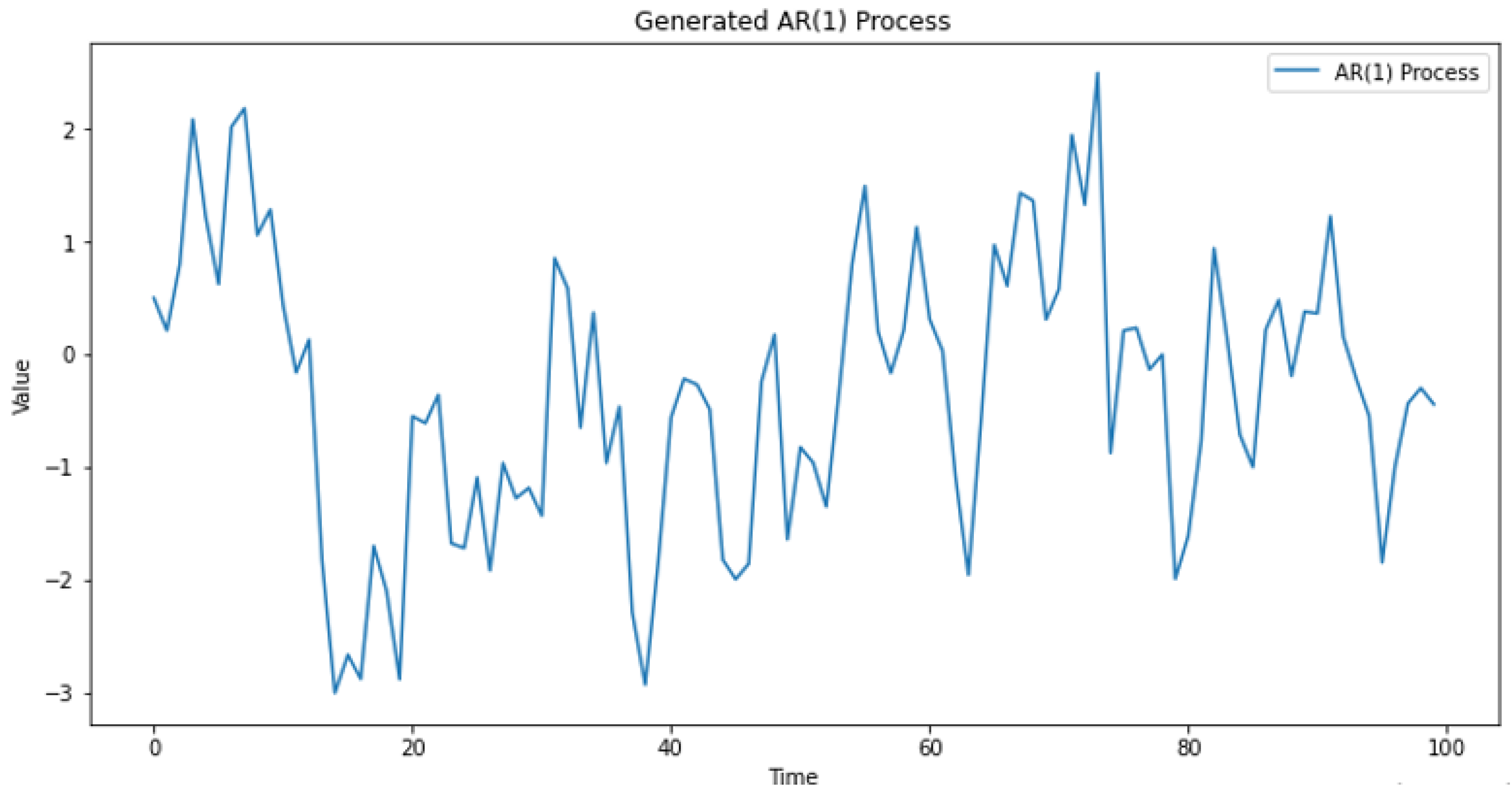
The methodology of this study involved generating a dataset that represents an autoregressive process AR(1) with residuals transformed into Extended Negative Dependence random variables (END) using the sine function, in Figure 1 and Figure 2 below.

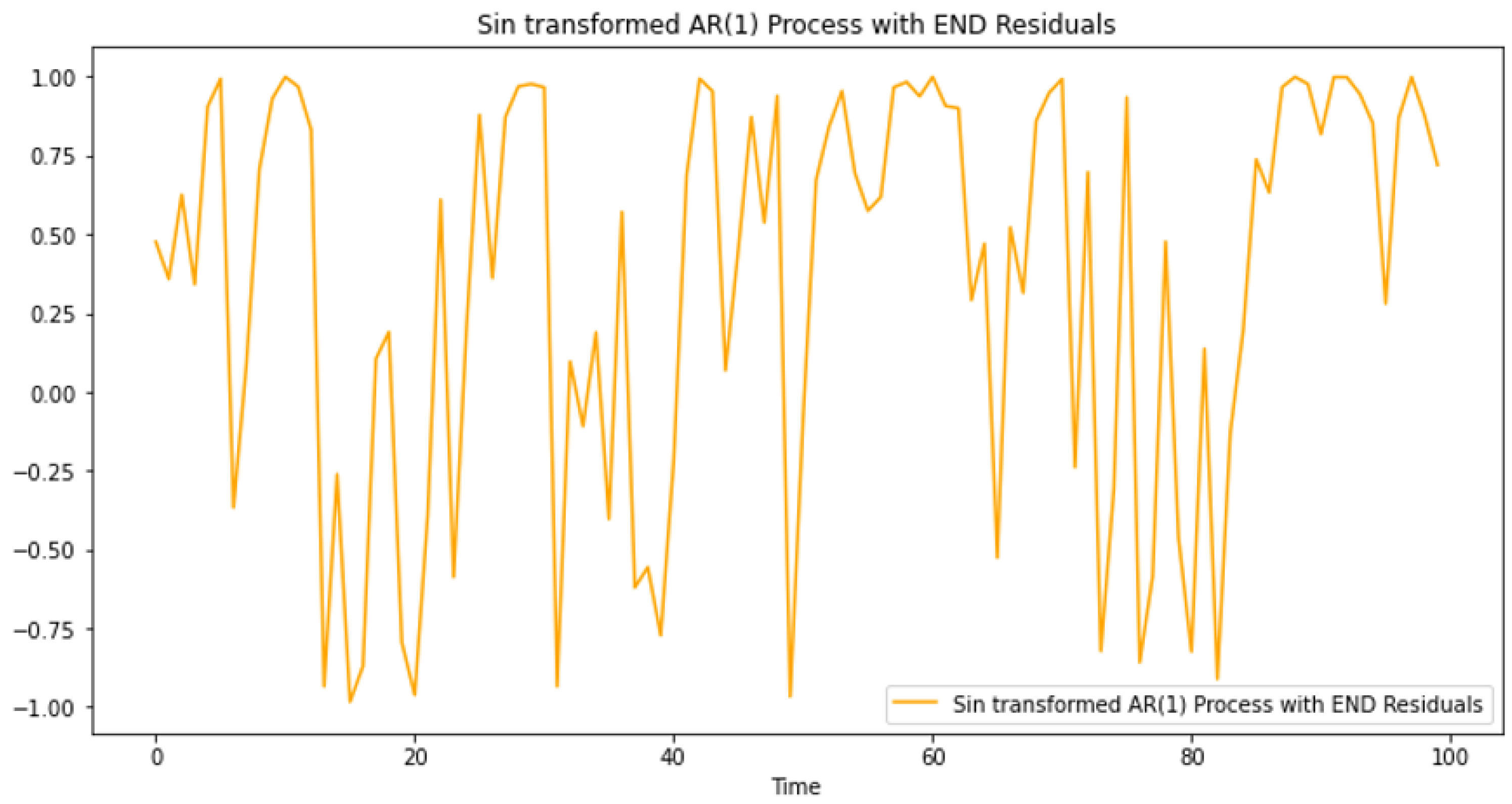
When we proceed to verify END properties for the transformed residuals, we find that the condition, for all k, ${0<\mathbb{E}\left(\right|Z-\mathbb{E}Z|}^k)\le {\phi }_z$, is not satisfied. Therefore, we apply an additional transformation using a sine function, Figure 3 below.

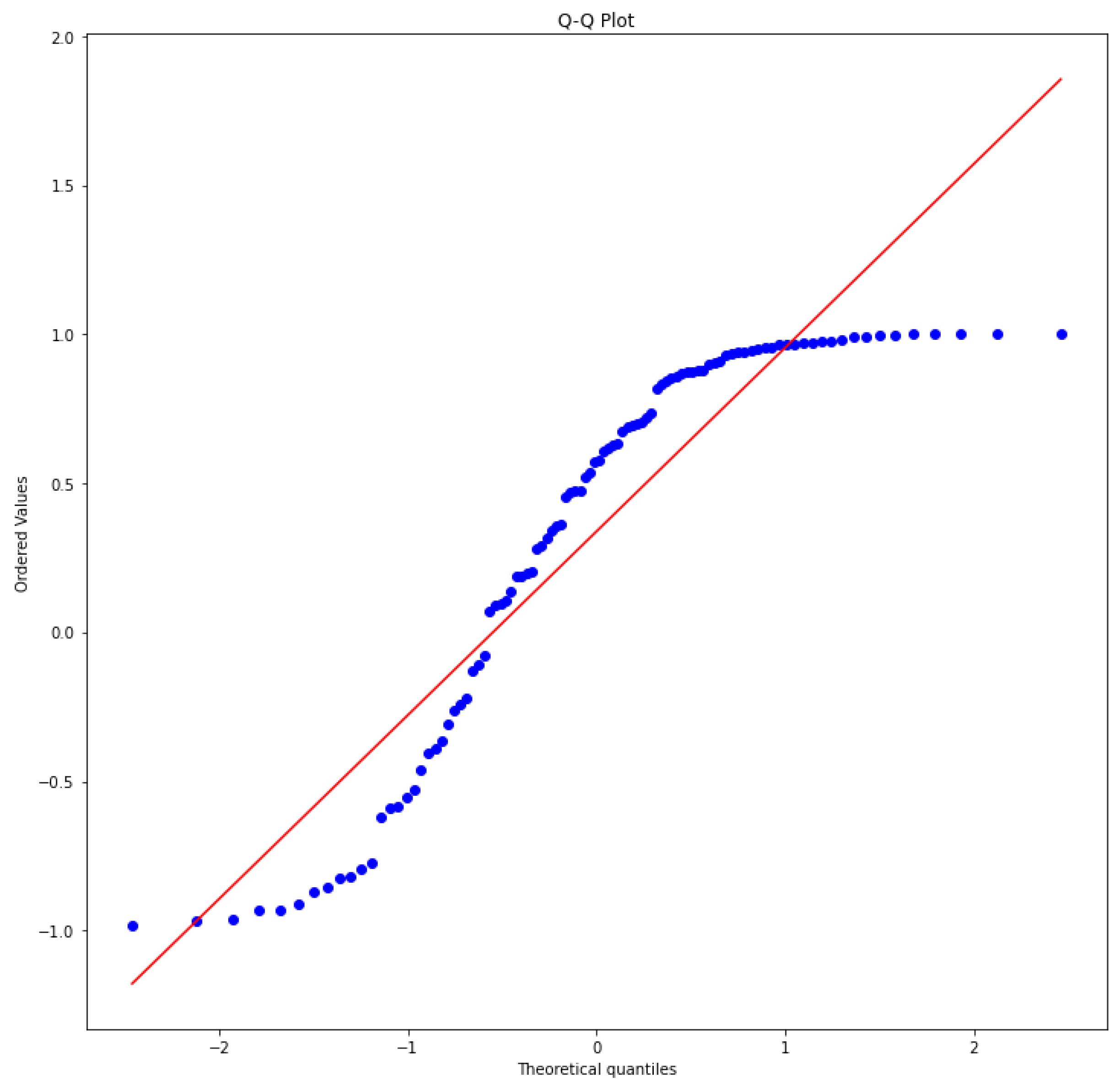
Before verifying the condition above for this final transformation, we ensure that the sine-transformed data remain Extended Negative Dependence random variables (ENDs) through moment conditions and the Q-Q plot in the Figure 4 below.

The points roughly follow a straight line from around −2.0 to 1.5 on the x-axis. This indicates that the data approximates a normal distribution.

Prior to delving into the concentration inequality, we rigorously confirm that the transformed residuals meet the conditions outlined by Theorem 1. Specifically, we validate that for all $k,$${0<\mathbb{E}\left(\right|Z-\mathbb{E}Z|}^k)\le {\phi }_z$.

Ensuring the meticulous verification of these conditions is crucial for laying the foundation for the subsequent analysis of concentration inequalities.

With these conditions confirmed, we proceed to compute the theoretical bound for the concentration inequality. The bound is expressed as

$$\mathbb{P}\left(\right|S_n-\mathbb{E}{S}_n|>n\xi )\le 4M{e}^{{\displaystyle \frac{-n\xi }{2}}\left[log\left({\displaystyle \frac{\xi }{2{\phi }_Z}}\right)-1\right]}$$

where M, $\xi$, and ${\phi }_Z$ are constants determined based on the characteristics of the transformed residuals.

Subsequently, we compute the actual probability of the sum of transformed residuals deviating from its expected value for varying sample sizes. This involves calculating the cumulative sum of the transformed data (Sn) and comparing it with the expected cumulative sum (ESn).

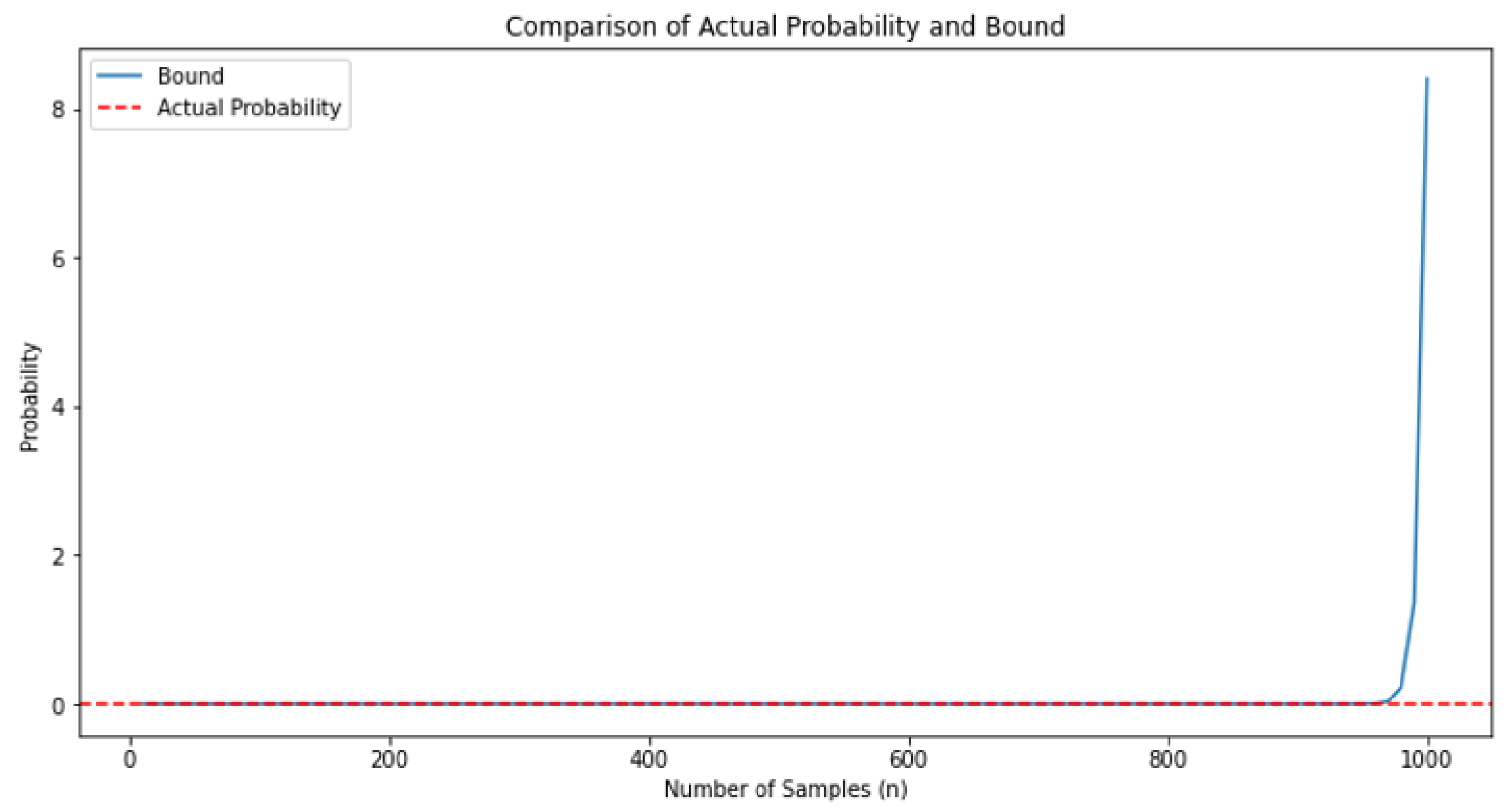
The culmination of our numerical illustration is visualized through a line plot. This plot showcases the theoretical bound alongside the actual probability for different sample sizes, offering a visual comparison of the concentration behavior in Figure 5 below.

The results obtained from the numerical illustration shed light on the concentration behavior of the sum of transformed residuals. The visual comparison of the theoretical bound and the actual probability reinforces the validity of the concentration inequality for the given dataset.

Furthermore, the verification of conditions ensures the applicability of Theorem 1 to the transformed residuals, affirming the foundational assumptions crucial for the subsequent analysis.

In conclusion, this section provides a comprehensive numerical illustration of concentration inequalities applied to transformed residuals from an autoregressive process. Through meticulous verification of conditions, calculation of theoretical bounds, and visual comparison with actual probabilities, we gain insights into the concentration behavior of the transformed data.

This analysis contributes to a deeper understanding of statistical properties in the context of EVT, particularly for non-random variables exhibiting extreme value behavior. The verified concentration inequalities provide a solid foundation for subsequent analyses and form a basis for further exploration into the tails of the distribution.

Through this illustration, we not only showcase the application of concentration inequalities but also emphasize the importance of thorough verification and visual representation in establishing the reliability of statistical results.

7. Conclusions

Our research investigates the complete convergence of Extended Negative Dependence (END) random variables and their applications in autoregressive AR(1) models. By employing exponential inequalities and specific inequalities for the likelihood of END variables, we demonstrate significant insights into their convergence properties. Our findings show that the proposed concentration inequalities effectively characterize the statistical behavior of END random variables.

The results from our theoretical analysis and numerical illustrations underscore the robustness of our approach. Specifically, the application of our methodology to AR(1) models reveals important dynamics and convergence properties of END variables, validating the practical significance of our theoretical contributions.

Moving forward, our methodology can be extended to other statistical models to further validate its applicability. Additionally, exploring higher-order moments and different tail behaviors in real-world datasets can enhance our understanding of extreme events and dependencies. This research lays a solid foundation for future studies, encouraging further collaboration and innovation in statistical analysis and extreme value theory.