On Lebesgue Constants
Abstract
1. Introduction
- Fejér [5] proved the formula
- Szegö [6] contributed with the formula
- Hardy [8] discovered two integral representationsLater, other mathematicians contributed with two-sided estimates. Zhao [9] discovered bilateral inequalities that help improve Watson’s asymptotic expansion formulae. In [3], new inequalities for the Lebesgue constants were established, which allowed the authors to obtain an asymptotic expansion of in terms of . More recently, other contributions have been published. Shakirov approximated the Lebesgue constant using a logarithmic function [10] and using the logarithmic–fractional–rational function [4]. The asymptotic behavior of was also studied in [11], although indirectly, since the authors studied the properties of the Dirichlet kernel, which is related to the integrand function appearing in (8). It must be remarked that (1) can be rewritten in the formwhere As is an odd integer, we are interested in treating the even case too. Therefore, the main goals of the paper are as follows:
- Consider the more general expressionkeeping the designation “Lebesgue constants”;
- Reproduce Fejér’s results using a simpler approach;
- Obtain simple asymptotic formulae.
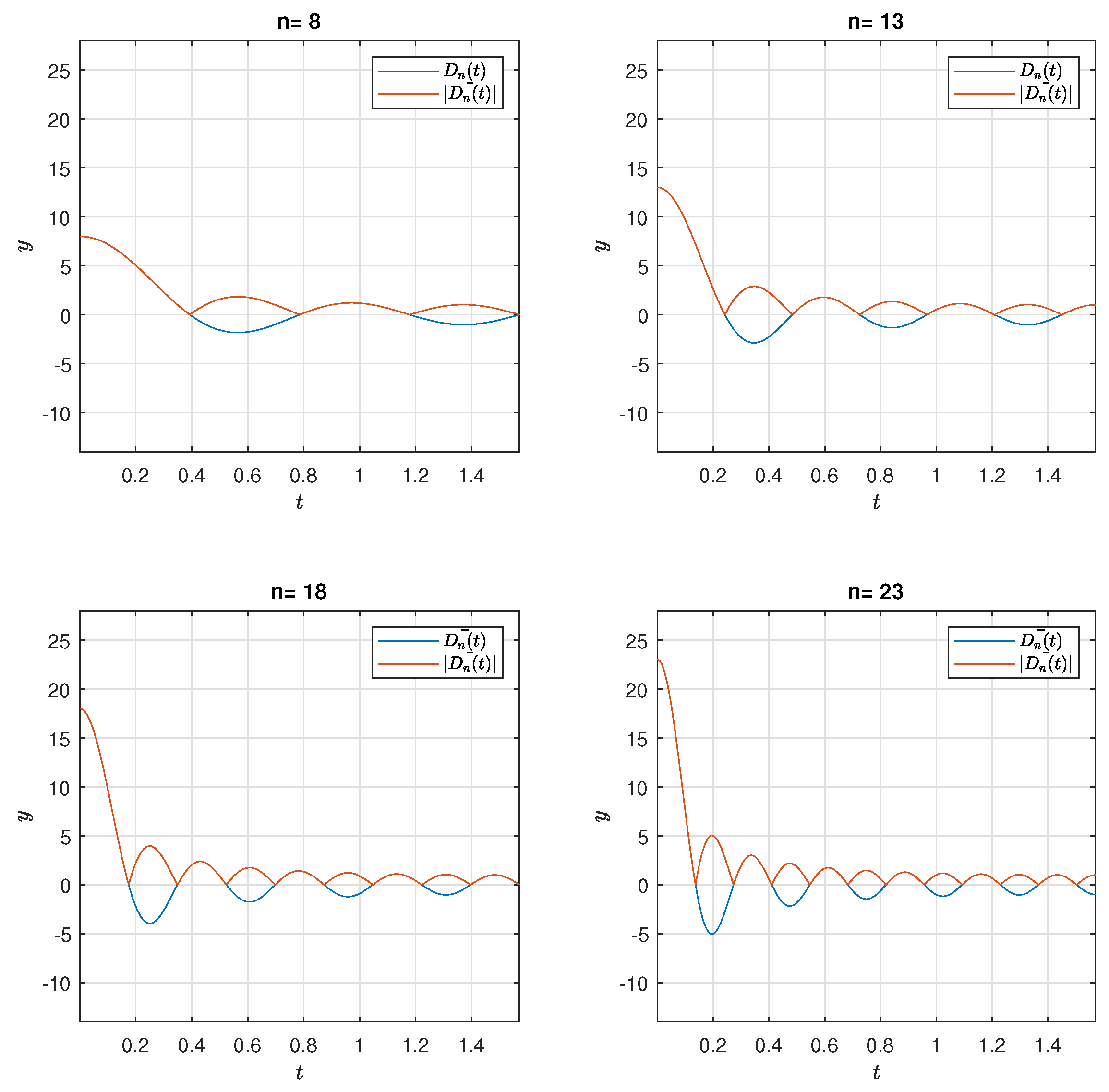
2. The Way to the Lebesgue Constants
3. New Formulation
3.1. Preliminaries
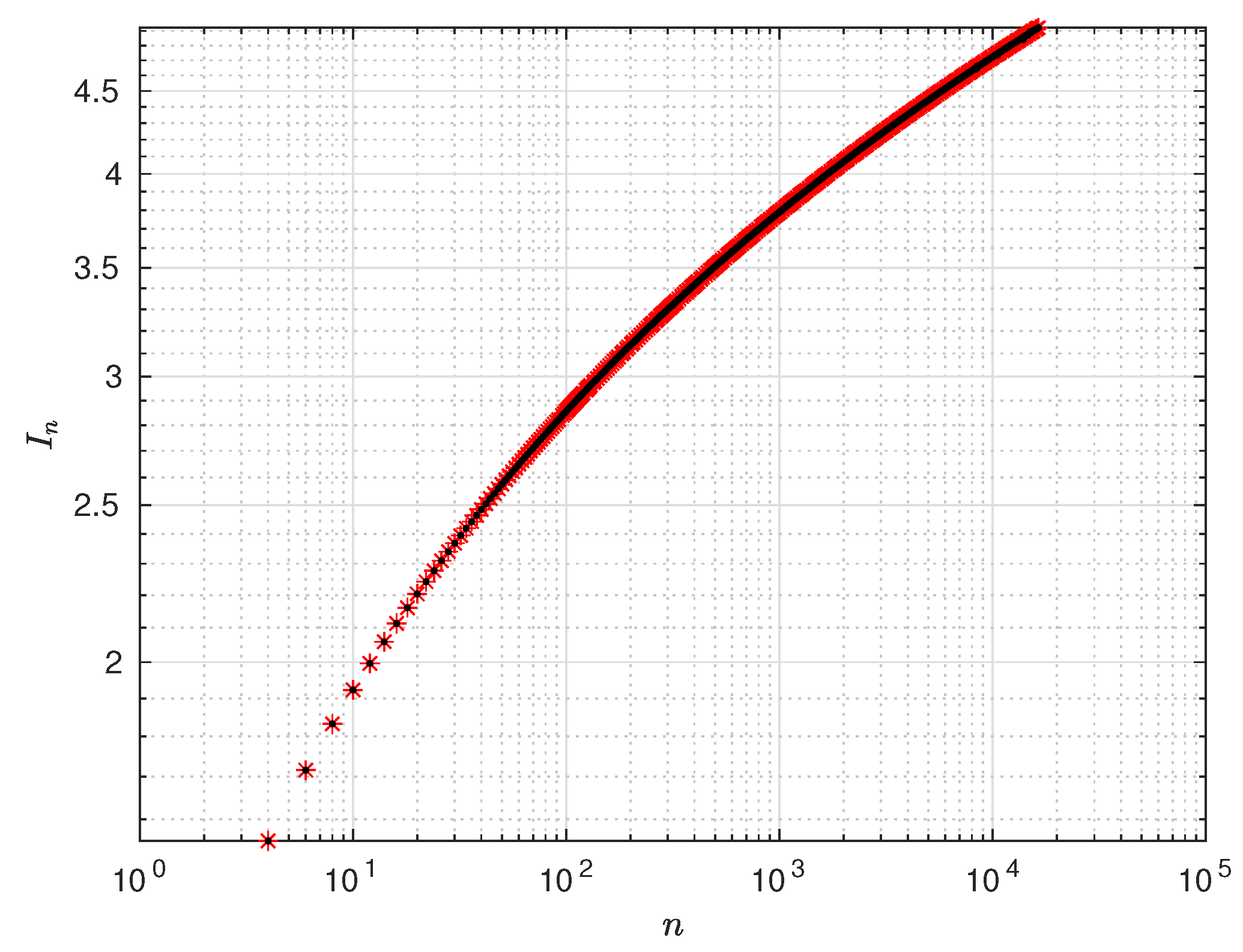
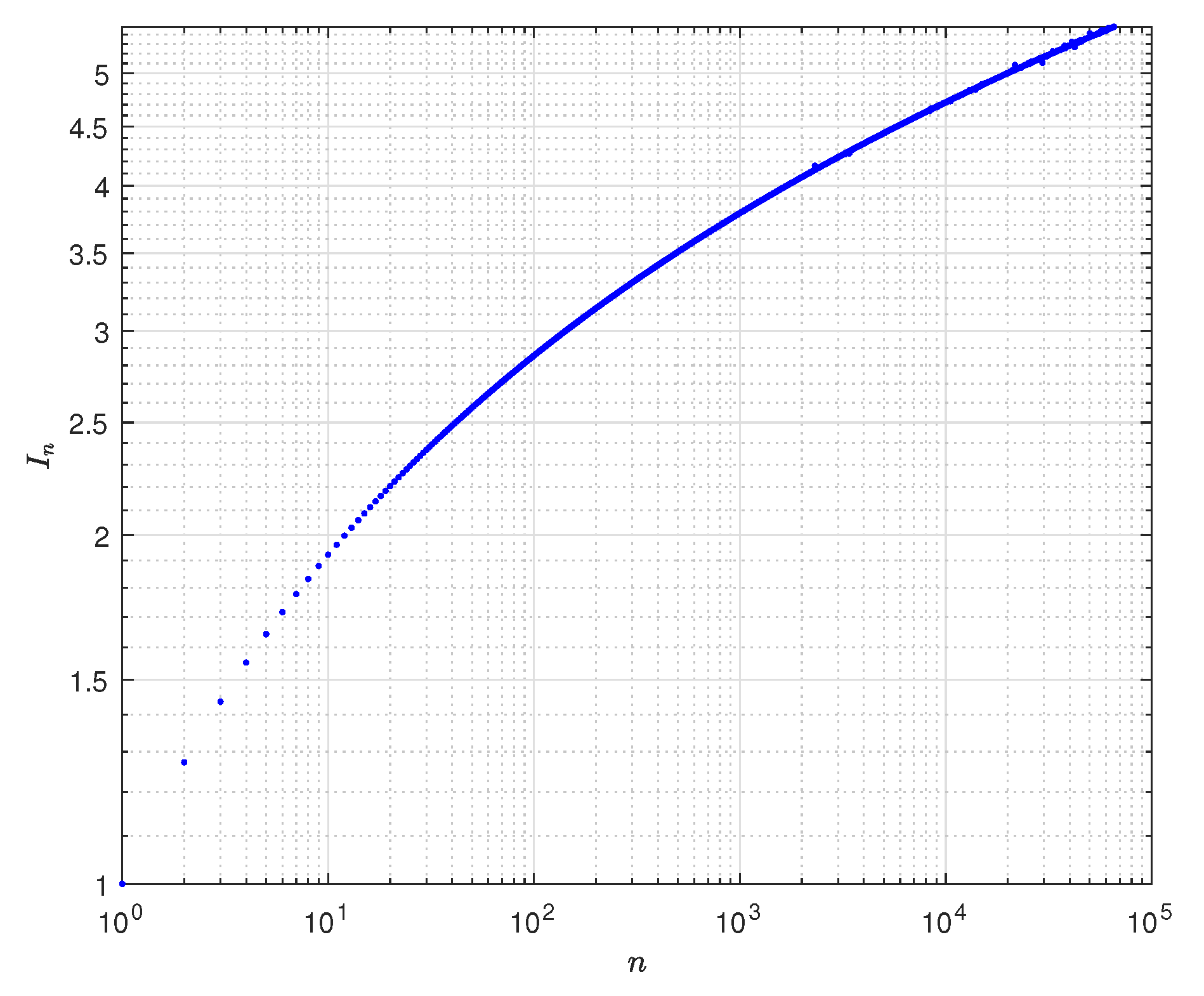
3.2. The Even n Case
3.3. The Odd n Case
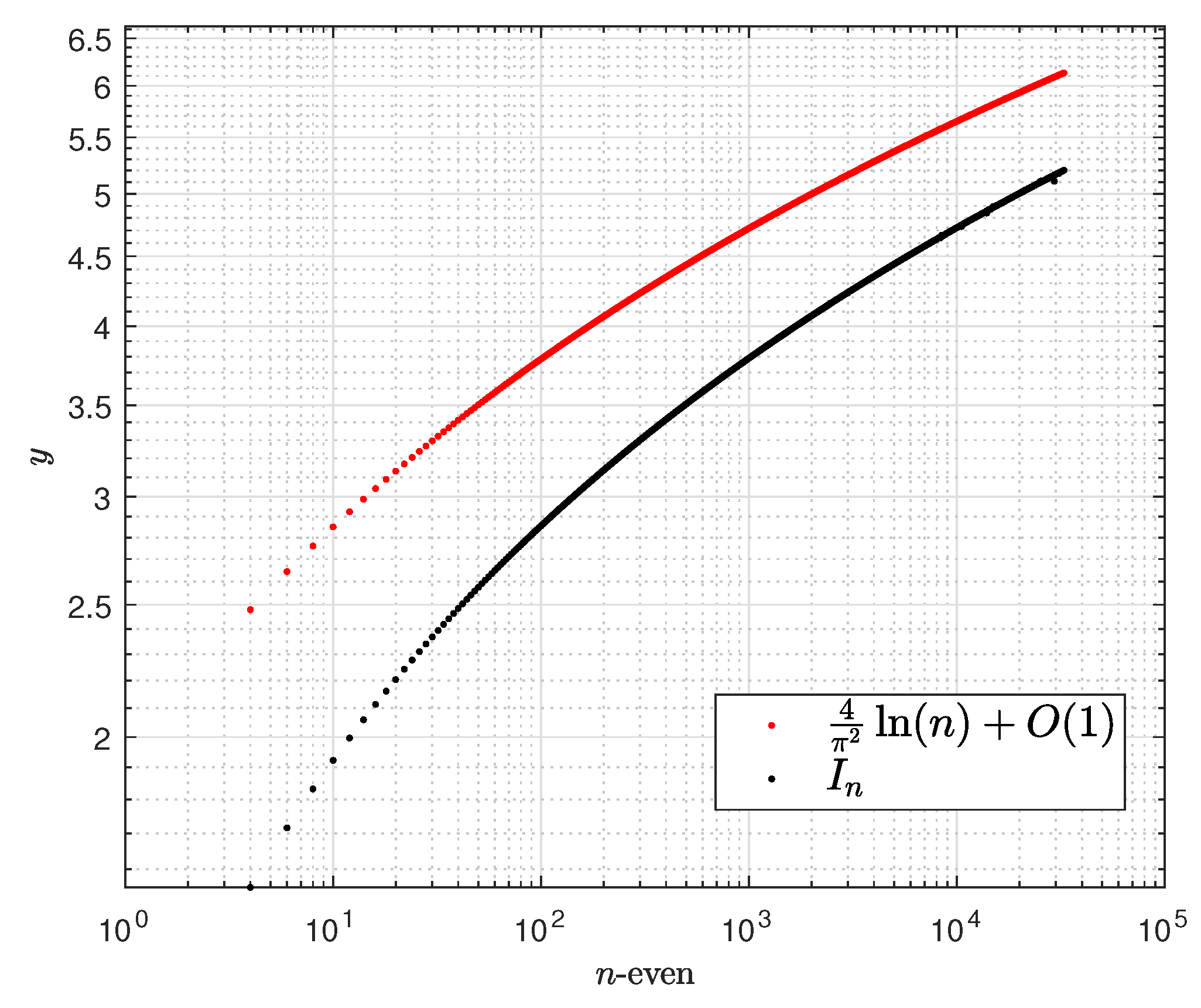
4. Asymptotic Behavior
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Finch, S. Mathematical Constants; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Lebesgue, H. Sur la représentation trigonométrique approchée des fonctions satisfaisant à une condition de Lipschitz. Société Mathématique Fr. 1910, 38, 184–210. [Google Scholar] [CrossRef]
- Chen, C.; Choi, J. Inequalities and asymptotic expansions for the constants of Landau and Lebesgue. Appl. Math. Comput. 2014, 248, 610–624. [Google Scholar] [CrossRef]
- Shakirov, I.A. Approximation of the Lebesgue constant of the Fourier operator by a logarithmic-fractional-rational function. Russ. Math. 2023, 67, 64–74. [Google Scholar] [CrossRef]
- Fejér, L. Sur les singularités de la série de Fourier des fonctions continues. In Annales Scientifiques de L’École Normale Supérieure; Elsevier: Amsterdam, The Netherlands, 1911; Volume 28, pp. 63–104. [Google Scholar]
- Szego, G. Über die Lebesgueschen konstanten bei den Fourierschen reihen. Math. Z. 1921, 9, 163–166. [Google Scholar] [CrossRef]
- Watson, G. The constants of Landau and Lebesgue. Quart. J. Math. 1930, 1, 310–318. [Google Scholar] [CrossRef]
- Hardy, G. Note on Lebesgue’s constants in the theory of Fourier series. J. Lond. Math. Soc. 1942, 1, 4–13. [Google Scholar] [CrossRef]
- Zhao, D. Some sharp estimates of the constants of Landau and Lebesgue. J. Math. Anal. Appl. 2009, 349, 68–73. [Google Scholar] [CrossRef]
- Shakirov, I. Approximation of the Lebesgue constant of the Fourier operator by a logarithmic function. Russ. Math. 2022, 66, 70–76. [Google Scholar] [CrossRef]
- Alvarez, J.; Guzmán-Partida, M. Properties of the Dirichlet kernel. Electron. J. Math. Anal. Appl. 2023, 11, 96–110. [Google Scholar] [CrossRef]
- Stein, E.; Shakarchi, R. Fourier Analysis: An Introduction; Princeton University Press: Princeton, NJ, USA, 2011; Volume 1. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ortigueira, M.D.; Bengochea, G. On Lebesgue Constants. Axioms 2024, 13, 505. https://doi.org/10.3390/axioms13080505
Ortigueira MD, Bengochea G. On Lebesgue Constants. Axioms. 2024; 13(8):505. https://doi.org/10.3390/axioms13080505
Chicago/Turabian StyleOrtigueira, Manuel Duarte, and Gabriel Bengochea. 2024. "On Lebesgue Constants" Axioms 13, no. 8: 505. https://doi.org/10.3390/axioms13080505
APA StyleOrtigueira, M. D., & Bengochea, G. (2024). On Lebesgue Constants. Axioms, 13(8), 505. https://doi.org/10.3390/axioms13080505