Modelling Up-and-Down Moves of Binomial Option Pricing with Intuitionistic Fuzzy Numbers
Abstract
1. Introduction
- We model uncertainty via IFNs, which generalize FNs, in an option pricing context. Introducing parameter quantification with IFNs allows for the incorporation of bipolar information; that is, capturing values that can actually take the parameter, as well as those that are definitely not [37]. It should not be understood that IFNs introduce more uncertainty in parameter estimation but rather introduce new information [38]. Although intuitionistic fuzzy uncertainty has been considered in some studies [39,40,41,42,43], it is quite residual and absent in fuzzy binomial modelling.
- We propose a methodology that allows for the adjustment of the volatility necessary to value the option as an IFN using the historical volatility approach [4] and the concept of coherent probability–possibility transformation [44]. This focus has been adopted to fit fuzzy number parameters in an FROP setting to price stock options [10], in a real options setting [45], and in the field of valuation of interest-sensitive instruments [46].
- We contribute to FROP in a binomial setting by critically proposing the modelling of up-and-down moves in the valuation of the path-dependent option under assessment. We compared the commonly used fuzzy literature CRR with the alternative of Rendleman and Bartter [7]. In this sense, given that the use of the binomial model is justified by its convergence to the BSM, the evaluation of binomial models is carried out by comparing the proximity of their calculated price with the BSM in a European option with the same characteristics as those intended to be evaluated [47].
2. Intuitionistic Fuzzy Estimates of Statistical Parameters and Intuitionistic Fuzzy Number Arithmetic
2.1. Fuzzy Numbers, Intuitionistic Fuzzy Numbers, and Distance between Intuitionistic Fuzzy Numbers
2.2. Fitting Statistical Parameters with Intuitionistic Fuzzy Numbers
- To determine historical volatility, the desired time horizon (e.g., 30 days, 60 days) must be specified. The choice of horizon will determine the core of the IFN that quantifies volatility.
- The time horizon for volatility affects the breadth of the membership and nonmembership functions: a shorter time horizon implies fewer observations for calculating volatility and broader confidence intervals (17) and (18).
- The percentiles used to set the upper and lower possibility functions determine their breadth. The percentiles associated with lower probabilities result in narrower membership and nonmembership functions. For example, using 90% rules for the lower possibility function and 95% for the upper possibility function would result in narrower -cuts.
2.3. Intuitionistic Fuzzy Number Arithmetic
3. An Extension Black–Scholes–Merton and Binomial Option Pricing Model for the Use of Intuitionistic Fuzzy Parameters
3.1. Pricing European Options with the Black–Scholes–Merton Model and Intuitionistic Fuzzy Parameters
3.2. Pricing European Options with a Binomial Model and Intuitionistic Fuzzy Parameters
- As expected, both the CRR and the RB converge to the BSM since when .
- For the in-the-money options, the number of times that the CRR and RB are the closest to the BSM is the same (50%). The RB provides the closest price when there is only one move, and the CRR provides the closest price when the number of moves is the maximum ( = 504).
- For out-of-the-money options, the RB tends to provide better approximations to the BSM. However, when the movement frequency is annual, the CRR is better, but when , the price closest to the BSM comes from the RB.
- For at-the-money options, the best model is the RB model, regardless of the movement frequency.
- The price equations are monotonic functions of volatility, so the extremes of and are easily programmable even in a spreadsheet. On the other hand, the calculation of the integrals to obtain and has been carried out via Simpson’s rule with the discretization of the -cuts, which in our case have been obtained as = 0, 0.25, 0.5, 0.75, 1, and 1 − . Thus, these calculations are also easily implemented with a spreadsheet.
4. Assessment of the Convergence of Two Alternative Binomial Moves Modelling to Black–Scholes–Merton Prices with Intuitionistic Fuzzy Volatility
4.1. Materials and Methods
- Step 1: We identified five scenarios of low volatility, five of medium volatility, and five of high volatility. The low-volatility scenarios are the 1st, 5th, 19th, 20th, and 30th percentiles of historical volatility. The medium volatility scenarios are determined from percentiles 40, 45, 50, 55, and 60 of the calculated standard deviations. The high-volatility scenarios are identified with 70th, 80th, 90th, 95th, and 99th percentiles. Table 4 shows the <0,1>-cut, <0.5,0.5>-cut, and <1,0>-cut of the volatility scenarios considered in this empirical application.
- Step 2: For these volatility scenarios, we fit an intuitionistic estimation using Equations (16)–(19). We used 95 and 99.7 rules to adjust the membership and nonmembership functions, respectively. Thus, with γ = 0.05, we obtain , and with γ* = 0.003, and so
- Step 3: We determined the prices of the evaluated European call options (for = 0.9, 1, 1.1, and = 1) for all evaluated volatility scenarios. To calculate the binomial prices, we used periodicities /504, 1/252, 1/48, 1/24, 1/12, 1/4, 1/2, 1}.
- Step 4: In all valuations, we determined the distance (5) between the value obtained with the BSM and the tested binomial models; that is, . Comparing the distances of the prices obtained with CRR and RB in a specific option, volatility scenario, and move frequency with respect to the benchmark, the BSM, allows us to establish which model converges better to the BSM.
- Step 5: We conducted three analyses of the convergence of the binomial IFN to the intuitionistic BSM as follows:
- We analysed the level of convergence for each degree of moneyness (in the money, out of the money, and at the money) separately, considering all volatility scenarios and moving frequencies together.
- We analysed the convergence levels by differentiating the degree of moneyness and movement frequency by considering conjointly all volatility scenarios. Within move frequencies, we differentiated between ‘low’ frequencies (monthly, quarterly, semiannual, and annual) and ‘high’ frequencies (every 12 h, daily, weekly, and every half month).
- We analysed the convergence levels by differentiating the moneyness degree and volatility scenarios without differentiating move periodicity. Within the volatility scenarios, we differentiated low-volatility, medium-volatility, and high-volatility scenarios, as indicated in Table 4.
4.2. Results
5. Conclusions and Further Research
Funding
Data Availability Statement
Conflicts of Interest
References
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–654. Available online: http://www.jstor.org/stable/1831029 (accessed on 13 October 2023). [CrossRef]
- Merton, R.C. Theory of rational option pricing. Bell J. Econ. Manag. Sci. 1973, 4, 141–183. [Google Scholar] [CrossRef]
- Hull, J.C. Options Futures and Other Derivatives; Pearson Education: New Delhi, India, 2008. [Google Scholar]
- Van der Hoek, J.; Elliott, R.J. Binomial Models in Finance; Springer: New York, NY, USA, 2006. [Google Scholar]
- Chance, D.M. A Synthesis of Binomial Option Pricing Models for Lognormally Distributed Assets. J. Appl. Financ. (Former. Financ. Pract. Educ.) 2008, 18, 38–56. [Google Scholar] [CrossRef]
- Cox, J.; Ross, S.; Rubinstein, M. Option Pricing: A Simplified Approach. J. Financ. Econ. 1979, 7, 229–263. [Google Scholar] [CrossRef]
- Rendleman, R.J., Jr.; Bartter, B.J. Two state option pricing. J. Financ. 1979, 34, 1092–1110. [Google Scholar]
- Trigeorgis, L. A log-transformed binomial numerical analysis method for valuing complex multioption investments. J. Financ. Quant. Anal. 1991, 26, 309–326. [Google Scholar] [CrossRef]
- Jabbour, G.M.; Kramin, M.V.; Young, S.D. Two-state option pricing: Binomial models revisited. J. Futures Mark. Futures Options Other Deriv. Prod. 2001, 21, 987–1001. [Google Scholar] [CrossRef]
- Chrysafis, K.A.; Papadopoulos, B.K. On theoretical pricing of options with fuzzy estimators. J. Comput. Appl. Math. 2009, 223, 552–566. [Google Scholar] [CrossRef]
- Carlsson, C.; Fuller, R. A fuzzy approach to real option valuation. Fuzzy Sets Syst. 2003, 139, 297–312. [Google Scholar] [CrossRef]
- Andrés-Sánchez, J. A systematic review of the interactions of fuzzy set theory and option pricing. Expert Syst. Appl. 2023, 223, 119868. [Google Scholar] [CrossRef]
- Muzzioli, S.; De Baets, B. Fuzzy approaches to option price modelling. IEEE Trans. Fuzzy Syst. 2016, 25, 392–401. [Google Scholar] [CrossRef]
- Romaniuk, M.; Hryniewicz, O. Interval-based, nonparametric approach for resampling of fuzzy numbers. Soft Comput. 2019, 23, 5883–5903. [Google Scholar] [CrossRef]
- Zmeskal, Z. Application of the fuzzy-stochastic methodology to appraising the firm value as a European call option. Eur. J. Oper. Res. 2001, 135, 303–310. [Google Scholar] [CrossRef]
- Wu, H.C. Pricing European options based on the fuzzy pattern of Black-Scholes formula. Comput. Oper. Res. 2004, 31, 1069–1081. [Google Scholar] [CrossRef]
- Guerra, M.L.; Sorini, L.; Stefanini, L. Option price sensitivities through fuzzy numbers. Comput. Math. Appl. 2011, 61, 515–526. [Google Scholar] [CrossRef]
- Kim, Y.; Lee, E.B. Optimal Investment Timing with Investment Propensity Using Fuzzy Real Options Valuation. Int. J. Fuzzy Syst. 2018, 20, 1888–1900. [Google Scholar] [CrossRef]
- Muzzioli, S.; Gambarelli, L.; De Baets, B. Indices for Financial Market Volatility Obtained Through Fuzzy Regression. Int. J. Inf. Technol. Decis. Mak. 2018, 17, 1659–1691. [Google Scholar] [CrossRef]
- Muzzioli, S.; Gambarelli, L.; De Baets, B. Option implied moments obtained through fuzzy regression. Fuzzy Optim. Decis. Mak. 2020, 19, 211–238. [Google Scholar] [CrossRef]
- Capotorti, A.; Figà-Talamanca, G. SMART-or and SMART-and fuzzy average operators: A generalized proposal. Fuzzy Sets Syst. 2020, 395, 1–20. [Google Scholar] [CrossRef]
- Anzilli, L.; Villani, G. Cooperative R&D investment decisions: A fuzzy real option approach. Fuzzy Sets Syst. 2023, 458, 143–164. [Google Scholar] [CrossRef]
- Zhang, H.; Watada, J. Fuzzy Levy-GJR-GARCH American option pricing model based on an infinite pure jump process. IEICE Trans. Inf. Syst. 2018, E101D, 1843–1859. [Google Scholar] [CrossRef]
- Nowak, P.; Pawłowski, M. Application of the Esscher Transform to Pricing Forward Contracts on Energy Markets in a Fuzzy Environment. Entropy 2023, 25, 527. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, Y. A discrete-time model of American put option in an uncertain environment. Eur. J. Oper. Res. 2003, 151, 153–166. [Google Scholar] [CrossRef]
- Muzzioli, S.; Torricelli, C. A multiperiod binomial model for pricing options in a vague world. J. Econ. Dyn. Control 2004, 28, 861–887. [Google Scholar] [CrossRef]
- Lee, C.F.; Tzeng, G.-H.; Wang, S.-Y. A fuzzy set approach for generalized CRR model: An empirical analysis of S&P 500 index options. Rev. Quant. Financ. Account. 2005, 25, 255–275. [Google Scholar] [CrossRef]
- Wang, G.X.; Wang, Y.Y.; Tang, J.M. Fuzzy Option Pricing Based on Fuzzy Number Binary Tree Model. IEEE Trans. Fuzzy Syst. 2022, 30, 3548–3558. [Google Scholar] [CrossRef]
- Meenakshi, K.; Kennedy, F.C. A study of european fuzzy put option buyers model on future contracts involving general trapezoidal fuzzy numbers. Glob. Stoch. Anal. 2021, 8, 47–59. [Google Scholar] [CrossRef]
- Meenakshi, K.; Kennedy, F.C. On some properties of American fuzzy put option model on fuzzy future contracts involving general linear octagonal fuzzy numbers. Adv. Appl. Math. Sci. 2021, 21, 331–342. [Google Scholar] [CrossRef]
- Zmeskal, Z. Generalized soft binomial American real option pricing model (fuzzy-stochastic approach). Eur. J. Oper. Res. 2010, 207, 1096–1103. [Google Scholar] [CrossRef]
- Ho, S.H.; Liao, S.H. A fuzzy real option approach for investment. Expert Syst. Appl. 2011, 38, 15296–15302. [Google Scholar] [CrossRef]
- Anzilli, L.; Facchinetti, G.; Pirotti, T. Pricing of minimum guarantees in life insurance contracts with fuzzy volatility. Inf. Sci. 2018, 460, 578–593. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Yin, J.B. Assessment of investment decisions in bulk shipping through fuzzy real options analysis. Marit. Econ. Logist. 2023, 25, 122–139. [Google Scholar] [CrossRef]
- Zhang, M.J.; Qin, X.Z.; Nan, J.X. Binomial tree model of the European option pricing based on the triangular intuitionistic fuzzy numbers. Syst. Eng. Theory Pract. 2013, 33, 34–40. [Google Scholar] [CrossRef]
- Zmeskal, Z.; Dluhosova, D.; Gurny, P.; Kresta, A. Generalized soft multimode real options model (fuzzy-stochastic approach). Expert Syst. Appl. 2022, 192, 116388. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. An overview of the asymmetric bipolar representation of positive and negative information in possibility theory. Fuzzy Sets Syst. 2009, 160, 1355–1366. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Gradualness, uncertainty and bipolarity: Making sense of fuzzy sets. Fuzzy Sets Syst. 2012, 192, 3–24. [Google Scholar] [CrossRef]
- Wu, L.; Liu, J.F.; Wang, J.T.; Zhuang, Y.M. Pricing for a basket of LCDS under fuzzy environments. SpringerPlus 2016, 5, 1747. [Google Scholar] [CrossRef]
- Wu, L.; Zhuang, Y.M.; Li, W. A New Default Intensity Model with Fuzziness and Hesitation. Int. J. Comput. Intell. Syst. 2016, 9, 340–350. [Google Scholar] [CrossRef]
- Wu, L.; Mei, X.B.; Sun, J.G. A New Default Probability Calculation Formula an Its Application under Uncertain Environments. Discret. Dyn. Nat. Soc. 2018, 2018, 3481863. [Google Scholar] [CrossRef]
- Ersen, H.Y.; Tas, O.; Kahraman, C. Intuitionistic fuzzy real-options theory and its application to solar energy investment projects. Eng. Econ. 2018, 29, 140–150. [Google Scholar] [CrossRef]
- Ersen, H.Y.; Tas, O.; Ugurlu, U. Solar Energy Investment Valuation with Intuitionistic Fuzzy Trinomial Lattice Real Option Model. IEEE Trans. Eng. Manag. 2023, 70, 2584–2593. [Google Scholar] [CrossRef]
- Dubois, D.; Folloy, L.; Mauris, G.; Prade, H. Probability–possibility transformations, triangular fuzzy sets, and probabilistic inequalities. Reliab. Comput. 2004, 10, 273–297. [Google Scholar] [CrossRef]
- Chrysafis, K.A.; Papadopoulos, B.K. Decision Making for Project Appraisal in Uncertain Environments: A Fuzzy-Possibilistic Approach of the Expanded NPV Method. Symmetry 2021, 13, 27. [Google Scholar] [CrossRef]
- Andrés-Sánchez, J. A Fuzzy-Random Extension of Jamshidian’s Bond Option Pricing Model and Compatible One-Factor Term Structure Models. Axioms 2023, 12, 668. [Google Scholar] [CrossRef]
- Hull, J.; White, A. The use of the control variate technique in option pricing. J. Financ. Quant. Anal. 1988, 23, 237–251. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Fuzzy numbers: An overview. In Readings in Fuzzy Sets and Intelligent Systems; Dubois, D., Prade, H., Yager, R.R., Eds.; Elsevier: Amsterdam, The Netherlands, 1993; pp. 112–148. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Kahraman, C.; Onar, Ç.; Öztayşi, B. Engineering economic analyses using intuitionistic and hesitant fuzzy sets. J. Intell. Fuzzy Syst. 2015, 29, 1151–1168. [Google Scholar] [CrossRef]
- Mitchell, H.B. Ranking-intuitionistic fuzzy numbers. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2004, 12, 377–386. [Google Scholar] [CrossRef]
- Arefi, M.; Taheri, S.M. Least-Squares Regression Based on Atanassov’s Intuitionistic Fuzzy Inputs–Outputs and Atanassov’s Intuitionistic Fuzzy Parameters. IEEE Trans. Fuzzy Syst. 2015, 23, 1142–1154. [Google Scholar] [CrossRef]
- Mohan, S.; Kannusamy, A.P.; Samiappan, V. A new approach for ranking of intuitionistic fuzzy numbers. J. Fuzzy Ext. Appl. 2020, 1, 15–26. [Google Scholar]
- Couso, I.; Montes, S.; Gil, P. The necessity of the strong α-cuts of a fuzzy set. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2001, 9, 249–262. [Google Scholar] [CrossRef]
- Mauris, G.; Lasserre, V.; Foulloy, L. A fuzzy approach for the expression of uncertainty in measurement. Measurement 2001, 29, 165–177. [Google Scholar] [CrossRef]
- Buckley, J.J. Fuzzy statistics: Hypothesis testing. Soft Comput. 2005, 9, 512–518. [Google Scholar] [CrossRef]
- Falsafain, A.; Taheri, S.M. On Buckley’s approach to fuzzy estimation. Soft Comput. 2011, 15, 345–349. [Google Scholar] [CrossRef]
- Sfiris, D.S.; Papadopoulos, B.K. Nonasymptotic fuzzy estimators based on confidence intervals. Inf. Sci. 2014, 279, 446–459. [Google Scholar] [CrossRef]
- Adjenughwure, K.; Papadopoulos, B. Fuzzy-statistical prediction intervals from crisp regression models. Evol. Syst. 2020, 11, 201–213. [Google Scholar] [CrossRef]
- Al-Kandari, M.; Adjenughwure, K.; Papadopoulos, K. A Fuzzy-Statistical Tolerance Interval from Residuals of Crisp Linear Regression Models. Mathematics 2020, 8, 1422. [Google Scholar] [CrossRef]
- Alostad, H.; Davulcu, H. Directional prediction of stock prices using breaking news on Twitter. Web Intell. 2017, 15, 1–17. [Google Scholar] [CrossRef]
- Parvathi, R.; Malathi, C.; Akram, M.; Atanassov, K. Intuitionistic fuzzy linear regression analysis. Fuzzy Optim. Decis. Mak. 2013, 12, 215–229. [Google Scholar] [CrossRef]
- Buckley, J.J.; Qu, Y. On using α-cuts to evaluate fuzzy equations. Fuzzy Sets Syst. 1990, 38, 309–312. [Google Scholar] [CrossRef]
- Black, F. The pricing of commodity contracts. J. Financ. Econ. 1976, 3, 167–179. [Google Scholar] [CrossRef]
- Thiagarajah, K.; Appadoo, S.S.; Thavaneswaran, A. Option valuation model with adaptive fuzzy numbers. Comput. Math. Appl. 2007, 53, 831–841. [Google Scholar] [CrossRef]
- Andrés-Sánchez, J. Pricing European Options with Triangular Fuzzy Parameters: Assessing Alternative Triangular Approximations in the Spanish Stock Option Market. Int. J. Fuzzy Syst. 2018, 20, 1624–1643. [Google Scholar] [CrossRef]
- Guerra, M.L.; Sorini, L.; Stefanini, L. Value Function Computation in Fuzzy Models by Differential Evolution. Int. J. Fuzzy Syst. 2017, 19, 1025–1031. [Google Scholar] [CrossRef]
- Li, H.; Ware, A.; Di, L.; Yuan, G.; Swishchuk, A.; Yuan, S. The application of nonlinear fuzzy parameters PDE method in pricing and hedging European options. Fuzzy Sets Syst. 2018, 331, 14–25. [Google Scholar] [CrossRef]
- Chen, H.M.; Hu, C.F.; Yeh, W.C. Option pricing and the Greeks under Gaussian fuzzy environments. Soft Comput. 2019, 23, 13351–13374. [Google Scholar] [CrossRef]
- Capotorti, A.; Figa-Talamanca, G. On an implicit assessment of fuzzy volatility in the Black and Scholes environment. Fuzzy Sets Syst. 2013, 223, 59–71. [Google Scholar] [CrossRef]
- Collan, M.; Carlsson, C.; Majlender, P. Fuzzy Black and Scholes real options pricing. J. Decis. Syst. 2003, 12, 391–416. [Google Scholar] [CrossRef]
- Tolga, A.Ç.; Kahraman, C.; Demircan, M.L. A Comparative Fuzzy Real Options Valuation Model using Trinomial Lattice and Black-Scholes Approaches: A Call Center Application. J. Mult.-Valued Log. Soft Comput. 2010, 16, 135. [Google Scholar]
- Boltürk, E.; Kahraman, C. Interval-valued and circular intuitionistic fuzzy present worth analyses. Informatica 2022, 33, 693–711. [Google Scholar] [CrossRef]
- Haktanır, E.; Kahraman, C. Intuitionistic fuzzy risk adjusted discount rate and certainty equivalent methods for risky projects. Int. J. Prod. Econ. 2023, 257, 108757. [Google Scholar] [CrossRef]
- Uzhga-Rebrov, O.; Grabusts, P. Methodology for Environmental Risk Analysis Based on Intuitionistic Fuzzy Values. Risks 2023, 11, 88. [Google Scholar] [CrossRef]
- Andrés-Sánchez, J.D. Pricing Life Contingencies Linked to Impaired Life Expectancies Using Intuitionistic Fuzzy Parameters. Risks 2024, 12, 29. [Google Scholar] [CrossRef]
- Di Persio, L.; Vettori, S. Markov Switching Model Analysis of Implied Volatility for Market Indexes with Applications to S&P 500 and DAX. J. Math. 2014, 2014, 753852. [Google Scholar] [CrossRef]
- Di Persio, L.; Honchar, O. Multitask machine learning for financial forecasting. Int. J. Circuits Syst. Signal Process. 2018, 12, 444–451. [Google Scholar]

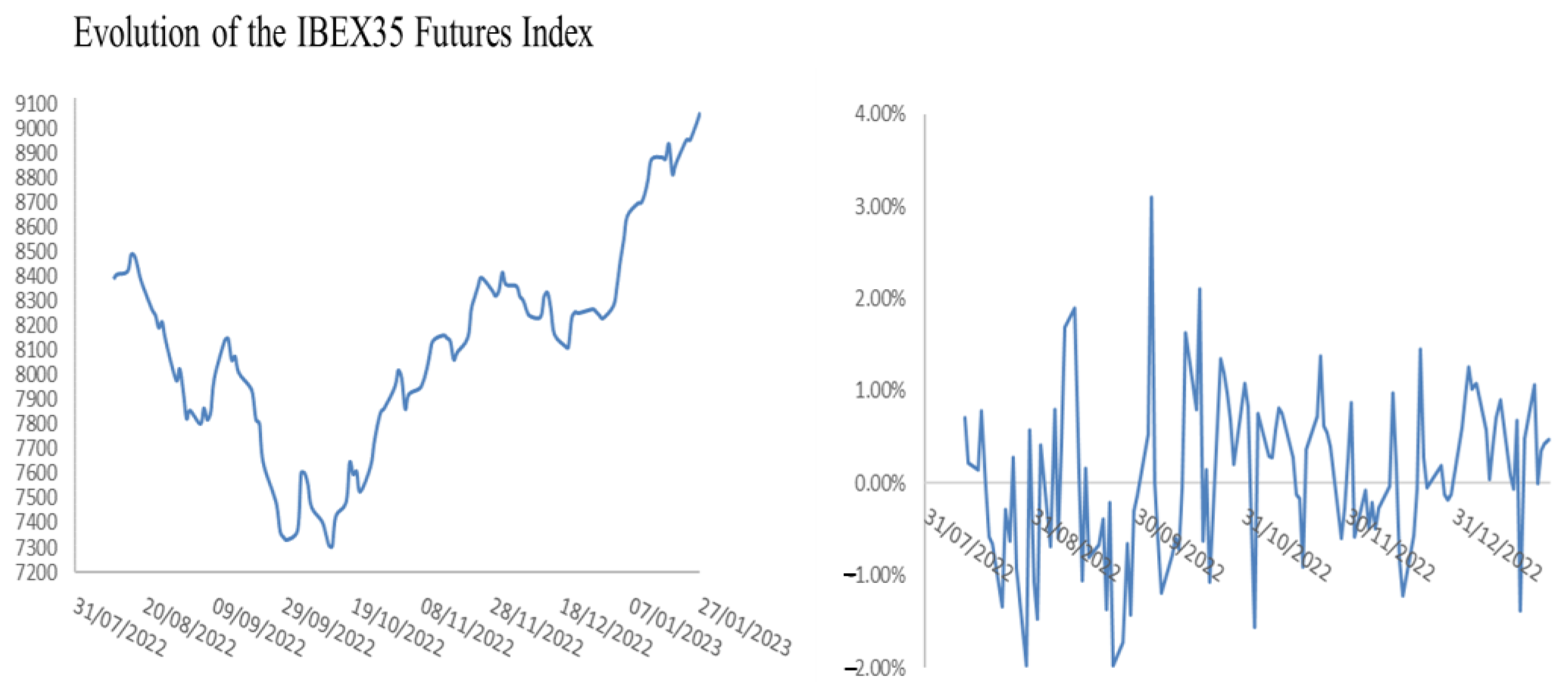

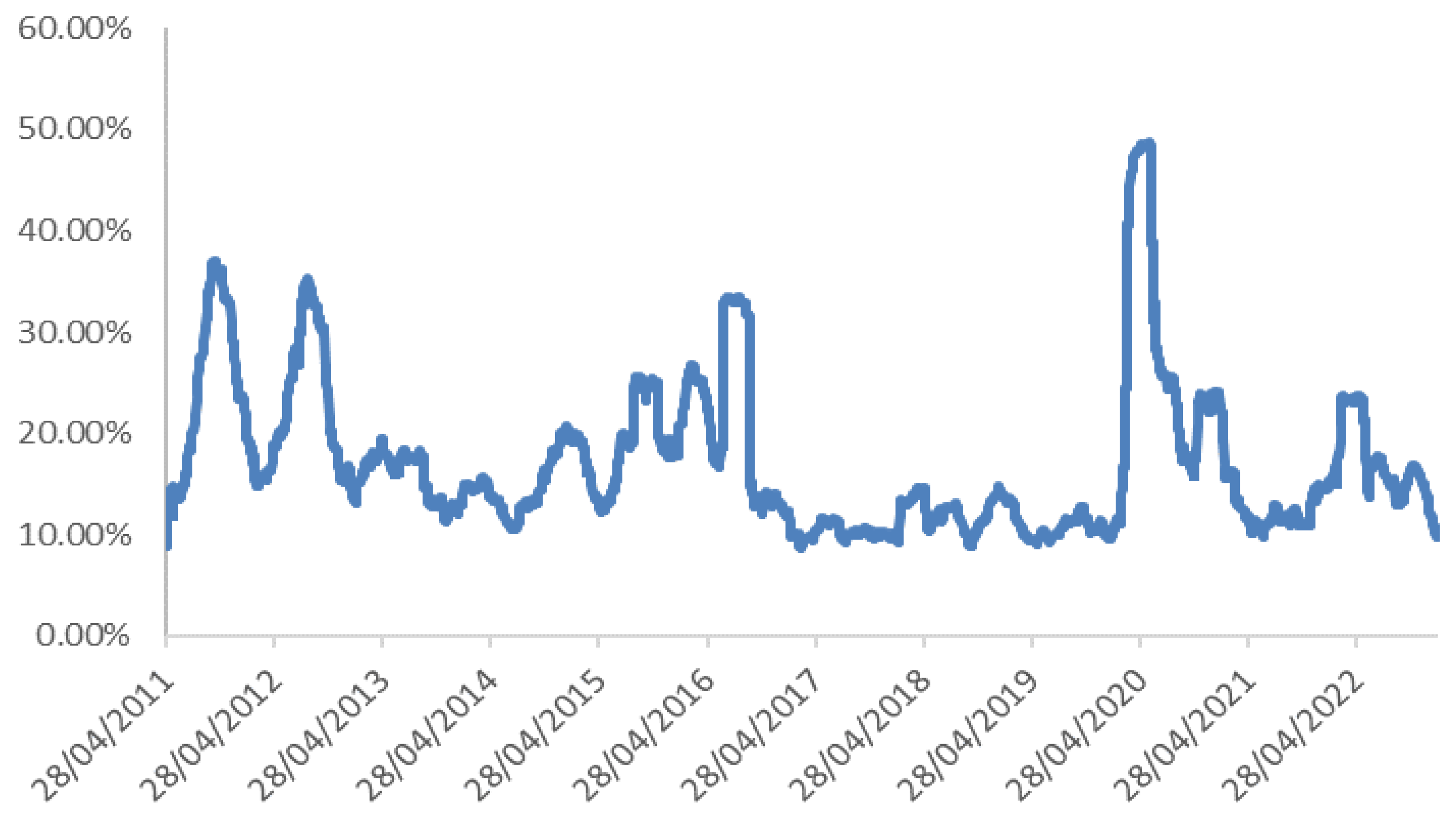
| K = 900 | |||||||
|---|---|---|---|---|---|---|---|
| h | n | BSM (a) | CRR (a) | CRR (b) | RB (a) | RB (b) | (c) |
| 1 | 1 | 107.83 | 101.87 | 8.401% | 102.97 | 7.417% | RB |
| 1/2 | 2 | 107.83 | 109.36 | 2.179% | 109.83 | 2.662% | CRR |
| 1/4 | 4 | 107.83 | 106.83 | 1.660% | 107.07 | 1.563% | RB |
| 1/12 | 12 | 107.83 | 107.83 | 0.395% | 107.94 | 0.374% | RB |
| 1/24 | 24 | 107.83 | 107.84 | 0.165% | 107.84 | 0.172% | CRR |
| 1/48 | 48 | 107.83 | 107.81 | 0.085% | 107.83 | 0.089% | CRR |
| 1/252 | 252 | 107.83 | 107.83 | 0.018% | 107.83 | 0.017% | RB |
| 1/504 | 504 | 107.83 | 107.83 | 0.009% | 107.83 | 0.009% | CRR |
| K = 1000 | |||||||
| h | n | BSM (a) | CRR (a) | CRR (b) | RB (a) | RB (b) | (c) |
| 1 | 1 | 40.85 | 51.18 | 34.909% | 51.04 | 34.461% | RB |
| 1/2 | 2 | 40.85 | 36.20 | 15.712% | 37.48 | 11.500% | RB |
| 1/4 | 4 | 40.85 | 38.40 | 8.288% | 39.34 | 5.181% | RB |
| 1/12 | 12 | 40.85 | 40.01 | 2.844% | 40.55 | 1.056% | RB |
| 1/24 | 24 | 40.85 | 40.43 | 1.431% | 40.80 | 0.221% | RB |
| 1/48 | 48 | 40.85 | 40.64 | 0.717% | 40.89 | 0.124% | RB |
| 1/252 | 252 | 40.85 | 40.81 | 0.137% | 40.89 | 0.124% | RB |
| 1/504 | 504 | 40.85 | 40.83 | 0.068% | 40.87 | 0.064% | RB |
| K = 1100 | |||||||
| h | n | BSM (a) | CRR (a) | CRR (b) | RB (a) | RB (b) | (c) |
| 1 | 1 | 10.36 | 4.61 | 90.444% | 2.97 | 109.045% | CRR |
| 1/2 | 2 | 10.36 | 12.98 | 35.153% | 12.48 | 28.995% | RB |
| 1/4 | 4 | 10.36 | 9.48 | 19.089% | 9.06 | 22.685% | CRR |
| 1/12 | 12 | 10.36 | 10.60 | 4.641% | 10.49 | 4.304% | RB |
| 1/24 | 24 | 10.36 | 10.36 | 2.127% | 10.38 | 2.040% | RB |
| 1/48 | 48 | 10.36 | 10.38 | 1.097% | 10.35 | 1.081% | RB |
| 1/252 | 252 | 10.36 | 10.36 | 0.208% | 10.36 | 0.219% | CRR |
| 1/504 | 504 | 10.36 | 10.36 | 0.108% | 10.36 | 0.106% | RB |
| K = 900 | |||||||
|---|---|---|---|---|---|---|---|
| h | n | BSM (a) | CRR (a) | CRR (b) | RB (a) | RB (b) | (c) |
| 1 | 1 | 130.33 | 136.40 | 6.425% | 140.19 | 10.295% | CRR |
| 1/2 | 2 | 130.33 | 136.08 | 6.208% | 134.95 | 5.181% | RB |
| 1/4 | 4 | 130.33 | 133.57 | 3.426% | 133.64 | 3.576% | CRR |
| 1/12 | 12 | 130.33 | 129.81 | 0.855% | 130.38 | 0.692% | RB |
| 1/24 | 24 | 130.33 | 130.69 | 0.470% | 130.40 | 0.365% | RB |
| 1/48 | 48 | 130.33 | 130.35 | 0.177% | 130.43 | 0.209% | CRR |
| 1/252 | 252 | 130.33 | 130.34 | 0.036% | 130.35 | 0.037% | CRR |
| 1/504 | 504 | 130.33 | 130.34 | 0.018% | 130.34 | 0.019% | CRR |
| K = 1000 | |||||||
| h | n | BSM (a) | CRR (a) | CRR (b) | RB (a) | RB (b) | (c) |
| 1 | 1 | 72.67 | 90.95 | 34.749% | 90.16 | 33.333% | RB |
| 1/2 | 2 | 72.67 | 64.41 | 15.713% | 68.31 | 8.482% | RB |
| 1/4 | 4 | 72.67 | 68.31 | 8.289% | 71.15 | 3.035% | RB |
| 1/12 | 12 | 72.67 | 71.18 | 2.844% | 72.76 | 0.247% | RB |
| 1/24 | 24 | 72.67 | 71.92 | 1.431% | 72.96 | 0.527% | RB |
| 1/48 | 48 | 72.67 | 72.30 | 0.717% | 72.94 | 0.502% | RB |
| 1/252 | 252 | 72.67 | 72.60 | 0.137% | 72.71 | 0.086% | RB |
| 1/504 | 504 | 72.67 | 72.64 | 0.068% | 72.66 | 0.042% | RB |
| K = 1100 | |||||||
| h | n | BSM (a) | CRR (a) | CRR (b) | RB (a) | RB (b) | (c) |
| 1 | 1 | 36.58 | 45.50 | 33.176% | 40.14 | 13.987% | RB |
| 1/2 | 2 | 36.58 | 42.52 | 23.032% | 43.30 | 25.578% | CRR |
| 1/4 | 4 | 36.58 | 40.40 | 14.503% | 39.90 | 12.453% | RB |
| 1/12 | 12 | 36.58 | 36.17 | 3.145% | 35.75 | 3.612% | CRR |
| 1/24 | 24 | 36.58 | 36.78 | 1.553% | 37.07 | 1.972% | CRR |
| 1/48 | 48 | 36.58 | 36.62 | 0.787% | 36.52 | 0.721% | RB |
| 1/252 | 252 | 36.58 | 36.60 | 0.161% | 36.59 | 0.162% | CRR |
| 1/504 | 504 | 36.58 | 36.59 | 0.075% | 36.58 | 0.074% | RB |
| Percentile | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Low volatility | 1% | 9.32% | 9.37% | 8.61% | 10.34% | 8.30% | 11.00% | 7.90% | 11.37% | 7.29% | 12.68% |
| 5% | 9.88% | 9.94% | 9.13% | 10.96% | 8.80% | 11.66% | 8.37% | 12.05% | 7.73% | 13.44% | |
| 10% | 10.28% | 10.34% | 9.50% | 11.41% | 9.16% | 12.13% | 8.71% | 12.54% | 8.04% | 13.99% | |
| 20% | 11.27% | 11.34% | 10.42% | 12.51% | 10.05% | 13.31% | 9.56% | 13.75% | 8.82% | 15.34% | |
| 30% | 12.55% | 12.62% | 11.59% | 13.92% | 11.18% | 14.81% | 10.63% | 15.30% | 9.81% | 17.07% | |
| Medium volatility | 40% | 13.44% | 13.51% | 12.41% | 14.91% | 11.97% | 15.86% | 11.39% | 16.39% | 10.51% | 18.28% |
| 45% | 14.04% | 14.12% | 12.97% | 15.58% | 12.51% | 16.57% | 11.90% | 17.12% | 10.98% | 19.09% | |
| 50% | 14.78% | 14.86% | 13.65% | 16.40% | 13.17% | 17.44% | 12.53% | 18.03% | 11.56% | 20.10% | |
| 55% | 15.66% | 15.75% | 14.46% | 17.38% | 13.95% | 18.48% | 13.27% | 19.10% | 12.24% | 21.30% | |
| 60% | 16.53% | 16.62% | 15.27% | 18.35% | 14.73% | 19.51% | 14.01% | 20.16% | 12.93% | 22.48% | |
| High volatility | 70% | 18.30% | 18.41% | 16.91% | 20.31% | 16.31% | 21.60% | 15.51% | 22.32% | 14.31% | 24.90% |
| 80% | 23.15% | 23.28% | 21.39% | 25.70% | 20.63% | 27.32% | 19.62% | 28.24% | 18.11% | 31.49% | |
| 90% | 26.71% | 26.86% | 24.67% | 29.64% | 23.80% | 31.52% | 22.64% | 32.58% | 20.89% | 36.33% | |
| 95% | 33.25% | 33.43% | 30.71% | 36.90% | 29.62% | 39.23% | 28.18% | 40.55% | 26.00% | 45.22% | |
| 99% | 47.87% | 48.15% | 44.23% | 53.13% | 42.66% | 56.50% | 40.58% | 58.39% | 37.44% | 65.12% | |
| Moneyness Degree | Strike Price | ρ | z | p Value |
|---|---|---|---|---|
| In the money | = 0.9 | 44.17% | −1.278 | 0.201 |
| At the money | = 1 | 100.00% | 10.954 | <0.001 |
| Out of the money | = 1.1 | 60.00% | 2.191 | 0.029 |
(h = 1, 1/2, 1/4, 1/12) | (h = 1/24, 1/48, 1/252, 1/504) | ||||||
|---|---|---|---|---|---|---|---|
| Moneyness Degree | Strike Price | ρ | z | p Value | ρ | z | p Value |
| In the money | = 0.9 | 53.33% | 0.516 | 0.606 | 36.67% | −2.066 | 0.039 |
| At the money | = 1 | 100% | 7.746 | <0.001 | 100.00% | 7.746 | <0.001 |
| Out of the money | = 1.1 | 55.00% | 0.775 | 0.439 | 63.33% | 2.066 | 0.039 |
| Low Volatility | Medium Volatility | High Volatility | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Moneyness Degree | Strike Price | ρ | z | p Value | ρ | z | p Value | ρ | z | p Value |
| In the money | = 0.9 | 50% | 0.000 | 1.000 | 32.5% | −2.214 | 0.027 | 50% | 0 | 1.000 |
| At the money | = 1 | 100% | 6.325 | <0.001 | 100% | 6.325 | <0.001 | 100% | 6.324 | <0.001 |
| Out of the money | = 1.1 | 45% | −0.632 | 0.527 | 80% | 3.795 | <0.001 | 55% | 0.632 | 0.527 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrés-Sánchez, J.d. Modelling Up-and-Down Moves of Binomial Option Pricing with Intuitionistic Fuzzy Numbers. Axioms 2024, 13, 503. https://doi.org/10.3390/axioms13080503
Andrés-Sánchez Jd. Modelling Up-and-Down Moves of Binomial Option Pricing with Intuitionistic Fuzzy Numbers. Axioms. 2024; 13(8):503. https://doi.org/10.3390/axioms13080503
Chicago/Turabian StyleAndrés-Sánchez, Jorge de. 2024. "Modelling Up-and-Down Moves of Binomial Option Pricing with Intuitionistic Fuzzy Numbers" Axioms 13, no. 8: 503. https://doi.org/10.3390/axioms13080503
APA StyleAndrés-Sánchez, J. d. (2024). Modelling Up-and-Down Moves of Binomial Option Pricing with Intuitionistic Fuzzy Numbers. Axioms, 13(8), 503. https://doi.org/10.3390/axioms13080503






