Abstract
This paper explores the inference for a constant-stress accelerated life test under a ranked set sampling scenario. When the lifetime of products follows the Fréchet distribution, and the failure times are collected under a maximum ranked set sampling with unequal samples, classical and Bayesian approaches are proposed, respectively. Maximum likelihood estimators along with the existence and uniqueness of model parameters are established, and the corresponding asymptotic confidence intervals are constructed based on asymptotic theory. Under squared error loss, Bayesian estimation and highest posterior density confidence intervals are provided, and an associated Monte-Carlo sampling algorithm is proposed for complex posterior computation. Finally, extensive simulation studies are conducted to demonstrate the performance of different methods, and a real-data example is also presented for applications.
Keywords:
accelerated life test; maximum ranked set sampling with unequal samples; Fréchet distribution; maximum likelihood estimation; Bayesian analysis MSC:
62F10; 62F15
1. Introduction
Accelerated Life Testing (ALT) is a method that involves testing products under conditions of stress levels higher than normal in order to predict their reliability under normal usage conditions. ALT is often conducted in lifetime experiments and reliability engineering, when the testing products feature high reliability and long life-cycles. Because accelerated life testing speeds up the product’s failure process, it can reduce the time and resources needed for long-term tracking of product performance, thereby saving on testing costs. In practice, accelerated life testing can be categorized by the method of stress application into constant-stress ALT, step-stress ALT, progressive-stress ALT and random stress ALT. In a constant-stress ALT, the product or a component is operated at a stress level higher than normal operating conditions, and the stress level is not increased or decreased during the test. In a step-stress ALT, the stress level to which a product or a component is subjected increases at some pre-specified moments, whereas in a progressive-stress ALT, the stress level continuously increases over time rather than remaining constant. In a random stress ALT, the stress levels vary randomly throughout the test, simulating the uncertainties encountered in actual use. These stress levels can be temperature, humidity, voltage, vibration, or any other type of stress that the product may experience during its normal life cycle. Additionally, to ensure the accuracy and validity of the test results, it is crucial to ensure that the failure mechanisms under high stress levels are the same as those under the normal operating conditions in the aforementioned accelerated life tests. Various inferences for ALTs have been widely discussed by many authors; see, for example, some recent contributions of Wu et al. [1], Kumar et al. [2], Wang et al. [3], Bai et al. [4], Alotaibi et al. [5], Wang and Yan [6] and Nassar et al. [7], among others. For more detailed information, interested readers may refer to Escobar and Meeker [8] for a comprehensive review.
In real-life experiments, simple random sampling (SRS) is commonly used to collect failure data from the population. However, when experiments are constrained by time and cost, the straightforward method of simple random sampling often proves to be less efficient. Consequently, based on the specific characteristics of the population and the objectives of the study, it may be worthwhile to consider other sampling techniques such as stratified sampling, systematic sampling, or cluster sampling, which might be more appropriate. Among numerous alternative schemes, the ranked set sampling (RSS) technique proposed by McIntyre [9] could improve the efficiency of SRS by using fewer sample resources. The proposed RSS scheme could be described as follows. Suppose that identical units are randomly selected from a population and are divided into n groups with size n in each group. For the i-th group , the test is conducted for all units, and the associated i-th smallest failure time, namely , is selected. Therefore, sample is observed as the corresponding RSS sample of size n. In this scenario, the schematic diagram of RSS can be described as follows:
It is worth noting that the RSS scheme may be an easy and inexpensive way to effectively collect failure information from the population. In addition, various authors have also demonstrated that the RSS gives more inferential efficiency than SRS from different perspectives (e.g., Almanjahie et al. [10], Al-Omari et al. [11], Yao et al. [12], Aljohani [13]). For some recent contributions, one could also refer to the works of Koshti and Kamalja [14], Sabry and Shaaban [15] and Bhushan and Kumar [16] among others.
Due to the potential advantages of the RSS method in saving experimental time and costs, as well as improving sampling efficiency, many alternative methods based on this method have been proposed in practice. For example, some are introduced as median ranked set sampling (Muttlak [17]), extreme ranked set sampling (Samawi et al. [18]), multi-stage RSS (Al-Saleh and Al-Omari [19]), as well as quartile RSS (Muttlak [20]), among others. Recently, Biradar and Santosha [21] proposed maximum ranked set sampling with unequal samples (MaxRSSU), which has attracted much attention in the literature. The MaxRSSU scenario is conducted with units in the sampling procedure. It is assumed that units are divided into n groups. For the i-th group with size i, the largest observation is selected from each group in the ranking process, and the MaxRSSU sample is then obtained as . Similarly, the MaxRSSU procedure is described as follows:
Correspondingly, if the minimum observation is collected by the above procedure, one has minimum ranked set sampling with unequal samples (MinRSSU) proposed by Al-Odat and Al-Saleh [22]. In the literature, both scenarios of MinRSSU and MaxRSSU are also referred to as moving extreme ranked set sampling (MERSS) in context. From the sketch of MERSS sampling, it is noted that its size is smaller than that of the traditional RSS scenario. This improvement reduces the sorting error caused by using the RSS scheme. There are also many studies for inference with MinRSSU and MaxRSSU schemes, for example, some recent contributions of Hassan and Alamri [23] and Chaudhary and Gupta [24], as well as references therein.
Due to the advantages of ALT and the RSS method in saving test time and costs, the use of the RSS method in ALT may improve the accuracy of statistical inference. Many scholars have discussed this aspect. For example, Kotb and El-Din [25] discussed the Bayesian estimation of unknown parameters of the Rayleigh distribution when the test data are ordered RSS under step-stress ALT. Hashem et al. [26] discussed the Bayesian inference of progressive-stress ALT based on the exponential distribution under Type-II censoring for SRS and ordered RSS. The results indicate that the estimates under ordered RSS are more effective compared to those obtained by SRS methods. Hashem and Abdel-Hamid [27] analyzed the statistical prediction of progressive-stress ALT using ordered RSS from Type-II censored data of the Rayleigh distribution, and the results indicate that the estimates calculated under ordered RSS are more effective than those under SRS.
To the best of our knowledge thus far, no attempt has been made on estimation for the constant-stress model and random stress model under the RSS scheme in the literature. However, given that the implementation of random stress ALT requires more sophisticated equipment and more resources, and that the data analysis is more complex, its application is limited. In contrast, constant-stress ALT is easier to implement because it does not require complex stress control equipment and has been widely used and verified. Therefore, this paper considers the estimation of the constant-stress model under the RSS scheme.
Suppose that X is a random variable from the Fréchet distribution, then the cumulative distribution function (CDF) and the probability density function (PDF) of X can be expressed, respectively, as
where and are scale and shape parameters, respectively. Correspondingly, the survival function (SF) and the hazard rate function (HRF) of Fréchet distribution can be written at mission time x as
The Fréchet distribution is a well-defined lifetime distribution, and it is commonly used to characterize variables associated with extreme phenomena like floods, rains and cash flow among other related fields. The Fréchet distribution has attracted the attention of a large number of authors such as Castillo et al. [28], Alotaibi et al. [29], Phaphan et al. [30] and Kanwal and Abbas [31]. For the details of this model, one can refer to Gómez et al. [32]. Due to the advantages of ALT and RSS technique and the potential theoretical and practical applications of the Fréchet distribution, this paper pursues the inference problem of the constant-stress model from the Fréchet distribution. Under the MaxRSSU scenario, inferential methods are developed under the classical and Bayesian procedures, respectively. Some potential contributions of this paper are as follows. Firstly, a new constant-stress model is proposed, and the MaxRSSU scheme is applied to the constant-stress model for analysis for the first time. In this context, the MaxRSSU method may allow for more flexible consideration of sample size allocation at different stress levels, which facilitates a more accurate modeling of the relationship between stress and lifetime. Additionally, it can enhance the sampling efficiency of traditional sampling techniques, particularly in scenarios where samples are scarce or the cost of sample acquisition is high, thereby contributing to the improved accuracy of estimates. Secondly, the existence and uniqueness of the maximum likelihood estimators of model parameters are established, which provides a solid theoretical foundation for likelihood-based numerical computations. Finally, the data analysis and model derivation of this study provide potential application value and a novel technical path for engineers to perform constant-stress ALT. Specifically, the application of research results helps to enhance the reliability and durability of products and may provide a scientific basis for the optimization of maintenance strategies, thereby facilitating the overall management of the product life cycle in practice.
The rest of this article is organized as follows. The testing procedure and model assumptions are presented in Section 2. Section 3 and Section 4 discuss maximum likelihood and Bayesian inference for model parameters, respectively. Some numerical simulations and a real life example are carried out in Section 5. Finally, concluding remarks are given in Section 6.
2. Model Description
2.1. Experimental Procedure under MaxRSSU
Consider a k stage constant-stress ALT with stress levels , where is the stress level under the use condition. Under stress level , suppose independent and identical units are put on a life-testing experiment. For the j-th testing group, one divides units into groups, and each group contains i units with . Following the MaxRSSU procedure, the MaxRSSU accelerated failure samples denoted as are collected under stress level , i.e., the MaxRSSU data from the stress level are conducted from the following procedure:
where represents the s-th order statistics from i-th groups under the stress level . Therefore, the following constant-stress MaxRSSU samples can be obtained as
For convenience, it is denoted as for concision.
2.2. Model Assumption
To conduct statistical inference based on the MaxRSSU accelerated data, the following basic assumptions are given:
- A1.
- Under stress levels , the lifetime of sample follows the Fréchet distribution with parameters and with CDF and PDF as follows:
- A2.
- The stress level changes only the scale parameter of the Fréchet distribution. Therefore,
- A3.
- Assume that the acceleration model is a logarithmic linear function of scale parameter , expressed as follows:where is a known function of stress level .
3. Classical Likelihood Estimation
In this section, maximum likelihood estimators (MLEs) of model parameters and acceleration coefficients are obtained, and the correspondingly asymptotic confidence intervals (ACIs) are also constructed by using asymptotic theory and the delta method.
3.1. Maximum Likelihood Estimation of Model Parameters
Let , the likelihood function of MaxRSSU accelerated sample (3) be expressed from Equation (4) as
where notation .
The associated log-likelihood function of and can be expressed from Equation (6) as
where the coefficient parameters a and b could be incorporated into above log-likelihood function via life-stress model (5).
From Equation (7), the MLEs and of coefficients and parameter can be obtained through standard procedure as the solutions of the following likelihood equations:
where , and the derivative of ℓ can be obtained by direct computation which is omitted for saving space. Clearly, there are no closed forms of the associated MLEs from the above likelihood equation. Therefore, numerical iterative approaches like the Newton–Raphson algorithm should be adopted for computation. However, such numerical methods sometimes may be sensitive to initial values and encounter convergence problems in this direct approach. Alternatively, a simpler way called profile likelihood approach is taken here to find the associated MLEs. Under such a procedure, the estimators that maximize the profile likelihood function are also the MLEs obtained from the full likelihood function.
The MLEs of model parameters are established below.
Theorem 1.
Proof.
See Appendix A. □
Substituting into the log-likelihood function and ignoring the additive constant terms, the profile log-likelihood function of can be deduced as
Theorem 2.
Proof.
See Appendix B. □
It is seen from Theorem 2 that the closed-form solution of the MLE does not exist from the likelihood equation in Equation (9). Therefore, an iterative approach termed as Algorithm 1 is proposed to find the MLE of numerically, where the convergence of such an algorithm is guaranteed by the Banach fixed-point theorem. In addition, the MLE of parameter could be further obtained from Theorem 2 as
| Algorithm 1: Iterative estimation of MLE . |
|
In addition, MLEs of the coefficient parameters a and b are obtained via least-square method based on the estimates of . From the life-stress model (5), the following expression with respect to a and b is denoted as
Then, taking derivatives with respect to a and b and setting them to zero, the MLEs of a and b are obtained as
Once the MLEs and of the acceleration coefficients a and b are obtained, the MLE of parameters under normal use stress level can be constructed based on the invariance principle as
In addition, the MLEs of reliability indices SF and HRF under normal use stress level can be obtained as
3.2. Approximate Confidence Intervals
It is noted that there are no closed forms of the MLE for the model parameters when MaxRSSU data are available. Therefore, the Fisher information matrix and asymptotic theory are implemented in this part to construct the associated ACIs of model parameters, acceleration coefficients and reliability indices.
Let with , and , then the second derivatives of the log-likelihood function can be obtained as
and other derivatives are zeros in this case.
Since the density function of can be expressed as
Then, the expectations of the negative second derivatives can be obtained as
and
where constant quantities , , and the detailed computation is presented in Appendix C.
Therefore, the expected Fisher information matrix can be written as
Under mild regularity conditions, the asymptotic distribution of the MLE can be constructed as
where notation is the inverse of the expected Fisher information matrix by substituting with its MLE provided as follows:
For arbitrary , a ACI of is given by
where is the upper -th quantile of the standard normal distribution.
In addition, let be the arbitrary function of parameters and , the asymptotic distribution of can be constructed by using the delta method as
where notations is the MLE of , and
Therefore, the ACI of can be further established as mentioned. In this manner, the ACIs of quantities a, b, , SF , HRF could be constructed consequently; the details are omitted here for concision and saving space.
4. Bayesian Estimation
Bayesian estimation appears to be advantageous in statistical inference, where its capability of incorporating prior information in decision making and data analysis make it attractive, especially when the sample size is not large enough. In this section, the Bayesian approach is presented for parameter estimation under the MaxRSSU scenario.
4.1. Prior Information
For Bayesian analysis, a flexible family of prior distributions is typically taken into account. Because of its flexibility, the gamma prior is widely adopted for modelling the historical information in our study. It is assumed that the parameters and have independent gamma priors with densities as follows:
and
where and are positive hyper-parameters, respectively.
From Equations (6), (14) and (15), the joint posterior density of parameters and can be expressed as
Therefore, for the arbitrary function as defined previously, the Bayes estimator of with respect to squared error loss can be expressed as
where notation . It is noted from Equation (17) that there is no closed form of the Bayes estimator . Therefore, a Monte-Carlo procedure with the Metropolis–Hastings (MH) sampling technique is implemented below to obtain the Bayes estimate, and the associated highest posterior density (HPD) credible intervals (CIs) are also constructed consequently.
4.2. Posterior Representation and MH Sampling
From Equation (16), the conditional posterior densities of and can be rewritten as
and
It is observed from Equation (18) that the parameter () follows a conditional posterior gamma distribution, namely with parameters and for given , whereas the conditional posterior density of the parameter cannot be reduced to some well-known distributions, unfortunately. Therefore, for obtaining the Bayes estimates and the HPD credible intervals, the MH sampling approach termed as Algorithm 2 is proposed for posterior computation with a normal proposal. The primary function of this algorithm is to indirectly generate a sequence of samples conforming to the posterior distribution in cases where direct sampling from the posterior distribution is not feasible, by constructing a Markov chain. By employing this algorithm on the conditional posterior density expressions (18) and (19), samples of and can be collected, thereby obtaining the corresponding Bayesian estimates. The specific application process can be seen in the flow of the algorithm. Specifically, when function is defined as the unknown model parameters and reliability indices, then one could find the associated Bayes point and HPD interval estimates in this manner.
| Algorithm 2: Metropolis-Hastings sampling technique |
|
5. Numerical Illustration
5.1. Simulation Studies
Extensive simulation experiments are carried out to investigate the performance of the proposed methods based on the MaxRSSU constant-stress failure times. The accuracy of the proposed point estimates are evaluated in terms of absolute bias (AB) and mean squared error (MSE), whereas the interval estimates are compared in terms of average length (AL) and coverage probability (CP), respectively.
In this study, a two-stage constant-stress model is considered for simulation, three sets of randomly chosen values of model parameters are used, and the associated hyper-parameters are taken due to parameter values in consequence, provided the prior means are the same as the original means. Therefore, the simulation experiments are conducted based on 10,000 repetitions, and the criteria quantities ABs, MSEs, CPs and ALs are reported in Table 1, Table 2 and Table 3, respectively, where the significance level is for interval estimates.

Table 1.
MLEs and Bayes estimates for parameters at with mission time .

Table 2.
MLEs and Bayes estimates for parameters at with mission time .

Table 3.
MLEs and Bayes estimates for parameters at with mission time .
Based on the listed results presented in Table 1, Table 2 and Table 3, the following conclusions for point and interval estimates could be observed as follows:
- For point estimates, both ABs and MSEs of MLEs and Bayesian results decrease with the increase in sample size n, which indicates the MLEs and the Bayesian estimates feature consistency properties and perform satisfactorily under simulation design scenarios.
- For a given n, Bayesian estimates are better than MLEs in terms of ABs and MSEs.
- When sample size n increases, the ALs of the Bayes HPD CIs and ACIs all decrease in general, whereas the CPs of the ACIs increase correspondingly.
- For a fixed n, in the vast majority of cases, the AL and CP of the Bayes HPD CIs are superior to those of the ACIs.
5.2. Real Data Illustrations
This subsection uses a set of real-life data to demonstrate the feasibility of the proposed method in this paper. The real data come from Stone [33], representing the accelerated life test data of insulation materials regarding voltage. In this data set, experimental data with accelerated stress levels kv and kv are selected, and the sample sizes are 20 in each stress level. For simplicity in the analysis, each datum is divided by 1000, and the transformed data from each stress level are provided in Table 4.

Table 4.
Complete accelerated life test data of insulation materials.
Before proceeding further, the goodness-of-fit is adopted to check whether the Fréchet distribution can be used as a suitable model to fit these data. By direct computation, the Kolmogorov–Smirnov (K-S) distances for the data under stress levels and are and , and the associated p-values are and , respectively. Therefore, there is no sufficient reason to reject the conclusion that the Fréchet distribution provides a reasonable model for these data. Furthermore, the probability–probability (P-P), quantile–quantile (Q-Q) and the plot of empirical cumulative distribution via theoretical distribution are presented in Figure 1, which also imply that the Fréchet distribution is a proper model to fit these real data. Similar works are also conducted by other authors, for example, Jana and Bera [34] indicated that the Fréchet model is a good fit for this data set under the estimation of stress-strength reliability perspective.
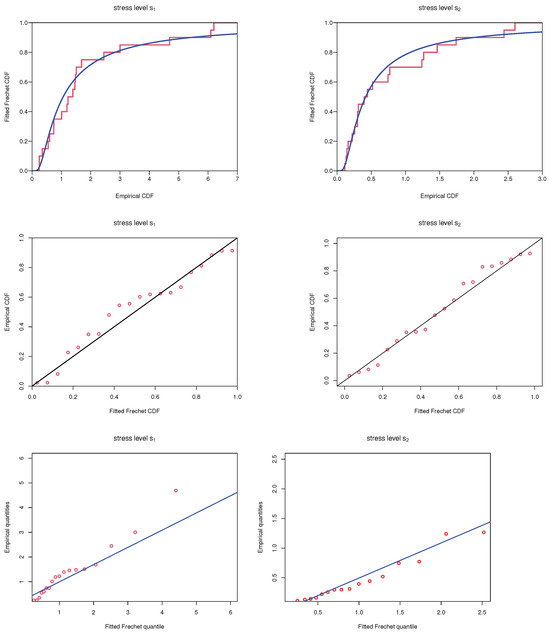
Figure 1.
Empirical cumulative distribution plot, P-P and Q-Q plots for the Fréchet distribuion under the real data.
Following the MaxRSSU scheme, we randomly select failure data of size from the origin data shown in Table 4 at each stress level and arrange them in ascending order, and the largest one was selected as the MaxRSSU sample. Therefore, the MaxRSSU accelerated failure times at each stress level are obtained as follows.
and
Following the suggestion of Nelson [35], when the accelerating stress is the voltage, the life-stress acceleration model is chosen as the inverse power rate model with . Therefore, based on the above generated MaxRSSU accelerated failure data, the model parameter and the coefficient and reliability index SF are estimated by the proposed maximum likelihood and Bayesian methods with normal stress level kv, where the significance level for interval estimates is taken to be , and the hyper-parameter is used as , provided that the prior mean becomes the expected value of the corresponding maximum likelihood estimates. In addition, the Bayes estimates are obtained based on 10,000 repetitions with 4000 burn-in time. The associated point and interval estimates are presented in Table 5, where the interval lengths for interval estimates are also provided in square brackets for illustration.

Table 5.
MLEs and Bayes estimates for unknown parameters obtained using the MaxRSSU method on real data at mission time .
It is noted from the results tabulated in Table 5 that the point estimates under the two methods are similar, and the Bayes HPD intervals perform better than the ACIs in terms of interval lengths. In addition, Figure 2 shows the plot of the profile log-likelihood function (9) under this real data example, and it is observed that the profile log-likelihood function is unimodal with respect to , which is consistent with the theoretical result of Theorem 2 giving the existence and uniqueness of MLE of the parameter .
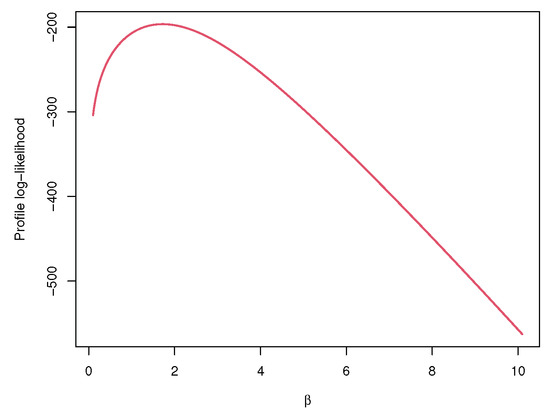
Figure 2.
Plot of the profile log-likelihood function for under real data.
For the sake of simplicity, we ignore the ordering information here and analyze the obtained data as a simple random sample. The corresponding estimation results are shown in Table 6. By comparing the results in Table 5 and Table 6, we find that under both the likelihood and Bayesian methods, the estimation results based on the MaxRSSU method are superior to those based on the SRS method. Similar findings have also been reported in many studies, for instance, Almanjahie et al. [10], Al-Omari et al. [11] and Aljohani [13].

Table 6.
MLEs and Bayes estimates for unknown parameters obtained using the SRS method on real data at mission time .
6. Conclusions
In this paper, statistical inference of the Fréchet model was conducted using classical maximum likelihood and Bayesian methods based on a constant-stress accelerated life test. The performance of different methods was evaluated through simulation research and a real data example, and the numerical results indicate that in situations with small sample sizes, Bayesian estimation outperforms traditional likelihood methods. In future research, we may further expand in the following directions. Firstly, the discussion of data types could be extended to other ranking set methods, such as the minimum ranked set sampling with unequal samples and the median ranked set sampling. Secondly, based on the MaxRSSU, we could further investigate other types of ALTs, such as step-stress ALT and random stress ALT. Finally, the optimal sampling scheme of MaxRSSU under accelerated life tests is interesting for future research.
Author Contributions
Methodology and Funding acquisition, L.W.; Methodology, Y.M.T. and Y.L.; Writing, J.L. and L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work of Liang Wang was supported by the Yunnan Fundamental Research Projects (No. 202401AT070116) and Yunnan Key Laboratory of Modern Analytical Mathematics and Applications (No. 202302AN360007).
Data Availability Statement
Data are contained within the article.
Acknowledgments
Authors would like to thank the editor and reviewers for their valuable comments and suggestions which improve this paper significantly.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Proof of Theorem 1.
By taking the first partial derivatives of the logarithmic likelihood function with respect to and setting them to zeros, one could obtain the conditional MLE of directly with
Further, the Hessian matrix of with given can be expressed as
and then, one could deduce from the extremum principle that the conditional MLEs achieve the maximum of the log-likelihood function. Therefore, the assertion is completed. □
Appendix B
Proof of Theorem 2.
By taking the direct derivative of the profile log-likelihood function (8), the likelihood equation shown in Equation (9) can be obtained as a consequence. In the following, the existence and uniqueness of the MLE are established.
Taking limitations at and ∞, it is noted that
where . Therefore, the function changes continuously from positive to negative with respect to parameter , and then, the MLE exists.
In addition, since
due to the Cauchy–Schwarz inequality, the function is an increasing function with respect to implying the MLE is unique. Therefore, the assertion is completed. □
Appendix C. Expectations of Negative Second Derivative Quantities
Since the density function of can be expressed as
then, the expectations of negative second derivative quantities can be obtained as
and
where constant quantities , .
References
- Wu, W.H.; Wang, B.X.; Chen, J.Y.; Miao, J.Z.; Guan, Q. Interval estimation of the two-parameter exponential constant stress accelerated life test model under Type-II censoring. Qual. Technol. Quant. Manag. 2023, 20, 751–762. [Google Scholar] [CrossRef]
- Kumar, D.; Nassar, M.; Dey, S.; Alam, F.M.A. On estimation procedures of constant stress accelerated life test for generalized inverse Lindley distribution. Qual. Reliab. Eng. Int. 2022, 38, 211–228. [Google Scholar] [CrossRef]
- Wang, X.F.; Wang, B.X.; Liang, W.J.; Jiang, P.H. Inference for constant stress accelerated life test under the proportional reverse hazards lifetime distribution. Qual. Reliab. Eng. Int. 2022, 38, 4223–4235. [Google Scholar] [CrossRef]
- Bai, X.C.; Shi, Y.M.; Ng, H.K.T. Statistical inference of Type-I progressively censored step-stress accelerated life test with dependent competing risks. Commun. Stat.-Theory Methods 2022, 51, 3077–3103. [Google Scholar] [CrossRef]
- Alotaibi, N.; Elbatal, I.; Almetwally, E.M.; Alyami, S.A.; Al-Moisheer, A.S.; Elgarhy, M. Bivariate step-stress accelerated life tests for the Kavya-Manoharan exponentiated Weibull model under progressive censoring with applications. Symmetry 2022, 14, 1791. [Google Scholar] [CrossRef]
- Wang, Y.; Yan, Z.Z. Statistical inference on accelerated life testing with dependent competing failure model under progressively Type-II censored data based on copula theory. Symmetry 2021, 37, 1396–1408. [Google Scholar] [CrossRef]
- Nassar, M.; Dey, S.; Wang, L.; Elshahhat, A. Estimation of Lindley constant-stress model via product of spacing with Type-II censored accelerated life data. Commun. Stat.-Simul. Comput. 2024, 53, 288–314. [Google Scholar] [CrossRef]
- Escobar, L.A.; Meeker, W.Q. A review of accelerated test model. Stat. Sci. 2006, 21, 552–577. [Google Scholar] [CrossRef]
- McIntyre, G. A method for unbiased selective sampling, using ranked sets. Aust. J. Agric. Res. 1952, 3, 385–390. [Google Scholar] [CrossRef]
- Almanjahie, I.M.; Ismail, M.; Cheema, A.N. Partial stratified ranked set sampling scheme for estimation of population mean and median. PLoS ONE 2023, 18, e0275340. [Google Scholar]
- Al-Omari, A.I.; Benchiha, S.; Almanjahie, I.M. Efficient estimation of two-parameter Xgamma distribution parameters using ranked set sampling design. Mathematics 2022, 10, 3170. [Google Scholar] [CrossRef]
- Yao, D.; Chen, W.; Yang, R.; Long, C. Fisher information in moving extreme ranked set sampling with application to parameter estimation. J. Syst. Sci. Complex. 2022, 35, 361–372. [Google Scholar] [CrossRef]
- Aljohani, H.M. Statistical inference for a novel distribution using ranked set sampling with applications. Heliyon 2024, 10, e26893. [Google Scholar] [CrossRef]
- Koshti, R.D.; Kamalja, K.K. Efficient estimation of a scale parameter of bivariate Lomax distribution by ranked set sampling. Calcutta Stat. Assoc. Bull. 2021, 73, 24–44. [Google Scholar] [CrossRef]
- Sabry, M.; Shaaban, M. Dependent ranked set sampling designs for parametric estimation with applications. Ann. Data Sci. 2020, 7, 357–371. [Google Scholar] [CrossRef]
- Bhushan, S.; Kumar, A. Predictive estimation approach using difference and ratio type estimators in ranked set sampling. J. Comput. Appl. Math. 2022, 410, 114214. [Google Scholar] [CrossRef]
- Muttlak, H. Median ranked set sampling. J. Appl. Stat. 1997, 6, 245–255. [Google Scholar]
- Samawi, H.M.; Ahmed, M.S.; Abu-Dayyeh, W. Estimating the population mean using extreme ranked set sampling. Biom. J. 1996, 38, 577–586. [Google Scholar] [CrossRef]
- Al-Saleh, M.F.; Al-Omari, A.I. Multistage ranked set sampling. Biom. J. 2002, 102, 273–286. [Google Scholar] [CrossRef]
- Muttlak, H.A. Investigating the use of quartile ranked set samples for estimating the population mean. Appl. Math. Comput. 2003, 146, 437–443. [Google Scholar] [CrossRef]
- Biradar, B.S.; Santosha, C.D. Estimation of the mean of the exponential distribution using maximum ranked set sampling with unequal samples. Open J. Stat. 2014, 4, 641–649. [Google Scholar] [CrossRef]
- Al-Odat, M.T.; Al-Saleh, M.F. A variation of ranked set sampling. J. Appl. Stat. Sci. 2001, 10, 137–146. [Google Scholar]
- Hassan, N.M.; Alamri, O.A. Estimation of Gumbel Distribution Based on Ordered Maximum Ranked Set Sampling with Unequal Samples. Axioms 2024, 13, 279. [Google Scholar] [CrossRef]
- Chaudhary, S.K.; Gupta, N. General weighted cumulative residual (past) extropy of minimum (maximum) ranked set sampling with unequal samples. Commun. Stat.-Theory Methods 2023, 1–21. [Google Scholar] [CrossRef]
- Kotb, M.S.; El-Din, M.M.M. Parametric inference for step-stress accelerated life testing from Rayleigh distribution under ordered ranked set sampling. IEEE Trans. Reliab. 2019, 71, 16–27. [Google Scholar] [CrossRef]
- Hashem, A.F.; Alyami, S.A.; Abdel-Hamid, A.H. Inference for a progressive-stress model based on ordered ranked set sampling under Type-II censoring. Mathematics 2022, 10, 2771. [Google Scholar] [CrossRef]
- Hashem, A.F.; Abdel-Hamid, A.H. Statistical prediction based on ordered ranked set sampling using Type-II censored data from the Rayleigh distribution under progressive-stress accelerated life tests. J. Math. 2023, 2023, 5211682. [Google Scholar] [CrossRef]
- Castillo, J.S.; Rojas, M.A.; Reyes, J. A more flexible extension of the Fréchet distribution based on the incomplete Gamma function and applications. Symmetry 2023, 15, 1608. [Google Scholar] [CrossRef]
- Alotaibi, R.; AL-Dayian, G.R.; Almetwally, E.M.; Rezk, H. Bayesian and non-Bayesian two-sample prediction for the Fréchet distribution under progressive type II censoring. AIP Adv. 2024, 14, 015137. [Google Scholar] [CrossRef]
- Phaphan, W.; Abdullahi, I.; Puttamat, W. Properties and Maximum Likelihood Estimation of the Novel Mixture of Fréchet Distribution. Symmetry 2023, 15, 1380. [Google Scholar] [CrossRef]
- Kanwal, T.; Abbas, K. Bootstrap confidence intervals of process capability indices Spmk, Spmkc and Cs for Frechet distribution. Qual. Reliab. Eng. Int. 2023, 39, 2244–2257. [Google Scholar] [CrossRef]
- Gómez, Y.M.; Barranco-Chamorro, I.; Castillo, J.S.; Gómez, H.W. An Extension of the Fréchet Distribution and Applications. Axioms 2024, 13, 253. [Google Scholar] [CrossRef]
- University of Waterloo (Ontario), Department of Electrical Engineering; Stone, G.C. Statistical Analysis of Accelerated Aging Tests on Solid Electrical Insulation; University of Waterloo: Waterloo, ON, Canada, 1978. [Google Scholar]
- Jana, N.; Bera, S. Interval estimation of multicomponent stress-strength reliability based on inverse Weibull distribution. Math. Comput. Simul. 2022, 191, 95–119. [Google Scholar] [CrossRef]
- Nelson, W.B. Accelerated Modeling-Statistical Models, Test Plans, and Data Analyses; Wiley: New York, NY, USA, 1990. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).