1. Introduction
Derivation, also known as differential operator, plays an important role in mathematical physics, such as homotopy Lie algebras [
1], differential Galois theory [
2], control theory and gauge theories of quantumj field theory [
3]. In [
4,
5], the authors studied associative algebras with derivations from the operadic point of view. Recently, in [
6], Tang and their collaborators considered Lie algebras with derivations from the cohomological point of view. Inspired by the work of [
6], associative algebras with derivations and pre-algebras with derivations have been studied in [
7,
8], respectively.
The solution of the modified classical Yang-Baxter equation, called modified
r-matrix, was introduced by Semenov-Tian-Shansky in [
9]. Recently, Jiang and Sheng [
10] developed the deformations of modified
r-matrices. Inspired from [
9,
10], the notion of modified
-differential Lie algebras was introduced in [
11]. Subsequently, the algebraic structures with modified operators were widely studied in [
12,
13,
14,
15,
16].
However, there have been very few studies about the modified
-differential left-symmetric algebras. Left-symmetric algebras (also called pre-Lie algebras) are nonassociative algebras, which were introduced by Cayley [
17] as a kind of rooted tree algebras and also introduced by Gerstenhaber [
18] when studying the deformation theory of rings and algebras. Left symmetric algebras have been widely used in geometry and physics, such as affine manifolds [
19], integrable systems, quantum Yang-Baxter Equations [
20,
21], Poisson brackets, operands, and complex and symplectic structures on Lie groups [
22]. See also [
23,
24,
25,
26,
27,
28,
29,
30,
31,
32] for more details. Thus, it is natural and necessary to study the modified
-differential left symmetric algebras.
Motivated by the work in [
8,
11,
12,
13], our main purpose is to study the representation and cohomology of the modified
-differential left symmetric algebras and applied them to the linear deformation, abelian extension, and skeletal modified
-differential left symmetric 2-algebras. The paper is organized as follows.
Section 2 introduces the representations of modified
-differential left-symmetric algebras. In
Section 3, we define a cohomology theory of modified
-differential left-symmetric algebras with coefficients in a representation, and apply it to the study of linear deformation. In
Section 4, we investigate abelian extensions of the modified
-differential left-symmetric algebras in terms of second cohomology groups. Finally, in
Section 5, we classify skeletal modified
-differential left-symmetric 2-algebras by using the third cohomology group. We then prove that strict modified
-differential left-symmetric 2-algebras are equivalent to the crossed modules of modified
-differential left-symmetric algebras.
All tensor products, vector spaces, and (multi)linear maps are over a field of characteristic 0.
2. Modified -Differential Left-Symmetric Algebras and Their Representations
This section introduces the notion of a modified -differential left-symmetric algebra and gives their representations.
Now let us recall some basic concepts of left-symmetric algebras from [
18,
24].
Definition 1 ([
18])
. Left-symmetric algebra (LSA in short) is a vector space with a bilinear product such that for , the associator:is symmetric in , i.e., :Denote it by . Remark 1. Let be a LSA. If we define a bilinear bracket as:then is a Lie algebra. Example 1. Let be a Lie algebra and be a linear map satisfying the Rota–Baxter equation:then, is a LSA, in which the LSA operation is . Definition 2. Let be a LSA and . If the linear map satisfiesthen ∂ is called a modified λ-differential operator (MλD operator in short). Moreover, the triple is called modified λ-differential left-symmetric algebra (MλDLSA in short), simply denoted by . Remark 2. Let ∂ be an MλD operator on a LSA . If then ∂ is a derivation on and is a LSA with a derivation. See [8] for LSAs with derivations. Definition 3. The homomorphism between MλDLSAs and is a linear map that satisfies and . In addition, if Φ is bijective, it is said that Φ is isomorphic from to .
Example 2. Let be a LSA. Then is an MλDLSA, where is an identity map.
Example 3. Let be an MλD Lie algebra (see [11], Definition 2.5). By Example 1, if , then is an MλDLSA. Example 4. Let be a two-dimensional LSA and be a basis, whose nonzero products are given as follows:Then the triple is a two-dimensional MλDLSA, where , for . Example 5. If is an MλDLSA, and for any , then is also an MDLSA.
Definition 4 ([
24])
. A representation of a LSA is a triple , where is a vector space, and are two linear maps such that for all : Definition 5. Let be a representation of a LSA . Then is called a representation of an MλDLSA if is endowed with a linear map satisfying the following equations: For example, given an MDLSA , there is a natural adjoint representation on itself. The corresponding representation maps and are given by and .
Proposition 1. The quadruple is a representation of an MλDLSA if and only if is an MλDLSA with the following maps:for all and . Proof. Firstly, it is easy to verify that
is a LSA. Furthermore, for any
and
, by Equations (
2)–(6) we have:
Hence,
is an M
DLSA.
Conversely, suppose
is an M
DLSA, then for any
and
, we have:
which implies that
and
. Therefore,
is a representation of
. □
3. Cohomology and Linear Deformations of Modified -Differential Left-Symmetric Algebras
This section defines the cohomology theory of an MDLSA with coefficients in a representation. Then the linear deformation of MDLSAs is studied by using low-order cohomology groups.
Let us first recall the cohomology theory of LSAs in [
30]. Let
be a LSA and
be a representation of it. Denote the
cochains of
with coefficients in
by
The coboundary map
, for
and
, as:
It has been proved in [
30] that
. The cohomology group of cochain complex
is denoted as
.
Let
be an M
DLSA and
be a representation of it. Inspired by [
12,
13], a linear map
is defined as:
Lemma 1. The map Γ defined above is a cochain map, that is, the diagram:
![Axioms 13 00380 i001]() is commutative.
is commutative. Proof. For any
and
we have:
and
From Equations (
1)–(4) and expanding Equations (
9) and (
10), we can deduce that
□
Definition 6. Let be an MλDLSA and be a representation of it. We define the cochain complex of with coefficients in to the negative shift of the mapping cone of Γ
, that is, let:and the coboundary operator is given by:for , the coboundary operator is given by: The cohomology of , denoted by , is called the cohomology of the MλDLSA with coefficients in . In particular, when , we just denote , by , , respectively, and call them the cochain complex, the cohomology of an MλDLSA , respectively.
Corollary 1. Let be an MλDLSA. Then, there is a short exact sequence of cochain complexes:Consequently, it induces a long exact sequence of cohomology groups: Next, we use the established cohomology theory to characterize linear deformations of MDLSAs.
Definition 7. Let be an MλDLSA. If for all , is still an MλDLSA over , where We say that generates a linear deformation of an MλDLSA .
Proposition 2. If generates a linear deformation of an MλDLSA , then is a 2-cocycle of the MλDLSA .
Proof. If
generates a linear deformation of an M
DLSA
, then for any
, we have:
Comparing coefficients of
on both sides of the above equations, we have:
and
Note that Equation (
11) is equivalent to
and that Equation (
12) is equivalent to
Therefore,
, that is,
is a 2-cocycle. □
Definition 8. Let and be two linear deformations of MλDLSA . We call them equivalent if there exists such that is a homomorphism from to , i.e., for all , the following equations hold: Proposition 3. If two linear deformations and are equivalent, then and are in the same cohomology class of .
Proof. Let
be an isomorphism. Expanding the equations and collecting coefficients of
t, we get from Equations (
13) and (14):
that is,
So,
and
are in the same cohomology class of
. □
Remark 3. If is equivalent to the undeformed deformation , we call the linear deformation of an MλDLSA trivial.
4. Abelian Extensions of Modified -Differential Left-Symmetric Algebras
This section mainly studies the abelian extensions of an MDLSA.
Definition 9. Let be an MλDLSA and an abelian MλDLSA with the trivial product . An abelian extension of by is a short exact sequence of morphisms of MλDLSAs:that is, there exists a commutative diagram:such that and , for i.e., is an abelian ideal of A section of an abelian extension of by is a linear map such that .
Definition 10. Let and be two abelian extensions of by . They are said to be isomorphic if there exists an MλDLSA isomorphism , such that the following diagram is commutative: Let
be an abelian extension of an M
DLSA
by
and
be a section of it. For any
, define
and
, respectively, by:
We further define linear maps
and
, respectively, by:
Obviously,
is isomorphic to
as vector spaces. Transfer the M
DLSA structure on
to that on
, we obtain an M
DLSA
, where
and
are given by:
In addition, we have an abelian extension
which is isomorphic to the original abelian extension (
15).
Proposition 4. With the above notations, is a representation of the MλDLSA .
Proof. For any
and
,
is an abelian ideal of
and
, and we have:
It is similar to see
Hence, this shows that
is a representation of the LSA
.
Moreover, by
we have:
By the same token,
. Hence, we deduce that
is a representation of
. □
Proposition 5. With the above notation, the pair is a 2-cocycle of the MλDLSA with coefficients in .
Proof. By
is an M
DLSA, for any
and
, we have:
Furthermore, the above two equations are equivalent to the following equations:
Using Equations (18) and (19), we have
and
, respectively. Therefore,
that is,
is a 2-cocycle. □
Let us now study the influence of different choices of sections.
Proposition 6. Let be an abelian extension of an MλDLSA by and be a section of it.
(i) Different choices of the section give the same representation on . Moreover, isomorphic abelian extensions give rise to the same representation of .
(ii) The cohomology class of does not depend on the choice of .
Proof. (i) Let
be another section of
and
be another representation of
constructed using the section
. By
for
, then we have:
which implies that
. Similarly, there is also
. Thus, different choices of the section
give the same representation on
.
Moreover, let
and
be two isomorphic abelian extensions of
by
with the associated isomorphism
such that the diagram in (
16) is commutative. Let
and
be two sections of
and
, respectively. By Proposition 4, we have
and
, which are their representations, respectively. Define
by
. As
, we have:
Thus, we obtain that
is a section of
. By
is an isomorphism of M
DLSAs such that
, for any
and
, we have:
which implies that
. Similarly, there is also
. Thus, isomorphic abelian extensions give rise to the same representation of
.
(ii) Let
be another section of
, by Proposition 5, we get another corresponding 2-cocycle
. Define
by
, for any
, we have:
Hence,
, that is
and
are in the same cohomological class in
. □
Next, we are ready to classify abelian extensions of an MDLSA.
Theorem 1. Abelian extensions of an MλDLSA by are classified by the second cohomology group .
Proof. Assume that
and
are two isomorphic abelian extensions of
by
with the associated isomorphism
such that the diagram in (
16) is commutative. Let
be a section of
. As
, we have:
Thus, we obtain that
is a section of
. Denote
. Since
is an isomorphism of M
DLSAs such that
, we have:
and
Thus, isomorphic abelian extensions gives rise to the same element in
.
Conversely, given two 2-cocycles
and
, we can construct two abelian extensions
and
via (
17). If they represent the same cohomology class in
, then there exists
such that:
We define
by
for all
Then, it is easy to verify that
is an isomorphism of these two abelian extensions
and
such that the diagram in (
16) is commutative. □
5. Skeletal Modified -Differential Left-Symmetric Algebras and Crossed Modules
In this section, first we classify skeletal MD left-symmetric 2-algebras via the third cohomology group. Then, we introduce the notion of a crossed module of MDLSAs, and show that they are equivalent to strict MD left-symmetric 2-algebras.
We first recall the definition of left-symmetric 2-algebras from [
31], which is the categorization of a LSA.
A left-symmetric 2-algebra is a quintuple
, where
is a linear map,
are bilinear maps, and
is a trilinear map, such that for any
and
, the following equations are satisfied:
Motivated by [
31,
32], we propose the concept of an M
D left-symmetric 2-algebra.
Definition 11. An MλD left-symmetric 2-algebra consists of a left-symmetric 2-algebra and an MλD 2-operator on , where , and , for any , satisfying the following equations:
We denote an MλD left-symmetric 2-algebra by .
An MD left-symmetric 2-algebra is said to be skeletal (resp. strict) if (resp. ).
Example 6. For any MλDLSA , is a strict MλD left-symmetric 2-algebra.
Proposition 7. Let be an MλD left-symmetric 2-algebra.
(i) If is skeletal or strict, then is an MλDLSA, where for .
(ii) If is strict, then is an MλDLSA, where for .
(iii) If is skeletal or strict, then is a representation of , where and for .
Proof. From Equations (20)–(25) and (27)–(30), (i), (ii), and (iii) can be obtained by direct verification. □
Theorem 2. There is a one-to-one correspondence between skeletal MλD left-symmetric 2-algebras and 3-cocycles of MλDLSAs.
Proof. Let
be an M
D left-symmetric 2-algebra. By Proposition 7, we can consider the cohomology of M
DLSA
with coefficients in the representation
. For any
, by Equation (26), we have:
By Equations (
8) and (31), it holds that
Thus,
which implies that
is a 3-cocycle of M
DLSA
with coefficients in the representation
.
Conversely, assume that is a 3-cocycle of MDLSA with coefficients in the representation . Then, is a skeletal MD left-symmetric 2-algebra, where and with for any . □
Next we introduce the concept of crossed modules of MDLSAs, which are equivalent to strict MD left-symmetric 2-algebras.
Definition 12. A crossed module of MλDLSAs is a quadruple , where and are MλDLSAs, is a homomorphism of MλDLSAs and is a representation of , for any , satisfying the following equations: Theorem 3. There is a one-to-one correspondence between strict MλD left-symmetric 2-algebras and crossed modules of MλDLSAs.
Proof. Let
be a strict M
D left-symmetric 2-algebra. By Proposition 7, we may construct a crossed module of M
DLSA
, where,
and
, for
. Based on Proposition 7, we only need to check that Equations (32) and (33) hold and
d is a homomorphism of M
DLSAs. In fact, by Equation (20), we have:
combining with Equation (27), which implies that
d is a homomorphism of M
DLSAs. Furthermore, we have:
Thus, we obtain a crossed module of M
DLSAs.
Conversely, a crossed module of M
DLSA
gives rise to a strict M
D left-symmetric 2-algebra
=
, where
are given by:
for all
. Direct verification shows that
is a strict M
D left-symmetric 2-algebra. □
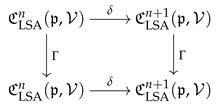 is commutative.
is commutative.




