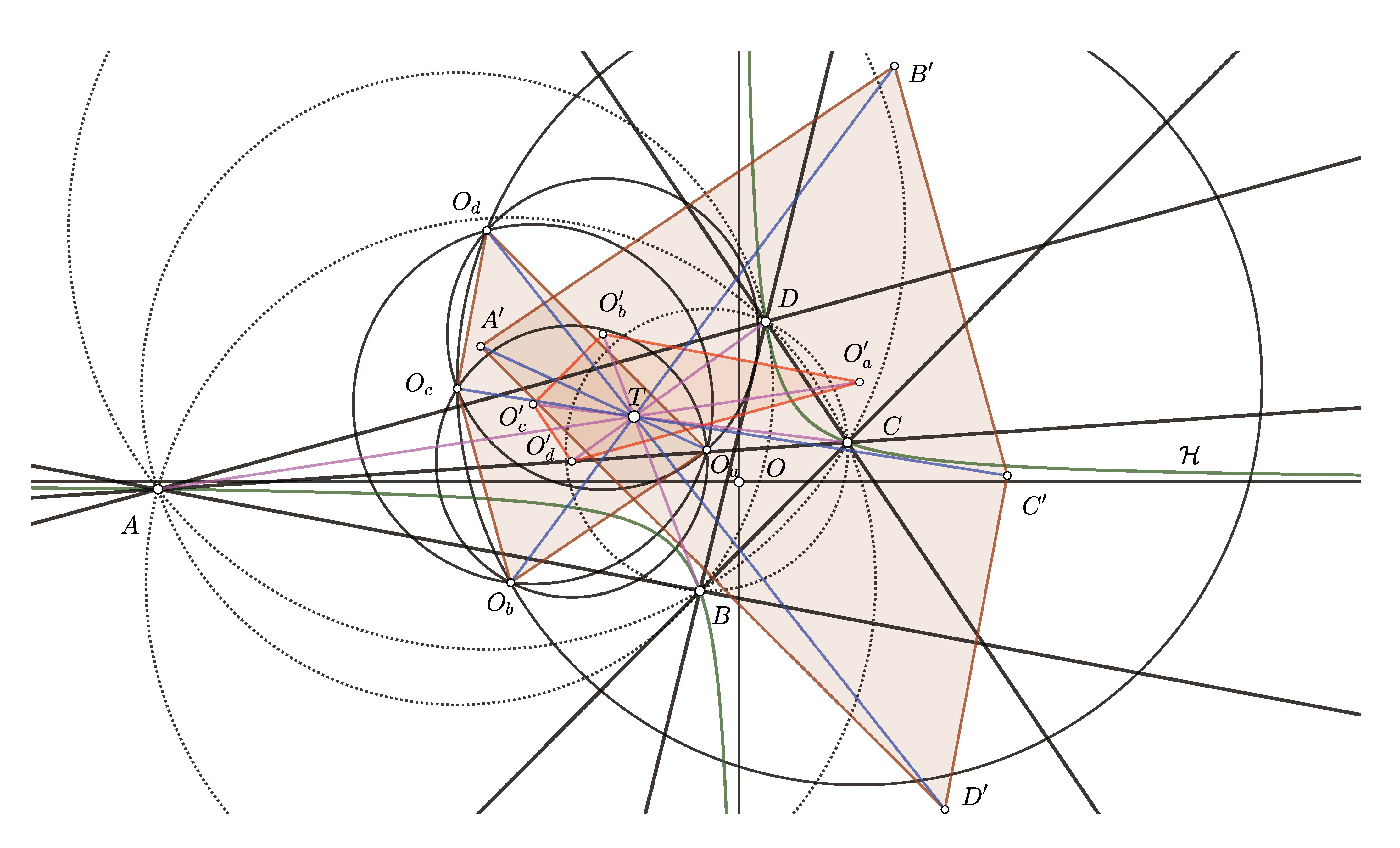Isoptic Point of the Complete Quadrangle

Abstract

In this paper, we study the complete quadrangle. We started this investigation in a few of our previous papers. In those papers and here, the rectangular coordinates are used to enable us to prove the properties of the rich geometry of a quadrangle using the same method. Now, we are focused on the isoptic point of the complete quadrangle $ABCD$, which is the inverse point to $A^{\prime },B^{\prime },C^{\prime },$ and $D^{\prime }$ with respect to circumscribed circles of the triangles $BCD$, $ACD$, $ABD$, and $ABC$, respectively, where $A^{\prime },B^{\prime },C^{\prime },$ and $D^{\prime }$ are isogonal points to $A,B,C,$ and D with respect to these triangles. In studying the properties of the quadrangle regarding its isoptic point, some new results are obtained as well.

1. Introduction

The geometry of a complete quadrangle is very rich and interesting, but all of its properties are proved in different ways. Our aim was to find a simple analytical tool with which it is possible to prove all of its properties using the same method. We have published several papers in this regard [1,2,3], where we present a unique method using rectangular coordinates that enables us to prove several properties of the complete quadrangle in a uniform way. This is the fourth work in the series of such papers, and it considers the isoptic point of the complete quadrangle. In the second section, we provide an overview of the previously mentioned method and important points and circles, which were all introduced in previous papers [1,2,3]. In the third section, we present numerous results on the isoptic point of the complete quadrangle proved using our new method. We end this paper with a Discussion section, where we distinguish our new original results and present the plan for our future work.

2. Materials and Methods

In [1], we introduced the choice of a suitable coordinate system and placed a complete quadrangle in such a system. First, we will mention important definitions and statements proved in [1,2].

The complete quadrangle $ABCD$ is formed by four vertices, $A,B,C,$ and D, and six lines, $AB$, $AC$, $AD$, $BC$, $BD$, and $CD$, representing the sides of the quadrangle. The opposite sides with no common vertex are $AB,CD$, $AC,BD$, and $AD,BC$. In all four papers, we set $ABCD$ in rectangular coordinates using four parameters: $a,b,c,d\ne 0$. In [1], we proved the following important fact: each quadrangle with no perpendicular opposite sides has a circumscribed rectangular hyperbola.

In the mentioned coordinate system, we obtain the following equation for this circumscribed hyperbola $\mathcal{H}$:

$$xy=1.$$

(1)

The center of this hyperbola is the point O, and we call it the center of the quadrangle $ABCD$ as well. The asymptotes of $\mathcal{H}$ are the axes of the quadrangle $ABCD$.

The vertices of $ABCD$ are

$$A=\left(a,\frac{1}{a}\right), B=\left(b,\frac{1}{b}\right), C=\left(c,\frac{1}{c}\right), D=\left(d,\frac{1}{d}\right),$$

(2)

and the sides are

$$\begin{array}{c}\hfill AB\dots x+aby=a+b,AC\dots x+acy=a+c,AD\dots x+ady=a+d\\ \hfill BC\dots x+bcy=b+c,BD\dots x+bdy=b+d,CD\dots x+cdy=c+d.\end{array}$$

(3)

The elementary symmetric functions in four variables—$a,b,c,$ and d—are very useful in our study [1]:

$$\begin{array}{c}\hfill s=a+b+c+d,q=ab+ac+ad+bc+bd+cd,\\ \hfill r=abc+abd+acd+bcd,p=abcd.\end{array}$$

(4)

There are many important points, lines, and circles related to the complete quadrangle, as introduced and proved in [1,2]. Here, we point out some of them that are important for further study in this paper.

The Euler’s circles of the triangles $BCD$, $ACD$, $ABD$, and $ABC$ are as follows:

$$\begin{array}{c}\hfill {\mathcal{N}}_a\dots 2bcd\left(x^2+y^2\right)+\left[1-bcd\left(b+c+d\right)\right]x-\left(b^2{c}^2{d}^2-bc-bd-cd\right)y=0,\\ \hfill {\mathcal{N}}_b\dots 2acd\left(x^2+y^2\right)+\left[1-abc\left(a+c+d\right)\right]x-\left(a^2{c}^2{d}^2-ac-ad-cd\right)y=0,\\ \hfill {\mathcal{N}}_c\dots 2abd\left(x^2+y^2\right)+\left[1-abd\left(a+b+d\right)\right]x-\left(a^2{b}^2{d}^2-ab-ad-bd\right)y=0,\\ \hfill {\mathcal{N}}_d\dots 2abc\left(x^2+y^2\right)+\left[1-abc\left(a+b+c\right)\right]x-\left(a^2{b}^2{c}^2-ab-ac-bc\right)y=0.\end{array}$$

(5)

The centers of these circles are

$$\begin{array}{ccc}\hfill N_a& =& \left(\frac{1}{4}\left(b+c+d-\frac{1}{bcd}\right),\frac{1}{4}\left(\frac{1}{b}+\frac{1}{c}+\frac{1}{d}-bcd\right)\right),\hfill \\ \hfill N_b& =& \left(\frac{1}{4}\left(a+c+d-\frac{1}{acd}\right),\frac{1}{4}\left(\frac{1}{a}+\frac{1}{c}+\frac{1}{d}-acd\right)\right),\hfill \\ \hfill N_c& =& \left(\frac{1}{4}\left(a+b+d-\frac{1}{abd}\right),\frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{d}-abd\right)\right),\hfill \\ \hfill N_d& =& \left(\frac{1}{4}\left(a+b+c-\frac{1}{abc}\right),\frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}-abc\right)\right).\hfill \end{array}$$

(6)

Denoting the orthocenters of the triangles $BCD$, $ACD$, $ABD$, and $ABC$ by $H_a,H_b,H_c,$ and $H_d$, respectively, we obtain their forms:

$$H_a=\left(-\frac{1}{bcd},-bcd\right),H_b=\left(-\frac{1}{acd},-acd\right),H_c=\left(-\frac{1}{abd},-abd\right),H_d=\left(-\frac{1}{abc},-abc\right).$$

(7)

The circumscribed circles of the triangles $ABC$, $ABD$, $ACD$, and $BCD$ are given by

$$\begin{array}{ccc}\hfill {\mathcal{K}}_a& \dots & bcd\left(x^2+y^2\right)-\left[1+bcd\left(b+c+d\right)\right]x-\left(b^2{c}^2{d}^2+bc+bd+cd\right)y\hfill \\ & & +b+c+d+bcd\left(bc+bd+cd\right)=0,\hfill \\ \hfill {\mathcal{K}}_b& \dots & acd\left(x^2+y^2\right)-\left[1+acd\left(a+c+d\right)\right]x-\left(a^2{c}^2{d}^2+ac+ad+cd\right)y\hfill \\ & & +a+c+d+acd\left(ac+ad+cd\right)=0,\hfill \\ \hfill {\mathcal{K}}_c& \dots & abd\left(x^2+y^2\right)-\left[1+abd\left(a+b+c\right)\right]x-\left(a^2{b}^2{d}^2+ab+ad+bd\right)y\hfill \\ & & +a+b+d++abd\left(ab+ad+bd\right)=0,\hfill \\ \hfill {\mathcal{K}}_d& \dots & abc\left(x^2+y^2\right)-\left[1+abc\left(a+b+c\right)\right]x-\left(a^2{b}^2{c}^2+ab+ac+bc\right)y\hfill \\ & & +a+b+c+abc\left(ab+ac+bc\right)=0\hfill \end{array}$$

(8)

with the centers

$$\begin{array}{ccc}\hfill O_a& =& \left(\frac{1}{2}\left(b+c+d+\frac{1}{bcd}\right),\frac{1}{2}\left(\frac{1}{b}+\frac{1}{c}+\frac{1}{d}+bcd\right)\right),\hfill \\ \hfill O_b& =& \left(\frac{1}{2}\left(a+c+d+\frac{1}{acd}\right),\frac{1}{2}\left(\frac{1}{a}+\frac{1}{c}+\frac{1}{d}+acd\right)\right),\hfill \\ \hfill O_c& =& \left(\frac{1}{2}\left(a+b+d+\frac{1}{abc}\right),\frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{d}+abd\right)\right),\hfill \\ \hfill O_d& =& \left(\frac{1}{2}\left(a+b+c+\frac{1}{abc}\right),\frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+abc\right)\right)\hfill \end{array}$$

(9)

and the radii

$${\rho }_a=\frac{1}{2}\left|\frac{a}{p}\right|\sqrt{{\lambda }^{\prime }{\mu }^{\prime }{\nu }^{\prime }},{\rho }_b=\frac{1}{2}\left|\frac{b}{p}\right|\sqrt{{\lambda }^{\prime }\mu \nu },{\rho }_c=\frac{1}{2}\left|\frac{c}{p}\right|\sqrt{\lambda {\mu }^{\prime }\nu },{\rho }_d=\frac{1}{2}\left|\frac{d}{p}\right|\sqrt{\lambda \mu {\nu }^{\prime }},$$

(10)

respectively, and we use the following abbreviations

$$\begin{array}{ccc}\hfill \lambda =a^2{b}^2+1,& \mu =a^2{c}^2+1,& \nu =a^2{d}^2+1,\hfill \\ \hfill {\lambda }^{\prime }=c^2{d}^2+1,& {\mu }^{\prime }=b^2{d}^2+1,& {\nu }^{\prime }=b^2{c}^2+1.\hfill \end{array}$$

(11)

The diagonal triangle $UVW$ of the quadrangle $ABCD$ is given by the vertices

$$\begin{array}{c}\hfill U=AB\cap CD=\left(\frac{ab(c+d)-cd(a+b)}{ab-cd},\frac{a+b-c-d}{ab-cd}\right),\\ \hfill V=AC\cap BD=\left(\frac{ac(b+d)-bd(a+c)}{ac-bd},\frac{a+c-b-d}{ac-bd}\right),\\ \hfill W=AD\cap BC=\left(\frac{ad(b+c)-bc(a+d)}{ad-bc},\frac{a+d-b-c}{ad-bc}\right),\end{array}$$

(12)

and the sides

$$\begin{array}{ccc}\hfill \mathcal{U}=VW& \dots & (a+b-c-d)x+\left[ab\right(c+d)-cd(a+b\left)\right]y=2(ab-cd),\hfill \\ \hfill \mathcal{V}=UW& \dots & (a+c-b-d)x+\left[ac\right(b+d)-bd(a+c\left)\right]y=2(ac-bd),\hfill \\ \hfill \mathcal{W}=UV& \dots & (a+d-b-c)x+\left[ad\right(b+c)-bc(a+d\left)\right]y=2(ad-bc).\hfill \end{array}$$

(13)

The vertices can be expressed as

$$U=\left(\frac{u^{\prime }}{u},\frac{u^{″}}{u}\right),V=\left(\frac{v^{\prime }}{v},\frac{v^{″}}{v}\right),W=\left(\frac{w^{\prime }}{w},\frac{w^{″}}{w}\right),$$

where $u,v,w,u^{\prime },v^{\prime },w^{\prime },u^{″},v^{″},$ and $w^{″}$ stand for

$$\begin{array}{ccc}\hfill u=ab-cd,& u^{\prime }=ab(c+d)-cd(a+b),& u^{″}=a+b-c-d,\hfill \\ \hfill v=ac-bd,& v^{\prime }=ac(b+d)-bd(a+c),& v^{″}=a+c-b-d,\hfill \\ \hfill w=ad-bc,& w^{\prime }=ad(b+c)-bc(a+d),& w^{″}=a+d-b-c.\hfill \end{array}$$

(14)

The orthocenter $H_{UVW}$ of the diagonal triangle $UVW$ is of the form

$$H_{UVW}=\left(\frac{u^{\prime }vw+u{v}^{\prime }w+uv{w}^{\prime }+u^{″}{v}^{″}{w}^{″}}{2uvw},\frac{u^{″}vw+u{v}^{″}w+uv{w}^{″}+u^{\prime }{v}^{\prime }{w}^{\prime }}{2uw}\right).$$

(15)

The line

$${\mathcal{W}}_o\dots (u^{″}vw+u{v}^{″}w+uv{w}^{″}-u^{\prime }{v}^{\prime }{w}^{\prime })x+(u^{\prime }vw+u{v}^{\prime }w+uv{w}^{\prime }-u^{″}{v}^{″}{w}^{″})y=4uvw$$

(16)

is Wallace’s line of the center O with respect to the triangle $UVW$.

The points $A^{\prime },B^{\prime },C^{\prime },$ and $D^{\prime }$ stand for the points isogonal to $A,B,C,$ and D with respect to the triangles $BCD$, $ACD$, $ABD$, and $ABC$, respectively. They are given by

$$\begin{array}{c}\hfill A^{\prime }=\left(\frac{2a-s}{p-1},\frac{r-2bcd}{p-1}\right),B^{\prime }=\left(\frac{2b-s}{p-1},\frac{r-2acd}{p-1}\right),\\ \hfill C^{\prime }=\left(\frac{2c-s}{p-1},\frac{r-2abd}{p-1}\right),D^{\prime }=\left(\frac{2d-s}{p-1},\frac{r-2abc}{p-1}\right).\end{array}$$

(17)

Moreover, the points $A,B,C,$ and D are centers of the circles $B^{\prime }{C}^{\prime }{D}^{\prime }$, $A^{\prime }{C}^{\prime }{B}^{\prime }$, $A^{\prime }{B}^{\prime }{D}^{\prime }$, and $A^{\prime }{C}^{\prime }{D}^{\prime }$. And the following relations are also valid:

$$\begin{array}{cc}\hfill & AB·CD=\left|\frac{(a-b)(c-d)}{p}\right|\sqrt{\lambda {\lambda }^{\prime }},AC·BD=\left|\frac{(a-c)(b-d)}{p}\right|\sqrt{\mu {\mu }^{\prime }},\\ & AD·BC=\left|\frac{(a-d)(b-c)}{p}\right|\sqrt{\nu {\nu }^{\prime }}\end{array}$$

(18)

where $\lambda ,{\lambda }^{\prime },\mu ,{\mu }^{\prime },\nu ,$ and ${\nu }^{\prime }$ are given in (11). The formula for two lines $\mathcal{L}$ and ${\mathcal{L}}^{\prime }$ with slopes $\frac{m}{n}$ and $\frac{m^{\prime }}{n^{\prime }}$ and their oriented angle $\angle (\mathcal{L},{\mathcal{L}}^{\prime })$,

$$tg\angle (\mathcal{L},{\mathcal{L}}^{\prime })=\frac{m^{\prime }n-m{n}^{\prime }}{m{m}^{\prime }+n{n}^{\prime }}.$$

(19)

is also of our interest.

3. Results

The line given by

$$(ab+ac+bc-a^2{b}^2{c}^2)x+(a^{2}bc+a{b}^{2}c+ab{c}^2-1)y=a^{2}b+a{b}^2+a^{2}c+a{c}^2+b^{2}c+b{c}^2+2abc$$

is incident to the points $O_d$ and $D^{\prime }$ given in (9) and (17); so, it is the line $O_d{D}^{\prime }$. However, the line passes through the point

$$T=\left(\frac{s}{p+1},\frac{r}{p+1}\right)$$

(20)

as well. By analogy, the point T is incident to lines $O_a{A}^{\prime },O_b{B}^{\prime },$ and $O_c{C}^{\prime }$ too. We will call this point an isoptic point of the quadrangle $ABCD$. The property described in Theorem 9 justifies this name.

Two points, $(x,y)$ and $(x^{\prime },y^{\prime })$, are conjugate points with respect to the circle ${\mathcal{K}}_d$ in (8) if the equality

$$\begin{array}{cc}& 2abc(x{x}^{\prime }+y{y}^{\prime })-[1+abc(a+b+c)](x+x^{\prime })-(a^2{b}^2{c}^2+ab+ac+bc)(y+y^{\prime })\\ & +2[a+b+c+abc(ab+ac+bc\left)\right]=0\end{array}$$

is valid.

For points $D^{\prime }$ and T from (17) and (20), we obtain

$$\begin{array}{ccc}\hfill 2abc(p^2-1)(x{x}^{\prime }+y{y}^{\prime })& =& 2abc[s(2d-s)+r(r-2abc)]=2abc(r^2-s^2+2ds-2abcr),\hfill \\ \hfill (p^2-1)(x+x^{\prime })& =& \left[\right(p+1\left)\right(2d-s)+(p-1\left)s\right]=2(dp+d-s),\hfill \\ \hfill (p^2-1)(y+y^{\prime })& =& \left[\right(p+1\left)\right(r-2abc)+(p-1\left)r\right]=2(rp-abcp-abc),\hfill \end{array}$$

and as the equality

$$\begin{array}{cc}& abc(r^2-s^2+2ds-2abcr)-[1+abc(a+b+c)](dp+d-s)\\ & -(a^2{b}^2{c}^2+ab+ac+bc)(rp-abcp-abc)+(p^2-1)[a+b+c+abc(ab+ac+bc)]=0\end{array}$$

is fulfilled, these points are conjugate points with respect to the circle ${\mathcal{K}}_d$. They are inverse points with respect to this circle as well because they are collinear to its center $O_d$. Hence, the following theorem, from [4], is valid:

Theorem 1. 

Let $ABCD$ be a complete quadrangle with the isoptic point T and let the $A^{\prime },B^{\prime },C^{\prime },$ and $D^{\prime }$ points be isogonal to the points $A,B,C,$ and D with respect to the triangles $BCD$, $ACD$, $ABD$, and $ABC$, respectively. The point T is the inverse point to $A^{\prime },B^{\prime },C^{\prime },$ and $D^{\prime }$ with respect to the circumcircles of $BCD$, $ACD$, $ABD$, and $ABC$, respectively.

In [4], the isogonal point T is called the tangential point of the quadrangle $ABCD$.

The perpendicular from the point T to the line $AB$ has the equation $abx-y=\frac{a+b}{p+1}$ because $abs-r=(a+b)u$ is valid. This line is incident to the point $T_{AB}=(\frac{a+b}{p+1},cd\frac{a+b}{p+1})$, which is incident as well to the line $AB$ with equation $x+aby=a+b$. Hence, the point $T_{AB}$ is the foot of the perpendicular from T to the line $AB$.

Let us study the point

$$O_D=\left(\frac{1}{2(p+1)}(a+b+c-abc{d}^2),\frac{1}{2d(p+1)}(ab{d}^2+ac{d}^2+bc{d}^2-1)\right).$$

The points $T_{AB}$ and $O_D$ have the differences of coordinates $\frac{1}{2d(p+1)}(ad+bd-cd+abc{d}^3)$ and $\frac{1}{2d(p+1)}(ac{d}^2+bc{d}^2-ab{d}^2+1)$. As ${(ad+bd-cd+abc{d}^3)}^2+{(ac{d}^2+bc{d}^2-ab{d}^2+1)}^2=(a^2{d}^2+1)(b^2{d}^2+1)(c^2{d}^2+1)$ is valid, then $4d^2{(p+1)}^2{O}_D{T}_{AB}^2={\lambda }^{\prime }{\mu }^{\prime }\nu$ holds. Based on the symmetry of this result on $a,b,$ and c, it follows that the point $O_D$ is the center of the pedal circle of the point T with respect to the triangle $ABC$ and that this circle has the radius $\frac{1}{\left|2d\right(p+1\left)\right|}\sqrt{{\lambda }^{\prime }{\mu }^{\prime }\nu }$. Similarly, the pedal circles of the point T with respect to the triangles $ABD$, $ACD$, and $BCD$ have the radii $\frac{1}{\left|2c\right(p+1\left)\right|}\sqrt{{\lambda }^{\prime }\mu {\nu }^{\prime }}$, $\frac{1}{\left|2b\right(p+1\left)\right|}\sqrt{\lambda {\mu }^{\prime }{\nu }^{\prime }}$, and $\frac{1}{\left|2a\right(p+1\left)\right|}\sqrt{\lambda \mu \nu }$, respectively. Comparing with (10), we can see that these radii are inversely proportional to the radii of the circles $ABC$, $ABD$, $ACD$, and $BCD$. However, the equality ${(ad+bd+cd-abc{d}^3)}^2+{(ac{d}^2+bc{d}^2+ab{d}^2-1)}^2=(a^2{d}^2+1)(b^2{d}^2+1)(c^2{d}^2+1)$, i.e., $4d^2{(p+1)}^2{O}_D{O}^2=\lambda {\mu }^{\prime }{\nu }^{\prime }$, holds, which leads to the following theorem.

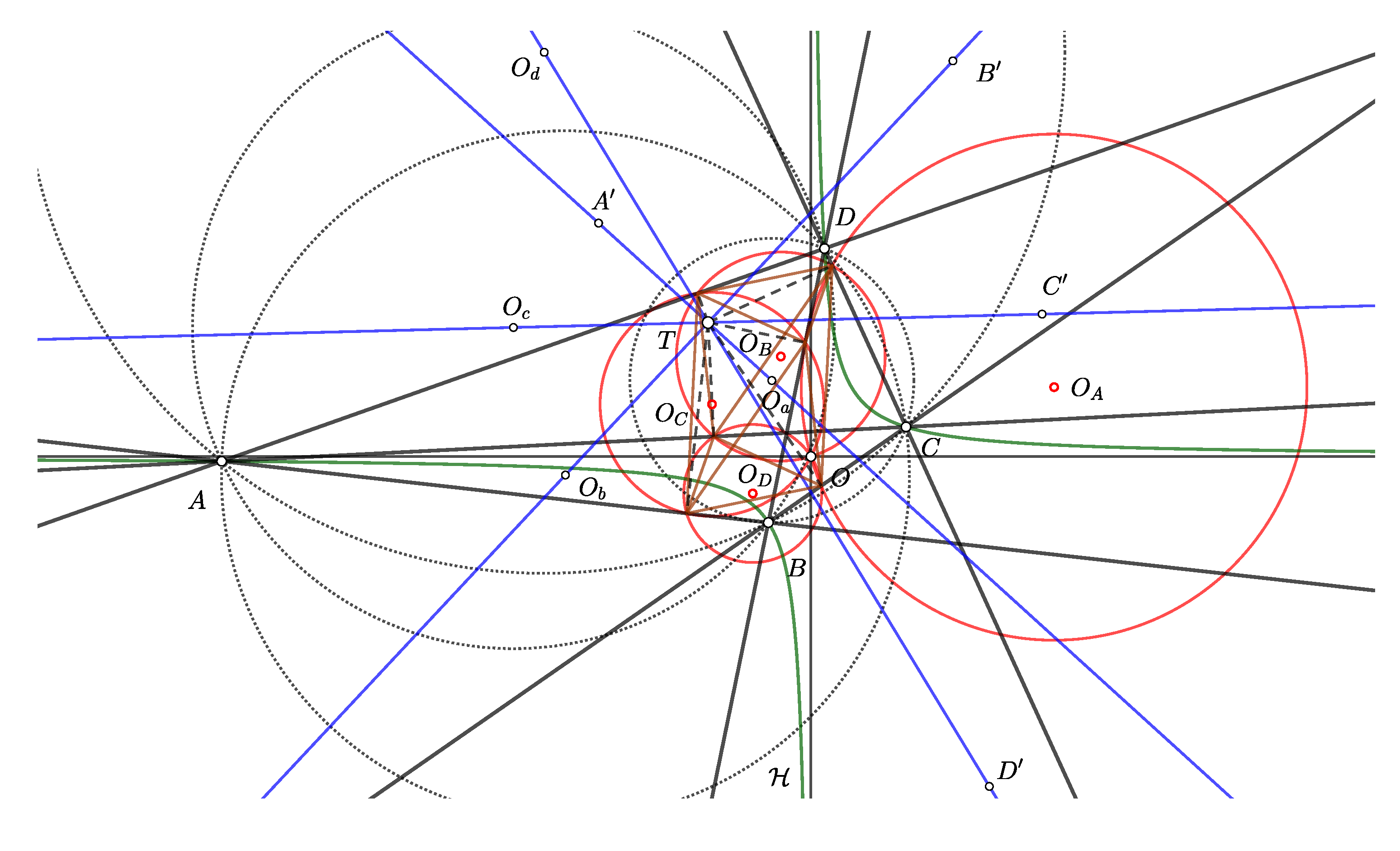
Theorem 2. 

Let $ABCD$ be a complete quadrangle with the center O and isoptic point T. The pedal circles of the point T with respect the triangles $ABC$, $ABD$, $ACD$, and $BCD$, respectively, are incident to the center O.

This is our an original statement; see the visualization of the theorem in Figure 1.

Let $T_{AB}^{\prime },T_{AC}^{\prime },T_{AD}^{\prime },T_{BC}^{\prime },T_{BD}^{\prime },$ and $T_{CD}^{\prime }$ be the points symmetric to T with respect to the lines $AB$, $AC$, $AD$, $BC$, $BD$, and $CD$. Then, we have, e.g., the equality $T_{AB}^{\prime }=2T_{AB}-T$, out of which the first equality from the two follows:

$$T_{AB}^{\prime }=\left(\frac{a+b-c-d}{p+1},\frac{cd(a+b)-ab(c+d)}{p+1}\right),T_{CD}^{\prime }=\left(\frac{c+d-a-b}{p+1},\frac{ab(c+d)-cd(a+b)}{p+1}\right)$$

The second equality follows from the first by substituting pairs $a,b$ and $c,d$. We can write it better in the form

$$\begin{array}{c}\hfill T_{AB}^{\prime }=\left(\frac{u^{″}}{p+1},-\frac{u^{\prime }}{p+1}\right),T_{CD}^{\prime }=\left(-\frac{u^{″}}{p+1},\frac{u^{\prime }}{p+1}\right).\end{array}$$

Analogously, we have

$$\begin{array}{c}\hfill T_{AC}^{\prime }=\left(\frac{v^{″}}{p+1},-\frac{v^{\prime }}{p+1}\right),T_{BD}^{\prime }=\left(-\frac{v^{″}}{p+1},\frac{v^{\prime }}{p+1}\right),\\ \hfill T_{AD}^{\prime }=\left(\frac{w^{″}}{p+1},-\frac{w^{\prime }}{p+1}\right),T_{BC}^{\prime }=\left(-\frac{w^{″}}{p+1},\frac{w^{\prime }}{p+1}\right),\end{array}$$

where $u^{\prime },u^{″},v^{\prime },v^{″},w^{\prime },$ and $w^{″}$ are given in (14). We have proved the next result:

Theorem 3. 

Let $ABCD$ be a complete quadrangle with the center O and isoptic point T. Points symmetric to T with respect to the sides of $ABCD$ form a hexagon symmetric with respect to the center O, and the feet of the perpendiculars from T to the sides of $ABCD$ form a hexagon symmetric with respect to the midpoint of T and O.

The result was reached in [4,5] and is shown in Figure 2.

The line $OU$ has the slope $\frac{u^{″}}{u^{\prime }}$, and the line $CD$ has the slope $-\frac{1}{cd}$, so due to (19),

$$tg\angle (UO,CD)=\frac{u^{\prime }+cd{u}^{″}}{u^{″}-cd{u}^{\prime }}$$

is valid. The line $AB$ has the slope $\frac{-1}{ab}$, and the line $UT$ has the slope $\frac{ru-(p+1)u^{″}}{su-(p+1)u^{\prime }}$, and due to the same formula,

$$tg\angle (AB,UT)=\frac{abru-ab(p+1)u^{″}+su-(p+1)u^{\prime }}{absu-ab(p+1)u^{\prime }-ru+(p+1)u^{″}}$$

(21)

holds. The numerator in (21), because of valid equality $ab{u}^{″}+u^{\prime }-(a+b)u=0$, is equal to

$$\begin{array}{c}\hfill abru+su-(p+1)(a+b)u=ab\left[ab\right(c+d)+cd(a+b\left)\right]u-p(a+b)u+(s-a-b)u=\\ \hfill =a^2{b}^2(c+d)u+(c+d)u=(a^2{b}^2+1)(c+d)u=(a^2+b^2+1)(u^{\prime }+cd{u}^{″})\end{array}$$

while because of

$$\begin{array}{c}\hfill absu-ru=\left[ab\right(a+b+c+d)-ab(c+d)-cd(a+b\left)\right]u=(ab-cd)(a+b)u=\\ \hfill (ab-cd)(a+b)u=(a+b)u^2=(u^{\prime }+ab{u}^{″})u\end{array}$$

the denominator is equal to

$$(p+1+abu)u^{″}-(abp+ab-u)u^{\prime }=(a^2{b}^2+1)u^{″}-(a^2{b}^2+1)cd{u}^{\prime }=(a^2{b}^2+1)(u^{″}-cd{u}^{\prime }),$$

Thus, finally, we obtain

$$tg\angle (AB,UT)=\frac{u^{\prime }+cd{u}^{″}}{u^{″}-cd{u}^{\prime }}=tg\angle (UO,CD).$$

We have just proved the following statement.

Theorem 4. 

Let $ABCD$ be a complete quadrangle with the center O and isoptic point T. The lines connecting O and T with a diagonal point of the quadrangle $ABCD$ are isogonal with respect to the pair of its opposite sides intersecting in this diagonal point.

Lines $TA$ and $TB$ have slopes

$$\frac{ar-p-1}{a(s-a-ap)},\frac{br-p-1}{b(s-b-bp)},$$

so due to (19), we obtain

$$tg\angle ATB=\frac{a(s-a-ap)(br-p-1)-b(s-b-bp)(ar-p-1)}{(ar-p-1)(br-p-1)+ab(s-a-ap)(s-b-bp)}.$$

For the numerator and denominator, we obtain the forms

$$(b-a)(c+d)(a^2{b}^2+1)(p+1)\mathrm{and}(a^2{b}^2+1)[{(p+1)}^2+ab(c^2+d^2)-cd(a^2+b^2)],$$

Hence,

$$tg\angle ATB=\frac{(b-a)(c+d)(p+1)}{{(p+1)}^2+ab(c^2+d^2)-cd(a^2+b^2)}.$$

(22)

Lines $AC$ and $BC$ have the slopes $-\frac{1}{ac}$ and $-\frac{1}{bc}$, so due to (19), we obtain the first out of the two analogous equalities:

$$tg\angle ACB=\frac{(b-a)c}{ab{c}^2+1},tg\angle ADB=\frac{(b-a)d}{ab{d}^2+1}.$$

(23)

out of which

$$\begin{array}{ccc}\hfill tg\left(\angle ACB+\angle ADB\right)& =& \frac{tg\angle ACB+tg\angle ADB}{1-tg\angle ACB·tg\angle ADB}\hfill \\ & =& \frac{(b-a)(c+d)(p+1)}{{(p+1)}^2+ab(c^2+d^2)-cd(a^2+b^2)}=tg\angle ATB\hfill \end{array}$$

easily follows. Hence, we have proved the first of six analogous statements.

Theorem 5. 

Let $ABCD$ be a complete quadrangle and T its isoptic point. The following statements are valid:

$$\begin{array}{cc}& tg\angle ATB=tg\angle ACB+tg\angle ADB,tg\angle ATC=tg\angle ABC+tg\angle ADC,\\ & tg\angle ATD=tg\angle ABD+tg\angle ACD,tg\angle BTC=tg\angle BAC+tg\angle BDC,\\ & tg\angle BTD=tg\angle BAD+tg\angle BCD,tg\angle CTD=tg\angle CAD+tg\angle CBD\end{array}$$

The same result can be found in [4,6], where the result is attributed to T. McHugh, and in [7]. See Figure 2.

Out of (17) and (20), for the slopes of lines $T{A}^{\prime }$ and $T{B}^{\prime }$, we obtain expressions

$$\frac{bc+bd+cd-b^2{c}^2{d}^2}{1-bcd(b+c+d)},\frac{ac+ad+cd-a^2{c}^2{d}^2}{1-acd(a+c+d)}$$

so due to (19),

$$\begin{array}{cc}\hfill & tg\angle A^{\prime }T{B}^{\prime }=\hfill \\ \hfill & \frac{(ac+ad+cd-a^2{c}^2{d}^2)[1-bcd(b+c+d)]-(bc+bd+cd-b^2{c}^2{d}^2)[1-acd(a+c+d)]}{(bc+bd+cd-b^2{c}^2{d}^2)(ac+ad+cd-a^2{c}^2{d}^2)+[1-bcd(b+c+d)][1-acd(a+c+d)]}\hfill \end{array}$$

is obtained. For the numerator and denominator, we obtain forms

$$(a-b)(c+d)(c^2{d}^2+1)(p+1)\mathrm{and}(c^2{d}^2+1)[{(p+1)}^2+ab(c^2+d^2)-cd(a^2+b^2)],$$

so because of (22),

$$tg\angle A^{\prime }T{B}^{\prime }=\frac{(a-b)(c+d)(p+1)}{{(p+1)}^2+ab(c^2+d^2)-cd(a^2+b^2)}=-tg\angle ATB.$$

Hence, we have proved the following.

Theorem 6. 

Let $ABCD$ be a complete quadrangle with the isoptic point T and $A^{\prime },B^{\prime },C^{\prime },$ and $D^{\prime }$ points isogonal to the points $A,B,C,$ and D with respect to the triangles $BCD$, $ACD$, $ABD$, and $ABC$, respectively. The pairs of lines $TA,T{A}^{\prime }$; $TB,T{B}^{\prime }$; $TC,T{C}^{\prime }$; and $TD,T{D}^{\prime }$ have the same bisectors. Lines $TA,TB,TC,$ and $TD$ have the same cross ratio as the lines $T{A}^{\prime }$, $T{B}^{\prime }$, $T{C}^{\prime }$, and $T{D}^{\prime }$.

The first statement from the previous theorem was reached in [8,9], and the second, in [10].

Let $\overline{D}$ be a point on the hyperbola $\mathcal{H}$ diametrically opposite to the point D, i.e., $\overline{D}=(-d,-\frac{1}{d})$. Then, the slope of the line $A\overline{D}$ is $\frac{1}{ad}$. As the line $AB$ has the slope $-\frac{1}{ab}$, then due to (19), the equality $tg\angle BA\overline{D}=\frac{ab+ad}{a^{2}bd-1}$ is obtained. As the line $AT$ has the slope $\frac{ar-p-1}{a(s-ap-a)}$, and the line $AC$ has the slope $-\frac{1}{ac}$, according to (19), we obtain the equality

$$tg\angle TAC=\frac{ab+ad}{a^{2}bd-1}=tg\angle BA\overline{D}.$$

Analogous equalities are valid for points B and C; hence, we have proved the following theorem.

Theorem 7. 

Let $ABCD$ be a complete quadrangle with the isoptic point T and circumscribed hyperbola $\mathcal{H}$. Let $\overline{A},\overline{B},\overline{C},$ and $\overline{D}$ be points on the hyperbola $\mathcal{H}$ diametrically opposite to the points $A,B,C,$ and D, respectively. The point T is an isogonal point to $\overline{A},\overline{B},\overline{C},$ and $\overline{D}$ with respect to the triangles $BCD,ACD,ABD,$ and $ABC$, respectively.

This result is in [8,9,10,11,12]. There is one more result regarding the fact that an isogonal image with respect to the triangle of any circumscribed conic is a line.

Theorem 8. 

Let $ABCD$ be a complete quadrangle and $\mathcal{H}$ be its circumscribed hyperbola. The lines that are isogonal images of $\mathcal{H}$ with respect to the triangles $BCD$, $ACD$, $ABD$, and $ABC$ are intersected at the point T, which is an isogonal point of the points $\overline{A},\overline{B},\overline{C},$ and $\overline{D}$ with respect to these triangles.

Specifically, the points $\overline{A},\overline{B},\overline{C},$ and $\overline{D}$ are incident to $\mathcal{H}$. A previous result can be found in [10].

For the distance of the point $O_d$ from (9) and T from (20), we obtain the equality

$$\begin{array}{ccc}\hfill 4p^2{(p+1)}^2{O}_d{T}^2& =& {[2sp-p(p+1)(a+b+c)-(p+1)d]}^2+\hfill \\ & & +{[2rp-(p+1)(abd+acd+bcd)-p(p+1)abc]}^2\hfill \end{array}$$

and then, after some computing, we also obtain

$$4p^2{(p+1)}^2{O}_d{T}^2={(p-1)}^2{d}^2(a^2{b}^2+1)(a^2{c}^2+1)(b^2{c}^2+1)={(p-1)}^2{d}^2\lambda \mu {\nu }^{\prime }.$$

This means that $O_{d}T=\frac{|p-1|}{2\left|abc\right(p+1\left)\right|}\sqrt{\lambda \mu {\nu }^{\prime }}$ is valid. Together with (10), the last equality in the series is obtained:

$${\rho }_a:O_{a}T={\rho }_b:O_{b}T={\rho }_c:O_{c}T={\rho }_d:O_{d}T=\left|\frac{p+1}{p-1}\right|,$$

(24)

And the rest is valid by analogy. This actually leads to the following theorem.

Theorem 9. 

Let $ABCD$ be a complete quadrangle and let its isoptic point T lie in the exterior of the circles $BCD,ACD,ABD,$ and $ABC$. These circles are seen from T under equal angels.

The result from the previous theorem can be found in [12], where it is attributed to G.T. Bennett. But also, the same result is in [4,7,11] as well.

The locus of points for which the ratio of distances to the centers of two given circles is equal to the ratio of the radii of these circles is a circle. This circle is called the circle of similitude. Let us note the following: if two given circles have the common point, then the point is incident to their circle of similitude. So, the circle of similitude for the circles ${\mathcal{K}}_a$ and ${\mathcal{K}}_b$ with the centers $O_a$ and $O_b$ and radii ${\rho }_a$ and ${\rho }_b$ is the locus of the point P such that $O_{a}P:O_{b}P={\rho }_a:{\rho }_b$ is valid, and this circle is incident to C and D. Out of (24), it follows that the isoptic point T is incident to this circle of similitude. Hence, we have proved the following theorem.

Theorem 10. 

Let $ABCD$ be a complete quadrangle. Its isoptic point T is the common point of the six circles of similitude of the pairs of the four circumcircles of the triangles $ABC$, $ABD$, $ACD$, and $BCD$.

This result can be found in [7,10,11,12], which is attributed to G.T. Bennett. See this result in Figure 3 as well.

For the point $D=(d,\frac{1}{d})$ and the point T from (20), we obtain

$$d^2{(p+1)}^{2}D{T}^2={[d^2(p+1)-ds]}^2+{(p+1-dr)}^2,$$

and after some computing, we also obtain

$$d^2{(p+1)}^{2}D{T}^2=(a^2{d}^2+1)(b^2{d}^2+1)(c^2{d}^2+1)={\lambda }^{\prime }{\mu }^{\prime }\nu ,$$

(25)

i.e., we have the last four analogous equalities:

$$\begin{array}{c}\hfill a^2{(p+1)}^{2}A{T}^2=\lambda \mu \nu ,b^2{(p+1)}^{2}B{T}^2=\lambda {\mu }^{\prime }{\nu }^{\prime },\\ \hfill c^2{(p+1)}^{2}C{T}^2={\lambda }^{\prime }\mu {\nu }^{\prime },d^2{(p+1)}^{2}D{T}^2={\lambda }^{\prime }{\mu }^{\prime }\nu .\end{array}$$

(26)

Because of $4p^2{{\rho }_d}^2=d^2\lambda \mu {\nu }^{\prime }$ in (10), it follows that $4p^2{(p+1)}^{2}D{T}^2{{\rho }_d}^2=\lambda \mu \nu {\lambda }^{\prime }{\mu }^{\prime }{\nu }^{\prime }$. Along with three more analogues equalities, we obtain

$$AT{\rho }_a=BT{\rho }_b=CT{\rho }_c=DT{\rho }_d,$$

(27)

and on the other side, from (27), we have

$${\left|p\right|(p+1)}^{4}AT·BT·CT·DT=\lambda \mu \nu {\lambda }^{\prime }{\mu }^{\prime }{\nu }^{\prime }.$$

(28)

As ${(a-b)}^2{c}^2+{(ab{c}^2+1)}^2=(a^2{c}^2+1)(b^2{c}^2+1)=\mu {\nu }^{\prime }$ is valid, then from the first formula from (23), we easily obtain the first of two analogous equalities,

$${sin}^2\angle ACB=\frac{1}{\mu {\nu }^{\prime }}{(a-b)}^2{c}^2,{sin}^2\angle ADB=\frac{1}{{\mu }^{\prime }\nu }{(a-b)}^2{d}^2,$$

(29)

for the sines of angels under which the side $AB$ of the quadrangle $ABCD$ is seen from C and D. There are ten more analogous equalities for the remaining five sides of the quadrangle. From the last two equalities and the last two equalities in (26), the equality ${sin}^2\angle ACB:{sin}^2\angle ADB=c^2{\mu }^{\prime }\nu :d^2\mu {\nu }^{\prime }=D{T}^2:C{T}^2$ follows, i.e., we finally have

$$sin\angle ACB:sin\angle ADB=DT:CT,$$

along with five more analogous statements. We can find them in [4].

For the power ${\pi }_d$ of the point T with respect to the circle $ABC$ from (8), we obtain

$$\begin{array}{ccc}& & abc{(p+1)}^2{\pi }_d=abc(s^2+r^2)-[1+abc(a+b+c)]s(p+1)\hfill \\ & & -(a^2{b}^2{c}^2+ab+ac+bc)r(p+1)+[a+b+c+abc(ab+ac+bc)]{(p+1)}^2,\hfill \end{array}$$

and then, after some calculations $abc{(p+1)}^2{\pi }_d=-d(a^2{b}^2+1)(a^2{c}^2+1)(b^2{c}^2+1)$ follows, i.e., the last equality is proved as follows:

$$\begin{array}{c}\hfill p{(p+1)}^2{\pi }_a=-a^2{\lambda }^{\prime }{\mu }^{\prime }{\nu }^{\prime },p{(p+1)}^2{\pi }_b=-b^2{\lambda }^{\prime }\mu \nu ,\\ \hfill p{(p+1)}^2{\pi }_c=-c^2\lambda {\mu }^{\prime }\nu ,p{(p+1)}^2{\pi }_d=-d^2\lambda \mu {\nu }^{\prime },\end{array}$$

(30)

where ${\pi }_a,{\pi }_b,$ and ${\pi }_c$ are powers of the point T with respect to the circles $BCD$, $ACD$, and $ABD$. If $p>0$, i.e., the quadrangle $ABCD$ is convex, then these powers of the point T are negative and the point T lies in the interior of each circle $BCD,ACD,ABD,$ and $ABC$, and if $p<0$, i.e., one of points $A,B,C,$ and D is placed into the area of the triangle formed by the remaining three points, then the mentioned powers of the point T are positive and T is outside of the circles $BCD,ACD,ABD,$ and $ABC$. Out of (30), it follows that $p^2{(p+1)}^8{\pi }_a{\pi }_b{\pi }_c{\pi }_d={\left(\lambda \mu \nu {\lambda }^{\prime }{\mu }^{\prime }{\nu }^{\prime }\right)}^2$. Because of (25), we have the equality $p^2{(p+1)}^{8}A{T}^{2}B{T}^{2}C{T}^{2}D{T}^2={\left(\lambda \mu \nu {\lambda }^{\prime }{\mu }^{\prime }{\nu }^{\prime }\right)}^2$, so ${\pi }_a{\pi }_b{\pi }_c{\pi }_d=A{T}^{2}B{T}^{2}C{T}^{2}D{T}^2$ is valid. We have just proved the following theorem.

Theorem 11. 

Let $ABCD$ be a complete quadrangle and T be its isoptic point. ${\pi }_a,{\pi }_b,{\pi }_c,$ and ${\pi }_d$ are denoted powers of the point T with respect to the circumscribed circles of the triangles $BCD,ACD,ABD,$ and $ABC$. Then, the following statement is valid"

$${\pi }_a{\pi }_b{\pi }_c{\pi }_d=A{T}^{2}B{T}^{2}C{T}^{2}D{T}^2.$$

The same result was proved in [4] in another way.

For the square of a distance between T and U, the equality ${(p+1)}^2{u}^{2}T{U}^2={(su-u^{\prime }-p{u}^{\prime })}^2+{(ru-p{u}^{″}-u^{″})}^2$ is fulfilled. As

$$\begin{array}{ccc}\hfill su& =& (a+b)u+(c+d)u=ab{u}^{″}+u^{\prime }+cd{u}^{″}+u^{\prime }=(ab+cd)u^{″}+2u^{\prime },\hfill \\ \hfill ru& =& ab(c+d)u+cd(a+b)u=ab(cd{u}^{″}+u^{\prime })+cd(ab{u}^{″}+u^{\prime })=(ab+cd)u^{\prime }+2p{u}^{″},\hfill \end{array}$$

then

$$\begin{array}{cc}\hfill & {(p+1)}^2{u}^{2}T{U}^2={[(ab+cd)u^{″}-(p-1)u^{\prime }]}^2+{[(ab+cd)u^{\prime }+(p-1)u^{″}]}^2=\hfill \\ \hfill & =[{(ab+cd)}^2+{(p-1)}^2]({u^{\prime }}^2+{u^{″}}^2)=(a^2{b}^2+1)(c^2{d}^2+1)({u^{\prime }}^2+{u^{″}}^2)=\lambda {\lambda }^{\prime }{u}^{2}O{U}^2,\hfill \end{array}$$

So, we reach the first out of three analogous equalities in the next theorem.

Theorem 12. 

Let $ABCD$ be a complete quadrangle; $UVW$, its diagonal triangle; and T, the isoptic point. For the distances $TU$, $TV$, and $TW$, the following equalities are valid:

$$TU=\frac{\sqrt{\lambda {\lambda }^{\prime }}}{|p+1|}OU,TV=\frac{\sqrt{\mu {\mu }^{\prime }}}{|p+1|}OV,TW=\frac{\sqrt{\nu {\nu }^{\prime }}}{|p+1|}OW$$

This result was reached in [4] as well.

From the first equality in (10), the equality $4p^2{\rho }_a^2=a^2{\lambda }^{\prime }{\mu }^{\prime }{\nu }^{\prime }$ is obtained. Together with the first equality from (30), it gives ${\pi }_d=-\frac{4p}{p+1}{\rho }_a^2$. Hence, we have the following theorem.

Theorem 13. 

Let $ABCD$ be a complete quadrangle and T be its isoptic point. The powers of the point T with respect to the circumscribed circles $BCD$, $ACD$, $ABD$, and $ABC$ are proportional to the squares of the radii of these circles. The distances of the point T to each vertex of $ABCD$ are reversely proportional to the radii of the circumscribed circle passing through the other three vertices.

The second statement in the previous theorem follows from (27). Both results can be found in [7].

For points $D^{\prime }$ in (17) and T in (20), we obtain

$$\begin{array}{ccc}\hfill {(p^2-1)}^2{D}^{\prime }{T}^2& =& {(2d+2pd-2ps)}^2+{(2r-2abc-2abcp)}^2\hfill \\ & =& 4d^2{[1-abc(a+b+c)]}^2+{(ab+ac+bc-a^2{b}^2{c}^2)}^2\hfill \\ & =& 4d^2(a^2{b}^2+1)(a^2{c}^2+1)(b^2{c}^2+1)=4d^2\lambda \mu {\nu }^{\prime },\hfill \end{array}$$

and together with the last equality from (26), the equality ${(p+1)}^4{(p-1)}^{2}D{T}^2{D}^{\prime }{T}^2=4\lambda \mu \nu {\lambda }^{\prime }{\mu }^{\prime }{\nu }^{\prime }$, i.e., ${(p+1)}^2|p-1|DT·D^{\prime }T=2\sqrt{\lambda \mu \nu {\lambda }^{\prime }{\mu }^{\prime }{\nu }^{\prime }}$ is obtained. Along with three more analogous equalities, we obtain the following theorem.

Theorem 14. 

Let $ABCD$ be a complete quadrangle; T, its isoptic point; and $A^{\prime }$, $B^{\prime }$, $C^{\prime }$, and $D^{\prime }$, points isogonal to $A,B,C,$ and D with respect to the triangles $BCD$, $ACD$, $ABD$, and $ABC$. Then,

$$AT·A^{\prime }T=BT·B^{\prime }T=CT·C^{\prime }T=DT·D^{\prime }T.$$

The previous result was proved in [8,9] as well. Together with the first statement in Theorem 6, our original statement is proved.

Theorem 15. 

Let $ABCD$ be a complete quadrangle; T, its isoptic point; and $A^{\prime }$, $B^{\prime }$, $C^{\prime }$, and $D^{\prime }$, points isogonal to $A,B,C,$ and D with respect to the triangles $BCD$, $ACD$, $ABD$, and $ABC$. The complete quadrangle $ABCD$ is mapped into the complete quadrangle $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ through the composition of a reflection with respect to the line through T and an inversion with the center in T.

For the points $O_d$ in (9) and $D^{\prime }$ in (20), we obtain

$$\begin{array}{ccc}\hfill 4p^2{(p-1)}^2{D}^{\prime }{O}_d^2& =& [p(p+1)s-{(p+1)}^{2}d]˘3+{[{(p+1)}^{2}abc-(p+1)r]}^2\hfill \\ & =& {(p+1)}^2{[p(a+b+c)-d]}^2+{[pabc-(abd+acd+bcd)]}^2\hfill \\ & =& {(p+1)}^2{d}^2{[abc(a+b+c)-1]}^2+{(a^2{b}^2{c}^2-ab-ac-bc)}^2\hfill \\ & =& {(p+1)}^2{d}^2(a^2{b}^2+1)(a^2{c}^2+1)(b^2{c}^2+1)={(p+1)}^2{d}^2\lambda \mu {\nu }^{\prime }.\hfill \end{array}$$

Along with already proved equality, $4p^2{(p+1)}^2{O}_d{T}^2={(p-1)}^2{d}^2\lambda \mu {\nu }^{\prime }$, it follows that $16p^4{D}^{\prime }{O_d^{\prime }}^2{O}_d{T}^2=d^4{\left(\lambda \mu {\nu }^{\prime }\right)}^2$. Out of (10), $16p^4{\rho }_d^4=d^4{\left(\lambda \mu {\nu }^{\prime }\right)}^2$ follows, so the following statement is valid.

Theorem 16. 

Let $ABCD$ be a complete quadrangle and T be its isoptic point, and let $A^{\prime },B^{\prime },C^{\prime },$ and $D^{\prime }$ be points isogonal to the points $A,B,C,$ and D with respect to the triangles $BCD$, $ACD$, $ABD$, and $ABC$. The following equalities are valid:

$$A^{\prime }{O}_a·O_{a}T={\rho }_a^2,B^{\prime }{O}_b·O_{b}T={\rho }_b^2,C^{\prime }{O}_c·O_{c}T={\rho }_c^2,D^{\prime }{O}_d·O_{a}T={\rho }_d^2$$

where $O_a,O_b,O_c,$ and $O_d$ and ${\rho }_a,{\rho }_b,{\rho }_c,$ and ${\rho }_d$ stand for the centers and radii of the circumcircles of $BCD$, $ACD$, $ABD$, and $ABC$, respectively.

The same result is in [8,9].

The points T and $\overline{D}$ are isogonal with respect to the triangle $ABC$. It is well known from the geometry of a triangle that there is a conic with foci T and $\overline{D}$ for which the square ${\beta }^2$ of the semi-minor axis $\beta$ is equal to the product of the distances of these foci to any side of the triangle. If we take into consideration that the studied conic is an ellipse or hyperbola and that we are calculating with oriented distances, then, for the point T from (20), the point $\overline{D}=(-d,-\frac{1}{d})$, and the line $AB$ with equation $x+aby-a-b=0$, we obtain

$$\begin{array}{ccc}\hfill \pm {\beta }^2& =& \frac{1}{\lambda }\left(\frac{s}{p+1}+ab\frac{r}{p+1}-a-b\right)(-d-ab\frac{1}{d}-a-b)\hfill \\ & =& -\frac{1}{d(p+1)\lambda }[s+abr-p(a+b)-a-b](ab+ad+bd+d^2)\hfill \\ & =& -\frac{1}{d(p+1)\lambda }[c+d+a^2{b}^2(c+d)+abcd(a+b)-p(a+b)](a+d)(b+d)\hfill \\ & =& -\frac{1}{d(p+1)\lambda }(a^2{b}^2+1)(c+d)(a+d)(b+d)=-\frac{1}{d(p+1)}(a+d)(b+d)(c+d).\hfill \end{array}$$

The distance between points T and $\overline{D}$ is given by

$$d^2{(p+1)}^2\overline{D}{T}^2={(pd+d+s)}^2{d}^2+{(rd+p+1)}^2.$$

The linear eccentricity $\gamma$ of the studied conic is $\frac{1}{2}\overline{D}T$. If $\alpha$ is its semi-major axis, then ${\alpha }^2=\gamma \pm {\beta }^2$ is valid. Hence, through a little bit of computing,

$$\begin{array}{ccc}\hfill 4d^2{(p+1)}^2{\alpha }^2& =& {(pd+d+s)}^2{d}^2+{(rd+p+1)}^2-4d(p+1)(a+d)(b+d)(c+d)\hfill \\ & =& (a^2{d}^2+1)(b^2{d}^2+1)(c^2{d}^2+1)={\lambda }^{\prime }{\mu }^{\prime }\nu =d^2{(p+1)}^{2}D{T}^2\hfill \end{array}$$

follow because of (25). And because of this, $2\alpha =DT$, so we have proved the following theorem.

Theorem 17. 

Let $ABCD$ be a complete quadrangle and T be its isoptic point. The major axis of the inscribed conics of the triangles $BCD,ACD,ABD,$ and $ABC$ with one focus in T is equal to the distance of this focus and the points $A,B,C,$ and D, respectively.

Let us denote the centers of the circles $O_b{O}_c{O}_d$, $O_a{O}_c{O}_d$, $O_a{O}_b{O}_d$, and $O_a{O}_b{O}_c$ by $O_a^{\prime },O_b^{\prime },O_c^{\prime },$ and $O_d^{\prime }$. The points $O_c$ and $O_d$ are incident to the bisector of the line segment $AB$, so the bisector of the line segment $O_c{O}_d$ is parallel to the line $AB$. Because the line $O_c{O}_d$ has the slope $-\frac{1}{ab}$ and it is incident to the midpoint of $O_d$ and $O_c$, it is easy to see that its equation is the first one of the next two:

$$\begin{array}{c}\hfill 4px+4abpy=4(a+b)p+(a^2{b}^2+1)(c+d)(p+1),\\ \hfill 4px+4acpy=4(a+c)p+(a^2{c}^2+1)(b+d)(p+1),\end{array}$$

And the second one is the equation of the bisector of the line segment $O_b{O}_d$. From these two equations, for the coordinates x and y of the point $O_a^{\prime }$, we obtain

$$x=\frac{1}{4p}(p+1)s-\frac{a}{4p}{(p-1)}^2,y=\frac{1}{4p}(p+1)r-\frac{1}{4ap}{(p-1)}^2.$$

Because of this, the point $O_a^{\prime }$ can be written in the form $O_a^{\prime }=\frac{1}{4p}{(p+1)}^{2}T-\frac{1}{4p}{(p-1)}^{2}A$, so $4p{O}_a^{\prime }+{(p-1)}^{2}A={(p+1)}^{2}T$, and furthermore, ${(p-1)}^2(T-A)=-4p(T-O_a^{\prime })$. Thus, homothety with center T and factor $\frac{1}{4p}{(p-1)}^2$ maps points $A,B,C,$ and D into points $O_a^{\prime },O_b^{\prime },O_c^{\prime },$ and $O_d^{\prime }$, respectively. The following result is proved.

Theorem 18. 

Let $ABCD$ be a complete quadrangle; T, its isoptic point; $O_a$, $O_b$, $O_c$, and $O_d$, the centers of the circles $BCD,ACD,ABD,$ and $ACD$, respectively; and $O_a^{\prime },O_b^{\prime },O_c^{\prime },$ and $O_d^{\prime }$, the centers of circles $O_b{O}_c{O}_d$, $O_a{O}_c{O}_d$, $O_a{O}_b{O}_d$, and $O_a{O}_b{O}_c$. The quadrangles $ABCD$ and $O_a^{\prime }{O}_b^{\prime }{O}_c^{\prime }{O}_d^{\prime }$ are similar.

This result was reached in [4] as well.

It is easy to check the equalities

$$\begin{array}{cc}& 2p(a+b+c+\frac{1}{abc})+(p-1)(d-a-b-c)=(p+1)(a+b+c+d)\\ & 2p(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+abc+(p-1)(abd+acd+bcd-abc)=(p+1)(abc+abd+acd+bcd),\end{array}$$

meaning that for the points $O_d$, $D^{\prime }$, and T, the equality $4p{O}_d+{(p-1)}^2{D}^{\prime }={(p+1)}^{2}T$ is fulfilled, and therefore, ${(p-1)}^2(T-D^{\prime })=-4p(T-O_d)$. Hence, homothety with center T and factor $-\frac{1}{4p}{(p-1)}^2$ maps the point $D^{\prime }$ into the point $O_d$, and by analogy, the points $A^{\prime },B^{\prime },$ and $C^{\prime }$ are mapped into $O_a,O_b,$ and $O_c$, respectively. Therefore, the same homothety maps the quadrangle $ABCD$ into the quadrangle $O_a^{\prime }{O}_b^{\prime }{O}_c^{\prime }{O}_d^{\prime }$, and the quadrangle $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ into the quadrangle $O_a{O}_b{O}_c{O}_d$. We obtained the isoptic point T of the quadrangle $ABCD$ as the common point of the connecting lines of the corresponding vertices of quadrangles $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ and $O_a{O}_b{O}_c{O}_d$. As the roles that $ABCD$ has for $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ and the quadrangle $O_a^{\prime }{O}_b^{\prime }{O}_c^{\prime }{O}_d^{\prime }$ for the quadrangle $O_a{O}_b{O}_c{O}_d$ are the same, and as the connecting lines of the corresponding vertices of quadrangles $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ and $O_a{O}_b{O}_c{O}_d$ are incident to the point T, we have proved the following original statement.

Theorem 19. 

Let $ABCD$ be a complete quadrangle and let $A^{\prime },B^{\prime },C^{\prime },$ and $D^{\prime }$ be points isogonal to the points $A,B,C,$ and D with respect to the triangles $BCD$, $ACD$, $ABD$, and $ABC$. The complete quadrangle $ABCD$ and the complete quadrangle $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ have the same isoptic point.

Quadrangles $ABCD$ and $O_a{O}_b{O}_c{O}_d$ have the same mutual relationship as well as relation to the point T as the quadrangles $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ and $ABCD$. So, as the point T is the inverse point to the points $A^{\prime },B^{\prime },C^{\prime },$ and $D^{\prime }$ with respect to the circles $BCD,ACD,ABD,$ and $ABC$, we have the following theorem.

Theorem 20. 

Let $ABCD$ be a complete quadrangle and T be its isoptic point. The point T is an inverse point to the points $A,B,C,$ and D with respect to the circles $O_b{O}_c{O}_d$, $O_a{O}_c{O}_d$, $O_a{O}_b{O}_d$, and $O_a{O}_c{O}_d$, where $O_a,O_b,O_c,$ and $O_d$ are the centers of the circumscribed circles $BCD$, $ACD$, $ABD$, and $ABC$, respectively.

This result was proved in [13,14]. Theorems 19 and 20 are visualized in Figure 4.

The equalities in (24) mean that the distances of the point T and each center of the circles $BCD$, $ACD$, $ABD$, and $ABC$ are proportional to the radii of these circles.

Theorem 21. 

Let $ABCD$ be a complete quadrangle and T be its isoptic point. The distances of the point T and the points $A,B,C,$ and D are proportional to the radii of circles $B^{\prime }{C}^{\prime }{D}^{\prime }$, $A^{\prime }{C}^{\prime }{D}^{\prime }$, $A^{\prime }{B}^{\prime }{D}^{\prime }$, and $A^{\prime }{B}^{\prime }{C}^{\prime }$, where $A^{\prime },B^{\prime },C^{\prime },$ and $D^{\prime }$ stand for points that are isogonal to the points $A,B,C,$ and D with respect to the triangles $BCD$, $ACD$, $ABD$, and $ABC$.

Again, the result can be found in [8,9].

For quadrangles $ABCD$, $O_a{O}_b{O}_c{O}_d$, and $O_a^{\prime }{O}_b^{\prime }{O}_c^{\prime }{O}_d^{\prime }$, we write them down in the form $A_0{B}_0{C}_0{D}_0$, $A_1{B}_1{C}_1{D}_1$, and $A_2{B}_2{C}_2{D}_2$, and then the quadrangle $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ can be written in the form $A_{-1}{B}_{-1}{C}_{-1}{D}_{-1}$. If we continue with this sequence in both directions, then for each $n\in \mathbb{Z}$, the points $A_{n+1},B_{n+1},C_{n+1},$ and $D_{n+1}$ are the centers of the circumscribed circles $B_n{C}_n{D}_n$, $A_n{C}_n{D}_n$, $A_n{B}_n{D}_n$, and $A_n{B}_n{C}_n$, and points $A_{n-1},B_{n-1},C_{n-1},$ and $D_{n-1}$ are isogonal to the points $A_n,B_n,C_n,$ and $D_n$ with respect to the triangles $B_n{C}_n{D}_n$, $A_n{C}_n{D}_n$, $A_n{B}_n{D}_n$, and $A_n{B}_n{C}_n$, respectively. Toward infinity for both sides of the sequence of the quadrangles, all the quadrangles have the same isoptic point T, where the same homothety with the center T maps the quadrangle $A_n{B}_n{C}_n{D}_n$ into $A_{n+2}{B}_{n+2}{C}_{n+2}{D}_{n+2}$ for each $n\in \mathbb{Z}$. Hence, all the quadrangles on the even places in the sequence are mutually homothetic, and the same fact is valid for the quadrangles on the odd places. However, two quadrangles in two adjacent places in the sequence do not have to be homothetic. This result can be found in several places [4,7,10]. The fact that the quadrangles $ABCD$ and $A_2{B}_2{C}_2{D}_2$ are similar was found in [15,16], and the fact that they are homothetic as well was found in [7,17], where the part of the point T being an inverse point to each vertex of the quadrangle $A_n{B}_n{C}_n{D}_n$ with respect to the circumscribed circles of the corresponding triangles of the quadrangle $A_{n+1}{B}_{n+1}{C}_{n+1}{D}_{n+1}$ was especially emphasized.

The normal of A to the line $AD$ with the slope $-\frac{1}{ad}$ has the equation $adx-y=a^{2}d-\frac{1}{a}$, and analogously, the normal of B to the line $BD$ has the equation $bdx-y=b^{2}d-\frac{1}{b}$. The intersection point of these lines is the point

$$C_D=\left(a+b+\frac{1}{abd},abd+\frac{a+b}{ab}\right),$$

which is a vertex of the antipedal triangle $A_D{B}_D{C}_D$ of D with respect to the triangle $ABC$. Analogously,

$$B_D=\left(a+c+\frac{1}{acd},acd+\frac{a+c}{ac}\right).$$

The bisector of the line segment $B_D{C}_D$ is parallel to the line $AD$ and has the equation

$$x+ady=a+d+\frac{p+1}{2p}(a^2{d}^2+1)(b+c).$$

(31)

It can be checked that the point

$$O_D^{\prime }=\left(\frac{p+1}{2p}s-\frac{1}{2p}(p^2+1)d,\frac{p+1}{2p}r-\frac{1}{2pd}(p^2+1)\right)$$

(32)

passes through the line (31), so because of symmetry on $a,b,$ and c, it follows that $O_D^{\prime }$ is the circumcenter of the triangle $A_D{B}_D{C}_D$. With the help of the forms of D and T in (20), the point $O_D^{\prime }$ can be written in the form $2p{O}_D^{\prime }={(p+1)}^{2}T-(p^2+1)D$, where for the oriented line segments, the ratio $T{O}_D^{\prime }:TD=-(p^2+1):2p$ is valid. Because of symmetry on $a,b,c,$ and d, we have the following theorem.

Theorem 22. 

Let $ABCD$ be a complete quadrangle. The quadrangles $O_A^{\prime }{O}_B^{\prime }{O}_C^{\prime }{O}_D^{\prime }$ and $ABCD$ are homothetic, where $O_A^{\prime },O_B^{\prime },O_C^{\prime },$ and $O_D^{\prime }$ are circumcenters of the antipedal triangles of the points $A,B,C,$ and D with respect to the triangles $BCD$, $ACD$, $ABD$, and $ABC$.

There was the same resut in [4] as well. In addition, we obtained the center of the homothety T, which is the isoptic point, and the factor of homothety is $-\frac{1}{2p}(p^2+1)$.

The symmetric functions in (14) of the values $u,v,w,u^{\prime },v^{\prime },w^{\prime },u^{″},v^{″},$ and $w^{″}$ can be expressed by values $s,q,r,$ and p, and the following identities are valid:

$$\begin{array}{ccc}\hfill u^{\prime }vw+u{v}^{\prime }w+uv{w}^{\prime }& =& 4pqs-8pr-r^{2}s\hfill \\ \hfill u^{″}{v}^{″}{w}^{″}& =& s^3-4qs+8r,\hfill \\ \hfill u^{″}vw+u{v}^{″}w+uv{w}^{″}& =& r{s}^2+8ps-4qr,\hfill \\ \hfill u^{\prime }{v}^{\prime }{w}^{\prime }& =& 4pqr-8p^{2}s-r^2,\hfill \\ \hfill uvw& =& p{s}^2-r^2=t,\hfill \end{array}$$

where $t=\frac{p-1}{p}$. Because of these, the point $H_{UVW}$ from (15) has the form

$$H_{UVW}=\left(\frac{1}{2t}(4pqs-8pr-r^{2}s+s^2-4qs+8r),\frac{1}{2t}(r{s}^2+8ps-4qr+4pqr-8p^{2}s-r^2)\right),$$

and the line (16) has an equation of the form

$$(r{s}^2+8ps-4qr-4pqr+8p^{2}s+r^2)x+(4pqs-8pr-r^{2}s-s^2+4qs-8r)y=4t.$$

(33)

As

$$\begin{array}{ccc}& & (p+1)(r{s}^2+8ps-4qr+4pqr-8p^{2}s-r^3)-2r(p{s}^2-r^2)=\hfill \\ & & =(p-1)(4pqr+4qr-r^3-8p^{2}s-8ps-r{s}^2),\hfill \\ & & (p+1)(4pqs-8pr-r^{2}s+s^3-4qs+8r)-2s(p{s}^2-r^2)=\hfill \\ & & =(p-1)(4pqs+4qs-8pr-8r-r^{2}s-s^3)\hfill \end{array}$$

is valid, then the line $T{H}_{UVW}$ has the slope

$$\frac{4pqr+4qr-r^3-8p^{2}s-8ps-r{s}^2}{4pqs+4qs-8pr-8r-r^{2}s-s^3}$$

which is equal to the slope of the line (33). Hence, we have the following.

Theorem 23. 

Let $ABCD$ be a complete quadrangle and $UVW$ be its diagonal quadrangle. The Wallace line of the center O with respect to the diagonal triangle $UVW$ is parallel to the line $T{H}_{UVW}$, where T is the isoptic point of $ABCD$, and $H_{UVW}$ is the orthocenter of $UVW$.

4. Discussion

Using rectangular coordinates for the complete quadrangle provides a new approach for the extensive geometry of complete quadrangles. It is possible to gather all of its properties and prove them in the same way. Here, we gathered the properties of the isoptic point of a quadrangle. Theorems 2, 15, and 19 are our original results, and we did not find these statements in the literature available to us. We have also studied the geometry of the complete quadrangle in the isotropic plane. Hence, we are planning to check and prove the results presented in this paper to see if they hold in the isotropic plane as well.