On Certain Properties of Parametric Kinds of Apostol-Type Frobenius–Euler–Fibonacci Polynomials
Abstract
1. Introduction
2. Two Parametric Kinds of Apostol-Type Frobenius–Euler–Fibonacci Polynomials
- (i)
- (ii)
3. Summation Formulae for Parametric Kinds of Apostol-Type Frobenius–Euler–Fibonacci Polynomials
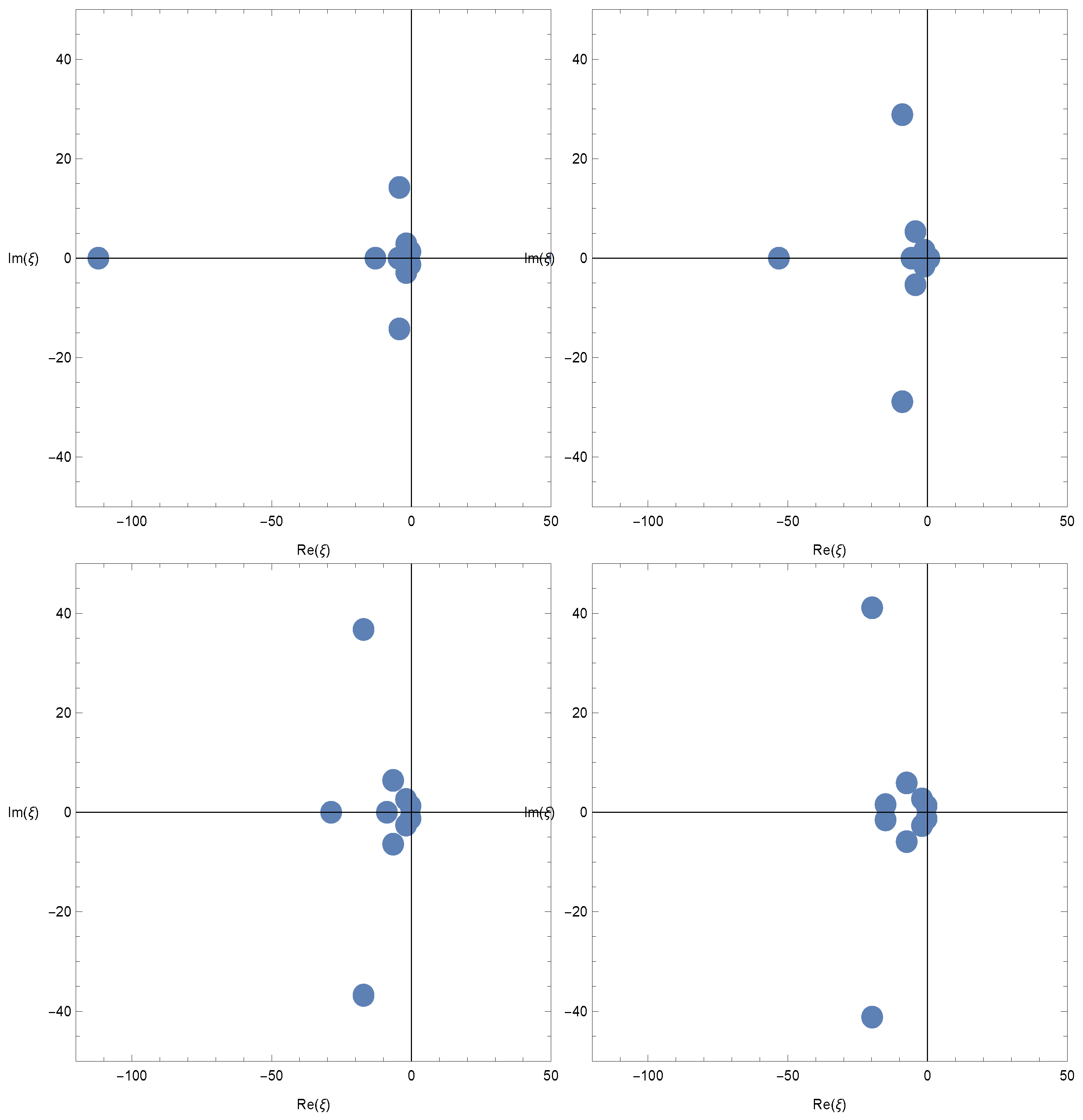
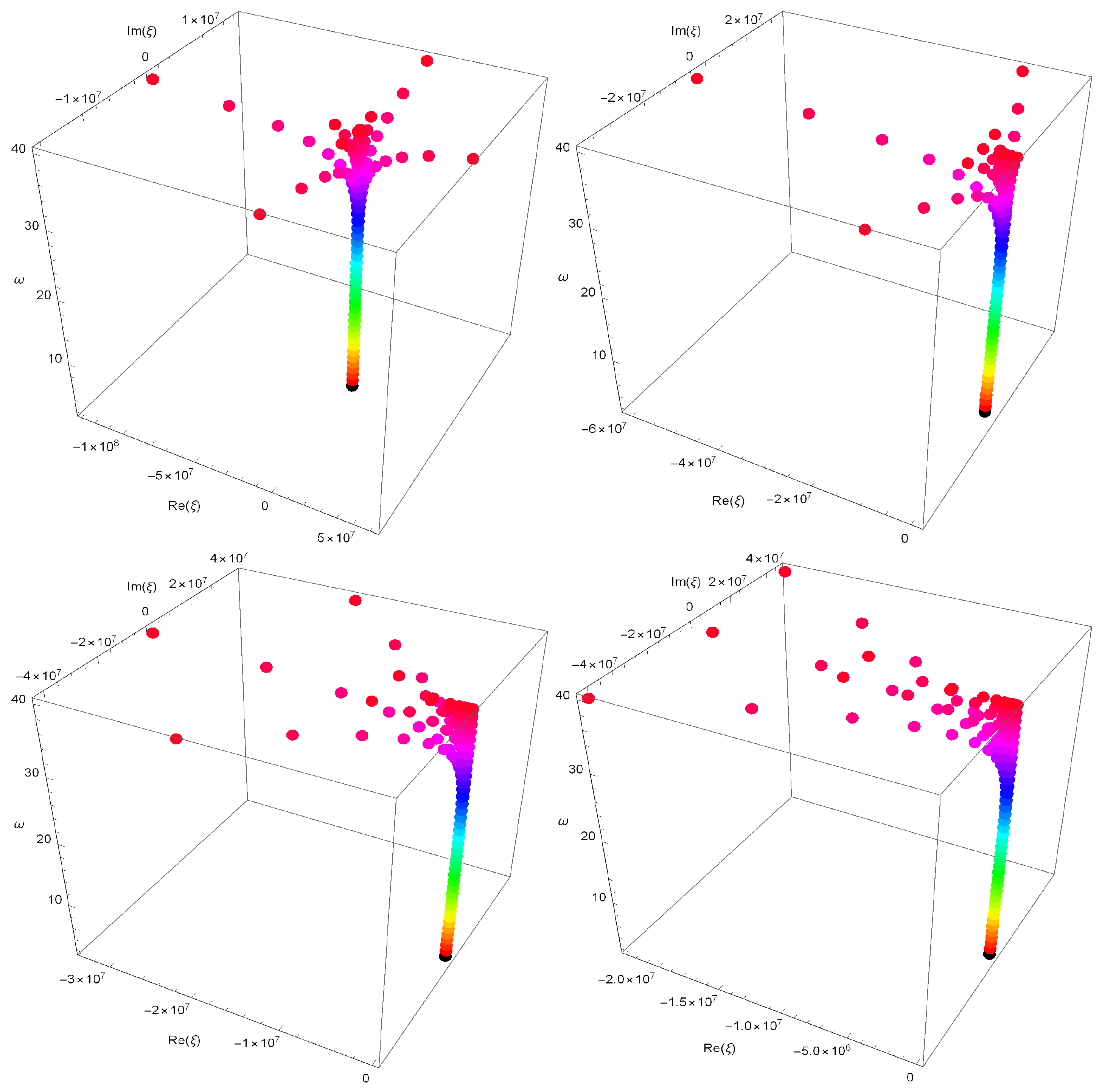
4. Approximate Roots for Cosine Apostol-Type Frobenius–Euler–Fibonacci Polynomials and Their Application
5. Approximate Roots for Sine Apostol-Type Frobenius–Euler–Fibonacci Polynomials and Their Application
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alam, N.; Khan, W.A.; Ryoo, C.S. A note on Bell-based Apostol-type Frobenius-Euler polynomials of complex variable with its certain applications. Mathematics 2022, 10, 2109. [Google Scholar] [CrossRef]
- Lyapin, A.P.; Akhtamova, S.S. Recurrence relations for the sections of the generating series of the solution to the multidimensional difference equation. Vestn. Udmurtsk. Univ. Mat. Mekh. 2021, 31, 414–423. [Google Scholar] [CrossRef]
- Carlitz, L. Eulerian numbers and polynomials. Mat. Mag. 1959, 32, 164–171. [Google Scholar] [CrossRef]
- Cakić, N.P.; Milovanović, G.V. On generalized Stirling number and polynomials. Math. Balk. N. Ser. 2004, 18, 241–248. [Google Scholar]
- Luo, Q.M.; Srivastava, H.M. Some generalization of the Apostol-Genocchi polynomials and Stirling numbers of the second kind. Appl. Math. Comput. 2011, 217, 5702–5728. [Google Scholar] [CrossRef]
- Kurt, B.; Simsek, Y. On the generalized Apostol-type Frobenius-Euler polynomials. Adv. Differ. Equ. 2013, 2013, 1. [Google Scholar] [CrossRef]
- Kim, D.S.; Kim, T. Some new identities of Frobenius-Euler numbers and polynomials. J. Inequal. Appl. 2012, 2012, 307. [Google Scholar] [CrossRef]
- Ryoo, C.S. A note on the Frobenius Euler polynomials. Proc. Jangjeon Math. Soc. 2011, 14, 495–501. [Google Scholar]
- Luo, Q.M.; Srivastava, H.M. Some generalizations of the Apostol-Bernoulli and Apostol-Euler polynomials. J. Math. Anal. Appl. 2005, 308, 290–302. [Google Scholar] [CrossRef]
- Jamei, M.J.; Milovanović, G.; Dagli, M.C. A generalization of the array type polynomials. Math. Morav. 2022, 26, 37–46. [Google Scholar] [CrossRef]
- Simsek, Y. Generating functions for generalized Stirling type numbers, Array type polynomials, Eulerian type polynomials and their applications. J. Fixed Point Theory Appl. 2013, 2013, 87. [Google Scholar] [CrossRef]
- Kus, S.; Tuglu, N.; Kim, T. Bernoulli F-polynomials and Fibo-Bernoulli matrices. Adv. Differ. Equ. 2019, 2019, 145. [Google Scholar] [CrossRef]
- Özvatan, M. Generalized Golden-Fibonacci Calculus and Applications. Ph.D. Thesis, Izmir Institute of Technology, Urla/Izmir, Turkey, 2018. [Google Scholar]
- Pashaev, O.K.; Nalci, S. Golden quantum oscillator and Binet–Fibonacci calculus. J. Phys. A Math. Theor. 2012, 45, 23. [Google Scholar] [CrossRef]
- Pashaev, O.K. Quantum calculus of Fibonacci divisors and infinite hierarchy of bosonic-fermionic golden quantum oscillators. Internat. J. Geom. Methods Modern Phys. 2021, 18, 32. [Google Scholar] [CrossRef]
- Krot, E. An introduction to finite fibonomial calculus. Centr. Eur. J. Math. 2004, 2, 754–766. [Google Scholar] [CrossRef]
- Pashaev, O.K.; Ozvatan, M. Bernoulli-Fibonacci Polynomials. arXiv 2020, arXiv:2010.15080. [Google Scholar]
- Gulal, E.; Tuglu, N. Apostol-Bernoulli-Fibonacci polynomials, Apostol-Euler-Fibonacci polynomials and their generating functions. Turk. J. Math. Comput. Sci. 2023, 15, 202–210. [Google Scholar] [CrossRef]
- Kızılateş, C.; Öztürk, H. On parametric types of Apostol Bernoulli-Fibonacci Apostol Euler-Fibonacci and Apostol Genocchi-Fibonacci polynomials via Golden calculus. AIMS Math. 2023, 8, 8386–8402. [Google Scholar] [CrossRef]
- Tuğlu, N.; Ercan, E. Some properties of Apostol Bernoulli Fibonacci and Apostol Euler Fibonacci Polynomials. In Proceedings of the ICMEE-2021, Ankara, Turkey, 16–18 September 2021; pp. 32–34. [Google Scholar]
- Alatawi, M.A.; Khan, W.A.; Kızılateş, C.; Ryoo, C.S. Some Properties of Generalized Apostol-type Frobenius-Euler-Fibonacci polynomials. Mathematics 2024, 12, 800. [Google Scholar] [CrossRef]
- Kılar, N.; Simsek, Y. Two Parametric Kinds of Eulerian-Type Polynomials Associated with Euler’s Formula. Symmetry 2019, 11, 1097. [Google Scholar] [CrossRef]
- Urieles, A.; Ramirez, W.; Ha, L.C.P.; Ortegac, M.J.; Arenas-Penaloza, J. On F-Frobenius-Euler polynomials and their matrix approach. J. Math. Comput. Sci. 2024, 32, 377–386. [Google Scholar] [CrossRef]

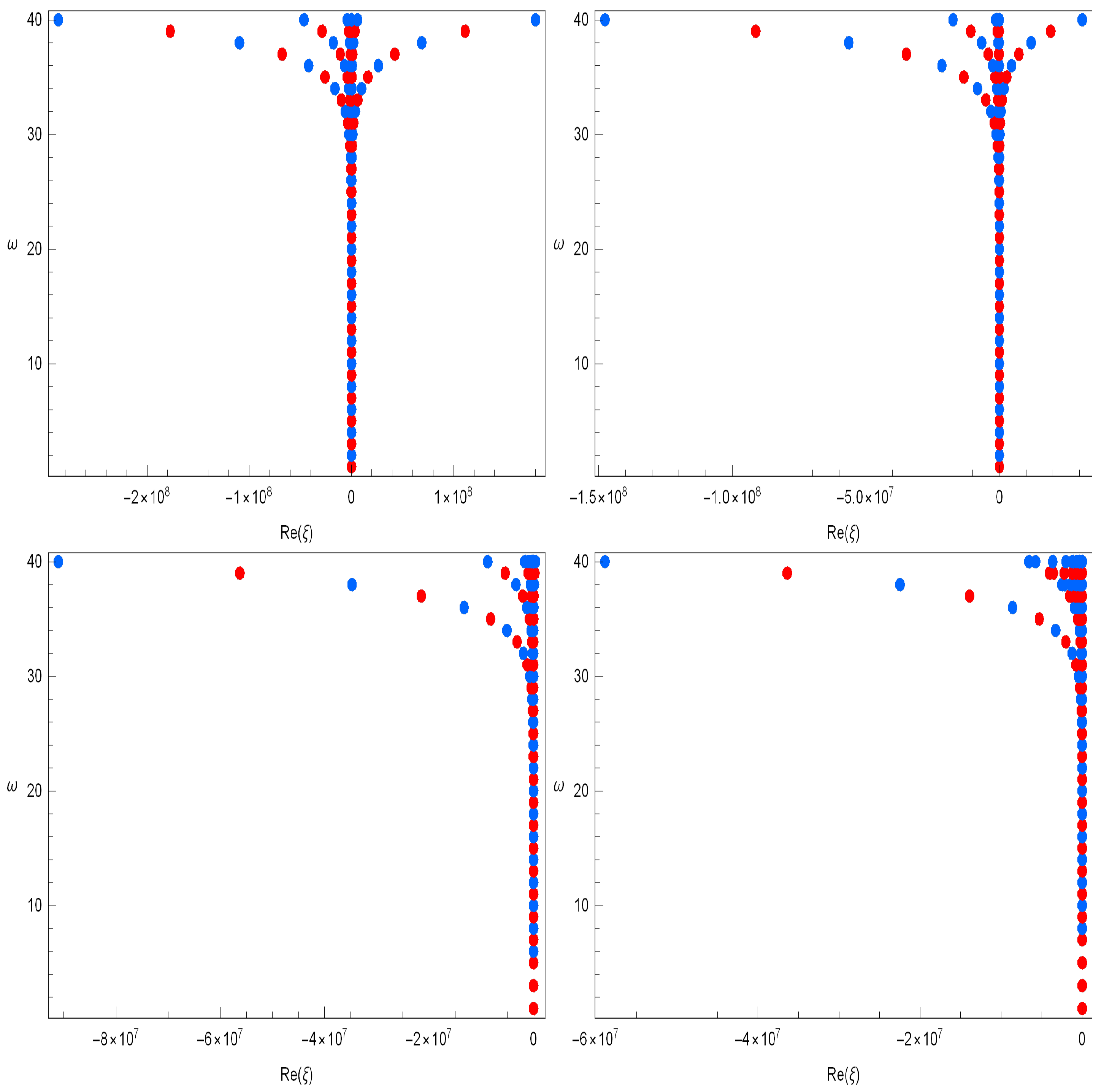
| Degree w | |
|---|---|
| 1 | −1.6216 |
| 2 | −0.81081–1.11721i, −0.81081 + 1.11721i |
| 3 | −2.5527, −0.3453–1.3890i, −0.3453 + 1.3890i |
| 4 | −2.1149 + 1.2065i, −2.1149–1.2065i, |
| −0.3176–1.6486i, −0.3176 + 1.6486i | |
| 5 | −4.9923, −1.0243 + 2.8171i, −1.0243–2.8171i, |
| −0.53363–1.25377i, −0.53363 + 1.25377i | |
| 6 | −6.6054, −2.8798, −1.4002 + 4.3170i, |
| −1.4002–4.3170i, −0.34373 + 1.21593i, −0.34373–1.21593i | |
| 7 | −11.829, −2.4479–7.1055i, −2.4479 + 7.1055i, −1.8300 + 1.8696i, |
| −1.8300–1.8696i, −0.34829 + 1.18791i, −0.34829–1.18791i | |
| 8 | −18.525, −4.0494, −3.8525–11.4136i, |
| −3.8525 + 11.4136i, −1.5458–2.4681i, −1.5458 + 2.4681i, | |
| −0.34158 + 1.07275i, −0.34158–1.07275i | |
| 9 | −30.369, −6.302 + 18.517i, −6.302–18.517i, |
| −3.8166 + 3.2636i, −3.8166–3.2636i, −1.9475–2.3368i, | |
| 1.9475 + 2.3368i, −0.31715 + 0.97703i, −0.31715–0.97703i |
| Degree w | |
|---|---|
| 2 | −1.6216 |
| 3 | −0.8108–1.4270i, −0.8108 + 1.4270i |
| 4 | −2.3585, −0.4424 + 1.7622i, −0.4424–1.7622i |
| 5 | −1.8208–2.1580i, −1.8208 + 2.1580i, |
| −0.6117 + 1.8334i, −0.6117–1.8334i | |
| 6 | −3.7216, −1.6884–3.8944i, −1.6884 + 3.8944i, |
| −0.5048–1.5492i, −0.5048 + 1.5492i | |
| 7 | −3.1006 + 2.3894i, −3.1006–2.3894i, −2.9654–5.8498i, |
| −2.9654 + 5.8498i, −0.4205–1.5019i, −0.4205 + 1.5019i | |
| 8 | −6.5500, −4.6320–9.7962i, −4.6320 + 9.7962i, −2.2337 + 2.8199i, |
| −2.2337–2.8199i, −0.3998–1.4437i, −0.3998 + 1.4437i | |
| 9 | −7.590–15.664i, −7.590 + 15.664i, −6.9050–3.0783i, |
| −6.9050 + 3.0783i, −2.1598–2.9826i, −2.1598 + 2.9826i, | |
| −0.3719–1.3842i, −0.3719 + 1.3842i | |
| 10 | −13.328, −12.221–25.464i, −12.221 + 25.464i, |
| −6.2140 + 5.1861i, −6.2140–5.1861i, −2.1195–2.7752i, | |
| −2.1195 + 2.7752i, −0.34922 + 1.33983i, −0.34922–1.33983i |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, H.; Khan, W.A.; Kızılateş, C.; Ryoo, C.S. On Certain Properties of Parametric Kinds of Apostol-Type Frobenius–Euler–Fibonacci Polynomials. Axioms 2024, 13, 348. https://doi.org/10.3390/axioms13060348
Guan H, Khan WA, Kızılateş C, Ryoo CS. On Certain Properties of Parametric Kinds of Apostol-Type Frobenius–Euler–Fibonacci Polynomials. Axioms. 2024; 13(6):348. https://doi.org/10.3390/axioms13060348
Chicago/Turabian StyleGuan, Hao, Waseem Ahmad Khan, Can Kızılateş, and Cheon Seoung Ryoo. 2024. "On Certain Properties of Parametric Kinds of Apostol-Type Frobenius–Euler–Fibonacci Polynomials" Axioms 13, no. 6: 348. https://doi.org/10.3390/axioms13060348
APA StyleGuan, H., Khan, W. A., Kızılateş, C., & Ryoo, C. S. (2024). On Certain Properties of Parametric Kinds of Apostol-Type Frobenius–Euler–Fibonacci Polynomials. Axioms, 13(6), 348. https://doi.org/10.3390/axioms13060348







