Nonuniform Sampling in L^p-Subspaces Associated with the Multi-Dimensional Special Affine Fourier Transform

Abstract

In this paper, the sampling and reconstruction problems in function subspaces of $L^p\left({\mathbb{R}}^n\right)$ associated with the multi-dimensional special affine Fourier transform (SAFT) are discussed. First, we give the definition of the multi-dimensional SAFT and study its properties including the Parseval’s relation, the canonical convolution theorems and the chirp-modulation periodicity. Then, a kind of function spaces are defined by the canonical convolution in the multi-dimensional SAFT domain, the existence and the properties of the dual basis functions are demonstrated, and the $L^p$-stability of the basis functions is established. Finally, based on the nonuniform samples taken on a dense set, we propose an iterative reconstruction algorithm with exponential convergence to recover the signals in a $L^p$-subspace associated with the multi-dimensional SAFT, and the validity of the algorithm is demonstrated via simulations.

1. Introduction

The well-known Shannon sampling theorem had a great impact on many engineering fields, such as communication and information processing, which provides a basic bridge between discrete and continuous signals [1]. However, it is not suitable for numerical realization due to the slow decay of the sinc function generating the bandlimited signal space. Moreover, many signals in the practical applications are not bandlimited. With the development of wavelet analysis, many sampling results have been generalized to more general shift-invariant spaces [2,3,4,5,6,7,8,9,10,11]. However, most results are studied in the framework of classical Fourier transform (FT).

In recent years, many sampling theories have been attempted to be established in the setting of more general integral transforms including the fractional Fourier transform (FrFT), the linear canonical transform (LCT) and the special affine Fourier transform (SAFT) [12,13,14,15,16,17,18,19,20,21]. The SAFT was first proposed in [22] for modeling optical systems and had been generally applied to signal processing, communications and quantum mechanics, which is a six-parameter integral transform and can contain many classical transforms as special cases, such as the FT, the FrFT, the Laplace transform and the LCT [23,24,25]. These results indicate that the studies related to one-dimensional signals in the SAFT domain have been relatively complete, but the results of multi-dimensional signals are rarely seen.

The SAFT is also called the offset linear canonical transform (OLCT) because it can be seen as a time-shifted and frequency-modulated version of the four-parameter LCT by introducing two extra flexible parameters. The LCT, as a tool for signal processing, had been intended to analyze multi-dimensional signals in the sense that a product of n-copies of the usual one-dimensional LCT was used [26,27]. Supported by the sampling theory, it has been widely applied to images and audio [28,29]. With the development of the sampling theory, the sampling of multi-dimensional signals will also have more potential applications, such as image scaling, and image super-resolution [27,30,31,32]. In addition, the conversion between different sample rates also plays an important role in communication, image processing, etc. All kinds of classical transform domains such as FT, FrFT, LCT and other one-dimensional sampling rate conversions or multi-dimensional extractions or interpolations with integer matrices are also proposed [33,34,35,36]. The SAFT, as the offset version of the LCT, is more flexible, so it is necessary to discuss the problems related to multi-dimensional signals in the SAFT transform domain.

As an extension of bandlimited signals in the SAFT domain, different function spaces associated with various types of convolutions are defined to model non-bandlimited signals, and the corresponding sampling theories are studied, such as the canonical convolution [14,16,17] and the SAFT-convolution [12,19]. However, all the involved function spaces are $L^2$-subspaces, and the discussion in the $L^p$-setting is still not explored. Motivated by the above observations, we will devote ourselves to the following problems:

• State the definition of the multi-dimensional special affine Fourier transform with multi-dimensional kernel and establish some basic conclusions including the inverse transform formula, the Parseval’s relation, the canonical convolution theorems and the chirp-modulation periodicity.
• Based on the proposed multi-dimensional SAFT and the canonical convolution in the multi-dimensional SAFT domain, introduce a class of $L^p$-subspaces and discuss the corresponding properties including the existence of the dual basis functions and the $L^p$-stability of the basis functions.
• The theory of nonuniform sampling in shift-invariant spaces of the $L^p$-setting associated with the classical FT has acquired great achievements [2,3]. Taking the existing results as a reference, consider the nonuniform sampling and reconstruction of signals in the $L^p$-subspaces associated with the multi-dimensional SAFT.

The paper is organized as follows. In Section 2, we give the definition of the multi-dimensional SAFT and its properties. In Section 3, a class of subspaces $V^p\left(\varphi \right)$ of $L^p\left({\mathbb{R}}^n\right)$ associated with the canonical convolution in the SAFT domain are discussed. In Section 4, an iterative reconstruction algorithm based on nonuniform samples is proposed to recover the signals living in the space $V^p\left(\varphi \right)$.

2. The Multi-Dimensional Special Affine Fourier Transform

In this section, we will give the definition of the multi-dimensional special affine Fourier transform and introduce its properties. Let

$$M=\left[\begin{array}{ccc}A& B& \mathbf{p}\\ C& D& \mathbf{q}\end{array}\right].$$

(1)

Here, $A,B,C,D$ are $n\ast n$ real matrices, $\mathbf{p},\mathbf{q}$ are $n\ast 1$ column vectors, and $M_1=\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]$ is a symplectic matrix, that is, $M_1^{T}J{M}_1=J$, where $J=\left[\begin{array}{cc}0& I_n\\ -I_n& 0\end{array}\right]$ and $I_n$ is a n-dimensional identity matrix. In the following, we only care about the case of $detB\ne 0$.

Definition 1.

For $f\in L^2\left({\mathbb{R}}^n\right)$, the multi-dimensional SAFT with respect to the matrix M is defined as

$$\begin{array}{cc}\hfill F_M\left(\mathbf{w}\right)& ={\int }_{{\mathbb{R}}^n}f\left(\mathbf{t}\right)K_M(\mathbf{w},\mathbf{t})d\mathbf{t}\hfill \\ \hfill & =\rho (n,B){\int }_{{\mathbb{R}}^n}f\left(\mathbf{t}\right)exp\left\{\frac{j}{2}({\mathbf{w}}^{T}D{B}^{-1}\mathbf{w}+\Omega B^{-T}\mathbf{w}+{\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t}-2{\mathbf{w}}^T{B}^{-T}\mathbf{t})\right\}d\mathbf{t},\hfill \end{array}$$

(2)

where $\rho (n,B)=\frac{1}{{\left(2\pi \right)}^{\frac{n}{2}}{|detB|}^{\frac{1}{2}}}$, $\Omega =2{(B\mathbf{q}-D\mathbf{p})}^T$, $\mathbf{t}={(t_1,t_2,\cdots ,t_n)}^T$ and $\mathbf{w}=$${(w_1,w_2,\cdots ,w_n)}^T.$

Similarly, for a sequence ${\left\{f\left(\mathbf{k}\right)\right\}}_{\mathbf{k}\in {\mathbb{Z}}^n}\in {\ell }^2\left({\mathbb{Z}}^n\right)$, the multi-dimensional SAFT transform is defined by

$$\begin{array}{cc}\hfill {\tilde{F}}_M\left(\mathbf{w}\right)& =\sum _{\mathbf{k}\in {\mathbb{Z}}^n}f\left(\mathbf{k}\right)K_M(\mathbf{w},\mathbf{k}).\hfill \end{array}$$

(3)

Lemma 1.

Let

$$\begin{array}{c}\hfill M^{-1}=\left[\begin{array}{ccc}{D}^T& -B^T& B\mathbf{q}-D\mathbf{p}\\ -C^T& A^T& B^{-T}{C}^{T}B\mathbf{p}-B^{-T}{A}^{T}B\mathbf{q}\end{array}\right].\end{array}$$

(4)

Then the multi-dimensional SAFT kernel satisfies the following properties:

(i)

$K_{M^{-1}}(\mathbf{t},\mathbf{w})=\overline{K_M(\mathbf{w},\mathbf{t})}.$

(ii)

${\int }_{{\mathbb{R}}^n}{K}_M(\mathbf{w},\mathbf{t})K_{M^{-1}}(\mathbf{z},\mathbf{w})d\mathbf{w}=\delta (\mathbf{t}-\mathbf{z}).$

Proof. 

(i) Since $M_1$ satisfies $M_1^{T}J{M}_1=J$, we have $A^{T}D-C^{T}B=I_n.$ Then

$$\begin{array}{cc}\hfill K_{M^{-1}}(\mathbf{t},\mathbf{w})& =\rho (n,B)exp\left\{\frac{j}{2}\right({\mathbf{t}}^T{A}^T\left(-B^{-T}\right)\mathbf{t}+2{\mathbf{t}}^T\left(-B^{-T}\right)\left(\left(-B^T\right)\left(B^{-T}{C}^{T}B\mathbf{p}-B^{-T}{A}^{T}B\mathbf{q}\right)\right.\hfill \\ \hfill & \left.-A^T(B\mathbf{q}-D\mathbf{p})\right)+{\mathbf{w}}^T\left(-B^{-T}\right)D^T\mathbf{w}+2{\mathbf{w}}^T\left(-B^{-1}\right)(B\mathbf{q}-D\mathbf{p})-2{\mathbf{t}}^T\left(-B^{-1}\right)\mathbf{w}\left)\right\}\hfill \\ \hfill & =\rho (n,B)exp\{-\frac{j}{2}({\mathbf{t}}^T{A}^T{B}^{-T}\mathbf{t}+2{\mathbf{t}}^T{B}^{-T}\mathbf{p}+{\mathbf{w}}^T{B}^{-T}{D}^T\mathbf{w}+2{\mathbf{w}}^T{B}^{-1}(B\mathbf{q}-D\mathbf{p})\hfill \\ \hfill & -2{\mathbf{t}}^T{B}^{-1}\mathbf{w}\left)\right\}\hfill \\ \hfill & =\rho (n,B)exp\{-\frac{j}{2}({\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t}+{\mathbf{w}}^{T}D{B}^{-1}\mathbf{w}+2{(B\mathbf{q}-D\mathbf{p})}^T{B}^{-T}\mathbf{w}\hfill \\ \hfill & -2{\mathbf{w}}^T{B}^{-T}\mathbf{t}\left)\right\}\hfill \\ \hfill & =\overline{K_M(\mathbf{w},\mathbf{t})}.\hfill \end{array}$$

(ii) It follows from (i) that

$$\begin{array}{cc}\hfill & {\int }_{{\mathbb{R}}^n}{K}_M(\mathbf{w},\mathbf{t})K_{M^{-1}}(\mathbf{z},\mathbf{w})d\mathbf{w}\hfill \\ \hfill =& {\int }_{{\mathbb{R}}^n}{K}_M(\mathbf{w},\mathbf{t})\overline{K_M(\mathbf{w},\mathbf{z})}d\mathbf{w}\hfill \\ \hfill =& {\rho }^2(n,B){\int }_{{\mathbb{R}}^n}exp\left\{\frac{j}{2}({\mathbf{w}}^{T}D{B}^{-1}\mathbf{w}+\Omega B^{-T}\mathbf{w}+{\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t}-2{\mathbf{w}}^T{B}^{-T}\mathbf{t})\right\}\hfill \\ \hfill & ·exp\left\{-\frac{j}{2}({\mathbf{w}}^{T}D{B}^{-1}\mathbf{w}+\Omega B^{-T}\mathbf{w}+{\mathbf{z}}^T{B}^{-1}A\mathbf{z}+2{\mathbf{p}}^T{B}^{-1}\mathbf{z}-2{\mathbf{w}}^T{B}^{-T}\mathbf{z})\right\}d\mathbf{w}\hfill \\ \hfill =& {\rho }^2(n,B)exp\left\{\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t}-{\mathbf{z}}^T{B}^{-1}A\mathbf{z}-2{\mathbf{p}}^T{B}^{-1}\mathbf{z}\right)\right\}\hfill \\ \hfill & ·{\int }_{{\mathbb{R}}^n}exp\{-j{\mathbf{w}}^T{B}^{-T}\left(\mathbf{t}-\mathbf{z}\right)\}d\mathbf{w}.\hfill \end{array}$$

(5)

Let ${\mathbf{w}}_{\mathbf{1}}=B^{-1}\mathbf{w}$. We can rewrite (5) as

$$\begin{array}{cc}\hfill & {\int }_{{\mathbb{R}}^n}{K}_M(\mathbf{w},\mathbf{t})K_{M^{-1}}(\mathbf{z},\mathbf{w})d\mathbf{w}\hfill \\ \hfill =& \frac{1}{{\left(2\pi \right)}^n|detB|}exp\left\{\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t}-{\mathbf{z}}^T{B}^{-1}A\mathbf{z}-2{\mathbf{p}}^T{B}^{-1}\mathbf{z}\right)\right\}\hfill \\ \hfill & ·{\int }_{{\mathbb{R}}^n}exp\{-j{{\mathbf{w}}_{\mathbf{1}}}^T\left(\mathbf{t}-\mathbf{z}\right)\}|detB|d{\mathbf{w}}_{\mathbf{1}}\hfill \\ \hfill =& \delta (\mathbf{t}-\mathbf{z}).\hfill \end{array}$$

□

Lemma 2.

For $f,g\in L^2\left({\mathbb{R}}^n\right)$, one has

$$\begin{array}{c}\hfill {⟨F_M,G_M⟩}_{L^2\left({\mathbb{R}}^n\right)}={⟨f,g⟩}_{L^2\left({\mathbb{R}}^n\right)}.\end{array}$$

(6)

Proof. 

Note that

$$\begin{array}{cc}\hfill F_M\left(\mathbf{w}\right)& =\frac{1}{{\left|detB\right|}^{\frac{1}{2}}}\mathcal{F}\left[f\left(\mathbf{t}\right)exp\left\{\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t}\right)\right\}\right]\left(B^{-1}\mathbf{w}\right)\hfill \\ \hfill & ·exp\left\{\frac{j}{2}\left({\mathbf{w}}^{T}D{B}^{-1}\mathbf{w}+\Omega B^{-T}\mathbf{w}\right)\right\}.\hfill \end{array}$$

(7)

Then, it follows from the Parseval’s formula in the FT domain that

$$\begin{array}{cc}\hfill & ⟨F_M\left(\mathbf{w}\right),G_M\left(\mathbf{w}\right)⟩\hfill \\ \hfill & =⟨\mathcal{F}\left[f\left(\mathbf{t}\right)exp\left\{\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t}\right)\right\}\right]\left({\mathbf{w}}_{\mathbf{1}}\right),\hfill \\ \hfill & \mathcal{F}\left[g\left(\mathbf{t}\right)exp\left\{\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t}\right)\right\}\right]\left({\mathbf{w}}_{\mathbf{1}}\right)⟩\hfill \\ \hfill & =⟨f\left(\mathbf{t}\right)exp\left\{\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t}\right)\right\},g\left(\mathbf{t}\right)exp\left\{\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t}\right)\right\}⟩\hfill \\ \hfill & =⟨f\left(\mathbf{t}\right),g\left(\mathbf{t}\right)⟩.\hfill \end{array}$$

When $f=g$, then the relation is the Plancherel’s formula in the multi-dimensional SAFT domain.

By the item (ii) of Lemma 1, one can obtain the inverse SAFT as

$$\begin{array}{cc}\hfill {\int }_{{\mathbb{R}}^n}{F}_M\left(\mathbf{w}\right)K_{M^{-1}}(\mathbf{t},\mathbf{w})d\mathbf{w}& ={\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}f\left(\mathbf{x}\right)K_M(\mathbf{w},\mathbf{x})d\mathbf{x}{K}_{M^{-1}}(\mathbf{t},\mathbf{w})d\mathbf{w}\hfill \\ \hfill & ={\int }_{{\mathbb{R}}^n}f\left(x\right){\int }_{{\mathbb{R}}^n}{K}_M(\mathbf{w},\mathbf{x})K_{M^{-1}}(\mathbf{t},\mathbf{w})d\mathbf{w}d\mathbf{x}\hfill \\ \hfill & ={\int }_{{\mathbb{R}}^n}f\left(\mathbf{x}\right)\delta \left(\mathbf{t}-\mathbf{x}\right)d\mathbf{x}\hfill \\ \hfill & =f\left(\mathbf{t}\right).\hfill \end{array}$$

(8)

□

Definition 2

([37]). Let N be a real and non-singular matrix of order n. Define the lattice generated by N as

$$\begin{array}{c}\hfill \mathbb{L}\left(N\right)=\left\{N\mathbf{k};\mathbf{k}\in {\mathbb{Z}}^n\right\}.\end{array}$$

(9)

For the lattice $\mathbb{L}\left(N\right)$, the unit-cell $\mathbb{U}\left(N\right)\subset {\mathbb{R}}^n$ is defined as

$$\begin{array}{c}\hfill \bigcup _{\mathbf{x}\in \mathbb{L}\left(N\right)}\left\{\mathbb{U}\left(N\right)+\mathbf{x}\right\}={\mathbb{R}}^n\end{array}$$

(10)

and

$$\begin{array}{c}\hfill \left\{\mathbb{U}\left(N\right)+\mathbf{x}\right\}\bigcap \left\{\mathbb{U}\left(N\right)+\mathbf{y}\right\}=\varnothing for\mathbf{x}\ne \mathbf{y}\in \mathbb{L}\left(N\right).\end{array}$$

(11)

The most convenient unit-cell is the parallelepiped given by

$$\begin{array}{c}\hfill \mathbb{U}\left(N\right)=\left\{N\mathbf{x};\mathbf{x}={\left(x_1,x_2,\cdots ,x_n\right)}^T,0\le x_i\le 1,i=1,\cdots ,n\right\}.\end{array}$$

(12)

Example 1.

If $n=2$ and $N=\left[\begin{array}{cc}1& 0\\ 0& 2\end{array}\right]$, then

$$\mathbb{L}\left(N\right)=\left\{N\mathbf{k}={(k_1,2k_2)}^T;\mathbf{k}={(k_1,k_2)}^T\in {\mathbb{Z}}^2\right\}$$

and $\mathbb{U}\left(N\right)=(0,1]\times (0,2]$.

Lemma 3.

For $p,q\in {\ell }^2\left({\mathbb{Z}}^n\right)$, one has

$$\begin{array}{c}\hfill {⟨{\tilde{P}}_M,{\tilde{Q}}_M⟩}_{L^2\left(\mathbb{U}\left(2\pi B\right)\right)}={⟨p,q⟩}_{{\ell }^2\left({\mathbb{Z}}^n\right)}.\end{array}$$

(13)

Proof. 

Let $\tilde{p}$ be a sequence such that

$$\begin{array}{c}\hfill \tilde{p}(\mathbf{k})=p\left(\mathbf{k}\right)exp\left\{\frac{j}{2}({\mathbf{k}}^T{B}^{-1}A\mathbf{k}+2p^T{B}^{-1}\mathbf{k})\right\},\mathbf{k}\in {\mathbb{Z}}^n.\end{array}$$

(14)

Note that

$$\begin{array}{cc}\hfill {\tilde{P}}_M\left(\mathbf{w}\right)& =\frac{1}{{\left|detB\right|}^{\frac{1}{2}}}\tilde{\mathcal{F}}\left[\tilde{p}\right]\left(B^{-1}\mathbf{w}\right)exp\left\{\frac{j}{2}\left({\mathbf{w}}^{T}D{B}^{-1}\mathbf{w}+\Omega B^{-T}\mathbf{w}\right)\right\},\hfill \end{array}$$

where $\tilde{\mathcal{F}}$ is the discrete FT. Then, one has

$$\begin{array}{cc}\hfill {⟨p,q⟩}_{{\ell }^2\left({\mathbb{Z}}^n\right)}& ={⟨\tilde{p},\tilde{q}⟩}_{{\ell }^2\left({\mathbb{Z}}^n\right)}\hfill \\ \hfill & ={⟨\tilde{\mathcal{F}}\left[\tilde{p}\right],\tilde{\mathcal{F}}\left[\tilde{q}\right]⟩}_{L^2\left({\left[0,2\pi \right]}^n\right)}\hfill \\ \hfill & ={⟨{\left|detB\right|}^{\frac{1}{2}}{\tilde{P}}_M\left(B\mathbf{w}\right),{\left|detB\right|}^{\frac{1}{2}}{\tilde{Q}}_M\left(B\mathbf{w}\right)⟩}_{L^2\left({\left[0,2\pi \right]}^n\right)}\hfill \\ \hfill & =\left|detB\right|{\int }_{{\left[0,2\pi \right]}^n}{\tilde{P}}_M\left(B\mathbf{w}\right)\overline{{\tilde{Q}}_M\left(B\mathbf{w}\right)}d\mathbf{w}.\hfill \end{array}$$

(15)

Note that

$$\begin{array}{cc}\hfill & \left\{B\mathbf{x}:\mathbf{x}=\left(x_1,x_2,\cdots ,x_n\right),0\le x_i\le 2\pi \right\}\hfill \\ \hfill & =\left\{2\pi B\mathbf{x}:\mathbf{x}=\left(x_1,x_2,\cdots ,x_n\right),0\le x_i\le 1\right\}\hfill \\ \hfill & =U\left(2\pi B\right).\hfill \end{array}$$

(16)

This together with (15) gives

$$\begin{array}{c}\hfill {⟨p,q⟩}_{{\ell }^2\left({\mathbb{Z}}^n\right)}={\int }_{U\left(2\pi B\right)}{\tilde{P}}_M\left(\mathbf{w}\right)\overline{{\tilde{Q}}_M\left(\mathbf{w}\right)}d\mathbf{w}={⟨{\tilde{P}}_M,{\tilde{Q}}_M⟩}_{L^2\left(\mathbb{U}\left(2\pi B\right)\right)}.\end{array}$$

□

The proposed multi-dimensional SAFT reduces to some special transforms when the sub-matrices of the matrix M take the particular forms. When $M=\left[\begin{array}{ccc}A& B& \mathbf{0}\\ C& D& \mathbf{0}\end{array}\right]$, the transform falls back to the multi-dimensional LCT

$$\begin{array}{c}\hfill {\mathcal{L}}_M\left[f\right]\left(\mathbf{w}\right)=\rho (n,B){\int }_{{\mathbb{R}}^n}f\left(\mathbf{t}\right)exp\left\{\frac{j}{2}({\mathbf{w}}^{T}D{B}^{-1}\mathbf{w}+{\mathbf{t}}^T{B}^{-1}A\mathbf{t}-2{\mathbf{w}}^T{B}^{-T}\mathbf{t})\right\}d\mathbf{t}\end{array}$$

(17)

defined in [37]. In particular,

if $A=D=\mathbf{0}$ and $B=-C=I_n$, it returns to the classical n-dimensional Fourier transform

$$\begin{array}{c}\hfill \mathcal{F}\left(\mathbf{w}\right)=\frac{1}{{\left(2\pi \right)}^{\frac{n}{2}}}{\int }_{{\mathbb{R}}^n}f\left(\mathbf{t}\right)exp\left\{-j{\mathbf{w}}^T\mathbf{t}\right\}d\mathbf{t}.\end{array}$$

(18)

Definition 3.

For $f,g\in L^2\left({\mathbb{R}}^n\right)$, the canonical convolution in the multi-dimensional SAFT domain is defined by

$$\begin{array}{c}\hfill (f\Theta g)\left(\mathbf{t}\right)={\int }_{{\mathbb{R}}^n}f\left(\mathbf{x}\right)g\left(\mathbf{t}-\mathbf{x}\right)exp\left\{-\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}-{\mathbf{x}}^T{B}^{-1}A\mathbf{x}+2{\mathbf{p}}^T{B}^{-1}(\mathbf{t}-\mathbf{x})\right)\right\}d\mathbf{x}.\end{array}$$

(19)

Lemma 4.

Let $h\left(\mathbf{t}\right)=(f\Theta g)\left(\mathbf{t}\right).$ Then, the multi-dimensional SAFT of h satisfies

$$\begin{array}{c}\hfill H_M\left(\mathbf{w}\right)={\left(2\pi \right)}^{\frac{n}{2}}{F}_M\left(\mathbf{w}\right)G\left(B^{-1}\mathbf{w}\right),\end{array}$$

(20)

where G is the multi-dimensional Fourier transform of g.

Proof. 

It follows from the definition of the multi-dimensional SAFT that

$$\begin{array}{cc}\hfill H_M\left(\mathbf{w}\right)& ={\int }_{{\mathbb{R}}^n}h\left(\mathbf{t}\right)K_M(\mathbf{w},\mathbf{t})d\mathbf{t}\hfill \\ \hfill & =\rho (n,B){\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}f\left(\mathbf{x}\right)g\left(\mathbf{t}-\mathbf{x}\right)exp\left\{-\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}-{\mathbf{x}}^T{B}^{-1}A\mathbf{x}+2{\mathbf{p}}^T{B}^{-1}\left(\mathbf{t}-\mathbf{x}\right)\right)\right\}\hfill \\ \hfill & ·exp\left\{\frac{j}{2}({\mathbf{w}}^{T}D{B}^{-1}\mathbf{w}+\Omega B^{-T}\mathbf{w}+{\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t}-2{\mathbf{w}}^T{B}^{-T}\mathbf{t})\right\}d\mathbf{x}d\mathbf{t}\hfill \\ \hfill & =\rho (n,B){\int }_{{\mathbb{R}}^n}f\left(\mathbf{x}\right)exp\left\{\frac{j}{2}({\mathbf{w}}^{T}D{B}^{-1}\mathbf{w}+\Omega B^{-T}\mathbf{w}+{\mathbf{x}}^T{B}^{-1}A\mathbf{x}+2{\mathbf{p}}^T{B}^{-1}\mathbf{x}-2{\mathbf{w}}^T{B}^{-T}\mathbf{x})\right\}\hfill \\ \hfill & ·{\int }_{{\mathbb{R}}^n}g\left(\mathbf{t}-\mathbf{x}\right)exp\{-j{\mathbf{w}}^T{B}^{-T}\left(\mathbf{t}-\mathbf{x}\right)\}d\mathbf{t}d\mathbf{x}\hfill \\ \hfill & ={\left(2\pi \right)}^{\frac{n}{2}}{F}_M\left(\mathbf{w}\right)G\left(B^{-1}\mathbf{w}\right).\hfill \end{array}$$

(21)

Similarly, the semi-discrete and discrete forms of the canonical convolution can be defined as

$$\begin{array}{c}\hfill (c\Theta f)\left(\mathbf{t}\right)=\sum _{\mathbf{k}\in {\mathbb{Z}}^n}c\left(\mathbf{k}\right)f\left(\mathbf{t}-\mathbf{k}\right)exp\left\{-\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}-{\mathbf{k}}^T{B}^{-1}A\mathbf{k}+2{\mathbf{p}}^T{B}^{-1}(\mathbf{t}-\mathbf{k})\right)\right\}\end{array}$$

and

$$\begin{array}{c}\hfill (c\Theta d)\left(\mathbf{k}\right)=\sum _{\mathbf{m}\in {\mathbb{Z}}^n}c\left(\mathbf{m}\right)d\left(\mathbf{k}-\mathbf{m}\right)exp\left\{-\frac{j}{2}\left({\mathbf{k}}^T{B}^{-1}A\mathbf{k}-{\mathbf{m}}^T{B}^{-1}A\mathbf{m}+2{\mathbf{p}}^T{B}^{-1}(\mathbf{k}-\mathbf{m})\right)\right\}\end{array}$$

for $c,d\in {\ell }^2\left({\mathbb{Z}}^n\right)$ and $f\in L^2\left({\mathbb{R}}^n\right)$, respectively. □

Lemma 5.

Let $h\left(\mathbf{t}\right)=\left({\left\{f\left(\mathbf{k}\right)\right\}}_{\mathbf{k}\in {\mathbb{Z}}^n}\Theta g(·)\right)\left(\mathbf{t}\right).$ Then, the multi-dimensional SAFT of h satisfies

$$\begin{array}{c}\hfill H_M\left(\mathbf{w}\right)={\left(2\pi \right)}^{\frac{n}{2}}{\tilde{F}}_M\left(\mathbf{w}\right)G\left(B^{-1}\mathbf{w}\right).\end{array}$$

(22)

Lemma 6.

Let $h\left(\mathbf{k}\right)=\left({\left\{f\left(\mathbf{m}\right)\right\}}_{\mathbf{m}\in {\mathbb{Z}}^n}\Theta {\left\{g\left(\mathbf{m}\right)\right\}}_{\mathbf{m}\in {\mathbb{Z}}^n}\right)\left(\mathbf{k}\right).$ Then, the multi-dimensional SAFT of ${\left\{h\left(\mathbf{k}\right)\right\}}_{\mathbf{k}\in {\mathbb{Z}}^n}$ satisfies

$$\begin{array}{c}\hfill {\tilde{H}}_M\left(\mathbf{w}\right)={\left(2\pi \right)}^{\frac{n}{2}}{\tilde{F}}_M\left(\mathbf{w}\right)\tilde{G}\left(B^{-1}\mathbf{w}\right),\end{array}$$

(23)

where $\tilde{G}$ is the multi-dimensional Fourier transform of the sequence g.

Lemma 7.

The SAFT of ${\left\{f\left(\mathbf{k}\right)\right\}}_{\mathbf{k}\in {\mathbb{Z}}^n}\in {\ell }^2\left({\mathbb{Z}}^n\right)$ satisfies the chirp-modulation periodicity as

$$\begin{array}{cc}\hfill & {\tilde{F}}_M(\mathbf{w}+2\pi B\mathbf{m})exp\left\{-\frac{j}{2}\left({(\mathbf{w}+2\pi B\mathbf{m})}^{T}D{B}^{-1}(\mathbf{w}+2\pi B\mathbf{m})+\Omega B^{-T}(\mathbf{w}+2\pi B\mathbf{m})\right)\right\}\hfill \\ \hfill & ={\tilde{F}}_M\left(\mathbf{w}\right)exp\left\{-\frac{j}{2}\left({\mathbf{w}}^{T}D{B}^{-1}\mathbf{w}+\Omega B^{-T}\mathbf{w}\right)\right\},\hfill \end{array}$$

(24)

where $\mathbf{m}={(m_1,m_2,\cdots ,m_n)}^T\in {\mathbb{Z}}^n.$

Proof. 

By the definition of the multi-dimensional SAFT, one has

$$\begin{array}{cc}\hfill & {\tilde{F}}_M(\mathbf{w}+2\pi B\mathbf{m})\hfill \\ \hfill & =\rho (n,B)\sum _{{\mathbf{k}\in \mathbb{Z}}^n}f\left(\mathbf{k}\right)exp\{\frac{j}{2}({(\mathbf{w}+2\pi B\mathbf{m})}^{T}D{B}^{-1}(\mathbf{w}+2\pi B\mathbf{m})+\Omega B^{-T}(\mathbf{w}+2\pi B\mathbf{m})+{\mathbf{k}}^T{B}^{-1}A\mathbf{k}\hfill \\ \hfill & +2{\mathbf{p}}^T{B}^{-1}\mathbf{k}-2{(\mathbf{w}+2\pi B\mathbf{m})}^T{B}^{-T}\mathbf{k})\}\hfill \\ \hfill & =\rho (n,B)\sum _{{\mathbf{k}\in \mathbb{Z}}^n}f\left(\mathbf{k}\right)exp\left\{\frac{j}{2}\left({\mathbf{w}}^{T}D{B}^{-1}\mathbf{w}+\Omega B^{-T}\mathbf{w}+{\mathbf{k}}^T{B}^{-1}A\mathbf{k}+2{\mathbf{p}}^T{B}^{-1}\mathbf{k}-2{\mathbf{w}}^T{B}^{-T}\mathbf{k}\right)\right\}\hfill \\ \hfill & ·exp\left\{\frac{j}{2}\left(2\pi {\left(B\mathbf{m}\right)}^{T}D{B}^{-1}(\mathbf{w}+2\pi B\mathbf{m})+{\mathbf{w}}^{T}D{B}^{-1}2\pi B\mathbf{m}+\Omega B^{-T}2\pi B\mathbf{m}-2{\left(2\pi B\mathbf{m}\right)}^T{B}^{-T}\mathbf{k}\right)\right\}\hfill \\ \hfill & =exp\left\{\frac{j}{2}\left(2\pi {\left(B\mathbf{m}\right)}^{T}D{B}^{-1}(\mathbf{w}+2\pi B\mathbf{m})+{\mathbf{w}}^{T}D{B}^{-1}2\pi B\mathbf{m}+\Omega B^{-T}2\pi B\mathbf{m}\right)\right\}{\tilde{F}}_M\left(\mathbf{w}\right)\hfill \\ \hfill & =exp\left\{\frac{j}{2}\left({(\mathbf{w}+2\pi B\mathbf{m})}^{T}D{B}^{-1}(\mathbf{w}+2\pi B\mathbf{m})+\Omega B^{-T}(\mathbf{w}+2\pi B\mathbf{m})\right)\right\}\hfill \\ \hfill & ·exp\left\{-\frac{j}{2}\left({\mathbf{w}}^{T}D{B}^{-1}\mathbf{w}+\Omega B^{-T}\mathbf{w}\right)\right\}{\tilde{F}}_M\left(\mathbf{w}\right).\hfill \end{array}$$

The desired result can be obtained by transposition. □

3. The Space Associated with the Canonical Convolution

In this section, we will define a class of subspaces in $L^p\left({\mathbb{R}}^n\right)$ which is related to the canonical convolution in the multi-dimension SAFT domain.

Let $1\le p\le \infty$. Define

$$\begin{array}{cc}\hfill V^p\left(\varphi \right)& =\left\{c\Theta \varphi \left(\mathbf{t}\right):c\in {\ell }^p\left({\mathbb{Z}}^n\right)\right\}\hfill \\ \hfill & =\left\{\sum _{\mathbf{k}\in {\mathbb{Z}}^n}c\left(\mathbf{k}\right)\varphi (\mathbf{t}-\mathbf{k})exp\left\{-\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}-{\mathbf{k}}^T{B}^{-1}A\mathbf{k}+2{\mathbf{p}}^T{B}^{-1}(\mathbf{t}-\mathbf{k})\right):c\in {\ell }^p\left({\mathbb{Z}}^n\right)\right\}\right\}.\hfill \end{array}$$

(25)

In the following, we will give a sufficient and necessary condition for the stability of the basis functions of $V^2\left(\varphi \right).$

Theorem 1.

Let ${\varphi }_{\mathbf{k}}\left(\mathbf{t}\right)=\varphi \left(\mathbf{t}-\mathbf{k}\right)exp\left\{-\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}-{\mathbf{k}}^T{B}^{-1}A\mathbf{k}+2{\mathbf{p}}^T{B}^{-1}(\mathbf{t}-\mathbf{k})\right)\right\}$. Then, ${\left\{{\varphi }_{\mathbf{k}}\left(\mathbf{t}\right)\right\}}_{\mathbf{k}\in {\mathbb{Z}}^n}$ is the Riesz basis of $V^2\left(\varphi \right)$ if and only if there exist constants $0<A_1\le B_1<\infty$ such that

$$A_1\le G_{\varphi ,M}\left(\mathbf{w}\right)\le B_1,\mathbf{w}\in U\left(2\pi B\right),$$

(26)

where $G_{\varphi ,M}\left(\mathbf{w}\right)\stackrel{def}{=}\sum _{\mathbf{m}\in {\mathbb{Z}}^n}{|\Phi (B^{-1}\mathbf{w}+2\pi \mathbf{m}\left)\right|}^2$ and Φ is the FT of ϕ.

Proof. 

For any $f\in V^2\left(\varphi \right)$, there exists a sequence $q\in {\ell }^2\left({\mathbb{Z}}^n\right)$ such that

$$\begin{array}{c}\hfill f\left(\mathbf{t}\right)=\sum _{\mathbf{k}\in {\mathbb{Z}}^n}q\left(\mathbf{k}\right){\varphi }_{\mathbf{k}}\left(\mathbf{t}\right).\end{array}$$

(27)

It follows from Lemma 5 that

$$\begin{array}{c}\hfill F_M\left(\mathbf{w}\right)={\left(2\pi \right)}^{\frac{n}{2}}{\tilde{Q}}_M\left(\mathbf{w}\right)\Phi \left(B^{-1}\mathbf{w}\right).\end{array}$$

(28)

Moreover, we know from Lemmas 2 and 7 that

$$\begin{array}{cc}\hfill {∥f∥}_{L^2\left({\mathbb{R}}^n\right)}^2& ={∥F_M∥}_{L^2\left({\mathbb{R}}^n\right)}^2\hfill \\ \hfill & ={\int }_{{\mathbb{R}}^n}{\left|{\left(2\pi \right)}^{\frac{n}{2}}{\tilde{Q}}_M\left(\mathbf{w}\right)\Phi \left(B^{-1}\mathbf{w}\right)\right|}^{2}d\mathbf{w}\hfill \\ \hfill & ={\left(2\pi \right)}^n\sum _{\mathbf{k}\in {\mathbb{Z}}^n}{\int }_{U\left(2\pi B\right)}{\left|{\tilde{Q}}_M(\mathbf{w}+2\pi B\mathbf{k})\right|}^2{\left|\Phi \left(B^{-1}\mathbf{w}+2\pi \mathbf{k}\right)\right|}^{2}d\mathbf{w}\hfill \\ \hfill & ={\left(2\pi \right)}^n{\int }_{U\left(2\pi B\right)}{\left|{\tilde{Q}}_M\left(\mathbf{w}\right)\right|}^2\sum _{\mathbf{k}\in {\mathbb{Z}}^n}{\left|\Phi \left(B^{-1}\mathbf{w}+2\pi \mathbf{k}\right)\right|}^{2}d\mathbf{w}\hfill \\ \hfill & ={\left(2\pi \right)}^n{\int }_{U\left(2\pi B\right)}{\left|{\tilde{Q}}_M\left(\mathbf{w}\right)\right|}^2{G}_{\varphi ,M}\left(\mathbf{w}\right)d\mathbf{w}.\hfill \end{array}$$

(29)

Similarly, it follows from the Parseval’s formula in Lemma 3 that

$$\begin{array}{cc}\hfill {∥q∥}_{{\ell }^2\left({\mathbb{Z}}^n\right)}^2& ={∥{\tilde{Q}}_M∥}_{L^2\left(U\left(2\pi B\right)\right)}^2={\int }_{U\left(2\pi B\right)}{\left|{\tilde{Q}}_M\left(\mathbf{w}\right)\right|}^{2}d\mathbf{w}.\hfill \end{array}$$

(30)

This together with (29) obtains the desired result. □

Theorem 2.

Suppose that ${\left\{{\varphi }_{\mathbf{k}}\left(\mathbf{t}\right)\right\}}_{\mathbf{k}\in {\mathbb{Z}}^n}$ is the Riesz basis of the space $V^2\left(\varphi \right)$, there exist the dual basis ${\left\{{\psi }_{\mathbf{k}}\left(\mathbf{t}\right)\right\}}_{\mathbf{k}\in {\mathbb{Z}}^n}$ of $V^2\left(\varphi \right)$ with

$${\psi }_{\mathbf{k}}\left(\mathbf{t}\right)=\psi \left(\mathbf{t}-\mathbf{k}\right)exp\left\{-\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}-{\mathbf{k}}^T{B}^{-1}A\mathbf{k}+2{\mathbf{p}}^T{B}^{-1}(\mathbf{t}-\mathbf{k})\right)\right\}$$

such that for $f\left(\mathbf{t}\right)\in L^2\left({\mathbb{R}}^n\right)$, the orthogonal projection operator $\mathrm{P}$ on $V^2\left(\varphi \right)$ can be given by

$$\begin{array}{c}\hfill \mathrm{P}f\left(\mathbf{t}\right)=\sum _{\mathbf{k}\in {\mathbb{Z}}^n}⟨f,{\psi }_{\mathbf{k}}⟩{\varphi }_{\mathbf{k}}\left(\mathbf{t}\right)=\sum _{\mathbf{k}\in {\mathbb{Z}}^n}⟨f,{\varphi }_{\mathbf{k}}⟩{\psi }_{\mathbf{k}}\left(\mathbf{t}\right).\end{array}$$

(31)

Moreover, one has

$$\begin{array}{c}\hfill \Psi \left(B^{-1}\mathbf{w}\right)=\frac{\Phi \left(B^{-1}\mathbf{w}\right)}{{\left(2\pi \right)}^n{G}_{\varphi ,M}\left(\mathbf{w}\right)},\end{array}$$

(32)

where Ψ is the FT of ψ.

Proof. 

Since ${\psi }_{\mathbf{k}}\left(\mathbf{t}\right)\in V^2\left(\varphi \right)$, then there exists a sequence $r\in {\ell }^2\left({\mathbb{Z}}^n\right)$ such that

$$\begin{array}{c}\hfill {\psi }_{\mathbf{0}}\left(\mathbf{t}\right)=\psi \left(\mathbf{t}\right)exp\left\{-\frac{j}{2}({\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t})\right\}=\sum _{\mathbf{k}\in {\mathbb{Z}}^n}r\left(\mathbf{k}\right){\varphi }_{\mathbf{k}}\left(\mathbf{t}\right)=r\Theta \varphi \left(\mathbf{t}\right).\end{array}$$

(33)

Taking the SAFT on both sides of (33), it follows from Lemma 5 that

$$\begin{array}{c}\hfill \rho (n,B)exp\left\{\frac{j}{2}({\mathbf{w}}^{T}D{B}^{-1}\mathbf{w}+\Omega B^{-T}\mathbf{w})\right\}\Psi \left(B^{-1}\mathbf{w}\right)={\tilde{R}}_M\left(\mathbf{w}\right)\Phi \left(B^{-1}\mathbf{w}\right).\end{array}$$

(34)

Note that

$$⟨{\psi }_{\mathbf{m}},{\varphi }_{\mathbf{k}}⟩=exp\left\{-\frac{j}{2}({\mathbf{m}}^T{B}^{-1}A\mathbf{k}+{\mathbf{k}}^T{B}^{-1}A\mathbf{m}-2{\mathbf{m}}^T{B}^{-1}A\mathbf{m})\right\}⟨{\psi }_{\mathbf{0}},{\varphi }_{\mathbf{k}-\mathbf{m}}⟩.$$

Then, one has

$$\begin{array}{cc}\hfill \delta \left(\mathbf{k}\right)& =⟨{\psi }_{\mathbf{0}},{\varphi }_{\mathbf{k}}⟩\hfill \\ \hfill & =⟨\sum _{\mathbf{m}\in {\mathbb{Z}}^n}r\left(\mathbf{m}\right){\varphi }_{\mathbf{m}}\left(\mathbf{t}\right),{\varphi }_{\mathbf{k}}\left(\mathbf{t}\right)⟩\hfill \\ \hfill & =\sum _{\mathbf{m}\in {\mathbb{Z}}^n}r\left(\mathbf{m}\right)⟨{\varphi }_{\mathbf{m}}\left(\mathbf{t}\right),{\varphi }_{\mathbf{k}}\left(\mathbf{t}\right)⟩\hfill \\ \hfill & =\sum _{\mathbf{m}\in {\mathbb{Z}}^n}r\left(\mathbf{m}\right)\lambda \left(\mathbf{k}-\mathbf{m}\right)exp\left\{-\frac{j}{2}\left({\mathbf{k}}^T{B}^{-1}A\mathbf{k}-{\mathbf{m}}^T{B}^{-1}A\mathbf{m}+2{\mathbf{p}}^T{B}^{-1}\left(\mathbf{k}-\mathbf{m}\right)\right)\right\}\hfill \\ \hfill & ={\left\{r\left(\mathbf{m}\right)\right\}}_{\mathbf{m}\in {\mathbb{Z}}^n}\Theta {\left\{\lambda \left(\mathbf{m}\right)\right\}}_{\mathbf{m}\in {\mathbb{Z}}^n}\left(\mathbf{k}\right),\hfill \end{array}$$

(35)

where $\lambda \left(\mathbf{k}-\mathbf{m}\right)=⟨\varphi \left(\mathbf{t}-\mathbf{m}\right),\varphi \left(\mathbf{t}-\mathbf{k}\right)⟩.$ Taking the SAFT on both sides of (35), it follows from Lemma 6 that

$$\begin{array}{c}\hfill \rho (n,B)exp\left\{\frac{j}{2}({\mathbf{w}}^{T}D{B}^{-1}\mathbf{w}+\Omega B^{-T}\mathbf{w})\right\}={\left(2\pi \right)}^{\frac{n}{2}}{\tilde{R}}_M\left(\mathbf{w}\right)\tilde{\Lambda }\left(B^{-1}\mathbf{w}\right),\end{array}$$

(36)

where $\tilde{\Lambda }$ is the discrete FT of $\lambda$. Moreover, we have

$$\begin{array}{cc}\hfill \lambda \left(\mathbf{k}-\mathbf{m}\right)& =⟨\varphi \left(\mathbf{t}-\mathbf{m}\right),\varphi \left(\mathbf{t}-\mathbf{k}\right)⟩\hfill \\ \hfill & =⟨exp\left\{-j{\mathbf{w}}^T\mathbf{m}\right\}\Phi \left(\mathbf{w}\right),exp\left\{-j{\mathbf{w}}^T\mathbf{k}\right\}\Phi \left(\mathbf{w}\right)⟩\hfill \\ \hfill & ={\int }_{{\mathbb{R}}^n}{|\Phi \left(\mathbf{w}\right)|}^{2}exp\left\{j{\mathbf{w}}^T\left(\mathbf{k}-\mathbf{m}\right)\right\}d\mathbf{w}\hfill \\ \hfill & =\sum _{{\mathbf{m}}_{\mathbf{1}}\in {\mathbb{Z}}^n}{\int }_{{[0,2\pi ]}^n}|\Phi \left(\mathbf{w}+2\pi {\mathbf{m}}_{\mathbf{1}}\right){|}^{2}exp\left\{j{\mathbf{w}}^T\left(\mathbf{k}-\mathbf{m}\right)\right\}d\mathbf{w}\hfill \\ \hfill & ={\int }_{{[0,2\pi ]}^n}\sum _{{\mathbf{m}}_{\mathbf{1}}\in {\mathbb{Z}}^n}|\Phi \left(\mathbf{w}+2\pi {\mathbf{m}}_{\mathbf{1}}\right){|}^{2}exp\left\{j{\mathbf{w}}^T\left(\mathbf{k}-\mathbf{m}\right)\right\}d\mathbf{w}.\hfill \end{array}$$

(37)

Then, we can obtain

$$\begin{array}{c}\hfill \tilde{\Lambda }\left(B^{-1}\mathbf{w}\right)={\left(2\pi \right)}^{\frac{n}{2}}{G}_{\varphi ,M}\left(\mathbf{w}\right).\end{array}$$

(38)

This together with (34) and (36) obtains

$$\begin{array}{c}\hfill \Psi \left(B^{-1}\mathbf{w}\right)=\frac{\Phi \left(B^{-1}\mathbf{w}\right)}{{\left(2\pi \right)}^n{G}_{\varphi ,M}\left(\mathbf{w}\right)},\end{array}$$

(39)

which means that the function $\psi$ exists because $G_{\varphi ,M}\left(\mathbf{w}\right)$ satisfies (26). □

Now, we introduce the Wiener amalgam space, more details can be found in [2]. A measurable function f belongs to $W\left(L^p\left({\mathbb{R}}^n\right)\right)$, $1\le p<\infty$, if it satisfies

$$\begin{array}{c}\hfill {∥f∥}_{W\left(L^p\left({\mathbb{R}}^n\right)\right)}^p=\sum _{\mathbf{k}\in {\mathbb{Z}}^n}\mathrm{ess}sup\left\{{\left|f\left(\mathbf{t}+\mathbf{k}\right)\right|}^p;\mathbf{t}\in {[0,1]}^n\right\}<\infty .\end{array}$$

(40)

If $p=\infty$, a measurable function f belongs to $W\left(L^{\infty }\left({\mathbb{R}}^n\right)\right)$ if it satisfies

$$\begin{array}{c}\hfill {∥f∥}_{W\left(L^{\infty }\left({\mathbb{R}}^n\right)\right)}=\underset{\mathbf{k}\in {\mathbb{Z}}^n}{sup}\{\mathrm{ess}sup\{\left|f\left(\mathbf{t}+\mathbf{k}\right)\right|;\mathbf{t}\in {[0,1]}^n\left\}\right\}<\infty .\end{array}$$

(41)

Note that $W\left(L^{\infty }\left({\mathbb{R}}^n\right)\right)$ coincides with $L^{\infty }\left({\mathbb{R}}^n\right)$. Let $W_0\left(L^p\left({\mathbb{R}}^n\right)\right)$ be the subspace of continuous functions in $W\left(L^p\left({\mathbb{R}}^n\right)\right).$

Lemma 8

([2]). If $\varphi \in W\left(L^1\left({\mathbb{R}}^n\right)\right),$ then the autocorrelation sequence

$$\begin{array}{c}\hfill a_{\mathbf{k}}={\int }_{{\mathbb{R}}^n}\varphi \left(\mathbf{t}\right)\overline{\varphi \left(\mathbf{t}-\mathbf{k}\right)}d\mathbf{t}\end{array}$$

(42)

belongs to ${\ell }^1\left({\mathbb{Z}}^n\right)$, and we have

$$\begin{array}{c}\hfill {∥a∥}_{{\ell }^1\left({\mathbb{Z}}^n\right)}\le {∥\varphi ∥}_{W\left(L^1\left({\mathbb{R}}^n\right)\right)}^2.\end{array}$$

(43)

Lemma 9

([2]). If $f\in L^p\left({\mathbb{R}}^n\right)$ and $g\in W\left(L^1\left({\mathbb{R}}^n\right)\right)$, then the sequence d defined by $d_{\mathbf{k}}={\int }_{{\mathbb{R}}^n}f\left(\mathbf{t}\right)\overline{g\left(\mathbf{t}-\mathbf{k}\right)}d\mathbf{t}$ belongs to ${\ell }^p\left({\mathbb{Z}}^n\right)$, and we have

$$\begin{array}{c}\hfill {∥d∥}_{{\ell }^p\left({\mathbb{Z}}^n\right)}\le {∥f∥}_{L^p\left({\mathbb{Z}}^n\right)}{∥g∥}_{W\left(L^1\left({\mathbb{R}}^n\right)\right)},1\le p\le \infty .\end{array}$$

(44)

Lemma 10

([22]). (Wiener’s Lemma) If $f\left(\mathbf{w}\right)=\sum _{\mathbf{k}\in {\mathbb{Z}}^n}{a}_{\mathbf{k}}exp\left\{j{\mathbf{w}}^T\mathbf{k}\right\}$ is an absolutely convergent Fourier series with coefficient sequence $a={\left(a_{\mathbf{k}}\right)}_{\mathbf{k}\in {\mathbb{Z}}^n}\in {\ell }^1\left({\mathbb{Z}}^n\right)$ and if $f\left(\mathbf{w}\right)\ne \mathbf{0}$ for all $\mathbf{w}\in {\mathbb{R}}^n$, then $\frac{1}{f}$ also has an absolutely convergent Fourier series $\frac{1}{f\left(\mathbf{w}\right)}=\sum _{\mathbf{k}\in {\mathbb{Z}}^n}{b}_{\mathbf{k}}exp\left\{j{\mathbf{w}}^T\mathbf{k}\right\}$ with coefficient sequence $b={\left(b_{\mathbf{k}}\right)}_{\mathbf{k}\in {\mathbb{Z}}^n}\in {\ell }^1\left({\mathbb{Z}}^n\right).$

Lemma 11.

If $f\in L^p\left({\mathbb{R}}^n\right)$ and $g\in W\left(L^1\left({\mathbb{R}}^n\right)\right)$, then the sequence d defined by

$$\begin{array}{c}\hfill d_{\mathbf{k}}={\int }_{{\mathbb{R}}^n}f\left(\mathbf{t}\right)\overline{g\left(\mathbf{t}-\mathbf{k}\right)}exp\left\{\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}-{\mathbf{k}}^T{B}^{-1}A\mathbf{k}+2{\mathbf{p}}^T{B}^{-1}\left(\mathbf{t}-\mathbf{k}\right)\right)\right\}d\mathbf{t}\end{array}$$

(45)

belongs to ${\ell }^p\left({\mathbb{Z}}^n\right)$, and we have

$$\begin{array}{c}\hfill {∥d∥}_{{\ell }^p\left({\mathbb{Z}}^n\right)}\le {∥f∥}_{L^p\left({\mathbb{R}}^n\right)}{∥g∥}_{W\left(L^1\left({\mathbb{R}}^n\right)\right)},1\le p\le \infty .\end{array}$$

(46)

Proof. 

Note that

$$\left|d_{\mathbf{k}}\right|\le {\int }_{{\mathbb{R}}^n}\left|f\left(\mathbf{t}\right)g\left(\mathbf{t}-\mathbf{k}\right)\right|d\mathbf{t}.$$

It follows from Lemma 9 that the result holds. □

Lemma 12.

Let $1\le p\le \infty$. If $\varphi \in W\left(L^1\left({\mathbb{R}}^n\right)\right)$ and $c\in {\ell }^p\left({\mathbb{Z}}^n\right)$, then the function

$$f\left(\mathbf{t}\right)=\sum _{\mathbf{k}\in {\mathbb{Z}}^n}c\left(\mathbf{k}\right)\varphi \left(\mathbf{t}-\mathbf{k}\right)exp\left\{-\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}-{\mathbf{k}}^T{B}^{-1}A\mathbf{k}+2{\mathbf{p}}^T{B}^{-1}\left(\mathbf{t}-\mathbf{k}\right)\right)\right\}$$

belongs to $W\left(L^p\left({\mathbb{R}}^n\right)\right)$ and

$$\begin{array}{c}\hfill {∥f∥}_{W\left(L^p\left({\mathbb{R}}^n\right)\right)}\le {∥c∥}_{{\ell }^p\left({\mathbb{Z}}^n\right)}{∥\varphi ∥}_{W\left(L^1\left({\mathbb{R}}^n\right)\right)}.\end{array}$$

(47)

Proof. 

Let $b_{\mathbf{k}}=\mathrm{ess}\underset{\mathbf{t}\in {[0,1]}^n}{sup}\left|\varphi \left(\mathbf{t}+\mathbf{k}\right)\right|$ and $d_{\mathbf{k}}=\mathrm{ess}\underset{\mathbf{t}\in {[0,1]}^n}{sup}\left|f\left(\mathbf{t}+\mathbf{k}\right)\right|.$ Note that

$$\begin{array}{cc}\hfill d_{\mathbf{k}}& =\mathrm{ess}\underset{\mathbf{t}\in {[0,1]}^n}{sup}\left|\sum _{\mathbf{m}\in {\mathbb{Z}}^n}c\left(\mathbf{m}\right){\varphi }_{\mathbf{m}}\left(\mathbf{t}+\mathbf{k}\right)\right|\hfill \\ \hfill & \le \mathrm{ess}\underset{\mathbf{t}\in {[0,1]}^n}{sup}\sum _{\mathbf{m}\in {\mathbb{Z}}^n}\left|c\left(\mathbf{m}\right)\right|\left|\varphi \left(\mathbf{t}+\mathbf{k}-\mathbf{m}\right)\right|\hfill \\ \hfill & \le \sum _{\mathbf{m}\in {\mathbb{Z}}^n}\left|c\left(\mathbf{m}\right)\right|b_{\mathbf{k}-\mathbf{m}}\hfill \end{array}$$

(48)

and ${∥b∥}_{{\ell }^1\left({\mathbb{Z}}^n\right)}={∥\varphi ∥}_{W\left(L^1\left({\mathbb{R}}^n\right)\right)}.$ Then, we can obtain

$${∥f∥}_{W\left(L^p\left({\mathbb{R}}^n\right)\right)}={∥d∥}_{{\ell }^p\left({\mathbb{Z}}^n\right)}\le {∥c∥}_{{\ell }^p\left({\mathbb{Z}}^n\right)}{∥b∥}_{{\ell }^1\left({\mathbb{Z}}^n\right)}={∥c∥}_{{\ell }^p\left({\mathbb{Z}}^n\right)}{∥\varphi ∥}_{W\left(L^1\left({\mathbb{R}}^n\right)\right)}.$$

□

Theorem 3.

Suppose that $\varphi \in W\left(L^1\left({\mathbb{R}}^n\right)\right)$ and ${\left\{\varphi { }_{\mathbf{k}}\left(\mathbf{t}\right)\right\}}_{\mathbf{k}\in {\mathbb{Z}}^n}$ is the Riesz basis of $V^2\left(\varphi \right)$, then the dual basis ψ is also in $W\left(L^1\left({\mathbb{R}}^n\right)\right)$.

Proof. 

It follows from Theorem 2 that there exists a $c\in {\ell }^2\left({\mathbb{Z}}^n\right)$ such that

$$\begin{array}{cc}\hfill {\psi }_{\mathbf{0}}\left(\mathbf{t}\right)& =\psi \left(\mathbf{t}\right)exp\left\{-\frac{j}{2}({\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t})\right\}\hfill \\ \hfill & =\sum _{\mathbf{k}\in {\mathbb{Z}}^n}c\left(\mathbf{k}\right)\varphi \left(\mathbf{t}-\mathbf{k}\right)exp\left\{-\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}-{\mathbf{k}}^T{B}^{-1}A\mathbf{k}+2{\mathbf{p}}^T{B}^{-1}\left(\mathbf{t}-\mathbf{k}\right)\right)\right\},\hfill \end{array}$$

(49)

which is equivalent to

$$\begin{array}{cc}\hfill \psi \left(\mathbf{t}\right)& =\sum _{\mathbf{k}\in {\mathbb{Z}}^n}c\left(\mathbf{k}\right)exp\left\{\frac{j}{2}({\mathbf{k}}^T{B}^{-1}A\mathbf{k}+2{\mathbf{p}}^T{B}^{-1}\mathbf{k})\right\}\varphi \left(\mathbf{t}-\mathbf{k}\right)\hfill \\ \hfill & =:\sum _{\mathbf{k}\in {\mathbb{Z}}^n}{c}_1\left(\mathbf{k}\right)\varphi \left(\mathbf{t}-\mathbf{k}\right).\hfill \end{array}$$

(50)

Moreover, we know from Theorem 2 that the FT of ${\left\{c{ }_1\left(\mathbf{k}\right)\right\}}_{\mathbf{k}\in {\mathbb{Z}}^n}$ is

$$\begin{array}{c}\hfill {\tilde{C}}_1\left(\mathbf{w}\right)=\frac{1}{{\left(2\pi \right)}^{\frac{3n}{2}}{\displaystyle \sum _{\mathbf{k}\in {\mathbb{Z}}^n}}{\left|\Phi (\mathbf{w}+2\pi \mathbf{k})\right|}^2},\mathbf{w}\in {\left[0,2\pi \right]}^n.\end{array}$$

(51)

By the Poisson summation formula, one has

$$\begin{array}{c}\hfill \sum _{\mathbf{k}\in {\mathbb{Z}}^n}{\left|\Phi (\mathbf{w}+2\pi \mathbf{k})\right|}^2=\sum _{\mathbf{k}\in {\mathbb{Z}}^n}⟨\varphi ,\varphi (·-\mathbf{k})⟩exp\left\{j{\mathbf{w}}^T\mathbf{k}\right\}.\end{array}$$

(52)

It follows from Lemma 8 that

$$\begin{array}{c}\hfill {\left\{⟨\varphi ,\varphi (·-\mathbf{k})⟩\right\}}_{\mathbf{k}\in {\mathbb{Z}}^n}\in {\ell }^1\left({\mathbb{Z}}^n\right).\end{array}$$

(53)

This together with (51) and Lemma 10 obtains $c_1\in {\ell }^1\left({\mathbb{Z}}^n\right).$ Then, $c\in {\ell }^1\left({\mathbb{Z}}^n\right).$ Finally, $\psi \in W\left(L^1\left({\mathbb{R}}^n\right)\right)$ follows from (50) and Lemma 12. □

Theorem 4.

Suppose that $\varphi \in W\left(L^1\left({\mathbb{R}}^n\right)\right),$ then

(i)

The space $V^p\left(\varphi \right)$ is a subspace of $L^p\left({\mathbb{R}}^n\right)$ and $W\left(L^p\left({\mathbb{R}}^n\right)\right)$ for $1\le p\le \infty .$

(ii)

If ${\left\{{\varphi }_{\mathbf{k}}\left(\mathbf{t}\right)\right\}}_{\mathbf{k}\in {\mathbb{Z}}^n}$ is a Riesz basis of $V^2\left(\varphi \right)$, then there exist constants $0<m_p\le M_p<\infty$ such that for any $c\in {\ell }^p\left({\mathbb{Z}}^n\right),$ one has

$$\begin{array}{c}\hfill m_p{∥c∥}_{{\ell }^p\left({\mathbb{Z}}^n\right)}\le {∥\sum _{\mathbf{k}\in {\mathbb{Z}}^n}c\left(\mathbf{k}\right){\varphi }_{\mathbf{k}}\left(\mathbf{t}\right)∥}_{L^p\left({\mathbb{R}}^n\right)}\le M_p{∥c∥}_{{\ell }^p\left({\mathbb{Z}}^n\right)}.\end{array}$$

(54)

(iii)

If $f\in V^p\left(\varphi \right)$, then we have the norm equivalences

$$\begin{array}{c}\hfill {∥f∥}_{L^p\left({\mathbb{R}}^n\right)}\approx {∥c∥}_{{\ell }^p\left({\mathbb{Z}}^n\right)}\approx {∥f∥}_{W\left(L^p\left({\mathbb{R}}^n\right)\right)}.\end{array}$$

(55)

Proof. 

Note that

$$\begin{array}{c}\hfill {∥f∥}_{L^p\left({\mathbb{R}}^n\right)}\le {∥f∥}_{W\left(L^p\left({\mathbb{R}}^n\right)\right)},1\le p\le \infty .\end{array}$$

(56)

This together with Lemma 12 obtains (i) and the right side of (54) holds. □

Now, we prove the left side of (54). Define the operator

$$\begin{array}{c}\hfill {\mathrm{T}}_{\varphi }c=\sum _{\mathbf{k}\in {\mathbb{Z}}^n}c\left(\mathbf{k}\right)\varphi \left(\mathbf{t}-\mathbf{k}\right)exp\left\{-\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}-{\mathbf{k}}^T{B}^{-1}A\mathbf{k}+2{\mathbf{p}}^T{B}^{-1}\left(\mathbf{t}-\mathbf{k}\right)\right)\right\},c\in {\ell }^p\left({\mathbb{Z}}^n\right)\end{array}$$

and the operator

$$\begin{array}{c}\hfill {\left({\mathrm{T}}_{\psi }^{*}f\right)}_{\mathbf{k}}={\int }_{{\mathbb{R}}^n}f\left(\mathbf{t}\right)\overline{\psi \left(\mathbf{t}-\mathbf{k}\right)}exp\left\{\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}-{\mathbf{k}}^T{B}^{-1}A\mathbf{k}+2{\mathbf{p}}^T{B}^{-1}\left(\mathbf{t}-\mathbf{k}\right)\right)\right\}d\mathbf{t},f\in L^p\left({\mathbb{R}}^n\right).\end{array}$$

It follows from Lemmas 11 and 12 that ${\mathrm{T}}_{\varphi }$ is a bounded map from ${\ell }^p\left({\mathbb{Z}}^n\right)$ to $L^p\left({\mathbb{R}}^n\right)$ and ${\mathrm{T}}_{\psi }^{*}$ is also a bounded map from $L^p\left({\mathbb{R}}^n\right)$ to ${\ell }^p\left({\mathbb{Z}}^n\right)$.

Let $f\left(\mathbf{t}\right)={\displaystyle \sum _{\mathbf{k}\in {\mathbb{Z}}^n}}c\left(\mathbf{k}\right){\varphi }_{\mathbf{k}}\left(\mathbf{t}\right)\in V^p\left(\varphi \right)$. Since ${\left\{{\varphi }_{\mathbf{k}}\left(\mathbf{t}\right)\right\}}_{\mathbf{k}\in {\mathbb{Z}}^n}$ and ${\left\{{\psi }_{\mathbf{m}}\left(\mathbf{t}\right)\right\}}_{\mathbf{m}\in {\mathbb{Z}}^n}$ are biorthogonal, $c\left(\mathbf{k}\right)=⟨f,{\psi }_{\mathbf{k}}\left(\mathbf{t}\right)⟩={\left(T_{\psi }^{*}f\right)}_{\mathbf{k}}$. Then

$${∥c∥}_{{\ell }^p\left({\mathbb{Z}}^n\right)}\le {∥T_{\psi }^{*}∥}_{op}{∥f∥}_{L^p\left({\mathbb{R}}^n\right)}.$$

Choosing $m_p={∥T_{\psi }^{*}∥}_{op}^{-1}$ obtains the desired result. The norm equivalences (55) follows from (54) and Lemma 12.

Theorem 5.

Let $1\le p\le \infty$. Suppose that $\varphi \in W_0\left(L^1\left({\mathbb{R}}^n\right)\right)$ and ${\left\{{\varphi }_{\mathbf{k}}\left(\mathbf{t}\right)\right\}}_{\mathbf{k}\in {\mathbb{Z}}^n}$ are the Riesz basis of $V^2\left(\varphi \right),$ then $V^p\left(\varphi \right)\subset W_0\left(L^p\left({\mathbb{R}}^n\right)\right)$.

Proof. 

It is obvious that $V^p\left(\varphi \right)\subset W\left(L^p\left({\mathbb{R}}^n\right)\right)$ follows from Lemma 12. Note that

$$\begin{array}{c}\hfill {∥f∥}_{L^{\infty }\left({\mathbb{R}}^n\right)}\le {∥f∥}_{W\left(L^p\left({\mathbb{R}}^n\right)\right)},1\le p\le \infty .\end{array}$$

(57)

Let $f\left(\mathbf{t}\right)={\displaystyle \sum _{\mathbf{k}\in {\mathbb{Z}}^n}}c\left(\mathbf{k}\right){\varphi }_{\mathbf{k}}\left(\mathbf{t}\right)\in V^p\left(\varphi \right)$ and $f_N\left(\mathbf{t}\right)={\displaystyle \sum _{{\parallel \mathbf{k}\parallel }_{\infty }\le N}}c\left(\mathbf{k}\right){\varphi }_{\mathbf{k}}\left(\mathbf{t}\right).$ If $1\le p<\infty ,$ then it follows from Lemma 12 and (57) that

$$\begin{array}{c}\hfill {∥f-f_N∥}_{L^{\infty }\left({\mathbb{R}}^n\right)}\le {\left(\sum _{{\parallel \mathbf{k}\parallel }_{\infty }>N}{\left|c\left(\mathbf{k}\right)\right|}^p\right)}^{\frac{1}{p}}{∥\varphi ∥}_{W\left(L^1\left({\mathbb{R}}^n\right)\right)},\end{array}$$

(58)

which means that $f_N\left(\mathbf{t}\right)$ uniformly converges to the continuous function $f\left(\mathbf{t}\right)$. □

Now, we will prove for the case $p=\infty$. Since $\varphi \in W_0\left(L^1\left({\mathbb{R}}^n\right)\right)$, there exists a sequence ${\phi }_N$ of continuous function with compact support such that

$$\begin{array}{c}\hfill \underset{N\to \infty }{lim}{∥\varphi -{\phi }_N∥}_{W\left(L^1\left({\mathbb{R}}^n\right)\right)}=0.\end{array}$$

(59)

Let

$$g_N\left(\mathbf{t}\right)=\sum _{\mathbf{k}\in {\mathbb{Z}}^n}c\left(\mathbf{k}\right){\phi }_N\left(\mathbf{t}-\mathbf{k}\right)exp\left\{-\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}-{\mathbf{k}}^T{B}^{-1}A\mathbf{k}+2{\mathbf{p}}^T{B}^{-1}\left(\mathbf{t}-\mathbf{k}\right)\right)\right\}.$$

Then, $g_N$ is continuous because the sum is locally finite. Using Lemma 12, we have

$$\begin{array}{cc}\hfill & {∥f-g_N∥}_{L^{\infty }\left({\mathbb{R}}^n\right)}\hfill \\ \hfill & ={∥\sum _{\mathbf{k}\in {\mathbb{Z}}^n}c\left(\mathbf{k}\right)(\varphi -{\phi }_N)\left(\mathbf{t}-\mathbf{k}\right)exp\left\{-\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}-{\mathbf{k}}^T{B}^{-1}A\mathbf{k}+2{\mathbf{p}}^T{B}^{-1}\left(\mathbf{t}-\mathbf{k}\right)\right)\right\}∥}_{L^{\infty }\left({\mathbb{R}}^n\right)}\hfill \\ \hfill & \le {∥c∥}_{{\ell }^{\infty }\left({\mathbb{Z}}^n\right)}{∥\varphi -{\phi }_N∥}_{W\left(L^1\left({\mathbb{R}}^n\right)\right)}.\hfill \end{array}$$

This together with (59) shows that $g_N\left(\mathbf{t}\right)$ uniformly converges to continuous function $f\left(\mathbf{t}\right)$.

4. Sampling and Reconstruction in $V^p\left(\varphi \right)$

In this section, we will discuss the sampling and reconstruction of signals in the space $V^p\left(\varphi \right)$.

Definition 4

([2]). A set $X=\{{\mathbf{t}}_i:i\in I\}$ is ${\gamma }_0$-dense in ${\mathbb{R}}^n$ if

$$\begin{array}{c}\hfill {\mathbb{R}}^n=\bigcup _{i\in I}{B}_{\gamma }\left({\mathbf{t}}_i\right)\forall \gamma >{\gamma }_0,\end{array}$$

(60)

where $B_{\gamma }\left({\mathbf{t}}_i\right)$ is a sphere with ${\mathbf{t}}_i$ as the center and γ as the radius.

Definition 5

([2]). We call ${\left\{{\beta }_i\right\}}_{i\in I}$ a bounded partition of unity associated with $X=\{{\mathbf{t}}_i:i\in I\}$, if

(i)

$0\le {\beta }_i\le 1$ for all $i\in I$;

(ii)

$supp{\beta }_i\subset B_{\gamma }\left({\mathbf{t}}_i\right)$;

(iii)

${\displaystyle \sum _{i\in I}}{\beta }_i\equiv 1.$

Moreover, we define the operator ${\mathrm{Q}}_{\mathrm{X}}$ as

$$\begin{array}{c}\hfill {\mathrm{Q}}_{\mathrm{X}}f=\sum _{i\in I}f\left({\mathbf{t}}_i\right){\beta }_i.\end{array}$$

(61)

Theorem 6.

Suppose that $\varphi \in W_0\left(L^1\left({\mathbb{R}}^n\right)\right)$, ${\left\{{\varphi }_{\mathbf{k}}\left(\mathbf{t}\right)\right\}}_{\mathbf{k}\in {\mathbb{Z}}^n}$ is a Riesz basis of $V^2\left(\varphi \right)$ and ${\left\{{\psi }_{\mathbf{k}}\left(\mathbf{t}\right)\right\}}_{\mathbf{k}\in {\mathbb{Z}}^n}\in V^2\left(\varphi \right)$ is the dual basis of ${\left\{{\varphi }_{\mathbf{k}}\left(\mathbf{t}\right)\right\}}_{\mathbf{k}\in {\mathbb{Z}}^n}.$ Then the orthogonal projection operator

$$\begin{array}{c}\hfill \mathrm{P}:f⟶\sum _{\mathbf{k}\in {\mathbb{Z}}^n}⟨f,{\psi }_{\mathbf{k}}⟩{\varphi }_{\mathbf{k}}\left(\mathbf{t}\right)\end{array}$$

(62)

is a bounded projection from $L^p\left({\mathbb{R}}^n\right)$ onto $V^p\left(\varphi \right)$ for $1\le p\le \infty$.

Proof. 

Note that

$$\begin{array}{c}\hfill \mathrm{P}f=\sum _{\mathbf{k}\in {\mathbb{Z}}^n}⟨f,{\psi }_{\mathbf{k}}⟩{\varphi }_{\mathbf{k}}\left(\mathbf{t}\right)={\mathrm{T}}_{\varphi }{\mathrm{T}}_{\psi }^{*}f,f\in L^p\left({\mathbb{R}}^n\right).\end{array}$$

(63)

Then, the desired result follows from the boundedness of the operators ${\mathrm{T}}_{\varphi }$ and ${\mathrm{T}}_{\psi }^{*}$ in the proof of Theorem 4. □

Lemma 13

([2]). Suppose that $\phi \in W_0\left(L^1\left({\mathbb{R}}^n\right)\right)$ and $\{\phi \left(\mathbf{t}-\mathbf{k}\right):\mathbf{k}\in {\mathbb{Z}}^n\}$ are the Riesz basis of $V_F^2\left(\phi \right)=\left\{{\displaystyle \sum _{\mathbf{k}\in {\mathbb{Z}}^n}}c\left(\mathbf{k}\right)\phi \left(\mathbf{t}-\mathbf{k}\right):c\in {\ell }^2\left({\mathbb{Z}}^n\right)\right\}$. Then, there exists a density $\gamma >0$ such that any f belonging to

$$\begin{array}{c}\hfill V_F^p\left(\phi \right)=\left\{\sum _{\mathbf{k}\in {\mathbb{Z}}^n}c\left(\mathbf{k}\right)\phi \left(\mathbf{t}-\mathbf{k}\right):c\in {\ell }^p\left({\mathbb{Z}}^n\right)\right\}\end{array}$$

(64)

can be recovered from its samples $\{f\left({\mathbf{t}}_i\right):{\mathbf{t}}_i\in X\}$ on any γ-dense set $X=\{{\mathbf{t}}_i:i\in I\}$ by the iterative algorithm

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{f}_1={\mathrm{P}}_{\mathrm{F}}{\mathrm{Q}}_{\mathrm{X}}f,\hfill \\ f_{k+1}={\mathrm{P}}_{\mathrm{F}}{\mathrm{Q}}_{\mathrm{X}}(f-f_k)+f_k,\hfill \end{array}\right.\end{array}$$

(65)

where ${\mathrm{P}}_{\mathrm{F}}$ is the bounded projection from $L^p\left({\mathbb{R}}^n\right)$ onto $V_F^p\left(\phi \right).$ Moreover, $f_k$ uniformly converges to f and

$$\begin{array}{c}\hfill {∥f-f_k∥}_{L^p\left({\mathbb{R}}^n\right)}\le {∥f-f_k∥}_{W\left(L^p\left({\mathbb{R}}^n\right)\right)}\le C{∥f∥}_{L^p\left({\mathbb{R}}^n\right)}{\alpha }^k,\end{array}$$

(66)

where $\alpha =\alpha \left(\gamma \right)<1.$

Define an operator $M_S$ as

$$\begin{array}{c}\hfill M_{S}f\left(\mathbf{t}\right)=exp\left\{-\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t}\right)\right\}f\left(\mathbf{t}\right).\end{array}$$

(67)

Then, we can provide the following iterative reconstruction algorithm.

Theorem 7.

Suppose that $\varphi \in W_0\left(L^1\left({\mathbb{R}}^n\right)\right)$ and ${\left\{{\varphi }_{\mathbf{k}}\left(\mathbf{t}\right)\right\}}_{\mathbf{k}\in {\mathbb{Z}}^n}$ are the Riesz basis of $V^2\left(\varphi \right)$. Then, there exists a density $\gamma >0$ such that any $f\in V^p\left(\varphi \right)$ can be recovered from its samples $\{f\left({\mathbf{t}}_i\right):{\mathbf{t}}_i\in X\}$ on any γ-dense set $X=\{t_i:i\in I\}$ by the iterative algorithm

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{f}_1=\mathrm{P}{M}_S{\mathrm{Q}}_{\mathrm{X}}{M}_S^{-1}f,\hfill \\ f_{k+1}=\mathrm{P}{M}_S{\mathrm{Q}}_{\mathrm{X}}{M}_S^{-1}(f-f_k)+f_k.\hfill \end{array}\right.\end{array}$$

(68)

Moreover, $f_k$ uniformly converges to f and

$$\begin{array}{c}\hfill {∥f-f_k∥}_{L^p\left({\mathbb{R}}^n\right)}\le {∥f-f_k∥}_{W\left(L^p\left({\mathbb{R}}^n\right)\right)}\le C{∥f∥}_{L^p\left({\mathbb{R}}^n\right)}{\alpha }^k,\end{array}$$

(69)

where $\alpha =\alpha \left(\gamma \right)<1.$

Proof. 

Note that

$$\begin{array}{cc}\hfill f\left(\mathbf{t}\right)& =\sum _{\mathbf{k}\in {\mathbb{Z}}^n}c\left(\mathbf{k}\right){\varphi }_{\mathbf{k}}\left(\mathbf{t}\right)\hfill \\ \hfill & =\sum _{\mathbf{k}\in {\mathbb{Z}}^n}c\left(\mathbf{k}\right)\varphi \left(\mathbf{t}-\mathbf{k}\right)exp\left\{-\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}-{\mathbf{k}}^T{B}^{-1}A\mathbf{k}+2{\mathbf{p}}^T{B}^{-1}\left(\mathbf{t}-\mathbf{k}\right)\right)\right\}\hfill \end{array}$$

(70)

is equivalent to

$$\begin{array}{cc}\hfill & exp\left\{\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t}\right)\right\}f\left(\mathbf{t}\right)\hfill \\ \hfill & =\sum _{\mathbf{k}\in {\mathbb{Z}}^n}c\left(\mathbf{k}\right)exp\left\{\frac{j}{2}\left({\mathbf{k}}^T{B}^{-1}A\mathbf{k}+2{\mathbf{p}}^T{B}^{-1}\mathbf{k}\right)\right\}\varphi \left(\mathbf{t}-\mathbf{k}\right).\hfill \end{array}$$

(71)

Let

$$g\left(\mathbf{t}\right)=exp\left\{\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t}\right)\right\}f\left(\mathbf{t}\right)$$

and $c{ }_2\left(\mathbf{k}\right)=c\left(\mathbf{k}\right)exp\left\{\frac{j}{2}\left({\mathbf{k}}^T{B}^{-1}A\mathbf{k}+2{\mathbf{p}}^T{B}^{-1}\mathbf{k}\right)\right\}.$ Then, $g\left(\mathbf{t}\right)\in V_F^p\left(\varphi \right)$. Since the FT of $\varphi$ satisfies (26), $\{\varphi \left(\mathbf{t}-\mathbf{k}\right):\mathbf{k}\in {\mathbb{Z}}^n\}$ is the Riesz basis of $V_F^2\left(\varphi \right).$ Then it follows from Lemma 13 that g can be recovered from its samples

$$g\left({\mathbf{t}}_i\right)=exp\left\{\frac{j}{2}\left({\mathbf{t}}_i^T{B}^{-1}A{\mathbf{t}}_i+2{\mathbf{p}}^T{B}^{-1}{\mathbf{t}}_i\right)\right\}f\left({\mathbf{t}}_i\right)$$

by the iterative algorithm

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{g}_1={\mathrm{P}}_{\mathrm{F}}{\mathrm{Q}}_{\mathrm{X}}g,\hfill \\ g_{k+1}={\mathrm{P}}_{\mathrm{F}}{\mathrm{Q}}_{\mathrm{X}}(g-g_k)+g_k.\hfill \end{array}\right.\end{array}$$

(72)

Moreover, $g_k$ uniformly converges to g and

$$\begin{array}{c}\hfill {∥g-g_k∥}_{L^p\left({\mathbb{R}}^n\right)}\le {∥g-g_k∥}_{W\left(L^p\left({\mathbb{R}}^n\right)\right)}\le C{∥g∥}_{L^p\left({\mathbb{R}}^n\right)}{\alpha }^k,\end{array}$$

(73)

where $\alpha =\alpha \left(\gamma \right)<1.$ Note that

$$\begin{array}{cc}\hfill {\mathrm{P}}_{\mathrm{F}}f\left(\mathbf{t}\right)& =\sum _{\mathbf{k}\in {\mathbb{Z}}^n}⟨f,\psi \left(\mathbf{t}-\mathbf{k}\right)⟩\varphi \left(\mathbf{t}-\mathbf{k}\right)\hfill \\ \hfill & =\sum _{\mathbf{k}\in {\mathbb{Z}}^n}⟨exp\left\{-\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t}\right)\right\}f,\psi \left(\mathbf{t}-\mathbf{k}\right)exp\left\{-\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}-{\mathbf{k}}^T{B}^{-1}A\mathbf{k}\right.\right..\hfill \\ \hfill & .\left.\left.+2{\mathbf{p}}^T{B}^{-1}\left(\mathbf{t}-\mathbf{k}\right)\right)\right\}⟩\varphi \left(\mathbf{t}-\mathbf{k}\right)exp\left\{-\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}-{\mathbf{k}}^T{B}^{-1}A\mathbf{k}+2{\mathbf{p}}^T{B}^{-1}\left(\mathbf{t}-\mathbf{k}\right)\right)\right\}\hfill \\ & ·exp\left\{\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t}\right)\right\}\hfill \\ \hfill & =\sum _{\mathbf{k}\in {\mathbb{Z}}^n}⟨exp\left\{-\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t}\right)\right\}f,{\psi }_{\mathbf{k}}⟩{\varphi }_{\mathbf{k}}\left(\mathbf{t}\right)exp\left\{\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t}\right)\right\}\hfill \\ \hfill & =exp\left\{\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t}\right)\right\}\mathrm{P}\left(exp\left\{-\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t}\right)\right\}f\right)\left(\mathbf{t}\right),\hfill \end{array}$$

which means that

$$\begin{array}{cc}\hfill & exp\left\{-\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t}\right)\right\}{\mathrm{P}}_{\mathrm{F}}f\left(\mathbf{t}\right)\hfill \\ & =\mathrm{P}\left(exp\left\{-\frac{j}{2}\left({\mathbf{t}}^T{B}^{-1}A\mathbf{t}+2{\mathbf{p}}^T{B}^{-1}\mathbf{t}\right)\right\}f\right)\left(\mathbf{t}\right).\hfill \end{array}$$

(74)

Therefore, the algorithm (72) can be rewritten as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{M}_S{g}_1=\mathrm{P}{M}_S{\mathrm{Q}}_{\mathrm{X}}{M}_S^{-1}f,\hfill \\ M_S{g}_{k+1}=\mathrm{P}{M}_S{\mathrm{Q}}_{\mathrm{X}}{M}_S^{-1}(f-M_S{g}_k)+M_S{g}_k.\hfill \end{array}\right.\end{array}$$

(75)

Let $f_k=M_S{g}_k.$ Then, (75) is equivalent to

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{f}_1=\mathrm{P}{M}_S{\mathrm{Q}}_{\mathrm{X}}{M}_S^{-1}f,\hfill \\ f_{k+1}=\mathrm{P}{M}_S{\mathrm{Q}}_{\mathrm{X}}{M}_S^{-1}(f-f_k)+f_k.\hfill \end{array}\right.\end{array}$$

(76)

Note that

$$\left|f-f_k\right|=\left|M_S(g-g_k)\right|=\left|g-g_k\right|.$$

Then, ${∥f-f_k∥}_{L^p\left({\mathbb{R}}^n\right)}={∥g-g_k∥}_{L^p\left({\mathbb{R}}^n\right)}$ and ${∥f-f_k∥}_{W\left(L^p\left({\mathbb{R}}^n\right)\right)}={∥g-g_k∥}_{W\left(L^p\left({\mathbb{R}}^n\right)\right)}$. Finally, the desired result follows from (73). □

Finally, we will give simulations to verify the proposed methods. Consider the matrix M, where the elements are $A=\left[\begin{array}{cc}\frac{1}{4}& 0\\ 0& \frac{1}{2}\end{array}\right]$, $B=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$, $C=\left[\begin{array}{cc}0& 0\\ 0& 0\end{array}\right]$, $D=\left[\begin{array}{cc}4& 0\\ 0& 2\end{array}\right]$, $\mathbf{p}=\left[\begin{array}{c}1\\ 0\end{array}\right]$, $\mathbf{q}=\left[\begin{array}{c}0\\ 1\end{array}\right]$ and a signal

$$f\left(\mathbf{t}\right)=sinc\left(t_1\right)sinc\left(t_2\right)exp\left\{-\frac{j}{2}\left(\frac{1}{4}{t}_1^2+2t_1\right)\right\}exp\left\{-\frac{j}{2}\left(\frac{1}{2}{t}_2^2+2t_2\right)\right\}$$

which is bandlimited in the multi-dimensional SAFT domain. Then, we use the proposed iterative algorithm (68) to reconstruct the signal f. The special affine spectrum of f, the sampled signal and the reconstructed signal are shown in Figure 1, Figure 2, Figure 3 and Figure 4.

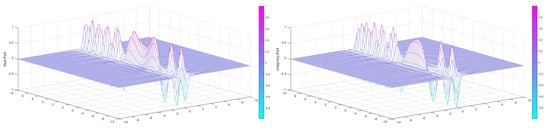
Figure 1. The real and imaginary parts of f.

Figure 2. The real and imaginary parts of the SAFT of f.

Figure 3. The real and imaginary parts after sampling f.

Figure 4. The real and imaginary parts of the reconstructed signal.