Ideals and Filters on Neutrosophic Topologies Generated by Neutrosophic Relations

Abstract

Recently, Milles and Hammami presented and studied the concept of a neutrosophic topology generated by a neutrosophic relation. As a continuation in the same direction, this paper studies the concepts of neutrosophic ideals and neutrosophic filters on that topology. More precisely, we offer the lattice structure of neutrosophic open sets of a neutrosophic topology generated via a neutrosophic relation and examine its different characteristics. Furthermore, we enlarge to this lattice structure the notions of ideals (respectively, filters) and characterize them with regard to the lattice operations. We end this work by studying the prime neutrosophic ideal and prime neutrosophic filter as interesting types of neutrosophic ideals and neutrosophic filters.

1. Introduction

The concept of neutrosophic sets was introduced by Smarandache [1] as a generalization of the concepts of fuzzy sets and intuitionistic fuzzy sets. The notion of a neutrosophic set is described by three degrees, truth membership function (T), indeterminacy membership function (I) and falsity membership function (F), in the non-standard unit interval, and it accomplished tremendous success in various areas of applications [2,3,4]. In particular, Wang et al. [5] presented the concept of a single-valued neutrosophic set as a subclass of the neutrosophic set which can be used in the field of scientific and engineering applications.

In the literature, there are many approaches to the concept of neutrosophic topological space. In [6], Smarandache presented neutrosophic topology on the non-standard interval. Later, Lupiáñez [7,8] proposed some notes about the relationship between Smarandache’s concept of neutrsophic topology and intuitionistic fuzzy topology. Others, such as Salama and Alblowi [9,10] studied neutrosophic topological spaces with various basic properties and characteristics. Recently, El-Gayyar [11] introduced the notion of smooth topological space in the setting of neutrosophic sets. For more details, see [12,13,14,15,16,17].

One of the essential tools in many branches of mathematics is the concepts of ideal and filter. For instance, ideals and filters appear in topology, boolean algebra, the extensive theory of representation of distributive lattices and in algebraic structures. In addition to their theoretical uses, ideals and filters are used in some branches of applied mathematics. In a neutrosophic setting, many researchers have examined and studied the neutrosophic ideals and neutrosophic filters in various frameworks and structures [18,19,20,21].

In this work, we apply Smarandache’s neutrosophic set to the notion of ideals and filters in a neutrosophic open-set lattice on neutrosophic topology generated by neutrosophic relation. We study its various properties and characterizations. We finally characterize them with regard to this lattice of meet and join operations.

The content of the present work is structured as follows. Section 2 provides an overview introduction to neutrosophic sets and relations. We recall the concept of a neutrosophic topology generated by a neutrosophic relation in Section 3, and then describe the lattice structure of neutrosophic open sets on a topology generated by a neutrosophic relation in Section 4. In Section 5, we establish the notions of neutrosophic ideals (respectively, neutrosophic filter) on the lattice of neutrosophic open sets, and some characterizations in terms of this lattice of meet and join operations and in terms of the corresponding level sets are given. In Section 6, we examine and characterize the notion of the prime neutrosophic ideal and prime neutrosophic filter as interesting types of neutrosophic ideals and neutrosophic filters. Section 7 concludes with some thoughts and suggestions for future works.

2. Preliminaries

This part contains some concepts and properties of neutrosophic sets and several related definitions that will be required throughout this work.

2.1. Neutrosophic Sets

The fuzzy set notion was defined by Zadeh [22].

Definition 1

([22]). Assume that $\mathcal{E}$ is a crisp set. A fuzzy set $\Omega =\{⟨\varsigma ,{\daleth }_{\Omega }\left(\varsigma \right)⟩\mid \varsigma \in \mathcal{E}$} is defined by a function of membership ${\daleth }_{\Omega }$ : $\mathcal{E}$$\to [0,1]$, with ${\daleth }_{\Omega }\left(\varsigma \right)$ as the degree of membership of an element ς in the fuzzy subset Ω for all $\varsigma \in \mathcal{E}$.

As a generalization of the idea of a fuzzy set, K, Atanassov proposed the intuitionistic fuzzy set in [23,24].

Definition 2

([23]). Assume that $\mathcal{E}$ is a classical set. An intuitionistic fuzzy set (IFS) Ω of $\mathcal{E}$ is an object of the model

$$\Omega =\{⟨\varsigma ,{\daleth }_{\Omega }\left(\varsigma \right),{\mathsf{Ϝ}}_{\Omega }\left(\varsigma \right)⟩\mid \varsigma \in \mathcal{E}\}$$

defined by a membership mapping ${\daleth }_{\Omega }:\mathcal{E}\to [0,1]$ and a non-membership mapping ${\mathsf{Ϝ}}_{\Omega }:\mathcal{E}\to [0,1]$, such that

$$0⩽{\daleth }_{\Omega }\left(\varsigma \right)+{\mathsf{Ϝ}}_{\Omega }\left(\varsigma \right)⩽1,for all\varsigma \in \mathcal{E}.$$

In [1], the author suggested the approach of a neutrosophic set as an extension of the approach of the IF-set. For an applied use of neutrosophic sets, the authors of [5] proposed a subclass of neutrosophic sets, which is the single-valued neutrosophic set (SVNS).

Definition 3

([1]). Assume that $\mathcal{E}$ is a classical set. A neutrosophic set (NS) Ω of $\mathcal{E}$ is an object of the model

$$\Omega =\{⟨\varsigma ,{\daleth }_{\Omega }\left(\varsigma \right),{\gimel }_{\Omega }\left(\varsigma \right),{\mathsf{Ϝ}}_{\Omega }\left(\varsigma \right)⟩\mid \varsigma \in \mathcal{E}\}$$

defined by a membership mapping ${\daleth }_{\Omega }$ from $\mathcal{E}$ to ${\mathcal{J}:=]}^{-}0,1^{+}[$ and an indeterminacy mapping ${\gimel }_{\Omega }$ from $\mathcal{E}$ to $\mathcal{J}$. Also, it is a non-membership mapping ${\mathsf{Ϝ}}_{\Omega }$ from $\mathcal{E}$ to $\mathcal{J}$ such that

$${ }^{-}0⩽{\daleth }_{\Omega }\left(\varsigma \right)+{\gimel }_{\Omega }\left(\varsigma \right)+{\mathsf{Ϝ}}_{\Omega }\left(\varsigma \right)⩽3^{+},for all\varsigma \in \mathcal{E}.$$

Remark 1. 

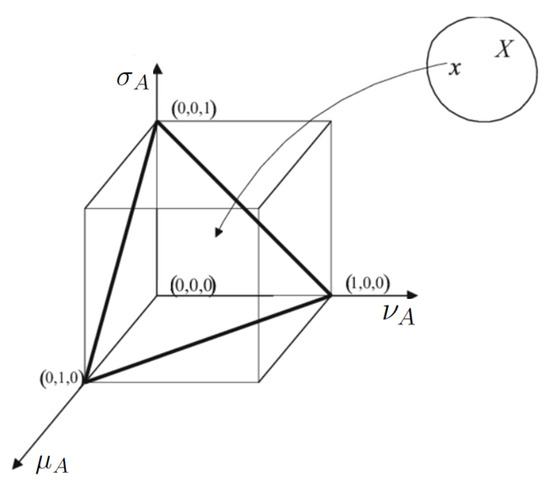
In the literature of neutrosophic logic, different notations are used to represent the functions introduced earlier. The most widely used symbols are μ (membership function), σ (indeterminacy function) and ν (non-membership function). See Figure 1.

Figure 1. Representation of a neutrosophic set.

Definition 4

([5]). Assume that $\mathcal{E}$ is a classical set. Define a single-valued neutrosophic set (SVNS) Ω of $\mathcal{E}$ as an object of the model

$$\Omega =\{⟨\varsigma ,{\daleth }_{\Omega }\left(\varsigma \right),{\gimel }_{\Omega }\left(\varsigma \right),{\mathsf{Ϝ}}_{\Omega }\left(\varsigma \right)⟩\mid \varsigma \in \mathcal{E}\}$$

defined by a truth membership mapping ${\daleth }_{\Omega }:\mathcal{E}\to [0,1]$, an indeterminacy membership mapping ${\gimel }_{\Omega }:\mathcal{E}\to [0,1]$ and a falsity membership mapping ${\mathsf{Ϝ}}_{\Omega }:\mathcal{E}\to [0,1].$

Obviously, IF-set is a neutrosophic set by setting ${\gimel }_{\Omega }\left(\varsigma \right)=1-{\daleth }_{\Omega }\left(\varsigma \right)-{\mathsf{Ϝ}}_{\Omega }\left(\varsigma \right)$. The family of all neutrosophic sets of the set $\mathcal{E}$ is indicated by $NS\left(\mathcal{E}\right)$.

For every two neutrosophic sets $\Omega$ and $\Delta$ of $\mathcal{E}$, many operations are defined (see, e.g., [5,25,26,27,28,29]). Only those relevant to the current work are presented below:

(i)

$\Omega \subseteq \Delta \mathrm{if}{\daleth }_{\Omega }\left(\varsigma \right)⩽{\daleth }_{\Delta }\left(\varsigma \right)\mathrm{and}{\gimel }_{\Omega }\left(\varsigma \right)⩽{\gimel }_{\Delta }\left(\varsigma \right)\mathrm{and}{\mathsf{Ϝ}}_{\Omega }\left(\varsigma \right)⩾{\mathsf{Ϝ}}_{\Delta }\left(\varsigma \right),\mathrm{for}\mathrm{all}\varsigma \in \mathcal{E};$

(ii)

$\Omega =\Delta \mathrm{if}{\daleth }_{\Omega }\left(\varsigma \right)={\daleth }_{\Delta }\left(\varsigma \right)\mathrm{and}{\gimel }_{\Omega }\left(\varsigma \right)={\gimel }_{\Delta }\left(\varsigma \right)\mathrm{and}{\mathsf{Ϝ}}_{\Omega }\left(\varsigma \right)={\mathsf{Ϝ}}_{\Delta }\left(\varsigma \right),\mathrm{for}\mathrm{all}\varsigma \in \mathcal{E};$

(iii)

$\Omega \cap \Delta =\{⟨\varsigma ,{\daleth }_{\Omega }\left(\varsigma \right)⋏{\daleth }_{\Delta }\left(\varsigma \right),{\gimel }_{\Omega }\left(\varsigma \right)⋏{\gimel }_{\Delta }\left(\varsigma \right),{\mathsf{Ϝ}}_{\Omega }\left(\varsigma \right)⋎{\mathsf{Ϝ}}_{\Delta }\left(\varsigma \right)⟩\mid \varsigma \in \mathcal{E}\};$

(iv)

$\Omega \cup \Delta =\{⟨\varsigma ,{\daleth }_{\Omega }\left(\varsigma \right)⋎{\daleth }_{\Delta }\left(\varsigma \right),{\gimel }_{\Omega }\left(\varsigma \right)⋎{\gimel }_{\Delta }\left(\varsigma \right),{\mathsf{Ϝ}}_{\Omega }\left(\varsigma \right)⋏{\mathsf{Ϝ}}_{\Delta }\left(\varsigma \right)⟩\mid \varsigma \in \mathcal{E}\};$

(v)

$\overline{\Omega }=\{⟨\varsigma ,{\mathsf{Ϝ}}_{\Omega }\left(\varsigma \right),{\gimel }_{\Omega }\left(\varsigma \right),{\daleth }_{\Omega }\left(\varsigma \right)⟩\mid \varsigma \in \mathcal{E}\};$

(vi)

$[\Omega ]=\{⟨\varsigma ,{\daleth }_{\Omega }\left(\varsigma \right),{\gimel }_{\Omega }\left(\varsigma \right),1-{\daleth }_{\Omega }\left(\varsigma \right)⟩\mid \varsigma \in \mathcal{E}\};$

(vii)

$⟨\Omega ⟩=\{⟨\varsigma ,1-{\mathsf{Ϝ}}_{\Omega }\left(\varsigma \right),{\gimel }_{\Omega }\left(\varsigma \right),{\mathsf{Ϝ}}_{\Omega }\left(\varsigma \right)⟩\mid \varsigma \in \mathcal{E}\}.$

Additionally, we need the following concept of $(\alpha ,\beta ,\gamma )$-cuts (which is also called “level sets”) of a neutrosophic set.

Definition 5.

Assume that Ω is a neutrosophic set of $\mathcal{E}$. The $(\alpha ,\beta ,\gamma )$-cut of Ω is a classical subset

$${\Omega }_{\alpha ,\beta ,\gamma }=\{\varsigma \in \mathcal{E}\mid {\daleth }_{\Omega }\left(\varsigma \right)⩾\alpha and{\gimel }_{\Omega }\left(\varsigma \right)⩾\beta and{\mathsf{Ϝ}}_{\Omega }\left(\varsigma \right)⩽\gamma \},$$

for some $0<\alpha ,\beta ,\gamma \le 1$.

Definition 6.

Assume that Ω is a neutrosophic set of $\mathcal{E}$. The support of Ω is the classical subset of $\mathcal{E}$, given by

$$\mathcal{S}(\Omega ):=\{\varsigma \in \mathcal{E}\mid {\daleth }_{\Omega }\left(\varsigma \right)\ne 0and{\gimel }_{\Omega }\left(\varsigma \right)\ne 0and{\mathsf{Ϝ}}_{\Omega }\left(\varsigma \right)\ne 0\}.$$

2.2. Neutrosophic Relations

In [30], the authors proposed the approach of neutrosophic relation as a generalization of fuzzy and IF-relation.

Definition 7

([30]). A neutrosophic binary relation (or, a neutrosophic relation, for short) from a set $\mathcal{E}$ to a set $\mathcal{Z}$ is a neutrosophic subset of $\mathcal{E}\times \mathcal{Z}$, i.e., it is an expression $\mathcal{N}$ expressed by

$$\mathcal{N}=\{⟨(\varsigma ,\sigma ),{\daleth }_{\mathcal{N}}(\varsigma ,\sigma ),{\gimel }_{\mathcal{N}}(\varsigma ,\sigma ),{\mathsf{Ϝ}}_{\mathcal{N}}(\varsigma ,\sigma )⟩\mid (\varsigma ,\sigma )\in \mathcal{E}\times \mathcal{Z}\},$$

where ${\daleth }_{\mathcal{N}}:\mathcal{E}\times \mathcal{Z}\to [0,1],and{\gimel }_{\mathcal{N}}:\mathcal{E}\times \mathcal{Z}\to [0,1]and{\mathsf{Ϝ}}_{\Omega }:\mathcal{E}\times \mathcal{Z}\to [0,1]$.

For any $(\varsigma ,\sigma )\in \mathcal{E}\times \mathcal{Z}$, the value ${\daleth }_{\mathcal{N}}(\varsigma ,\sigma )$ is named the degree of a membership of $(\varsigma ,\sigma )$ in $\mathcal{N}$; ${\gimel }_{\mathcal{N}}(\varsigma ,\sigma )$ is named the degree of indeterminacy of $(\varsigma ,\sigma )$ in $\mathcal{N}$; and ${\mathsf{Ϝ}}_{\mathcal{N}}(\varsigma ,\sigma )$ is said to be the degree of non-membership of $(\varsigma ,\sigma )$ in $\mathcal{N}$.

Example 1. 

Suppose $\mathcal{E}=\{{\rho }_1,{\rho }_2,{\rho }_3,{\rho }_4,{\rho }_5\}$. Then, the neutrosophic relation $\mathcal{N}$ of $\mathcal{E}$ is given by

$$\mathcal{N}=\{⟨(\varsigma ,\sigma ),{\daleth }_{\mathcal{N}}(\varsigma ,\sigma ),{\gimel }_{\mathcal{N}}(\varsigma ,\sigma ),{\mathsf{Ϝ}}_{\mathcal{N}}(\varsigma ,\sigma )⟩\mid \varsigma ,\sigma \in \mathcal{E}\},$$

such that ${\daleth }_{\mathcal{N}},{\gimel }_{\mathcal{N}}$ and ${\mathsf{Ϝ}}_{\mathcal{N}}$ are given by the following tables.

${\daleth }_{\mathbf{R}}(.,.)$	${\mathit{\rho }}_{\mathbf{1}}$	${\mathit{\rho }}_{\mathbf{2}}$	${\mathit{\rho }}_{\mathbf{3}}$	${\mathit{\rho }}_{\mathbf{4}}$	${\mathit{\rho }}_{\mathbf{5}}$
${\rho }_1$	$3.5\times {10}^{-1}$	0	0	$3.5\times {10}^{-1}$	$3\times {10}^{-1}$
${\rho }_2$	0	$4\times {10}^{-1}$	0	$3.5\times {10}^{-1}$	$4.5\times {10}^{-1}$
${\rho }_3$	$2\times {10}^{-1}$	0	$6.5\times {10}^{-1}$	0	$7\times {10}^{-1}$
${\rho }_4$	0	0	0	1	0
${\rho }_5$	$2.5\times {10}^{-1}$	$3.5\times {10}^{-1}$	0	0	$6\times {10}^{-1}$

${\gimel }_{\mathbf{R}}(.,.)$	${\mathit{\rho }}_{\mathbf{1}}$	${\mathit{\rho }}_{\mathbf{2}}$	${\mathit{\rho }}_{\mathbf{3}}$	${\mathit{\rho }}_{\mathbf{4}}$	${\mathit{\rho }}_{\mathbf{5}}$
${\rho }_1$	$5\times {10}^{-1}$	$5\times {10}^{-1}$	$4.2\times {10}^{-1}$	$2\times {10}^{-1}$	0
${\rho }_2$	$6\times {10}^{-1}$	$1.2\times {10}^{-1}$	$4\times {10}^{-1}$	$8\times {10}^{-1}$	$1\times {10}^{-1}$
${\rho }_3$	0	1	$2\times {10}^{-2}$	$7.5\times {10}^{-1}$	$1.5\times {10}^{-1}$
${\rho }_4$	$3.3\times {10}^{-1}$	1	$8.8\times {10}^{-1}$	0	$1\times {10}^{-1}$
${\rho }_5$	$2\times {10}^{-1}$	$5.5\times {10}^{-1}$	1	$5.5\times {10}^{-1}$	$3\times {10}^{-1}$

${\mathsf{Ϝ}}_{\mathbf{R}}(.,.)$	${\mathit{\rho }}_{\mathbf{1}}$	${\mathit{\rho }}_{\mathbf{2}}$	${\mathit{\rho }}_{\mathbf{3}}$	${\mathit{\rho }}_{\mathbf{4}}$	${\mathit{\rho }}_{\mathbf{5}}$
${\rho }_1$	0	1	$4\times {10}^{-1}$	$2.5\times {10}^{-1}$	$2.5\times {10}^{-1}$
${\rho }_2$	$3\times {10}^{-1}$	$3.5\times {10}^{-1}$	$2\times {10}^{-1}$	$3.5\times {10}^{-1}$	$1\times {10}^{-1}$
${\rho }_3$	$8\times {10}^{-1}$	1	0	$8.5\times {10}^{-1}$	$1.5\times {10}^{-1}$
${\rho }_4$	1	1	1	0	1
${\rho }_5$	$7\times {10}^{-1}$	$5.5\times {10}^{-1}$	1	$9\times {10}^{-1}$	$3\times {10}^{-1}$

Next, the following notions need to be recalled.

Definition 8 

([31]). Let $\mathcal{N}$ and $\mathcal{M}$ be two neutrosophic relations from a set $\mathcal{E}$ to a set $\mathcal{Z}$.

(i) 

The transposea (inverse) ${\mathcal{N}}^t$ of $\mathcal{N}$ is the neutrosophic relation from the universe $\mathcal{Z}$ to the universe $\mathcal{E}$ defined by

$${\mathcal{N}}^t=\{⟨(\varsigma ,\sigma ),{\daleth }_{{\mathcal{N}}^t}(\varsigma ,\sigma ),{\gimel }_{{\mathcal{N}}^t}(\varsigma ,\sigma ),{\mathsf{Ϝ}}_{{\mathcal{N}}^t}(\varsigma ,\sigma )⟩\mid (\varsigma ,\sigma )\in \mathcal{E}\times \mathcal{Z}\},$$

where

$$\left\{\begin{array}{cc}\hfill {\daleth }_{{\mathcal{N}}^t}(\varsigma ,\sigma )=& {\daleth }_{\mathcal{N}}(\sigma ,\varsigma )\\ \hfill \mathrm{and}& \\ \hfill {\gimel }_{{\mathcal{N}}^t}(\varsigma ,\sigma )=& {\gimel }_{\mathcal{N}}(\sigma ,\varsigma )\\ \hfill \mathrm{and}& \\ \hfill {\mathsf{Ϝ}}_{{\mathcal{N}}^t}(\varsigma ,\sigma )=& {\mathsf{Ϝ}}_{\mathcal{N}}(\sigma ,\varsigma )\end{array}\right.$$

for every $(\varsigma ,\sigma )\in \mathcal{E}\times \mathcal{Z}.$

(ii) 

$\mathcal{N}$ is said to be contained in $\mathcal{M}$ (or we say that $\mathcal{M}$ contains $\mathcal{N}$) and is indicated by $\mathcal{N}\subseteq \mathcal{M}$; if for all $(\varsigma ,\sigma )\in \mathcal{E}\times \mathcal{Z}$, it holds that

$${\daleth }_{\mathcal{N}}(\varsigma ,\sigma )⩽{\daleth }_{\mathcal{M}}(\varsigma ,\sigma ),{\gimel }_{\mathcal{N}}(\varsigma ,\sigma )⩽{\gimel }_{\mathcal{M}}(\varsigma ,\sigma )and{\mathsf{Ϝ}}_{\mathcal{N}}(\varsigma ,\sigma )⩾{\mathsf{Ϝ}}_{\mathcal{M}}(\varsigma ,\sigma ).$$

(iii) 

The intersection (respectively, the union) of two neutrosophic relations $\mathcal{N}$ and $\mathcal{M}$ from a universe $\mathcal{E}$ to a universe $\mathcal{Z}$ is a neutrosophic relation defined as

$$\begin{array}{cc}\hfill \mathcal{N}\cap \mathcal{M}=& \{⟨(\varsigma ,\sigma ),min({\daleth }_{\mathcal{N}}(\varsigma ,\sigma ),{\daleth }_{\mathcal{M}}(\varsigma ,\sigma )),min({\gimel }_{\mathcal{N}}(\varsigma ,\sigma ),{\gimel }_{\mathcal{M}}(\varsigma ,\sigma )),\hfill \\ \hfill & max({\mathsf{Ϝ}}_{\mathcal{N}}(\varsigma ,\sigma ),{\mathsf{Ϝ}}_{\mathcal{M}}(\varsigma ,\sigma ))⟩\mid (\varsigma ,\sigma )\in \mathcal{E}\times \mathcal{Z}\}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \mathcal{N}\cup \mathcal{M}=& \{⟨(\varsigma ,\sigma ),max({\daleth }_{\mathcal{N}}(\varsigma ,\sigma ),{\daleth }_{\mathcal{M}}(\varsigma ,\sigma ))max({\gimel }_{\mathcal{N}}(\varsigma ,\sigma ),{\gimel }_{\mathcal{M}}(\varsigma ,\sigma )),\hfill \\ & min({\mathsf{Ϝ}}_{\mathcal{N}}(\varsigma ,\sigma ),{\mathsf{Ϝ}}_{\mathcal{M}}(\varsigma ,\sigma ))⟩\mid (\varsigma ,\sigma )\in \mathcal{E}\times \mathcal{Z}\}.\hfill \end{array}$$

Definition 9 

([31]). Let $\mathcal{N}$ be a neutrosophic relation from a set $\mathcal{E}$ into itself.

(i) 

Reflexivity: ${\daleth }_{\mathcal{N}}(\varsigma ,\varsigma )={\gimel }_{\mathcal{N}}(\varsigma ,\varsigma )=1and{\mathsf{Ϝ}}_{\mathcal{N}}(\varsigma ,\varsigma )=0$, for all $\varsigma \in \mathcal{E}$.

(ii) 

Symmetry: for all $\varsigma ,\sigma \in \mathcal{E}$, then

$$\left\{\begin{array}{c}\hfill {\daleth }_{\mathcal{N}}(\varsigma ,\sigma )={\daleth }_{\mathcal{N}}(\sigma ,\varsigma )\\ \hfill {\gimel }_{\mathcal{N}}(\varsigma ,\sigma )={\gimel }_{\mathcal{N}}(\sigma ,\varsigma )\\ \hfill {\mathsf{Ϝ}}_{\mathcal{N}}(\varsigma ,\sigma )={\mathsf{Ϝ}}_{\mathcal{N}}(\sigma ,\varsigma )\end{array}.\right.$$

(iii) 

Antisymmetry: for all $\varsigma ,\sigma \in \mathcal{E}$, $\varsigma \ne \sigma$, then

$$\left\{\begin{array}{c}\hfill {\daleth }_{\mathcal{N}}(\varsigma ,\sigma )\ne {\daleth }_{\mathcal{N}}(\sigma ,\varsigma )\\ \hfill {\gimel }_{\mathcal{N}}(\varsigma ,\sigma )\ne {\gimel }_{\mathcal{N}}(\sigma ,\varsigma )\\ \hfill {\mathsf{Ϝ}}_{\mathcal{N}}(\varsigma ,\sigma )\ne {\mathsf{Ϝ}}_{\mathcal{N}}(\sigma ,\varsigma )\end{array}.\right.$$

(iv) 

Transitivity: $\mathcal{N}\circ \mathcal{N}\subset \mathcal{N}$, i.e., ${\mathcal{N}}^2\subset \mathcal{N}$.

3. Neutrosophic Topology Generated by Neutrosophic Relation

In this part, we will recall the concept of topology generated by relation in a neutrosophic setting [32] as an extension of the fuzzy topology generated by the fuzzy relation given in [33]. Moreover, several properties of this structure are investigated.

Definition 10. 

Let $\mathcal{E}$ be a universe and $\mathcal{N}=\{⟨(\varsigma ,\sigma ),{\daleth }_{\mathcal{N}}(\varsigma ,\sigma ),{\gimel }_{\mathcal{N}}(\varsigma ,\sigma ),{\mathsf{Ϝ}}_{\mathcal{N}}(\varsigma ,\sigma )⟩\mid \varsigma ,\sigma \in \mathcal{E}\}$ be a neutrosophic relation of $\mathcal{E}$. Then, for all $\varsigma \in \mathcal{E}$, the neutrosophic sets ${\mathcal{L}}_{\varsigma }$ and ${\mathcal{R}}_{\varsigma }$ are defined by

$${\daleth }_{{\mathcal{L}}_{\varsigma }}\left(\sigma \right)={\daleth }_{\mathcal{N}}(\sigma ,\varsigma ),{\gimel }_{{\mathcal{L}}_{\varsigma }}\left(\sigma \right)={\gimel }_{\mathcal{N}}(\sigma ,\varsigma ) and {\mathsf{Ϝ}}_{{\mathcal{L}}_{\varsigma }}\left(\sigma \right)={\mathsf{Ϝ}}_{\mathcal{N}}(\sigma ,\varsigma ), for every \sigma \in \mathcal{E};$$

$${\daleth }_{{\mathcal{R}}_{\varsigma }}\left(\sigma \right)={\daleth }_{\mathcal{N}}(\varsigma ,\sigma ),{\gimel }_{{\mathcal{R}}_{\varsigma }}\left(\sigma \right)={\gimel }_{\mathcal{N}}(\varsigma ,\sigma ) and {\mathsf{Ϝ}}_{{\mathcal{R}}_{\varsigma }}\left(\sigma \right)={\mathsf{Ϝ}}_{\mathcal{N}}(\varsigma ,\sigma ), for every \sigma \in \mathcal{E};$$

they are named, respectively, the lower and the upper contours of ς.

We symbolize the neutrosophic topology generated by the family of all lower contours with ${\tau }_1$, and the neutrosophic topology generated by the family of all upper contours with ${\tau }_2$. Therefore, we symbolize the neutrosophic topology generated by S, the family of all lower and upper contours, with ${\tau }_{\mathcal{N}}$, and it is named the neutrosophic topology generated by $\mathcal{N}$.

Remark 2. 

Since the neutrosophic set ${\mathcal{L}}_{\varsigma }$ (respectively, ${\mathcal{R}}_{\varsigma }$) is defined from the neutrosophic relation $\mathcal{N}$, then, in that case

$$0⩽{\daleth }_{{\mathcal{L}}_{\varsigma }}+{\gimel }_{{\mathcal{L}}_{\varsigma }}+{\mathsf{Ϝ}}_{{\mathcal{L}}_{\varsigma }}⩽3,$$

respectively,

$$0⩽{\daleth }_{{\mathcal{R}}_{\varsigma }}+{\gimel }_{{\mathcal{R}}_{\varsigma }}+{\mathsf{Ϝ}}_{{\mathcal{R}}_{\varsigma }}⩽3,$$

for all $\varsigma \in \mathcal{E}$.

Example 2. 

Suppose $\mathcal{E}=\{\varsigma ,\sigma \}$ and $\mathcal{N}$ is a neutrosophic relation of $\mathcal{E}$, given by

${\mathbf{\daleth }}_{\mathcal{N}}(.,.)$	$\mathbf{\varsigma }$	$\mathbf{\sigma }$
$\varsigma$	0.6	0.8
$\sigma$	0.3	0.7

${\mathbf{\gimel }}_{\mathcal{N}}(.,.)$	$\mathbf{\varsigma }$	$\mathbf{\sigma }$
$\varsigma$	0.3	0.1
$\sigma$	0.6	0.2

${\mathsf{Ϝ}}_{\mathcal{N}}(.,.)$	$\mathbf{\varsigma }$	$\mathbf{\sigma }$
$\varsigma$	0.3	0.1
$\sigma$	0.6	0.2

So, ${\mathcal{L}}_{\varsigma },{\mathcal{L}}_{\sigma },{\mathcal{R}}_{\varsigma }$ and ${\mathcal{R}}_{\sigma }$ are the neutrosophic sets of $\mathcal{E}$ given by the following values:

$$\begin{array}{ccc}\hfill {\mathcal{L}}_{\varsigma }& =& \{⟨\varsigma ,0.6,0.3,0.3⟩;⟨\sigma ,0.3,0.6,0.6⟩\};\hfill \\ \hfill {\mathcal{L}}_{\sigma }& =& \{⟨\varsigma ,0.8,0.1,0.1⟩;⟨\sigma ,0.7,0.2,0.2⟩\};\hfill \\ \hfill {\mathcal{R}}_{\varsigma }& =& \{⟨\varsigma ,0.6,0.3,0.3⟩;⟨\sigma ,0.8,0.1,0.1⟩\};\hfill \\ \hfill {\mathcal{R}}_{\sigma }& =& \{⟨\varsigma ,0.3,0.6,0.6⟩;⟨\sigma ,0.7,0.2,0.2⟩\}.\hfill \end{array}$$

Note that

$${\mathcal{L}}_{\varsigma }\subset {\mathcal{L}}_{\sigma },{\mathcal{L}}_{\varsigma }\subset {\mathcal{R}}_{\sigma },{\mathcal{R}}_{\sigma }\subset {\mathcal{R}}_{\varsigma }and{\mathcal{R}}_{\sigma }\subset {\mathcal{L}}_{\sigma }.$$

Then, the neutrosophic topology ${\tau }_{\mathcal{R}}$ is generated by

$$S=\{{\mathcal{L}}_{\varsigma },{\mathcal{L}}_{\sigma }\}\cup \{{\mathcal{R}}_{\varsigma },{\mathcal{R}}_{\sigma }\}.$$

Hence,

$${\tau }_{\mathcal{R}}=\{\varnothing ,\mathcal{E},{\mathcal{L}}_{\varsigma },{\mathcal{L}}_{\sigma },{\mathcal{R}}_{\varsigma },{\mathcal{R}}_{\sigma },{\mathcal{L}}_{\varsigma }\cap {\mathcal{R}}_{\sigma },{\mathcal{L}}_{\sigma }\cap {\mathcal{R}}_{\varsigma },{\mathcal{L}}_{\varsigma }\cup {\mathcal{R}}_{\sigma },{\mathcal{L}}_{\sigma }\cup R_{\varsigma }\}.$$

Proposition 1. 

Assume that $\mathcal{E}$ is a classical set and $\mathcal{N}$ is a neutrosophic symmetric relation of $\mathcal{E}$. Then, it holds that ${\tau }_1={\tau }_2$.

Proof. 

Assume that $\mathcal{N}$ is a neutrosophic symmetric relation of $\mathcal{E}$; so for every $\varsigma ,\sigma \in \mathcal{E}$, it holds that

$${\daleth }_{\mathcal{N}}(\varsigma ,\sigma )={\daleth }_{\mathcal{N}}(\sigma ,\varsigma ),{\gimel }_{\mathcal{N}}(\varsigma ,\sigma )={\gimel }_{\mathcal{N}}(\sigma ,\varsigma )\mathrm{and}{\mathsf{Ϝ}}_{\mathcal{N}}(\varsigma ,\sigma )={\mathsf{Ϝ}}_{\mathcal{N}}(\sigma ,\varsigma ).$$

Then, in such a case,

$${\daleth }_{{\mathcal{L}}_{\varsigma }}\left(\sigma \right)={\daleth }_{{\mathcal{R}}_{\varsigma }}\left(\sigma \right),{\gimel }_{{\mathcal{L}}_{\varsigma }}\left(\sigma \right)={\gimel }_{{\mathcal{R}}_{\varsigma }}\left(\sigma \right)\mathrm{and}{\mathsf{Ϝ}}_{{\mathcal{L}}_{\varsigma }}\left(\sigma \right)={\mathsf{Ϝ}}_{{\mathcal{R}}_{\varsigma }}\left(\sigma \right).$$

Therefore, ${\mathcal{L}}_{\varsigma }={\mathcal{R}}_{\varsigma }$, for all $\varsigma \in \mathcal{E}$. We can determine that ${\tau }_1={\tau }_2$. □

Remark 3. 

If $\mathcal{N}$ is a neutrosophic preorder relation, then the neutrosophic topology generated by $\mathcal{N}$ is a generalization of the Alexandrov topology introduced in [34].

4. The Lattice of Neutrosophic Open Sets on a Topology Generated by a Neutrosophic Relation

The purpose of this part is to study the lattice structure of neutrosophic open sets on a topology generated by a neutrosophic relation. First, we introduce the notion of neutrosophic intersection and union between neutrosophic open sets.

Definition 11. 

Let ${\tau }_{\mathcal{N}}$ be the neutrosophic topology of the set $\mathcal{E}$ generated by the relation $\mathcal{N}$ and let ${\mathcal{W}}_1$ and ${\mathcal{W}}_2$ be two neutrosophic open sets of ${\tau }_{\mathcal{N}}$. The intersection of ${\mathcal{W}}_1$ and ${\mathcal{W}}_2$ (in symbols, ${\mathcal{W}}_1⋒{\mathcal{W}}_2$) is a neutrosophic open set V such that

$$\begin{array}{cc}\hfill {\daleth }_V\left({\varsigma }_i\right)=& min({\daleth }_{{\mathcal{W}}_1}\left({\varsigma }_i\right),{\daleth }_{{\mathcal{W}}_2}\left({\varsigma }_i\right)),\hfill \\ \hfill {\gimel }_V\left({\varsigma }_i\right)=& min({\gimel }_{{\mathcal{W}}_1}\left({\varsigma }_i\right),{\gimel }_{{\mathcal{W}}_2}\left({\varsigma }_i\right)),\hfill \\ \hfill {\mathsf{Ϝ}}_V\left({\varsigma }_i\right)=& max({\mathsf{Ϝ}}_{{\mathcal{W}}_1}\left({\varsigma }_i\right),{\mathsf{Ϝ}}_{{\mathcal{W}}_2}\left({\varsigma }_i\right))\hfill \end{array}$$

for all $x_i\in \mathcal{E}$. Furthermore, $\underset{i\in I}{⋒}{\mathcal{W}}_i$ is the neutrosophic open set of $\mathcal{E}$ containing all ${\mathcal{W}}_i$.

Definition 12. 

Let ${\tau }_{\mathcal{N}}$ be the neutrosophic topology of the set $\mathcal{E}$ generated by the relation $\mathcal{N}$ and let ${\mathcal{W}}_1$ and ${\mathcal{W}}_2$ be two neutrosophic open sets of ${\tau }_{\mathcal{N}}$. The union of ${\mathcal{W}}_1$ and ${\mathcal{W}}_2$ (in symbols, ${\mathcal{W}}_1⋓{\mathcal{W}}_2$) is a neutrosophic open set V such that

$$\begin{array}{cc}\hfill {\daleth }_V\left({\varsigma }_i\right)=& max({\daleth }_{{\mathcal{W}}_1}\left({\varsigma }_i\right),{\daleth }_{{\mathcal{W}}_2}\left({\varsigma }_i\right)),\hfill \\ \hfill {\gimel }_V\left({\varsigma }_i\right)=& max({\gimel }_{{\mathcal{W}}_1}\left({\varsigma }_i\right),{\gimel }_{{\mathcal{W}}_2}\left({\varsigma }_i\right)),\hfill \\ \hfill {\mathsf{Ϝ}}_V\left({\varsigma }_i\right)=& min({\mathsf{Ϝ}}_{{\mathcal{W}}_1}\left({\varsigma }_i\right),{\mathsf{Ϝ}}_{{\mathcal{W}}_2}\left({\varsigma }_i\right))\hfill \end{array}$$

for all ${\varsigma }_i\in \mathcal{E}.$ Furthermore, $\underset{i\in I}{⋓}{\mathcal{W}}_i$ is a greater neutrosophic open set of $\mathcal{E}$ containing all ${\mathcal{W}}_i$.

In the following theorem, we provide the lattice of neutrosophic open sets of a neutrosophic topology generated by neutrosophic relation.

Theorem 1. 

Let $\mathcal{E}$ be a universe, $\mathcal{N}$ be a neutrosophic relation of $\mathcal{E}$ and ${\tau }_{\mathcal{N}}$ be a neutrosophic topology generated by $\mathcal{N}$. Then, the family

$$\mathfrak{L}=\{{\mathcal{W}}_i\mid {\mathcal{W}}_{i}is a neutrosophic open set on{\tau }_{\mathcal{N}}\}$$

is a lattice.

Proof. 

Assume that $\left\{{\mathcal{W}}_i\right\}$ is a set of neutrosophic open sets of ${\tau }_{\mathcal{N}}$. Definition of neutrosophic topology guarantees that $\left\{{\mathcal{W}}_i\right\}$ is a non-empty set.

Now, let ${\mathcal{W}}_1$ and ${\mathcal{W}}_2$ be two neutrosophic open sets. It is easy to check that ${\mathcal{W}}_1⋐{\mathcal{W}}_1$, i.e., the neutrosophic reflexivity, and if we assume that ${\mathcal{W}}_1⋐{\mathcal{W}}_2$ and ${\mathcal{W}}_2⋐{\mathcal{W}}_1$, in which case, ${\mathcal{W}}_1={\mathcal{W}}_2$, i.e., the neutrosophic antisymmetry.

To verify the neutrosophic transitivity, we assume that ${\mathcal{W}}_1⋐{\mathcal{W}}_2$ and ${\mathcal{W}}_2⋐{\mathcal{W}}_3$, in which case ${\mathcal{W}}_1⋐{\mathcal{W}}_3$, i.e., the neutrosophic transitivity. Hence, $(\mathfrak{L},⋐)$ is a neutrosophic poset of $\mathcal{E}$. Also, the leastaupper bound (respectively, the greatest lower bound) of ${\mathcal{W}}_1$ and ${\mathcal{W}}_2$ coincides with the intersection of neutrosophic open sets (respectively, the union of neutrosophic open sets), i.e.,

$${\mathcal{W}}_1⋏{\mathcal{W}}_2={\mathcal{W}}_1⋒{\mathcal{W}}_2,(\mathrm{resp}.{\mathcal{W}}_1⋎{\mathcal{W}}_2={\mathcal{W}}_1⋓{\mathcal{W}}_2).$$

Then, we can determine that $(\mathfrak{L},⋐)$ is a lattice of $\mathcal{E}.$ □

Hence, $(\mathfrak{L},⋐)$ is a neutrosophic poset of $\mathcal{E}$. Also, the greatestalower bound (respectively, the leastaupper bound) of ${\mathcal{W}}_1$ and ${\mathcal{W}}_2$ coincides with the union of neutrosophic open sets (respectively, the intersection of neutrosophic open sets), i.e.,

$$(\mathrm{resp}.{\mathcal{W}}_1⋎{\mathcal{W}}_2={\mathcal{W}}_1⋓{\mathcal{W}}_2),{\mathcal{W}}_1⋏{\mathcal{W}}_2={\mathcal{W}}_1⋒{\mathcal{W}}_2.$$

Example 3. 

Let $\mathcal{E}=\{\varsigma ,\sigma \}$ and $\mathcal{N}$ be a neutrosophic relation of $\mathcal{E}$ given by the following:

${\mathbf{\daleth }}_{\mathcal{N}}(.,.)$	$\mathbf{\varsigma }$	$\mathbf{\sigma }$
$\varsigma$	0.6	0.8
$\sigma$	0.3	0.7

${\mathbf{\gimel }}_{\mathcal{N}}(.,.)$	$\mathbf{\varsigma }$	$\mathbf{\sigma }$
$\varsigma$	0.3	0.1
$\sigma$	0.6	0.2

${\mathsf{Ϝ}}_{\mathcal{N}}(.,.)$	$\mathbf{\varsigma }$	$\mathbf{\sigma }$
$\varsigma$	0.3	0.1
$\sigma$	0.6	0.2

Consider the neutrosophic topology ${\tau }_{\mathcal{N}}$ of Example 2. Then, $\mathfrak{L}=\{{\mathcal{W}}_i\mid {\mathcal{W}}_{i}is a neutrosophic$ open set and ${\tau }_{\mathcal{N}}\}$ is a lattice.

Remark 4. 

To avoid the confusion, we will use the symbols $(⋐,⋓,⋒)$ to refer to the order, max, and min on the lattice structure $\mathfrak{L}$ and $(⩽,⋎,⋏)$ to refer toathe usual order, max, and min on the unit interval $[0,1]$.

Proposition 2. 

Let $\mathcal{E}$ be a finite universe and $\mathfrak{L}=\left\{{\mathcal{W}}_i\right\}$ is the lattice structure of all neutrosophic open sets on topology ${\tau }_{\mathcal{N}}$ generated by neutrosophic relation $\mathcal{N}$. Then, $\mathfrak{L}$ is complete.

Proof. 

Let $\mathfrak{L}=\left\{{\mathcal{W}}_i\right\}$ be the lattice of neutrosophic open sets on neutrosophic topology ${\tau }_R$ generated by the neutrosophic relation $\mathcal{N}$. Let $\Omega =\left\{{\mathcal{W}}_j\right\}$ be a subset of $\mathfrak{L}$ under the neutrosophic inclusion between the neutrosophic open sets defined above. Since $\mathfrak{L}$ is a finite lattice, then $⋒U_j\in \mathfrak{L}$, which shows that $\Omega$ has anainfimum. Thus, $\mathfrak{L}$ is complete. □

Corollary 1. 

Let $\mathfrak{L}$ be the complete lattice of all neutrosophic open sets of neutrosophic topology generated by neutrosophic relation; then $\mathfrak{L}$ is bounded. Indeed, the least element of $\mathfrak{L}$ is $0_{\mathfrak{L}}=\varnothing =⋒U_i$ and the greatest element of $\mathfrak{L}$ is $1_{\mathfrak{L}}=\mathcal{E}=⋓U_i$.

Corollary 2. 

Let $\mathfrak{L}$ be the lattice of neutrosophic open sets of neutrosophic topology ${\tau }_R$ generated by neutrosophic relation $\mathcal{N}$, then $\mathfrak{L}$ is distributive and therefore modular.

Hartmanis in 1958 proved that the lattice structure of all topologies on a finite universe is complemented. The following proposition shows that the lattice structure of neutrosophic open sets of a topology generated by neutrosophic relation is also complemented.

Proposition 3. 

Let $\mathfrak{L}$ be the lattice of open neutrosophic sets of neutrosophic topology ${\tau }_{\mathcal{N}}$ generated by the neutrosophic relation $\mathcal{N}$, then $\mathfrak{L}$ is complemented.

Proof. 

Indeed, every element ${\mathcal{W}}_{i_0}$ has a complement ${\mathcal{W}}_{j_0}$ such that ${\mathcal{W}}_{i_0}⋒{\mathcal{W}}_{j_0}=0_{\mathfrak{L}}$ and ${\mathcal{W}}_{i_0}⋓{\mathcal{W}}_{j_0}=1_{\mathfrak{L}}.$ Hence, $\mathfrak{L}$ is complemented. □

Corollary 3. 

The fact that $\mathfrak{L}$ is a distributive lattice and complemented with the least element $0_{\mathfrak{L}}=\varnothing$ and the greatest element $1_{\mathfrak{L}=\mathcal{E}}$, then $\mathfrak{L}$ is a boolean algebra indicated by $(\mathfrak{L},⋒,⋓,0_{\mathfrak{L}},1_{\mathfrak{L}})$.

Proof. 

Directly from Corollary 2 and Proposition 3. □

5. Ideals and Filters on the Lattice of Neutrosophic Open Sets

The study of ideals and neutrosophic filters on the lattice structure of neutrosophic open sets is presented in this section. We describe them both in terms of the corresponding level sets and terms of lattice structure operations.

5.1. Definitions and Properties

Definition 13.

A neutrosophic set $\mathcal{D}$ of $\mathfrak{L}$ is named a neutrosophic ideal if for all $\Phi ,\Psi \in \mathfrak{L}$, the following conditions hold:

(i) 

${\daleth }_{\mathcal{D}}(\Phi \cup \Psi )⩾{\daleth }_{\mathcal{D}}(\Phi )⋏{\daleth }_{\mathcal{D}}(\Psi );$

(ii) 

${\daleth }_{\mathcal{D}}(\Phi \cap \Psi )⩾{\daleth }_{\mathcal{D}}(\Phi )⋎{\daleth }_{\mathcal{D}}(\Psi );$

(iii) 

${\gimel }_{\mathcal{D}}(\Phi \cup \Psi )⩾{\gimel }_{\mathcal{D}}(\Phi )⋏{\gimel }_{\mathcal{D}}(\Psi );$

(iv) 

${\gimel }_{\mathcal{D}}(\Phi \cap \Psi )⩾{\gimel }_{\mathcal{D}}(\Phi )⋎{\gimel }_{\mathcal{D}}(\Psi );$

(v) 

${\mathsf{Ϝ}}_{\mathcal{D}}(\Phi \cup \Psi )⩽{\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋎{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi );$

(vi) 

${\mathsf{Ϝ}}_{\mathcal{D}}(\Phi \cap \Psi )⩽{\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋏{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi ).$

Definition 14.

A neutrosophic set F of $\mathfrak{L}$ is said to be a neutrosophic filter if for all $\Phi ,\Psi \in \mathfrak{L}$, the following conditions hold:

(i) 

${\daleth }_F(\Phi \cup \Psi )⩾{\daleth }_F(\Phi )⋎{\daleth }_F(\Psi );$

(ii) 

${\daleth }_F(\Phi \cap \Psi )⩾{\daleth }_F(\Phi )⋏{\daleth }_F(\Psi );$

(iii) 

${\gimel }_F(\Phi \cup \Psi )⩾{\gimel }_F(\Phi )⋎{\gimel }_F(\Psi );$

(iv) 

${\gimel }_F(\Phi \cap \Psi )⩾{\gimel }_F(\Phi )⋏{\gimel }_F(\Psi );$

(v) 

${\mathsf{Ϝ}}_F(\Phi \cup \Psi )⩽{\mathsf{Ϝ}}_F(\Phi )⋏{\mathsf{Ϝ}}_F(\Psi );$

(vi) 

${\mathsf{Ϝ}}_F(\Phi \cap \Psi )⩽{\mathsf{Ϝ}}_F(\Phi )⋎{\mathsf{Ϝ}}_F(\Psi ).$

In the following proposition, we show the relationship between ideal and filter on a lattice structure of neutrosophic open sets.

Proposition 4. 

Let $\mathfrak{L}$ be the lattice structure of neutrosophic open sets, ${\mathfrak{L}}^d$ be the dual-order lattice, and let $\Phi \in S\left(\mathfrak{L}\right)$. So, it holds that Φ is a neutrosophic ideal of $\mathfrak{L}$ if and only if Φ is a neutrosophic filter of ${\mathfrak{L}}^d$ and vice versa.

Proof. 

Let $\Phi$ be a neutrosophic ideal of $\mathfrak{L}$, then the six conditions of Definition 13 hold. From the principle of duality, which we obtained by replacing each meet operation (respectively, join operation) by its dual, we then obtained the six conditions of Definition 14. Therefore, $\Phi$ becomes a neutrosophic filter of ${\mathfrak{L}}^d$. □

This result will be useful in the following.

Proposition 5. 

Let $\mathfrak{L}$ be the lattice structure of neutrosophic open sets, and Φ and Ψ be two neutrosophic sets of $\mathfrak{L}$. Then, we have the following:

(i) 

If Φ and Ψ are two neutrosophic ideals of $\mathfrak{L}$, then $\Phi ⋒\Psi$ is a neutrosophic ideal of $\mathfrak{L}$;

(ii) 

If Φ and Ψ are two neutrosophic filters of $\mathfrak{L}$, then $\Phi ⋒\Psi$ is a neutrosophic filter of $\mathfrak{L}$.

5.2. Characterizations of Neutrosophic Ideals and Filters in Terms of Their Level Sets

The following result discusses the relationship between neutrosophic ideal and neutrosophic filter and their support on the lattice of open sets.

Proposition 6. 

Let $\mathcal{D}$ and F be two neutrosophic sets of $\mathfrak{L}$. Then, the following hold:

(i) 

If $\mathcal{D}$ is a neutrosophic ideal, then the support of $\mathcal{D}$ is an ideal of $\mathfrak{L}$.

(ii) 

If F is a neutrosophic filter, then the support F is a filter of $\mathfrak{L}$.

Proof. 

(i) Let $\mathcal{D}$ be a neutrosophic ideal of $\mathfrak{L}$. We prove that $\mathcal{S}\left(\mathcal{D}\right)$ is an ideal of $\mathfrak{L}$.

(a) Assume that $\Phi \in \mathcal{S}\left(\mathcal{D}\right)$ and $\Psi ⋐\Phi$. Therefore, it implies that

$${\daleth }_{\mathcal{D}}(\Phi )\ne 0,{\gimel }_{\mathcal{D}}(\Phi )\ne 0,{\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )\ne 0.$$

Because $\Psi ⋐\Phi$, we have $\Phi ⋒\Psi =\Psi$. Consequently,

$${\daleth }_{\mathcal{D}}(\Psi )={\daleth }_{\mathcal{D}}(\Phi ⋒\Psi )⩾{\daleth }_{\mathcal{D}}(\Phi )⋎{\daleth }_{\mathcal{D}}(\Psi ).$$

So,

$${\daleth }_{\mathcal{D}}(\Psi )⩾{\daleth }_{\mathcal{D}}(\Phi )\ne 0.$$

Similarly, we can determine that

$${\gimel }_{\mathcal{D}}(\Phi )\ne 0\mathrm{and}{\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )\ne 0.$$

Hence, $\Psi \in \mathcal{S}\left(\mathcal{D}\right)$.

(b) Assume that $\Phi ,\Psi \in \mathcal{S}\left(\mathcal{D}\right)$. We prove that $\Phi ⋓\Psi \in \mathcal{S}\left(\mathcal{D}\right).$ The fact that $\mathcal{D}$ is a neutrosophic ideal, it thus holds by Definition 13 that

$${\daleth }_{\mathcal{D}}(\Phi ⋓\Psi )⩾{\daleth }_{\mathcal{D}}(\Phi )⋏{\daleth }_{\mathcal{D}}(\Psi )\ne 0.$$

Similarly, we show that

$${\gimel }_{\mathcal{D}}(\Phi ⋓\Psi )\ne 0\mathrm{and}{\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋓\Psi )\ne 0.$$

Thus, $\Phi ⋓\Psi \in \mathcal{S}\left(\mathcal{D}\right).$ Therefore, $\mathcal{S}\left(\mathcal{D}\right)$ is an ideal of $\mathfrak{L}$.

(ii) Analogously from (i) and Proposition 4. □

We establish the concept of ideal and filter on the lattice structure of open sets in terms of its level sets in the following result.

Theorem 2. 

Let $\mathcal{D}$ and F be two neutrosophic sets of $\mathfrak{L}$:

(i) 

$\mathcal{D}$ is a neutrosophic ideal equivalent to that when its level sets are ideals of $\mathfrak{L}$;

(ii) 

F is a neutrosophic filter equivalent to that when its level sets are filters of $\mathfrak{L}$.

Proof. 

(i) Let $\Phi$ be a neutrosophic ideal of $\mathfrak{L}$ and ${\mathcal{D}}_{\alpha ,\beta ,\gamma }$ their level sets, with $0<\alpha ,\beta ,\gamma \le 1$.

(a) Assume that $\Phi \in {\mathcal{D}}_{\alpha ,\beta ,\gamma }$ and $\Psi ⋐\Phi$. By Definition 13 of a neutrosophic ideal, it states that

$${\daleth }_{\mathcal{D}}(\Psi )⩾{\daleth }_{\mathcal{D}}(\Phi ),{\gimel }_{\mathcal{D}}(\Psi )⩾{\gimel }_{\mathcal{D}}(\Phi )\mathrm{and}{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi )⩽{\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ).$$

Since,

$${\daleth }_{\mathcal{D}}(\Phi )⩾\alpha ,{\gimel }_{\mathcal{D}}(\Phi )⩾\beta \mathrm{and}{\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⩽\gamma ,$$

we obtain

$${\daleth }_{\mathcal{D}}(\Psi )⩾\alpha ,{\gimel }_{\mathcal{D}}(\Psi )⩾\beta \mathrm{and}{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi )⩽\gamma .$$

Hence, $\Psi \in {\mathcal{D}}_{\alpha ,\beta ,\gamma }$.

(b) Let $\Phi ,\Psi \in {\mathcal{D}}_{\alpha ,\beta ,\gamma }$, then it holds that

$${\daleth }_{\mathcal{D}}(\Phi )⩾\alpha ,{\gimel }_{\mathcal{D}}(\Phi )⩾\beta ,{\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⩽\gamma$$

and

$${\daleth }_{\mathcal{D}}(\Psi )⩾\alpha ,{\gimel }_{\mathcal{D}}(\Psi )⩾\beta ,{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi )⩽\gamma .$$

By Definition 13 of a neutrosophic ideal, it holds that

$$\begin{array}{cc}\hfill {\daleth }_{\mathcal{D}}(\Phi ⋓\Psi )⩾& {\daleth }_{\mathcal{D}}(\Phi )⋏{\daleth }_{\mathcal{D}}(\Psi )⩾\alpha ,\hfill \\ \hfill {\gimel }_{\mathcal{D}}(\Phi ⋓\Psi )⩾& {\gimel }_{\mathcal{D}}(\Phi )⋏{\gimel }_{\mathcal{D}}(\Psi )⩾\beta ,\hfill \\ \hfill {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋓\Psi )⩽& {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋎{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi )⩽\gamma .\hfill \end{array}$$

Hence, $\Phi ⋓\Psi \in {\mathcal{D}}_{\alpha ,\beta ,\gamma }.$

Consequently, ${\mathcal{D}}_{\alpha ,\beta ,\gamma }$ is an ideal of $\mathfrak{L}$, for all $0<\alpha ,\beta ,\gamma \le 1$.

Inversely, we suppose that all level sets of $\mathcal{D}$ are ideals of $\mathfrak{L}$. We prove that $\mathcal{D}$ is a neutrosophic ideal of $\mathfrak{L}$. Let $\Phi ,\Psi \in \mathfrak{L}$ with

$$\alpha ={\daleth }_{\mathcal{D}}(\Phi )⋏{\daleth }_{\mathcal{D}}(\Psi ),\beta ={\gimel }_{\mathcal{D}}(\Phi )⋏{\gimel }_{\mathcal{D}}(\Psi )\mathrm{and}\gamma ={\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋎{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi ).$$

The fact that ${\mathcal{D}}_{\alpha ,\beta ,\gamma }$ is an ideal of $\mathfrak{L}$ assures that $\Phi ⋓\Psi \in {\mathcal{D}}_{\alpha ,\beta ,\gamma }$, for all $0<\alpha ,\beta ,\gamma \le 1$. Then, we can determine that

$${\daleth }_{\mathcal{D}}(\Phi ⋓\Psi )⩾\alpha ,{\gimel }_{\mathcal{D}}(\Phi ⋓\Psi )⩾\beta \mathrm{and}{\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋓\Psi )⩽\gamma .$$

Thus,

$$\begin{array}{cc}\hfill {\daleth }_{\mathcal{D}}(\Phi ⋓\Psi )⩾& {\daleth }_{\mathcal{D}}(\Phi )⋏{\daleth }_{\mathcal{D}}(\Psi ),\hfill \\ \hfill {\gimel }_{\mathcal{D}}(\Phi ⋓\Psi )⩾& {\gimel }_{\mathcal{D}}(\Phi )⋏{\gimel }_{\mathcal{D}}(\Psi ),\hfill \\ \hfill {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋓\Psi )⩽& {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋎{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi ).\hfill \end{array}$$

Similarly, we can prove conditions (ii), (iv) and (vi) on Definition 13. Therefore, $\mathcal{D}$ is a neutrosophic ideal of $\mathfrak{L}$.

(ii) It follows in the same way by using Proposition 4 and (i). □

5.3. Basic Characterizations of Neutrosophic Ideals (Respectively, Filters)

This part provides a significant characterization of neutrosophic ideals (respectively, filters).

Theorem 3. 

Let $\mathfrak{L}$ be the lattice structure of neutrosophic open sets. Then, it holds that $\mathcal{D}$ is a neutrosophic ideal of $\mathfrak{L}$ if and only if the following conditions are satisfied:

(i) 

${\daleth }_{\mathcal{D}}(\Phi ⋓\Psi )={\daleth }_{\mathcal{D}}(\Phi )⋏{\daleth }_{\mathcal{D}}(\Psi );$

(ii) 

${\gimel }_{\mathcal{D}}(\Phi ⋓\Psi )={\daleth }_{\mathcal{D}}(\Phi )⋏{\daleth }_{\mathcal{D}}(\Psi );$

(iii) 

${\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋓\Psi )={\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋎{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi )$, for all $\Phi ,\Psi \in \mathfrak{L}.$

Proof. 

Let $\mathcal{D}$ be a neutrosophic ideal of $\mathfrak{L}$, then for all $\Phi ,\Psi \in \mathfrak{L}$. Then

$$\begin{array}{cc}\hfill {\daleth }_{\mathcal{D}}(\Phi ⋓\Psi )⩾& {\daleth }_{\mathcal{D}}(\Phi )⋏{\daleth }_{\mathcal{D}}(\Psi ),\hfill \\ \hfill {\gimel }_{\mathcal{D}}(\Phi ⋓\Psi )⩾& {\gimel }_{\mathcal{D}}(\Phi )⋏{\gimel }_{\mathcal{D}}(\Psi ),\hfill \\ \hfill {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋓\Psi )⩽& {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋎{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi ).\hfill \end{array}$$

Since $\Phi ⋐\Phi ⋓\Psi$ and $\Psi ⋐\Phi ⋓\Psi$, it follows by the monotonicity that

$${\daleth }_{\mathcal{D}}(\Phi )⩾{\daleth }_{\mathcal{D}}(\Phi ⋓\Psi ),{\gimel }_{\mathcal{D}}(\Phi )⩾{\gimel }_{\mathcal{D}}(\Phi ⋓\Psi )$$

and

$${\daleth }_{\mathcal{D}}(\Psi )⩾{\daleth }_{\mathcal{D}}(\Phi ⋓\Psi ),{\gimel }_{\mathcal{D}}(\Psi )⩾{\gimel }_{\mathcal{D}}(\Phi ⋓\Psi ).$$

Hence,

$${\daleth }_{\mathcal{D}}(\Phi )⋏{\daleth }_{\mathcal{D}}(\Phi )⩾{\daleth }_{\mathcal{D}}(\Phi ⋓\Psi )and{\gimel }_{\mathcal{D}}(\Phi )⋏{\gimel }_{\mathcal{D}}(\Psi )⩾{\gimel }_{\mathcal{D}}(\Phi ⋓\Psi ).$$

Thus,

$${\daleth }_{\mathcal{D}}(\Phi ⋓\Psi )={\daleth }_{\mathcal{D}}(\Phi )⋏{\daleth }_{\mathcal{D}}(\Psi )and{\gimel }_{\mathcal{D}}(\Phi ⋓\Psi )={\gimel }_{\mathcal{D}}(\Phi )⋏{\gimel }_{\mathcal{D}}(\Psi ).$$

Also, since

$$\Phi ⋐\Phi ⋓\Psi \mathrm{and}\Psi ⋐\Phi ⋓\Psi ,$$

we obtain from the monotonicity that

$${\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⩽{\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋓\Psi )and{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi )⩽{\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋓\Psi ).$$

Hence,

$${\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋎{\mathsf{Ϝ}}_{\mathcal{D}}(\Delta )⩽{\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋓\Delta ).$$

Thus,

$${\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋓\Psi )={\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋎{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi ).$$

Inversely, assume that

$$\begin{array}{cc}\hfill {\daleth }_{\mathcal{D}}(\Phi ⋓\Psi )=& {\daleth }_{\mathcal{D}}(\Phi )⋏{\daleth }_{\mathcal{D}}(\Psi ),\hfill \\ \hfill {\gimel }_{\mathcal{D}}(\Phi ⋓\Psi )=& {\gimel }_{\mathcal{D}}(\Phi )⋏{\gimel }_{\mathcal{D}}(\Delta ),\hfill \\ \hfill {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋓\Psi )=& {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋎{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi ),\mathrm{for}\mathrm{all}\Phi ,\Psi \in \mathfrak{L}.\hfill \end{array}$$

Easily, we can see that

$$\begin{array}{cc}\hfill {\daleth }_{\mathcal{D}}(\Phi ⋓\Psi )⩾& {\daleth }_{\mathcal{D}}(\Phi )⋏{\daleth }_{\mathcal{D}}(\Psi ),\hfill \\ \hfill {\gimel }_{\mathcal{D}}(\Phi ⋓\Psi )⩾& {\gimel }_{\mathcal{D}}(\Phi )⋏{\gimel }_{\mathcal{D}}(\Psi ),\hfill \\ \hfill {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋓\Psi )⩽& {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋎{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi ),\mathrm{for}\mathrm{all}\Phi ,\Psi \in \mathfrak{L}.\hfill \end{array}$$

Now, we show that

$$\begin{array}{cc}\hfill {\daleth }_{\mathcal{D}}(\Phi ⋒\Psi )⩾& {\daleth }_{\mathcal{D}}(\Phi )⋎{\daleth }_{\mathcal{D}}(\Psi ),\hfill \\ \hfill {\gimel }_{\mathcal{D}}(\Phi ⋒\Psi )⩾& {\gimel }_{\mathcal{D}}(\Phi )⋎{\gimel }_{\mathcal{D}}(\Psi ),\hfill \\ \hfill {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋒\Psi )⩽& {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋏{\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ),\mathrm{for}\mathrm{all}\Phi ,\Psi \in \mathfrak{L}.\hfill \end{array}$$

Since

$$\Psi ⋓(\Phi ⋒\Psi )=\Phi \mathrm{and}\Psi ⋓(\Phi ⋒\Psi )=\Psi ,$$

we can determine that

$$\begin{array}{cc}\hfill {\daleth }_{\mathcal{D}}(\Phi ⋓(\Phi ⋒\Psi ))=& {\daleth }_{\mathcal{D}}(\Phi ),\hfill \\ \hfill {\gimel }_{\mathcal{D}}(\Phi ⋓(\Phi ⋒\Psi ))=& {\gimel }_{\mathcal{D}}(\Phi ),\hfill \\ \hfill {\daleth }_{\mathcal{D}}(\Psi ⋓(\Phi ⋒\Psi ))=& {\daleth }_{\mathcal{D}}(\Psi ),\hfill \\ \hfill {\gimel }_{\mathcal{D}}(\Psi ⋓(\Phi ⋒\Psi ))=& {\gimel }_{\mathcal{D}}(\Psi ).\hfill \end{array}$$

From conditions (i) and (ii), we conclude that

$$\begin{array}{cc}\hfill {\daleth }_{\mathcal{D}}(\Phi )⋏{\daleth }_{\mathcal{D}}(\Phi ⋒\Psi )=& {\daleth }_{\mathcal{D}}(\Phi ),\hfill \\ \hfill {\gimel }_{\mathcal{D}}(\Phi )⋏{\gimel }_{\mathcal{D}}(\Phi ⋒\Psi )=& {\gimel }_{\mathcal{D}}(\Phi ),\hfill \\ \hfill {\daleth }_{\mathcal{D}}(\Psi )⋏{\daleth }_{\mathcal{D}}(\Phi ⋒\Psi )=& {\daleth }_{\mathcal{D}}(\Psi ),\hfill \\ \hfill {\gimel }_{\mathcal{D}}(\Psi )⋏{\gimel }_{\mathcal{D}}(\Phi ⋒\Psi )=& {\gimel }_{\mathcal{D}}(\Psi ).\hfill \end{array}$$

Hence,

$$\begin{array}{cc}\hfill {\daleth }_{\mathcal{D}}(\Phi ⋒\Psi )⩾& {\daleth }_{\mathcal{D}}(\Phi ),\hfill \\ \hfill {\gimel }_{\mathcal{D}}(\Phi ⋒\Psi )⩾& {\gimel }_{\mathcal{D}}(\Phi ),\hfill \\ \hfill {\daleth }_{\mathcal{D}}(\Phi ⋒\Psi )⩾& {\daleth }_{\mathcal{D}}(\Psi ),\hfill \\ \hfill {\gimel }_{\mathcal{D}}(\Phi ⋒\Psi )⩾& {\gimel }_{\mathcal{D}}(\Psi ).\hfill \end{array}$$

Thus,

$$\begin{array}{cc}\hfill {\daleth }_{\mathcal{D}}(\Phi ⋒\Psi )⩾& {\daleth }_{\mathcal{D}}(\Phi )⋎{\daleth }_{\mathcal{D}}(\Psi ),\hfill \\ \hfill {\gimel }_{\mathcal{D}}(\Phi ⋒\Psi )⩾& {\gimel }_{\mathcal{D}}(\Phi )⋎{\gimel }_{\mathcal{D}}(\Psi ),\mathrm{for}\mathrm{all}\Phi ,\Psi \in \mathfrak{L}.\hfill \end{array}$$

In the same way, we obtain that

$${\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋒\Psi )⩽{\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋏{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi ),\mathrm{for}\mathrm{all}\Phi ,\Psi \in \mathfrak{L}.$$

Therefore, $\mathcal{D}$ is a neutrosophic of $\mathfrak{L}$. □

Similarly, the following result provides a characterization of neutrosophic filters of neutrosophic open-set lattice in terms of its operation.

Theorem 4. 

Let $\mathfrak{L}$ be the lattice of neutrosophic open sets. Then, it holds that F is a neutrosophic filter of $\mathfrak{L}$ if and only if the following conditions are satisfied:

(i) 

${\daleth }_F(\Phi ⋒\Psi )={\daleth }_F(\Phi )⋏{\daleth }_F(\Psi );$

(ii) 

${\gimel }_F(\Phi ⋒\Psi )={\gimel }_F(\Phi )⋏{\gimel }_F(\Psi );$

(iii) 

${\mathsf{Ϝ}}_F(\Phi ⋒\Psi )={\mathsf{Ϝ}}_F(\Phi )⋎{\mathsf{Ϝ}}_F(\Psi )forall\Phi ,\Psi \in \mathfrak{L}.$

Proof. 

Directly from Theorem 3 and Proposition 4. □

As results of the above theorems, we can obtain the following properties of ideals and filters on a neutrosophic open-set lattice.

Corollary 4. 

Let $\mathcal{D}$ be a neutrosophic ideal of $\mathfrak{L}$ and $\Phi ,\Psi \in \mathfrak{L}$. If $\Phi \subseteq \Psi$, then

$${\daleth }_{\mathcal{D}}(\Phi )⩾{\daleth }_{\mathcal{D}}(\Psi ),{\gimel }_{\mathcal{D}}(\Phi )⩾{\gimel }_{\mathcal{D}}(\Psi )and{\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⩽{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi ),$$

i.e., the mappings ${\daleth }_{\mathcal{D}},{\gimel }_{\mathcal{D}}$ are antitone and ${\mathsf{Ϝ}}_{\mathcal{D}}$ is monotone.

Corollary 5. 

Let F be a neutrosophic filter of $\mathfrak{L}$ and $\Phi ,\Psi \in \mathfrak{L}$. If $\Phi \subseteq \Psi$, then

$${\daleth }_F(\Phi )⩽{\daleth }_F(\Psi ),{\gimel }_F(\Phi )⩽{\gimel }_F(\Psi )and{\mathsf{Ϝ}}_F(\Phi )⩾{\mathsf{Ϝ}}_F(\Psi ),$$

i.e., the mappings ${\daleth }_F,{\gimel }_F$ are monotone and ${\mathsf{Ϝ}}_F$ is antitone.

The following result characterizes fuzzy ideals (respectively, fuzzy filters) of open-set lattice.

Corollary 6. 

For every fuzzy set $\mathcal{D}$ and F of $\mathfrak{L}$, the following equivalences hold:

(i) 

$\mathcal{D}$ is a fuzzy ideal of $\mathfrak{L}$ equivalent to ${\daleth }_{\mathcal{D}}(\Phi ⋓\Psi )={\daleth }_{\mathcal{D}}(\Phi )⋏{\daleth }_{\mathcal{D}}(\Psi )$;

(ii) 

F is a fuzzy filter of $\mathfrak{L}$ equivalent to ${\daleth }_F(\Phi ⋒\Psi )={\daleth }_F(\Phi )⋏{\daleth }_F(\Psi )$, for all $\Phi ,\Psi \in \mathfrak{L}.$

Proof. 

(i) The fact that fuzzy ideal is a neutrosophic ideal of $\mathfrak{L}$ by setting ${\gimel }_{\mathcal{D}}(\Phi )=0$ and ${\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )=1-{\daleth }_{\mathcal{D}}(\Phi )$, Theorem 3 assures that $\mathcal{D}$ is a fuzzy ideal of $\mathfrak{L}$ if and only if ${\daleth }_{\mathcal{D}}(\Phi ⋓\Psi )={\daleth }_{\mathcal{D}}(\Phi )⋏{\daleth }_{\mathcal{D}}(\Psi )$, for all $\Phi ,\Psi \in \mathfrak{L}.$

(ii) It follows from Proposition 4 and (i). □

Similarly, the following result shows a characterization of intuitionistic fuzzy ideals and filters of the open-set lattice.

Corollary 7. 

For any intuitionistic fuzzy sets $\mathcal{D}$ and F of $\mathfrak{L}$, the following equivalences hold:

(i) 

$\mathcal{D}$ is an intuitionistic fuzzy ideal of $\mathfrak{L}$ if and only if for all $\Phi ,\Psi \in \mathfrak{L},$ the following conditions are satisfied:

(a)

${\daleth }_{\mathcal{D}}(\Phi ⋓\Psi )={\daleth }_{\mathcal{D}}(\Phi )⋏{\daleth }_{\mathcal{D}}(\Psi )$;

(b)

${\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋓\Psi )={\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋎{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi )$.

(ii) 

F is an intuitionistic fuzzy filter of $\mathfrak{L}$ if and only if for all $\Phi ,\Psi \in \mathfrak{L},$ the following conditions are satisfied:

(a)

${\daleth }_F(\Phi ⋒\Psi )={\daleth }_F(\Phi )⋏{\daleth }_F(\Psi )$;

(b)

${\mathsf{Ϝ}}_F(\Phi ⋒\Psi )={\mathsf{Ϝ}}_F(\Phi )⋎{\mathsf{Ϝ}}_F(\Psi )$.

Proof. 

(i) Since every intuitionistic fuzzy ideal is a neutrosophic ideal of $\mathfrak{L}$ by putting ${\gimel }_{\mathcal{D}}(\Phi )=1-{\daleth }_{\mathcal{D}}(\Phi )-{\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )$, it holds by Theorem 3 that $\mathcal{D}$ is an intuitionistic fuzzy ideal of $\mathfrak{L}$ if and only if for all $\Phi ,\Psi \in \mathfrak{L},$ the following conditions hold:

(a)

${\daleth }_{\mathcal{D}}(\Phi ⋓\Psi )={\daleth }_{\mathcal{D}}(\Phi )⋏{\daleth }_{\mathcal{D}}(\Psi )$;

(b)

${\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋓\Psi )={\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋎{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi )$.

(ii) Directly via (i) and Proposition 4. □

6. Prime Neutrosophic Ideals and Filters of $\mathfrak{L}$

In this part of the paper, we study the concept of prime neutrosophic ideals (respectively, prime neutrosophic filters) of $\mathfrak{L}$ as interesting types of neutrosophic ideals (respectively, neutrosophic filters).

6.1. Characterizations of Prime Neutrosophic Ideals and Filters

We apply the previous characterizations of neutrosophic ideals (respectively, neutrosophic filters) to the prime neutrosophic ideals (respectively, prime neutrosophic filters) of $\mathfrak{L}$.

Definition 15. 

A neutrosophic ideal $\mathcal{D}$ of the lattice $\mathfrak{L}$ is said to be a prime neutrosophic ideal if, for all $\Phi ,\Psi \in \mathfrak{L}$, the following conditions apply:

(i) 

${\daleth }_{\mathcal{D}}(\Phi ⋒\Psi )⩽{\daleth }_{\mathcal{D}}(\Phi )⋎{\daleth }_{\mathcal{D}}(\Psi )$;

(ii) 

${\gimel }_{\mathcal{D}}(\Phi ⋒\Psi )⩽{\gimel }_{\mathcal{D}}(\Phi )⋎{\gimel }_{\mathcal{D}}(\Psi )$;

(iii) 

${\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋒\Psi )⩾{\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋏{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi ).$

Definition 16. 

A neutrosophic filter F of the lattice $\mathfrak{L}$ is said to be a prime neutrosophic filter if, for all $\Phi ,\Psi \in \mathfrak{L}$, the following conditions apply:

(i) 

${\daleth }_F(\Phi ⋓\Psi )⩽{\daleth }_F(\Phi )⋎{\daleth }_F(\Psi )$;

(ii) 

${\gimel }_F(\Phi ⋓\Psi )⩽{\gimel }_F(\Phi )⋎{\gimel }_F(\Psi )$;

(iii) 

${\mathsf{Ϝ}}_F(\Phi ⋓\Psi )⩾{\mathsf{Ϝ}}_F(\Phi )⋏{\mathsf{Ϝ}}_F(\Psi ).$

The next theorem shows a basic characterization of prime neutrosophic ideals.

Theorem 5. 

Let $\mathcal{D}$ be a neutrosophic subset of $\mathfrak{L}$. Then,

$\mathcal{D}$ is a prime neutrosophic ideal of $\mathfrak{L}$ if and only if the following conditions hold:

(i) 

${\daleth }_{\mathcal{D}}(\Phi ⋓\Psi )={\daleth }_{\mathcal{D}}(\Phi )⋏{\daleth }_{\mathcal{D}}(\Psi )$;

(ii) 

${\daleth }_{\mathcal{D}}(\Phi ⋒\Psi )={\daleth }_{\mathcal{D}}(\Phi )⋎{\daleth }_{\mathcal{D}}(\Psi )$;

(iii) 

${\gimel }_{\mathcal{D}}(\Phi ⋓\Psi )={\gimel }_{\mathcal{D}}(\Phi )⋏{\gimel }_{\mathcal{D}}(\Psi )$;

(iv) 

${\gimel }_{\mathcal{D}}(\Phi ⋒\Psi )={\gimel }_{\mathcal{D}}(\Phi )⋎{\gimel }_{\mathcal{D}}(\Psi )$;

(v) 

${\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋓\Psi )={\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋎{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi )$;

(vi) 

${\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋒\Psi )={\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋏{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi ),for all\Phi ,\Psi \in \mathfrak{L}$.

Proof. 

Let $\mathcal{D}$ be a prime neutrosophic ideal of $\mathfrak{L}$. We prove (i), as the others can be proved similarly. By the aforementioned hypothesis, we have that

$${\daleth }_{\mathcal{D}}(\Phi ⋓\Psi )⩾{\daleth }_{\mathcal{D}}(\Phi )⋏{\daleth }_{\mathcal{D}}(\Psi ),\mathrm{for}\mathrm{every}\Phi ,\Psi \in \mathfrak{L}.$$

It follows by Definition 13 that

$${\daleth }_{\mathcal{D}}(\Phi )={\daleth }_{\mathcal{D}}(\Phi ⋒(\Omega ⋓\Psi ))⩾{\daleth }_{\mathcal{D}}(\Phi ⋓\Psi )\mathrm{and}{\daleth }_{\mathcal{D}}(\Psi )={\daleth }_{\mathcal{D}}(\Psi ⋒(\Phi ⋓\Psi ))⩾{\daleth }_{\mathcal{D}}(\Phi ⋓\Psi ).$$

Thus,

$${\daleth }_{\mathcal{D}}(\Phi )⋏{\daleth }_{\mathcal{D}}(\Psi )⩾{\daleth }_{\mathcal{D}}(\Phi ⋓\Psi ).$$

Therefore,

$${\daleth }_{\mathcal{D}}(\Phi ⋓\Psi )={\daleth }_{\mathcal{D}}(\Phi )⋏{\daleth }_{\mathcal{D}}(\Psi ).$$

Inversely, if we assume that ${\daleth }_{\mathcal{D}}$, ${\gimel }_{\mathcal{D}}$ and ${\mathsf{Ϝ}}_{\mathcal{D}}$ satisfy the above conditions, then it is clear that $\mathcal{D}$ is a prime neutrosophic ideal of $\mathfrak{L}$. □

Similarly, the following theorem shows a characterization of prime neutrosophic filters.

Theorem 6. 

Let $\mathcal{D}$ be a neutrosophic subset of $\mathfrak{L}$. Then, $\mathcal{D}$ is a prime neutrosophic filter of $\mathfrak{L}$ if and only if the following conditions hold:

(i) 

${\daleth }_F(\Phi ⋓\Psi )={\daleth }_F(\Phi )⋎{\daleth }_F(\Psi )$;

(ii) 

${\daleth }_F(\Phi ⋒\Psi )={\daleth }_F(\Phi )⋏{\daleth }_F(\Psi )$;

(iii) 

${\gimel }_F(\Phi ⋓\Psi )={\gimel }_F(\Phi )⋎{\gimel }_F(\Psi )$;

(iv) 

${\gimel }_F(\Phi ⋒\Psi )={\gimel }_F(\Phi )⋏{\gimel }_F(\Psi )$;

(v) 

${\mathsf{Ϝ}}_F(\Phi ⋓\Psi )={\mathsf{Ϝ}}_F(\Phi )⋏{\mathsf{Ϝ}}_F(\Psi )$;

(vi) 

${\mathsf{Ϝ}}_F(\Phi ⋒\Psi )={\mathsf{Ϝ}}_F(\Phi )⋎{\mathsf{Ϝ}}_F(\Psi )$.

Proof. 

Direct application of Proposition 4 and Theorem 5. □

Example 4. 

Let $\mathcal{E}=\{a,b\}$ and $\mathfrak{L}=\{\varphi ,\Phi ,\Psi ,\mathcal{E}\}$ be a lattice of $\mathcal{E}$ with $\Phi =\{⟨a,0.4,0.3,0.1⟩\mid a\in \mathcal{E}\}$ and $\Psi =\{⟨b,0.1,0.3,0.4⟩\mid b\in \mathcal{E}\}$. Then, according to Definitions 15 and 16, we have the following:

(i) 

$\mathcal{D}=\{⟨a,0.2,0.3,0.1⟩,⟨b,0.3,0.4,0.1⟩\mid a,b\in \mathcal{E}\}$ is a prime neutrosophic ideal of $\mathfrak{L}.$

(ii) 

$F=\{⟨a,0.5,0.2,0.3⟩,⟨b,0.4,0.1,0.2⟩\mid a,b\in \mathcal{E}\}$ is a prime neutrosophic filter of $\mathfrak{L}.$

6.2. Operations of Prime Neutrosophic Ideals and Prime Neutrosophic Filters

We present some basic operations of prime neutrosophic ideals (respectively, prime neutrosophic filters).

Proposition 7. 

Suppose ${\left({\Phi }_i\right)}_{i\in I}$ is a set of neutrosophic sets of $\mathfrak{L}$:

(i) 

If ${\Phi }_i$ is a prime neutrosophic ideal of $\mathfrak{L}$, then $\underset{i\in I}{\cap }{\Phi }_i$ is a prime neutrosophic ideal of $\mathfrak{L}$;

(ii) 

If ${\Phi }_i$ is a prime neutrosophic filter of $\mathfrak{L}$, then $\underset{i\in I}{\cap }{\Phi }_i$ is a prime neutrosophic filter of $\mathfrak{L}$.

Proof. 

(i) Let ${\Phi }_i$ be a prime neutrosophic ideal of $\mathfrak{L}$. From Proposition 5, it holds that $\underset{i\in I}{\cap }{\Phi }_i$ is a neutrosophic ideal of $\mathfrak{L}$. Now, we show that $\underset{i\in I}{\cap }{\Phi }_i$ is prime. Let $\Phi ,\Psi \in \mathfrak{L}$ with $\Phi ⋒\Psi \in \underset{i\in I}{\cap }{\Phi }_i$. Then, in that case, $\Phi ⋒\Psi \in {\Phi }_i$. Since for all $i\in I$, ${\Phi }_i$ is a prime neutrosophic ideal, in that case

$$\begin{array}{cc}\hfill {\daleth }_{{\Phi }_i}(\Phi ⋒\Psi )⩽& {\daleth }_{{\Phi }_i}(\Phi )⋎{\daleth }_{{\Phi }_i}(\Psi ),\hfill \\ \hfill {\gimel }_{{\Phi }_i}(\Phi ⋒\Psi )⩽& {\gimel }_{{\Phi }_i}(\Phi )⋎{\gimel }_{{\Phi }_i}(\Psi ),\hfill \\ \hfill {\mathsf{Ϝ}}_{{\Phi }_i}(\Phi ⋒\Psi )⩾& {\mathsf{Ϝ}}_{{\Phi }_i}(\Phi )⋏{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi ),\mathrm{for} \mathrm{every}i\in I.\hfill \end{array}$$

We can determine that

$$\begin{array}{cc}\hfill {\daleth }_{\underset{i\in I}{\cap }{\Phi }_i}(\Phi ⋒\Psi )⩽& {\daleth }_{{\Phi }_i}(\Phi ⋒\Psi )⩽{\daleth }_{{\Phi }_i}(\Phi )⋎{\daleth }_{{\Phi }_i}(\Psi ),\hfill \\ \hfill {\gimel }_{\underset{i\in I}{\cap }{\Phi }_i}(\Phi ⋒\Psi )⩽& {\gimel }_{{\Phi }_i}(\Phi ⋒\Psi )⩽{\gimel }_{{\Phi }_i}(\Phi )⋎{\gimel }_{{\Phi }_i}(\Psi ),\hfill \\ \hfill {\mathsf{Ϝ}}_{\underset{i\in I}{\cap }{\Phi }_i}(\Phi ⋒\Psi )⩾& {\mathsf{Ϝ}}_{{\Phi }_i}(\Phi ⋒\Delta )⩾{\mathsf{Ϝ}}_{{\Phi }_i}(\Phi )⋏{\mathsf{Ϝ}}_{\mathcal{D}}(\Delta ),\mathrm{for} \mathrm{every}i\in I.\hfill \end{array}$$

Hence,

$$\begin{array}{cc}\hfill {\daleth }_{\underset{i\in I}{\cap }{\Phi }_i}(\Phi ⋒\Psi )⩽& \underset{i\in I}{\bigwedge }({\daleth }_{{\Phi }_i}(\Phi )⋎{\daleth }_{{\Phi }_i}(\Psi )),\hfill \\ \hfill {\gimel }_{\underset{i\in I}{\cap }{\Phi }_i}(\Phi ⋒\Psi )⩽& \underset{i\in I}{\bigwedge }({\gimel }_{{\Phi }_i}(\Phi )⋎{\gimel }_{{\Phi }_i}(\Psi )),\hfill \\ \hfill {\mathsf{Ϝ}}_{\underset{i\in I}{\cap }{\Phi }_i}(\Phi ⋒\Psi )⩾& \underset{i\in I}{\bigvee }({\mathsf{Ϝ}}_{{\Phi }_i}(\Phi )⋏{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi )).\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill {\daleth }_{\underset{i\in I}{\cap }{\Phi }_i}(\Phi ⋒\Psi )⩽& {\daleth }_{\underset{i\in I}{\cap }{\Phi }_i}(\Omega )⋎{\daleth }_{\underset{i\in I}{\cap }{\Phi }_i}(\Psi ),\hfill \\ \hfill {\gimel }_{\underset{i\in I}{\cap }{\Phi }_i}(\Phi ⋒\Psi )⩽& {\gimel }_{\underset{i\in I}{\cap }{\Phi }_i}(\Phi )⋎{\gimel }_{\underset{i\in I}{\cap }{\Phi }_i}(\Psi ),\hfill \\ \hfill {\mathsf{Ϝ}}_{\underset{i\in I}{\cap }{\Phi }_i}(\Omega ⋒\Psi )⩾& {\mathsf{Ϝ}}_{\underset{i\in I}{\cap }{\Phi }_i}(\Phi )⋏{\mathsf{Ϝ}}_{\underset{i\in I}{\cap }{\Phi }_i}(\Psi ).\hfill \end{array}$$

We conclude that $\underset{i\in I}{\cap }{\Phi }_i$ is a prime neutrosophic ideal of $\mathfrak{L}$.

(ii) Directly by Proposition 4 and (i). □

Next, we study the complement property between the prime neutrosophic ideal and prime neutrosophic filter.

Proposition 8. 

Let $\mathcal{D}$ be a neutrosophic set of $\mathfrak{L}$; the following equivalences hold:

(i) 

$\mathcal{D}$ is a prime neutrosophic ideal if and only if $\overline{\mathcal{D}}$ is a prime neutrosophic filter of $\mathfrak{L}$;

(ii) 

$\mathcal{D}$ is a prime neutrosophic filter if and only if $\overline{\mathcal{D}}$ is a prime neutrosophic ideal of $\mathfrak{L}$.

Proof. 

(i) Let $\mathcal{D}$ be a prime neutrosophic ideal, for all $\Phi ,\Psi \in \mathfrak{L}$, Proposition 5 provides that

$${\daleth }_{\overline{\mathcal{D}}}(\Phi ⋓\Psi )={\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋓\Psi )={\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋎{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi )={\daleth }_{\overline{\mathcal{D}}}(\Phi )⋎{\daleth }_{\overline{\mathcal{D}}}(\Psi )$$

and

$${\daleth }_{\overline{\mathcal{D}}}(\Phi ⋒\Psi )={\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋒\Psi )={\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋏{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi )={\daleth }_{\overline{\mathcal{D}}}(\Phi )⋏{\daleth }_{\overline{\mathcal{D}}}(\Psi ).$$

Similarly, we show that

$$\begin{array}{cc}\hfill {\gimel }_{\overline{\mathcal{D}}}(\Phi ⋓\Psi )=& {\gimel }_{\overline{\mathcal{D}}}(\Phi )⋎{\gimel }_{\overline{\mathcal{D}}}(\Psi ),\hfill \\ \hfill {\gimel }_{\overline{\mathcal{D}}}(\Phi ⋒\Psi )=& {\gimel }_{\overline{\mathcal{D}}}(\Phi )⋏{\gimel }_{\overline{\mathcal{D}}}(\Psi ),\hfill \\ \hfill {\mathsf{Ϝ}}_{\overline{\mathcal{D}}}(\Phi ⋓\Psi )=& {\mathsf{Ϝ}}_{\overline{\mathcal{D}}}(\Phi )⋏{\mathsf{Ϝ}}_{\overline{\mathcal{D}}}(\Psi ),\hfill \\ \hfill {\mathsf{Ϝ}}_{\overline{\mathcal{D}}}(\Phi ⋒\Psi )=& {\mathsf{Ϝ}}_{\overline{\mathcal{D}}}(\Phi )⋎{\mathsf{Ϝ}}_{\overline{\mathcal{D}}}(\Psi ).\hfill \end{array}$$

By Proposition 6, $\overline{\mathcal{D}}$ is a prime neutrosophic filter of $\mathfrak{L}$. The inverse follows from Proposition 4 and the first implication.

(ii) Directly by the concerned that $\mathcal{D}=\overline{\overline{\mathcal{D}}}$ and (i). □

Example 5. 

Consider the prime neutrosophic ideal $\mathcal{D}$ of $\mathfrak{L}=\{\varphi ,\Phi ,\Psi ,\mathcal{E}\}$ given in Example 4. Then, according to Definition 16, the complement

$$\overline{\mathcal{D}}=\{⟨a,0.1,0.3,0.2⟩,⟨b,0.3,0.4,0.1⟩\mid a,b\in \mathcal{E}\}$$

is a prime neutrosophic filter of $\mathfrak{L}.$

Proposition 9. 

Let $\mathcal{D}$ and F be two neutrosophic sets of $\mathfrak{L}$; the following equivalences hold:

(i) 

$\mathcal{D}$ is a prime neutrosophic ideal if and only if $\left[\mathcal{D}\right]$ is a prime neutrosophic ideal;

(ii) 

F is a prime neutrosophic filter if and only if $\left[F\right]$ is a prime neutrosophic filter.

Proof. 

(i) Let $\mathcal{D}$ be a prime neutrosophic ideal of a lattice $\mathfrak{L}.$ It is obvious that $\left[\mathcal{D}\right]=\{⟨\Phi ,{\daleth }_{\mathcal{D}}(\Phi ),{\gimel }_{\mathcal{D}}(\Phi ),1-{\daleth }_{\mathcal{D}}(\Phi )⟩\mid \Phi \in \mathfrak{L}\}$ is a neutrosophic ideal of $\mathfrak{L}$. Now, we show that $\left[\mathcal{D}\right]$ is prime. We have that

$${\daleth }_{\left[\mathcal{D}\right]}(\Phi ⋒\Psi )={\daleth }_{\mathcal{D}}(\Phi ⋒\Psi )={\daleth }_{\mathcal{D}}(\Phi )⋎{\daleth }_{\Phi }(\Psi )={\daleth }_{\left[\mathcal{D}\right]}(\Phi )⋎{\daleth }_{\left[\mathcal{D}\right]}(\Psi )$$

and

$${\gimel }_{\left[\mathcal{D}\right]}(\Phi ⋒\Psi )={\gimel }_{\mathcal{D}}(\Phi ⋒\Psi )={\gimel }_{\mathcal{D}}(\Phi )⋎{\gimel }_{\mathcal{D}}(\Psi )={\gimel }_{\left[\mathcal{D}\right]}(\Phi )⋎{\gimel }_{\left[\mathcal{D}\right]}(\Psi ).$$

Also,

$$\begin{array}{ccc}\hfill {\mathsf{Ϝ}}_{\left[\mathcal{D}\right]}(\Phi ⋒\Psi )& =& 1-{\daleth }_{\mathcal{D}}(\Phi ⋒\Psi )\hfill \\ & =& 1-({\daleth }_{\mathcal{D}}(\Phi )⋎{\daleth }_{\mathcal{D}}(\Psi ))\hfill \\ & =& (1-{\daleth }_{\mathcal{D}}(\Phi ))⋏(1-{\daleth }_{\mathcal{D}}(\Psi ))\hfill \\ & =& {\mathsf{Ϝ}}_{\left[\mathcal{D}\right]}(\Phi )⋏{\mathsf{Ϝ}}_{\left[\mathcal{D}\right]}(\Psi ).\hfill \end{array}$$

We can determine that $\left[\mathcal{D}\right]$ is a prime neutrosophic ideal of $\mathfrak{L}.$ Inversely, let $\left[\mathcal{D}\right]$ be a prime neutrosophic ideal. By using the same proof, we conclude that $\mathcal{D}$ is a prime neutrosophic ideal of $\mathfrak{L}.$

(ii) It follows from Proposition 4 and (i). □

Proposition 10. 

Let $\mathcal{D}$ and F be two neutrosophic sets of $\mathfrak{L}$:

(i) 

$\mathcal{D}$ is a prime neutrosophic ideal if and only if $⟨\mathcal{D}⟩$ is a prime neutrosophic ideal;

(ii) 

F is a prime neutrosophic filter if and only if $⟨F⟩$ is a prime neutrosophic filter.

Proof. 

The proof of this property is analogous to that of Proposition 9 by using the definition of $⟨\mathcal{D}⟩$ instead of $\left[\mathcal{D}\right]$. □

The following result discusses the relationship between the prime neutrosophic ideal (respectively, prime neutrosophic filter) and its support of the lattice of open sets.

Proposition 11. 

Let $\mathcal{D}$ and F be two neutrosophic sets of $\mathfrak{L}$:

(i) 

If $\mathcal{D}$ is a prime neutrosophic ideal, then the support $\mathcal{S}\left(\mathcal{D}\right)$ is a prime ideal of $\mathfrak{L}$.

(ii) 

If F is a prime neutrosophic filter, then the support $\mathcal{S}\left(F\right)$ is a prime filter of $\mathfrak{L}$.

Proof. 

(i) Let $\mathcal{D}$ be a prime neutrosophic ideal of the lattice $\mathfrak{L}$. Proposition 6 confirms that $\mathcal{S}\left(\mathcal{D}\right)$ is an ideal of $\mathfrak{L}$.

Now, we show that $\mathcal{S}\left(\mathcal{D}\right)$ is prime. Let $\Phi ,\Psi \in \mathfrak{L}$ with $\Phi ⋒\Psi \in \mathcal{S}\left(\mathcal{D}\right)$. We have

$$\begin{array}{cc}\hfill {\daleth }_{\mathcal{D}}(\Phi ⋒\Psi )\ne & 0,\hfill \\ \hfill {\gimel }_{\mathcal{D}}(\Phi ⋒\Psi )\ne & 0,\hfill \\ \hfill {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋒\Psi )\ne & 0.\hfill \end{array}$$

Since $\mathcal{D}$ is a prime neutrosophic ideal of $\mathfrak{L}$, then

$$\begin{array}{cc}\hfill {\daleth }_{\mathcal{D}}(\Phi )⋎{\daleth }_{\mathcal{D}}(\Psi )=& {\daleth }_{\mathcal{D}}(\Phi ⋒\Psi )\ne 0,\hfill \\ \hfill {\gimel }_{\mathcal{D}}(\Phi )⋎{\gimel }_{\mathcal{D}}(\Psi )=& {\gimel }_{\mathcal{D}}(\Phi ⋒\Psi )\ne 0,\hfill \\ \hfill {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋏{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi )=& {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋒\Psi )\ne 0.\hfill \end{array}$$

This implies that either $({\daleth }_{\mathcal{D}}(\Phi )\ne 0,{\gimel }_{\mathcal{D}}(\Phi )\ne 0\mathrm{and}{\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )\ne 0)$ or $({\daleth }_{\mathcal{D}}(\Psi )\ne 0,{\gimel }_{\mathcal{D}}(\Psi )\ne 0\mathrm{and}{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi )\ne 0)$. Thus, either $\Phi \in \mathcal{S}\left(\mathcal{D}\right)$ or $\Psi \in \mathcal{S}\left(\mathcal{D}\right)$. Therefore, $\mathcal{S}\left(\mathcal{D}\right)$ is a prime ideal of $\mathfrak{L}$.

(ii) Directly by using Proposition 4 and (i). □

Similarly, we obtain the following agreement that describes the level sets of the prime neutrosophic ideals, (respectively, prime neutrosophic filters).

Theorem 7. 

Let $\mathcal{D}$ and F be two neutrosophic sets of $\mathfrak{L}$. Then, the following hold:

(i) 

$\mathcal{D}$ is a prime neutrosophic ideal if and only if its level sets are prime ideals.

(ii) 

F is a prime neutrosophic filter if and only if its level sets are prime filters.

Proof. 

(i) By Proposition 2, $\mathcal{D}$ is a neutrosophic ideal of $\mathfrak{L}$ if and only if ${\mathcal{D}}_{\alpha ,\beta ,\gamma }$ are ideals of $\mathfrak{L}$ for all $0<\alpha ,\beta ,\gamma \le 1$. We shall prove the primality property. Let $\mathcal{D}$ be a prime neutrosophic ideal of $\mathfrak{L}$, and let $\Phi ,\Psi \in \mathfrak{L}$ with $\Phi ⋒\Psi \in {\mathcal{D}}_{\alpha ,\beta ,\gamma }$. Then, from Theorem 5, it holds that

$$\begin{array}{cc}\hfill ({\daleth }_{\mathcal{D}}(\Phi ⋒\Psi )=& {\daleth }_{\mathcal{D}}(\Phi )⋎{\daleth }_{\mathcal{D}}(\Psi )⩾\alpha ,\hfill \\ \hfill {\gimel }_{\mathcal{D}}(\Phi ⋒\Psi )=& {\gimel }_{\mathcal{D}}(\Phi )⋎{\gimel }_{\mathcal{D}}(\Psi )⩾\beta ,\hfill \\ \hfill {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋒\Psi )=& {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋏{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi )⩽\gamma ).\hfill \end{array}$$

This implies that either $({\daleth }_{\mathcal{D}}(\Phi )⩾\alpha$, ${\gimel }_{\mathcal{D}}(\Phi )⩾\beta$ and ${\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⩽\gamma )$ or $({\daleth }_{\mathcal{D}}(\Psi )⩾\alpha$, ${\gimel }_{\mathcal{D}}(\Psi )⩾\beta$ and ${\mathsf{Ϝ}}_{\mathcal{D}}(\Psi )⩽\gamma ).$ Thus, either $\Phi \in {\mathcal{D}}_{\alpha ,\beta ,\gamma }$ or $\Psi \in {\mathcal{D}}_{\alpha ,\beta ,\gamma }.$ Therefore, ${\mathcal{D}}_{\alpha ,\beta ,\gamma }$ are primeaideals for all $0<\alpha ,\beta ,\gamma \le 1$. Inversely, let ${\mathcal{D}}_{\alpha ,\beta ,\gamma }$ be prime ideals for all $0<\alpha ,\beta ,\gamma \le 1$ where $\mathcal{D}$ is not a prime neutrosophic ideal of $\mathfrak{L}$. Then, it follows that there exist $\Phi ,\Psi \in \mathfrak{L}$ such that

$$\begin{array}{cc}\hfill {\daleth }_{\mathcal{D}}(\Phi ⋒\Psi )>& {\daleth }_{\mathcal{D}}(\Phi )⋎{\daleth }_{\mathcal{D}}(\Psi ),\hfill \\ \hfill {\gimel }_{\mathcal{D}}(\Phi ⋒\Psi )>& {\gimel }_{\mathcal{D}}(\Phi )⋎{\gimel }_{\mathcal{D}}(\Psi ),\hfill \\ \hfill {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋒\Psi )<& {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )⋏{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi ).\hfill \end{array}$$

This implies that

$$\begin{array}{cc}\hfill {\daleth }_{\mathcal{D}}(\Phi ⋒\Psi )>& {\daleth }_{\mathcal{D}}(\Phi )\mathrm{and}{\daleth }_{\mathcal{D}}(\Phi ⋒\Psi )>{\daleth }_{\mathcal{D}}(\Psi ),\hfill \\ \hfill {\gimel }_{\mathcal{D}}(\Phi ⋒\Psi )>& {\gimel }_{\mathcal{D}}(\Phi )\mathrm{and}{\gimel }_{\mathcal{D}}(\Phi ⋒\Psi )>{\gimel }_{\mathcal{D}}(\Psi ),\hfill \\ \hfill {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋒\Psi )<& {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )\mathrm{and}{\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋒\Psi )<{\mathsf{Ϝ}}_{\mathcal{D}}(\Psi ).\hfill \end{array}$$

If we put

$$\begin{array}{cc}\hfill {\daleth }_{\mathcal{D}}(\Phi ⋒\Psi )=& \alpha ,\hfill \\ \hfill {\gimel }_{\mathcal{D}}(\Phi ⋒\Psi )=& \beta ,\hfill \\ \hfill {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi ⋒\Psi )=& \gamma \hfill \end{array}$$

we obtain

$$\begin{array}{cc}\hfill {\daleth }_{\mathcal{D}}(\Phi )<& \alpha ,\hfill \\ \hfill {\gimel }_{\mathcal{D}}(\Phi )<& \beta ,\hfill \\ \hfill {\mathsf{Ϝ}}_{\mathcal{D}}(\Phi )>& \gamma ,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\daleth }_{\mathcal{D}}(\Psi )<& \alpha ,\hfill \\ \hfill {\gimel }_{\mathcal{D}}(\Psi )<& \beta ,\hfill \\ \hfill {\mathsf{Ϝ}}_{\mathcal{D}}(\Psi )>& \gamma .\hfill \end{array}$$

Hence,

$$\Phi ⋒\Psi \in {\mathcal{D}}_{\alpha ,\beta ,\gamma }and\Phi ,\Psi \notin {\mathcal{D}}_{\alpha ,\beta ,\gamma },$$

which contradicts the concerned that ${\mathcal{D}}_{\alpha ,\beta ,\gamma }$ are prime ideals of $\mathfrak{L}$ for all $0<\alpha ,\beta ,\gamma \le 1$.

Consequently, $\mathcal{D}$ is a prime neutrosophic ideal.

(ii) Derive through Proposition 4 and (i). □

Example 6. 

Let us consider the lattice $\mathfrak{L}=\{\varphi ,\Phi ,\Psi ,\mathcal{E}\}$ given in Example 4 and let

$$\mathcal{D}=\{⟨a,0.2,0.3,0.1⟩,⟨b,0.3,0.4,0.1⟩\mid a,b\in \mathcal{E}\}$$

be a prime neutrosophic ideal of $\mathfrak{L}.$ Then, for any $0<\alpha ,\beta ,\gamma \le 1$, ${\mathcal{D}}_{\alpha ,\beta ,\gamma }$ are crisp ideals of $\mathfrak{L}$.

7. Conclusions

The structure of the neutrosophic open-set lattice on a topology generated by a neutrosophic relation is described in this study. We have defined the concepts of neutrosophic ideals and neutrosophic filters on that lattice in terms of their level sets and meet and join operations. In addition, we have examined and defined the concepts of prime neutrosophic filters and ideals as fascinating subsets of neutrosophic ideals and filters. This work mostly discussed neutrosophic ideals and neutrosophic filters on the lattice structure of neutrosophic open sets. However, we think that other types of neutrosophic ideals and neutrosophic filters will also be very interesting in more general structures in future works.